Numerical Optimization of Neuro-Fuzzy Models Using Evolutionary Algorithms for Electricity Demand Forecasting in Pre-Tertiary Institutions
Abstract
1. Introduction
1.1. Related Works
1.2. Research Gap and Motivation
1.3. Contributions of the Study
- It develops two evolutionary-based adaptive neuro-inference systems for electricity forecasting in lower-to-middle-income pre-tertiary education institutions;
- It investigates the effect of two renowned clustering techniques, namely subtractive clustering and fuzzy c-means, and other pivotal hyperparameters on model accuracy;
- It identifies the optimal model and compares it with three different variants, stand-alone ANFIS, and other hybrid models.
2. Materials and Methods
2.1. Data
2.2. Adaptive Neuro-Fuzzy Inference System
2.3. Clustering Methods
2.3.1. Fuzzy C-Means Method
2.3.2. Subtractive Clustering (SC) Method
2.4. Evolution-Based Soft Computing for ANFIS
2.4.1. Genetic Algorithm-Based ANFIS
2.4.2. Particle Swarm Optimization-Based ANFIS
2.5. Model Performance Evaluation
3. Results and Discussion
3.1. Overview of Case Studies
3.1.1. Case A: Evaluation of Hybrid Model Performance in Pre-Tertiary Institution A
3.1.2. Case B: Evaluation of Hybrid Model Performance in Pre-Tertiary Institution B
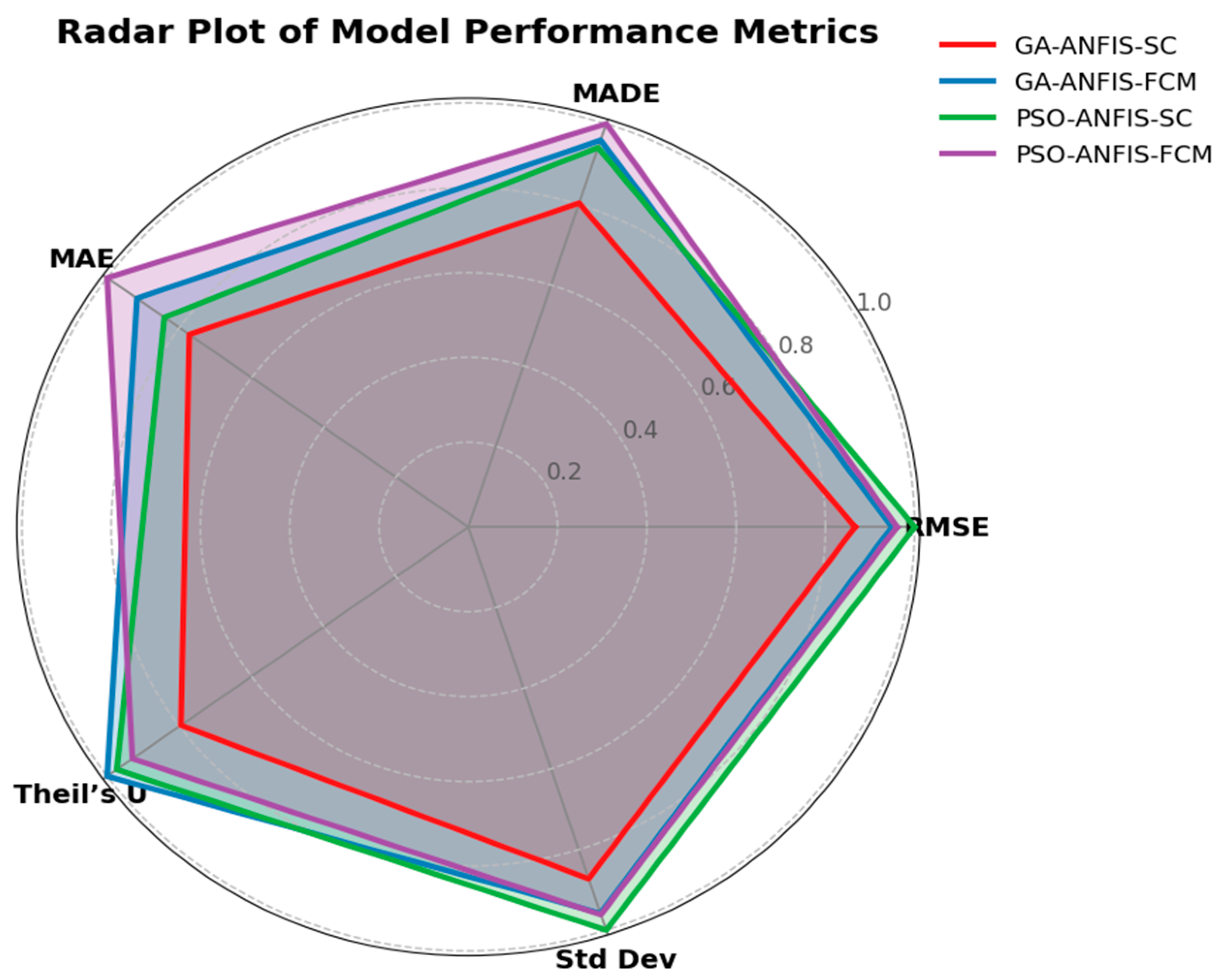
3.2. Performance Comparison Between the Optimal Sub-Models of Case A and Case B
3.3. Overall Optimal Model
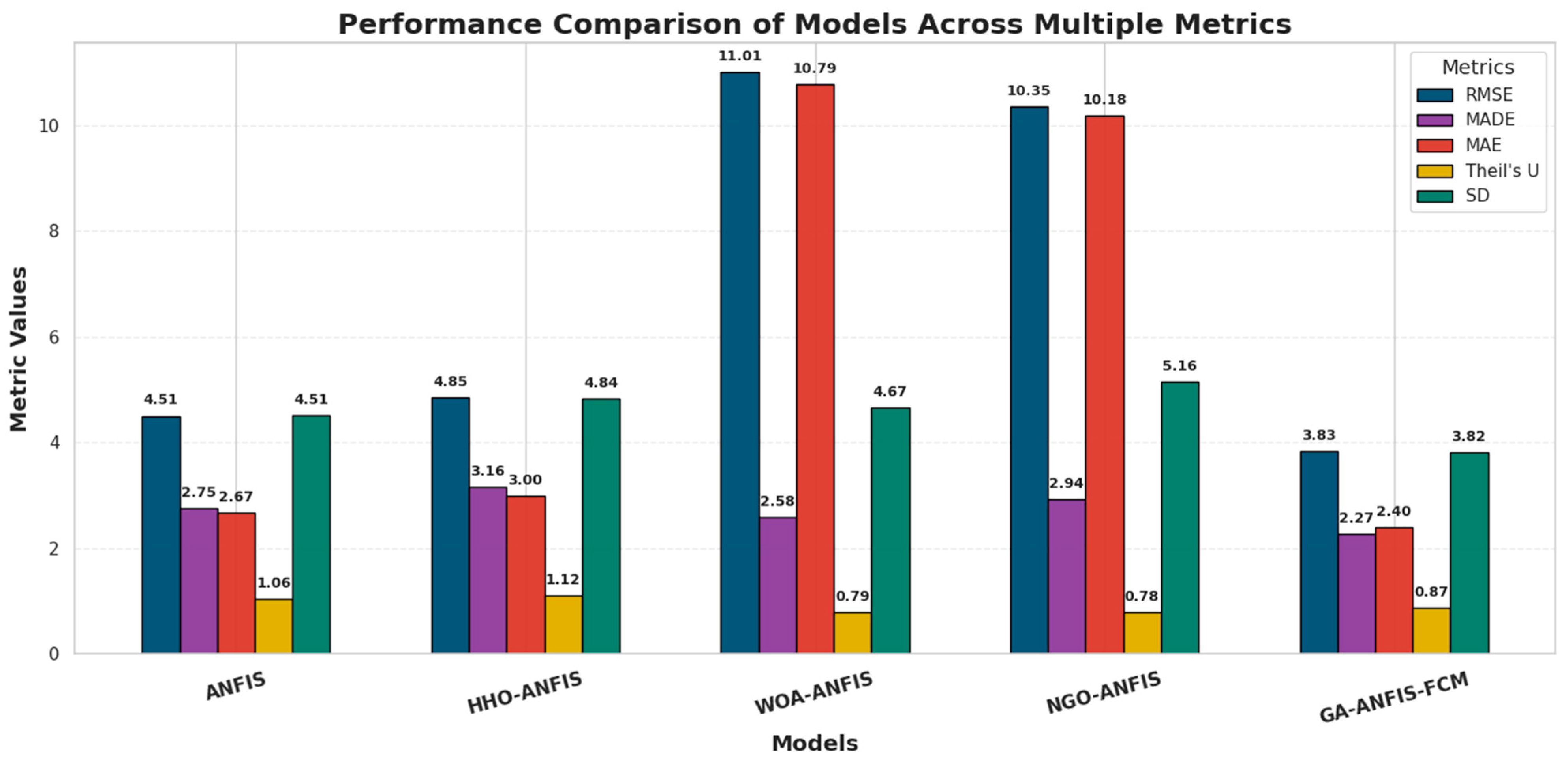
3.4. Comparison of Optimal Model with Other Variants
3.4.1. Impact of GA Selection Methods
3.4.2. Benchmarking Against Other Metaheuristic Algorithms
3.5. Limitations and Future Work
4. Conclusions
- Energy prediction in pre-tertiary schools is often overlooked. However, understanding their needs is vital to ensure adequate support is provided in order to achieve educational goals, especially in low-to-middle-income settings.
- Our findings showed that the merger of genetic algorithm, fuzzy c-means clustering technique, and a moderate number of clusters (4) presents an artificial intelligence scheme that can serve as an evidence-based energy-management policies for educational buildings in resource-constrained settings.
- The choice of selection method in genetic algorithm can impact the performance of GA-based ANFIS models. In addition, the choice of clustering hyperparameters such as number of clusters and clustering radius has a significant impact on the GA-ANFIS models.
- The application of standalone ANFIS may not offer the most accurate model and it is necessary to optimize its parameters using intelligent evolutionary algorithms.
- To sum up, this study provides an important insight into the efficacy of the GA-ANFIS-FCM hybrid model in predicting energy consumption in lower-to-middle-income pre-tertiary education institutions. The developed model can contribute helpful insights for policy makers in making informed energy decisions for lower-to-middle-income pre-tertiary education institutions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANFIS | Adaptive neuro-fuzzy inference systems |
| ANN | Artificial neural networks |
| GP | Grid partitioning |
| SC | Subtractive clustering |
| FCM | Fuzzy c-means |
| CR | Clustering radius |
| RMSE | Root Mean Square Error |
| SD | Standard Deviation |
| SVM | Support Vector Machine |
| MAE | Mean Absolute Error |
| RCoV | Coefficient of Variation |
| CVRMSE | Coefficient of Variation of the Root Mean Square Error |
| MADE | Mean Absolute Deviation Error |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| FIS | Fuzzy inference systems |
| MF | Membership Function |
| DTW | Dynamic Time Warping |
| LSTM | Long short-term memory networks |
| CNN | Convolutional Neural Networks |
References
- Masebinu, S.O.; Akinlabi, E.T.; Muzenda, E.; Aboyade, A.O. Techno-Economics and Environmental Analysis of Energy Storage for a Student Residence under a South African Time-of-Use Tariff Rate. Energy 2017, 135, 413–429. [Google Scholar] [CrossRef]
- Arinaitwe, A.; Aikiriza, F.A.; Kakooza, J.B.; Bagire, V. Sustainable Energy Consumption in African Higher Institutions of Learning: The Nexus of Top Management Commitment and Institutional Pressures. IIMBG J. Sustain. Bus. Innov. 2024, 3, 21–36. [Google Scholar] [CrossRef]
- Akpahou, R.; Mensah, L.D.; Quansah, D.A.; Kemausuor, F. Energy Planning and Modeling Tools for Sustainable Development: A Systematic Literature Review. Energy Rep. 2024, 11, 830–845. [Google Scholar] [CrossRef]
- Ritchie, H.; Rosado, P.; Roser, M. Energy. Our World in Data; Global Change Data Lab: Oxford, UK, 2023. [Google Scholar]
- Jain, S.; Jain, P.K. The Rise of Renewable Energy Implementation in South Africa. Energy Procedia 2017, 143, 721–726. [Google Scholar] [CrossRef]
- Ye, Y.; Koch, S.F. Measuring Energy Poverty in South Africa Based on Household Required Energy Consumption. Energy Econ. 2021, 103, 105553. [Google Scholar] [CrossRef]
- Adedeji, P.A.; Akinlabi, S.; Ajayi, O.; Madushele, N. Non-Linear Autoregressive Neural Network (NARNET) with SSA Filtering for a University Energy Consumption Forecast. Procedia Manuf. 2019, 33, 176–183. [Google Scholar] [CrossRef]
- Ukoba, K.; Olatunji, K.O.; Adeoye, E.; Jen, T.C.; Madyira, D.M. Optimizing Renewable Energy Systems through Artificial Intelligence: Review and Future Prospects. Energy Environ. 2024, 35, 3833–3879. [Google Scholar] [CrossRef]
- REN21 RENEWABLES 2017 GLOBAL STATUS REPORT. Available online: https://www.ren21.net/gsr-2017/ (accessed on 12 June 2025).
- Adedeji, P.; Madushele, N.; Akinlabi, S. Adaptive Neuro-Fuzzy Inference System (ANFIS) for a Multi-Campus Institution Energy Consumption Forecast in South Africa. In Proceedings of the International Conference on Industrial Engineering and Operations Management, Washington, DC, USA, 27–29 September 2018; pp. 950–958. [Google Scholar]
- Department of Energy. A Survey of Energy Related Behaviour and Perceptions in South Africa; Government Printer: Mumbai, Maharashtra, 2013. [Google Scholar]
- Minelli, F.; Ciriello, I.; Minichiello, F.; D’Agostino, D. From Net Zero Energy Buildings to an Energy Sharing Model—The Role of NZEBs in Renewable Energy Communities. Renew Energy 2024, 223, 120110. [Google Scholar] [CrossRef]
- Ragupathi, C.; Dhanasekaran, S.; Vijayalakshmi, N.; Salau, A.O. Prediction of Electricity Consumption Using an Innovative Deep Energy Predictor Model for Enhanced Accuracy and Efficiency. Energy Rep. 2024, 12, 5320–5337. [Google Scholar] [CrossRef]
- van der Meer, D.W.; Shepero, M.; Svensson, A.; Widén, J.; Munkhammar, J. Probabilistic Forecasting of Electricity Consumption, Photovoltaic Power Generation and Net Demand of an Individual Building Using Gaussian Processes. Appl. Energy 2018, 213, 195–207. [Google Scholar] [CrossRef]
- Kim, H.; Park, S.; Kim, S. Time-Series Clustering and Forecasting Household Electricity Demand Using Smart Meter Data. Energy Rep. 2023, 9, 4111–4121. [Google Scholar] [CrossRef]
- Ramos, D.; Faria, P.; Morais, A.; Vale, Z. Using Decision Tree to Select Forecasting Algorithms in Distinct Electricity Consumption Context of an Office Building. Energy Rep. 2022, 8, 417–422. [Google Scholar] [CrossRef]
- Yang, H.; Ran, M.; Zhuang, C. Prediction of Building Electricity Consumption Based on Joinpoint−Multiple Linear Regression. Energies 2022, 15, 8543. [Google Scholar] [CrossRef]
- Shijer, S.S.; Jassim, A.H.; Al-Haddad, L.A.; Abbas, T.T. Evaluating Electrical Power Yield of Photovoltaic Solar Cells with K-Nearest Neighbors: A Machine Learning Statistical Analysis Approach. E-Prime Adv. Electr. Eng. Electron. Energy 2024, 9, 100674. [Google Scholar] [CrossRef]
- Jónsson, T.; Pinson, P.; Nielsen, H.A.; Madsen, H. Exponential Smoothing Approaches for Prediction in Real-Time Electricity Markets. Energies 2014, 7, 3710–3732. [Google Scholar] [CrossRef]
- Mi, J.; Fan, L.; Duan, X.; Qiu, Y. Short-Term Power Load Forecasting Method Based on Improved Exponential Smoothing Grey Model. Math. Probl. Eng. 2018, 2018, 3894723. [Google Scholar] [CrossRef]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A Review on Time Series Forecasting Techniques for Building Energy Consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Tarmanini, C.; Sarma, N.; Gezegin, C.; Ozgonenel, O. Short Term Load Forecasting Based on ARIMA and ANN Approaches. Energy Rep. 2023, 9, 550–557. [Google Scholar] [CrossRef]
- Mohammed, N.A.; Al-Bazi, A. An Adaptive Backpropagation Algorithm for Long-Term Electricity Load Forecasting. Neural Comput. Appl. 2021, 34, 477. [Google Scholar] [CrossRef]
- Elbeltagi, E.; Wefki, H. Predicting Energy Consumption for Residential Buildings Using ANN through Parametric Modeling. Energy Rep. 2021, 7, 2534–2545. [Google Scholar] [CrossRef]
- Oladipo, S.O.; Sun, Y.; Amole, A.O. Analysis of the Impact of Clustering Techniques and Parameters on Evolutionary-Based Hybrid Models for Forecasting Electricity Consumption. IEEE Access 2023, 11, 82838–82856. [Google Scholar] [CrossRef]
- Jang, J.S.R. ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Ani, K.A.; Agu, C.M. Predictive Comparison and Assessment of ANFIS and ANN, as Efficient Tools in Modeling Degradation of Total Petroleum Hydrocarbon (TPH). Clean. Waste Syst. 2022, 3, 100052. [Google Scholar] [CrossRef]
- Ghenai, C.; Al-Mufti, O.A.A.; Al-Isawi, O.A.M.; Amirah, L.H.L.; Merabet, A. Short-Term Building Electrical Load Forecasting Using Adaptive Neuro-Fuzzy Inference System (ANFIS). J. Build. Eng. 2022, 52, 104323. [Google Scholar] [CrossRef]
- Bilgili, M.; Yildirim, A.; Ozbek, A.; Celebi, K.; Ekinci, F. Long Short-Term Memory (LSTM) Neural Network and Adaptive Neuro-Fuzzy Inference System (ANFIS) Approach in Modeling Renewable Electricity Generation Forecasting. Int. J. Green Energy 2021, 18, 578–594. [Google Scholar] [CrossRef]
- Rathor, R.D.; Bharagava, A. Day Ahead Regional Electrical Load Forecasting Using ANFIS Techniques. J. Inst. Eng. Ser. B 2020, 101, 475–495. [Google Scholar] [CrossRef]
- Chévez, P.; Martini, I. Applying Neural Networks for Short and Long-Term Hourly Electricity Consumption Forecasting in Universities: A Simultaneous Approach for Energy Management. J. Build. Eng. 2024, 97, 110612. [Google Scholar] [CrossRef]
- Begić Juričić, H.; Krstić, H. Comparing MLR and ANN Models for School Building Electrical Energy Prediction in Osijek-Baranja County in Croatia. Energy Rep. 2024, 12, 3595–3606. [Google Scholar] [CrossRef]
- Stošović, M.A.; Radivojević, N.; Ivanova, M. Electricity Consumption Prediction in an Electronic System Using Artificial Neural Networks. Electronics 2022, 11, 3506. [Google Scholar] [CrossRef]
- Al-Qaness, M.A.A.; Elaziz, M.A.; Ewees, A.A. Oil Consumption Forecasting Using Optimized Adaptive Neuro-Fuzzy Inference System Based on Sine Cosine Algorithm. IEEE Access 2018, 6, 68394–68402. [Google Scholar] [CrossRef]
- Naik, M.; Abiodun, B.J. Modelling the Potential of Land Use Change to Mitigate the Impacts of Climate Change on Future Drought in the Western Cape, South Africa. Theor. Appl. Climatol. 2024, 155, 6371–6392. [Google Scholar] [CrossRef]
- Botai, C.M.; Botai, J.O.; De Wit, J.P.; Ncongwane, K.P.; Adeola, A.M. Drought Characteristics over the Western Cape Province, South Africa. Water 2017, 9, 876. [Google Scholar] [CrossRef]
- Samuels, J.A.; Michael-Ahile, T.; Booysen, M.J. (Thinus) Dataset on Electricity Usage Measurement for Lower-to-Middle-Income Primary and Secondary Schools in Western Cape, South Africa. Data Brief 2025, 59, 111321. [Google Scholar] [CrossRef]
- Rahman, M.S.; Ali, M.H. Adaptive Neuro Fuzzy Inference System (ANFIS)-Based Control for Solving the Misalignment Problem in Vehicle-to-Vehicle Dynamic Wireless Charging Systems. Electronics 2025, 14, 507. [Google Scholar] [CrossRef]
- Kamarian, S.; Yas, M.H.; Pourasghar, A.; Daghagh, M. Application of Firefly Algorithm and ANFIS for Optimisation of Functionally Graded Beams. J. Exp. Theor. Artif. Intell. 2014, 26, 197–209. [Google Scholar] [CrossRef]
- Petković, D.; Ćojbašić, Ž.; Nikolić, V.; Shamshirband, S.; Mat Kiah, M.L.; Anuar, N.B.; Abdul Wahab, A.W. Adaptive Neuro-Fuzzy Maximal Power Extraction of Wind Turbine with Continuously Variable Transmission. Energy 2014, 64, 868–874. [Google Scholar] [CrossRef]
- Jayaprabha, M.; Felcy, P. A Review of Clustering, Its Types and Techniques. Int. J. Innov. Sci. Res. Technol. 2018, 3, 127–130. [Google Scholar]
- Chiu, S.L. Fuzzy Model Identification Based on Cluster Estimation. J. Intell. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar] [CrossRef]
- Sayeed, M.S.; Hossen, M.J.; Rahman, A.; Samsuddin, K.; Rokhani, F. A Modified Hybrid Fuzzy Clustering Algorithm for Data Partitions. Aust. J. Basic Appl. Sci. 2011, 5, 674–681. [Google Scholar]
- Deb, A.K. Introduction to Soft Computing Techniques: Artificial Neural Networks, Fuzzy Logic and Genetic Algorithms. Soft Comput. Text. Eng. 2011, 3–24. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Kennedy, R.E.J. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Hossain, M.; Mekhilef, S.; Afifi, F.; Halabi, L.M.; Olatomiwa, L.; Seyedmahmoudian, M.; Horan, B.; Stojcevski, A. Application of the Hybrid ANFIS Models for Long Term Wind Power Density Prediction with Extrapolation Capability. PLoS ONE 2018, 13, e0193772. [Google Scholar] [CrossRef] [PubMed]
- Olatunji, K.O.; Adeleke, O.; Jen, T.-C.; Madyira, D.M. Impact of Acidic Pretreatment on Biomethane Yield from Xyris Capensis: Experimental and In-Depth Data-Driven Insight. Processes 2025, 13, 1997. [Google Scholar] [CrossRef]
- Rajabi, A.; Eskandari, M.; Ghadi, M.J.; Li, L.; Zhang, J.; Siano, P. A Comparative Study of Clustering Techniques for Electrical Load Pattern Segmentation. Renew. Sustain. Energy Rev. 2020, 120, 109628. [Google Scholar] [CrossRef]
- Sharma, N.; Katyal, R. Investigation on Combined Impacts of Different Clustering Techniques and Enhanced K-Means Algorithm. Commun. Comput. Inf. Sci. 2025, 2238 CCIS, 251–260. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; The MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Mills, K.L.; Filliben, J.J.; Haines, A.L. Determining Relative Importance and Effective Settings for Genetic Algorithm Control Parameters. Evol. Comput. 2015, 23, 309–342. [Google Scholar] [CrossRef]
- Ghahramani, M.; Shiri, N. An Adaptive Neuro-Fuzzy Inference System Optimized by Genetic Algorithm for Brain Tumour Detection in Magnetic Resonance Images. IET Image Process 2024, 18, 1358–1372. [Google Scholar] [CrossRef]
- Savrun, M.M.; İnci, M. Adaptive Neuro-Fuzzy Inference System Combined with Genetic Algorithm to Improve Power Extraction Capability in Fuel Cell Applications. J. Clean Prod. 2021, 299, 126944. [Google Scholar] [CrossRef]
- Arana-Jimenez, M.; Dogan, O.; Avvad, H. Fuzzy Clustering Based on Activity Sequence and Cycle Time in Process Mining. Axioms 2025, 14, 351. [Google Scholar] [CrossRef]
- Thong, P.H.; Canh, H.T.; Lan, L.T.H.; Huy, N.T.; Giang, N.L. Multi-View Picture Fuzzy Clustering: A Novel Method for Partitioning Multi-View Relational Data. Comput. Mater. Contin. 2025, 83, 5461–5485. [Google Scholar] [CrossRef]
- Onakpojeruo, E.P.; Uzun, B.; David, L.R.; Ozsahin, I.; Ozsahin, D.U. Selection Techniques in Genetic Algorithm. In Proceedings of the International Conference on Developments in eSystems Engineering, DeSE, Khorfakkan, UK, 6–8 November 2024; pp. 411–416. [Google Scholar] [CrossRef]
- Nemati, K.; Refahi Sheikhani, A.H.; Kordrostami, S.; Khoshhal Roudposhti, K. New Hybrid Feature Selection Approaches Based on ANN and Novel Sparsity Norm. J. Electr. Comput. Eng. 2024, 2024, 7112770. [Google Scholar] [CrossRef]
- Haq, E.U.; Ahmad, I.; Hussain, A.; Almanjahie, I.M. A Novel Selection Approach for Genetic Algorithms for Global Optimization of Multimodal Continuous Functions. Comput. Intell. Neurosci. 2019, 2019, 8640218. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Deb, K. A Comparative Analysis of Selection Schemes Used in Genetic Algorithms. Found. Genet. Algorithms 1991, 1, 69–93. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris Hawks Optimization: Algorithm and Applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubálovský, Š.; Trojovský, P. Northern Goshawk Optimization: A New Swarm-Based Algorithm for Solving Optimization Problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Karaboga, D.; Kaya, E. Adaptive Network Based Fuzzy Inference System (ANFIS) Training Approaches: A Comprehensive Survey. Artif. Intell. Rev. 2018, 52, 2263–2293. [Google Scholar] [CrossRef]
- Ghordoyee Milan, S.; Roozbahani, A.; Arya Azar, N.; Javadi, S. Development of Adaptive Neuro Fuzzy Inference System –Evolutionary Algorithms Hybrid Models (ANFIS-EA) for Prediction of Optimal Groundwater Exploitation. J. Hydrol. 2021, 598, 126258. [Google Scholar] [CrossRef]



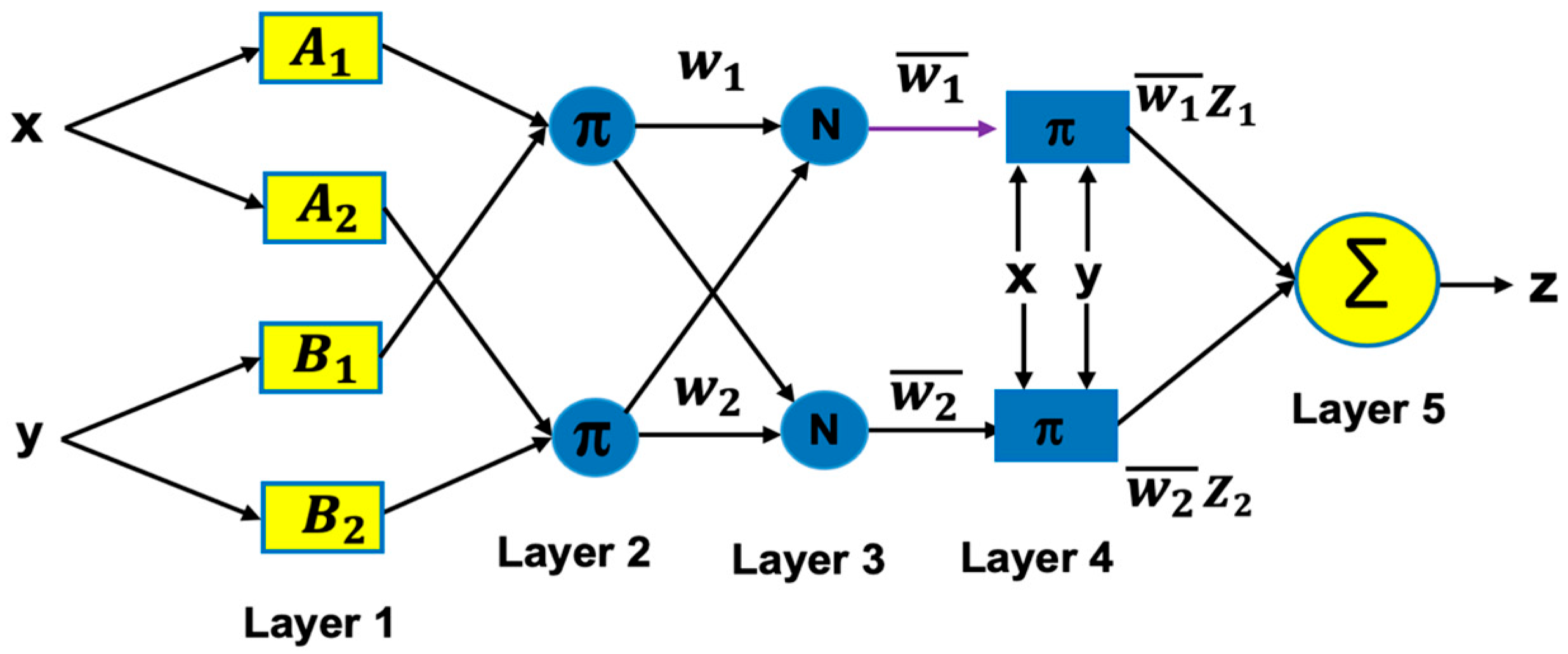
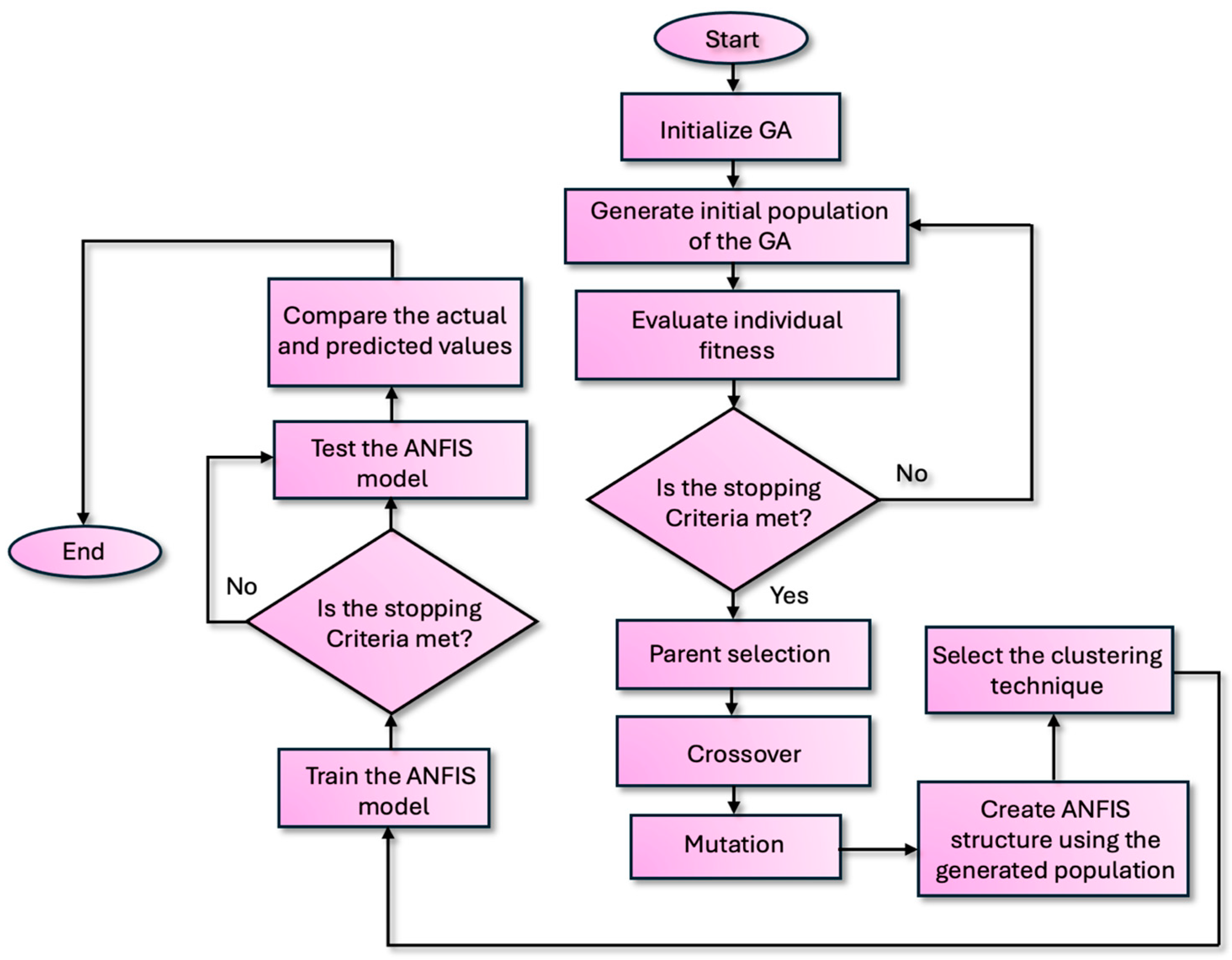












| Reference | Model/Machine Learning Used | Work Performed/Contributions | Area of Application |
|---|---|---|---|
| Meer et al. [14] | Gaussian Processes (GPs) | Utilized GPs for probabilistic forecasting of residential electricity consumption. | Residential building |
| Kim et al. [15] | Various (ARIMA, DSHW, TBATS, NNAR, NARX) | Forecasted household electricity demand using time-series clustering. | Residential |
| Ramos et al. [16] | ANN, k-NN, decision trees | Used decision trees to select forecasting algorithms for an office building. | Office building |
| Tarmanini et al. [22] | ARIMA, ANN | Compared ARIMA and ANN for short-term load forecasting. | Residential |
| Mohammed et al. [23] | ANN, Adaptive Backpropagation Algorithm (ABPA) | Developed an improved ANN with an adaptive algorithm for long-term load forecasting. | General |
| Elbeltagi et al. [24] | ANN | Presented an ANN-based methodology to predict residential building energy usage. | Residential building |
| Ghenai et al. [28] | Adaptive Neuro-Fuzzy Inference System (ANFIS) | Developed an ANFIS model for very short-term energy-consumption forecasts. | Educational building |
| Bilgili et al. [29] | LSTM, ANFIS | Applied LSTM and ANFIS to forecast renewable electricity generation. | Renewable energy generation |
| Rathor et al. [30] | ANFIS | Developed ANFIS models for day-ahead regional electrical load forecasting. | Regional |
| Pedro et al. [31] | Neural Networks | Developed simultaneous short-term and long-term electricity-forecasting models for a university. | University building |
| Ana et al. [32] | ANN, Multiple Linear Regression (MLR) | Compared ANN and MLR models for predicting school building energy consumption. | School building |
| Miona et al. [33] | RNN, LSTM, GRU | Proposed a method for electricity-consumption prediction using various recurrent neural networks. | Cold storage facility |
| Present Study | Hybrid ANFIS models: optimized with GA and PSO utilized with Subtractive Clustering (SC) and Fuzzy C-Means (FCM) | Developed hybrid evolutionary-based ANFIS models for electricity forecasting, investigating the impact of clustering and hyperparameters. | Lower-to-middle-income pre-tertiary schools in Western Cape, South Africa |
| Quintile | Case | Learners | School Type | Educators |
|---|---|---|---|---|
| 1 | Case A | 1405 | Primary | 43 |
| 2 | Case B | 1159 | Combined | 29 |
| Parameters | Names | Values |
|---|---|---|
| SC | Cluster radius (CR) | 3–7 |
| FCM | Minimum improvement | 0.3–0.6 |
| Number of exponents for partitioning matrix | 1 × 10−5 | |
| Number of clusters | 2 | |
| General settings of the hybrid models | 100 | |
| Population size | 100 | |
| Number of inputs | 4 | |
| Number of outputs | 1 | |
| GA | 0.40 | |
| 0.15 | ||
| Selection mechanism | Roulette wheel | |
| PSO | 2 | |
| 2 | ||
| 0.99 | ||
| 1 |
| Clustering Radius | RMSE | MADE | MAE | Theil’s U | SD | |
|---|---|---|---|---|---|---|
| GA-ANFIS-SC | 0.3 | 6.1207 | 3.7070 | 3.7277 | 0.8764 | 6.1333 |
| 0.4 | 5.3640 | 3.1917 | 3.2396 | 0.8035 | 5.3641 | |
| 0.5 | 6.1626 | 3.7538 | 3.8520 | 0.9299 | 6.1588 | |
| 0.6 | 6.1572 | 3.5279 | 3.6018 | 0.9834 | 6.1649 | |
| 0.7 | 6.0727 | 3.6245 | 3.7618 | 0.9093 | 6.0611 |
| No. of Clusters | RMSE | MADE | MAE | Theil’s U | SD | |
|---|---|---|---|---|---|---|
| GA-ANFIS-FCM | 2 | 6.5763 | 4.3244 | 4.2307 | 1.1353 | 6.5782 |
| 3 | 6.1397 | 3.8515 | 3.7314 | 1.1402 | 6.1375 | |
| 4 | 5.8777 | 3.8117 | 3.8466 | 1.0097 | 5.8886 | |
| 5 | 6.4433 | 4.1355 | 4.0181 | 1.1248 | 6.4486 | |
| 6 | 6.3044 | 4.1147 | 4.0945 | 1.0504 | 6.3181 | |
| 7 | 7.1538 | 4.5693 | 4.2497 | 1.2525 | 7.1165 |
| Clustering Radius | RMSE | MADE | MAE | U | SD | |
|---|---|---|---|---|---|---|
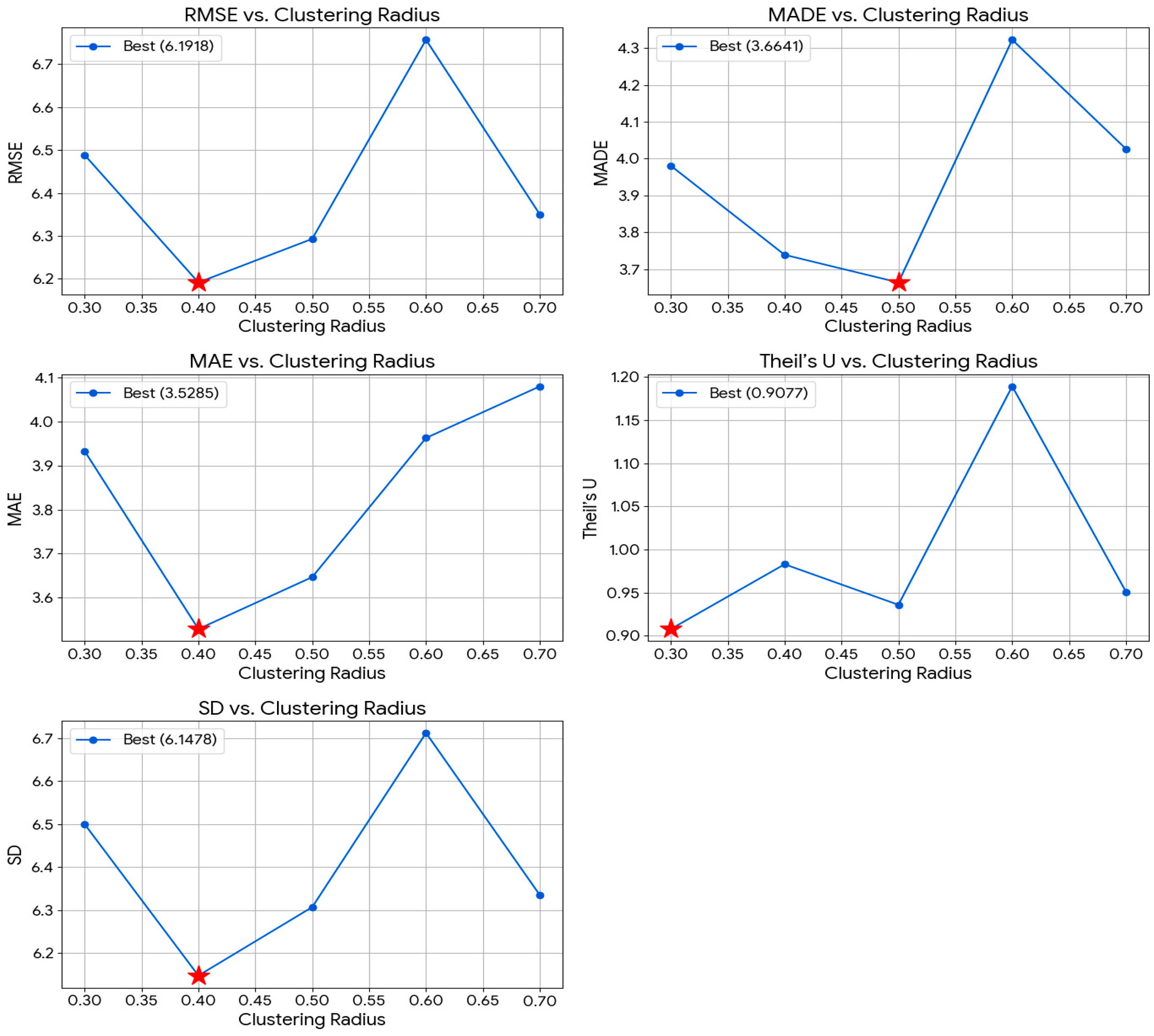
| PSO-ANFIS-SC | 0.3 | 6.4885 | 3.9808 | 3.9334 | 0.9077 | 6.5002 |
| 0.4 | 6.1918 | 3.7391 | 3.5285 | 0.9828 | 6.1478 | |
| 0.5 | 6.2932 | 3.6641 | 3.6466 | 0.9358 | 6.3071 | |
| 0.6 | 6.7566 | 4.3226 | 3.9631 | 1.1891 | 6.7125 | |
| 0.7 | 6.3501 | 4.0263 | 4.0805 | 0.9508 | 6.3352 |
| No. of Clusters | RMSE | MADE | MAE | Theil’s U | SD | |
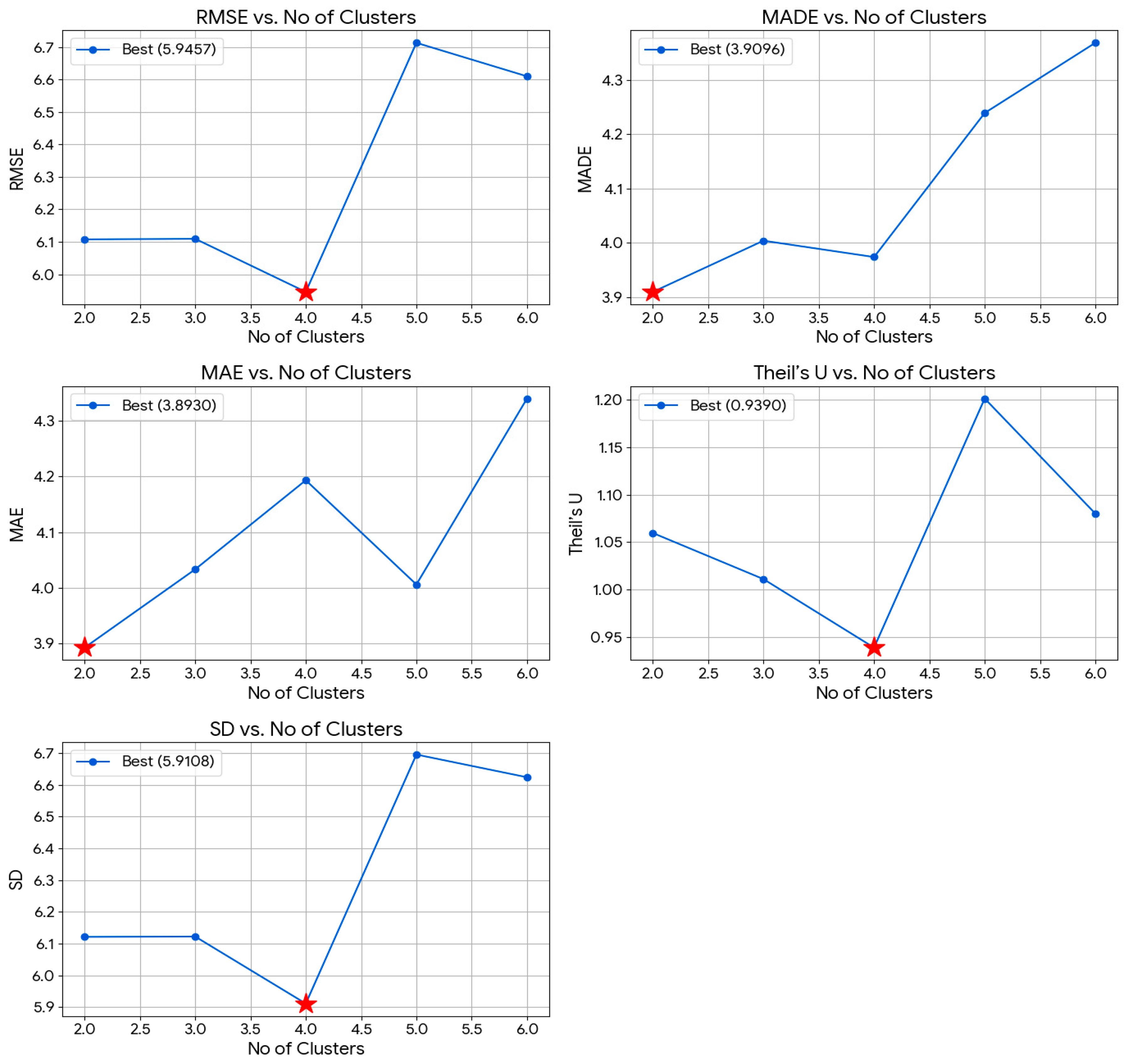
|---|---|---|---|---|---|---|
| PSO-ANFIS-FCM | 2 | 6.1074 | 3.9096 | 3.8930 | 1.0596 | 6.1209 |
| 3 | 6.1092 | 4.0039 | 4.0335 | 1.0111 | 6.1219 | |
| 4 | 5.9457 | 3.9738 | 4.1933 | 0.9390 | 5.9108 | |
| 5 | 6.7127 | 4.2390 | 4.0063 | 1.2010 | 6.6951 | |
| 6 | 6.6095 | 4.3682 | 4.3398 | 1.0800 | 6.6236 |
| Clustering Radius | RMSE | MADE | MAE | Theil’s U | SD | |
|---|---|---|---|---|---|---|
| GA-ANFIS-SC | 0.3 | 4.2432 | 2.5385 | 2.5373 | 0.8466 | 4.2527 |
| 0.4 | 4.2857 | 2.5341 | 2.5733 | 0.8568 | 4.2807 | |
| 0.5 | 4.1968 | 2.4838 | 2.5385 | 0.9045 | 4.2024 | |
| 0.6 | 4.0090 | 2.3966 | 2.4791 | 0.9110 | 4.0087 | |
| 0.7 | 4.7708 | 2.8786 | 2.8106 | 1.0713 | 4.7792 |
| No. of Clusters | RMSE | MADE | MAE | Theil’s U | SD | |
|---|---|---|---|---|---|---|
| GA-ANFIS-FCM | 2 | 4.2809 | 2.6677 | 2.6697 | 0.9752 | 4.2905 |
| 3 | 5.1983 | 3.2716 | 3.0480 | 1.2216 | 5.1909 | |
| 4 | 3.8305 | 2.2677 | 2.3957 | 0.8703 | 3.8176 | |
| 5 | 4.2583 | 2.5812 | 2.5558 | 1.0019 | 4.2667 | |
| 6 | 4.9699 | 2.9590 | 2.7765 | 1.1623 | 4.9625 |
| Clustering Radius | RMSE | MADE | MAE | Theil’s U | SD | |
|---|---|---|---|---|---|---|
| PSO-ANFIS-SC | 0.3 | 4.4344 | 2.5462 | 2.5546 | 0.9319 | 4.4443 |
| 0.4 | 4.8002 | 2.8950 | 2.7962 | 1.0286 | 4.7937 | |
| 0.5 | 4.2761 | 2.5997 | 2.4457 | 0.9915 | 4.2591 | |
| 0.6 | 4.2773 | 2.4102 | 2.4123 | 0.9272 | 4.2869 | |
| 0.7 | 4.7509 | 2.7719 | 2.6655 | 1.0422 | 4.7538 |
| Number of Clusters | RMSE | MADE | MAE | Theil’s U | SD | |
|---|---|---|---|---|---|---|
| PSO-ANFIS-FCM | 2 | 4.2002 | 2.4928 | 2.6475 | 0.9194 | 4.1853 |
| 3 | 4.1914 | 2.5125 | 2.6042 | 0.9698 | 4.1918 | |
| 4 | 4.8235 | 2.9979 | 3.0110 | 0.9947 | 4.8340 | |
| 5 | 4.4595 | 2.7226 | 2.7093 | 1.0328 | 4.4695 | |
| 6 | 4.2867 | 2.6464 | 2.7206 | 0.9616 | 4.2891 |
| Model | RMSE | MADE | MAE | Theil’s U | SD | |
|---|---|---|---|---|---|---|
| GA-ANFIS-SC | Cluster radius: 0.4 | 5.3640 | 3.1917 | 3.2396 | 0.8035 | 5.3641 |
| GA-ANFIS-FCM | Number of clusters: 4 | 5.8777 | 3.8117 | 3.8466 | 1.0097 | 5.8886 |
| PSO-ANFIS-SC | Cluster radius: 0.4 | 6.1918 | 3.7391 | 3.5285 | 0.9828 | 6.1478 |
| PSO-ANFIS-FCM | Number of clusters: 4 | 5.9457 | 3.9738 | 4.1933 | 0.9390 | 5.9108 |
| Model | RMSE | MADE | MAE | Theil’s U | SD | |
|---|---|---|---|---|---|---|
| GA-ANFIS-SC | Clustering radius: 0.6 | 4.0090 | 2.3966 | 2.4791 | 0.9110 | 4.0087 |
| GA-ANFIS-FCM | Number of clusters: 4 | 3.8305 | 2.2677 | 2.3957 | 0.8703 | 3.8176 |
| PSO-ANFIS-SC | Clustering radius: 0.6 | 4.2773 | 2.4102 | 2.4123 | 0.9272 | 4.2869 |
| PSO-ANFIS-FCM | Number of clusters: 2 | 4.2002 | 2.4928 | 2.6475 | 0.9194 | 4.1853 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oladipo, S.O.; Akuru, U.B.; Okoro, O.I. Numerical Optimization of Neuro-Fuzzy Models Using Evolutionary Algorithms for Electricity Demand Forecasting in Pre-Tertiary Institutions. Mathematics 2025, 13, 2648. https://doi.org/10.3390/math13162648
Oladipo SO, Akuru UB, Okoro OI. Numerical Optimization of Neuro-Fuzzy Models Using Evolutionary Algorithms for Electricity Demand Forecasting in Pre-Tertiary Institutions. Mathematics. 2025; 13(16):2648. https://doi.org/10.3390/math13162648
Chicago/Turabian StyleOladipo, Stephen O., Udochukwu B. Akuru, and Ogbonnaya I. Okoro. 2025. "Numerical Optimization of Neuro-Fuzzy Models Using Evolutionary Algorithms for Electricity Demand Forecasting in Pre-Tertiary Institutions" Mathematics 13, no. 16: 2648. https://doi.org/10.3390/math13162648
APA StyleOladipo, S. O., Akuru, U. B., & Okoro, O. I. (2025). Numerical Optimization of Neuro-Fuzzy Models Using Evolutionary Algorithms for Electricity Demand Forecasting in Pre-Tertiary Institutions. Mathematics, 13(16), 2648. https://doi.org/10.3390/math13162648








