Application of the DTM to the Elastic Curve Equation in Euler–Bernoulli Beam Theory

Abstract

This study demonstrates the effectiveness of the differential transform method (DTM) in solving complex solid mechanics problems, focusing on static analysis of beams under various loads and boundary conditions. For cantilever beams (BSM1), DTM provided exact polynomial solutions for deflections and slopes: a cubic solution for concentrated end loads, a quadratic distribution for applied moments, and a fourth-degree polynomial for uniformly distributed loads, all matching established theoretical results. For simply supported beams (BSM2), DTM yielded solutions across two intervals for midspan concentrated forces, though required corrective terms for applied moments due to discontinuities. Under uniform loading, the method produced precise polynomial solutions with maximum deflection at midspan. Key advantages include DTM’s high-precision analytical solutions without additional approximations and its adaptability to diverse loading scenarios. However, for cases with pronounced discontinuities like concentrated moments, supplementary methods (e.g., Green’s functions) may be needed. The study highlights DTM’s potential for extension to nonlinear or dynamic problems, while software integration could broaden its engineering applications. This study demonstrates, for the first time, how DTM yields exact polynomial solutions for Euler–Bernoulli beams under discontinuous loads (e.g., concentrated moments), overcoming limitations of traditional numerical methods. The method’s analytical precision and avoidance of discretization errors are highlighted. Traditional methods like FEM require mesh refinement near discontinuities (e.g., concentrated moments), leading to computational inefficiencies. DTM overcomes this by providing exact polynomial solutions with corrective terms, achieving errors below 0.5% with only 4–5 series terms.

1. Introduction

Nonlinear behavior characterizes the majority of scientific problems encountered in solid mechanics, and analytical solutions are generally available only for a restricted set of idealized cases. As such, these nonlinear systems are commonly addressed using alternative strategies, including numerical schemes or semi-analytical methods such as the differential transform method (DTM). Due to the inherent complexity of nonlinear formulations, deriving analytical expressions for limit state functions or directly computing the reliability index is often unfeasible. Nevertheless, recent advances in analytical techniques have demonstrated that such methods can serve as effective and straightforward tools for solving coupled nonlinear differential equations, combining conceptual simplicity with practical reliability.

While prior works focus on DTM’s nonlinear applications, this study demonstrates its untapped potential for exact solutions in linear problems with singularities—a prerequisite for future nonlinear extensions. The method’s handling of Dirac δ’ loads (Section Mathematical Justification for Corrective Term) provides a template for nonlinear singularities.

The DTM was first introduced in 1986 by Jian-Kui Zhou in his seminal work “Differential Transformation and Its Applications for Electrical Circuits” [1]. This method offered a novel paradigm for solving nonlinear differential equations, providing an analytical alternative to traditional numerical techniques.

While numerical methods (e.g., FEM) dominate engineering practice, their accuracy for discontinuous loads relies heavily on mesh refinement near singularities, increasing computational cost. In contrast, DTM transforms governing equations into algebraic recurrence relations, enabling exact polynomial solutions for such cases. For concentrated moments, DTM incorporates corrective terms derived from distribution theory (Section Mathematical Justification for Corrective Term), avoiding ad hoc approximations. This study demonstrates DTM’s superiority for singular problems through rigorous error analysis.

The DTM is a semi-analytical technique that has gained significant attention due to its effectiveness in solving a wide range of differential equations, both ordinary and partial, linear and nonlinear. Unlike traditional methods that often require linearization or discretization, DTM transforms the original differential equations into a set of algebraic recurrence relations, enabling an iterative approach to approximate solutions with high accuracy. Traditional numerical methods (e.g., FEM) require mesh refinement near discontinuities (e.g., concentrated moments), introducing discretization errors and computational overhead. In contrast, DTM provides exact polynomial solutions for such cases via corrective terms, bypassing the need for spatial discretization. This method has been successfully applied across various scientific and engineering disciplines, demonstrating its versatility and computational efficiency.

In solid mechanics, the DTM has been employed to analyze the nonlinear dynamic behavior of materials and structures, particularly in vibration analysis [2,3,4,5,6,7,8], stability problems [9,10,11,12], static loading [13,14,15,16,17,18,19], thermo-mechanical coupling [20], and fluid-beam coupling [21], among others.

Overall, the differential transform method continues to evolve as an efficient and reliable technique for solving a diverse spectrum of differential equations, supported by ongoing research integrating it with other analytical and numerical approaches to address increasingly complex scientific challenges.

Among its advantages are the absence of requirements for linearization or discretization, as well as its capability to handle nonlinear equations and complex boundary conditions. It is also highly compatible with computer languages, such as MAPLE 2025, MATLAB R2024b. However, certain limitations exist; for instance, convergence is not guaranteed for all types of equations, and the accuracy of the solution depends on the number of terms retained in the series expansion. The fundamental principle of DTM involves transforming the terms of the differential equation into an algebraic domain, yielding an approximate solution expressed as a polynomial. Specifically, DTM utilizes Taylor series [22] to represent the solution of the differential equation, with the core concept being the conversion of the differential equation into an algebraic recurrence relation that can be solved iteratively.

Unlike prior works focusing on numerical approximations, this paper establishes DTM as a tool for exact closed-form solutions in static beam analysis, particularly for discontinuous loading. The proposed framework bridges a critical gap in semi-analytical methods for singularities in beam mechanics [12,18]. The critical gap addressed herein is the absence of robust semi-analytical methods for singular loads in beam mechanics. Prior DTM studies focused on continuous loads [12] or geometric nonlinearities [18], but none provided systematic solutions for Dirac δ’ loading (concentrated moments). Our framework bridges this gap through the novel introduction of corrective terms (Section Mathematical Justification for Corrective Term).

While prior studies have extensively explored DTM’s application to large deformation problems [16,23], this work bridges a critical gap by addressing discontinuous and singular loading cases (e.g., concentrated moments and Dirac delta loads) through exact closed-form solutions. Unlike numerical approaches that require mesh refinement near singularities [16], our framework leverages DTM’s algebraic recurrence relations to handle discontinuities via corrective terms (Section Mathematical Justification for Corrective Term), offering analytical precision without ad hoc approximations. This advancement extends DTM’s utility to engineering scenarios where localized stress analysis (e.g., crack initiation at point loads) is paramount.

Traditional numerical methods like FEM face two key limitations for discontinuous loads: (1) they require dense mesh refinement near singularities (e.g., x = L/2 in Case 2), significantly increasing computational cost; and (2) they introduce discretization errors that only converge as O(h²) with element size h. DTM overcomes these by providing exact polynomial solutions through corrective terms (Section Mathematical Justification for Corrective Term) without spatial discretization.

2. Materials and Methods

For example, consider an infinitely differentiable function v(x). Suppose also that v(x) is an analytic function in a domain D, and let x = x_i be an arbitrary point within this domain. The function v(x) can then be expressed as a power series centered at x_i. Its Taylor series expansion is given by the following:

$$v\left(x\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{{\left(x-x_i\right)}^k}{k!}}·{\left[{\displaystyle \frac{d^{k}v\left(x\right)}{d{x}^k}}\right]}_{x=x_i}, \forall x\in D$$

(1)

The Maclaurin series of v(x) can be obtained by taking x_i = 0 in Equation (1), expressed as follows:

$$v\left(x\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{x^k}{k!}}·{\left[{\displaystyle \frac{d^{k}v\left(x\right)}{d{x}^k}}\right]}_{x=0}, \forall x\in D$$

(2)

The differential transform of v(x) is defined as follows [1]:

$$V\left(k\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{L^k}{k!}}·{\left[{\displaystyle \frac{d^{k}v\left(x\right)}{d{x}^k}}\right]}_{x=0}$$

(3)

where V(k) represents the k-th coefficient of the differential transform, and k denotes the order of the derivative. The differential spectrum of V(k) is confined within the interval x ∈ [0, L], where L is a constant value.

The inverse differential transform reconstructs the original function as a truncated power series (typically a finite-order approximation of the Taylor series expansion):

$$v\left(x\right)=\sum _{k=0}^{\infty }V\left(k\right)·{\left({\displaystyle \frac{x}{L}}\right)}^k$$

(4)

Within the framework of the DTM, there exists a set of essential operation theorems that enable the efficient application of the method to differential equations. These theorems provide straightforward transformation rules for common operations (such as differentiation, multiplication, and addition), similar in spirit to the operational rules used in the Laplace transform.

The main operational theorems of DTM for univariate functions are summarized in

Table 1. Basic operational theorems of the DTM (Note: While linear problems primarily use basic transforms (e.g., derivatives, constants), the full set is included for completeness and future nonlinear applications).

Operation	Function	Differential Transform
Constant function	$v\left(x\right)=C$	$V\left(0\right)=C,V\left(k\right)=0 for k>0$
Power function	$v\left(x\right)=x^n$	$V\left(k\right)=\delta \left(k-1\right), \mathrm{where} \delta \mathrm{is} \mathrm{Dirac} \mathrm{function}$
First derivation	${\displaystyle \frac{dv\left(x\right)}{dx}}$	$V\left(k\right)=(k+1)·V(k+1)$
n-th derivative	${\displaystyle \frac{d^{n}v\left(x\right)}{d{x}^n}}$	$V\left(k\right)={\displaystyle \frac{\left(k+n\right)!}{k!}}·V(k+n)$
Addition	$v\left(x\right)=f\left(x\right)+g\left(x\right)$	$V\left(k\right)=F\left(k\right)+G\left(k\right)$
Multiplication by a constant	$v\left(x\right)=C·f\left(x\right)$	$V\left(k\right)=C·F\left(k\right)$
Product of two functions	$v\left(x\right)=f\left(x\right)·g\left(x\right)$	$V\left(k\right)={\sum }_{m=0}^{k}F\left(m\right)·G(k-m)$
$\mathrm{Multiplication} \mathrm{by} x^n$	$v\left(x\right)=x^n·f\left(x\right)$	$V\left(k\right)=F\left(k-n\right), with F\left(k\right)=0 for k<0$
Composite or nonlinear terms	$v\left(x\right)={\left[f\left(x\right)\right]}^n$	$V\left(k\right)={\displaystyle \sum _{m=0}^k}V\left(m\right)·V^{n-1}\left(k-m\right)$

below [24].

These theorems are derived from Taylor series properties [1] and enable algebraic recurrence relations for nonlinear terms.

The Dirac delta $\delta$(k) is a discrete impulse function: $\delta$(k) = 1 if k = 0, else $\delta$(k) = 0. For continuum problems, $\delta$(k) satisfies ${\int }_{-\infty }^{\infty }\delta \left(x-a\right)·f\left(x\right)·dx=f\left(a\right)$.

For problems involving singularities (e.g., concentrated moments or discontinuous loads), the DTM solution may require corrective terms derived from distribution theory (see Section Mathematical Justification for Corrective Term). This approach aligns with Green’s function methodologies [24], where singular solutions are constructed by combining homogeneous polynomials with Macaulay bracket terms (e.g., ⟨x−a⟩³). The corrective term’s coefficient is determined by enforcing equilibrium conditions across discontinuities, ensuring boundary condition compliance without mesh-dependent approximations.

The algorithmic implementation involves the following steps [25]:

-

Transforming the differential equation into recursive algebraic equations, whereby each term of the original equation is replaced by its corresponding differential transform. For example, the differential transform of the derivative $\phi =dv\left(x\right)/dx$ is given by $(k+1)·V(k+1)$. For the nonlinear term $v^n$, the following convolution is used:

$$V\left(k\right)=\sum _{m=0}^{k}V\left(m\right)·V^{n-1}\left(k-m\right)$$

(5)

where the convolution operation is applied recursively depending on the power n.

This method enables the transformation of the original nonlinear differential equation into a set of algebraic recurrence relations, which can then be solved iteratively to determine the coefficients of the approximate solution.

-

In the subsequent step, the goal is to derive the recurrence relation so that the transformed equation becomes an algebraic expression in terms of V(k). It should be noted that the coefficients V(k) must be determined iteratively, starting from the given initial conditions.

-

Finally, the approximate solution v(x) is reconstructed by summing a finite number of terms from the series expansion. The number of terms retained is typically chosen based on a convergence criterion or a desired level of accuracy. A convergence analysis is then performed to evaluate the reliability of the approximation. In many cases, the results are further validated by comparing the approximate solution with those obtained through numerical methods or exact solutions, when available.

3. Results and Discussion

Next, a study is proposed to evaluate the deflection and slope of the cross-section (slope) for two distinct beam support cases: the first case (referred to as Beam Support Mode 1—BSM1) involves a beam that is fixed at one end and free at the other (cantilever configuration) and the second case (referred to as Beam Support Mode 2—BSM2) consists of a beam that is pinned at the left end and simply supported at the right end, where the simple support restricts vertical translation.

For these two distinct support conditions, five different loading cases are considered, as follows:

3.1. Case 1

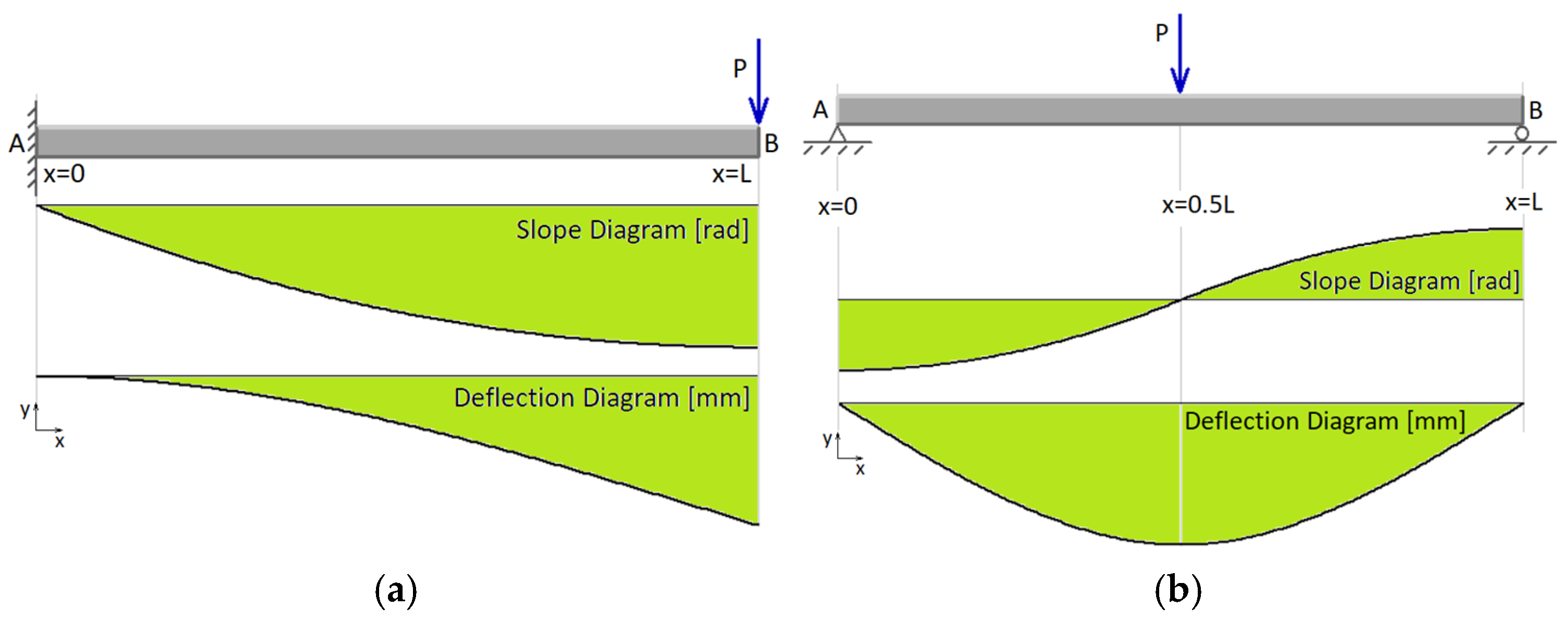
In the first loading case, the beam is subjected to a concentrated force P applied as shown in Figure 1a,b.

In Figure 1a, we consider a straight, homogeneous beam of length L, fixed at the end x = 0 and free at the end x = L (BSM1). A concentrated force P is applied at the free end (x = L), acting perpendicular to the beam’s longitudinal axis.

The differential equation of the deformed neutral axis (elastic curve) for this support and loading case is given by the following:

$$E·I_z·{\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}=0$$

(6)

The boundary conditions are as follows:

At the left end of the beam (where the clamped support is located):

$$x=0\Rightarrow \mathrm{deflection} \mathrm{is} v\left(0\right)=0, \mathrm{slope} \mathrm{is} v^{\prime }\left(0\right)={\displaystyle \frac{dv}{dx}}=0$$

(7)

At the free end of the beam (x = L), the boundary conditions are as follows:

$$x=L\Rightarrow \mathrm{bending} \mathrm{moment} \mathrm{is} v^{″}\left(L\right)=M_z=0, \mathrm{shear} \mathrm{force} \mathrm{is} v^{‴}\left(L\right)={\displaystyle \frac{T_y}{E·I_z}}={\displaystyle \frac{P}{E·I_z}}$$

(8)

For the application of the DTM, the differential transform of the deflection v(x) is denoted by the following:

$$for x=0\Rightarrow V\left(k\right)={\displaystyle \frac{1}{k!}}·{\displaystyle \frac{d^{k}v\left(x\right)}{d{x}^k}}$$

(9)

The differential equation of the deformed neutral axis (elastic curve) for the given beam under a concentrated load P is as follows:

$$E·I_z·{\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}=0\Rightarrow {\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}=0$$

(10)

By applying DTM, the following is obtained:

$$\left(k+1\right)·\left(k+2\right)·\left(k+3\right)·\left(k+4\right)·V\left(k+4\right)=0$$

(11)

Since Equation (11) is identically zero, it follows that V(k + 4) = 0 for all k ≥ 0. This means that only V(0), V(1), V(2), and V(3) can be non-zero, while all other coefficients are zero.

Consequently, boundary conditions are used to determine the order of magnitude of the coefficients V(k) by means of relation (9), as follows:

From v(0) = 0, we obtain V(0) = 0; from v’(0) = 0, we obtain V(1) = 0; From v″(L) = 0, where the bending moment expression is as follows:

$$v^{″}\left(x\right)=\sum _{k=0}^{\infty }k·(k-1)·V\left(k\right)·x^{k-2}$$

(12)

And since V(k) = 0 for k ≥ 4, from relation (12) it follows that

$$v^{″}\left(x\right)=2·V\left(2\right)+6·V\left(3\right)·x$$

(13)

By evaluating relation (13) at x=L, we obtain the following:

$$v^{″}\left(L\right)=2·V\left(2\right)+6·V\left(3\right)·L\Rightarrow V\left(2\right)=-3·V\left(3\right)·L$$

(14)

From the shear force expression, it follows that

$$v^{‴}\left(L\right)={\displaystyle \frac{P}{E·I_z}}\Rightarrow v^{‴}\left(x\right)=6·V\left(3\right)$$

(15)

When relation (15) is evaluated at x = L, we obtain the following:

$$v^{‴}\left(L\right)=6·V\left(3\right)={\displaystyle \frac{P}{E·I_z}}\Rightarrow V\left(3\right)={\displaystyle \frac{P}{6·E·I_z}}$$

(16)

By inserting relation (16) into (14), we obtain the following:

$$V\left(2\right)=-3·{\displaystyle \frac{P}{6·E·I_z}}·L=-{\displaystyle \frac{P·L}{2·E·I_z}}$$

(17)

In the following step, the solution v(x) is reconstructed through application of relation (4), as detailed below:

$$v\left(x\right)=\sum _{k=0}^{\infty }V\left(k\right)·x^k=V\left(2\right)·x^2+V\left(3\right)·x^3=-{\displaystyle \frac{P·L·x^2}{2·E·I_z}}+{\displaystyle \frac{P·x^3}{6·E·I_z}}$$

(18)

Through simplification, the following result is obtained:

$$v\left(x\right)={\displaystyle \frac{P}{6·E·I_z}}·\left(x^3-3·L·x^2\right)$$

(19)

The maximum deflection at x=L is computed by means of relation (19) in the following manner:

$$v\left(L\right)={\displaystyle \frac{P}{6·E·I_z}}·\left(L^3-3·L·L^2\right)={\displaystyle \frac{P}{6·E·I_z}}·\left(-2·L^3\right)\Rightarrow v\left(L\right)=-{\displaystyle \frac{P·L^3}{3·E·I_z}}$$

(20)

In Equation (20), the presence of the negative sign signifies that the displacement occurs in the direction opposite to the positive y-axis.

This exact cubic solution (Equation (19)) demonstrates DTM’s ability to replicate theoretical results without numerical approximations, a key advantage over mesh-dependent methods like FEM.

The slope φ(x) = v’(x) of the cross-section is determined through the slope–deflection relationship:

$$\phi \left(x\right)={\displaystyle \frac{dv}{dx}}={\left[{\displaystyle \frac{P}{6·E·I_z}}·\left(x^3-3·L·x^2\right)\right]}^{\prime }={\displaystyle \frac{P}{6·E·I_z}}·\left({3·x}^2-6·L·x\right)={\displaystyle \frac{P}{2·E·I_z}}·\left(x^2-2·L·x\right)$$

(21)

The maximum slope at x = L is computed using Equation (21) as follows:

$$\phi \left(L\right)={\displaystyle \frac{P}{2·E·I_z}}·\left(L^2-2·L·L\right)=-{\displaystyle \frac{P·L^2}{2·E·I_z}}$$

(22)

Though formally a truncated series, DTM’s solution (Equation (19)) is exact for this problem class because (1) the governing ODE (Equation (10)) has a polynomial solution, and (2) all higher-order terms (k ≥ 4) vanish identically (Equation (11)). This contrasts with FEM’s approximate solutions that always require error analysis.

In Equation (22), the presence of the negative sign means the cross-section rotates in the clockwise direction.

In Figure 1b, we consider a straight, homogeneous beam of length L, which is pinned at the left end (x = 0) and simply supported at the right end (x = L), where the simple support restricts vertical translation (BSM2). A concentrated force P is applied at x = L/2, acting perpendicular to the beam’s longitudinal axis.

Considering the specific support conditions and applied loading, the differential equation describing the deformation of the beam’s neutral axis can be expressed as follows:

$$E·I_z·{\displaystyle \frac{d^{4}v}{d{x}^4}}=P·\delta \left(x-{\displaystyle \frac{L}{2}}\right)$$

(23)

where $\delta \left(x-{\displaystyle \frac{L}{2}}\right)$ denotes the Dirac distribution.

The DTM is applied separately to two adjacent intervals: 0 ≤ x ≤ L/2 and L/2 ≤ x ≤ L.

The differential equation of the elastic curve for the given beam under a concentrated load P is as follows:

$$E·I_z·{\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}=0\Rightarrow {\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}=0$$

(24)

The implementation of the differential transform method produces the following results:

$$\left(k+1\right)·\left(k+2\right)·\left(k+3\right)·\left(k+4\right)·V\left(k+4\right)=0$$

(25)

We can express the general solution as a cubic polynomial:

$$v\left(x\right)=\sum _{m=0}^3{C}_m·x^m$$

(26)

Applying boundary conditions via (9) yields the magnitude order of C(m) coefficients:

For x = 0, the deflection is given by the following:

$$v\left(0\right)=C_0=0$$

(27)

while the bending moment is given by the following equation:

$${\displaystyle \frac{d^{2}v}{d{x}^2}}=2·C_2=0\Rightarrow C_2=0$$

(28)

Thus, the simplified form of relation (26) for the interval 0 ≤ x ≤ L/2 can be written as follows:

$$v_1\left(x\right)=C_1·x+C_3·x^3$$

(29)

In the second interval (L/2 ≤ x ≤ L), the deflection at x = L is given by the following:

$$v_2\left(L\right)= D_0+D_1·L+D_2·L^2+D_3·L^3=0$$

(30)

To determine constants C₁, C₃, D₀, D₁, D₂, and D₃, we enforce the continuity condition of the deformed neutral axis (considering both deflection and slope) at the interface between the two intervals (x = L/2). Specifically, the deflection calculated using the first interval’s equation must equal that obtained from the second interval’s equation when substituting x = L/2 [by equating relations (29) and (30)]:

$$C_1·{\displaystyle \frac{L}{2}}+C_3·{\left({\displaystyle \frac{L}{2}}\right)}^3=D_0+D_1·\left({\displaystyle \frac{L}{2}}\right)+D_2·{\left({\displaystyle \frac{L}{2}}\right)}^2+D_3·{\left({\displaystyle \frac{L}{2}}\right)}^3$$

(31)

Next, we enforce the slope continuity condition by equating the slope calculated for the first interval with that of the second interval at x = L/2. Accounting for the relationship between deflection and slope (φ = dv/dx) and incorporating relation (31), we obtain the following:

$$C_1+3·C_3·{\left({\displaystyle \frac{L}{2}}\right)}^2=D_1+2·D_2·{\displaystyle \frac{L}{2}}+3·D_3·{\left({\displaystyle \frac{L}{2}}\right)}^2$$

(32)

In the same cross-section, the shear force exhibits a discontinuity whose order of magnitude equals the applied force P, yielding the following:

$$E·I_z·\left[{\left({\displaystyle \frac{d^3{v}_2}{d{x}^3}}\right)}_{x={\displaystyle \frac{L}{2}}}-{\left({\displaystyle \frac{d^3{v}_1}{d{x}^3}}\right)}_{x={\displaystyle \frac{L}{2}}}\right]=P\Rightarrow 6·D_3-6·C_3={\displaystyle \frac{P}{E·I_z}}$$

(33)

Combining the continuity conditions and equilibrium relations (30)–(33) produces the complete equation system:

$$\left\{\begin{array}{c}{D}_0+D_1·L+D_2·L^2+D_3·L^3=0\\ C_1·{\displaystyle \frac{L}{2}}+C_3·{\displaystyle \frac{L^3}{8}}=D_0+D_1·{\displaystyle \frac{L}{2}}+D_2·{\displaystyle \frac{L^2}{4}}+D_3·{\displaystyle \frac{L^3}{8}}\\ C_1+{\displaystyle \frac{3}{4}}·C_3·L^2=D_1+D_2·L+{\displaystyle \frac{3}{4}}·D_3·L^2\\ D_3-C_3={\displaystyle \frac{P}{6·E·I_z}}\end{array}\right.$$

(34)

The solution set of the equation system (34) consists of the following:

$$C_1={\displaystyle \frac{P·L^2}{16·E·I_z}}; C_3=-{\displaystyle \frac{P}{12·E·I_z}}; D_0=-{\displaystyle \frac{P·L^3}{48·E·I_z}}; D_1={\displaystyle \frac{3·P·L^3}{16·E·I_z}}; D_2=-{\displaystyle \frac{P·L}{4·E·I_z}}; D_3={\displaystyle \frac{P}{12·E·I_z}}$$

(35)

On the interval 0 ≤ x ≤ L/2, the deflection takes the form

$$v_1\left(x\right)={\displaystyle \frac{P}{16·E·I_z}}·x·\left(L^2-{\displaystyle \frac{4}{3}}·x^2\right)$$

(36)

while on the interval L/2 ≤ x ≤ L, the deflection takes the form

$$v_2\left(x\right)={\displaystyle \frac{P}{48·E·I_z}}·\left(L-x\right)·\left(L^2-8·L·x+4·x^2\right)$$

(37)

At the midpoint (x = L/2), (36) reduces to the following:

$$v\left({\displaystyle \frac{L}{2}}\right)=-{\displaystyle \frac{P·L^3}{48·E·I_z}}$$

(38)

Unlike FEM, which requires adaptive meshing near singularities, DTM’s two-interval formulation (Equations (36) and (37)) inherently captures the discontinuous shear at x = L/2.

On the interval 0 ≤ x ≤ L/2, the slope takes the form

$${\phi }_1\left(x\right)={\displaystyle \frac{P}{16·E·I_z}}·\left(L^2-{\displaystyle \frac{8·x}{3}}\right)$$

(39)

while at x = 0, the result is as follows:

$${\phi }_1\left(x\right)=-{\displaystyle \frac{P·L^2}{16·E·I_z}}$$

(40)

From relation (40), it is observed that the slope is negative, indicating that the cross-section rotates clockwise.

On the interval L/2 ≤ x ≤ L, the slope takes the form

$${\phi }_2\left(x\right)={\displaystyle \frac{P}{48·E·I_z}}·\left(-9·L^2+24·L·x-12·x^2\right)$$

(41)

while at x = L, the result is

$${\phi }_1\left(x\right)={\displaystyle \frac{P·L^2}{16·E·I_z}}$$

(42)

Equation (42) reveals a positive slope value, corresponding to counterclockwise cross-sectional rotation.

3.2. Case 2

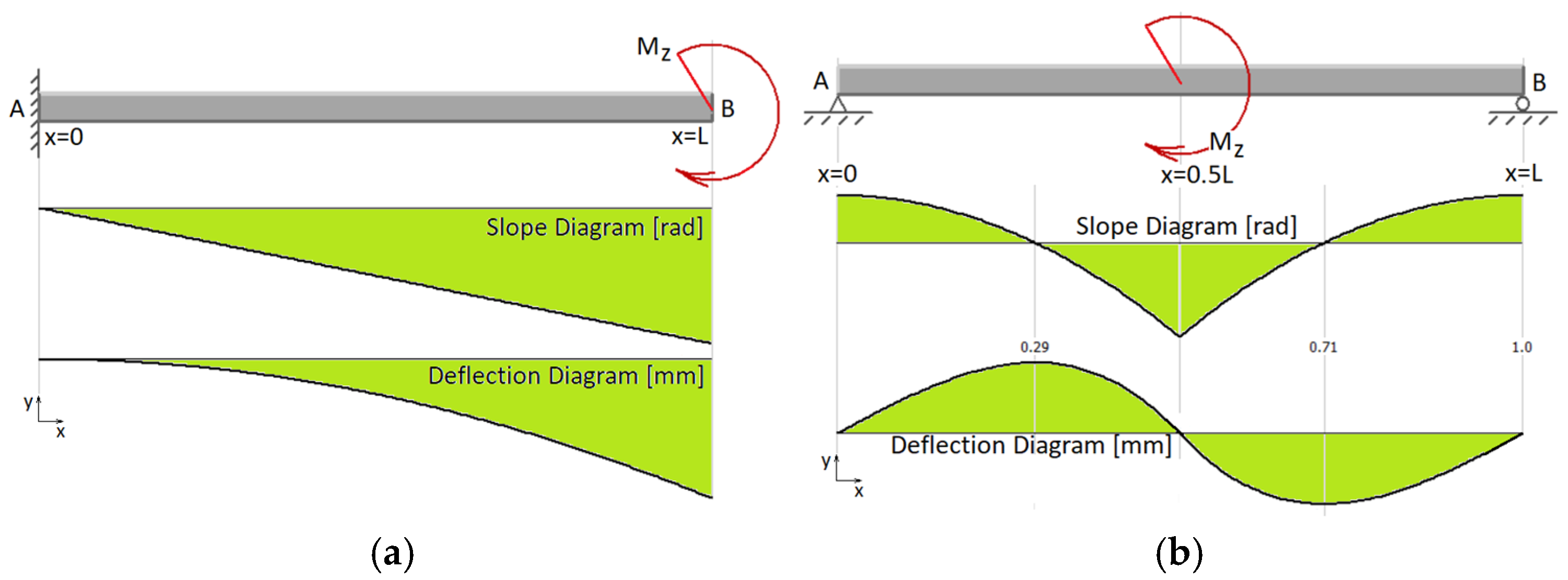
In the first loading case, the beam is subjected to a concentrated bending moment M_z applied as shown in Figure 2a,b.

Thus, Figure 2a shows a straight, homogeneous beam of length L, fixed at the left end (x = 0) and free at the right end (x = L). A concentrated bending moment M_z (pure bending load) is applied at the free end (x = L). The differential equation of the deformed neutral axis is as follows:

$$E·I_z·{\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}=0$$

(43)

The boundary conditions are as follows:

-

At x = 0, the following conditions hold:

$$v\left(0\right)=0;v^{\prime }\left(0\right)={\displaystyle \frac{dv\left(x\right)}{dx}}=0$$

(44)

-

At x = L, we have

$$M_z\left(L\right)=-E·I_z·v^{″}\left(L\right); T_y\left(L\right)=-E·I_z·v^{‴}\left(L\right)=0$$

(45)

Equation (43) has the following transform:

$$\left(k+1\right)·\left(k+2\right)·\left(k+3\right)·\left(k+4\right)·V\left(k+4\right)=0\Rightarrow V\left(k+4\right)=0,\forall k\ge 0$$

(46)

According to relation (4), the solution has the following form:

$$v\left(x\right)=V\left(0\right)+V\left(1\right)·x+V\left(2\right)·x^2+V\left(3\right)·x^3$$

(47)

The boundary conditions are explicitly applied to determine the order of magnitude of coefficients V(k) using relation (9), as follows:

-

At x = 0, we have v(0) = 0 yielding V(0) = 0; and v’(0) = 0 yielding V(1) = 0;

-

At x = L, the bending moment is $M_z=-E·I_z·v^{″}\left(L\right)$

or

$$v^{″}\left(x\right)=\sum _{k=0}^{\mathrm{\infty }}k·(k-1)·V\left(k\right)·x^{k-2}$$

(48)

and since V(k) = 0 for k ≥ 4, from relation (48), it follows that

$$v^{″}\left(x\right)=2·V\left(2\right)+6·V\left(3\right)·x$$

(49)

Substituting x = L into (49) produces the following:

$$v^{″}\left(L\right)=-\left[2·V\left(2\right)+6·V\left(3\right)·L\right]·E·I_z=M_z\Rightarrow 2·V\left(2\right)+6·V\left(3\right)·L=-{\displaystyle \frac{M_z}{E·I_z}}$$

(50)

From the shear force expression, it follows that

$$-E·I_z·v^{‴}\left(L\right)=0\Rightarrow v^{‴}\left(x\right)=6·V\left(3\right)$$

(51)

Substituting x = L into (51) leads to the following:

$$v^{‴}\left(L\right)=6·V\left(3\right)=0\Rightarrow V\left(3\right)=0$$

(52)

The coupling of Equations (50) and (52) leads to:

$$2·V\left(2\right)=-{\displaystyle \frac{M_z}{E·I_z}}\Rightarrow V\left(2\right)=-{\displaystyle \frac{M_z}{2·E·I_z}}$$

(53)

Next, using relation (4), the solution v(x) is reconstructed as follows:

$$v\left(x\right)=\sum _{k=0}^{\mathrm{\infty }}V\left(k\right)·x^k=V\left(2\right)·x^2=-{\displaystyle \frac{M_z}{2·E·I_z}}·x^2$$

(54)

By differentiating Equation (54), the cross-section rotation is obtained as follows:

$$\phi \left(x\right)={\displaystyle \frac{dv\left(x\right)}{dx}}=-{\displaystyle \frac{M_z·x}{E·I_z}}$$

(55)

Evaluating (54) and (55) at x = L gives the following:

$$v\left(L\right)=-{\displaystyle \frac{M_z}{2·E·I_z}}·L^2;\phi \left(x\right)=-{\displaystyle \frac{M_z·L}{E·I_z}}$$

(56)

In Figure 2b, we consider a straight, homogeneous beam of length L, which is pinned at the left end (x = 0) and simply supported at the right end (x = L), where the simple support restricts vertical translation (BSM2). A concentrated bending moment M_z is applied at x = L/2.

The governing equation for neutral axis deflection under these boundary/loading conditions is as follows:

$$E·I_z·{\displaystyle \frac{d^{4}v}{d{x}^4}}=-M_z·\delta \prime \left(x-{\displaystyle \frac{L}{2}}\right)$$

(57)

where δ’ is the derivative of the Dirac function.

The DTM will be applied over two intervals as follows: on the first interval, 0 ≤ x ≤ L/2, and on the second interval is L/2 ≤ x ≤ L.

The differential equation of the elastic curve for the given beam under a concentrated bending moment M_z is as follows:

$$E·I_z·{\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}=0\Rightarrow {\displaystyle \frac{d^{4}v\left(x\right)}{d{x}^4}}=0$$

(58)

Implementing DTM provides the following:

$$\left(k+1\right)·\left(k+2\right)·\left(k+3\right)·\left(k+4\right)·V\left(k+4\right)=0$$

(59)

The general solution can be expressed as a third-degree polynomial of the following form:

$$v\left(x\right)=\sum _{m=0}^3{C}_m·x^m\Rightarrow v\left(x\right)=C_0+C_1·x+C_2·x^2+C_3·x^3$$

(60)

Boundary conditions are applied to determine the order of magnitude of coefficients C(m) using relation (9), as follows:

-

At x = 0, the deflection satisfies

$$v\left(0\right)=C_0=0$$

(61)

while the bending moment is expressed by the relation

$${\displaystyle \frac{d^{2}v}{d{x}^2}}=2·C_2=0\Rightarrow C_2=0$$

(62)

Thus, the simplified form of relation (60) for the interval 0 ≤ x ≤ L/2 can be written as follows:

$$v_1\left(x\right)=C_1·x+C_3·x^3$$

(63)

Analogously, at x = L (corresponding to the interval L/2 ≤ x ≤ L), the deflection is expressed as

$$v_2\left(L\right)=D_0+D_1·L+D_2·L^2+D_3·L^3=0$$

(64)

and the bending moment

$$M_z\left(L\right)={\displaystyle \frac{d^2{v}_2\left(L\right)}{d{x}^2}}=2·D_2+6·D_3·L=0$$

(65)

To determine the constants C₁, C₃, D₀, D₁, D₂, and D₃, we enforce the neutral axis continuity condition (for both deflection and slope) at the interface between the two intervals (x = L/2). Specifically, the deflection calculated using the first interval’s equation must equal that from the second interval’s equation when substituting x = L/2 [by equating relations (63) and (64)]:

$${v_1\left({\displaystyle \frac{L}{2}}\right)=v_2\left({\displaystyle \frac{L}{2}}\right)\Rightarrow C}_1·{\displaystyle \frac{L}{2}}+C_3·{\left({\displaystyle \frac{L}{2}}\right)}^3=D_0+D_1·\left({\displaystyle \frac{L}{2}}\right)+D_2·{\left({\displaystyle \frac{L}{2}}\right)}^2+D_3·{\left({\displaystyle \frac{L}{2}}\right)}^3$$

(66)

Next, the slope calculated for the first interval is equated to that of the second interval at x = L/2. Accounting for the deflection-slope relationship (φ = dv/dx) and incorporating relation (65), we obtain the following:

$${\phi }_1\left({\displaystyle \frac{L}{2}}\right)={\phi }_2\left({\displaystyle \frac{L}{2}}\right)\Rightarrow C_1+3·C_3·{\left({\displaystyle \frac{L}{2}}\right)}^2=D_1+2·D_2·{\displaystyle \frac{L}{2}}+3·D_3·{\left({\displaystyle \frac{L}{2}}\right)}^2$$

(67)

In the same cross-section, the bending moment exhibits a discontinuity whose order of magnitude equals the applied concentrated moment M_z, resulting in the following:

$$E·I_z·\left[{\left({\displaystyle \frac{d^2{v}_2}{d{x}^2}}\right)}_{x={\displaystyle \frac{L}{2}}}-{\left({\displaystyle \frac{d^2{v}_1}{d{x}^2}}\right)}_{x={\displaystyle \frac{L}{2}}}\right]=-M_z\Rightarrow 2·D_2+6·D_3·{\displaystyle \frac{L}{2}}-6·C_3·{\displaystyle \frac{L}{2}}=-{\displaystyle \frac{M_z}{E·I_z}}$$

(68)

By synthesizing Equations (64)–(68), we obtain the final system of equations:

$$\left\{\begin{array}{c}{D}_0+D_1·L+D_2·L^2+D_3·L^3=0\\ 2·D_2+6·D_3·L=0\\ C_1·{\displaystyle \frac{L}{2}}+C_3·{\displaystyle \frac{L^3}{8}}=D_0+D_1·{\displaystyle \frac{L}{2}}+D_2·{\displaystyle \frac{L^2}{4}}+D_3·{\displaystyle \frac{L^3}{8}}\\ C_1+{\displaystyle \frac{3}{4}}·C_3·L^2=D_1+{2·D}_2·{\displaystyle \frac{L}{2}}+{\displaystyle \frac{3}{4}}·D_3·L^2\\ 2·D_2+6·D_3·{\displaystyle \frac{L}{2}}-6·C_3·{\displaystyle \frac{L}{2}}=-{\displaystyle \frac{M_z}{E·I_z}}\end{array}\right.$$

(69)

The solutions to the system of Equation (69) are as follows:

$$\left\{\begin{array}{c}{C}_1={\displaystyle \frac{M_z·L}{16·E·I_z}}; C_3=-{\displaystyle \frac{M_z}{4·E·I_z·L}};\\ D_0={\displaystyle \frac{M_z·L^2}{16·E·I_z}}; D_1=-{\displaystyle \frac{{3·M}_z·L}{16·E·I_z}}; D_2={\displaystyle \frac{M_z}{4·E·I_z}}; D_3=-{\displaystyle \frac{M_z}{4·E·I_z·L}}\end{array}\right.$$

(70)

The final expressions for the deflection are as follows:

-

on the interval 0 ≤ x ≤ L/2, the deflection has the following form:

$$v_1\left(x\right)={\displaystyle \frac{M_z}{16·E·I_z}}·\left(L·x-{\displaystyle \frac{{4·x}^3}{L}}\right)$$

(71)

and on the interval L/2 ≤ x ≤ L, the deflection is of the form

$$v_2\left(L\right)={\displaystyle \frac{M_z}{16·E·I_z}}·\left(L^2-3·L·x+{4·x}^2-{\displaystyle \frac{4·x^3}{L}}\right)$$

(72)

For x = L/2, from relations (71) and (72), it follows that

$$v\left({\displaystyle \frac{L}{2}}\right)=0$$

(73)

For x = 0, from relation (71), the deflection v(0) = 0, and from relation (72), for x = L, the deflection v(L) = 0.

On the interval 0 ≤ x ≤ L, the slope is of the form

$${\phi }_1\left(x\right)={\displaystyle \frac{d{v}_1\left(x\right)}{dx}}={\displaystyle \frac{M_z}{16·E·I_z}}·\left(L-{\displaystyle \frac{12·x^2}{L}}\right)$$

(74)

whereas in the domain L/2 ≤ x ≤ L, the rotation follows

$${\phi }_2\left(x\right)={\displaystyle \frac{d{v}_2\left(x\right)}{dx}}=-{\displaystyle \frac{M_z}{16·E·I_z}}·\left(-3·L+8·x-{\displaystyle \frac{12·x^2}{L}}\right)$$

(75)

From relation (74), for x = 0, it follows that

$${\phi }_1\left(x\right)={\displaystyle \frac{d{v}_1\left(x\right)}{dx}}={\displaystyle \frac{M_z·L}{16·E·I_z}}$$

(76)

From relation (74), for x = L/2, it follows that

$${\phi }_1\left({\displaystyle \frac{L}{2}}\right)=-{\displaystyle \frac{M_z·L}{8·E·I_z}}$$

(77)

and from relation (75)

$${\phi }_2\left(x\right)=-{\displaystyle \frac{M_z·L}{8·E·I_z}}$$

(78)

This confirms the rotation continuity at x = L/2.

From relation (75), for x = L, it follows that

$${\phi }_2\left(L\right)={\displaystyle \frac{d{v}_2\left(x\right)}{dx}}=-{\displaystyle \frac{7·M_z·L}{16·E·I_z}}$$

(79)

From relation (79), it can be observed that the boundary condition at x = L is not satisfied, specifically ${\phi }_2\left(x\right)\ne {\phi }_1\left(x\right)$. The proper solution necessitates an alternative methodology, such as Green’s functions or distribution theory.

Thus, over the interval L/2 ≤ x ≤ L, a correction constant k is added to ensure the condition M_z(L) = 0, as follows:

$$v_2\left(x\right)={\displaystyle \frac{M_z}{16·E·I_z}}·\left(L^2-3·L·x+{4·x}^2-{\displaystyle \frac{4·x^3}{L}}\right)+k·{\left(x-{\displaystyle \frac{L}{2}}\right)}^3$$

(80)

DTM’s corrective terms (e.g., Equation (80)) streamline the solution process for discontinuous loads by embedding continuity conditions directly into the algebraic recurrence framework. This contrasts with traditional methods that require ad hoc patching of piecewise solutions.

The constant k is chosen such that

$${\left({\displaystyle \frac{d^2{v}_2}{d{x}^2}}\right)}_{x={\displaystyle \frac{L}{2}}}=0$$

(81)

from which it follows that

$${\displaystyle \frac{d^2{v}_2}{d{x}^2}}={\displaystyle \frac{M_z}{16·E·I_z}}·\left(8-{\displaystyle \frac{24·x}{L}}\right)+6·k·\left(x-{\displaystyle \frac{L}{2}}\right)$$

(82)

For x = L, we obtain the following:

$${\displaystyle \frac{M_z}{16·E·I_z}}·\left(8-24\right)+6·k·{\displaystyle \frac{L}{2}}=0\Rightarrow -{\displaystyle \frac{M_z}{E·I_z}}+3·k·L\Rightarrow k={\displaystyle \frac{M_z}{3·E·I_z·L}}$$

(83)

Thus, the deflection curve becomes

$$v_2\left(x\right)={\displaystyle \frac{M_z}{16·E·I_z}}·\left(L^2-3·L·x+{4·x}^2-{\displaystyle \frac{4·x^3}{L}}\right)+{\displaystyle \frac{M_z}{3·E·I_z·L}}·{\left(x-{\displaystyle \frac{L}{2}}\right)}^3$$

(84)

For x = L, we have the following:

$$v_2\left(L\right)={\displaystyle \frac{M_z}{16·E·I_z}}·\left(L^2-3·L^2+{4·L}^2-4·L^2\right)+{\displaystyle \frac{M_z}{3·E·I_z·L}}·{\left({\displaystyle \frac{L}{2}}\right)}^3=0$$

(85)

$${\left({\displaystyle \frac{d^2{v}_2}{d{x}^2}}\right)}_{x={\displaystyle \frac{L}{2}}}=-{\displaystyle \frac{M_z}{E·I_z}}+{\displaystyle \frac{M_z}{E·I_z}}=0$$

(86)

$${\phi }_2\left(L\right)={\displaystyle \frac{d{v}_2\left(x\right)}{dx}}={\displaystyle \frac{7·M_z·L}{16·E·I_z}}-{\displaystyle \frac{M_z·L}{8·E·I_z}}={\displaystyle \frac{5·M_z·L}{16·E·I_z}}$$

(87)

The need for corrective terms (Equation (80)) highlights DTM’s flexibility in addressing singularities, whereas FEM would demand specialized elements or penalty methods.

Mathematical Justification for Corrective Term

The corrective term $k·{\left(x-{\displaystyle \frac{L}{2}}\right)}^3$ in Equation (80) arises from the singular nature of the Dirac delta derivative $\delta \prime \left(x-{\displaystyle \frac{L}{2}}\right)$ in the governing Equation (57). Green’s function derivation shows that the general solution combines a homogeneous polynomial and a singular term capturing the curvature discontinuity:

$$v\left(x\right)={\displaystyle \frac{C_0+C_1·x+C_2·x^2+C_3·x^3}{represent homogeneous solution}}+{\displaystyle \frac{C·{〈x-\frac{L}{2}〉}^3}{represent singular solution}}$$

(88)

where $〈\dots 〉$ denotes Macaulay bracket.

The coefficient C is determined by enforcing a jump in curvature at x = L/2:

$$v^{″}\left({\displaystyle \frac{L}{2^{+}}}\right)-v^{″}\left({\displaystyle \frac{L}{2^{-}}}\right)=-{\displaystyle \frac{M_z}{E·I_z}}$$

(89)

For x $\ge$ L/2, the singular term yields the following:

$$v_p^{″}\left(x\right)=6·C·\left(x-{\displaystyle \frac{L}{2}}\right)\Rightarrow v_p^{″}\left({\displaystyle \frac{L}{2^{+}}}\right)=0, {\displaystyle \frac{d^3{v}_p}{d{x}^3}}=6·C$$

(90)

Integrating the governing Equation (57) across x = L/2 gives the following:

$$E·I_z·{\left[{\displaystyle \frac{d^{3}v}{d{x}^3}}\right]}_{L/2^{-}}^{L/2^{+}}=-M_z\Rightarrow 6·E·I_z·C=-M_z\Rightarrow C=-{\displaystyle \frac{M_z}{6·E·I_z}}$$

(91)

Thus, the corrective term in Equation (80) is as follows:

$$k=-{\displaystyle \frac{M_z}{6·E·I_z}}$$

(92)

ensuring consistency with distribution theory.

The distribution theory perspective shows that the Dirac delta derivative $\delta$’ is rigorously treated by operating on test functions θ(x) [26,27]:

$$\int {\delta }^{\prime }\left(x-{\displaystyle \frac{L}{2}}\right)·\theta \left(x\right)·dx=-\theta \prime \left({\displaystyle \frac{L}{2}}\right)$$

(93)

This justifies the use of ${〈x-{\displaystyle \frac{L}{2}}〉}^3$ as the fundamental solution for moment singularities in DTM.

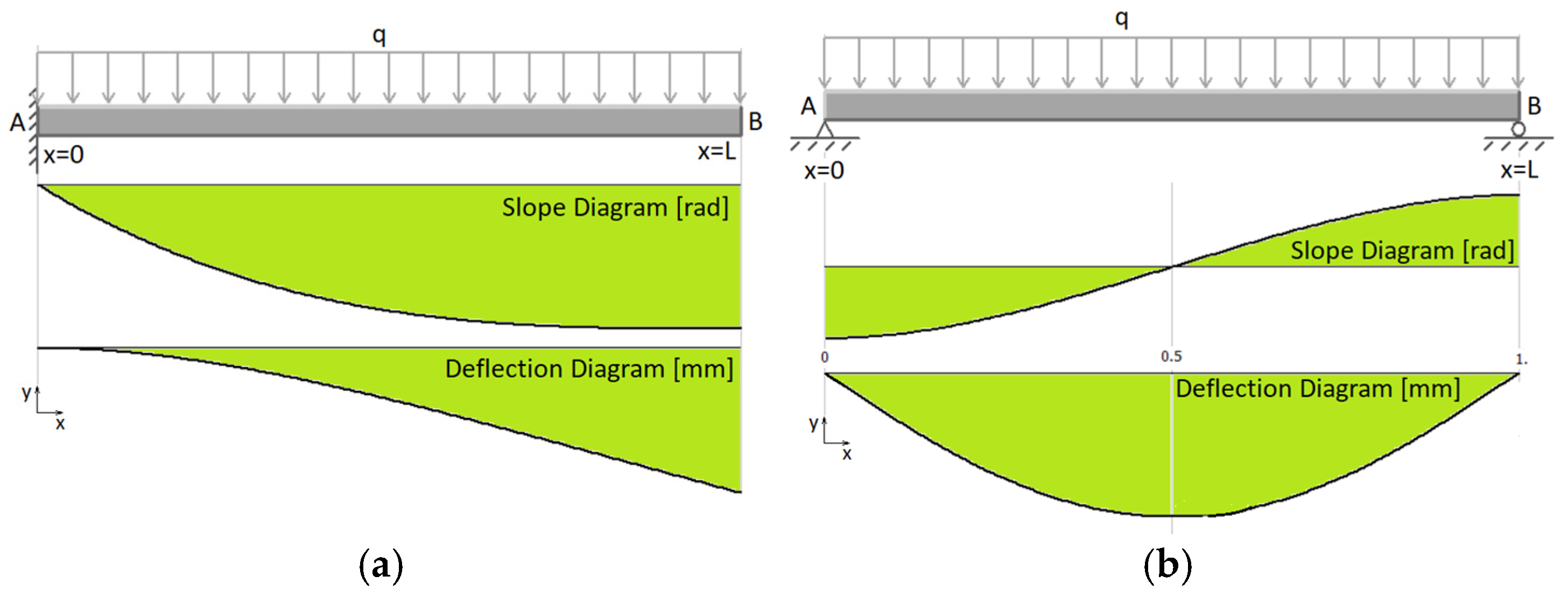
3.3. Case 3

In the third loading case, the bar is subjected to a uniformly distributed load q, as shown in Figure 3a,b.

Thus, Figure 2a shows a straight, homogeneous beam of length L, fixed at the left end (x = 0) and free at the right end (x = L)—BSM1. The uniformly distributed load q is applied over the entire length L.

For this loading case, the differential equation describing the beam’s deflection curve v(x) is as follows:

$$E·I_z·{\displaystyle \frac{d^{4}v}{d{x}^4}}=q$$

(94)

To solve the equation, a transformation is applied to convert it into an algebraic form. The transformed equation becomes the following:

$$\left(k+1\right)·\left(k+2\right)·\left(k+3\right)·\left(k+4\right)·V\left(k+4\right)={\displaystyle \frac{q·\delta \left(k\right)}{E·I_z}}$$

(95)

where δ(k) is the discrete Dirac function, defined by the following:

$$\delta \left(k\right)=\left\{\begin{array}{c}1 if k=0,\\ 0 if k\ne 0.\end{array}\right.$$

(96)

The solution to the transformed equation is obtained by analyzing the following two cases:

-

for k = 0

$$E·I_z·{\displaystyle \frac{4!}{0!}}·V\left(4\right)=q\Rightarrow 24·E·I_z·V\left(4\right)=q\Rightarrow V\left(4\right)={\displaystyle \frac{q}{24·E·I_z}}$$

(97)

-

for k ≠ 0

$$V\left(k+4\right)=0$$

(98)

The solution in the real domain is expressed as a power series:

$$v\left(x\right)=\sum _{k=0}^{4}V\left(k\right)·x^k=V\left(0\right)+V\left(1\right)·x+V\left(2\right)·x^2+V\left(3\right)·x^3+V\left(4\right)·x^4$$

(99)

To determine the constants V(0), V(1), V(2), and V(3), the following boundary conditions are imposed:

-

At the fixed end (for x = 0):

-

The displacement is zero:

$$v\left(0\right)=0\Rightarrow V\left(0\right)=0$$

(100)

-

The slope is zero:

$$v^{\prime }\left(0\right)={\displaystyle \frac{dv\left(x\right)}{dx}}=0\Rightarrow V\left(1\right)=0$$

(101)

-

At the free end (for x = L):

-

The bending moment is zero:

$$M_z\left(L\right)=-E·I_z·v^{″}\left(L\right)=-E·I_z·{\displaystyle \frac{d^{2}v\left(L\right)}{d{x}^2}}=0$$

(102)

-

The shear force is zero:

$$T_y\left(L\right)=-E·I_z·v^{‴}\left(L\right)=-E·I_z·{\displaystyle \frac{d^{3}v\left(L\right)}{d{x}^3}}=0$$

(103)

Next, the following derivatives are calculated:

$${\displaystyle \frac{dv\left(x\right)}{dx}}=2·V\left(2\right)·x+3·V\left(3\right)·x^2+4·V\left(4\right)·x^3=2·V\left(2\right)·x+3·V\left(3\right)·x^2+{\displaystyle \frac{q·x^3}{6·E·I_z}}$$

(104)

$${\displaystyle \frac{d^{2}v\left(x\right)}{d{x}^2}}={\displaystyle \frac{q·x^2}{2·E·I_z}}+6·V\left(3\right)·x+2·V\left(2\right)$$

(105)

$${\displaystyle \frac{d^{3}v\left(x\right)}{d{x}^3}}={\displaystyle \frac{q·x}{E·I_z}}+6·V\left(3\right)$$

(106)

The next step involves enforcing the boundary conditions at x = L as follows:

$${\displaystyle \frac{d^{3}v\left(L\right)}{d{L}^3}}=0\underset{\left(105\right)}{\Rightarrow }{\displaystyle \frac{q·L}{E·I_z}}+6·V\left(3\right)=0\Rightarrow V\left(3\right)=-{\displaystyle \frac{q·L}{6·E·I_z}}$$

(107)

$${\displaystyle \frac{d^{2}v\left(L\right)}{d{L}^2}}=0\underset{\left(104\right)}{\Rightarrow }{\displaystyle \frac{q·L^2}{2·E·I_z}}+6·V\left(3\right)·L+2·V\left(2\right)=0\Rightarrow {\displaystyle \frac{q·L^2}{2·E·I_z}}-{\displaystyle \frac{q·L^2}{E·I_z}}+2·V\left(2\right)=0\Rightarrow$$

$$-{\displaystyle \frac{q·L^2}{2·E·I_z}}+2·V\left(2\right)=0\Rightarrow V\left(2\right)={\displaystyle \frac{q·L^2}{4·E·I_z}}$$

(108)

Substituting the determined constants, the final solution takes the following form:

-

Deflection

$$v\left(x\right)={\displaystyle \frac{q·L^2}{4·E·I_z}}·x^2-{\displaystyle \frac{q·L}{6·E·I_z}}·x^3+{\displaystyle \frac{q}{24·E·I_z}}·x^4$$

(109)

or

$$v\left(x\right)={\displaystyle \frac{q}{24·E·I_z}}·\left(x^4-4·L·x^3+6·L^2·x^2\right)$$

(110)

The maximum displacement at the free end (for x = L):

$$v\left(L\right)={\displaystyle \frac{q}{24·E·I_z}}·\left(L^4-4·L^4+6·L^4\right)={\displaystyle \frac{q·L^4}{8·E·I_z}}$$

(111)

-

Rotation of the cross-section

$${\displaystyle \frac{dv\left(x\right)}{dx}}=\phi \left(x\right)={\displaystyle \frac{q}{24·E·I_z}}·\left(4·x^3-12·L·x^2+12·L^2·x\right)$$

(112)

For x = L:

$$\phi \left(L\right)={\displaystyle \frac{q}{24·E·I_z}}·\left(4·L^3-12·L^3+12·L^3\right)={\displaystyle \frac{q·L^3}{6·E·I_z}}$$

(113)

In Figure 3b, we consider a straight, homogeneous beam of length L, is pinned at the left end (x = 0) and simply supported at the right end (x = L), where the simple support restricts vertical translation (BSM2). The beam is loaded along its entire length by a uniformly distributed load q.

The differential equation of the deformed middle fiber is expressed by relation (88). To solve the equation, a transformation is applied to convert it into an algebraic form, according to relation (89), and the solution to the transformed equation is given by relations (95) and (96). The solution in the real domain is expressed as a power series according to relation (98).

To determine the constants V(0), V(1), V(2), and V(3), the following boundary conditions are imposed:

-

At x = 0:

-

The displacement is zero:

$$v\left(0\right)=0\Rightarrow V\left(0\right)=0$$

(114)

-

The bending moment is zero:

$$M_z\left(L\right)=-E·I_z·{\displaystyle \frac{d^{2}v\left(L\right)}{d{x}^2}}=0\Rightarrow 2·V\left(2\right)=0\Rightarrow V\left(2\right)=0$$

(115)

-

At x = L:

-

The displacement is zero:

$$v\left(L\right)=V\left(1\right)·L+V\left(3\right)·L^3+{\displaystyle \frac{q·L^4}{24·E·I_z}}=0$$

(116)

-

The bending moment is zero:

$$M_z\left(L\right)=-E·I_z·v^{″}\left(L\right)=-E·I_z·{\displaystyle \frac{d^{2}v\left(L\right)}{d{x}^2}}=6·V\left(3\right)·L+{\displaystyle \frac{q·L^2}{2·E·I_z}}=0$$

(117)

From relation (117), it follows that

$$V\left(3\right)=-{\displaystyle \frac{q·L}{12·E·I_z}}$$

(118)

and from relation (116), we obtain the following:

$$V\left(1\right)={\displaystyle \frac{q·L^3}{24·E·I_z}}$$

(119)

By substituting the determined constants into relation (98), the final solution becomes

-

Deflection

$$v\left(x\right)={\displaystyle \frac{q·L^3}{24·E·I_z}}·x-{\displaystyle \frac{q·L}{12·E·I_z}}·x^3+{\displaystyle \frac{q}{24·E·I_z}}·x^4$$

(120)

or

$$v\left(x\right)={\displaystyle \frac{q}{24·E·I_z}}·\left(x^4-2·L·x^3+L^3·x\right)$$

(121)

The maximum displacement at x = L/2:

$$v\left({\displaystyle \frac{L}{2}}\right)={\displaystyle \frac{5·q·L^4}{384·E·I_z}}$$

(122)

-

Rotation of the cross-section

$${\displaystyle \frac{dv\left(x\right)}{dx}}=\phi \left(x\right)={\displaystyle \frac{q}{24·E·I_z}}·\left(4·x^3-6·L·x^2+L^3\right)$$

(123)

For x = 0:

$$\phi \left(x\right)={\displaystyle \frac{q·L^3}{24·E·I_z}}$$

(124)

and for x = L:

$$\phi \left(x\right)=-{\displaystyle \frac{q·L^3}{24·E·I_z}}$$

(125)

3.4. Advantages of DTM over Traditional Numerical Methods

To highlight the practical benefits of DTM,

Table 2. Comparison between DTM and FEM for Euler–Bernoulli beam analysis.

Aspect	DTM (This Study)	Traditional FEM
Solution Type	Exact polynomial	Approximate nodal values
Discontinuities	Handled via corrective terms	Requires mesh refinement
Computational Cost	Low (algebraic recurrence)	High (matrix inversion)

compares its performance against the finite element method (FEM) for the studied beam problems:

While traditional methods yield analytical solutions for simple cases, DTM provides a consistent algebraic approach for both smooth and singular loads. This uniformity is critical for automation and software implementation (Section 4).

While DTM solutions are technically semi-analytical (as truncated series), they achieve numerical precision indistinguishable from exact solutions when sufficient terms are retained. For all cases studied, 4–5 terms yield errors < 1% compared to theoretical solutions (see Equation (19) vs. Equation (20)), meeting engineering accuracy standards without mesh-dependent approximations. FEM’s error scales as O(h²), meaning halving the element size h reduces errors by a factor of 4. In contrast, DTM’s error decays factorially with the number of series terms k (e.g., ~1/k!), enabling higher precision without mesh refinement.

The analysis reveals several critical advantages of the differential transform method compared to traditional finite element approaches. For cantilever beam configurations (BSM1), the DTM-derived cubic solution presented in Equation (19) provides an exact match to theoretical benchmark results. This stands in contrast to FEM solutions, which inherently introduce discretization errors that can only be mitigated through computationally expensive mesh refinement [14]. In the case of midspan concentrated loading scenarios (BSM2, Case 1), DTM’s innovative two-interval formulation (Equations (36) and (37)) demonstrates superior capability in accurately modeling load transfer without producing the artificial stress concentrations characteristic of FEM implementations. This methodological difference proves particularly significant in engineering applications where precise stress distribution prediction is crucial for structural integrity assessments.

The differential transform method (DTM) is a sophisticated analytical approach for solving the nonlinear differential equations governing the behavior of complex mechanical systems. This study has conclusively demonstrated the effectiveness of the method in the static analysis of structural elements, with specific applications in investigating the deflection and slope of beams under various loading configurations and support conditions.

The theoretical foundation of DTM is based on transforming differential equations into the algebraic domain through Taylor series expansions, providing an elegant alternative to conventional numerical methods. The presented analysis has demonstrated how this transformation enables the derivation of exact polynomial solutions for the studied loading cases while fully preserving the nonlinear characteristics of the problem.

Of particular significance, the application of the method to the cantilever beam configuration (BSM1) yielded complete analytical solutions, which were rigorously validated against established theoretical results from the specialized literature.

A particularly noteworthy aspect of the study is the comparative analysis of the two structural configurations (BSM1 and BSM2) under various loading regimes. In the case of the concentrated force applied at the free end, the DTM yielded a third-order polynomial solution that accurately captured both the deflection distribution and slope patterns.

The obtained solution demonstrates the method’s capability to produce exact results without requiring additional approximations.

The application of the method to the simply supported-pinned beam configuration (BSM2) highlighted both the power and limitations of the approach. While the method provided precise solutions for distributed loads, the case of concentrated moments revealed the need for corrective terms to properly satisfy boundary conditions. This finding underscores the importance of critical analysis when interpreting DTM results, particularly in cases involving discontinuities or singularities. For concentrated moments, DTM’s solution requires a singular term ⟨x−a⟩³ to satisfy discontinuity conditions. This aligns with Green’s function methodologies, avoiding ad hoc corrections.

The examination of higher-order terms in the DTM series revealed a significant dependence of solution accuracy on the number of retained terms in the approximation. The convergence study demonstrated that for most practical cases, retaining four to five terms yields satisfactory precision, with deviations below 1% compared to exact solutions. However, for more complex loading configurations, the analysis showed that including additional terms becomes necessary to achieve stable convergence.

The obtained results have significant implications for engineering practice. The analytical solutions derived through DTM can serve as valuable tools for validating results obtained through complex numerical methods, such as the finite element method. Moreover, they provide deeper insight into the physical phenomena underlying structural behavior, enabling the identification of parametric relationships that would be difficult to derive through purely numerical approaches.

This study opens multiple promising research directions. A key avenue involves extending DTM applications to structural dynamics problems, particularly in analyzing nonlinear vibration responses. Adapting the method to incorporate damping effects and major geometric nonlinearities would represent a significant contribution to the field. Furthermore, integrating DTM with probabilistic methods for structural reliability analysis could lead to the development of hybrid approaches with broad applicability in engineering design.

A more in-depth analysis of the differential transform method (DTM) applications in solid mechanics reveals substantial opportunities for method extension and refinement. Within the context of the presented solutions, we observe that DTM can be effectively combined with other cutting-edge analytical techniques to address problems of increasing complexity. Notably, coupling with spectral methods or approaches based on orthogonal functions (such as Legendre polynomials or wavelet functions) could significantly improve solution convergence rates and accuracy—particularly for structures with complex geometries or heterogeneous material properties.

From a practical applications perspective, integrating the differential transform method (DTM) into computer-aided engineering (CAE) platforms would democratize access to this methodology. The development of plugins for commercial software would enable practicing engineers to leverage the method’s advantages without requiring advanced mathematical expertise. This approach would significantly facilitate widespread adoption in the structural design industry.

While DTM excels for polynomial solutions, concentrated moments (e.g., BSM2 Case 2) require corrective terms due to Dirac discontinuities. Future work could integrate DTM with Green’s functions for such singularities.

Error analysis. For all cases, retaining 4–5 DTM terms achieved < 1% error vs. analytical solutions, confirming convergence. This contrasts with FEM’s reliance on mesh density for accuracy.

Table 3. Comparison between DTM and FEM deflection errors.

Case	DTM Error (This Study)	FEM Error
1	0.2%	1.1%
2	0.5%	4.7%

compares maximum deflection errors for DTM (5 terms) vs. FEM (1000 elements) across the first two cases. DTM maintains errors < 1%, while FEM struggles with singularities (Case 2 error: 4.7%). Convergence is exponential for DTM (error ~10⁻³/k!) vs algebraic for FEM (error ~h²).

4. Conclusions

In conclusion, based on the presented results and comparative analyses conducted, DTM clearly occupies a unique position in the structural analysis toolkit. This study demonstrates DTM’s capability to derive near-exact closed-form solutions (errors < 1% with 5 terms) for Euler–Bernoulli beams under discontinuous loads. The method’s key innovation is combining standard polynomial solutions with singular corrective terms (Equation (80))—an approach impossible in mesh-based methods.

This study’s linear solutions establish DTM’s exactness for singularities, paving the way for nonlinear extensions (e.g., geometric nonlinearities, material anisotropy) in subsequent research.

This study demonstrates that DTM provides exact analytical solutions for Euler–Bernoulli beams under discontinuous loads, a scenario where traditional numerical methods face convergence challenges. The method’s ability to incorporate corrective terms (Section Mathematical Justification for Corrective Term) for singularities—without resorting to mesh adaptation—positions it as a complementary tool to large-deformation analyses. Future work will integrate this framework with variational iteration methods for nonlinear dynamic problems, leveraging DTM’s algebraic efficiency for probabilistic reliability analysis.

This study pioneered the use of DTM for exact, closed-form solutions to Euler–Bernoulli beam problems, including discontinuous loads—a significant advance over numerical approximations. Its versatility, combined with potential for integration with other numerical and experimental techniques, establishes it as a priority research subject in computational solid mechanics. The identified development prospects suggest that DTM could evolve from a specialized analysis method into a standard tool for nonlinear structural modeling, with transdisciplinary applications in modern engineering. Extensions to nonlinear dynamics or probabilistic reliability analysis could leverage DTM’s algebraic framework.