Abstract
Seismic retrofitting of reinforced concrete (RC) structures is essential for improving resilience and extending service life, particularly in regions with outdated building codes. However, selecting the optimal retrofitting strategy requires balancing multiple interdependent sustainability criteria—economic, environmental, and social—under expert-based uncertainty. This study presents a fuzzy hybrid multi-criteria decision-making (MCDM) approach that combines DEMATEL, DANP, and TOPSIS to represent causal interdependencies, derive interlinked priority weights, and rank retrofit alternatives. The assessment applies three complementary life cycle-based tools—cost-based, environmental, and social sustainability analyses following LCCA, LCA, and S-LCA frameworks, respectively—to evaluate three commonly used retrofitting strategies: RC jacketing, steel jacketing, and carbon fiber-reinforced polymer (CFRP) wrapping. The fuzzy-DANP methodology enables accurate modeling of feedback among sustainability dimensions and improves expert consensus through causal mapping. The findings identify CFRP as the top-ranked alternative, primarily attributed to its enhanced performance in both environmental and social aspects. The model’s robustness is confirmed via sensitivity analysis and cross-method validation. This mathematically grounded framework offers a reproducible and interpretable tool for decision-makers in civil infrastructure, enabling sustainability-oriented retrofitting under uncertainty.
Keywords:
fuzzy MCDM; DEMATEL-ANP; life cycle assessment; seismic retrofit; sustainability; uncertainty modeling; circular economy; reinforced concrete; decision-making; multi-criteria analysis MSC:
90C70; 90C29; 90C30; 90C90
1. Introduction
Achieving sustainable and resilient infrastructure requires decision-making strategies that ensure structural safety and optimize environmental and social outcomes across the building life cycle. In seismic-prone regions, retrofitting existing reinforced concrete (RC) buildings has gained priority over demolition, as it offers both environmental and economic advantages by extending service life and reducing resource consumption and carbon emissions [1]. Many of these buildings were constructed before implementing modern seismic codes, particularly in low- and middle-income countries where construction practices often lack technical supervision [2]. As a result, load-bearing elements—especially RC columns—frequently exhibit structural deficiencies that necessitate targeted retrofitting interventions. Standard retrofit techniques include concrete confinement with RC overlays, steel encasement techniques, and fiber-reinforced polymer (FRP) laminates, which are recognized for improving seismic performance [3,4].
In response, governmental bodies and researchers have promoted updated design codes, zoning regulations, and best practices to improve the safety of existing structures [5]. More recently, circular economy (CE) principles have been introduced into the retrofitting paradigm to minimize demolition waste, promote material reuse, and support long-term sustainability [6]. Such strategies are aligned with international decarbonization goals, particularly in the context of the cement industry, which accounts for approximately 8% of global CO2 emissions [7]. Sustainability-oriented retrofit decisions are consistent with the Sustainable Development Goals (SDGs) [8].
Reusing existing building stock is an effective way to reduce embodied carbon and construction-related emissions [9]. However, given the large number of structures requiring seismic upgrades, the overall environmental impact of widespread retrofitting can still be significant [10]. Despite growing interest in sustainability assessments, Life Cycle Assessment (LCA) methods remain underutilized in retrofitting compared to new construction [11,12]. Although Life Cycle Costing (LCC) and Environmental LCA have been applied in seismic retrofit studies [13,14,15], the social dimension remains underdeveloped in methodology and implementation.
Social Life Cycle Assessment (S-LCA), a method to evaluate social impacts of products and processes, still faces key challenges such as fragmented indicators, limited stakeholder involvement, and inconsistent methodologies [16]. Leichter and Picardo [17] observed that the social dimension is frequently omitted from retrofit evaluations due to the absence of universally accepted S-LCA frameworks. This omission limits the comprehensiveness of Life Cycle Sustainability Assessments and weakens the analytical basis for socially informed decisions.
Compounding these limitations is the challenge of making decisions under uncertainty, limited budgets, and conflicting objectives. In such multi-dimensional scenarios, traditional single-criterion optimization is insufficient [18]. Multi-criteria decision-making (MCDM) techniques have become crucial for evaluating retrofit strategies across heterogeneous criteria [19]. These include economic performance, structural functionality, and environmental impact, as shown in studies by Formisano et al. [20], Fiore et al. [21], and Santa-Cruz et al. [22]. Life Cycle-based Assessments have also been combined with MCDM to support strategy evaluation [23,24,25].
Among the most common MCDM techniques, the Analytic Hierarchy Process (AHP) and the TOPSIS method (Technique for Preference by Similarity to an Ideal Solution) are often preferred for their interpretability and low input burden [26]. However, both methods typically assume that evaluation criteria are independent—an assumption rarely satisfied in sustainability modeling, where trade-offs and interrelations are the norm [27].
The Analytic Network Process (ANP) method mitigates this constraint by enabling interactions between criteria through a network structure, albeit at the cost of significantly increasing the number of pairwise comparisons required [28]. To alleviate this burden, the Decision-Making Trial and Evaluation Laboratory (DEMATEL) approach is commonly combined with the ANP in the form of the DANP framework, which captures causal relationships and relative importance among criteria [29]. These methods have been widely adopted in sustainability research domains. Classical applications of the ANP and DANP have been used in urban renewal [30] and green building performance evaluation [31], where modeling interdependencies enhances the explanatory power of MCDM models.
To account for vagueness and subjective uncertainty inherent in expert judgments, fuzzy set theory—mainly triangular fuzzy numbers—has been integrated with these methods. The resulting fuzzy ANP, fuzzy DEMATEL, and fuzzy DANP methods improve robustness and realism in the presence of linguistic ambiguity. Such fuzzy-hybrid approaches have proven effective across diverse domains, including renewable energy supplier selection [32], sustainable rental housing planning [33], smart manufacturing assessment [34], and business information system evaluation [35]. The practical strength of fuzzy-DANP has also been demonstrated in innovation assessment for sustainable construction in developing countries [36,37]. Table 1 summarizes representative studies addressing seismic retrofitting and sustainability-oriented MCDM frameworks, highlighting their scope, methodological tools, and main outcomes.

Table 1.
Summary of studies on sustainability-oriented seismic retrofit decisions.
Despite these advances, few studies have applied fuzzy-DANP with LCA methods to address seismic retrofitting problems. In particular, there is limited evidence of frameworks that simultaneously model interdependencies among sustainability dimensions and handle expert-based uncertainty.
This study addresses these limitations by simultaneously (i) integrating economic, environmental, and social pillars via LCC, LCA, and S-LCA; (ii) applying fuzzy-DANP to model interdependencies under uncertainty; and (iii) validating results with both compensatory and non-compensatory MCDM techniques.
In response to these gaps, this work introduces a hierarchical MCDM framework integrating fuzzy-DANP with Life Cycle Assessment methods. The proposed model evaluates and ranks seismic retrofitting strategies for RC columns with inadequate confinement based on sustainability’s economic, ecological, and societal pillars. Specifically, this study seeks to (1) model the causal relationships among sustainability criteria through fuzzy DEMATEL and DANP modeling; (2) assess the performance of retrofitting alternatives through LCCA, LCA, and S-LCA; and (3) prioritize seismic retrofit strategies using the TOPSIS method under fuzzy-weighted criteria.
2. Mathematical Framework and Decision-Making Methodology
A four-phase methodological framework was developed to determine the optimal retrofitting alternative by integrating sustainability’s economic, environmental, and social dimensions. This framework enables a structured assessment of the chosen criteria based on life cycle methodologies. It supports the identification of interrelationships among sustainability indicators, the calculation of their relative importance, and the ranking of retrofitting strategies. Figure 1 presents the methodological sequence, organized into four main stages.
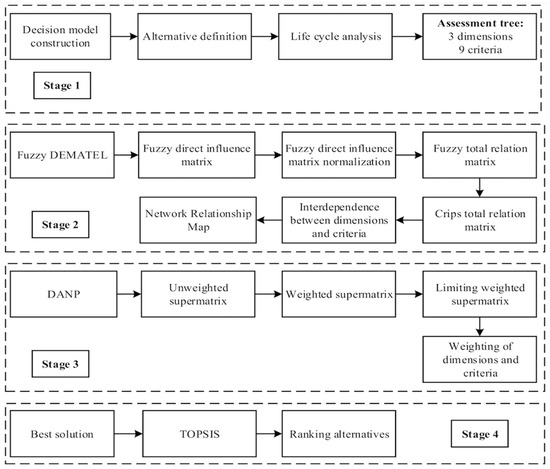
Figure 1.
Fuzzy DEMATEL–DANP–TOPSIS decision framework.
During the initial stage, the decision model was established by identifying and selecting nine pertinent criteria, each reflecting a distinct facet of sustainability. In the second stage, the fuzzy DEMATEL method was applied to construct the network relationship map (NRM), revealing the cause-and-effect links between the various dimensions and evaluation criteria. The third phase utilized the DANP approach to calculate the importance levels of each criterion, taking into account their interrelated influences. Finally, the TOPSIS technique was used to rank the retrofitting alternatives based on sustainability considerations.
2.1. Life Cycle-Based Multi-Dimensional Decision Model
The decision model integrates nine sustainability criteria, classified into three dimensions—economic, environmental, and social—based on life cycle-based assessments. The model adopts a cradle-to-grave perspective, encompassing all relevant phases: material production, transportation, construction and installation, preventive maintenance, and end-of-life (EoL) processes. Each criterion was carefully selected to reflect sustainability performance throughout service life. This structure ensures technical comparability of retrofitting options and considers long-term impacts.
2.2. Interdependency Modeling via Fuzzy DEMATEL
Alternative methods, such as Interpretive Structural Modeling (ISM), Structural Equation Modeling (SEM), Bayesian networks, or cognitive mapping, were considered; however, they either lack quantitative weighting capabilities or do not explicitly capture bidirectional influences among criteria. The DANP approach integrates DEMATEL’s ability to map cause-and-effect relationships with ANP’s network-based weighting scheme, enabling a reduction in the number of required pairwise comparisons while retaining the capacity to model feedback loops. This balance between analytical rigor and respondent effort has been highlighted in the sustainability assessment literature as a key factor for ensuring expert participation and consistent judgments.
Four main approaches represent the fusion of DEMATEL and ANP techniques: ANP utilizing normalized relationship matrices, ANP that models internal dependencies, cluster-weighted ANP, and the DANP method that integrates these elements [29]. DANP builds upon the strengths of both DEMATEL and ANP, offering a structured mechanism to address interdependencies within multi-criteria systems. By utilizing a total influence matrix, this method reduces the cognitive complexity associated with conventional pairwise comparisons in ANP, allowing for the concurrent modeling of cause–effect interactions among criteria [36]. Nonetheless, DANP alone cannot handle the linguistic vagueness or epistemic uncertainty inherent in expert judgments. As conventional MCDA techniques struggle to capture such imprecision, the integration of fuzzy logic improves representational accuracy [37].
Triangular fuzzy numbers (TFNs) were adopted due to their simplicity in representing linguistic terms, reduced computational complexity compared to trapezoidal or Gaussian fuzzy numbers, and proven performance in engineering decision contexts where expert judgments are expressed qualitatively. TFNs require fewer parameters to model uncertainty, which minimizes elicitation burden on experts while preserving sufficient accuracy for ranking and weighting purposes. This choice aligns with numerous sustainability-oriented MCDM studies in the construction sector that report high interpretability and robust aggregation properties when TFNs are applied to pairwise comparison data.
2.2.1. Construction of the Expert-Derived Fuzzy Influence Matrix
The direct influence matrix A = [aij]nxn is meticulously constructed utilizing a calibrated five-point ordinal scale, spanning from 0 (denoting no influence) to 4 (signifying powerful influence). Subject matter experts employ this scale to rigorously evaluate the pairwise direct effects exerted by one dimension or criterion upon another. Table 2 delineates the associated fuzzy linguistic scale, wherein qualitative judgments are systematically transformed into TFNs expressed as triplets (l, m, n) [38]. Each matrix entry aij quantitatively represents the magnitude of influence the element ai imposes on element aj. Separate and specialized influence matrices are independently developed for the overarching sustainability dimensions and the granular evaluation criteria to ensure precision in capturing interdependencies. The final aggregated fuzzy influence matrices were obtained using the fuzzy average operator applied component-wise to the triangular parameters (l, m, u), a method widely adopted in fuzzy MCDM to preserve the shape and interpretability of expert-based distributions. Tables S1 and S2 (Supplementary Materials) present the complete set of fuzzy direct influence matrices obtained from each expert before aggregation. For transparency, Table S1 presents the dimension-level fuzzy direct influence matrices, and Table S2 for criteria, illustrating the conversion of linguistic terms to triangular fuzzy numbers, as described in Table 2.

Table 2.
Fuzzy scale for evaluating expert influence.
2.2.2. Normalization of Fuzzy Influence Values
The matrix A is multiplied by a normalization factor s, using Equations (1) and (2), to obtain the normalized influence matrix of the dimensions/criteria.
2.2.3. Computation and Defuzzification of the Total Influence Matrix
The fuzzy direct relationship matrix is developed based on Equation (3). To extract the crisp values for the total relationship matrix Tf, the CFCS (Converting the Fuzzy Data into Crisp Scores) method introduced by Opricovic and Tzeng [39] was utilized. This technique has proven efficient for defuzzification in MCDM models that integrate crisp and fuzzy criteria. The defuzzified total relationship matrix T was constructed for the dimensions and criteria.
2.2.4. Deriving Centrality and Causality from the Influence Structure
In the total relationship matrix T, the influence of the ith dimension/group on the jth dimension/group is represented by tij. The total relationship matrix for dimensions is designated TD, while that for criteria is designated TC. To ascertain the most influential and most affected values, the row and column values of the total relationship matrix are summed by Equations (4) and (5). The row totals, named D, express the cumulative effect a given factor imposes on others. Conversely, the column totals, known as R, indicate the aggregate influence that factor experiences from the rest. The NRM plots (D + R) along the x-axis measure the overall intensity of influences both given and received, known as centrality or prominence. Meanwhile, (D − R) is plotted on the y-axis and termed relation, which allows the classification of factors into cause-and-effect groups. A positive value means the factor is a cause; a negative value means it is an effect.
2.3. Deriving Interdependent Weights Using DANP
A total relationship matrix was constructed for the dimensions (TD) and criteria (TC). The NRM of the ANP was captured using the fuzzy DEMATEL for the dimensions and criteria. The following section will present an overview of the fundamental steps to applying the DANP method [29].
2.3.1. Construction of the Unweighted Supermatrix
The matrix TC, associated with the matrix TD, is called Equation (6). First, a normalized total relationship matrix is constructed by normalizing each submatrix. The sum of the rows of each submatrix in the TC is used to obtain a value, and then each row is divided by this value to achieve normalization. Next, the unweighted supermatrix is formed by transposing each block within the normalized total relationship matrix, resulting in the matrix WC, as defined in Equation (7).
2.3.2. Weighting via Dimension-Adjusted Supermatrix
In the direct relationship matrix for the dimensions, a threshold value is established following the creation of the total relationship matrix, where minor effects are disregarded [29]. To obtain an appropriate NRM, the decision-maker (DM) needs to determine a threshold value ρ representing the minimum level of influence. If this threshold is set too low, the resulting map becomes overly complex, making it difficult to extract relevant information. Conversely, if the threshold is too high, many elements become isolated, losing their connections with other factors [40]. Within the total relationship matrix TD for the dimensions, influences below the threshold are set to zero. Afterwards, the sums of each row in this modified matrix are calculated and used to generate the normalized total relationship matrix by dividing each element by its respective row sum, as indicated in Equation (8). This normalized matrix is then utilized to weight the unweighted supermatrix, resulting in the weighted supermatrix WW, as defined by Equation (9).
2.3.3. Convergence to the Limiting Supermatrix of Global Weights
The weighted supermatrix is a stochastic matrix with positive values in each column, where each column is normalized so that its elements sum to one. By iteratively multiplying the matrix WW by itself, the process continues until the matrix stabilizes—meaning further multiplications no longer cause significant changes. The limiting supermatrix has identical columns that capture the final priority weights, reflecting the elements’ relative importance and interdependencies.
2.4. Prioritization of Retrofit Alternatives via TOPSIS Ranking
The TOPSIS method [41] evaluated and selected the optimal alternative. TOPSIS has proven to be an effective method for evaluating retrofitting alternatives in seismic decision-making contexts, as noted by Caterino and Cosenza [42]. The method assesses each option based on its relative closeness to the ideal solution ( and distance from the least favorable scenario (. This is quantified through the performance index , which integrates both aspects to rank alternatives comprehensively.
3. Case Study: Fuzzy MCDM for Retrofit Evaluation
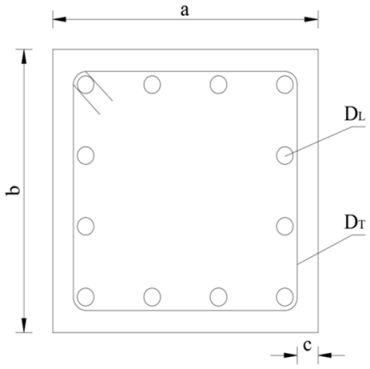
Adopting a comprehensive systems approach, this study seeks to determine the most appropriate seismic retrofit solution for reinforced concrete columns in high-seismicity areas. One of the most common structural deficiencies in such contexts is inadequate transverse reinforcement, which significantly compromises ductility and performance under cyclic loading [43]. This research builds on the column and retrofit methods previously proposed by Villalba et al. [25]; however, their study did not address social life cycle factors, cross-dimensional dependencies, or uncertainties based on expert opinions. The column under consideration is a centrally located first-story column in a four-story reinforced concrete structure in Quito, Ecuador—a city exposed to high seismicity and volcanic risk, with a substantial stock of non-engineered buildings [44]. The functional unit corresponds to a retrofitted reinforced concrete column, with all alternatives designed to achieve equivalent structural performance over a 50-year service life. Table 3 summarizes the key characteristics of the column to be retrofitted.

Table 3.
Main parameters of the reinforced concrete column.
The first retrofitting strategy involves a reinforced concrete jacket (RC) with a 75 mm thickness, compressive strength of 32 MPa, and 12 longitudinal Ø12 mm rebars complemented by Ø10 mm stirrups at 75 mm spacing. A structural adhesive enhances the bond between the new and existing concrete. The second option is a welded steel jacket (ST) composed of 4 mm thick ASTM A572 Grade 50 steel plates, fully adhered using structural epoxy. The third alternative utilizes a carbon fiber-reinforced polymer (CFRP) wrapping system, composed of two layers of unidirectional carbon fabric (0.333 mm thickness, 3800 MPa tensile strength, and 1.55% elongation at break). All retrofitting strategies incorporate specific maintenance measures to ensure long-term performance and user safety [45]. These strategies include targeted maintenance actions such as carbonation prevention for reinforced concrete, anti-corrosion coatings for steel components, and fire-resistant mortar applied to steel and CFRP retrofit options.
The analysis follows a cradle-to-grave approach, encompassing stages such as resource extraction, construction activities, transportation, routine maintenance, and EoL management. Nine criteria were selected to represent sustainability’s economic, environmental, and social dimensions. Priority was given to user-centric factors: comfort, architectural compatibility, and minimal disruption [26].
3.1. Evaluation of Economic Impacts via Life Cycle Cost Assessment
Villalba et al. [25] updated cost data for each alternative using the CYPE construction cost database. The LCC includes design and testing (semi-destructive tests, quality control), construction (materials, equipment, labor), preventive maintenance, and EoL activities such as demolition, transport, and recycling or disposal. Future costs were discounted at 2% to reflect social discounting principles aligned with intergenerational equity [46]. Three economic criteria were considered: design/testing (Q1), construction (Q2), and maintenance and EoL costs (Q3).
3.2. Analyzing Environmental Impacts Using Life Cycle Analysis
The environmental impact assessment utilized LCA data from Villalba et al. [25], considering four key life cycle stages: material production, transportation, construction and maintenance, and EoL disposal. A zero discount rate was applied to prevent distortions in impacts occurring beyond a 100-year horizon [47]. Inventory information was obtained from the BEDEC and Ecoinvent databases, and modeling was conducted using the OpenLCA 2.0.4 software. The ReCiPe Endpoint method (H/H perspective) was employed, addressing three impact categories: ecosystem quality (measured in species·year, Q4), human health (DALYs, Q5), and resource scarcity (USD, Q6).
3.3. Assessment of Social Performance Through Social Life Cycle Assessment
Although developing within the construction industry, S-LCA faces challenges such as limited data availability and the absence of standardized indicators [48,49]. This research used the SOCA v2 database—combined with PSILCA and Ecoinvent—to ensure methodological alignment with the environmental LCA [50]. A cradle-to-grave perspective guided the analysis. The CFRP data were derived from aviation-grade sources and adjusted using the work of Akbar and Liew [51] to reflect composite materials for building applications. Due to a lack of region-specific data, global averages were adopted [52].
The Social Impact Weighting Methodology generated 55 indicators, categorized into four stakeholder groups: Workers, Value Chain Actors, Society, and Local Community. These were further broken down into 20 social subcategories, addressing issues such as child labor, workplace safety, corruption, and Indigenous rights [53]. All social impacts were measured using the Mean Risk per Hour (MRH) method, which allows a comparison among retrofit options. For analysis purposes, impacts were grouped into two combined criteria: Local Community and Workers (Q7), and Society and Value Chain Actors (Q8). The third social criterion is functionality (Q9), assessed via architectural impact and construction time. Architectural compatibility was rated through AHP-based pairwise comparison using expert judgments from Villalba et al. [25]. Construction time was extracted and normalized from Pour [54]. These indicators are among the most recurrent in the social retrofit MCDM literature [26].
3.4. Aggregation of Weighted Criteria and Final Decision
The decision model integrates three sustainability dimensions through nine representative criteria: three each for economic (Q1–Q3), environmental (Q4–Q6), and social (Q7–Q9) pillars. Experts were selected using purposive sampling to ensure academic and professional practice representation. Inclusion criteria comprised (i) at least 8 years of experience in seismic structural engineering, retrofitting, or sustainability assessment; (ii) documented participation in retrofit projects or peer-reviewed publications in the field; and (iii) familiarity with multi-criteria decision-making tools. The final panel included five structural engineers and one architect, with combined expertise covering LCC, LCA, and S-LCA applications in the built environment. The weighting process used fuzzy-DEMATEL, where TFNs mitigate subjectivity and capture cognitive vagueness.
Table 4 provides a summary of the impact values corresponding to all criteria and alternatives. The subsequent steps (Section 4 and Section 5) used these values to determine the alternatives’ global priorities and rankings. The model configuration adheres to recent advances in MCDM frameworks that integrate fuzziness, causality, and sustainability simultaneously, comparable to the hybrid ANP-ELECTRE IS system developed by Sánchez-Garrido et al. [55], albeit adapted here for interdependent and uncertain criteria using fuzzy-DANP.

Table 4.
Multi-dimensional impact assessment of seismic retrofit options.
4. Analysis of the Results
4.1. Causal Structure of Sustainability Criteria via Fuzzy DEMATEL
Using the established decision model, the three sustainability dimensions and their nine related criteria were assessed through the fuzzy DEMATEL approach. The analysis began with constructing non-negative influence matrices (3 × 3 for sustainability dimensions and 9 × 9 for criteria), representing the direct and indirect relationships among the elements. Table 5 presents the defuzzified total relationship matrix for the dimensions, obtained via Equations (1)–(3). To enhance interpretability, a threshold value ρ was applied—computed as the average of the matrix elements (1.0486)—following the guidance of Sufiyan et al. [38] in similar applications in sustainability modeling.

Table 5.
Aggregated influence matrix among sustainability dimensions.
The results indicate that the economic dimension exerts the most decisive influence on the social dimension, followed—though less intensely—by its impact on the environmental dimension. Conversely, the environmental dimension affects only the social dimension. In contrast, the social dimension exhibits mutual interactions with economic and environmental components, emphasizing its integrative and reactive character within the system.
Table 6 provides the total relationship matrix at the criteria level, highlighting in bold those elements exceeding the threshold (0.0912), which were used to construct the NRM. These values define the directionality of influence arrows in the NRM (Figure 2), helping to visualize the causal hierarchy among indicators.

Table 6.
Total influence matrix among sustainability criteria.
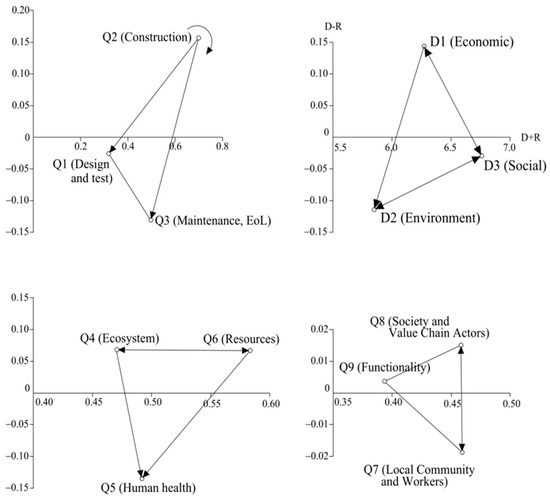
Figure 2.
Causal network of sustainability criteria based on fuzzy DEMATEL.
The (D + R) and (D − R) indicators in Table 7 quantify each element’s relative importance and causality. Among the three dimensions, the social dimension exhibits the highest centrality (D + R), followed by the economic and environmental dimensions. The economic dimension acts predominantly as a causal driver, while the social and environmental dimensions behave more as dependent effects.

Table 7.
Centrality and causality scores of dimensions and criteria.
At the criteria level, the most influential elements (high D values) are construction costs, resources, ecosystems, society, and value chain actors. High dependence (R values) is observed for maintenance and end-of-life costs, human health, and construction costs. Construction costs exhibit the highest centrality overall, underscoring their dual role as cause and effect in system dynamics.
Figure 2 displays the NRM constructed from Table 6, where only relationships exceeding the influence threshold are shown to improve visual clarity. This graphical representation provides an intuitive understanding of causal interactions and is aligned with prior studies advocating hybrid MCDM frameworks with visual tools, such as Sánchez-Garrido et al. [55].
Further disaggregation reveals that construction costs (Q2) are the principal driver within the economic dimension, whereas maintenance and EoL costs are primarily dependent factors. Resources and ecosystems act as dominant causes in the environmental dimension, while human health is influenced. In the social dimension, the functionality criterion—although not central—exerts a measurable influence on construction costs, suggesting a link between architectural design decisions and economic performance.
4.2. Final Global Weights Derived from the Fuzzy-DEMATEL-DANP Supermatrix
The unweighted supermatrix Wc, generated via Equation (7) and shown in Table 8, was adjusted using the weighting coefficients from Table 6. It was then normalized following Equations (8) and (9). After raising the matrix to the sixth power, it converged to a stable steady-state form, allowing for the extraction of local and global weights (see Table 9).

Table 8.
Unweighted supermatrix from fuzzy DEMATEL-DANP.

Table 9.
Weight allocation across dimensions and associated indicators.
The results confirm the relative importance of the sustainability dimensions, with the social dimension holding the highest weight (0.4462), followed by the environmental (0.3225) and economic (0.2313) dimensions. Within the economic group, construction costs (Q2) dominate, while resources (Q6) lead the environmental criteria. In the social domain, the most influential elements are local community and workers (Q7), society and value chain actors (Q8), followed by social functionality (Q9).
The five most influential criteria overall—based on global weights—are as follows:
- Local community and workers (Q7);
- Society and value chain actors (Q8);
- Resources (Q6);
- Functionality (Q9);
- Construction costs (Q2).
This result emphasizes the preeminence of social criteria in retrofit decision-making, especially when uncertainty and interdependencies are explicitly modeled through fuzzy-DANP.
4.3. Ranking of Retrofit Strategies Based on TOPSIS Closeness Coefficients
The initial evaluation involved a disaggregated analysis of life cycle components: economic, environmental, and social indicators. Figure 3 summarizes the performance of each retrofitting alternative (RC, ST, CFRP) under these three dimensions.
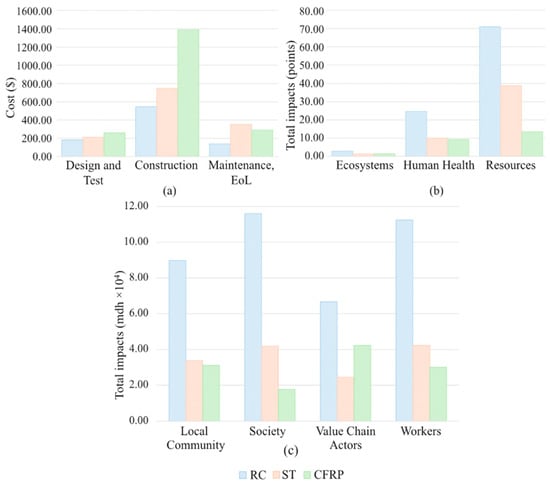
Figure 3.
Outcomes of the life cycle analyses. (a) LCC. (b) LCA. (c) S-LCA.
From an economic standpoint, RC is the most cost-effective option, showing a superior performance across all life cycle stages. In contrast, ST shows higher costs at all stages, with particularly high EoL expenditures. CFRP exhibits the highest upfront cost—154% greater than RC—but potentially compensates through a superior performance in environmental and social criteria.
Regarding environmental impact, all strategies exhibit their highest burdens in the resource depletion category, followed by human health impacts. RC performs the worst across all metrics. ST and CFRP reduce human health impacts by up to 59% and 62%, respectively, with CFRP also achieving an 81% reduction in resource-related impacts.
Regarding social performance, RC again performs the worst, especially concerning society and workers. ST provides a 63% reduction in social impact, while CFRP achieves the best overall social performance, with up to an 85% improvement in the society category. Interestingly, ST slightly outperforms CFRP in the value chain actor criterion.
Figure 4 displays the normalized performance of each alternative across the nine criteria. RC scores lowest in all economic indicators but highest in environmental and social impacts. CFRP exhibits strong results in key environmental areas (resources, human health) and excels in social indicators, particularly functionality, due to a shorter construction time and reduced disruption.
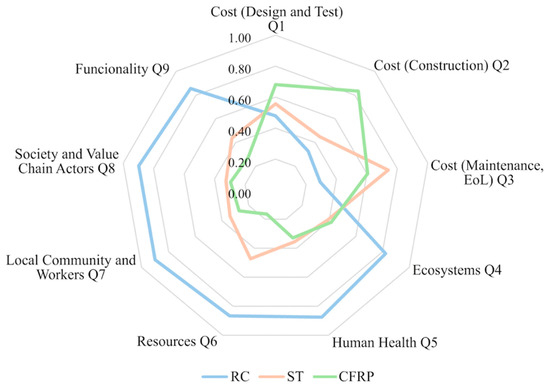
Figure 4.
Normalized evaluation criteria values.
When applying the final weights from the fuzzy-DANP model and computing the closeness coefficients through the TOPSIS procedure, the resulting ranking is presented in Table 10. CFRP ranks as the most sustainable retrofit option, followed closely by ST, with RC consistently rated lowest.

Table 10.
Ranking of alternatives based on evaluation.
5. Discussion of Results
Applying circular economy principles in retrofitting existing structures enhances sustainability across the entire life cycle by extending the service life and reducing resource consumption. However, conventional MCDM methods such as the AHP assume criterion independence, which is often unrealistic in complex engineering contexts. This study addresses that limitation by employing a hybrid approach that integrates fuzzy DEMATEL, DANP, and TOPSIS to capture the causal interactions and mutual influences among the economic, environmental, and social dimensions relevant to seismic retrofitting decisions for reinforced concrete columns.
The AHP remains one of the most prevalent MCDM methods owing to its straightforward pairwise comparison approach [56]. Nevertheless, it imposes a hierarchical structure and does not accommodate feedback loops. While the ANP allows interdependence [57], it introduces cognitive and computational complexity, which may hinder expert consistency unless simplifications are introduced [29].
The DANP method addresses these limitations by combining the direct influence structure of DEMATEL with the supermatrix-based weighting mechanism of the ANP. It employs a simplified linguistic scale to construct an NRM and determine normalized weights. As Manupati et al. [30] noted, DANP enhances expert consensus by reducing the questionnaire length, clarifying causal structures, and improving interpretability—thus balancing methodological rigor and practical usability.
One limitation of DANP is its lack of an intrinsic consistency ratio, unlike the AHP or ANP. The calculation of consistency indices is paramount in ensuring the accuracy of the judgments made by DMs. However, this does not necessarily imply that the judgments are correct [58]. To mitigate this, the proposed model incorporates fuzzy logic—specifically, TFNs to handle uncertainty and vagueness inherent in expert assessments [59]. This hybridization improves the reliability and mathematical robustness of the weighting process, especially under vague or imprecise decision environments.
This approach aligns with the network-based hybrid MCDM framework proposed by Sánchez-Garrido et al. [55], who combined adaptive the ANP and ELECTRE IS to assess sustainable building design alternatives with exclusively quantitative variables. They reported that their method reduced the required expert comparisons by approximately 92%, and that inter-method variability exceeded 70% for some criteria, highlighting the relevance of method selection. Our fuzzy-DANP model furthers this line of work by offering visual transparency through network maps and numerical robustness through fuzzification, aligning with the mathematical modeling standards.
From an environmental standpoint, our LCA findings are consistent with Palacios Muñoz et al. [60], who identified CFRP as a superior retrofit material due to reduced resource consumption and life cycle impact. They also noted that epoxy-free steel variants may achieve comparable or better performance, reinforcing the notion that material innovation is critical in long-term sustainability.
Social impacts remain an underexplored dimension in structural retrofitting studies. Aligned with prior observations by Hosseinijou et al. [61], the analysis indicates that steel-based solutions tend to outperform concrete regarding social sustainability. Nevertheless, the body of research examining the social effects of CFRP remains scarce. This work contributes to closing that gap by being among the first to embed S-LCA within a fuzzy MCDM decision framework for retrofit evaluation—thereby expanding the analytical perspective and promoting a more comprehensive assessment of infrastructural performance [50,62].
To verify the stability of the findings, two sensitivity analyses were performed.
Weight perturbation analysis across 26 scenarios, including ±20% deviations and equal weighting. In 22 of these, CFRP consistently ranked first. Only in cases where environmental weights were significantly reduced and cost was prioritized did ST match CFRP. These findings underscore the importance of transparent weight calibration and highlight how expert priorities can shift final decisions. This aligns with the argument by Backes and Traverso [63], who cautioned against oversimplified compensatory mechanisms across sustainability dimensions. Similarly, Tan et al. [64] emphasize the need for comprehensive MCDM frameworks that capture complex interrelations among sustainability criteria, reinforcing the robustness of hybrid approaches. Figure 5 illustrates these ranking shifts across scenarios.
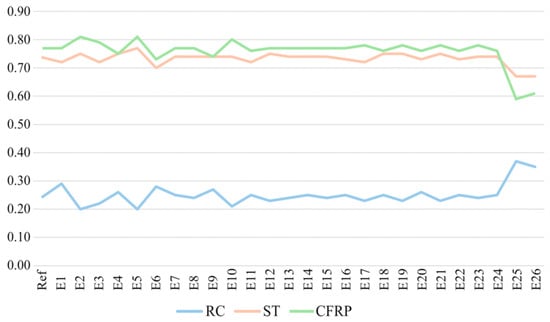
Figure 5.
Analysis of sensitivity in dimension and criteria weights.
Cross-method validation using four alternative MCDM techniques—SAW, VIKOR, COPRAS, and EDAS—employing the same fuzzy-DANP weights. All methods except VIKOR ranked CFRP highest, with VIKOR favoring ST. Figure 6 visualizes these rankings, providing triangulated evidence of the model’s consistency. A non-compensatory validation was conducted using the ELECTRE I method [55], applying the same fuzzy-DANP weights. The results highlighted CFRP and ST as the top alternatives. This outcome reinforces the robustness of the decision model under both compensatory and non-compensatory aggregation logics, which is relevant in safety-critical decision contexts where trade-offs between criteria should be cautiously interpreted. This confirms the reliability of the fuzzy-DEMATEL-DANP–TOPSIS framework and its applicability in real-world conditions with incomplete or uncertain data.
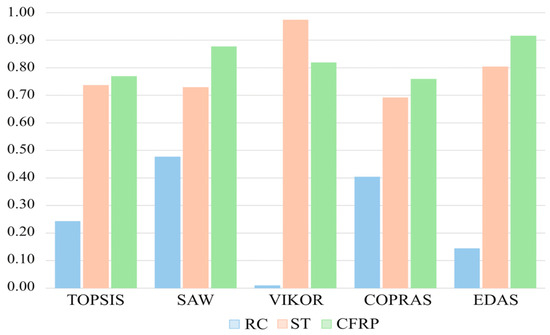
Figure 6.
Sensitivity analysis using multiple MCDMs.
According to Baykasoğlu and Gölcük [28], a robust MCDM framework should satisfy three main conditions: hierarchical structure, interdependency modeling, and uncertainty management. Our integrated approach fulfills all three by combining fuzzy set theory with causal mapping and matrix-based convergence analysis. Based on an expert credibility graph, visual influence structures, and a stable supermatrix, the resulting decision model offers a reproducible, generalizable, and mathematically sound framework for sustainability-driven decision-making in civil infrastructure projects.
6. Conclusions
This study develops an integrated decision-making model to support sustainability-oriented choices for retrofitting seismic-vulnerable reinforced concrete structures. The model integrates fuzzy DEMATEL, DANP, and TOPSIS into a mathematically structured architecture capable of capturing causal interdependencies and non-compensatory trade-offs across economic, environmental, and social criteria. Uncertainty stemming from expert judgment is modeled using TFNs, ensuring linguistic vagueness is incorporated without sacrificing analytical rigor.
The core methodological contribution lies in transforming classical MCDM logic—typically reliant on independence and compensation assumptions—into a hierarchical fuzzy network structure that quantifies mutual influence among indicators. This allows for both the propagation of influence within the system and the derivation of global priority weights through a stable supermatrix. The proposed model enhances sustainability evaluations’ transparency, scalability, and reproducibility under uncertainty.
The framework was applied to a real-world case involving retrofitting reinforced concrete columns using CFRP, steel jacketing, and RC jacketing. Results show that CFRP offers the most sustainable performance despite its higher initial cost due to its lower environmental and social burdens over the life cycle. Steel jacketing provides a balanced performance, while RC jacketing exhibits lower sustainability across multiple indicators. Robustness checks under different weighting schemes consistently preserved the relative ranking of the retrofit alternatives.
The main practical contribution lies in providing DMs with a structured classification of retrofitting alternatives aligned with circular economy principles and life cycle thinking. The model offers actionable guidance for engineers, contractors, and policymakers in contexts where technical feasibility, sustainability, and uncertainty must be jointly addressed.
However, this study is not without limitations. First, the model assumes that the three alternatives are structurally equivalent in performance, which may not always hold in other retrofit contexts. Second, fuzzy logic effectively captures linguistic imprecision, but it does not model more profound epistemic uncertainty or hesitation. Third, the applicability of the criteria weights is case-dependent and may vary by geographic, regulatory, or socioeconomic context.
Future research may explore integrating neutrosophic or hesitant fuzzy sets to better reflect the ambiguity in expert judgment or using dynamic weighting schemes based on Bayesian updating. Additionally, incorporating metaheuristic optimization methods or expanding the model to multi-stakeholder or multi-objective frameworks could enhance its robustness and policy relevance. The proposed framework is also suitable for extension to broader domains such as resilient infrastructural planning, climate-adaptive design, or asset management under uncertainty.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/math13162649/s1, Table S1: Fuzzy direct influence matrices of dimensions; Table S2: Fuzzy direct influence matrices of criteria.
Author Contributions
All authors contributed substantially to the development of this work. The conceptual framework and overall design were formulated collaboratively by P.V., A.J.S.-G., L.Y.-B., and V.Y. Leading the methodological development and execution of the case study, P.V. also drafted the initial version of the manuscript. A.J.S.-G. conducted a comprehensive technical review, refined the analytical components, and finalized the manuscript for submission. L.Y.-B. contributed to the improvement of the written content. V.Y. supervised the entire research process and secured the necessary funding. All authors have read and agreed to the published version of the manuscript.
Funding
This study was support by grant PID2023-150003OB-I00, funded by MICIU/AEI/10.13039/501100011033 and by “ERDF/EU”.
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author(s).
Acknowledgments
The first author is grateful to the Universidad Central del Ecuador for funding to pursue a doctoral program at the Universitat Politècnica de València.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RC | Reinforced concrete |
| FRP | Fiber-reinforced polymer |
| CE | Circular economy |
| SDGs | Sustainable Development Goals |
| LCA | Life Cycle Assessment |
| LCC | Life Cycle Costing |
| S-LCA | Social Life Cycle Assessment |
| MCDM | Multi-criteria decision-making |
| AHP | Analytic Hierarchy Process |
| TOPSIS | Technique for Preference by Similarity to an Ideal Solution |
| ANP | Analytic Network Process |
| DEMATEL | Decision-Making Trial and Evaluation Laboratory |
| CBA | Choosing by advantages |
| NRM | Network relationship map |
| EoL | End of life |
| ISM | Interpretive Structural Modeling |
| SEM | Structural Equation Modeling |
| TFNs | Triangular fuzzy numbers |
| CFCS | Converting the Fuzzy Data into Crisp Scores |
| DM | Decision-maker |
| ST | Steel jacket |
| CFRP | Carbon fiber-reinforced polymer |
References
- Silva, R.; Surra, E.; Quelhas, B.; Costa, A.A.; Lapa, N.; Delerue-Matos, C. Advantages of structural inspection and diagnosis for traditional buildings refurbishment: A life cycle assessment perspective. Build. Environ. 2022, 223, 109485. [Google Scholar] [CrossRef]
- Feliciano, D.; Arroyo, O.; Carrillo, J.; Liel, A.B.; Murray, P.B. Framework to assess the seismic performance of non-engineered masonry infilled RC frame buildings accounting for material uncertainty. Structures 2023, 50, 1191–1203. [Google Scholar] [CrossRef]
- Ding, Y.; Zeng, B.; Zhou, Z.; Wei, Y.; Zhu, M. Seismic retrofitting of RC columns using stainless steel grid-reinforced UHPC jackets in plastic hinge zone. J. Build. Eng. 2024, 84, 108637. [Google Scholar] [CrossRef]
- Ozcan, O.; Binici, B. A drift capacity prediction model for retrofitted reinforced concrete columns. Mag. Concr. Res. 2022, 74, 236–250. [Google Scholar] [CrossRef]
- Hoyos, M.C.; Silva, V. Exploring benefit cost analysis to support earthquake risk mitigation in Central America. Int. J. Disaster Risk Reduct. 2022, 80, 103162. [Google Scholar] [CrossRef]
- Corona, B.; Shen, L.; Reike, D.; Rosales Carreón, J.; Worrell, E. Towards sustainable development through the circular economy—A review and critical assessment on current circularity metrics. Resour. Conserv. Recycl. 2019, 151, 104498. [Google Scholar] [CrossRef]
- Farahzadi, L.; Tellnes, L.G.F.; Shafei, B.; Kioumarsi, M. Life-cycle environmental assessment of ultra-high-performance concrete with sustainable materials and fiber substitutions. Clean Eng. Technol. 2024, 23, 100846. [Google Scholar] [CrossRef]
- Scrucca, F.; Ingrao, C.; Barberio, G.; Matarazzo, A.; Lagioia, G. On the role of sustainable buildings in achieving the 2030 UN sustainable development goals. Environ. Impact Assess. Rev. 2023, 100, 107069. [Google Scholar] [CrossRef]
- Besen, P.; Boarin, P. Integrating energy retrofit with seismic upgrades to future-proof built heritage: Case studies of unreinforced masonry buildings in Aotearoa New Zealand. Build. Environ. 2023, 241, 110512. [Google Scholar] [CrossRef]
- Salgado, R.A.; Apul, D.; Guner, S. Life cycle assessment of seismic retrofit alternatives for reinforced concrete frame buildings. J. Build. Eng. 2020, 28, 101064. [Google Scholar] [CrossRef]
- Lei, H.; Li, L.; Yang, W.; Bian, Y.; Li, C.-Q. An analytical review on application of life cycle assessment in circular economy for built environment. J. Build. Eng. 2021, 44, 103374. [Google Scholar] [CrossRef]
- Palacios-Munoz, B.; Peuportier, B.; Gracia-Villa, L.; López-Mesa, B. Sustainability assessment of refurbishment vs. new constructions by means of LCA and durability-based estimations of buildings lifespans: A new approach. Build. Environ. 2019, 160, 106203. [Google Scholar] [CrossRef]
- Cavalieri, F.; Bellotti, D.; Caruso, M.; Nascimbene, R. Comparative evaluation of seismic performance and environmental impact of traditional and dissipation-based retrofitting solutions for precast structures. J. Build. Eng. 2023, 79, 107918. [Google Scholar] [CrossRef]
- Pushkar, S.; Halperin, I.; Ribakov, Y. Life-cycle assessment of contemporary and classical seismic retrofitting approaches applied to a reinforced concrete building in Israel. Buildings 2022, 12, 1854. [Google Scholar] [CrossRef]
- Vitiello, U.; Salzano, A.; Asprone, D.; Di Ludovico, M.; Prota, A. Life-cycle assessment of seismic retrofit strategies applied to existing building structures. Sustainability 2016, 8, 1275. [Google Scholar] [CrossRef]
- Dong, Y.; Ng, S.T.; Liu, P. Towards the principles of life cycle sustainability assessment: An integrative review for the construction and building industry. Sustain. Cities Soc. 2023, 95, 104604. [Google Scholar] [CrossRef]
- Leichter, M.; Piccardo, C. Assessing life cycle sustainability of building renovation and reconstruction: A comprehensive review of case studies and methods. Build. Environ. 2024, 262, 111817. [Google Scholar] [CrossRef]
- Sun, C.; Li, S.; Deng, Y. Determining Weights in Multi-Criteria Decision Making Based on Negation of Probability Distribution under Uncertain Environment. Mathematics 2020, 8, 191. [Google Scholar] [CrossRef]
- Figueiredo, K.; Pierott, R.; Hammad, A.W.A.; Haddad, A. Sustainable material choice for construction projects: A life cycle sustainability assessment framework based on BIM and Fuzzy-AHP. Build. Environ. 2021, 196, 107805. [Google Scholar] [CrossRef]
- Formisano, A.; Castaldo, C.; Chiumiento, G. Optimal seismic upgrading of a reinforced concrete school building with metal-based devices using an efficient multi-criteria decision-making method. Struct. Infrastruct. Eng. 2017, 13, 1373–1389. [Google Scholar] [CrossRef]
- Fiore, P.; Donnarumma, G.; Falce, C.; D’Andria, E.; Sicignano, C. An AHP-based methodology for decision support in integrated interventions in school buildings. Sustainability 2020, 12, 10181. [Google Scholar] [CrossRef]
- Santa-Cruz, S.; Cordova-Arias, C.; Brioso, X.; Vazquez-Rowe, I. Transparency-based protocol for decision-making regarding seismic rehabilitation projects of public buildings. Int. J. Disaster Risk Reduct. 2021, 55, 102116. [Google Scholar] [CrossRef]
- Vázquez-Rowe, I.; Córdova-Arias, C.; Brioso, X.; Santa-Cruz, S. A method to include life cycle assessment results in choosing by advantage (CBA) multicriteria decision analysis. A case study for seismic retrofit in Peruvian primary schools. Sustainability 2021, 13, 8139. [Google Scholar] [CrossRef]
- Clemett, N.; Gallo, W.W.C.; O’Reilly, G.J.; Gabbianelli, G.; Monteiro, R. Optimal seismic retrofitting of existing buildings considering environmental impact. Eng. Struct. 2022, 250, 113391. [Google Scholar] [CrossRef]
- Villalba, P.; Sánchez-Garrido, A.J.; Yepes, V. Life cycle evaluation of seismic retrofit alternatives for reinforced concrete columns. J. Clean Prod. 2024, 455, 142290. [Google Scholar] [CrossRef]
- Villalba, P.; Sánchez-Garrido, A.; Yepes, V. A review of multi-criteria decision-making methods for building assessment, selection, and retrofit. J. Civ. Eng. Manag. 2024, 30, 465–480. [Google Scholar] [CrossRef]
- Salas, J.; Yepes, V. Urban vulnerability assessment: Advances from the strategic planning outlook. J. Clean Prod. 2018, 179, 544–558. [Google Scholar] [CrossRef]
- Yucesan, M.; Mete, S.; Serin, F.; Celik, E.; Gul, M. An Integrated Best-Worst and Interval Type-2 Fuzzy TOPSIS Methodology for Green Supplier Selection. Mathematics 2019, 7, 182. [Google Scholar] [CrossRef]
- Gölcük, İ.; Baykasoğlu, A. An analysis of DEMATEL approaches for criteria interaction handling within ANP. Expert Syst. Appl. 2016, 46, 346–366. [Google Scholar] [CrossRef]
- Manupati, V.K.; Ramkumar, M.; Samanta, D. A multi-criteria decision making approach for the urban renewal in Southern India. Sustain. Cities Soc. 2018, 42, 471–481. [Google Scholar] [CrossRef]
- Shao, Q.-G.; Liou, J.J.H.; Weng, S.-S.; Chuang, Y.-C. Improving the Green Building Evaluation System in China Based on the DANP Method. Sustainability 2018, 10, 1173. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, C.-Y.; Cheng, H.-C. Fuzzy Multi-Criteria Decision-Making Model for Supplier Evaluation and Selection in a Wind Power Plant Project. Mathematics 2019, 7, 417. [Google Scholar] [CrossRef]
- Jiang, W.; Qiu, W.L.; Lin, S.-H.; Lv, H.; Zhao, X.; Cong, H. A New Hybrid Decision-Making Model for Promoting Sustainable Social Rental Housing. Sustainability 2023, 15, 6420. [Google Scholar] [CrossRef]
- Abdullah, F.M.; Al-Ahmari, A.M.; Anwar, S. An Integrated Fuzzy DEMATEL and Fuzzy TOPSIS Method for Analyzing Smart Manufacturing Technologies. Processes 2023, 11, 906. [Google Scholar] [CrossRef]
- Kang, H.-Y.; Lee, A.H.I.; Chan, Y.-C. An Integrated Fuzzy Multi-Criteria Decision-Making Approach for Evaluating Business Process Information Systems. Mathematics 2019, 7, 982. [Google Scholar] [CrossRef]
- Kaklauskas, A.; Zavadskas, E.K.; Binkyte-Veliene, A.; Kuzminske, A.; Cerkauskas, J.; Cerkauskiene, A.; Valaitiene, R. Multiple Criteria Evaluation of the EU Country Sustainable Construction Industry Lifecycles. Appl. Sci. 2020, 10, 3733. [Google Scholar] [CrossRef]
- Van Nguyen, M. Drivers of innovation towards sustainable construction: A study in a developing country. J. Build. Eng. 2023, 80, 107970. [Google Scholar] [CrossRef]
- Sufiyan, M.; Haleem, A.; Khan, S.; Khan, M.I. Evaluating food supply chain performance using hybrid fuzzy MCDM technique. Sustain. Prod. Consum. 2019, 20, 40–57. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Defuzzification within a multicriteria decision model. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2003, 11, 635–652. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Chiang, C.-H.; Li, C.-W. Evaluating intertwined effects in e-learning programs: A novel hybrid MCDM model based on factor analysis and DEMATEL. Expert Syst. Appl. 2007, 32, 1028–1044. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Methods for Multiple Attribute Decision Making. In Multiple Attribute Decision Making: Methods and Applications—A State-of-the-Art Survey; Springer-Verlag: Berlin/Heidelberg, Germany, 1981; pp. 973–978. [Google Scholar] [CrossRef]
- Caterino, N.; Cosenza, E. A multi-criteria approach for selecting the seismic retrofit intervention for an existing structure accounting for expected losses and tax incentives in Italy. Eng. Struct. 2018, 174, 840–850. [Google Scholar] [CrossRef]
- Kagermanov, A.; Ceresa, P.; Morales, E.; Poveda, J.; O’Connor, J. Seismic performance of RC buildings during the M(W)7.8 Muisne (Ecuador) earthquake on April 2016: Field observations and case study. Bull. Earthq. Eng. 2017, 15, 5167–5189. [Google Scholar] [CrossRef]
- Pacheco, D.; Mercerat, E.D.; Courboulex, F.; Bonilla, L.F.; Laurendeau, A.; Alvarado, A. Profiling the Quito basin (Ecuador) using seismic ambient noise. Geophys. J. Int. 2022, 228, 1419–1437. [Google Scholar] [CrossRef]
- Yepes, V.; Torres-Machi, C.; Chamorro, A.; Pellicer, E. Optimal pavement maintenance programs based on a hybrid greedy randomized adaptive search procedure algorithm. J. Civ. Eng. Manag. 2016, 22, 540–550. [Google Scholar] [CrossRef]
- Sánchez-Garrido, A.J.; Navarro, I.J.; Yepes, V. Optimizing reactive maintenance intervals for the sustainable rehabilitation of chloride-exposed coastal buildings with MMC-based concrete structure. Environ. Impact Assess. Rev. 2026, 116, 108110. [Google Scholar] [CrossRef]
- Lueddeckens, S.; Saling, P.; Guenther, E. Temporal issues in life cycle assessment—A systematic review. Int. J. Life Cycle Assess 2020, 25, 1385–1401. [Google Scholar] [CrossRef]
- Ayassamy, P.; Pellerin, R. Social Life-Cycle Assessment in the Construction Industry: A Review of Characteristics, Limitations, and Challenges of S-LCA through Case Studies. Sustainability 2023, 15, 14569. [Google Scholar] [CrossRef]
- Backes, J.G.; Traverso, M. Social Life Cycle Assessment in the Construction Industry: Systematic Literature Review and Identification of Relevant Social Indicators for Carbon Reinforced Concrete. Environ. Dev. Sustain. 2024, 26, 7199–7233. [Google Scholar] [CrossRef]
- Huang, Q.; Sun, Y.; Guo, Q.; Li, Q.; Zhang, Y.; Li, X.; Wang, L. Social life cycle assessment and its methodological challenges: A bibliometric and content analysis. J. Ind. Ecol. 2025, 29, 264–278. [Google Scholar] [CrossRef]
- Akbar, A.; Liew, K.M. Multicriteria performance evaluation of fiber-reinforced cement composites: An environmental perspective. Compos. B Eng. 2021, 218, 108937. [Google Scholar] [CrossRef]
- Jiang, T.; Yin, P.; Jin, Q. Performances of typical photovoltaic module production from the perspective of life cycle sustainability assessment. Sustain. Energy Technol. Assess 2024, 64, 103703. [Google Scholar] [CrossRef]
- Benoit, C.; Mazijn, B.; Margni, M.; Roy, P.O.; Jolliet, O.; Weidema, B.; Ciroth, A.; Rosenbaum, R.K.; Mueller-Wenk, R.; Pennington, D.W.; et al. The guidelines for social life cycle assessment of products: Just in time! Int. J. Life Cycle Assess 2010, 15, 156–163. [Google Scholar] [CrossRef]
- Pour, M.T. Prioritization of methods for seismic retrofitting of structures. J. Eng. Sci. Technol. 2015, 10, 64–80. [Google Scholar]
- Sánchez-Garrido, A.J.; Navarro, I.J.; García, J.; Yepes, V. An Adaptive ANP & ELECTRE IS-Based MCDM Model Using Quantitative Variables. Mathematics 2022, 10, 2009. [Google Scholar] [CrossRef]
- Jorge-García, D.; Estruch-Guitart, V.; Aragonés-Beltrán, P. How does the type of MCDM method affect the results of the prioritization and assessment of ecosystem services? A case study in the Ebro River Delta (Spain). J. Clean Prod. 2023, 429, 139637. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Yin, Z.-Y.; Zhou, A.; Shen, S.-L. MCDM-based flood risk assessment of metro systems in smart city development: A review. Environ. Impact Assess. Rev. 2023, 101, 107154. [Google Scholar] [CrossRef]
- Sánchez-Garrido, A.J.; Navarro, I.J.; Yepes, V. Sustainable preventive maintenance of MMC-based concrete building structures in a harsh environment. J. Build. Eng. 2024, 95, 110155. [Google Scholar] [CrossRef]
- Pushpakumara, B.H.J.; Jayasinghe, J.A.S.P. Development of a carbon emission based rating model for buildings. Clean Eng. Technol. 2024, 21, 100764. [Google Scholar] [CrossRef]
- Palacios-Munoz, B.; Gracia-Villa, L.; Zabalza-Bribian, I.; Lopez-Mesa, B. Simplified structural design and LCA of reinforced concrete beams strengthening techniques. Eng. Struct. 2018, 174, 418–432. [Google Scholar] [CrossRef]
- Hosseinijou, S.A.; Mansour, S.; Shirazi, M.A. Social life cycle assessment for material selection: A case study of building materials. Int. J. Life Cycle Assess 2014, 19, 620–645. [Google Scholar] [CrossRef]
- Navarro, I.J.; Villalba, I.; Yepes-Bellver, L.; Alcalá, J. Social life cycle assessment of railway track substructure alternatives. J. Clean. Prod. 2024, 450, 142008. [Google Scholar] [CrossRef]
- Backes, J.G.; Traverso, M. Life cycle sustainability assessment as a metrics towards SDGs agenda 2030. Curr. Opin. Green Sustain. Chem. 2022, 38, 100683. [Google Scholar] [CrossRef]
- Tan, Y.; Karbassi Yazdi, A.; Antunes, J.; Wanke, P.; Gunasekaran, A.; Corrêa, H.L.; Coluccio, G. The Quest for an ESG Country Rank: A Performance Contribution Analysis/MCDM Approach. Mathematics 2024, 12, 1865. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).