Abstract
The emergence of deep vision models such as convolutional neural networks and vision transformers has revolutionized computer vision, enabling significant advancements in image classification, object detection, and segmentation. In parallel, the rapid development of quantum computing has spurred interest in quantum machine learning (QML), which integrates the strengths of quantum computation with the representational power of deep learning. In QML, parameterized quantum circuits offer the potential to capture complex image features, define complex decision boundaries, and provide other computational advantages. This paper investigates hybrid quantum-classical vision architectures, with a focus on hybrid quantum-classical convolutional neural networks and hybrid quantum-classical vision transformers. These hybrid models explore both quantum pre-processing and post-processing of data, respectively, where quantum circuits are strategically integrated into the data pipeline to enhance model performance. Our results suggest that these hybrid models can enhance accuracy and computational efficiency in vision-related tasks, even with the constraints of current noisy intermediate-scale quantum devices.
Keywords:
convolutional neural network; image classification; neural networks; quantum computing; vision transformer MSC:
81P68
1. Introduction
The rapid evolution of artificial intelligence (AI), particularly fueled by transformative progress in deep learning, has fundamentally reshaped numerous domains, including computer vision [1,2], natural language processing (NLP) [3], robotics [4], and autonomous systems [5]. One of the most significant milestones in this trajectory is the emergence of “Big-AI", referring to large-scale models composed of billions of parameters. Notable examples include large language models (LLMs) [6] and generative pretrained transformers (GPTs) [7], which have demonstrated unprecedented capabilities in understanding, generating, and interpreting complex multimodal data. These models leverage massive datasets and advanced neural architectures to perform tasks ranging from natural language understanding to code generation and decision-making [8].
In parallel, vision models have undergone a similar scale-up in both architectural depth and representational power [9]. The integration of transformer-based designs into vision pipelines has further accelerated this growth, enabling deep vision models to process high-dimensional visual data with improved accuracy and generalization [10,11]. These advancements have catalyzed breakthroughs across a broad spectrum of real-world applications, including image classification, object detection, semantic segmentation, medical diagnostics, autonomous navigation, industrial automation, and remote sensing.
Among these models, vision transformers (ViTs) adapt transformer architectures
from NLP to vision tasks by dividing images into patches, embedding them linearly,
and using self-attention to capture long-range dependencies. ViTs offer advantages over
convolutional neural networks (CNNs) in modeling global context, flexibility to input
sizes, and parallelism. They achieve competitive or superior performance on large-scale
classification tasks when trained on large datasets or with extensive pre-training [12]. However, ViTs lack convolutional inductive bias, making them prone to overfitting on
limited data. They are also compute- and memory-intensive due to the quadratic complexity
of self-attention. While CNNs excel at local feature extraction with efficiency, ViTs provide
global receptive fields with higher resource demands [13,14].
Quantum computing introduces fundamentally new computational paradigms by exploiting principles such as quantum superposition, entanglement, and interference [15]. At the intersection of quantum computing and machine learning lies quantum machine
learning (QML), a rapidly evolving field that aims to harness quantum mechanical advantages
to improve learning algorithms [16,17]. Among the most promising approaches
within QML are hybrid quantum-classical (HQC) models, which integrate parametrized
quantum circuits (PQCs) with classical optimization and inference frameworks. These
hybrid systems exploit the expressive power of quantum circuits to operate within exponentially
large Hilbert spaces, enabling them to compactly represent and manipulate
highly complex functions and correlations in data [18,19]. Furthermore, quantum circuits inherently support the generation of highly non-linear transformations, which have been shown to improve performance across various machine learning tasks [20,21,22].
There has been a growing body of research exploring hybrid quantum–classical models
for vision applications. Several studies have proposed frameworks that embed PQCs
into classical CNN pipelines to enhance feature expressiveness and reduce model complexity [23,24,25,26]. For instance, shallow quantum circuits have been integrated between classical convolutional and dense layers for image classification tasks, demonstrating competitive accuracy with reduced trainable parameters under noise-free conditions [20]. More recently, researchers have begun exploring quantum-enhanced Transformer architectures, where quantum circuits replace or augment attention modules to model long-range dependencies [27,28]. These hybrid models aim to combine the parallelism and scalability of classical Transformers with the representational power of quantum processing.
In this paper, we further explore these two prominent types of HQC vision models:
the hybrid quantum-classical convolutional neural network (HQC-CNN) and the hybrid
quantum-classical vision transformer (HQC-ViT). The HQC-CNN architecture incorporates
a quantum convolutional layer to extract unique and intricate features from images that
are difficult to extract using the classical computer. These are then passed on to a classical
convolutional model, which is then trained and used for image classification tasks. On
the other hand, the HQC-ViT architecture integrates attention mechanisms with quantum
circuit layers to improve overall model performance. To evaluate the effectiveness of
these hybrid models, we train them on the MNIST dataset. For benchmarking purposes, a baseline model with an identical classical architecture—excluding the quantum layer—is also trained on the same dataset to assess the comparative advantage offered by the quantum layer.
The structure of this paper is as follows: Section 2 provides a brief overview of the fundamentals of quantum computing and QML, along with a discussion of the HQC models employed in this work. Section 3 presents the proposed model architectures and describes the dataset used for evaluation. Section 4 reports the experimental results with comprehensive performance analysis, while Section 5 provides a discussion of the challenges in QML. Finally, Section 6 concludes the paper.
2. Preliminary
2.1. Quantum Computing
Quantum computing is based on manipulating quantum bits, or qubits, which, unlike classical bits that exist in states 0 or 1, can exist in superpositions of both states. A single qubit is represented as a linear combination of the computational basis states:
where and , which represents the orthonormal basis for , known as the computational basis, and , are the probability amplitudes obeying .
A fundamental component of quantum computing is the use of quantum gates, analogous to classical logic gates, denoted by a unitary operator . The Pauli gates (X, Y, and Z) and the Hadamard gate are examples of single-qubit quantum gates. Another important class of single-qubit quantum gates are the rotation gates, which perform unitary transformations by rotating the qubit state around the Bloch sphere’s principal axes: X, Y, and Z. These gates are parameterized by a continuous rotation angle and are represented by unitary matrices acting on the two-dimensional Hilbert space of a single qubit. The rotation gates are denoted as , , and , corresponding to rotations about the X, Y, and Z axes, respectively [29]. In the computational basis , their matrix representations are given by the following:
These rotation gates form the building blocks of many PQCs used in variational quantum algorithms and QML models. Their ability to continuously adjust quantum states is critical for optimizing circuit behavior in response to data-driven learning tasks.
In order to have a complete set of gates for quantum computation, two-qubit gates are also necessary. One of the most used two-qubit gates is the Controlled NOT (CNOT) gate, which flips the state of the target qubit if the control qubit is in the state and leaves it unchanged if the control qubit is in the state . The CNOT gate is represented in the computational basis as
After the information in the qubits is processed by the quantum gates, the computation result needs to be read out using quantum measurement. The measurement in a quantum computer can be implemented by projection into the basis of the Hilbert space. Using the computational basis in single-qubit case, we have the measurement operators and with outcome 0 and 1, respectively, where . Given the state , the probability of obtaining the measurement outcome is given by
where .
2.2. QML
QML is a rapidly emerging field at the intersection of quantum computing and AI.
It aims to enhance machine learning (ML) models by leveraging the computational advantages
offered by quantum mechanics. QML focuses specifically on designing and implementing machine learning algorithms that are either entirely executed on quantum hardware or operate in HQC configurations. In its narrow definition, adopted in this work, QML refers to machine learning models that utilize quantum computers for training, inference, or both, using classical data inputs. The potential advantages include improved model expressivity, faster convergence in optimization landscapes, and access to high-dimensional Hilbert spaces for feature representation that are otherwise intractable classically.
This capacity to work in high-dimensional vector spaces equips quantum models with a powerful mechanism for feature representation, enabling the extraction of patterns and relationships that are often intractable or inefficient to capture using classical methods. Moreover, PQCs are capable of implementing highly expressive and non-linear transformations, making them particularly well-suited for tasks such as classification, regression, and generative modeling. These non-linear mappings, which arise through quantum gate compositions and measurement statistics, form the backbone of QML algorithms and contribute to their theoretical potential for outperforming classical counterparts in specific domains.
However, fully quantum deep learning models remain impractical to run at useful scales today due to hardware constraints, quantum circuits large enough to encode high-resolution images, or very deep quantum networks would suffer from prohibitive noise and qubit requirements. Therefore, HQC architectures have emerged as a promising near-term approach. In HQC machine learning models, a quantum computer is employed to execute specific subroutines or layers within a broader learning architecture, while the remaining components, such as extensive data processing, model orchestration, and training loops, are handled by classical hardware. This division of labor exploits the complementary strengths of both computational paradigms.
A key enabler of hybrid architectures is the use of variational quantum circuits (VQCs),
which are PQCs containing trainable gate rotations. These parameters are optimized by a classical computer using iterative learning strategies akin to those employed in training neural networks. After each forward pass through the quantum circuit, a classical optimizer updates the gate parameters by minimizing a cost function—typically defined via measurement outcomes, such as classification loss. This variational principle allows quantum circuits to adapt to data and learn meaningful representations, even in the presence of quantum noise, making them well-suited to current noisy intermediate-scale quantum (NISQ)
devices [30]. By maintaining shallow circuit depths and modest qubit counts, hybrid ML models can operate within present hardware limitations while potentially demonstrating quantum advantages on specialized tasks.
2.3. HQC-CNN
The HQC-CNN model combines a quantum convolutional layer with a CNN. The quantum layer pre-processes the data before it is fed as input to the CNN. An illustration of the model can be seen in Figure 1.
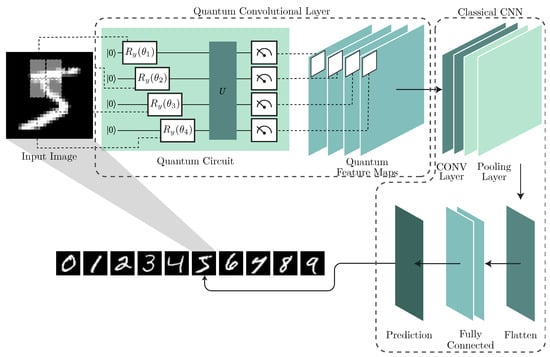
Figure 1.
Proposed HQC-CNN architecture.
Inspired by classical convolutional layers, quantum convolutional layers operate by applying parameterized or random quantum circuits to local patches of input images, enabling the extraction of hierarchical features. Unlike their classical counterparts, quantum circuits are capable of generating highly entangled and non-linear transformations that may be intractable for classical systems to simulate. This capability stems from their intrinsic access to high-dimensional Hilbert spaces, which facilitates the encoding of richer representations. Consequently, quantum convolutional architectures can offer a promising pathway towards achieving quantum advantage in image-based machine learning tasks.
The application of a quantum convolutional layer can be broadly decomposed into three stages: input encoding, unitary transformation, and measurement. Let the input image be denoted by , where H, W, and C represent the height, width, and number of channels, respectively. This image is partitioned into local patches of size , analogous to the convolutional kernels in classical CNN architectures. Each patch is encoded into a quantum state using angle encoding, typically implemented via parameterized single-qubit rotation gates. The qubits used are n, where . The general form of the encoding is given by the following:
where denotes the resulting quantum state, corresponds to the encoded pixel value, and represents the set of allowable rotation gates.
Following the encoding stage, a unitary transformation is applied using either a variational quantum circuit or a predefined random circuit. These circuits are designed to operate on the encoded patches to extract hierarchical features, functioning similarly to convolutional filters in classical networks. A typical quantum circuit layer comprises a combination of single-qubit rotations and two-qubit entangling gates. Deeper quantum pre-processing can be achieved by stacking multiple such layers. This can be represented as follows:
The final stage involves measurement in the computational basis. This process collapses the quantum state and yields classical binary outcomes (0 or 1) corresponding to the state of each qubit. These measurements serve as the output feature maps for subsequent processing in the classical post-processing pipeline. The quantum-generated feature maps are subsequently passed to a CNN, which continues the processing pipeline by applying additional convolutional, dense, and normalization layers. This hybrid architecture enables the extraction of high-level semantic features and ultimately produces the final classification output.
2.4. HQC-ViT
ViT architecture reformulates image processing through a sequence-based approach, where an input image is divided into N non-overlapping patches . An illustration of the model can be seen in Figure 2.
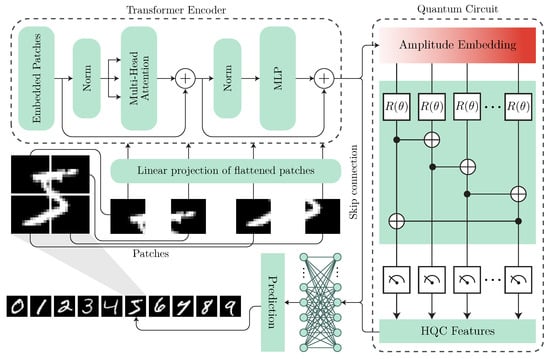
Figure 2.
Proposed HQC-ViT architecture.
Each patch is linearly projected into a D-dimensional embedding space. The resulting
patch embeddings, augmented with positional encodings, are processed by a stack of transformer
blocks composed of multi-head self-attention (MSA) and feed-forward networks
(FFN). The self-attention mechanism computes pairwise interactions between patches as follows:
where denote the query, key, and value matrices, respectively, derived via learned linear projections.
In a HQC-ViT, a PQC is introduced to transform classical embeddings by leveraging the high-dimensional Hilbert space of quantum states. A classical feature vector is encoded into a quantum state via a unitary operator :
where are trainable parameters and n denotes the number of qubits. The quantum encoding introduces non-linear feature transformations that are inaccessible to classical networks.
HQC-ViT quantum circuits typically consist of variational layers comprising entanglement gates like CNOT, CZ, and parameterized single-qubit rotation gates like , and . A common encoding scheme is amplitude embedding, which maps into the quantum state:
followed by entangling operations and measurements in the Pauli basis. The expectation values of observables are computed as follows:
and serve as non-linear activations fed back into the classical transformer pipeline.
By integrating quantum modules with ViT structures, HQC-ViT enables hybrid processing that benefits from both quantum expressivity and classical scalability. This architecture facilitates learning of complex image representations, while remaining compatible with gradient-based optimization methods.
2.5. Prospective Advantage of Adding Quantum Layers in ML Models
2.5.1. Nonlinear Feature Transformation
The feature transformation implemented by a quantum layer is inherently nonlinear due to three sequential effects [31]. First, the data encoding stage embeds classical patch values into quantum amplitudes and phases, altering the representational geometry of the input space. Second, the application of entangling quantum gates mixes these components in a nonclassical manner, producing complex correlations that cannot be replicated by purely linear operations. Third, projective measurement introduces a probabilistic collapse of the quantum state into classical outputs, acting as a nonlinear activation mechanism. This process parallels the concept of random nonlinear features in classical ML.
2.5.2. High-Dimensional Quantum Feature Space
Random quantum circuits within a quantum layer generate feature mappings into high-dimensional Hilbert spaces, where similarities between data points correspond to overlaps between quantum states [21]. Such mappings can provide efficient access to complex kernel functions that may be computationally expensive or infeasible to evaluate classically. This expanded representational capacity enables the separation of data patterns that may remain inseparable under the lower-dimensional feature transformations produced by conventional convolutional layers [22].
2.5.3. Expressive Power Beyond Classical Architectures
Entanglement within quantum layers enables the compact representation of high-order feature correlations. Studies on the expressive power of PQCs have demonstrated their ability to capture complex statistical dependencies and probability distributions beyond the capacity of comparable classical neural network architectures [18]. This expressivity stems from the ability of quantum circuits to realize volume-law entanglement and to simulate certain classes of circuits whose output distributions are intractable for classical computation.
3. Methods
3.1. HQC-CNN
Our quantum convolutional layer design is based on the architecture proposed in [31], with the key distinction that we directly utilize the raw expectation values obtained from quantum measurements, foregoing any additional classical post-processing. The input images are partitioned into local regions and sequentially processed using kernel sizes of , , and , with a stride of 2. We performed separate model training and testing for each of these three kernel sizes to systematically evaluate their impact on classification performance.
For encoding, we adopt angle encoding by applying gates, where the rotation angles are linearly scaled by a factor of from the raw pixel values. Each patch is encoded into a quantum circuit comprising n qubits. Subsequently, a random unitary transformation is applied to the encoded state. The quantum circuit consists of a single layer composed of randomly selected single-qubit rotation gates and two-qubit entangling gates. Although the circuit depth can be increased to enhance the quantum feature extraction capability, a single-layer configuration was employed in this work to maintain simplicity. Final measurements are performed in the computational basis (or Pauli-Z basis), producing binary outcomes.
Analogous to the classical convolution operation, where each kernel maps input values to different output channels, the quantum measurements yield n classical bits that are mapped to n output channels. This results in a multi-channel output image, where each channel corresponds to a distinct quantum-derived feature map. By scanning across the entire input image, the model constructs a spatially consistent, multi-channel representation capturing quantum-enhanced features. All quantum operations were simulated using a state vector simulator provided by the PennyLane framework.
As discussed earlier, the quantum pre-processed data is fed into a CNN for the task of image classification. A custom CNN architecture was designed, comprising convolutional and max-pooling layers for hierarchical feature extraction, followed by fully connected dense layers and dropout for regularization. The rectified linear unit (ReLU) activation function was applied to all intermediate layers, while a ‘softmax’ activation was used in the output layer to produce class probabilities. The complete architecture of the CNN model is illustrated in Figure 3. The model was compiled using the sparse categorical cross-entropy loss function and optimized with the ‘RMSprop’ optimizer. Training was performed for 30 epochs with a batch size of 16, while all other hyperparameters were kept at their default values. The entire implementation was carried out using the TensorFlow framework.
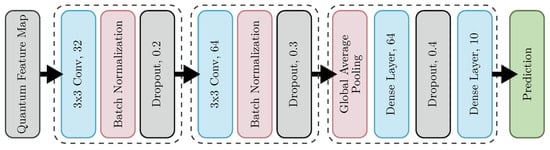
Figure 3.
Detailed illustration of the CNN model layers in the HQC-CNN framework.
We used the MNIST handwritten digit dataset, consisting of grayscale images of size and their corresponding digit labels (0–9), as the benchmark for evaluating the quantum model. To manage computational complexity, we restricted the dataset to a subset of 7000 images for training and 3000 images for testing. All image pixel values were normalized to the range by dividing by 255. For model validation, the training set was further split into training and validation subsets using an 80/20 ratio. Specifically, 80% of the 7000 training images were retained for training, while the remaining 20% (i.e., 1400 images) were used for validation.
3.2. HQC-ViT
The classical component of our HQC-ViT architecture utilizes a (ViT) to extract initial image features. As in the previous configuration, the MNIST dataset is employed for evaluation. The complete architecture of the model is illustrated in Figure 4. Each input image is divided into non-overlapping patches of size , facilitating localized feature extraction. Each patch is then flattened and linearly projected into a dimensional embedding space. To retain spatial information, learnable positional embeddings are added to the patch embeddings. The resulting sequence is processed by a transformer encoder
(TFE) comprising four layers (), where each layer consists of (MSA) with four heads (), a two-layer (FFN) with hidden dimension , as well as layer normalization and residual connections. The final output of the ViT frontend is a 10-dimensional feature vector tailored to match the input requirement of the subsequent quantum processing stage.
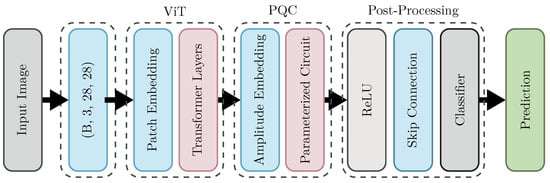
Figure 4.
Detailed illustration of the HQC-ViT model layers.
This 10-dimensional feature vector is passed to the quantum layer, implemented as a (PQC) using the PennyLane framework. This quantum component, referred to as
quantum neural network (QNET), operates on classical features using quantum computational principles. The vector is embedded into the amplitudes of a 10-qubit quantum state using amplitude embedding, whereby classical data is encoded into the probability amplitudes of the quantum state. The embedded state is then processed by a five-layer qml.BasicEntanglerLayers circuit, which includes trainable rotation gates and entangling CNOT gates. These layers enable the extraction of complex, high-order correlations. Following quantum evolution, Pauli-Z expectation values are measured across all qubits, producing a 10-dimensional vector of quantum-enhanced (HQC) features. The quantum circuit is fully integrated with the PyTorch (version 3.10) pipeline using pennylane.qnn.TorchLayer for end-to-end hybrid training.
Post-quantum processing is performed in the classical domain. The HQC features are passed through a ReLU activation function to introduce non-linearity. A key design element is the inclusion of a skip connection: the activated HQC features are added to the original 10-dimensional feature vector from the ViT frontend. This additive fusion ensures that both classical and quantum features contribute to the final representation, enhancing expressiveness and information flow. The resulting combined vector is passed through a final linear layer, mapping it to the 10 output classes of the MNIST dataset to produce the classification logits.
To conform with standard transformer input formats, the grayscale MNIST images were expanded to three channels. A balanced training subset of 10,000 images was curated, containing 1000 samples per digit class. Model generalization was evaluated on the full MNIST test set of 10,000 images, with standard normalization applied to all inputs.
Both the ViT and the HQC-ViT models were trained for 20 epochs using the ‘Adam’ optimizer with a learning rate of and the ‘CrossEntropyLoss’ function. A batch size of 128 was used during training, while a batch size of 512 was used for efficient testing. The best-performing model checkpoint, based on test accuracy, was saved during training.
4. Results
The classification performance of the classical and the hybrid models was evaluated on the MNIST test dataset. For the case of HQC-CNN, the training accuracy and loss are shown in Figure 5. The CNN achieved an overall accuracy of 94.07%, with macro-averaged precision, recall, and F1-score of 0.9452, 0.9383, and 0.9399, respectively. In comparison, the HQC-CNN model with a quantum kernel achieved an accuracy of 92.67%, with corresponding macro-averaged metrics of 0.9315 (precision), 0.9281 (recall), and 0.9270 (F1-score). The kernel outperformed the classical baseline, achieving 95.17% accuracy, with macro-averaged precision, recall, and F1-score of 0.9525, 0.9508, and 0.9511, respectively. The best results were observed with the quantum kernel, which attained 95.23% accuracy, along with macro-averaged precision, recall, and F1-score of 0.9537, 0.9523, and 0.9524. These findings highlight that increasing the quantum kernel size in HQC-CNN models can lead to improved classification performance, surpassing both smaller quantum kernels and purely classical counterparts. This demonstrates the potential of quantum-enhanced feature extraction in vision-based ML tasks.
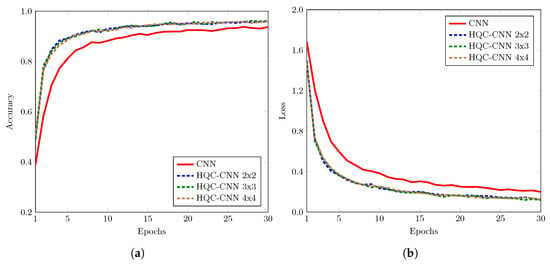
Figure 5.
Training (a) accuracy and (b) loss of simple CNN model and HQC-CNN model.
In the case of HQC-ViT, experimental results show a slight but consistent improvement over the ViT on the MNIST test dataset. Training accuracy and loss are shown in Figure 6. The HQC-ViT achieved an accuracy of 92.40%, marginally outperforming the ViT, which achieved 92.20%. In terms of precision, recall, and F1-score, HQC-ViT reported values of 0.9248, 0.9240, and 0.9241, respectively, compared to 0.9224, 0.9220, and 0.9216 for the ViT.
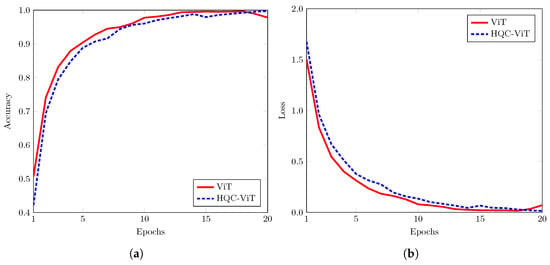
Figure 6.
Training (a) accuracy and (b) loss of simple ViT and HQC-ViT model.
To evaluate the impact of hybrid schemes on model complexity, Table 1 and Table 2 present a comparison of trainable parameters. The classical CNN has the highest parameter count, while HQC-CNN variants with larger quantum kernels progressively reduce parameters and improve performance. This is due to , where increased channel depth and reduced spatial size yield fewer activations and lower parameter loads in dense layers. Thus, larger quantum kernels produce more compact models with better accuracy, without altering the network’s core structure. On the other hand, transformer-based models show minimal change in parameter count. The HQC-ViT maintains a similar parameter count to the classical ViT, yet outperforms it in accuracy and macro-averaged metrics. This indicates that quantum-enhanced encoding can improve transformer performance with negligible architectural overhead. Overall, hybridization offers a compact and effective design strategy for both CNN and transformer models.

Table 1.
Trainable parameter comparison for CNN and HQC-CNN variants using different quantum kernel sizes.

Table 2.
Trainable parameter comparison for ViT and HQC-ViT.
5. Discussion
Although the performance gains are modest, they suggest that integrating quantum components can offer meaningful improvements in classical ML pipelines. In these HQC frameworks, we have used shallow quantum circuits, which can be implemented on NISQ hardware with limited qubit count. In this section, we will discuss some of the challenges regarding QML implementation on physical hardware and training of larger datasets.
NISQ hardware operates without full quantum error correction, making computations highly vulnerable to environmental disturbances [30]. Sources of noise include qubit decoherence, control imperfections, and cross-talk between qubits, each of which can introduce significant gate and measurement errors. Over time, this cumulative noise alters the quantum state, reducing computational fidelity and leading to unreliable results [32]. To limit these effects, current QML models must be designed with minimal qubit counts and shallow circuit depths, ensuring that they can be executed before decoherence dominates.
A fundamental and often performance-limiting step in QML is the encoding of classical data into the quantum state of a processor. This procedure, known as data embedding, presents a significant bottleneck, especially for large datasets [16]. While encoding strategies such as amplitude encoding offer exponential compactness in terms of qubit requirements, they necessitate deep and complex quantum circuits for state preparation [33]. On noisy hardware, the depth of these circuits is a critical liability; the accumulated noise during the encoding process can easily destroy the encoded information, thereby negating any potential quantum advantage.
The execution of a QML algorithm is inherently probabilistic, requiring multiple runs of a quantum circuit to accumulate sufficient measurement statistics for each data point or batch. This repetition is both time-consuming and computationally demanding. When performed on cloud-based quantum platforms, additional user-facing constraints such as long queue times and restricted hardware availability further extend the total runtime. As a result, scaling QML to datasets with millions of entries is presently impractical from both temporal and financial standpoints.
Another major obstacle to scaling QML models is the barren plateau phenomenon. In variational or gradient-based QML algorithms, certain model architectures exhibit an exponential decay in the variance of the cost function gradient as the number of qubits increases. This produces an optimization landscape that is nearly flat, severely limiting the effectiveness of gradient-based methods. Consequently, barren plateaus represent a critical barrier to the trainability of deep QML models [34].
Overall, the practical deployment of QML remains constrained by a combination of hardware limitations and training challenges. Reliable execution on physical devices requires addressing noise, limited qubit connectivity, and the data encoding bottleneck. Simulators are essential for prototyping QML architectures and evaluating their potential under ideal or configurable noise models. The proof-of-concept studies, as in this paper, can provide valuable insights into model configurations and potential quantum advantage. Notably, consistent improvements observed even with limited-depth circuits highlight the promise of HQC models in ML. As quantum hardware advances toward fault-tolerant architectures with scalable qubit counts and robust error correction, the deployment of deep, expressive, and powerful QML models will become feasible, enabling fundamentally new paradigms.
6. Conclusions
This work explored the effectiveness of HQC neural network architectures for vision task of classification. Two hybrid models were investigated: the HQC-CNN, which integrates quantum convolutional layers into a classical CNN, and the HQC-ViT, which combines a classical ViT with a PQC. Experimental results demonstrated that hybrid models, even with shallow quantum circuits, can contribute beneficial representational capacity in image recognition tasks. As quantum hardware continues to evolve, the approaches presented in this work may serve as viable foundations for scalable, high-performance quantum-enhanced deep learning systems.
Author Contributions
Conceptualization, S.M.A.R.; methodology, S.M.A.R. and U.I.P.; software, S.M.A.R. and U.I.P.; validation, S.M.A.R.; formal analysis, S.M.A.R.; investigation, S.M.A.R.; resources, S.M.A.R., U.I.P. and U.K.; data curation, S.M.A.R.; writing—original draft preparation, S.M.A.R., U.I.P. and U.K.; writing—review and editing, S.M.A.R., U.K., K.L. and H.S.; visualization, U.I.P. and H.S.; supervision, H.S.; project administration, H.S.; funding acquisition, H.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) under RS-2025-00556064 and by the MSIT (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP-2025-2021-0-02046) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation).
Data Availability Statement
The data presented in this study are available in the MNIST Handwritten Digit Database at https://yann.lecun.org/exdb/mnist/index.html. These data were derived from the following resources available in the public domain: MNIST Dataset—Yann LeCun, Corinna Cortes, and Christopher J.C. Burges, https://yann.lecun.org/exdb/mnist/index.html (accessed on 13 August 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| CNOT | Controlled-NOT |
| CNN | Convolutional Neural Network |
| HQC | Hybrid Quantum–Classical |
| HQC-CNN | Hybrid Quantum–Classical Convolutional Neural Network |
| HQC-ViT | Hybrid Quantum–Classical Vision Transformer |
| ML | Machine Learning |
| PQC | Parameterized Quantum Circuit |
| QML | Quantum Machine Learning |
| ViT | Vision Transformer |
References
- Zhang, J.; Huang, J.; Jin, S.; Lu, S. Vision-Language Models for Vision Tasks: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 5625–5644. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in Vision: A Survey. ACM Comput. Surv. 2022, 54, 1–41. [Google Scholar] [CrossRef]
- Khurana, D.; Koli, A.; Khatter, K.; Singh, S. Natural Language Processing: State of the Art, Current Trends and Challenges. Multimed. Tools Appl. 2023, 82, 3713–3744. [Google Scholar] [CrossRef] [PubMed]
- Soori, M.; Arezoo, B.; Dastres, R. Artificial Intelligence, Machine Learning and Deep Learning in Advanced Robotics: A Review. Cogn. Robot. 2023, 3, 54–70. [Google Scholar] [CrossRef]
- Tang, Y.; Zhao, C.; Wang, J.; Zhang, C.; Sun, Q.; Zheng, W.X.; Du, W.; Qian, F.; Kurths, J. Perception and Navigation in Autonomous Systems in the Era of Learning: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9604–9624. [Google Scholar] [CrossRef]
- Chang, Y.; Wang, X.; Wang, J.; Wu, Y.; Yang, L.; Zhu, K.; Chen, H.; Yi, X.; Wang, C.; Wang, Y.; et al. A Survey on Evaluation of Large Language Models. ACM Trans. Intell. Syst. Technol. 2024, 15, 1–45. [Google Scholar] [CrossRef]
- Yenduri, G.; Ramalingam, M.; Selvi, G.C.; Supriya, Y.; Srivastava, G.; Maddikunta, P.K.R.; Raj, G.D.; Jhaveri, R.H.; Prabadevi, B.; Wang, W.; et al. GPT (Generative Pre-Trained Transformer)—A Comprehensive Review on Enabling Technologies, Potential Applications, Emerging Challenges, and Future Directions. IEEE Access 2024, 12, 54608–54649. [Google Scholar] [CrossRef]
- Harshvardhan, G.; Gourisaria, M.K.; Pandey, M.; Rautaray, S.S. A Comprehensive Survey and Analysis of Generative Models in Machine Learning. Comput. Sci. Rev. 2020, 38, 100285. [Google Scholar] [CrossRef]
- Guo, M.; Xu, T.; Liu, J.; Liu, Z.; Jiang, P.; Mu, T.; Zhang, S.; Martin, R.R.; Cheng, M.; Hu, S. Attention Mechanisms in Computer Vision: A Survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Bhojanapalli, S.; Chakrabarti, A.; Glasner, D.; Li, D.; Unterthiner, T.; Veit, A. Understanding Robustness of Transformers for Image Classification. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 10231–10241. [Google Scholar]
- Chen, C.R.; Fan, Q.; Panda, R. CrossViT: Cross-Attention Multi-Scale Vision Transformer for Image Classification. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 357–366. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual/Vienna, Austria, 3–7 May 2021; pp. 1–21. [Google Scholar]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent Advances in Convolutional Neural Networks. Pattern Recogn. 2018, 77, 354–377. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A Survey of Convolutional Neural Networks: Analysis, Applications, and Prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Schuld, M.; Petruccione, F. Machine Learning with Quantum Computers; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Hsieh, M.; Liu, T.; Tao, D. Expressive Power of Parametrized Quantum Circuits. Phys. Rev. Res. 2020, 2, 033125. [Google Scholar] [CrossRef]
- Rizvi, S.M.A.; Ulum, M.S.; Asif, N.; Shin, H. Neural Networks with Variational Quantum Circuits. In Proceedings of the International Conference on Industrial Networks and Intelligent Systems Programs (INISCOM), Ho Chi Minh, Vietnam, 2–3 August 2023. [Google Scholar]
- Wang, A.; Hu, J.; Zhang, S.; Li, L. Shallow Hybrid Quantum-Classical Convolutional Neural Network Model for Image Classification. Quantum Inf. Process 2024, 23, 17. [Google Scholar] [CrossRef]
- Schuld, M.; Killoran, N. Quantum Machine Learning in Feature Hilbert Spaces. Phys. Rev. Lett. 2019, 122, 040504. [Google Scholar] [CrossRef] [PubMed]
- Havlíček, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chowb, J.M.; Gambetta, J.M. Supervised learning with quantum-enhanced feature spaces. Nature 2019, 567, 209–212. [Google Scholar] [CrossRef]
- Huang, S.; An, W.; Zhang, D.; Zhou, N. Image Classification and Adversarial Robustness Analysis Based on Hybrid Quantum–Classical Convolutional Neural Network. Opt. Commun. 2023, 533, 129287. [Google Scholar] [CrossRef]
- Li, W.; Chu, P.; Liu, G.; Tian, Y.; Qiu, T.; Wang, S. An Image Classification Algorithm Based on Hybrid Quantum Classical Convolutional Neural Network. Quantum Eng. 2022, 2022, 5701479. [Google Scholar] [CrossRef]
- Fan, F.; Shi, Y.; Guggemos, T.; Zhu, X.X. Hybrid Quantum-Classical Convolutional Neural Network Model for Image Classification. IEEE Trans. Neural Netw. 2023, 34, 5981–5994. [Google Scholar] [CrossRef]
- Liu, J.; Lim, K.H.; Wood, K.L.; Huang, W.; Guo, C.; Huang, H.L. Hybrid quantum-classical convolutional neural networks. Sci. China Phys. Mech. Astron. 2021, 64, 290311. [Google Scholar] [CrossRef]
- Cherrat, E.A.; Kerenidis, I.; Mathur, N.; Landman, J.; Strahm, M.; Li, Y.Y. Quantum Vision Transformers. Quantum 2024, 8, 1265. [Google Scholar] [CrossRef]
- Tariq, S.; Arfeto, B.E.; Khalid, U.; Kim, S.; Duong, T.Q.; Shin, H. Deep Quantum-Transformer Networks for Multimodal Beam Prediction in ISAC Systems. IEEE Internet Things J. 2024, 11, 29387–29401. [Google Scholar] [CrossRef]
- Wilde, M.M. Quantum Information Theory, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Henderson, M.; Shakya, S.; Pradhan, S.; Cook, T. Quanvolutional neural networks: Powering image recognition with quantum circuits. Quant. Mach. Intell. 2020, 2, 2. [Google Scholar] [CrossRef]
- Sarovar, M.; Proctor, T.; Rudinger, K.; Young, K.; Nielsen, E.; Blume-Kohout, R. Detecting crosstalk errors in quantum information processors. Quantum 2020, 4, 321. [Google Scholar] [CrossRef]
- Möttönen, M.; Vartiainen, J.J.; Bergholm, V.; Salomaa, M.M. Transformation of quantum states using uniformly controlled rotations. Quantum Inf. Comput. 2005, 5, 467–473. [Google Scholar] [CrossRef]
- McClean, J.R.; Boixo, S.; Smelyanskiy, V.N.; Babbush, R.; Neven, H. Barren plateaus in quantum neural network training landscapes. Nat. Commun. 2018, 9, 4812. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).