Nonlocal Prior Mixture-Based Bayesian Wavelet Regression with Application to Noisy Imaging and Audio Data
Abstract
1. Introduction
2. Bayesian Hierarchical Model
2.1. Observation Model
2.2. Wavelet Coefficient Model
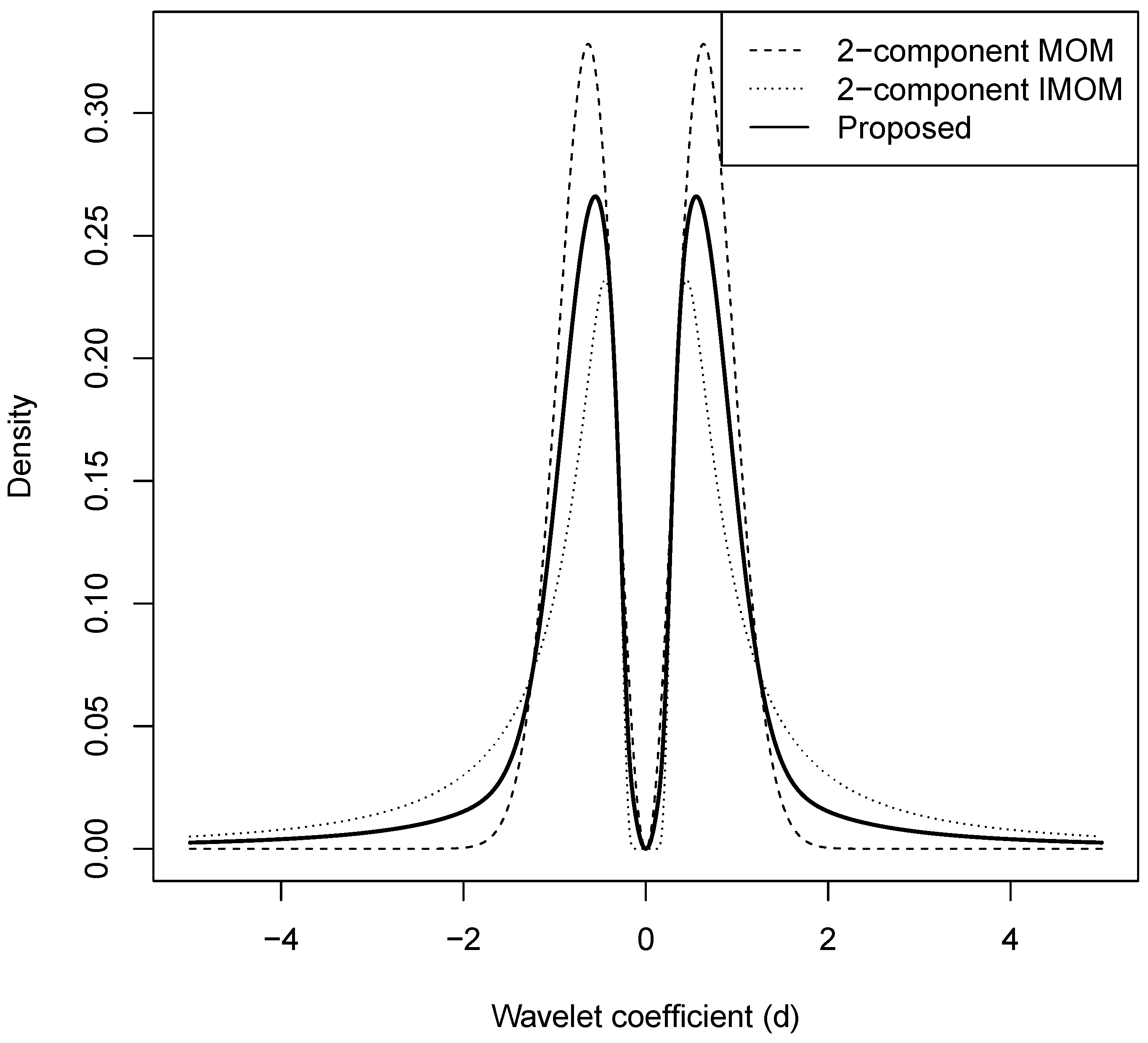
2.3. Mixture Prior for the Wavelet Coefficients
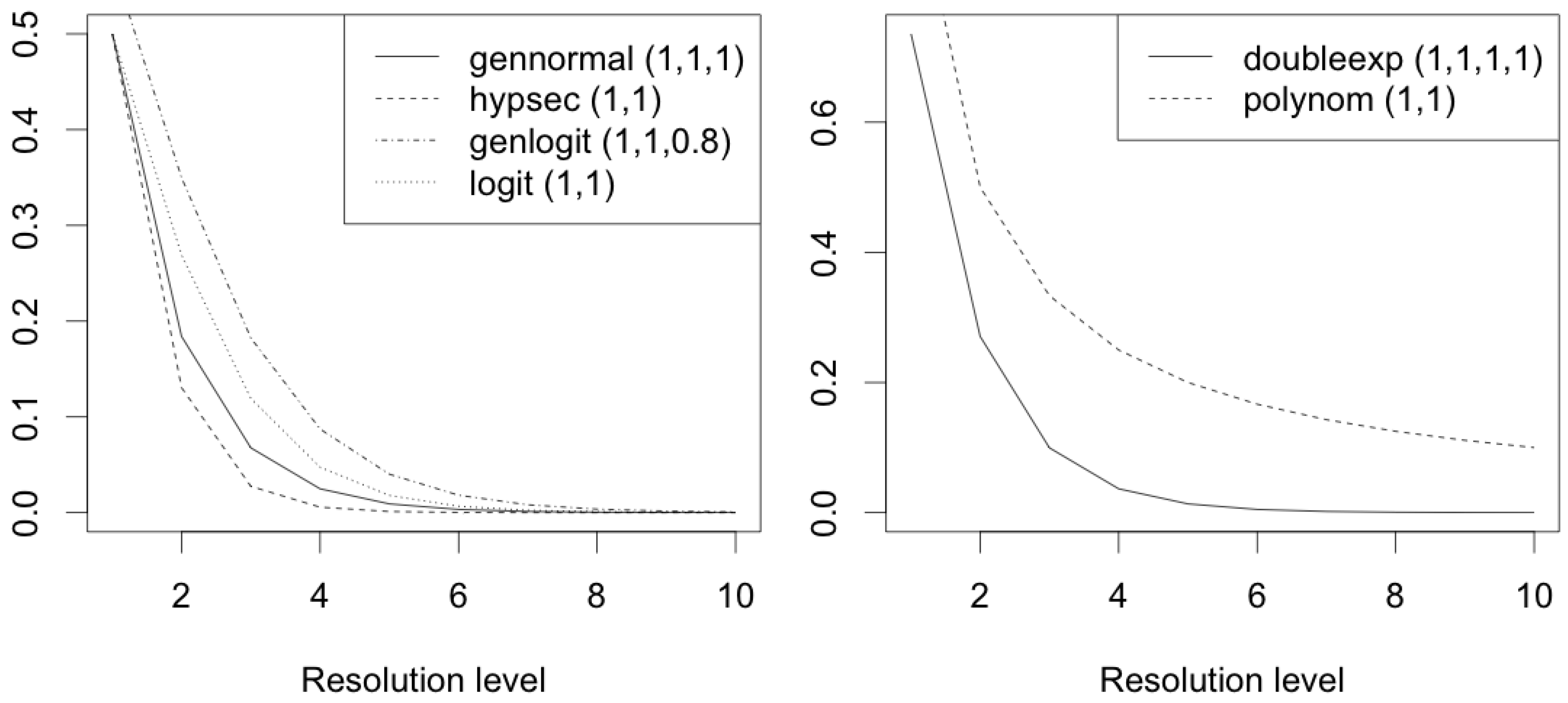
2.4. Hyperparameter Specifications
- (a)
- Generalized logit or Richards decay specifications, given byThis form corresponds to a flexible S-shaped decay curve that reduces to standard logistic decay when (or ) and controls the steepness of the curve equal to one.
- (b)
- Hyperbolic secant decay specifications, given byThis form, although less intuitive, is also sigmoid-like but with heavier tails and slower decay than logistic, indicating that the mixture parameters approach one more slowly with a smoother transition. (or ) controls steepness and (or ) controls shift.
- (c)
- Generalized normal decay specifications, given byThis form is most flexible and can mimic normal CDF, Laplace CDF, and many other distributions, but also most complex. Whereas (or ) controls tail behavior with larger values indicating lighter tails, others control scale and shift.
- (d)
- Double exponential decay specifications, given by
3. Inference
3.1. Hyperparameter Estimation
3.2. Posterior Distribution
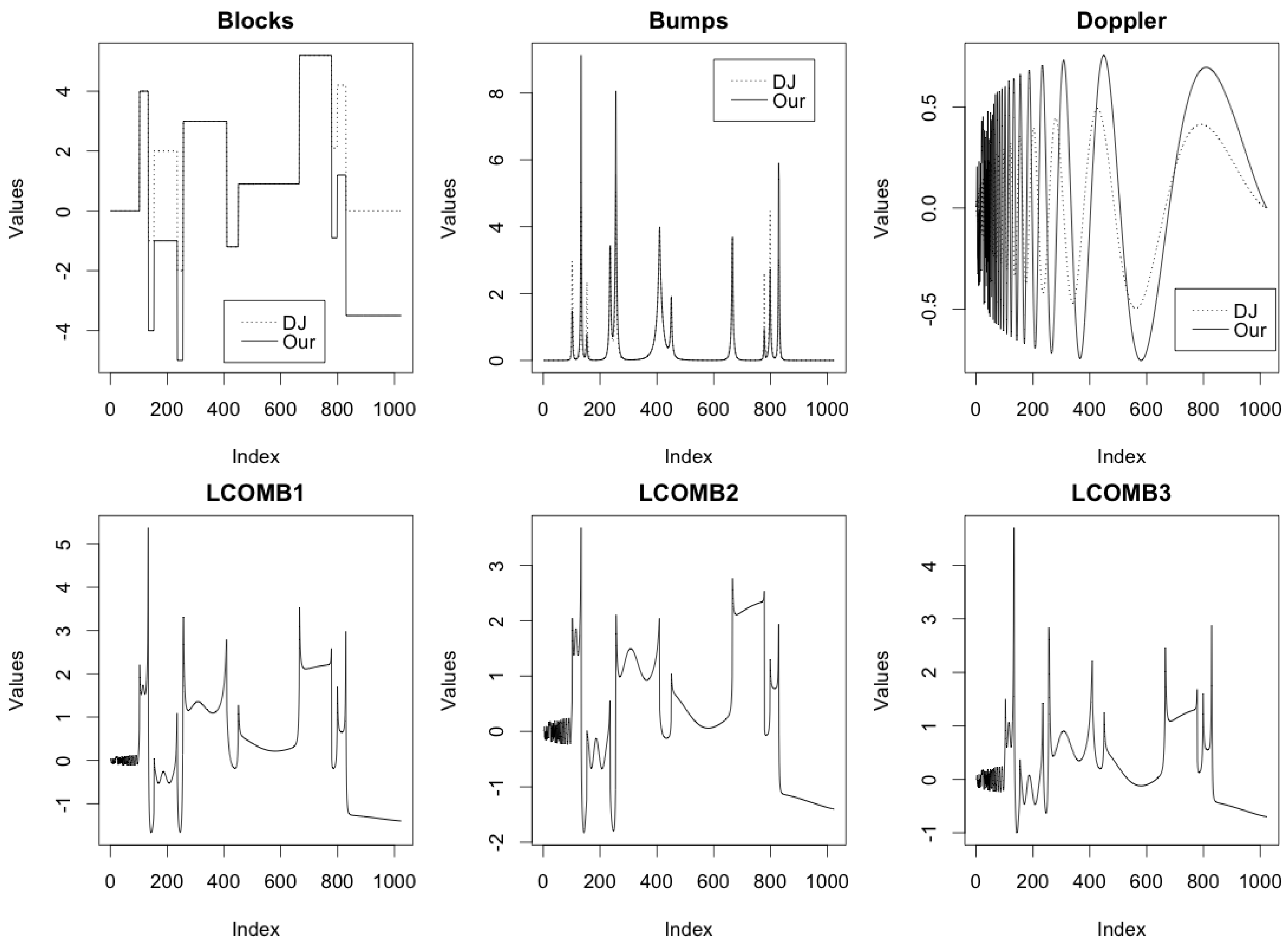
4. Simulation Study
- ,
- ;
- ,
- ,
- ;
- (a)
- For every function, the highest frequency of best performance was shown by a three-component mixture method (with one tie with a two-component mixture method for the blocks function), which is proposed in the current work.
- (b)
- Out of all eight three-component mixture methods, the one with generalized normal specification for the mixture probabilities and double exponential decay specification for the scale parameters (mixture-gennormal-doubleexp) showed the maximum number of best performances in total (12 times) for all the test functions. This was followed by the method using logit specification for the mixture probabilities and polynomial decay specification for the scale parameters (mixture-logit-polynom) (11 times) and the method using generalized normal specification for the mixture probabilities and polynomial decay specification for the scale parameters (mixture-logit-polynom) (9 times).
- (c)
- Considering only the test functions lcomb1, lcomb2, and lcomb3 that represent signals with mixed characteristics in various proportions, the mixture-gennormal-doubleexp method showed the maximum number of best performances (10 times).
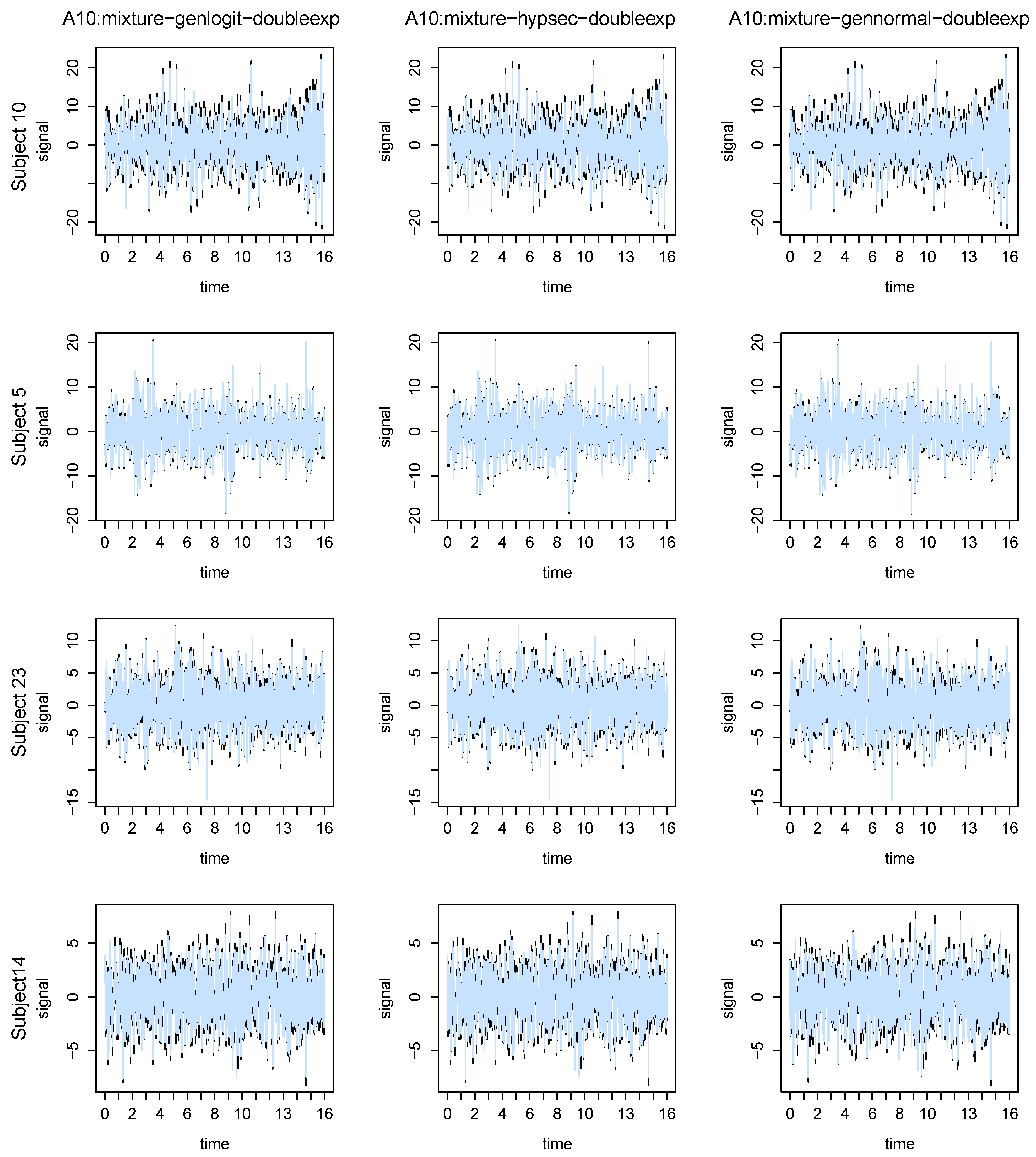
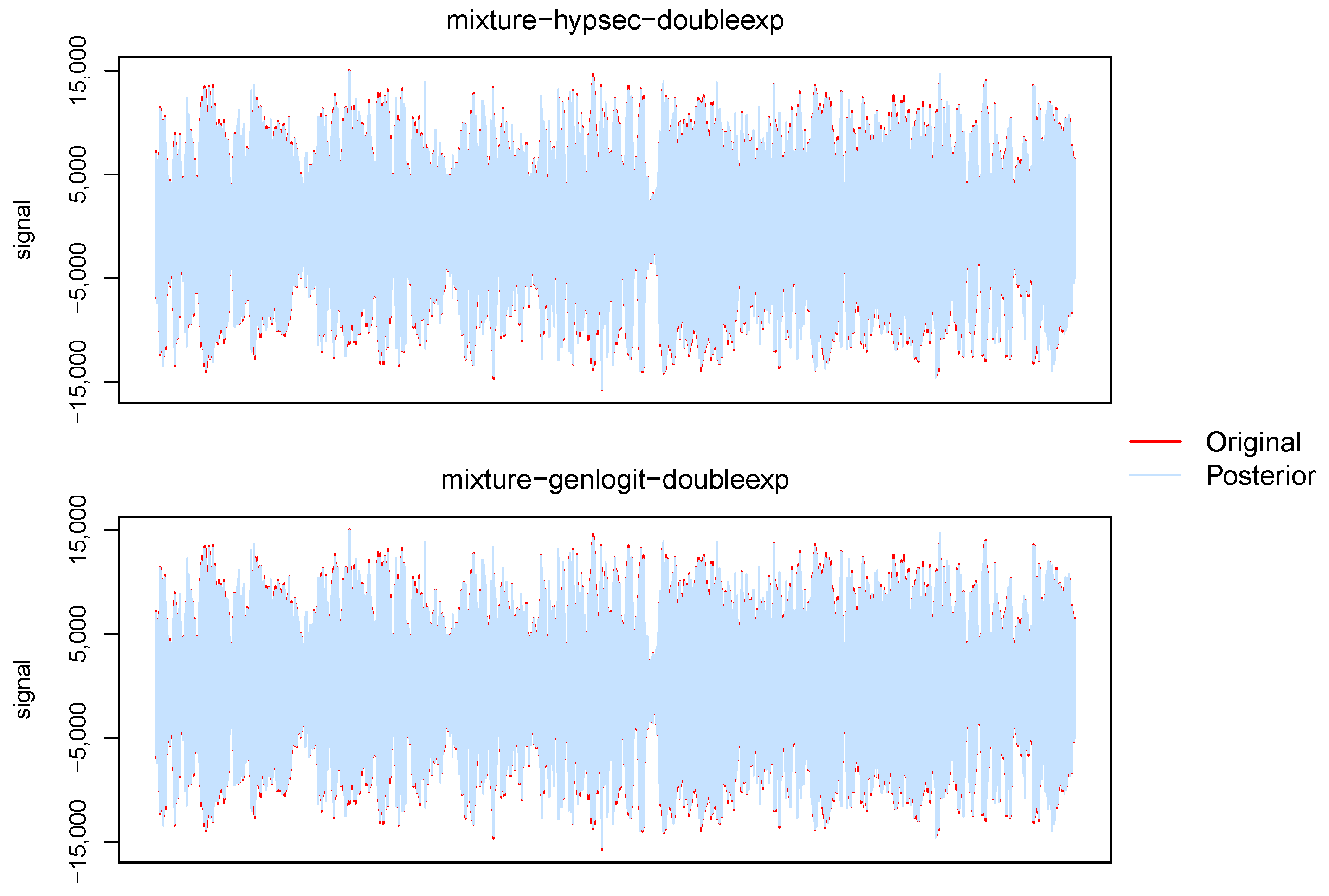
5. EEG Meditation Study
6. Musical Sound Study
7. Discussion
- (a)
- We introduce a three-component spike-and-slab prior for the wavelet coefficients. This structure is particularly suited for modeling highly dispersed signals. The slab component is a mixture of two nonlocal priors—the MOM and IMOM priors, which offer enhanced adaptability to signal characteristics.
- (b)
- We propose flexible and previously unexplored hyperparameter specifications. These include generalized logit (or Richards), hyperbolic secant, and generalized normal decay specifications for the mixture probabilities, as well as a double exponential decay structure for the scale parameter. These enhancements provide improved flexibility and accuracy in modeling complex signal patterns, as demonstrated in our simulation study.
- (c)
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MOM prior | Moment prior |
| IMOM prior | Inverse moment prior |
| NLP | Nonlocal prior |
| SNR | Signal-to-noise ratio |
| MSE | Mean squared error |
| EEG | Electroencephalogram |
Appendix A
Appendix A.1. Proof of Result 1
Appendix A.2. Proof of Result 2
References
- Chipman, H.A.; Kolaczyk, E.D.; McCulloch, R.E. Adaptive Bayesian Wavelet Shrinkage. J. Am. Stat. Assoc. 1997, 92, 1413–1421. [Google Scholar] [CrossRef]
- Clyde, M.; Parmigiani, G.; Vidakovic, B. Multiple shrinkage and subset selection in wavelets. Biometrika 1998, 85, 391–401. [Google Scholar] [CrossRef]
- Abramovich, F.; Sapatinas, T.; Silverman, B. Wavelet thresholding via a Bayesian approach. J. R. Stat. Soc. Ser. B 1998, 60, 725–749. [Google Scholar] [CrossRef]
- Sanyal, N.; Ferreira, M.A. Bayesian hierarchical multi-subject multiscale analysis of functional {MRI} data. NeuroImage 2012, 63, 1519–1531. [Google Scholar] [CrossRef] [PubMed]
- Clyde, M.; George, E.I. Flexible empirical Bayes estimation for wavelets. J. R. Stat. Soc. Ser. B 2000, 62, 681–698. [Google Scholar] [CrossRef]
- Johnstone, I.M.; Silverman, B.W. Empirical Bayes Selection of Wavelet Thresholds. Ann. Stat. 2005, 33, 1700–1752. [Google Scholar] [CrossRef]
- dos Santos Sousa, A.R. A Bayesian wavelet shrinkage rule under LINEX loss function. Res. Stat. 2024, 2, 2362926. [Google Scholar] [CrossRef]
- Sanyal, N.; Ferreira, M.A. Bayesian wavelet analysis using nonlocal priors with an application to FMRI analysis. Sankhya B 2017, 79, 361–388. [Google Scholar] [CrossRef]
- Johnson, V.; Rossell, D. On the use of non-local prior densities in Bayesian hypothesis tests. J. R. Stat. Soc. Ser. B 2010, 72, 143–170. [Google Scholar] [CrossRef]
- Johnson, V.; Rossell, D. Bayesian model selection in high-dimensional settings. J. Am. Stat. Assoc. 2012, 107, 649–660. [Google Scholar] [CrossRef]
- Rossell, D.; Telesca, D. Nonlocal priors for high-dimensional estimation. J. Am. Stat. Assoc. 2017, 112, 254–265. [Google Scholar] [CrossRef]
- Sanyal, N.; Lo, M.T.; Kauppi, K.; Djurovic, S.; Andreassen, O.A.; Johnson, V.E.; Chen, C.H. GWASinlps: Non-local prior based iterative SNP selection tool for genome-wide association studies. Bioinformatics 2019, 35, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Mallat, S. A Wavelet Tour of Signal Processing, Third Edition: The Sparse Way, 3rd ed.; Academic Press, Inc.: Cambridge, MA, USA, 2008. [Google Scholar] [CrossRef]
- Vidakovic, B. Nonlinear Wavelet Shrinkage with Bayes Rules and Bayes Factors. J. Am. Stat. Assoc. 1998, 93, 173–179. [Google Scholar] [CrossRef]
- Vidakovic, B.; Ruggeri, F. BAMS Method: Theory and Simulations. Sankhyā Indian J. Stat. Ser. B 2001, 63, 234–249. [Google Scholar]
- Portilla, J.; Strela, V.; Wainwright, M.; Simoncelli, E. Image denoising using scale mixtures of Gaussians in the wavelet domain. IEEE Trans. Image Process. 2003, 12, 1338–1351. [Google Scholar] [CrossRef]
- Cutillo, L.; Jung, Y.Y.; Ruggeri, F.; Vidakovic, B. Larger posterior mode wavelet thresholding and applications. J. Stat. Plan. Inference 2008, 138, 3758–3773. [Google Scholar] [CrossRef]
- Crouse, M.; Nowak, R.; Baraniuk, R. Wavelet-based statistical signal processing using hidden Markov models. IEEE Trans. Signal Process. 1998, 46, 886–902. [Google Scholar] [CrossRef]
- Chang, S.; Yu, B.; Vetterli, M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Process. 2000, 9, 1532–1546. [Google Scholar] [CrossRef]
- Figueiredo, M.; Nowak, R. Wavelet-based image estimation: An empirical Bayes approach using Jeffrey’s noninformative prior. IEEE Trans. Image Process. 2001, 10, 1322–1331. [Google Scholar] [CrossRef]
- Boubchir, L.; Boashash, B. Wavelet denoising based on the MAP estimation using the BKF Prior with application to images and EEG signals. IEEE Trans. Signal Process. 2013, 61, 1880–1894. [Google Scholar] [CrossRef]
- Reményi, N.; Vidakovic, B. Wavelet shrinkage with double Weibull prior. Commun. Stat. Simul. Comput. 2015, 44, 88–104. [Google Scholar] [CrossRef]
- Afshari, M.; Lak, F.; Gholizadeh, B. A new Bayesian wavelet thresholding estimator of nonparametric regression. J. Appl. Stat. 2017, 44, 649–666. [Google Scholar] [CrossRef]
- Sousa, A.R.d.S.; Garcia, N.L.; Vidakovic, B. Bayesian wavelet shrinkage with beta priors. Comput. Stat. 2021, 36, 1341–1363. [Google Scholar] [CrossRef]
- dos Santos Sousa, A.R. Bayesian wavelet shrinkage with logistic prior. Commun. Stat. Simul. Comput. 2022, 51, 4700–4714. [Google Scholar] [CrossRef]
- Vidakovic, B. Statistical Modeling by Wavelets; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar] [CrossRef]
- Antoniadis, A.; Bigot, J.; Sapatinas, T. Wavelet Estimators in Nonparametric Regression: A Comparative Simulation Study. J. Stat. Softw. 2001, 6, 1–83. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Adapting to Unknown Smoothness via Wavelet Shrinkage. J. Am. Stat. Assoc. 1995, 90, 1200–1224. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M.; Kerkyacharian, G.; Picard, D. Wavelet Shrinkage: Asymptopia? J. R. Stat. Soc. Ser. B 1995, 57, 301–369. [Google Scholar] [CrossRef]
- Donoho, D.; Johnstone, J. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Nason, G.P. Wavelet Shrinkage Using Cross-Validation. J. R. Stat. Soc. Ser. B 1996, 58, 463–479. [Google Scholar] [CrossRef]
- Abramovich, F.; Benjamini, Y. Adaptive thresholding of wavelet coefficients. Comput. Stat. Data Anal. 1996, 22, 351–361. [Google Scholar] [CrossRef]
- Nason, G. Wavethresh: Wavelets Statistics and Transforms, version 4.7.3; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar] [CrossRef]
- Brandmeyer, T.; Delorme, A. Reduced mind wandering in experienced meditators and associated EEG correlates. Exp. Brain Res. 2018, 236, 2519–2528. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Sanyal, N. NLPwavelet: Bayesian Wavelet Analysis Using Non-Local Priors, version 1.1; R Foundation for Statistical Computing: Vienna, Austria, 2025. [Google Scholar] [CrossRef]
- International Telecommunication Union. Perceptual Evaluation of Speech Quality (PESQ): An Objective Method for End-to-End Speech Quality Assessment of Narrow-Band Telephone Networks and Speech Codecs; Rec. P.862; International Telecommunication Union: Geneva, Switzerland, 2001. [Google Scholar]
- Taal, C.H.; Hendriks, R.C.; Heusdens, R.; Jensen, J. A short-time objective intelligibility measure for time-frequency weighted noisy speech. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 4214–4217. [Google Scholar] [CrossRef]

| Method | blocks | bumps | doppler | lcomb1 | lcomb2 | lcomb3 | Total |
|---|---|---|---|---|---|---|---|
| mom-logit-polynom | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| mom-logit-doubleexp | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| mom-genlogit-polynom | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| mom-genlogit-doubleexp | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| mom-hypsec-polynom | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| mom-hypsec-doubleexp | 3 | 0 | 0 | 0 | 0 | 0 | 3 |
| mom-gennormal-polynom | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| mom-gennormal-doubleexp | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| imom-logit-polynom | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| imom-logit-doubleexp | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| imom-genlogit-polynom | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| imom-genlogit-doubleexp | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| imom-hypsec-polynom | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| imom-hypsec-doubleexp | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| imom-gennormal-polynom | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| imom-gennormal-doubleexp | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| mixture-logit-polynom | 1 | 6 | 0 | 1 | 3 | 0 | 11 |
| mixture-logit-doubleexp | 0 | 1 | 2 | 1 | 2 | 1 | 7 |
| mixture-genlogit-polynom | 2 | 1 | 2 | 0 | 1 | 2 | 8 |
| mixture-genlogit-doubleexp | 3 | 0 | 0 | 0 | 1 | 0 | 4 |
| mixture-hypsec-polynom | 1 | 0 | 4 | 1 | 1 | 0 | 7 |
| mixture-hypsec-doubleexp | 0 | 1 | 0 | 4 | 1 | 2 | 8 |
| mixture-gennormal-polynom | 0 | 3 | 2 | 1 | 1 | 2 | 9 |
| mixture-gennormal-doubleexp | 0 | 0 | 2 | 4 | 1 | 5 | 12 |
| Total | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanyal, N. Nonlocal Prior Mixture-Based Bayesian Wavelet Regression with Application to Noisy Imaging and Audio Data. Mathematics 2025, 13, 2642. https://doi.org/10.3390/math13162642
Sanyal N. Nonlocal Prior Mixture-Based Bayesian Wavelet Regression with Application to Noisy Imaging and Audio Data. Mathematics. 2025; 13(16):2642. https://doi.org/10.3390/math13162642
Chicago/Turabian StyleSanyal, Nilotpal. 2025. "Nonlocal Prior Mixture-Based Bayesian Wavelet Regression with Application to Noisy Imaging and Audio Data" Mathematics 13, no. 16: 2642. https://doi.org/10.3390/math13162642
APA StyleSanyal, N. (2025). Nonlocal Prior Mixture-Based Bayesian Wavelet Regression with Application to Noisy Imaging and Audio Data. Mathematics, 13(16), 2642. https://doi.org/10.3390/math13162642






