A Mathematical Method for Optimized Decision-Making and Performance Improvement Through Training and Employee Reallocation Under Resistance to Change
Abstract
1. Introduction
- Existing models do not incorporate real-time, dynamic adaptation to employee resistance and training needs during organizational change.
- Current approaches use traditional communication tools, such as interviews, seminars, and information sessions. These tools are time-consuming and inflexible, making them unable to respond immediately to RtC and training requirements.
- Additionally, most models treat human resource allocation as a static process, overlooking the dynamic nature of employees’ behavior and their evolving resistance throughout the change process.
- The development of a dynamic EDMO model, which simultaneously monitors and optimizes multiple and often conflicting objectives (performance versus cost).
- Evaluation of the model’s effectiveness in real-time training and monitoring in terms of improving performance and cost stabilization.
- Comparison of the dynamic model with traditional static and dynamic models in terms of their ability to respond to complex and evolving conditions of organizational change.
2. Literature Review
2.1. Change Management Models
2.2. Dynamic Multi-Objective Optimization Problems
3. The Performance Improvement Through Training and Employee Reallocation (PITTER) Method
3.1. Problem Description
- (i)
- The number of employees remains constant throughout the change process.
- (ii)
- The initial performance of each employee is known.
- (iii)
- The initial cost for each employee is known.
- (iv)
- Each employee can perform all tasks.
- (v)
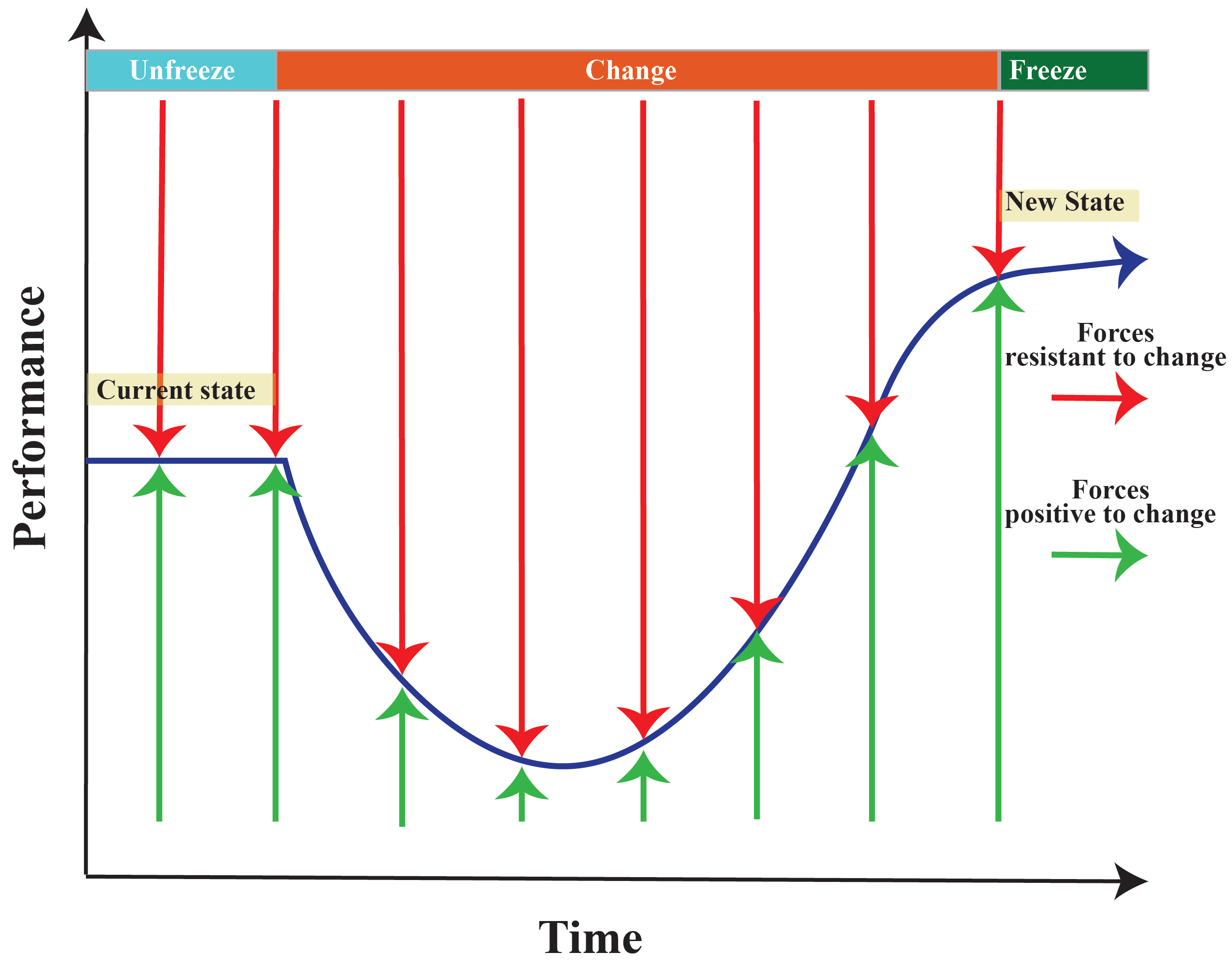
- During the change period, each employee presents a resistance that follows the change curve model [5].
- (vi)
- This resistance is reduced when training is provided.
- (vii)
- Training is cumulative for each employee (i.e., its effect adds up over time) and is discontinued when the employee no longer exhibits resistance that affects their performance.
3.2. Description of the PITTER Application
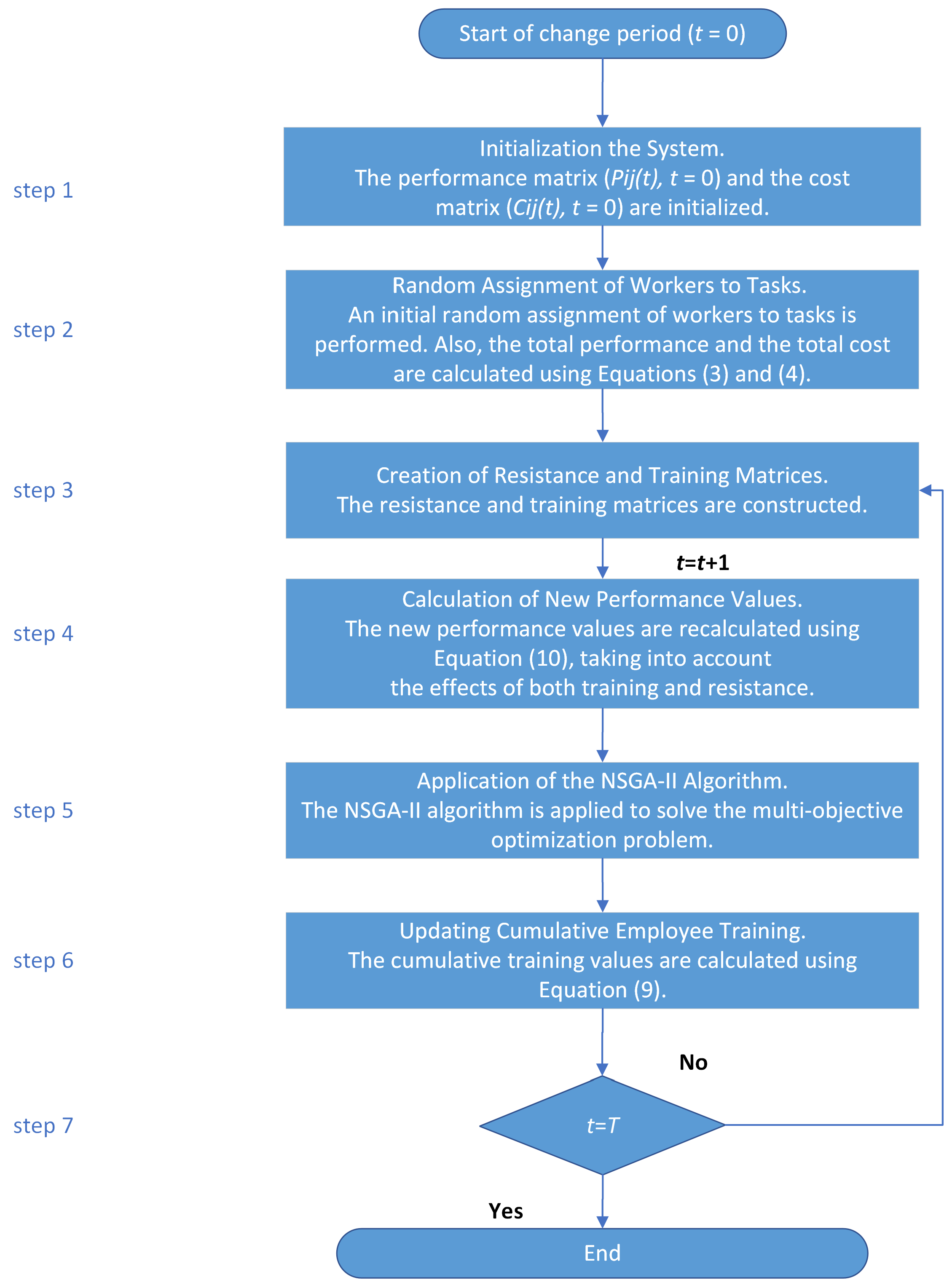
- Step 1:
- Initialization of the System. The number n of workers and jobs, which is assumed to be equal, is determined. Then, the initial cost matrix is formulated, which includes the cost of each worker i in each job j. At the same time, the initial performance matrix () is initialized, which has the same dimensions as the cost matrix.
- Step 2:
- Random Assignment of Workers to Tasks. An initial random assignment of workers to available tasks is performed. The use of randomness at this stage serves to create a neutral initial state for the system. At this point, no resistance to their change of position has yet developed on the part of the workers, so no training process is needed. Immediately afterwards, the total performance and the total cost of the assignment are calculated, based on the corresponding Equations (3) and (4).
- Step 3:
- Creation of Resistance and Training Matrices. At each time step t, the resistance matrix is constructed for each pair of worker i and task position j through a process that is described in detail in the Experiments Section. Based on the resistance matrix values, the corresponding training matrix is obtained using Equation (8), which determines the level of training that must be provided to each employee i in order to reduce their resistance during the change process. The matrices have the same dimensions .
- Step 4:
- Calculation of New Performance Values. The performance of each employee is recalculated using Equation (10), which takes into account the effects of both training and resistance.
- Step 5:
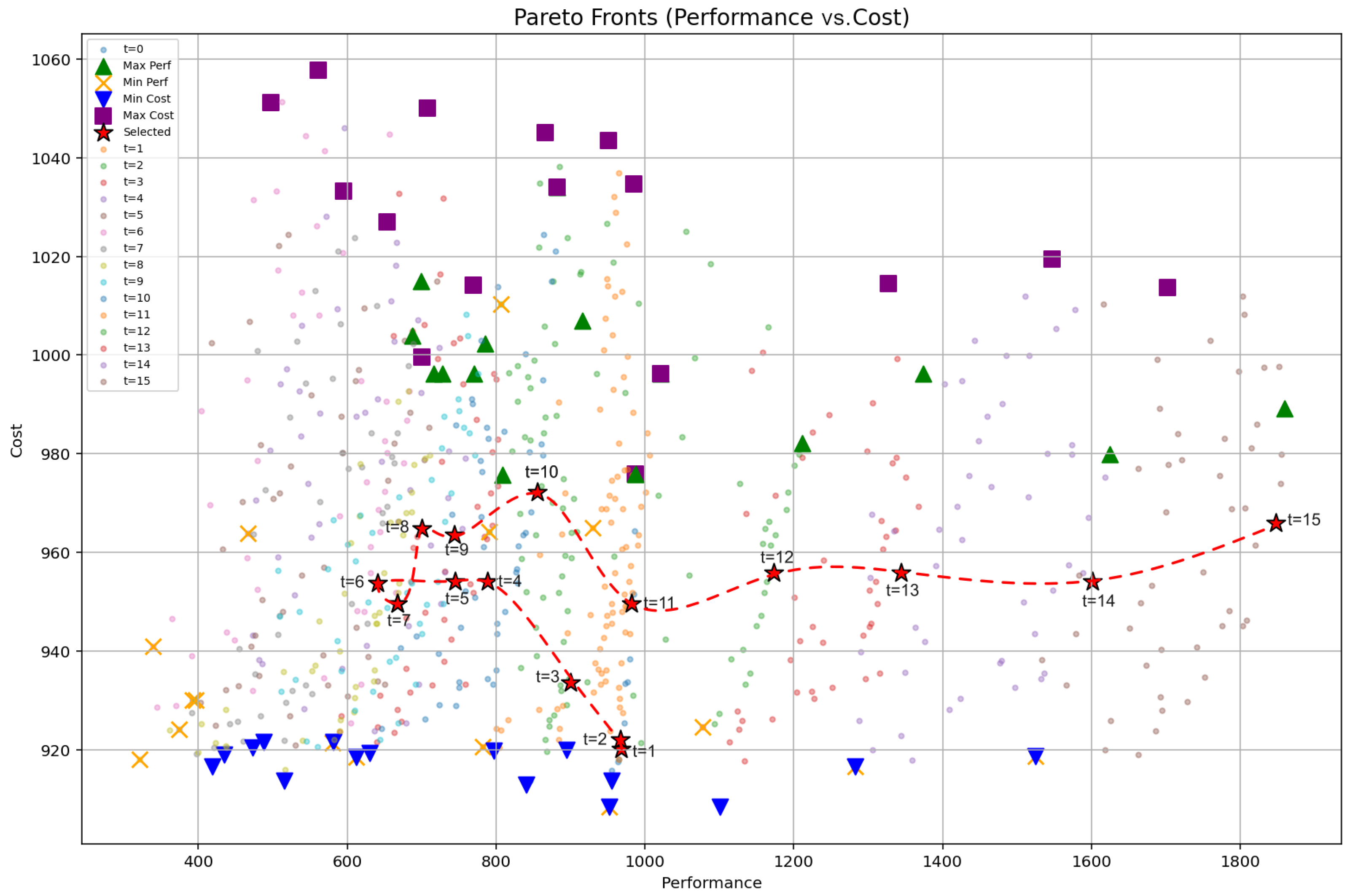
- Application of the NSGA-II Algorithm. The NSGA-II algorithm is applied to solve the multi-objective problem comprising two objectives: maximizing the total performance and minimizing the total assignment cost, as described in Equations (3) and (4). Based on the Pareto front, one of the non-dominated solutions is selected through a process that is described in detail in the Experiments Section.
- Step 6:
- Step 7:
- Repeating the Process. Steps 3–6 are repeated for each time step , simulating the full duration of the organizational change process. At each time step, both the total performance and the total assignment cost are recalculated. The total performance is calculated as the sum of the performance values in the selected assignment pairs, and the total cost is calculated as the sum of the assignment costs for the same pairs. Furthermore, the current generation of NSGA-II algorithm solutions is used as the initial conditions in the next time step.
4. Experiments and Results
4.1. First Experiment: Algorithm Implementation
- is the distance of solution i from the ideal point;
- is the total performance of solution i;
- is the total assignment cost of solution i;
- is the highest performance across all solutions;
- is the lowest cost across all solutions.
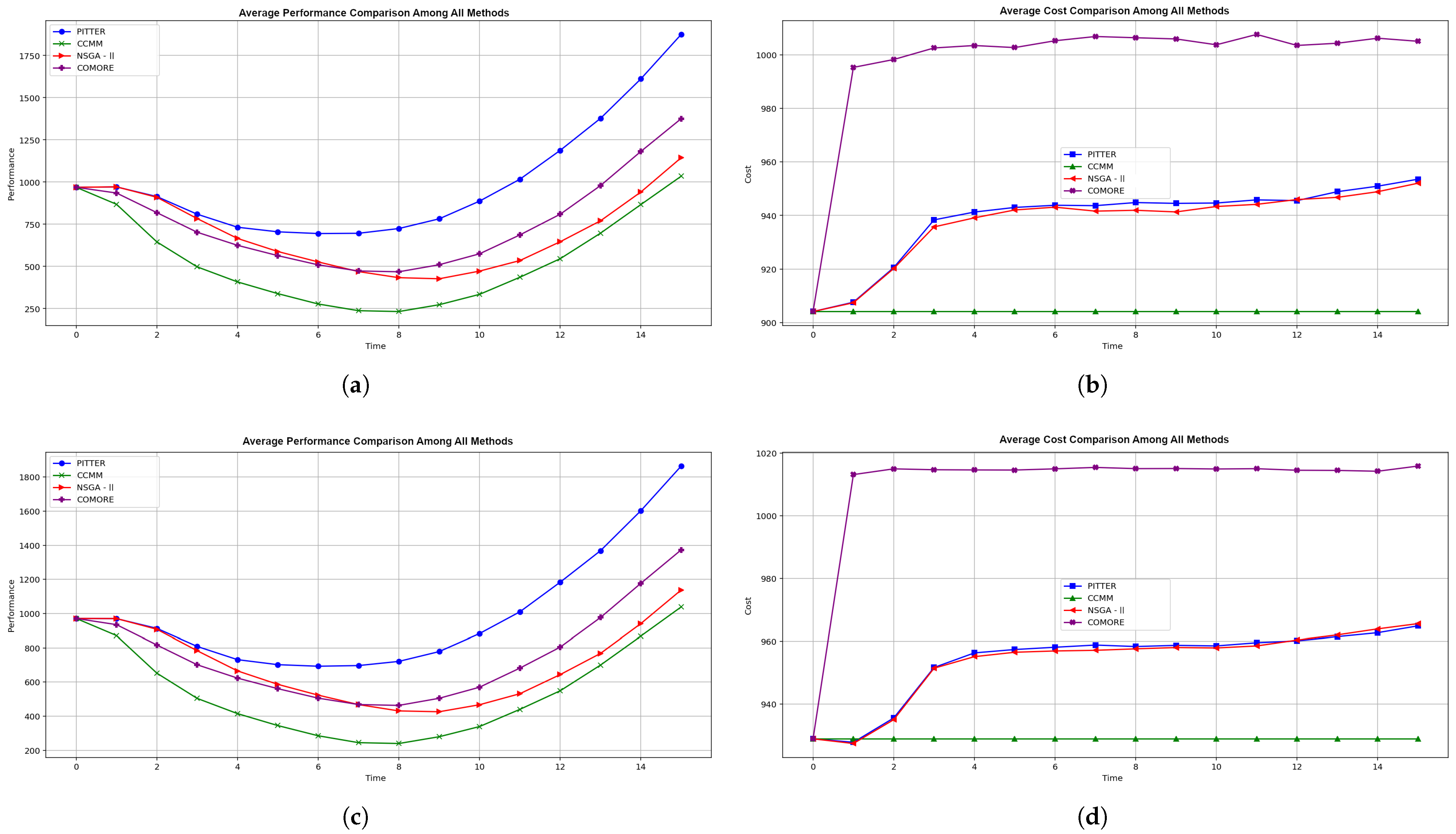
4.2. First Experiment: Results and Analysis
4.3. Second Experiment: Algorithm Implementation
5. Conclusions and Limitations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RtC | Resistance to Change |
| HRAP | Human Resource Allocation Problem |
| NuRe | Nurse Reallocation |
| CoMoRe | Continuous Monitoring and Reallocation |
| CCMM | Classical Change Management Model |
| DMOPs | Dynamic Multi-Objective Optimization Problems |
| EDMO | Evolutionary Dynamic Multi-Objective Optimization |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| TPI | Total Performance Improvement |
References
- Al-Haddad, S.; Kotnour, T. Integrating the organizational change literature: A model for successful change. J. Organ. Chang. Manag. 2015, 28, 234–262. [Google Scholar] [CrossRef]
- Burnes, B.; Jackson, P. Success and failure in organizational change: An exploration of the role of values. J. Chang. Manag. 2011, 11, 133–162. [Google Scholar] [CrossRef]
- Cândido, C.; Santos, S. Strategy implementation: What is the failure rate? J. Manag. Organ. 2015, 21, 237–262. [Google Scholar] [CrossRef]
- Kunert, S.; von der Weth, R. Failure in Projects; Springer International Publishing: Cham, Switzerland, 2018; pp. 47–66. [Google Scholar] [CrossRef]
- Elrod, P.D.; Tippett, D.D. The “death valley” of change. J. Organ. Chang. Manag. 2002, 15, 273–291. [Google Scholar] [CrossRef]
- Stouten, J.; Rousseau, D.; Cremer, D.D. Successful organizational change: Integrating the management practice and scholarly literatures. Acad. Manag. Ann. 2018, 12, 752–788. [Google Scholar] [CrossRef]
- Warrick, D. Revisiting resistance to change and how to manage it: What has been learned and what organizations need to do. Bus. Horizons 2023, 66, 433–441. [Google Scholar] [CrossRef]
- Reineholm, C.; Lundqvist, D.; Wallo, A. Change competence: An integrative literature review. Work 2024, 79, 569–584. [Google Scholar] [CrossRef]
- Armenakis, A.; Harris, S.; Mossholder, K. Creating Readiness for Organizational Change. Hum. Relat. 1993, 46, 681–703. [Google Scholar] [CrossRef]
- Piderit, S.K. Rethinking resistance and recognizing ambivalence: A multidimensional view of attitudes toward an organizational change. Acad. Manag. Rev. 2000, 25, 783–794. [Google Scholar] [CrossRef]
- Kotter, J.P.; Schlesinger, L.A. Choosing Strategies for Change. Harv. Bus. Rev. 2008, 86, 130–139+162. [Google Scholar]
- Armenakis, A.A.; Harris, S.G. Reflections: Our Journey in Organizational Change Research and Practice. J. Chang. Manag. 2009, 9, 127–142. [Google Scholar] [CrossRef]
- Ford, J.; Ford, L.; D’Amelio, A. Resistance to change: The rest of the story. Acad. Manag. Rev. 2008, 33, 362–377. [Google Scholar] [CrossRef]
- Thundiyil, T.G.; Chiaburu, D.S.; Oh, I.S.; Banks, G.C.; Peng, A.C. Cynical About Change? A Preliminary Meta-Analysis and Future Research Agenda. J. Appl. Behav. Sci. 2015, 51, 429–450. [Google Scholar] [CrossRef]
- Grama, B.; Todericiu, R. Change, Resistance to Change and Organizational Cynicism. Stud. Bus. Econ. 2017, 11, 47–54. [Google Scholar] [CrossRef]
- Oreg, S. Resistance to change: Developing an individual differences measure. J. Appl. Psychol. 2003, 88, 680–693. [Google Scholar] [CrossRef]
- Ferrari, F. Skills mismatch and change confidence: The impact of training on change recipients’ self-efficacy. Eur. J. Train. Dev. 2022, 47, 69–90. [Google Scholar] [CrossRef]
- Coch, L.; French, J. Overcoming Resistance to Change. Hum. Relat. 1948, 1, 512–532. [Google Scholar] [CrossRef]
- Oreg, S. Resistance to Change and Performance: Toward a More Even-Handed View of Dispositional Resistance. J. Appl. Behav. Sci. 2018, 54, 88–107. [Google Scholar] [CrossRef]
- Jiang, S.; Zou, J.; Yang, S.; Yao, X. Evolutionary Dynamic Multi-objective Optimisation: A Survey. ACM Comput. Surv. 2023, 55, 1–47. [Google Scholar] [CrossRef]
- Ros, A.D.; Vainieri, M.; Bellé, N. An Overview of Reviews: Organizational Change Management Architecture. J. Chang. Manag. 2023, 23, 113–142. [Google Scholar] [CrossRef]
- Oreg, S.; Vakola, M.; Armenakis, A. Change Recipients’ Reactions to Organizational Change: A 60-Year Review of Quantitative Studies. J. Appl. Behav. Sci. 2011, 47, 461–524. [Google Scholar] [CrossRef]
- Lomba-Portela, L.; Domínguez-Lloria, S.; Pino-Juste, M.R. Resistances to Educational Change: Teachers’ Perceptions. Educ. Sci. 2022, 12, 359. [Google Scholar] [CrossRef]
- Panagiotopoulos, F.; Fragidis, L.; Chatzis, V. A Nurse Reallocation method for successful change management during Electronic Health Record systems implementations. In Proceedings of the ACM International Conference Proceeding Series, Lamia, Greece, 24–26 November 2023; pp. 150–155. [Google Scholar] [CrossRef]
- Panagiotopoulos, F.; Chatzis, V. A Continuous Monitoring and Reallocation Method for Successful Decisions in Change Management. Algorithms 2025, 18, 184. [Google Scholar] [CrossRef]
- Lewin, K. Frontiers in Group Dynamics: Concept, Method and Reality in Social Science; Social Equilibria and Social Change. Hum. Relat. 1947, 1, 5–41. [Google Scholar] [CrossRef]
- Burnes, B. The Origins of Lewin’s Three-Step Model of Change. J. Appl. Behav. Sci. 2020, 56, 32–59. [Google Scholar] [CrossRef]
- Beer, M.; Eisenstat, R.; Spector, B. Why change programs don’t produce change. Harv. Bus. Rev. 1990, 68, 158–166. [Google Scholar]
- Hiatt, J.M.; Creasey, T.J. Change Management: The People Side of Change; Prosci Learning Center Publications: Fort Collins, CO, USA, 2012. [Google Scholar]
- Picado Argüello, B.; González-Prida, V. Integrating Change Management with a Knowledge Management Framework: A Methodological Proposal. Information 2024, 15, 406. [Google Scholar] [CrossRef]
- Arazmjoo, H.; Rahmanseresht, H. A multi-dimensional meta-heuristic model for managing organizational change. Manag. Decis. 2020, 58, 526–543. [Google Scholar] [CrossRef]
- Maes, G.; Hootegem, G.V. A systems model of organizational change. J. Organ. Chang. Manag. 2019, 32, 725–738. [Google Scholar] [CrossRef]
- McDermott, O.; Antony, J.; Sony, M.; Looby, E. A critical evaluation and measurement of organisational readiness and adoption for continuous improvement within a medical device manufacturer. Int. J. Manag. Sci. Eng. Manag. 2023, 18, 145–155. [Google Scholar] [CrossRef]
- Hutzschenreuter, A.K.; Bosman, P.A.N.; La Poutré, H. Evolutionary multiobjective optimization for dynamic hospital resource management. In International Conference on Evolutionary Multi-Criterion Optimization, 5467 LNCS; Springer: Berlin/Heidelberg, Germany, 2010; pp. 320–334. [Google Scholar] [CrossRef]
- Zeng, H.; Nie, S. Multiobjective optimization allocation of multi-skilled workers considering the skill heterogeneity and time-varying effects in unit brake production lines. Eng. Rep. 2024, 6, e12774. [Google Scholar] [CrossRef]
- Miguel, F.M.; Frutos, M.; Méndez, M.; Tohmé, F.; González, B. Comparison of MOEAs in an Optimization-Decision Methodology for a Joint Order Batching and Picking System. Mathematics 2024, 12, 1246. [Google Scholar] [CrossRef]
- Adekoya, A.; Helbig, M. Decision-Maker’s Preference-Driven Dynamic Multi-Objective Optimization. Algorithms 2023, 16, 504. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, J.; Hou, Z.; Liu, Y.; Zou, J.; Xia, Y.; Yang, S. A novel preference-driven evolutionary algorithm for dynamic multi-objective problems. Swarm Evol. Comput. 2024, 89, 101638. [Google Scholar] [CrossRef]
- Ran, X.; Suyaroj, N.; Tepsan, W.; Lei, M.; Ma, H.; Zhou, X.; Deng, W. A novel fuzzy system-based genetic algorithm for trajectory segment generation in urban global positioning system. J. Adv. Res. 2025; in press. [Google Scholar] [CrossRef]
- Deng, W.; Wang, J.; Guo, A.; Zhao, H. Quantum differential evolutionary algorithm with quantum-adaptive mutation strategy and population state evaluation framework for high-dimensional problems. Inf. Sci. 2024, 676, 120787. [Google Scholar] [CrossRef]
- Song, Y.; Song, C. Adaptive evolutionary multitask optimization based on anomaly detection transfer of multiple similar sources. Expert Syst. Appl. 2025, 283, 127599. [Google Scholar] [CrossRef]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
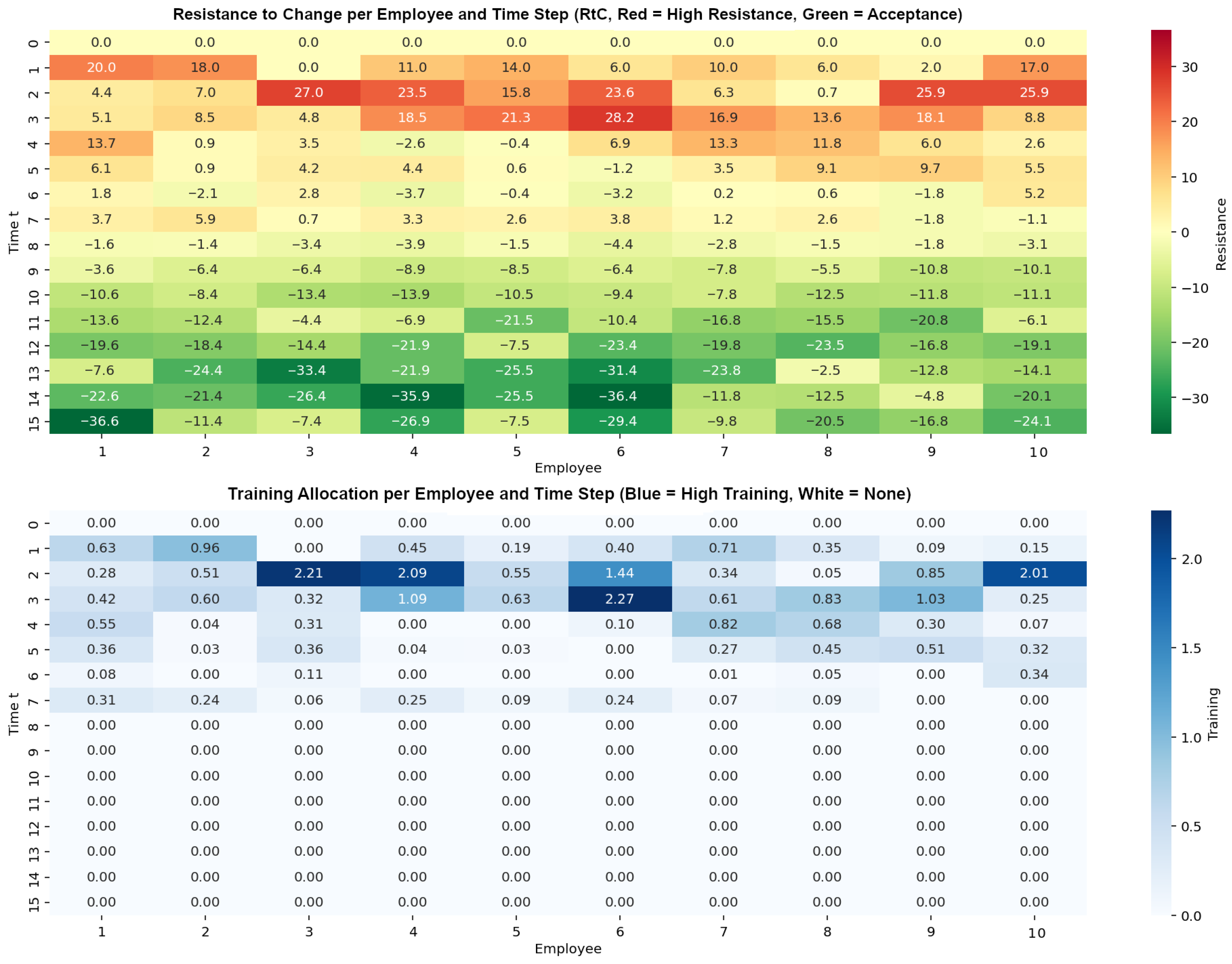
| TIME (t) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Resistance limits | [0,20] | [0,44] | [0,30] | [0,18] | [0,14] | [0,12] | [0,8] | [-] |
| TIME (t) | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Resistance limits | [0,−8] | [0,−12] | [0,−20] | [0,−22] | [0,−30] | [0,−34] | [0,−34] | [-] |
| Performance ((t = 0)) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Jobs () | ||||||||||
| Workers () | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 95 | 90 | 93 | 93 | 97 | 99 | 93 | 95 | 92 | 94 |
| 2 | 97 | 96 | 98 | 98 | 100 | 91 | 96 | 97 | 97 | 98 |
| 3 | 91 | 95 | 99 | 98 | 99 | 94 | 93 | 90 | 93 | 95 |
| 4 | 90 | 92 | 93 | 98 | 91 | 93 | 93 | 93 | 97 | 90 |
| 5 | 91 | 99 | 99 | 90 | 100 | 94 | 97 | 93 | 92 | 97 |
| 6 | 92 | 90 | 90 | 94 | 95 | 95 | 96 | 98 | 94 | 91 |
| 7 | 94 | 99 | 100 | 100 | 98 | 91 | 91 | 97 | 99 | 99 |
| 8 | 93 | 96 | 97 | 92 | 90 | 93 | 95 | 99 | 100 | 94 |
| 9 | 94 | 96 | 94 | 94 | 93 | 94 | 94 | 98 | 94 | 93 |
| 10 | 100 | 97 | 95 | 95 | 90 | 91 | 95 | 99 | 93 | 90 |
| Cost ((t = 0)) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Jobs () | ||||||||||
| Workers () | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 95 | 87 | 89 | 96 | 106 | 116 | 112 | 88 | 114 | 92 |
| 2 | 86 | 102 | 99 | 103 | 102 | 94 | 116 | 101 | 100 | 106 |
| 3 | 115 | 94 | 88 | 94 | 107 | 89 | 95 | 94 | 91 | 115 |
| 4 | 93 | 106 | 84 | 82 | 101 | 108 | 106 | 102 | 96 | 105 |
| 5 | 97 | 100 | 93 | 99 | 89 | 93 | 94 | 106 | 91 | 114 |
| 6 | 91 | 84 | 107 | 98 | 105 | 102 | 101 | 98 | 106 | 91 |
| 7 | 112 | 112 | 105 | 99 | 108 | 98 | 101 | 104 | 99 | 108 |
| 8 | 90 | 113 | 111 | 92 | 102 | 88 | 114 | 99 | 101 | 86 |
| 9 | 107 | 83 | 85 | 96 | 95 | 93 | 108 | 92 | 102 | 106 |
| 10 | 99 | 117 | 101 | 112 | 91 | 113 | 99 | 98 | 95 | 103 |
| Workers (i) | Jobs (j) | Performance ((t = 0)) | Cost |
|---|---|---|---|
| 1 | 10 | 94 | 92 |
| 2 | 1 | 97 | 86 |
| 3 | 3 | 99 | 88 |
| 4 | 4 | 98 | 82 |
| 5 | 5 | 100 | 89 |
| 6 | 7 | 96 | 101 |
| 7 | 9 | 99 | 99 |
| 8 | 6 | 93 | 88 |
| 9 | 2 | 96 | 83 |
| 10 | 8 | 99 | 98 |
| Total | – | 971 | 906 |
| Resistance ((t = 0)) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Jobs () | ||||||||||
| Workers () | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 12 | 6 | 5 | 10 | 17 | 16 | 2 | 6 | 1 | 12 |
| 2 | 7 | 17 | 2 | 1 | 8 | 6 | 11 | 0 | 7 | 19 |
| 3 | 6 | 8 | 11 | 2 | 3 | 9 | 12 | 17 | 6 | 9 |
| 4 | 19 | 1 | 14 | 16 | 3 | 3 | 12 | 7 | 15 | 18 |
| 5 | 13 | 15 | 11 | 7 | 11 | 9 | 19 | 4 | 3 | 8 |
| 6 | 15 | 15 | 15 | 19 | 18 | 8 | 4 | 3 | 0 | 5 |
| 7 | 17 | 13 | 19 | 14 | 1 | 14 | 14 | 2 | 13 | 0 |
| 8 | 5 | 3 | 0 | 7 | 10 | 3 | 20 | 6 | 4 | 13 |
| 9 | 20 | 13 | 13 | 6 | 0 | 12 | 2 | 2 | 0 | 3 |
| 10 | 6 | 20 | 0 | 10 | 20 | 1 | 7 | 15 | 2 | 12 |
| Training ((t = 0)) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Jobs () | ||||||||||
| Workers () | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 0.32 | 0.35 | 0.32 | 0.76 | 0.89 | 1.03 | 0.15 | 0.28 | 0.07 | 0.64 |
| 2 | 0.55 | 0.45 | 0.08 | 0.05 | 0.46 | 0.10 | 0.62 | 0.00 | 0.49 | 0.90 |
| 3 | 0.35 | 0.64 | 0.82 | 0.12 | 0.22 | 0.58 | 0.62 | 0.90 | 0.30 | 0.61 |
| 4 | 1.26 | 0.05 | 1.27 | 1.22 | 0.09 | 0.12 | 0.87 | 0.18 | 0.62 | 1.02 |
| 5 | 0.97 | 0.68 | 0.74 | 0.31 | 0.53 | 0.41 | 1.28 | 0.33 | 0.19 | 0.65 |
| 6 | 0.95 | 0.40 | 1.02 | 1.02 | 1.36 | 0.41 | 0.29 | 0.10 | 0.00 | 0.28 |
| 7 | 1.49 | 0.83 | 0.53 | 0.47 | 0.09 | 1.27 | 0.26 | 0.09 | 0.61 | 0.00 |
| 8 | 0.30 | 0.15 | 0.00 | 0.38 | 0.32 | 0.11 | 0.86 | 0.36 | 0.13 | 0.68 |
| 9 | 1.29 | 0.60 | 0.49 | 0.39 | 0.00 | 0.48 | 0.17 | 0.13 | 0.00 | 0.10 |
| 10 | 0.37 | 1.06 | 0.00 | 0.35 | 1.50 | 0.02 | 0.29 | 0.48 | 0.15 | 0.70 |
| Population Size | Generations | Crossover Probability | Mutation Probability |
|---|---|---|---|
| 100 | 200 | 0.7 | 1/n |
| Total Performance | ||||||||
|---|---|---|---|---|---|---|---|---|
| Time | PITTER | CV | CCMM | CV | NSGA-II | CV | CoMoRe | CV |
| 0 | 969 | 0.27% | 969 | 0.27% | 969 | 0.27% | 969 | 0.27% |
| 1 | 971 | 0.41% | 868 | 2.35% | 972 | 0.40% | 935 | 1.01% |
| 2 | 914 | 1.17% | 645 | 6.23% | 910 | 1.37% | 819 | 2.63% |
| 3 | 810 | 2.66% | 497 | 9.82% | 783 | 3.08% | 703 | 4.05% |
| 4 | 732 | 3.76% | 408 | 12.71% | 666 | 4.48% | 625 | 4.71% |
| 5 | 705 | 4.43% | 339 | 16.04% | 588 | 5.43% | 564 | 5.39% |
| 6 | 695 | 4.84% | 277 | 19.67% | 527 | 6.27% | 509 | 5.95% |
| 7 | 696 | 5.21% | 238 | 23.59% | 470 | 7.38% | 473 | 6.45% |
| 8 | 725 | 5.10% | 233 | 24.01% | 433 | 7.83% | 468 | 6.51% |
| 9 | 782 | 5.25% | 273 | 20.44% | 427 | 7.71% | 510 | 6.17% |
| 10 | 887 | 5.08% | 335 | 16.85% | 472 | 7.37% | 575 | 6.05% |
| 11 | 1017 | 4.62% | 436 | 13.82% | 535 | 6.98% | 687 | 5.56% |
| 12 | 1188 | 4.87% | 546 | 11.58% | 646 | 5.72% | 809 | 4.67% |
| 13 | 1378 | 4.62% | 697 | 9.57% | 770 | 5.10% | 979 | 4.23% |
| 14 | 1611 | 4.79% | 867 | 8.62% | 941 | 4.45% | 1181 | 3.66% |
| 15 | 1875 | 4.54% | 1035 | 8.63% | 1144 | 4.43% | 1376 | 3.40% |
| Total Performance | ||||||||
|---|---|---|---|---|---|---|---|---|
| Time | PITTER | CV | CCMM | CV | NSGA-II | CV | CoMoRe | CV |
| 0 | 971 | 0.02% | 971 | 0.02% | 971 | 0.02% | 971 | 0.02% |
| 1 | 970 | 0.23% | 871 | 2.19% | 970 | 0.18% | 935 | 0.92% |
| 2 | 913 | 1.19% | 652 | 6.92% | 908 | 1.25% | 817 | 2.50% |
| 3 | 809 | 2.78% | 504 | 10.90% | 784 | 2.87% | 701 | 3.69% |
| 4 | 731 | 3.88% | 415 | 13.86% | 665 | 4.23% | 623 | 4.58% |
| 5 | 702 | 4.44% | 345 | 17.13% | 586 | 5.05% | 561 | 5.24% |
| 6 | 693 | 4.76% | 285 | 21.35% | 523 | 5.87% | 506 | 6.07% |
| 7 | 697 | 5.24% | 245 | 25.10% | 468 | 6.70% | 468 | 6.62% |
| 8 | 721 | 5.38% | 240 | 25.63% | 431 | 7.45% | 463 | 6.69% |
| 9 | 779 | 5.52% | 279 | 22.16% | 426 | 7.50% | 505 | 6.23% |
| 10 | 883 | 5.30% | 339 | 18.55% | 467 | 7.16% | 570 | 5.71% |
| 11 | 1010 | 5.29% | 440 | 14.80% | 532 | 6.41% | 682 | 5.02% |
| 12 | 1184 | 5.03% | 549 | 12.46% | 644 | 5.63% | 804 | 4.41% |
| 13 | 1368 | 4.87% | 699 | 10.24% | 768 | 4.99% | 977 | 3.97% |
| 14 | 1603 | 4.62% | 868 | 9.05% | 941 | 4.25% | 1177 | 3.65% |
| 15 | 1865 | 4.45% | 1039 | 8.13% | 1138 | 3.91% | 1373 | 3.44% |
| Total Performance Improvement (%) | ||||||
|---|---|---|---|---|---|---|
| Repetitions | 100 | 1000 | ||||
| Time () | PITTER vs. CCMM | PITTER vs. NSGA-II | PITTER vs. CoMoRe | PITTER vs. CCMM | PITTER vs. NSGA-II | PITTER vs. CoMoRe |
| 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 1 | 11.87 | -0.10 | 3.85 | 11.37 | 0.00 | 3.74 |
| 2 | 41.71 | 0.44 | 11.60 | 40.03 | 0.55 | 11.75 |
| 3 | 62.98 | 3.45 | 15.22 | 60.52 | 3.19 | 15.41 |
| 4 | 79.41 | 9.91 | 17.12 | 76.14 | 9.92 | 17.34 |
| 5 | 107.96 | 19.90 | 25.00 | 103.48 | 19.80 | 25.13 |
| 6 | 150.90 | 31.88 | 36.54 | 143.16 | 32.50 | 36.96 |
| 7 | 192.44 | 48.09 | 47.15 | 184.49 | 48.93 | 48.93 |
| 8 | 211.16 | 67.44 | 54.91 | 200.42 | 67.29 | 55.72 |
| 9 | 186.45 | 83.14 | 53.33 | 179.21 | 82.86 | 54.26 |
| 10 | 164.78 | 87.92 | 54.26 | 160.47 | 89.08 | 54.91 |
| 11 | 133.26 | 90.09 | 48.03 | 129.55 | 89.85 | 48.09 |
| 12 | 117.58 | 83.90 | 46.85 | 115.66 | 83.85 | 47.26 |
| 13 | 97.70 | 78.96 | 40.76 | 95.71 | 78.13 | 40.02 |
| 14 | 85.81 | 71.20 | 36.41 | 84.68 | 70.35 | 36.19 |
| 15 | 81.16 | 63.90 | 36.26 | 79.50 | 63.88 | 35.83 |
| Total Cost | ||||||||
|---|---|---|---|---|---|---|---|---|
| Repetitions | 100 | 1000 | ||||||
| Time () | PITTER | CCMM | NSGA-II | CoMoRe | PITTER | CCMM | NSGA-II | CoMoRe |
| 0 | 904 | 904 | 904 | 904 | 929 | 929 | 929 | 929 |
| 1 | 908 | 904 | 907 | 995 | 928 | 929 | 927 | 1013 |
| 2 | 921 | 904 | 920 | 998 | 936 | 929 | 935 | 1015 |
| 3 | 938 | 904 | 936 | 1003 | 952 | 929 | 951 | 1015 |
| 4 | 941 | 904 | 939 | 1003 | 956 | 929 | 955 | 1015 |
| 5 | 943 | 904 | 942 | 1003 | 957 | 929 | 957 | 1015 |
| 6 | 944 | 904 | 943 | 1005 | 958 | 929 | 957 | 1015 |
| 7 | 944 | 904 | 942 | 1007 | 959 | 929 | 957 | 1015 |
| 8 | 945 | 904 | 942 | 1006 | 958 | 929 | 958 | 1015 |
| 9 | 945 | 904 | 941 | 1006 | 959 | 929 | 958 | 1015 |
| 10 | 945 | 904 | 943 | 1004 | 959 | 929 | 958 | 1015 |
| 11 | 946 | 904 | 944 | 1008 | 960 | 929 | 959 | 1015 |
| 12 | 946 | 904 | 946 | 1003 | 960 | 929 | 960 | 1015 |
| 13 | 949 | 904 | 947 | 1004 | 961 | 929 | 962 | 1015 |
| 14 | 951 | 904 | 949 | 1006 | 963 | 929 | 964 | 1014 |
| 15 | 954 | 904 | 952 | 1005 | 965 | 929 | 966 | 1016 |
| Time (t) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Employee () | Tasks () | |||||||||||||||
| 1 | 10 | 10 | 2 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 6 | 1 | 1 | 2 |
| 3 | 3 | 3 | 6 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 4 | 4 | 4 | 8 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 4 | 6 | 4 | 6 | 6 | 6 |
| 5 | 5 | 5 | 5 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 8 | 4 | 1 | 4 | 8 | 8 |
| 6 | 7 | 7 | 7 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| 7 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| 8 | 6 | 6 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 6 | 2 | 2 | 2 | 2 | 1 |
| 9 | 2 | 2 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 2 | 10 | 10 | 10 | 4 | 4 |
| 10 | 8 | 8 | 4 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 10 | 8 | 8 | 8 | 10 | 10 |
| Total Performance | ||||||||
|---|---|---|---|---|---|---|---|---|
| Time | PITTER | CV | CCMM | CV | NSGA-II | CV | CoMoRe | CV |
| 0 | 9694 | 0.24% | 9694 | 0.24% | 9694 | 0.24% | 9694 | 0.24% |
| 1 | 9701 | 0.23% | 8706 | 0.70% | 9703 | 0.24% | 9852 | 0.11% |
| 2 | 8888 | 0.69% | 6498 | 2.30% | 8862 | 0.66% | 9255 | 0.31% |
| 3 | 7369 | 1.73% | 5006 | 3.30% | 7178 | 1.93% | 8480 | 0.43% |
| 4 | 6560 | 2.11% | 4105 | 4.32% | 5987 | 2.35% | 7831 | 0.62% |
| 5 | 6304 | 2.21% | 3403 | 5.42% | 5278 | 2.49% | 7280 | 0.81% |
| 6 | 6254 | 2.27% | 2802 | 6.57% | 4695 | 2.86% | 6782 | 0.83% |
| 7 | 6315 | 2.34% | 2406 | 7.62% | 4203 | 3.25% | 6434 | 0.92% |
| 8 | 6614 | 2.49% | 2356 | 7.76% | 3888 | 3.55% | 6386 | 0.93% |
| 9 | 7235 | 2.22% | 2757 | 6.62% | 3879 | 3.35% | 6832 | 0.91% |
| 10 | 8292 | 2.16% | 3354 | 5.53% | 4318 | 3.00% | 7528 | 0.76% |
| 11 | 9532 | 2.10% | 4359 | 4.24% | 4970 | 2.69% | 8765 | 0.74% |
| 12 | 11,204 | 1.90% | 5456 | 3.56% | 6041 | 2.47% | 10,125 | 0.68% |
| 13 | 12,986 | 1.93% | 6954 | 3.07% | 7229 | 2.31% | 12,051 | 0.61% |
| 14 | 15,203 | 1.90% | 8652 | 2.63% | 8842 | 2.14% | 14,261 | 0.52% |
| 15 | 17,676 | 1.77% | 10,354 | 2.51% | 10,721 | 1.80% | 16,419 | 0.60% |
| Total Performance Improvement (%) | |||
|---|---|---|---|
| Time () | PITTER vs. CCMM | PITTER vs. NSGA-II | PITTER vs. CoMoRe |
| 0 | 0.00 | 0.00 | 0.00 |
| 1 | 11.43 | −0.02 | −1.53 |
| 2 | 36.78 | 0.30 | −3.97 |
| 3 | 47.20 | 2.66 | −13.10 |
| 4 | 59.80 | 9.58 | −16.22 |
| 5 | 85.24 | 19.45 | −13.40 |
| 6 | 123.23 | 33.20 | −7.79 |
| 7 | 162.51 | 50.24 | −1.86 |
| 8 | 180.70 | 70.13 | 3.58 |
| 9 | 162.48 | 86.52 | 5.91 |
| 10 | 147.20 | 92.02 | 10.15 |
| 11 | 118.67 | 91.78 | 8.75 |
| 12 | 105.35 | 85.45 | 10.65 |
| 13 | 86.75 | 79.65 | 7.76 |
| 14 | 75.72 | 71.93 | 6.60 |
| 15 | 70.72 | 64.87 | 7.66 |
| Average Total Cost | ||||
|---|---|---|---|---|
| Time () | PITTER | CCMM | NSGA-II | CoMoRe |
| 0 | 9245 | 9245 | 9245 | 9245 |
| 1 | 9224 | 9245 | 9220 | 9985 |
| 2 | 9292 | 9245 | 9262 | 9988 |
| 3 | 9420 | 9245 | 9394 | 9986 |
| 4 | 9454 | 9245 | 9424 | 9990 |
| 5 | 9433 | 9245 | 9422 | 10,000 |
| 6 | 9431 | 9245 | 9419 | 9996 |
| 7 | 9426 | 9245 | 9413 | 10,008 |
| 8 | 9415 | 9245 | 9400 | 10,007 |
| 9 | 9406 | 9245 | 9394 | 10,003 |
| 10 | 9396 | 9245 | 9386 | 9996 |
| 11 | 9385 | 9245 | 9378 | 9998 |
| 12 | 9384 | 9245 | 9384 | 9998 |
| 13 | 9382 | 9245 | 9385 | 10,000 |
| 14 | 9390 | 9245 | 9396 | 9988 |
| 15 | 9405 | 9245 | 9405 | 9990 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panagiotopoulos, F.; Chatzis, V. A Mathematical Method for Optimized Decision-Making and Performance Improvement Through Training and Employee Reallocation Under Resistance to Change. Mathematics 2025, 13, 2619. https://doi.org/10.3390/math13162619
Panagiotopoulos F, Chatzis V. A Mathematical Method for Optimized Decision-Making and Performance Improvement Through Training and Employee Reallocation Under Resistance to Change. Mathematics. 2025; 13(16):2619. https://doi.org/10.3390/math13162619
Chicago/Turabian StylePanagiotopoulos, Fotios, and Vassilios Chatzis. 2025. "A Mathematical Method for Optimized Decision-Making and Performance Improvement Through Training and Employee Reallocation Under Resistance to Change" Mathematics 13, no. 16: 2619. https://doi.org/10.3390/math13162619
APA StylePanagiotopoulos, F., & Chatzis, V. (2025). A Mathematical Method for Optimized Decision-Making and Performance Improvement Through Training and Employee Reallocation Under Resistance to Change. Mathematics, 13(16), 2619. https://doi.org/10.3390/math13162619







