Abstract
Industrial systems operating under severe mission environment are frequently confronted with intricate failure behaviors arising from system internal degradation and extrinsic stresses, posing an elevating challenge to system survivability and mission reliability. Mission termination strategies are attracting increasing attention as an intuitive and effective means to mitigating catastrophic mission-induced risk. However, how to manage coupled risk arising from competing fault processes, particularly when these modes are interdependent, has been rarely reported in existing works. To bridge this gap, this study delves into a dynamic risk control policy for continuously degrading systems operating under a random shock environment, which yields competing and dependent fault processes. An optimal mission termination policy is developed to minimize risk-centered losses throughout the mission execution, whose optimization problem constitutes a finite-time Markov decision process. Some critical structural properties associated with the optimal policy are derived, and by leveraging these structures, the alerting threshold for implementing mission termination procedure is formally established. Alternative risk control policies are introduced for comparison, and experimental evaluations substantiate the superior model capacity in risk mitigation.
MSC:
90B25
1. Introduction
A large variety of real-world, safety-critical systems operate under harsh and even extreme working conditions, including, but not limited to, oceans, plateaus, near space, and polar regions, creating significant failure risk that endangers mission completion and personnel/equipment [1,2,3,4,5,6,7,8,9]. It is therefore of pivotal importance to devise effective risk control strategies that alleviate risk-induced losses of mission-critical systems. Enabled by notable technological strides in sensing and data interpretation capabilities, the online monitoring, prediction, and control of mission risk is becoming increasingly feasible in mission-critical systems such as unmanned aerial vehicles, ocean-going ships, and reusable rockets [10,11,12,13,14,15,16].
Condition-Based Maintenance (CBM) has been demonstrated as an effective risk control methodology [17,18,19,20,21,22,23]. CBM procedures are conducted primarily based on information collected through condition monitoring, which suggest repairs/replacement actions upon the initialization of a warning system state [24,25,26,27,28,29,30]. However, such procedures usually require a system shut-down, which may not be feasible for a system executing critical, uninterruptable missions. Moreover, in cases where system failure may lead to severe safety hazards and tremendous economic losses, it is preferable to terminate the mission immediately once the system reaches a degraded condition to ensure that the system survives rather than conducting repair actions for ensuring mission success [31,32,33,34,35,36].
Mission termination strategies, as an intuitive means to balance system survivability and mission reliability, have been attracting increasing attention in the recent literature [37,38,39,40,41,42]. Analogous to CBM, mission abort policies benefit from advancement of sensor technology, allowing policy optimization based on degradation levels [43]. Qiu et al. [44] proposed an optimal abort policy leveraging the number of minor failures as decision variables. Yang et al. [45] designed a mission termination strategy that strives to balance the potential hazards resulting from either unsuccessful mission execution or system malfunctions. They developed a dynamic age-based abort framework that integrates the information system’s degradation level, age condition, and estimated RUL. Additionally, Yang et al. [46] designed an optimal mission termination strategy under a fixed-duration mission setup, based on early warning signal information. Cha et al. [47] explored an efficient strategy for premature mission termination for partially repairable heterogeneous systems. Some researchers have also formulated mission abort policies within the framework of the MDP. For example, Zhao et al. [48] developed a decision model for early termination in systems undergoing deterioration characterized by a Gamma-type stochastic progression, using system degradation as the decision variable. Cheng et al. [49] analyzed the best combination of inspection and termination strategies for systems with incomplete observability.
Mission safety, in many examples, is also severely endangered by external environmental shocks, particularly when exposed to harsh natural environments [50]. Levitin et al. [51] developed a policy addressing mission termination and rescue operations in system deployments operating in stochastic shock environments. They proposed an optimization algorithm that balances mission success probability and system survival probability in order to guide the determination of the termination indicator. Additionally, Levitin et al. [52] developed a termination strategy applied to systems exposed to shock-driven stochastic settings, using shock frequency as a benchmark for abort decisions. Zhao et al. [53] analyzed a two-variable-based abort scheme for mission-executing systems in systems operating under random shock environments and multiple failure modes, and demonstrated the superior model performance via benchmarking experiments against several heuristic-based strategies.
Although previous studies have devised several classes of effective risk control policies associated with distinct failure models, studies on mission termination strategies for systems enduring multiple failure modes and complex mission environments have been rarely reported. In fact, prevailing existing mission abort strategies focused exclusively on dealing with single system failure modes, either internal degradation (either continuous degradation or discrete state transition) or external random shocks [54,55,56]. There is, however, a lack of comprehensive analysis for mission abort methodologies that is able to control the integrated risk stimulated by both internal degradation and external environmental shocks, which is usually the case for many practical mission-oriented systems. It is therefore of both theoretical and realistic interest to develop advanced mission abort strategies and associated modes that are able to simultaneously control both types of failure modes, particularly when these modes are physically/statistically interacted.
To bridge the gap addressed previously, we delve deep into an innovative risk-aware mission termination strategy for systems exposed to coupling risks of both endogenous performance degradation and external environmental shocks. In contrast to previous studies, the proposed framework develops a stochastic modeling approach to characterize the interdependence between both failure modes, and accordingly accounts for the coupling implication of competing failures on malfunction risk throughout the mission execution. The mission reliability model under the competing failure mode is formulated, whose key affecting parameters are thoroughly investigated. Building upon the reliability model, we develop a dynamic mission termination strategy that balances system survivability and mission reliability by controlling the accumulated damage due to dependent failure modes.
A distinguished feature of the proposed methodology is that it, for the first time, constructs a tractable, dynamic risk control framework that is applicable to competing and dependent failure modes. We theoretically show that the risk control problem of interest constitutes a finite-time Markov decision process, whose mission-loss-related value function possesses a monotonous behavior. By exploiting these findings, we establish the optimal abort control limit. In particular, we show that the control limit is a non-decreasing function of the number of condition monitoring. To our knowledge, this is the first trial to devise adaptive control limit policies for managing competing failure modes, which significantly promotes the decision accuracy and efficiency under complex mission environment. The scientific contribution to this paper is summarized as follows:
- ■
- A tractable risk control methodology is developed to manage coupling mission-critical risks of dependent fault processes stemming from both (a) endogenous degradation and (b) extrinsic environmental damage;
- ■
- The model we propose enables the dynamic control of anticipated loss throughout the mission implementation, which is realized by striving for a global trade-off between system survivability and mission reliability;
- ■
- A series of structural properties corresponding to optimal termination decisions are rigorously established, which constitutes a global dynamic threshold-restriction risk control policy. Such findings allow for efficient risk mitigation with an intuitive decision rule, which substantially streamlines computation effort;
- ■
- Comprehensive comparative experiments are conducted on mission risk control of unmanned aerial vehicle, which substantiate the superior model performance in mitigating anticipated risk losses with considerable efficiency.
The remainder of this paper is structured as follows. Section 2 presents the fundamental problem associated with failure evolution and prevention under dependent fault processes. Section 3 formulates the risk control model, analyzes its structural properties to enhance decision efficiency and accuracy, and presents heuristic policies for comparison. Section 4 conducts comparative experiments to validate the model. Section 5 presents the discussion and concludes the paper.
2. Problem Description
We investigate a dynamic risk control policy for a safety-critical system that is required to execute a continuous mission under a coupling risk environment, where malfunction creates a safety hazard which arises from endogenous state degradation in conjunction with an external environmental shock. The core idea is to manage such an integrated risk throughout the mission execution in order to strive a balance between the following: (a) promoting mission success possibility, and (b) ensuring system survivability. In what follows, we introduce the fundamental problem with regard to the interdependent failure modes that affects mission execution, and accordingly devise risk-aware mission termination strategies. Following the strategy, the fundamental reliability and mission reliability characteristics are established, and by exploiting these characteristics, the mission risk model is formulated.
To better illustrate the practical relevance of the problem setting before delving into the mathematical formulation, consider the following motivating example. An unmanned aerial vehicle (UAV) may be tasked with a long-duration environmental monitoring mission over a remote area. During the mission, the UAV is subject to continuous performance degradation—such as battery capacity loss, sensor drift, and structural fatigue—as well as sudden environmental shocks like turbulence or abrupt wind gusts. Either type of failure event can jeopardize mission success and lead to the total loss of the UAV. In such contexts, timely and well-informed mission termination decisions are essential to mitigate catastrophic losses while maintaining a high probability of mission completion. The methodology proposed in this paper aims to determine these optimal abort decisions based on real-time health monitoring information, balancing system survivability and mission reliability.
2.1. Underlying Failure Evolution
Consider an industrial system executing a critical mission within a duration of . During the mission, the system encounters continuous degradation governed by a stochastic process . The system fails once the accumulated degradation attains a pre-specified threshold , which simultaneously causes an immediate mission failure. Here, we characterize the underlying degradation through a Brownian motion (i.e., Wiener process, a continuous-time stochastic process with stationary, normally distributed increments) with shift and diffusion , which yields [57]. Such a process is selected owing to its tractable mathematical properties and physical interpretability, which scales well for various degradation signals such as vibration, temperature, acoustic emission, flow rate, etc., [58]. In particular, the degradation under this process yields an independent, Gaussian distributed increment, which facilitates analytically structural analysis particularly when complicated by other failure modes [59].
Apart from endogenous degradation damage, the mission-critical system simultaneously confronts random environmental shocks during the mission execution. The arrival process of external shocks admits a homogeneous Poisson process (a stochastic process that models the occurrence of random events over time, with independent inter-arrival times following an exponential distribution) with an invariant intensity . In practical engineering scenarios, external shocks such as violent turbulence, abrupt structural load, or sudden electromagnetic interference may lead to immediate system failure, independent of the cumulative degradation state. For example, a UAV experiencing extreme vibrations during rapid maneuvers could suffer instantaneous actuator failure or sensor detachment. On the other hand, even if the system survives a shock, it may still incur damage that accelerates internal degradation. For instance, repetitive shock-induced stress can exacerbate fatigue in structural joints, increase battery wear, or cause drift in sensor calibration. Such accumulated effects, although not immediately fatal, raise the long-term failure risk. Therefore, the impact of external shock to system survivability is two-fold: (a) causing an immediate, catastrophic system failure with a probability ; and (b) accumulating a random amount of degradation damage, provided that it successfully survives the shock with a probability . Given that the degradation accumulation follows Gaussian distribution, the integrated system degradation can be formulated as follows:
where is the Gaussian distributed degradation increment due to the -th shock. This yields the following:
and is the number of unfatal shocks experienced at time .
2.2. Dynamic Mission Termination for Risk Control
To control the operational risk during the mission, the system degradation severity is monitored equidistantly at an interval of , which yields for execution convenience. In other words, there are at most inspections throughout the mission. Following the monitored outcome, the following control limit termination policy is adopted for mission risk control.
- ■
- Mission termination. Upon the -th monitoring epoch, if the system’s degradation level exceeds a predetermined termination control limit , , the mission is terminated immediately to avoid catastrophic failure risk, but at a cost of immediate mission failure.
- ■
- Mission continuity. Otherwise, if the accumulated degradation is below the limit L at the -th monitoring epoch, continue the mission and wait for the subsequent condition monitoring.
Notably, the control limit is an unknown and optimizable variable, whose value is stochastically related to the number of inspections . This actually constitutes a dynamic control limit policy that determines the mission termination action based simultaneously on (a) whether the system has entered a worn-out or severe defective status, and (b) whether there is sufficient remaining mission time. The optimization procedure of this control limit policy will be specified in the rest of the paper.
3. Methodology
3.1. Fundamental Model Formulation
This section is devoted to formulating the mission termination model under the aforementioned dependent fault processes. To this end, the reliability model governed by both mission properties and fault evolution patterns is established, following which a mission termination model is developed to minimize the associated loss arising from both mission failure and system fault processes.
To begin with, we establish the basic system reliability model under the previously devised mission termination strategy, which serves as a fundamental basis for the subsequent strategy optimization. To this end, let denote the degradation level of the system at the -th degradation monitoring. Then, the number of condition monitoring implemented , the number of shocks experienced , and the monitored degradation magnitude collaboratively constitute the state space of the mission-critical system . Following this, the operational reliability of the system at time t is formulated as follows:
With the reliability model derived previously, we are able to formulate the mission termination decision model to minimize the risk-induced loss throughout the mission. The sequential decision model of interest constitutes a finite-time Markov decision process (MDP, a mathematical framework for modeling sequential decision problems where outcomes are partly random and partly under the control of a decision-maker). For model formulation purposes, we first introduce the cost structure associated with the control policy.
If the system fails due to either excessive degradation or external shock, a total cost of is incurred, where and represent the costs of mission failure and system failure, respectively. If, however, the degradation at the -th inspection exceeds the threshold , the termination action is selected, incurring a mission failure cost . If the system remains operational until the mission is successfully completed, a reward of is gained. The cost of each monitoring is .
As stated previously, a finite-time Markov Decision Process is leveraged to formulate the sequential decision-making approach. To this end, let and denote the expected costs associated with terminating and continuing the mission, respectively. Also, define the total number of inspections to be . Then, for the given state , we formulate the Bellman equation that minimizes the expected total mission-induced loss, , as
where . The formulation of is as follows
As stated previously, a revenue is earned if the system remains operational until the mission is completed. Otherwise, an integrated cost of mission and system failures is incurred. As a consequence, the boundary condition is given as follows:
If no system failure occurs, the system state transitions from to with . The transition probability density is formulated as
where denotes the probability of the system experiencing external random shocks during the state transition, which can be expressed as follows:
Then the reliability of the system upon the subsequent monitoring interval is given by
Summing up these formulas, the value function under the proposed risk control policy is formulated as
The risk loss function formulated above enables us to explore the structural characteristics of the optimal risk control policy, and thereby explore the existence and monotonicity of the optimal mission termination threshold, as we will explicitly show in the next part.
3.2. Structural Properties for Risk Prevention
Following the mission termination model established above, this part delves into the structural properties of the value function corresponding to the optimal mission abort strategy. By exploiting these structures, we are able to conduct an in-depth analytical discussion on the existence and statistical properties of the optimal control threshold that minimizes the total loss. To begin with, we provide the key definition with respect to random order.
Definition 1.
A random variable X is said to be stochastically smaller than a random Y in a stochastic order provided , denoted by .
By Definition 1, we can conclude that, provided that is a non-decreasing function and , always holds (see the stochastic order properties in Shaked and Shanthikumar [60]). Building upon this critical definition, we can derive the following properties.
Proposition 1.
The random variable
is stochastically non-decreasing in .
The proof of Proposition 1 is left to Appendix A. Proposition 1 establishes the monotonicity of system degradation, revealing that a high degradation level is more likely to lead to a severe future degradation evolution, on condition that external stochastic shocks do not cause immediate system failure. Leveraging this conclusion allows us to derive the monotony properties of the cost value function, as we will show in Proposition 2.
Proposition 2.
For a fixed n, the optimal value function is a non-decreasing function of the degradation measurement x. At the same time, for a fixed degradation severity x,
is a non-increasing function of the inspection number n.
The proof process is placed in Appendix B. Proposition 2 establishes the monotonicity nature of the optimal value function with respect to two key variables: (a) the number of inspections n, and (b) the degradation severity of the system level x. On one hand, a higher level of degradation accumulation corresponds to a higher expected mission-induced loss. On the other hand, for the given severity of system degradation, the anticipated loss decreases with the number of completed inspections. Utilizing both degradation monotony nature and value function structures, one can prove the existence of the risk-aware control limit and associated statistical properties, as indicated in Theorem 1.
Theorem 1.
For a given inspection period n, there always exists a control limit
, such that if
, aborting the mission is always the optimal decision; if, conversely, , continuing the mission is the optimal decision. The abort control limit is a non-decreasing function of n.
The proof process is left to Appendix C. Theorem 1 provides the theoretical foundation for determining the optimal control limits with respect to the mission continuation or termination based on system degradation evaluation. Through the structural analysis, the reasonability of setting adaptive risk control limit is well verified, which provides an intuitive and informed indicator from a mission management perspective. Another core finding is that, as the mission progresses, the abort control limit increases monotonically with the number of inspections, even though process or parameter uncertainties of the degradation/shock process are not involved. This is mainly attributed to the fact that operators may conduct aggressive and controllable risk control actions to alleviate mission failure losses if the residual mission time is short.
A graph illustration of Theorem 1 is presented in Figure 1, which summarizes four possible exclusive scenarios under this threshold-constriction termination policy: (A) mission success, (B) proactive mission termination, (C) unexpected failure attributed to degradation accumulation, and (D) unexpected failure due to fatal shock. At each inspection, the system’s degradation level is compared with a corresponding dynamic optimal mission risk control threshold to determine whether to continue the mission. In Figure 1A, the degradation trajectory always remains below the non-decreasing termination threshold, leading to successful completion. Figure 1B reveals that the degradation level exceeds the dynamic threshold at a certain inspection, triggering an instant mission termination to avert severe failure consequences. Figure 1C,D, in contrast, state two distinct system malfunction scenarios stemming from either excessive degradation or fatal shock, prior to mission termination. This set of figures visually discloses the dynamics of the risk-aware termination strategy driven by both mission duration and real-time degradation, which provides an explicit and intuitive termination suggestion for managers.
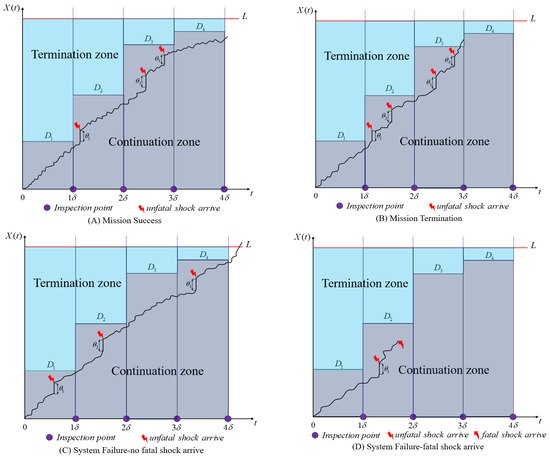
Figure 1.
Illustration of the threshold-constraint termination policy.
Building upon the foregoing findings, we are able to develop a reinforced computation algorithm for the efficient search of optimal solutions, as indicated in Algorithm 1 (The value iteration algorithm for determining optimal termination solution). The inspection interval is set to be , and the continuous system degradation state is discretized into small enough intervals [61]. Based on the algorithm, the value function at any monitoring point can be calculated in a sequential manner, and the optimal value function and the corresponding risk control thresholds can be determined.
Proposition 3.
The system mission reliability provided the non-decreasing nature of risk control limit in mission operational time (as indicated in Theorem 1) can be explicitly formulated as follows:
The proof is left to Appendix D. The reliability dynamics revealed in Proposition 3, in conjunction with the risk threshold established in Theorem 1, can aid in an efficient evaluation of real-time risk degree for mission completion, facilitating a structured risk decision-making process to improve precision.
| Algorithm 1 Optimal Mission Risk Control Policy Based on Value Iteration Algorithm |
 |
3.3. Heuristic Abort Policies for Comparison
This part introduces two heuristic mission abort policies for performance comparison. These policies have been reported in previous abort or maintenance models owing to their intuitiveness and implementation convenience. In the following, we formulate the risk control model under these policies.
- ■
- Comparative policy A: invariant threshold policy
In contrast to the gradually increasing mission abort threshold policy described earlier, this policy assumes a fixed mission abort threshold . That is, at each inspection epoch, if the system’s degradation level exceeds a fixed abort threshold, a mission abort action is executed. Under this policy, the value function becomes as follows:
which can be further specified as the following:
- ■
- Comparative policy B: no action taken
This policy presumes that no mission abort action is taken throughout the mission, implying that only two outcomes are possible: mission success or system failure. To derive the value function under this policy, we set the mission abort threshold to infinity. In this case, the value function is expressed as follows:
which can be further specified as follows:
4. Numerical Experiment
The environmental monitoring mission conducted by an unmanned aerial vehicle (UAV) is employed as an experimental scenario to validate the effectiveness of the proposed mission risk control policy and model. During the mission, the UAV’s health condition progressively deteriorates due to intrinsic performance degradation and fatigue accumulation caused by external environmental factors. For instance, the UAV’s structural components may experience fatigue damage due to prolonged operation, compounded by environmental influences such as continuous vibrations, temperature fluctuations, and humidity changes. When this degradation reaches a critical threshold, the UAV fails.
Moreover, the UAV is susceptible to extreme environmental shocks, which can directly induce failures. For example, during rapid maneuvers or in turbulent conditions, strong vibrations may compromise the stability of critical connections, leading to structural component failure. Such UAV failures can result in dual losses for decision-makers: the mission’s failure and the loss of the machine itself. Furthermore, the fall of a UAV may cause additional property damage or pose significant safety risks to personnel. Consequently, timely assessment of UAV health status and the implementation of risk control interventions are essential to ensure operational safety, enhance the UAV’s survival probability, and minimize mission losses.
The health status of UAVs can be comprehensively evaluated through collecting health monitoring signals, such as vibration data and battery capacity, to derive a health index that reflects its degradation level. The UAV’s performance degradation is monitored through a combination of signals, including vibration amplitude from accelerometers, rotational velocity variations from gyroscopes, battery capacity and discharge rate trends, as well as control surface response time. These indicators collectively form the health index used in modeling the Wiener process-based degradation path. Decision-makers can utilize monitoring information to assess the UAV’s condition and make informed risk control decisions. To better validate the proposed risk control strategy, the probability of random shocks directly causing system failure was set to a very small value during the case verification process, without affecting the numerical experimental results.
4.1. Optimal Risk Control Policy
The mission requires the UAV to monitor and collect environmental data for 60 h on an area’s environment, and to be brought back every 6 hours to recharge and collect the necessary health information to assess its status. That is, the duration of the mission is and inspections are performed at fixed intervals . Therefore, the total number of inspections is set to .
The health index of the UAV is evaluated by a combination of various types of information, such as mechanical and structural condition monitoring information including vibration signals and flight control signal deviations, and energy status information including battery capacity and discharge curves. The deterioration process of the health index is modeled by the Wiener process, involving external random shocks, and the parameters are estimated based on historical data. The corresponding degradation and impact parameters are given as follows: the drift parameter is , the diffusion parameter is . External random shocks arrive according to a homogeneous Poisson process, with intensity as . The degradation increment of the UAV system caused by these shocks follows a normal distribution, with a mean of and a variance of . The failure threshold is . The costs associated with information collection, mission failure, and system failure are set to , , and , respectively, with a unit of $. Under the degradation–shock parameters and cost parameters set above, this section presents the optimal mission risk control policy.
In Figure 2, the risk control chart is divided into two parts by a monotonic threshold: the upper part where the abort action is performed, and the lower half where the system continues to perform the mission. The monotonicity of the threshold corresponds to Theorem 1, that as the mission progresses, the decision-maker becomes more tolerant of the health status. Next, we explored the control chart variation regarding cost. Under a fixed system failure cost, as the cost of mission failure increases, the area of mission termination becomes smaller; that is, decision-makers will take more radical measures to try to complete the mission and have a higher tolerance for the health of the system. This is reflected by a shrinking upper section in the diagram.
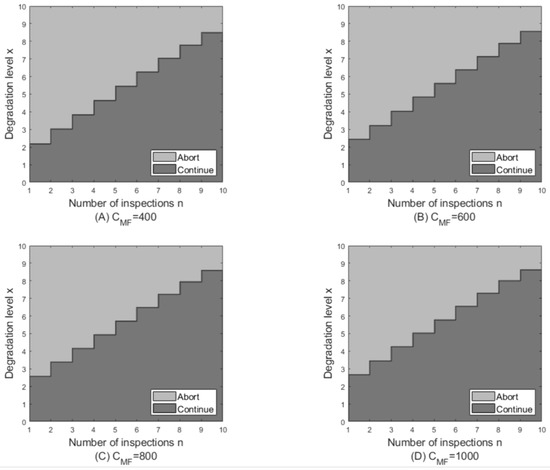
Figure 2.
Optimal mission risk control policy when .
Figure 3 illustrates the optimal mission abort policy under varying system failure costs, given a fixed mission failure cost. The figure demonstrates that as the system failure cost increases, the mission abort threshold decreases, leading to a broader abort region (i.e., the threshold line moves downward). This relationship arises because a higher system failure cost prompts decision-makers to prioritize the survivability of the system over mission completion. In particular, as the system failure cost grows, the emphasis on preventing system failure progressively outweighs the importance of accomplishing the mission. This shift reflects the increasing importance assigned to preserving the system in scenarios where failure entails greater consequences. Figure 2 and Figure 3 highlight how different cost components influence the risk control decision.
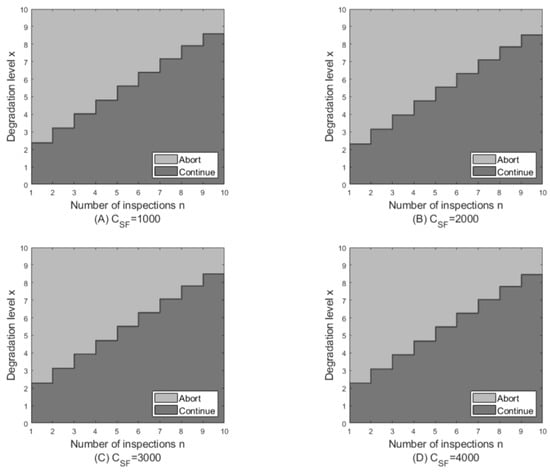
Figure 3.
Optimal mission risk control policy when .
4.2. Sensitivity Analysis
In addition to cost parameters, the degradation characteristics of the UAV itself play a more critical role in shaping the control strategy. Factors such as production conditions, maintenance history, and operational environments can cause UAVs of the same model to exhibit significant variability in their degradation parameters, introducing heterogeneity into their performance and reliability. Therefore, it is essential to investigate the impact of these degradation parameters, as understanding their influence can offer valuable insights for decision-makers. Such analysis can guide the adjustment of control strategies, enabling the adoption of either more aggressive or more conservative approaches tailored to the specific conditions of each UAV.
As shown in Figure 4, the mission abort threshold decreases as the drift parameter increases. A higher drift parameter accelerates the rate of system damage degradation, necessitating a lower control threshold to manage the heightened risk of system failure. Similarly, Figure 5 demonstrates that as the intensity of external random shocks increases, the mission risk control policy follows a similar trend. This behavior reflects the need to prioritize system survivability and mitigate the elevated risk of failure caused by stronger external shocks. Together, these trends highlight the importance of dynamically adjusting control thresholds to account for both internal degradation dynamics and external uncertainties.
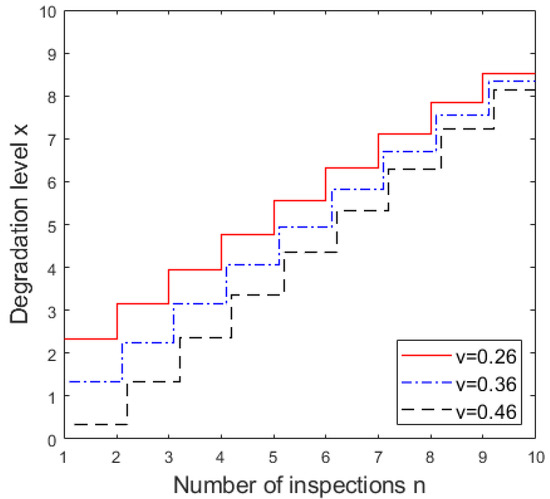
Figure 4.
Sensitivity of the drift parameter of the Wiener process.
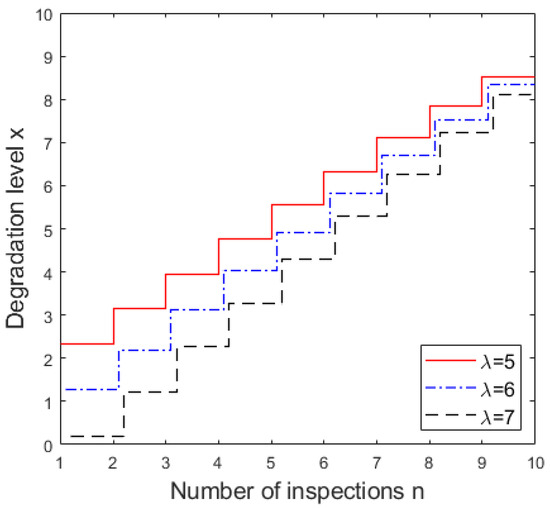
Figure 5.
Sensitivity of the random shock intensity.
Figure 6 depicts the variation in system reliability with respect to degradation for different drift parameters of the Wiener process. A larger drift parameter indicates a faster progression of the system toward the degraded state. Consequently, for the same level of degradation, the system is more likely to reach the failure threshold sooner. As a result, an increased drift parameter corresponds to a higher probability of system failure, thereby leading to a reduction in system reliability. This highlights the critical impact of the drift parameter on system performance and the importance of accounting for it in reliability assessments.
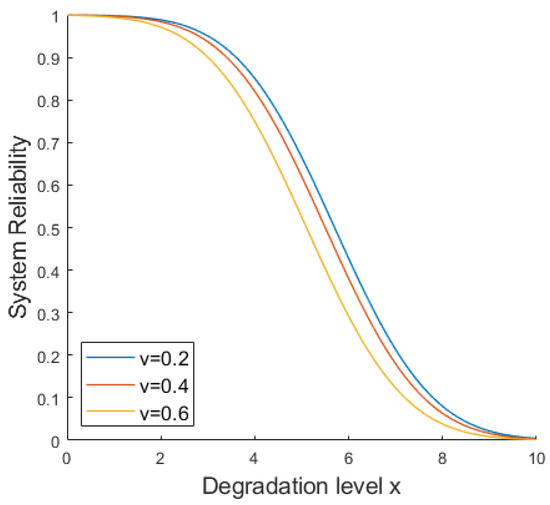
Figure 6.
System reliability curves under different drift parameters.
4.3. Comparison with Alternative Policies
In this section, we present a comparison of the optimal mission risk control policy with two benchmark policies. Table 1 and Table 2 illustrate the impact of two critical mission cost parameters on the average total cost of the mission system under identical degradation paths.

Table 1.
Cost comparison between the optimal policy and contrast policies under different .

Table 2.
Cost comparison between the optimal policy and contrast policies under different .
The results clearly show that the optimal policy significantly outperforms the two benchmark policies in minimizing the total cost. Unlike the optimal policy, the fixed abort threshold policy uses a constant mission abort threshold and lacks the flexibility to adapt decision-making based on the system’s degradation state. This rigidity increases the likelihood of higher mission failure costs, highlighting the limitations of the fixed threshold approach in dynamic environments. The never abort policy completely disregards the risks of mission failure and system failure during the mission execution process, resulting in significantly higher costs compared to the other two policies.
5. Discussion and Conclusions
This study investigates the optimal risk control policy for mission systems subject to competing failures caused by internal degradation and external random shocks. The system degradation process is modeled as a Wiener process, while the arrival of external shocks follows a homogeneous Poisson process. Innovatively, we integrate the impact of random shocks into the degradation trajectory itself: each shock adds a normally distributed increment to the degradation level, explicitly coupling the two failure modes. The decision problem is formulated as a Markov decision process in which the controller chooses whether to continue the mission or abort to avoid escalating failure risk and downstream costs. Within this framework, the optimal mission-abort policy is characterized by a control limit rule with respect to the observable degradation state.
Through rigorous analysis, we establish key structural properties of the value function and the associated risk control limit. In particular, we prove the existence of an optimal mission risk control policy and the monotonicity of the optimal threshold with respect to the degradation level, thereby providing a clear theoretical characterization of how the policy responds to system deterioration under coupled degradation–shock dynamics. Numerical validation demonstrates the superiority of the optimal risk control policy. Across a range of operating regimes, it yields lower total mission costs than fixed-threshold and heuristic alternatives by adaptively timing termination to the evolving degradation state and realized shocks. Sensitivity analyses further reveal how changes in degradation rate, shock frequency, and cost parameters shift the control limit and the resulting mission outcomes, offering transparent guidance for calibration and deployment. Finally, comparative experiments against two contrast policies highlight that the proposed approach effectively balances inspection, mission failure, and system failure costs, leading to substantial cost reductions and improved reliability. Taken together, the combination of model formulation, theoretical analysis, and computational evidence shows that explicitly accounting for the coupling of different failure modes can materially improve mission risk control in practice.
This study can be extended in several directions. First, while this work focuses on risk control policies for single-stage mission systems, it can be extended to systems executing multi-stage missions, where the model parameters vary with different mission stages. In this extension, simulation analysis could be performed to verify the applicability of the proposed model under stage-dependent operational conditions. Second, due to system heterogeneity, degradation parameters are often challenging to determine from prior data. Updating system degradation parameters based on real-time monitoring data and formulating mission risk control policies based on parameter learning results would be a more effective approach. In future work, we plan to integrate parameter learning mechanisms—such as Bayesian updating—into the framework, enabling dynamic recalibration of degradation and shock parameters during mission execution. This extension is expected to enhance the adaptability and robustness of the proposed risk control methodology. Lastly, incorporating the randomness of mission durations presents an interesting avenue for future research. Allowing mission length to vary stochastically would enable the framework to capture a wider range of operational scenarios, particularly those where the duration is influenced by environmental or operational uncertainties. Although such an extension would increase the complexity of the model, it would significantly broaden its applicability in real-world mission planning.
Author Contributions
Methodology, Z.K.; formal analysis, Z.K.; writing—original draft preparation, Z.K. and Y.M.; writing—review and editing, Y.M., B.W. and K.G.; visualization, Z.K.; supervision, K.G.; All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grant No. 72101010) and the Basic Technical Research Project of China (Grant No. JSZL2018601B004).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
Abbreviations
| Acronyms | |
| CBM | Condition-Based Maintenance |
| MDP | Markov decision process |
| Probability density function | |
| RUL | Remaining useful lifetime |
| Notations | |
| Mission duration | |
| System failure threshold | |
| System deterioration value at time | |
| Shift parameter of the Wiener process | |
| Diffusion parameter of the Wiener process | |
| Number of external shocks up to time | |
| Intensity of the external shocks | |
| The probability of system failure directly caused by external shocks | |
| Inspection interval | |
| Total number of inspections | |
| Mission risk control limit at the -th inspection | |
| The costs of mission failure | |
| The costs of system failure | |
| Reward for successful completion of task | |
| The cost of each inspection |
Appendix A
Proof of Proposition 1.
We start by defining two separate realizations of the degradation monitoring -th inspection as or (), and the degradation level at the -th inspection as . Additionally, we define the total number of unfatal shocks experienced during two successive inspection epoch as . We then have ; the following inequation holds
It is evident that, provided that the number of unfatal shocks experienced remain the same, a higher initial degradation level corresponds to a higher expected degradation level. This conclusion can be generalized to arbitrary shock number occasions as follows:
By Definition 1, one obtains , which completes the proof. □
Appendix B
Proof of Proposition 2.
We start by demonstrating that is a non-decreasing function of x. By Proposition 1, is stochastically non-decreasing in . Then, the following inequation holds
Evidently, is a constant whose value is not associated the degradation severity x. Accordingly, it can be proved that is also non-decreasing in x, and is non-decreasing in x for any value of shock number n. Additionally, it is evident from Equation (7) that is a non-decreasing function with respect to x. Summing up all these monotonicity verifies that the value function is a non-decreasing function of x.
Recall from previous discussions that the degradation increments in almost non-negative. As a consequence, we can obtain the following:
Moreover, the following obviously holds:
Combining the two inequalities yields the following: , which completes the proof. □
Appendix C
Proof of Theorem 1.
Stemming from the insights of Proposition 2, it can be obtained that is non-decreasing in x. Since is a constant, the term is also non-decreasing in x. Since the difference intersects with zero for a specific value of x, for all values of x greater than this value, aborting the mission is always the optimal choice. In other words, there always exists a control limit , such that for , it is optimal to abort the mission; otherwise, for , it is optimal to continue the mission. For , it follows from Proposition 2 that
Therefore, the control limit satisfies , which concludes the proof. □
Appendix D
Proof of Proposition 3.
Recall that the mission termination limit possesses a non-decreasing nature with respect to the inspection count. Consequently, the mission is accomplished successfully only if the following two conditions are simultaneously fulfilled: (a) no degradation failure emerges during the entire mission; (b) no fatal shock arrives; (c) the monitored degradation at the n-th inspection, , always falls below the termination control limit . Let denote the increment of the system degradation at the nth detection relative to the last inspection, and denote the PDF of the degradation increment , which are formulated as
Accordingly, the unconditional probability density of each degradation increment is obtained by marginalizing the conditional Gaussian density over the Poisson-distributed shock counts, i.e.,
Because the increments are mutually independent, the joint density of the vector factorizes into the product . Mission reliability is therefore the probability that amounts to integrating the joint density over the nested domain
Accordingly, the mission reliability can be obtained, which closes the proof. □
References
- Qiu, Q.; Li, R.; Zhao, X. Failure risk management: Adaptive performance control and mission abort decisions. Risk Anal. 2025, 45, 421–440. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Wei, F.; Ma, X.; Qiu, Q. Controlling mission hazards through integrated abort and spare support optimization. Risk Anal. 2025. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ma, X.; Wei, F.; Yang, L.; Qiu, Q. Dynamic scheduling of intelligent group maintenance planning under usage availability constraint. Mathematics 2022, 10, 2730. [Google Scholar] [CrossRef]
- Levitin, G.; Xing, L.; Dai, Y. A new self-adaptive mission aborting policy for systems operating in uncertain random shock environment. Reliab. Eng. Syst. Saf. 2024, 248, 110184. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Qiu, Q.; Wang, J. Risk control of mission-critical systems: Abort decision-makings integrating health and age conditions. IEEE Trans. Ind. Inform. 2022, 18, 6887–6894. [Google Scholar] [CrossRef]
- Zheng, R.; Fang, H.; Peng, Z. Condition-based maintenance for a balanced system considering dependent soft and hard failures. Comput. Ind. Eng. 2024, 197, 110550. [Google Scholar] [CrossRef]
- Yang, L.; Wei, F.; Qiu, Q. Mission risk control via joint optimization of sampling and abort decisions. Risk Anal. 2024, 44, 666–685. [Google Scholar] [CrossRef]
- Cheng, Y.; Wei, Y.; Liao, H. Optimal sampling-based sequential inspection and maintenance plans for a heterogeneous product with competing failure modes. Reliab. Eng. Syst. Saf. 2022, 218, 108181. [Google Scholar] [CrossRef]
- Yang, L.; Sun, Q.; Ye, Z.S. Designing mission abort strategies based on early-warning information: Application to UAV. IEEE Trans. Ind. Inform. 2019, 16, 277–287. [Google Scholar] [CrossRef]
- Zheng, R.; Fang, H.; Song, Y. A condition-based maintenance policy for a two-component balanced system with dependent degradation processes. Reliab. Eng. Syst. Saf. 2024, 252, 110483. [Google Scholar] [CrossRef]
- Levitin, G.; Xing, L.; Huang, H.Z. Cost effective scheduling of imperfect inspections in systems with hidden failures and rescue possibility. Appl. Math. Model. 2019, 68, 662–674. [Google Scholar] [CrossRef]
- Chai, X.; Chen, B.; Zhao, X. Optimal mission abort decisions for multi-component systems considering multiple abort criteria. Mathematics 2023, 11, 4922. [Google Scholar] [CrossRef]
- Zheng, R.; Xing, Y.; Ren, X. Multilevel preventive replacement for a system subject to internal deterioration, external shocks, and dynamic missions. Reliab. Eng. Syst. Saf. 2023, 239, 109507. [Google Scholar] [CrossRef]
- Wei, Y.; Cheng, Y. An optimal two-dimensional maintenance policy for self-service systems with multi-task demands and subject to competing sudden and deterioration-induced failures. Reliab. Eng. Syst. Saf. 2025, 255, 110628. [Google Scholar] [CrossRef]
- Alhamad, K.; Alkhezi, Y. Hybrid genetic algorithm and tabu search for solving preventive maintenance scheduling problem for cogeneration plants. Mathematics 2024, 12, 1881. [Google Scholar] [CrossRef]
- Yang, L.; Li, G.; Zhang, Z.; Ma, X.; Zhao, Y. Operations & maintenance optimization of wind turbines integrating wind and aging information. IEEE Trans. Sustain. Energy 2020, 12, 211–221. [Google Scholar] [CrossRef]
- Levitin, G.; Finkelstein, M. Optimal mission abort policy for systems operating in a random environment. Risk Anal. 2018, 38, 795–803. [Google Scholar] [CrossRef]
- Cheng, G.; Zhou, B.; Qi, F.; Li, L. Modeling condition-based maintenance and replacement strategies for an imperfect production-inventory system. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 1858–1871. [Google Scholar] [CrossRef]
- Yan, R.; Zhu, X.; Zhu, X.; Peng, R. Joint optimisation of task abortions and routes of truck-and-drone systems under random attacks. Reliab. Eng. Syst. Saf. 2023, 235, 109249. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, L. State-based opportunistic maintenance with multifunctional maintenance windows. IEEE Trans. Reliab. 2020, 70, 1481–1494. [Google Scholar] [CrossRef]
- Shishkin, P.V.; Malozyomov, B.V.; Martyushev, N.V.; Sorokova, S.N.; Efremenkov, E.A.; Valuev, D.V.; Qi, M. Development of a mathematical model of operation reliability of mine hoisting plants. Mathematics 2024, 12, 1843. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, T.; Ma, X.; Wang, J.; Peng, R.; Yang, L. System maintenance optimization under structural dependency: A dynamic grouping approach. IEEE Syst. J. 2024, 18, 1605–1616. [Google Scholar] [CrossRef]
- Yan, R.; Zhu, X.; Zhu, X.; Peng, R. Optimal routes and aborting strategies of trucks and drones under random attacks. Reliab. Eng. Syst. Saf. 2022, 222, 108457. [Google Scholar] [CrossRef]
- Tan, L.; Wei, F.; Ma, X.; Peng, R.; Xiao, H.; Yang, L. Systemic Condition-based Maintenance Optimization Under Inspection Uncertainties: A Customized Multi-Agent Reinforcement Learning Approach. IEEE Trans. Reliab. 2025. [Google Scholar] [CrossRef]
- Hu, Q.; Qi, F. Maintenance policy optimization for buffered serial systems considering energy-saving based on dual time windows. Appl. Math. Model. 2023, 117, 687–704. [Google Scholar] [CrossRef]
- Wang, J.; Yang, L.; Ma, X.; Peng, R. Joint optimization of multi-window maintenance and spare part provisioning policies for production systems. Reliab. Eng. Syst. Saf. 2021, 216, 108006. [Google Scholar] [CrossRef]
- Levitin, G.; Xing, L.; Dai, Y. Optimal aborting in cumulative parallel missions with individual and common shocks. Reliab. Eng. Syst. Saf. 2025, 262, 111197. [Google Scholar] [CrossRef]
- Wei, F.; Wang, J.; Ma, X.; Yang, L.; Qiu, Q. An Optimal Opportunistic Maintenance Planning Integrating Discrete-and Continuous-State Information. Mathematics 2023, 11, 3322. [Google Scholar] [CrossRef]
- Wei, Y.; Cheng, Y.; Liao, H. Fleet Service Reliability Analysis of Self-Service Systems Subject to Failure-Induced Demand Switching and a Two-Dimensional Inspection and Maintenance Policy. IEEE Trans. Autom. Sci. Eng. 2024, 22, 10029–10044. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Ma, X.; Qiu, Q.; Peng, R. A prognosis-centered intelligent maintenance optimization framework under uncertain failure threshold. IEEE Trans. Reliab. 2023, 73, 115–130. [Google Scholar] [CrossRef]
- Wei, Y.; Li, A.; Cheng, Y.; Li, Y. An optimal multi-level inspection and maintenance policy for a multi-component system with a protection component. Comput. Ind. Eng. 2025, 201, 110898. [Google Scholar] [CrossRef]
- Ma, X.; Han, R.; Chen, Y.; Qiu, Q.; Yan, R.; Yang, L. Intelligent spare ordering and replacement optimisation leveraging adaptive prediction information. Reliab. Eng. Syst. Saf. 2024, 252, 110420. [Google Scholar] [CrossRef]
- Wu, T.; Wei, F.; Yang, L.; Ma, X.; Hu, L. Maintenance optimization of k-out-of-n load-sharing systems under continuous operation. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6329–6341. [Google Scholar] [CrossRef]
- Shang, L.; Liu, B.; Gao, K.; Yang, L. Random Warranty and Replacement Models Customizing from the Perspective of Heterogeneity. Mathematics 2023, 11, 3330. [Google Scholar] [CrossRef]
- Ji, Z.; Chen, Y.; Ma, X.; Cai, Y.; Yang, L. Hierarchical condition-based maintenance planning for corrosion process considering natural environmental impact. Reliab. Eng. Syst. Saf. 2024, 243, 109856. [Google Scholar] [CrossRef]
- Zheng, R. Structured replacement policies for a system subject to random mission types. Nav. Res. Logist. 2024, 71, 1055–1069. [Google Scholar] [CrossRef]
- Wang, J.; Ma, X.; Yang, L.; Qiu, Q.; Shang, L.; Wang, J. A hybrid inspection-replacement policy for multi-stage degradation considering imperfect inspection with variable probabilities. Reliab. Eng. Syst. Saf. 2024, 241, 109629. [Google Scholar] [CrossRef]
- Wu, D.; Han, R.; Ma, Y.; Yang, L.; Wei, F.; Peng, R. A two-dimensional maintenance optimization framework balancing hazard risk and energy consumption rates. Comput. Ind. Eng. 2022, 169, 108193. [Google Scholar] [CrossRef]
- Wei, F.; Tan, L.; Ma, X.; Xiao, H.; Patel, D.; Lee, C.G.; Yang, L. A hybrid prognostic framework: Stochastic degradation process with adaptive trajectory learning to transfer historical health knowledge. Mech. Syst. Signal Process. 2025, 224, 112171. [Google Scholar] [CrossRef]
- Wang, J.; Ma, X.; Gao, K.; Zhao, Y.; Yang, L. Condition-based maintenance management for two-stage continuous deterioration with two-dimensional inspection errors. Qual. Reliab. Eng. Int. 2024, 40, 3691–3708. [Google Scholar] [CrossRef]
- Xing, L. Reliability in Internet of Things: Current status and future perspectives. IEEE Internet Things J. 2020, 7, 6704–6721. [Google Scholar] [CrossRef]
- Qiu, Q.; Kou, M.; Chen, K.; Deng, Q.; Kang, F.; Lin, C. Optimal stopping problems for mission-oriented systems considering time redundancy. Reliab. Eng. Syst. Saf. 2021, 205, 107226. [Google Scholar] [CrossRef]
- Wang, J.; Longyan, T.; Ma, X.; Gao, K.; Jia, H.; Yang, L. Prognosis-driven reliability analysis and replacement policy optimization for two-phase continuous degradation. Reliab. Eng. Syst. Saf. 2023, 230, 108909. [Google Scholar] [CrossRef]
- Qiu, Q.; Cui, L.; Wu, B. Dynamic mission abort policy for systems operating in a controllable environment with self-healing mechanism. Reliab. Eng. Syst. Saf. 2020, 203, 107069. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Ma, X. A state-age-dependent opportunistic intelligent maintenance framework for wind turbines under dynamic wind conditions. IEEE Trans. Ind. Inform. 2023, 19, 10434–10443. [Google Scholar] [CrossRef]
- Yang, L.; Ye, Z.; Lee, C.G.; Yang, S.F.; Peng, R. A two-phase preventive maintenance policy considering imperfect repair and postponed replacement. Eur. J. Oper. Res. 2019, 274, 966–977. [Google Scholar] [CrossRef]
- Cha, J.H.; Finkelstein, M.; Levitin, G. Optimal mission abort policy for partially repairable heterogeneous systems. Eur. J. Oper. Res. 2018, 271, 818–825. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, J.; Qiu, Q.; Chen, K. Optimal inspection and mission abort policies for systems subject to degradation. Eur. J. Oper. Res. 2021, 292, 610–621. [Google Scholar] [CrossRef]
- Cheng, G.; Li, L.; Shangguan, C.; Yang, N.; Jiang, B.; Tao, N. Optimal joint inspection and mission abort policy for a partially observable system. Reliab. Eng. Syst. Saf. 2023, 229, 108870. [Google Scholar] [CrossRef]
- Levitin, G.; Finkelstein, M.; Huang, H.Z. Optimal mission abort policies for multistate systems. Reliab. Eng. Syst. Saf. 2020, 193, 106671. [Google Scholar] [CrossRef]
- Levitin, G.; Finkelstein, M.; Dai, Y. Mission abort policy optimization for series systems with overlapping primary and rescue subsystems operating in a random environment. Reliab. Eng. Syst. Saf. 2020, 193, 106590. [Google Scholar] [CrossRef]
- Levitin, G.; Finkelstein, M.; Dai, Y. State-based mission abort policies for multistate systems. Reliab. Eng. Syst. Saf. 2020, 204, 107122. [Google Scholar] [CrossRef]
- Zhao, X.; Chai, X.; Sun, J.; Qiu, Q. Optimal bivariate mission abort policy for systems operate in random shock environment. Reliab. Eng. Syst. Saf. 2021, 205, 107244. [Google Scholar] [CrossRef]
- Yin, J.; Cui, L. Reliability analysis for shock systems based on damage evolutions via Markov processes. Nav. Res. Logist. 2023, 70, 246–260. [Google Scholar] [CrossRef]
- Jia, H.; Peng, R.; Yang, L.; Wu, T.; Liu, D.; Li, Y. Reliability evaluation of demand-based warm standby systems with capacity storage. Reliab. Eng. Syst. Saf. 2022, 218, 108132. [Google Scholar] [CrossRef]
- Wang, X.; Balakrishnan, N.; Guo, B. Residual life estimation based on nonlinear-multivariate Wiener processes. J. Stat. Comput. Simul. 2015, 85, 1742–1764. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, S.; Ma, X.; Chen, Y.; Jia, H.; Dai, W. Group machinery intelligent maintenance: Adaptive health prediction and global dynamic maintenance decision-making. Reliab. Eng. Syst. Saf. 2024, 252, 110426. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, S.; Peng, R.; Qiu, Q.; Yang, L. An inspection-based replacement planning in consideration of state-driven imperfect inspections. Reliab. Eng. Syst. Saf. 2023, 232, 109064. [Google Scholar] [CrossRef]
- Li, M.; Ma, X.; Zhang, X.; Peng, R.; Yang, J. Reliability analysis of nonrepairable cold-standby system based on the Wiener process. In Proceedings of the 2017 2nd International Conference on System Reliability and Safety (ICSRS), Milan, Italy, 20–22 December 2017; IEEE: New York, NY, USA, 2017; pp. 151–155. [Google Scholar]
- Shaked, M.; Shanthikumar, J.G. Stochastic Orders; Springer: New York, NY, USA, 2007. [Google Scholar]
- Elwany, A.H.; Gebraeel, N.Z.; Maillart, L.M. Structured replacement policies for components with complex degradation processes and dedicated sensors. Oper. Res. 2011, 59, 684–695. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).