Integrated Process Planning and Scheduling Framework Using an Optimized Rule-Mining Approach for Smart Manufacturing

Abstract

Manufacturing industries are undergoing a significant transformation toward Smart Manufacturing (SM) to meet the ever-evolving demands for customized products. A major obstacle in this transition is the integration of Computer-Aided Process Planning (CAPP) with Scheduling. This integration poses challenges because of conflicting objectives that must be balanced, resulting in the Integrated Process Planning and Scheduling problem. In response to these challenges, this research introduces a novel hybridized machine learning optimization approach designed to assign and sequence setups in Dynamic Flexible Job Shop environments via dispatching rule mining, accounting for real-time disruptions such as machine breakdowns. This approach connects CAPP and scheduling by considering setups as dispatching units, ultimately reducing makespan and improving manufacturing flexibility. The problem is modeled as a Dynamic Flexible Job Shop problem. It is tackled through a comprehensive methodology that combines mathematical programming, heuristic techniques, and the creation of a robust dataset capturing priority relationships among setups. Empirical results demonstrate that the proposed model achieves a 42.6% reduction in makespan, improves schedule robustness by 35%, and reduces schedule variability by 27% compared to classical dispatching rules. Additionally, the model achieves an average prediction accuracy of 92% on unseen instances, generating rescheduling decisions within seconds, which confirms its suitability for real-time Smart Manufacturing applications.

Nomenclature

Model Indices:

$J$: Number of jobs

$j$: The index of jobs of {1, 2, …, $J$}

$m$: Number of machines

$k$: The index of machine {1, 2, …, $m$}

$n_j$: Number of setups in a job $j$

$i$: The index of setup $\{1, 2, \dots ,n_j\}$

Model Parameters:

$P_{i,j,k}$: Processing Time of setup i of job j on machine k

$M$: A very large positive number

$m_{i,j,k}$: A subset of machines eligible to process setup $i$

$m_{i,j,k}$ ⊆ ($m_1,m_2,\dots ,m_k$)

$S_{ij}:$: Setup $i$ of job $j$

$T_{MTBD}^k$ = Mean time between breakdowns of the machine $k$

${TH}_k$: Breakdown probability threshold of the machine $k$

Decision Variables:

$x_{i,j,k}$ = $\left\{\begin{array}{c}1, if the setup i of job j is processed on machine k\\ 0 otherwise\end{array}\right.$

$s_{i,j,k}$: Start time of the setup i of job j on machine k

$Z_{i,i^{\prime },j,j^{\prime },k}$ = $\left\{\begin{array}{c}1, if the setup i of job j precedes setup i^{\prime }of job j^{\prime } on machine k\\ 0 otherwise\end{array}\right.$

$C_{max}$: Makespan

$e_{i,j,k}$: Completion time of the setup $i$ of job $j$ on machine $k$

$t_{bd}^k$: Breakdown time of machine $k$; it is a random variable.

1. Introduction

Over the last three decades, the manufacturing industry has undergone significant evolution from traditional processes to the Smart Manufacturing (SM) era. This transformation has been driven by the growing demand for highly customized products. As a result, production planning and scheduling now face extraordinary challenges that require real-time and flexible approaches. Manufacturing systems must autonomously adapt process plans and production schedules to dynamic environments.

Computer-Aided Process Planning (CAPP) plays a crucial role in linking design and manufacturing, encompassing decisions related to raw materials, processes, machines, and sequencing of operations. Traditional CAPP largely depends on the knowledge and experience of human experts, potentially leading to inefficient decision-making and non-optimal solutions) [1]. This approach is often non-generalizable and cannot meet the flexibility required for mass customization [2]. Due to the capability of computers to aid planning activities with increased speed and accuracy, the CAPP problem has been gaining popularity among researchers [3,4] Wu [5] defined CAPP as a combination of tasks involving translating a part’s geometric model into machining features, determining suitable machining resources and operations, and selecting the most cost-effective setup plan and operation sequence, considering design and manufacturing constraints. Most CAPP systems use either a variant approach (retrieving and modifying existing plans) or a generative approach (developing plans based on part geometry) [6]. Despite the efforts, few CAPP systems can significantly improve manufacturing because of the highly complex and dynamic aspects [3].

Scheduling allocates manufacturing jobs to manufacturing resources over a specific time interval. The scheduling function depends on the job arrival pattern, operation precedence relation, and the number of available resources and determines the most suitable time to execute an operation on a machine tool. In summary, scheduling is an optimization problem where the objective is to manufacture final products in the shortest possible time, considering resource capacity limitations [7]. CAPP and scheduling are two distinct manufacturing activities; however, they are closely related. CAPP can also be considered a manufacturing resource management function; however, CAPP and scheduling objectives are often incompatible and frequently in conflict. Where scheduling typically considers manufacturing resources with time-based objectives, CAPP primarily focuses on minimizing manufacturing costs and product quality objectives. Traditionally, CAPP and Scheduling are performed sequentially, with scheduling occurring after CAPP. This approach has some significant drawbacks. According to Li et al. [8], the process planner creates a process plan for individual jobs within the sequential approach. The capacity limitation of resources and uncertain events, such as delays, urgent orders, and machine breakdowns, are not considered in this stage. During the scheduling phase, the fixed process plan often becomes infeasible due to changing production conditions. Thus, it is crucial to study the overlap between CAPP and scheduling objectives to effectively handle disruptions on the production floor.

The integrated CAPP and scheduling problem in this research involves completing $J$ jobs on $m$ machines, each comprising multiple setups ($n_j$). This problem is modeled as a Flexible Job Shop Scheduling Problem (FJSP). The goal is to assign setups to machines and schedule them to minimize makespan while maintaining the proper sequence of setups within each job. This choice is motivated by two practical considerations: (1) makespan is the most direct indicator of system responsiveness in Smart Manufacturing, and (2) a single-objective formulation enables real-time computation, which is essential for online rescheduling. The research adopts a hybrid two-stage strategy: a fast localization algorithm assigns each setup to the machine that offers the minimum processing time, thereby generating an initial route. Given these assignments, a novel dispatching rule mining (DRM) algorithm yields near-instant schedules suitable for dynamic rescheduling. This decomposition keeps the solution lightweight enough for real-time use while still treating routing and sequencing decisions within a unified workflow.

The primary novelty of this research lies in the development of a real-time hybrid framework that integrates routing and sequencing to adapt schedules in response to disruptions dynamically. In particular, this approach enables setups interrupted by disruptions, such as machine breakdowns, to be automatically reassigned to available machines and rescheduled. This work introduces a dedicated MILP formulation for setup-level sequencing and applies a supervised learning–based dispatching rule mining model to support fast, data-driven rescheduling decisions.

The research has several key contributions:

• Conducting an in-depth analysis of existing literature on Integrated Process Planning and Scheduling (IPPS), providing a comprehensive understanding of the field.
• Developing an initial schedule that jointly solves machine assignment and sequencing problems.
• Formulating a Mixed-Integer Linear Programming (MILP) model for efficient setup sequencing.
• Creating a machine learning model to extract dispatching rules and enhance scheduling efficiency.
• Validating the developed model in real-world scenarios.
• Demonstrating the model’s ability to adapt to changing manufacturing environments, including rescheduling after unexpected events.

This introduction has provided an overview of the research problem, objectives, and contributions. As for the remaining sections of the article: Section 2 is a literature review; the employed methodology is presented in Section 3; the experimental setup is detailed in Section 4; and finally, our conclusions and recommendations for future research are given in Section 5.

2. Literature Review

This section presents a critical review of the relevant literature, followed by a discussion on the existing knowledge gaps.

2.1. Review of IPPS

The IPPS problem is one of the most intricate problems for manufacturing systems [9]. In most research papers addressing the IPPS problem, it is typically dissected into three subproblems: (i) the selection of process plans, (ii) the allocation of machines, and (iii) scheduling [10]. The conventional approach to addressing this problem involves first choosing the process plan, followed by the subsequent allocation and scheduling of operations [10,11]. Recent reviews also highlight that the integration of process planning and scheduling remains an active area of research, with emerging solutions leveraging data-driven and learning-based methods to improve flexibility [12].

All of these approaches consider operations as the dispatching unit. Operation sequencing is a common problem for both process planning and scheduling functions. For CAPP, operations of a job are sequenced with objectives such as minimizing machining costs [13]. In the case of scheduling, operations are sequenced to complete jobs in the shortest possible time [14,15,16,17]. This creates conflict between the objective of CAPP and scheduling. Process planning often involves trade-offs among cost, quality, production time, and resource utilization. For example, using a slower machine that consumes less energy and produces might be cost-effective, but it increases production time. On the contrary, scheduling decisions often prioritize time over cost. This can lead to situations where machines are frequently set up or reconfigured for different jobs, which may not be the most efficient manufacturing approach. Recent studies have also emphasized the importance of balancing time- and cost-related objectives within integrated frameworks, proposing adaptive setup planning and multi-objective optimization approaches to address these trade-offs [18].

Now, setup planning can play a crucial role in bridging the gap in this conflict [19]. Setup planning is a pivotal task within CAPP that guides workpiece setup, influencing manufacturability, production efficiency, costs, and the integration of CAD/CAPP/CAM/CNC, thus advancing intelligent manufacturing [18]. It is divided into three sub-tasks: setup generation by grouping manufacturing operations, operation sequencing within a setup, and setup sequencing [20,21]. Many works dedicated to the IPPS problem have acknowledged the importance of setup planning for integrating CAPP and the Scheduling function. For instance, ref. [22] proposed adaptive setup grouping strategies for minimization of cost and makespan, and maximization of machine utilization for alternative machines (3-axis, 4-axis, 5-axis, etc.) for a single part. They have focused on grouping operations for a workpiece and assigning each setup to suitable machines, following a cross-machine setup approach. However, they neglected the importance of addressing the true integration of the process planning and scheduling problem, which should involve the consideration of n parts to be processed on m machines. To solve the issue, ref. [19] proposed a cross-machine setup planning approach for multiple parts and grouped operations simultaneously targeting various objectives; however, this research does not consider the routing and sequencing task of the problem. Ref. [23] introduced a hybrid Lamarckian Layered Genetic Algorithm to integrate planning and scheduling in Engineer-To-Order projects, improving solution robustness and reducing schedule instability in the presence of design uncertainty.

There has been growing interest in Adaptive Setup Planning (ASP), which generates machine-specific setups triggered by dynamic schedules [24]. ASP helps adapt to unforeseen events, such as changes in machine availability or tools, and reduces the time needed for re-planning. Therefore, setups should be considered the dispatching unit rather than operations. Early work by [24] emphasized this approach. More recent studies have refined ASP by incorporating reconfigurable resources and uncertainty [25]. Ref. [26] proposed a multi-agent deep reinforcement learning method integrating layout optimization and scheduling, demonstrating improved adaptability and reduced makespan in flexible assembly systems.

From the literature review (

Table 1. Synthesis matrix of IPPS literature.

Reference	$\mathit{j}$$\times \mathit{m}$	SP			Routing		Sequencing		uncertainty		Objective
		O. Grouping	O. Sequencing	S. Sequencing	$\mathit{O}$	$\mathit{S}$	$\mathit{O}$	$\mathit{S}$	Static	Dynamic	CAPP	Scheduling
[28]	1 × $m$				√					√	tol, SF	MFT, $\#J_{tk}$
[29]	1 × $m$	√				√				√	$P_s$, $\#S$
[24]	1 × $m$	√				√				√	C, $M_{utl}$	$C_{max}$
[30]	1 × $m$	√				√				√	C, $M_{utl}$	$C_{max}$
[31]	1 × $m$	√				√				√	C, $M_{utl}$	$C_{max}$
[32]	1 × $m$	√			√				√		C, $M_{utl}$	$C_{max}$
[33]	1 × $m$	√			√				√		$M_{utl}$	$C_{max}$
[13]	1 × $m$	√			√				√		C, $M_{utl}$	$C_{max}$
[19]	$n$ × $m$	√			√				√		C, $M_{utl}$, $\#S$	$C_{max}$
[10]	$n$ × $m$				√		√		√			$C_{max}$
[34]	$n$ × $m$				√		√		√			$C_{max}$
[20]		√	√	√							$\#S$
[21]		√	√	√							$\#S$
[35]	1 × $m$	√	√	√	√
[5]	1 × $m$	√	√		√						$C$, $E_s$
[25]	1 × 1 (Reconfigurable)	√			√						$C$
[36]			√								$C$
[37]		√	√							√
[38]		√	√	√							$\#S$
[39]	1 × $m$	√	√	√		√			√		$C$
[40]		√	√	√
[41]	1 × $m$	√	√	√		√					$C$
[18]		√		√							$C$
Current Articles	$\mathit{n}\times \mathit{m}$	√	√	√		√		√		√	$\#\mathit{S}$	$C_{max}$

($j$ = job, $m$ = machine, $O$ = operation, $S$ = setup, $\#S$ = number of setups, $C$ = cost, $M_{utl}$ = machine utilization, tol = tolerance, SF = surface finish, $P_s$ = part stability, MFT = mean flow time, $\#J_{tk}$ = no of tardy job, $C_{max}$ = makespan, $E_s$ = stacking error; boldfaced entries indicate attributes of the current article.)

), it becomes apparent that most previous research has primarily concentrated on addressing the process plan selection and routing problem under static conditions. While some studies have demonstrated the potential to adapt setup plans to changing shop floor conditions, they have not effectively tackled the sequencing problem within dynamic scenarios. Ref. [27] developed an integrated optimization framework for large-scale, multi-job multitasking batch plants, highlighting the challenges and benefits of simultaneously coordinating planning and scheduling decisions.

However, static scheduling becomes outdated when unforeseen events occur on the shop floor due to unrealistic assumptions considered during its creation. Ref. [42] point out in their review that deterministic scheduling assumptions, such as known and fixed processing times and the absence of machine failures, render these static schedules impractical in real-world situations. As Industry 4.0 continues to evolve, the production system is gaining enhanced flexibility; this progress comes hand in hand with added intricacies in production scheduling. Manufacturing systems inevitably face unpredictable disruptions, causing changes in planned activities due to factors such as shifts in resource availability, order arrivals or cancelations, and longer processing times. Consequently, there arises a necessity for scheduling mechanisms to swiftly adapt to these potential disruptions and efficiently re-optimize the operational sequences in real-time [43].

Therefore, this research takes a novel approach by treating the setups for each job or workpiece as the dispatching and scheduling unit. The goal is to incorporate the problem of CAPP within the dynamic scheduling framework. This innovative approach allows for the development of a one-shot solution method for the integrated CAPP and scheduling problem. Furthermore, it facilitates the reconfigurability of the process plan, as highlighted by Azab and ElMaraghy in 2007) [12]. Building upon these foundational IPPS studies, the following section examines dynamic scheduling approaches that enable real-time adaptation to disruptions in Smart Manufacturing environments.

2.2. Dynamic Scheduling for Smart Manufacturing

The challenge of managing schedules while accounting for real-time events (i.e., disruptions) is referred to as dynamic scheduling. The purpose of this scheduling type is to offer a partial or complete reconfiguration of the production schedule to mitigate the effects of disruptions [44]. Research has developed into dynamic scheduling to address real-time disruptions, treating it as a series of static scheduling problems that require periodic revision or updates triggered by real-time events. The methodology of Dynamic scheduling can be grouped into proactive-reactive and predictive-reactive approaches [43,45]. The aim of the predictive-reactive approach is to develop a preliminary schedule that seeks to mitigate the effects of uncertain events on overall system performance [46]. To adjust the preliminary schedule or reschedule, we need to answer two questions: when and how to react to uncertain events. Three policies—periodic, event-driven, and hybrid rescheduling—are suggested in the literature to address the questions of when to reschedule and how to reschedule. Schedule repair and complete rescheduling are also tackled in the literature [45].

Existing scheduling methodologies can be grouped into three categories: exact approaches, meta-heuristic algorithms, and heuristic approaches [45,47]. Exact approaches based on mathematical modeling have been used to ensure better performance than other heuristic methods in terms of finding optimal solutions. Approaches such as mixed-integer linear programming and branch and bound can find the optimal solutions for small or mid-size scheduling problems [47]. However, they are computationally inefficient for large-scale problems because they cannot solve the problems in polynomial times [47]. Metaheuristics [e.g., simulated annealing (SA), tabu search, genetic algorithms (GAs)] are widely applied to solve large scheduling problems [45]. For instance, ref. [48] proposed a Q-Learning-based NSGA-II algorithm for a dynamic flexible job shop with transportation resources. However, metaheuristic algorithms are often time-consuming and computationally intensive, making them challenging to apply in real-time scheduling environments [49]. Although they can outperform heuristics in terms of solution quality and robustness, their implementation and tuning are complex, and few studies have successfully applied them in dynamic scheduling contexts [50]. Recent studies have advanced dynamic scheduling for flexible job shops by applying reinforcement learning and deep learning approaches, including NeuroEvolution of Augmenting Topologies (NEAT) models for real-time rescheduling under uncertainty [51] and Improved Double Deep Q-networks for rescheduling under machine breakdown scenarios [52].

Currently, in the literature, a common and popular way of dynamically scheduling jobs is by implementing dispatching rules. Dispatching rules are efficient, simple, and capable of instantly solving scheduling problems by assigning a priority for every job in the waiting queue and are frequently used in practice due to their ease of implementation and quick computation time [42,53,54,55]. However, as dispatching rules are traditionally derived from empirical or analytical studies, their performance depends on the state the system is in at each moment [45]. To resolve this limitation and boost their effectiveness/performance, machine learning algorithms arise as a promising solution [43,45,56]. Among the two approaches of dynamic scheduling, a knowledge-based system is capable of extracting implicit knowledge from earlier system simulations to determine the best dispatching rule for each possible system state. Additionally, heuristic approaches that combine threshold- and priority-based dispatching rules within discrete-event simulation frameworks have demonstrated improvements in flow time and system responsiveness [57]. Moreover, ref. [58] proposed novel heuristics and dispatching rules for online scheduling with predicted release time jobs, showing significant improvements in total weighted tardiness in dynamic single-machine environments, which could inform future research extensions to flexible job shops.

The main algorithm types in the field of dispatching rule development are case-based reasoning (CBR), neural networks, inductive learning, and reinforcement learning. The Inductive Learning Algorithm (ILA) is an iterative and inductive machine learning approach employed to generate a set of classification rules, typically presented in the “IF-THEN” format, based on a given set of examples. This algorithm progressively refines its rule set through successive iterations, appending newly generated rules to the existing set. Ref. [49] propose a hybrid simulation–optimization–data mining approach to generate JSP solutions by tabu search and identify the dominant relationship between competing jobs with predefined attributes. A decision tree is subsequently employed to dispatch jobs efficiently in real-time. Ref. [59] constructed a data mining dynamic scheduling model to assign Dispatching Rules (DRs) from a DR library to different scheduling subproblems in real-time. Ref. [60] have also developed a decision tree learning model to select dispatch jobs in real-time. Habib) [61] have developed a GA-data mining approach to automatically assign different dispatching rules to machines based on the jobs in the queues. This work tried to address the dominance or priority of different jobs. Ref. [62] are among the pioneers in developing a data mining-based approach to discovering new dispatching rules for the operation sequencing of multiple jobs. They used a decision tree to discover key scheduling decisions from production data. Ref. [47] have taken an approach to developing operation assignment and sequencing rules using random forests. Ref. [63] introduced an incremental learning approach for dynamic parallel machine scheduling with sequence-dependent setups, showing that periodically retrained neural networks outperform metaheuristics and DRL-based methods in minimizing tardiness.

From this review, it becomes evident that despite substantial progress in integrated process planning and scheduling (IPPS), existing methods continue to face unresolved challenges. Most approaches still rely on static scheduling assumptions or treat routing and sequencing separately, limiting their adaptability in dynamic environments. Additionally, traditional models predominantly use operations as the scheduling unit, overlooking the benefits of setup-level sequencing for enhancing flexibility and efficiency. Few studies offer practical solutions that dynamically reassign and resequence setups under disruptions while remaining computationally efficient. These gaps underscore the need for integrated, real-time frameworks that combine optimization and machine learning to support adaptive scheduling in Smart Manufacturing.

It is also clear that developing a dispatching rule mining system for dynamic setup sequencing can be beneficial for addressing the current gap in the integrated CAPP and Scheduling problem. Based on the literature review presented, this study adopts a predictive-reactive approach to effectively sequence setups on the shop floor, addressing the gap in process planning and scheduling objectives. By integrating machine learning and optimization within a unified framework, the schedule can be dynamically adjusted in response to these disruptions, all while ensuring that the fundamental objectives of the Integrated CAPP and Scheduling problem remain unviolated. On this note [64] demonstrated a complementary digital twin-driven dynamic scheduling strategy for complex product assembly, illustrating how real-time monitoring and multi-objective optimization can enhance both production efficiency and stability—a direction for extending the proposed approach in this article, as outlined in Section 5.

3. Methodology

We introduce a novel approach that combines machine learning (data mining) and optimization techniques to address the integrated CAPP and Scheduling problem (see Figure 1). The proposed approach first assigns setups to available machines on the shop floor. Secondly, setups are sequenced on an assigned machine by learning the best dispatching rule through a Machine Learning Optimization model. Initially, mathematical programming is used to generate solutions to train a dispatching rule mining model. The primary objective of this approach is to establish a set of rules that guide dispatching decisions in sequencing setups within a flexible job shop scheduling environment. Thus, initial nominal solutions for small problem instances are generated as sources of learning rules for scheduling. Once the solutions have been obtained, they are transformed into learning data by constructing new attributes. In this research, the term ‘attributes’ refers to the set of all data related to the scheduling decisions. For each one of these setups, operations within the setup are sequenced optimally. Finally, in the event of a random machine breakdown, the initial schedule is adjusted by reassigning disrupted setups to the new available machine and sequencing them using the mined dispatching rules.

The methodology for the online rescheduling is described as follows:

• Initially, a simulation module generates a series of problem instances relevant to real-world scheduling systems. Alternatively, historical data from the manufacturing system can be used in place of this. These problem instances are then stored in an instance database.
• Subsequently, the optimization module generates solutions for a subset of these instances, from which the initial training dataset is created. These solutions represent a collection of well-informed scheduling decisions that could potentially benefit the manufacturing system. These scheduling decisions form valuable scheduling knowledge, stored in a scheduling database, and utilized by a learning process to construct a decision tree. This decision tree is then used to generate the dispatching rule for the setups. Notably, it is a dynamic sequencing model that can be updated with changes in resources.

Figure 2 illustrates the dispatching rule mining approach framework for sequencing the setups, which consists of the following steps:

• FJSP instances are generated and collected from real production data.
• A subset of instances is solved using a routing algorithm and MILP sequencing model to obtain high-quality initial schedules.
• Scheduling decisions are transformed into labeled data by extracting raw and engineered attributes from setup pairs.
• A supervised learning algorithm, such as Random Forest, is trained to classify sequencing priorities based on the constructed dataset.
• Later, the generated rule can also be used to dynamically sequence setups in real-time, including rescheduling events.

Figure 2. Rule mining procedure for the initial nominal schedule.

Figure 2. Rule mining procedure for the initial nominal schedule.

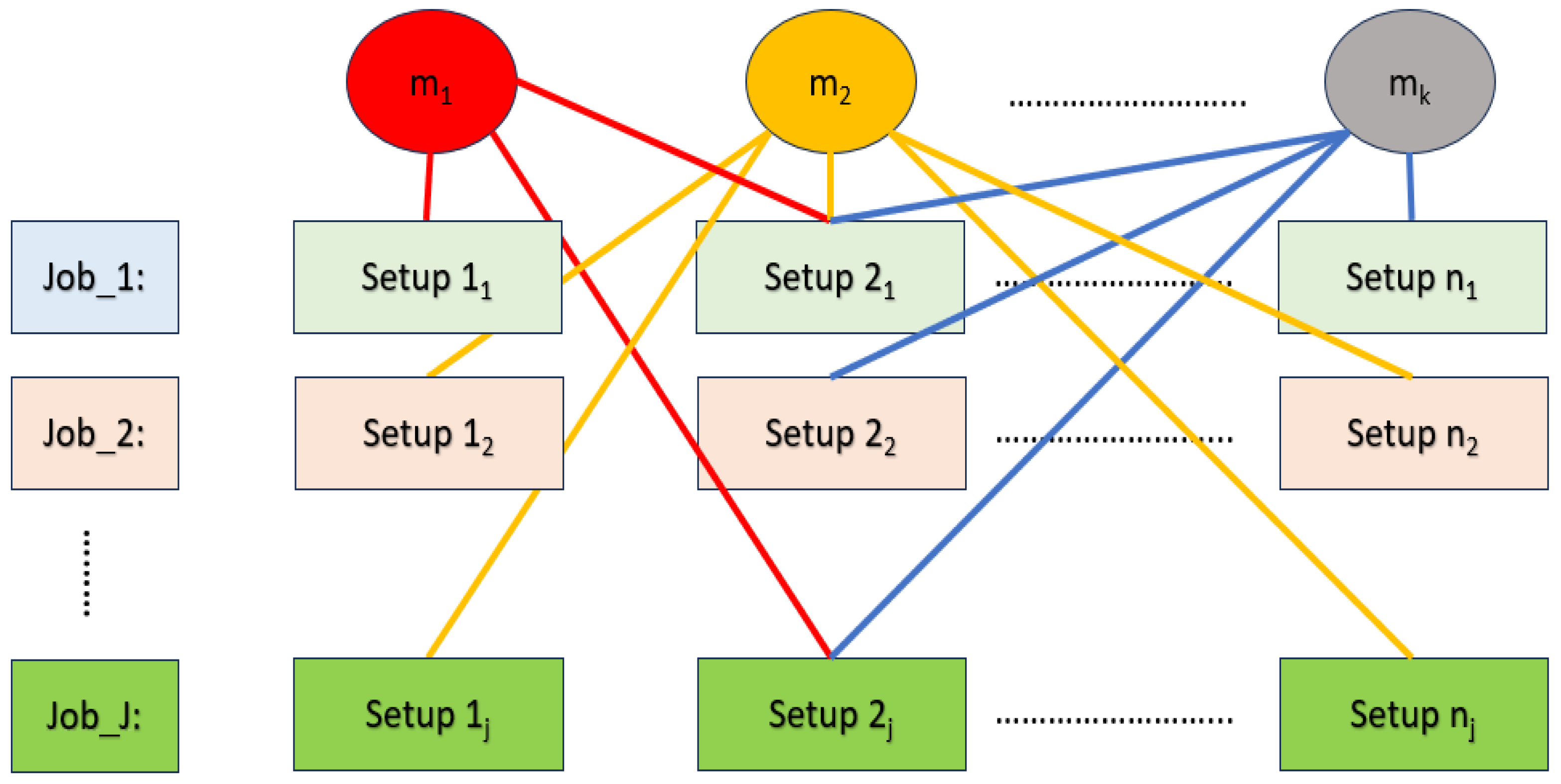
3.1. Solving the FJSP

The Flexible Job Shop Scheduling Problem (FJSP) considered in this research involves assigning and sequencing multiple setups for each job across a set of alternative machines. Each setup can be processed by more than one machine with varying processing times, and all setups within a job must adhere to predefined precedence constraints. This structure results in a combinatorial search space that grows rapidly with the number of jobs, setups, and machines. A schematic overview of the FJSP is presented in Figure 3.

The FJSP instance can be divided into two sub-problems: a routing problem and a sequencing problem. The routing sub-problem involves assigning each operation to a suitable machine. In contrast, the scheduling sub-problem focuses on determining the order in which operations should be performed while considering precedence constraints. The sequencing problem is for sequencing assigned operations to machines and is equivalent to the classical job shop scheduling problem. These two sub-problems have been shown to be NP-hard [47].

The Flexible Job Shop Problem (FJSP) can be approached using two main strategies: concurrent approaches and hierarchical approaches. Hierarchical approaches offer a structured method for independently handling assignments and sequencing decisions, thereby reducing the complexity of the problem.

A hierarchical methodology is employed to address the research problem in this research study. Specifically, a rule-based algorithm is adopted to tackle the routing problem, thereby transforming the initial problem into a form that can be effectively analyzed and compared with a classical job shop sequencing problem.

3.1.1. Solving the Routing Sub-Problem/Machine Assignment

The routing sub-problem is a crucial aspect of production scheduling, involving the assignment of each operation or task to a suitable machine or workstation. This is a fundamental step in optimizing the production process, as it determines the sequence in which tasks are executed and allocates resources.

Solving the routing sub-problem aims to minimize production costs, maximize efficiency and utilization, reduce makespan, or achieve other specific objectives depending on the manufacturing environment and requirements. Various algorithms and techniques, such as mathematical optimization, heuristics, and simulation, can be used to address the routing sub-problem and find an optimal or near-optimal assignment of operations to machines.

In this study, we have employed the Approach by Localization (AL), as summarized in Algorithm 1, which enables us to address the resource allocation challenge and construct an ideal assignment model [65,66]. This method considers both the time it takes to complete tasks and the load on each machine, which is the total processing time of the operations assigned to it. The process involves identifying, for each operation, the machine with the shortest processing time, locking in that assignment, and subsequently adding this time to all the following entries in the same column (updating the machine’s workload). This is illustrated in

Table 2. Approach by localization.

	M1	M2	M3		M1	M2	M3		M1	M2	M3		M1	M2	M3
s11	7	6	4		7	6	5		11	6	5		7	6	4
s12	4	8	5		4	8	6		4	8	6		4	8	5
s13	9	5	4		9	5	5		13	5	5	…	9	5	4
s21	2	5	1		2	5	1		6	5	1		2	5	1
s22	4	6	8		4	6	9		8	6	9		4	6	8

Machine workload updates are in boldface; highlighted cells show the final assigned machines (solution of the routing problem).

, where bold values correspond to workload updates.

Algorithm 1. Algorithm for solving the routing subproblem.
Input:	FJSP problem instance
Output:	Route of Jobs
	For index in range(length_input):
	row = random_select	# Get the current row by random selection
	get row_min get min_column_index	# assign setup in machine with min_pt
	for i in range(index + 1, len(length_input)):
	row_val += row_min	# Add the minimum value to the subsequent rows in the same column
	End For
	End For

3.1.2. Solving the Sequencing of Setups Sub-Problem/Job Shop Scheduling (JSP)

Once the assignments are settled, the problem becomes akin to a classical JSP problem. We just need to determine the sequence of the setups on the machines. The sequencing is feasible if it respects the natural, logical precedence relationship among the setups of the same job, i.e., setup $S_{ij}$ cannot be processed before setup $S_{ij+1}$. In this study, the sequencing of the initial assignments is obtained by solving the following Mixed Integer Linear Programming (MILP) model, which is formulated as follows:

The problem considers $n$ jobs that must be processed on $m$ machines. Each job consists of a total of $n_j$ setups. Each setup $S_{ij}$ must be assigned to a machine $k$ and find the sequence of the job $j$. The setup planning solution includes and sets the precedence between the setups of a job. The objective is to minimize the maximum makespan. The model assumptions are defined as follows:

Assumptions:

(1)

All the jobs and machines are available at time zero.

(2)

Each machine can perform at most one operation at any time.

(3)

Transportation time is not considered.

(4)

Processing time includes setup time.

(5)

Job pre-emption is not allowed.

(6)

The setup numbers are indicative of their natural logical sequence within a job.

The MILP model is listed as follows:

$$\mathrm{Min} C_{max}$$

(1)

s.t.,

$$s_{i,j,k}\le M\ast x_{i,j,k}\forall \mathrm{i},\mathrm{j},\mathrm{k}$$

(2)

$$\begin{gathered} s_{i+1,j,k}\ge s_{i,j,k}+P_{i,j,k}\ast x_{i,j,k} \\ \forall i=1\dots (n_j-1),\mathrm{j},\mathrm{k},x_{i+1,j,k}=1,x_{i,j,k}=1 \end{gathered}$$

(3)

$$\begin{gathered} s_{i+1,j,k^{\prime }}\ge s_{i,j,k}+P_{i,j,k}\ast x_{i,j,k} \\ \forall i=1\dots (n_j-1),j,k^{\prime }:k\ne k^{\prime },k,x_{i+1,j,k^{\prime }}=1,x_{i,j,k}=1 \end{gathered}$$

(4)

$$\begin{gathered} s_{i^{\prime }{j}^{\prime }k}\ge s_{ijk}+P_{ijk}\ast x_{ijk}-M\left(3-Z_{i{i}^{\prime }j{j}^{\prime }k}-x_{i^{\prime }{j}^{\prime }k}-x_{ijk}\right) \\ \forall i,i^{\prime }:i\ne i^{\prime },j,j^{\prime }:j\ne j^{\prime },k,x_{i^{\prime }{j}^{\prime }k}=1,x_{ijk}=1 \end{gathered}$$

(5)

$$\begin{gathered} s_{ijk}\ge s_{i^{\prime }{j}^{\prime }k}+P_{i^{\prime }{j}^{\prime }k}\ast x_{i^{\prime }{j}^{\prime }k}-M\left(3-Z_{i{i}^{\prime }j{j}^{\prime }k}-x_{i^{\prime }{j}^{\prime }k}-x_{ijk}\right) \\ \forall i,i^{\prime }:i\ne i^{\prime },j,j^{\prime }:j\ne j^{\prime },k,x_{i^{\prime }{j}^{\prime }k}=1,x_{ijk}=1 \end{gathered}$$

(6)

$$C_{max}\ge {\sum }_{k=1}^K{s}_{ijk}+{{\sum }_{k=1}^K{x}_{ijk}\ast P}_{ijk}\forall i,j,k$$

(7)

$$s_{ijk},C_{max}\ge 0 \forall i,j,k$$

(8)

$$Z_{i{i}^{\prime }j{j}^{\prime }k}\in \{0,1\} i,i^{\prime }:i\ne i^{\prime },j,j^{\prime }:j\ne j^{\prime },k$$

(9)

The objective function in Equation (1) minimizes the makespan of all setups. Constraint (2) defines the completion time of each setup on its assigned machine. Constraints (3) and (4) enforce precedence relationships within each job, ensuring that setups are processed in the correct order. Constraints (5) and (6) prevent overlapping of setups belonging to different jobs on the same machine by establishing mutual exclusivity. Constraint (7) specifies the maximum makespan as a positive value. Constraint (8) ensures that all start times and makespan values are non-negative. Finally, Constraint (9) defines the binary and continuous decision variables used in the model.

The goal of the experiment is to solve the problem instance and generate high-quality solutions (in terms of makespan). OR-Tools2 (ORT), an open-source solver developed by Google [67,68]. In this research, we utilized Google’s OR-Tools to determine the optimal sequence for the initial assignment. Concerning the solvers’ version, we use version 9.6 for OR-Tools. We have decided to use the CP-SAT solver because CP-SAT has proven to be better on average, as reported in the literature, is fairly easy to implement, and is compatible with other necessary Python 3.10 libraries and packages [67,68]. The experiment is conducted on a system equipped with a 3 GHz Intel Core i7 4-Core (11th Gen), 16 GB of DDR4 RAM, and a 256 GB M2 SSD.

3.1.3. Sequencing the Operations Within a Setup

The literature on the problem of sequencing operations is rich. Any of the developed existing models or heuristics (e.g., [12,69]) can be used for the purpose depending on the complexity of the problem.

3.2. Construction of Data Mining Dataset from Initial Solution

Creating an appropriate training dataset is a pivotal aspect of the entire rule-mining procedure. When viewed from the perspective of setup sequencing, the primary objective is to identify the preferred order in which setups should be prioritized for dispatching among a collection of schedulable setups, regardless of whether they belong to the same or different jobs and are intended for the same machine at a specific moment. By extracting this knowledge from the training dataset, we can determine the sequence for dispatching the next setup at any given time. Subsequently, this knowledge can be used to generate dispatching lists for any combination of jobs and machines, provided that the assignment or routing for each setup is known.

3.2.1. Attribute Selection

Attribute selection is the task of identifying the most suitable set of attributes for a classifier, aiming to reduce the number of attributes while maximizing the separation between classes [49]. This process is crucial for the effectiveness of subsequent model induction since it helps eliminate redundant and irrelevant attributes. However, it is also important to note that the attributes recorded as part of the available data may not always be the most relevant or useful for the data mining process, making the creation of new attributes a necessary consideration.

A priority relationship can be established between jobs, with sequencing based on their processing time, due date, and other relevant factors [49,62,70]. Th1is priority relationship can be reduced by only considering two setups on the same machine, among schedulable jobs, at any given instance for comparison. However, proper attribute selection is essential for capturing this relationship.

Furthermore, both the selection of raw attributes from production data and the creation of new attributes are closely tied to the objectives of the scheduling problem. Objectives related to making span require different attributes to be considered compared to objectives pertaining to flow time or tardiness. For example, attributes related to processing time, precedence relationship, and associated statistics are more suitable for makespan or completion time-based objectives. Similarly, attributes related to deadlines and associated statistics are more suitable for objectives based on tardiness.

Additionally, the attributes recorded as part of the raw production data may not be the most useful for the data mining itself. Thus, the creation of new attributes must be considered [49,62,70]. Combining raw attributes through arithmetic operations can lead to the creation of new valuable attributes, as pointed out by [62]. However, it is important to avoid having a large set of attributes, as they are often not independent of each other, which can make the process computationally impractical [46].

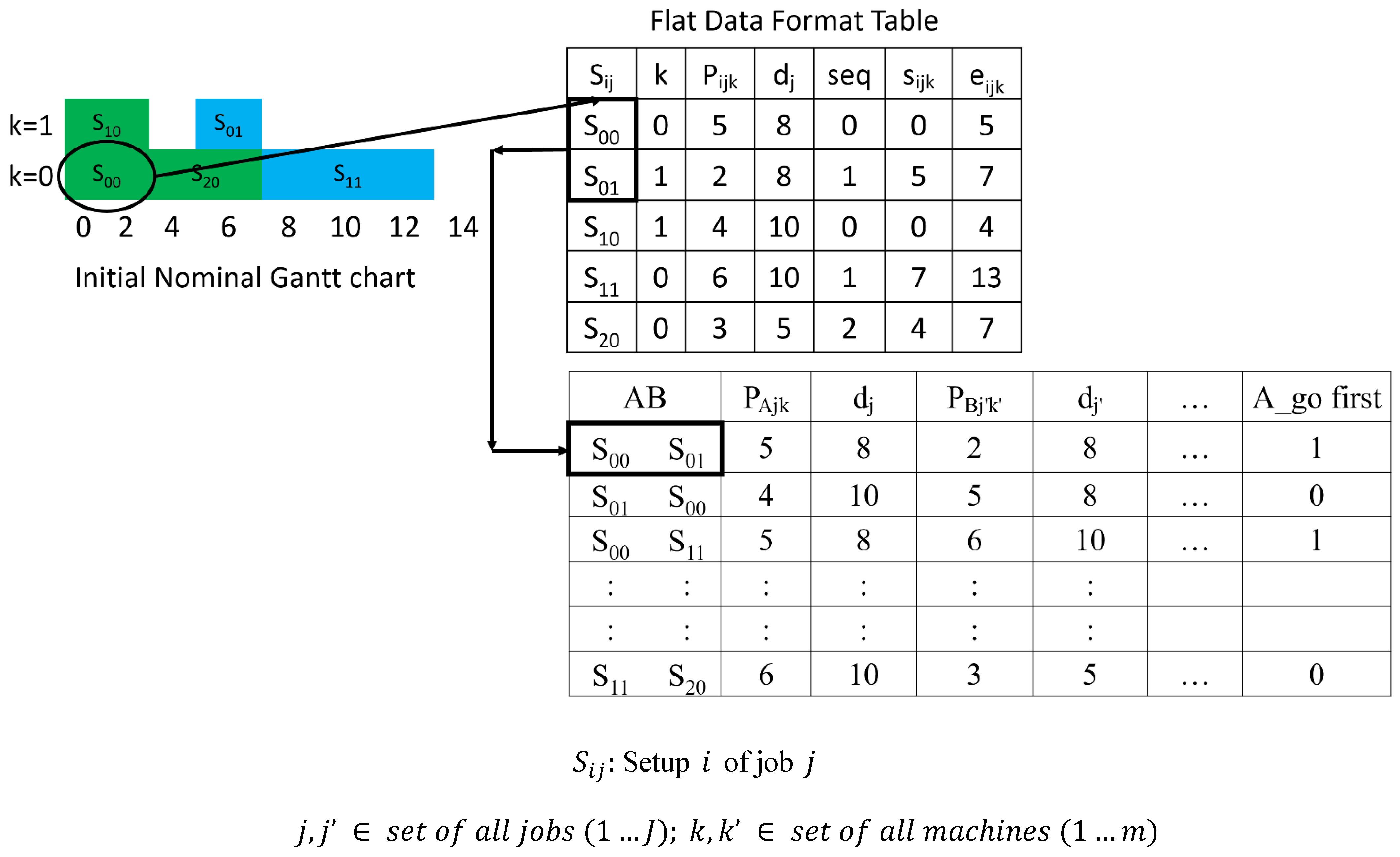
3.2.2. Creation of Training Dataset

The goal of this step is to convert the initial nominal scheduling solution into training data. From the previous steps, nominal solutions for each problem instance are saved as a flat data file. The columns represent separate data attributes, and each row of the file represents the schedule of a setup. The training dataset for sequencing setups is then generated by following two steps, as shown in Figure 4.

• First, the first setup in the schedule list is selected, and all setups that can be processed at the start time are taken. Subsequently, all possible combinations of setup pairs are selected. Thus, for a problem instance with $j$ jobs each having $i$ setups, there will be $2·C_2^{i·j}$ possible setup pairs.
• Then, rows for all possible pairs of setups are appended to a dataset with their attributes.

Figure 4. Process of training dataset generation.

Figure 4. Process of training dataset generation.

3.3. Development of Dispatching Rule Mining Model

The setup sequencing rule or dispatching rule is mined using the following supervised learning methodology. The implementation details are described in the following sections.

3.3.1. Preprocessing of the Data

Preprocessing the data, including feature selection and data cleaning, such as handling missing values, outliers, inconsistent or skewed values, removing duplicates, ensuring data format consistency, correcting typos, errors, dealing with irrelevant or redundant information, etc. In the present scenario, case studies have been meticulously crafted through simulation. Nevertheless, it is crucial to emphasize the importance of this step, especially when working with datasets derived from real-world manufacturing systems.

3.3.2. Model Selection

The choice of potential classifiers suitable for the problem depends on the problem’s complexity, dataset size, interpretability needs, and available algorithms. For this research, a range of supervised learning classifiers was considered to evaluate different algorithm families and their suitability for dispatching rule prediction. Random Forest (RF) is an ensemble method that aggregates the outputs of multiple decision trees, offering robustness against overfitting and the ability to capture complex feature interactions. K-Nearest Neighbors (KNN) is a non-parametric, instance-based classifier that assigns classes based on the majority vote among nearest neighbors in the feature space. The Support Vector Machine (SVM) constructs an optimal hyperplane to separate classes with the maximum margin, using kernel functions to handle non-linear boundaries when needed. Naive Bayes is a probabilistic model that assumes conditional independence among features and calculates class probabilities using Bayes’ theorem. Logistic Regression models the relationship between features and class probabilities using a logistic function, providing interpretable coefficients and probabilistic outputs. These classifiers were selected to cover a spectrum of linear, non-linear, probabilistic, and ensemble approaches.

3.3.3. Parameter Tuning

Identify hyperparameters specific to the chosen models (e.g., learning rate, number of trees, regularization strength) that affect model performance. We investigated the typical variation in parameters for each learning algorithm. This section provides a summary of the parameters employed for each learning algorithm [71].

Random Forest (RF): The number of trees in the forest varies between 50 and 500. The number of features to consider when looking for the best split was 1, 2, 4, 6, 8, and 11.

KNN: We used 10 values of $k$, ranging from $k = 1$ to (number of sample). The standard Euclidean distance was used as the metric for distance computation.

SVM: The following kernels were used: linear, polynomial degree 3, and radial with kernel varying coefficient (1/(n_features * X.var()), 1/n_features, 0.001, 0.01, 0.5, and 1).

Naive Bayes (NB): We employed Gaussian Naive Bayes.

Logistic Regression (LR): Regularized logistic regression is employed. Tolerance was varied by a factor of 10 from 10⁻⁵ to 10⁵.

3.3.4. Cross Validation

This study uses stratified K-fold CV on the dataset to perform 5- and 10-fold cross-validation. The dataset is shuffled to have representative folds.

3.3.5. Model Evaluation Metrics

In this research, the best-performing model based on its performance on the cross-validation set is selected and assessed against the test set, which it has never seen before. This gives an estimate of its generalization ability. To evaluate the performance, the approach proposed by [71] has been adopted. In this evaluation process, we have calculated performance metrics based on seven evaluation parameters: Accuracy (ACC), F-score (FSC), Receiver Operating Characteristic (ROC) score, Precision (APR), Recall (REC), Root Mean Square Error (RMS), and Mean Cross-Entropy (MXE), as well as the Execution Time (TIME).

3.4. Reconfiguration of Initial Nominal Schedule Under Disruption

This section explains the rescheduling strategy. The rescheduling strategy employs dynamic adjustments to the existing schedule, prioritizing the reassignment of affected jobs to alternative available machines. This ensures production can resume as swiftly as possible following a breakdown event. In this research, we have considered an FJSP with a machine breakdown problem based on the following assumptions:

Assumptions:

-

The occurrence of machine failures is modeled as following an exponential distribution.

-

During a production cycle, only one machine will experience a breakdown.

3.4.1. Machine Breakdown Distribution

According to the assumption of [72], the breakdown probability follows the exponential distribution shown in Equation (10):

$$P_k= \left\{\begin{array}{c}0, when t\le 0 or {t=r}_{bk}\\ 1-e^{-\mathrm{\lambda }t}, when 0<t<r_{bk}\end{array}\right.$$

(10)

where $P_k$ = Probability of machine failure, $r_{bk}$ = Estimated repair time, $\lambda = 1/$Mean time between two successive breakdowns.

Following this assumption, this article introduces a Monte Carlo simulation-based approach to model the probability of breakdowns occurring over a production cycle. The simulation model is implemented using Python 3.10, leveraging the random and matplotlib libraries.

Simulation model for Machine Breakdown:

• Setting the Mean Time Between Breakdowns ($\lambda$): The mean time between breakdowns (lambda) is a key parameter that influences the simulation’s behavior. This parameter is user-adjustable, enabling the exploration of various real-time scenarios and system characteristics.
• Generating Random Breakdown Times: Using an exponential distribution, the simulation generates random breakdown times for each machine independently. We conduct 1000 simulations for each machine to collect data on breakdown times.
• Calculating Breakdown Probability: We compute each machine’s breakdown probabilities at various time points. This allows us to construct cumulative probability curves specific to each machine.

In this research, if the probability function exceeds a specified threshold, the machine will experience a breakdown. Multiple breakdowns are not considered to simplify the problem.

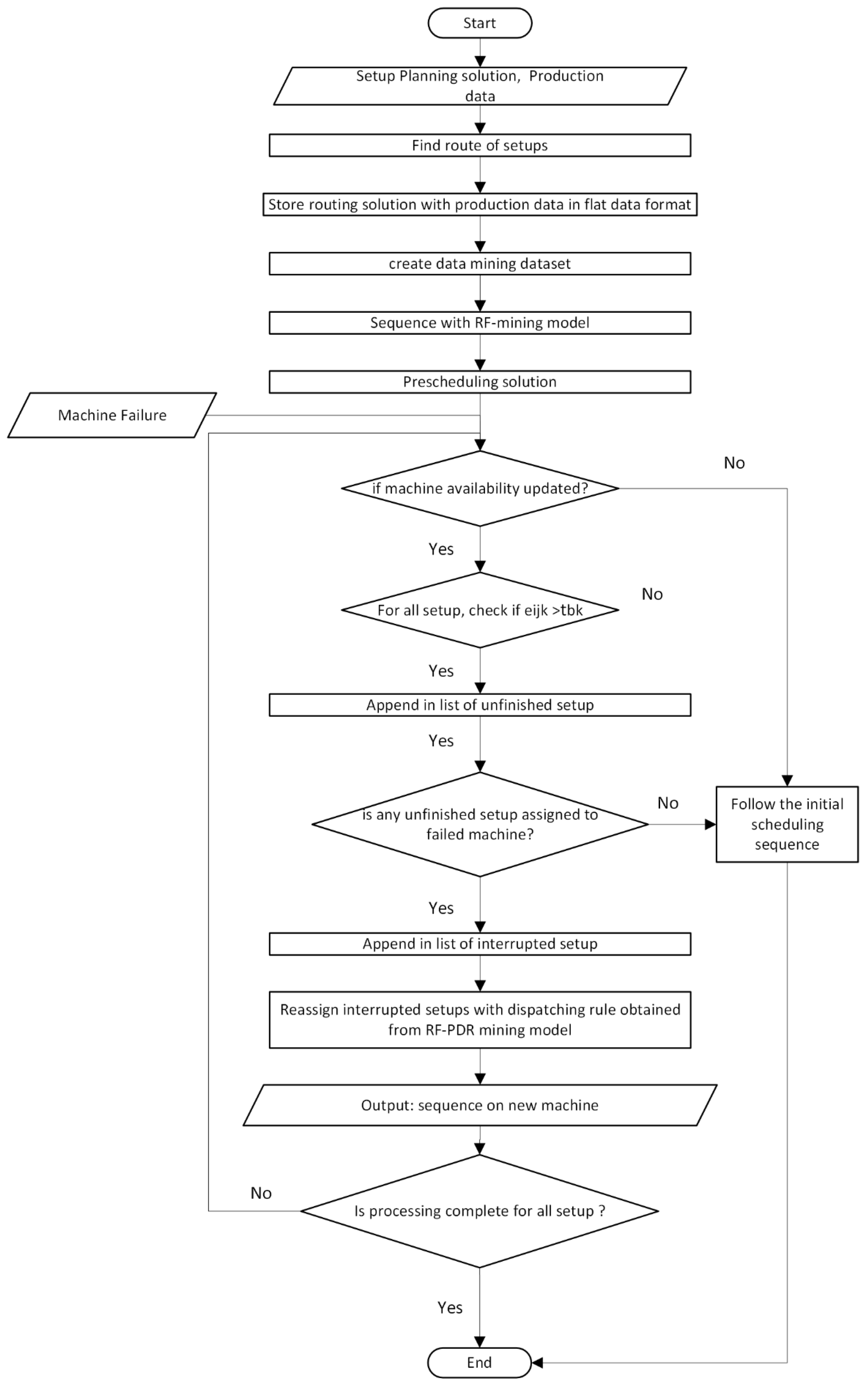
3.4.2. Online Rescheduling Framework

In traditional static scheduling, production plans are generated once and executed without modification, often becoming infeasible when disruptions occur on the shop floor, whether related to machines, material handling, or job profiles. By contrast, dynamic scheduling continuously monitors the production environment and triggers rescheduling actions in response to events, e.g., machine breakdowns, material delays, changes in priority. This study adopts a dynamic scheduling approach, as shown in the flowchart illustrated in Figure 5, which integrates real-time monitoring with dispatching rule mining to adapt sequencing decisions during execution:

Assuming an initial state at $t = 0$, where the probability of machine breakdown is zero, the prescheduling process is initiated on the job floor, and setups are executed in accordance with the initial nominal scheduling solution. In instances where no machine breakdown occurs, this schedule becomes the realized schedule. As the probability of machine breakdown surpasses a predefined threshold, machine failures are anticipated. Subsequently, the following decision criteria must be evaluated:

• Identification of Interrupted Setups: A critical assessment is conducted for all setups in progress on the broken machine at the time of breakdown. Setups categorized as “interrupted setups” if their scheduled end time exceeds the breakdown time.
• Reassignment of Interrupted Setups: To resume production without delay, these interrupted setups must be reassigned to currently available, eligible machines. This reassignment is executed following a localization heuristic approach.
• Sequencing of Interrupted Setups: Once the setups have been reassigned to new machines, their sequence is determined using a dispatching rule derived from the RF-PDR mining model.
• Continuation of the Rescheduling Process: The rescheduling process is iteratively executed until the machine is repaired and brought back into operational condition. Throughout this process, the current availability of resources is continuously considered to ensure optimal scheduling decisions.

This rescheduling framework is designed to effectively address machine breakdowns, minimizing disruption to production processes and optimizing resource utilization systematically and adaptively.

3.4.3. Robust and Stability Measures of Rescheduling

The rescheduling implemented on the job floor is characterized by two crucial attributes: robustness and stability. Developing a rescheduling system that embodies robustness and stability is imperative to mitigate the impact of unforeseen disruptions. In this study, the robustness and stability metrics are adopted from [64] and defined in Equation (11):

$$\mathrm{Robustness}, \mathrm{RM} = {\displaystyle \frac{C_{maxR}-C_{maxP}}{C_{maxP}}}\times 100\mathrm{\%}$$

(11)

where $C_{maxR}$ = makespan after rescheduling and $C_{maxP}$ = makespan of prescheduling.

The stable measures as in Equation (12):

$$\mathrm{SM} = \min {\displaystyle \frac{{\sum }_{j=1}^{n^{\prime }}{\sum }_{i=1}^{q\prime }{|C}_{ijP}-C_{ijR}|}{{\sum }_{j=1}^n{n}_j}}$$

(12)

where $n^{\prime }$ = number of unfinished and currently in-progress jobs, $n$ = total number of jobs, $q\prime$ = number of unfinished and currently in-progress setups of the job $i$, $C_{ijP}$ = predicted completion time for setup $i$ of job $j$ in the prescheduling phase, $C_{ijR}$ = completion time for setup $i$ of job $j$ in the rescheduling process.

4. Experimental Setup

A simulation module is used to generate instances of the relevant scheduling problem. The experimental configurations were chosen to align with problem sizes commonly studied in the literature, where moderate-scale scenarios serve as benchmarks for validating dynamic scheduling frameworks. This enables a transparent comparison with established methods, ensuring that model performance can be rigorously evaluated. Larger-scale instances remain a valuable direction for future work. In our experiments, we created three sets of similarly sized static FJSP instances: FJSP_5 which consists of five jobs and three machines described in

Table 3. Considered parameters for the case study.

Parameters	FJSP_5
Number of jobs	5
Range setups per job	2–3
Number of machines	3
Minimum number of equivalent machines per setup (flexibility: $f$)	2
Range of processing time per setup (hours)	10–50
Tightness factor of the due date	0.8–1.2

. These specific problem instances were generated randomly, following the parameters outlined in the methodology introduced by [20]. All jobs are assumed to be available simultaneously at time zero. The discrete uniform distribution between 10 and 50 is used to generate the operation processing times. The due date of each job was specified by a date tightness parameter, as in [73]. The due date formula is shown in Equation (13):

$$d_i= r_j+c * {\sum }_{j=1}^{n_i}{\overline{P}}_{ij}$$

(13)

where $c$ = tightness factor of the due date, $n_i$ = number of operations of the job $i$, $r_j=$ release date of job $j$ (notably, $r_j=0 \forall j$), and ${\overline{P}}_{ij}$ = average processing time of setup $i$ of job $j$, given all the candidate machines that can carry out the setup.

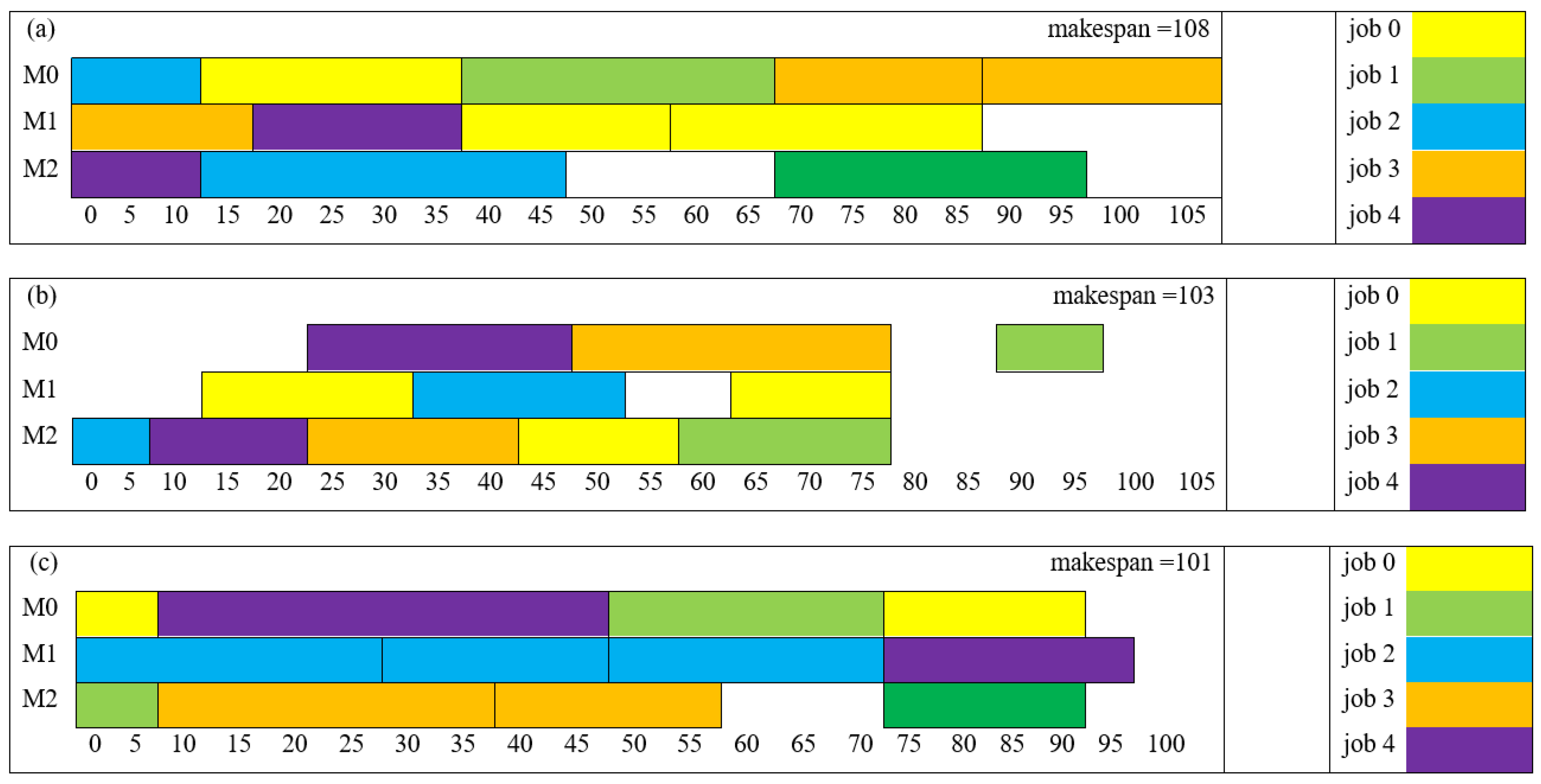
Following the methodology outlined in Section 3.1, we initially obtained nominal solutions encompassing routing and sequencing decisions. Figure 6 illustrates the Gantt chart derived from these obtained solutions.

This study considers 11 attributes, which are categorized into two types: raw and constructed. The four raw attributes are the setup processing time ($p_{ijk}$) and the due date of the job ($d_j$). These are considered directly from production data. Constructed attributes can further be divided into two types. Composite attributes and categorical attributes. Two composite attributes are built with basic arithmetic operations following the methodology proposed by [62,70]. The categorical attributes represent binary variables used to indicate a direct comparison between two setups, A and B. When the raw attribute value of A exceeds that of B, the categorical value is set to 1. Conversely, when the raw attribute value of A is less than that of B, the categorical value is set to −1. For all other situations, the categorical value is set to 0. In this research, five categorical attributes are also constructed to capture the priority, delay, and precedence relationship among setups. Details of the attributes are shown in

Table 4. Considered attributes for rule mining.

Type	Feature/Attributes	Notation
Raw	processing time of setup A	p_A
	processing time of setup B	p_B
	due data of the A	d_A
	due data of the B	d_B
Constructed	if processing time of A is higher than B (categorical)	p_A>B
	if due date of A is higher than B (categorical)	d_A>B
	processing time difference	p_A-B
	Due date difference	d_A-B
	if A and B has precedence relationship (categorical)	$Z_{i{i}^{\prime }j}$
	if A precedes B (categorical)	$Z_{ij}$ > $Z_{i^{\prime }j }$
	if A and B processed on same machine (categorical)	$x_{i{i}^{\prime }k}$

.

Subsequently, these solutions are arranged in a flat-file format to assemble the dataset required for rule mining, as detailed in

Table 5. Initial nominal solution in flat data format.

${\mathit{S}}_{\mathit{i}\mathit{j}}$	$\mathit{k}$	${\mathit{P}}_{\mathit{i}\mathit{j}\mathit{k}}$	${\mathit{d}}_{\mathit{j}}$	$\mathit{s}\mathit{e}\mathit{q}.$	${\mathit{s}}_{\mathit{i}\mathit{j}\mathit{k}}$	${\mathit{e}}_{\mathit{i}\mathit{j}\mathit{k}}$
s00	0	23	49.2	1	16	39
s01	1	21	49.2	2	39	60
s02	1	27	49.2	3	60	87
s10	0	31	44.4	2	39	70
s11	2	29	44.4	2	70	99
s20	0	16	45.2	0	0	16
s21	2	30	45.2	1	18	48
s30	1	18	48	0	0	18
s31	0	19	48	3	70	89
s32	0	19	48	4	89	108
s40	2	18	42.8	0	0	18
s41	1	21	42.8	1	18	39

$S_{ij}$ = setup ID, $k$ = assigned machine, $P_{ijk}$ = processing time of $S_{ij}$ on $k$, $d_j$ = due date of job $j$, $seq.$ = sequence of $S_{ij}$ on k, $s_{ijk}$ = start time of $S_{ij}$ on $k$, $e_{ijk}$ = completion time of $S_{ij}$ on $k.$

. Each row within the flat data file corresponds to a specific setup, while the columns encapsulate relevant production data. The next step involved crafting a training dataset from these flat files by aggregating all feasible setup pairs and their corresponding attributes for each case study. In total, we generated 313 setup pairs from these three case studies.

4.1. Findings of Parameter Tuning and Model Selection

To rigorously evaluate the performance of our model, we employed a systematic approach. We began by selecting 250 setup-pair instances at random from a comprehensive dataset compiled from three distinct case studies. These instances were divided into training and testing sets, with 5-fold cross-validation applied to each trial to ensure robustness and reduce bias. The experimentation involved training models and selecting optimal parameters for predicting sequences between two setups.

The following are the key findings from model parameter tuning:

• RF Classifier: The RF classifier with 500 trees and 11 features consistently outperformed other configurations across all evaluation metrics. However, it is important to note that the computational time increased significantly, from 3 s for 50 trees to 16 s for 500 trees. Interestingly, beyond 300 trees, the performance metrics exhibited minimal change. Hence, for the RF classifier, a balance between computational efficiency and performance led us to select the model with 300 trees and 11 features for building the rule mining model, referred to as the RF-PDR mining model.
• K-Nearest Neighbors (KNN) Classifier: In the case of KNN, a k-value of 1 yielded the best metrics. However, the computational time was minimal for all k-values, making it a computationally efficient choice.
• Support Vector Machine (SVM) Classifier: SVM exhibited similar performance across various parameter combinations. Models with a linear kernel and a scale coefficient consistently outperformed others. SVM models were also relatively efficient in terms of execution time.
• Logistic Regression (LR) Classifier: LR showed the weakest performance across all metrics, with limited variation based on parameter selection. The best results were obtained with a tolerance value of 0.001.

The following are the key findings from normalized performance metrics:

To facilitate a fair and comprehensive comparison across different algorithms, performance metrics are normalized using z-scores. This enabled us to objectively evaluate and select the best model for learning dispatching rules.

Table 6. Normalized Scores for each learning algorithm by metrics (average over 5-folds).

Model	Combinations	ACC	FSC	ROC	APR	REC	RMS	MXE	MEAN	TIME
RF (num_trees, num_Features)	100, 1	0.643	0.570	0.593	0.591	0.609	0.500	0.333	0.548	0.980
	100, 6	0.738	0.670	0.701	0.705	0.696	0.375	0.251	0.591	0.927
	100, 11	0.810	0.748	0.691	0.773	0.783	0.188	0.186	0.597	0.950
	300, 1	0.857	0.783	0.845	0.864	0.739	0.250	0.137	0.639	2.735
	300, 6	0.857	0.783	0.845	0.864	0.739	0.250	0.137	0.639	2.735
	300, 11	0.925	0.890	0.907	0.919	0.917	0.108	0.078	0.643	2.353
	500, 1	0.952	0.913	0.948	0.909	0.913	0.125	0.069	0.690	4.324
	500, 6	1.000	0.957	1.000	1.000	1.000	0.063	0.029	0.721	4.586
	500, 11	1.000	1.000	1.000	1.000	1.000	0.000	0.000	0.714	4.703
KNN	k = 1	0.833	0.714	1.000	1.000	0.875	0.750	1.000	0.882	0.000
	k = 20	0.667	0.714	0.706	0.833	0.625	0.750	0.902	0.742	0.006
	k = 50	0.500	0.429	0.412	0.500	0.375	0.875	0.902	0.570	0.009
	k = 80	0.500	0.429	0.412	0.500	0.375	0.875	0.902	0.570	1.000
NB		0.167	0.000	0.118	0.000	0.125	1.000	0.627	0.291	0.061
LR (tol.)	tol = 0.0001	0.167	0.000	0.118	0.000	0.125	1.000	0.618	0.290	0.064
	tol = 0.001	0.167	0.000	0.000	0.000	0.125	1.000	0.608	0.271	0.061
	tol = 1	0.083	0.000	0.000	0.000	0.125	1.000	0.598	0.258	0.061
	tol = 100	0.083	0.029	0.000	0.000	0.125	1.000	0.588	0.261	0.067
	tol = 10,000	0.083	0.026	0.000	0.000	0.125	1.000	0.582	0.267	0.061
SVM (kernel, coeff.)	‘linear’, ‘scale’	0.500	0.286	0.412	0.500	0.375	0.875	0.853	0.543	0.067
	‘rbf’, ‘scale’	0.500	0.286	0.412	0.333	0.375	0.938	0.833	0.525	0.067
	‘poly’, ‘scale’	0.333	0.286	0.412	0.333	0.000	0.938	0.804	0.444	0.079
	‘linear’, ‘auto’	0.333	0.286	0.412	0.333	0.250	0.875	0.804	0.470	0.070
	‘rbf’, ‘auto’	0.333	0.286	0.412	0.333	0.250	0.938	0.804	0.479	0.061
	‘poly’, ‘auto’	0.333	0.143	0.118	0.333	0.250	0.938	0.706	0.403	0.055
	‘linear’, 0.001	0.333	0.143	0.118	0.000	0.250	0.938	0.735	0.360	0.070
	‘rbf’, 0.001	0.333	0.143	0.118	0.167	0.250	0.938	0.716	0.381	0.070
	‘poly’, 0.001	0.167	0.143	0.118	0.167	0.250	1.000	0.706	0.364	0.076
	‘linear’, 0.01	0.167	0.143	0.118	0.167	0.250	1.000	0.696	0.363	0.073
	‘rbf’, 0.01	0.167	0.000	0.118	0.167	0.125	1.000	0.676	0.322	0.070
	‘poly’, 0.01	0.167	0.100	0.118	0.167	0.125	1.000	0.667	0.335	0.070
	‘linear’, 1	0.167	0.100	0.118	0.000	0.125	1.000	0.657	0.309	0.055
	‘rbf’, 1	0.167	0.086	0.059	0.167	0.150	1.000	0.645	0.325	0.052
	‘poly’, 1	0.000	0.143	0.059	0.000	0.125	1.000	0.637	0.281	0.052

In the table, the algorithm with the best performance on each metric is boldfaced.

presents the normalized values for each algorithm on each of the seven metrics and execution time, calculated as the average over 5-fold cross-validation across different parameter combinations.

Upon aggregating the results across all seven metrics, RF emerged as the superior model. Following RF, KNN exhibited the next best performance, while LR consistently performed the poorest across all metrics.

Considering both performance and computational efficiency, we selected the RF classifier with 300 trees and 11 features to construct the RF-PDR mining model. This decision strikes a balance between robust predictive capabilities and manageable computational demands, making it an ideal choice for learning dispatching rules in our context. This selection ensures that the RF-PDR mining model can provide effective sequencing recommendations for setups in a flexible job shop scheduling environment, thereby optimizing manufacturing operations. The comprehensive evaluation process presented in this section underpins our confidence in the chosen model’s ability to deliver real-world value.

4.2. Evaluation of Generalization Capability of the RF-PDR Mining Model

The effectiveness and generalization capability of our Random Forest (RF)-based dispatching rule mining model were rigorously assessed through extensive testing on new, unseen problem instances. In this section, we present the results of these tests, highlighting the model’s ability to predict sequencing schedules for setups within a flexible job shop scheduling environment. To assess the model’s generalization prowess, we conducted experiments where we excluded instances generated from one specific problem instance and utilized instances generated from the remaining two problem training datasets.

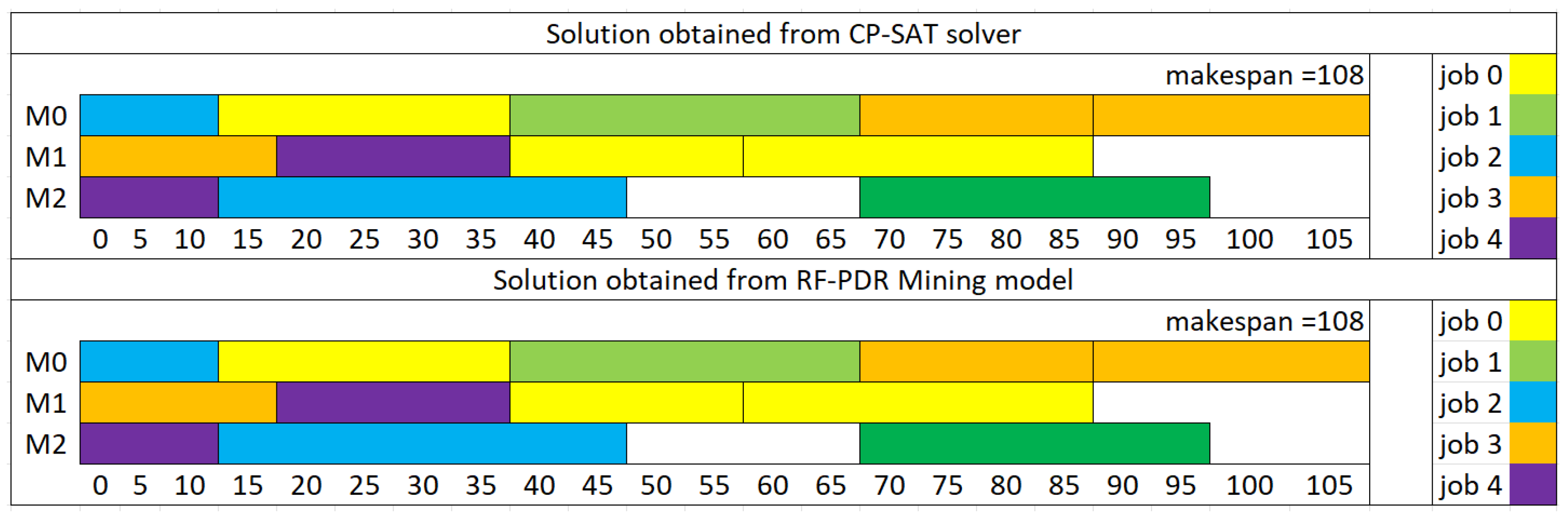
The RF-Dispatching Rule Mining Model displayed remarkable performance in these instances. In the first case, labeled as FJSP5_C1 with perfect prediction, the model flawlessly predicted the sequencing schedule for all setups, achieving a flawless match with the optimization solver’s solutions (Figure 7).

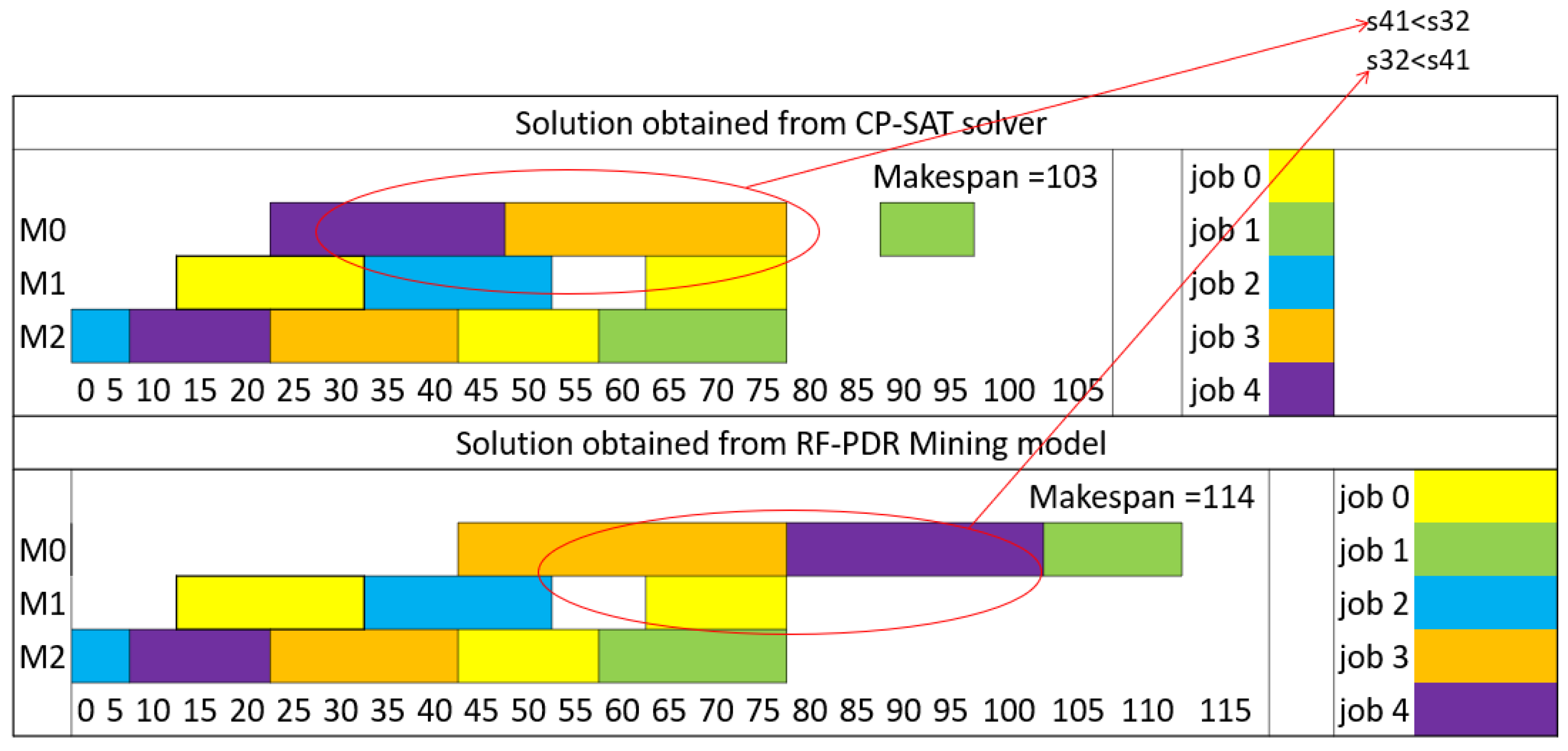
Moving on to the second and third instances, labeled as FJSP5_C2 and FJSP5_C3, the model continued to exhibit high accuracy. It successfully predicted the sequencing schedule for most setups, aligning perfectly with the solutions obtained from the solver. However, in both of these cases, there was a minor discrepancy in one sequence, where the model’s prediction slightly diverged from the solver’s output (Figure 8 and Figure 9). Importantly, these deviations did not disrupt the natural sequence of setups within the jobs.

Overall, these results emphasize the robustness and generalization capabilities of the RF-Dispatching Rule Mining Model. It proves its adaptability to diverse scheduling scenarios and consistently provides reliable sequencing recommendations, showcasing its impressive performance across different instances.

The RF-based dispatching rule mining model demonstrates its effectiveness and generalization potential, making it a valuable tool for improving scheduling efficiency in real-world manufacturing environments. Further refinement and ongoing testing with a broader range of instances will continue to enhance its performance and applicability.

4.3. Comparison with Classical Dispatching Rule

To assess the effectiveness of the dispatching rules derived from the RF-PDR (Random Forest-Dispatching Rule) mining model, we conducted a comparison with two well-established classical dispatching rules: Earliest Due Date (EDD) and Shortest Processing Time (SPT). The objective of this comparison was to evaluate the performance of the RF-PDR mining model in generating sequencing recommendations for setups within a flexible job shop scheduling environment. In our experiment, we randomly divided the problem instances into training and testing sets, with 60% of the instances used for training and the remaining instances reserved for testing. This partitioning ensured an unbiased evaluation of the dispatching rules on unseen data.

Table 7 provides a detailed overview of the makespan ($C_{max}$) for three testing instances, each characterized by the number of jobs ($j$), the number of machines ($k$), and the number of setups within each job ($i$). The table presents the makespan results for the RF-PDR mining model, SPT, and EDD dispatching rules. Results are discussed as follows:

• RF-PDR vs. SPT: In the comparison between the RF-PDR mining model and the SPT dispatching rule, it is evident that the RF-PDR model consistently outperforms SPT in terms of makespan. RF-PDR achieves a lower makespan for each testing instance, indicating more efficient scheduling. The percentage deviation between RF-PDR and SPT is also presented, highlighting the significant improvement achieved by the RF-PDR model.
• Instance FJSP5_C1: RF-PDR achieves a makespan of 108, while SPT results in a considerably higher makespan of 169, representing a 36% improvement.
• Instance FJSP5_C2: RF-PDR again demonstrates superior performance with a makespan of 114, compared to SPT’s 166, resulting in a 31% improvement.
• Instance FJSP5_C3: In this instance, RF-PDR achieves a makespan of 108, whereas SPT yields a makespan of 141, indicating a 23% improvement.
• RF-PDR vs. EDD: Similarly, when comparing the RF-PDR mining model with the EDD dispatching rule, RF-PDR consistently delivers better makespan results. The percentage deviation highlights the superior performance of the RF-PDR model.
• Instance FJSP5_C1: RF-PDR achieves a makespan of 108, while EDD results in a makespan of 166, marking a 35% improvement.
• Instance FJSP5_C2: RF-PDR’s makespan of 114 outperforms EDD’s makespan of 198 by 42%.
• Instance FJSP5_C3: In this instance, RF-PDR’s makespan of 108 is substantially better than EDD’s makespan of 169, indicating a 36% improvement.

The RF-PDR mining model exhibits clear superiority in terms of makespan when compared to the classical dispatching rules, SPT, and EDD. This demonstrates the potential of data-driven dispatching rules in enhancing scheduling efficiency and optimizing manufacturing operations. Further research can explore the model’s performance on a wider range of problem instances and its applicability to real-world manufacturing environments. The superior performance of the dispatching rule obtained from the RF-PDR mining model can be attributed to its adaptability and ability to discover implicit knowledge from production data. Unlike classical dispatching rules, often designed for specific manufacturing systems with fixed sequencing criteria, the RF-PDR model leverages attributes derived from real production data. As a result, the RF-PDR model can dynamically adjust its sequencing recommendations based on the unique characteristics of each problem instance, leading to more efficient scheduling. It harnesses the power of machine learning to uncover hidden patterns and correlations within the data, ultimately outperforming traditional dispatching rules.

Table 7. Comparison of the mined dispatching rule with the SPT and EDD dispatching rules.

Instance	$\mathit{j}$$\times \mathit{k}$	$\mathit{i}$	${\mathit{C}}_{\mathit{m}\mathit{a}\mathit{x}}$
			RF-PDR	SPT	% dev	EDD	% dev
FJSP5_C1	5 × 3	2–3	108	169	36%	166	35%
FJSP5_C2	5 × 3	2–3	114	166	31%	198	42%
FJSP5_C3	5 × 3	2–3	108	141	23%	169	36%

Table 7. Comparison of the mined dispatching rule with the SPT and EDD dispatching rules.

Instance	$\mathit{j}$$\times \mathit{k}$	$\mathit{i}$	${\mathit{C}}_{\mathit{m}\mathit{a}\mathit{x}}$
			RF-PDR	SPT	% dev	EDD	% dev
FJSP5_C1	5 × 3	2–3	108	169	36%	166	35%
FJSP5_C2	5 × 3	2–3	114	166	31%	198	42%
FJSP5_C3	5 × 3	2–3	108	141	23%	169	36%

4.4. Rescheduling with RF-PDR Mining Model

In the experimental setup designed to evaluate the efficacy of the rescheduling framework, we consider the predicted solution for FJSP_C3 as the initial nominal solution.

Table 8. Initial nominal solution for Case Study 3 in a flat data format.

Setup_ID	Eligible Machine			Solution
	${\mathit{m}}_0$	${\mathit{m}}_1$	${\mathit{m}}_2$	Assigned Mid	Start	End
s00	10	13		0	0	10
s01	20	12	23	0	75	95
s10	25		11	2	0	11
s11	27	18	20	0	48	75
s12	44	26	15	2	75	90
s20	47	30	27	1	0	30
s21	27	18		1	30	48
s22		25	29	1	48	73
s30	35	22	18	2	11	40
s31	19	27	0	2	40	58
s40	38		23	0	10	48
s41	38	28	29	1	73	101

represents the solution in a flat data format.

4.4.1. Machine Breakdown Simulation

The simulation model focuses on predicting breakdown times for three machines. The parameter for each machine is considered as follows:

Input parameters:

• Mean time between two successive breakdowns:

λ_m1 = 30 h,

λ_m2 = 80 h,

λ_m3 = 120 h.

• Threshold, $T{H}_{bk}$ = 0.7 [64].

Output:

• Breakdown time (refer to Figure 10):

$t_{bd}^{mo}$ = 45 h,

$t_{bd}^{m1}$ >120 h,

$t_{bd}^{m2}$> 120 h.

Figure 10. Breakdown probabilities.

Figure 10. Breakdown probabilities.

4.4.2. Identification of Disrupted Setups

A compiled list of disrupted setups in conjunction with the presently available machines is generated using the formula: $e_{ijk}$ > $t_{bd}^k$. This compilation is presented in

Table 9. Setup status after machine breakdown.

Setup_ID	Current Eligible Machine		Solution			Status
	m1	m2	Assigned m_ID	Start	End
s01	12	23	-	-	-	Interrupted
s11	18	20	-	-	-	Interrupted
s40		23	-	-	-	Interrupted
s21	18		1	30	48	Unfinished
s22	25	29	1	48	73	Unfinished
s41	28	29	1	73	101	Unfinished
s12	26	15	2	75	90	Unfinished
s31	27	18	2	40	58	Unfinished

, wherein a “status” column has been included to categorize the setups into two distinct classifications: “Interrupted” and “Unfinished.”

In Table 9, “Interrupted” setups due to disruption on the shop floor necessitate reassignment and resequencing on currently eligible machines. In contrast, “Unfinished” setups indicate those that have already been assigned and sequenced on the available machines, but have not been finished yet.

4.4.3. Online Re-Scheduling of the Interrupted Setups

In accordance with the localization heuristics approach, the interrupted jobs have been subjected to reassignment. In

Table 10. Updated routing of interrupted setups.

Setup_ID	${\mathit{m}}_1$	${\mathit{m}}_2$
s01	12	23
s11	18	20
s40		23

, the boldfaced cells denote the updated routing assignments.

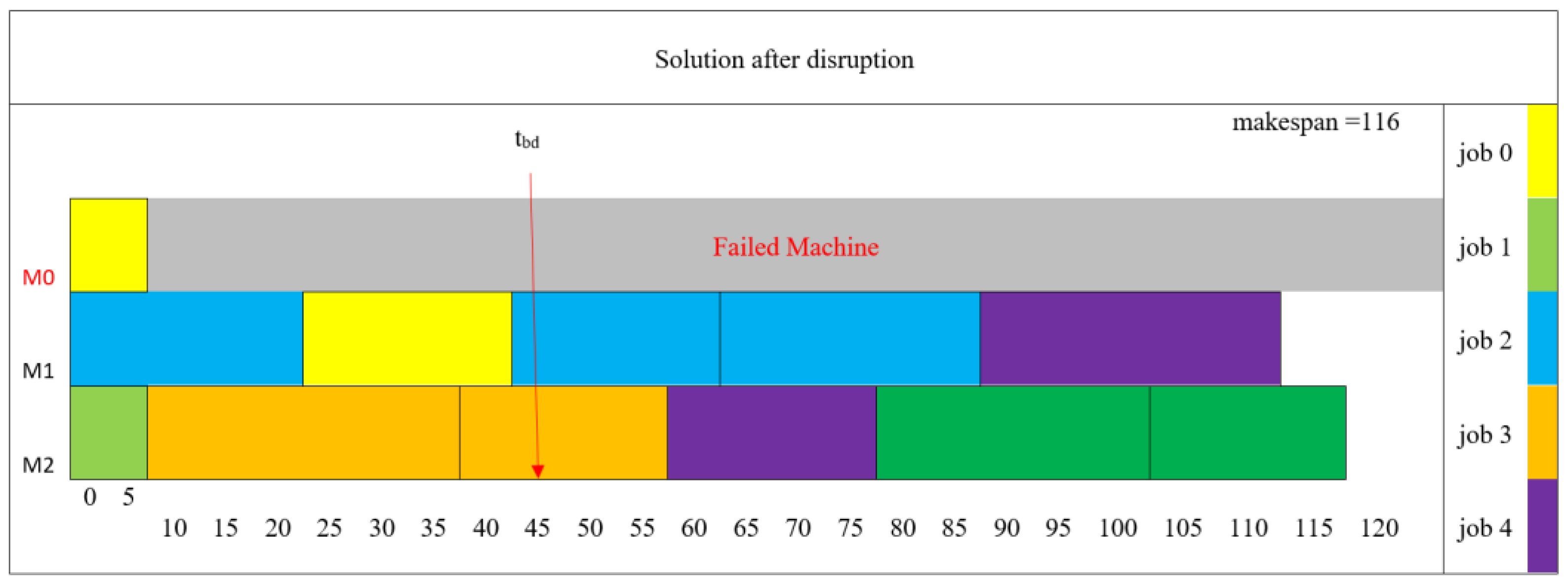
Subsequently, a revised sequence for the interrupted setups on eligible machines has been derived utilizing the RF-PDR mining model. This online re-scheduled solution is visually depicted in Figure 11. The shadow block on the failed machine stands for the idle time interval (the time length is equal to the repair time). As a result of this rescheduling effort, the makespan has been reduced to 116 h. When the now-broken machine becomes operational, unfinished setups can then be scheduled, considering updated machine availability, following the same approach.

4.4.4. Online Re-Scheduling Robustness and Stability Measure

To assess the efficacy of the proposed re-scheduling approach, a comparative evaluation was conducted, juxtaposing the sequenced results obtained through this approach with those derived from two widely adopted classical dispatching rules: SPT (Shortest Processing Time) and EDD (Earliest Due Date).

Table 11. Comparative analysis with classical dispatching rules.

	${\mathit{C}}_{\mathit{m}\mathit{a}\mathit{x}}$	RM%	SM
RF-PDR	116	12.93	25.8
SPT	144	33.33	21.4
EDD	152	40.7	52.6

presents a comprehensive overview of the performance metrics related to robustness and stability.

The comparison illustrates that the RF-PDR approach yields the lowest $C_{max}$ value of 116 h, indicating the shortest completion time among the considered approaches. Additionally, it exhibits the lowest RM%, signifying robustness in minimizing deviations from the optimal solution. Furthermore, the RF-PDR approach boasts a substantial SM value of 25.8, indicating its capability to maintain stability in scheduling operations.

In contrast, the classical dispatching rules, SPT and EDD, exhibit higher $C_{max}$ values, greater RM% deviations, and SM values, suggesting comparatively inferior performance. These findings underscore the superior performance of the RF-PDR model in achieving efficient and stable re-scheduling outcomes.

5. Conclusions and Future Research Directions

This study proposes a hybrid framework that combines machine learning and optimization to integrate CAPP and scheduling in Smart Manufacturing environments. The model defines setups as the primary dispatching unit and employs supervised learning to extract sequencing rules from optimized solutions. Experimental evaluations demonstrate that the Random Forest–based dispatching rule mining approach achieves a 42.6% reduction in makespan compared to classical rules, such as SPT and EDD, across all test scenarios. The approach improves schedule robustness by approximately 35% and reduces the standard deviation of makespan by 27%, indicating more stable and reliable performance under dynamic disruptions. In addition, the model achieved an average prediction accuracy of 92% on unseen problem instances, highlighting strong generalization capability. The proposed method also demonstrates practical computational efficiency, as rescheduling decisions are generated efficiently, supporting real-time applications in dynamic job shop environments. Comparative experiments further confirmed that the hybrid approach consistently outperformed baseline heuristics and maintained performance advantages across different instance configurations. These results confirm that combining routing optimization and dynamic sequencing significantly enhances responsiveness, adaptability, and schedule stability in flexible job shop scheduling problems.

In conclusion, this research aims to enhance the efficiency, responsiveness, and overall integrity of manufacturing processes by integrating process planning and scheduling within the context of Smart Manufacturing. However, several avenues for future work can further enhance the proposed approach’s understanding, application, and impact. In our proposed approach, it is important to note that the generation of an optimal routing has not been explicitly addressed within the scope of this research. Instead, we have adopted a heuristic approach for assigning setups, where the attainment of optimality in the initial nominal solution is not guaranteed. Consequently, this heuristic assignment process can impact the quality of the sequencing solution. One important direction for future work is to extend the framework to a multi-objective formulation, incorporating trade-offs beyond makespan, such as processing time, cost, or machine utilization, thereby allowing the system to dynamically balance priorities in real-world production scenarios. This could be explored using multi-objective optimization techniques. Another promising avenue for future research lies in addressing the routing sub-problem through the utilization of unsupervised learning techniques. This could potentially enhance the efficiency and effectiveness of the overall approach by autonomously discovering optimal routing strategies.