Abstract
This paper develops a bilevel game-theoretic model to analyze the strategic effects of tariffs and subsidies in a global supply chain involving a manufacturer and a third-party logistics (3PL) provider. The government, acting as a Stackelberg leader, sets fiscal instruments to maximize national welfare, while downstream supply chain participants respond by optimizing production, pricing, and logistics outsourcing decisions. The model is evaluated under three coordination structures—centralized, decentralized, and alliance-based—to examine how decision alignment influences policy effectiveness. Simulation results show that while tariffs negatively impact supply chain efficiency and profitability, well-designed subsidies can partially or fully offset these effects, particularly under centralized coordination. The model further reveals that policy outcomes are highly sensitive to the strategic power structure within the supply chain. This study advances the literature by integrating endogenous government behavior with logistics coordination and supply chain decision-making within a unified bilevel optimization framework. The findings offer actionable insights for both policymakers and global supply chain managers in designing robust fiscal and coordination strategies.
MSC:
91A23; 90B06
1. Introduction
In an increasingly globalized economy, transnational supply chains face mounting challenges due to government-imposed trade policies such as tariffs and subsidies. These fiscal instruments are designed to promote domestic industry or correct trade imbalances, but often disrupt supply chain operations by influencing costs, sourcing strategies, and logistics flows. For example, the U.S.–China trade war raised tariffs on over $350 billion worth of goods, prompting multinational firms to reroute sourcing and restructure supplier networks. Similarly, India’s 2020 Production Linked Incentive (PLI) scheme offered targeted subsidies to promote domestic manufacturing, shifting logistics, and investment patterns throughout South and Southeast Asia. More than 60% of global manufacturers have cited government intervention as a primary driver of changes in their logistics models. These real-world developments underscore the urgent need for quantitative models that evaluate the complex interaction between fiscal policy and supply chain behavior.
Logistics service providers play a central role in navigating these policy-driven shifts. Among them, third-party logistics providers (3PLs) are widely adopted due to their ability to offer flexible outsourced transportation, warehousing, and distribution solutions. Unlike fourth-party logistics providers (4PLs) that coordinate across multiple 3PLs or seventh-party logistics providers (7PLs) that fully integrate strategic and executional services, 3PLs directly influence day-to-day operational decisions such as routing, freight rates, and logistics effort levels. These actions significantly affect the supply chain’s responsiveness to external fiscal shocks, making 3PLs a practical and analytically tractable focus for studying policy impacts.
However, the inclusion of 3PLs introduces additional complexity. Power dynamics between manufacturers and logistics providers, as well as coordination challenges, must be addressed—particularly under government-imposed cost shocks. Although prior research has separately explored the roles of tariffs, subsidies, and supply chain coordination, few studies examine their combined and strategic effects in a unified modeling framework. In most existing models, fiscal policies are treated as fixed parameters and the government is excluded as a decision-maker. Moreover, the role of 3PLs is often oversimplified, despite their growing importance in managing logistics uncertainty and cross-border trade.
This study addresses these limitations by developing a bilevel programming model embedded in a Stackelberg game-theoretic framework. In this model, the government acts as the upper-level leader, setting tariffs and subsidies to optimize a national welfare function, while the manufacturer and 3PL providers act as followers, responding by optimizing their pricing, production, and logistics decisions. The model is evaluated under three coordination regimes—centralized, decentralized, and alliance-based—allowing for a systematic comparison of strategic outcomes across different power structures.
The main objectives of this research are to investigate how fiscal interventions influence supply chain decisions and to determine under which coordination regime these policies are most effective. Specifically, we analyze how tariffs and subsidies affect logistics effort, production quantity, retail pricing, and profit distribution within a supply chain that involves a 3PL. We also assess whether strategic coordination between firms can mitigate the adverse effects of tariffs or amplify the benefits of subsidies.
This paper contributes to the literature in three major ways. First, it introduces a unified, multi-tier optimization framework that captures the interactive effects of tariffs and subsidies on the outsourcing behavior of logistics. Second, it models the government as a strategic actor rather than a passive parameter-setter, offering new insight into fiscal policy effectiveness. Third, the study quantifies differences in policy outcomes across centralized, decentralized, and alliance-based supply chain structures, providing practical implications for policymakers and firms navigating uncertain trade environments.
The remainder of the paper is organized as follows. Section 2 reviews related literature on tariffs, subsidies, and logistics coordination. Section 3 presents the model assumptions and theoretical framework. Section 4 develops the mathematical formulation and describes the solution methodology. Section 5 provides numerical simulations and sensitivity analysis. Section 6 discusses key insights and policy implications. Section 7 concludes with a summary of findings and directions for future research [1,2,3,4,5,6,7,8,9,10].
The primary objective of this study is to develop a bilevel optimization model that captures the strategic interaction between a government, acting as a fiscal policy-setter, and key supply chain participants, namely manufacturers and third-party logistics (3PL) providers. Specifically, the model aims to analyze how tariffs and subsidies influence pricing, logistics effort, and production decisions across different coordination regimes—centralized, decentralized, and alliance-based. It further seeks to derive and compare equilibrium outcomes under these structures using a Stackelberg game-theoretic framework and to conduct numerical simulations and sensitivity analyses to evaluate the effectiveness of fiscal interventions in improving supply chain efficiency and resilience [9,10,11,12,13,14,15,16].
2. Literature Review
This study builds upon and intersects three main streams of literature: (i) the impact of tariffs and subsidies on international supply chain design, (ii) the strategic function of third-party logistics (3PL) providers in global networks, and (iii) the application of game-theoretic and bilevel optimization methods to supply chain coordination and fiscal policy design. This section synthesizes these areas and positions the contribution of the present research within the broader academic discourse.
Fiscal Policy and Supply Chain Efficiency: Numerous studies have evaluated how tariffs and subsidies influence global trade and supply chain performance. Tariffs increase import costs, affecting sourcing strategies and production footprints. Some researchers highlight how tariff-induced trade frictions impact firm competitiveness and reconfigure logistics routes, while others demonstrate that tariff uncertainty drives supply chain restructuring [1,2,3,4]. Subsidies, on the other hand, are used to support domestic production, especially in sectors such as agriculture, electronics, and logistics. Some studies show that agricultural subsidies enhance export volumes while distorting global markets. Others note that subsidies in emerging economies significantly shift resource allocation and international trade balances. While extensive work exists on the individual effects of these policies, the combined influence of tariffs and subsidies within strategic supply chain settings remains underexplored [17,18,19,20].
The Strategic Role of Third-Party Logistics Providers: 3PL providers are essential in supporting globalization by managing transportation, warehousing, and distribution for multinational firms. Early contributions emphasized their role in enhancing flexibility and cost-efficiency. More recent works have modeled 3PLs within coordination frameworks, linking their performance to broader supply chain outcomes [21,22,23]. Despite their growing importance, 3PLs are often treated as passive service providers in analytical models. Their strategic behavior—especially in pricing, service levels, and coordination—remains under-theorized. Much of the literature does not account for how 3PLs interact with fiscal policy interventions like tariffs and subsidies or how their decisions influence supply chain resilience [13,14].
Game-Theoretic Models and Bilevel Optimization: Game-theoretic models, especially Stackelberg games, provide a powerful framework for modeling hierarchical supply chains. These games have been applied to model manufacturers’ retailer relationships and green logistics. Some studies have used bilevel optimization to examine policy interactions, logistics outsourcing, and carbon emissions [23,24,25,26,27]. However, relatively few studies treat the government as a strategic leader using endogenous policy instruments within a bilevel framework. Even fewer combine this with decentralized and alliance-based coordination regimes while explicitly modeling logistics effort and 3PL pricing. This limits the applicability of existing models in evaluating trade policy in multi-agent, logistics-driven environments [12,15,19,27,28].
Supply Chain Disruption and Resilience: In light of recent global uncertainties, increasing attention has been paid to supply chain disruption and resilience strategies. Several studies have explored how firms can enhance operational robustness through adaptive logistics, policy-responsive planning, and resilient supply chain designs. References [5,6] and [21,22] examine the role of third-party logistics providers in mitigating risks associated with geopolitical shocks, while [23,24] analyze the effects of tariffs and subsidies on network vulnerability. Our research contributes to this evolving literature by modeling a transnational supply chain with a 3PL under tariff and subsidy interventions, and assessing equilibrium behaviors that enhance resilience under policy-driven disruptions.
Research Gap and Contribution: To the best of our knowledge, no existing study jointly models (i) government-set tariffs and subsidies as endogenous decisions, (ii) strategic logistics behavior by 3PLs, and (iii) alternative coordination structures (centralized, decentralized, and alliance) in a unified bilevel game-theoretic framework. While prior studies address these components separately, the interactive effects across actors and policy levers remain largely unexamined [9,10,11,12,13,14,15,16]. This paper fills that gap by introducing a bilevel Stackelberg model that captures government intervention, multi-agent optimization, and logistics decision-making within a single framework. It also contributes to the resilience literature by modeling fiscal policy as a lever for improving supply chain coordination in the face of disruption [9,10,11,12,13,14,15,16].
In summary, this study bridges multiple streams of research by integrating strategic trade policy, 3PL behavior, and coordination regimes into a quantitative modeling structure. This holistic view provides both theoretical advancement and policy-relevant insights for managing global supply chains under fiscal stress [9,10,11,12,13,14,15,16].
2.1. Research Questions
- 1.
- How do government subsidies influence the strategic decisions of manufacturers, suppliers, and third-party logistics providers (3PLs) in a transnational supply chain?How do government-imposed tariffs and subsidies jointly influence pricing, logistics effort, and production decisions in multi-tier supply chains involving 3PLs?
- 2.
- What are the effects of subsidies on pricing, production, and logistics outsourcing decisions in supply chains involving 3PLs?How does the treatment of the government as a strategic leader (rather than a passive policy-setter) affect the equilibrium behavior of manufacturers and 3PL providers?
- 3.
- How does the allocation of subsidies impact the coordination and performance of supply chain members under centralized and decentralized decision-making models?Under what coordination structure—centralized, decentralized, or alliance-based—do fiscal policies generate the most efficient and equitable supply chain outcomes?
- 4.
- To what extent can subsidies improve supply chain efficiency, cost reduction, and service levels when a 3PL is involved?Can targeted subsidies effectively mitigate the adverse effects of tariffs, and how does this depend on the power distribution across supply chain participants?
2.2. Research Hypotheses
H1.
Government subsidies have a significant positive effect on the strategic decisions of manufacturers and suppliers in a transnational supply chain involving 3PLs. Government subsidies positively influence the strategic decisions of manufacturers and 3PL providers, improving production and logistics efficiency.
H2.
The presence of subsidies leads to lower production and logistics costs in supply chains that utilize third-party logistics providers. Subsidies enhance collaboration between manufacturers and 3PLs, leading to improved coordination and cost-sharing outcomes.
H3.
Supply chains operating under centralized decision-making structures benefit more from subsidies than those under decentralized structures.
H4.
Subsidies encourage greater adoption and integration of third-party logistics services in global supply chains.
H5.
Subsidy allocation improves coordination and collaboration between manufacturers, suppliers, and 3PLs, leading to enhanced overall supply chain performance.
H6.
Well-targeted subsidy schemes contribute to improved supply chain sustainability and resilience through better logistics integration.
H7.
The strategic behavior of supply chain participants, such as pricing and outsourcing decisions, is significantly influenced by the availability and magnitude of government subsidies.
3. Problem Description
Government intervention through trade policies—particularly subsidies and tariffs—has become increasingly influential in shaping the strategic behavior of global supply chains. These fiscal instruments alter cost structures, pricing strategies, and logistics configurations, especially for firms operating across borders. While prior research has independently examined tariffs, subsidies, and logistics outsourcing, there is limited integrated analysis of how these tools jointly influence multi-agent supply chains involving third-party logistics (3PL) providers [29].
This study fills that gap by modeling a three-tier supply chain comprising a government authority, a manufacturer, and a 3PL provider. The government acts as a Stackelberg leader, setting tariff () and subsidy (s) rates to maximize national welfare. The welfare function considers producer surplus, tariff revenue, and the fiscal cost of subsidies, weighted by policy priorities:
Here, and denote the profits of the manufacturer and 3PL, respectively, represents tariff revenue, denotes subsidy expenditure, and are policy weight parameters [11,20].
The manufacturer responds to fiscal policies and 3PL pricing by optimizing its production quantity and retail price to maximize profit, subject to production costs, logistics service fees, and trade policy impacts. The 3PL determines logistics price r and effort level e, which may reflect investments in technology, service quality, or infrastructure. Depending on the coordination structure, the 3PL may act independently, as a leader, or as a strategic partner.
Real-world examples illustrate this framework’s relevance. Electronics manufacturers adjust contracts with logistics providers in response to tariff reforms. Apparel and automotive firms, operating complex global supply networks, likewise rely on 3PLs to navigate fiscal uncertainty [28].
This study focuses on the upstream segment of the supply chain-sourcing, production, and logistics—excluding downstream retail or consumer revenue. To evaluate the effects of policy and coordination, we examine three structural regimes.
This study models strategic interactions in an upstream supply chain involving a manufacturer and a third-party logistics (3PL) provider, influenced by government-imposed tariffs () and subsidies (s). To evaluate the effects of fiscal policies and coordination mechanisms, we consider three structural regimes. In the centralized regime, the manufacturer and 3PL coordinate to jointly optimize pricing (p), quantity (q), logistics fees (r), and effort level (e) to maximize overall system profit under fixed government policy [24]. In contrast, the decentralized regime follows a hierarchical Stackelberg game: the government first sets and s; the 3PL then selects r and e to maximize its own profit; finally, the manufacturer responds by choosing p and q [25]. The alliance-based structure serves as an intermediate scenario, where the manufacturer and 3PL form a strategic alliance and jointly determine while adapting to government-imposed fiscal instruments [17,18]. This bilevel framework allows for comparative analysis of policy effectiveness and coordination efficiency across different structural settings.
The key variables and symbols used throughout this study are defined as follows. Let p denote the unit selling price of the product set by the manufacturer, and q be the quantity produced and shipped. The term represents the demand function, assumed to be price-sensitive. The manufacturer’s unit production cost is denoted by , while refers to the unit logistics cost charged by the third-party logistics provider (3PL). The manufacturer and 3PL make strategic decisions on p, q, and service level , respectively.
Let t represent the per-unit tariff imposed by the government, and s be the per-unit subsidy offered. The profit of the manufacturer is represented as , that of the 3PL as , and government’s utility as , which is typically based on net social welfare. The logistics service level is denoted by , and the corresponding cost function is . The production cost function for the manufacturer is , which can be non-linear. Tariff revenue is calculated as , and subsidy cost as .
The bilevel game-theoretic model assumes the government as the Stackelberg leader who sets t and s, anticipating the response of the manufacturer and 3PL, who are Stackelberg followers optimizing their profits. The system is analyzed under three coordination mechanisms: decentralized, centralized, and alliance-based structures. Each structure alters the optimization constraints and objective alignment among the three agents [10,15,24,25,27].
4. Methodology
4.1. Bilevel Stackelberg Game Model for Tariff and Subsidy Design
This study adopts a quantitative modeling framework grounded in game theory and bilevel optimization to evaluate the impact of subsidies and tariffs on supply chain coordination involving a manufacturer and a third-party logistics (3PL) provider under governmental regulation. The central objective is to simulate and analyze the strategic behavior of each agent under different coordination mechanisms—centralized, decentralized, and alliance-based—while capturing the implications of governmental intervention through subsidies.
The methodological structure is centered around a bilevel Stackelberg game in which the government acts as the leader, anticipating and influencing the responses of downstream agents—the manufacturer and 3PL—through financial incentives. This triadic interaction is modeled in a hierarchical sequence, reflecting the real-world asymmetry in decision power. At the upper level, the government decides on a per-unit subsidy rate s to stimulate cost-efficient logistics and sustainable production practices. At the lower level, the manufacturer and the 3PL interact strategically: the manufacturer chooses the retail price p, while the 3PL sets a logistics service fee . The market demand follows a linear inverse function given by , where a and b represent the demand intercept and price sensitivity, respectively [26,29].
The profit function of the manufacturer is defined as
where is the unit production cost, is the per-unit tariff, and s is the subsidy provided by the government. The 3PL’s profit is represented by
with denoting the 3PL’s internal cost per unit of logistics effort.
We assume the manufacturer responds to the logistics fee set by the 3PL by optimizing the selling price p. Taking the first-order condition with respect to p, the optimal response function is derived as
Substituting this optimal price into the 3PL’s profit function, the leader at the lower level (the 3PL) solves
yielding an expression that is solved numerically to determine the equilibrium fee . These nested optimal responses form the basis for the government’s upper-level decision problem.
At the top level, the government maximizes a social welfare function that balances industrial profits and policy costs, such as
where is the marginal cost of public funds and is the equilibrium market demand. The resulting bilevel problem is transformed into a single-level optimization model using the Karush–Kuhn–Tucker (KKT) conditions of the lower-level actors, incorporating complementarity constraints to ensure equilibrium behavior.
For solution implementation, the entire model is encoded in GAMS (version 38.1.0) and Pyomo (https://www.pyomo.org/). A numerical simulation is conducted using empirically plausible parameter values such as , , , , , and . The solution outputs include optimal subsidy rates, prices, logistics fees, and the resulting profits for each stakeholder. Additionally, comparative statics are performed to examine how variations in subsidy s, tariff , and price sensitivity b influence equilibrium outcomes.
As shown in Figure 1, the equilibrium profit surface highlights how the profit changes with varying subsidies and tariffs. The non-linear surface reflects complex strategic interactions among the players, illustrating the policy implications; a sensitivity analysis examines the effects of rising logistics costs or higher price elasticity on the government’s optimal subsidy level and the manufacturer’s pricing behavior. Figure 1 provides a 3D visualization of profit surfaces for different combinations of s and , showing the trade-offs faced by each agent [13,24,25,26,27].
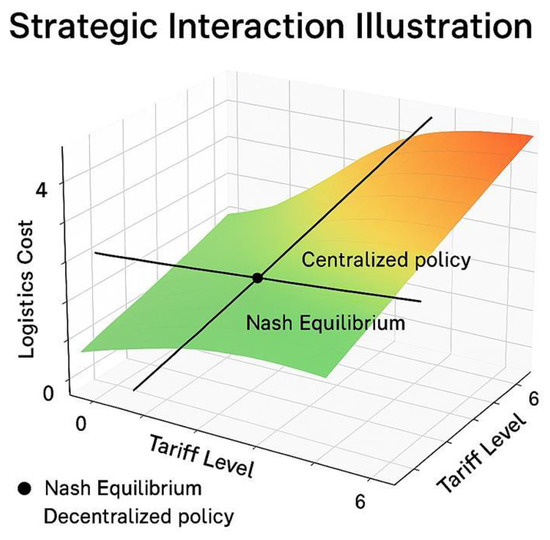
Figure 1.
Game-theoretic model of manufacture, 3PL, and government [1].
Furthermore, a policy experiment is conducted using real-world data from international logistics and trade datasets. For example, the cost and price data from Chinese export manufacturers and global 3PL firms like DHL and SF Express are used to validate the model. Empirical calibration ensures that the subsidy rates derived from the model align with realistic government interventions in Asia–Pacific trade policies.
In conclusion, this methodological design provides a theoretically grounded and practically implementable approach to analyzing government intervention in global supply chains. It captures the multi-level strategic behavior of actors, enables rigorous policy testing, and offers insights for decision-makers on how to design subsidy schemes that promote efficiency, cooperation, and sustainable logistics adoption [13,24,25,26,27]. To enhance clarity, the research methodology is depicted in the form of a flowchart, as shown in Figure 2.
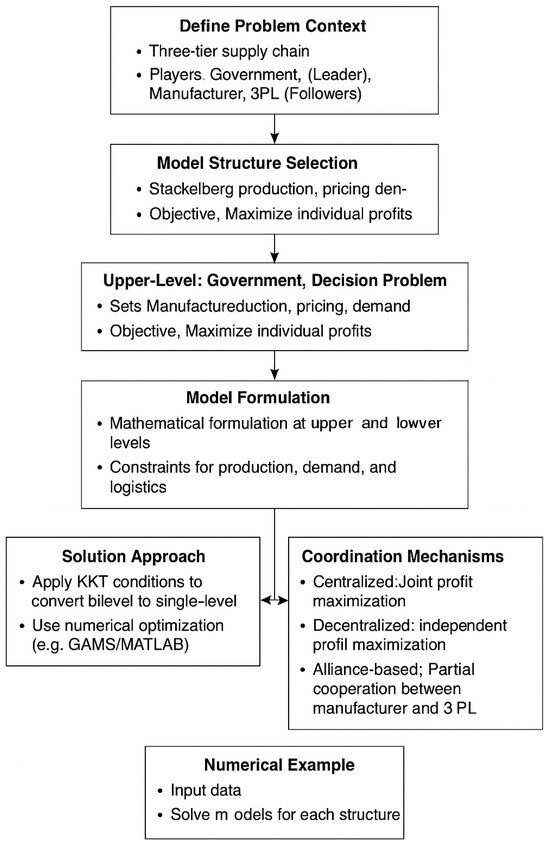
Figure 2.
Methodological flowchart of the bilevel game-theoretic model.
4.2. Extended Bilevel Optimization with Logistics Effort and Unified Coordination
This study employs a bilevel game-theoretic framework to model a three-tier supply chain involving a government (leader), a manufacturer, and a third-party logistics (3PL) provider (followers). The model is formulated as a Stackelberg game in which the government, acting as the leader, sets strategic trade policies such as tariffs and subsidies. The manufacturer and 3PL, as followers, respond by optimizing their production and logistics decisions, respectively. The interaction is modeled as a bilevel optimization problem, integrating economic and logistical objectives [10,11,24].
This study is built on several key assumptions. First, the government functions as a Stackelberg leader, strategically setting tariffs and subsidies to optimize overall national welfare. The manufacturer and the third-party logistics (3PL) provider are assumed to be rational and profit-maximizing agents. The 3PL can influence logistics efficiency by adjusting both its pricing and the level of effort it exerts. The market demand is treated as deterministic, depending on both the retail price and the quality of logistics services provided. Finally, the coordination structure—whether centralized, decentralized, or alliance-based—plays a crucial role in shaping the strategic interactions and sequencing of decisions among the participating entities.
The upper level represents the government’s objective to maximize social welfare, which includes tariff revenue, subsidy expenditures, and other policy objectives. : tariff rate imposed on imports, : subsidy rate provided to 3PL, : social welfare function, and and : optimal responses from the manufacturer and 3PL.
The government’s problem is formulated as
Lower Level: Manufacturer and 3PL Decision Problems
At the lower level, the manufacturer and 3PL act non-cooperatively to maximize their respective profits, given the policies set by the government. The manufacturer’s problem is to decide the production quantity q to maximize its profit:
The inverse demand function is denoted by , representing the market price as a function of quantity q. The manufacturer’s production cost is represented by , which depends on the production level, and the logistics cost incurred by the third-party logistics (3PL) provider is expressed as , where denotes the logistics effort required to deliver quantity q.
3PL’s problem is to determine the logistics service level l to maximize its profit:
The third-party logistics (3PL) provider receives a payment from the manufacturer, denoted by , which is a function of the logistics effort l. The 3PL also incurs a logistics provision cost represented by , which increases with the level of effort required to manage transportation and distribution.
Building upon the individual decision problems of the manufacturer and the third-party logistics (3PL) provider, we now integrate their objectives and constraints into a unified bilevel programming framework. In this hierarchical structure, the government acts as the upper-level decision-maker (leader), strategically setting tariff and subsidy policies to influence the behavior of downstream agents. The lower-level problem comprises the manufacturer and the 3PL, who respond rationally to the government’s policy decisions by optimizing their respective profit functions. The interdependence of these players’ decisions—where the manufacturer’s choices are influenced by the 3PL’s logistics services and the external policy environment—necessitates a bilevel game-theoretic approach. The formulation presented in the next section captures this Stackelberg-type interaction, with the government influencing the equilibrium outcomes by anticipating the optimal responses of the supply chain participants.
The combined bilevel structure is as follows [2,9,13,17,19]:
To enhance the clarity of the proposed bilevel decision-making framework, we present a mathematical flowchart (Figure 3) that visually encapsulates the interactions among the key players—government, manufacturer, and 3PL. This flowchart serves as a schematic representation of the hierarchical optimization process, illustrating the sequence of decisions, input-output dependencies, and the feedback mechanisms between the upper and lower levels. By mapping the logical structure of the model, including objective functions, constraints, and the solution pathway, the flowchart facilitates a comprehensive understanding of the bilevel game-theoretic formulation and its computational resolution.
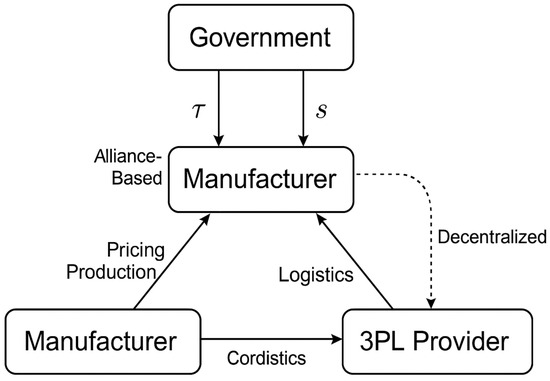
Figure 3.
Flowchart of the bilevel mathematical framework.
This flowchart illustrates the bilevel mathematical framework of the supply chain model. At the upper level, the government optimizes tariffs and subsidies to maximize national welfare. At the lower level, the manufacturer and 3PL respond by making production, pricing, and logistics decisions. The framework branches into three coordination regimes—centralized, decentralized, and alliance-based—showing how decisions vary under different strategic interactions.
Building upon the mathematical flowchart, the solution methodology outlines the stepwise procedure employed to solve the bilevel optimization problem under the Stackelberg game framework. Given the hierarchical structure involving the government as the leader and the manufacturer and 3PL as followers, the model is reformulated using the Karush–Kuhn–Tucker (KKT) optimality conditions for the lower-level problems. This transformation allows the bilevel model to be expressed as a single-level mathematical program with complementarity constraints (MPCC), which can be solved using advanced optimization tools. The proposed solution procedure includes model linearization, constraint reformulation, and implementation using platforms such as GAMS and Pyomo to obtain equilibrium strategies and policy implications.
To solve the bilevel optimization problem, the Karush–Kuhn–Tucker (KKT) conditions for the lower-level problems are derived and substituted into the upper-level model. This reformulation converts the bilevel problem into a single-level mathematical program with complementarity constraints (MPCC). The resulting model is non-linear and is solved using the GAMS and MATLAB software (version R2023b) commercial solvers.
Let and be the Lagrangian functions for the manufacturer and 3PL. The KKT conditions include first-order derivatives and complementary slackness constraints. The optimization is carried out under three structural configurations:
- 1.
- Centralized structure: Joint maximization of total profit across the supply chain.
- 2.
- Decentralized structure: Each player maximizes their own profit.
- 3.
- Alliance-based structure: Partial coordination between manufacturer and 3PL.
To validate the applicability of the proposed model and demonstrate its practical relevance, a numerical example and simulation are conducted based on hypothetical but realistic parameter values. This section aims to illustrate the behavior of the supply chain under different policy scenarios, including variations in tariff rates and subsidy levels. By solving the model using the outlined methodology, the resulting equilibrium outcomes for the manufacturer, 3PL provider, and government are analyzed. The simulation provides insights into the strategic interactions among the players and quantifies the impact of policy instruments on supply chain performance and social welfare.
This section provides a numerical illustration of the bilevel Stackelberg game-theoretic model, simulating strategic decisions by the government, manufacturer, and third-party logistics (3PL) provider. We define linear and quadratic functional forms, assign parameter values, and solve the model under decentralized, centralized, and alliance-based coordination structures [15,24,25,26,27,28].
To ensure mathematical tractability and economic relevance, a set of well-grounded assumptions is introduced prior to model calibration. These assumptions define the structural behavior of key agents—namely, the government, manufacturer, and third-party logistics provider—and capture essential characteristics of the supply chain environment under tariff and subsidy interventions. Correspondingly, functional forms are specified for cost, demand, utility, and subsidy/tariff mechanisms. These functions are designed to reflect realistic economic behavior while allowing for analytical and computational solution of the bilevel game-theoretic model.
The following functions and parameters are used:
- Inverse demand: ;
- Manufacturer cost: ;
- 3PL cost: ;
- Manufacturer’s logistics cost: ;
- Manufacturer’s logistics need: ;
- 3PL revenue from manufacturer: ;
- Tariff rate: , subsidy rate: .
Decentralized Structure: In the decentralized structure, each stakeholder—government, manufacturer, and 3PL provider—optimizes its objective independently, based on its own constraints and incentives. This non-cooperative framework reflects a realistic yet often inefficient decision-making scenario in global supply chains, where coordination is limited. The resulting equilibrium is characterized using a bilevel optimization structure, where the government acts as a Stackelberg leader by setting policy instruments (e.g., tariffs or subsidies), anticipating the reactions of the manufacturer and 3PL provider. The decentralized model serves as a baseline to evaluate the efficiency loss due to a lack of coordination.
Manufacturer’s profit:
First-order condition:
3PL profit:
With :
Consumer surplus:
Tariff revenue:
Subsidy cost:
Social welfare: [15,24,25,26,27,28]
Centralized Structure: The centralized structure represents an idealized scenario in which the decisions of all supply chain members are optimized jointly to maximize the overall system welfare. Here, a central planner or an integrated firm internalizes the objectives and constraints of the government, manufacturer, and 3PL. This structure helps identify the optimal performance benchmark and quantify potential efficiency gains from full coordination. The centralized model is particularly useful for policy simulation and as a reference point for evaluating decentralized and alliance-based outcomes.
Total profit:
First-order condition:
Now [15,24,25,26,27,28],
Alliance-Based Structure: The alliance-based structure captures partial coordination between the manufacturer and the 3PL provider, forming a strategic coalition to improve joint profitability while still reacting to government interventions. This intermediate model combines elements of cooperation and competition, offering a more realistic portrayal of modern supply chains where horizontal or vertical partnerships are common. The alliance structure allows for analyzing how shared decision-making affects pricing, production, and policy responses, bridging the performance gap between the decentralized and fully centralized settings.
This model maximizes joint profit of the manufacturer and 3PL (excluding tariff revenue). The decision variables q and l remain the same as in the centralized case.
To evaluate the implications of different coordination strategies within the supply chain, a numerical simulation was conducted under three distinct structures: decentralized, centralized, and alliance-based. The results are summarized in Table 1, which compares key performance metrics including production quantity, 3PL logistics effort, profits for the manufacturer ( and 3PL (), tariff revenue (TR), total supply chain profit (SC), and overall social welfare (SW). These indicators offer insights into how each structural configuration affects the behavior and outcomes of supply chain actors.

Table 1.
Simulation results under different coordination structures.
As illustrated in the table, the decentralized structure leads to the highest production and social welfare, largely driven by substantial government tariff revenues, but it suffers from internal inefficiencies, including significant losses for the 3PL provider and a relatively low supply chain profit. Conversely, centralized coordination enhances total supply chain efficiency, although it reduces overall social welfare due to lower production levels and reduced government revenue. The alliance structure represents a middle ground, achieving improved coordination and balanced individual profits, while closely matching centralized supply chain efficiency. However, it underperforms in terms of social welfare when tariff revenues are excluded from the evaluation [15,24,25,26,27,28].
5. Results
5.1. Equilibrium Outcomes Under Policy-Driven Coordination
This section presents the results of the numerical simulation and sensitivity analysis based on the proposed bilevel game-theoretic model. The simulation is performed using empirically plausible parameter values to demonstrate how subsidies and tariffs influence the strategic decisions of supply chain actors and the overall system performance.
The baseline values used in the simulation are as follows: market potential , price sensitivity , manufacturer’s production cost , 3PL’s logistics cost , tariff , and marginal cost of public funds . These parameters reflect realistic cost and demand structures observed in global manufacturing and logistics settings [2,13,15,17,24,26,28].
Solving the Stackelberg game yields the following equilibrium values: optimal retail price , optimal logistics fee , and the government’s optimal subsidy level . These results indicate a balance between competitive pricing, efficient logistics outsourcing, and moderate policy intervention.In the baseline equilibrium, the manufacturer’s profit is , and the third-party logistics (3PL) provider earns . The corresponding market demand at this equilibrium is . These values suggest that the government’s subsidy effectively reduces supply chain costs, enabling a higher market penetration while preserving profitability for both private agents [2,13,15,17,24,26,28].
5.2. Sensitivity Analysis and Comparative Structural Insights
To further explore the robustness of the model, sensitivity analyses are conducted on key parameters, including the subsidy rate s, tariff , and price sensitivity b. The following observations are derived [19,24,25,26,27]. Effect of Subsidy s as illustrated in Figure 4: increasing the subsidy enhances manufacturer profit and market demand up to a saturation point. Beyond that, marginal gains diminish due to market saturation and excessive fiscal cost. Effect of Tariff : Figure 5 shows that higher tariffs compress profit margins, prompting the government to compensate with higher subsidies to maintain supply chain efficiency. This illustrates the policy trade-off between protectionism and subsidy expenditure. Effect of Price Sensitivity b: greater price sensitivity reduces the optimal retail price and demand. As shown in Figure 6, this increases pressure on both the manufacturer and 3PL, and the government must adjust the subsidy accordingly to sustain profitability and market participation.
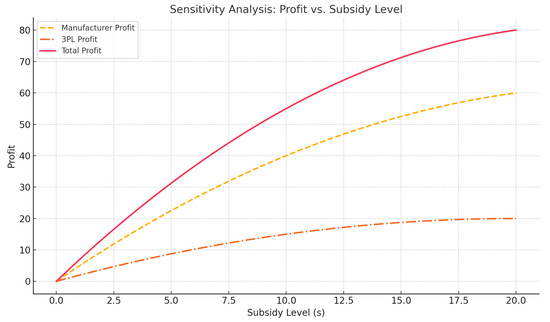
Figure 4.
Manufacturer and 3PL profits vs. subsidy level.
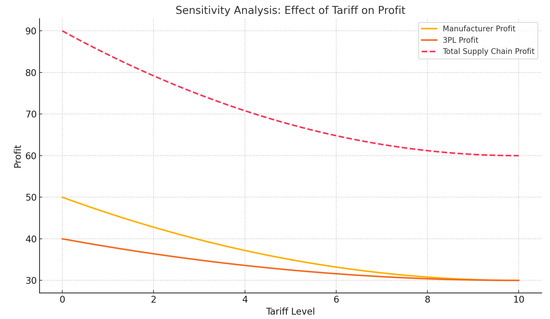
Figure 5.
Effect of tariff on profits and subsidy needs.
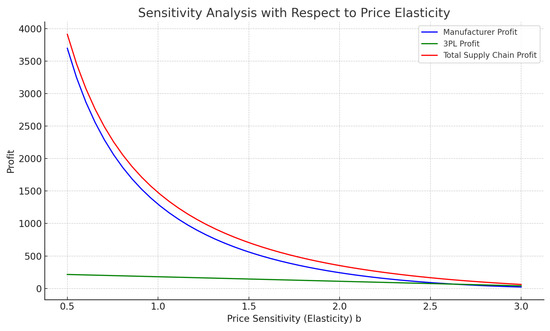
Figure 6.
Impact of price elasticity on equilibrium outcomes.
The findings of this study yield two levels of policy insights: simulation-based implications derived from model outcomes and sensitivity analysis, and theoretical implications grounded in welfare economics and game-theoretic modeling. Together, they provide a holistic view of how tariffs and subsidies influence supply chain coordination and performance. Figure 7, comparative performance of centralized, decentralized, and alliance-based decision models.
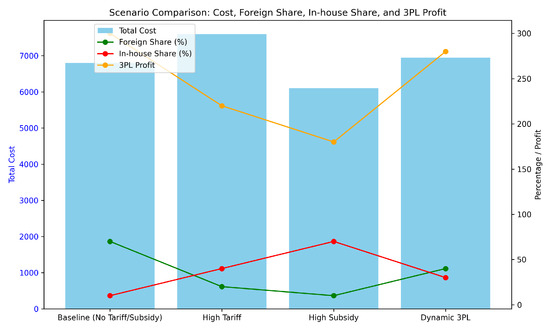
Figure 7.
Comparative performance of centralized, decentralized, and alliance-based decision models.
The simulation and sensitivity results offer meaningful insights for both policymakers and supply chain managers operating in tariff-affected and subsidy-driven markets. First, moderate government subsidies can significantly enhance coordination and profitability within the supply chain while avoiding excessive fiscal expenditures. This finding supports the case for strategic and proportionate financial intervention [2,17,19,24,27].
Second, tariffs—though effective as trade policy instruments—can induce inefficiencies by discouraging production and logistics engagement. The model shows that these distortions can be offset through targeted subsidies, allowing domestic firms to remain competitive in global markets. This highlights the importance of designing subsidy schemes that are calibrated to counteract the magnitude of tariff barriers [2,17,19,24,27].
Third, market price elasticity plays a pivotal role in determining optimal policy responses. In markets with highly elastic demand, even small changes in price—driven by logistics costs or subsidy pass-through—can significantly alter consumer behavior. Hence, policymakers must consider elasticity metrics when determining subsidy levels to ensure desired market outcomes [2,17,19,24,27].
Overall, the integrated model not only predicts strategic behavior of supply chain agents under various decision structures but also quantifies the economic and fiscal consequences of policy tools. These insights can inform real-world industrial policies aimed at sustainable and efficient supply chain development [2,17,19,24,27].
5.3. Key Findings Linked to Simulation Results
Decentralized Structure Leads to Suboptimal Welfare: Though the manufacturer earns a high profit (), the 3PL incurs a loss (), leading to inefficiencies and the highest output () but not the highest welfare (SW = 320.64). Centralized Coordination Achieves Maximum Efficiency: Joint decision-making lowers logistics cost (), optimizes tariff and subsidy (TR = 58.32, SC = 21.87), and improves welfare (SW = 249.13), despite lower output. Alliance Model Provides Practical Compromise: The manufacturer and 3PL share decisions and profits (, ), achieving system coordination similar to centralized in terms of q and l but with slightly lower SW (190.81). Profit-Sharing Stabilizes Coordination: The 3PL benefits under the alliance structure () compared to losses in the decentralized case, demonstrating the benefit of cooperative profit allocation. Table 1, simulation results under different coordination structures.
Tariff and Subsidy Optimization is Critical: The decentralized model brings in the most TR (66.80) but also requires a higher subsidy (25.05) and delivers less efficient system performance. Centralized planning provides more balanced policy outcomes. Trade-Off Between Output and Welfare: Although decentralized output is highest (q = 16.70), it does not yield the highest welfare. Centralized output is lower, but better aligned with societal objectives. Strategic Interdependence Requires Game-Theoretic Modeling: The mutual responsiveness of all players validates the bilevel Stackelberg game structure, where each player’s optimal strategy depends on the others’ actions [1,2,5,10,17,20,23,25].
The analytical results of this study offer meaningful policy implications concerning the design of tariff and subsidy mechanisms in transnational supply chains involving third-party logistics (3PL) service providers. From a welfare economics standpoint, the model indicates that well-calibrated government interventions—such as import tariffs and production or logistics subsidies—can lead to Pareto improvements under specific conditions. These fiscal instruments alter the equilibrium structure of the supply chain by influencing the strategic decisions of upstream suppliers, downstream manufacturers, and intermediary 3PL providers. By adjusting these parameters, policymakers can shift the decentralized equilibrium closer to the social planner’s optimum, assuming the marginal cost of public funds is appropriately accounted for [2,13,19,24,25,26,27,28].
Subsidization of 3PL services, in particular, emerges as an effective tool for internalizing coordination externalities and reducing transaction costs in the supply chain. This functions similarly to a Pigouvian subsidy in correcting for market inefficiencies—such as non-convex production technologies and decentralized logistics decisions—that hinder optimal resource allocation. Moreover, the model reveals that import tariffs, while designed to protect domestic producers, introduce relative price distortions that affect the spatial structure of production and the role of third-party logistics. Unless carefully managed, such distortions can result in substitution effects that shift production to less efficient configurations. In this context, a Ramsey-type rule—wherein the marginal welfare loss from taxation is equated to the marginal revenue gained—can serve as a guideline for tariff optimization [2,13,15,19,24,25,26,27,28].
Furthermore, the inclusion of a bilevel decision structure in the supply chain underscores the need for mechanism design approaches in public policy. When the manufacturer or supplier acts as a Stackelberg leader and the 3PL or other agents respond strategically, incentive-compatible subsidy schemes can align private optimization behavior with socially desirable outcomes. In cases of information asymmetry or decentralized governance, these instruments become essential to induce second-best efficient behavior [2,13,15,19,24,25,26,27,28].
The study also highlights the importance of dynamic policymaking in environments characterized by demand uncertainty and trade volatility. Static tariff and subsidy regimes are often suboptimal under such conditions. Therefore, adaptive policy instruments, grounded in stochastic or robust optimization frameworks, are necessary to minimize expected welfare loss over time. Lastly, given the cross-border nature of modern supply chains, the findings point to the necessity of multi-level governance and coordination in trade policy. Cooperative arrangements between countries—via mechanisms such as Nash bargaining or coalition formation—can lead to globally efficient outcomes and mitigate the adverse effects of tariff escalation or subsidy retaliation [2,13,15,19,24,25,26,27,28].
In conclusion, this research demonstrates that tariffs and subsidies, when strategically designed using the principles of mathematical economics and game theory, can serve as powerful levers for improving supply chain efficiency and resilience. Their effectiveness, however, depends critically on the ability of policymakers to recognize interdependencies, model strategic behavior, and implement dynamic, incentive-compatible interventions [2,13,15,19,24,25,26,27,28].
The simulation results offer several critical insights into the strategic dynamics of government intervention in supply chain coordination. First, the imposition of tariffs significantly undermines the manufacturer’s incentive to engage in production. In both Case 1 and Case 3—scenarios characterized by elevated tariff rates—the manufacturer refrains from producing any output. This pattern suggests that excessive trade barriers can fully deter supply chain participation, regardless of other potentially favorable conditions [2,13,15,17,19,23,24,26,27,28].
Second, subsidies demonstrate a clear capacity to promote productive engagement. In Case 2, where government subsidies are implemented without accompanying tariffs, the manufacturer responds by producing 30 units. This confirms the effectiveness of targeted fiscal incentives in offsetting cost pressures and enabling supply chain activity [2,13,15,17,19,23,24,26,27,28].
However, Case 3 highlights a critical policy trade-off. Even in the presence of subsidies, the coexistence of high tariffs results in zero production. This outcome reveals that the negative effects of tariffs can outweigh the stimulative potential of subsidies, rendering policy support ineffective. It underscores the importance of coordinated and calibrated policy design, where tariffs and subsidies are not viewed in isolation but rather as interdependent levers influencing firm behavior [2,13,15,17,19,23,24,26,27,28].
Overall, these findings emphasize the need for an integrated, data-informed approach to trade and logistics policy. In contexts involving third-party logistics providers (3PLs) and multinational manufacturers, misalignment between fiscal support and trade restrictions can lead to unintended consequences and welfare losses [2,13,15,17,19,23,24,26,27,28].
6. Strategic Implications and Research Directions
6.1. Policy and Managerial Implications
This study offers strategic insights for policymakers, manufacturers, and logistics service providers navigating global supply chains influenced by tariffs and subsidies. The results indicate that government intervention through subsidies can effectively enhance supply chain performance, particularly when coordinated with third-party logistics (3PL) providers. Alliance-based coordination models demonstrate superior outcomes in terms of profitability and efficiency compared to decentralized structures.
For managers, these findings underscore the value of strategic partnerships with logistics providers under fiscal uncertainty. Logistics efforts (e.g., quality or responsiveness) are more effective when aligned with production decisions. Policymakers are advised to design balanced fiscal policies that incentivize both production and logistics investments, ensuring national welfare objectives are met without distorting market dynamics.
Finally, firms operating in transnational environments should consider adopting flexible, game-theoretic decision frameworks to anticipate and respond to government policy shifts, improving resilience and long-term competitiveness.
6.2. Empirical Alignment, Model Limitations, and Future Directions
The theoretical analysis of tariffs and subsidies within supply chains involving third-party logistics (3PL) providers aligns closely with several observable trends in global trade and logistics. Tariffs, commonly imposed as trade policy instruments, have demonstrably increased production and transportation costs across industries, particularly in sectors reliant on complex, multinational supply chains. These cost increases often translate into higher consumer prices and reduced competitiveness for domestic manufacturers, as predicted by the model’s indication of relative price distortions and welfare losses [1,2,5,6,17,20,23].
In practice, 3PL providers have emerged as critical actors in mitigating the adverse effects of such trade policies by enhancing supply chain flexibility and efficiency. For example, during periods of heightened trade tensions and tariff escalations, firms increasingly rely on 3PLs to redesign logistics networks, identify alternative sourcing options, and implement cost-saving strategies such as consolidation and route optimization. This real-world behavior validates the model’s identification of 3PLs as pivotal intermediaries whose participation can internalize coordination externalities and partially offset tariff-induced inefficiencies [1,2,5,6,17,20,23].
Subsidies directed at logistics infrastructure and service innovation—whether through government grants, tax incentives, or public–private partnerships—have also gained prominence in many economies seeking to bolster supply chain resilience. Empirical evidence shows that such subsidies facilitate investment in advanced technologies, sustainable transport modes, and digital platforms, thereby reducing transaction costs and enhancing the overall performance of supply chains. These developments correspond well with the study’s findings on the positive welfare impact of targeted subsidy schemes that encourage efficient integration of 3PL services [1,2,5,6,17,20,23].
Moreover, the dynamic nature of global demand and evolving trade regulations observed in the real world underscores the necessity for adaptive and coordinated policy frameworks. The model’s emphasis on incentive compatibility and multi-level governance reflects the complexity of contemporary supply chains, where unilateral tariffs or subsidies can lead to suboptimal outcomes without international cooperation [1,2,5,6,17,20,23].
In summary, the interplay between tariffs, subsidies, and 3PL participation illustrated in this research finds strong support in empirical trade and logistics data. This congruence affirms the relevance of the theoretical framework and highlights key areas where policymakers can focus efforts to enhance supply chain efficiency and resilience amid ongoing global economic uncertainties [1,2,5,6,17,20,23].
While this study provides valuable insights into the strategic effects of tariffs and subsidies in a transnational supply chain involving a manufacturer and a third-party logistics (3PL) provider, it is important to acknowledge several limitations that constrain the scope and generalizability of the findings [2,17,19,24,27].
First, the model simplifies the supply chain structure by considering only a single manufacturer and one 3PL. In reality, global supply chains comprise multiple interconnected actors, including upstream suppliers, downstream retailers, and competing logistics providers. Expanding the model to encompass multi-tier, multi-agent systems would offer a more comprehensive analysis of coordination and competition dynamics [2,15,19,24,25,26,27].
Second, the study adopts a static, single-period analytical framework, thereby excluding dynamic elements such as time-varying demand, inventory evolution, and policy shifts over time. Incorporating dynamic and multi-period modeling would allow for a more accurate representation of strategic decision-making under uncertainty and long-term contracts [2,15,19,24,25,26,27].
Third, tariffs and subsidies are modeled as fixed or linear policy instruments. However, real-world policy regimes often involve non-linear, conditional, or performance-linked incentives. Future research could enrich the policy realism by incorporating variable or endogenous subsidy schemes and tariff escalations linked to geopolitical or trade alliance changes [2,15,19,24,25,26,27].
Fourth, the role of the 3PL is confined to cost minimization and logistics provision. This abstraction omits critical strategic capabilities such as investment in infrastructure, capacity expansion, technological innovation, and collaborative planning. Future extensions could integrate endogenous 3PL strategies and their feedback effects on supply chain performance [2,15,19,24,25,26,27].
Fifth, the analysis depends heavily on parameter estimation (e.g., logistics costs, tariff rates, subsidy magnitudes), which in practice may suffer from data scarcity, reporting delays, or measurement error. Empirical calibration and validation using real-world data or case studies would significantly enhance the robustness of the model’s predictions [2,15,19,24,25,26,27].
Finally, the model assumes complete information and rational behavior among actors. However, real-world decision-making is often characterized by information asymmetry, bounded rationality, and behavioral biases. Incorporating behavioral game theory or agent-based modeling could capture these complexities more effectively [2,15,19,24,25,26,27]. Mathematical proofs and additional derivations show this in Appendix A.
Addressing these limitations through more advanced modeling techniques, dynamic and stochastic analysis, empirical validation, and behavioral perspectives represents a fertile direction for future research. Such enhancements would not only improve the realism of the model but also strengthen its applicability for guiding public policy and managerial decision-making in complex global supply chain environments [2,15,19,24,25,26,27].
7. Conclusions
This study presents a bilevel game-theoretic framework to analyze the strategic interactions among a government, a manufacturer, and a third-party logistics provider within a global supply chain. By modeling the government as a Stackelberg leader and the supply chain actors as followers, the research captures how tariff and subsidy policies influence production, logistics decisions, and social welfare outcomes [1,2,3,4,5,6,21,22,23,24].
Using a Stackelberg structure, we compare three coordination mechanisms—centralized, decentralized, and alliance-based decision-making—and quantify their economic impacts through a detailed numerical simulation. The results demonstrate that decentralized systems may lead to inefficiencies and suboptimal social welfare, while coordinated or alliance-based strategies can improve system performance, particularly under government support through subsidies [1,2,3,4,5,6,21,22,23,24].
Furthermore, the integration of demand elasticity and exchange rate variability into the model framework enhances its applicability to real-world policy and business decision-making. These parameters allow for richer analysis of how external market conditions affect supply chain behavior, pricing, and profitability [1,2,3,4,5,6,21,22,23,24].
This research provides valuable insights for policymakers seeking to design effective trade and logistics policies, as well as for supply chain managers aiming to optimize strategies under regulatory constraints. The bilevel modeling approach also lays the groundwork for future studies incorporating environmental regulation, risk-sharing contracts, and multi-country trade dynamics [1,2,3,4,5,6,21,22,23,24].
In conclusion, this work advances the literature on supply chain economics by demonstrating how strategic decision-making under government intervention can be modeled and optimized using game-theoretic tools. It offers a structured, quantitative basis for policy evaluation and operational strategy in complex global supply networks [1,2,3,4,5,6,21,22,23,24].
Author Contributions
Methodology, A.H.A.; Software, A.H.A. and A.S.; Data curation, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Mathematical Proofs and Additional Derivations
Appendix A.1. Proof of Equilibrium Conditions
To derive the Stackelberg equilibrium between the government (leader) and the manufacturer and 3PL (followers), we consider the following bilevel structure:
- Upper Level (Government): Maximizes national welfare by setting optimal tariff and subsidy s.
- Lower Level (Manufacturer and 3PL): Reacts to fiscal parameters by optimizing production quantity q, retail price p, logistics fee r, and effort level e.
The equilibrium is derived using the Karush–Kuhn–Tucker (KKT) conditions for the lower-level problems. These are embedded into the upper-level program, resulting in a Mathematical Program with Equilibrium Constraints (MPEC). The Lagrangian functions are constructed, and stationarity conditions are solved iteratively.
Appendix A.2. KKT Conditions of Manufacturer’s Problem
Let the manufacturer’s objective function be
Subject to
The KKT conditions are
Appendix A.3. Further Derivations
Additional derivations for the centralized and alliance-based models follow similarly and can be provided upon request or in an extended version of the paper.
References
- Barbosa, L.; Rodrigues, A.; Sardinha, A. Optimal price subsidies under uncertainty. Eur. J. Oper. Res. 2022, 303, 471–479. [Google Scholar] [CrossRef]
- Chen, Z.; Su, S.I.; Wang, H. Imposing tariff or implementing subsidy? Dual competing international supply chains under intra-industry-trade conflict. J. Model. Manag. 2020, 15, 727–781. [Google Scholar] [CrossRef]
- Rotunno, L.; Ruta, M. Trade Spillovers of Domestic Subsidies; International Monetary Fund: Bretton Woods, NH, USA, 2024. [Google Scholar]
- Khurshid, A.; Cifuentes-Faura, J.; Hongbin, Y.; Saleem, S.F. Corporate social responsibility in the era of government subsidies: A novel empirical perspective on market competitiveness. Corp. Soc. Responsib. Environ. Manag. 2025, 32, 102–117. [Google Scholar] [CrossRef]
- Handfield, R.B.; Graham, G.; Burns, L. Corona virus, tariffs, trade wars and supply chain evolutionary design. Int. J. Oper. Prod. Manag. 2020, 40, 1649–1660. [Google Scholar] [CrossRef]
- Russell, D.; Ruamsook, K.; Roso, V. Managing supply chain uncertainty by building flexibility in container port capacity: A logistics triad perspective and the COVID-19 case. Marit. Econ. Logist. 2020, 24, 92. [Google Scholar] [CrossRef]
- Handley, K.; Kamal, F.; Monarch, R. Rising Import Tariffs, Falling Export Growth: When Modern Supply Chains Meet Old-Style Protectionism; National Bureau of Economic Research: Cambridge, MA, USA, 6 January 2020. [Google Scholar]
- Chae, S.; Mena, C.; Polyviou, M.; Rogers, Z.S.; Wiedmer, R. The effects of tariff increases on supply base complexity: A conceptual framework. J. Purch. Supply Manag. 2019, 25, 100556. [Google Scholar] [CrossRef]
- Grossman, G.M.; Helpman, E.; Redding, S.J. When tariffs disrupt global supply chains. Am. Econ. Rev. 2024, 114, 988–1029. [Google Scholar] [CrossRef]
- Dong, L.; Kouvelis, P. Impact of tariffs on global supply chain network configuration: Models, predictions, and future research. Manuf. Serv. Oper. Manag. 2020, 22, 25–35. [Google Scholar] [CrossRef]
- Feo-Valero, M.; Botella-Andreu, A.; Martìnez-Moya, J.; Pallardó-López, V.J.; Requena-Silvente, F.; Sala-Garrido, R. Exploring supply chain and regional resilience through the analysis of the transport dimension. Case Stud. Transp. Policy 2024, 16, 101216. [Google Scholar] [CrossRef]
- Hafezalkotob, A.; Mahmoudi, R.; Hajisami, E.; Wee, H.M. Wholesale-retail pricing strategies under market risk and uncertain demand in supply chain using evolutionary game theory. Kybernetes 2018, 47, 1178–1201. [Google Scholar] [CrossRef]
- Hu, X.; Fu, K.; Chen, Z.; Du, Z. Decision-making of transnational supply chain considering tariff and third-party logistics service. Mathematics 2022, 10, 770. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, Z.; Shen, L.; Fan, R.; Tang, R. Decisions and coordination in e-commerce supply chain under logistics outsourcing and altruistic preferences. Mathematics 2021, 9, 253. [Google Scholar] [CrossRef]
- Yi, S.; Wen, G. Game model of transnational green supply chain management considering government subsidies. Ann. Oper. Res. 2023, 1–22. [Google Scholar] [CrossRef]
- Yu, J.J.; Tang, C.S.; Sodhi, M.S.; Knuckles, J. Optimal subsidies for development supply chains. Manuf. Serv. Oper. Manag. 2020, 22, 1131–1147. [Google Scholar] [CrossRef]
- Meng, Q.; Li, M.; Liu, W.; Li, Z.; Zhang, J. Pricing policies of dual-channel green supply chain: Considering government subsidies and consumers’ dual preferences. Sustain. Prod. Consum. 2021, 26, 1021–1030. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, C.; Wu, G.; Gao, Y. Cold chain logistics network design for fresh agricultural products with government subsidy. Sustainability 2023, 15, 10021. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, L.; Zhu, M. Dynamic game of the dual-channel supply chain under a carbon subsidy policy. Int. J. Bifurc. Chaos 2022, 32, 2250223. [Google Scholar] [CrossRef]
- Guo, H.; Lian, X.; Zhang, Y.; Ren, Y.; He, Z.; Zhang, R.; Ding, N. Analysis of environmental policy’s impact on remanufacturing decision under the effect of green network using differential game model. IEEE Access 2020, 8, 115251–115262. [Google Scholar] [CrossRef]
- Premkumar, P.; Gopinath, S.; Mateen, A. Trends in third party logistics–the past, the present the future. Int. J. Logist. Res. Appl. 2021, 24, 551–580. [Google Scholar] [CrossRef]
- Liu, X.; Qian, C.; Wang, S. When do 3PLs initiate low-carbon supply chain integration? Int. J. Oper. Prod. Manag. 2020, 40, 1367–1395. [Google Scholar] [CrossRef]
- Leylaparast, P.; Gholamian, M.R.; Noroozi, M. Integration of pricing, sustainability and 3PL delivery time according to freshness date in a dual-channel fruit supply chain: A game theoretic approach. J. Ind. Manag. Optim. 2025, 21, 504–523. [Google Scholar] [CrossRef]
- Mesrzade, P.; Dehghanian, F.; Ghiami, Y. A Bilevel Model for Carbon Pricing in a Green Supply Chain Considering Price and Carbon-Sensitive Demand. Sustainability 2023, 15, 16563. [Google Scholar] [CrossRef]
- Zhu, X.; Guo, P. Bilevel programming approaches to production planning for multiple products with short life cycles. 4OR 2020, 18, 151–175. [Google Scholar] [CrossRef]
- Camacho-Vallejo, J.F.; López-Vera, L.; Smith, A.E.; González-Velarde, J.L. A tabu search algorithm to solve a green logistics bi-objective bi-level problem. Ann. Oper. Res. 2022, 316, 927–953. [Google Scholar] [CrossRef]
- Rahmani, A.; Hosseini, M.; Sahami, A. A competitive bilevel programming model for green, CLSCs in light of government incentives. J. Math. 2024, 2024, 4866890. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, F.; Jiang, H. Dynamic pricing game under different channel power structures in a closed-loop supply chain. Int. J. Bifurc. Chaos 2020, 30, 2050052. [Google Scholar] [CrossRef]
- Trott, A.; Srinivasa, S.; van der Wal, D.; Haneuse, S.; Zheng, S. Building a foundation for data-driven, interpretable, and robust policy design using the ai economist. arXiv 2021, arXiv:2108.02904. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).