Generalized Antiorthotomics of (n, m)-Cusp Curves

Abstract

In optics, light rays emitted from a light source form a wavefront (orthotomic) upon reflection by a mirror. The mirror is referred to as an antiorthotomic of the orthotomic. The investigation of the relationship between orthotomics and antiorthotomics constitutes an interesting problem in physics. However, the study becomes ambiguous when the orthotomic exhibits singular points. In this paper, we define generalized antiorthotomics of (n, m)-cusp curves in the Euclidean plane by using the singular curve theory. We demonstrate that the singular points of the generalized antiorthotomic sweep out the evolute of the (n, m)-cusp curve. We also investigate the behavior and singular characteristics of the antiorthotomic of the (n, m)-cusp curve. Moreover, we define parallels for (n, m)-cusp curves and reveal the relationship between parallels and generalized antiorthotomics. Finally, repeated antiorthotomics are studied, which is useful for identifying the characteristics of (n, m)-cusp curves.

1. Introduction

The study of special submanifolds has garnered significant attention from mathematicians and physicists. For instance, wavefronts, particularly in optics, are instrumental in physics research and can be represented as involutes of caustics (see [1,2,3,4,5]). B. Gu and Y. Zhang developed a wavefront reconstructor using a damped transpose matrix of the influence function. This development offered a valuable tool for testing, evaluating, and optimizing adaptive optics systems (see [6]). In [7], S. Sorgato et al. proposed a wavefront-matching procedure, which enables the design of optics with prescribed intensity for non-symmetric configurations in 3D. Y. Nishizaki et al. presented a new class of deep learning wavefront sensor which could simplify both the optical hardware and image processing in wavefront sensing (see [8]). In [9], J. Kung and E. Manche investigated the effects of wavefront-guided and wavefront-optimized technology on the subjective quality of vision using different laser platforms. In this paper, we concentrate on wavefronts in a classical optical system, where reflection occurs when a light source illuminates a mirror. In accordance with [10,11,12,13], a concise description of the optical system is provided as follows (see Figure 1). Consider a mirror M as an $(n-1)$-dimensional submanifold embedded in n-dimensional Euclidean space ${\mathbb{R}}^n$, with F representing a light source in ${\mathbb{R}}^n$. In this context, there exists an $(n-1)$-dimensional submanifold $W,$ where its normal lines align with the ray lines generated from F upon reflection on M. W is called a wavefront. In geometrical optics, W is also referred to as an orthotomic of M with respect to $F,$ and conversely, M is called an antiorthotomic of W with respect to F. In the study of geometric optics and differential geometry, orthotomic and antiorthotomic curves are classically related as reflection counterparts with respect to a fixed point or line. While the orthotomic of a curve corresponds to the reflected rays, the antiorthotomic captures the inverse reflection geometry. These constructions are closely connected to the notions of secondary caustics and isotels in caustic theory, where secondary caustics refer to the orthogonal trajectory of reflected rays, and isotels describe loci of equal optical path length.

Figure 1. Orthotomic and antiorthotomic.

The study of the orthotomic was initially explored in [14]. J. Xiong introduced the concepts of spherical orthotomic and spherical antiorthotomic, along with determining their local diffeomorphic types in [15]. In geometrical optics, a fundamental problem involves determining the orthotomic through a mirror (antiorthotomic) and a light source. In [16], N. Alamo and C. Criado addressed the inverse problem by proposing a method to construct a family of mirrors, denoted as $M_a$, parameterized by a real number $a>0$. These mirrors can generate reflected rays normal to W from the light source F. $M_a$ is called a generalized antiorthotomic or a-antiorthotomic of W relative to $F.$ Actually, the construction of $M_a$ involves taking the envelopes of ellipsoids or hyperboloids, both sharing the foci F and a point varying on W. The distance between the two vertices is equal to $2a$. Notably, when $a=0,$ the ellipsoids or hyperboloids degenerate into hyperplanes that are parallel to the tangent hyperplanes of $M_a.$ In this case, the generalized antiorthotomic $M_a$ essentially reduces to the antiorthotomic M.

While regular curves and their antiorthotomics have been studied, the investigation of the antiorthotomics of singular curves is equally crucial. Singular curves are significant as they are prevalent in practical scenarios and represent a generalization of regular curves. In [17], T. Fukui delved into the local differential geometry of singular curves with finite multiplicities. In [18], C. Zhang and D. Pei analyzed the behavior and the singular property of the evolute of an $(n,m)$-cusp curve which may have singular points. Furthermore, they established a one-to-one correspondence between the orthotomics and the caustics of $(n,m)$-cusp curves in [19]. Then D. Pei et al. investigated generalized Bertrand curves and nullcone fronts of framed curves in Lorentz–Minkowski 3-space in [20,21]. As the orthotomics we studied here are singular curves, their antiorthotomics will inevitably exhibit singular points. One of the main motives of our study is to investigate the geometric properties of the antiorthotomic near singular points. This is also a part of our research projects about the classification and characterization of singularities for curves and surfaces ([22,23,24]).

We consider the orthotomic as an $(n,m)$-cusp curve instead of a regular curve, and construct the a-antiorthotomic $M_a$ from the $(n,m)$-cusp curve and a light source point F. Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an $(n,m)$-cusp curve and F the origin of ${\mathbb{R}}^2$. Suppose $a>0$ and $h_a$ is the ellipse or hyperbola which has the foci F and a point on $\mathit{\gamma }.$ One of the directrices closest to F is denoted as $d.$ Based on fundamental knowledge of conic curves, as detailed in [25], $h_a$ represents the locus of the point $p\in {\mathbb{R}}^2$ such that the ratio of the distance from p to F and the distance from p to d is a constant, denoted as the eccentricity e. For any $t_0\in I,$ the value of e is $\parallel \mathit{\gamma }\left(t_0\right)\parallel /2a$. $h_a\left(t_0\right)$ represents an ellipse or a hyperbola depending on the eccentricity $0<e<1$ or $e>1$, respectively. When $e=1$ or $e=0,$$h_a\left(t_0\right)$ becomes either a straight line passing through F and $\mathit{\gamma }\left(t_0\right)$ or a circle centered at F, respectively. It forms a family of conic curves as $t_0$ varies in I. The envelope of the family of conic curves is defined as the a-antiorthotomic of $\mathit{\gamma }$ relative to F (see Figure 2).

Figure 2. A cusp orthotomic $\mathit{\gamma }\left(t\right)$, an ellipse $h_a\left(t_0\right)$ and an a-antiorthotomic $M_a$.

In order to study $M_a$, we give the equation of $h_a$. Let Q be the intersection point of the directrix d and the straight line passing through F and $\mathit{\gamma }\left(t_0\right)$, then the distance between Q and the center of $h_a$ is $a/e.$ Thus, we have

$$Q=\mathit{\gamma }\left(t_0\right)/2-(a/e)\mathit{\gamma }\left(t_0\right)/\parallel \mathit{\gamma }\left(t_0\right)\parallel .$$

Since $e=\parallel \mathit{\gamma }\left(t_0\right)\parallel /2a$, the equation for Q can be rewritten as follows:

$$Q=\mathit{\gamma }\left(t_0\right)·(1/2-2a^2/\parallel \mathit{\gamma }\left(t_0\right){\parallel }^2).$$

For any $p\in h_a\left(t_0\right),$ we have $(p-Q)·(\mathit{\gamma }\left(t_0\right)/\parallel \mathit{\gamma }\left(t_0\right)\parallel )e\pm \parallel p\parallel =0.$ It follows that

$$\begin{array}{c}\hfill {\displaystyle \mathit{\gamma }\left(t_0\right)·\left(p-\frac{\mathit{\gamma }\left(t_0\right)}{2}\right)+2a^2\pm 2a\parallel p\parallel =0.}\end{array}$$

(1)

Notably, when $a=0,$$h_a\left(t_0\right)$ acts as a perpendicular bisector of the line segment with endpoints F and $\mathit{\gamma }\left(t_0\right)$.

Thus, for any $a\ge 0,$ a family of curves ${\left\{h_a\left(t_0\right)\right\}}_{t_0\in I}$ is defined using the map $f_a:I\times {\mathbb{R}}^2\to \mathbb{R},$ where ${\displaystyle f_a(t_0,p)=\mathit{\gamma }\left(t_0\right)·(p-\mathit{\gamma }\left(t_0\right)/2)+2a^2\pm 2a\left|p\right|,}$ so that for any fixed $t_0\in I$ the zero set of the map $f_{a,t_0}:{\mathbb{R}}^2\to \mathbb{R}$ given by $f_{a,t_0}\left(p\right)=f_a(t_0,p)$ is $h_a\left(t_0\right).$ Then the envelope $M_a$ of the family curves $h_a\left(t\right)$ is composed of points p that satisfy

$${\displaystyle f_a(\mathit{\gamma }\left(t\right),p)=\mathit{\gamma }\left(t\right)·\left(p-\frac{\mathit{\gamma }\left(t\right)}{2}\right)+2a^2\pm 2a\parallel p\parallel =0}$$

and

$$\begin{array}{c}\hfill {\displaystyle \frac{d{f}_a}{dt}(\mathit{\gamma }\left(t\right),p)=\left(p-\mathit{\gamma }\left(t\right)\right)·\frac{d\mathit{\gamma }}{dt}\left(t\right)=0.}\end{array}$$

(2)

On the other hand, we find that the normal line $r_n$ of $\mathit{\gamma }$ can be also given by Equation (2). Therefore, the a-antiorthotomic of $\mathit{\gamma }$ is naturally defined as follows:

$$\begin{array}{c}\hfill M_a\left[\mathit{\gamma }\right]\left(t\right)=\bigcup _{t\in I}{h}_a\left(t\right)\cap r_n\left(t\right).\end{array}$$

(3)

By the above notions, we can give an explicit parametrization of the a-antiorthotomic $M_a$. Let $\mathit{n}\left(t\right)$ be the modified unit normal vector of $\mathit{\gamma }\left(t\right)$ defined in Section 2, so that $\mathit{n}$ is a smooth vector field along $\mathit{\gamma }$ even if $\mathit{\gamma }$ is a cusp curve. Then $M_a$ can be given by

$$\begin{array}{c}\hfill M_a\left[\mathit{\gamma }\right]\left(t\right)=\mathit{\gamma }\left(t\right)+\lambda \left(t\right)·\mathit{n}\left(t\right),\end{array}$$

(4)

where $\lambda \left(t\right)$ is determined by the condition $M_a\left[\mathit{\gamma }\right]\left(t\right)\in h_a\left(t\right)$, which satisfies

$$\begin{array}{c}\hfill {\displaystyle \mathit{\gamma }\left(t\right)·\left(M_a\left[\mathit{\gamma }\right]\left(t\right)-\frac{\mathit{\gamma }\left(t\right)}{2}\right)+2a^2\pm 2a\parallel M_a\left[\mathit{\gamma }\right]\left(t\right)\parallel =0.}\end{array}$$

(5)

Combining Equations (4) and (5), by a straightforward calculation, $\lambda \left(t\right)$ has two values:

$$\begin{array}{c}\hfill {\displaystyle {\lambda }_{a^{+}}\left(t\right)=\frac{4a^2-{\parallel \mathit{\gamma }\left(t\right)\parallel }^2}{4a+2\left(\mathit{\gamma }\right(t)·\mathit{n}(t\left)\right)}\mathrm{and}{\lambda }_{a^{-}}\left(t\right)=\frac{4a^2-{\parallel \mathit{\gamma }\left(t\right)\parallel }^2}{-4a+2\left(\mathit{\gamma }\right(t)·\mathit{n}(t\left)\right)}.}\end{array}$$

(6)

For the choice of $\lambda \left(t\right),$ the a-antiorthotomic $M_a$ consists of two parts, $M_{a^{+}}$ and $M_{a^{-}}.$ They are parameterized by

$$\begin{array}{c}\hfill M_{a^{+}}\left[\mathit{\gamma }\right]\left(t\right)=\mathit{\gamma }\left(t\right)+{\lambda }_{a^{+}}\left(t\right)·\mathit{n}\left(t\right)\end{array}$$

(7)

and

$$\begin{array}{c}\hfill M_{a^{-}}\left[\mathit{\gamma }\right]\left(t\right)=\mathit{\gamma }\left(t\right)+{\lambda }_{a^{-}}\left(t\right)·\mathit{n}\left(t\right)\end{array}$$

(8)

respectively. Specifically, we have $M_{a^{+}}=M_{a^{-}}=M$ if $a=0$.

This paper is structured as follows. In Section 2, we introduce the differential geometry of $(n,m)$-cusp curves. Section 3 presents the proof that singular points of the generalized antiorthotomic sweep out the evolute of cusp curve, and establishes a one-to-one correspondence between antiorthotomics and cusp curves. In Section 4, we define parallels of cusp curves and explore the relationship between parallels and generalized antiorthotomics. Finally, in Section 5, we study the repeated antiorthotomics of cusp curves, and demonstrate how the k-th antiorthotomics is determined by the $(n,m)$-cusp curves.

All maps considered here are differential of class ${\mathcal{C}}^{\infty }$.

2. Preliminaries

In this section, we introduce some necessary notations and concepts of $(n,m)$-cusp curves in the Euclidean plane. Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be a smooth curve, where $I\in \mathbb{R}$ is an open interval. If $t_0\in I$ satisfies the following two conditions:

(1)

$\text{det}({\mathit{\gamma }}^{\left(n\right)}\left(t_0\right),{\mathit{\gamma }}^{\left(j\right)}\left(t_0\right))=0,(j=1,2,\dots ,m-1)$,

(2)

$\text{det}({\mathit{\gamma }}^{\left(n\right)}\left(t_0\right),{\mathit{\gamma }}^{\left(m\right)}\left(t_0\right))\ne 0$,

where n and m are integers satisfying $1\le n<m$ and ${\mathit{\gamma }}^{\left(i\right)}\left(t\right)={\displaystyle \frac{d^i\mathit{\gamma }}{d{t}^i}}\left(t\right),$ we say that $t=t_0$ is an $(n,m)$-cusp point, and $\mathit{\gamma }$ is an $(n,m)$-cusp curve. It is known that the classical Frenet–Serret-type frame does not work for singular curves. Fortunately, C. Zhang and D. Pei introduced a new moving frame to study the geometric properties of $(n,m)$-cusp curves as follows (for details, see [18]).

Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an $(n,m)$-cusp curve. Without losing generality, we choose $t=0$ as the cusp point in this paper. Define two unit orthogonal vectors as

$${\displaystyle \mathit{t}\left(t\right)=\frac{\mathit{\gamma }\prime \left(t\right)/t^{n-1}}{\parallel \mathit{\gamma }\prime \left(t\right)/t^{n-1}\parallel }}$$

and

$$\mathit{n}\left(t\right)=\mathit{J}\left(\mathit{t}\left(t\right)\right),$$

where $\mathit{J}$ is the anti-clockwise rotation by ${\displaystyle \frac{\pi }{2}}$ on ${\mathbb{R}}^2$. $\mathit{t}\left(t\right)$ and $\mathit{n}\left(t\right)$ are called the modified tangent vector and the modified normal vector of $\mathit{\gamma }\left(t\right)$, respectively. We refer to $\left\{\mathit{\gamma }\right(t);\mathit{t}(t),\mathit{n}(t\left)\right\}$ a modified frame of the $(n,m)$-cusp curve $\mathit{\gamma }$, and we have the following formula:

$${\displaystyle \frac{d}{dt}\left(\begin{array}{c}\mathit{t}\left(t\right)\\ \mathit{n}\left(t\right)\end{array}\right)=\left(\begin{array}{cc}0& f\left(t\right)\\ -f\left(t\right)& 0\end{array}\right)\left(\begin{array}{c}\mathit{t}\left(t\right)\\ \mathit{n}\left(t\right)\end{array}\right),}$$

where

$$f\left(t\right)=\left\{\begin{array}{cc}\parallel \mathit{\gamma }\prime \left(t\right)\parallel sgn\left(t^{m+n-1}\right)\kappa \left(t\right),\hfill & \mathrm{if}t\ne 0,\hfill \\ \alpha (n,m)\parallel {\mathit{\gamma }}^{\left(n\right)}{\left(t\right)\parallel }^{(m-n)/n}{t}^{m-n-1}\kappa (n,m),\hfill & \mathrm{if}t=0,\hfill \end{array}\right.$$

and

$$\left\{\begin{array}{c}{\displaystyle \kappa \left(t\right)=\frac{\parallel \mathit{\gamma }\prime \left(t\right)\times \mathit{\gamma }″\left(t\right)\parallel }{\parallel \mathit{\gamma }\prime {\left(t\right)\parallel }^3},}\hfill \\ {\displaystyle \kappa (n,m)=\frac{\parallel {\mathit{\gamma }}^{\left(n\right)}\left(0\right)\times {\mathit{\gamma }}^{\left(m\right)}\left(0\right)\parallel }{\parallel {\mathit{\gamma }}^{\left(n\right)}{\left(0\right)\parallel }^{(n+m)/n}},}\hfill \\ {\displaystyle \alpha (n,m)=\frac{(m-n)(n-1)!}{(m-1)!}.}\hfill \end{array}\right.$$

The function $f\left(t\right)$ is called the associate function of $\mathit{\gamma },$ and $sgn\left(t^{m+n-1}\right)$ denotes the sign function of $t^{m+n-1}$.

In the field of differential geometry concerning regular curves, it is well-established that the evolute of a planar curve represents the locus of centers of osculating circles of the curve. An equivalent description states that the envelope of the normal lines of a planar curve defines its evolute. Now, we introduce the definition of the evolute of an $(n,m)$-cusp curve. Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an $(n,m)$-cusp curve. Since $\mathit{\gamma }$ is a regular curve in the case of $n=1,$ we choose the arc length parameter s. Then $\left\{\mathit{\gamma }\right(s);\mathit{t}(s),\mathit{n}(s\left)\right\}$ represents the classical Frenet–Serret-type frame, and the evolute of $\mathit{\gamma }$ is defined by:

$$\begin{array}{c}\hfill {\displaystyle Ev\left(\mathit{\gamma }\right)\left(s\right)=\mathit{\gamma }\left(s\right)+\frac{1}{\kappa \left(s\right)}\mathit{n}\left(s\right),}\end{array}$$

(9)

where $\kappa$ denotes the curvature function of $\mathit{\gamma }.$ If $n\ne 1,$ the evolute of $\mathit{\gamma }$ is defined as follows:

$$\begin{array}{c}\hfill {\displaystyle Ev\left(\mathit{\gamma }\right)\left(t\right)=\mathit{\gamma }\left(t\right)+\frac{\mathit{\gamma }\prime \left(t\right)·\mathit{t}\left(t\right)}{f\left(t\right)}\mathit{n}\left(t\right).}\end{array}$$

(10)

It was proved in [18] that the value of ${\displaystyle \underset{t\to 0}{lim}\frac{\mathit{\gamma }\prime \left(t\right)·\mathit{t}\left(t\right)}{f\left(t\right)}}$ depends on n and $m,$ and the following holds:

(1)

${\displaystyle \underset{t\to 0}{lim}\frac{\mathit{\gamma }\prime \left(t\right)·\mathit{t}\left(t\right)}{f\left(t\right)}=0}$ if $m<2n,$ $Ev\left(\mathit{\gamma }\right)\left(0\right)=\mathit{\gamma }\left(0\right)$.

(2)

${\displaystyle \underset{t\to 0}{lim}\frac{\mathit{\gamma }\prime \left(t\right)·\mathit{t}\left(t\right)}{f\left(t\right)}=c\ne 0}$ if $m=2n,$ $Ev\left(\mathit{\gamma }\right)\left(0\right)=\mathit{\gamma }\left(0\right)+c\mathit{n}\left(0\right)$.

(3)

${\displaystyle \underset{t\to 0}{lim}\frac{\mathit{\gamma }\prime \left(t\right)·\mathit{t}\left(t\right)}{f\left(t\right)}=+\infty }$ if $m>2n$ and m is even, the straight line spanned by $\mathit{n}\left(0\right)$ is the asymptotic line of the evolute. Moreover, the evolute approximates the normal line of $\mathit{\gamma }$ along the positive direction at $t=0$.

(4)

${\displaystyle \underset{t\to 0^{\pm }}{lim}\frac{\mathit{\gamma }\prime \left(t\right)·\mathit{t}\left(t\right)}{f\left(t\right)}=\pm \infty }$ if $m>2n$ and m is odd, the straight line spanned by $\mathit{n}\left(0\right)$ is the asymptotic line of the evolute. Additionally, the right (resp. left) side of the evolute approximates the normal line of $\mathit{\gamma }$ along the positive(resp. negative)direction at $t=0$.

3. Singularities of $\mathit{a}$-Antiorthotomics

We investigate the a-antiorthotomic of an $(n,m)$-cusp curve focusing on singularities in this section. The relationship between the singularities of a-antiorthotomics and the evolutes of cusp curves is elucidated as follows:

Theorem 1.

Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an (n, m)-cusp curve with the modified frame $\left\{\mathit{\gamma }\right(t);\mathit{t}(t),\mathit{n}(t\left)\right\}$ and $M_a\left[\mathit{\gamma }\right]\left(t\right)$ the a-antiorthotomic of $\mathit{\gamma }\left(t\right).$ Then the singularities of $M_a\left[\mathit{\gamma }\right]\left(t\right)$ sweep out the evolute of $\mathit{\gamma }\left(t\right).$

Proof. 

We consider $M_{a^{-}}\left[\mathit{\gamma }\right]\left(t\right)$ first; Equations (6) and (8) yield the representation of $M_{a^{-}}\left[\mathit{\gamma }\right]\left(t\right)$ as follows:

$$\begin{array}{c}\hfill M_{a^{-}}\left[\mathit{\gamma }\right]\left(t\right)=\mathit{\gamma }\left(t\right)+{\displaystyle \frac{4a^2-\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{-4a+2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}\mathit{n}\left(t\right).\end{array}$$

(11)

Case 1: When $n=1$, the arc length parameter s can be employed, yielding

$$\begin{array}{cc}& \left(M_{a^{-}}\left[\mathit{\gamma }\right]\right)\prime \left(s\right)\hfill \\ \hfill =& {\displaystyle \frac{2\left[2a-\left(\mathit{\gamma }\left(s\right)·\mathit{n}\left(s\right)\right)\right]\left(\mathit{\gamma }\left(s\right)·\mathit{t}\left(s\right)\right)+\kappa \left(s\right)\left[4a^2-\left(\mathit{\gamma }\left(s\right)·\mathit{\gamma }\left(s\right)\right)\right]\left(\mathit{\gamma }\left(s\right)·\mathit{t}\left(s\right)\right)}{2{\left[-2a+\left(\mathit{\gamma }\left(s\right)·\mathit{n}\left(s\right)\right)\right]}^2}}\mathit{n}\left(s\right)\hfill \\ & +\mathit{t}\left(s\right)-\kappa \left(s\right){\displaystyle \frac{4a^2-\left(\mathit{\gamma }\left(s\right)·\mathit{\gamma }\left(s\right)\right)}{-4a+2\left(\mathit{\gamma }\left(s\right)·\mathit{n}\left(s\right)\right)}}\mathit{t}\left(s\right)\hfill \\ \hfill =& {\displaystyle \frac{2\left[2a-\left(\mathit{\gamma }\left(s\right)·\mathit{n}\left(s\right)\right)\right]\left(\mathit{\gamma }\left(s\right)·\mathit{t}\left(s\right)\right)+\kappa \left(s\right)\left[4a^2-\left(\mathit{\gamma }\left(s\right)·\mathit{\gamma }\left(s\right)\right)\right]\left(\mathit{\gamma }\left(s\right)·\mathit{t}\left(s\right)\right)}{2{\left[-2a+\left(\mathit{\gamma }\left(s\right)·\mathit{n}\left(s\right)\right)\right]}^2}}\mathit{n}\left(s\right)\hfill \\ & +\left[1-\kappa \left(s\right){\displaystyle \frac{4a^2-\left(\mathit{\gamma }\left(s\right)·\mathit{\gamma }\left(s\right)\right)}{-4a+2\left(\mathit{\gamma }\left(s\right)·\mathit{n}\left(s\right)\right)}}\right]\mathit{t}\left(s\right).\hfill \end{array}$$

If $s_0\in I$ is a singular point of $M_{a^{-}}\left[\mathit{\gamma }\right]\left(s\right),$ then $\left(M_{a^{-}}\left[\mathit{\gamma }\right]\right)\prime \left(s_0\right)=0.$ Namely $s_0$ is a singular point if and only if

$${\displaystyle \frac{2\left[2a-\left(\mathit{\gamma }\left(s_0\right)·\mathit{n}\left(s_0\right)\right)\right]\left(\mathit{\gamma }\left(s_0\right)·\mathit{t}\left(s_0\right)\right)+\kappa \left(s_0\right)\left[4a^2-\left(\mathit{\gamma }\left(s_0\right)·\mathit{\gamma }\left(s_0\right)\right)\right]\left(\mathit{\gamma }\left(s_0\right)·\mathit{t}\left(s_0\right)\right)}{2{\left[-2a+\left(\mathit{\gamma }\left(s_0\right)·\mathit{n}\left(s_0\right)\right)\right]}^2}}=0$$

and

$$1-\kappa \left(s_0\right){\displaystyle \frac{4a^2-\left(\mathit{\gamma }\left(s_0\right)·\mathit{\gamma }\left(s_0\right)\right)}{-4a+2\left(\mathit{\gamma }\left(s_0\right)·\mathit{n}\left(s_0\right)\right)}}=0.$$

By calculation, we have

$${\displaystyle \frac{4a^2-\left(\mathit{\gamma }\left(s_0\right)·\mathit{\gamma }\left(s_0\right)\right)}{-4a+2\left(\mathit{\gamma }\left(s_0\right)·\mathit{n}\left(s_0\right)\right)}}={\displaystyle \frac{1}{\kappa \left(s_0\right)}},$$

which means ${\lambda }_{a^{-}}\left(s_0\right)={\displaystyle \frac{1}{\kappa \left(s_0\right)}}.$ According to the definition of the evolute of a regular curve, we obtain that $M_{a^{-}}\left[\mathit{\gamma }\right]\left(s_0\right)$ lies on the evolute of the cusp curve $\mathit{\gamma }$.

Case 2: When $n\ne 1$, we use the parameter t. We have

$$\begin{array}{cc}\hfill & \left(M_{a^{-}}\left[\mathit{\gamma }\right]\right)\prime \left(t\right)\hfill \\ \hfill =& {\displaystyle \frac{2\left[2a-\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)\right]\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\prime \left(t\right)\right)+f\left(t\right)\left[4a^2-\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)\right]\left(\mathit{\gamma }\left(t\right)·\mathit{t}\left(t\right)\right)}{2{\left[-2a+\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)\right]}^2}}\mathit{n}\left(t\right)\hfill \\ \hfill & +\mathit{\gamma }\prime \left(t\right)-f\left(t\right){\displaystyle \frac{4a^2-\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{-4a+2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}\mathit{t}\left(t\right)\hfill \\ \hfill =& {\displaystyle \frac{2\left[2a-\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)\right]\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\prime \left(t\right)\right)+f\left(t\right)\left[4a^2-\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)\right]\left(\mathit{\gamma }\left(t\right)·\mathit{t}\left(t\right)\right)}{2{\left[-2a+\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)\right]}^2}}\mathit{n}\left(t\right)\hfill \\ \hfill & +\left[sgn\left(t^{n-1}\right){\left(\mathit{\gamma }\prime \left(t\right)·\mathit{\gamma }\prime \left(t\right)\right)}^{{\displaystyle \frac{1}{2}}}-f\left(t\right){\displaystyle \frac{4a^2-\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{-4a+2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}\right]\mathit{t}\left(t\right),\hfill \end{array}$$

where $f\left(t\right)$ is the associate function of $\mathit{\gamma }$. If $t_0\in I$ is a singular point of $M_{a^{-}}\left[\mathit{\gamma }\right]\left(t\right),$ then $\left(M_{a^{-}}\left[\mathit{\gamma }\right]\right)\prime \left(t_0\right)=0.$ Namely $t_0$ is a singular point if and only if

$${\displaystyle \frac{2\left[2a-\left(\mathit{\gamma }\left(t_0\right)·\mathit{n}\left(t_0\right)\right)\right]\left(\mathit{\gamma }\left(t_0\right)·\mathit{\gamma }\prime \left(t_0\right)\right)+f\left(t_0\right)\left[4a^2-\left(\mathit{\gamma }\left(t_0\right)·\mathit{\gamma }\left(t_0\right)\right)\right]\left(\mathit{\gamma }\left(t_0\right)·\mathit{t}\left(t_0\right)\right)}{2{\left[-2a+\left(\mathit{\gamma }\left(t_0\right)·\mathit{n}\left(t_0\right)\right)\right]}^2}}=0$$

and

$$sgn\left(t_0^{n-1}\right){\left({\mathit{\gamma }}^{\prime }\left(t_0\right)·\mathit{\gamma }\prime \left(t_0\right)\right)}^{{\displaystyle \frac{1}{2}}}-f\left(t_0\right){\displaystyle \frac{4a^2-\left(\mathit{\gamma }\left(t_0\right)·\mathit{\gamma }\left(t_0\right)\right)}{-4a+2\left(\mathit{\gamma }\left(t_0\right)·\mathit{n}\left(t_0\right)\right)}}=0.$$

When $t_0\ne 0,$ by calculation, we have

$${\displaystyle \frac{4a^2-\left(\mathit{\gamma }\left(t_0\right)·\mathit{\gamma }\left(t_0\right)\right)}{-4a+2\left(\mathit{\gamma }\left(t_0\right)·\mathit{n}\left(t_0\right)\right)}}={\displaystyle \frac{sgn\left(t_0^{n-1}\right){\left({\mathit{\gamma }}^{\prime }\left(t_0\right)·\mathit{\gamma }\prime \left(t_0\right)\right)}^{\frac{1}{2}}}{f\left(t_0\right)}},$$

which means ${\displaystyle {\lambda }_{a^{-}}\left(t_0\right)=\frac{\mathit{\gamma }\prime \left(t_0\right)·\mathit{t}\left(t_0\right)}{f\left(t_0\right)}.}$ Moreover, ${\displaystyle \underset{t\to 0}{lim}\frac{\mathit{\gamma }\prime \left(t\right)·\mathit{t}\left(t\right)}{f\left(t\right)}}$ depends on the relation between n and m, the same as the case for evolutes. By the definition of the evolute of an $(n,m)$-cusp curve, the conclusion holds. The proof for the case of $\lambda ={\lambda }_{a^{+}}$ follows similarly. This completes the proof. □

Example 1.

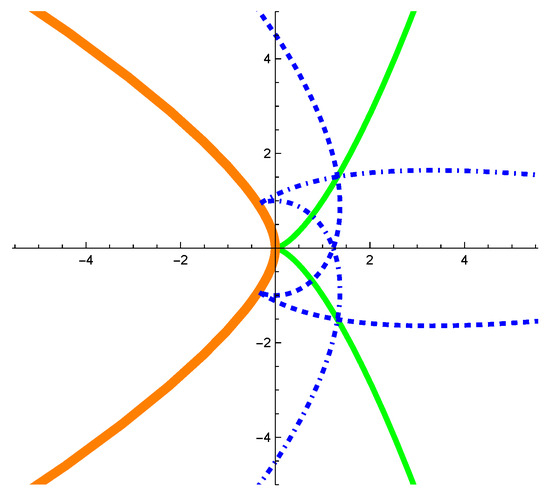
Let $\mathit{\gamma }:(-2,2)\to {\mathbb{R}}^2$ be a $(2,3)$-cusp curve which is defined by $\mathit{\gamma }\left(t\right)=(t^2,t^3).$ It follows that

$$\mathit{n}\left(t\right)={\displaystyle \frac{1}{\sqrt{4+9t^2}}}(-3t,2).$$

Take $a=1,$ and according to Equations (7) and (8), $M_{1^{+}}\left[\mathit{\gamma }\right]\left(t\right)$ and $M_{1^{-}}\left[\mathit{\gamma }\right]\left(t\right)$ are parameterized by

$$M_{1^{+}}\left[\mathit{\gamma }\right]\left(t\right)=\left(t^2+{\displaystyle \frac{-12t+3t^5+3t^7}{4\sqrt{4+9t^2}-2t^3}},t^3+{\displaystyle \frac{4-t^4-t^6}{2\sqrt{4+9t^2}-t^3}}\right)$$

and

$$M_{1^{-}}\left[\mathit{\gamma }\right]\left(t\right)=\left(t^2+{\displaystyle \frac{-12t+3t^5+3t^7}{-4\sqrt{4+9t^2}-2t^3}},t^3+{\displaystyle \frac{4-t^4-t^6}{-2\sqrt{4+9t^2}-t^3}}\right)$$

respectively. By calculation, the evolute of $\mathit{\gamma }$ is parameterized by

$$Ev\left(\mathit{\gamma }\right)\left(t\right)=\left(-t^2-{\displaystyle \frac{9t^4}{2}},{\displaystyle \frac{4t}{3}}+4t^3\right).$$

According to Theorem 1, the singularities of $M_{1^{+}}\left[\mathit{\gamma }\right]\left(t\right)$ and $M_{1^{-}}\left[\mathit{\gamma }\right]\left(t\right)$ both lie on $Ev\left(\mathit{\gamma }\right)\left(t\right)$ (see Figure 3).

Figure 3. The thin curve represents $\mathit{\gamma }\left(t\right)$, the thick curve represents $Ev\left(\mathit{\gamma }\right)\left(t\right),$ the dotdashed curve and the dashed curve represent $M_{1^{+}}\left[\mathit{\gamma }\right]\left(t\right)$ and $M_{1^{-}}\left[\mathit{\gamma }\right]\left(t\right)$, respectively.

We discuss the behavior of the antiorthotomic of an $(n,m)$-cusp curve at the cusp point. Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an $(n,m)$-cusp curve with the modified Frenet–Serret-type frame $\left\{\mathit{\gamma }\right(t);\mathit{t}(t),\mathit{n}(t\left)\right\}$ and $\mathit{\gamma }\left(0\right)=\mathbf{0}.$ If $a=0,$ then the antiorthotomic of $\mathit{\gamma }\left(t\right)$ is given by

$$\begin{array}{c}\hfill M\left[\mathit{\gamma }\right]\left(t\right)=\mathit{\gamma }\left(t\right)-{\displaystyle \frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}\mathit{n}\left(t\right).\end{array}$$

(12)

As $\mathit{\gamma }\left(t\right)$ is an $(n,m)$-cusp curve and $t=0$ being its cusp point, it follows that $(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right))=O\left(t^{2n}\right)$ and $(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right))=O\left(t^m\right),$ where $O\left(t^k\right)$ signifies the infinitesimal of the same order as $t^k$ at $t=0.$ Considering the value of

$$\underset{t\to 0}{lim}-{\displaystyle \frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}},$$

we have

$$\left\{\begin{array}{cc}{\displaystyle \underset{t\to 0}{lim}-\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}=0,}\hfill & \mathrm{m}<2\mathrm{n},\hfill \\ {\displaystyle \underset{t\to 0}{lim}-\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}=c\ne 0,}\hfill & \mathrm{m}=2\mathrm{n},\hfill \\ {\displaystyle \underset{t\to 0}{lim}-\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}=+\infty \mathrm{or}-\infty ,}\hfill & \mathrm{m}>2\mathrm{n}\text{and}\mathrm{m}\text{is}\text{even},\hfill \\ {\displaystyle \underset{t\to 0^{\pm }}{lim}-\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}=\pm \infty \mathrm{or}\mp \infty ,}\hfill & \mathrm{m}>2\mathrm{n}\text{and}\mathrm{m}\text{is}\text{odd}.\hfill \end{array}\right.$$

Consequently:

(1)

When $m<2n,$ the antiorthotomic and $\mathit{\gamma }$ coincide at $t=0,$ meaning

$$M\left[\mathit{\gamma }\right]\left(0\right)=\mathit{\gamma }\left(0\right).$$

(2)

When $m=2n,$ the antiorthotomic coincides with the normal line of $\mathit{\gamma }$ at $t=0,$ which means

$$M\left[\mathit{\gamma }\right]\left(0\right)=\mathit{\gamma }\left(0\right)+c\mathit{n}\left(0\right).$$

(3)

When $m>2n,$ the normal line spanned by $\mathit{n}\left(0\right)$ becomes the asymptotic line of the antiorthotomic. Additionally, if m is even, the two sides of the antiorthotomic approximate the normal line of $\mathit{\gamma }$ infinitely along the same direction at $t=0.$ If m is odd, the two sides of the antiorthotomic approximate the normal line of $\mathit{\gamma }$ infinitely along the opposite direction at $t=0$.

Proposition 1.

Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an $(n,m)$-cusp curve. Suppose that $\mathit{\gamma }\left(0\right)=\mathbf{0}$ and $m<2n$, then $t=0$ is the $(2n-m,n)$-cusp point of the antiorthotomic $M\left[\mathit{\gamma }\right]\left(t\right)$ and $M\left[\mathit{\gamma }\right]\left(0\right)=\mathit{\gamma }\left(0\right)=\mathbf{0}$.

Proof. 

From the above discussion, it follows that $M\left[\mathit{\gamma }\right]\left(0\right)=\mathit{\gamma }\left(0\right)$ if $2n>m.$ According to Equation (12), we have

$$\parallel M\left[\mathit{\gamma }\right]\left(t\right)\parallel =O\left(t^{2n-m}\right).$$

Moreover, we calculate that

$${\left(M\left[\mathit{\gamma }\right]\right)}^{\prime }\left(t\right)=\mathit{\gamma }\prime \left(t\right)+\lambda \prime \left(t\right)\mathit{n}\left(t\right)-\lambda \left(t\right)f\left(t\right)\mathit{t}\left(t\right)$$

and

$$\left(M\left[\mathit{\gamma }\right]\right)″\left(t\right)=\mathit{\gamma }″\left(t\right)+\left(\lambda ″\left(t\right)+\lambda \left(t\right)f^2\left(t\right)\right)\mathit{n}\left(t\right)-\left(2\lambda \prime \left(t\right)f\left(t\right)+\lambda \left(t\right)f\prime \left(t\right)\right)\mathit{t}\left(t\right),$$

where

$$\lambda \left(t\right)=-{\displaystyle \frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}.$$

Thus, we have

$$\parallel \left(M\left[\mathit{\gamma }\right]\right)\prime \left(t\right)\parallel =O\left(t^{2n-m-1}\right)$$

and

$$\begin{array}{cc}\hfill & \det \left(\left(M\left[\mathit{\gamma }\right]\right)\prime \left(t\right),\left(M\left[\mathit{\gamma }\right]\right)″\left(t\right)\right)\hfill \\ \hfill =& \left(\lambda ″\left(t\right)+\lambda \left(t\right)f^2\left(t\right)\right)\parallel \mathit{\gamma }\prime \left(t\right)\times \mathit{n}\left(t\right)\parallel -\left(2\lambda \prime \left(t\right)f\left(t\right)+\lambda \left(t\right)f\prime \left(t\right)\right)\parallel \mathit{\gamma }\prime \left(t\right)\times \mathit{t}\left(t\right)\parallel \hfill \\ \hfill & +\parallel \mathit{\gamma }\prime \left(t\right)\times \mathit{\gamma }″\left(t\right)\parallel +\lambda \prime \left(t\right)\parallel \mathit{\gamma }″\left(t\right)\times \mathit{n}\left(t\right)\parallel -\lambda \left(t\right)f\left(t\right)\parallel \mathit{\gamma }″\left(t\right)\times \mathit{t}\left(t\right)\parallel \hfill \\ \hfill & -2\lambda \prime 2\left(t\right)f\left(t\right)-\lambda \left(t\right)\lambda \prime \left(t\right)f\prime \left(t\right)-\lambda \left(t\right)\lambda ″\left(t\right)f\left(t\right)-{\lambda }^2\left(t\right)f^3\left(t\right)\hfill \\ \hfill =& O\left(t^{3n-m-3}\right).\hfill \end{array}$$

According to [14], $M\left[\mathit{\gamma }\right]\left(t\right)$ is an $(n_e,m_e)$-cusp curve with the cusp point $t=0,$ where

$$\left\{\begin{array}{c}{n}_e-1=2n-m-1,\hfill \\ n_e+m_e-3=3n-m-3.\hfill \end{array}\right.$$

Therefore, we have

$$(n_e,m_e)=(2n-m,n).$$

This completes the proof. □

We provide some examples as follows.

Example 2.

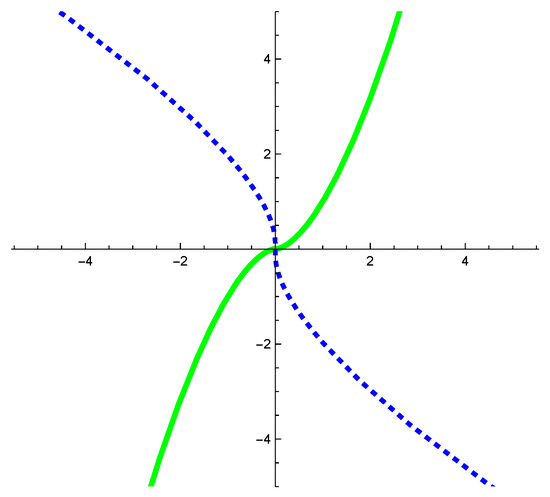
Let $\mathit{\gamma }:(-2,2)\to {\mathbb{R}}^2$ be a $(3,5)$-cusp curve which is defined by $\mathit{\gamma }\left(t\right)=(t^3,t^5).$ It follows that

$$\mathit{n}\left(t\right)={\displaystyle \frac{1}{\sqrt{9+25t^4}}}(-5t^2,3).$$

By Equation (12), we have

$$M\left[\mathit{\gamma }\right]\left(t\right)=\left(-{\displaystyle \frac{t^3}{4}}-{\displaystyle \frac{5t^7}{4}},{\displaystyle \frac{3t}{4}}+{\displaystyle \frac{7t^5}{4}}\right),$$

which is a $(1,3)$-cusp curve. By Proposition 1, $t=0$ is a $(1,3)$-cusp point of $M\left[\mathit{\gamma }\right]\left(t\right)$ and $M\left[\mathit{\gamma }\right]\left(0\right)=\mathit{\gamma }\left(0\right)=\mathbf{0}.$ By calculation, the evolute of $\mathit{\gamma }$ is parameterized by

$$Ev\left(\mathit{\gamma }\right)\left(t\right)=\left(-{\displaystyle \frac{t^3}{2}}-{\displaystyle \frac{25t^7}{6}},{\displaystyle \frac{9t}{10}}+{\displaystyle \frac{7t^5}{2}}\right).$$

For $t=0$, we have $M\left[\mathit{\gamma }\right]\left(0\right)=Ev\left(\mathit{\gamma }\right)\left(0\right)=\mathit{\gamma }\left(0\right)=\mathbf{0}$ (see Figure 4).

Figure 4. The solid curve represents $\mathit{\gamma }\left(t\right),$ and the dashed curve represents $M\left[\mathit{\gamma }\right]\left(t\right)$.

Example 3.

Let $\mathit{\gamma }:(-2,2)\to {\mathbb{R}}^2$ be a $(2,4)$-cusp curve which is defined by

$$\mathit{\gamma }\left(t\right)=\left({\displaystyle \frac{t^2}{2}}+{\displaystyle \frac{t^3}{3}},{\displaystyle \frac{t^4}{4}}+{\displaystyle \frac{t^5}{5}}\right).$$

It follows that

$$\mathit{n}\left(t\right)={\displaystyle \frac{1}{\sqrt{1+t^4}}}(-t^2,1).$$

By Equation (12), we have

$$\begin{array}{cc}\hfill M\left[\mathit{\gamma }\right]\left(t\right)=& \left(-{\displaystyle \frac{t^2{\left(\frac{1}{2}+\frac{t}{3}\right)}^2+t^6{\left(\frac{1}{4}+\frac{t}{5}\right)}^2}{\frac{1}{2}+\frac{4}{15}t}}+{\displaystyle \frac{t^2}{2}}+{\displaystyle \frac{t^3}{3}},{\displaystyle \frac{{\left(\frac{1}{2}+\frac{t}{3}\right)}^2+t^4{\left(\frac{1}{4}+\frac{t}{5}\right)}^2}{\frac{1}{2}+\frac{4}{15}t}}\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{t^4}{4}}+{\displaystyle \frac{t^5}{5}}\right)\hfill \end{array}$$

and

$$M\left[\mathit{\gamma }\right]\left(0\right)=\mathit{\gamma }\left(0\right)+{\displaystyle \frac{1}{2}}(0,1).$$

Since $m=2n,$ the antiorthotomic coincides with the normal line of $\mathit{\gamma }$ at $t=0$ (see Figure 5).

Figure 5. The solid curve represents $\mathit{\gamma }\left(t\right),$ and the dashed curve represents $M\left[\mathit{\gamma }\right]\left(t\right)$.

Example 4.

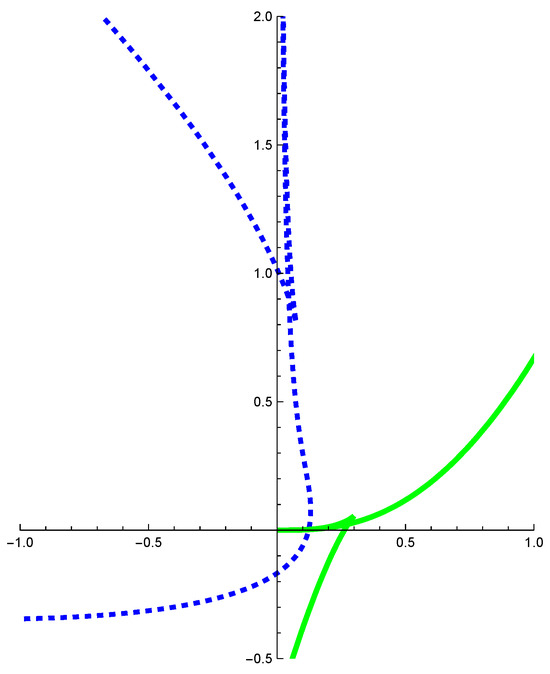
Let $\mathit{\gamma }:(-2,2)\to {\mathbb{R}}^2$ be a $(2,6)$-cusp curve which is defined by

$$\mathit{\gamma }\left(t\right)=\left({\displaystyle \frac{t^2}{2}}+{\displaystyle \frac{t^5}{5}},{\displaystyle \frac{t^6}{6}}+{\displaystyle \frac{t^9}{9}}\right).$$

It follows that

$$\mathit{n}\left(t\right)={\displaystyle \frac{1}{\sqrt{1+t^8}}}(-t^4,1).$$

By Equation (12), we have

$$\begin{array}{cc}\hfill M\left[\mathit{\gamma }\right]\left(t\right)=& \left(-{\displaystyle \frac{{\left(\frac{t}{2}+\frac{t^4}{5}\right)}^2+{\left(\frac{t^5}{6}+\frac{t^8}{9}\right)}^2}{\frac{2}{3}+\frac{8t^3}{45}}}+{\displaystyle \frac{t^2}{2}}+{\displaystyle \frac{t^5}{5}},{\displaystyle \frac{{\left(\frac{1}{2}+\frac{t^3}{5}\right)}^2+{\left(\frac{t^4}{6}+\frac{t^7}{9}\right)}^2}{\frac{2t^2}{3}+\frac{8t^5}{45}}}\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{t^6}{6}}+{\displaystyle \frac{t^9}{9}}\right).\hfill \end{array}$$

Since $m>2n$ and m is even, the two sides of the antiorthotomic approximate the normal line of $\mathit{\gamma }$ infinitely along the same direction at $t=0$ (see Figure 6).

Figure 6. The solid curve represents $\mathit{\gamma }\left(t\right),$ and the dashed curve represents $M\left[\mathit{\gamma }\right]\left(t\right)$.

Example 5.

Let $\mathit{\gamma }:(-2,2)\to {\mathbb{R}}^2$ be a $(3,7)$-cusp curve which is defined by $\mathit{\gamma }\left(t\right)=(t^3,t^7).$ It follows that

$$\mathit{n}\left(t\right)={\displaystyle \frac{1}{\sqrt{9+49t^8}}}(-7t^4,3).$$

By Equation (12), we have

$$M\left[\mathit{\gamma }\right]\left(t\right)=\left({\displaystyle \frac{t^3}{8}}-{\displaystyle \frac{7t^{11}}{8}},{\displaystyle \frac{3}{8t}}+{\displaystyle \frac{11t^7}{8}}\right).$$

Since $m>2n$ and m is odd, the two sides of the antiorthotomic approximate the normal line of $\mathit{\gamma }$ infinitely along the opposite direction at $t=0$ (see Figure 7).

Figure 7. The solid curve represents $\mathit{\gamma }\left(t\right),$ and the dashed curve represents $M\left[\mathit{\gamma }\right]\left(t\right)$.

4. Parallels and $\mathit{a}$-Antiorthotomics of $(\mathit{n},\mathit{m})$-Cusp Curves

In this section, we define parallels of an $(n,m)$-cusp curve and investigate their relationship with a-antiorthotomics. Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an $(n,m)$-cusp curve with the modified Frenet–Serret-type frame $\left\{\mathit{\gamma }\right(t);\mathit{t}(t),\mathit{n}(t\left)\right\}.$ A parallel of $\mathit{\gamma }$ is a curve obtained by moving each point on $\mathit{\gamma }$ along $\mathit{n}\left(t\right)$ by a fixed distance b, which is defined as

$$\begin{array}{c}\hfill {\mathit{\gamma }}_b\left(t\right)=\mathit{\gamma }\left(t\right)+b\mathit{n}\left(t\right).\end{array}$$

(13)

Proposition 2.

Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an $(n,m)$-cusp curve with the modified frame $\left\{\mathit{\gamma }\right(t);\mathit{t}(t),\mathit{n}(t\left)\right\},$ and ${\mathit{\gamma }}_b\left(t\right)$ a parallel of $\mathit{\gamma }\left(t\right).$ Then the singularities of ${\mathit{\gamma }}_b\left(t\right)$ sweep out the evolute of $\mathit{\gamma }\left(t\right).$

Proof. 

By taking the derivative of ${\mathit{\gamma }}_b\left(t\right)$, we have

$$\begin{array}{cc}\hfill {\mathit{\gamma }}_b\prime \left(t\right)& =\mathit{\gamma }\prime \left(t\right)-bf\left(t\right)\mathit{t}\left(t\right)=[sgn\left(t^{n-1}\right){\left(\mathit{\gamma }\prime \left(t\right)·\mathit{\gamma }\prime \left(t\right)\right)}^{{\displaystyle \frac{1}{2}}}-bf\left(t\right)]\mathit{t}\left(t\right),\hfill \end{array}$$

where $f\left(t\right)$ is the associate function. $t_0\in I$ is a singular point if and only if ${\mathit{\gamma }}_b\prime \left(t_0\right)=0.$ Namely, $t_0$ is a singular point if and only if

$$sgn\left(t_0^{n-1}\right){\left({\mathit{\gamma }}^{\prime }\left(t_0\right)·\mathit{\gamma }\prime \left(t_0\right)\right)}^{{\displaystyle \frac{1}{2}}}-bf\left(t_0\right)=0.$$

When $t_0\ne 0,$ by calculation, we have

$$b={\displaystyle \frac{sgn\left(t_0^{n-1}\right){\left(\mathit{\gamma }\prime \left(t_0\right)·\mathit{\gamma }\prime \left(t_0\right)\right)}^{\frac{1}{2}}}{f\left(t_0\right)}},$$

which means ${\displaystyle b=\frac{\mathit{\gamma }\prime \left(t_0\right)·\mathit{t}\left(t_0\right)}{f\left(t_0\right)}.}$ Moreover, ${\displaystyle \underset{t\to 0}{lim}\frac{\mathit{\gamma }\prime \left(t\right)·\mathit{t}\left(t\right)}{f\left(t\right)}}$ depends on the relation between n and m, the same as the case for the evolute. According to the definition of the evolute of an $(n,m)$-cusp curve, the consequent holds. This completes the proof. □

By combining Theorem 1 and Proposition 2, it is observed that the singularities of parallels and a-antiorthotomics both sweep out the evolute of $\mathit{\gamma }$. To further elucidate the relationship between parallels and a-antiorthotomics, we have the following theorem.

Theorem 2.

Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an (n, m)-cusp curve with the modified frame $\left\{\mathit{\gamma }\right(t);\mathit{t}(t),\mathit{n}(t\left)\right\},$ and ${\mathit{\gamma }}_b\left(t\right)$ a parallel of $\mathit{\gamma }\left(t\right).$ Then we have the following assertions:

(1) 

$\mathrm{If}b=2a_1-2a_2,$ then $M_{a_2^{+}}\left[{\mathit{\gamma }}_b\right]\left(t\right)=M_{a_1^{+}}\left[\mathit{\gamma }\right]\left(t\right).$

(2) 

$\mathrm{If}b=-2a_1-2a_2,$ then $M_{a_2^{+}}\left[{\mathit{\gamma }}_b\right]\left(t\right)=M_{a_1^{-}}\left[\mathit{\gamma }\right]\left(t\right).$

(3) 

$\mathrm{If}b=-2a_1+2a_2,$ then $M_{a_2^{-}}\left[{\mathit{\gamma }}_b\right]\left(t\right)=M_{a_1^{-}}\left[\mathit{\gamma }\right]\left(t\right).$

(4) 

$\mathrm{If}b=2a_1+2a_2,$ then $M_{a_2^{-}}\left[{\mathit{\gamma }}_b\right]\left(t\right)=M_{a_1^{+}}\left[\mathit{\gamma }\right]\left(t\right).$

Here $a_1,a_2\ge 0$ are constants.

Proof. 

For the case of $b=2a_1-2a_2,$ according to Equations (6) and (7), we have

$$\begin{array}{cc}\hfill M_{a_2^{+}}\left[{\mathit{\gamma }}_b\right]\left(t\right)& ={\mathit{\gamma }}_b\left(t\right)+{\displaystyle \frac{4a_2^2-\left({\mathit{\gamma }}_b\left(t\right)·{\mathit{\gamma }}_b\left(t\right)\right)}{4a_2+2\left({\mathit{\gamma }}_b\left(t\right)·\mathit{n}\left(t\right)\right)}}\mathit{n}\left(t\right)\hfill \\ & =\mathit{\gamma }\left(t\right)+b\mathit{n}\left(t\right)+{\displaystyle \frac{4a_2^2-\left(\mathit{\gamma }\left(t\right)+b\mathit{n}\left(t\right)·\mathit{\gamma }\left(t\right)+b\mathit{n}\left(t\right)\right)}{4a_2+2\left(\mathit{\gamma }\left(t\right)+b\mathit{n}\left(t\right)·\mathit{n}\left(t\right)\right)}}\mathit{n}\left(t\right)\hfill \\ & =\mathit{\gamma }\left(t\right)+{\displaystyle \frac{{\left(2a_2+b\right)}^2-\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{4a_2+2b+2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}\mathit{n}\left(t\right)\hfill \\ & =\mathit{\gamma }\left(t\right)+{\displaystyle \frac{4a_1^2-\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{4a_1+2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}\mathit{n}\left(t\right)\hfill \\ & =M_{a_1^{+}}\left[\mathit{\gamma }\right]\left(t\right).\hfill \end{array}$$

By the same method, we can demonstrate assertions $\left(2\right),\left(3\right),\left(4\right).$ This completes the proof. □

The following example is provided to illustrate Proposition 2 and Theorem 2.

Example 6.

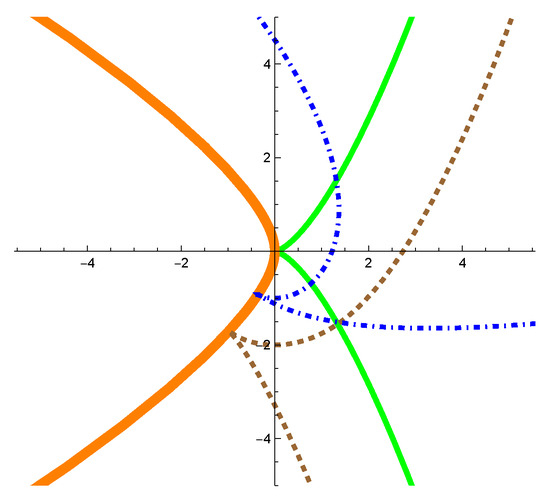
Let $\mathit{\gamma }:(-2,2)\to {\mathbb{R}}^2$ be a $(2,3)$-cusp curve which is defined by $\mathit{\gamma }\left(t\right)=(t^2,t^3).$ Let $a_1=1,a_2=2$ and $b=2a_1-2a_2=-2,$ then the parallel ${\mathit{\gamma }}_{-2}\left(t\right)$ of $\mathit{\gamma }\left(t\right)$ is parameterized by

$${\mathit{\gamma }}_{-2}\left(t\right)=\left(t^2+{\displaystyle \frac{6t}{\sqrt{4+9t^2}}},t^3-{\displaystyle \frac{4}{\sqrt{4+9t^2}}}\right).$$

By calculation, we have

$$M_{2^{+}}\left[{\mathit{\gamma }}_{-2}\right]\left(t\right)=M_{1^{+}}\left[\mathit{\gamma }\right]\left(t\right)=\left(t^2+{\displaystyle \frac{-12t+3t^5+3t^7}{4\sqrt{4+9t^2}-2t^3}},t^3+{\displaystyle \frac{4-t^4-t^6}{2\sqrt{4+9t^2}-t^3}}\right).$$

According to Theorem 2, we also have $M_{2^{+}}\left[{\mathit{\gamma }}_{-2}\right]\left(t\right)=M_{1^{+}}\left[\mathit{\gamma }\right]\left(t\right).$ Moreover, reviewing Example 1, the evolute of $\mathit{\gamma }\left(t\right)$ is parameterized by

$$Ev\left(\mathit{\gamma }\right)\left(t\right)=\left(-t^2-{\displaystyle \frac{9t^4}{2}},{\displaystyle \frac{4t}{3}}+4t^3\right).$$

According to Theorem 1 and Proposition 2, the singularities of $M_{1^{+}}\left[\mathit{\gamma }\right]\left(t\right)$ and ${\mathit{\gamma }}_{-2}\left(t\right)$ both lay on $Ev\left(\mathit{\gamma }\right)\left(t\right)$ (see Figure 8).

Figure 8. The thin curve represents $\mathit{\gamma }\left(t\right)$, the thick curve represents $Ev\left(\mathit{\gamma }\right)\left(t\right),$ the dashed curve represents ${\mathit{\gamma }}_{-2}\left(t\right)$ and the dotdashed curve represents $M_{2^{+}}\left[{\mathit{\gamma }}_{-2}\right]\left(t\right)$(or $M_{1^{+}}\left[\mathit{\gamma }\right]\left(t\right)$).

5. $\mathit{k}$-th Antiorthotomics of $(\mathit{n},\mathit{m})$-Cusp Curves

In this section, we investigate the k-th antiorthotomic of an $(n,m)$-cusp curve, which corresponds to the k-th mirror in the optical system. Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an $(n,m)$-cusp curve with the modified Frenet–Serret-type frame $\left\{\mathit{\gamma }\right(t);\mathit{t}(t),\mathit{n}(t\left)\right\}.$ From now on, we denote the antiorthotomic $M\left[\mathit{\gamma }\right]\left(t\right)$ as $M^1\left[\mathit{\gamma }\right]\left(t\right).$ We delineate two distinct cases as follows.

Case 1: $\mathit{\gamma }\left(t\right)$ does not pass through the origin.

According to Equation (12), the representation of the 2-th antiorthotomic of $\mathit{\gamma }\left(t\right)$ is given by

$$M^2\left[\mathit{\gamma }\right]\left(t\right)=M^1\left[\mathit{\gamma }\right]\left(t\right)-{\displaystyle \frac{\left(M^1\left[\mathit{\gamma }\right]\left(t\right)·M^1\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^1\left[\mathit{\gamma }\right]\left(t\right)·{\mathit{n}}_1\left(t\right)\right)}}{\mathit{n}}_1\left(t\right),$$

where ${\mathit{n}}_1\left(t\right)$ is the modified unit normal vector of $M^1\left[\mathit{\gamma }\right]\left(t\right)$.

Lemma 1.

Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an $(n,m)$-cusp curve with the modified Frenet–Serret-type frame $\left\{\mathit{\gamma }\right(t);\mathit{t}(t),\mathit{n}(t\left)\right\}.$ Then the vector ${\mathit{n}}_1\left(t\right)$ is parallel to $\mathit{\gamma }\left(t\right)$.

Proof. 

By Equation (12), we have

$$\begin{array}{cc}\hfill \left(M^1\left[\mathit{\gamma }\right]\right)\prime \left(t\right)=& -{\displaystyle \frac{2\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\prime \left(t\right)\right)\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)+f\left(t\right)\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)\left(\mathit{\gamma }\left(t\right)·\mathit{t}\left(t\right)\right)}{2{\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}^2}}\mathit{n}\left(t\right)\hfill \\ \hfill & +\mathit{\gamma }\prime \left(t\right)+f\left(t\right){\displaystyle \frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}\mathit{t}\left(t\right),\hfill \end{array}$$

so that

$$\begin{array}{cc}\hfill & \left(\left(M^1\left[\mathit{\gamma }\right]\right)\prime \left(t\right)·\mathit{\gamma }\left(t\right)\right)\hfill \\ \hfill =& -{\displaystyle \frac{2\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\prime \left(t\right)\right)\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)+f\left(t\right)\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)\left(\mathit{\gamma }\left(t\right)·\mathit{t}\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}\hfill \\ \hfill & +\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\prime \left(t\right)\right)+f\left(t\right){\displaystyle \frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)\left(\mathit{\gamma }\left(t\right)·\mathit{t}\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}\hfill \\ \hfill =& 0.\hfill \end{array}$$

This implies that ${\mathit{n}}_1\left(t\right)$ is parallel to $\mathit{\gamma }\left(t\right)$. □

By Lemma 1, it follows from $\mathit{\gamma }\left(t\right)\ne \mathbf{0}$ that

$$\begin{array}{cc}\hfill M^2\left[\mathit{\gamma }\right]\left(t\right)& =M^1\left[\mathit{\gamma }\right]\left(t\right)-{\displaystyle \frac{\left(M^1\left[\mathit{\gamma }\right]\left(t\right)·M^1\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left({\displaystyle M^1\left[\mathit{\gamma }\right]\left(t\right)·\frac{\mathit{\gamma }\left(t\right)}{\parallel \mathit{\gamma }\left(t\right)\parallel }}\right)}}{\displaystyle \frac{\mathit{\gamma }\left(t\right)}{\parallel \mathit{\gamma }\left(t\right)\parallel }}\hfill \\ \hfill & =M^1\left[\mathit{\gamma }\right]\left(t\right)-{\displaystyle \frac{\left(M^1\left[\mathit{\gamma }\right]\left(t\right)·M^1\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^1\left[\mathit{\gamma }\right]\left(t\right)·\mathit{\gamma }\left(t\right)\right)}}\mathit{\gamma }\left(t\right).\hfill \end{array}$$

By repeating this process, we can obtain the k-th antiorthotomic of $\mathit{\gamma }\left(t\right)$ as follows:

$$\begin{array}{c}\hfill M^k\left[\mathit{\gamma }\right]\left(t\right)=M^{(k-1)}\left[\mathit{\gamma }\right]\left(t\right)-{\displaystyle \frac{\left(M^{(k-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(k-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^{(k-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(k-2)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}{M}^{(k-2)}\left[\mathit{\gamma }\right]\left(t\right),\end{array}$$

(14)

where $k=2,3,4,···$ and $M^0\left[\mathit{\gamma }\right]\left(t\right)$ denotes $\mathit{\gamma }\left(t\right)$. More precisely, we have the following theorem.

Theorem 3.

With the above notations and conditions, we have the following relationship:

$$\begin{array}{c}\hfill M^k\left[\mathit{\gamma }\right]\left(t\right)=M^{(k-1)}\left[\mathit{\gamma }\right]\left(t\right)-{\displaystyle \frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{4{\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}^2}}{M}^{(k-2)}\left[\mathit{\gamma }\right]\left(t\right),(k=2,3,4,···).\end{array}$$

(15)

Proof. 

According to Equation (14), we just need to prove

$$\begin{array}{c}\hfill {\displaystyle \frac{\left(M^k\left[\mathit{\gamma }\right]\left(t\right)·M^k\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^k\left[\mathit{\gamma }\right]\left(t\right)·M^{(k-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}={\displaystyle \frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{4{\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}^2}}\end{array}$$

(16)

holds for $k=1,2,3···.$ Let $k=1$, and we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\left(M^1\left[\mathit{\gamma }\right]\left(t\right)·M^1\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^1\left[\mathit{\gamma }\right]\left(t\right)·\mathit{\gamma }\left(t\right)\right)}}\hfill \\ \hfill =& {\displaystyle \frac{\left({\displaystyle \mathit{\gamma }\left(t\right)-\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}\mathit{n}\left(t\right)}\right)·\left({\displaystyle \mathit{\gamma }\left(t\right)-\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}\mathit{n}\left(t\right)}\right)}{2\left({\displaystyle \mathit{\gamma }\left(t\right)-\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}\mathit{n}\left(t\right)}\right)·\mathit{\gamma }\left(t\right)}}\hfill \\ \hfill =& {\displaystyle \frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{4{\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}^2}}.\hfill \end{array}$$

Thus, Equation (16) is valid for $k=1.$ We assume that Equation (16) holds for $k\le l,$ then we have

$${\displaystyle \frac{\left(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^l\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}={\displaystyle \frac{\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-2)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}={\displaystyle \frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{4{\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}^2}}.$$

It follows that

$$\left(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^l\left[\mathit{\gamma }\right]\left(t\right)\right)={\displaystyle \frac{\left(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}{\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-2)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}.$$

By Equation (14), we have

$$M^l\left[\mathit{\gamma }\right]\left(t\right)=M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)-{\displaystyle \frac{\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-2)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}{M}^{(l-2)}\left[\mathit{\gamma }\right]\left(t\right).$$

Therefore,

$$\begin{array}{cc}\hfill & (M^l\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right))\hfill \\ \hfill =& -{\displaystyle \frac{\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-2)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-2)}\left[\mathit{\gamma }\right]\left(t\right)\right)\hfill \\ \hfill & +\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right).\hfill \end{array}$$

Thus, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{(M^{(l+1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l+1)}\left[\mathit{\gamma }\right]\left(t\right))}{2(M^{(l+1)}\left[\mathit{\gamma }\right]\left(t\right)·M^l\left[\mathit{\gamma }\right]\left(t\right))}}\hfill \\ \hfill =& {\displaystyle \frac{{\displaystyle M^l\left[\mathit{\gamma }\right]\left(t\right)-\frac{(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^l\left[\mathit{\gamma }\right]\left(t\right))}{2(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right))}{M}^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)}}{2\left({\displaystyle M^l\left[\mathit{\gamma }\right]\left(t\right)-\frac{(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^l\left[\mathit{\gamma }\right]\left(t\right))}{2(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right))}{M}^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)}\right)·M^l\left[\mathit{\gamma }\right]\left(t\right)}}\hfill \\ \hfill & ·\left(M^l\left[\mathit{\gamma }\right]\left(t\right)-{\displaystyle \frac{(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^l\left[\mathit{\gamma }\right]\left(t\right))}{2(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right))}}{M}^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)\hfill \\ \hfill =& {\displaystyle \frac{\left(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^l\left[\mathit{\gamma }\right]\left(t\right)\right)\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}{4{\left(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}^2}}\hfill \\ \hfill =& {\displaystyle \frac{\left(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right){\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}^2}{4{\left(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}^2\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-2)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}\hfill \\ \hfill =& {\displaystyle \frac{\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-2)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}·{\displaystyle \frac{\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^l\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}\hfill \\ \hfill =& {\displaystyle \frac{\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^{(l-1)}\left[\mathit{\gamma }\right]\left(t\right)·M^{(l-2)}\left[\mathit{\gamma }\right]\left(t\right)\right)}}\hfill \\ \hfill =& {\displaystyle \frac{\left(\mathit{\gamma }\right(t)·\mathit{\gamma }(t\left)\right)}{4{(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right))}^2}}.\hfill \end{array}$$

It means that Equation (16) holds for $k=l+1,$ thereby concluding the proof. □

Case 2: $\mathit{\gamma }\left(t\right)$ passes through the origin. We study the k-th antiorthotomic $M^k\left[\mathit{\gamma }\right]\left(t\right)$ subdividing into two cases based on whether the origin corresponds to the cusp point of $\mathit{\gamma }\left(t\right)$.

Case 2a: $\mathit{\gamma }\left(0\right)\ne \mathbf{0}$. We assume that $\mathit{\gamma }\left(t_0\right)$ is the origin and $k\ge 2$.

When $t\ne t_0,$ the expression for $M^k\left[\mathit{\gamma }\right]\left(t\right)$ remains Equation (15).

When $t=t_0,$$M^k\left[\mathit{\gamma }\right]\left(t_0\right)$ depends on the value of ${\displaystyle \underset{t\to t_0}{lim}\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{4{\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}^2}.}$ Specifically,

(1)

if ${\displaystyle \underset{t\to t_0}{lim}\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{4{\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}^2}=0,}$ then $M^k\left[\mathit{\gamma }\right]\left(t_0\right)=\mathit{\gamma }\left(t_0\right)$;

(2)

if ${\displaystyle \underset{t\to t_0}{lim}\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{4{\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}^2}=c,}$ then $M^k\left[\mathit{\gamma }\right]\left(t_0\right)=M^{(k-1)}\left[\mathit{\gamma }\right]\left(t_0\right)-c{M}^{(k-2)}\left[\mathit{\gamma }\right]\left(t_0\right)$;

(3)

if ${\displaystyle \underset{t\to t_0}{lim}\frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{4{\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}^2}=\infty ,}$ then $M^k\left[\mathit{\gamma }\right]\left(t_0\right)$ does not exist.

Case 2b: $\mathit{\gamma }\left(0\right)=\mathbf{0}$. The following theorem characterizes the relationship between $M^k\left[\mathit{\gamma }\right]\left(t\right)$ and $\mathit{\gamma }\left(t\right)$ at the cusp point $t=0$.

Theorem 4.

Let $\mathit{\gamma }:I\to {\mathbb{R}}^2$ be an (n, m)-cusp curve and $\mathit{\gamma }\left(0\right)=\mathbf{0}$. If $m<2n$, then $t=0$ is a $\left((k+1)n-km,kn-(k-1)m\right)$-cusp point of $M^k\left[\mathit{\gamma }\right]\left(t\right)$ and $M^k\left[\mathit{\gamma }\right]\left(0\right)=\mathbf{0},$ where $1\le k<{\displaystyle \frac{n}{m-n}}$ is a positive integer.

Proof. 

Since $m,n\in {\mathbb{N}}^{+}$ and $n<m<2n,$ there must exist a unique $i\in {\mathbb{N}}^{+}$ such that

$${\displaystyle \frac{n}{m-n}}-1\le i<{\displaystyle \frac{n}{m-n}}.$$

It is equivalent to

$$\left\{\begin{array}{c}(i+1)n>im,\hfill \\ (i+2)n\le (i+1)m.\hfill \end{array}\right.$$

Proposition 1 implies that for $k=1,t=0$ is a $(2n-m,n)$-cusp point of $M^1\left[\mathit{\gamma }\right]\left(t\right)$ and $M^1\left[\mathit{\gamma }\right]\left(0\right)=\mathbf{0}$. This confirms that the consequent holds for $k=1.$ If $i\ge 2$, assume the consequent holds for $k\le i-1,$ then $t=0$ is an $\left(in-(i-1)m,(i-1)n-(i-2)m\right)$-cusp point of $M^{(i-1)}\left[\mathit{\gamma }\right]\left(t\right)$ and $M^{(i-1)}\left[\mathit{\gamma }\right]\left(0\right)=\mathbf{0}.$ Since

$$2[in-(i-1\left)m\right]-\left[\right(i-1)n-(i-2\left)m\right]=(i+1)n-im>0,$$

it follows again from Proposition 1 that $t=0$ is an $\left((i+1)n-im,in-(i-1)m\right)$-cusp point of $M^i\left[\mathit{\gamma }\right]\left(t\right)$ and $M^{\left(i\right)}\left[\mathit{\gamma }\right]\left(0\right)=\mathbf{0}.$ Thus, the consequent holds for $k=i.$ Moreover, because

$$2\left[\right(i+1)n-im]-[in-(i-1\left)m\right]=(i+2)n-(i+1)m\le 0.$$

By the analysis before Proposition 1, we obtain that $M^{(i+1)}\left[\mathit{\gamma }\right]\left(0\right)\ne \mathbf{0},$ which means that the consequent does not hold for $k=i+1.$ This completes the proof. □

The above theorem shows that the number of repeated antiorthotomics of $\mathit{\gamma }$ is entirely determined by m and $n.$ We provide an example to demonstrate Theorem 4.

Example 7.

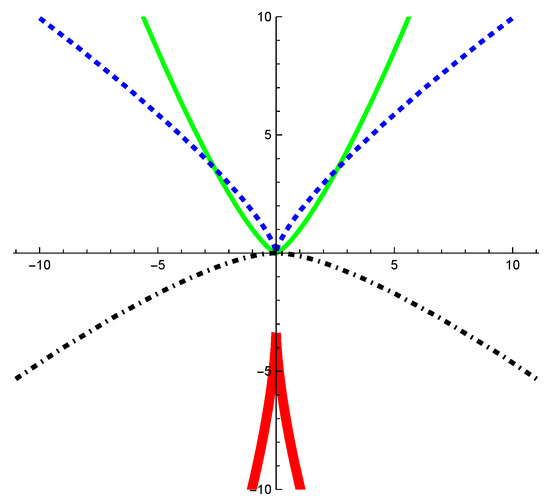
Let $\mathit{\gamma }:(-2,2)\to {\mathbb{R}}^2$ be a $(3,4)$-cusp curve which is defined by $\mathit{\gamma }\left(t\right)=(t^3,t^4).$ Since ${\displaystyle \frac{n}{m-n}}=3,$ then $i=2$ follows. By Theorem 4, $M^1\left[\mathit{\gamma }\right]\left(t\right)$ and $M^2\left[\mathit{\gamma }\right]\left(t\right)$ have cusp points at $t=0.$ By calculation, we have

$$\mathit{n}\left(t\right)={\displaystyle \frac{1}{\sqrt{9+16t^2}}}(-4t,3).$$

Then $M^1\left[\mathit{\gamma }\right]\left(t\right)$ is obtained as follows:

$$\begin{array}{cc}\hfill M^1\left[\mathit{\gamma }\right]\left(t\right)& =\mathit{\gamma }\left(t\right)-{\displaystyle \frac{\left(\mathit{\gamma }\left(t\right)·\mathit{\gamma }\left(t\right)\right)}{2\left(\mathit{\gamma }\left(t\right)·\mathit{n}\left(t\right)\right)}}\mathit{n}\left(t\right)=\left(-t^3-2t^5,{\displaystyle \frac{3t^2}{2}}+{\displaystyle \frac{5t^4}{2}}\right),\hfill \end{array}$$

which is a $(2,3)$-cusp curve. By Theorem 4, it is also known that $M^1\left[\mathit{\gamma }\right]\left(t\right)$ is a $(2,3)$-cusp curve at $t=0$ and $M^1\left[\mathit{\gamma }\right]\left(0\right)=\mathbf{0}$. By the representation of $M^1\left[\mathit{\gamma }\right]\left(t\right)$, we calculate that

$${\mathit{n}}_1\left(t\right)={\displaystyle \frac{1}{\sqrt{1+t^2}}}(-1,-t).$$

Then $M^2\left[\mathit{\gamma }\right]\left(t\right)$ is parameterized by

$$\begin{array}{cc}\hfill M^2\left[\mathit{\gamma }\right]\left(t\right)& =M^1\left[\mathit{\gamma }\right]\left(t\right)-{\displaystyle \frac{\left(M^1\left[\mathit{\gamma }\right]\left(t\right)·M^1\left[\mathit{\gamma }\right]\left(t\right)\right)}{2\left(M^1\left[\mathit{\gamma }\right]\left(t\right)·{\mathit{n}}_1\left(t\right)\right)}}{\mathit{n}}_1\left(t\right)\hfill \\ \hfill & =\left(-{\displaystyle \frac{9t}{4}}-{\displaystyle \frac{29t^3}{4}}-6t^5,-{\displaystyle \frac{3t^2}{4}}-{\displaystyle \frac{15t^4}{4}}-4t^6\right),\hfill \end{array}$$

which is a $(1,2)$-cusp curve. It also follows from Theorem 4 that $M^2\left[\mathit{\gamma }\right]\left(t\right)$ is a $(1,2)$-cusp curve at $t=0$ and $M^2\left[\mathit{\gamma }\right]\left(0\right)=\mathbf{0}$. Moreover, we calculate $M^3\left[\mathit{\gamma }\right]\left(t\right)$ as follows:

$$M^3\left[\mathit{\gamma }\right]\left(t\right)=\left({\displaystyle \frac{7t^3}{2}}+{\displaystyle \frac{21t^5}{2}}+8t^7,-{\displaystyle \frac{27}{8}}-{\displaystyle \frac{63t^2}{4}}-{\displaystyle \frac{203t^4}{8}}-14t^6\right),$$

and it is clear that $M^3\left[\mathit{\gamma }\right]\left(0\right)\ne \mathbf{0}$ (see Figure 9).

Figure 9. The thin curve represents $\mathit{\gamma }\left(t\right),$ the dashed curve represents $M^1\left[\mathit{\gamma }\right]\left(t\right),$ the dotdashed curve represents $M^2\left[\mathit{\gamma }\right]\left(t\right),$ the thick curve represents $M^3\left[\mathit{\gamma }\right]\left(t\right)$.

6. Conclusions

In this paper, we have introduced generalized antiorthotomics of $(n,m)$-cusp curves in the plane. We have then investigated the singular property of generalized antiorthotomics. Since evolutes and parallels can be explained as caustics and wavefronts, respectively, from the viewpoint of Legendrian singularity theory, we have established the connections between evolutes, parallels and generalized antiorthotomics. At last, we have studied the behavior of k-th antiorthotomics of $(n,m)$-cusp curves which correspond to the multi-mirror in optics.