Abstract
We study Thurstone-motivated paired comparison models from the perspective of data evaluability, focusing on cases where datasets cannot be directly evaluated. Despite this limitation, such datasets may still contain extractable information. Three main strategies are known in the literature: increasing the number of options, inserting artificial data through perturbation methods, and requesting new real comparisons. We propose a new approach closely related to the latter two. We analyze the structure of the data and introduce the concept of the optimal limit point, related to the supremum of the log-likelihood function. We prove a theorem for determining optimal limit points based on the data structure, which characterizes the information content of the available dataset. We also prove a theorem linking optimal limit points to the limiting behavior of evaluation results obtained via perturbations, thereby explaining why different perturbation methods may yield different outcomes. In addition, we propose a new perturbation method that adds the minimum possible amount of artificial data. Furthermore, the method identifies the most informative object pairs for new real comparisons, enabling a full evaluation of the dataset.
MSC:
62C86; 90B50; 62J15
1. Introduction
Deep learning is among the most popular evaluation methods. Excellent surveys that detail both the methods and their applications include, for example, [1,2,3]. The range of applications is extremely broad, including image processing [4], speech recognition [5], traffic prediction [6], healthcare [7], recommender systems [8], and weather forecasting [9], among others. A common feature of these methods is the requirement for relatively large amounts of data to ensure reliable performance.
Despite the widespread use of neural networks, relatively few papers have been published on their application to ranking problems [10]. In [11], the authors compared the performance of paired (pairwise) comparison methods and a deep learning approach in the context of the top European football leagues. They concluded that, when ranking the leagues separately, all paired comparison methods and the neural network performed well. However, for the aggregated ranking, the deep learning method was limited due to the small amount of available data, whereas the paired comparison methods remained effective. Although deep learning methods hold fantastic potential and their development is explosively fast, at the current stage of research, they cannot replace specialized evaluation methods in cases of a small amount of data.
Pairwise comparisons are common in practical applications when the amount of data is limited. They are frequently applied in decision making [12,13], education [14,15], politics [16,17], healthcare [18,19], psychology [20,21], economy [22], social sciences [23,24], architecture [25], and even in sports performance evaluation [11,26]. One can find numerous further applications in the new book by Mazurek [27] as well.
The most frequently used paired comparison method is based on pairwise comparison matrices (PCMs). The most commonly used variant is the analytic hierarchy process [28,29]. In this method, the verbal decisions are converted into the numbers 1, 3, 5, 7, 9, and their reciprocals, and the resulting reciprocal symmetric PCM is evaluated by the eigenvector method [30] or by the logarithmic least squares methods [31]. In the methods based on the PCMs, one of the key issues is the consistency/inconsistency of the data. Various methods have been developed to measure inconsistency [32,33], and reducing inconsistency is also the subject of many publications [27,34].
Another branch of paired comparison models has a stochastic background. These models are inspired by Thurstone’s idea [35]; we call them Thurstone-motivated models. The original assumptions have been generalized in many ways: the distribution of the latent random variables [36,37,38]; the number of options that can be chosen in decisions [39,40,41,42]; incorporation of home-field advantage [43,44]; consideration of time effects [45]; and so on. The model parameters are estimated based on the comparison results. The most preferable parameter estimation method is the maximum likelihood estimation (MLE) method, which has favorable asymptotic properties and additional benefits, such as constructing confidence intervals and testing hypotheses [46]. However, when applying maximum likelihood estimation, it is necessary to determine whether the likelihood function attains its maximum value and whether the maximizing argument is unique. This requires analyzing the likelihood function—or its logarithm—from the perspective of mathematical analysis, as done in [47,48]. If the maximum value is attained and the argument is unique, we obtain a unique strength value for each object and a unique ranking based on the comparison data. We refer to this case as evaluable data.
Nevertheless, sometimes there are cases when the data derived from pairwise comparisons cannot be evaluated, meaning that the strengths of individual objects to be evaluated cannot be determined definitively based on the data. From a mathematical perspective, this occurs when the maximum value of the likelihood function is not attained, or when it is attained at multiple arguments. We refer to this scenario as having non-evaluable data. However, even in such cases, the data contain information that we would like to extract. For example, we might possess relevant information about the relative positions of certain objects within a ranking or rating. To ensure evaluability, additional information must be introduced into the system. There are three different approaches to achieve this: modifying the model for another option number, inserting artificial comparison results, or requesting additional real comparisons and incorporating their results into the data.
The first case—that is, changing the number of options—can sometimes be implemented, while in other cases it cannot. For example, if we are evaluating the results of a sports tournament, it may be feasible to increase or decrease the option number. If we distinguish between ‘much better’ and ‘slightly better’ options instead of simply ‘better’; we introduce additional information. When evaluating opinions gathered through questionnaires, the possible responses determine the maximum number of options. The number of options cannot be increased; although it can be decreased, this does not improve evaluability. The potential method of ensuring evaluability by changing the number of options is analyzed in [49].
The second case—i.e., making artificial data supplements—is called data perturbation. It was considered in the papers of Conner and Grant [50] and Yan [51] in the case of two- and three-option Bradley–Terry models. The original data do not contain all the information about the complete system, but by making the data evaluable, some of the information (e.g., partial information about ranking—about subsets) can be extracted. The insertion of new data is intended to address this task. Data modification can be performed in several ways. It is a natural requirement to make as few modifications as possible. However, this approach only allows for limited information retrieval. As it turns out, by analyzing the structure of the dataset, we can still extract information about some of the entities. However, for other entities, sometimes nothing definitive can be stated.
Although [50,51] proved the convergence of the evaluation results obtained by their perturbation methods, they did not provide the values of the limits. Moreover, different perturbation techniques may yield different results, even in their limits. This is surprising, as the log-likelihood function was modified only slightly in each case. It is also unsettling: What causes these different limits? The reason for this phenomenon has not yet been explored. Under what conditions do different perturbation methods produce the same or different evaluation results in their limits? What information can be extracted from the available dataset?
To address this, we investigate the supremum rather than the maximum of the log-likelihood function and introduce the concept of the optimal limit point. Based on a detailed analysis of the data structure, we determine the optimal limit point(s). These, together with the data structure, capture all information contained in the available dataset. We clarify the conditions under which the optimal limit point is unique and when it is not. Our results apply to a wide class of distributions for the differences of the latent random variables. Moreover, we prove a theorem that establishes a connection between optimal limit points and perturbation methods, thereby explaining why different perturbation methods may lead to different results in their limits.
The third case, to enlarge the data set, i.e., requesting further real comparison results, is the most natural approach, but it is sometimes impossible. In cases of completed, previously conducted studies, or even the evaluation of sports championships, obtaining new data is not always possible. If it is still possible to obtain additional data, it matters how many comparisons we request. Moreover, it is very useful to know which pairs are worth comparing. The structural analysis of the available data and the elaborated new perturbation algorithm also answer this problem.
In addition to generalizing the scope of applicability of previously published perturbation methods, this paper presents four main contributions in information extraction in case of non-evaluable data: (a) analyzing the data structure; (b) introducing the concept of the optimal limit point, which characterizes the information contained in the dataset; (c) establishing a connection between this new concept and perturbation methods; and (d) developing a new algorithm for determining the optimal supplements in terms of inserted edges or additional comparisons.
The structure of the paper is as follows: Section 2 summarizes the model under investigation and presents the necessary and sufficient condition for data evaluability. Section 3 contains the analysis of the data structure. On the one hand, it is the basis of the theoretical results in Section 6, containing the determination of the optimal limit points and theoretical results between the perturbation methods and the optimal limit points. On the other hand, data structure analysis the basis of a new special perturbation method, named S. Section 4 presents the perturbation methods known from the literature, along with a simple modification (M) and a new algorithm (S) based on the structural analysis of the data. Section 5 presents some interesting special examples of different data structures, along with perturbation algorithms. Section 7 contains numerical results related to different methods of data supplementation, highlighting the properties of the individual methods. In Section 8, the results of a tennis tournament are analyzed, serving as an interesting application of the findings presented in the paper. Finally, the paper concludes with a short summary.
2. The Investigated Model
Let us denote the objects to be evaluated by the numbers . The Thurstone-motivated models have a stochastic background; it is assumed that the current performances of the objects are random variables denoted by , for , with the expectations . These expectations are the strengths of the objects. Decisions comparing two objects i and j are related to the difference between these latent random variables, i.e., . We can separate the expectations as follows:
where are independent identically distributed random variables with the common cumulative distribution function (c.d.f.) F. F is assumed to be three times continuously differentiable, where . The probability density function of F is , which is symmetric to zero (i.e., , ). Moreover, the logarithm of f is strictly concave. The set of these c.d.f.s is denoted by . Logistic distribution and Gaussian distribution belong to this set, among many other distributions. If is Gaussian-distributed, then we call it the Thurstone model [35]. If the distribution F is logistic, i.e.,
we speak about the Bradley–Terry model [36].
We note that the assumption of a common cumulative distribution function F is usual in the literature. From a mathematical point of view, one could assume a specific c.d.f. for each pair , with the only requirement being that . Such a model is investigated in [37].
The simplest model in terms of structure is the two-option model. In the case of the two-option model, the differences are compared to zero: the decision ‘better’/‘worse’ (relating i to j) indicates whether the difference (1) is positive or negative, respectively. The set of real numbers is divided into two disjoint parts by the point zero. If the difference of the latent random variables is negative, then the object i is ‘worse’ than object j, while if , then i is ‘better’ than j. Denote the possible options by , . Figure 1 represents the intervals of the set of real numbers belonging to the decisions.
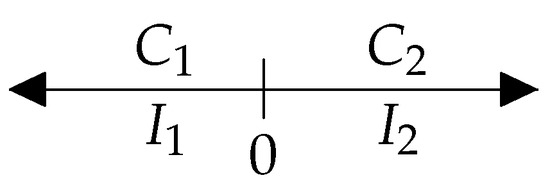
Figure 1.
The options in decisions and the intervals belonging to them in a two-option model.
If only two options are allowed, then the probabilities of ‘worse’ and ‘better’ can be expressed as
and
respectively.
The data are included in a three-dimensional () data matrix A. Its elements represent the number of comparisons in which decision is the outcome when objects i and j are compared. In detail, is the number of comparisons when object i is ‘worse’ than object j, while is the number of comparisons when object i is ‘better’ than object j. Of course, for , and . Assuming independent decisions, the likelihood function is
The log-likelihood function, denoted by , is the logarithm of the above and is given by
One can see that the likelihood Function (5), and also the log-likelihood Function (6), depend only on the differences of the parameters ; hence, one parameter (or the sum of all parameters) can be fixed. Let us fix . The maximum likelihood estimation of the parameters is the argument at the maximum value of (5), or equivalently, of (6); that is,
Introduce notation
We will refer to them as weights to distinguish this exponential form from the original one. If the distributions of the differences are logistic, then Equations (3) and (4) can be written in the following equivalent form:
The log-likelihood function is
which has to be maximized under the conditions
Explicitly, the maximum likelihood estimate of the parameter vector is given by
This is the standard form of the two-option Bradley–Terry model [36]. We note that the maximum can also be found under the constraint .
To find the maximum value of Function (6) or (11), it is not necessary for to be integer-valued. This fact will be used in the perturbation step when the original data matrices A are transformed into matrices with nonnegative elements.
We note that every additive term in (6) and (11) is negative, or, if , is zero. Therefore, the log-likelihood function itself can only take negative values under the constraint or (12), respectively. The log-likelihood function has a finite supremum, which can be negative or zero. The limits of some terms in (6) and (11) can be zero if for some indices i, or, equivalently, if for some indices i, respectively.
In this parameter estimation method, the key issue is the existence of the maximum value and the uniqueness of its argument. If the maximum is not attained, we cannot provide the estimated values. If the argument is not unique, we cannot determine which of the values should be chosen as the estimate. The existence and the uniqueness are guaranteed by the Theorem 1, proved in [47], for the Bradley–Terry model and in [48] for general distributions. To present it, let us first introduce the following definitions.
Definition 1
(Graph of comparisons defined by data set A). Let the objects to be evaluated be the nodes of the graph . There exists an undirected edge between nodes i and j () if .
Definition 2
(Directed graph defined by data set A). Let the objects to be evaluated be the nodes of the graph . There exists a directed edge between nodes i and j, directed from i to j (), if .
It may happen that there is a directed edge from i to j and also a directed edge from j to i.
We note that if the graph is not connected, then the data set A is non-evaluable, since the maximum, if it is attained, can be reached at multiple arguments. Even if is connected, it is still possible that A is non-evaluable; see Examples 1–3. We now present the criterion for data evaluability.
Theorem 1
If the graph is strongly connected, then the graph is also connected. In the case of a two-option model, there are two possible reasons why the data set may not be evaluable: (1) the graph is not connected, meaning that there are separate components that are not compared with other parts; or, (2) there exists an object, or a subset of objects, that has only one-way comparison results—either always ‘better’ or always ‘worse’—with respect to all other objects or subsets. These issues are examined and analyzed in Section 3.
3. Data Structure Analysis
First, consider the connected subgraphs of that cannot be enlarged. These subgraphs will be called maximal connected subgraphs. These will be denoted by , where is the number of the maximal connected subgraphs of . It is clear that there is no edge between the nodes belonging to different maximal connected subgraphs, and . If , then the graph is connected. If , there is no comparison between the elements of the different maximal connected subgraphs; therefore, there is no information about how the strengths of the objects in different subgraphs relate to each other. Yan did not address this case. We also mainly focus on the case where .
Second, consider the strongly connected components of the maximal connected subgraphs—that is, those strongly connected subgraphs that cannot be enlarged. Let u denote the index of a maximal connected subgraph, where . Furthermore, let the strongly connected components of be denoted by , where , and denotes the number of strongly connected components of the maximal connected subgraph . We define a ’supergraph’ corresponding to based on the edges between nodes in different strongly connected components. This supergraph characterizes the relationships among the strongly connected components of . Essentially, we merge the nodes within each component and remove the edges between them. The edges between the nodes of the supergraph are then defined corresponding to the edges between the nodes in the different strongly connected components, as if merging them too. The supergraph characterizes the relations among the strongly connected components of . For the sake of simplicity, we denote the maximal connected subgraphs by X.
Definition 3
(The supergraph characterizing the directed connections in a maximal connected subgraph). Let X be a maximal connected subgraph of , and let be the directed graph consisting of the nodes in X and the original directed edges between them. Denote the strongly connected components of by , …, , where is the number of strongly connected components in . The supergraph , corresponding to X, consists of nodes, referred to as super-nodes. Two super-nodes a and b (with ) are connected by a directed super-edge from a to b if there exists an object and such that . The edge from a to b is called an outgoing edge from a and an incoming edge to b.
We make the following observations:
- A
- The connection between two super-nodes can only be one-way.If there are multiple edges between the elements of different strongly connected components, then they must all have the same direction. If directed edges exist in both directions between two super-nodes, then there would exist elements in the two strongly connected components such that , with and . This implies that , which contradicts the assumption that and are distinct strongly connected components.
- B
- The supergraph does not contain a directed cycle; that is, it is acyclic.If there was a directed cycle in the supergraph, let us denote it by , with . Find those object pairs of the form between which there exist directed edges in that generate the edges of the supergraph. This means that and are elements of the strongly connected component corresponding to the super-node . The upper indices ‘(out)’ and ‘(in)’ indicate the direction of the edges; moreover, , and . In each strongly connected component, there is a directed path between any two elements; in particular, and for are connected via a directed edge. Consequently, starting from , we can find a directed cycle in that includes objects from different strongly connected components, which leads to a contradiction.
- C
- The supergraph is not strongly connected. If we omit the directions of the edges between the super-nodes of the supergraph and we replace the directed edges with undirected ones, the obtained undirected graph is connected through these undirected edges.If the supergraph was strongly connected, it would contain a cycle. The connected property is the consequence of the connectedness of X.
- D
- There exists at least one super-node in the supergraph that has only an outgoing super-edge.Assume the opposite of the statement. This means that every super-node has either only incoming super-edges or both incoming and outgoing super-edges. It is not possible that all super-nodes have only incoming super-edges, since each incoming super-edge must also be an outgoing super-edge for another super-node.If every super-node has both incoming and outgoing super-edges, then start from such a super-node and find the super-node from which it has an incoming super-edge. This new super-node must also have an incoming super-edge. This is because, by assumption, the set of super-nodes with only outgoing super-edges is empty, and the current node cannot belong to the set of super-nodes with only incoming super-edges, since it has an outgoing super-edge.Repeat this process until the set of selectable super-nodes is exhausted, i.e., you must choose a super-node that has already appeared, thereby forming a directed cycle—again contradicting condition C. Hence, the original statement D must be true.
Now, we can define the levels of the super-nodes of the supergraph by the following algorithm. Level 0, called top level, contains the super-nodes that have only outgoing edges. We note that there are no connections between these super-nodes because they all have only outgoing edges. Now, remove these super-nodes from the supergraph along with their outgoing edges. If there are super-nodes that have not yet been classified into a level, there must be super-nodes in the remaining part of the supergraph that have no edges or have only outgoing edges. If the th level (for ) has been constructed, then these latter super-nodes will form the ith level. The process continues until all super-nodes are classified into a level.
If there is more than one maximal connected subgraph, then each of them gives rise to a separate supergraph. These supergraphs are disconnected from one another.
Examples illustrating the levels in the supergraph are contained in Section 5.
A very similar levelization process, applied in genetics, is presented in [52].
4. Perturbation Methods
4.1. Previously Defined Perturbation Methods and a Modification
First, Conner and Grant published a paper [50] dealing with the idea that every data set can be evaluable if every comparison data is increased by a value. In this case, the perturbed data matrix will be denoted by , and its elements—the perturbed data—are as follows:
Definition 4
(Perturbation by Conner and Grant denoted by C).
Regardless of the data matrix A, perturbation C inserts data. Now, we can formulate the following statement.
Theorem 2.
Let . Then, the perturbed data matrix is evaluable.
Proof.
Regardless of the matrix A, the graph of connection is a complete comparison graph, and is a complete directed comparison graph. Recalling Theorem 1, the statement is obvious. □
We note that Conner and Grant proved this statement only in the case of the Bradley–Terry model, but it is also true for general . Yan modified the method in [51] so that additions were made only for pairs that were originally compared.
Definition 5
(Perturbation given by Yan denoted by Y).
We can observe that this method does not make every data matrix A evaluable. Yan proved the following statement only for the Bradley–Terry model: The perturbed data matrix is evaluable if and only if is connected. This statement also holds for the case where .
Theorem 3.
Let . The perturbed data matrix is evaluable if and only if is connected.
Proof.
Perturbation Y makes every connection in into directed connections in both directions in . If is connected, then there is an undirected path between any objects i and j; therefore, there is a directed path from i to j in . If there is no path between i and j, where , then there is no directed path in both directions between them in ; therefore, is not strongly connected, i.e., is not evaluable. □
This method also may insert unnecessary data; if there is a directed edge from i to j, and also from j to i, the added value does not improve evaluability.
To remove some unnecessary supplements from the perturbed matrix constructed by Yan, we can define the following perturbation method.
Definition 6
(Modified Yan perturbation method denoted by M).
The condition , and , expresses that there is at least one comparison between objects i and j, and all such comparisons are either consistently ‘better’ or consistently ‘worse’. In the case of perturbation method M, the amount of insertion is less than or equal to that in method Y. Now, we can state the following.
Theorem 4.
Let . The perturbed matrix can be evaluated if and only if the graph is connected.
Proof.
Perturbation M makes additions if the compared pair has only one-directed connections; then, every connection becomes a directed edge in both directions in the graph . As is connected, is strongly connected; therefore, is evaluable. If is not connected, then is not strongly connected; therefore, cannot be evaluated. □
It is easy to see that the perturbation method M might insert perturbations even in cases where they are not necessary. Therefore, we aimed to develop an algorithm that adds supplements only when needed. To achieve this, we used the data structure analysis of the data matrix A.
4.2. Algorithm for Perturbation Based on Data Structure
Now, we can construct a new perturbation algorithm based on the data structure. It will be called the S algorithm. The steps for the algorithm are the following:
- I.
- Data structure analysis: Identify all maximal connected subgraphs of the graph .
- II.
- Data structure analysis: Determine the strongly connected components of each maximal connected subgraph.
- III.
- Data structure analysis: construct the supergraph of each maximal connected subgraph. Determine the levels and identify the nodes that are placed at the top level. Then, identify the objects belonging to the super-nodes located at top level.
- IV.
- Evaluation of subsets: Evaluate each strongly connected component at the top level based exclusively on the data between its elements.
- V.
- Connection of the strongly connected components in the maximal connected subgraphs: For each leveled supergraph, construct two chains of unidirectional edges. An -perturbation connects the element with the highest -coordinate in the ith strongly connected component to the element with the lowest -coordinate in the th strongly connected component. The first chain contains the top level strongly connected components. The second chain contains those strongly connected components that do not have any outgoing edges. Arrange them in decreasing order according to their level. Finally, add an -perturbation from the strongest object of last element of the second chain to the weakest object of the first element of the first chain. If the coordinates are not uniquely determined, choose among the appropriate ones the lowest number. Data modification involves the following: If the set of inserted directed edges is denoted by , we have
- VI.
- Evaluation of the maximal connected subgraphs: Step V makes every maximal connected subgraph evaluable; evaluate them based exclusively on the data between the elements within each subgraph.
- VII.
- Connection of the maximal connected subgraphs: Connect the maximal connected subgraphs with a chain of unidirectional perturbations into a cycle such that the element with the highest -coordinate in the ith maximal connected subgraph has a perturbation to the element with the lowest -coordinate in the th maximal connected subgraph.
Theorem 5.
The algorithm consisting of Steps I–VII renders any data set A evaluable in a finite number of steps. The original data set A cannot be made evaluable with less than the number of additions in the algorithm.
Proof.
Since for any data set A, the graph has finitely many maximal connected subsets and finitely many strongly connected components, Steps I–VII terminate after a finite number of iterations. In Step I, the disjoint set union algorithm can be used. In Step II, Tarjan’s algorithm [53] can be used. In Step III, an algorithm presented at the bottom of Section 3, which assigns the super-nodes with no incoming super-edges to the top level, can be used.
The second part of the theorem is easy to see. □
Note that Step VII can be applied in the case of the Y and M algorithms to connect the maximal connected subgraphs if is not connected.
In order to make it easier to reproduce the aforementioned S perturbation algorithm, we provide a flowchart and a pseudocode of the algorithm. The pseudocode is presented in Algorithm 1. The flowchart can be seen in Figure 2.
| Algorithm 1 The pseudocode of the S perturbation. |
|
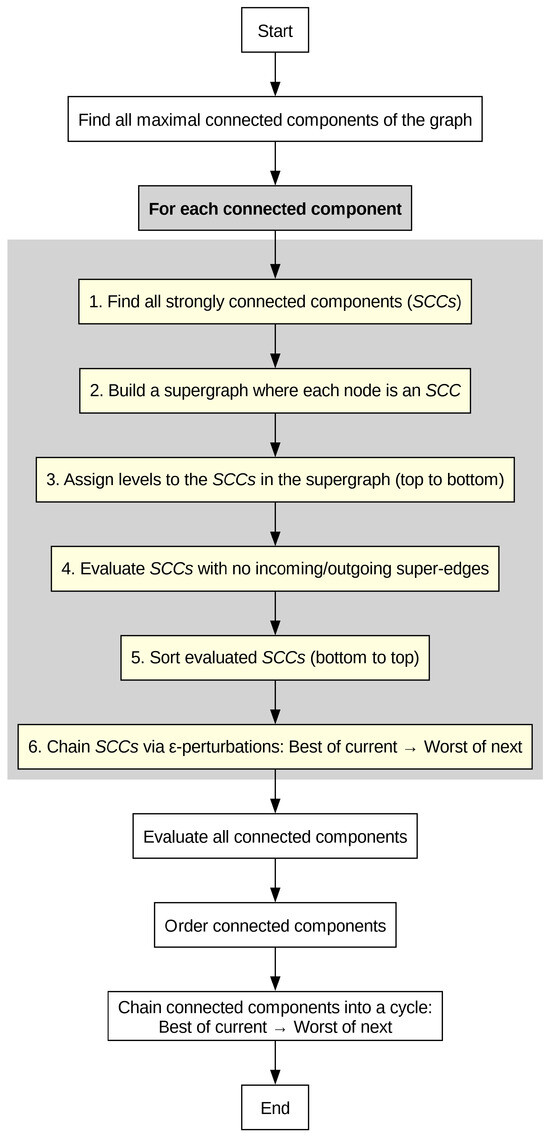
Figure 2.
A flowchart of the S perturbation.
Comparing the C, Y, and M perturbation methods to S, we can state the following. While the former algorithms insert edges based on certain values in the data—often unnecessarily—the S algorithm, after analyzing the structure of the entire dataset, inserts only those edges that are strictly necessary to ensure evaluability. As we will see later, this leads to faster convergence to the optimal limit point and significantly reduces the number of artificial edges.
5. Examples
We present some simple data structures that are worth demonstrating because they are easy to follow and understand. The first example is as follows.
Example 1.
The number of objects equals three. There is a comparison between any two objects. Moreover,
The graph of Example 1 and the supergraph belonging to it can be seen in Figure 3.
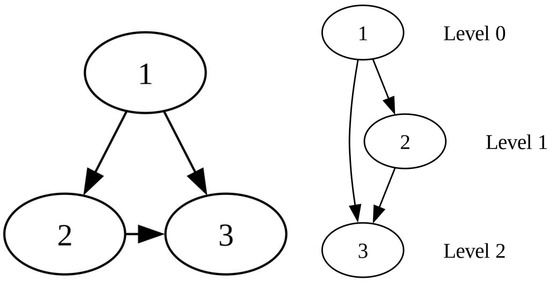
Figure 3.
The graph and the supergraph with its levels, corresponding to Example 1.
The ranking of the objects intuitively is clear: object 1 is the best, then object 2 is the next, and finally, object 3 follows. Recalling Theorem 1, it is clear that (18) is non-evaluable. To gain deeper insight, we now examine the log-likelihood Function (6) in detail under the condition .
Let
Introducing , and , we have
strictly monotonically increasing if x moves strictly monotonically increasing. Although the maximal value is not attained, the log-likelihood Function (19) can get arbitrarily close to zero, so its limit is equal to its supremum. The boundary point corresponding to the supremum is =, or . We will call it the optimal limit point, as it is the limit of a parameter setting along which the log-likelihood function tends to its supremum.
Whether we apply the C, Y, or M perturbation, the perturbed data matrices will be the same. The perturbed data matrices can be evaluated, and the results of the evaluations for different values are shown in Table 1. It can be seen that

Table 1.
The optimal parameter values in the case of different values and perturbation methods C, M, and Y using the Bradley–Terry model. Data are shown as in Example 1.
The S algorithm inserts an edge from the object 3 to the object 1 in this direction. Table 2 contains the estimated weights for different values.

Table 2.
The optimal parameter values in the case of different values and perturbation method S using the Bradley–Terry model. Data are shown as in Example 1.
Table 2 shows that also holds in this case. Furthermore, the convergence is quicker compared to the other perturbation cases.
Example 2.
In our second example, the number of objects equals three again. There is no connection between the objects 1 and 2. Moreover, let
The graph from Example 2 and its corresponding supergraph with its levels are shown in Figure 4.
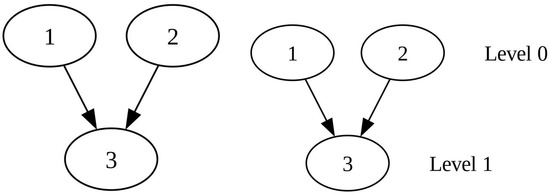
Figure 4.
The graph and the supergraph with its levels, corresponding to Example 2.
In this case, we do not have any direct information about the relationship between objects 1 and 2. The only clue may be how many times they proved to be better than object 3. Based on this, the intuitive ranking is either or , depending on which value of and is greater.
The log-likelihood Function (6) with is
It can be easily seen that if and , both strictly monotonically decreasing, then is strictly monotonically increasing. We can again state that the maximum does not exist, but the supremum of the log-likelihood function is 0. This value can be approached arbitrarily closely, independently of and . Condition does not determine the value of ; it can be zero, positive, a negative real number, ∞, or −∞. The optimal limit points are of the followings: . Turning to , we get , where , with . There is no connection between the strongly connected components on the level; therefore, we have flexibility in choosing their weights. This observation will also be used again later. By performing the C, Y, M, and S perturbations, we can see that , but and differ from them. The S perturbation method inserts two edges: one from 3 to 1 and another from 1 to 2. As is connected, the perturbed data matrices can be evaluated. The results of the evaluations of the perturbed data , , and are contained in Table 3, Table 4, and Table 5, respectively.

Table 3.
The estimated parameter values in the case of C perturbation method and different perturbation values using the Bradley–Terry model. Data are shown as in Example 2, with .

Table 4.
The estimated parameter values in the case of Y and M perturbation methods and different perturbation values using the Bradley–Terry model. Data are shown as in Example 2, with .

Table 5.
The estimated parameter values in the case of S perturbation method and different perturbation values using the Bradley–Terry model. Data are shown as in Example 2, with .
Based on the numerical results, one can observe that in the case of the Y (and M) perturbation,
but this is not the case for the C perturbation method. The property
can be analytically proven in this example if we use perturbation. We draw the reader’s attention to the fact that the limit of differs from the limit of , which equals the limit of .
Here,
with , ,
with and , and
with and .
We can conclude that the ranking of the objects coincides with our intuition in all four perturbation methods.
Example 3.
The third example is taken from Yan’s paper ([51], Example 1) and consists of four objects to be evaluated. The data are the following:
The graph of Example 3 and the corresponding supergraph with its levels can be seen in Figure 5.
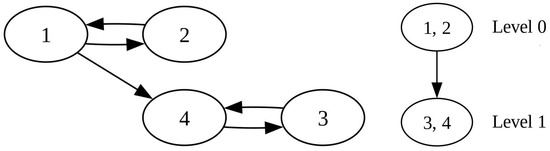
Figure 5.
The graph and the supergraph with its levels, corresponding to Example 3.
Now we have two levels of the supergraph, and both levels have only one strongly connected component. Intuition suggests that the ranking is in decreasing order.
Fix , as usual. The log-likelihood function given in Equation (6) is as follows:
The sum contains three well-separated parts. The first consists exclusively of the terms that involve the parameters of the objects in the level 0, i.e., objects 1 and 2. Now,
The second part serves as a bridge between the elements of level 0 and level 1. It contains the terms that include parameters from objects in both levels.
Finally, the last part contains those terms in which the parameters corresponding to the elements of level 1 are included, i.e.,
One can observe that does not depend on the variables and and can be maximized in itself. Therefore, find the maximum value of ; denote the first and second arguments . After some analytical computations, we get . Then, find the maximum value of . The argument is not unique in this case; the coordinates can be shifted. Let a possible argument of the third and fourth coordinates be . We can prove that holds.
The value of does not change if we substitute , , and , where . Consequently,
The log-likelihood function tends to its supremum, and the optimal limit point is . If we use the Bradley–Terry model, the optimal limit point is . are the estimated weights of objects 1 and 2 based only on the comparison results between these two objects. Formally, contains the comparison data between objects 1 and 2. It can be easily seen that .
In this example, all four perturbation methods produce different perturbed data matrices. In the case of perturbation method C, Table 6 presents the results.

Table 6.
The estimated parameter values applying C perturbation method in the case of different perturbation values using the Bradley–Terry model. Data are shown as in Example 3.
In the Bradley–Terry model, applying the Y perturbation, the estimated weights in Example 3 can be computed analytically. They are as follows:
with
By applying the M perturbation, the estimated weights are the following:
where
One can see that in all three perturbations,
Moreover,
Moreover, in the case of the M perturbation method, the equalities
hold for any .
Perturbation method S inserts a directed edge from object 4 to object 2. The results of the evaluation of these perturbed matrices for different values are contained in Table 7.

Table 7.
The estimated parameter values applying S perturbation method in the case of different perturbation values using the Bradley–Terry model. Data are shown as in Example 3.
From Table 7, it can be seen that , and the convergence is quicker than in the cases of C, Y, and M perturbations. One can prove analytically that the equality
holds again.
In this case as well, the rankings agree with the intuition.
Finally, Table 8 contains the numbers of inserted edges in the case of different perturbation methods.

Table 8.
The numbers of inserted edges in the case of different perturbation methods.
One can see that the S perturbation method inserts the fewest edges, always only as many as are absolutely necessary. In [54], the authors suggested applying Bayesian parameter estimation with gamma prior distributions. Example 3 was analyzed in [51] using the mentioned method, and the results are presented in Section 5, Table 6, of the paper [51]. Based on this, we can see that, for different parameters of the prior distributions, the results do not approach the optimal limit point—even in the case of the parameter setting suggested by the authors.
6. Characterization of the Optimal Limit Point Based on the Data Structure
Our observations on Examples 1, 2, and 3 help us to formulate a statement about the optimal limit points. In the presented examples, the log-likelihood function does not attain its maximum; however, its supremum can be approached arbitrarily closely. We can find trajectories along which the supremum can be approximated. The arguments of these trajectories have limits: these limit points are the optimal limit points. These points are not in the domain of the log-likelihood function, but they lie on the boundary of the domain (possibly including the value of ). In Example 2, we realized that the supremum can be approached on different trajectories which result in more than one optimal limit points. At the same time, different perturbation methods lead to different evaluation results in the limit as approaches zero.
The main idea of finding these trajectories is the following: Separate the terms of the sum (6) into specific groups—those between objects belonging to strongly connected components on the same level and those between components on different levels. We show that the terms between objects from different levels are increasing and tend to zero, while the terms between objects on the same level can be optimized independently, since there is no connection between the strongly connected components on the same level.
Assume that is connected, but is not strongly connected.
We will need some notations. The structure of the notations is the following: Letter is for the strongly connected component itself, while the set of objects in it. The upper index refers to the level of the strongly connected component of the objects; the lower index is for the identifier of the strongly connected component at its level. The notations are detailed as follows:
- Let the number of strongly connected components of be , where .
- Let the number of the level of the supergraph constructed on the basis of be , where , and let the levels be indexed by .
- Let the strongly connected components be denoted by , where s refers to the level (, and l is the index of the strongly connected component being on the level s, i.e., .
- Let the index set of objects belonging to the objects in strongly connected component be .
- Let be the indices of the objects in strongly connected components that belong to super-nodes at the sth level, i.e., .
- Let the sum of the terms in the log-likelihood function be denoted by , which exclusively contains those parameters belonging to the lth strongly connected component at level s, i.e.,
- Let
- Let the sum of the terms be denoted by , which depend exclusively on the parameters of the objects at level and at level , i.e.,
- Let denote the sum of the terms that depend on the parameters of the objects at different levels, i.e.,
Lemma 1.
The log-likelihood Function (6) equals
Proof.
Due to the construction of the levels of the supergraph, there is no comparison between objects on the same level but in different strongly connected components, i.e., for if and , with and . Therefore, the terms in the log-likelihood function can be grouped into two separate parts. One part contains terms that depend only on parameters included in the fixed strongly connected components; these are contained in . The other part consists of terms involving parameters from strongly connected components on different levels; these are included in . □
We now turn to the optimization of .
Lemma 2.
for can be optimized by maximizing for every index and separately.
Proof.
Taking into consideration (44), the maximum of corresponds to the maximum of separated terms. Since every object is in a unique strongly connected component, the sum achieves its maximum when each reaches its maximum. For a fixed strongly connected component, the maximum of the log-likelihood function exists, and the argument is unique if we fix one parameter in each strongly connected component. Consequently, the arguments of the maximal values are only uniquely determined up to a translation in every strongly connected component. □
After maximizing the sum of the terms arising from the same strongly connected components, let us examine those belonging to different strongly connected components. Since there is no edge between two components at the same level, we only need to deal with the terms associated with objects belonging to components at different levels. It will be shown that the sum of these terms converges to zero along certain sequences, while the terms within the same strongly connected components remain maximal.
Lemma 3.
Fixing a parameter setting and making the transformation
then
Proof.
We show that every term (45) tends to zero if . If , then, there are only ‘better’ results between the elements in and , i.e., , for and , as the objects i and j belong to different levels. Moreover, the terms tend to 1 if , as the arguments of F tend to . Therefore, their logarithms tend to the largest value, which is zero. Consequently, the sum of them will tend to zero as well. □
Lemma 4.
With the transformation of (48), we have
Proof.
Lemma 5.
where is the maximum likelihood estimate of the expectations based on the comparison data between the objects in . The appropriate data sets are denoted by . The estimated values are unique only apart from translation.
Proof.
Recalling Lemmas 1 and 2, and taking into account Lemmas 3 and 4, we get the statement. □
Now we turn to one of the main theorems in the section. It is for the determination of optimal limit point(s). Its essence can be summarized as follows. Suppose that is connected but is not strongly connected. Considering the original form, optimize the log-likelihood functions separately in each strongly connected component at level 0 by fixing one parameter to zero. These values can be shifted separately by the same value for a fixed strongly connected component. Use these shifted arguments’ coordinates for the appropriate coordinates of . All other coordinates have to be .
If we consider the exponential form (8), optimize the log-likelihood function separately within each strongly connected component at level 0. These yield estimated weights based on the local comparison results, which involve only the objects within the given strongly connected component. Take an arbitrary normalized vector with non-negative coordinates whose dimension equals the number of strongly connected components at level 0. These coordinates will serve as multipliers for the estimated weights within the strongly connected components. The multipliers are constant within each strongly connected component but may differ across components. The coordinates corresponding to the objects at level 0 will be the values obtained as a result of this multiplication. Assign zero to all remaining coordinates.
For the sake of the formal statement and the proof, we introduce a further notation: the function h defines a one-to-one correspondence between the indices of the objects in the strongly connected components and their original values. For example, suppose object 7 is in the third strongly connected component at level 0, and it is the fourth element in that component. Then, , and the seventh coordinate of the optimal limit point corresponds to the fourth estimated parameter in . This is expressed as .
Now, we can state the following.
Theorem 6.
Suppose that is connected, and is not strongly connected.
- I.
- The optimal limit points can be expressed as follows:Here, are the estimated expectations of the objects in the strongly connected components . The estimation is performed exclusively based on the data of after fixing one parameter to 0. These values are shifted by an arbitrary constant .
- II.
- If we turn to the exponential form of (8), the optimal limit points are as follows:Here, are the estimated weights computed by exclusively applying the data of the strongly connected component . for are arbitrary non-negative constant values belonging to the lth strongly connected component on the top level, with .
- III.
- If there is only one strongly connected component at the top level, then, by fixing one parameter in to zero, there is a unique optimal limit point, and it is
- IV.
- Turning to the exponential form of (8), if there is only one strongly connected component at the top level, the optimal limit point, under the constraint , is unique and equals
Proof.
I. Recall Lemma 5 and note that the Function (46) is strictly increasing as .
II. Take the exponential transformations, with , and normalize. The possible translations in the strongly connected components are incorporated into the values.
III. From I, we know that the coordinates corresponding to the indices of the strongly connected components at the top level can be determined independently by fixing one expectation, and they can be shifted. From I, we know that the coordinates corresponding to the indices of the strongly connected components at the top level can be determined independently by fixing one expectation, and they can be shifted. Since there is only one strongly connected component at the top level, the possibility of shifting corresponds to fixing a single coordinate. All other coordinates, belonging to the strongly connected components below the top level, are equal to .
IV. From II, we know that the non-zero coordinates of the optimal limit points are the weighted averages of the normalized weights corresponding to the objects in the strongly connected components at the top level. Since there is only one strongly connected component, the weighted average equals the original weights, and the other coordinates are zero. □
Note that the optimal limit point may depend on the distribution of the differences , but which coordinates are zero depends only on the data structure, i.e., the supergraph.
Theorem 6 clarifies the conditions under which the optimal limit point is unique or non-unique. In practice, non-uniqueness may allow the decision maker to assign weights to the objects within certain strongly connected components at level 0 at their own discretion. In such cases of non-evaluability, it is advisable to avoid relying on this possibility and instead request additional comparisons to ensure that decisions are based on reliable comparison results. The optimal pairs are explored by the S algorithm. This remark clearly also holds when the comparison graph is disconnected. In such a case, nothing can be said about the relationship between the separate components, so it is very important to perform comparisons between elements of different subsets.
An interesting question is the relationship between the optimal limit points and the evaluation results based on the perturbed data matrices for small values of . In [50], the authors proved that, in the case of the Bradley–Terry model,
exists. The same argumentation as in [50] is true for Y, M, and S perturbations. Therefore, we can conclude that , , and exist. Although the proof cannot be directly generalized for the case of , simulation results support that in this case the same statements hold. Moreover, based on Examples 1–3 and simulations, we conjecture that these limits coincide with one of the optimal limit points. Example 2 shows that these limits may differ from each other. Nevertheless, if the optimal limit point is unique (i.e., there is only one strongly connected component at the top level); then,
If contains more than one maximal connected subgraph, we do not have any information about the relations of the subgraphs. Consequently, we cannot make a reliable evaluation. It may happen that two subgraphs have approximately the same distribution in terms of the strength of the objects within them, but it is also possible that every element in one group is stronger than all the elements in the other group. Think, for example, of teams playing in Serie A and Serie D in the Italian football league system.
Now, we turn to the relation between the optimal limit points and the limit of the evaluation results based on perturbed data if
Theorem 7 (Assume that is connected).
Consider the Bradley–Terry model, and let be a general ε-perturbation of the data matrix A, i.e.,
keeping the property . Let us assume that the perturbed data matrix is evaluable. Then,
exists and is equal to an optimal limit point .
If there exists a unique optimal limit point, then the limits of the evaluations, , are the same when applying any perturbation method.
Proof.
Let us carefully go through Conner and Grant’s proofs in [50]. On the basis of Theorem 1.1 in [50] one can see that the limit exists. A slight modification of the proof of Theorem 3.3 in [50] guarantees that if there is a directed path from i to j, then is bounded (simply replace by 1 or by the number of the inserted edges). If there is a directed path from i to j but there is no directed path from j to i, then
The condition “there is a directed path from i to j but there is no directed path from j to i” means that i and j are in strongly connected components on different levels, and the level of i is less than the level of j. The optimal limit points have this property: their coordinates are equal to 0 for objects outside strongly connected components at the top level. Moreover, if objects i and j are in the same strongly connected component at the top level, Theorem 3.5 in [50] guarantees that
Here, is the data matrix reduced to the current strongly connected component. As the strongly connected components can be separately optimized to approach the supremum of the log-likelihood function, this property aligns with that observed in optimal limit points. Hence, the limit of the coordinates computed by an arbitrary -perturbation method constitutes an optimal limit point. If there is only one optimal limit point, then the limit of the evaluation results obtained using different perturbation methods must be the same. This is the case in Examples 1 and 3. If there is more than one optimal limit point, the limits of the evaluation results obtained from different perturbation methods may differ. This is illustrated in Example 2 using perturbations C, , and S.
If we take the logarithm of the limit of different coordinates, we get the same statement for the additive form of the Bradley–Terry model. □
From the above, it follows that for each G perturbation method that makes evaluable data matrix A, one can construct sequences along which the log-likelihood function, which converges to its supremum.
We note that, although the proof is valid only for the Bradley–Terry model, the authors believe that the statement remains valid when a general c.d.f. is applied.
7. Comparison of the Perturbation Methods by Computer Simulations
We performed computer simulations to compare the properties of different perturbation methods, focusing on the similarity of rankings and the number of inserted data. We applied the Bradley–Terry model and randomly chose an initial weight vector. We compared the results to this vector, as we are interested in the extent of information retrieval compared to the original rankings. The steps of the simulations are the following:
- ST_I
- Generate uniformly distributed values for in the interval (0, 1), and normalize them. These will be called the original weights. Determine the ranking defined by them; it is referred to as the original ranking.
- ST_II
- ST_III
- Randomly generate edges according to the number of comparisons and also generate data corresponding to the edges according to the probabilities computed in ST_II.
- ST_IV
- Check whether the data are evaluable or not, and consider only the cases when they are not evaluable, but the comparison graph is connected.
- ST_V
- Apply the perturbations C, Y, M, and S to the data. Compute the numbers of the inserted edges.
- ST_VI
- Evaluate the perturbed data matrices.
- ST_VII
- Compare the ranking defined by the estimates to the original ranking by computing Spearman [55] and Kendall rank correlations [56].
- ST_VIII
- Repeat the steps ST_I to ST_VII as many times as the simulation number indicates.
- ST_IX
- Take the averages over the simulations and determine the standard deviation of the quantities computed in steps ST_V and ST_VII.
simulations were performed. We chose as the number of objects, and the number of comparisons was set to 20, 40, 60, and 80. The ratios of connected but not strongly connected graphs were 87.48%, 65.38%, 34.5%, and 23.61%, respectively, in these cases. We have investigated the mentioned cases. For the values and , Table 9, Table 10, Table 11 and Table 12 present the results for the C, Y, M, and S perturbation methods, respectively. The comparison numbers appear in the first column under “c.n.” The second column of the tables shows the average numbers of insertions (i.e., artificial data) along with the standard deviations, separated by semicolons. Following these, the tables report the average values and standard deviations of Spearman’s and Kendall’s rank correlations between the original and estimated rankings.

Table 9.
The number of inserted edges, as well as average values and standard deviations of Spearman’s and Kendall’s rank correlations, related to the initial parameter setting for random comparison data with 20, 40, 60, and 80 comparisons using C perturbation in the case of objects.

Table 10.
The average number and the standard deviation of inserted edges and the average values and standard deviations of Spearman’s and Kendall’s rank correlations related to the initial parameter setting for random comparison data with 20, 40, 60, and 80 comparisons using Y perturbation in the case of objects.

Table 11.
The average number and the standard deviation of inserted edges, as well as the average values and standard deviations of Spearman’s and Kendall’s rank correlations, related to the initial parameter setting for random comparison data with 20, 40, 60, and 80 comparisons using M perturbation in the case of objects.

Table 12.
The average number and the standard deviation of inserted edges, as well as the average values and standard deviations of Spearman’s and Kendall’s rank correlations, related to the initial parameter settings for random comparison data with 20, 40, 60, and 80 comparisons using S perturbation in the case of objects.
Looking at the correlation coefficients, we observe that as the number of comparisons increases, the average values increase in the case of all four perturbation methods. Meanwhile, the standard deviations decrease with the growing number of comparisons.
From Table 9, Table 10, Table 11 and Table 12, Spearman’s correlation coefficients show that, based on 20 comparisons, the original rankings can be reconstructed to a moderate extent on average, while with 60 and 80 comparisons, the reconstruction is efficient. The same conclusion can be drawn from the Kendall’s coefficients. A larger comparison number results in better information retrieval with lower uncertainty across all four perturbation cases.
Comparing the different methods with the same number of comparisons, we observe that the average values and dispersions are very similar across all four perturbation methods. Usually, the averages corresponding to are slightly larger than those corresponding to . The examination of the perturbation case is interesting because it involves the insertion of data that could also occur in reality. From Table 9, Table 10, Table 11 and Table 12, we can see that both rank correlation coefficients across all four perturbations tend toward similar values as decreases. This trend is especially apparent in graphs based on 60 and 80. It is also evident that perturbation C yields the most favorable rank correlation coefficient values, followed by Y, M, and finally S. However, the differences among the correlation values are minimal.
The substantial difference is in the average number of inserted edges. Perturbation S inserts significantly less edges compared to the other perturbations. We can also see that perturbations Y and M seem to add more and more edges in graphs with higher edge counts, while S adds less edges as the number of original edges increases. The average values of around 1 and 2.5 indicate that the comparison data require only a few well-assigned new comparison data to become evaluable. The information retrieval is similarly effective as with the other perturbation methods that use a lot of artificial data. Therefore, it may be worthwhile to request real comparison data if possible. The S algorithm, which is based on data structure analysis, reveals which pairs should be compared.
Similar phenomena are observed for larger numbers of objects. Table 13 reports the average numbers of inserted edges and Spearman and Kendall correlation coefficients, together with the standard deviations, for objects and 200 comparisons. In this setting, 98% of the random graph of comparisons are connected, but the directed graph is not strongly connected. The standard deviations are considerably smaller than for objects. The averages and standard deviations are very close to each other for the different methods. The number of inserted edges for algorithm S is only a fraction (less than 1%) of that required by the other algorithms.

Table 13.
The average number and the standard deviation of the numbers of inserted edges, as well as the average values and standard deviations of Spearman’s and Kendall’s rank correlations, related to the initial parameter setting for random comparison data with 200 comparisons using all investigated perturbations in the case of objects.
We also examined the convergence properties of the different methods. In Table 14, we present the differences between the optimal limit point and the evaluation results obtained by different perturbation methods when the optimal limit point is unique. The number of objects was , and the number of comparisons was 200. About 50% of the random comparison graphs were connected, but the directed graphs were not strongly connected, with only one strongly connected component at the top level. We can see that the S algorithm shows the best convergence property with the smallest average distances and with the smallest standard deviations. The same can be stated if we investigate the rank correlations between the rankings of the evaluations applying perturbed data and ranking of the optimal limit point. Regarding convergence in rank correlations, the best method is perturbation S, as shown in Table 15 and Table 16.

Table 14.
The average values and standard deviations of the Euclidean distances between evaluation results obtained by perturbations and the optimal limit points for random data with 200 comparisons, considering all perturbations in the case where there are n = 50 objects.

Table 15.
The average values and standard deviations of Spearman’s rank correlations when compared to the optimal limit point for random comparison data with 200 comparisons for each investigated perturbation in the case of objects.

Table 16.
The average values and standard deviations of Kendall’s rank correlations when compared to the optimal limit point for random optimal comparison data with 200 comparisons for each investigated perturbation in the case of objects.
We also examined the runtime of the perturbation methods. The results can be seen in Table 17. The simulations were run on a laptop with an AMD Ryzen 3 5425U processor. We can see that perturbations C, Y, and M share similar average running times, with M having a slightly higher value than the other two. Despite perturbation S having the worst average runtime, we can confidently say that this perturbation is computable within a short amount of time, as the average value concerning one simulation is below s.

Table 17.
The average runtimes of all perturbations across multiple object and comparison numbers. The runtime values are for simulations and measured in seconds (s). (o.n. = object number; c.n. = number of comparisons.)
8. An Application for Analyzing the Results of a Sports Tournament
Applications of pairwise comparison for evaluating tennis players can be found in the literature [57,58]. The presented method is based on a pairwise comparison matrix whose elements are constructed by dividing the number of wins by the number of defeats. However, this construction requires modification if only one match is played between any two players—which is typically the case in a tournament. Therefore, we will apply a Thurstone-motivated method to estimate the weights of the participants in the 2019 ATP Finals based on the match results of this tournament.
A tennis match ends with the victory of one of the players; therefore, the result can be considered the outcome of a comparison allowing two options, ‘better’ and ‘worse’. If Player 1 defeats Player 2, then Player 1 is considered the ‘better’ player in this comparison (match), and Player 2 is considered to be ‘worse’ in this comparison.
The 2019 ATP Finals was a men’s year-end tennis tournament featuring eight participants, which was held in London. The players were Matteo Berrettini (B), Novak Djokovic (D), Roger Federer (F), Daniil Medvedev (M), Rafael Nadal (N), Dominic Thiem (TH), Stefanos Tsitsipas (TS), and Alexander Zverev (Z). The match results can be found on the webpage [59].
Figure 6 represents the directed graph and the supergraph, along with its levels. It can be seen that the results cannot be fully evaluated, as Medvedev was defeated by all the other competitors he played against; consequently, the graph is not strongly connected. Nevertheless, the graph is connected. The data structure analysis reveals two strongly connected components: one at level 0 containing seven players and another at level 1 consisting of a single player—Medvedev. Therefore, according to Theorem 6 IV, we can obtain the optimal limit point by evaluating the results of the 7 players among themselves and setting Medvedev’s coordinate to 0. Perturbation C and insert 56 data and 30 data, respectively, while perturbation S only inserts 1: a win of Medvedev over Berrettini.
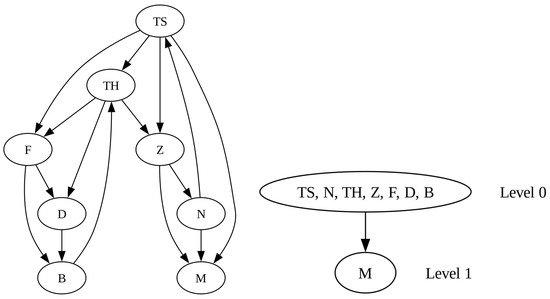
Figure 6.
The graph and the supergraph with its levels corresponding to the 2019 ATP Finals.
Applying the Bradley–Terry model, the optimal limit point, and the estimated weights evaluated by perturbations C, , and S with values and , the results are contained in Table 18 and Table 19, respectively. To obtain evaluable data, the inserted artificial comparison result is a Medvedev’s win over Berrettini when the S algorithm is applied. If a new match were to be scheduled, the most advisable pairing would be Medvedev versus Berrettini. The results of the evaluation in this case (assuming Medvedev’s win over Berrettini) are presented in the last column of Table 18. It would have been a conceivable result if they had played each other, since so far Medvedev had won three out of three matches against Berrettini.

Table 18.
The optimal limit point and the estimated weights of the tennis players of 2019 ATP Finals based on the results of the matches evaluated by different perturbation methods applying using Bradley–Terry model.

Table 19.
The optimal limit point and the estimated weights of the tennis players of 2019 ATP Finals based on the results of the matches evaluated by different perturbation methods applying using Bradley–Terry model.
Although the C and perturbations do not alter the ranking based on the optimal limit point, the S perturbation results in a modified ranking. In this case, Medvedev moves ahead of Berrettini and Djokovic, which is understandable, since he has a win over Berrettini. Nadal’s strength increases due to the rise in Medvedev’s strength. Thiem’s strength decreases as a result of Berrettini’s weakened performance due to the assumed loss—so much so that he falls behind the strengthening Zverev in the rankings.
The rankings by the different methods coincide, and the weights computed by perturbation are close to the optimal limit point. The highest-ranked and the lowest-ranked player are the tournament winner and the last-place finisher, respectively. Thiem can be considered the runner-up in the tournament, as he reached the final but was defeated there, but applying Thurstone-motivated methods, he is only the third in weights. This can be explained by the fact that his wins, except for the one against Zverev, were against lower-ranked players: Djokovic and Berrettini. Apart from Tsitsipas, Thiem was also overtaken by Nadal, whose weights turned out to be surprisingly high. This is because Nadal was able to defeat the strongest player, Tsitsipas, and was defeated only by a mid-weight player, Zverev. The method’s ability to take into account the opponent’s strengths—not just the result achieved against them—is clearly demonstrated through this example as well.
The results obtained using this method can be used by the organizers when distributing the prize money, even though the tournament players cannot be ranked using the usual scoring method, or when determining the players to be placed in each seed group for organizing a new tournament.
We also attempted to evaluate the above match results using RankNet neural network. We conducted an extremely large number of experiments, but in many cases, the result was NaN, meaning the neural network did not produce an evaluation output. With an extremely low learning rate (), we did obtain results, but the outcome still depended on which matches were placed in the training, validation, and testing sets. Therefore, evaluation using a neural network is not recommended at this stage.
9. Summary
In this paper, non-evaluable data were investigated in terms of their information content in two-option Thurstone-motivated models by applying a general cumulative distribution function. Since the maximum of the log-likelihood function was not attained in this case, we instead considered its supremum.
By finding trajectories that approach the supremum, we regarded the limits of their arguments as optimal limit points. As a theoretical result, we proved that these can be determined by analyzing the data structure, and their uniqueness can also be characterized on the basis of the data structure (Theorem 6).
Furthermore, we proved another statement (Theorem 7) that reveals a connection between perturbation methods and optimal limit points.
Based on knowledge of the data structure, we developed a new perturbation algorithm that inserts as few data points as possible to make the dataset evaluable. This knowledge also allows us to identify pairs for which real comparison data should be collected in order to make the available dataset evaluable.
Numerical experiments show that the convergence of the newly developed algorithm S to the optimal limit point was the best among the investigated perturbation methods.
This research has been conducted for two-option Thurstone-motivated models. It would be worthwhile to investigate the characteristics of non-evaluable data in multi-option models, to develop perturbation methods for them, and to compare these methods in terms of information content under different distance metrics.
Author Contributions
Conceptualization: C.M. and É.O.-M.; methodology: C.M.; software: B.K.; validation: B.K.; writing—original draft preparation: É.O.-M.; writing—review and editing: É.O.-M. and C.M.; visualization: B.K.; supervision: C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was implemented through the TKP2021-NVA-10 project with the support provided by the Ministry of Culture and Innovation of Hungary from the National Research, Development, and Innovation Fund, which is financed under the 2021 Thematic Excellence Programme funding scheme.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are public and are available on https://en.wikipedia.org/wiki/2019_ATP_Finals, which was last accessed on 4 July 2025.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Raghu, M.; Schmidt, E. A Survey of Deep Learning for Scientific Discovery. arXiv 2020, arXiv:2003.11755. [Google Scholar]
- Dong, S.; Wang, P.; Abbas, K. A survey on deep learning and its applications. Comp. Sci. Rev. 2021, 40, 100379. [Google Scholar] [CrossRef]
- Heydari, S.; Mahmoud, Q.H. Tiny Machine Learning and On-Device Inference: A Survey of Applications, Challenges, and Future Directions. Sensors 2025, 25, 3191. [Google Scholar] [CrossRef]
- Trigka, M.; Dritsas, E. A Comprehensive Survey of Deep Learning Approaches in Image Processing. Sensors 2025, 25, 531. [Google Scholar] [CrossRef] [PubMed]
- Kheddar, H.; Hemis, M.; Himeur, Y. Automatic speech recognition using advanced deep learning approaches: A survey. Inf. Fusion 2024, 109, 102422. [Google Scholar] [CrossRef]
- Almukhalfi, H.; Noor, A.; Noor, T.H. Traffic Management Approaches Using Machine Learning and Deep Learning Techniques: A Survey. Eng. Appl. Artif. Intell. 2024, 133, 108147. [Google Scholar] [CrossRef]
- Abdel-Jaber, H.; Devassy, D.; Al Salam, A.; Hidaytallah, L.; El-Amir, M. A Review of Deep Learning Algorithms and Their Applications in Healthcare. Algorithms 2022, 15, 71. [Google Scholar] [CrossRef]
- Gheewala, S.; Xu, S.; Yeom, S. In-Depth Survey: Deep Learning in Recommender Systems—Exploring Prediction and Ranking Models, Datasets, Feature Analysis, and Emerging Trends. Neural Comput. Appl. 2025, 37, 10875–10947. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Zhang, C.; Li, N. Machine Learning Methods for Weather Forecasting: A Survey. Atmosphere 2025, 16, 82. [Google Scholar] [CrossRef]
- Guo, J.; Fan, Y.; Pang, L.; Yang, L.; Ai, Q.; Zamani, H.; Wu, C.; Croft, W.B.; Cheng, X. A deep look into neural ranking models for information retrieval. Inf. Process. Manag. 2020, 57, 102067. [Google Scholar] [CrossRef]
- Gyarmati, L.; Orbán-Mihálykó, É.; Mihálykó, C.; Vathy-Fogarassy, Á. Aggregated Rankings of Top Leagues’ Football Teams: Application and Comparison of Different Ranking Methods. Appl. Sci. 2023, 13, 4556. [Google Scholar] [CrossRef]
- Kou, G.; Ergu, D.; Lin, C.; Chen, Y. Pairwise comparison matrix in multiple criteria decision making. Technol. Econ. Dev. Econ. 2016, 22, 738–765. [Google Scholar] [CrossRef]
- Ramík, J. Pairwise comparison matrices in decision-making. In Pairwise Comparisons Method: Theory and Applications in Decision Making, Lecture Notes in Economics and Mathematical Systems; Springer: Cham, Switzerland, 2020; pp. 17–65. [Google Scholar]
- Kosztyán, Z.T.; Orbán-Mihálykó, É; Mihálykó, C.; Csányi, V.V.; Telcs, A. Analyzing and clustering students’ application preferences in higher education. J. Appl. Stat. 2020, 47, 2961–2983. [Google Scholar] [CrossRef]
- Crompvoets, E.A.; Béguin, A.A.; Sijtsma, K. Adaptive pairwise comparison for educational measurement. J. Educ. Behav. Stat. 2020, 45, 316–338. [Google Scholar] [CrossRef]
- Francis, B.; Dittrich, R.; Hatzinger, R.; Penn, R. Analysing partial ranks by using smoothed paired comparison methods: An investigation of value orientation in Europe. J. R. Stat. Soc. Ser. C Appl. Stat. 2002, 51, 319–336. [Google Scholar] [CrossRef]
- Tarrow, S. The strategy of paired comparison: Toward a theory of practice. Comp. Polit. Stud. 2010, 43, 230–259. [Google Scholar] [CrossRef]
- McKenna, S.P.; Hunt, S.M.; McEwen, J. Weighting the seriousness of perceived health problems using Thurstone’s method of paired comparisons. Int. J. Epidemiol. 1981, 10, 93–97. [Google Scholar] [CrossRef]
- Radwan, N.; Farouk, M. The growth of internet of things (IoT) in the management of healthcare issues and healthcare policy development. Int. J. Technol. Innov. Manag. 2021, 1, 69–84. [Google Scholar] [CrossRef]
- Mayor-Silva, L.I.; Romero-Saldaña, M.; Moreno-Pimentel, A.G.; Álvarez-Melcón, Á.; Molina-Luque, R.; Meneses-Monroy, A. The role of psychological variables in improving resilience: Comparison of an online intervention with a face-to-face intervention. A randomised controlled clinical trial in students of health sciences. Nurse Educ. Today 2021, 99, 104778. [Google Scholar] [CrossRef] [PubMed]
- Yap, A.U.; Zhang, M.J.; Cao, Y.; Lei, J.; Fu, K.Y. Comparison of psychological states and oral health–related quality of life of patients with differing severity of temporomandibular disorders. J. Oral Rehabil. 2022, 49, 177–185. [Google Scholar] [CrossRef]
- Kazibudzki, P.T.; Trojanowski, T.W. Quantitative Evaluation of Sustainable Marketing Effectiveness: A Polish Case Study. Sustainability 2024, 16, 3877. [Google Scholar] [CrossRef]
- Brandt, F.; Lederer, P.; Suksompong, W. Incentives in social decision schemes with pairwise comparison preferences. Games Econ. Behav. 2023, 142, 266–291. [Google Scholar] [CrossRef]
- Meng, X.; Shaikh, G.M. Evaluating environmental, social, and governance criteria and green finance investment strategies using fuzzy AHP and fuzzy WASPAS. Sustainability 2023, 15, 6786. [Google Scholar] [CrossRef]
- Milošević, M.R.; Milošević, D.M.; Stanojević, A.D.; Stević, D.M.; Simjanović, D.J. Fuzzy and interval AHP approaches in sustainable management for the architectural heritage in smart cities. Mathematics 2021, 9, 304. [Google Scholar] [CrossRef]
- Held, L.; Vollnhals, R. Dynamic rating of European football teams. IMA J. Manag. Math. 2005, 16, 121–130. [Google Scholar] [CrossRef]
- Mazurek, J. Advances in Pairwise Comparisons; Springer: Cham, Switzerland, 2023. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. How to make a decision: The Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision-making with the AHP: Why is the principal eigenvector necessary. Eur. J. Oper. Res. 2003, 145, 85–91. [Google Scholar] [CrossRef]
- Bozóki, S.; Fülöp, J.; Rónyai, L. On optimal completion of incomplete pairwise comparison matrices. Math. Comput. Model. 2010, 52, 318–333. [Google Scholar] [CrossRef]
- Kazibudzki, P.T. Redefinition of triad’s inconsistency and its impact on the consistency measurement of pairwise comparison matrix. J. Appl. Math. Comput. Mech. 2016, 15, 71–78. [Google Scholar] [CrossRef]
- Brunelli, M. A survey of inconsistency indices for pairwise comparisons. Int. J. Gen. Syst. 2018, 47, 751–771. [Google Scholar] [CrossRef]
- Aguarón, J.; Escobar, M.T.; Moreno-Jiménez, J.M. Reducing inconsistency measured by the geometric consistency index in the analytic hierarchy process. Eur. J. Oper. Res. 2021, 288, 576–583. [Google Scholar] [CrossRef]
- Thurstone, L. A law of comparative judgment. Psychol. Rev. 1927, 34, 273–286. [Google Scholar] [CrossRef]
- Bradley, R.A.; Terry, M.E. Rank analysis of incomplete block designs: I. The method of paired comparisons. Biometrika 1952, 39, 324–345. [Google Scholar] [CrossRef]
- Orbán-Mihálykó, É.; Mihálykó, C.; Koltay, L. Incomplete paired comparisons in case of multiple choice and general log-concave probability density functions. Cent. Eur. J. Oper. Res. 2019, 27, 515–532. [Google Scholar] [CrossRef]
- Stern, H. Are all linear paired comparison models empirically equivalent? Math. Soc. Sci. 1992, 23, 103–117. [Google Scholar] [CrossRef]
- Glenn, W.A.; David, H.A. Ties in paired-comparison experiments using a modified Thurstone-Mosteller model. Biometrics 1960, 16, 86–109. [Google Scholar] [CrossRef]
- Rao, P.V.; Kupper, L.L. Ties in paired-comparison experiments: A generalization of the Bradley-Terry model. J. Am. Stat. Assoc. 1967, 62, 194–204. [Google Scholar] [CrossRef]
- Agresti, A. Analysis of ordinal paired comparison data. J. R. Stat. Soc. Ser. C Appl. Stat. 1992, 41, 287–297. [Google Scholar] [CrossRef]
- Orbán-Mihálykó, É.; Mihálykó, C.; Koltay, L. A generalization of the Thurstone method for multiple choice and incomplete paired comparisons. Cent. Eur. J. Oper. Res. 2019, 27, 133–159. [Google Scholar] [CrossRef]
- Huang, T.K.; Weng, R.C.; Lin, C.J.; Ridgeway, G. Generalized Bradley-Terry models and multi-class probability estimates. J. Mach. Learn. Res. 2006, 7, 85–115. [Google Scholar]
- Islam, M.M.; Khan, J.R.; Raheem, E. Bradley-Terry model for assessing the performance of ten ODI cricket teams adjusting for home ground effect. J. Data Sci. 2017, 16, 657–668. [Google Scholar] [CrossRef]
- Cattelan, M.; Varin, C.; Firth, D. Dynamic Bradley–Terry modelling of sports tournaments. J. R. Stat. Soc. Ser. C Appl. Stat. 2013, 62, 135–150. [Google Scholar] [CrossRef]
- Eliason, S.R. Maximum Likelihood Estimation: Logic and Practice; Sage Publications: Thousand Oaks, CA, USA, 1993. [Google Scholar]
- Ford, L.R. Solution of a ranking problem from binary comparisons. Am. Math. Mon. 1957, 64, 28–33. [Google Scholar] [CrossRef]
- Gyarmati, L.; Orbán-Mihálykó, É.; Mihálykó, C. Comparative analysis of the existence and uniqueness conditions of parameter estimation in paired comparison models. Axioms 2023, 12, 575. [Google Scholar] [CrossRef]
- Gyarmati, L.; Mihálykó, C.; Orbán-Mihálykó, É. Algorithm for option number selection in stochastic paired comparison models. Algorithms 2024, 17, 410. [Google Scholar] [CrossRef]
- Conner, G.R.; Grant, C.P. An extension of Zermelo’s model for ranking by paired comparisons. Eur. J. Appl. Math. 2000, 11, 225–247. [Google Scholar] [CrossRef]
- Yan, T. Ranking in the generalized Bradley–Terry models when the strong connection condition fails. Commun. Stat. Theory Methods 2016, 45, 340–353. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, Y. A novel efficient graph model for the multiple longest common subsequences (MLCS) problem. Front. Genet. 2017, 8, 104. [Google Scholar] [CrossRef]
- Tarjan, R. Depth-First Search and Linear Graph Algorithms. SIAM J. Comput. 1972, 2, 146–160. [Google Scholar] [CrossRef]
- Caron, F.; Doucet, A. Efficient Bayesian Inference for Generalized Bradley–Terry Models. Mathematics 2012, 21, 174–196. [Google Scholar] [CrossRef]
- Walpole, R.E.; Myers, R.H.; Myers, S.L.; Ye, K. Probability and Statistics for Engineers and Scientists; Macmillan: New York, NY, USA, 1993. [Google Scholar]
- Abdi, H. The Kendall Rank Correlation Coefficient. In Encyclopedia of Measurement and Statistics; Sage: Thousand Oaks, CA, USA, 2007; pp. 508–510. [Google Scholar]
- Bozóki, S.; Csató, L.; Temesi, J. An Application of Incomplete Pairwise Comparison Matrices for Ranking Top Tennis Players. Eur. J. Oper. Res. 2016, 248, 211–218. [Google Scholar] [CrossRef]
- Temesi, J.; Szádoczki, Z.; Bozóki, S. Incomplete pairwise comparison matrices: Ranking top women tennis players. J. Oper. Res. Soc. 2024, 75, 145–157. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/2019_ATP_Finals (accessed on 4 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).