Abstract
In a world increasingly dependent on digital computers, understanding the relationship between information theory and thermodynamics is essential. A recent attempt to address this issue was made by A. De Vos who, using a reversible model within the framework of finite-time thermodynamics, derived Carnot’s law, Landauer’s principle, Ohm’s law, and even Moore’s law. Following De Vos et al., this paper first recovers the efficiency of Curzon and Ahlborn, and then establishes the so-called endoreversible Landauer principle for a traditional computer gate, assuming the gate operates in the Maximum Power regime. However, two other regimes are particularly important: the Omega function and the Efficient Power function. By considering these, we obtain the corresponding thermodynamic efficiencies and compare them against that of the Maximum Power regime.
Keywords:
Landauer´s principle; finite time thermodynamics; Omega function; Efficient Power function MSC:
80-10; 80M50; 94-10
1. Introduction
Since 1961, when Rolf Landauer demonstrated the close relationship between information theory and thermodynamics, a series of articles [1,2,3,4] elaborated what later became known as the erasure principle or Landauer’s principle. This principle postulates that the deletion of information is inherently accompanied by energy dissipation. Landauer showed that a small quantity of heat, proportional to thermal energy, is required to erase a bit of information. A direct implication of this irreversible process is the increase of entropy in the environment. From the beginning, Landauer’s principle was so disturbing, that during the following years many scientists began to work on its experimental demonstration [5,6,7,8,9,10,11].
In general, this is not surprising: computing, like all processes occurring at a finite rate, necessarily involves some dissipation. Since heat generation limits speed and storage capacity in modern microprocessors, it is crucial to determine to what extent this problem is fundamental. Within this context, A. De Vos [12,13] developed a model of an endoreversible engine that performs computation logically through a series of reversible computing steps. To this end, De Vos et al. proposed a model of logic gates based on the Curzon and Ahlborn [14] thermodynamic model of an engine operating at non-zero speed—the so-called infinite engine. This consists of a reversible core where heat is converted into work, together with two irreversible elements for heat transport. This approach proved useful, as it enables tasks to be performed in finite time. The model was thus named the endoreversible model for logic gates. Under this framework, a logic gate was modeled that could reproduce Carnot efficiency, Landauer’s principle, and even Ohm’s law.
A few years after the postulation of the second law of thermodynamics, James C. Maxwell illustrated the probabilistic nature of the second law [15]. Since then, a very interesting question has been what happens with this law if information is introduced into the system, and even more so what happens if the information is relevant at a microscopic scale, as is the case with quantum systems. It is perhaps in this sense that De Vos et al. [12] introduce the concept of microentropy, attempting to quantify the average amount of information needed to specify the exact microstate of a system. From the point of view of statistical mechanics, these requirements require that for a system with n microstates, it must possess multiple and distinct metastable states. In other words, ergodicity must be broken for a specific timescale. In practice, this means that its phase space is split into m ergodic regions, one for each informational state [16].
To adopt the latter approach, a mesoscopic theory is necessary, and some attempts in this direction are made by Parrondo et al., among others [16,17,18]. However, our approach is macroscopic using the Finite Time Thermodynamics FTT approximation. Then, following the ideas of De Vos, this article addresses the problem of deriving the energetics of an endoreversible engine, taking into account that the engine comprises two parts (one reversible and one irreversible, not only the reversible part as in De Vos et al. [12]): (a) a core with a reversible gate, and (b) two transport channels, one for supplying the input information and the other for draining the output information.
A key advantage observed in the results obtained by Curzon and Ahlborn (later generalized in the FTT framework) is that their optimal efficiency values are much closer to those observed in real engines [19]. Within FTT, several objective functions have been introduced under different optimization criteria, and many models of heat engines operating as real devices have been proposed and analyzed. The importance of these models lies in the fact that the energy production processes observed in various systems often follow similar principles.
In this article, we also derive the endoreversible—or Curzon and Ahlborn—efficiency for a traditional computational gate, assuming it operates in the Maximum Power regime. However, two other particularly relevant regimes, the Omega function and the Efficient Power functions, are also considered. By analyzing these functions, we compute the corresponding thermodynamic efficiencies and compare them with that of the Maximum Power regime.
The paper is organized as following, Section 1 presents a brief introduction to the Landauer´s principle studied by De Vos et al. [12] in the context of Finite Time Thermodynamics. Section 2 presents a model for an endoreversible computer gate and Section 3 presents an analysis of the thermodynamics of the endoreversible computer gate model. Finally, Section 4 presents a brief discussion and some concluding remarks.
2. Model for a Endoreversible Computer Gate
2.1. De Vos Model for a Reversible Computer Gate
In 2020, De Vos et al. [12] published a notable article comparing the endoreversible framework to Landauer’s principle [1,2]. The primary objective of De Vos was to describe computing tasks thermodynamically at non-zero speed, i.e., within finite time. To achieve this, De Vos et al. introduced a simple endoreversible model for a computer gate, consisting of the following components (see Figure 1):
- A core part containing a reversible gate;
- Two transport channels: one for providing input information and another for extracting output information.
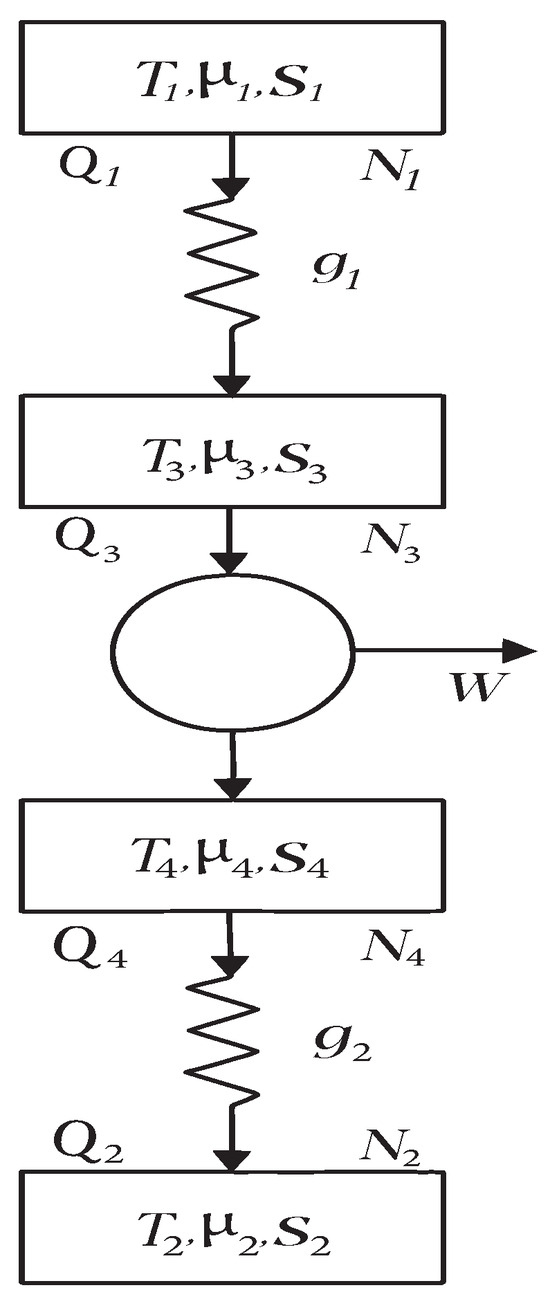
Figure 1.
Endoreversible computer gate model. The core is modeled as a reversible engine with two heat reservoirs: one at temperature , supplying heat , and the other at temperature , absorbing heat . The reversible part also includes a converter that generates work W. In addition, two parameters are introduced for each reservoir: entropy S and chemical potential . Thus, in addition to heat flow Q, each reservoir also provides (or absorbs) a matter flow N.
The core is modeled as a reversible engine (Carnot engine) with two heat reservoirs: one at temperature , supplying heat , and the other at temperature , absorbing heat . The reversible part also includes a converter that generates work W. To model the computational gate, De Vos et al. [12] introduced two additional parameters for each reservoir: macroentropy S (associated with information entropy) and chemical potential (of the information-carrying particles). Thus, in addition to heat flow Q, each reservoir also provides (or absorbs) a matter flow N.
By applying the three fundamental conservation laws of reversible thermodynamics:
- Conservation of energy: , indicating that the total energy output from the converter is zero. It is worth mentioning that, in conventional electronic computers, the particles are electrons and the particle flow N is (up to a constant) equal to the electric current I. In this sense, it is possible to postulate that there exists a conservation of mater implying that the total amount of matter leaving the convertor is zero. Thus, assuming the conservation of matter, the equation for the conservation of energy is true only if should not depend on .
- Conservation of matter: , indicating that the total output of matter of the converter is zero.
- Conservation of entropy: , indicating that the total entropy output of the converter is zero.
De Vos et al. [12] derived the work output of the reversible part for three special cases:
- Carnot’s Law: When and , the work is , yielding an efficiency , which is the Carnot´s formula for a reversible engine working between the temperatures and .
- Landauer’s Principle: When and , the work is .
- Gibbs’ Law: When and , the work is .
2.2. Endoreversible Computer Gate Model
In the 1970s, the field of finite-time thermodynamics (FTT) emerged with the aim of modeling thermal engines more realistically than classical equilibrium thermodynamics allowed.
Among the models in FTT, the Curzon–Ahlborn (CA) engine (see Figure 1) attracted significant attention. This model consists of two thermal reservoirs, one at temperature and the other at , connected through two irreversible components to a reversible part: a Carnot engine located between two intermediate reservoirs at temperatures and . The defining feature of this model is the endoreversibility hypothesis, which asserts that entropy production occurs only in the coupling between the working fluid and the surroundings. This was a key advancement toward modeling real-world engines, as it allowed for a global, positive entropy production.
Inspired by these ideas, it is possible to introduce an endoreversible model for a computer gate consisting of:
- A reversible computational gate.
- An irreversible structure for the transport of heat and information. The input side—analogous to one of the irreversible components of the CA engine—is connected to the reversible gate reservoir at temperature , while the output side—another irreversible channel—extracts heat and information and connects to the second reservoir at temperature , as shown in Figure 1.
In Figure 1, the input and output information registers are defined with fixed boundary conditions: , and , respectively. Similarly, intermediate reservoirs are characterized by variables and .
We now proceed to apply the three fundamental conservation laws of thermodynamics:
- Conservation of Matter:
- Conservation of Energy:
- Conservation of Entropy in the reversible part:where for this purpose we define the total energy [20]: .
3. Thermodynamics of the Endoreversible Model for a Computer Gate
3.1. Thermal Efficiency: The Special Case of the Curzon and Ahlbort Efficiency
Now, it is clear from Equation (2) that
Taking into account Equation (3) and assuming that , we obtain the following.
which, after some algebra, results in,
Due to Equation (2), we have to note that we cannot speak of the “heat current through the thermal conductor”, as the heat entering at one end, which is not equal to the heat leaving it at the other end, because the terminals are different chemical potentials . Therefore, we have
such that the amount of chemical energy is degraded to heat during transport from reservoir 1 to reservoir 3. Analogously, is larger than by an amount , obtaining;
If we postulate that in the irreversible part the efficiency is given by:
Then, Equation (10) transforms into
Now, taking into account Equation (8) and a linear law for the heat flux,
and
where and are called conductances and these constants are mainly dependent on the material properties and geometry of the particle channel it is possible to obtain,
Then, solving for yields:
Finally, from Equation (12) and taking into account Equation (17), it is easy to obtain the work output W as,
Finally, assuming that the particle drifts and are caused by the difference of the two potentials and (in conventional electronic computers, the particles are electrons, where the particle flow N is proportional to the electric current and the chemical potential is proportional to the voltage; we maintain the quantities N and , in order not to exclude unconventional computing, e.g., computation by means of ions, photons, fermions, etc.), we have a linear transport equation, that is, Ohm’s law ( with ) which we obtain as follows:
For the special case in which and (to maintain particle conservation , it is possible to have the same chemical potentials or “voltages” in the reservoirs at temperatures and ), respectively, Equation (19) transforms into:
For this special case, the point at which the function (Equation (20)) reaches its maximum value is determined by condition . Applying this condition yields the following.
which is the well-known expression for the efficiency obtained by Curzon and Ahlborn [14] in their seminal work on endoreversible heat engines. This expression is particularly relevant for processes occurring at non-zero speed, where tasks are completed within a finite time.
For the Maximum Power function, the point at which the function (Equation (20)) reaches its maximum value is obtained similarly from condition . As shown in Figure 2, the Maximum Power function is plotted against , and the maximum is clearly observed for this special case at .
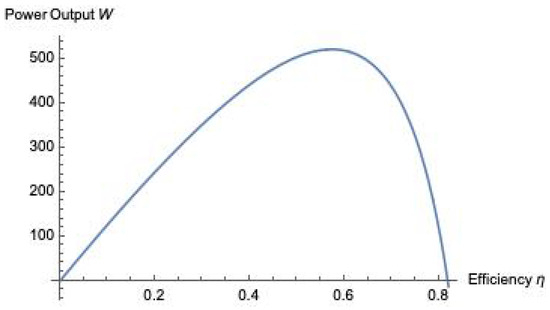
Figure 2.
Maximum Power output W vs. , for the special case in which and .
3.2. Endoreversible Landauer’s Principle for a Computer Gate Model
According to Equation (3), the total entropy in the reversible part is given by
Now, assuming that , , , and , from this last equation we obtain,
Substituting Equations (13) and (14) into Equation (22) obtains
which after some algebra results in,
where we are assuming that and . Then, substituting Equation (24) into Equations (13) and (14) yields,
and
Moreover, recalling that the total energy in the irreversible part is given by (Equation (2))
Equation (27) represents the work output for the endoreversible computer gate.
For the special case in which , and , we obtain the Landauer´s endoreversible principle for a computer gate,
3.3. Some Other Different Operation Regimes Regimes
Since the publication of the Curzon and Alhborn paper in 1975, it has been clear that one of the main results obtained from the model is the efficiency expression , which has since become known as the Curzon–Ahlborn efficiency. This result is independent of model parameters and depends solely on the temperatures of the heat reservoirs, resembling the expression obtained by Carnot [21] for a reversible theoretical cycle, .
It seems that the first problem, in optimization thermodynamics (review the following ref. [22] for a more detailed description of the topic) was the “Maximum Power problem” (solved by Carnot [21]), about a form of thermodynamic cycle that receives heat from a source of infinite capacity and gives heat to a source with less temperature, for which the power of the heat engine would be maximum [22]. Much later, the problem of the Maximum Power cycle was solved by Curzon and Alhborn [14].
An important advantage of the results obtained by Curzon and Ahlborn, later generalized within the framework of FTT, is that the optimal efficiency values more closely resemble those observed in real machines [19]. Within the context of FTT, several objective functions have been introduced to optimize under different criteria, and numerous models of heat engines that operate as real devices have been proposed and analyzed. The significance of these models lies in the fact that the energy production processes they describe are governed by similar underlying principles.
In the present article, we have already derived the endoreversible, or Curzon–Ahlborn, efficiency for a traditional computational gate (see Equation (21)), assuming the gate operates in the Maximum Power regime. However, there are two other particularly important regimes that will be analyzed in the following sections.
3.3.1. The Omega Function
The Omega function was proposed as part of a unified optimization criterion [19], representing the best compromise between energy benefits and losses in a device. In Finite Time Thermodynamics (FTT), the physical meaning is a kind of trade-off between useful energy and lost energy for a given heat device, such as an engine or refrigerator. It balances maximum useful energy output with unavoidable losses [19]. One notable advantage of this function is that it does not explicitly require the expression of entropy or any other environmental parameters, unlike other objective functions such as the Exergy or Ecological criteria [23,24].
The Omega function is defined as [25]:
where is the maximum attainable efficiency of an engine and is always equal to or less than the Carnot efficiency , that is, . The function is equivalent to another trade-off function known as Ecological function [23] when . Additionally, if we consider that the efficiency of the system is given by: and taking into account that , then for this system, the expression for the Omega function is given by,
Then, substituting Equation (19) into Equation (29) we get the Omega function for the endoreversible computer gate:
For the special case in which and , Equation (30) transforms into,
For the Omega function, the point at which the function (Equation (32)) reaches its maximum value is determined by condition , as shown in Figure 3, where the Omega function is plotted against , and the maximum is clearly seen for this special case at .
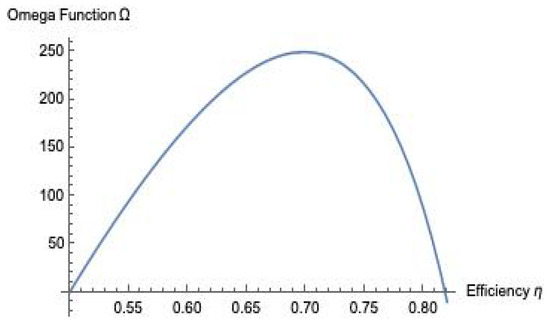
Figure 3.
Omega function vs. , for the special case in which and .
Moreover, previous studies reveal a close relationship between the Ecological function [23] and the Omega function [25] in terms of their behavior; see, for example, [26,27]. A particularly interesting property observed in the Ecological regime is that the efficiency satisfies the relation , where is the Carnot efficiency and is the Curzon–Ahlborn efficiency for thermal engines operating between the same thermal reservoirs. This relationship, known as the Semisum property, was first introduced by Arias et al. [28]. Notably, in our case, the validity of this property is clearly evident when comparing the behavior of the Omega function with the Semisum value: and .
3.3.2. The Efficient Power
In 2006, Yilmaz et al. [29] proposed a new performance criterion for thermal engines known as Efficient Power (EP). This criterion, which has been directly applied to Carnot, Brayton, Diesel engines, and other systems, incorporates the effects of design by defining Efficient Power as the product of power output and cycle efficiency , as expressed by the following equation.
If we substitute Equation (19) into Equation (32) we get the efficient power function for the endoreversible computer gate:
For the special case in which and , Equation (33) transforms into,
For the Efficient Power function, the point at which the function (Equation (34)) reaches its maximum value is determined by the condition . As shown in Figure 4, the Efficient Power function is plotted against , and the maximum is clearly observed for this special case at .
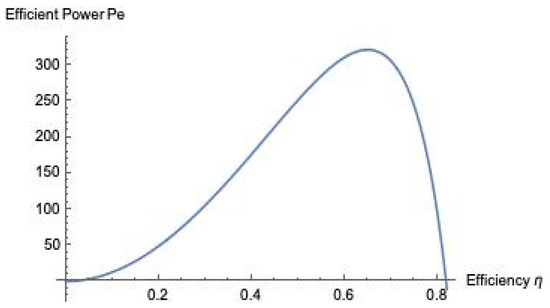
Figure 4.
Efficient Power function vs. , for the special case in which and .
3.4. Some Consequences of Landauers’s Principle
Landauer’s principle [1] establishes a very important relationship between thermodynamics and information theory. In principle, this establishes that the erasure of one bit of information in any computational systems (mainly in classical computers, but in general in systems where information is manipulated at small scales, such as in molecular and cell biology, artificial nano-devices or quantum computation), must be accompanied by a minimum amount of energy dissipation as heat. This dissipation is inevitable because of the increase in entropy associated with the loss of information. The energy cost of erasing one bit of information is given by [1,30]:
where is the Boltzmann constant (), is the temperature of the hot reservoir shown in Figure 1 and represents the reduction in the number of microstates from two to one.
However, is related with efficiency, for instance in the case of the Curzon and Alhborn efficiency, as:
For the special case of Carnot´s efficiency, the energy cost would be:
Additionally, using the approximation founded by for the Omega function Sanchez-Salas et al. [31], it is possible to find, for the Omega Function efficiency, the following expression:
Then, comparison between Equations (38)–(40) are shown in Figure 5.
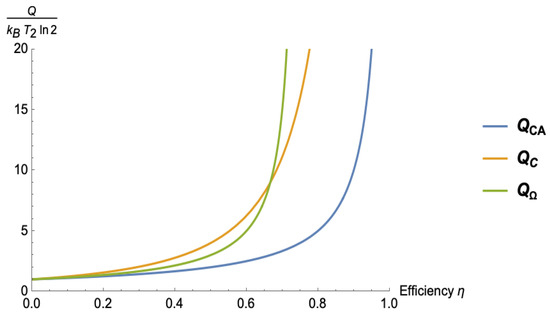
Figure 5.
Amount of energy dissipation as heat Q as function of Efficiency , for three different optimization criteria, namely: Curzon and Alhborn , Carnot , and Omega Function , respectively.
4. Discussion and Concluding Remarks
In a seminal and thought-provoking paper, Rolf Landauer [1] demonstrated a fundamental connection between information theory and thermodynamics. His central insight was that the act of erasing information is inherently accompanied by a certain amount of energy dissipation. Due to the experimental challenges associated with observing this effect at the single-particle level in the low-dissipation regime, empirical verification of Landauer’s principle only emerged in the second decade of the 21st century [5,6,7,8,9,10,11]. In a world increasingly reliant on digital computation, and with quantum computing on the horizon, it is crucial to deepen our understanding of the thermodynamic implications of information processing. A notable contribution in this direction was made by A. De Vos [12], who used a reversible model within the framework of finite-time thermodynamics to derive both Carnot’s law and Landauer’s principle from a theoretical point of view.
Building on Landauer’s insights and assuming that the information in traditional computers is transported by electrons, we extended De Vos’s reversible model by incorporating a matter flow. With this extension, we first recovered the Curzon–Ahlborn efficiency (see Equation (21)), noting that the maximum value in this context is . Second, we introduced what we refer to as the endoreversible Landauer principle for a computational gate (see Equation (28)).
In conventional computers, information is erased during the computational process, that is, . In contrast to reversible computers, no information is erased, and thus, . The understanding of reversible computing is very important in the sense of trying to design efficient computing systems and thereby minimize energy dissipation. According to Equation (28), if the objective is to minimize heat generation, this can be achieved in two distinct ways: (a) by ensuring that , as proposed by De Vos et al. [12], or (b) by making the total resistance negligible, , a condition that resembles superconductivity. Superconducting materials that exhibit zero electrical resistance can significantly reduce energy dissipation. These materials work at relative low temperatures, and then the immediate consequence is the design and development of materials with high thermal conductivity to facilitate efficient heat transfer.
Furthermore, we present a finite-time thermodynamic optimization based on three distinct criteria: Maximum Power Output, Maximum Omega Function, and Maximum Efficient Power. Our findings indicate that the efficiencies satisfy the ordering . These results suggest that operating under the Omega optimization criterion yields higher efficiency compared to the other two criteria. Finally, we observe that the Omega function satisfies the semisum property, a fact that is noteworthy within this theoretical framework.
Finally, in classical computers, when we take into account the information erased, this is in strong relation with the dissipation of energy and at the same time sets a theoretical lower limit of any computational process. The future design of energy-computing systems could be focused on a kind of trade-off in which computational operations avoid erasures of information and at the same time minimize the dissipation of energy.
The integration of Landauer’s principle with the Finite Time Thermodynamics provides a theoretical framework to relate the thermodynamic properties of the system (for instance, the efficiency) and the information processing. In this sense, Figure 5 shows the minimum energy dissipation associated with the loss of one bit of information as a function of efficiency considering it in terms of the optimization criteria. It is interesting that, for a given (for example ), the amount of energy dissipated is greater for the Carnot criterion than for the Omega function criterion, and the latter is even greater than the Curzon–Alhborn criterion, that is, .
In this sense, it is well known that the experimental set-up which tries to understand if work needed to erase a single bit of information (information processing requires work!) corresponds to the free energy difference between the initial and final states of the system, and seeking for this free energy, a colloidal particle confined in a double-well potential can be used as a single-bit memory. A custom-built vertical optical tweezers is used to realize a two-state system: a silica bead (radius ) is trapped at the focus of a laser beam (wavelength 1024 nm) which is rapidly switched (at a rate of 10 Khz) between two positions (separated by ) using an acousto-optic deflector. A disk-shaped cell (18 mm in diameter, 1 mm in depth) is filled with a solution of beads dispersed in bidistilled water at low concentration [9].
This additional work is proportional (translated as a change in free energy) to the global entropy production, and thus, quantifies thermodynamic efficiency. This reveals a trade-off between information and energy. Then, in order to achieve certain efficiency, we need to find the minimally dissipative protocol which takes into account constraints in space and time. Thus, in the protocol aforementioned, we could change some physical quantities to search for the validity of some of the mentioned regimes, for instance, the changing of the energy barrier height relative to the thermal energy, as well as the protocol total time duration or intuitively the dissipated work must be a function of the system length scale, that is, it is more difficult to move the distributions of particles with information long distances in the same time. Then, by taking into account different dissipative protocols in the well-established set-ups, we can test different optimization criteria, which can achieve significant reductions in energy dissipation (regardless of whether the system is classical, quantum or biological), and thus, have more sustainable efficient computing technologies.
Author Contributions
Conceptualization, J.C.C.-E.; methodology, formal analysis, investigation, J.C.C.-E., R.T.P.-H., J.C.P.-P. and D.L.-L.; visualization, writing—review and editing, data curation, J.C.C.-E. and M.S.-P.; software, validation, writing—original draft preparation; resources, supervision, project administration, funding acquisition, J.C.C.-E., R.T.P.-H., J.C.P.-P., D.L.-L. and M.S.-P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded in part by the economic support program of the Secretaría de Ciencia, Humanidades, Tecnología e Innovación (Secihti), and the Secretaría de Investigación y Posgrado (SIP) of the Instituto Politécnico Nacional under grants no. SIP-20251347 and Proyecto multidisciplinario no. SIP-3398.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon request.
Acknowledgments
The authors would like to thank the Instituto Politécnico Nacional of México (Secretaría Académica, SIP, COFAA, CIC), and the SECIHTI for their support in the development of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Keyes, R.W.; Landauer, R. Minimal energy dissipation in logic. IBM J. Res. Dev. 1970, 14, 152–157. [Google Scholar] [CrossRef]
- Bennett, C.H.; Landauer, R. The fundamental physical limits of computation. Sci. Am. 1985, 253, 48–57. [Google Scholar] [CrossRef]
- Landauer, R. Information is physical. Phys. Today 1991, 44, 23–29. [Google Scholar] [CrossRef]
- Bérut, A.; Arakelyan, A.; Petrosyan, A.; Ciliberto, S.; Dillenschneider, R.; Lutz, E. Experimental verification of Landauer’s principle linking information and thermodynamics. Nature 2012, 483, 187–189. [Google Scholar] [CrossRef]
- Orlov, A.O.; Lent, C.S.; Thorpe, C.C.; Boechler, G.P.; Snider, G.L. Experimental test of Landauer’s Principle at the sub-kBT level. Jpn. J. Appl. Phys. 2012, 51, 06FE10. [Google Scholar] [CrossRef]
- Gavrilov, M.; Chétrite, R.; Bechhoefer, J. Direct measurement of weakly nonequilibrium system entropy is consistent with Gibbs–Shannon form. Proc. Natl. Acad. Sci. USA 2017, 114, 11097–11102. [Google Scholar] [CrossRef]
- Ciliberto, S. Information and thermodynamics: Experimental verification of Landauer’s erasure principle. In Proceedings of the APS March Meeting Abstracts, San Antonio, TX, USA, 2–6 March 2015; Volume 2015, p. Z3–005. [Google Scholar]
- Bérut, A.; Petrosyan, A.; Ciliberto, S. Detailed Jarzynski equality applied to a logically irreversible procedure. Europhys. Lett. 2013, 103, 60002. [Google Scholar] [CrossRef]
- Zulkowski, P.R.; DeWeese, M.R. Optimal finite-time erasure of a classical bit. Phys. Rev. E 2014, 89, 052140. [Google Scholar] [CrossRef]
- Aimet, S.; Tajik, M.; Tournaire, G.; Schüttelkopf, P.; Sabino, J.; Sotiriadis, S.; Guarnieri, G.; Schmiedmayer, J.; Eisert, J. Experimentally probing Landauer’s principle in the quantum many-body regime. Nat. Phys. 2025, 1–6. [Google Scholar] [CrossRef]
- De Vos, A. Endoreversible models for the thermodynamics of computing. Entropy 2020, 22, 660. [Google Scholar] [CrossRef] [PubMed]
- Andresen, B.; Salamon, P. Future perspectives of finite-time thermodynamics. Entropy 2022, 24, 690. [Google Scholar] [CrossRef] [PubMed]
- Curzon, F.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Leff, H.S.; Rex, A.F. Maxwell’s Demon: Entropy, Information, Computing; Princeton University Press: Princeton, NJ, USA, 1990. [Google Scholar]
- Parrondo, J.M.; Horowitz, J.M.; Sagawa, T. Thermodynamics of information. Nat. Phys. 2015, 11, 131–139. [Google Scholar] [CrossRef]
- Proesmans, K.; Ehrich, J.; Bechhoefer, J. Finite-time Landauer principle. Phys. Rev. Lett. 2020, 125, 100602. [Google Scholar] [CrossRef]
- Gadomski, A.; Karpiński, K. Erasure by friction: An over-scales-manifesting estimation of the nanoscale (quantum) coefficient of friction. J. Phys. D Appl. Phys. 2025, 58, 135310. [Google Scholar] [CrossRef]
- Velasco, S.; Roco, J.; Medina, A.; White, J.; Hernández, A.C. Optimization of heat engines including the saving of natural resources and the reduction of thermal pollution. J. Phys. D Appl. Phys. 2000, 33, 355. [Google Scholar] [CrossRef]
- Callen, H. Thermodynamics; Wiley: New York, NY, USA, 1960; pp. 45–46. [Google Scholar]
- Carnot, S. Reflections on the motive power of fire, and on machines fitted to develop that power. Bachelier 1824, 108, 1824. [Google Scholar]
- Tsirlin, A.M.; Balunov, A.I.; Sukin, I.A. Finite-Time Thermodynamics: Problems, Approaches, and Results. Entropy 2025, 27, 649. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization: The Method of Thermodynamic Optimization of Finite-Size Systems and Finite-Time Processes; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Hernández, A.C.; Medina, A.; Roco, J.; White, J.; Velasco, S. Unified optimization criterion for energy converters. Phys. Rev. E 2001, 63, 037102. [Google Scholar] [CrossRef]
- Salas, N.S.; Velasco, S.; Hernández, A.C. Unified working regime of irreversible Carnot-like heat engines with nonlinear heat transfer laws. Energy Convers. Manag. 2002, 43, 2341–2348. [Google Scholar] [CrossRef]
- Chimal, J.; Sánchez, N.; Ramírez, P. Thermodynamic Optimality criteria for biological systems in linear irreversible thermodynamics. J. Phys. Conf. Ser. 2017, 792, 012082. [Google Scholar] [CrossRef]
- Arias-Hernández, L.; Angulo-Brown, F. A general property of endoreversible thermal engines. J. Appl. Phys. 1997, 81, 2973–2979. [Google Scholar] [CrossRef]
- Yilmaz, T. A new performance criterion for heat engines: Efficient power. J. Energy Inst. 2006, 79, 38–41. [Google Scholar] [CrossRef]
- Bormashenko, E. Landauer’s Principle: Past, Present and Future. Entropy 2025, 27, 437. [Google Scholar] [CrossRef]
- Sanchez-Salas, N.; López-Palacios, L.; Velasco, S.; Calvo Hernández, A. Optimization criteria, bounds, and efficiencies of heat engines. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2010, 82, 051101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).