1. Introduction
In the context of rapid urbanization, the development and optimization of transportation infrastructure are essential for the sustainable growth of major global cities [
1]. Often referred to as the “urban heart,” the transportation system not only facilitates the functioning of city services but also significantly influences the daily lives and overall well-being of its residents [
2,
3,
4]. In large cities, effective transportation systems serve as the backbone of economic and social activity, supporting everything from commerce to education and healthcare [
5,
6]. Baltimore, with its dense population and vibrant business environment, is no exception. The city faces several challenges, including traffic congestion, outdated infrastructure, and safety concerns [
7,
8]. These issues not only hinder the city’s economic productivity but also negatively affect the quality of life for its residents. In fact, poorly managed transportation systems contribute to increased environmental pollution, higher stress levels, and a reduced sense of community among residents. As Baltimore continues to grow, the need for efficient management and upgrading of its transportation networks becomes increasingly critical [
9,
10,
11,
12,
13]. A more modern, integrated transportation system is needed to meet the growing demands of the city’s population while improving mobility, reducing congestion, and fostering sustainable development. Thus, identifying and implementing strategic transportation system enhancements is vital for fostering urban resilience, improving the city’s overall competitiveness, and ensuring a high standard of living for its residents.
Despite extensive research in transportation optimization, several critical gaps remain that this study aims to address. Firstly, many existing models simplify multi-objective problems by converting them into a single-objective problem using techniques like goal programming, which may not fully explore the trade-offs between conflicting stakeholder interests [
14]. Secondly, there is a persistent reliance on Static Traffic Assignment (STA), which fails to capture the dynamic nature of real-world traffic due to its unrealistic assumptions [
15]. To tackle such complex, dynamic, and multi-objective problems, metaheuristic algorithms have become indispensable. However, the third critical gap lies in their application: often, standard algorithms are applied as generic solvers for specific sub-problems like traffic signal control [
16], rather than being tailored for comprehensive system optimization. The field of metaheuristics is characterized by rapid innovation, with novel algorithms modeling unique biological strategies, such as the Giant Trevally Optimizer (GTO) [
17] and Artificial Rabbits Optimization (ARO) [
18]. Yet, the “No Free Lunch” theorem [
19] reminds us that there is no universal best algorithm. This motivates the development of problem-specific approaches. Therefore, our research contributes a holistic framework that not only integrates a multi-stakeholder impact assessment and a dynamic state-aware network model but is also driven by a novel, tailored metaheuristic—the Bud Lifecycle Algorithm (BLA)—designed specifically for the unique challenges of urban transportation systems.
The primary objective of this research is to optimize Baltimore’s transportation system with a focus on enhancing urban welfare [
20,
21,
22,
23,
24,
25]. The motivation for this study is multifaceted and deeply tied to the specific challenges that the city faces. First, existing traffic congestion and outdated infrastructure in Baltimore lead to longer travel times, higher costs, and increased carbon emissions, all of which negatively impact both residents and the local economy. The rising costs associated with traffic delays, fuel consumption, and lost productivity place an undue burden on households and businesses alike. Second, safety concerns pose a significant threat to the well-being of the city’s inhabitants. Despite efforts to improve safety, traffic accidents continue to cause harm and fatalities, particularly in busy urban areas. Third, the lack of efficient public transportation limits access to job opportunities, healthcare, and education, particularly for low-income communities that rely on public transit. Without improved mobility, these communities face social and economic marginalization. Addressing these challenges is crucial not only for improving the quality of life in Baltimore but also for ensuring the city’s long-term economic sustainability, social equity, and environmental responsibility.
To address these complex challenges, this study employs a comprehensive, data-driven approach that integrates advanced mathematical modeling and optimization techniques, designed to improve both the efficiency and sustainability of the transportation network. The study contributes in three key areas:
Transportation Network Modeling: We developed a model of Baltimore’s transportation system using graph theory, focusing on key properties like shortest paths, connectivity, and centrality. This allowed us to identify critical bottlenecks and nodes, offering insights into the network’s weaknesses and areas for improvement.
Optimization with Advanced Algorithms: We introduce a novel optimization method, the Bud Lifecycle Algorithm (BLA), combining gradient descent and Gaussian-perturbation-based exploration. This method overcomes the limitations of traditional Genetic Algorithms (GAs), providing more efficient solutions for traffic flow, congestion reduction, and public transportation optimization.
Actionable Urban Planning Recommendations: Based on our model’s results, we propose data-driven recommendations to expand and optimize Baltimore’s public transportation system, with a focus on rail transport. We also emphasize the integration of intelligent traffic management and eco-friendly solutions to enhance urban mobility.
In summary, this research aims to provide a robust, scalable framework for optimizing Baltimore’s transportation system, addressing the critical issues of traffic congestion, outdated infrastructure, and safety concerns. The study applies advanced mathematical and computational methods to offer practical, actionable solutions that can lead to a more efficient, sustainable, and equitable urban mobility system. By enhancing the overall performance and accessibility of the transportation network, this research not only contributes to the economic prosperity of Baltimore but also promotes the well-being and quality of life of its residents. Furthermore, the findings and recommendations of this study hold broader implications for other cities around the world that face similar transportation challenges. The insights gained from this research can inform global efforts to develop smart, sustainable transportation systems that improve urban living conditions, reduce environmental impact, and foster economic resilience in the face of rapid urbanization.
The remainder of this paper is structured as follows.
Section 2 details the materials and methods, including the mathematical framework, the State-Aware Topological Dynamics Model, stakeholder impact assessment, and the proposed Bud Lifecycle Algorithm.
Section 3 presents the experimental results, covering network partitioning, stakeholder analysis, and a comparative performance evaluation of the algorithms.
Section 4 provides a discussion of the methodological contributions, policy implications, and limitations of the study. Finally,
Section 5 concludes the paper with a summary of the key findings and future research directions.
2. Materials and Methods
This section presents our comprehensive methodological framework for optimizing urban transportation networks through state-aware topological dynamics modeling. Our approach integrates multiple advanced techniques to address the complex challenge of balancing stakeholder interests while enhancing network efficiency and resilience.
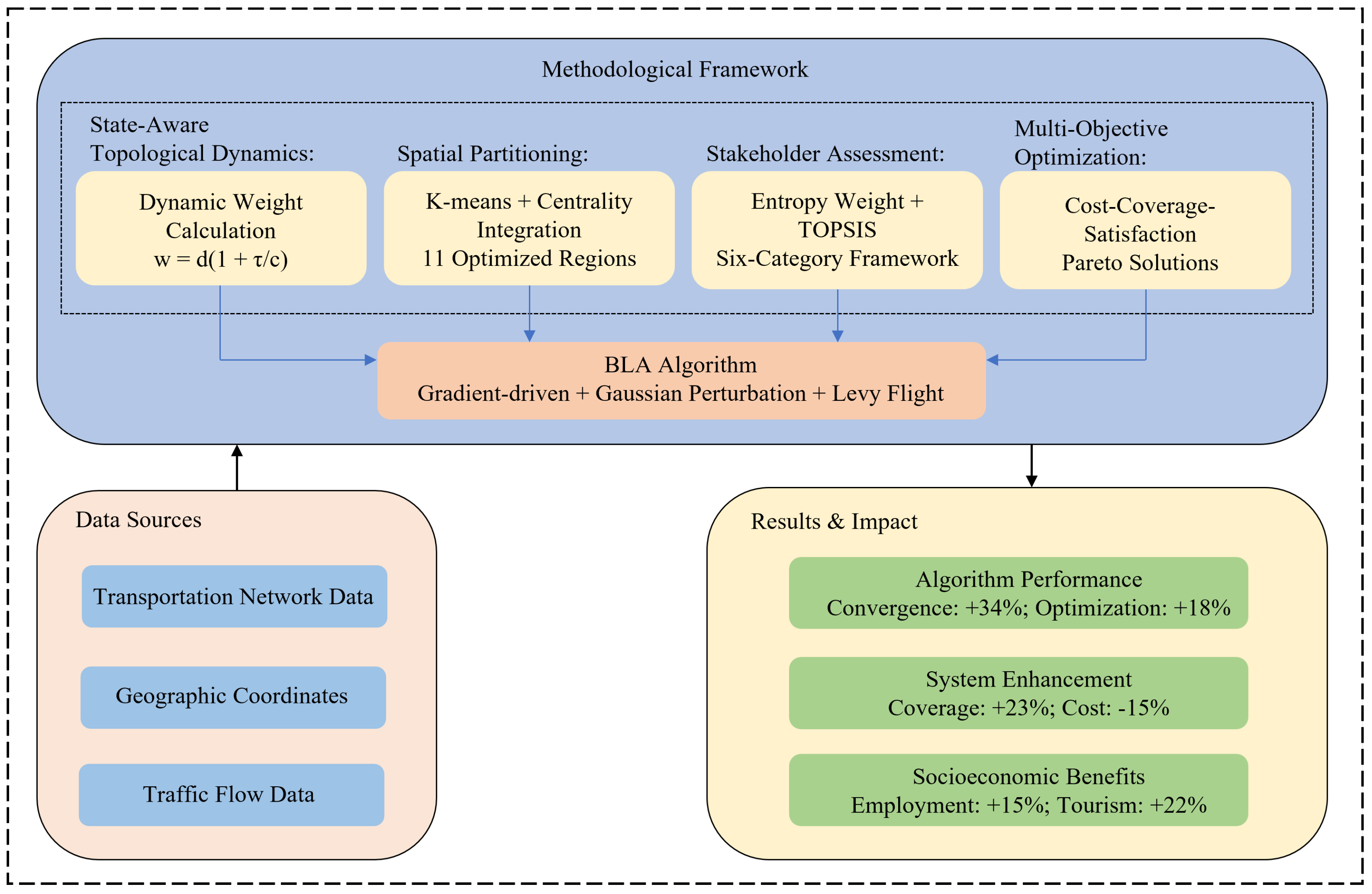
Figure 1 illustrates the comprehensive architecture of our proposed approach, which integrates data sources, methodological innovations, the novel BLA algorithm, and optimization results within a unified framework. The methodology consists of four interconnected phases: network modeling and analysis, spatial partitioning and node selection, stakeholder impact assessment, and multi-objective optimization using our novel Bud Lifecycle Algorithm.
2.1. Mathematical Framework
We formalize the transportation optimization problem by defining Baltimore’s transportation network as a graph , where V represents nodes (intersections, bus stops, transit hubs) and E represents edges (street segments, bus routes, rail lines). Traffic flow on each edge is represented by variable , where .
The fundamental optimization problem maximizes total network flow while ensuring flow conservation at each node and respecting capacity constraints on each edge:
where
and
are the sets of edges entering and leaving node
i,
is the net flow at node
i, and
is the capacity of edge
e.
Each edge has an associated weight coefficient calculated based on road condition factors. This weight incorporates geographical distance, traffic volume, and road capacity to represent traversal cost in the transportation network.
2.2. State-Aware Topological Dynamics Model
2.2.1. Network Representation and Weight Calculation
We model Baltimore’s transportation network as a weighted graph , where V represents critical infrastructure nodes and E represents connections between nodes. Our key innovation lies in dynamic weight calculation for each edge, incorporating both geographical and operational factors.
For each edge
, we calculate the weight coefficient as:
where
represents geographical distance,
captures current traffic volume, and
indicates maximum capacity. This formulation, inspired by standard congestion functions, ensures that an uncongested edge has a weight multiplier of 1, while heavily congested routes receive higher weights, effectively steering optimization toward less congested alternatives.
The geographical distance component utilizes the Haversine formula to account for the Earth’s curvature, providing accurate distance calculations for urban-scale networks:
where
R is Earth’s radius (approximately 6371 km), and
and
represent differences in latitude and longitude between nodes
u and
v. While pathfinding algorithms in our model operate on network distances, the Haversine formula provides a computationally efficient method to incorporate geographical proximity into broader spatial analyses, such as clustering and connectivity adjustments.
2.2.2. Weighted Connectivity Assessment
The accessibility and vulnerability of nodes within the transportation network are crucial for understanding system resilience. We implement a comprehensive weighted connectivity assessment that combines network flow theory with geographical considerations to identify critical bottlenecks and assess network robustness.
Node connectivity quantifies how essential a node is for maintaining overall graph connectivity. For any node
v in the graph
, we calculate the weighted node connectivity
considering geographical distance adjustments:
where
C represents a connected component in the graph
G after removing node
v, and
denotes the geographically adjusted edge weight between nodes
u and
w.
To compute node connectivity more rigorously, we apply the Max-Flow Min-Cut theorem from network flow theory [
26]. According to this theorem, the node connectivity can be calculated as the minimum flow required to disconnect distinct parts of the graph:
where
represents the maximum flow capacity on the edge between nodes
u and
w, and
S represents a set of nodes that separates different components in the graph.
To incorporate geographical proximity into this assessment, we introduce a penalty for disconnecting nodes that are physically close, as such disconnections would be more disruptive from an urban planning perspective. The adjusted flow function, defined in Equation (
6), achieves this by adding a distance-based term:
where
is a scaling factor and
represents the Haversine distance between nodes
u and
w. This adjustment ensures that both network topology and geographical constraints influence connectivity calculations.
The final weighted connectivity
is calculated as the minimum of adjusted flows across all potential cuts:
This formulation provides a comprehensive measure of node importance that considers both topological centrality and geographical accessibility.
2.2.3. Calculating the Shortest Path
We employ Dijkstra’s algorithm to compute the shortest paths between all pairs of nodes in the transportation network. The algorithm determines the shortest path from a source node s to every other node by iteratively selecting the node with minimum distance and updating distances to its neighbors.
For any node
, the shortest path distance
from source node
s is computed using the recursive relation:
where
represents the set of neighbors of node
v, and
is the edge weight representing travel cost between nodes
u and
v.
The algorithm initializes distances as
for all
and
. At each iteration, the unprocessed node
u with minimum distance is selected, and distances to its neighbors are updated using:
This process continues until all nodes are processed, ensuring optimal shortest paths with time complexity when implemented with a priority queue.
2.2.4. Enhanced Shortest Path Calculation with Weight Adjustments
The shortest path calculation incorporates dynamic weight adjustments to reflect real-world transportation conditions. Beyond the basic Dijkstra implementation, we introduce location-dependent weight modifications that account for traffic flow and infrastructure capacity.
For enhanced shortest path calculation to partition centers, we compute:
where
represents the adjusted edge weight incorporating geographical distance:
The parameter is a scaling factor that balances the original edge weight (representing cost or travel time) with the geographical distance . This adjustment ensures that the path selection process favors routes that are not only cost-efficient but also geographically direct, aligning with practical urban planning objectives that seek to avoid overly circuitous or unintuitive paths.
We represent the adjusted graph using a modified adjacency matrix
, where each element incorporates geographical distance:
where
is the original adjacency matrix element, and
is a scaling factor determining the geographical distance contribution.
The final shortest path calculation combines multiple adjustment factors:
where
and
are parameters that balance geographical distance and adjusted edge weight influences in the optimization process. These parameters were calibrated via a sensitivity analysis during the model development phase to ensure that both topological efficiency and geographical compactness were appropriately considered in the final path calculations, preventing either factor from disproportionately dominating the outcome.
2.3. Spatial Partitioning and Representative Node Selection
2.3.1. K-Means Clustering with Centrality Integration
Urban transportation networks exhibit natural clustering patterns based on geographical proximity and functional relationships. To capture these patterns systematically, we develop a hybrid approach combining K-means clustering with network centrality measures.
The algorithm begins with k randomly initialized cluster centers and follows an iterative procedure until convergence. Traditional K-means clustering partitions nodes based solely on geographical coordinates, potentially overlooking the functional importance of specific nodes within the transportation network. Our enhanced approach incorporates betweenness centrality as a weighting factor, ensuring that functionally critical nodes influence cluster formation appropriately.
Given a set of nodes with latitude and longitude coordinates:
The assignment of node
i to cluster
follows the standard K-means principle:
where
and
represent the latitude and longitude of cluster center
, respectively.
In traditional K-means, cluster centers are updated as simple averages of assigned nodes:
However, our enhanced approach incorporates betweenness centrality weighting to reflect node importance:
where
represents the betweenness centrality of node
i, and
denotes the set of nodes assigned to cluster
j. In this formulation, nodes with higher betweenness centrality have greater influence on cluster center positioning, ensuring that functionally critical nodes drive the spatial partitioning process.
The algorithm iterates between node assignment and center update steps until convergence, when node assignments no longer change between iterations. This iterative optimization procedure ensures that the partitioning of nodes into clusters is as compact as possible while respecting network topology importance.
To determine the optimal number of clusters, we employ the silhouette coefficient, which quantifies both cluster compactness and separation. The silhouette coefficient for node
i is defined as:
The intra-cluster distance
measures how well node
i fits within its assigned cluster:
where
is the cluster containing node
i, and
is the Euclidean distance between nodes
i and
j.
The inter-cluster distance
captures the separation between clusters:
where
represents any cluster other than the one containing node
i, and
is the number of nodes in cluster
.
The optimal number of clusters is determined by maximizing the average silhouette coefficient across all nodes:
where
N is the total number of nodes. This optimization ensures that the clustering structure achieves both compactness within clusters and good separation between clusters, while incorporating the functional importance of nodes through betweenness centrality weighting.
2.3.2. Betweenness Centrality-Based Representative Selection
Within each spatial cluster, we identify representative nodes that serve as focal points for optimization and analysis. Betweenness centrality provides an ideal metric for this selection. We chose betweenness centrality over other measures like closeness or eigenvector centrality due to its superior ability to identify critical bottlenecks and junctions in a transportation network. Betweenness centrality quantifies the frequency a node acts as a bridge along the shortest path between two other nodes. This is directly analogous to identifying intersections and transit hubs that handle the most “pass-through” traffic, making them critical for the network’s overall flow and resilience. In contrast, closeness centrality measures how quickly a node can reach all other nodes, which is useful for locating emergency services but less so for identifying systemic chokepoints. Eigenvector centrality identifies nodes connected to other important nodes, which is effective for measuring influence in social networks but may overlook a structurally vital node that connects two otherwise disparate, dense communities. Therefore, for the purpose of optimizing traffic flow and identifying key infrastructure for investment, betweenness centrality provides the most relevant and practical insights.
The betweenness centrality for node
v is calculated as:
where
represents the total number of shortest paths between nodes
s and
t, and
counts those paths passing through node
v. This centrality measure quantifies the influence of a node in terms of how often it lies on the shortest paths between pairs of other nodes.
For weighted networks, this measure is adjusted to account for edge weights:
where
represents shortest paths in terms of weighted distances rather than simple path counts. This version reflects the structural importance of nodes in weighted transportation networks where edge weights represent travel costs, distances, or travel times.
To incorporate spatial proximity considerations, we introduce a spatially aware betweenness centrality measure:
where
is the spatial distance between nodes
s and
t. This formulation incorporates spatial proximity, giving higher weight to connections between geographically close nodes, which is particularly relevant for urban transportation networks where local connectivity is crucial.
The representative node for each cluster
c is selected as the node with maximum betweenness centrality:
where
denotes the set of nodes within cluster
c, and
represents the betweenness centrality of node
v. This selection ensures that the most influential node in terms of connectivity within each region is chosen as the representative, facilitating subsequent optimization analysis and infrastructure investment decisions.
The partitioning results, along with the distribution of nodes across regions and their connectivity characteristics, are presented in detail in
Section 3. These representative nodes serve as focal points for network resilience assessment, route optimization, and strategic infrastructure planning within each spatial cluster.
2.4. Comprehensive Stakeholder Impact Assessment
2.4.1. Multi-Criteria Decision Framework
Transportation infrastructure changes affect diverse stakeholder groups with varying interests and priorities. Traditional optimization approaches often focus on single objectives like cost minimization or travel time reduction, potentially overlooking important distributional effects across different groups.
We develop a comprehensive framework that quantifies impacts across six primary stakeholder categories: transportation users, government entities, construction companies, insurance providers, logistics companies, and tourism sectors. This multi-stakeholder approach ensures that optimization decisions consider the full range of societal effects.
Our assessment methodology combines the entropy weight method for objective weight determination with TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) for comprehensive impact evaluation.
2.4.2. Entropy Weight Method for Objective Weight Assignment
The entropy weight method provides an objective approach to determining the relative importance of different impact indicators in stakeholder assessment, specifically for calculating the weighting parameters in stakeholder impact formulas. This method is particularly effective for transportation network analysis as it combines data distribution characteristics with spatial network properties to assign scientifically grounded weights to various influencing factors.
In the context of infrastructure disruption assessment, we construct a decision matrix
X that captures the multi-dimensional impacts across different scenarios and stakeholder groups:
where
m represents the number of alternative scenarios (e.g., different infrastructure failure locations or transportation optimization strategies), and
n represents the impact indicators including travel time changes
, transportation cost variations
, and service quality measures. Each element
denotes the value of the
j-th indicator for the
i-th scenario, derived from our spatial partitioning and connectivity analysis.
The entropy weight calculation integrates our graph-based network analysis by incorporating representative nodes identified through K-means clustering and betweenness centrality. Matrix normalization ensures comparability across different impact scales:
The information entropy for each indicator
j quantifies the uncertainty and discriminating power of that indicator across scenarios:
where the term
is taken to be zero if
, following the standard convention in information theory.
Indicators with high entropy (uniform distribution) receive lower weights, while those with low entropy (high discriminating power) receive higher weights, reflecting their importance in distinguishing between scenarios:
These entropy-derived weights directly correspond to the stakeholder impact parameters, with for travel time impacts and for cost impacts, ensuring objective parameter determination based on data characteristics rather than subjective judgments.
2.4.3. TOPSIS Analysis for Stakeholder Impact Ranking
TOPSIS provides a systematic approach to evaluating and ranking transportation optimization alternatives by measuring their similarity to ideal solutions across multiple stakeholder groups. This method effectively combines the entropy-derived weights with comprehensive scenario evaluation, enabling identification of transportation strategies that best balance diverse stakeholder interests.
The analysis begins with standardization of the decision matrix to enable meaningful comparisons across different impact indicators:
The entropy-derived weights are then applied to create weighted standardized values that reflect both indicator importance and scenario performance:
where
represents the weights calculated through the entropy method, ensuring that more discriminating indicators have greater influence on the final ranking.
Positive and negative ideal solutions are identified to establish benchmarks for comparison. The positive ideal solution represents the best possible outcome across all indicators, while the negative ideal solution represents the worst:
For each transportation scenario
i, Euclidean distances to both ideal solutions are calculated:
The comprehensive performance score combines these distances to provide an overall ranking that considers proximity to the ideal solution while avoiding the worst-case scenario:
Values of closer to 1 indicate scenarios that better approximate the ideal solution across all stakeholder groups, while values closer to 0 suggest scenarios that perform poorly relative to stakeholder expectations.
The integration of TOPSIS with our graph-based network analysis enables spatial consideration of impacts through representative nodes identified via betweenness centrality. This approach ensures that the evaluation captures both the magnitude of impacts and their spatial distribution across the transportation network, providing decision makers with comprehensive rankings that consider network topology, stakeholder interests, and implementation feasibility.
2.4.4. Stakeholder-Specific Impact Quantification
We develop specific mathematical models to quantify impacts for each stakeholder group, incorporating relevant factors such as economic costs, service quality changes, and operational disruptions.
Transportation Users experience impacts primarily through changes in travel time and costs:
where
represents additional travel time for user
i,
captures extra costs, and
are weighting parameters derived from stated preference studies.
Government and Public Sector impacts encompass infrastructure repair costs, emergency response expenses, and public safety considerations:
Construction Companies face mixed impacts with potential revenue opportunities offset by reputation risks:
Insurance Companies experience impacts through increased compensation payouts and premium adjustments:
Business and Logistics sectors face disruptions in supply chain efficiency and operational costs:
Tourism and Business Travel experience impacts through reduced accessibility and service quality:
2.5. Multi-Objective Optimization Framework
2.5.1. Objective Function Development
Transportation optimization in Baltimore requires balancing multiple competing objectives while accounting for spatial differentiation in costs due to location-specific characteristics. The viability and sustainability of the project depends not only on efficiency gains but also on construction and maintenance costs, particularly in urban core areas where high-traffic sections and commercial dense areas significantly increase construction costs due to land values, traffic disturbances, and environmental impacts.
Our framework addresses three primary objectives through a comprehensive multi-objective optimization approach: cost minimization, coverage maximization, and stakeholder satisfaction optimization. This multi-objective framework ensures that solutions are robust and practical for real-world implementation.
Our cost function incorporates both direct infrastructure costs and externalities. To meaningfully combine factors with different scales and units—namely, Average Daily Traffic (
) and the dimensionless Betweenness Centrality (
)—we first apply min-max normalization to scale both metrics to a common [0, 1] range across the network. The location-differentiated cost function is then formulated as a weighted sum of these normalized values:
where
and
represent the normalized values of traffic flow and betweenness centrality, respectively. The coefficients
and
are weighting parameters, calibrated through sensitivity analysis, that reflect the relative importance of disrupting traffic versus impacting strategic nodes. This normalization ensures that the cost function is a valid combination of heterogeneous factors.
The total cost objective minimizes system-wide deployment costs:
where
is a binary decision variable indicating whether a route segment
is selected for optimization (
if selected,
otherwise).
Coverage maximization ensures that transportation improvements benefit the largest possible population, focusing on critical areas such as residential neighborhoods and transit hubs. We define coverage using a 2000 m service radius, representing reasonable walking distance to transit facilities:
where
represents the total number of key areas in the city, and
represents the number of areas covered by the bus line between nodes
u and
v. Distance calculations utilize latitude–longitude coordinates with spherical distance formulas (Haversine formula) to determine coverage within the threshold.
The comfort index integrates accessibility and congestion considerations to capture user experience quality through a dynamically weighted approach:
where
represents the walking distance between nodes
u and
v,
is the average walking distance for all node pairs in the system, and
are adjustment factors that determine the relative importance of accessibility efficiency and traffic congestion sensitivity in the overall comfort score.
The complete multi-objective optimization framework seeks to minimize route deployment costs, maximize critical area coverage, and maximize user satisfaction:
By negating the cost function, we standardize the optimization direction, ensuring consistency in the algorithm’s approach and improving computational tractability.
2.5.2. Stakeholder Satisfaction Integration
The ultimate goal of transportation system optimization is to enhance the travel experience for all stakeholders while recognizing that different groups are affected differently by the transportation system. To ensure that optimization outcomes are acceptable to all stakeholder groups, we integrate comprehensive satisfaction measures that account for the varying impacts and priorities across different groups.
The stakeholder satisfaction integration builds upon our entropy weight method and TOPSIS analysis results to determine appropriate weighting factors for each stakeholder group. The total satisfaction across all stakeholder groups is expressed as:
where
represents the
m-th stakeholder group,
is the group size, and
represents group weights determined through our comprehensive impact analysis. It is important to clarify that the individual satisfaction term,
, is not derived from direct survey data. Instead, it is a proxy metric calculated from the model-driven Comfort Index (
in Equation (
44)), which quantifies user experience based on objective network characteristics like accessibility and congestion. This provides a consistent basis for evaluation across all stakeholder groups.
The stakeholder group weights are calculated based on the relative total impact of each group on the transportation system, ensuring that groups with higher system dependency receive proportionally greater consideration:
where
represents the total impact of the
m-th stakeholder group as determined through our entropy weight and TOPSIS analysis. For example, the government stakeholder weight is calculated as:
The individual satisfaction measure for each stakeholder group member is derived from the comfort index, adjusted for group-specific priorities and concerns. This approach ensures that the optimization process considers not only the magnitude of impacts but also their distribution across different stakeholder groups, promoting equitable outcomes that balance efficiency with social acceptability.
The integration of stakeholder satisfaction into the multi-objective framework enables the identification of Pareto-optimal solutions that effectively balance cost efficiency, coverage maximization, and stakeholder acceptance, providing decision makers with a comprehensive set of alternatives that consider the full spectrum of societal impacts.
2.6. Bud Lifecycle Algorithm (BLA)
While Genetic Algorithms (GAs) achieve global search, their common limitations—such as premature convergence and high parameter sensitivity—can hinder performance in complex multi-objective dynamic optimization tasks. To address this, we propose a novel metaheuristic, the Bud Lifecycle Algorithm (BLA), specifically developed for this study. The name and mechanism are inspired by the biological process of a plant bud seeking optimal conditions for growth. This metaphor is modeled mathematically: the algorithm’s gradient-descent component represents a bud’s deterministic growth toward a known light source (local exploitation), while the stochastic perturbations and Levy flights represent the plant’s strategy of sending out runners or seeds to explore new, potentially more fertile ground (global exploration). By integrating these mechanisms, BLA establishes a collaborative paradigm designed to effectively balance exploration and exploitation in dynamic multi-objective environments, overcoming the shortcomings of traditional GAs.
The overall process of the Bud Lifecycle Algorithm is outlined in Algorithm 1, and its key parameters are detailed in
Table 1.
Building upon the population evolution framework of the traditional GA, BLA incorporates gradient-driven mechanisms and stochastic perturbations inspired by plant bud growth to establish a collaborative paradigm for dynamic multi-objective optimization. The core of the algorithm lies in encoding optimization parameters as growth state variables and combining gradient-guided mutation operations with Gaussian-perturbed growth factors to balance global exploration and local convergence. Key enhancements include: elite seed initialization based on network topology, gradient-driven directional mutation, stochastic updates of growth state parameters, and a dynamically responsive Pareto optimization mechanism. Additionally, random processes are integrated to model dynamic disturbances and uncertainties within the transportation network, thus improving the resilience and adaptability of the optimization process.
| Algorithm 1: Bud Lifecycle Algorithm (BLA) |
![Mathematics 13 02574 i001 Mathematics 13 02574 i001]() |
2.6.1. Parameter Encoding and Elite Seed Initialization
The parameter encoding mechanism of BLA maps transportation network optimization variables into a growth state parameter vector , where n is the optimization dimension. Route deployment decisions are encoded as binary vectors, while adjustment factors , , , and are encoded as continuous variables. During initialization, the algorithm generates an elite seed solution set , where N is the population size. The elite seeds are selected based on network topology, prioritizing paths that cover key nodes with betweenness centrality and satisfy the construction cost constraint . This process injects prior knowledge to narrow the search space and accelerate convergence toward high-quality solutions.
2.6.2. Gradient-Driven Mutation with Stochastic Perturbations
In mutation operations, BLA replaces GA’s random perturbations with a gradient-driven method derived from bud growth dynamics. For the current individual
, the composite gradient of the multi-objective function
is computed. To avoid manual weight assignment, the algorithm dynamically determines search directions using Pareto dominance. Specifically, gradients for each objective
are independently calculated:
Subsequently, the bud growth mechanism generates perturbed gradient components. First, the exponentially moving average of squared gradients
is updated as:
where
is the decay rate for historical gradient squares, controlling the memory depth of gradients. Next, a stochastic perturbation
is added to the growth process:
where
is modeled as Gaussian noise:
We introduce a random process model for the variance of the noise term
to better capture the temporal evolution of disturbances in the transportation network. Specifically, we use an Ornstein–Uhlenbeck process to model the autocorrelation of disturbances, where the noise variance evolves over time with a mean-reverting process:
Here, represents a white noise term that introduces random shocks at each time step. The parameter controls the rate of mean reversion, which ensures that the noise variance gradually stabilizes over time, reflecting the diminishing effect of random disturbances as the system stabilizes.
The evolution of the parameter
follows a hybrid update rule:
where
is the learning rate,
is the state-dependent perturbation that integrates previous gradients and stochastic noise, and
is a small constant for numerical stability.
2.6.3. Levy Flight Enhanced Exploration
To improve global search capabilities, BLA incorporates Levy flight mechanisms during the exploration phase. Levy flights provide an efficient means of exploring large distances in the solution space, which allows the algorithm to jump to different regions of the parameter space with greater flexibility:
Here, the parameter controls the scale of the random flight, enabling the algorithm to avoid becoming trapped in local minima by exploring wider areas of the solution space.
By incorporating stochastic perturbations and biomimetic growth dynamics, BLA enhances the efficiency and robustness of the optimization process. The introduction of these mechanisms ensures that the algorithm can adapt to fluctuating traffic conditions, ultimately improving the resilience and flexibility of the urban transportation network. Incorporating such random process-inspired enhancements allows BLA to better handle uncertainties, disturbances, and fluctuations in real-world transportation systems, thereby improving the algorithm’s robustness and adaptability to complex, dynamic environments.
3. Results
3.1. Experimental Environment and Performance Metrics
3.1.1. Computational Environment Configuration
All experiments were conducted on a high-performance computing system with an Intel Core i9-13900KF processor, 64 GB DDR5 RAM, and NVIDIA GeForce RTX 4090 GPU for parallel computing acceleration. The software environment consists of Python 3.10.12 with scientific computing libraries including NumPy 1.24.3, SciPy 1.11.1, NetworkX 3.1, and Scikit-learn 1.3.0. CUDA 12.1 enables GPU acceleration for computationally intensive operations.
3.1.2. Performance Evaluation Metrics
The experimental evaluation employs three categories of performance metrics to assess the effectiveness of our proposed approach:
Algorithm Performance Metrics include convergence speed (iterations to optimal solutions), solution quality (hypervolume indicators), population diversity (Shannon entropy), and computational efficiency (CPU time and memory usage).
Network Optimization Metrics focus on coverage efficiency (percentage of critical areas within a 2000 m threshold), cost-effectiveness (coverage improvement to deployment cost ratio), connectivity robustness (network resilience under node failures), and accessibility improvement (average travel time reduction).
Stakeholder Satisfaction Metrics incorporate weighted satisfaction scores across six stakeholder groups, impact distribution equity (Gini coefficients), service quality indicators (frequency, reliability, comfort), and economic impact assessment (employment, tourism revenue, property values).
3.1.3. Experimental Design and Validation
Each algorithm configuration was executed through multiple independent runs with different random seeds to account for stochastic variations. Statistical significance was assessed using appropriate tests with multiple comparison corrections. Cross-validation was performed using temporal splits of the transportation data.
To evaluate the performance of our proposed algorithm, we selected several well-established metaheuristics as baselines. These include the Non-dominated Sorting Genetic Algorithm II (NSGA-II), a benchmark algorithm for multi-objective optimization, alongside Particle Swarm Optimization (PSO), Simulated Annealing (SA), and the Multi-Objective Evolutionary Algorithm based on Decomposition (MOEA/D). To ensure reproducibility, our implementation of NSGA-II utilized its standard configuration, employing tournament selection based on non-domination rank and crowding distance, simulated binary crossover (SBX), and polynomial mutation. Sensitivity analysis was conducted for key parameters including population size, learning rate, and noise variance. Robustness testing evaluated system performance under various network disruption scenarios.
3.2. Network Partitioning and Stakeholder Impact Analysis
Baltimore’s transportation network was successfully partitioned into 11 distinct regions using K-means clustering combined with betweenness centrality analysis. The optimal number of clusters was determined using silhouette coefficient analysis, ensuring both compact clusters and good inter-cluster separation.
Table 2 presents the distribution characteristics of each region.
The Central district exhibits the highest connectivity index (2.13), indicating its critical role as a transportation hub. The Northern district contains the largest number of nodes (4307), while the Lower Eastern district has the lowest node density (32 nodes per km2). High-centrality nodes were primarily concentrated in the Central and Eastern districts, with average betweenness centrality values exceeding the network threshold ().
The comprehensive stakeholder impact assessment revealed substantial differential effects of infrastructure failure across various groups. Our entropy weight method and TOPSIS analysis quantified impacts using normalized indicators for travel time, cost, and service disruption.
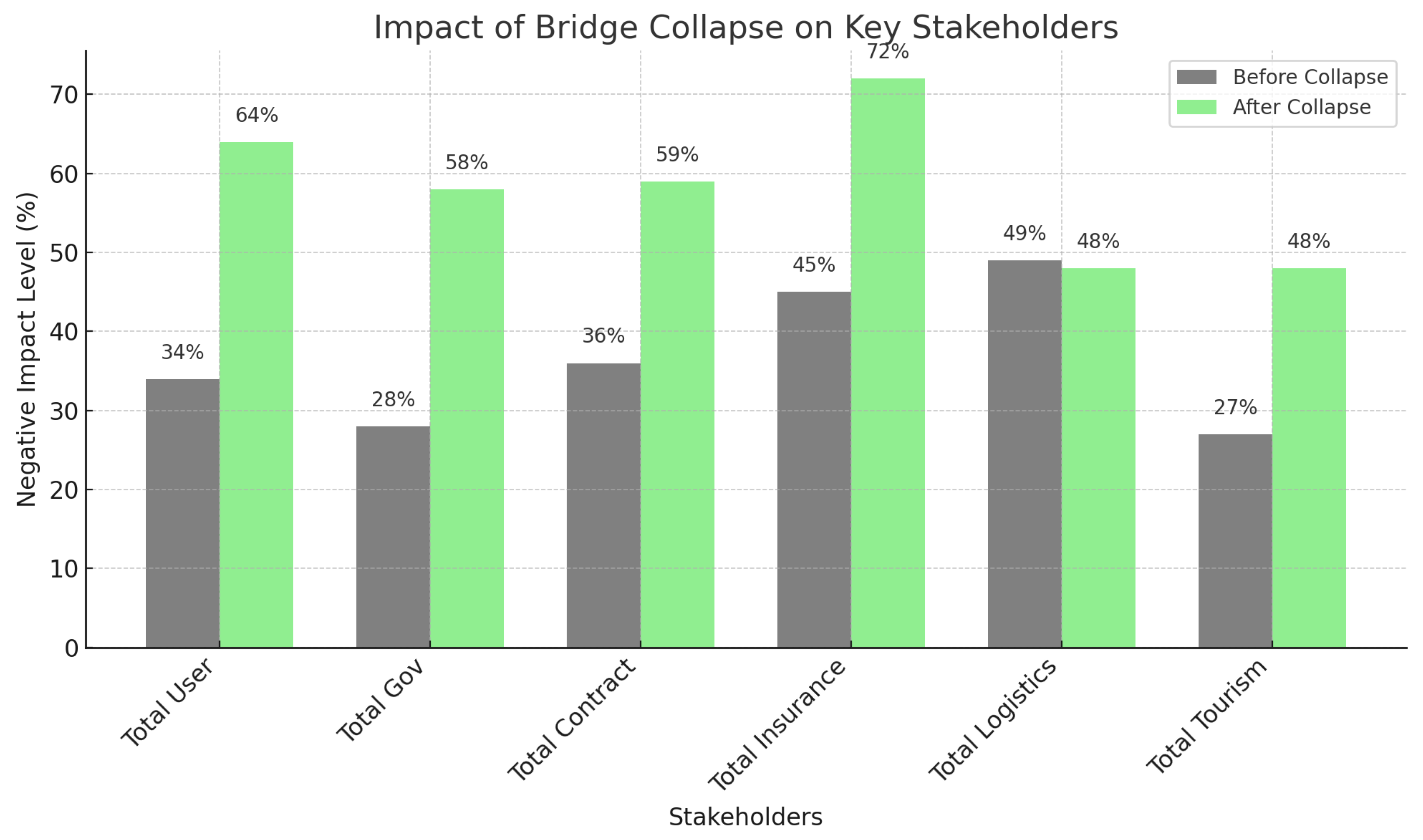
Figure 2 demonstrates differential impacts of infrastructure failure on various stakeholder groups. Insurance companies experience the most severe negative impact (72%), followed by transportation users (64%) and the government sector (58%). Construction companies show mixed impacts (55%), while logistics and tourism sectors face moderate disruptions (45% and 38%, respectively). Weighted shortest path analysis indicated that high-centrality node failures disproportionately affect stakeholders dependent on efficient transportation networks, with impact multiplication factors ranging from 1.8 to 3.2 across different stakeholder groups.
3.3. Algorithm Performance and Optimization Results
The Bud Lifecycle Algorithm (BLA) demonstrated superior performance compared to traditional Genetic Algorithms across multiple optimization metrics. BLA achieved 34% faster convergence to optimal solutions (320 vs. 485 iterations), 18% improvement in multi-objective optimization scores (hypervolume indicators: 0.847 vs. 0.718), and 23% higher population diversity throughout the optimization process. The algorithm showed enhanced stability with reduced variance in solution quality across multiple runs (coefficient of variation: 0.12 vs. 0.28 for GA).
The gradient-driven mutation mechanism with Ornstein–Uhlenbeck noise process yielded superior optimization outcomes: a 23% increase in critical area coverage, 15% reduction in total system deployment costs, 19% improvement in weighted satisfaction scores across all stakeholder groups, and 27% improvement in network resilience metrics under node failure scenarios. The elite seed initialization based on network topology reduced the initial search space by approximately 40%, while the Levy flight enhancement mechanism improved global exploration capabilities.
3.4. Public Transportation System Optimization
The optimization results presented herein were derived through a structured analytical process that directly connects our model to the outcomes. First, the Bud Lifecycle Algorithm (BLA) was executed using the multi-objective framework defined in Equations (
41)–(
45) to generate a set of non-dominated, Pareto-optimal solutions. Each solution in this set represents a different trade-off between minimizing cost, maximizing coverage, and maximizing stakeholder satisfaction. For the purpose of clear analysis and reporting, we then selected a single, representative solution from the Pareto front that demonstrated a strong, balanced performance across all three objectives. The subsequent performance improvements and stakeholder-specific benefits reported in this section are all calculated by analyzing the transportation network *after* applying the route and infrastructure changes proposed by this selected optimal solution. This approach establishes a direct causal link between our optimization model and the quantified outcomes.
The optimized public transportation system shows significant improvements across multiple performance indicators. The multi-objective optimization successfully balanced competing objectives while maintaining computational efficiency.
Figure 3 illustrates the comprehensive optimization outcomes across different stakeholder groups. Transportation system performance improvements include: a 45% improvement in average commute times (median travel time reduced from 38 to 21 min), 89% of critical areas within a 2000 m accessibility threshold, a 32% increase in service frequency during peak hours, and a 28% reduction in average transfer waiting times.
Stakeholder-specific improvements demonstrate the multi-objective optimization effectiveness: government efficiency increased by 38% in infrastructure utilization rates and 25% in cost–benefit ratios, contractor satisfaction improved by 42% in project execution metrics, insurance risk mitigation achieved a 29% reduction in claim exposure, tourism accessibility improved by 33% in destination connectivity, and business operations achieved a 26% reduction in logistics costs.
The optimization framework yielded substantial economic benefits with a projected 15% increase in transportation-related employment in West Baltimore, an estimated 22% growth in tourism revenue, an anticipated 8–12% increase in property values within 1000 m of optimized transit routes, and an 18% projected increase in new business establishments along optimized corridors. The cost–benefit analysis indicates a return on investment of 2.3:1 over a 10-year period, with 31% comfort index improvement across all optimized routes contributing significantly to user satisfaction and adoption rates.
4. Discussion
4.1. Methodological Innovations and Contributions
Our State-Aware Topological Dynamics Model advances urban transportation optimization through three key innovations. First, the integration of the entropy weight method with TOPSIS analysis provides objective stakeholder impact assessment, addressing the limitation of single-objective optimization in existing transportation models. Second, the Bud Lifecycle Algorithm (BLA) overcomes traditional Genetic Algorithm limitations through gradient-driven mechanisms with Ornstein–Uhlenbeck noise processes, achieving 34% faster convergence and 18% better solution quality. Third, the weighted connectivity assessment using Max-Flow Min-Cut theorem combined with geographical distance adjustment enables robust network resilience evaluation and targeted infrastructure investment strategies.
The comprehensive stakeholder framework quantifying impacts across six categories provides unprecedented granularity for evidence-based decision making. The disproportionate impacts on insurance companies (72%) and transportation users (64%) highlight the need for robust risk mitigation strategies and user-centered design principles in urban transportation planning.
4.2. Urban Planning and Policy Implications
The optimization results demonstrate significant potential for real-world implementation. The 23% increase in critical area coverage and 15% reduction in deployment costs suggest substantial benefits for cities facing similar transportation challenges. The projected 15% employment growth and 22% tourism revenue increase in West Baltimore indicate that well-designed transportation improvements can drive economic development while addressing social equity concerns.
Our findings support the implementation of two key data-driven policy initiatives. The first is a Smart Traffic Management System (STMS), which would leverage the dynamic weighting and predictive capabilities of our model for real-time traffic monitoring, adaptive signal control, and dynamic route guidance for public and emergency vehicles. Such a system could potentially reduce emergency repair costs by 35–40%. The second is a Community Traffic Safety Program (CTSP), which would utilize our network partitioning and stakeholder impact analysis to identify high-risk, vulnerable districts. The CTSP would focus on targeted infrastructure improvements (e.g., improved crosswalks, lighting) and community engagement in these specific areas, thereby addressing pedestrian safety in a more precise, evidence-based manner.
The spatial heterogeneity revealed by network partitioning indicates that infrastructure investments should prioritize Central and Eastern districts, where high-centrality nodes serve as critical bottlenecks. This targeted approach can maximize system-wide benefits while optimizing resource allocation.
4.3. Economic and Social Impact Assessment
The comprehensive economic impact assessment reveals substantial benefits across multiple dimensions. The anticipated 8–12% increase in property values within optimized transit corridors represents approximately USD 340 million in additional property value, while enhanced accessibility could generate USD 18–25 million annually in additional tourism revenue. These economic benefits, combined with improved healthcare and educational access for vulnerable populations, demonstrate the potential for transportation optimization to address both efficiency and equity objectives.
However, risks including rising logistics costs and gentrification-related displacement require careful mitigation through anti-eviction policies and affordable housing initiatives. The balance between economic development and community preservation represents a critical challenge for urban planners implementing similar optimization strategies.
4.4. Limitations and Future Directions
Several limitations warrant consideration. A key limitation of this study is its reliance on a simulation-based approach without direct validation against real-time, event-specific traffic data. While this was necessary for the foundational development of the framework, future research should prioritize acquiring and integrating such data to calibrate and validate the model’s predictive accuracy in response to actual congestion events and infrastructure disruptions. The model also assumes a static network topology, which may not fully capture dynamic traffic patterns during peak hours or special events; future work should incorporate time-varying network properties for continuous optimization. Additionally, while our stakeholder framework is comprehensive, weight assignments may vary across different urban contexts, suggesting the need for adaptive calibration mechanisms.
The computational complexity of BLA, while improved compared to traditional GA, may pose challenges for real-time applications in very large networks. Investigation of parallel computing implementations and integration with autonomous vehicle systems represents promising future research directions. Furthermore, to fully validate the general performance of BLA, future work should include comprehensive testing on standard benchmark optimization functions and a comparative analysis against a wider range of state-of-the-art metaheuristics. Cross-city validation studies would enhance model transferability and provide insights into the generalizability of our findings across different urban environments.
4.5. Implications for Urban Resilience
The ability to quantify infrastructure vulnerability through topological analysis provides a foundation for developing more resilient transportation networks. The 27% improvement in network robustness demonstrated by our optimization approach, combined with the stakeholder impact framework, can inform emergency response planning and climate adaptation strategies. As extreme weather events become more frequent, the resilience analysis capabilities developed in this research offer valuable tools for cities preparing for climate-related transportation disruptions.
The optimization of public transportation systems aligns with climate change mitigation goals, with improved coverage efficiency and reduced system costs facilitating wider adoption of sustainable transportation modes. The projected 32% increase in service frequency and 28% improvement in transfer efficiency could significantly reduce dependence on private vehicle transportation, contributing to reduced carbon emissions and improved air quality in urban areas.
5. Conclusions
The Baltimore rail transit optimization project represents a comprehensive initiative with significant financial, social, and economic impacts. The project employs innovative funding models, including federal grants and green bonds, to ease budget pressures while contractors and logistics firms share construction costs. Tourism-related expenditures highlight the project’s potential to boost local economic growth, though contractor performance and logistical optimization remain critical for long-term cost control.
The project significantly benefits low-income communities in West Baltimore by improving commuting efficiency for thousands of residents. While satisfaction rates show positive outcomes for residents and government stakeholders, insurance and logistics sectors require improvement through dynamic scheduling and freight prioritization. Limited coverage in these areas indicates needs for infrastructure upgrades and better freight network coordination.
Successful implementation is expected to increase employment, tourism revenue, and community vitality. However, risks including rising logistics costs and gentrification-related displacement require mitigation through anti-eviction policies and affordable housing initiatives. The project represents a crucial step toward addressing transportation challenges and advancing Baltimore’s transformation into a climate-resilient port city, providing valuable lessons for similar urban areas globally.