A Spectral Approach to Variable-Order Fractional Differential Equations: Improved Operational Matrices for Fractional Jacobi Functions
Abstract
1. Introduction
2. Core Definition of Liouville–Caputo VOFDs
3. Shifted Jacobi Polynomials and Fractional Jacobi Functions
3.1. Analytical Framework: Shifted JP Basis Functions
3.2. Introducing Generalized FJFs
4. Operational Matrices for Both ODs and VOFDs of
5. Numerical Handling for MTVOFDE Subject to ICs
5.1. Homogeneous ICs
5.2. Nonhomogeneous ICs
| Algorithm 1 GFJCOPMM algorithm |
|
- Array: For creating and manipulating arrays, which are used to hold coefficients and operational matrices throughout the computations.
- NSolve: For finding numerical solutions to nonlinear algebraic equations; it is utilized to compute the zeros of or, alternatively, the points .
- FindRoot: For solving equations by finding roots; it is essential in handling the nonlinear aspects of our system, using a zero initial approximation.
- JacobiP: For generating , which serve as basis functions that provide the foundation for approximating the solution in our collocation method.
- D: To compute ordinary derivatives to determine the defined residuals.
- LCaputoD: To compute Liouville–Caputo fractional derivatives to determine the defined residuals.
- Table: For generating lists and arrays of values based on specified formulas, particularly for collocation points and other parameterized data.
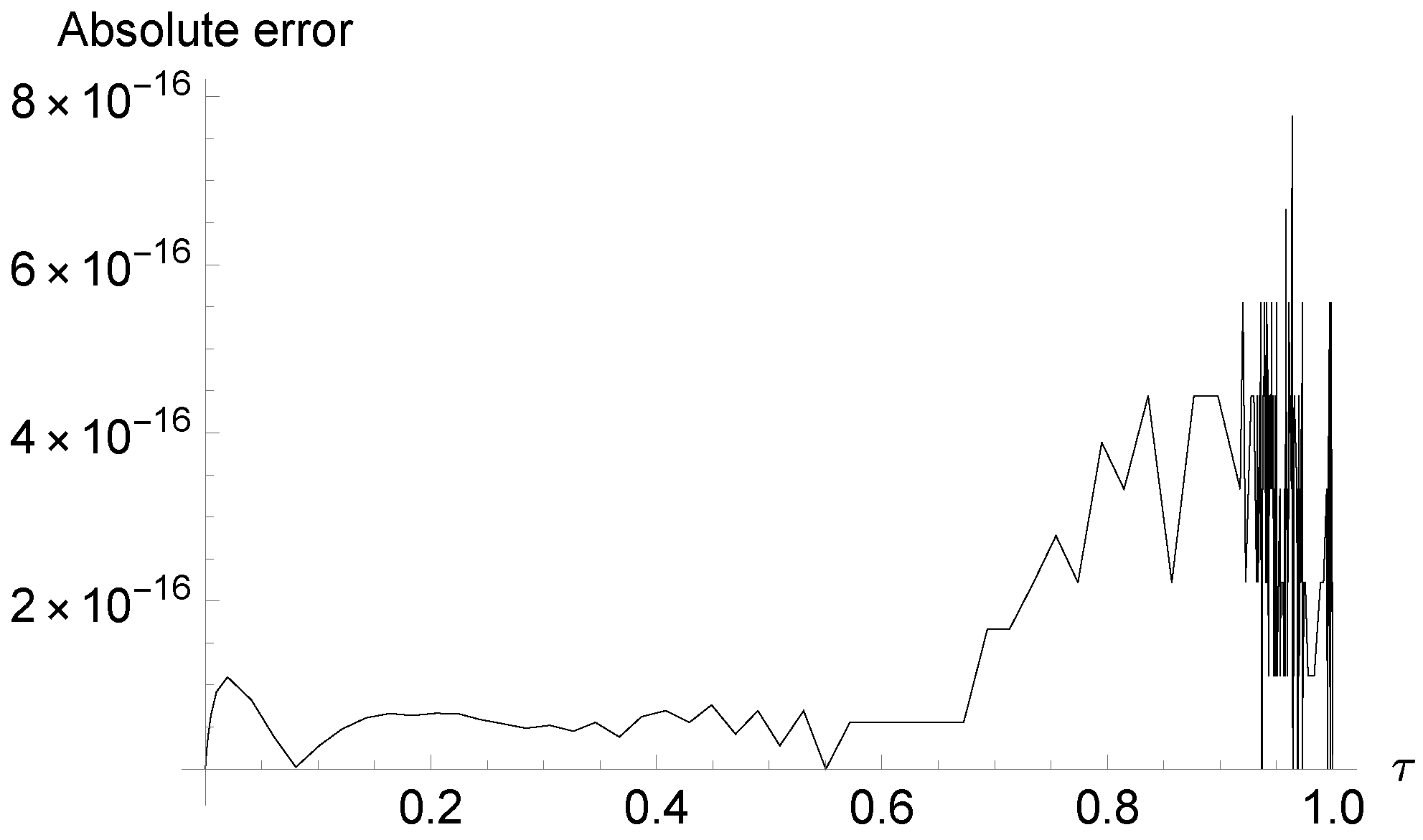
6. Error Analysis and Convergence Results
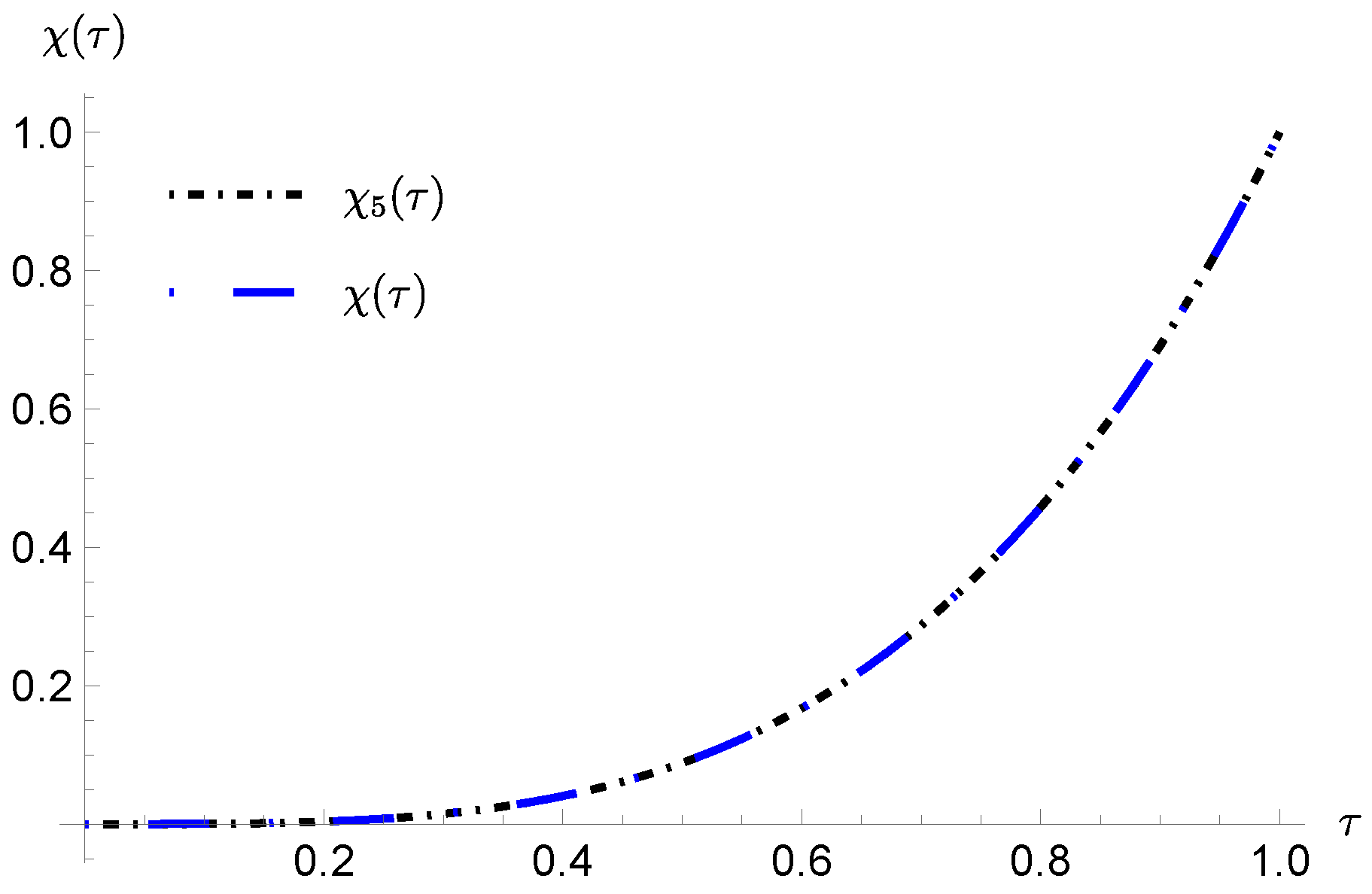
7. Numerical Simulations
| GFJCOPMM | Ref. [21] | Ref. [19] | Ref. [18] | |
|---|---|---|---|---|
| 0.2 | 0 | 8.091305 | 1.818101 | 0 |
| 0.4 | 0 | 2.024535 | 1.817213 | 8.881784 |
| 0.6 | 0 | 9.564669 | 1.820765 | 1.776356 |
| 0.8 | 0 | 1.696030 | 1.818989 | 1.776356 |
| 1.0 | 0 | 1.734222 | 1.818989 | 0 |
| 0 | 0 | 1.29 | 3.00 | 4.85 | 5.55 | 1.00 | 1.33 | |
| 7.49 | 1.71 | 2.47 | 1.81 | 5.51 | 5.14 | |||
| CPU time | 0.133 | 0.301 | 0.402 | 0.431 | 0.445 | 0.551 | ||
| 1 | 1 | 1.92 | 3.31 | 9.18 | 1.11 | 5.00 | 7.76 | |
| 5.73 | 1.54 | 3.42 | 3.63 | 3.54 | 3.51 | |||
| CPU time | 0.124 | 0.313 | 0.404 | 0.426 | 0.428 | 0.514 | ||
| −1/2 | 1/2 | 1.67 | 5.47 | 1.25 | 1.35 | 8.88 | 7.77 | |
| 9.90 | 2.42 | 4.32 | 3.92 | 5.15 | 2.50 | |||
| CPU time | 0.120 | 0.309 | 0.398 | 0.410 | 0.419 | 0.497 | ||
| 1/2 | −1/2 | 1.44 | 2.72 | 7.10 | 8.46 | 7.78 | 7.78 | |
| 5.43 | 1.33 | 2.41 | 2.31 | 6.50 | 6.33 | |||
| CPU time | 0.129 | 0.381 | 0.422 | 0.443 | 0.447 | 0.552 |
| GFJCOPMM | [36] | |||||
|---|---|---|---|---|---|---|
| 0.2 | 3.18 | 1.06 | 5.81 | 5.69 | 9.75 | 8.06 |
| 0.4 | 1.37 | 1.25 | 1.25 | 2.34 | 8.02 | 6.34 |
| 0.6 | 1.22 | 1.11 | 0 | 2.78 | 7.03 | 5.53 |
| 0.8 | 2.18 | 1.11 | 5.00 | 2.52 | 5.97 | 4.59 |
| 1.0 | 1.16 | 4.44 | 1.11 | 1.66 | 2.89 | 1.95 |
| Ref. [49] (k = 2 and M = 7) | |||
|---|---|---|---|
| 0.0 | 0 | 8.43745 × | 1.26942 × |
| 0.1 | 0 | 1.42121 × | 2.00086 × |
| 0.2 | 0 | 1.95085 × | 2.94462 × |
| 0.3 | 0 | 1.95085 × | 2.86427 × |
| 0.4 | 0 | 1.47103 × | 1.51048 × |
| 0.5 | 0 | 1.13654 × | 3.96870 × |
| 0.6 | 0 | 8.98023 × | 3.60302 × |
| 0.7 | 0 | 7.46806 × | 3.23654 × |
| 0.8 | 0 | 6.97788 × | 2.85101 × |
| 0.9 | 0 | 7.78465 × | 2.39836 × |
| 1.0 | 0 | 1.02211 × | 1.76092 × |
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maayah, B.; Arqub, O.A.; Alnabulsi, S.; Alsulami, H. Numerical solutions and geometric attractors of a fractional model of the cancer-immune based on the Atangana-Baleanu-Caputo derivative and the reproducing kernel scheme. Chin. J. Phys. 2022, 80, 463–483. [Google Scholar] [CrossRef]
- Berredjem, N.; Maayah, B.; Arqub, O.A. A numerical method for solving conformable fractional integro-differential systems of second-order, two-points periodic boundary conditions. Alex. Eng. J. 2022, 61, 5699–5711. [Google Scholar] [CrossRef]
- Arqub, O.A.; Rabah, A.B.; Momani, S. A spline construction scheme for numerically solving fractional Bagley-Torvik and Painlevé models correlating initial value problems concerning the Caputo-Fabrizio derivative approach. Int. J. Mod. Phys. C. 2023, 34, 2350115. [Google Scholar] [CrossRef]
- Almeida, R.; Tavares, D.; Torres, D.F.M. The Variable-Order Fractional Calculus of Variations; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Odzijewicz, T.; Malinowska, A.B.; Torres, D.F.M. Noether’s theorem for fractional variational problems of variable order. Cent. Eur. J. Phys. 2013, 11, 691–701. [Google Scholar] [CrossRef]
- Chen, S.; Liu, F.; Burrage, K. Numerical simulation of a new two-dimensional variable-order fractional percolation equation in non-homogeneous porous media. Comput. Math. Appl. 2014, 67, 1673–1681. [Google Scholar] [CrossRef]
- Samko, S.G.; Ross, B. Integration and differentiation to a variable fractional order. Integr. Transf. Spec. Funct. 1993, 1, 277–300. [Google Scholar] [CrossRef]
- Coimbra, C.F.M.; Soon, C.M.; Kobayashi, M.H. The variable viscoelasticity operator. Ann. Phys. 2005, 14, 378–389. [Google Scholar]
- Ostalczyk, P.W.; Duch, P.; Brzeziński, D.W.; Sankowski, D. Order Functions Selection in the Variable-Fractional-Order PID Controller. In Advances in Modelling and Control of Non-Integer-Order Systems; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2015; Volume 320, pp. 159–170. [Google Scholar]
- Rapaić, M.R.; Pisano, A. Variable-order fractional operators for adaptive order and parameter estimation. IEEE Trans. Autom. Contr. 2013, 59, 798–803. [Google Scholar] [CrossRef]
- Izadi, M.; Yüzbaşı, Ş.; Adel, W. Two novel Bessel matrix techniques to solve the squeezing flow problem between infinite parallel plates. Comput. Math. Math. Phys. 2021, 61, 2034–2053. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. Variable-order particle dynamics: Formulation and application to the simulation of edge dislocations. Philos. Trans. R. Soc. A 2020, 378, 20190290. [Google Scholar] [CrossRef]
- Blaszczyk, T.; Bekus, K.; Szajek, K.; Sumelka, W. Approximation and application of the Riesz-Caputo fractional derivative of variable order with fixed memory. Meccanica 2022, 57, 861–870. [Google Scholar] [CrossRef]
- Sheikhi, S.; Matinfar, M.; Firoozjaee, M.A. Numerical solution of variable-order differential equations via the Ritz approximation method by shifted Legendre polynomials. Int. J. Appl. Comput. Math. 2021, 7, 22. [Google Scholar] [CrossRef]
- Abbasi, Z.; Izadi, M.; Hosseini, M.M. A highly accurate matrix method for solving a class of strongly nonlinear BVP arising in modeling of human shape corneal. Math. Methods Appl. Sci. 2023, 46, 1511–1527. [Google Scholar] [CrossRef]
- Izadi, M.; Sene, N.; Adel, W.; El-Mesady, A. The Layla and Majnun mathematical model of fractional order: Stability analysis and numerical study. Results Phys. 2023, 51, 106650. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Wu, L. An operational matrix of fractional differentiation of the second kind of Chebyshev polynomial for solving multiterm variable order fractional differential equation. Math. Probl. Eng. 2016, 2016, 7126080. [Google Scholar] [CrossRef]
- El-Sayed, A.A.; Baleanu, D.; Agarwal, P. A novel Jacobi operational matrix for numerical solution of multi-term variable-order fractional differential equations. J. Taibah Univ. Sci. 2020, 14, 963–974. [Google Scholar] [CrossRef]
- Nagy, A.M.; Sweilam, N.H.; El-Sayed, A.A. New operational matrix for solving multiterm variable order fractional differential equations. J. Comput. Nonlinear Dyn. 2018, 13, 011001. [Google Scholar] [CrossRef]
- Wang, L.F.; Ma, Y.P.; Yang, Y.Q. Legendre polynomials method for solving a class of variable order fractional differential equation. CMES-Comp. Model. Eng. 2014, 101, 97–111. [Google Scholar]
- Chen, Y.M.; Wei, Y.Q.; Liu, D.Y.; Yu, H. Numerical solution for a class of nonlinear variable order fractional differential equations with Legendre wavelets. Appl. Math. Lett. 2015, 46, 83–88. [Google Scholar] [CrossRef]
- Heydari, M.H.; Hooshmandasl, M.R.; Cattani, C.; Hariharan, G. An optimization wavelet method for multi variable-order fractional differential equations. Fundam. Inform. 2017, 151, 255–273. [Google Scholar] [CrossRef]
- Moustafa, M.; Youssri, Y.H.; Atta, A.G. Explicit Chebyshev Petrov–Galerkin scheme for time-fractional fourth-order uniform Euler–Bernoulli Pinned–Pinned beam equation. Nonlinear Eng. 2023, 12, 20220308. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Atta, A.G. Fejér-quadrature collocation algorithm for solving fractional integro-differential equations via Fibonacci polynomials. Contemp. Math. 2024, 5, 296–308. [Google Scholar] [CrossRef]
- Ahmed, H.M. A new first finite class of classical orthogonal polynomials operational matrices: An application for solving fractional differential equations. Contemp. Math. 2023, 4, 974–994. [Google Scholar] [CrossRef]
- Iqbal, S.; Francisco, M.; Mohammed, K.A.K.; Mohammad, E.S. A novel Elzaki transform homotopy perturbation method for solving time-fractional non-linear partial differential equations. Bound. Value Probl. 2022, 2022, 91. [Google Scholar] [CrossRef]
- Martínez, F.; Mohammed, K.A.K. On the Martínez–Kaabar fractal–fractional reduced Pukhov differential transformation and its applications. Mathematics 2025, 13, 352. [Google Scholar] [CrossRef]
- Hafez, R.M.; Youssri, H.Y. Legendre-collocation spectral solver for variable-order fractional functional differential equations. Comput. Methods Differ. Equ. 2020, 8, 99–110. [Google Scholar]
- Mallawi, F.; Alzaidy, J.F.; Hafez, R.M. Application of a Legendre collocation method to the space–time variable fractional-order advection–dispersion equation. J. Taibah Uni. Sci. 2019, 13, 324–330. [Google Scholar] [CrossRef]
- Hafez, R.M.; Youssri, Y.H. Jacobi collocation scheme for variable-order fractional reaction-subdiffusion equation. Comput. Appl. Math. 2018, 37, 5315–5333. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Taha, T.M.; Abdelkawy, M.A.; Hafez, R.M. On numerical methods for fractional differential equation on a semi-infinite interval. In Fractional Dynamics; Sciendo Migration: Warsaw, Poland, 2015; pp. 191–218. [Google Scholar]
- Bushnaq, S.; Shah, K.; Tahir, S.; Ansari, K.J.; Sarwar, M.; Abdeljawad, T. Computation of numerical solutions to variable order fractional differential equations by using non-orthogonal basis. AIMS Math. 2022, 7, 10917–10938. [Google Scholar] [CrossRef]
- Chen, Y.M.; Liu, L.Q.; Li, B.F.; Sun, Y. Numerical solution for the variable order linear cable equation with Bernstein polynomials. Appl. Math. Comput. 2014, 238, 329–341. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F.; Chen, J.; Turner, I.; Anh, V. Numerical techniques for the variable order time fractional diffusion equation. Appl. Math. Comput. 2012, 218, 10861–10870. [Google Scholar] [CrossRef]
- Moghaddam, B.P.; Machado, J.A.T. Extended algorithms for approximating variable order fractional derivatives with applications. J. Sci. Comput. 2017, 71, 1351–1374. [Google Scholar] [CrossRef]
- Nemati, S.; Pedro, M.L.; Delfim, F.M.T. Numerical solution of variable-order fractional differential equations using Bernoulli polynomials. Fractal Fract. 2021, 5, 219. [Google Scholar] [CrossRef]
- Shen, J.; Tang, T.; Wang, L. Spectral Methods: Algorithms, Analysis and Applications; Springer: Berlin, Germany, 2011; Volume 41. [Google Scholar]
- Ashry, H.; Abd-Elhameed, W.M.; Moatimid, G.M.; Youssri, Y.H. Robust shifted Jacobi-Galerkin method for solving linear hyperbolic telegraph type equation. Palestine J. Math. 2022, 11, 504–518. [Google Scholar]
- Abd-Elhameed, W.M.; Ahmed, H.M.; Youssri, Y.H. A new generalized Jacobi Galerkin operational matrix of derivatives: Two algorithms for solving fourth-order boundary value problems. Adv. Differ. Equ. 2016, 2016, 22. [Google Scholar] [CrossRef]
- Sabermahani, S.; Ordokhani, H.; Hassani, H. General Lagrange scaling functions: Application in general model of variable order fractional partial differential equations. Comput. Appl. Math 2021, 40, 269. [Google Scholar] [CrossRef]
- Ahmed, H.M. Enhanced shifted Jacobi operational matrices of derivatives: Spectral algorithm for solving multiterm variable-order fractional differential equations. Bound. Value Probl. 2023, 2023, 108. [Google Scholar] [CrossRef]
- Abd El-Hady, M.; El-Gamel, M.; Emadifar, H. Analysis of RL electric circuits modeled by fractional Riccati IVP via Jacobi-Broyden Newton algorithm. PLoS ONE 2025, 20, e0316348. [Google Scholar] [CrossRef]
- Ahmed, H.M. New generalized Jacobi polynomial Galerkin operational matrices of derivatives: An algorithm for solving boundary value problems. Fractal Fract. 2024, 8, 199. [Google Scholar] [CrossRef]
- Youssri, Y.H.; Ismail, M.I.; Atta, A.G. Chebyshev Petrov-Galerkin procedure for the time-fractional heat equation with nonlocal conditions. Phys. Scr. 2023, 99, 015251. [Google Scholar] [CrossRef]
- Singh, H.; Srivastava, H.M. Jacobi collocation method for the approximate solution of some fractional-order Riccati differential equations with variable coefficients. Physica A 2019, 523, 1130–1149. [Google Scholar] [CrossRef]
- Ahmed, H.M. Highly accurate method for a singularly perturbed coupled system of convection–diffusion equations with Robin boundary conditions. J. Nonlinear Math. Phys. 2024, 31, 17. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Izadi, M.; Adel, W. Robust and accurate numerical framework for multi-dimensional fractional-order telegraph equations using Jacobi/Jacobi–Romanovski spectral technique. Bound. Value Prob. 2024, 2024, 131. [Google Scholar] [CrossRef]
- Kazem, S.; Abbasbandy, S.; Kumar, S. Fractional-order Legendre functions for solving fractional-order differential equations. Appl. Math. Model. 2013, 37, 5498–5510. [Google Scholar] [CrossRef]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. Fractional-order Bernoulli wavelets and their applications. Appl. Math. Model. 2016, 40, 8087–8107. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. Shifted fractional-order Jacobi orthogonal functions: Application to a system of fractional differential equations. Appl. Math. Model. 2016, 40, 832–845. [Google Scholar] [CrossRef]
- Yin, F.; Song, J.; Wu, Y.; Zhang, L. Numerical solution of the fractional partial differential equations by the two-dimensional fractional-order Legendre functions. Abstr. Appl. Anal. 2013, 2013, 562140. [Google Scholar] [CrossRef]
- Izadi, M.; Cattani, C. Generalized Bessel polynomial for multi-order fractional differential equations. Symmetry 2020, 12, 1260. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Alghamdi, M.M.; Taha, T.M. A new modified generalized Laguerre operational matrix of fractional integration for solving fractional differential equations on the half line. Adv. Differ. Equ. 2012, 2012, 179. [Google Scholar] [CrossRef]
- Shahriyar, M.R.B.; Ismail, F.; Aghabeigi, S.; Ahmadian, A.; Salahshour, S. An eigenvalue-eigenvector method for solving a system of fractional differential equations with uncertainty. Math. Probl. Eng. 2013, 2013, 579761. [Google Scholar] [CrossRef]
- Eghbali, A.; Johansson, H.; Saramäki, T. A method for the design of Farrow-structure based variable fractional-delay FIR filters. Signal Process. 2013, 93, 1341–1348. [Google Scholar] [CrossRef]
- Yu, C.; Teo, K.L.; Dam, H.H. Design of allpass variable fractional delay filter with signed powers-of-two coefficients. Signal Process. 2014, 95, 32–42. [Google Scholar] [CrossRef]
- Cooper, G.R.J.; Cowan, D.R. Filtering using variable order vertical derivatives. Comput. Geosci. 2004, 30, 455–459. [Google Scholar] [CrossRef]
- Tseng, C.-C. Design of variable and adaptive fractional order FIR differentiators. Signal Process. 2006, 86, 2554–2566. [Google Scholar] [CrossRef]
- Coimbra, C.F.M. Mechanics with variable-order differential operators. Ann. Phys. 2003, 515, 692–703. [Google Scholar] [CrossRef]
- Szegö, G. Orthogonal Polynomials; American Mathematical Society: Providence, RI, USA, 1975; Volume XXIII. [Google Scholar]
- Kamali, F.; Saeedi, H. Generalized fractional-order Jacobi functions for solving a nonlinear systems of fractional partial differential equations numerically. Math. Methods Appl. Sci. 2018, 41, 3155–3174. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D.; Burden, A.M. Numerical Analysis; Cengage Learning: Boston, MA, USA, 2015. [Google Scholar]
- Jeffrey, A.; Dai, H.H. Handbook of Mathematical Formulas and Integrals; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Irandoust-Pakchin, S.; Kheiri, H.; Abdi-Mazraeh, S. Efficient computational algorithms for solving one class of fractional boundary value problems. Comp. Math. Math. Phys. 2013, 53, 920–932. [Google Scholar] [CrossRef]
- Hassani, H.; Dahaghin, M.S.; Heydari, H. A new optimized method for solving variable-order fractional differential equations. J. Math. Ext. 2017, 11, 85–98. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, H.M.; Izadi, M.; Cattani, C. A Spectral Approach to Variable-Order Fractional Differential Equations: Improved Operational Matrices for Fractional Jacobi Functions. Mathematics 2025, 13, 2544. https://doi.org/10.3390/math13162544
Ahmed HM, Izadi M, Cattani C. A Spectral Approach to Variable-Order Fractional Differential Equations: Improved Operational Matrices for Fractional Jacobi Functions. Mathematics. 2025; 13(16):2544. https://doi.org/10.3390/math13162544
Chicago/Turabian StyleAhmed, Hany M., Mohammad Izadi, and Carlo Cattani. 2025. "A Spectral Approach to Variable-Order Fractional Differential Equations: Improved Operational Matrices for Fractional Jacobi Functions" Mathematics 13, no. 16: 2544. https://doi.org/10.3390/math13162544
APA StyleAhmed, H. M., Izadi, M., & Cattani, C. (2025). A Spectral Approach to Variable-Order Fractional Differential Equations: Improved Operational Matrices for Fractional Jacobi Functions. Mathematics, 13(16), 2544. https://doi.org/10.3390/math13162544








