Safety Analysis of Subway Station Under Seepage Force Using a Continuous Velocity Field
Abstract
1. Introduction
2. Methodology
2.1. Upper Bound Theorem
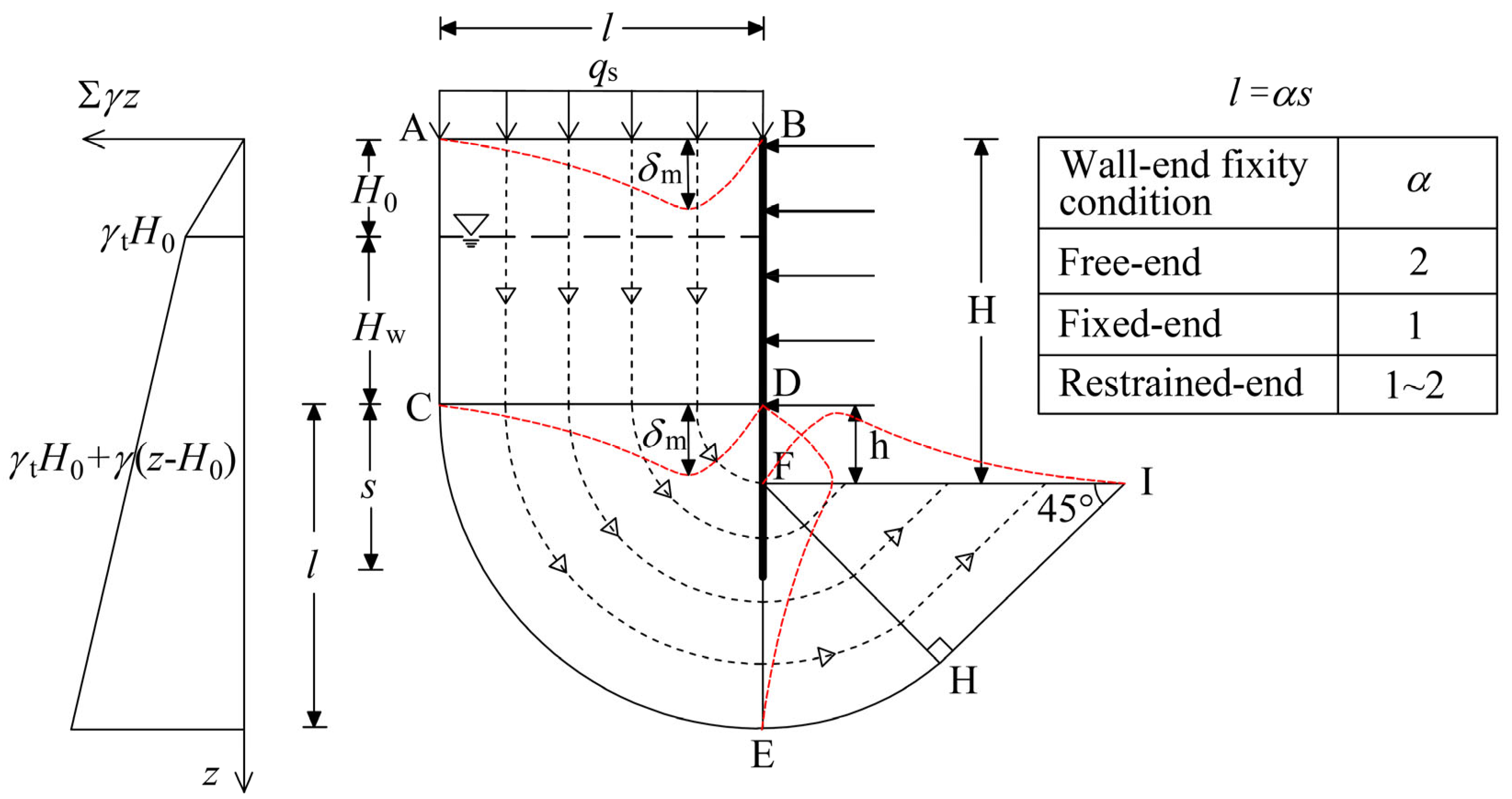
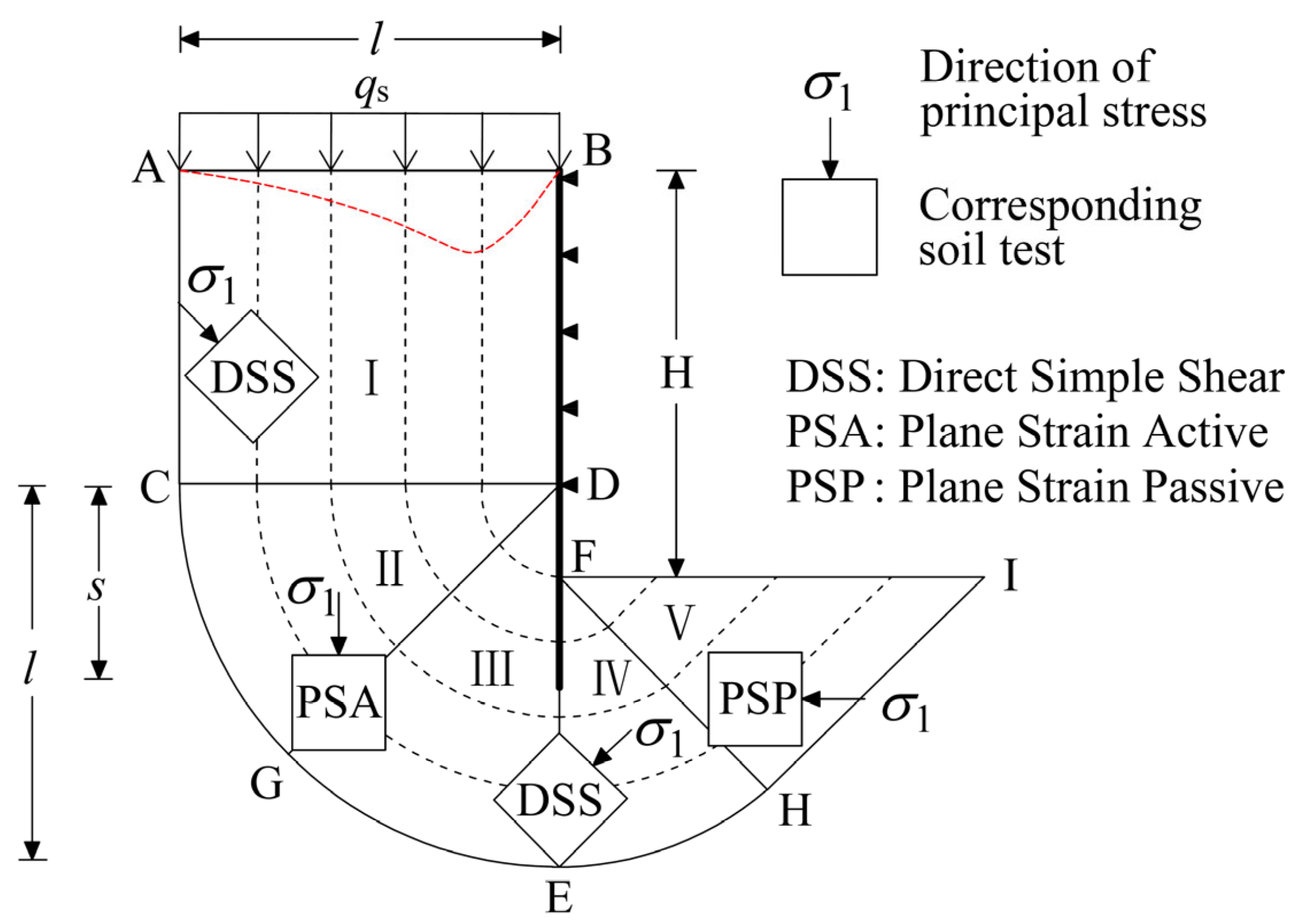
2.2. Continuous Deformation Field of the Station Pit
3. Kinematic Analysis of the Station Pit
3.1. External Work Rate Calculation
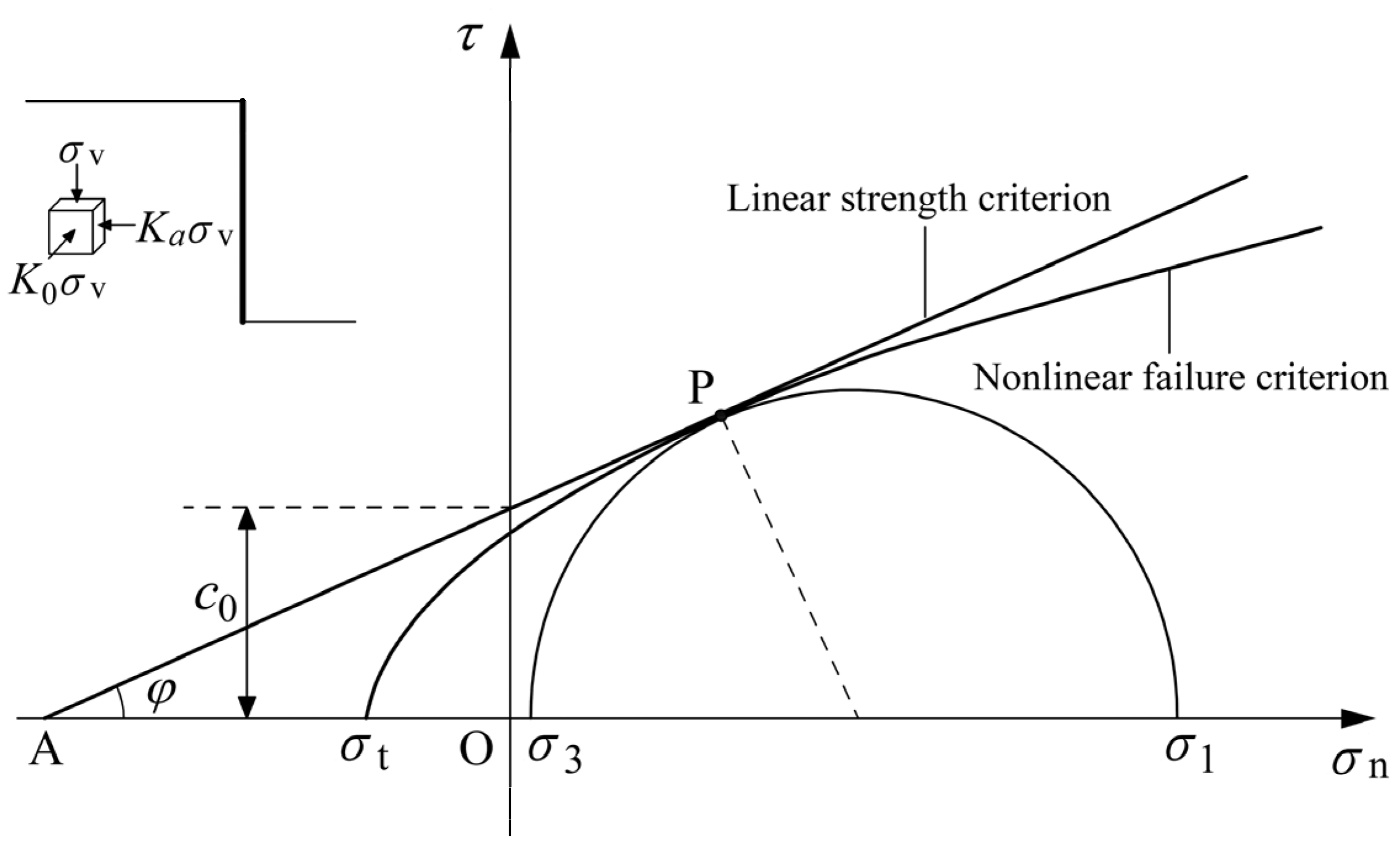
3.2. Plastic Shear Energy Calculation
4. Results and Discussion
4.1. Comparison
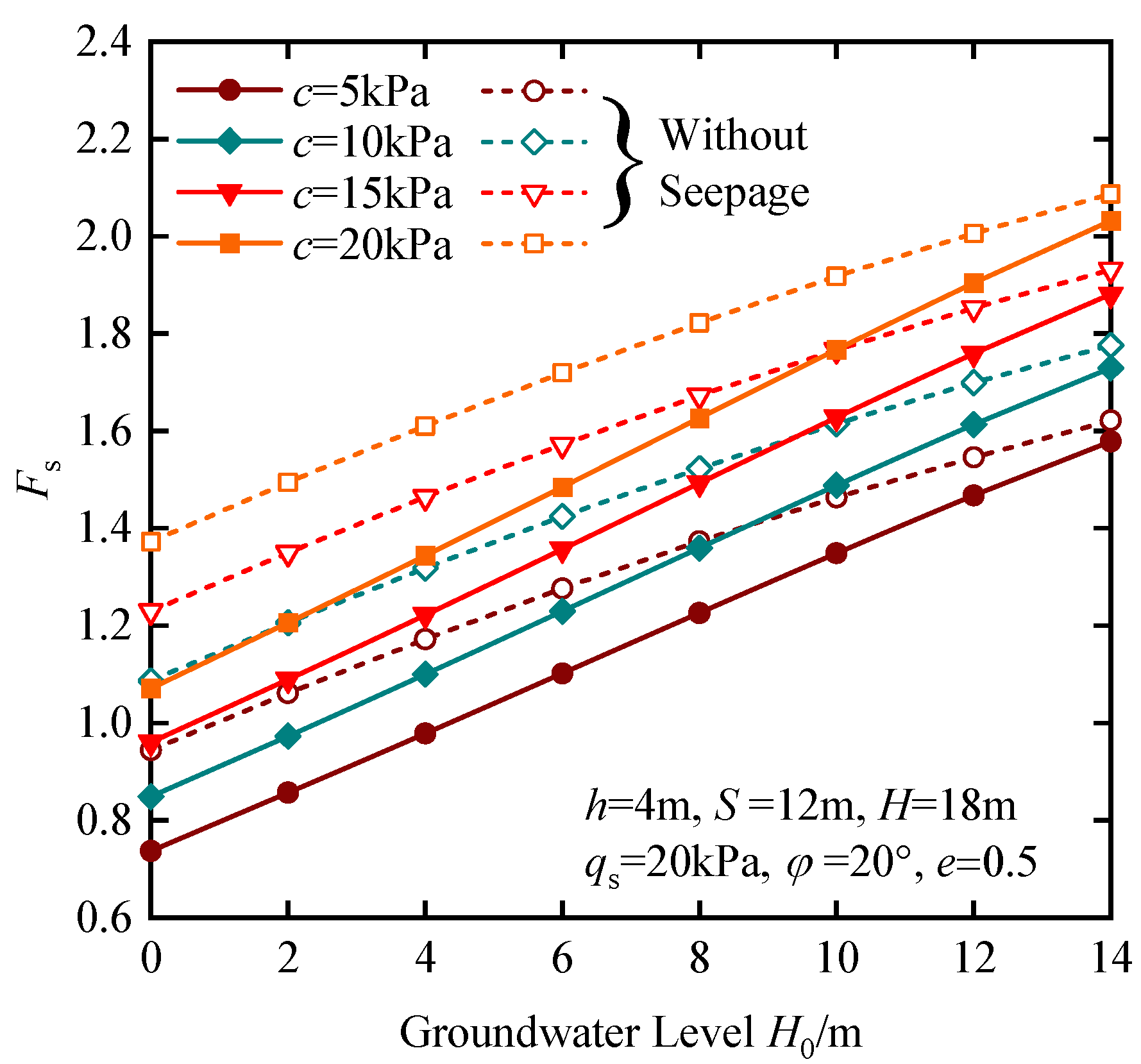
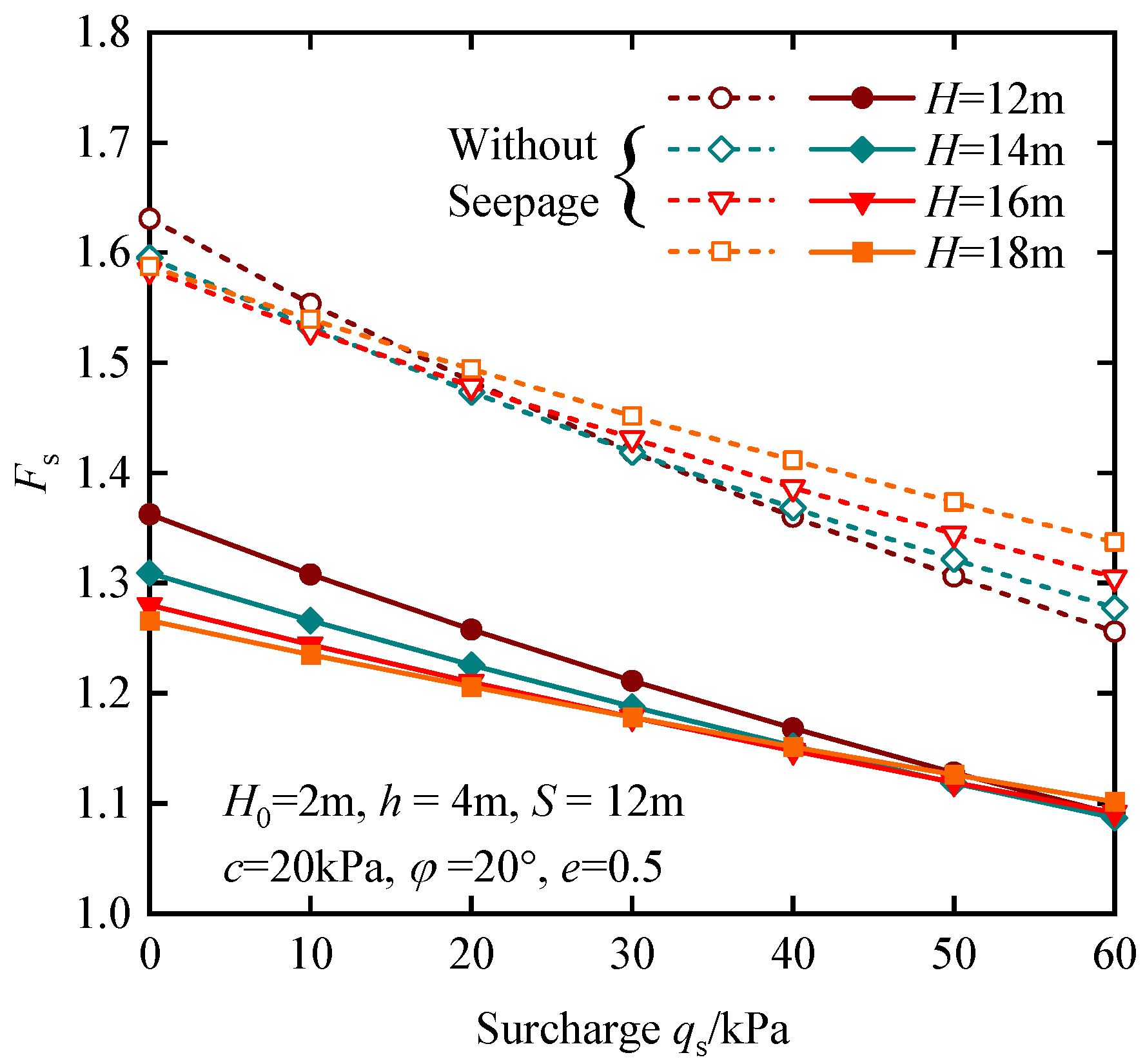
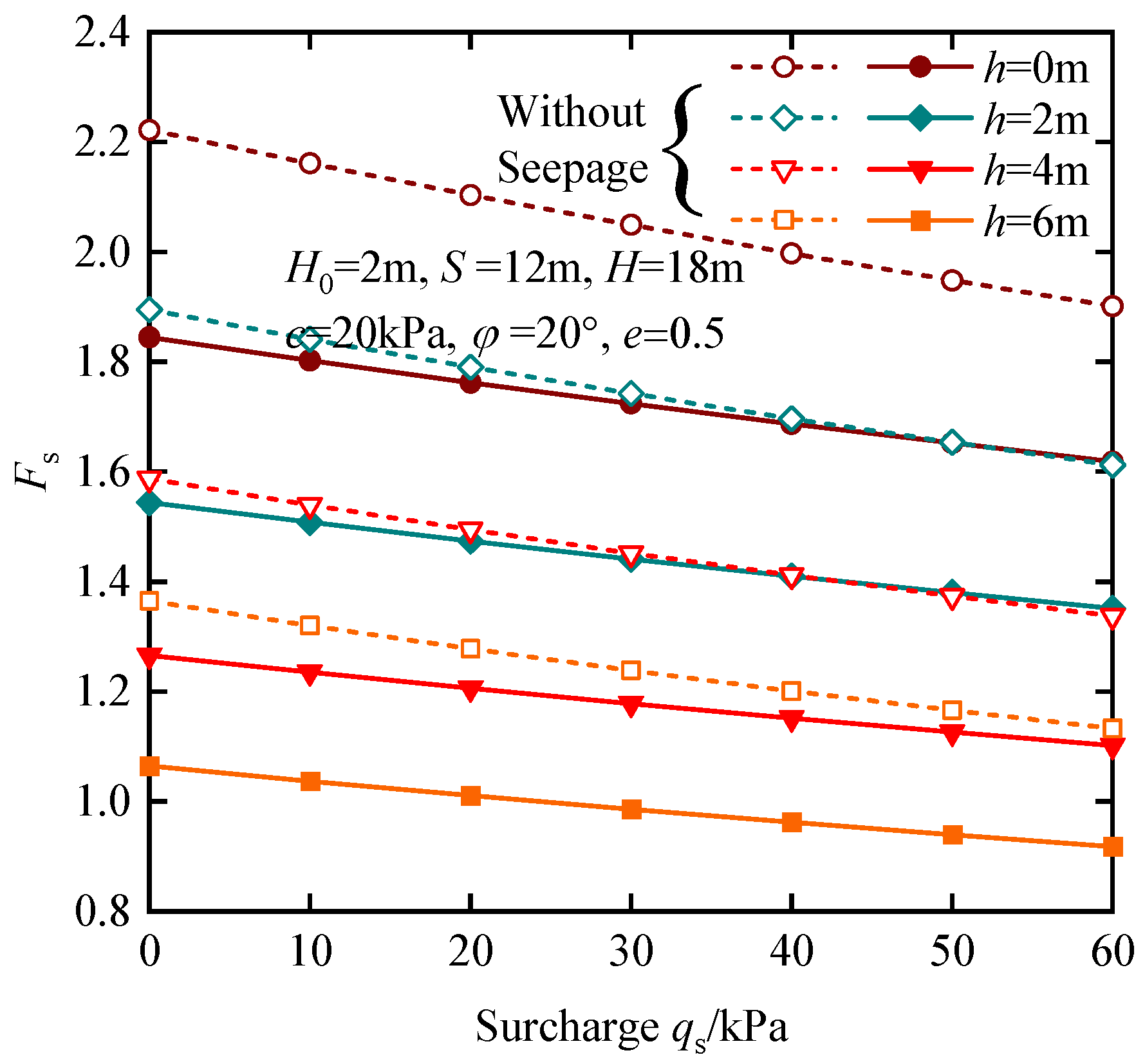
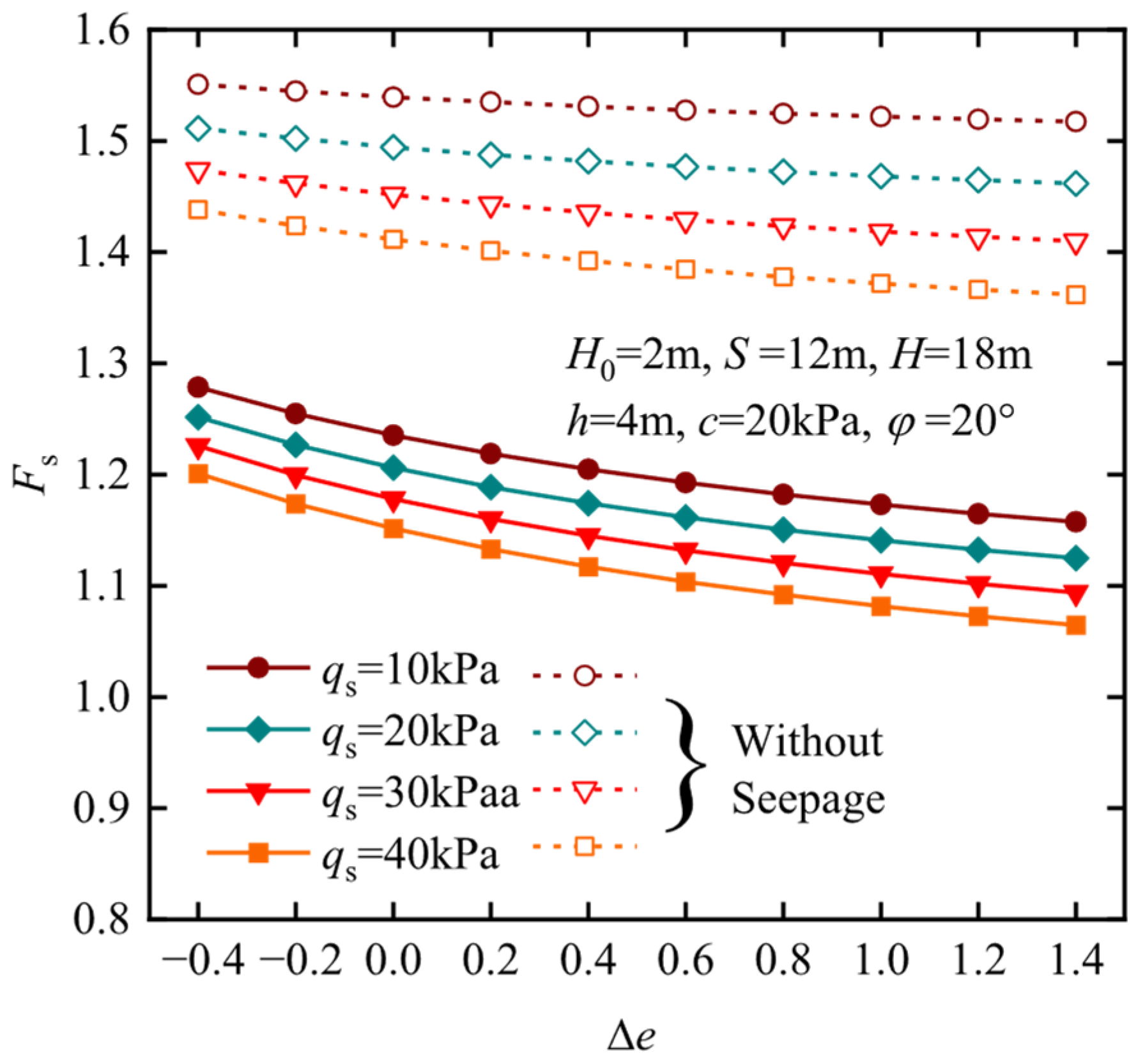
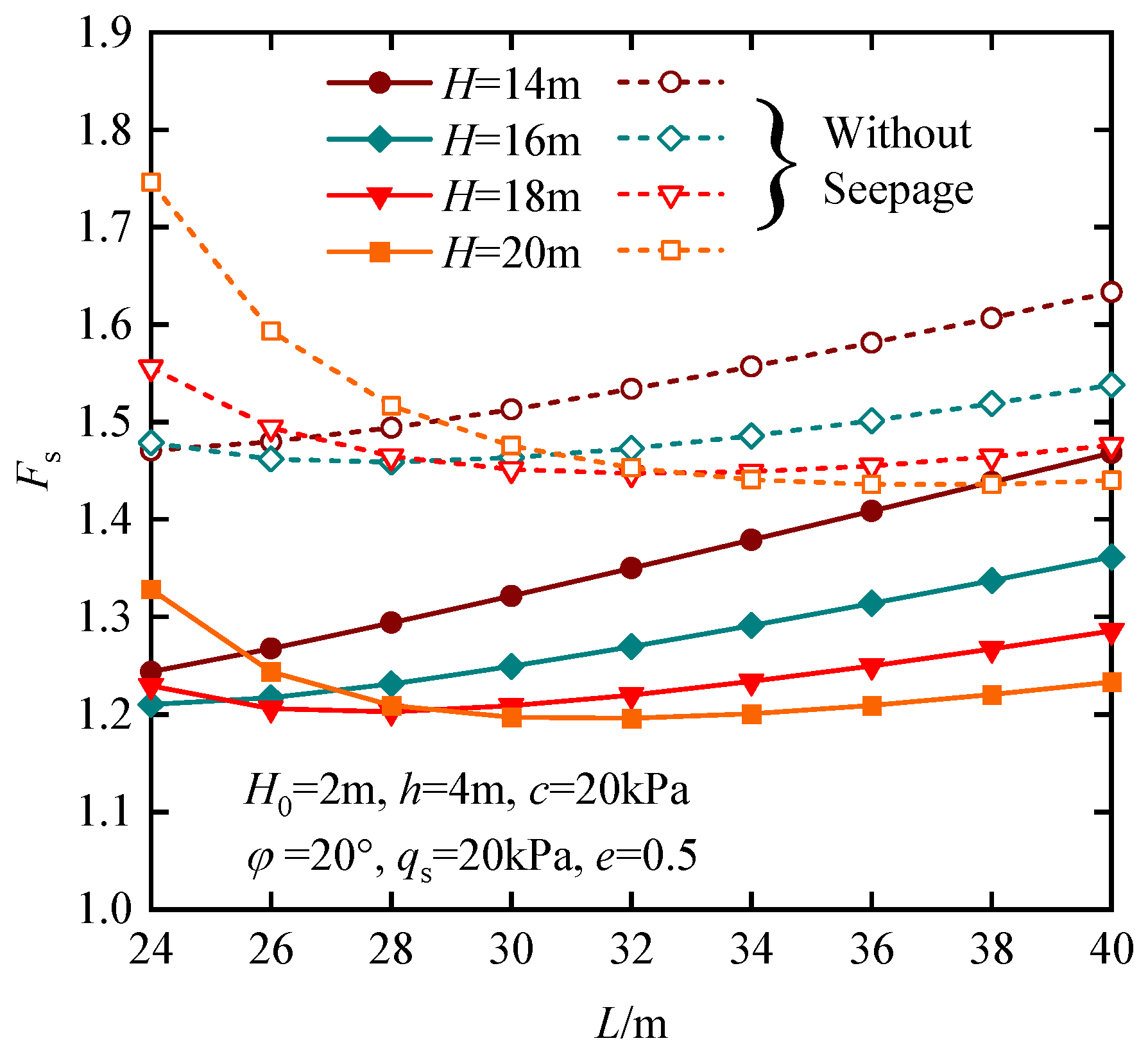
4.2. Parametric Studies
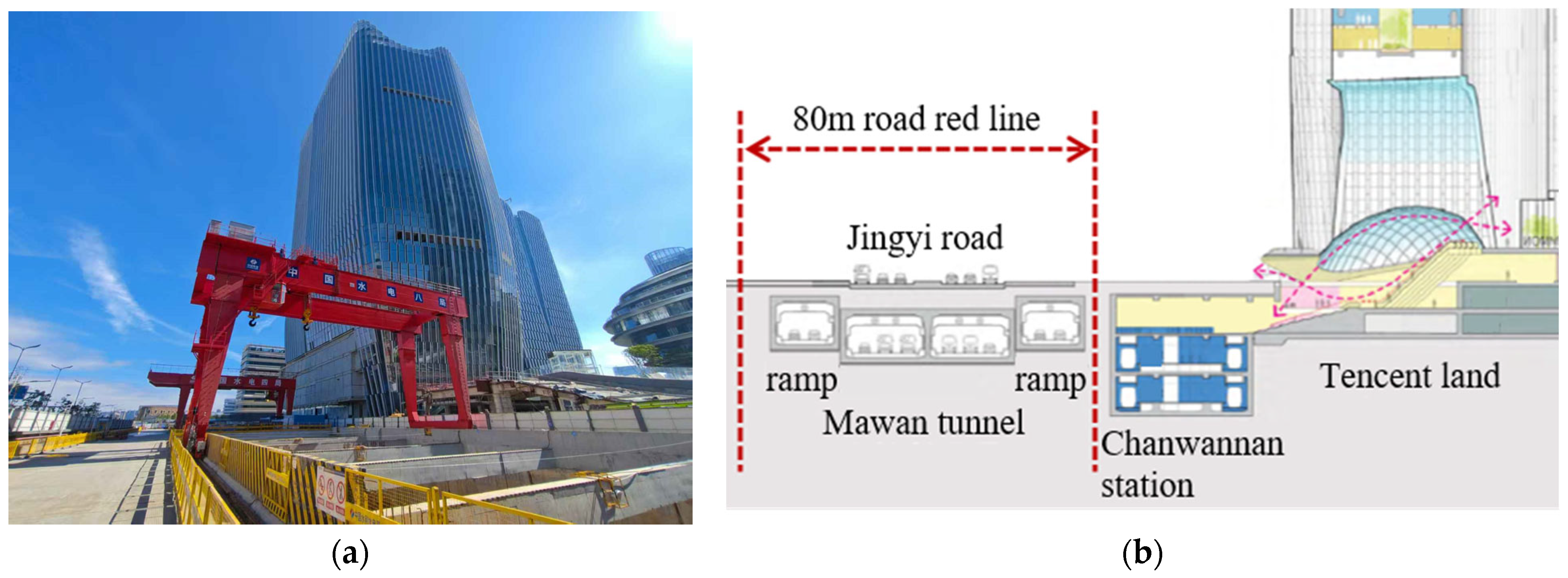
4.3. Engineering Application
5. Conclusions
- (1)
- The increase in seepage force caused by an increase in groundwater level and excess pore water pressure significantly reduces the anti-uplift stability of the station pit. Permeation pressure is an important factor influencing the stability of station pits.
- (2)
- The factors that affect the anti-uplift stability of the station pit include the following: seepage force (fs), soil shear strength (c and φ), embedded depth of retaining wall (D), and variation in soil particle (e). An increase in the embedding depth can increase the anti-uplift safety factor of the station pit when the excavation depth is small. When the excavation depth becomes larger, the anti-uplift safety factor might decrease due to the increase in the range of deformation influence.
- (3)
- The previous calculation methods ignore the influence of seepage force. This work attempts to extend the calculation method for the anti-uplift stability of deep station pits in geological formations that are sensitive to the influence of groundwater seepage pressure. Through engineering application and comparison, the predicted results of the proposed procedure without considering seepage are close to those of classic formulas, and considering seepage can better predict the stability of station pits.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| A, B | nondimensional parameters | maximum of surface subsidence, m | |
| plastic strain | work resulted from gravity, kJ | ||
| surface force on boundary S, kPa | work resulted from , kJ | ||
| stress tensor, kPa | work resulted from , kJ | ||
| kinematic admissible velocity field, m/s | shear strength of soils, kPa | ||
| distributed load, kPa | unit weight of soils, kN/m3 | ||
| pore water pressure, kPa | engineering shear strain | ||
| seepage force, kPa | active earth pressure coefficient | ||
| distance between surface and water level, m | internal friction angle, ° | ||
| excavation depth, m | cohesion, kPa | ||
| distance between last support to excavation level, m | gradient of shear strength, kN/m3 | ||
| H−h−H0, m | surface surcharge, kPa | ||
| influence range of excavation, m; | nondimensional parameter | ||
| length from the bottom of the wall to the lowest internal support, m | plastic shear energy, kJ | ||
| deformation parameter | vertical effective stress, kPa | ||
| surface subsidence, m | foundation width, m | ||
| e | void ratio | effective weight of soils, kN/m3 |
References
- Hashash, Y.M.A.; Whittle, A.J. Ground movement prediction for deep excavations in soft clay. J. Geotech. Eng. 1996, 122, 474–486. [Google Scholar] [CrossRef]
- Goh, A.T.C. Assessment of basal stability for braced excavation systems using the finite element method. Comput. Geotech. 1990, 10, 325–338. [Google Scholar] [CrossRef]
- Faheem, H.; Cai, F.; Ugai, K.; Hagiwara, T. Two-dimensional base stability of excavations in soft soils using FEM. Comput. Geotech. 2003, 30, 141–163. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, W.; Han, L. Determination of groundwater buoyancy reduction coefficient in clay: Model tests, numerical simulations and machine learning methods. Undergr. Space 2023, 13, 228–240. [Google Scholar] [CrossRef]
- Zhong, J.H.; Yang, X.L. Seismic stability of three-dimensional slopes considering the nonlinearity of soils. Soil Dyn. Earthq. Eng. 2021, 140, 106334. [Google Scholar] [CrossRef]
- Yang, X.L.; Wang, J.M. Ground movement prediction for tunnels using simplified procedure. Tunn. Undergr. Space Technol. 2011, 26, 462–471. [Google Scholar] [CrossRef]
- Qin, H.; Huang, M.; Ma, S. Multi-block upper bound method for basal heave stability analysis of braced excavations in clay. Chin. J. Rock Mech. Eng. 2010, 29, 73–81. [Google Scholar]
- Huang, M.; Yu, S. Upper bound analysis of basal stability in undrained clay based on block set mechanism. Chin. J. Geotech. Eng. 2012, 34, 1440–1447. [Google Scholar]
- Ukritchon, B.; Whittle, A.J.; Sloan, S.W. Undrained stability of braced excavations in clay. J. Geotech. Geoenviron. ASCE 2003, 129, 738–755. [Google Scholar] [CrossRef]
- Yang, X.L.; Li, L.; Yin, J.H. Seismic and static stability analysis for rock slopes by a kinematical approach. Geotechnique 2004, 54, 543–549. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L.; Li, T.Z. Static and seismic stability assessment of 3D slopes with cracks. Eng. Geol. 2020, 265, 105450. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Yang, X.L. Unified solution of safety factors for three-dimensional compound slopes considering local and global instability. Comput. Geotech. 2023, 155, 105227. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Yang, X.L. Pseudodynamic analysis of three-dimensional fissured slopes reinforced with piles. Int. J. Geomech. 2022, 23, 04022315. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L. Three-dimensional active earth pressure under transient unsaturated flow conditions. Comput. Geotech. 2020, 123, 103559. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L. Active earth pressure for soils with tension cracks under steady unsaturated flow conditions. Can. Geotech. J. 2018, 55, 1850–1859. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Zhu, J.Q.; Yang, X.L. Three-dimensional active earth pressures for unsaturated backfills with cracks considering steady seepage. Int. J. Geomech. 2023, 23, 04022270. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Li, Z.W.; Dias, D. Seismic stability of cracked rock slopes based on physics-informed neural networks. Int. J. Rock Mech. Min. 2025, 192, 106147. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Zhang, W.; Sun, W.; Fu, J.; Xiao, T.; Dai, Z. A physics-informed data-driven model for landslide susceptibility assessment in the Three Gorges Reservoir area. Geosci. Front. 2023, 14, 101621. [Google Scholar] [CrossRef]
- Li, Z.W.; Yang, X.L. Stability of 3D slope under steady unsaturated flow condition. Eng. Geol. 2018, 242, 150–159. [Google Scholar] [CrossRef]
- Li, T.Z.; Gong, W.P.; Tang, H.M.; Zhang, L.M. A meshed kinematical approach for 3D slope stability analysis. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 2913–2930. [Google Scholar] [CrossRef]
- Yang, X.L.; Huang, F. Collapse mechanism of shallow tunnel based on nonlinear Hoek–Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 686–691. [Google Scholar] [CrossRef]
- Li, T.Z.; Pan, Q.; Dias, D. Active learning relevant vector machine for reliability analysis. Appl. Math. Model. 2021, 89, 381–399. [Google Scholar] [CrossRef]
- Zhong, J.; Yang, X.; Chian, S.; Chen, H.; Hou, C. Revisiting the face stability of rock tunnels in the Hoek–Brown strength criterion with tension cutoff. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 2061–2084. [Google Scholar] [CrossRef]
- Li, T.Z.; Yang, X.L. New approach for face stability assessment of tunnels driven in nonuniform soils. Comput. Geotech. 2020, 121, 103412. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Yang, X.L. Pseudo-dynamic analysis of a 3D tunnel face in inclined weak strata. Undergr. Space 2023, 12, 156–166. [Google Scholar] [CrossRef]
- Xie, Y.; Zhou, D.; Liao, H.; Zhu, J. Failure Mode of Tunnel Face Under Transient Unsaturated Seepage with Temperature Influence. Mathematics 2025, 13, 1311. [Google Scholar] [CrossRef]
- Sun, W.; Liu, H.; Zhang, W.; Liu, S.; Gao, X. Investigation on overburden thickness considering face and anti-floating stability of shallow shield tunnel. Comput. Geotech. 2023, 160, 105562. [Google Scholar] [CrossRef]
- Zhong, J.H.; Hou, C.T.; Yang, X.L. Three-dimensional face stability analysis of rock tunnels excavated in Hoek-Brown media with a novel multi-cone mechanism. Comput. Geotech. 2023, 154, 105158. [Google Scholar] [CrossRef]
- Zhong, J.H.; Yang, X.L. Kinematic analysis of the three-dimensional stability for tunnel faces by pseudodynamic approach. Comput. Geotech. 2020, 128, 103802. [Google Scholar] [CrossRef]
- Yi, C.; Senent, S.; Jimenez, R. Effect of advance drainage on tunnel face stability using limit analysis and numerical simulations. Tunn. Undergr. Space Technol. 2019, 93, 103105. [Google Scholar] [CrossRef]
- Li, T.Z.; Dias, D.; Li, Z.W. Failure potential of a circular tunnel face under steady-state unsaturated flow condition. Comput. Geotech. 2020, 117, 103231. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Face stability analysis of circular tunnels driven by a pressurized shield. J. Geotech. Geoenviron. 2009, 136, 215–229. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, D. An Analytical Framework for Assessing the Unsaturated Bearing Capacity of Strip Footings under Transient Infiltration. Mathematics 2023, 11, 3480. [Google Scholar] [CrossRef]
- Liu, J.; Xu, S.; Yang, X.L. Modified pseudo dynamic bearing capacity of strip footing on rock masses. Comput. Geotech. 2022, 150, 104897. [Google Scholar] [CrossRef]
- Yang, X.L.; Yin, J.H. Upper bound solution for ultimate bearing capacity with a modified Hoek–Brown failure criterion. Int. J. Rock Mech. Min. 2005, 42, 550–560. [Google Scholar] [CrossRef]
- Chang, M.F. Basal stability analysis of braced cuts in clay. J. Geotech. Geoenviron. 2000, 126, 276–279. [Google Scholar] [CrossRef]
- Zhang, W.G.; Goh, A.T.C.; Goh, K.H.; Chew, O.Y.S.; Zhou, D.; Zhang, R. Performance of braced excavation in residual soil with groundwater drawdown. Undergr. Space 2018, 3, 150–165. [Google Scholar] [CrossRef]
- Huang, M.; Yu, S.; Qin, H. Upper bound method for basal stability analysis of braced excavations in K0-consolidated clays. China Civ. Eng. J. 2011, 44, 101–108. [Google Scholar] [CrossRef]
- Huang, M.; Du, Z.; Song, C. Effects of inserted depth of wall penetration on basal stability of foundation pits in clay. Chin. J. Geotech. Eng. 2011, 33, 1097–1103. [Google Scholar]
- Du, Z.; Huang, M. Analysis for basal stability of braced excavation in nonhomogeneous and anisotropic clay. Rock Soil Mech. 2013, 34, 455–467. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Tang, Y. Basal-heave Stability of Excavations Considering Groundwater Level and Pore Water Pressure Fluctuations by Upper Bound Method. Rock Soil Mech. 2011, 12, 3653–3659. [Google Scholar] [CrossRef]
- Osman, A.S.; Bolton, M.D. Ground movement predictions for braced excavations in undrained clay. J. Geotech. Geoenviron. 2006, 132, 465–477. [Google Scholar] [CrossRef]
- Wang, M.; Zeng, Z.; Jiang, Y.; Liu, D. Upper Limit Analysis of Continuous Deformation Field Infiltration Force on Anti-uplift Instability of Foundation Pit. J. Railw. Eng. Soc. 2019, 36, 12–18. [Google Scholar]
- Huang, M.; Tang, Z.; Yuan, J. Basal stability analysis of braced excavations with embedded walls in undrained clay using the upper bound theorem. Tunn. Undergr. Space Technol. 2018, 79, 231–241. [Google Scholar] [CrossRef]

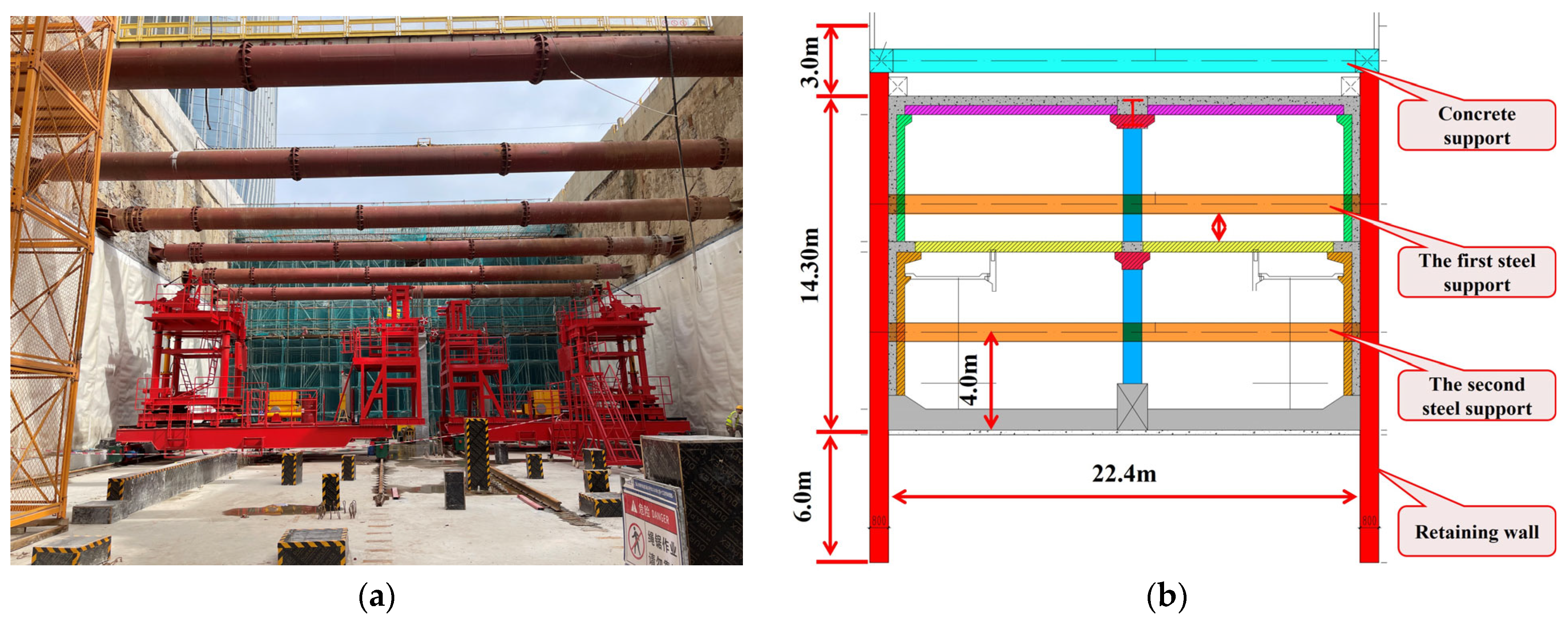
| Foundation Width | B | 40 m |
| Soil unit weight | γ | 18 kN/m3 |
| Internal friction angle | φ | 0° |
| Undrained strength ratio | cu/σv | 0.33 |
| Distance of last support to excavation level | h | 2.5 m |
| Vertical effective stress | σv | (8.19z + 24.5) kPa |
| H/m | s/m | Factor of Safety, Fs | ||||
|---|---|---|---|---|---|---|
| Terzaghi Mechanism | Prandtl Mechanism | Upper-Bound Finite Element | Multi-Block Mechanism | This Work | ||
| 10.0 | 5.0 | 1.69 | 1.72 | 1.21 | 1.22 | 1.58 |
| 15.0 | 7.5 | 1.45 | 1.48 | 1.23 | 1.29 | 1.62 |
| 22.5 | 20.0 | 1.66 | 1.69 | 1.11 | 1.62 | 1.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Zhou, D.; Chen, Q.; Gu, S. Safety Analysis of Subway Station Under Seepage Force Using a Continuous Velocity Field. Mathematics 2025, 13, 2541. https://doi.org/10.3390/math13152541
Cheng Z, Zhou D, Chen Q, Gu S. Safety Analysis of Subway Station Under Seepage Force Using a Continuous Velocity Field. Mathematics. 2025; 13(15):2541. https://doi.org/10.3390/math13152541
Chicago/Turabian StyleCheng, Zhufeng, De Zhou, Qiang Chen, and Shuaifu Gu. 2025. "Safety Analysis of Subway Station Under Seepage Force Using a Continuous Velocity Field" Mathematics 13, no. 15: 2541. https://doi.org/10.3390/math13152541
APA StyleCheng, Z., Zhou, D., Chen, Q., & Gu, S. (2025). Safety Analysis of Subway Station Under Seepage Force Using a Continuous Velocity Field. Mathematics, 13(15), 2541. https://doi.org/10.3390/math13152541





