The Set of Numerical Semigroups with Frobenius Number Belonging to a Fixed Interval

Abstract

Let a and b be positive integers such that $a<b$ and $[a,b]=\{x\in \mathbb{N}\mid a\le x\le b\}.$ In this work, we will show that $\mathcal{A}\left(\right[a,b\left]\right)=\{S\mid S$ is a numerical semigroup whose Frobenius number belongs to $[a,b]\}$ and is a covariety. This fact allows us to present an algorithm which computes all the elements from $\mathcal{A}\left(\right[a,b\left]\right).$ We will prove that $\mathcal{A}\left(\right[a,b],m)=\{S\in \mathcal{A}([a,b])\mid S$ has multiplicity $m\}$ and is a ratio-covariety. As a consequence, we will show an algorithm which calculates all the elements belonging to $\mathcal{A}\left(\right[a,b],m).$ Based on the above results, we will develop an interesting algorithm that calculates all numerical semigroups with a given multiplicity and complexity.

1. Introduction

In this paper, $\mathbb{Z}$ will denote the set of integers, and the set of non-negative integers will be denoted by $\mathbb{N}.$ We will say that a subset M of $\mathbb{N}$ is a submonoid of $(\mathbb{N},+)$; if $0\in M$, and given $a,b\in M$, then $a+b\in M.$ A submonoid S of $(\mathbb{N},+)$ is a numerical semigroup if it has finite complement in $\mathbb{N}$.

Given S is a numerical semigroup, then $\mathrm{m}\left(S\right)=min(S\setminus \{0\left\}\right)$, $\mathrm{F}\left(S\right)=\max \{z\in \mathbb{Z}\mid z\notin S\}$ and $\mathrm{g}\left(S\right)=♯(\mathbb{N}\setminus S)$ (where $♯X$ denotes the cardinality of a set X) will be called the multiplicity, Frobenius number, and genus of S, respectively.

Let X be a nonempty subset of $\mathbb{N}$. Then, the submonoid of $(\mathbb{N},+)$ generated by X, is the set

$$\langle X\rangle =\{a_1{x}_1+\dots +a_n{x}_n\mid n\in \mathbb{N}\setminus \left\{0\right\},\{x_1,\dots ,x_n\}\subseteq Xand\{a_1,\dots ,a_n\}\subseteq \mathbb{N}\}.$$

It is verified that $\langle X\rangle$ is a numerical semigroup if and only if $\gcd \left(X\right)=1$ (see [1] (Lema 2.1)).

Let M be a submonoid of $(\mathbb{N},+)$ such that $M=\langle X\rangle$. In this case, the set X is a system of generators of M. In addition, if $M\ne \langle Y\rangle$ for all $Y⊊X$, then X is called a minimal system of generators of M. Every submonoid of $(\mathbb{N},+)$ has a unique minimal system of generators. In addition, it is finite (see [1] (Corollary 2.8)). We use $\mathrm{msg}\left(M\right)$ to denote the minimal system of generators of M. We call the embedding dimension of $M,$ denoted by $\mathrm{e}\left(M\right),$ the cardinlity of $\mathrm{msg}\left(M\right).$

For numerical semigroups, there exists a problem which consists of looking for formulas to compute the Frobenius number and the genus of a numerical semigroup from its minimal system of generators. This problem is known as the Frobenius problem (see [2]). For numerical semigroups with two embedding dimensions, this problem was solved in [3]. But at this moment, for numerical semigroups of embedding dimension greater than or equal to three, the problem is open, although it has been, and continues to be, extensively researched (see, for instance [4,5,6,7,8,9]).

The relationship between Frobenius number, genus, and embedding dimension has also been a problem widely considered in mathematical research. In fact, H. S. Wilf conjectures in [10] that if S is a numerical semigroup, then $\mathrm{e}\left(S\right)\mathrm{g}\left(S\right)\le \left(\mathrm{e}\right(S)-1)\left(\mathrm{F}\right(S)+1).$ Nowadays, this question is still open and has become one of the main problems in the theory of numerical semigroups. This conjecture has been proved for many families of numerical semigroups (see, for instance [11,12,13,14,15,16]).

Readers not familiar with the study of numerical semigroups may find the nomenclature surprising: multiplicity, genus, embedding dimension, etc. …

With respect to this, we will say that, in the literature, there is a long list of publications devoted to the study of analytically irreducible Noetherian local domains via their semigroup of values, with these groups being numerical semigroups (see, e.g., [17,18,19,20,21]). All these invariants have interpretation in this context, and hence their names.

Throughout this work, a and b will denote positive integers such that $a<b$ and $[a,b]=\{x\in \mathbb{N}\mid a\le x\le b\}.$

It is denoted that $\mathcal{A}\left(\right[a,b\left]\right)=\{S\mid S\mathrm{is}a\mathrm{numerical}\mathrm{and}\mathrm{F}(S)\in [a,b\left]\right\}.$ We will begin Section 2 by stating that $\mathcal{A}\left(\right[a,b\left]\right)$ is a covariety. This fact will allow us to arrange the elements of $\mathcal{A}\left(\right[a,b\left]\right)$ in the form of a tree. As a consequence, we will obtain an algorithm that allows for the computing of all the elements of $\mathcal{A}\left(\right[a,b\left]\right).$ In Section 3, we will study the genus of the elements that belong to $\mathcal{A}\left(\right[a,b\left]\right).$ We will prove that $\{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}\left([a,b]\right)\}=\left[\lceil {\displaystyle \frac{a+1}{2}}\rceil ,b\right],$ where $\lceil q\rceil =min\{z\in \mathbb{Z}\mid q\le z\}$ for $q\in \mathbb{Q}$, and we will present an algorithm that calculates all the elements of $\mathcal{A}\left(\right[a,b\left]\right)$ with a fixed genus.

If m is a positive integer, then we denote that

$$\mathcal{A}\left(\right[a,b],m)=\{S\in \mathcal{A}([a,b])\mid \mathrm{m}(S)=m\}.$$

We will start Section 4 by showing that $\mathcal{A}\left(\right[a,b],m)$ is a ratio-covariety. This fact will allow us to arrange the elements of $\mathcal{A}\left(\right[a,b],m)$ into a tree. Consequently, we will provide an algorithm that allows us to calculate all the elements of $\mathcal{A}\left(\right[a,b],m).$ In this section, we will also see the genus that the elements of $\mathcal{A}\left(\right[a,b],m)$ can have.

Let $\mathrm{\Delta }$ be a numerical semigroup. An idea of $\mathrm{\Delta }$ is a nonempty subset I of $\mathrm{\Delta }$ such that $I+\mathrm{\Delta }\subseteq I.$ If I is an ideal of $\mathrm{\Delta },$ then $I\cup \left\{0\right\}$ is a numerical semigroup. This fact leads us to give the following definition. An $\mathrm{I}\left(\mathrm{\Delta }\right)$-semigroup is a numerical semigroup S such that $S\setminus \left\{0\right\}$ is an ideal of $\mathrm{\Delta }.$ We denote that $\mathcal{J}\left(\mathrm{\Delta }\right)=\{S\mid S\mathrm{is}\mathrm{an}\mathrm{I}(\mathrm{\Delta })\text{-}\mathrm{semigroup}\}.$ If $\mathcal{F}$ is a family of numerical semigroups, then we denote by ${\displaystyle \mathcal{J}\left(\mathcal{F}\right)=\bigcup _{\mathrm{\Delta }\in \mathcal{F}}\mathcal{J}\left(\mathrm{\Delta }\right).}$

The complexity of a numerical semigroup S is $\mathrm{C}\left(S\right)=min\{k\in \mathbb{N}\mid S\in {\mathcal{J}}^k\left(\mathbb{N}\right)\},$ where ${\mathcal{J}}^k\left(\mathbb{N}\right)=\mathcal{J}\left({\mathcal{J}}^{k-1}\left(\mathbb{N}\right)\right).$

If m and c are positive integers, then we denote by

$$\mathcal{R}(m,c)=\{S\mid S\mathrm{is}a\mathrm{numerical}\mathrm{semigroup,},\mathrm{m}(S)=mand\mathrm{C}(S)=c\}.$$

We will begin Section 5 by showing that

$$\mathcal{R}(m,c)=\mathcal{A}\left(\right[(c-1)m+1,(c-1)m+m-1],m)$$

and, consequently, we will transfer to $\mathcal{R}(m,c)$ all the results obtained in Section 4.

A set X is a $\mathcal{R}(m,c)$-set if $X\cap \{m,\to \}=\varnothing$ (where the symbol → means that every integer greater than or equal to m belongs to the set) and $X\subseteq S$ for some $S\in \mathcal{R}(m,c).$ If X is a $\mathcal{R}(m,c)$-set, then we denote by $\mathcal{R}(m,c)\left[X\right]$ the intersection of all elements of $\mathcal{R}(m,c)$ containing $X.$ If $S=\mathcal{R}(m,c)\left[X\right],$ then we say that X is a $\mathcal{R}(m,c)$-system of generators of $S.$ If $S=\mathcal{R}(m,c)\left[X\right]$ and $S\ne \mathcal{R}(m,c)\left[Y\right]$ for all $Y⊊X,$ then we will say that X is a $\mathcal{R}(m,c)$-minimal system of generators of $S.$ In Section 5, we prove that every element S of $\mathcal{R}(m,c)$ has a unique $\mathcal{R}(m,c)$-minimal system of generators. The cardinality of the $\mathcal{R}(m,c)$-minimal system of generators of S is called the $\mathcal{R}(m,c)$-rank of $S.$ We finish Section 5 by studying the elements of $\mathcal{R}(m,c)$ with $\mathcal{R}(m,c)$-rank 1.

2. The Tree Associated with $\mathcal{A}\left(\right[\mathbf{a},\mathbf{b}\left]\right)$

A covariety is a nonempty family $\mathcal{C}$ of numerical semigroups that fulfills the following conditions:

(1)

$\mathcal{C}$ has minimum, with respect to set inclusion.

(2)

If $\{S,T\}\subseteq \mathcal{C}$, then $S\cap T\in \mathcal{C}$.

(3)

If $S\in \mathcal{C}$ and $S\ne min\left(\mathcal{C}\right)$, then $S\setminus \left\{\mathrm{m}\right(S\left)\right\}\in \mathcal{C}$.

Our first aim in this section will be to show that $\mathcal{A}\left(\right[a,b\left]\right)$ is a covariety.

The following result is well known and easy to prove.

Lemma 1.

Let S and T be numerical semigroups and $x\in S.$ Then, the following conditions hold:

1. 

$S\cap T$ is a numerical semigroup and $\mathrm{F}(S\cap T)=\max \left\{\mathrm{F}\right(S),\mathrm{F}(T\left)\right\}.$

2. 

$S\setminus \left\{x\right\}$ is a numerical semigroup if and only if $x\in \mathrm{msg}\left(S\right).$

3. 

$\mathrm{m}\left(S\right)=min\left(\mathrm{msg}\left(S\right)\right).$

If $n\in \mathbb{N}\setminus \left\{0\right\},$ then we denote by $\mathrm{\Delta }\left(n\right)=\{0,n+1,\to \}.$ It is clear that $\mathrm{\Delta }\left(n\right)$ is a numerical semigroup and $\mathrm{F}\left(\mathrm{\Delta }\right(n\left)\right)=n.$

Proposition 1.

$\mathcal{A}\left(\right[a,b\left]\right)$ is a covariety.

Proof. 

We have the following:

• It is clear that $\mathrm{\Delta }\left(b\right)$ is the minimum of $\mathcal{A}\left(\right[a,b\left]\right).$
• If $\{S,T\}\subseteq \mathcal{A}\left(\right[a,b\left]\right),$ then by applying Lemma 1, we deduce that $S\cap T\in \mathcal{A}\left(\right[a,b\left]\right)$.
• Let $S\in \mathcal{A}\left(\right[a,b\left]\right)$ such that $S\ne \mathrm{\Delta }\left(b\right);$ then, $\mathrm{m}\left(S\right)<b.$ By applying Lemma 1, we have $S\setminus \left\{\mathrm{m}\right(S\left)\right\}$ as a numerical semigroup. Moreover, $a\le \mathrm{F}\left(S\right)\le \mathrm{F}(S\setminus \{\mathrm{m}\left(S\right)\left\}\right)\le b$, and so $S\setminus \left\{\mathrm{m}\right(S\left)\right\}\in \mathcal{A}\left(\right[a,b\left]\right).$

   □

A graph G is a pair $(V,E)$, where V is a nonempty set and E is a subset of $\left\{\right(u,v)\in V\times V\mid u\ne v\}$. The elements of V and E are called vertices and edges of G, respectively.

A path (of length n) connecting the vertices x and y of G is a sequence of different edges of the form $(v_0,v_1),(v_1,v_2),\dots ,(v_{n-1},v_n)$ such that $v_0=x$ and $v_n=y$.

A graph G is a tree if there exists a vertex r (known as the root of G) such that, for any other vertex x of G, there exists a unique path connecting x and r. If $(u,v)$ is an edge of the tree G, we say that u is a child of v.

Define the graph $\mathrm{G}\left(\mathcal{A}\right([a,b]\left)\right)$ in the following way: $\mathcal{A}\left(\right[a,b\left]\right)$ is its set of vertices and $(S,T)\in \mathcal{A}\left(\right[a,b\left]\right)\times \mathcal{A}\left(\right[a,b\left]\right)$ is an edge if and only if $T=S\setminus \left\{\mathrm{m}\right(S\left)\right\}.$

By applying Proposition 1 and [22] (Proposition 2.3), we obtain the following result.

Proposition 2.

$\mathrm{G}\left(\mathcal{A}\right([a,b]\left)\right)$ is a tree and $\mathrm{\Delta }\left(\mathcal{A}\right([a,b]\left)\right)$ is its root.

Observe that we can build a tree recursively, starting from the root and joining each vertex, already built, with its children by means of an edge.

We now show what the children of an arbitrary vertex of tree $\mathrm{G}\left(\mathcal{A}\right([a,b]\left)\right)$ look like. For this, we first need to introduce the following concept.

Let S be a numerical semigroup. We will say that an integer x is a special gap of $S,$ if $x\notin S$ and $S\cup \left\{x\right\}$ is a numerical semigroup. We denote, by $\mathrm{SG}\left(S\right)$, the set formed by the special gaps of $S.$

By applying Proposition 1 and [22] (Proposition 2.4), we obtain the following result.

Proposition 3.

If $S\in \mathcal{A}\left(\right[a,b\left]\right),$ then the set formed by the children of S in the tree $\mathrm{G}\left(\mathcal{A}\right([a,b]\left)\right)$ is $\{S\cup \{x\}\mid x\in \mathrm{SG}(S),x<\mathrm{m}(S)andS\cup \{x\}\in \mathcal{A}([a,b]\left)\right\}.$

Lemma 2.

Let $S\in \mathcal{A}\left(\right[a,b\left]\right)$ and $x\in \mathrm{SG}\left(S\right)$ such that $x<\mathrm{m}\left(S\right).$ Then, $S\cup \left\{x\right\}\notin \mathcal{A}\left(\right[a,b\left]\right)$ if and only if $S=\mathrm{\Delta }\left(a\right)$ and $x=a.$

Proof. 

(Necessity). If $x\ne \mathrm{F}\left(S\right),$ then $\mathrm{F}(S\cup \{x\left\}\right)=\mathrm{F}\left(S\right)$ and so $S\cup \left\{x\right\}\in \mathcal{A}\left(\right[a,b\left]\right).$ Then, we can assume that $x=\mathrm{F}\left(S\right).$ Therefore, $\mathrm{F}\left(S\right)=x<\mathrm{m}\left(S\right)$, and so $S=\{0,x+1,\to \}=\mathrm{\Delta }\left(x\right).$ If $\mathrm{\Delta }\left(x\right)\in \mathcal{A}\left(\right[a,b\left]\right)$ and $\mathrm{\Delta }\left(x\right)\cup \left\{x\right\}\notin \mathcal{A}\left(\right[a,b\left]\right),$ then we deduce that $x=a.$ Consequently, $S=\mathrm{\Delta }\left(a\right)$ and $x=a.$

(Sufficiency). Trivial.

   □

By applying Proposition 3 and Lemma 2, we obtain the following result.

Proposition 4.

If $S\in \mathcal{A}\left(\right[a,b\left]\right),$ then the set formed by the children of S in the tree $\mathrm{G}\left(\mathcal{A}\right([a,b]\left)\right)$ is as follows:

1. 

$\{S\cup \{x\}\mid x\in \mathrm{SG}(S)andx<\mathrm{m}(S\left)\right\}$ if $S\ne \mathrm{\Delta }\left(a\right).$

2. 

$\left\{\mathrm{\Delta }\right(a)\cup \{x\}\mid x\in \mathrm{SG}(\mathrm{\Delta }\left(a\right))\setminus \{a\left\}\right\}$ if $S=\mathrm{\Delta }\left(a\right).$

Our aim now is to present an algorithm for calculating $\mathcal{A}\left(\right[a,b\left]\right)$. For this, we introduce some concepts and results.

If S is a numerical semigroup and $n\in S\setminus \left\{0\right\},$ then we define the Apéry set (see [23]) of n in S as $\mathrm{Ap}(S,n)=\{s\in S\mid s-n\notin S\}.$

From [1] (Lemma 2.4), we can deduce the following.

Lemma 3.

Let S be a numerical semigroup and $n\in S\setminus \left\{0\right\}.$ Then, $\mathrm{Ap}(S,n)=\{0=w(0),$$w\left(1\right),\dots ,w(n-1)\}$, where $w\left(i\right)$ is the element of S that is least congruent with i modulo n for all $i\in \{0,\dots ,n-1\}.$

Remark 1.

Remarks 1 and 2 from [22] prove that if S is a numerical semigroup and we know $\mathrm{Ap}(S,n)$ for some $n\in S\setminus \left\{0\right\},$ then

1. 

We can easily calculate $\mathrm{SG}\left(S\right).$

2. 

We can obtain effortlessly $\mathrm{Ap}(S\cup \{x\},n)$ for all $x\in \mathrm{SG}\left(S\right).$

Now we have all the necessary elements to present the algorithm which computes $\mathcal{A}\left(\right[a,b\left]\right)$ (Algorithm 1).

Algorithm 1: Computation of $\mathcal{A}\left(\right[a,b\left]\right)$

Input: Positive integers a and b such that $a<b.$ Output: $\mathcal{A}\left(\right[a,b\left]\right).$ (1) $\mathcal{A}\left(\right[a,b\left]\right)=\left\{\mathrm{\Delta }\right(b\left)\right\},$$B=\left\{\mathrm{\Delta }\right(b\left)\right\}$ and $\mathrm{Ap}\left(\mathrm{\Delta }\right(b),b+1)=\{0,b+2,b+3,\dots ,$$2b+1\}.$ (2) For every $S\in B$, compute $\theta \left(S\right)=\left\{\begin{array}{ccc}\{x\in \mathrm{SG}(S)\mid x<\mathrm{m}(S\left)\right\}\hfill & if& \hfill S\ne \mathrm{\Delta }\left(a\right),\\ \{x\in \mathrm{SG}(S)\mid x\ne a\}\hfill & if& \hfill S=\mathrm{\Delta }\left(a\right).\end{array}\right.$ (3) If ${\displaystyle \bigcup _{S\in B}\theta \left(S\right)=\varnothing ,}$ then return $\mathcal{A}\left(\right[a,b\left]\right).$ (4) ${\displaystyle C:=\bigcup _{S\in B}\{S\cup \left\{x\right\}\mid x\in \theta \left(S\right)\}.}$ (5) $\mathcal{A}\left(\right[a,b\left]\right):=\mathcal{A}\left(\right[a,b\left]\right)\cup C$ and $B:=C.$ (6) For every $S\in B$, compute $\mathrm{Ap}(S,b+1)$ and go to Step $\left(2\right).$

In the following example, we can see how the algorithm works.

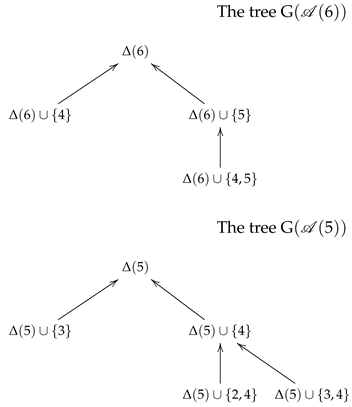
Example 1.

We are going to compute $\mathcal{A}\left(\right[5,6\left]\right)$ by using Algoritm 1

• $\mathcal{A}\left(\right[5,6\left]\right)=\left\{\mathrm{\Delta }\right(6\left)\right\},$$B=\left\{\mathrm{\Delta }\right(6\left)\right\}$ and $\mathrm{Ap}\left(\mathrm{\Delta }\right(6),7)=\{0,8,9,10,11,12,13\}.$
• $\theta \left(\mathrm{\Delta }\right(6\left)\right)=\{4,5,6\}.$
• $C=\left\{\mathrm{\Delta }\right(6)\cup \{4\},\mathrm{\Delta }(6)\cup \{5\},\mathrm{\Delta }(6)\cup \{6\left\}\right\}.$
• $\mathcal{A}\left(\right[5,6\left]\right)=\left\{\mathrm{\Delta }\right(6),\mathrm{\Delta }(6)\cup \{4\},\mathrm{\Delta }(6)\cup \{5\},\mathrm{\Delta }(6)\cup \{6\left\}\right\},$$B=\left\{\mathrm{\Delta }\right(6)\cup \{4\},\mathrm{\Delta }(6)\cup \{5\},\mathrm{\Delta }(6)\cup \{6\left\}\right\}.$
• $\mathrm{Ap}\left(\mathrm{\Delta }\right(6)\cup \{4\},7)=\{0,4,8,9,10,12,13\},$$\mathrm{Ap}\left(\mathrm{\Delta }\right(6)\cup \{5\},7)=\{0,5,8,9,10,11,13\},$$\mathrm{Ap}\left(\mathrm{\Delta }\right(6)\cup \{6\},7)=\{0,6,8,9,10,11,12\}.$
• $\theta \left(\mathrm{\Delta }\right(6)\cup \{4\left\}\right)=\varnothing ,$$\theta \left(\mathrm{\Delta }\right(6)\cup \{5\left\}\right)=\left\{4\right\},$$\theta \left(\mathrm{\Delta }\right(6)\cup \{6\left\}\right)=\{3,4\}.$
• $C=\left\{\mathrm{\Delta }\right(6)\cup \{4,5\},\mathrm{\Delta }(6)\cup \{3,6\},\mathrm{\Delta }(6)\cup \{4,6\left\}\right\}.$
• $\mathcal{A}\left(\right[5,6\left]\right)=\left\{\mathrm{\Delta }\right(6),\mathrm{\Delta }(6)\cup \{4\},\mathrm{\Delta }(6)\cup \{5\},\mathrm{\Delta }(6)\cup \{6\},\mathrm{\Delta }(6)\cup \{4,5\},\mathrm{\Delta }(6)\cup \{3,6\},\mathrm{\Delta }(6)$$\cup \{4,6\}\}$ and $B=\left\{\mathrm{\Delta }\right(6)\cup \{4,5\},\mathrm{\Delta }(6)\cup \{3,6\},\mathrm{\Delta }(6)\cup \{4,6\left\}\right\}.$
• $\mathrm{Ap}\left(\mathrm{\Delta }\right(6)\cup \{4,5\},7)=\{0,4,5,8,9,10,13\},$$\mathrm{Ap}\left(\mathrm{\Delta }\right(6)\cup \{3,6\},7)=\{0,3,6,8,9,11,12\},$
  $\mathrm{Ap}\left(\mathrm{\Delta }\right(6)\cup \{4,6\},7)=\{0,4,6,8,9,10,12\}.$
• $\theta \left(\mathrm{\Delta }\right(6)\cup \{4,5\left\}\right)=\varnothing =\theta \left(\mathrm{\Delta }\right(6)\cup \{3,6\left\}\right)$ and $\theta \left(\mathrm{\Delta }\right(6)\cup \{4,6\left\}\right)=\{2,3\}.$
• $C=\left\{\mathrm{\Delta }\right(6)\cup \{2,4,6\},\mathrm{\Delta }(6)\cup \{3,4,6\left\}\right\}.$
• $\mathcal{A}\left(\right[5,6\left]\right)=\left\{\mathrm{\Delta }\right(6),\mathrm{\Delta }(6)\cup \{4\},\mathrm{\Delta }(6)\cup \{5\},\mathrm{\Delta }(6)\cup \{6\},\mathrm{\Delta }(6)\cup \{4,5\},\mathrm{\Delta }(6)\cup \{3,6\},\mathrm{\Delta }(6)$$\cup \{4,6\},\mathrm{\Delta }\left(6\right)\cup \{2,4,6\},\mathrm{\Delta }\left(6\right)\cup \{3,4,6\}\}$ and $B=\left\{\mathrm{\Delta }\right(6)\cup \{2,4,6\},\mathrm{\Delta }(6)\cup \{3,4,6\left\}\right\}.$
• $\mathrm{Ap}\left(\mathrm{\Delta }\right(6)\cup \{2,4,6\},7)=\{0,2,4,6,8,10,12\}$ and $\mathrm{Ap}\left(\mathrm{\Delta }\right(6)\cup \{3,4,6\},7)=\{0,3,4,6,8,$$9,12\}.$
• $\theta \left(\mathrm{\Delta }\right(6)\cup \{2,4,6\left\}\right)=\varnothing$ and $\theta \left(\mathrm{\Delta }\right(6)\cup \{3,4,6\left\}\right)=\varnothing .$

Therefore, Algorithm 1 returns $\mathcal{A}\left(\right[5,6\left]\right)=\left\{\mathrm{\Delta }\right(6),\mathrm{\Delta }(6)\cup \{4\},\mathrm{\Delta }(6)\cup \{5\},\mathrm{\Delta }(6)\cup \{6\},\mathrm{\Delta }(6)\cup \{4,5\},\mathrm{\Delta }(6)\cup \{3,6\},\mathrm{\Delta }(6)\cup \{4,6\},\mathrm{\Delta }(6)\cup \{2,4,6\},\mathrm{\Delta }(6)\cup \{3,4,6\left\}\right\}.$

The tree $\mathrm{G}\left(\mathcal{A}\right([5,6]\left)\right)$ can be drawn easily by using Example 1.

If F is a positive integer, then we denote that

$$\mathcal{A}\left(F\right)=\{S\mid S\mathrm{is}a\mathrm{numerical}\mathrm{semigroup}\mathrm{and}\mathrm{F}(S)=F\}.$$

The following result has an immediate demonstration.

Proposition 5.

The set $\left\{\mathcal{A}\right(F)\mid F\in [a,b\left]\right\}$ is a partition of $\mathcal{A}\left(\right[a,b\left]\right).$

In [22] (Proposition 2.2), it is proven that $\mathcal{A}\left(F\right)$ is a covariety. Accordingly, Proposition 5 decomposes the covariety $\mathcal{A}\left(\right[a,b\left]\right)$ into smaller covarieties. Moreover, Algorithm 1 from [22] computes $\mathcal{A}\left(F\right).$ Consequently, we have an alternative algorithm to the Algorithm 1 for calculating $\mathcal{A}\left(\right[a,b\left]\right).$ This is Algorithm 2.

Algorithm 2: Computation of $\mathcal{A}\left(\right[a,b\left]\right)$

Input: Positive integers a and b such that $a<b.$ Output: $\mathcal{A}\left(\right[a,b\left]\right).$ (1) For every $F\in [a,b]$, compute $\mathcal{A}\left(F\right)$ by using Algorithm 1 of [22]. (2) Return ${\displaystyle \mathcal{A}\left([a,b]\right)=\bigcup _{F=a}^b\mathcal{A}\left(F\right).}$

In [22], the graph $\mathrm{G}\left(\mathcal{A}\right(F\left)\right)$ is defined as follows: $\mathcal{A}\left(F\right)$ is its set of vertices and $(S,T)\in \mathcal{A}\left(F\right)\times \mathcal{A}\left(F\right)$ is an edge if and only if $T=S\setminus \left\{\mathrm{m}\right(S\left)\right\}.$ Additionally, it is proven that $\mathrm{G}\left(\mathcal{A}\right(F\left)\right)$ is a tree with root $\mathrm{\Delta }\left(F\right).$ We finish this section by drawing the trees for $F\in \{5,6\}.$

3. The Genus of the Elements of $\mathcal{A}\left(\right[\mathbf{a},\mathbf{b}\left]\right)$

The following result can be deduced from [1] (Lemma 2.14).

Lemma 4.

If S is a numerical semigroup, then ${\displaystyle ⌈\frac{\mathrm{F}\left(S\right)+1}{2}⌉\le \mathrm{g}\left(S\right)\le \mathrm{F}\left(S\right).}$

A numerical semigroup is irreducible if it cannot be expressed as the intersection of two numerical semigroups properly containing it. The following result is [1] (Corollary 4.5).

Lemma 5.

A numerical semigroup S is irreducible if and only if ${\displaystyle \mathrm{g}\left(S\right)=⌈\frac{\mathrm{F}\left(S\right)+1}{2}⌉.}$

The following result is deduced from [24] (Theorem 1).

Lemma 6.

Let S be a numerical semigroup. Then, S is irreducible if and only if S is maximal in the set of all numerical semigroups with Frobenius number $\mathrm{F}\left(S\right).$

As $\mathrm{F}\left(\mathrm{\Delta }\right(F\left)\right)=F,$ the set of all numerical semigroups with Frobenius number F is nonempty. By applying Lemma 6, we obtain the following result.

Lemma 7.

If F is a positive integer, then there exists at least one irreducible numerical semigroup with Frobenius number $F.$

Let S be a numerical semigroup. An element $s\in S$ will be labelled small if $s<\mathrm{F}\left(S\right).$ We denote, by $\mathrm{N}\left(S\right)$, the set of all small elements of $S.$ The cardinality of $\mathrm{N}\left(S\right)$ is denoted by $\mathrm{n}\left(S\right).$ Note that $\mathrm{n}\left(S\right)+\mathrm{g}\left(S\right)=\mathrm{F}\left(S\right)+1.$

Proposition 6.

If F is a positive integer, then $\{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}\left(F\right)\}=\left[⌈{\displaystyle \frac{F+1}{2}}⌉,F\right].$

Proof. 

By applying Lemmas 5 and 7, we deduce that there exists a numerical semigroup S such that $\mathrm{F}\left(S\right)=F$ and $\mathrm{g}\left(S\right)=⌈{\displaystyle \frac{F+1}{2}}⌉.$ We recursively define the following sequence of numerical semigroups: $S_0=S$ and $S_{n+1}=\left\{\begin{array}{ccc}{S}_n\setminus \left\{\mathrm{m}\left(S_n\right)\right\}\hfill & if& \hfill \mathrm{m}\left(S_n\right)<F,\\ \mathrm{\Delta }\left(F\right)\hfill & & \hfill otherwise.\end{array}\right.$

It is clear that $S=S_0⊊S_1⊊\dots ⊊S_{\mathrm{n}\left(S\right)-1}=\mathrm{\Delta }\left(F\right)$ and that $\{\mathrm{g}\left(S_0\right),\mathrm{g}\left(S_1\right),\dots ,\mathrm{g}\left(S_{\mathrm{n}\left(S\right)-1}\right)\}$$=\left[⌈{\displaystyle \frac{F+1}{2}}⌉,F\right].$ As $\{S=S_0,S_1,\dots ,S_{\mathrm{n}\left(S\right)-1}\}\subseteq \mathcal{A}\left(F\right),$ by applying Lemma 4, we can conclude that $\{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}\left(F\right)\}=\left[⌈{\displaystyle \frac{F+1}{2}}⌉,F\right].$    □

We now aim to generalise Proposition 6 to $\mathcal{A}\left(\right[a,b\left]\right).$ That is, we want to see that there are positive integers $\alpha$ and $\beta$ such that $\left\{\mathrm{g}\right(S)\mid S\in \mathcal{A}([a,b]\left)\right\}=[\alpha ,\beta ].$

Proposition 7.

The following are verified:

1. 

$min\{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}\left([a,b]\right)\}=⌈{\displaystyle \frac{a+1}{2}}⌉.$

2. 

$\max \left\{\mathrm{g}\right(S)\mid S\in \mathcal{A}([a,b]\left)\right\}=b.$

3. 

$\{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}\left([a,b]\right)\}=\left[⌈{\displaystyle \frac{a+1}{2}}⌉,b\right].$

Proof. 

1.

If $S\in \mathcal{A}\left(\right[a,b\left]\right),$ then $\mathrm{F}\left(S\right)\ge a$, and by using Lemma 4, we have $\mathrm{g}\left(S\right)\ge ⌈{\displaystyle \frac{\mathrm{F}\left(S\right)+1}{2}}⌉\ge ⌈{\displaystyle \frac{a+1}{2}}⌉.$ By Lemma 7, we know that there is an irreducible numerical semigroup T such that $\mathrm{F}\left(T\right)=a.$ Then, by Lemma 5, we have ${\displaystyle \mathrm{g}\left(T\right)=⌈\frac{a+1}{2}⌉.}$ Therefore, $min\{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}\left([a,b]\right)\}=⌈{\displaystyle \frac{a+1}{2}}⌉.$

2.

By Proposition 1, we know that $\mathrm{\Delta }\left(b\right)$ is the minimum of $\mathcal{A}\left(\right[a,b\left]\right).$ Then, we can easily deduce $\max \left\{\mathrm{g}\right(S)\mid S\in \mathcal{A}([a,b]\left)\right\}=\mathrm{g}\left(\mathrm{\Delta }\right(b\left)\right)=b.$

3.

Let T be an element of $\mathcal{A}\left(\right[a,b\left]\right)$ such that $\mathrm{g}\left(T\right)=⌈{\displaystyle \frac{a+1}{2}}⌉$, and let $(S_0,S_1),(S_1,S_2),\dots ,(S_{n-1},S_n)$ be the unique path in the tree $\mathrm{G}\left(\mathcal{A}\right([a,b]\left)\right)$ connecting T and $\mathrm{\Delta }\left(b\right).$ Then, it is clear that $\{\mathrm{g}\left(S_0\right),\mathrm{g}\left(S_1\right),\dots ,\mathrm{g}\left(S_n\right)\}=\left[⌈{\displaystyle \frac{a+1}{2}}⌉,b\right].$

   □

Our next aim is to present an algorithm that calculates all elements of $\mathcal{A}\left(\right[a,b\left]\right)$ with a given genus.

Let G be a tree and let v be one of its vertices. The depth of v, denoted by $d\left(v\right)$, is the length of the only path connecting v with the root of G. By definition, we will say that the root has zero depth. If $n\in \mathbb{N},$ denote by $\mathrm{N}(G,n)=\{v\in V\mid d(v)=n\}.$ The height of G is $\mathrm{h}\left(G\right)=\max \{k\in \mathbb{N}\mid \mathrm{N}(G,k)\ne \varnothing \}.$

The following result has immediate proof.

Proposition 8.

With the previous notation,

1. 

$\mathrm{N}\left(G\right(\mathcal{A}\left(\right[a,b\left]\right)),n)=\{S\in \mathcal{A}([a,b])\mid \mathrm{g}(S)=b-n\}.$

2. 

$\mathrm{N}\left(G\right(\mathcal{A}\left(\right[a,b\left]\right)),n+1)=\{S\mid S\mathit{is}\mathrm{a}\mathit{child}\mathit{of}\mathit{some}\mathit{element}\mathit{of}\mathrm{N}(G\left(\mathcal{A}\right([a,b]\left)\right),n\left)inthetreeG\right(\mathcal{A}\left(\right[a,b\left]\right)\left)\right\}.$

3. 

$\mathrm{h}\left(G\left(\mathcal{A}\left([a,b]\right)\right)\right)=b-⌈{\displaystyle \frac{a+1}{2}}⌉.$

The following algorithm (Algorithm 3) computes all the elements of $\mathcal{A}\left(\right[a,b\left]\right)$ with a fixed genus.

Algorithm 3: Computation of $\{S\in \mathcal{A}([a,b])\mid \mathrm{g}(S)=g\}$

Input: An integer g such that $⌈{\displaystyle \frac{a+1}{2}}⌉\le g\le b.$ Output: $\{S\in \mathcal{A}([a,b])\mid \mathrm{g}(S)=g\}$. (1) $H=\left\{\mathrm{\Delta }\right(b\left)\right\}$, $i=b.$ (2) If $i=g$, then return $H.$ (3) For each $S\in H$, compute $\theta \left(S\right).$ (4) $H={\bigcup }_{S\in H}\left\{S\cup \left\{x\right\}\mid x\in \theta \left(S\right)\right\}$, $i=i-1$ and go to Step $\left(2\right).$

   We will proceed to illustrate how the previous algorithm works with an example.

Example 2.

We are going to compute the set $\{S\in \mathcal{A}([5,6])\mid \mathrm{g}(S)=4\}$ by applying Algorithm 3. Note that $⌈{\displaystyle \frac{5+1}{2}}⌉\le 4\le 6.$

• $H=\left\{\mathrm{\Delta }\right(6\left)\right\}$, $i=6.$
• $\theta \left(\mathrm{\Delta }\right(6\left)\right)=\{4,5,6\}.$
• $H=\left\{\mathrm{\Delta }\right(6)\cup \{4\},\mathrm{\Delta }(6)\cup \{5\},\mathrm{\Delta }(6)\cup \{6\left\}\right\}$, $i=5.$
• $\theta \left(\mathrm{\Delta }\right(6)\cup \{4\left\}\right)=\varnothing ,$$\theta \left(\mathrm{\Delta }\right(6)\cup \{5\left\}\right)=\left\{4\right\},$$\theta \left(\mathrm{\Delta }\right(6)\cup \{6\left\}\right)=\{3,4\}.$
• $H=\left\{\mathrm{\Delta }\right(6)\cup \{4,5\},\mathrm{\Delta }(6)\cup \{3,6\},\mathrm{\Delta }(6)\cup \{4,6\left\}\right\}$, $i=4.$

Algorithm 3 returns

$$\{S\in \mathcal{A}([5,6])\mid \mathrm{g}(S)=4\}=\left\{\mathrm{\Delta }\right(6)\cup \{4,5\},\mathrm{\Delta }(6)\cup \{3,6\},\mathrm{\Delta }(6)\cup \{4,6\left\}\right\}.$$

We conclude this section by noting that, from the tree $\mathrm{G}\left(\mathcal{A}\right([5,6]\left)\right)$ pictured after Example 1, we can deduce that

• $\mathrm{N}\left(G\right(\mathcal{A}\left(\right[5,6\left]\right)),0)=\left\{\mathrm{\Delta }\right(6\left)\right\}.$
• $\mathrm{N}\left(G\right(\mathcal{A}\left(\right[5,6\left]\right)),1)=\left\{\mathrm{\Delta }\right(6)\cup \{4\},\mathrm{\Delta }(6)\cup \{5\},\mathrm{\Delta }(6)\cup \{6\left\}\right\}.$
• $\mathrm{N}\left(G\right(\mathcal{A}\left(\right[5,6\left]\right)),2)=\left\{\mathrm{\Delta }\right(6)\cup \{4,5\},\mathrm{\Delta }(6)\cup \{3,6\},\mathrm{\Delta }(6)\cup \{4,6\left\}\right\}.$
• $\mathrm{N}\left(G\right(\mathcal{A}\left(\right[5,6\left]\right)),3)=\left\{\mathrm{\Delta }\right(6)\cup \{2,4,6\},\mathrm{\Delta }(6)\cup \{3,4,6\left\}\right\}.$
• $\mathrm{h}\left(G\right(\mathcal{A}\left(\right[5,6\left]\right)\left)\right)=3.$

4. The Elements of $\mathcal{A}\left(\right[\mathbf{a},\mathbf{b}\left]\right)$ with Fixed Multiplicity

If m is a positive integer, then we denote by $\mathcal{A}\left(\right[a,b],m)=\{S\in \mathcal{A}([a,b])\mid \mathrm{m}(S)=m\}.$

Note that $\mathbb{N}$ is the unique numerical semigroup with multiplicity 1. Therefore, henceforth, we shall assume that $m\ge 2.$

For integers p and $q,$ we say that p divides q if there exists an integer r such that $q=rp,$ and we denote this by $p\mid q.$ Otherwise, p does not divide q, and we denote this by $p\nmid q.$

Also note that if $m|a$ ($m|b$, respectively), then $\mathcal{A}\left(\right[a,b],m)=\mathcal{A}\left(\right[a+1,b],m)$ ($\mathcal{A}\left(\right[a,b],m)=\mathcal{A}\left(\right[a,b-1],m)$, respectively).

In the rest of this paper, m will denote an integer greater than or equal to 2; a and b will be positive integers such that $a<b,$$m\nmid a$ and $m\nmid b.$

If S is a numerical semigroup such that $S\ne \mathbb{N},$ the ratio of S is $\mathrm{r}\left(S\right)=min\{s\in S\mid \mathrm{m}(S)\nmid s\}.$ Note that $\mathrm{r}\left(S\right)=min\left(\mathrm{msg}\right(S)\setminus \{\mathrm{m}\left(S\right)\left\}\right).$

A ratio-covariety is a nonempty family $\mathcal{R}$ of numerical semigroups fulfilling the following conditions:

(1)

There is the minimum of $\mathcal{R}$, denoted by $min\left(\mathcal{R}\right).$

(2)

If $\{S,T\}\subseteq \mathcal{R}$, then $S\cap T\in \mathcal{R}$.

(3)

If $S\in \mathcal{R}$ and $S\ne min\left(\mathcal{R}\right)$, then $S\setminus \left\{\mathrm{r}\right(S\left)\right\}\in \mathcal{R}$.

Observe that if $S\in \mathcal{A}\left(\right[a,b],m),$ then $m\le b+1.$ Moreover, if $m=b+1,$ then $\mathcal{A}\left(\right[a,b],m)=\left\{\mathrm{\Delta }\right(b\left)\right\}.$ So, in what follows, without loss of generality, it is possible to assume $m<b.$

Proposition 9.

$\mathcal{A}\left(\right[a,b],m)$ is a ratio-covariety.

Proof. 

The following is verified.

• It is clear that $\mathrm{\Delta }(b,m)=\langle m\rangle \cup \{b+1,\to \}$ is the minimum of $\mathcal{A}\left(\right[a,b],m).$
• By applying Lemma 1, it is easy to deduce that if $\{S,T\}\subseteq \mathcal{A}\left(\right[a,b],m)$, then $S\cap T\in \mathcal{A}\left(\right[a,b],m).$
• To conclude the proof, we will show that if $S\in \mathcal{A}\left(\right[a,b],m)$ and $S\ne \mathrm{\Delta }(b,m),$ then $S\setminus \left\{\mathrm{r}\right(S\left)\right\}\in \mathcal{A}\left(\right[a,b],m).$ As $\mathrm{r}\left(S\right)\in \mathrm{msg}\left(S\right),$ then, by applying Lemma 1, we know that $S\setminus \left\{\mathrm{r}\right(S\left)\right\}$ is a numerical semigroup. As $S\ne \mathrm{\Delta }(b,m),$ then $m<\mathrm{r}\left(S\right)<b$ and so $\mathrm{m}(S\setminus \{\mathrm{r}\left(S\right)\left\}\right)=m$ and $\mathrm{F}\left(S\right)\le \mathrm{F}(S\setminus \{\mathrm{r}\left(S\right)\left\}\right)\le b.$ Consequently, $S\setminus \left\{\mathrm{r}\right(S\left)\right\}\in \mathcal{A}\left(\right[a,b],m).$

   □

Define the graph $\mathrm{G}\left(\mathcal{A}\right([a,b],m\left)\right)$ in the following way: $\mathcal{A}\left(\right[a,b],m)$ is its set of vertices and $(S,T)\in \mathcal{A}\left(\right[a,b],m)\times \mathcal{A}\left(\right[a,b],m)$ is an edge if and only if $T=S\setminus \left\{\mathrm{r}\right(S\left)\right\}.$

By applying Proposition 1 and [25] (Propositions 3 and 4), we obtain the following result.

Proposition 10.

$\mathrm{G}\left(\mathcal{A}\right([a,b],m\left)\right)$ is a tree with root $\mathrm{\Delta }(b,m).$ Moreover, if $S\in \mathcal{A}\left(\right[a,b],m),$ then the set formed by the children of S in the tree $\mathrm{G}\left(\mathcal{A}\right([a,b],m\left)\right)$ is $\{S\cup \{x\}\mid x\in \mathrm{SG}(S),m<x<\mathrm{r}(S)$$andS\cup \left\{x\right\}\in \mathcal{A}\left(\right[a,b],m)\}.$

The following result is easily provable.

Lemma 8.

Let $S\in \mathcal{A}\left(\right[a,b],m)$ and $x\in \mathrm{SG}\left(S\right)$ such that $m<x.$ Then, $S\cup \left\{x\right\}\in \mathcal{A}\left(\right[a,b],m)$ if and only if $x\ne \mathrm{F}\left(S\right)$ or $x=\mathrm{F}\left(S\right)$ and $[a,\mathrm{F}(S)-1]⊈S.$

Proposition 10 can be reformulated by applying Lemma 8, as follows.

Proposition 11.

$\mathrm{G}\left(\mathcal{A}\right([a,b],m\left)\right)$ is a tree with root $\mathrm{\Delta }(b,m).$ Moreover, if $S\in \mathcal{A}\left(\right[a,b],m),$ then the set formed by the children of S in the tree $\mathrm{G}\left(\mathcal{A}\right([a,b],m\left)\right)$ is $\{S\cup \{x\}\mid x\in \mathrm{SG}(S),m<x<\mathrm{r}(S)$$andx\ne \mathrm{F}\left(S\right)\}\cup \alpha (S),$ where

$$\alpha \left(S\right)=\left\{\begin{array}{ccc}\{S\cup \{\mathrm{F}\left(S\right)\left\}\right\}\hfill & if& m<\mathrm{F}\left(S\right)<\mathrm{r}\left(S\right)and[a,\mathrm{F}(S)-1]⊈S,\hfill \\ \varnothing \hfill & & otherwise.\hfill \end{array}\right.$$

If S is a numerical semigroup, then we denote by

$$\lambda \left(S\right)=\{x\in \mathrm{SG}(S)\mid \mathrm{m}(S)<x<\mathrm{r}(S)\mathrm{and}x\ne \mathrm{F}(S\left)\right\}\cup \mu \left(S\right),$$

where

$$\mu \left(S\right)=\left\{\begin{array}{ccc}\left\{\mathrm{F}\right(S\left)\right\}\hfill & \mathrm{if}& \mathrm{m}\left(S\right)<\mathrm{F}\left(S\right)<\mathrm{r}\left(S\right)\mathrm{and}[a,\mathrm{F}(S)-1]⊈S,\hfill \\ \varnothing \hfill & & \mathrm{otherwise}.\hfill \end{array}\right.$$

Algorithm 4: Computation of $\mathcal{A}\left(\right[a,b],m)$

Input: Positive integers $a,b$ and m such that $m\ge 2,$$m\nmid a$, $m\nmid b$, $m<b$ and $a<b.$ Output: $\mathcal{A}\left(\right[a,b],m).$ (1) Compute $\mathrm{Ap}\left(\mathrm{\Delta }\right(b,m),m).$ (2) $\mathcal{A}\left(\right[a,b],m)=\left\{\mathrm{\Delta }\right(b,m\left)\right\},$$B=\left\{\mathrm{\Delta }\right(b,m\left)\right\}.$ (3) For every $S\in B$, compute $\lambda \left(S\right).$ (4) If ${\displaystyle \bigcup _{S\in B}\lambda \left(S\right)=\varnothing ,}$ then return $\mathcal{A}\left(\right[a,b],m).$ (5) ${\displaystyle C=\bigcup _{S\in B}\{S\cup \left\{x\right\}\mid x\in \lambda \left(S\right)\}.}$ (6) $\mathcal{A}\left(\right[a,b],m):=\mathcal{A}\left(\right[a,b],m)\cup C$ and $B=C.$ (7) For every $S\in B$, compute $\mathrm{Ap}(S,m)$ and go to Step $\left(3\right).$

Now we will illustrate the previous algorithm.

Example 3.

We are going to compute $\mathcal{A}\left(\right[5,6],4)$ by using Algorithm 4

• $\mathrm{Ap}\left(\mathrm{\Delta }\right(6,4),4)=\{0,7,9,10\}.$
• $\mathcal{A}\left(\right[5,6],4)=\left\{\mathrm{\Delta }\right(6,4\left)\right\},$$B=\left\{\mathrm{\Delta }\right(6,4\left)\right\}.$
• $\lambda \left(\mathrm{\Delta }\right(6,4\left)\right)=\{5,6\}.$
• $C=\left\{\mathrm{\Delta }\right(6,4)\cup \{5\},\mathrm{\Delta }(6,4)\cup \{6\left\}\right\}.$
• $\mathcal{A}\left(\right[5,6],4)=\left\{\mathrm{\Delta }\right(6,4),\mathrm{\Delta }(6,4)\cup \{5\},\mathrm{\Delta }(6,4)\cup \{6\left\}\right\},$$B=\left\{\mathrm{\Delta }\right(6,4)\cup \{5\},\mathrm{\Delta }(6,4)\cup \{6\left\}\right\},$
• $\mathrm{Ap}\left(\mathrm{\Delta }\right(6,4)\cup \{5\},4)=\{0,5,7,10\},$$\mathrm{Ap}\left(\mathrm{\Delta }\right(6,4)\cup \{6\},4)=\{0,6,7,9\}.$
• $\lambda \left(\mathrm{\Delta }\right(6,4)\cup \{5\left\}\right)=\varnothing$ and $\lambda \left(\mathrm{\Delta }\right(6,4)\cup \{6\left\}\right)=\varnothing .$

Therefore, Algorithm 4 returns

$$\mathcal{A}\left(\right[5,6],4)=\left\{\mathrm{\Delta }\right(6,4),\mathrm{\Delta }(6,4)\cup \{5\},\mathrm{\Delta }(6,4)\cup \{6\left\}\right\}.$$

Our next goal now will be to see what genus the elements of $\mathcal{A}\left(\right[a,b],m)$ have. The following result can be deduced from [26] (Proposition 4.2).

Lemma 9.

Let F be a positive integer. If ${\displaystyle m\le \frac{F+2}{2}}$ and $m\nmid F,$ then there exists at least an irreducible numerical semigroup such that $\mathrm{F}\left(S\right)=F$ and $\mathrm{m}\left(S\right)=m.$

Lemma 10.

Let F be an integer such that $F\ge m-1$ and $m\nmid F$. Then

$$min\left\{\mathrm{g}\right(S)\mid Sisanumericalsemigroup,\mathrm{F}(S)=Fand\mathrm{m}(S)=m\}=$$

$$\left\{\begin{array}{ccc}m-1\hfill & if& \hfill F=m-1,\\ m\hfill & if& \hfill m<F<2m,\\ ⌈{\displaystyle \frac{F+1}{2}}⌉\hfill & if& \hfill F>2m.\end{array}\right.$$

Proof. 

Let S be a numerical semigroup such that $\mathrm{F}\left(S\right)=F$ and $\mathrm{m}\left(S\right)=m.$ We consider the following cases:

• If $F=m-1,$ then $S=\{0,m,\to \}$ and so $\mathrm{g}\left(S\right)=m-1.$
• If $m<F<2m,$ then $\mathrm{g}\left(S\right)\ge m.$ Besides, it is clear that $\{0,m,\to \}\setminus \left\{F\right\}$ is a numerical semigroup with multiplicity $m,$ Frobenius number F and genus $m.$
• If $F>2m,$ then by Lemmas 5 and 9, we know that there is a numerical semigroup with multiplicity $m,$ Frobenius number F and genus $⌈{\displaystyle \frac{F+1}{2}}⌉.$ In addition, by Lemma 4, we know that if S is a numerical semigroup and $\mathrm{F}\left(S\right)=F,$ then $\mathrm{g}\left(S\right)\ge ⌈{\displaystyle \frac{F+1}{2}}⌉.$

□

Note that if S is a numerical semigroup with multiplicity $m,$ then $\mathrm{F}\left(S\right)\ge m-1.$ We will therefore assume from now on that $m-1\le a<b,$$m\ge 2,$$m\nmid a$ and $m\nmid b.$

If $q\in \mathbb{Q}$, we denote by $\lfloor q\rfloor =\max \{z\in \mathbb{Z}\mid z\le q\}.$

Lemma 11.

We have

$$\max \{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}([a,b],m)\}=b-⌊{\displaystyle \frac{b}{m}}⌋.$$

Proof. 

This is enough to observe that $\mathrm{\Delta }(b,m)$ is the minimum of $\mathcal{A}\left(\right[a,b],m)$ and $\mathrm{g}\left(\mathrm{\Delta }(b,m)\right)=b-⌊{\displaystyle \frac{b}{m}}⌋.$ □

Proposition 12.

The following are verified:

1. 

If $a=m-1,$ then $\{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}([a,b],m)\}=\left[a,b-⌊{\displaystyle \frac{b}{m}}⌋\right].$

2. 

If $m<a<2m,$ then $\{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}([a,b],m)\}=\left[m,b-⌊{\displaystyle \frac{b}{m}}⌋\right].$

3. 

If $2m<a,$ then $\{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}([a,b],m)\}=\left[⌈{\displaystyle \frac{a+1}{2}}⌉,b-⌊{\displaystyle \frac{b}{m}}⌋\right].$

Proof. 

By Lemma 10, we know that

1.

If $a=m-1,$ then $min\left\{\mathrm{g}\right(S)\mid S\in \mathcal{A}([a,b],m\left)\right\}=a.$

2.

If $m<a<2m,$ then $min\left\{\mathrm{g}\right(S)\mid S\in \mathcal{A}([a,b],m\left)\right\}=m.$

3.

If $2m<a,$ then $min\{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}([a,b],m)\}=⌈{\displaystyle \frac{a+1}{2}}⌉.$

By Lemma 11, we know that $\max \{\mathrm{g}\left(S\right)\mid S\in \mathcal{A}([a,b],m)\}=b-⌊{\displaystyle \frac{b}{m}}⌋.$

To conclude the proof, it will be enough note that if $T\in \mathcal{A}\left(\right[a,b],m),$$\mathrm{g}\left(T\right)=min\left\{\mathrm{g}\right(S)\mid S\in \mathcal{A}([a,b],m\left)\right\}$ and $(S_0,S_1),(S_1,S_2),\dots ,(S_{\mathrm{n}\left(S\right)-1},S_n)$ is the unique path in the tree $\mathrm{G}\left(\mathcal{A}\right([a,b],m\left)\right)$ that connects T and $\mathrm{\Delta }(b,m),$ then $\{\mathrm{g}\left(S_0\right),\mathrm{g}\left(S_1\right),\dots ,\mathrm{g}\left(S_n\right))\}=\left[\mathrm{g}\left(T\right),b-⌊{\displaystyle \frac{b}{m}}⌋\right].$ □

5. Numerical Semigroups with a Given Multiplicity and Complexity

A numerical semigroup is ordinary if $S=\{0,\mathrm{m}(S),\to \}.$ A numerical semigroup S is elemental if $\mathrm{m}\left(S\right)<\mathrm{F}\left(S\right)<2\mathrm{m}\left(S\right).$ The following result is straightforward to obtain.

Proposition 13.

The following holds:

$\{S\mid Sisanelementalnumericalsemigroupand\mathrm{m}(S)=m\}=\left\{\right\{0,m,2m,\to \}\cup A\mid A⊊\{m+1,\dots ,2m-1\left\}\right\}.$

Intuitively, the ordinary numerical semigroups are the easiest to study, and the elementary numerical semigroups are the next easiest.

In [27], it is shown that $\mathcal{J}\left(\mathbb{N}\right)$ is the set formed by all the ordinary numerical semigroup, and ${\mathcal{J}}^2\left(\mathbb{N}\right)=\mathcal{J}\left(\mathcal{J}\left(\mathbb{N}\right)\right)$ is the set formed by all elemental numerical semigroups. This fact leads us to give the following definition. The complexity of a numerical semigroup S is $\mathrm{C}\left(S\right)=min\{k\in \mathbb{N}\mid S\in {\mathcal{J}}^k\left(\mathbb{N}\right)\}.$ The following result is [27] (Corollary 21).

Proposition 14.

If S is a numerical semigroup, then $\mathrm{C}\left(S\right)=⌊{\displaystyle \frac{\mathrm{F}\left(S\right)}{\mathrm{m}\left(S\right)}}⌋+1.$

If m and c are positive integers, then we denote by

$$\mathcal{R}(m,c)=\{S\mid S\mathrm{is}a\mathrm{numerical}\mathrm{semigroup},\mathrm{m}(S)=mand\mathrm{C}(S)=c\}.$$

It is clear that $\mathbb{N}$ is the unique numerical semigroup with multiplicity 1 and as $\mathrm{F}\left(\mathbb{N}\right)=-1;$ then, by applying Proposition 14, we have $\mathrm{C}\left(\mathbb{N}\right)=0.$ Note that if S is a numerical semigroup and $S\ne \mathbb{N}$ then $\mathrm{F}\left(S\right)\ge 1$ and, by Proposition 14, we have $\mathrm{C}\left(S\right)\ge 1.$ We also observe that if $c\in \mathbb{N}\setminus \left\{0\right\},$ then $\mathcal{R}(2,c)=\{\langle 2,2c+1\rangle \}.$ In what follows in this paper, we assume that m and c are integers such that $m\ge 3$ and $c\ge 2.$

Proposition 15.

We have

$$\mathcal{R}(m,c)=\mathcal{A}\left(\left[\right(c-1)m+1,(c-1)m+m-1],m\right).$$

Proof. 

This is enough to note that $S\in \mathcal{R}(m,c)$ if and only if $\mathrm{m}\left(S\right)=m$ and $\mathrm{C}\left(S\right)=⌊{\displaystyle \frac{\mathrm{F}\left(S\right)}{m}}⌋+1=c.$ □

As a consequence of Propositions 9 and 15, we have the following result.

Corollary 1.

$\mathcal{R}(m,c)$ is a ratio-covariety, and $\mathrm{P}(m,c)=\langle m\rangle \cup \{cm,\to \}$ is its minimum.

Define the graph $\mathrm{G}\left(\mathcal{R}\right(m,c\left)\right)$ in the following way: $\mathcal{R}(m,c)$ is its set of vertices, and $(S,T)\in \mathcal{R}(m,c)\times \mathcal{R}(m,c)$ is an edge if and only if $T=S\setminus \left\{\mathrm{r}\right(S\left)\right\}.$

If $\{p,q\}\subseteq \mathbb{Z}$ and $q\ne 0$, we denote, by p $\mathrm{mod}$ q, the remainder of the division of p by q. By applying Propositions 11 and 15, we deduce the following result.

Corollary 2.

$\mathrm{G}\left(\mathcal{R}\right(m,c\left)\right)$ is a tree with root $\mathrm{P}(m,c).$ Moreover, if $S\in \mathcal{R}(m,c),$ then the set formed by the children of S in the tree $\mathrm{G}\left(\mathcal{R}\right(m,c\left)\right)$ is $\{S\cup \{x\}\mid x\in \mathrm{SG}(S),m<x<\mathrm{r}(S)$$andx\ne \mathrm{F}\left(S\right)\}\cup \mathrm{A}(S)$, where

$$\mathrm{A}\left(S\right)=\left\{\begin{array}{ccc}\{S\cup \mathrm{F}(S\left)\right\}\hfill & if& \mathrm{m}<\mathrm{F}\left(S\right)<\mathrm{r}\left(S\right)and\hfill \\ & & \left[\mathrm{F}\right(S)-(\mathrm{F}\left(S\right)\mathrm{mod}m),\mathrm{F}(S)-1]⊈S,\hfill \\ \varnothing \hfill & & otherwise.\hfill \end{array}\right.$$

The following result is easily provable.

Proposition 16.

With the previous notation, $\mathcal{R}(m,2)=\left\{\right\{0,m,2m,\to \}\cup A\mid A⊊\{m+1,\dots ,2m-1\left\}\right\}.$ Moreover, $\left\{\mathrm{g}\right(S)\mid S\in \mathcal{R}(m,2\left)\right\}=\{m,m+1,\dots ,2m-2\}.$

The following result is obtained by applying Propositions 12 and 15.

Proposition 17.

If m and c are integers greater than or equal to 3, then $\{\mathrm{g}\left(S\right)\mid S\in \mathcal{R}(m,c)\}=\left[⌈{\displaystyle \frac{(c-1)m+2}{2}}⌉,c(m-1)\right].$

A set X is a $\mathcal{R}(m,c)$-set if it verifies the following conditions:

1.

$X\cap \mathrm{P}(m,c)=\varnothing ;$

2.

$X\subseteq S$ for some $S\in \mathcal{R}(m,c).$

If X is a $\mathcal{R}(m,c)$-set, then we denote, by $\mathcal{R}(m,c)\left[X\right],$ the intersection of all elements of $\mathcal{R}(m,c)$ containing $X.$

As $\mathcal{R}(m,c)$ is a finite set, by Corollary 1, we deduce that the intersection of elements from $\mathcal{R}(m,c)$ is, again, an element of $\mathcal{R}(m,c).$ As a consequence, the following result holds.

Proposition 18.

If X is a $\mathcal{R}(m,c)$-set, then $\mathcal{R}(m,c)\left[X\right]$ is the smallest element of $\mathcal{R}(m,c)$, with respect to set inclusion order, containing $X.$

If X is a $\mathcal{R}(m,c)$-set and $S=\mathcal{R}(m,c)\left[X\right],$ then we will say that X is a $\mathcal{R}(m,c)$-system of generators of $S.$ In addition, if $S\ne \mathcal{R}(m,c)\left[Y\right]$ for all $Y⊊X,$ then X will be called a $\mathcal{R}(m,c)$-minimal system of generators of $S.$

Our next goal will be to demonstrate that every element of $\mathcal{R}(m,c)$ has a unique $\mathcal{R}(m,c)$-minimal system of generators.

By applying Corollary 1 and [25] (Lemma 13), the following result is obtained.

Lemma 12.

If $S\in \mathcal{R}(m,c),$ then $X=\{x\in \mathrm{msg}(S)\mid x\notin \mathrm{P}(m,c\left)\right\}$ is a $\mathcal{R}(m,c)$-set and $\mathcal{R}(m,c)\left[X\right]=S.$

Proposition 19.

If $S\in \mathcal{R}(m,c),$ then $X=\{x\in \mathrm{msg}(S)\mid x\notin \mathrm{P}(m,c\left)\right\}$ is the unique $\mathcal{R}(m,c)$-minimal system of generators of $S.$

Proof. 

In accordance with Lemma 12, to prove the proposition, it will suffice to demonstrate that if Y is an $\mathcal{R}(m,c)$-set and $S=\mathcal{R}(m,c)\left[Y\right],$ then $X\subseteq Y.$ If $X⊈Y,$ then there is $x\in X\setminus Y.$ By applying Lemma 1, we say that $S\setminus \left\{x\right\}$ is a numerical semigroup. As $x\notin \mathrm{P}(m,c),$ we easily deduce that $S\setminus \left\{x\right\}\in \mathcal{R}(m,c).$ If $Y\subseteq S$ and $x\notin Y,$ then $Y\subseteq S\setminus \left\{x\right\}.$ By Proposition 18, we have $S=\mathcal{R}(m,c)\left[Y\right]\subseteq S\setminus \left\{x\right\},$ which is absurd. □

If $S\in \mathcal{R}(m,c),$ then we denote, by $\mathcal{R}(m,c)\mathrm{msg}\left(S\right)$, the unique $\mathcal{R}(m,c)$-minimal system of generators of $S.$ The cardinality of $\mathcal{R}(m,c)\mathrm{msg}\left(S\right)$ is called the $\mathcal{R}(m,c)$-rank of S, and it will denote, by $\mathcal{R}(m,c),\mathrm{rank}\left(S\right).$

Example 4.

Let $S=\langle 5,7,9\rangle =\{0,5,7,9,10,12,14,\to \}.$ Then, $\mathrm{m}\left(S\right)=5,$$\mathrm{F}\left(S\right)=13$, and by applying Proposition 14, we have $\mathrm{C}\left(S\right)=3.$ Therefore, $S\in \mathcal{R}(5,3).$ As $\mathrm{P}(5,3)=\{0,5,10,15,\to \},$ then $\{x\in \mathrm{msg}(S)\mid x\notin \mathrm{P}(5,3\left)\right\}=\{7,9\}.$ By applying Proposition 19, we have $\mathcal{R}(5,3)\mathrm{msg}\left(S\right)=\{7,9\}$ and $\mathcal{R}(5,3)\mathrm{rank}\left(S\right)=2.$

By applying Proposition 19 and [25] (Lemmas 14 and 15, along with Proposition 11) we obtain the following result.

Proposition 20.

If $S\in \mathcal{R}(m,c),$ then we have the following conditions.

(1) 

$\mathcal{R}(m,c)\mathrm{rank}\left(S\right)\le \mathrm{e}\left(S\right)-1;$

(2) 

$\mathcal{R}(m,c)\mathrm{rank}\left(S\right)=0$ if and only if $S=\mathrm{P}(m,c);$

(3) 

If $S\ne \mathrm{P}(m,c),$ then $\mathrm{r}\left(S\right)\in \mathcal{R}(m,c)\mathrm{msg}\left(S\right);$

(4) 

$\mathcal{R}(m,c)\mathrm{rank}\left(S\right)=1$ if and only if $\mathcal{R}(m,c)\mathrm{msg}\left(S\right)=\left\{\mathrm{r}\right(S\left)\right\}.$

We now aim to describe the elements of $\mathcal{R}(m,c)$ with $\mathcal{R}(m,c)\mathrm{rank}\left(S\right)=1.$ The following result is deduced from [3].

Lemma 13.

If $\{\alpha ,\beta \}\subseteq \mathbb{N}\setminus \{0,1\}$ and $\gcd \{\alpha ,\beta \}=1,$ then $\mathrm{F}(\langle \alpha ,\beta \rangle )=\alpha \beta -\alpha -\beta .$

Proposition 21.

It is verified that $S\in \mathcal{R}(m,c)$ and $\mathcal{R}(m,c)\mathrm{rank}\left(S\right)=1$ if and only if one of the following conditions is true:

1. 

$S=\langle m,km+i\rangle \cup \{cm,\to \}$ for some $(k,i)\in \{1,\dots ,c-1\}\times \{1,\dots ,m-1\}$ such that $\gcd \{m,i\}\ne 1.$

2. 

$S=\langle m,km+i\rangle \cup \{cm,\to \}$ for some $(k,i)\in \{1,\dots ,c-1\}\times \{1,\dots ,m-1\}$ such that $\gcd \{m,i\}=1$ and ${\displaystyle km+i>\frac{cm}{m-1}.}$

Proof. 

(Necessity). If $S\in \mathcal{R}(m,c)$ and $\mathcal{R}(m,c)\mathrm{rank}\left(S\right)=1$, then, by Proposition 20, we know that $\mathcal{R}(m,c)\mathrm{msg}\left(S\right)=\left\{\mathrm{r}\right(S\left)\right\}.$ By applying Proposition 19, we have that $\left\{\mathrm{r}\right(S\left)\right\}=\{x\in \mathrm{msg}(S)\mid x\notin \mathrm{P}(m,c\left)\right\}.$ We consider two cases:

1.

If $\gcd \{m,\mathrm{r}(S\left)\right\}\ne 1,$ then $\mathrm{r}\left(S\right)=km+i,$ with $k\in \{1,\dots ,c-1\},$$i\in \{1,\dots ,m-1\}$ and $\gcd \{m,i\}\ne 1.$ Additionally, $S=\langle m,km+i\rangle \cup \{cm,\to \}.$

2.

If $\gcd \{m,\mathrm{r}(S\left)\right\}=1,$ then $\mathrm{r}\left(S\right)=km+i,$ with $k\in \{1,\dots ,c-1\},$$i\in \{1,\dots ,m-1\}$ and $\gcd \{m,i\}=1.$ Moreover, $\mathrm{F}(\langle m,km+i\rangle )>(c-1)m.$ By applying Lemma 13, we have $m(km+i)-m-km-i>(c-1)m.$ Therefore, ${\displaystyle km+i>\frac{cm}{m-1}.}$

(Sufficiency). Two cases are distinguished:

1.

If $(k,i)\in \{1,\dots ,c-1\}\times \{1,\dots ,m-1\}$ and $\gcd \{m,i\}\ne 1,$ then we can easily deduce that $S=\langle m,km+i\rangle \cup \{cm,\to \}$ is a numerical semigroup with multiplicity m and Frobenius number $cm-1.$ By applying Proposition 14, we have $S\in \mathcal{R}(m,c).$ Moreover, $\{x\in \mathrm{msg}(S)\mid x\notin \mathrm{P}(m,c\left)\right\}=\{km+i\}.$ By Proposition 19, we obtain $\mathcal{R}(m,c)\mathrm{msg}\left(S\right)=\{km+i\}$. Hence, $\mathcal{R}(m,c)\mathrm{rank}\left(S\right)=1.$

2.

Suppose now that $(k,i)\in \{1,\dots ,c-1\}\times \{1,\dots ,m-1\},$$\gcd \{m,i\}=1$ and ${\displaystyle km+i>\frac{cm}{m-1}.}$ Let $S=\langle m,km+i\rangle \cup \{cm,\to \}.$ As ${\displaystyle km+i>\frac{cm}{m-1};}$ then, by Lemma 13, we have $\mathrm{F}(\langle m,km+i\rangle )>(c-1)m$ and so $F\left(S\right)\in \left[\right(c-1)m+1,cm-1].$ Consequently, $S\in \mathcal{R}(m,c).$ Moreover, $\{x\in \mathrm{msg}(S)\mid x\notin \mathrm{P}(m,c\left)\right\}=\{km+i\}.$ Finally, by using Proposition 19, we have $\mathcal{R}(m,c)\mathrm{rank}\left(S\right)=1.$

□

Example 5.

We are going to calculate the set $\{S\in \mathcal{R}(4,6)\mid \mathcal{R}(4,6\left)\mathrm{rank}\right(S)=1\}.$ For this, we apply Proposition 21.

1. 

Taking $k\in \{1,2,3,4,5\}$ and $i=2,$ we obtain $\langle 4,6\rangle \cup \{24,\to \},$$\langle 4,10\rangle \cup \{24,\to \},$$\langle 4,14\rangle \cup \{24,\to \},$$\langle 4,18\rangle \cup \{24,\to \}$ and $\langle 4,22\rangle \cup \{24,\to \}.$

2. 

We will consider two cases:

• Taking $k\in \{1,2,3,4,5\},$$i=1$ and ${\displaystyle k·4+1>\frac{6·4}{3}=8,}$ we obtain $\langle 4,9\rangle \cup \{24,\to \},$$\langle 4,13\rangle \cup \{24,\to \},$$\langle 4,17\rangle \cup \{24,\to \}$ and $\langle 4,21\rangle \cup \{24,\to \}.$
• Taking $k\in \{1,2,3,4,5\},$$i=3$ and $k·4+3>8,$ we obtain $\langle 4,11\rangle \cup \{24,\to \},$$\langle 4,15\rangle \cup \{24,\to \},$$\langle 4,19\rangle \cup \{24,\to \}$ and $\langle 4,23\rangle \cup \{24,\to \}.$

Therefore, $\{S\in \mathcal{R}(4,6)\mid \mathcal{R}(4,6\left)\mathrm{rank}\right(S)=1\}=\{\langle 4,6,25,27\rangle ,\langle 4,10,25,27\rangle ,\langle 4,14,25,27\rangle ,\langle 4,18,25,27\rangle ,$ $\langle 4,22,25,27\rangle ,\langle 4,9\rangle ,\langle 4,13,27\rangle ,\langle 4,17,26,27\rangle ,\langle 4,21,26,27\rangle ,\langle 4,11,25\rangle ,\langle 4,15,25,26\rangle ,\langle 4,19,25,26\rangle ,\langle 4,23,25,26\rangle \}.$