Inbound Truck Scheduling for Workload Balancing in Cross-Docking Terminals

Abstract

The rapid growth of e-commerce and advances in information and communication technologies have placed increasing pressure on last-mile delivery companies to enhance operational productivity. As investments in logistics infrastructure require long-term planning, maximizing the efficiency of existing terminal operations has become a critical priority. This study proposes a mathematical model for inbound truck scheduling that simultaneously minimizes truck waiting times and balances workload across temporary inventory storage located at outbound chutes in cross-docking terminals. The model incorporates a dynamic rescheduling strategy that updates the assignment of inbound trucks in real time, based on the latest terminal conditions. Numerical experiments, based on real operational data, demonstrate that the proposed approach significantly outperforms conventional strategies such as First-In First-Out (FIFO) and Random assignment in terms of both load balancing and truck turnaround efficiency. In particular, the proposed model improves workload balance by approximately 10% and 12% compared to the FIFO and Random strategies, respectively, and it reduces average truck waiting time by 17% and 18%, thereby contributing to more efficient workflow and alleviating bottlenecks. The findings highlight the practical potential of the proposed strategy for improving the responsiveness and efficiency of parcel distribution centers operating under fixed infrastructure constraints. Future research may extend the proposed approach by incorporating realistic operational factors, such as cargo heterogeneity, uncertain arrivals, and terminal shutdowns due to limited chute storage.

1. Introduction

The parcel delivery industry has gradually expanded due to the growth of the e-commerce market [1]. As consumers increasingly prioritize rationality and convenience, shifting their purchasing behavior from offline to online platforms, the industry is expected to continue growing. In particular, the ability to differentiate delivery services and efficiently manage the increasing volume of parcels is a key competitive advantage for the global companies. To strengthen global competitiveness and improve parcel handling efficiency, many parcel delivery companies are adopting cross-docking terminals [2]. The implementation of cross-docking terminals is becoming more common across various industries [3]. A cross-docking terminal is a logistics facility where incoming cargoes are rapidly sorted and transferred directly to outbound trucks without long-term storage. This approach enables faster delivery and reduces inventory holding costs compared to traditional warehousing [4].

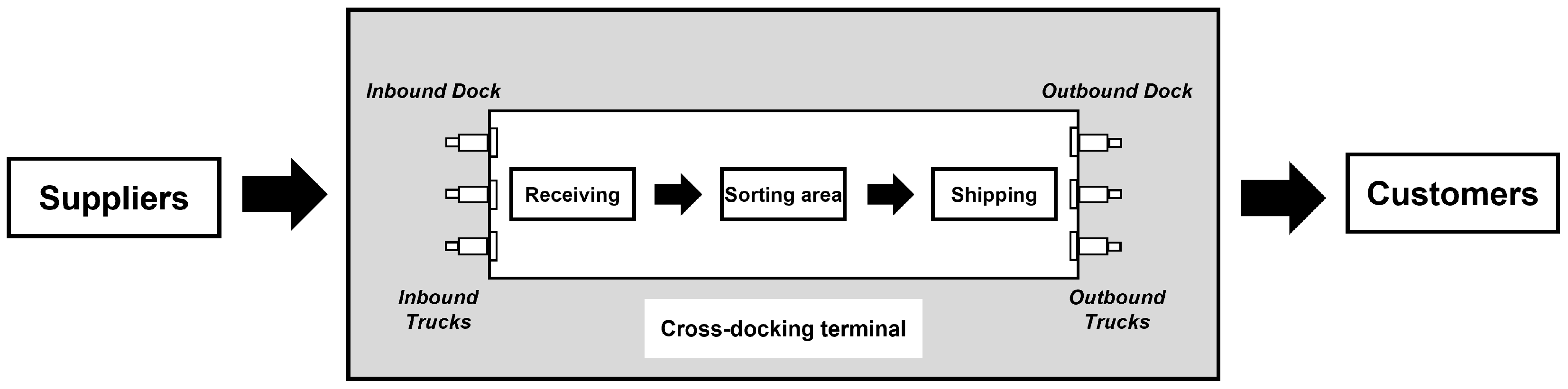
A cross-docking terminal is typically divided into three main areas: an inbound dock, where inbound trucks unload parcels; a sorting area, where parcels are classified; and an outbound dock, where sorted parcels are loaded onto outbound trucks, as illustrated in Figure 1. In the past, all operations in cross-docking terminals relied on manual labor for handling and transporting parcels. However, with technological advancements, these terminals now automate the process using equipment such as forklifts and conveyor belt systems [5]. Particularly, parcel companies that handle large volumes in cross-docking terminals have driven technological advancements through various studies and operational innovations [6].

Previous studies primarily focused on the initial setup of cross-docking terminals, which are considered part of the capital-intensive industry [7]. Once a conveyor belt system is established in a cross-docking terminal, making physical modifications or integrating new equipment requires substantial investment in both cost and time. Therefore, parcel companies are focusing on optimization and automation techniques to overcome the limitations of existing processing capacity and efficiently manage cross-docking terminals. In particular, truck scheduling is one of the most crucial operations in determining the processing capacity of parcel hub terminals. When truck scheduling is effectively performed, arriving inbound trucks are appropriately assigned to available docks, allowing cargo to be efficiently transferred to outbound trucks after passing through sorting processes or temporary inventory storage within the terminal. In actual operations, the arrival patterns of inbound trucks are irregular, and the type and quantity of cargo loaded on each truck can vary significantly. If inbound truck scheduling is not properly managed, it may result in workload imbalances or bottlenecks due to cargo being concentrated at specific docks or outbound docks. Therefore, in this study, we focus on the inbound truck scheduling problem to enhance workload balancing and improve the operational efficiency of cross-docking terminals.

In cross-docking terminals, the truck scheduling problem primarily refers to the scheduling of inbound trucks. Since each outbound dock is designated for a predefined delivery destination, outbound trucks can be easily directed to their corresponding docks based on their destinations. In contrast, inbound trucks do not have designated docks, making it essential to promptly allocate arriving inbound trucks to available inbound docks without delay. In previous studies, this problem was relatively simple due to the inability to access information about the parcels inside inbound trucks. These allocation strategies lacked information of parcel destinations, resulting in an unbalanced distribution of unloaded parcels across outbound docks and causing operational bottlenecks as volumes gradually increase. With advancements in technology, it is now possible to obtain detailed parcel information in advance, making optimization based on this data increasingly important. Therefore, this study proposes an inbound truck scheduling strategy that utilizes pre-identified parcel information to balance the workload across outbound docks and enhance operational efficiency.

This study proposes a dynamic inbound truck scheduling model that simultaneously considers the state of temporary inventory storage in the outbound docks and the waiting time of inbound trucks. The proposed model assigns trucks to the docks using a dynamic rescheduling strategy after reflecting the terminal’s latest information, including the temporary inventory level at each outbound chute whenever the inbound docks of the cross-docking terminal are idle. Specifically, after each inbound truck completes its process, the system evaluates the level of temporary inventory storage at each outbound chute and the waiting time of remaining inbound trucks in real time, and it then optimally assigns the next truck to an available dock. This dynamic approach enables the scheduling process to flexibly respond to real-time changes within the terminal, such as the accumulation of temporary inventory storage, and contributes to minimizing the overall operational time of the terminal. This study conducts numerical experiments based on real terminal data to validate the effectiveness of the proposed strategy, and it confirms that it outperforms conventional real-time assignment methods in terms of temporary inventory management and truck waiting time.

The structure of this paper is as follows. In Section 2, we review the existing research on the inbound truck scheduling problem. We describe the problem and the assumptions for developing the model in Section 3. In Section 4, we present a proposed mathematical model and introduce a dynamic rescheduling strategy for solving inbound truck scheduling problem with real-world environments in Section 5. We validate the proposed methodology through numerical experiments and comparative analysis in Section 6. In Section 7, we discuss the practical implications and limitations of the proposed methodology. Finally, we conclude in Section 8.

2. Literature Review

Cross-docking is a logistics strategy in which inbound parcels delivered by trucks are not stored in warehouses for long periods, but instead are immediately sorted and reallocated according to customer demand before being loaded onto outbound trucks for delivery. This approach offers several advantages, including reduced inventory costs, shorter logistics lead times, and improved space utilization. As a result, extensive research has been conducted to enhance the operational efficiency of cross-docking systems. Major research areas include handling equipment scheduling, terminal layout optimization, and truck scheduling. Among these, this study focuses on the truck scheduling problem and aims to review relevant prior studies in this area.

Early studies on truck scheduling problems primarily focused on minimizing costs associated with early arrivals and delayed departures by incorporating time-related constraints. Boysen et al. [8] addressed the problem of minimizing total completion time by simultaneously scheduling and assigning inbound and outbound trucks to dock doors. Boysen et al. [9] addressed the inbound truck scheduling problem with the objective of minimizing the arrival time of parcels at the docks connected to their designated outbound trucks. Gallo et al. [10] proposed a stochastic Mixed-Integer Linear Programming (MILP) model combined with a genetic algorithm to reduce penalty costs caused by uncertainty in truck arrival times and Molavi et al. [11] developed a scheduling model that simultaneously considers the prioritization of outbound trucks and parcel classification, aiming to minimize earliness and tardiness penalties. Recently, studies have expanded beyond time-based optimization to improve overall system efficiency by diversifying objective functions. Chargui et al. [12] introduced a MILP model that accounts for multiple dock doors and heterogeneous temporary storage zones and Taghizadeh et al. [13] proposed a multi-objective optimization model that considers both makespan and parcel transfer costs to better reflect realistic operational settings. Nogueira et al. [14] modeled the multi-door sequencing problem in cross-docking terminals as a parallel machine environment and proposed a deterministic heuristic and a mathematical model to minimize the overall makespan. This study overcame the limitations of conventional flow-shop- based approaches and emphasized the effectiveness of the parallel environment based model by demonstrating superior performance across instances of various sizes. Theophilus et al. [15] investigated the truck scheduling problem in a cold-chain cross-docking terminal, explicitly accounting for product perishability. Their study proposed a comprehensive cost minimization objective function that incorporates truck waiting time, service time, delayed departure time, temporary storage cost, and product decay cost, in addition to conventional time-related constraints.

In addition to time and objective function-based models, recent research has increasingly focused on enhancing scheduling flexibility by accounting for the diversity of truck types. Shahmardan and Sajadieh [16] proposed an integrated model that enables flexible parcel handling between inbound and outbound trucks by leveraging the partial unloading capability of compound trucks and solved it using a reinforcement learning-based simulated annealing algorithm. Moussavi et al. [17] presented a model that dynamically synchronizes the allocation of products, trucks, and destinations to link inbound operations with just-in-time demand. Meanwhile, Pan et al. [18] introduced a repeated loading strategy tailored for fresh food distribution to improve truck turnaround rates while minimizing product deterioration. Zheng et al. [19] proposed a MILP model for a cold chain cross-docking environment that handles chilled and frozen products separately, considering dual operations of storage zones and truck types (chilled/frozen) based on product characteristics. Meanwhile, Shahabi-Shahmiri et al. [20] proposed a cross-docking network optimization model that simultaneously considers heterogeneous vehicles, product perishability, and split delivery conditions to minimize total transportation cost, time, and product freshness degradation penalty. These studies demonstrate that considering truck-type heterogeneity significantly enhances the practical applicability of truck scheduling models in real-world cross-docking environments.

Uncertainties in operational factors such as truck arrival times and service durations have a significant impact on the efficiency of cross-docking systems. Accordingly, robust scheduling techniques that account for such uncertainties have emerged as a critical area of research. Xi et al. [21] proposed a two-stage conflict-robust optimization model designed to minimize docking conflicts and further enhanced the model by incorporating a scenario-based K-means clustering approach to define a multi-scenario uncertainty set. They also improved computational efficiency through a column-and-constraint generation algorithm. Nasiri et al. [22] presented a predictive-reactive scheduling framework that updates the initial plan in response to real-time truck arrival information, emphasizing the importance of properly designing the triggering conditions and scope for rescheduling. Vincent et al. [23] derived a polyhedral-based robust optimization model and proposed an adaptive large neighborhood search algorithm to solve the vehicle routing and cross-docking problem under demand uncertainty. This study was designed to ensure schedule feasibility and cost efficiency under demand uncertainty, and it provides practical implications through sensitivity analysis on the cost-robust trade-off.

In addition to time-oriented approaches, constraints on temporary inventory storage have increasingly been recognized as critical factors in cross-docking operations. Kusuma [24] proposed a multi-agent-based scheduling model that dynamically adjusts truck flow based on the status of temporary inventory storage and introduced a truck changeover strategy to prevent overflow by relocating trucks waiting at the dock. Chargui et al. [12] developed a MILP model that considers multiple storage zones segmented by product type and proposed a framework that dynamically determines whether to perform direct transfer or storage-transfer operations, as well as the appropriate routing for each case. Yu and Egbelu [25] proposed an integrated scheduling model that realistic cross-docking conditions with limited temporary storage space aiming to compromise the asynchronous time gaps between inbound and outbound trucks. Such an approach, which explicitly incorporates temporary storage space into the model, is considered an effective means to ensure flexibility and stability while maintaining the continuous flow of cross-docking operations.

Finally, truck scheduling research aimed at addressing the real-time nature and dynamic changes of logistics operations has also been actively conducted. Boysen [26] addressed the truck scheduling problem in cross-docking terminals by considering the following three objectives: flow time, processing time, and tardiness minimization. To solve the problem, a dynamic programming approach and simulated annealing were employed. Wu et al. [27] performed real-time truck entry and exit optimization under conditions without temporary inventory storage by applying a hybrid metaheuristic algorithm based on particle swarm optimization, simulated annealing, and variable neighborhood search. Cubillos et al. [28] introduced a partially observable Markov decision process based on estimated time of arrival information to reflect real-time uncertainties, and they coordinated policy feasibility and performance through an information-penalty-based dual bound technique. In addition, Torbali and Alpan [29] proposed a real-time truck scheduling model for cross-docking environments with a single inbound and outbound door. This model combines multi-agent simulation and discrete-event simulation to dynamically manage resource conflicts among trucks and achieve high adaptability. Furthermore, Nasiri et al. [22] proposed a predictive-reactive scheduling framework to reflect the uncertainty of truck arrival times in real time and respond flexibly. This approach integrates a predictive phase, which generates an initial schedule based on estimated arrivals, with a reactive phase that dynamically adjusts the schedule upon the observation of actual arrivals, while simultaneously considering dock resource utilization and schedule stability constraints. By comparing various rescheduling policies, the study derived a trade-off point between performance and stability, contributing to the development of practical truck operation strategies in a real-time environment.

The contributions of this study are as follows. First, previous research has typically focused on specific aspects of the inbound truck scheduling problem, including time constraints, and responsiveness to real-time conditions. However, these factors have often been considered independently or under simplified assumptions. This study develops an integrated scheduling model that simultaneously considers truck waiting times and temporary inventory storage. By jointly incorporating these two critical factors, the proposed model effectively mitigates chute congestion and enhances the overall operational efficiency of cross-docking terminals. Second, unlike conventional static scheduling approaches that rely on pre-determined assignments, this study introduces a real-time rescheduling strategy in the inbound truck scheduling problem. Scheduling decisions are dynamically updated whenever an inbound dock becomes idle, based on the latest system information. This enables the proposed method to flexibly respond to real-time disturbances, such as unexpected truck arrivals or unloading delays. Third, the proposed method accounts for compound trucks—vehicles that, after completing unloading at inbound docks, proceed to outbound docks for loading operations. This operational characteristic, which has received limited attention in prior studies, reflects real-world conditions and enables better coordination between inbound and outbound flows. Lastly, a quadratic objective function is formulated to capture the nonlinear interaction between inventory imbalance and truck waiting time, which cannot be effectively represented using linear models. This formulation improves the model’s ability to balance resource utilization and reflect realistic operational constraints, thereby enhancing both its accuracy and practical applicability.

3. Problem Description

3.1. Inbound Truck Scheduling

In a hub terminal, trucks can be categorized into inbound trucks, outbound trucks, and compound trucks. Inbound and outbound trucks have single roles: inbound trucks deliver parcels to the terminal, while outbound trucks transport parcels out of the terminal. Compound trucks perform both functions. After completing the unloading operations, compound trucks proceed to the outbound docks to reload parcels for subsequent dispatch. This characteristic of compound trucks enhances parcel handling efficiency and optimizes resource utilization within the terminal. However, determining the unloading sequence becomes more complicated when operating multiple-functional trucks simultaneously. Therefore, this study investigates an unloading sequence decision-making method for scenarios in which both inbound and compound trucks are operated together.

The challenge of determining the unloading sequence and optimizing dock assignment for inbound trucks in a terminal is referred to as the inbound truck scheduling problem. Conventional terminals temporarily store unloaded parcels in warehouses for later dispatch, as illustrated in Figure 2. In contrast, cross-docking terminals, depicted in Figure 3, immediately sort parcel via conveyor belts after unloading, subsequently dispatching it through outbound docks without interim warehouse storage. In the illustrations, the color of each parcel represents its outbound destination (i.e., the outbound dock it should be sent to), while the shape indicates the parcel type. Parcels with the same color are sorted to the same outbound dock, and those with the same shape share the same handling characteristics. This operational method of cross-docking terminals maximizes efficiency; however, it is susceptible to bottlenecks, particularly when specific outbound docks are overwhelmed by parcel within a short period due to improper unloading sequences that do not account for the current state of the outbound chutes. Bottlenecks occur when the volume of cargo exceeds a chute’s handling capacity per unit time, causing temporary accumulation in the temporary inventory storage near the chute area. When this congestion reaches saturation, dock lines experience operational stoppages and delays, further impacting other trucks scheduled for dispatch through the same dock and ultimately reducing overall terminal operational efficiency.

To prevent such issues, effective truck scheduling must incorporate comprehensive consideration of anticipated truck arrival parcel information and temporary inventory storage of the chute rather than simply assigning inbound docks based on arrival sequences. In practice, terminals leverage transportation management systems to obtain the parcel load information of scheduled trucks in advance, which serves as a foundation for efficient dock assignment and truck scheduling.

The goal of inbound truck scheduling is to minimize the total terminal operation time and to maximize parcel handling per unit time. There are two main strategies to achieve the goal. One is to perform fast matching between docks and trucks in order to reduce dock idle time. The other is to prevent temporary inventory storage at chutes, which helps avoid stoppages along the dock lines and stabilizes the flow of parcels. Hub terminals often experience a high volume of truck arrivals within short time windows, which leads to the consistently high utilization of inbound docks. In this environment, distributing parcel loads across outbound chutes based on the information of parcel accumulation in the temporary inventory storage is a more effective way to reduce overall operational time. However, minimizing truck waiting time and balancing temporary inventory storage across chutes can be conflicting objectives. Focusing solely on reducing waiting times may lead to congestion at specific chutes, while prioritizing inventory balance can delay truck assignments. To address this trade-off, this study proposes an approach the simultaneously considers both temporary inventory availability at chutes and truck waiting times.

3.2. Assumptions

This study proposes a Mixed-Integer Quadratic Programming (MIQP) model that simultaneously considers the spare capacity of temporary inventory storage (bottom load) and truck waiting times. The model considers the balancing of outbound chute congestion and truck waiting time in the allocation process simultaneously, thereby aiming to improve overall terminal operational efficiency. The assumptions made for the development of the MIQP model are as follows:

• Parcels are homogeneous in size and type; differences in cargo characteristics are not considered [30].
• The cargo volume for each truck is known in advance [22].
• Once a truck is assigned to a dock, its cargo is immediately added to the temporary inventory storage of the corresponding chute [11].
• Travel time from arrival point to dock is negligible and not considered [4].
• The truck waiting area has unlimited capacity [11].
• Each truck occupies the assigned dock until unloading is complete [29].
• The state of temporary inventory storage at each outbound chute is assumed to be known at each rescheduling instance [22].

4. Mathematical Model

In this section, we present the MIQP model for the inbound truck scheduling with temporary inventory storage. The following subsections describe the notation, objective function, and constraints used in the model.

4.1. Notation

The notation of the MIQP model is defined in

Table 1. Notation.

Symbol	Description
I	Set of inbound trucks.
K	Set of inbound docks.
S	Set of outbound chutes.
T	Current time in minutes.
M	A large constant (Big-M).
$\alpha$	Weight parameter controlling the trade-off between truck waiting time and inventory balance in the objective function.
$a_i$	Arrival time of inbound truck i.
$b_i$	Allocation time of unloading for inbound truck i.
$m_s$	Initial available temporary inventory storage capacity of outbound chute $s\in S$.
$p_s$	Number of parcels currently stored in outbound chute s at time T.
${\mathrm{inb}}_{is}$	Number of parcels from inbound truck i to outbound chute s.
${\mathrm{cmp}}_{is}$	Number of parcels from truck i to outbound chute s if it is a compound truck; otherwise, 0.
${\mathrm{margin}}_s$	Remaining temporary inventory storage capacity of outbound chute s at time T, i.e., $m_s-p_s$.
$x_{ik}$	Binary decision variable; equals 1 if truck i is assigned to dock k, and 0 otherwise.
$t_s$	Temporary inventory storage capacity of outbound chute s before assignment of truck i.
$z_s$	Temporary inventory storage capacity of outbound chute s after assignment of truck i.
$z_{max}$	Maximum value of $z_s$ across all outbound chutes.
$z_{min}$	Minimum value of $z_s$ across all outbound chutes.

.

4.2. Multi-Objective Optimization Model

The following MIQP model, constructed using the parameters and decision variables introduced above, consists of two objective functions.

$$\begin{array}{cccc}\hfill \left[\mathrm{M}1\right]& min(z_{max}-z_{min})\hfill & \hfill & \hfill \end{array}$$

(1)

$$\begin{array}{cccc}\hfill & min\sum _{i\in I}\sum _{k\in K}(b_i-a_i)x_{ik}\hfill & \hfill & \hfill \end{array}$$

(2)

subject to the following:

$$\begin{array}{cccc}\hfill \sum _{k\in K}{x}_{ik}& \le 1,\hfill & \hfill & \forall i\in I\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \sum _{i\in I}{x}_{ik}\le 1,& \hfill & \hfill \forall k\in K\end{array}$$

(4)

$$\begin{array}{ccc}\hfill \sum _{i\in I}\sum _{k\in K}{x}_{ik}=min\left\{\right|I|,|K\left|\right\},& \hfill & \hfill \forall i\in I,\forall k\in K\end{array}$$

(5)

$$\begin{array}{ccc}\hfill b_i\ge T-M\left(1-\sum _{k\in K}{x}_{ik}\right),& \hfill & \hfill \forall i\in I\end{array}$$

(6a)

$$\begin{array}{ccc}\hfill b_i\le T+M\left(1-\sum _{k\in K}{x}_{ik}\right),& \hfill & \hfill \forall i\in I\end{array}$$

(6b)

$$\begin{array}{ccc}\hfill b_i\ge a_i,& \hfill & \hfill \forall i\in I\end{array}$$

(6c)

$$\begin{array}{ccc}\hfill t_s={\mathrm{margin}}_s-\sum _{i\in I}\sum _{k\in K}({\mathrm{inb}}_{i,s}-{\mathrm{cmp}}_{i,s})x_{ik},& \hfill & \hfill \forall s\in S\end{array}$$

(7)

$$\begin{array}{ccc}\hfill z_s=min\{t_s,m_s\},& \hfill & \hfill \forall s\in S\end{array}$$

(8)

$$\begin{array}{ccc}\hfill z_{max}=\underset{s\in S}{max}{z}_s,& \hfill & \hfill \forall s\in S\end{array}$$

(9a)

$$\begin{array}{ccc}\hfill z_{min}=\underset{s\in S}{min}{z}_s,& \hfill & \hfill \forall s\in S\end{array}$$

(9b)

$$\begin{array}{ccc}\hfill x_{ik}\in \{0,1\},& \hfill & \hfill \forall i\in I,\forall k\in K\end{array}$$

(10)

$$\begin{array}{ccc}\hfill b_i,t_s,z_s,z_{max},z_{min}\ge 0,& \hfill & \hfill \forall i\in I,\forall s\in S\end{array}$$

(11)

The first objective function (1) represents the balancing of temporary inventory storage across outbound chutes. This objective minimizes the difference between the maximum and minimum temporary inventory storage among the chutes, thereby achieving load balancing. The second objective function (2) corresponds to the total waiting time of inbound trucks. This objective minimizes the total waiting time of inbound trucks, which is defined as the cumulative time from each truck’s arrival at the terminal to its assignment to a dock. Both objective functions are recalculated at each scheduling round. Constraint (3) ensures that each inbound truck is assigned to exactly one inbound dock, while Constraint (4) enforces that only one truck can be assigned to each dock at any given time. Constraint (5) guarantees that the number of trucks scheduled per round does not exceed the number of idle docks or the number of trucks in the waiting queue, whichever is smaller. Constraints (6a)–(6c) ensure that the start time of unloading for each truck is not earlier than its arrival time. Constraint (7) computes the remaining temporary inventory storage for outbound chute s immediately after truck assignment. Constraint (8) imposes that the updated temporary storage at any chute cannot exceed its initial capacity. Constraints (9a)–(9b) define the maximum and minimum values of the temporary inventory storage capacities across all outbound chutes after the assignment of trucks. Constraint (10) defines the binary nature of the assignment decision variables, while Constraint (11) specifies that the remaining variables are continuous and non-negative.

4.3. Weighted Sum Reformulation

The proposed model addresses a trade-off between balancing temporary inventory storage across outbound chutes and minimizing the total waiting time of inbound trucks. To resolve this trade-off, we adopt the weighted sum method to reformulate the multi-objective problem as a single-objective problem [31,32].

In this approach, one of the objective functions is multiplied by a parameter $\alpha$ and added to the other objective. Parameter $\alpha$ reflects the relative importance of balancing temporary inventory storage across outbound chutes. In Section 6, we conduct a sensitivity analysis to evaluate the model’s response to variations in $\alpha$ and to assess the overall robustness of the model with respect to this trade-off. The resulting single-objective function is given in Equation (12).

$$\begin{array}{cccc}\hfill \left[\mathrm{M}2\right]& min\alpha (z_{max}-z_{min})+\sum _{i\in I}\sum _{k\in K}(b_i-a_i)x_{ik}\hfill & \hfill & \hfill \end{array}$$

(12)

subject to the following:

$$\mathrm{Constraints}\left(3\right)–\left(11\right)$$

5. Dynamic Rescheduling Strategy

This study employs a dynamic rescheduling strategy that updates the state of temporary inventory storage each time an inbound truck completes its unloading operation. By integrating real-time terminal information into the scheduling process, the strategy allows adaptive responses to operational uncertainties through repeated reoptimization based on a pre-established mathematical model [33,34,35].

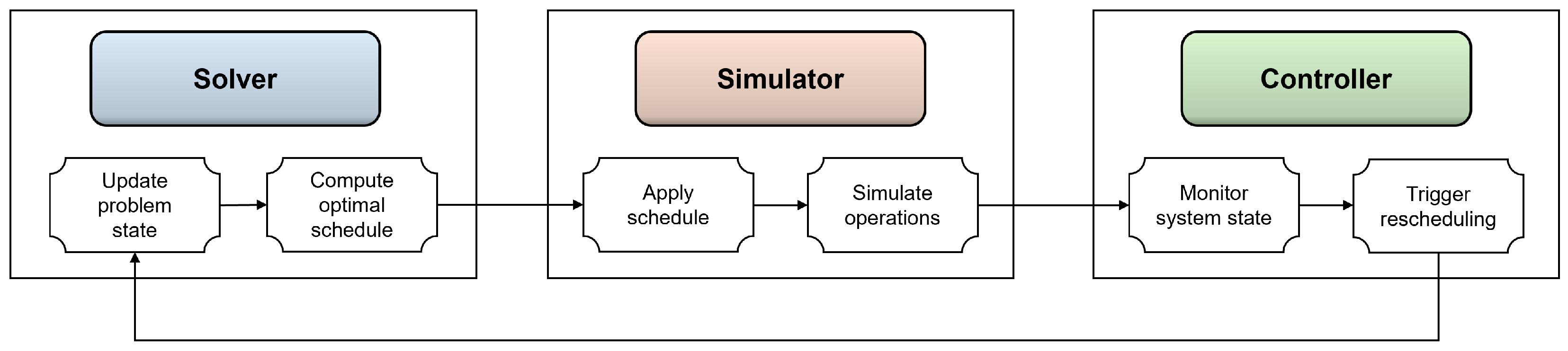
As illustrated in Figure 4, the proposed strategy comprises three main modules: the Solver, Simulator, and Controller. The Solver generates an optimal inbound truck schedule using the proposed mathematical model, aiming to minimize the imbalance in temporary storage across chutes and the waiting time of inbound trucks. Each time an inbound dock becomes idle, the Solver receives the latest status of temporary inventory storage capacity and waiting trucks, updates the scheduling problem, and computes a new optimal assignment.

The Controller monitors the system state throughout the simulation and determines when rescheduling should be triggered. For instance, when an inbound dock becomes available, the Controller invokes the Solver to compute an updated schedule. This process ensures that the system adapts to ongoing changes, reducing the deviation from optimality and maintaining real-time operational efficiency.

The Simulator captures real-world uncertainty by modeling truck arrival times as probabilistic variables. Using the each truck’s arrival time and cargo information, the Simulator forms a pool of inbound trucks and updates their waiting times and the temporary inventory storage capacity of each outbound chute dynamically. This simulation environment enables the performance evaluation of the schedules generated by the Solver under realistic conditions.

Although model-based plans are valid within a short time window, prediction errors accumulate as operations evolve due to unforeseen events or stochastic disturbances. To address this, the proposed strategy incorporates iterative reoptimization that reflects updated system states and outcomes. This continuous adjustment improves responsiveness to fluctuations in truck arrivals and chute congestion, thereby enhancing the robustness and practical applicability of the scheduling approach.

To provide a formal and modular representation of the proposed dynamic rescheduling framework, Algorithm 1 describes the overall procedure at 1-min intervals, explicitly reflecting the roles of the Solver, Simulator, and Controller modules.

Algorithm 1: Dynamic inbound truck scheduling framework

To illustrate the effect of dynamic rescheduling, consider the example shown in Figure 5, where the temporary inventory storage capacity is limited to eight units distributed across multiple outbound chutes. If trucks are scheduled strictly based on their arrival order (a–b–c), cargo from truck a may overload chutes 1 and 2, resulting in temporary inventory congestion. This can cause line stoppages and delay subsequent operations, thereby reducing overall terminal efficiency.

In contrast, if truck assignment priorities are determined by giving equal weight to both the available temporary inventory storage of each outbound chute and the waiting time of the trucks, truck b may be allocated first, thereby reducing the likelihood of immediate bottlenecks. While this reduces the risk of immediate overloading, it may result in uneven inventory distribution over time, eventually causing downstream bottlenecks.

To mitigate this, the proposed strategy assigns higher priority to balancing temporary inventory storage across chutes. In this case, truck c, which arrived later, may be assigned first to maintain inventory balance and prevent congestion. This approach allows for more effective long-term operations, reducing the likelihood of bottlenecks and improving the overall performance of the cross-docking terminal.

6. Numerical Experiments

6.1. Experimental Environment and Dataset

In this study, the experimental dataset was constructed based on 30 days of operational data collected from Company A’s cross-docking terminal in Korea. The dataset includes the actual unloading volume and arrival time of each inbound truck, and it was used to configure the simulation environment. The ratio between inbound and outbound docks was modeled to reflect the actual ratio of 1:3 observed at the terminal. Rescheduling was performed when an inbound dock becomes idle, and to evaluate the robustness of the proposed model with respect to the number of inbound docks, numerical experiments were conducted by varying the number of inbound docks to 30, 40, and 50. The unloading speed of each truck was set to 100 parcels per minute, and a truck was assumed to occupy its assigned dock until the unloading process was completed. To prevent terminal shutdown caused by bottlenecks, the initial temporary inventory storage capacity of each outbound chute ($m_s$) was set to a sufficiently large value of 100,000 in all experiments. To assess the effectiveness of the proposed methodology under a cross-docking terminal environment, we compared our approach with two strategies that are commonly used in practice, due to the lack of recent studies addressing exactly the same situation as ours. The first strategy is the First-In First-Out (FIFO) strategy, in which trucks are assigned strictly according to their order of arrival in the queue. The second strategy is the Random strategy, which assigns inbound trucks randomly without any prioritization.

To quantitatively evaluate the performance of each strategy in allocating inbound trucks efficiently, the following two performance indicators were used: the average imbalance of temporary inventory storage across outbound chutes and the average truck waiting time. The experiments were executed on a computer equipped with a 2.10 GHz 13th Gen Intel(R) Core(TM) i7-13700 processor and 32.0 GB RAM, running the Windows 11 operating system. The MIQP model was solved using the Gurobi 12.0 optimization solver.

6.2. Sensitivity Analysis

This section presents a sensitivity analysis of the weighting parameter $\alpha$ in the proposed MIQP model. There is an inherent trade-off between minimizing the waiting time of inbound trucks and balancing temporary inventory storage across outbound chutes. If only truck waiting time is minimized, congestion may be concentrated at specific chutes, while prioritizing only the balancing of temporary inventory storage may increase the waiting time for trucks. This trade-off is controlled by the weighting parameter $\alpha$ in the objective function. By varying $\alpha$, we investigate the model’s responsiveness to this trade-off and its overall robustness.

The experiments were conducted in a simulation environment consisting of 148 outbound docks and inbound docks set to 30, 40, and 50, respectively, to evaluate the robustness of the model with respect to terminal scale. For each case, the value of $\alpha$ (1, 10, 100, 1000, and 10,000) was varied, and 30 independent simulation runs were performed for each setting to ensure statistical stability.

Model performance was evaluated using two key indicators. The first is temporary inventory storage balancing, measured by $z_{max}-z_{min}$, which represents the difference between the maximum and minimum remaining capacities among outbound chutes. A smaller value indicates a more evenly distributed chute load. The second indicator is average truck waiting time, represented by Waiting_Time, defined as the total waiting time of all inbound trucks divided by the number of trucks processed per day. Lower values indicate more efficient truck-to-dock assignments and reduced congestion. The results of the sensitivity analysis are summarized in

Table 2. Sensitivity analysis results by number of inbound docks and parameter $\alpha$.

Number of Inbound Docks	$\mathit{\alpha }$	${\mathit{z}}_{max}-{\mathit{z}}_{min}$	Waiting_Time
30	1	4994.41	30.06
	10	4861.45	28.97
	100	4818.62	28.92
	1000	4830.99	28.49
	10,000	4824.36	28.97
40	1	5332.33	12.04
	10	5295.67	11.70
	100	5264.39	11.75
	1000	5289.32	11.64
	10,000	5276.06	11.66
50	1	5801.37	3.75
	10	5751.06	3.65
	100	5751.49	3.65
	1000	5739.12	3.60
	10,000	5738.34	3.61

.

The experimental results indicate that both performance indicators exhibit minimal variation not only across different $\alpha$ values but also with changes in the number of docks (i.e., terminal scale). No significant degradation in either metric was observed, even at extreme values of $\alpha$, suggesting that the proposed model is robust to changes in the weighting parameter. The lowest average truck waiting time was achieved at $\alpha =1000$, while the best balance in temporary inventory storage was observed at $\alpha =$ 10,000. Although slight performance improvements were identified for specific values of $\alpha$, the overall system performance remained stable throughout the tested range.

These findings demonstrate that the proposed scheduling model is not highly sensitive to parameter tuning. This characteristic enhances its practicality for real-world deployment, where extensive parameter calibration is often infeasible. In particular, the ability to maintain consistent performance across varying operational priorities makes the model suitable for real-time scheduling in dynamic terminal environments. Therefore, in this study, the parameter setting of $\alpha =$ 10,000 was used, as it resulted in the best performance with respect to minimizing $z_{max}-z_{min}$.

6.3. Performance Comparison by Strategy

In this section, a comparative experiment was conducted to verify the effectiveness of the proposed strategy against the following two conventional methods: First-In First-Out (FIFO) strategy and the Random strategy. Each strategy was evaluated through 30 independent simulation runs under a configuration with 50 inbound docks. Two performance indicators were used as follows: (1) temporary inventory storage balancing, measured by $z_{max}-z_{min}$, and (2) average truck waiting time, denoted as Waiting_Time. The average results are summarized in

Table 3. Performance comparison of scheduling strategies (50 inbound docks).

Strategy	${\mathit{z}}_{max}-{\mathit{z}}_{min}$	Waiting_Time
Proposed strategy	5738.34	3.61
FIFO	6411.25	4.36
Random	6502.39	4.38

.

The results demonstrate that the proposed strategy outperforms both benchmark methods across all performance criteria. Specifically, the proposed strategy achieves approximately 10% and 12% improvements in inventory storage balance compared to FIFO and Random strategies, respectively. Additionally, it reduces average truck waiting time by 17% and 18% relative to FIFO and Random strategies, respectively. These results indicate that the proposed strategy effectively distributes overall system workload, enabling both improved chute load balancing and shorter truck waiting times. Consequently, the proposed strategy proves to be a practical and robust approach for enhancing both operational throughput and stability in cross-docking terminals.

6.4. Performance Comparison by Number of Inbound Docks and Outbound Docks

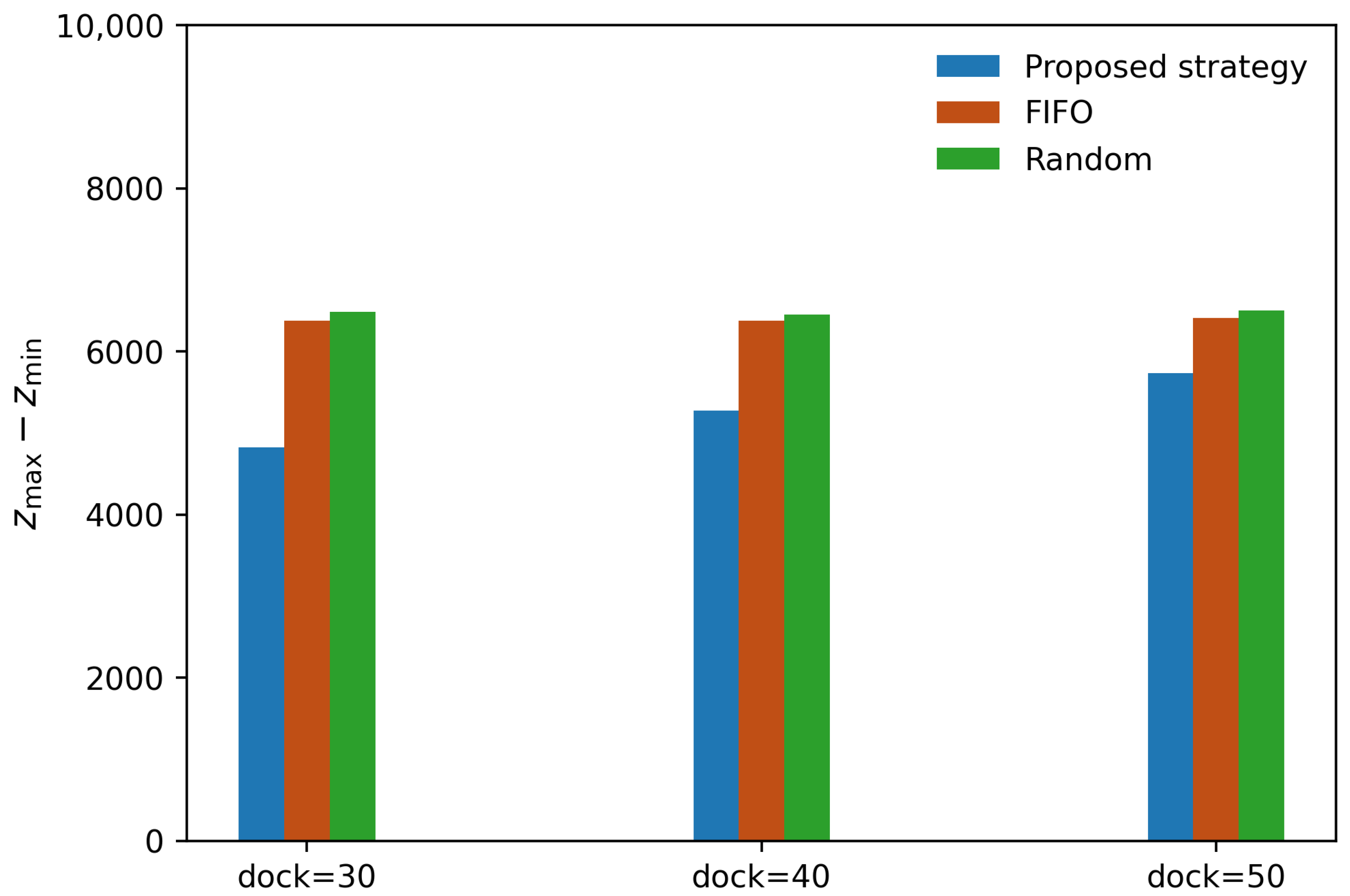
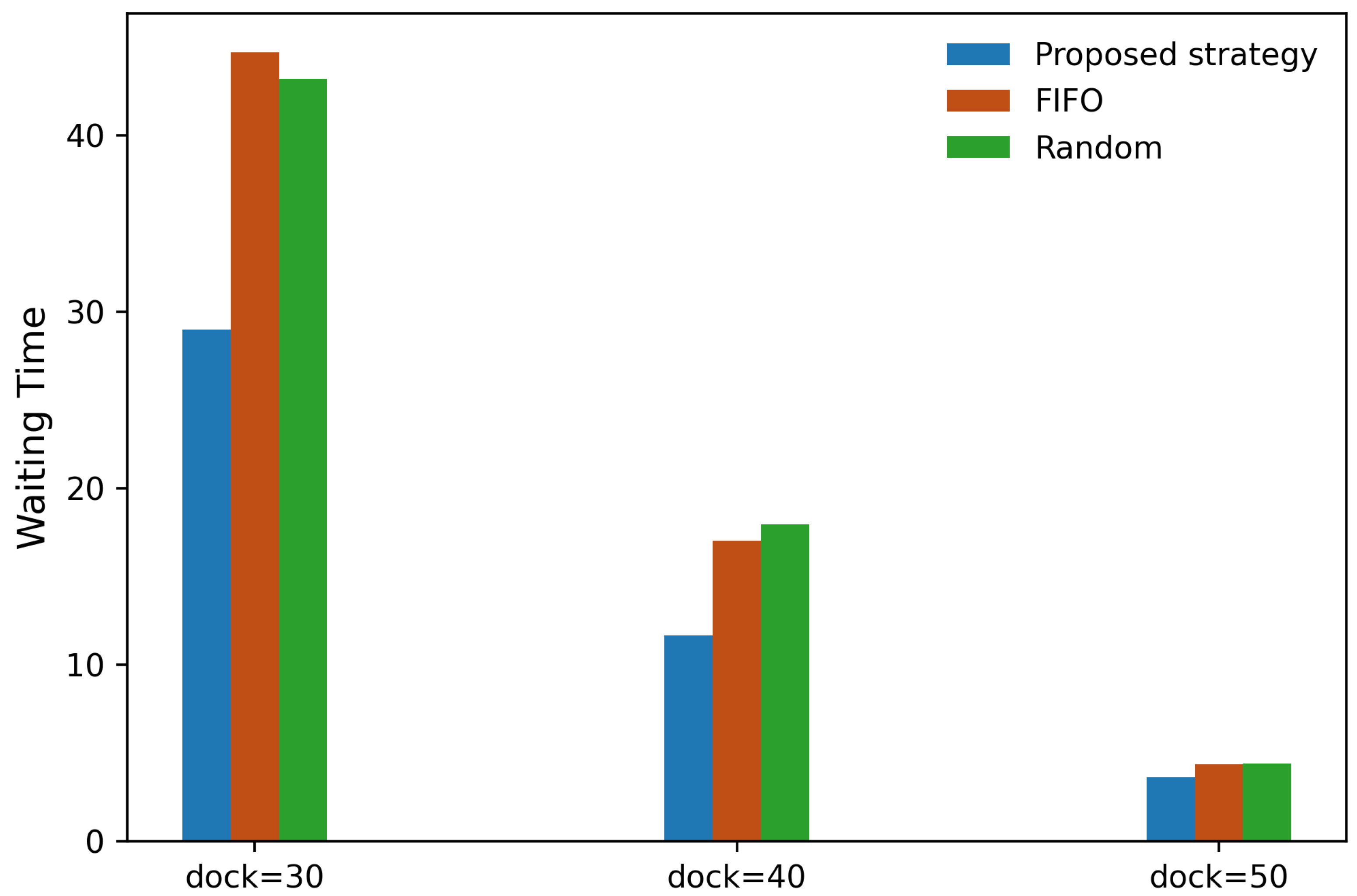
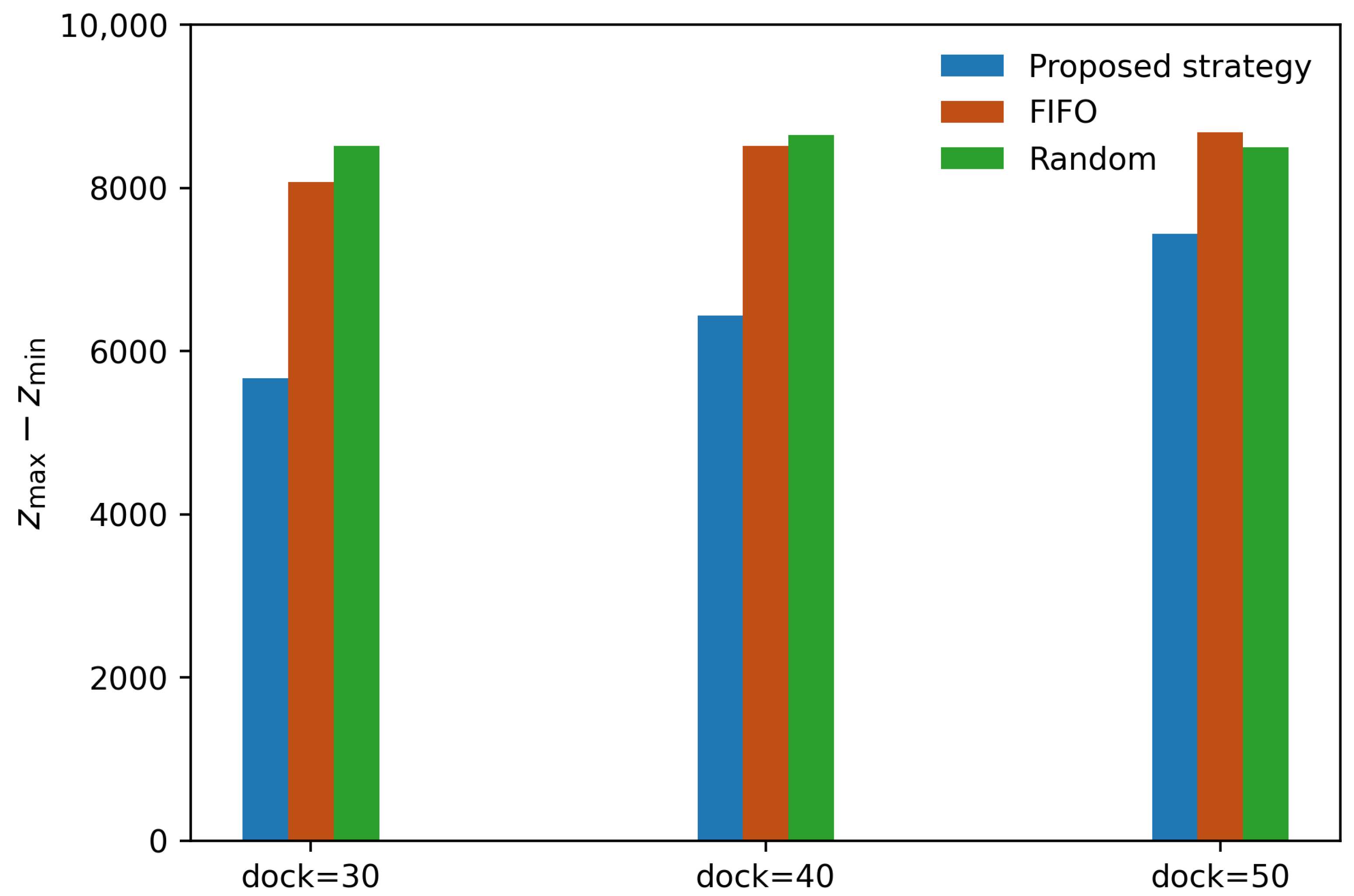
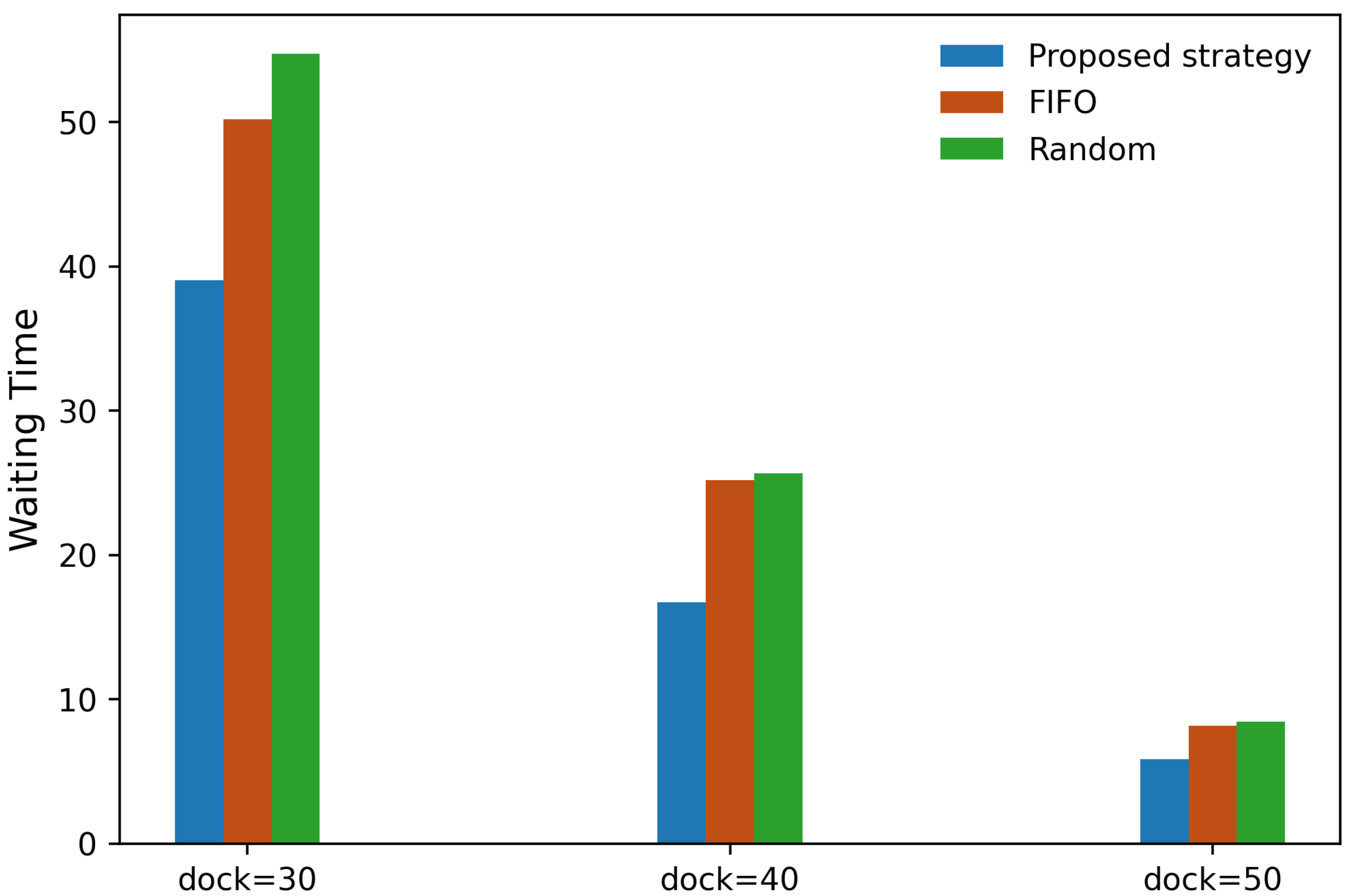
To further evaluate the robustness of the proposed strategy under varying capacity conditions, a comparative analysis was conducted using different numbers of inbound docks (30, 40, and 50) and outbound docks (98 and 148). The proposed strategy was compared with two baseline methods: FIFO and Random strategies. The performance comparison of each strategy across various combinations of inbound dock and outbound dock configurations is summarized in

Table 4. Performance comparison across different numbers of inbound and outbound docks.

Number of Outbound Docks	Number of Inbound Docks	Strategy	${\mathit{z}}_{max}-{\mathit{z}}_{min}$	Waiting_Time
98	30	Proposed strategy	5667.13	39.04
		FIFO	8071.07	50.20
		Random	8510.23	54.72
	40	Proposed strategy	6547.79	16.75
		FIFO	8513.03	25.17
		Random	8664.64	25.65
	50	Proposed strategy	7439.42	5.86
		FIFO	8682.27	8.17
		Random	8495.44	8.47
148	30	Proposed strategy	4824.36	28.97
		FIFO	6380.85	44.68
		Random	6488.31	43.20
	40	Proposed strategy	5276.06	11.66
		FIFO	6380.72	17.02
		Random	6453.52	17.95
	50	Proposed strategy	5738.34	3.61
		FIFO	6411.25	4.36
		Random	6502.39	4.38

and illustrated in Figure 6, Figure 7, Figure 8 and Figure 9.

The results demonstrate that the proposed strategy consistently outperforms the FIFO and Random strategies across all dock configurations. In terms of inventory storage balancing, the proposed strategy achieved improvements of approximately 24%, 17%, and 10% compared to FIFO and 26%, 18%, and 12% compared to Random, under the combination of 148 outbound docks and 30, 40, and 50 inbound docks, respectively. Under the combination of 98 outbound docks and 30, 40, and 50 inbound docks, it achieved improvements of approximately 30%, 23%, and 14% compared to FIFO and 33%, 24%, and 12% compared to Random, respectively. Similarly, average truck waiting time was reduced by approximately 35%, 31%, and 17% relative to FIFO, and by 33%, 35%, and 18% relative to Random under the 148 outbound dock configuration. For the 98 outbound dock configuration, average truck waiting time was reduced by approximately 22%, 33%, and 28% compared to FIFO and 29%, 35%, and 31% compared to Random for 30, 40, and 50 inbound docks, respectively.

The results demonstrate that the proposed strategy performs robustly across different terminal configurations, consistently outperforming the benchmarks in reducing truck waiting times and improving dock utilization. The degree of performance improvement depends on the terminal configuration. When more outbound docks are available, workload balancing becomes inherently easier across all strategies, which narrows the performance gap. Likewise, with a larger number of inbound docks, overall congestion is alleviated, resulting in shorter truck queues and reducing the room for further gains. These findings underscore the practical utility of the proposed strategy, particularly in resource-constrained settings where effective scheduling is most critical.

7. Discussion

This study demonstrates both academic and practical value by empirically validating that dynamic inbound truck scheduling can enhance workload balancing and reduce truck waiting times in cross-docking terminal operations. The model’s ability to alleviate dock bottlenecks and improve system stability through real-time operational updates offers meaningful implications for terminal operators and decision makers. Furthermore, unlike most prior studies that focused on a single objective or employed static heuristics, our model simultaneously optimizes multiple operational goals. This expands the scope of dynamic scheduling research and contributes to practical applications in cross-docking logistics.

This study has several limitations. First, it assumes all cargoes are homogeneous in size and shape. However, in real-world settings, cargoes often vary significantly, and such complete information is rarely available. Second, the model omits the travel time from truck arrival points to docks, although these times can affect scheduling accuracy in practice. These idealized assumptions may limit the applicability of the model in practice, and the presence of system uncertainty or cargo heterogeneity may reduce solution quality. Third, although our objective function incorporates workload balancing to mitigate dock bottlenecks, we assumed a large temporary storage capacity (e.g., 100,000 units), eliminating the possibility of terminal shutdowns caused by chute congestion. In practice, such shutdowns may occur and lead to additional operational costs and service disruptions.

Future research could address these limitations and extend the model in several directions. First, if outbound truck information can be known in advance and integrated with inbound truck scheduling to simultaneously consider both loading and unloading operations, a more comprehensive optimization of cargo flows within the terminal can be achieved. Second, incorporating realistic factors—such as heterogeneous cargo characteristics, uncertain truck arrivals and service times, incomplete information, and non-negligible internal travel times—would improve practical applicability. Third, the model could be extended by incorporating terminal shutdowns resulting from chute bottlenecks due to limited temporary inventory storage capacity. Finally, validating the proposed strategy with real operational data from large-scale, multi-terminal environments would provide stronger evidence of its scalability and industrial relevance.

8. Conclusions

This study proposed a dynamic inbound truck scheduling model that jointly considers temporary inventory storage and truck waiting times to enhance the operational efficiency of cross-docking terminals. The proposed model integrates a real-time rescheduling strategy that is triggered whenever an inbound dock becomes idle. By continuously reflecting the latest status of outbound dock capacity and waiting truck queues, the strategy aims to minimize both dock load imbalance and average truck waiting times.

Simulation experiments confirmed that the proposed strategy significantly outperforms conventional scheduling strategies such as FIFO and Random assignment across the following two key performance indicators: temporary inventory storage balancing and truck waiting time. The model effectively prevents dock congestion and reduces overall system delays, particularly under constrained dock availability, thereby enhancing the stability and responsiveness of cross-docking terminal operations.

In future research, the applicability and practical usefulness of the model can be further enhanced by expanding it to reflect the real-world constraints and dynamics of terminal operations by addressing bottleneck-induced shutdowns and minimizing operational costs and by validating the proposed strategies using actual large-scale and multi-terminal operational data.