A Random Riemann–Liouville Integral Operator

Abstract

In this work, we propose a definition of the random fractional Riemann–Liouville integral operator, where the order of integration is given by a random variable. Within the framework of random operator theory, we study this integral with a random kernel and establish results on the measurability of the random Riemann–Liouville integral operator, which we show to be a random endomorphism of $L^1[a,b]$. Additionally, we derive the semigroup property for these operators as a probabilistic version of the constant-order Riemann–Liouville integral. To illustrate the behavior of this operator, we present two examples involving different random variables acting on specific functions. The sample trajectories and estimated probability density functions of the resulting random integrals are then explored via Monte Carlo simulation.

1. Introduction

The Riemann–Liouville integral operator (R-L IO) can be seen as a generalization of Cauchy’s formula for the iterated integral of a suitably regular function. It plays a fundamental role in fractional calculus, serving as the basis for defining both the Riemann–Liouville and Caputo fractional derivatives. These derivatives have been widely used to model real-world and complex phenomena that exhibit properties such as memory, scale dependence, and self-similarity. Memory phenomena appear in different disciplines such as dielectric relaxation and the charge–discharge of supercapacitors [1]; the self-similarity property is considered a intrinsic feature of complex phenomena and fractal objects, which are related to long-term memory and scaling laws, to mention a few [2,3]. In this sense, models that use fractional operators such as the Riemann–Liouville integral and the Caputo derivative have been applied to the study of memory and the self-similarity of complex phenomena. The order of the fractional operator can be physically interpreted as an index of memory or forgetfulness [1] and it is related to the fractal dimension [4]. There are phenomena with properties of memory, scale, and self-similarity where these qualities do not remain constant in time and space [5,6]. Therefore, it is appropriate to model the order of the fractional operator as a random variable [7,8].

In the pioneering works of [7,9], fractional differential equations with randomly distributed derivative orders were introduced, and the behavior of their solutions was analyzed using numerical techniques and Monte Carlo simulations. However, these studies did not investigate the probabilistic properties of the operators themselves or of the resulting solutions. Later, in [8], the authors explored such operators under the assumption that the fractional order is a simple random variable. Building upon this foundation, the present work advances the theory by extending the classical semigroup property of fractional integrals to the random setting, laying the groundwork for further developments in stochastic fractional calculus.

In this work, our main contribution is to extend the results of [8] by considering the order of the integral operator as a continuous random variable, which leads to the definition of a random Riemann–Liouville integral operator. This operator is analyzed within the framework of random operator theory, where we establish its measurability and demonstrate that it defines a random endomorphism on the space $L^1[a,b]$. We study its probabilistic properties and proving that it satisfies a random version of the semigroup property, analogous to the classical constant-order case. The results obtained here are expected to play a crucial role in the formulation and analysis of fractional differential equations with a random order, as they enable a fractional version of the Fundamental Theorem of Calculus under randomness, providing the theoretical foundation for the development of random fractional integrodifferential equations, which was the central motivation of this work.

2. Preliminaries

For a better understanding, we first recall some foundational concepts related to random variables in Banach spaces and random operators.

Let $\mathfrak{B}$ be a Banach space equipped with the norm ${\parallel ·\parallel }_{\mathfrak{B}}$. A function $X:\Omega \to \mathbb{R}$, defined on a probability space $(\Omega ,\mathcal{A},P)$, is called a real-valued random variable if it is measurable with respect to the Borel $\sigma$-algebra, $\sigma \left(\mathbb{R}\right)$, generated by the open subsets of $\mathbb{R}$; that is,

$$X^{-1}\left(\sigma \left(\mathbb{R}\right)\right)\subset \mathcal{A}.$$

In order to extend the above notion to the case where the random variable takes values in a Banach space $\mathfrak{B}$, let us consider that $\sigma \left(\mathfrak{B}\right)$ is the $\sigma$-algebra generated by the Borel subsets of $\mathfrak{B}$.

Definition 1

([10]). A random variable of values in a Banach space $\mathfrak{B}$ is a function $X:\Omega \to \mathfrak{B}$ such that

$$X^{-1}\left(B\right)\in \mathcal{A},\forall B\in \sigma \left(\mathfrak{B}\right).$$

In particular, if the range of X is a finite subset of $\mathfrak{B}$, then X is said to be a simple random variable.

Definition 2

([10]). The random variable $X:\Omega \to \mathfrak{B}$ is said to be a strong random variable if there exists a sequence of simple random variables $\left\{X_n\right\}$ that converge to X almost surely; that is to say,

$$\underset{n\to \infty }{lim}{\parallel X_n\left(\omega \right)-X\left(\omega \right)\parallel }_{\mathfrak{B}}=0,$$

for each $\omega \in \Omega -A_0$, where $A_0\in \mathcal{A}$ and $P\left(A_0\right)=0$.

From Definition 1, it is natural to consider the Banach space $\mathfrak{L}\left({\mathfrak{B}}_1,{\mathfrak{B}}_2\right)$ of all linear and bounded transformations between the Banach spaces ${\mathfrak{B}}_1$ and ${\mathfrak{B}}_2$; this space is equipped with the uniform norm

$${∥L∥}_{\mathfrak{L}}=\underset{{\parallel x\parallel }_{{\mathfrak{B}}_1}\le 1}{sup}{∥Lx∥}_{{\mathfrak{B}}_2},L\in \mathfrak{L}\left({\mathfrak{B}}_1,{\mathfrak{B}}_2\right).$$

To define a random variable that takes values in said operator space, use $\sigma \left(\mathfrak{L}\left({\mathfrak{B}}_1,{\mathfrak{B}}_2\right)\right)$ the $\sigma$-algebra generated by the Borel sets of $\mathfrak{L}\left({\mathfrak{B}}_1,{\mathfrak{B}}_2\right)$, then $\mathcal{L}:\Omega \to \mathfrak{L}\left({\mathfrak{B}}_1,{\mathfrak{B}}_2\right)$ is a random operator between the spaces of Banach ${\mathfrak{B}}_1$ and ${\mathfrak{B}}_2$ if

$${\mathcal{L}}^{-1}\left(B\right)\in \mathcal{A},\forall B\in \sigma \left(\mathfrak{L}\left({\mathfrak{B}}_1,{\mathfrak{B}}_2\right)\right).$$

Definition 3

([10]). Let ${\left\{{\mathcal{L}}_n\right\}}_{n\in \mathbb{N}}$ be a sequence of simple random operators that take values in $\mathfrak{L}\left({\mathfrak{B}}_1,{\mathfrak{B}}_2\right)$. If such a sequence converges almost surely to $\mathcal{L}\in \mathfrak{L}({\mathfrak{B}}_1,{\mathfrak{B}}_2)$ in the uniform norm, $\mathcal{L}:\Omega \to \mathfrak{L}\left({\mathfrak{B}}_1,{\mathfrak{B}}_2\right)$ is said to be a uniform random operator.

From the previous definition, we can determine that if $\mathcal{L}:\Omega \to \mathfrak{L}({\mathfrak{B}}_1,{\mathfrak{B}}_2)$ is a uniform random operator then $\mathcal{L}\left(\omega \right)x$ is a strong random variable that takes values in ${\mathfrak{B}}_2$ for each $x\in {\mathfrak{B}}_1$.

In the particular case where ${\mathfrak{B}}_1={\mathfrak{B}}_2=\mathfrak{B}$, the random operator $\mathcal{L}$ is referred to as a uniform random endomorphism of $\mathfrak{B}$.

3. Main Contributions

Let $(\Omega ,\mathcal{F},P)$ be a complete probability space and $\xi :\Omega \to {\mathbb{R}}_{+}$ a simple non-negative real-valued random variable; that is, a function such that the image $\xi (\Omega )$ is a finite subset of ${\mathbb{R}}_{+}$, $\xi (\Omega )=\{a_1,a_2,\dots ,a_k\}$, $k\in \mathbb{N}$. Also, it must be satisfied that

$$A_i=\left[\omega :\xi \left(\omega \right)=a_i\right]\in \mathcal{F},$$

for $i=1,\dots ,k$. Let us note that ${\cup }_i{A}_i=\Omega$ and $A_i\cap A_j=\varnothing$ for $i\ne j$, and therefore the simple random variable $\xi$ admits the representation

$$\xi \left(\omega \right)=\sum _{i=1}^k{a}_i{\chi }_{A_i}\left(\omega \right),$$

(1)

where ${\chi }_A(·)$ denotes the indicator function of the event A (${\chi }_A\left(\omega \right):=\left\{\begin{array}{cc}1,& \mathrm{if} \omega \in A,\hfill \\ 0,& \mathrm{otherwise}.\hfill \end{array}\right.$).

Let ${\mathcal{E}}_{+}$ denote the collection of all simple non-negative real-valued random variables defined in the same probability space.

Definition 4.

Let $\xi \left(\omega \right)\in {\mathcal{E}}_{+}$. The operator $I_a^{\xi \left(\omega \right)}$, defined for $\varphi \in L_1[a,b]$ by means of

$$I_a^{\xi \left(\omega \right)}\phi \left(t\right):={\displaystyle \frac{1}{\Gamma \left(\xi \right(\omega \left)\right)}}{\int }_a^t{(t-s)}^{\xi \left(\omega \right)-1}\phi \left(s\right)ds,$$

(2)

for $a\le t\le b$ and $\Gamma (·)$ is the Gamma function, referred to as the simple Riemann–Liouville random integral operator.

Since $\xi \left(\omega \right)$ is a simple random variable of non-negative real values by (1), it follows that

$${\displaystyle I_a^{\xi \left(\omega \right)}\phi \left(t\right)={\displaystyle \frac{1}{\Gamma \left({\displaystyle \sum _{i=1}^k{\alpha }_i{\chi }_{A_i}\left(\omega \right)}\right)}}{\int }_a^t{(t-s)}^{{\displaystyle \sum _{i=1}^k{\alpha }_i{\chi }_{A_i}\left(\omega \right)-1}}\phi \left(s\right)ds.}$$

Let us note that the integral on the right-hand side takes a unique value $I_a^{{\alpha }_i}\phi \left(t\right)$ depending on whether $\omega \in A_i$ for $i=1,2,\dots ,n$. Therefore,

$$\begin{array}{ccc}\hfill {\displaystyle {\displaystyle \frac{1}{\Gamma \left({\sum }_{i=1}^k{\alpha }_i{\chi }_{A_i}\left(\omega \right)\right)}}{\int }_a^t{(t-s)}^{{\sum }_{i=1}^k{\alpha }_i{\chi }_{A_i}\left(\omega \right)-1}\phi \left(s\right)ds}& =& {\displaystyle \sum _{i=1}^k\left({\displaystyle \frac{1}{\Gamma \left({\alpha }_i\right)}}{\int }_a^t{(t-s)}^{{\alpha }_i-1}\phi \left(s\right)ds\right){\chi }_{A_i}\left(\omega \right)}\hfill \\ & & \\ & =& {\displaystyle \sum _{i=1}^k{I}_a^{{\alpha }_i}\phi \left(t\right){\chi }_{A_i}\left(\omega \right)}\hfill \\ & & \\ & =& {\displaystyle \sum _{i=1}^k{\Phi }_{{\alpha }_i}\left(t\right){\chi }_{A_i}\left(\omega \right),}\hfill \end{array}$$

where ${\Phi }_{{\alpha }_i}\left(t\right)=I_a^{{\alpha }_i}\phi \left(t\right)$. Thus, the rank of $I_a^{\xi \left(\omega \right)}$, $R_I=\{{\Phi }_{{\alpha }_1}\left(t\right),\dots ,{\Phi }_{{\alpha }_k}\left(t\right)\}$ is finite for each $\phi \in L_1[a,b]$.

Now, let us consider the measurable space $(L_1[a,b],{\mathcal{B}}_{L_1})$ where ${\mathcal{B}}_{L_1}$ is the $\sigma$-algebra of the Borel sets of the space $L_1[a,b]$. It follows that for each $B\in {\mathcal{B}}_{L_1}$

$$\left[\omega :I_a^{\xi \left(\omega \right)}\phi \left(t\right)\in B\right]=\bigcup _{{\Phi }_{{\alpha }_i}\left(t\right)\in B\cap R_I}\left[\omega :I_a^{\xi \left(\omega \right)}\phi \left(t\right)={\Phi }_{{\alpha }_i}\left(t\right)\right]\in \mathcal{F}.$$

Thus, for each $\phi \in L_1[a,b]$, $I_a^{\xi \left(\omega \right)}\phi \left(t\right)$ is a simple $L_1[a,b]$-valued random variable.

Theorem 1.

Let $\xi \left(\omega \right)={\sum }_{i=1}^n{a}_i{\chi }_{A_i}\left(\omega \right)$ and $\eta \left(\omega \right)={\sum }_{j=1}^m{b}_j{\chi }_{B_j}\left(\omega \right)$ be two elements of ${\mathcal{E}}_{+}$ and $\phi \in L_1[a,b]$. Then,

$$I_a^{\xi \left(\omega \right)}{I}_a^{\eta \left(\omega \right)}\phi \left(t\right)=I_a^{\xi \left(\omega \right)+\eta \left(\omega \right)}\phi \left(t\right),$$

with a probability of one and almost everywhere in $[a,b]$.

Proof. 

By Definition 4 and [8],

$$\begin{array}{ccc}\hfill I_a^{\xi \left(\omega \right)}{I}_a^{\eta \left(\omega \right)}\phi \left(t\right)& =& {\displaystyle {\displaystyle \frac{1}{\Gamma \left({\sum }_{i,j}(a_i+b_j){\chi }_{A_i\cap B_j}\left(\omega \right)\right)}}{\int }_a^t\phi \left(u\right){(t-u)}^{{\sum }_{i,j}(a_i+b_j){\chi }_{A_i\cap B_j}\left(\omega \right)-1}du.}\hfill \end{array}$$

Note that the event $\left[\omega :I_a^{\xi \left(\omega \right)}{I}_a^{\eta \left(\omega \right)}\phi \left(t\right)=I_a^{\xi \left(\omega \right)+\eta \left(\omega \right)}\phi \left(t\right)\right]$ coincides with all $A_i\cap B_j\ne \varnothing$. Therefore,

$$P\left[\omega :I_a^{\xi \left(\omega \right)}{I}_a^{\eta \left(\omega \right)}\phi \left(t\right)=I_a^{\xi \left(\omega \right)+\eta \left(\omega \right)}\phi \left(t\right)\right]=P\left[\bigcup _i\bigcup _j{A}_i\cap B_j\right]=P\left[\Omega \right]=1.$$

□

Theorem 2.

Let $X:\Omega \to {\mathbb{R}}_{+}$ be a positive random variable. Then, $I_a^X$ is a uniform random operator from $L_1[a,b]$ to itself.

Proof. 

Let $\phi \in L_1[a,b]$; then, for every $\omega \in \Omega$ we have

$$\begin{array}{ccc}\hfill \left|I_a^X\phi \left(t\right)\right|& =& \left|{\displaystyle \frac{1}{\Gamma \left(X\right)}{\int }_a^t{(t-s)}^{X-1}\phi \left(s\right)ds}\right|\hfill \\ & & \\ & \le & {\displaystyle \frac{1}{\Gamma \left(X\right)}{\int }_a^t{(t-s)}^{X-1}\left|\phi \left(s\right)\right|ds}\hfill \\ & & \\ & \le & {\displaystyle \frac{1}{\Gamma \left(X\right)}{\int }_0^{b-a}{u}^{X-1}\left|\phi (t-u)\right|du.}\hfill \end{array}$$

Using the generalized Minkowski inequality [11], we have

$$\begin{array}{ccc}\hfill \parallel I_a^X{\phi \parallel }_{L_1}& =& {\displaystyle {\int }_a^b\left|\frac{1}{\Gamma \left(X\right)}{\int }_a^t{(t-s)}^{X-1}\phi \left(s\right)ds\right|dt}\hfill \\ \hfill & & \\ \hfill & \le & {\displaystyle {\int }_a^b\left[{\displaystyle \frac{1}{\Gamma \left(X\right)}{\int }_0^{b-a}{u}^{X-1}\left|\phi (t-u)\right|du}\right]dt}\hfill \\ \hfill & & \\ \hfill & \le & {\displaystyle \frac{1}{\Gamma \left(X\right)}{\int }_0^{b-a}{u}^{X-1}du{\int }_a^b\left|\phi (t-u)\right|dt}\hfill \\ \hfill & & \\ \hfill & \le & {\displaystyle \frac{{(b-a)}^X}{\Gamma (X+1)}}{\parallel \phi \parallel }_{L_1}.\hfill \end{array}$$

(3)

Since X is a random variable, we know that there exists a sequence $\left\{{\xi }_n\right\}$ of simple random variables of non-negative values such that ${\xi }_n\to X$, when $n\to \infty$ almost surely. For the elements of such a sequence, let us consider the sequence of simple Riemann–Liouville random integral operators $\left\{I_a^{{\xi }_n\left(\omega \right)}\right\}$. For each $\phi \in L_1[a,b]$, such operators are simple $L_1[a,b]$-valued random variables. For such $\omega \in \Omega$, we have

$$\begin{array}{ccc}\hfill I_a^X\phi \left(t\right)-I_a^{{\xi }_n\left(\omega \right)}\phi \left(t\right)& =& {\displaystyle {\int }_a^t\left[{\displaystyle \frac{{(t-s)}^{X-1}}{\Gamma \left(X\right)}}-{\displaystyle \frac{{(t-s)}^{{\xi }_n\left(\omega \right)-1}}{\Gamma \left({\xi }_n\left(\omega \right)\right)}}\right]\phi \left(s\right)ds}\hfill \\ & & \\ & =& {\displaystyle \left[{\displaystyle \frac{1}{\Gamma \left(X\right)}}-{\displaystyle \frac{1}{\Gamma \left({\xi }_n\left(\omega \right)\right)}}\right]{\int }_a^t{(t-s)}^{X-1}\phi \left(s\right)ds}\hfill \\ & & \\ & & {\displaystyle +{\displaystyle \frac{1}{\Gamma \left({\xi }_n\left(\omega \right)\right)}}{\int }_a^t\left[{(t-s)}^{X-1}-{(t-s)}^{{\xi }_n\left(\omega \right)-1}\right]\phi \left(s\right)ds}\hfill \\ & & \\ & =& T_1\left(\omega \right)\phi +T_2\left(\omega \right)\phi .\hfill \end{array}$$

Now, we use (3) for $T_1\left(\omega \right)\phi$,

$$\begin{array}{ccc}\hfill {∥T_1\left(\omega \right)\phi ∥}_{L_1}& \le & {\parallel \phi \parallel }_{L_1}\left|1-{\displaystyle \frac{\Gamma \left(X\right)}{\Gamma \left({\xi }_n\left(\omega \right)\right)}}\right|{\displaystyle \frac{{(b-a)}^X}{\Gamma (X+1)}}.\hfill \end{array}$$

On the other hand, we have

$$\begin{array}{ccc}\hfill \left|T_2\left(\omega \right)\phi \left(t\right)\right|& =& \left|{\displaystyle {\displaystyle \frac{1}{\Gamma \left({\xi }_n\left(\omega \right)\right)}}{\int }_a^t\left[{(t-s)}^{X-1}-{(t-s)}^{{\xi }_n\left(\omega \right)-1}\right]\phi \left(s\right)ds}\right|\hfill \\ & & \\ & =& \left|{\displaystyle {\displaystyle \frac{1}{\Gamma \left({\xi }_n\left(\omega \right)\right)}}{\int }_0^{t-a}\left[u^{X-1}-u^{{\xi }_n\left(\omega \right)-1}\right]\phi (t-u)du}\right|\hfill \\ & & \\ & \le & {\displaystyle {\displaystyle \frac{1}{\Gamma \left({\xi }_n\left(\omega \right)\right)}}{\int }_0^{b-a}\frac{|1-u^{{\xi }_n\left(\omega \right)-X}|}{u^{1-X}}\left|\phi (t-u)\right|du.}\hfill \end{array}$$

Now, by applying the generalized Minkowski inequality, we get

$$\begin{array}{ccc}\hfill {∥T_2\left(\omega \right)\phi ∥}_{L_1}& \le & {\displaystyle {\parallel \phi \parallel }_{L_1}{\displaystyle \frac{1}{\Gamma \left({\xi }_n\left(\omega \right)\right)}}{\int }_0^{b-a}{\displaystyle \frac{|1-u^{{\xi }_n\left(\omega \right)-X}|}{u^{1-X}}}du.}\hfill \end{array}$$

From these two inequalities, we obtain

$$\begin{array}{ccc}\hfill \underset{{\parallel \phi \parallel }_{L_1}\le 1}{sup}{\parallel I_a^X\phi -I_a^{{\xi }_n\left(\omega \right)}\phi \parallel }_{L_1}& \le & \left|1-{\displaystyle \frac{\Gamma \left(X\right)}{\Gamma \left({\xi }_n\left(\omega \right)\right)}}\right|{\displaystyle \frac{{(b-a)}^X}{\Gamma (X+1)}}\hfill \\ & & \\ & & {\displaystyle +{\displaystyle \frac{1}{\Gamma \left({\xi }_n\left(\omega \right)\right)}}{\int }_0^{b-a}{\displaystyle \frac{|1-u^{{\xi }_n\left(\omega \right)-X}|}{u^{1-X}}}du.}\hfill \end{array}$$

Therefore, the right-hand side integral converges to 0, when $n\to \infty$, and since the function $\Gamma (·)$ is continuous, then $\underset{n\to \infty }{lim}{\parallel I_a^X-I_a^{{\xi }_n\left(\omega \right)}\parallel }_{\mathfrak{L}}=0$. According to Definition 3, we find that $I_a^X$ is a uniform random operator from $L_1[a,b]$ to itself. □

Definition 5.

Let $X:\Omega \to {\mathbb{R}}_{+}$ be a random variable. The operator $I_a^X$, defined on $L_1[a,b]$ by means of

$$I_a^X\phi \left(t\right):={\displaystyle \frac{1}{\Gamma \left(X\right)}}{\int }_a^t{(t-s)}^{X-1}\phi \left(s\right)ds,$$

for $a\le t\le b$, is called the random fractional Riemann–Liouville integral operator.

If X takes values in $R\subseteq {\mathbb{R}}_{+}$ and has the probability density function $f_X$, by Fubini’s Theorem [12], we can obtain

$$\begin{array}{ccc}\hfill E\left(I_a^X\phi \left(t\right)\right)& =& E\left({\displaystyle {\int }_a^t{\displaystyle \frac{{(t-s)}^{X-1}}{\Gamma \left(X\right)}}\phi \left(s\right)ds}\right)\hfill \\ & & \\ & =& {\displaystyle {\int }_{\Omega }{\int }_a^t{\displaystyle \frac{{(t-s)}^{X-1}}{\Gamma \left(X\right)}}\phi \left(s\right)dsdP}\hfill \\ & & \\ & =& {\displaystyle {\int }_a^t\phi \left(s\right){\int }_R{\displaystyle \frac{{(t-s)}^{x-1}}{\Gamma \left(x\right)}}{f}_X\left(x\right)dxds}\hfill \\ & & \\ & =& {\displaystyle {\int }_a^{t}E\left({\displaystyle \frac{{(t-s)}^{X-1}}{\Gamma \left(X\right)}}\right)\phi \left(s\right)ds.}\hfill \end{array}$$

Now, if X and Y are two random variables with the joint density function $f_{X,Y}$ that take values in $R_1\times R_2\subseteq {\mathbb{R}}_{+}^2$, then the covariance function is expressed as

$$\begin{array}{ccc}\hfill Cov\left(I_a^X\phi \left(t\right),I_a^Y\phi \left(t\right)\right)& =& {\displaystyle {\int }_a^t{\int }_a^t{\int }_{R_2}{\int }_{R_1}\phi \left(s\right)\phi \left(u\right){\displaystyle \frac{{(t-s)}^{x-1}{(t-u)}^{y-1}}{\Gamma \left(x\right)\Gamma \left(y\right)}}}\hfill \\ & & \\ & & \times \left(f_{X,Y}(x,y)-f_X\left(x\right)f_Y\left(y\right)\right)dxdydsdu,\hfill \end{array}$$

where $f_X$ and $f_Y$ are the marginal density functions of X and Y, respectively.

Proposition 1.

Let X and Y be two random variables of non-negative values. Then, the operator composition $I_a^{X\left(\omega \right)}{I}_a^{Y\left(\omega \right)}$ is a uniform random operator of the space $L_1[a,b]$ itself.

Proof. 

Let $\left\{{\eta }_n\left(\omega \right)\right\}$ be a sequence of simple random variables such that ${\eta }_n\left(\omega \right)\to Y$ when $n\to \infty$. Now, for each $\omega \in \Omega$, define $Z_n\left(\omega \right)=I_a^X{I}_a^{{\eta }_n\left(\omega \right)}$. Note that $Z_n\left(\omega \right)$ is a uniform random operator for each $n\in \mathbb{N}$. We have

$$\begin{array}{ccc}\hfill {∥{\displaystyle I_a^X{I}_a^Y\phi -Z_n\left(\omega \right)\phi }∥}_{L_1}& =& {∥{\displaystyle I_a^X\left(\left(I_a^Y-I_a^{{\eta }_n\left(\omega \right)}\right)\phi \right)}∥}_{L_1}\hfill \\ & & \\ & \le & {\displaystyle \frac{{(b-a)}^X}{\Gamma (X+1)}}{∥\left(I_a^Y-I_a^{{\eta }_n\left(\omega \right)}\right)\phi ∥}_{L_1}.\hfill \end{array}$$

Therefore, ${∥I_a^X{I}_a^Y-Z_n\left(\omega \right)∥}_{\mathfrak{L}}\to 0$, when $n\to \infty$, a.s. □

Theorem 3.

Let X and Y be two random variables defined on the probability space $(\Omega ,\mathcal{A},P)$ and $\phi \in L_1[a,b]$. Then,

$$I_a^X{I}_a^Y\phi =I_a^{X+Y}\phi ,$$

almost surely in $\Omega \times [a,b]$.

Proof. 

Let $\left\{{\xi }_n\right\}$ and $\left\{{\eta }_n\right\}$ be two sequences of simple random variables such that ${\xi }_n\to X$ and ${\eta }_n\to Y$ when $n\to \infty$ almost surely. For each $\omega \in \Omega$,

$$\begin{array}{ccc}\hfill {∥I_a^X{I}_a^Y-I_a^{{\xi }_n\left(\omega \right)}{I}_a^{{\eta }_n\left(\omega \right)}∥}_{\mathfrak{L}}& \le & {∥I_a^X∥}_{\mathfrak{L}}{∥I_a^Y-I_a^{{\eta }_n\left(\omega \right)}∥}_{\mathfrak{L}}\hfill \\ & & \\ & & +{∥I_a^X-I_a^{{\xi }_n\left(\omega \right)}∥}_{\mathfrak{L}}{∥I_a^{{\eta }_n\left(\omega \right)}∥}_{\mathfrak{L}},\hfill \end{array}$$

then $I_a^{{\xi }_n\left(\omega \right)}{I}_a^{{\eta }_n\left(\omega \right)}\to I_a^X{I}_a^Y$ when $n\to \infty$. According to Theorem 1, the random operators $I_a^{{\xi }_n\left(\omega \right)}{I}_a^{{\eta }_n\left(\omega \right)}$ and $I_a^{{\xi }_n\left(\omega \right)+{\eta }_n\left(\omega \right)}$ are indistinguishable for each $n\in \mathbb{N}$; i.e., for each $\omega \in \Omega -A_0$, we have $I_a^{X\left(\omega \right)}{I}_a^{Y\left(\omega \right)}=I_a^{X\left(\omega \right)+Y\left(\omega \right)}$, where $P\left(A_0\right)=0$. Consequently, $I_a^X{I}_a^Y\phi =I_a^{X+Y}\phi$ almost surely in $\Omega \times [a,b]$. □

Example

In this section, we obtain the random fractional Riemann–Liouville integral operator for some given functions in $L^1$.

The numerical experiments presented in this work were implemented using the R programming language [13], with the aid of the packages ggplot2 [14], ggridges, [15] and MittagLeffleR [16]. The simulation procedure involved the following steps:

• We define functions in R software to evaluate the random Riemann–Liouville integral operators.
• Trajectory simulation: we generated 100 trajectories using 1000 discretization points over the interval $[0,1]$. For each trajectory, a sample of 1000 random variables was generated from a Beta distribution and transformed to constrain the order within the considered intervals. The functions in Step 1 were evaluated for each realization.
• The trajectories were plotted using the ggplot2 package, allowing the visualization of the operator’s behavior over time for different random realizations.
• To approximate the probability density function of the operator at fixed times, 1000 samples of the random variable were generated (using a transformed Beta distribution). A set of evaluation times was chosen. At each time point, the operator was evaluated across all samples.
• From the resulting data, the estimated densities were visualized using density ridge plots (ggridges), allowing an intuitive view of how the randomness in the operator order affects the distribution of its output at various time points.

This simulation approach allows both the visualization of sample trajectories and the estimation of the probability density of the operator’s output via Monte Carlo sampling.

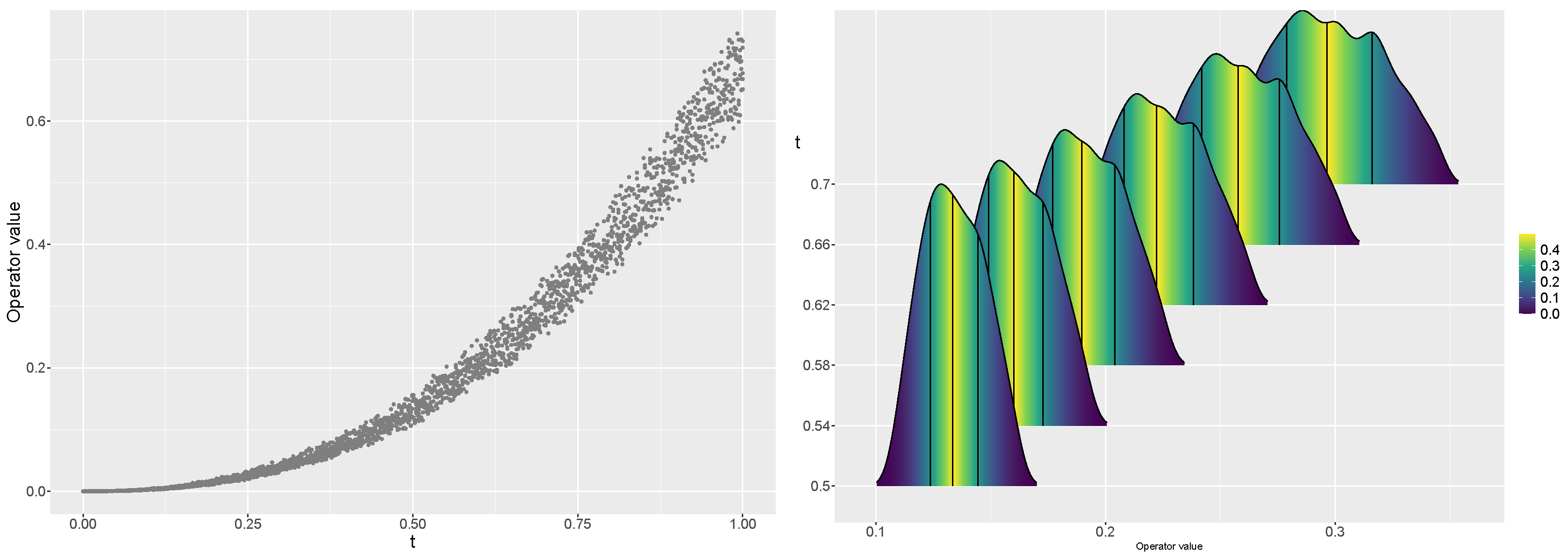
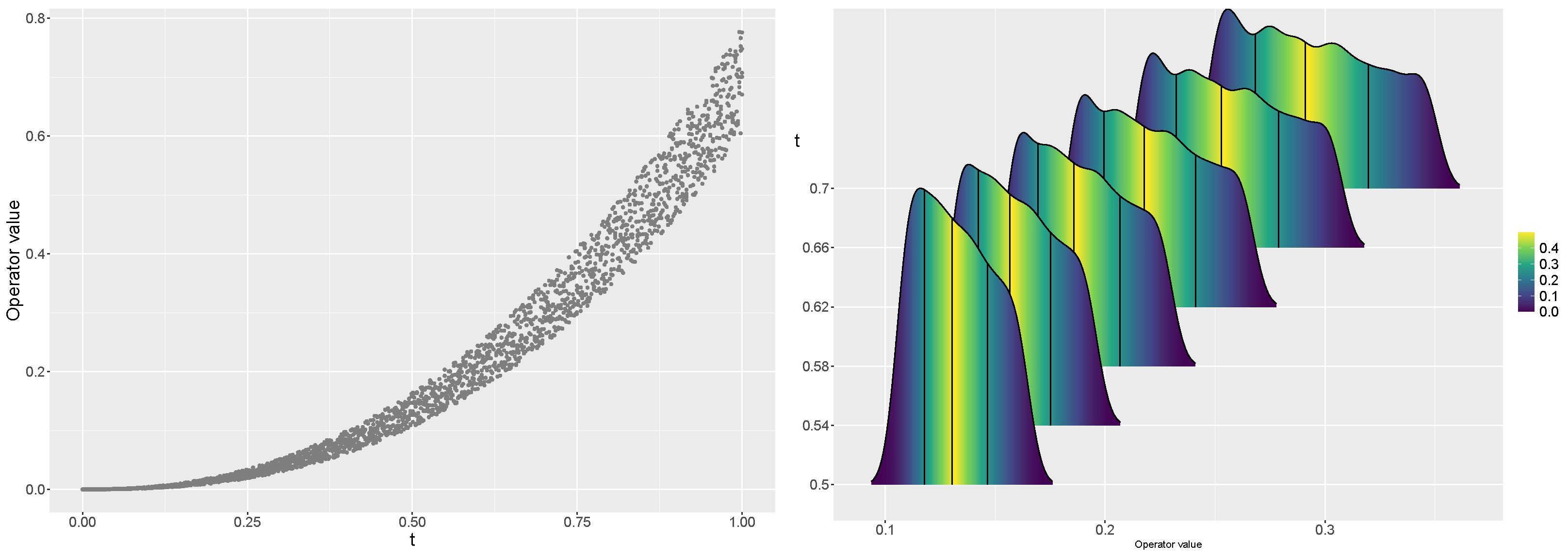
Example 1.

If $\phi \left(t\right)={(t-a)}^{\lambda }$, $\lambda >-1$ and $X:\Omega \to {\mathbb{R}}_{+}$ is a random variable, then

$$\begin{array}{ccc}\hfill I_a^X\phi \left(t\right)& =& {\displaystyle {\displaystyle \frac{1}{\Gamma \left(X\right)}}{\int }_a^t{(t-a)}^{X-1}{(s-a)}^{\lambda }ds}\hfill \\ \hfill & & \\ \hfill & =& \Gamma (\lambda +1){\displaystyle \frac{{(t-a)}^{X+\lambda }}{\Gamma (X+\lambda +1)}}.\hfill \end{array}$$

(4)

In Figure 1, we show the sample trajectories and density functions of (4) for different values of t, $a=0$, $\lambda =2$ and $X=(Y+1)/4$, where $Y\sim Beta(2,2)$.

In Figure 2, we show the sample trajectories and density functions of (4), for different values of t, $a=0$, $\lambda =2$, and $X\sim U(0.25,0.5)$.

Let us note that the points of the sample trajectories show a general power law trend; it is also appreciated that the variability increases with t. Also, we can observe that $\left\{I_a^X\phi :t\in [a,b]\right\}$ is a non-stationary process.

Example 2.

Now let us consider $\phi \left(t\right)=exp\left(\lambda \right(t-a\left)\right)$, $\lambda \ne 0$ and $X:\Omega \to {\mathbb{R}}_{+}$ is a random variable, then

$$\begin{array}{ccc}\hfill I_a^X\phi \left(t\right)& =& {\displaystyle {\displaystyle \frac{1}{\Gamma \left(X\right)}}{\int }_a^t{(t-s)}^{X-1}exp\left(\lambda (s-a)\right)ds}\hfill \\ \hfill & & \\ \hfill & =& {\displaystyle \sum _{n=0}^{\infty }{\displaystyle \frac{{\lambda }^n{(t-a)}^{X+n}}{\Gamma (X+n+1)}}}\hfill \\ \hfill & & \\ \hfill & =& {(t-a)}^X{E}_{1,X+1}\left(\lambda (t-a)\right),\hfill \end{array}$$

(5)

where $E_{\alpha ,\beta }\left(t\right)={\sum }_{k=0}^{\infty }{\displaystyle \frac{t^k}{\Gamma (\alpha k+\beta )}}$ is the two-parameter Mittag-Leffler function.

In Figure 3, we show the sample trajectories and density functions of (5) for different values of t, $a=0$, $\lambda =-{\displaystyle \frac{3}{2}}\pi$ and $X=(Y+1)/4$, where $Y\sim Beta(2,2)$.

In Figure 4, we show the sample trajectories and density functions of (5) for different values of t, $a=0$, $\lambda =-{\displaystyle \frac{3}{2}}\pi$ and $X\sim U(0.25,0.5)$.

The points of the sample trajectories are dispersed with respect to a well-determined general trend, which increases at the beginning to later show a gradual decay. The variability is greater around the maximum value of said tendency to decrease at the right end of the variation interval of t.

4. Conclusions

Under the theory of random operators, we introduced a generalization of the fractional Riemann–Liouville integral operator, considering the order of the integral given by a random variable. An important result is that the semigroup property for these operators was derived as a probabilistic version of the constant-order Riemann–Liouville integral, which enables the implementation of a fractional version of the Fundamental Theorem of Calculus under randomness, leading naturally to the formulation of random fractional integrodifferential equations. Finally, two illustrative examples were given to explore the action of this random operator on particular functions considering different random variables.

A direction for future work is the application of the main theorem developed in this work to the study of nonlinear fractional differential equations with random order. In particular, equations such as the fractional logistic equation or systems of nonlinear equations could benefit from this framework, allowing for a more realistic modeling of phenomena where memory and scaling effects vary in a stochastic manner.