LLM-Guided Ensemble Learning for Contextual Bandits with Copula and Gaussian Process Models
Abstract
1. Introduction
- Employs vine copulas to capture rich, nonlinear dependencies among contextual variables;
- Incorporates GARCH processes to simulate heteroskedastic, non-Gaussian reward noise;
- Utilizes GP-based bandit policies enhanced with dynamic, LLM-guided policy selection;
- Demonstrates through extensive experiments the superiority of this integrated approach in managing skewed, heavy-tailed, and volatile reward distributions.
2. Methods
2.1. Overview
2.2. Context Generation via GARCH and Copula Modeling
2.2.1. GARCH(1,1) Volatility Modeling
- is the conditional variance of dimension j at time t;
- is the long-term variance constant;
- measures sensitivity to recent squared innovations ;
- captures the persistence of past variance ,
2.2.2. Copula-Based Dependence Modeling
2.2.3. Copula-Based Dependence Structure
- is the pseudo-observation of the j-th variable at time t;
- is the rank of among ;
- T is the total number of observations.
2.3. Reward Simulation
- denotes the reward for arm at time t;
- is the PIT-transformed contextual input for arm k, obtained through a copula model to capture dependence across arms;
- is the inverse CDF (quantile function) of the Beta distribution;
- and are shape parameters controlling the distribution’s skewness and variance.
- Higher values of relative to result in right-skewed distributions (more probability mass near 1);
- Higher values of relative to lead to left-skewed distributions (more mass near 0);
- Equal values of and yield symmetric distributions (e.g., the uniform distribution when ).
2.4. GP Reward Estimation
- is the latent reward function for arm k evaluated at input ;
- denotes a GP prior;
- is the mean function, often assumed to be zero;
- is the covariance (kernel) function, typically chosen as the squared exponential (RBF) kernel, as follows:with hyperparameters ℓ (length-scale) and (signal variance).
- Predictive mean ;
- Predictive variance ,
2.5. Bandit Policies and LLM Integration
2.5.1. Classical Policies
- TS: For each round t, the algorithm draws a sample from the GP posterior predictive distribution for each arm k given the current context , and selects the arm with the highest sampled reward:where and are the GP posterior predictive mean and variance for arm k. This method balances exploration and exploitation through posterior sampling [7].
- UCB: At each time t, the algorithm selects the arm that maximizes an upper confidence bound:where
- –
- is the GP posterior predictive mean;
- –
- is the posterior predictive standard deviation;
- –
- is a tunable parameter that controls the degree of exploration.
Larger values of favor more exploration. This approach encourages arms with either high expected reward or high uncertainty [1]. - Epsilon-Greedy: This strategy selects the empirically best arm (highest predicted mean reward) with probability , and a random arm with probability as follows:where is a hyperparameter controlling exploration [5].
2.5.2. Ensemble Policy with LLM Guidance
- is the posterior predictive mean reward for arm k under the GP model, given the PIT-transformed context ;
- is the reward estimate from an LLM (e.g., GPT-4 [15]) conditioned on contextual information and a summary of recent regret or reward history ;
- is a tunable weighting hyperparameter that balances the contribution of model-based statistical prediction and LLM-based semantic inference.
- Fixed: chosen via offline validation (e.g., cross-validation or grid search) to minimize cumulative regret;
- Adaptive: dynamically updated during online learning, for instance by tracking the relative predictive accuracy or uncertainty of the GP and LLM components.
2.6. Adaptive Policy Selection via LLM
- For , actions are selected using classical model-based policies (e.g., TS or UCB), relying exclusively on GP reward estimates .
- For , the LLM is queried to determine either the next policy or to provide reward guidance through the ensemble formulation (see Equation (7)).
- convergence of posterior uncertainty ();
- stabilization of cumulative regret slopes;
- entropy of policy selection history.
2.7. LLM Prompt Engineering
2.7.1. Reward Prediction Prompt
Given context vector: , and arm index: k, along with recent reward history: [summary of last m rewards], predict the reward in the range [0, 1].
2.7.2. Policy Selection Prompt
“Given recent bandit performance metrics: [tabular summary of last n rounds including rewards, regrets, and selected policies], choose one policy from: TS, UCB, Epsilon-greedy, ensemble. Respond with only the policy name.”
2.7.3. Caching and Robustness
2.8. Evaluation Metrics
2.8.1. Cumulative Regret
2.8.2. Cumulative and Average Reward
2.8.3. Confidence Intervals and Replications
2.8.4. Policy Switching Dynamics
2.8.5. Per-Arm Performance
- -
- Mean reward received when each arm k was selected;
- -
- Selection frequency per arm under each policy p.
3. Simulation Setup
3.1. Context Generation via Functional Volatility and Copula Transformation
- is the matrix of contextual features with T time points and d feature dimensions;
- Each row represents the context vector at time t.
- Heteroskedastic Context Generation
- is the conditional variance of dimension j at time t;
- is the constant base volatility;
- controls sensitivity to past shocks ;
- governs persistence of volatility;
- are independent standard normal innovations;
- Stationarity is ensured by .
- Copula-Based Dependency Modeling
- We transform the GARCH-generated contexts into pseudo-observations using empirical cumulative distribution function (CDF) ranks as follows:ensuring uniform marginals suitable for copula modeling;
- A high-dimensional Vine Copula is fitted to the data using the RVineStructureSelect algorithm;
- This copula captures flexible nonlinear and tail dependencies between features;
- The probability integral transform (PIT) from the fitted copula yields the final transformed contextual inputs , which serve as bandit model inputs.
- Time-Varying Reward Volatility
- is the conditional reward variance for arm k at time t;
- , , and are fixed parameters;
- represents reward noise innovations;
- These parameters model volatility persistence () and responsiveness to recent shocks;
- This setup reflects financial-style volatility clustering to stress-test policy robustness under realistic, time-varying uncertainty.
- Distinguish volatility variables: for context dimension j, for arm k’s reward volatility;
- GARCH introduces temporal dependence, while Vine Copula models cross-sectional dependence among contexts;
- Each arm’s reward noise is modeled separately to allow arm-specific volatility dynamics.
3.2. Reward Generation
- is the reward at time t for arm a;
- A is the total number of arms;
- is the probability integral transform (PIT) value corresponding to arm a at time t, obtained from copula-based transformations of context;
- is the quantile function (inverse cumulative distribution function) of the Beta distribution parameterized by positive shape parameters .
- produces a left-skewed distribution (mass near 0), modeling sparse or conservative rewards;
- produces a right-skewed distribution (mass near 1), modeling optimistic rewards with heavier tails.
3.3. Reward Modeling via Gaussian Processes
- is the unknown reward function for arm a evaluated at context ;
- The mean function is assumed zero for simplicity;
- The covariance kernel is the squared exponential (RBF) kernel, given bywhere
- –
- is the signal variance;
- –
- l is the length-scale controlling smoothness;
- –
- is a small noise term (nugget) added for numerical stability;
- –
- is the Kronecker delta function (1 if , else 0).
3.4. Bandit Policies Evaluated
- TS: Sample a rewardthen select the arm with the highest sampled reward:
- UCB: Select the arm maximizing the UCB score:balancing exploitation and exploration.
- Epsilon-Greedy: With probability , select a random arm; otherwise, select the arm with the highest posterior mean:
- LLM-Guided Policies:
- –
- LLM-Reward: Uses predicted reward estimates from an LLM (mocked in simulation) to select the arm with highest predicted reward;
- –
- LLM-Policy: Dynamically selects among TS, UCB, Epsilon-greedy, or LLM-Reward policies by querying an LLM based on recent performance summaries.
3.5. Simulation Protocol
- Total time steps: ;
- Context dimension: ;
- Number of arms: .
3.6. Evaluation Metrics and Replications
- Mean Reward:where is the reward at time t for replication r.
- Cumulative Regret:representing the cumulative loss compared to always playing the best arm.
- Confidence Intervals (95%):where is the empirical mean and is the sample standard deviation over replications.
3.7. Empirical Results
- LLM-Reward: A policy guided by LLM reward prediction;
- Epsilon-Greedy: Selects a random arm with probability , otherwise exploits the best-known arm;
- UCB: Selects arms by maximizing upper confidence bounds to balance exploration and exploitation;
- TS: Samples from posterior reward distributions for probabilistic action selection.
- Mean R: Average reward obtained by the policy; higher values indicate better performance;
- SD R: Standard deviation of the reward across replications; lower values indicate more stable results;
- Mean Reg: Mean cumulative regret, defined as the total difference between the optimal arm’s reward and the chosen arm’s reward; lower values indicate more efficient learning;
- SD Reg: Standard deviation of cumulative regret, reflecting variability in performance across replications.
- : Left-skewed Beta distribution modeling sparse or conservative rewards.
- : Right-skewed Beta distribution modeling optimistic rewards with heavier tails.
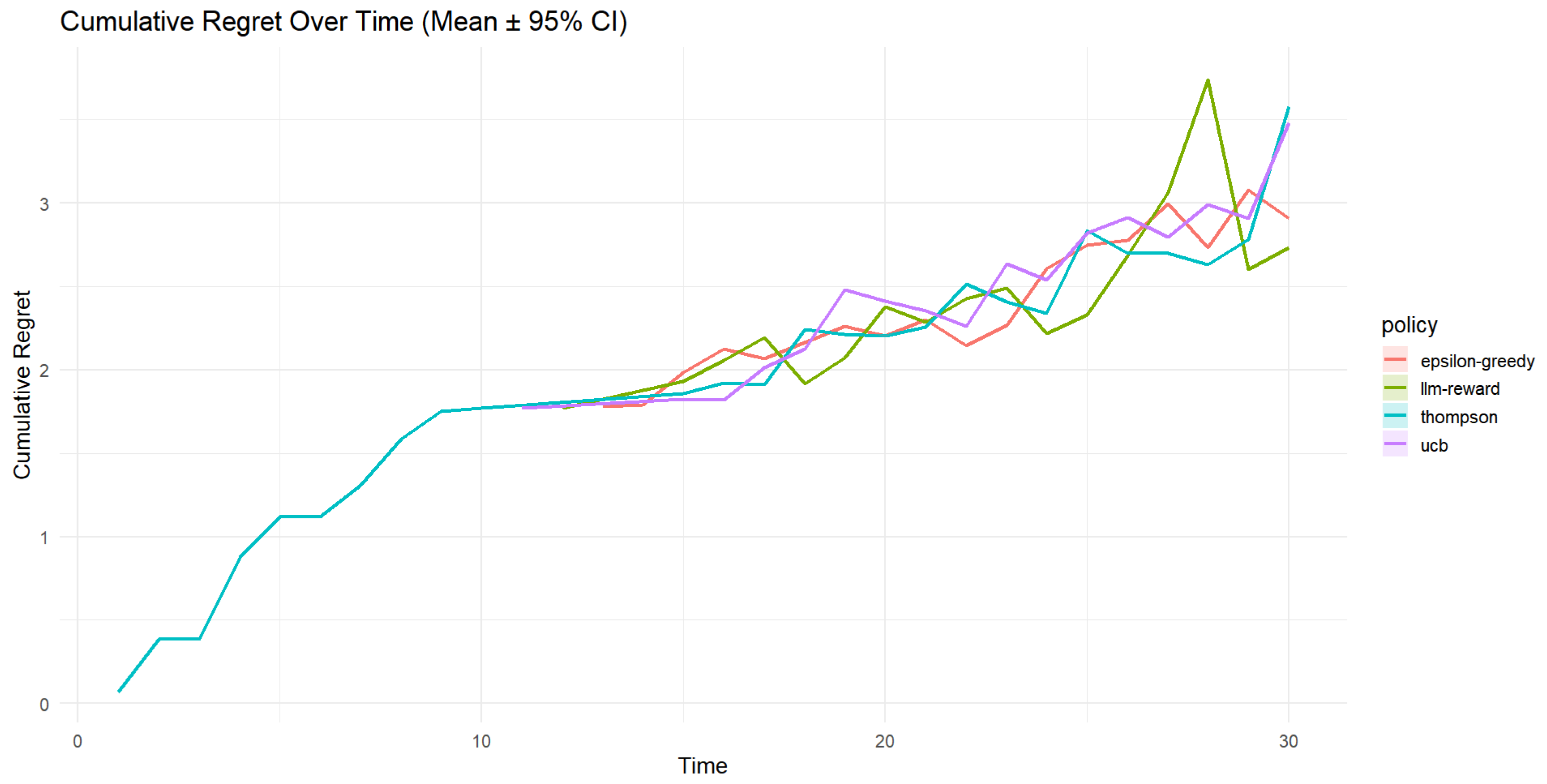
- Cumulative Regret (Figure 4)
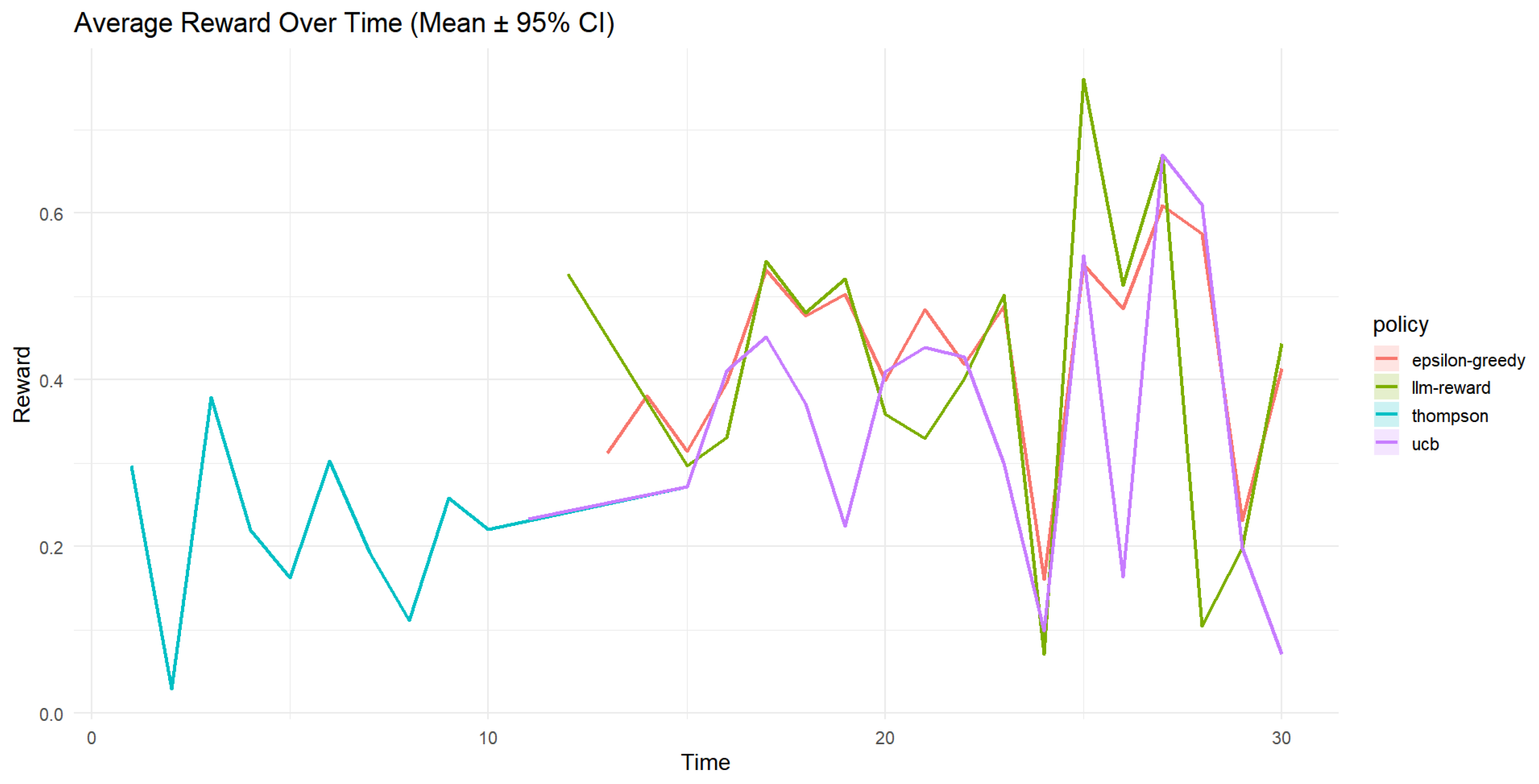
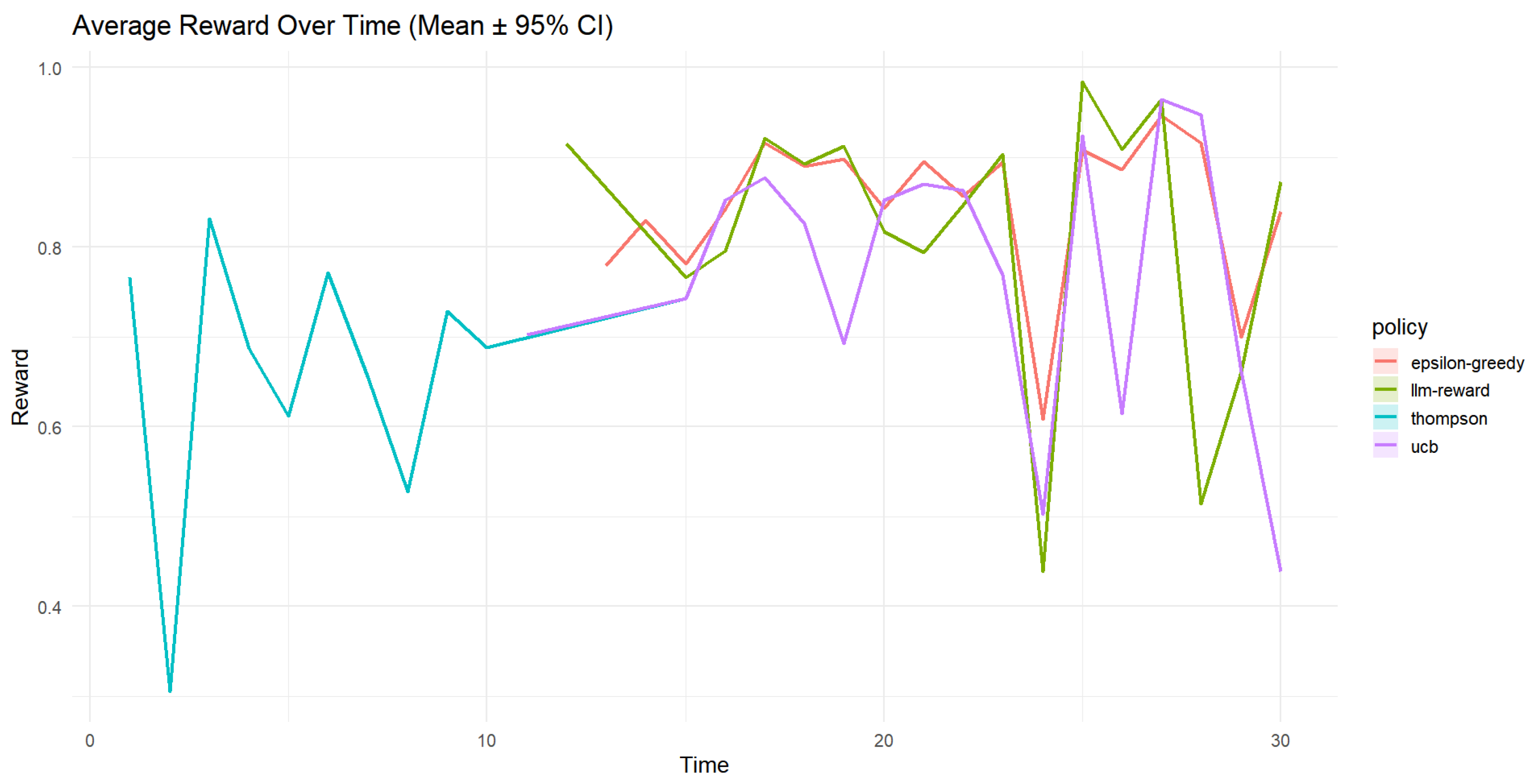
- Average Reward (Figure 5)
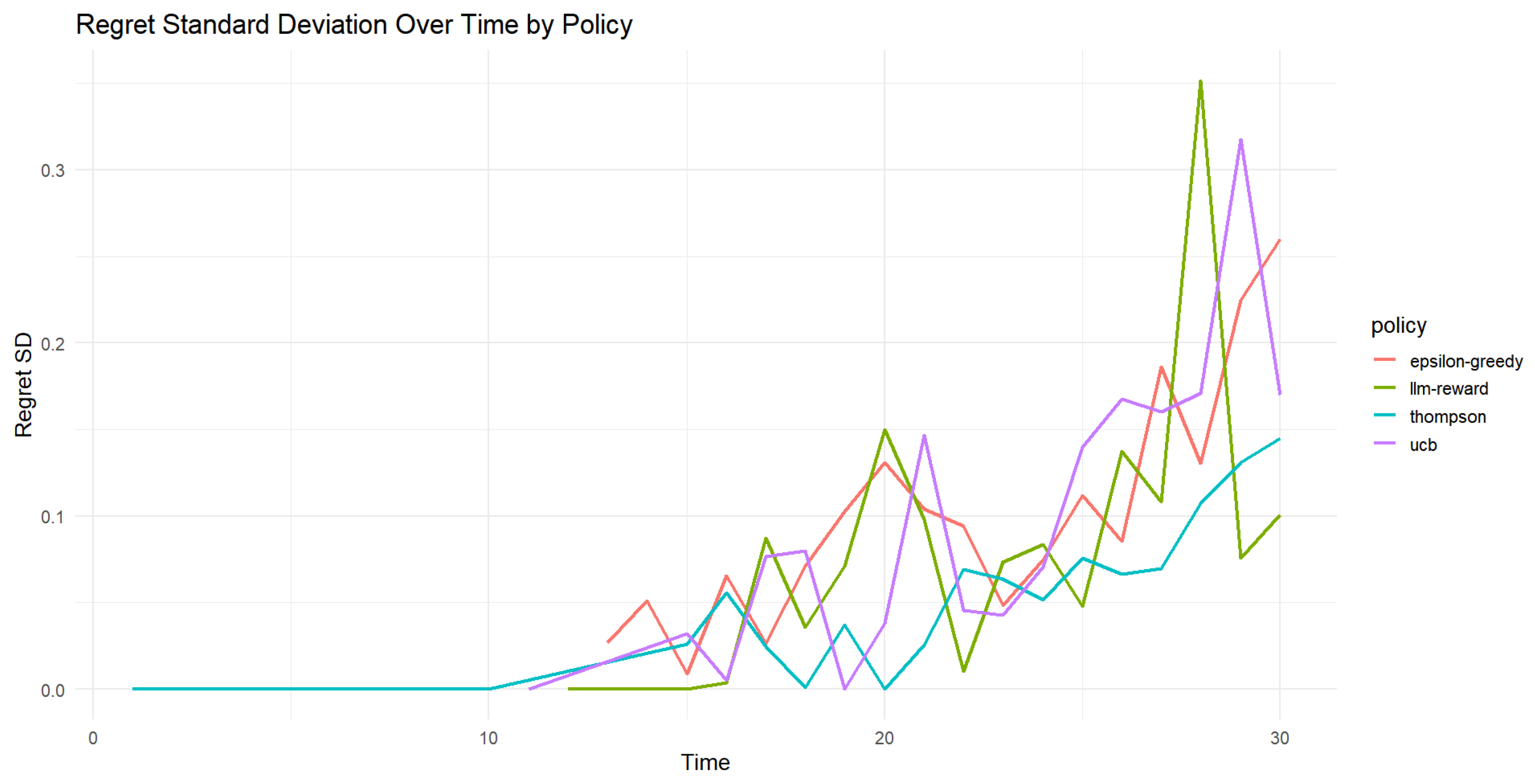
- Regret Variability (Figure 6)
4. Conclusions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Auer, P.; Cesa-Bianchi, N.; Fischer, P. Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 2002, 47, 235–256. [Google Scholar] [CrossRef]
- Langford, J.; Zhang, T. The Epoch-Greedy Algorithm for Multi-armed Bandits with Side Information. Adv. Neural Inf. Process. Syst. 2007, 20. [Google Scholar]
- Li, L.; Chu, W.; Langford, J.; Schapire, R.E. A contextual-bandit approach to personalized news article recommendation. In Proceedings of the 19th International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; Association for Computing Machinery: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Lai, T.L.; Robbins, H. Asymptotically efficient adaptive allocation rules. Adv. Appl. Math. 1985, 6, 4–22. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Srinivas, N.; Krause, A.; Kakade, S.M.; Seeger, M. Gaussian Process Optimization in the Bandit Setting: No Regret and Experimental Design. In Proceedings of the International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Agrawal, S.; Goyal, N. Thompson Sampling for Contextual Bandits with Linear Payoffs. In Proceedings of the International Conference on Machine Learning (ICML), Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Engle, R.F. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]
- Zakoian, J.-M. Threshold Heteroskedastic Models. J. Econ. Dyn. Control 1994, 18, 931–955. [Google Scholar] [CrossRef]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Czado, C. Analyzing Dependent Data with Vine Copulas: A Practical Guide with R; Springer: Berlin, Germany, 2019. [Google Scholar]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Olya, B.A.M.; Mohebian, R.; Moradzadeh, A. A new approach for seismic inversion with GAN algorithm. J. Seism. Explor. 2024, 33, 1–36. [Google Scholar]
- OpenAI. GPT-4 Technical Report. 2023. Available online: https://arxiv.org/abs/2303.08774 (accessed on 10 May 2025).
- Kim, J.-M. Gaussian Process with Vine Copula-Based Context Modeling for Contextual Multi-Armed Bandits. Mathematics 2025, 13, 2058. [Google Scholar] [CrossRef]
- Francq, C.; Zakoian, J.-M. GARCH Models: Structure, Statistical Inference and Financial Applications, 2nd ed.; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]


| Policy | Mean R | SD R | Mean Reg | SD Reg | Mean R | SD R | Mean Reg | SD Reg |
|---|---|---|---|---|---|---|---|---|
| LLM-Reward | 0.4440 | 0.0000 | 2.7300 | 0.1190 | 0.8730 | 0.0000 | 2.5400 | 0.1010 |
| Epsilon-Greedy | 0.4140 | 0.0992 | 2.9100 | 0.2700 | 0.8400 | 0.1110 | 2.5500 | 0.2600 |
| UCB | 0.0707 | 0.0000 | 3.4800 | 0.1830 | 0.4390 | 0.0000 | 3.1000 | 0.1700 |
| Thompson | 0.0707 | 0.0000 | 3.5800 | 0.0911 | 0.4390 | 0.0000 | 3.2600 | 0.1450 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-M. LLM-Guided Ensemble Learning for Contextual Bandits with Copula and Gaussian Process Models. Mathematics 2025, 13, 2523. https://doi.org/10.3390/math13152523
Kim J-M. LLM-Guided Ensemble Learning for Contextual Bandits with Copula and Gaussian Process Models. Mathematics. 2025; 13(15):2523. https://doi.org/10.3390/math13152523
Chicago/Turabian StyleKim, Jong-Min. 2025. "LLM-Guided Ensemble Learning for Contextual Bandits with Copula and Gaussian Process Models" Mathematics 13, no. 15: 2523. https://doi.org/10.3390/math13152523
APA StyleKim, J.-M. (2025). LLM-Guided Ensemble Learning for Contextual Bandits with Copula and Gaussian Process Models. Mathematics, 13(15), 2523. https://doi.org/10.3390/math13152523







