A Transfer Learning Approach for Diverse Motion Augmentation Under Data Scarcity

Abstract

Motion-capture data provide high accuracy but are difficult to obtain, necessitating dataset augmentation. To our knowledge, no prior study has investigated few-shot generative models for motion-capture data that address both quality and diversity. We tackle the diversity loss that arises with extremely small datasets (n ≤ 10) by applying transfer learning and continual learning to retain the rich variability of a larger pretraining corpus. To assess quality, we introduce MFMMD (Motion Feature-Based Maximum Mean Discrepancy)—a metric well-suited for small samples—and evaluate diversity with the multimodality metric. Our method embeds an Elastic Weight Consolidation (EWC)-based regularization term in the generator’s loss and then fine-tunes the limited motion-capture set. We analyze how the strength of this term influences diversity and uncovers motion-specific characteristics, revealing behavior that differs from that observed in image-generation tasks. The experiments indicate that the transfer learning pipeline improves generative performance in low-data scenarios. Increasing the weight of the regularization term yields higher diversity in the synthesized motions, demonstrating a marked uplift in motion diversity. These findings suggest that the proposed approach can effectively augment small motion-capture datasets with greater variety, a capability expected to benefit applications that rely on diverse human-motion data across modern robotics, animation, and virtual reality.

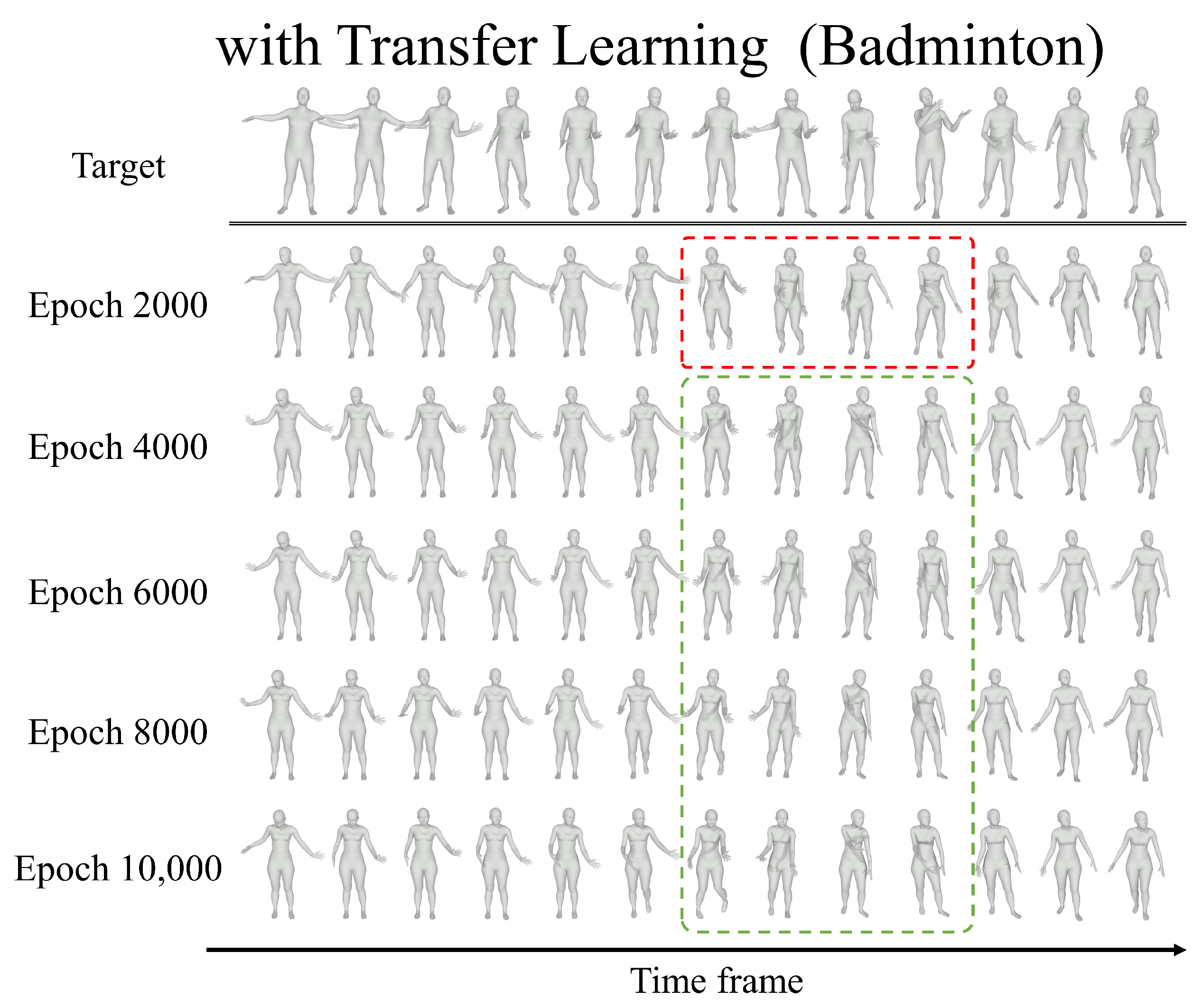
1. Introduction

Quantifying human motion through high-fidelity, marker-based motion-capture recordings remains pivotal for robotics, because these precise trajectories provide the kinematic ground truth required to model, predict, and replicate human movement across diverse tasks [1]. Anchoring control policies to accurate spatiotemporal data enables manipulators and social robots to navigate safely around people, while wearable exoskeletons can synchronize assistive torques with a user’s intent in real time. Large-scale motion libraries further power AI algorithms that synthesize realistic behaviors in virtual avatars, humanoid robots, and adaptive exoskeletons [2], thereby advancing metaverse interfaces and reinforcement-learning-based gait assistance [3]. In short, the continuing progress of modern robotics is strongly supported by the same high-precision, marker-based motion-capture datasets that furnish reliable ground truth for modeling and replicating human movement [1].

While marker-based motion-capture data provide the most important foundation for quantifying human movement, their limited availability makes data augmentation increasingly necessary [4]. Although this technique remains one of the most accurate ways to record motion, setting up the capture environment is expensive, and each session demands considerable time and skilled personnel. These constraints restrict the large-scale datasets that most AI methods still assume. The shortage is especially severe for uncommon or highly specialized movements that rarely appear in public repositories. These gaps hinder AI applications for specialized movements in wearable robot design [5], sports science [6], and AI-based motion prediction [7,8]. Augmentation techniques offer a practical way to enlarge small recordings without further capture sessions [9,10]. In short, because marker-based motion-capture data are both essential and scarce, augmenting limited, specialized datasets remains a pivotal step for advancing human-motion research.

As generative models have advanced, extensive research has been conducted to apply these techniques to motion-capture data, though most studies have focused on generating motions based on large-scale datasets. While these approaches have made significant contributions to producing high-quality human motions, they are not well-suited for augmenting specialized movements that cannot be obtained from public datasets, where researchers must collect their own limited samples for specific applications. Various fields, particularly biomechanics, have successfully applied generative models to address the challenges of motion-capture data acquisition, but these studies have primarily concentrated on fidelity while offering limited consideration of diversity in generated motions. Furthermore, these attempts have either not employed techniques tailored for few-shot learning or have lacked a comprehensive analyses of how these techniques affect the fidelity and diversity of generated motions and what their optimal application is. This limitation poses a significant challenge for augmenting marker-based datasets representing specific motions not included in open datasets, where collecting large amounts of data is impractical.

One of the challenging aspects of few-shot learning research for motion-capture data is that there are no optimized metrics for evaluating generated motion data from small motion-capture datasets. Evaluating generative models presents unique challenges compared to supervised learning tasks due to the absence of ground truth labels. Metrics like accuracy are unsuitable for quantitative assessment in such scenarios. In image generation research, this issue has been addressed through alternative evaluation methods like the Fréchet Inception Distance (FID) [11]. FID measures the similarity between distributions of real and generated images by extracting high-level features using a pretrained Inception v3 model, and it has been widely used as an indicator of fidelity and diversity. While FID has also been applied to evaluate generative models for motion synthesis, it has limitations when dealing with small sample sizes due to its reliance on normality assumptions and instability under such conditions. These limitations are particularly relevant when augmenting motion-capture datasets with limited original samples.

Alternative metrics such as Kernel Inception Distance (KID) [12] have been proposed to address FID’s instability with small datasets. Unlike FID, KID employs an unbiased estimator that remains stable even when working with limited samples, making it potentially more suitable for few-shot learning scenarios. However, KID still relies on the Inception model for feature extraction, which presents fundamental limitations when evaluating motion data. The Inception architecture was specifically designed and pretrained for image classification tasks, making it inherently unsuitable for capturing the temporal dynamics, biomechanical constraints, and kinematic relationships that characterize human motion. This architectural mismatch means that even with improved statistical stability, KID may not effectively capture the semantic quality and diversity of generated motion sequences, highlighting the need for motion-specific evaluation frameworks.

This study aims to analyze how few-shot learning techniques can be applied to motion data augmentation using generative models for uncommon and specialized motions and how these techniques can improve the fidelity and diversity of generated data. To our knowledge, this is the first study to systematically analyze the effects of few-shot learning techniques on the fidelity and diversity of generated data in marker-based motion-capture dataset augmentation using generative models and to determine the optimal application methods. To achieve this objective, we propose two key strategies: first, we apply transfer learning and Elastic Weight Consolidation (EWC), a continual learning technique, to motion-capture data augmentation; second, we introduce Motion Feature-Based Maximum Mean Discrepancy (MFMMD), which is well-suited for evaluating distributional distances between small-scale motion-capture datasets, and we use it to assess the quality of generated data.

In summary, this study makes several key contributions:

• Few-Shot Learning Framework for Motion Data Augmentation: We introduce the first systematic approach that applies few-shot learning techniques, specifically transfer learning and Elastic Weight Consolidation (EWC), to motion-capture data augmentation for uncommon and specialized motions, addressing the diversity constraints encountered with extremely limited dataset sizes.
• Comprehensive Analysis of Fidelity–Diversity Trade-Offs: To our knowledge, this is the first study to systematically analyze how few-shot learning techniques affect both the fidelity and diversity of generated data in marker-based motion-capture dataset augmentation, providing insights into optimal application methods for generative models.
• Motion Feature-Based Maximum Mean Discrepancy (MFMMD): We propose MFMMD as a novel evaluation metric specifically designed to assess semantic similarity between original and generated motion datasets effectively. Unlike existing metrics such as FID and KID, MFMMD remains stable even with limited samples by leveraging Maximum Mean Discrepancy combined with a motion-specific feature extractor, addressing the fundamental limitations of inception-based metrics for motion data evaluation.

2. Related Work

2.1. Human-Motion Generation

Research on generative models for human-motion synthesis has evolved along several complementary directions. Early studies learned large-scale motion corpora and embedded them in low-dimensional latent spaces to generate natural, diverse movements. Motegi et al. employed a convolutional auto-encoder for feature extraction and a variational auto-encoder (VAE) to model the latent probability distribution [13]. Their system produced realistic motions in a 32-dimensional space, with certain axes corresponding to controllable body parts such as the arms or legs.

Xi et al. addressed the difficulty of obtaining sufficient human movement data and the need for a generative model that controls the action type while maintaining authenticity and natural style variability [14]. They aimed to balance spatial and temporal information in CNN-based architectures and find a good pseudo-image representation for 3D skeletal data. They proposed a conditional Deep Convolutional Generative Adversarial Network (DC-GAN) applied to Tree Structure Skeleton Image (TSSI) pseudo-images, enabling the generation of qualitatively correct skeletal human movements for 60 action classes. They also modified the DC-GAN’s deconvolution operation to eliminate checkerboard artifacts and demonstrated the importance of joint reordering in TSSI for realistic skeletons.

Subsequently, Guo et al. addressed the task of generating 3D motion sequences conditioned on predefined action types [15]. To overcome the limitations of 2D modeling and the entanglement of joint coordinates with motion trajectories, they proposed a conditional temporal VAE based on a Lie-algebra representation. This formulation decouples skeletal anatomy, temporal dynamics, and scale; faithfully encodes anatomical constraints; mitigates motion “jitter”; and accelerates training. They also introduced the HumanAct12 dataset and refined the pose annotations of NTU-RGB-D.

In a related vein, Yu et al. tackled long-range skeleton-based action generation [16]. Observing that previous methods treated joints like image pixels and yielded distorted motions, they designed a self-attention-based Graph Convolutional Network (SA-GCN). By adaptively sparsifying a global action graph in the temporal domain, SA-GCN exhibits both computational efficiency and modeling power, generating high-quality long-range sequences directly from Gaussian noise and class labels without pretraining.

Petrovich et al. removed the need for an initial pose or seed sequence by formulating ACTOR, a Transformer encoder–decoder trained with a VAE objective [17]. Unlike autoregressive LSTM or GRU baselines that regress toward an average pose or drift over time, ACTOR outputs an entire sequence in a single pass and avoids such degeneration. It represents the first attempt to learn action-conditional sequence-level embeddings and can transform noisy monocular video estimates into realistic 3D motions while simultaneously de-noising them.

Moving beyond action labels, Guo et al. explored the challenging problem of generating 3D motion directly from text [18]. To satisfy the requirements of textual faithfulness, variable sequence length, and diversity, they introduced a two-stage pipeline—text-to-length sampling followed by text-to-motion generation—centered on a motion-snippet code that captures local semantic context. They further released HumanML3D, a large-scale dataset containing 14,616 motion clips paired with 44,970 textual descriptions.

To enhance expressiveness, Tevet et al. presented MotionCLIP, a 3D motion auto-encoder for which its latent space is aligned with CLIP [19]. By injecting CLIP’s rich semantic structure, the model yields a more continuous and disentangled motion manifold, enabling text-to-motion synthesis, out-of-domain actions, fine-grained editing, and understanding of abstract language commands.

The same authors subsequently proposed the Motion Diffusion Model (MDM), a classifier-free diffusion generator specialized for human motion [20]. Built on a Transformer backbone, MDM predicts the denoised sample at each diffusion step, permitting geometry-aware loss functions (e.g., position, foot-contact, velocity). Despite modest computational demands, the model achieves state-of-the-art results on text-to-motion and action-to-motion benchmarks and supports inpainting for motion completion and editing.

Most recently, Hu et al. identified slow sampling and error accumulation in diffusion- and GPT-based pipelines. Their Motion Flow Matching (MFM) model reduces sampling complexity from thousands of diffusion steps to only ten while retaining competitive performance [21]. As the first application of flow matching to human motion, MFM introduces “sampling trajectory rewriting,” an ODE-style framework that offers a novel paradigm for motion editing.

While these generative approaches produce high-fidelity motions via large-scale training, they do not address few-shot data-augmentation strategies for specialized actions—a critical gap given the difficulty of collecting motion-capture data for rare or complex behaviors.

2.2. Motion-Capture Data Augmentation

Human motion-capture data underpin a wide range of biomechanical studies and downstream applications, yet collecting high-quality recordings is time-consuming, expensive, and reliant on participant availability. These logistical constraints routinely produce datasets that are too small to unlock the full potential of modern deep-learning pipelines [22].

To alleviate this scarcity, early augmentation strategies applied simple numerical transformations—for example, injecting Gaussian noise into marker trajectories or synthesizing joint-angle curves [9,22]. Although such techniques inflate sample counts, they rarely preserve biomechanical realism and typically ignore coupled kinetic signals such as ground-reaction forces (GRFs) [22].

Recent research has therefore shifted toward generative deep-learning frameworks. Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs) can create synthetic motions that are visually and statistically similar to real recordings [9]. Bicer et al. used GANs to co-generate marker data and GRFs [22], whereas Perrone et al. demonstrated that VAEs, owing to their training stability, outperform GANs when only modest quantities of MoCap are available [23]. Maeda et al. further combined a VAE with inverse-kinematics correction to enforce physical plausibility [9].

Despite these advances, all existing approaches falter when confronted with truly extreme data scarcity—that is, “few-shot” regimes of fewer than a dozen sequences. Under such conditions GANs suffer from mode collapse, slashing output diversity, while VAEs still inherit biases from the limited priors embedded in the tiny training set. Physics-based post-processing can mitigate some artifacts but requires heavy computation and, in the case of inverse-kinematics pipelines, substantial manual annotation.

Crucially, no prior study has systematically investigated how different design choices in few-shot generative frameworks govern the resulting trade-off between motion fidelity and motion diversity when only a handful of samples are available. In other words, the literature lacks a principled analysis linking model design to downstream data quality and variability. This leaves open the question of which architectural or training strategies best preserve biomechanical realism while expanding the synthesized motion range under extreme data scarcity.

3. Materials and Methods

3.1. Datasets

In our study, we employ the AMASS dataset [24], which unifies multiple motion-capture collections under a common skeletal representation. AMASS comprises data from 500 subjects, totaling 3722 min and 17,916 motion sequences. For pretraining, we utilize the full AMASS corpus except for the HDM05 subset. HDM05 is itself included within AMASS but contains unique motions not found elsewhere in AMASS. During fine-tuning, we isolate HDM05 and focus on three specific motion categories: badminton (10 sequences), locomotion with weights (9 sequences), and kicking and punching (11 sequences) [25]. These represent unique motion types with limited occurrences in the AMASS collection. By training on these 30 sequences across diverse but sparse motion categories, we simulate a limited-data scenario and highlight the challenges of generating realistic specialized motions with minimal samples.

3.2. Data Processing

We used motion-capture data in the Skinned Multi-Person Linear (SMPL) format [26], which is the standard skeletal representation adopted by the AMASS dataset. We excluded 3D translation coordinates, hand joints, and facial expressions, as these aspects were beyond the scope of our research. To leverage the success of GAN models in image generation, we transformed the motion sequences into a single RGB image format—referred to as a pseudo-image [14,27]—as shown in Figure 1.

The complete motion sequence $\mathbf{S}$ is arranged as

$$\mathbf{S}=\left[\begin{array}{c}{\mathbf{s}}_1\\ ⋮\\ {\mathbf{s}}_T\end{array}\right]\in {\mathbb{R}}^{T\times 3J}$$

(1)

where T denotes the number of time frames, and J denotes the number of joints. Each row is defined by

$${\mathbf{s}}_t=\left[{\mathbf{v}}_{t,1}^{⊺},{\mathbf{v}}_{t,2}^{⊺},\dots ,{\mathbf{v}}_{t,J}^{⊺}\right]\in {\mathbb{R}}^{1\times 3J}$$

(2)

concatenating the axis–angle vectors ${\mathbf{v}}_{t,j}^{⊺}\in {\mathbb{R}}^{1\times 3}$ for all joints at frame t. Accordingly, ${\mathbf{s}}_t$ encodes the joint-angle data for frame t. The superscript ⊺ denotes the vector transpose operator, ensuring that each ${\mathbf{v}}_{t,j}$ is treated as a row vector when concatenated.

This $\mathbf{S}$ is converted into a pseudo-image tensor $\mathcal{I}$

$$\mathcal{I}\in {\mathbb{R}}^{3\times T\times J}$$

(3)

by reshaping and reassigning channels so that

$$\mathcal{I}(c,t,j)=v_{c,t,j}\left(c=1,2,3;t=1,\dots ,T;j=1,\dots ,J\right).$$

(4)

Each pixel in the pseudo-image represents a normalized component $v_{c,t,j}$ of the transposed motion vector ${\mathbf{v}}_{t,j}^{⊺}$. The first dimension c encodes the channel (R, G, and B) obtained from the three axis–angle components, the second dimension corresponds to the temporal index t, and the third dimension maps to the joint index j. This configuration enables the convolutional layers to learn temporal dynamics along the frame axis while simultaneously capturing spatial correlations across joints within the motion data.

However, converting T frames into an $H\times W$ image inevitably subsamples the temporal axis. Therefore, a lower pseudo-image resolution compresses more frames into each pixel row, increasing the chance of temporal detail loss. Smaller images (e.g., 128 × 128) boosted computational efficiency but caused noticeable motion degradation when sequences were reconstructed, whereas larger images preserved detail at the cost of higher memory and runtime. Pilot tests showed that resolutions below 256 × 256 produced motions that human evaluators judged as different actions, whereas 256 × 256 offered a balance—no severe perceptual loss yet appreciable savings over full-size rendering.

3.3. Elastic Weight Consolidation (EWC)

We introduce Elastic Weight Consolidation (EWC) to preserve source-domain diversity when fine-tuning a pretrained generator on a small motion-capture dataset. EWC was originally proposed for continual learning in classification models to alleviate the catastrophic forgetting that occurs when a neural network is trained sequentially on multiple datasets [28]. Inspired by the observation that the brain maintains previously acquired knowledge by reducing the plasticity of synapses that are vital for earlier tasks, EWC constrains changes in parameters that were important for previous tasks, thereby sustaining performance on both old and new tasks [28].

Beyond continual learning, EWC has also proven to be effective in transfer-based few-shot image generation, where it enables the production of diverse images from only a handful of samples [29]. Achieving strong performance on a new domain without sacrificing knowledge of the original domain hinges on accurately estimating each parameter’s importance. EWC accomplishes this by leveraging Fisher information, which quantifies how much information a dataset carries about the parameters of a probability distribution [28,29].

Parameters with higher Fisher information are considered more important to the source task and therefore receive stronger regularization during fine-tuning. Because Fisher information equals the variance of the score function—the gradient of the log-likelihood—it can be estimated as

$$F_i={\mathbb{E}}_x\left[{\left({\displaystyle \frac{\partial }{\partial {\theta }_{S,i}}}L(x\mid {\theta }_{S,i})\right)}^2\right]$$

(5)

Here, $F_i$ denotes the Fisher information associated with parameter ${\theta }_{S,i}$, and $L(x\mid \theta )$ represents the log-likelihood of $p(x\mid \theta )$. The symbol ${\theta }_{S,i}$ refers to the i-th parameter of the generator pretrained on the source data. In this work, we approximate L by applying a sigmoid activation to the discriminator output, and x corresponds to synthetic pseudo-images produced by the generator.

The EWC loss ${\mathcal{L}}_{\mathrm{ewc}}$ subsequently regulates each parameter during fine-tuning according to its Fisher information:

$${\mathcal{L}}_{\mathrm{ewc}}=\sum _i{F}_i{({\theta }_i-{\theta }_{S,i})}^2$$

(6)

During fine-tuning, the pretrained parameter ${\theta }_{S,i}$ remains fixed, and only the current parameter ${\theta }_i$ is updated.

To compute Fisher information, we transform the discriminator’s raw logits via a sigmoid activation. This mapping yields probabilistic outputs $p\left(x\right)\in (0,1)$ that represent the likelihood that a motion frame x originates from the generator’s distribution. The resulting Bernoulli likelihood ensures that the score function is derived from a valid probability model, thereby fulfilling the theoretical requirement for Fisher information.

Because the motion sequences are converted into pseudo-image form, they remain continuous and highly structured. The discriminator—already trained to separate real from synthetic trajectories—captures both temporal coherence and inter-joint correlations. Leveraging its sigmoid-based likelihood therefore provides a principled and sensitive weighting scheme when estimating how each generator parameter influences the probability of observing a specific motion sample.

3.4. Generative Model Implementation Details

For the data augmentation phase, we incorporate both adversarial loss and EWC loss to enhance diversity and preserve fidelity with limited data. Since we employ a Wasserstein GAN with a gradient penalty (WGAN-GP) framework, the adversarial component is based on Wasserstein loss. Pretraining was performed for 100 epochs with a batch size of 128 and a learning rate of 0.0001 using the Adam optimizer. Fine-tuning then proceeded for 10,000 epochs with a batch size of 10, maintaining the same learning rate and optimizer settings. To balance temporal resolution and computational efficiency, the motion-capture sequences were processed at 256 × 256 pixel resolution.

Pretraining was carried out on eight NVIDIA Tesla V100 cards. (NVIDIA Corporation, Santa Clara, CA, USA). Using approximately 18,000 motion sequence samples, 100 epochs required 17 h. Fine-tuning was executed on a single NVIDIA RTX 3090 (NVIDIA Corporation, Santa Clara, CA, USA). Optimizing the network for 10,000 epochs on 10 motion sequence samples completed in 8 h.

The total loss used in this study consists of adversarial loss and EWC loss, combined with a weight as shown in (7). ${\mathcal{L}}_{\mathrm{adv}}$ represents adversarial loss, while ${\mathcal{L}}_{\mathrm{ewc}}$ denotes EWC loss, which is designed to enhance diversity by retaining pretrained features in the source data. The term ${\lambda }_{\mathrm{ewc}}$ is the weighting factor that balances the contributions of adversarial loss and EWC loss during the training process.

$$\mathcal{L}={\mathcal{L}}_{\mathrm{adv}}+{\lambda }_{\mathrm{ewc}}{\mathcal{L}}_{\mathrm{ewc}}$$

(7)

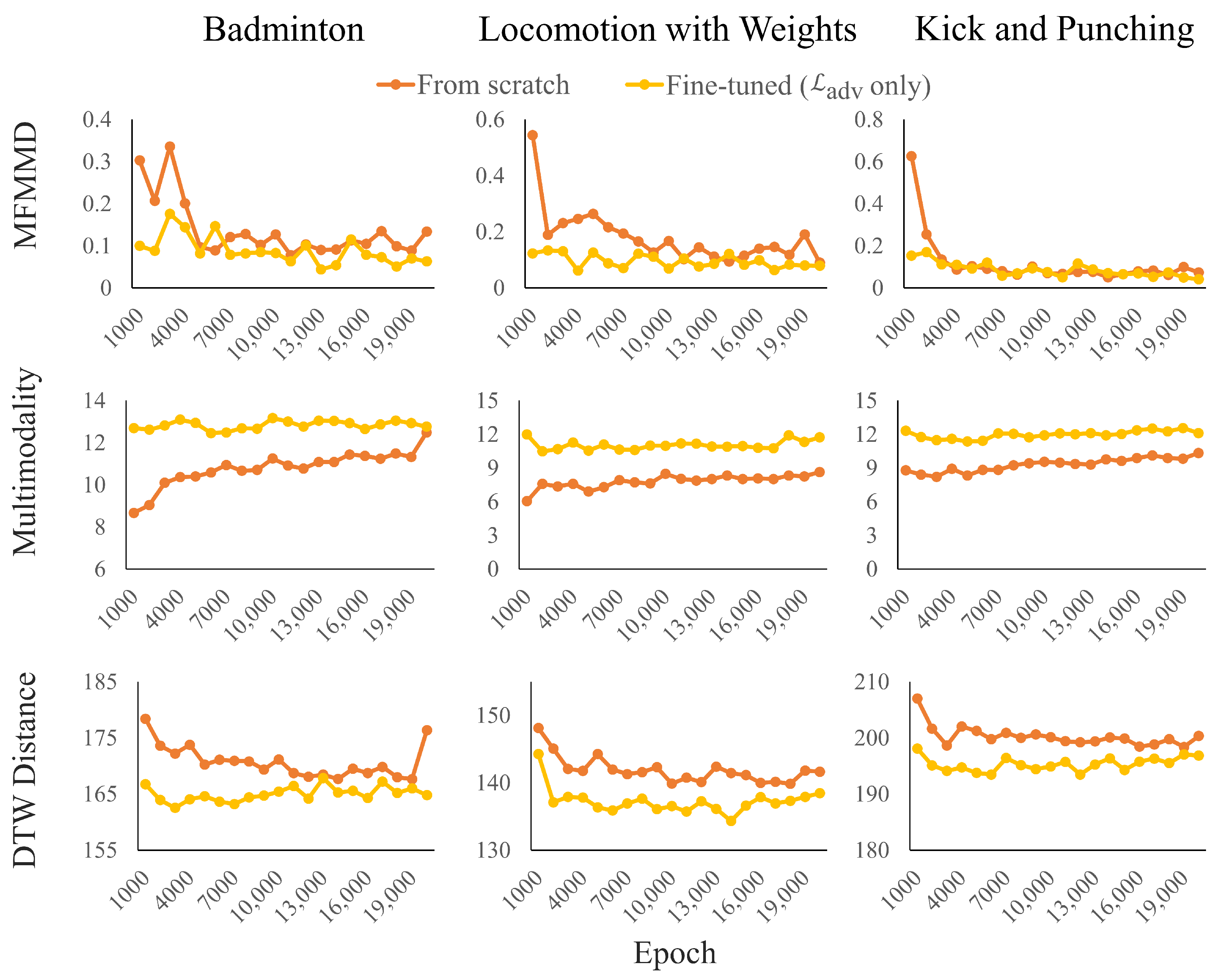
To assess the impact of transfer learning on the diversity of generated motion data, we compared two setups on a target dataset of 10 sequences: (1) a model trained from scratch using only adversarial loss and (2) a model pretrained on a source dataset of approximately 17,000 sequences and then fine-tuned using only adversarial loss. Furthermore, to evaluate the effect of EWC loss on motion diversity, we compared the adversarial-only transfer model with transfer models incorporating EWC loss at varying weights (${\lambda }_{\mathrm{ewc}}$ = 500; 5000; 50,000; and 500,000).

3.5. Framework

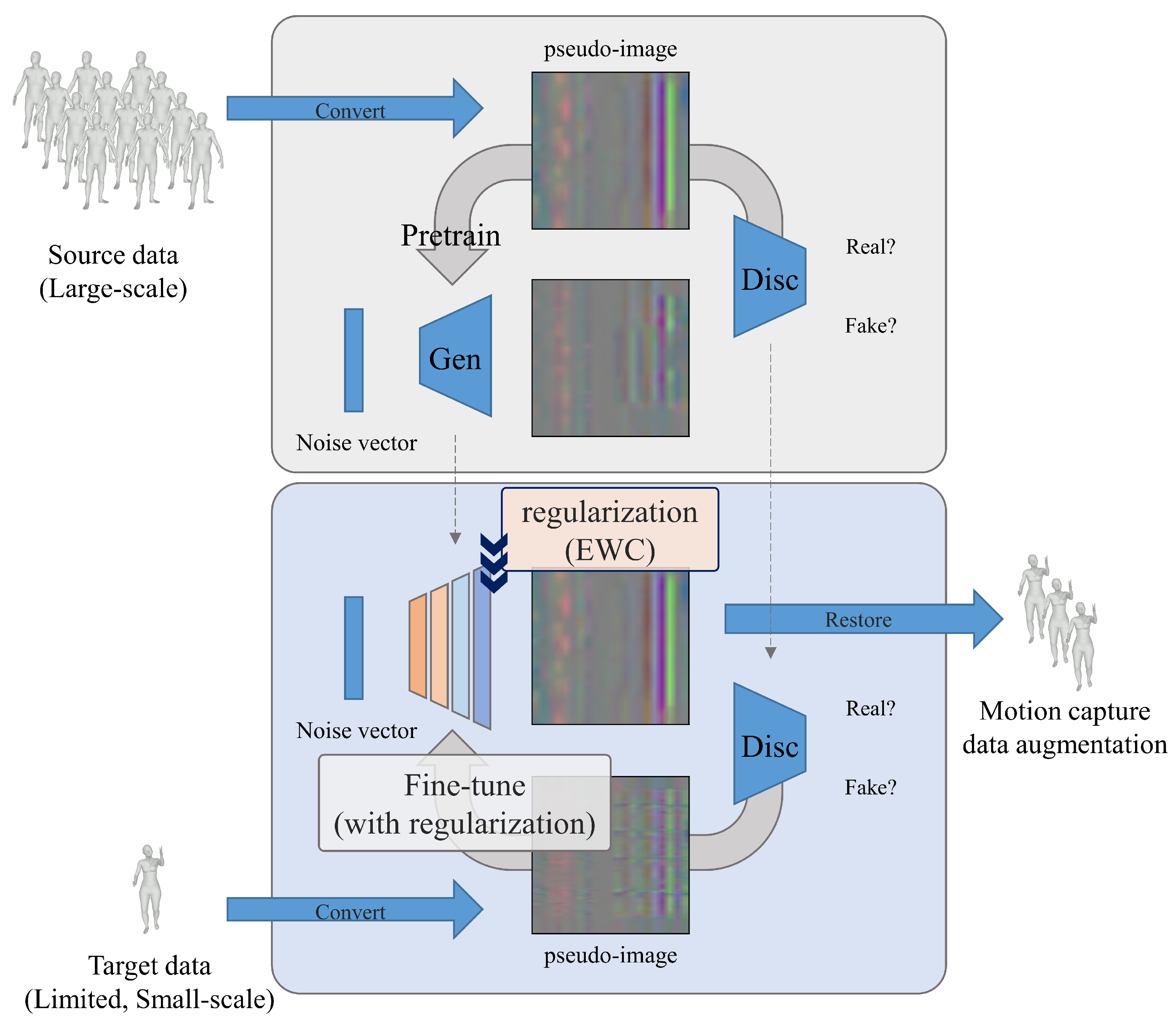
Figure 2 illustrates our proposed comprehensive framework for diverse motion augmentation under data scarcity conditions. The framework employs a two-stage transfer learning approach that leverages knowledge from large-scale source datasets to enhance the quality and diversity of generated motions when fine-tuning on extremely limited target datasets.

The framework begins with a pretraining phase where the generator learns fundamental human-motion patterns from a comprehensive source dataset containing diverse movement types. This pretraining stage enables the model to acquire rich representations of general human-motion dynamics, kinematic constraints, and anatomical relationships that serve as a robust foundation for subsequent specialization. The generator, implemented as a WGAN-GP architecture, learns to map random noise vectors to realistic motion sequences represented in pseudo-image format, capturing both spatial joint correlations and temporal motion patterns.

During the fine-tuning phase, the pretrained generator is adapted to the target domain containing only a handful of specialized motion sequences. To address the critical challenge of maintaining diversity while adapting to the limited target data, we introduce Elastic Weight Consolidation (EWC) as a regularization mechanism. The EWC regularizer strategically preserves the knowledge encoded in the pretrained model by constraining parameter updates based on their importance to the source task, as quantified by Fisher information values.

The Fisher information serves as a principled measure of parameter importance, with higher values indicating parameters that are more critical to the pretrained model’s performance on the source domain. During fine-tuning, parameters with high Fisher information values receive stronger regularization constraints, preventing them from deviating significantly from their pretrained values. This selective constraint mechanism allows the model to adapt to the target domain while retaining the diverse motion patterns learned during pretraining.

The framework’s effectiveness stems from its ability to balance two competing objectives: adaptation to the target domain and preservation of source domain diversity. By applying EWC regularization, the model can effectively leverage the rich variability present in the large-scale source dataset while gradually adapting to the specific characteristics of the target motions. This approach proves particularly beneficial in few-shot learning scenarios where traditional fine-tuning approaches often suffer from overfitting and catastrophic forgetting, leading to reduced diversity in generated motions.

The complete loss function integrates both adversarial training objectives and EWC regularization, with the regularization strength controlled by the hyperparameter ${\lambda }_{\mathrm{ewc}}$. This design enables fine-grained control over the trade-off between target domain adaptation and source domain knowledge preservation, allowing practitioners to adjust the framework’s behavior based on specific application requirements and the degree of specialization needed for the target motions.

3.6. Evaluation

In this study, we evaluated the quality of the generated motion data using two metrics: motion feature-based MMD and multimodality. The motion feature-based MMD and multimodality were computed using a Fully Convolutional Network (FCN)-based action classifier as a feature extractor. The details of each evaluation metric and the feature extractor are described below.

3.6.1. Feature Extractor

To compute motion feature-based MMD and multimodality, a feature vector must be extracted from the motion data. Since there is no standardized motion feature extractor, we employed an FCN-based action classifier, which has demonstrated strong performance in time-series classification [30]. While FCN represents a simple yet powerful framework for time-series data classification, its convolutional architecture inherently focuses on local feature patterns due to the nature of convolution operations. This characteristic may potentially limit the model’s ability to capture long-term temporal dependencies that span extended time horizons within motion sequences.

However, this limitation is mitigated in the context of human-motion recognition, where the most critical information for accurate motion understanding typically resides in the changes and patterns occurring within temporally adjacent frames. Fundamental biomechanical principles suggest that the most discriminative features for motion classification emerge from local temporal variations, such as joint velocity changes, and short-term coordination patterns. Consequently, the FCN’s emphasis on local temporal relationships aligns well with the inherent characteristics of human-motion data, making its potential limitations as a feature extractor for motion-capture sequences relatively constrained. This alignment between FCN’s architectural strengths and the temporal structure of human-motion data supports its effectiveness as a feature extraction mechanism for our evaluation framework.

3.6.2. Motion Feature-Based MMD

To estimate the distributional distance between the limited original motion data and the generated data, we employed a novel evaluation metric, motion feature-based MMD, which is derived from the Maximum Mean Discrepancy (MMD) [31]. While the Fréchet Inception Distance (FID) [15,20,32] has been widely used in prior studies, it is known to be unstable with respect to small sample sizes and requires a normality assumption [33]. Given the constraints of our study, MMD was chosen as a more suitable metric for evaluating the distribution of small-scale motion datasets.

For MFMMD, we applied a multi-scale Gaussian kernel to the extracted motion features $\mathbf{v}$. Let $\mathbf{V}=\{{\mathbf{v}}_1,{\mathbf{v}}_{\mathbf{2}},\dots ,{\mathbf{v}}_{\mathbf{m}}\}$ represent the motion feature set of real data and $\widehat{\mathbf{V}}=\{\widehat{{\mathbf{v}}_1},\widehat{{\mathbf{v}}_2},\dots ,\widehat{{\mathbf{v}}_n}\}$ denote the motion feature set of generated data. The motion feature-based MMD is formulated as follows:

$$\begin{array}{cc}\hfill {\mathrm{MMD}}_{\mathrm{motion}\mathrm{feature}}^2(\mathbf{V},\widehat{\mathbf{V}})=& {\displaystyle \frac{1}{m(m-1)}}\sum _{i\ne j}{k}_{\mathrm{multi}}({\mathbf{v}}_i,{\mathbf{v}}_j)\hfill \\ & +{\displaystyle \frac{1}{n(n-1)}}\sum _{i\ne j}{k}_{\mathrm{multi}}(\widehat{{\mathbf{v}}_i},\widehat{{\mathbf{v}}_j})-{\displaystyle \frac{2}{mn}}\sum _{i=1}^m\sum _{j=1}^n{k}_{\mathrm{multi}}({\mathbf{v}}_i,\widehat{{\mathbf{v}}_j})\hfill \end{array}$$

(8)

where the multi-scale Gaussian kernel is defined as

$$k_{\mathrm{multi}}(\mathbf{v},\widehat{\mathbf{v}})=\sum _{i=1}^{M}exp\left(-{\displaystyle \frac{\left|\right|\mathbf{v}-\widehat{\mathbf{v}}{\left|\right|}^2}{{\sigma }_i^2}}\right)$$

(9)

Here, M represents the number of kernels, and ${\sigma }_i^2$ denotes the bandwidth of each kernel.

In this study, we generated 1000 samples for each of the 10 real motion data sequences and calculated the MFMMD. The experiment was repeated 20 times. Additionally, the MFMMD values were multiplied by 1000 for easier readability.

3.6.3. Multimodality

To evaluate the diversity of motion data generated by our augmentation method, we also calculated a metric called multimodality [15,20,34]. Since the primary objective of this research is to enhance the diversity of generated motion data, higher multimodality values are considered desirable. Multimodality was calculated as the average distance across all combinations of motion features $\widehat{\mathbf{v}}$ and ${\widehat{\mathbf{v}}}^{\prime }$ from two sets of samples generated by the model. Each set contained $S_l$ samples. Similarly to the MFMMD evaluation, we generated 1000 samples per set ($S_l=1000$) and repeated the experiment 20 times.

$$\mathrm{Multimodality}={\displaystyle \frac{1}{S_l}}\sum _{i=1}^{S_l}{\parallel {\hat{\mathbf{v}}}_i-{\widehat{\mathbf{v}}}_i^{\prime }\parallel }_2$$

(10)

3.6.4. Dynamic Time Warping Distance

To provide a more intuitive fidelity measure that captures temporal alignment quality, we incorporated the Dynamic Time-Warping (DTW) distance [35] into our evaluation protocol. DTW distance offers a complementary perspective to MFMMD by explicitly measuring how well generated motion sequences preserve the temporal dynamics of the original data, making it particularly suitable for evaluating motion-capture data where temporal coherence is crucial.

To compute this metric, we first align each generated motion sequence with its corresponding ground-truth sequence using the DTW algorithm. The DTW algorithm finds the optimal alignment between two time series by allowing for temporal distortions while preserving the overall shape and order of the sequences. We then sum the DTW distances of all joint-angle trajectories within each sequence pair and average this value over every valid pair in the dataset. This approach provides a comprehensive assessment of temporal fidelity across all degrees of freedom in the skeletal representation.

The DTW distance is particularly valuable in our evaluation framework because it explicitly compensates for temporal shifts and variations in sequence timing that may occur during the generation process. Unlike point-to-point distance measures that require strict temporal correspondence, DTW offers a robust estimate of how closely the generated motions follow the original temporal patterns while allowing for natural variations in timing. This characteristic makes the DTW distance especially relevant for motion-capture data evaluation, where maintaining the natural flow and rhythm of human movement is essential for realistic augmentation.

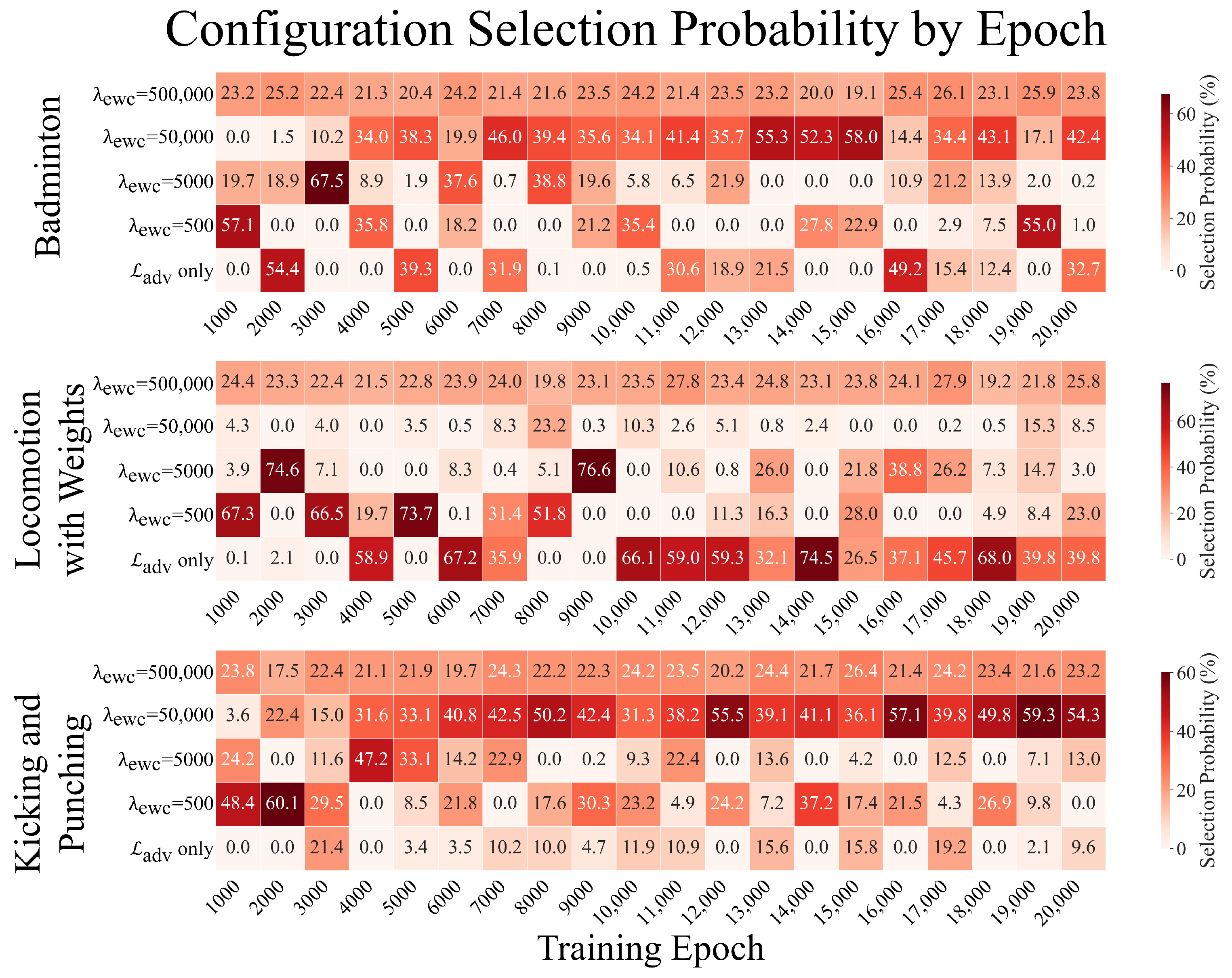
3.6.5. Monte Carlo-Based Sensitivity Analysis for Hyperparameter Optimization

To systematically evaluate the robustness of our ${\lambda }_{\mathrm{ewc}}$ optimization and assess the stability of our findings across different weighting schemes, we conducted a Monte Carlo-based sensitivity analysis. This approach quantifies how frequently each ${\lambda }_{\mathrm{ewc}}$ configuration emerges as optimal under randomly sampled weight combinations, providing insights into the reliability of our hyperparameter selection.

The sensitivity analysis proceeded through the following steps:

1.

Metric Standardization: For each training epoch, we standardized the three evaluation metrics (MFMMD, multimodality, and DTW) using Z-score normalization to ensure comparable scales across different measures.

2.

Direction Alignment: Since lower values are preferable for MFMMD and DTW distance while higher values are desirable for multimodality, we applied sign inversion to MFMMD and DTW scores:

$$\begin{array}{cc}\hfill & Z_{\mathrm{MFMMD}}=-(\mathrm{MFMMD}-{\mu }_{\mathrm{MFMMD}})/{\sigma }_{\mathrm{MFMMD}}\hfill \\ \hfill & Z_{\mathrm{multimodality}}=(\mathrm{multimodality}-{\mu }_{\mathrm{multimodality}})/{\sigma }_{\mathrm{multimodality}}\hfill \\ \hfill & Z_{\mathrm{DTW}}=-(\mathrm{DTW}-{\mu }_{\mathrm{DTW}})/{\sigma }_{\mathrm{DTW}}\hfill \end{array}$$

3.

Random Weight Sampling: We generated 2000 weight combinations using a symmetric Dirichlet distribution, Dir(1,1,1), ensuring unbiased sampling across the 3-simplex where $w_1+w_2+w_3=1$.

4.

Composite Score Calculation: For each weight combination w and ${\lambda }_{\mathrm{ewc}}$ configuration, we computed the following weighted sum:

$$\mathrm{Score}=w_1\times Z_{\mathrm{MFMMD}}+w_2\times Z_{\mathrm{multimodality}}+w_3\times Z_{\mathrm{DTW}}$$

(11)

5.

Optimal Configuration Identification: For each weight combination, we identified the ${\lambda }_{\mathrm{ewc}}$ configuration that achieved the highest composite score.

6.

Selection Probability Estimation: We calculated the proportion of weight combinations for which each ${\lambda }_{\mathrm{ewc}}$ configuration was selected as optimal, providing a robust measure of hyperparameter sensitivity.

4. Results

4.1. Transfer Learning Effects

Figure 3 compares the Motion Feature Maximum Mean Discrepancy (MFMMD), multimodality, and DTW distance metrics for motion data generated by two models: one trained from scratch on only ten samples and the other pretrained on approximately 20,000 samples and then fine-tuned. The pretrained model, having acquired knowledge of diverse human motions from the source data, demonstrates superior performance across all evaluation metrics from the earliest epochs.

The experimental results demonstrate that transfer learning provides substantial advantages over training from scratch, with benefits extending far beyond mere convergence acceleration to encompass fundamental improvements in motion quality and diversity.

4.1.1. Quantitative Performance Improvements

The pretrained model consistently outperforms the from-scratch approach across all evaluation metrics. In terms of fidelity, transfer learning produces samples with significantly lower MFMMD values, indicating that the generated motion distribution more closely matches the target dataset. The DTW distance analysis further confirms that pretrained models generate motions with superior temporal alignment and better preservation of original motion dynamics compared to from-scratch training. This improvement in temporal fidelity is particularly crucial for motion-capture data, where maintaining the natural flow and rhythm of human movement is essential for realistic augmentation.

Beyond fidelity improvements, the pretrained model demonstrates enhanced diversity capabilities, yielding higher multimodality scores that reflect the rich variability present in the source dataset. This indicates successful leverage of diverse motion patterns learned during pretraining to generate a wider variety of motions, even when fine-tuned on extremely limited target data.

4.1.2. Motion Quality and Biomechanical Realism

Transfer learning not only accelerates convergence but fundamentally enhances the quality of generated motion sequences compared to models trained from scratch. As illustrated in Figure 4, the qualitative differences extend beyond training efficiency to encompass critical aspects of motion realism and biomechanical plausibility.

Models trained from scratch frequently generate motions that violate basic physical constraints and anatomical limitations. In the badminton dataset, the from-scratch model fails to properly represent the smashing motion, as highlighted by the red dashed regions, while the fine-tuned model successfully captures this specialized athletic movement. Similarly, when generating locomotion with weights motions, the from-scratch approach produces sequences where legs overlap in biomechanically impossible configurations. Most critically, in kicking and punching motion generation, the from-scratch model creates sequences where one leg penetrates through another—a clear violation of physical reality that would never occur in actual human movement.

4.1.3. Convergence Speed and Training Efficiency

The temporal analysis of training progression reveals significant differences in convergence patterns between the two approaches. Qualitative visualizations demonstrate that from-scratch training requires approximately 6000 epochs to converge toward recognizable badminton serve postures (Figure 5), while pretrained models achieve similar target motions much more rapidly at approximately 4000 epochs (Figure 6). This accelerated convergence, combined with superior metric performance throughout the training process, establishes transfer learning as a robust foundation for motion augmentation tasks under data scarcity conditions.

4.1.4. Implications for Motion Generation

These findings underscore that transfer learning serves as a critical mechanism for ensuring the generation of anatomically plausible and biomechanically realistic motion sequences. The combination of improved fidelity, enhanced diversity, and accelerated convergence represents a significant advantage over training from scratch, where models typically struggle with limited expressiveness, poor temporal coherence, and fundamental violations of physical constraints. This comprehensive improvement addresses the core challenges encountered when augmenting specialized motion datasets with extremely limited samples.

4.2. Application of the Elastic Weight Consolidation Loss

In addition to simple fine-tuning, we explored the effect of incorporating the EWC loss—a technique that is widely used in continual learning [28] and previously applied to GANs with limited data [29]—to enhance the diversity of generated motions. EWC loss leverages each parameter’s Fisher information as an importance metric, penalizing changes to critical parameters while allowing less important ones to adapt. This approach preserves the pretrained model’s core knowledge during fine-tuning.

By integrating EWC loss, we aim to mitigate overfitting to the target dataset and encourage greater diversity in the generated motions. Figure 7 plots multimodality and MFMMD, respectively, for different values of the EWC weight ${\lambda }_{\mathrm{ewc}}$. As ${\lambda }_{\mathrm{ewc}}$ increases, the model retains more of the source data’s diversity, yielding higher multimodality. However, a trade-off becomes apparent: A higher ${\lambda }_{\mathrm{ewc}}$ also slightly increases MFMMD, indicating a modest shift away from the target distribution. This trade-off is visually confirmed in Figure 8, where higher ${\lambda }_{\mathrm{ewc}}$ values lead the model to generate motions that are somewhat less similar to those in the target dataset.

While the MFMMD and multimodality metrics demonstrate consistent trends across different motion types, the DTW distance exhibits notably distinct behavior, particularly for the locomotion-with-weights dataset in Figure 7. Unlike other motion categories, the locomotion-with-weights sequences show significantly lower DTW distance values and remain relatively unresponsive to variations in EWC loss applications. This distinctive pattern can be attributed to the inherently limited diversity within the locomotion-with-weights dataset, where the constrained range of motion variations results in lower average DTW distances between generated and original sequences. The reduced diversity in this dataset also necessitates larger ${\lambda }_{\mathrm{ewc}}$ values compared to other motion categories to effectively suppress overfitting during fine-tuning, as the model requires stronger regularization to prevent converging to the narrow distribution of available samples. These findings highlight a critical consideration for maximizing the effectiveness of the proposed augmentation approach: practitioners must ensure that target datasets are sufficiently diverse to avoid overly constrained distributions. In cases where datasets with limited diversity have already been collected, compensatory measures such as applying larger ${\lambda }_{\mathrm{ewc}}$ values become essential to achieve optimal augmentation results and prevent the model from collapsing into overly specific motion patterns.

4.3. Monte Carlo Sensitivity Analysis Results

Figure 9 presents the selection probabilities for each ${\lambda }_{\mathrm{ewc}}$ configuration across different training epochs. These probabilities represent the fraction of 2000 randomly sampled weight combinations for which each configuration emerged as optimal.

Figure 10 illustrates the evolution of selection probabilities across training epochs. The prominence of ${\lambda }_{\mathrm{ewc}}=50,000$ (shown in purple) throughout the training process confirms its consistent superiority under various evaluation criteria weightings. The relatively stable selection probabilities after epoch 10,000 suggest convergence to a stable hyperparameter ranking.

The results demonstrate that ${\lambda }_{\mathrm{ewc}}$ = 50,000 consistently exhibits the highest selection probability across most training epochs, indicating robust performance across diverse weighting schemes. This finding supports our primary conclusion that ${\lambda }_{\mathrm{ewc}}$ = 50,000 provides the optimal balance between fidelity and diversity for motion augmentation tasks.

5. Discussion

5.1. Research Objectives and Expected Outcomes

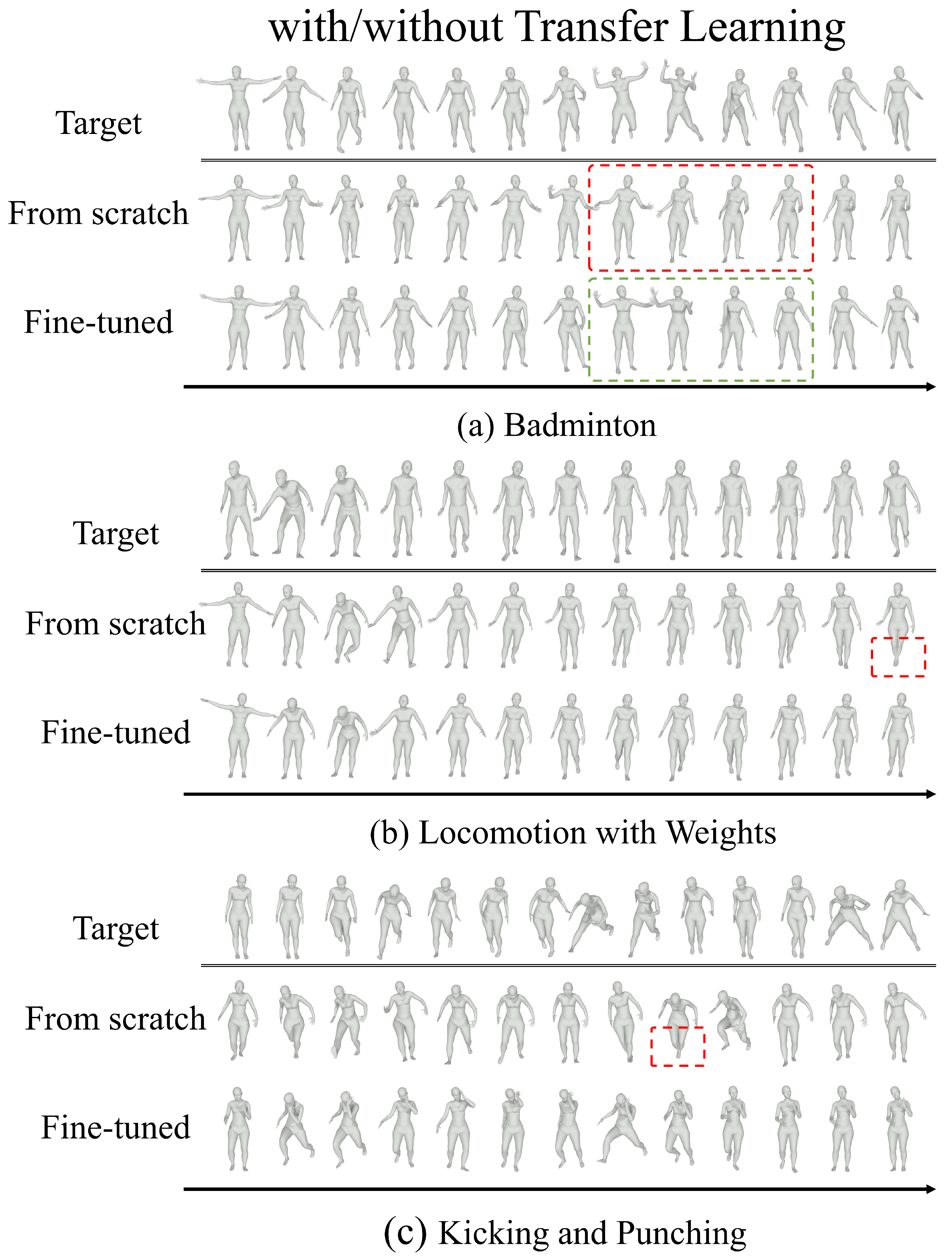
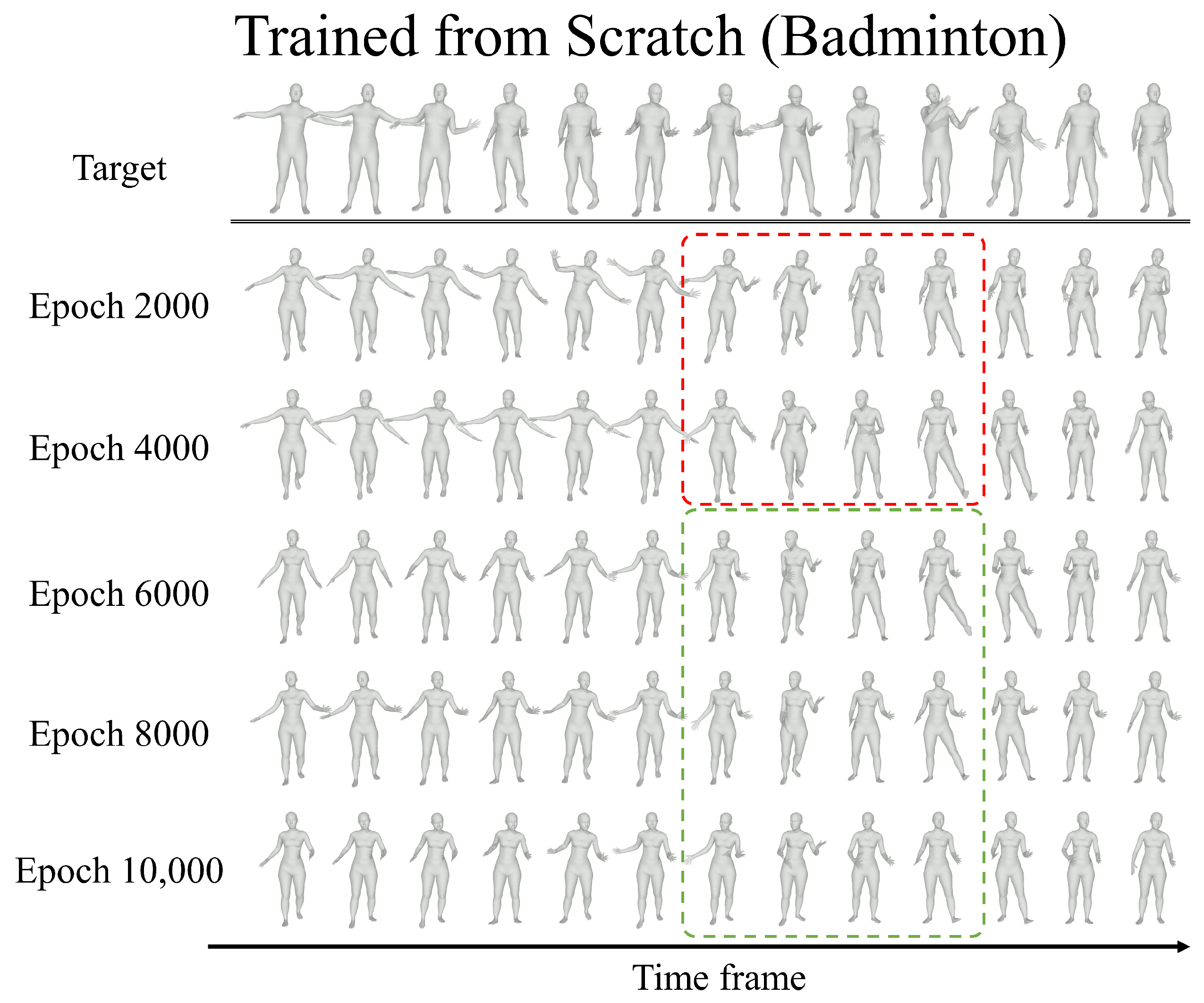
In this study, we investigate whether transfer learning and the Elastic Weight Consolidation (EWC) loss can enhance the diversity of motions generated by a generative adversarial network (GAN) trained on an extremely small set of motion-capture samples. Although the target dataset itself contains very few examples, we show that leveraging the diversity of a large source dataset and preserving its critical features via the EWC loss substantially increases the variability of the augmented target motions.

The Monte Carlo sensitivity analysis strongly supports ${\lambda }_{\mathrm{ewc}}$ = 50,000 as the optimal hyperparameter choice, demonstrating consistent superiority across diverse weighting schemes and training epochs. This probabilistic validation enhances the generalizability of our findings and provides practitioners with confidence in applying our methodology to their specific applications.

Our approach enables the augmentation of rare or hard-to-acquire motions—those not readily available in public datasets—by collecting only a handful of motion-capture sequences and synthesizing additional samples. This capability reduces the complexity, time, and labor required for extensive motion-capture campaigns while still producing a wide range of specialized actions.

As artificial intelligence continues to advance, both the size and diversity of training data remain core determinants of model performance. Marker-based motion capture is costly and resource-intensive, making it difficult to assemble large datasets, particularly for niche or proprietary motions. Although state-of-the-art AI methods in action recognition, motion prediction, and text-to-motion generation excel on movements included in their training sets, they struggle to generalize to unseen actions. Addressing the challenge of adding data for previously untrained motions is therefore crucial.

The techniques presented here not only improve the usability and performance of AI models that rely on motion-capture data but also generalize beyond the specific WGAN-GP framework used in our experiments. Transfer learning and EWC loss can be applied to a broad spectrum of generative models, suggesting that future adaptations may yield even higher quality and greater diversity in synthesized motion data.

5.2. Limitations

5.2.1. Transfer Learning Characteristics of Motion Versus Image Data

While augmenting a GAN’s adversarial loss with EWC loss increases the diversity of generated motions, it also tends to push the outputs away from the target distribution. Empirically, we observe an increase in MFMMD between generated and real target motions, and our qualitative evaluations confirm a semantic drift in the synthesized sequences.

We attribute this limitation to fundamental differences in how Fisher information is distributed across network parameters when modeling motion data versus image data. In convolutional image generators, early layers typically encode overall structure and style, whereas later layers capture fine details [36]. Figure 11a shows that the average Fisher information per layer is substantially higher in the later layers of our motion generator. Consequently, the EWC penalty preserves these detail-oriented parameters during fine-tuning, forcing adaptation to occur primarily in the early layers that govern global motion patterns.

In image-based GANs enhanced with EWC loss, such as the model in [29], this behavior proves advantageous for tasks like facial style transfer: The network maintains the essential facial structure (eyes, nose, and mouth) while adjusting style in the initial layers, thereby achieving both closeness to the target domain and increased diversity. By contrast, our motion-to-pseudo-image conversion (Figure 11b) reveals that while global motion trajectories remain similar after fine-tuning, detailed joint movements deviate. Because the parameters responsible for these details are heavily constrained by high Fisher information, the model cannot adequately adapt them to the target domain. This constraint explains why, in our experiments, multimodality improves but MFMMD also increases.

5.2.2. Data-Quality Sensitivity

Because the target set typically contains fewer than a dozen sequences, even one low-quality sample (e.g., motion-tracking drift or occlusion) can disproportionately skew the learned distribution and degrade both fidelity and diversity. We caution that this risk necessitates strict preprocessing or outlier filtering, especially when only a handful of examples are available.

5.2.3. Dependence on Large-Scale Pretraining

Our approach presumes access to a closely related, high-volume source dataset for pretraining. Consequently, it is not applicable to domains where no comparable repository exists, such as specialized animal-motion capture. We explicitly note that the method cannot be transferred to those scenarios without first curating a sufficiently large surrogate corpus.

5.3. Future Works

5.3.1. Motion-Aware Fisher Information Estimation for Few-Shot Learning

Current Fisher information estimation relies on discriminator outputs designed for pseudo-image representations, which may not effectively capture the biomechanical constraints and temporal dependencies inherent in human motion. Future research should develop motion-aware Fisher information estimators that account for joint hierarchies, kinematic chains, and anatomical constraints specific to human movement.

Advanced approaches could incorporate skeletal topology awareness into Fisher information computation, weighting parameters based on their influence on biomechanically critical joints (e.g., spine, pelvis) versus peripheral joints. This motion-specific parameter importance assessment could significantly improve diversity preservation during few-shot fine-tuning by ensuring that anatomically meaningful motion patterns are retained from the source domain.

5.3.2. Adaptive Regularization for Motion-Capture Data Scarcity

The fixed ${\lambda }_{\mathrm{ewc}}$ weighting approach presents limitations when target datasets exhibit varying degrees of motion complexity and diversity. Future work should investigate adaptive regularization schemes that automatically adjust the EWC strength based on target dataset characteristics, such as motion complexity, joint coordination patterns, and temporal variability.

Motion complexity metrics could guide regularization strength selection, with simpler repetitive motions (e.g., walking cycles) requiring stronger regularization to prevent overfitting, while complex multi-joint coordination tasks (e.g., sports movements) benefiting from reduced constraints to allow adaptation. This approach would eliminate the need for manual hyperparameter tuning and provide more robust augmentation across diverse motion-capture scenarios.

5.3.3. Hierarchical Motion Representation for Few-Shot Transfer

Current pseudo-image representations may lose critical hierarchical relationships between body segments that are essential for realistic motion generation. Future research should explore hierarchical motion encodings that explicitly preserve joint parent–child relationships and kinematic dependencies during few-shot learning.

Multi-scale temporal modeling could address the challenge of capturing both local joint movements and global coordination patterns within limited sample scenarios. This approach would involve developing specialized architectures that process motion data at multiple temporal resolutions, enabling effective transfer of both fine-grained joint dynamics and overall movement strategies from source to target domains.

5.3.4. Motion-Capture Quality Assessment and Data Curation

Given the extreme sensitivity of few-shot learning to data quality, future work should develop automated quality assessment frameworks specifically designed for motion-capture data curation in augmentation pipelines. These systems would detect and filter problematic sequences (marker drift, occlusions, and anatomical violations) before they contaminate the limited target datasets.

Biomechanical plausibility scoring could be integrated into the data preprocessing pipeline, ensuring that only physiologically realistic motion sequences are used for few-shot learning. This quality assurance mechanism becomes critical when working with specialized motions where even a single corrupted sequence can significantly impact augmentation performance.

5.3.5. Cross-Domain Motion Transfer for Specialized Applications

The methodology’s applicability to cross-domain motion transfer presents significant opportunities for specialized applications where direct motion capture is challenging or impossible. Future research should investigate transfer learning approaches that bridge different motion-capture modalities (e.g., optical to inertial sensor data) or adapt motions across different subject populations (e.g., able-bodied to impaired movement patterns).

Domain-specific adaptation techniques could enable the augmentation of highly specialized motion datasets in fields such as rehabilitation robotics, occupational ergonomics, and adaptive prosthetics, where collecting large-scale training data is particularly challenging due to ethical constraints and participant availability.

5.3.6. Evaluation Metrics for Few-Shot Motion Augmentation

The development of motion-specific evaluation frameworks tailored for few-shot learning scenarios represents a critical research direction. Current metrics may not adequately capture the nuanced requirements of motion augmentation, particularly regarding the preservation of biomechanical constraints and the assessment of motion diversity in extremely limited sample settings.

Future work should establish standardized benchmarking protocols for few-shot motion augmentation that incorporate biomechanical validity assessments, temporal coherence measures, and diversity quantification specifically designed for motion-capture data. These comprehensive evaluation frameworks would enable more reliable comparisons of augmentation techniques and facilitate the development of improved methods for specialized motion synthesis applications.

6. Conclusions

In this work, we demonstrated that combining transfer learning with Elastic Weight Consolidation (EWC) substantially enhances the diversity of motion-capture data generated by a GAN trained on very limited samples. Although the pretrained model yields lower MFMMD and higher multimodality than a from-scratch counterpart, the addition of EWC introduces a trade-off, modestly increasing the distance from the target distribution. Our Fisher information analysis reveals that detail-oriented parameters in later layers are heavily constrained by EWC, limiting the model’s ability to adapt fine movements. To address these challenges, we propose future directions, including fixed-length motion patches, transformer-based generators, diffusion-model frameworks augmented with regularization techniques like EWC, and the application of pretrained motion classifiers with likelihood functions to estimate Fisher information more accurately. Collectively, our findings provide a promising foundation for generating diverse, high-quality motion data from few samples and point toward tailored few-shot learning strategies for motion capture.