Rainfall Forecasting Using a BiLSTM Model Optimized by an Improved Whale Migration Algorithm and Variational Mode Decomposition
Abstract
1. Introduction
2. Materials and Methods
2.1. VMD
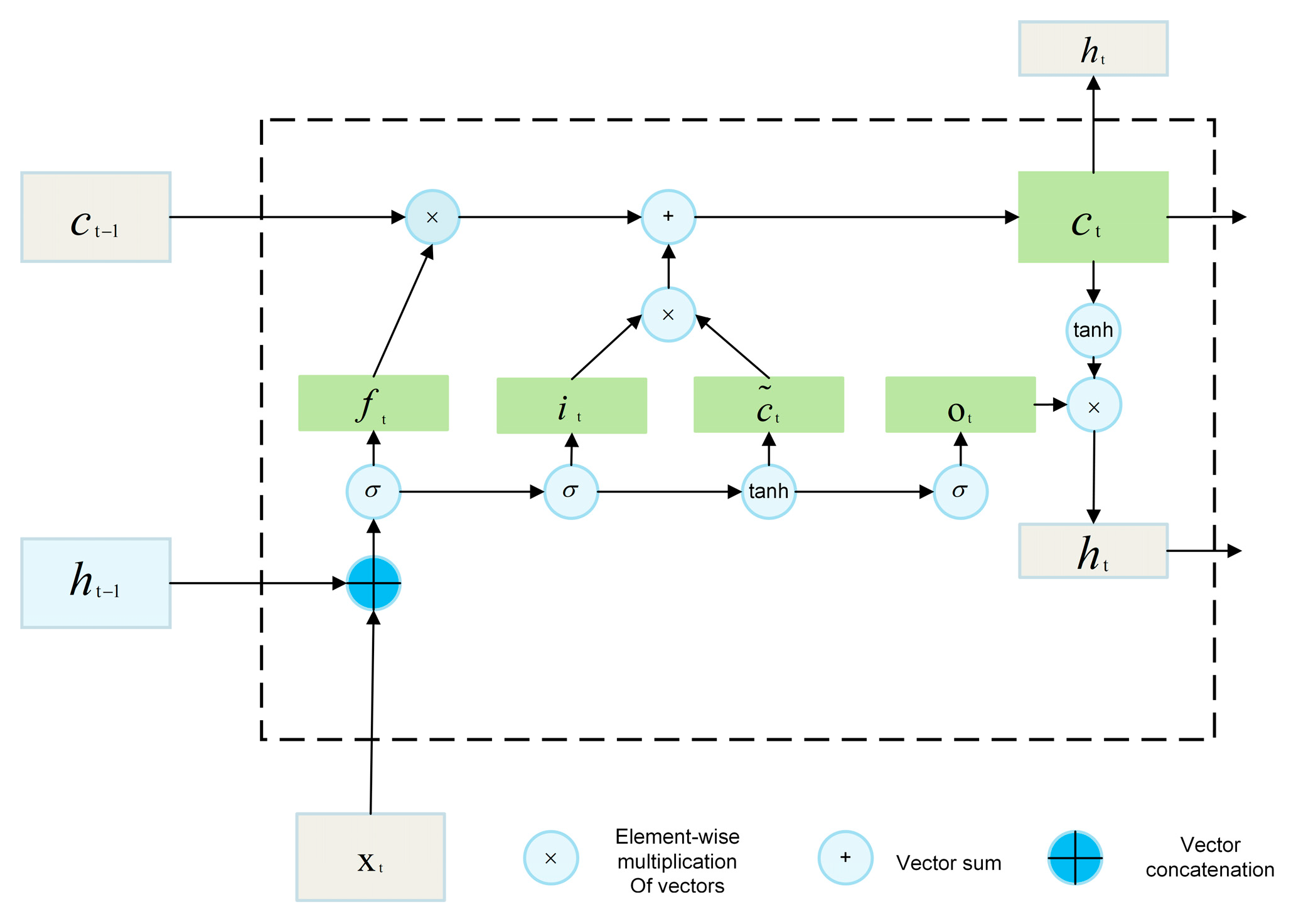
2.2. Rainfall Prediction Model: BiLSTM
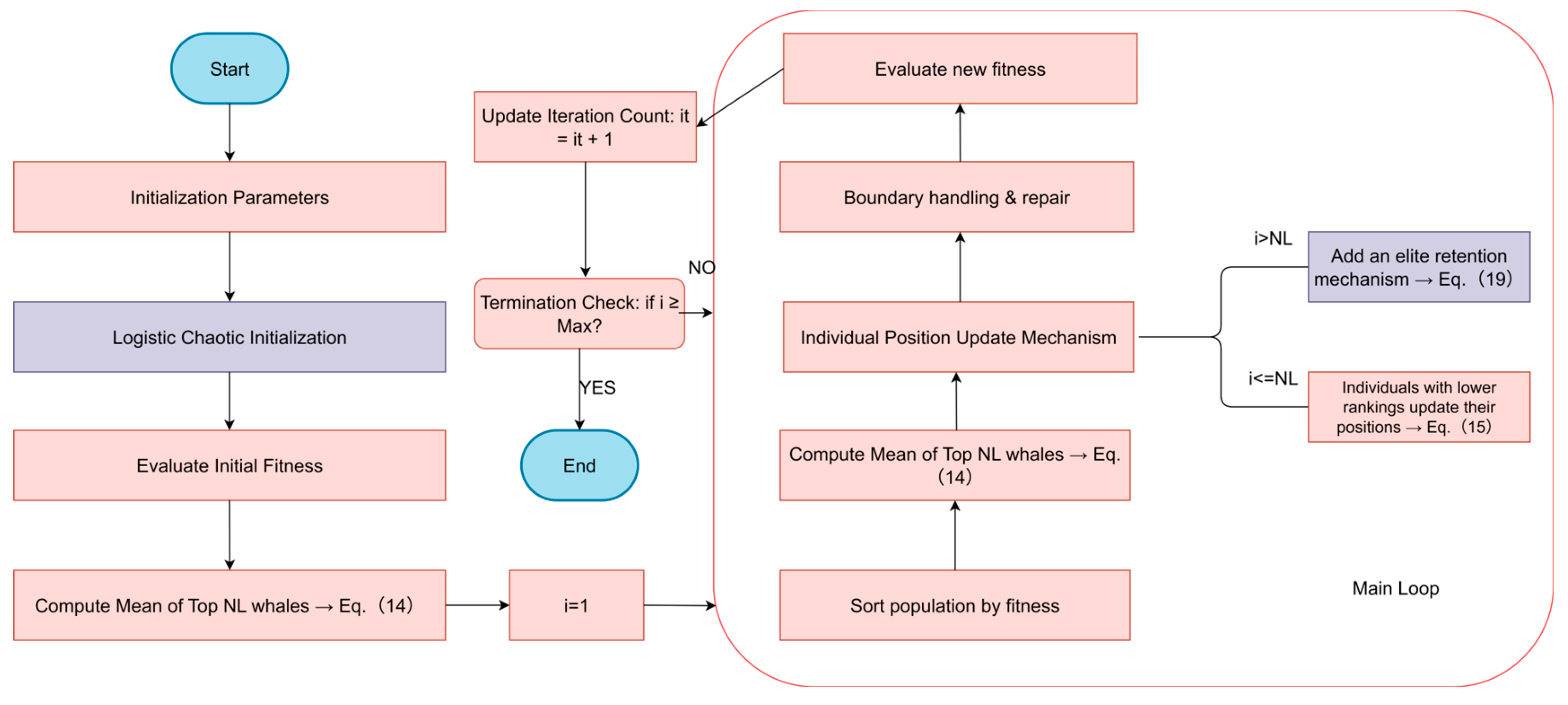
2.3. IWMA
2.3.1. The Original WMA
- Population initialization phase
- 2.
- Following Phase for Inexperienced Whales
- denotes the new position of the i-th non-leader individual;
- rand(1,D) represents a uniformly distributed random number within the interval [0, 1];
- denotes the Hadamard product;
- is the current best solution in the population;
- is the total population size, and is the number of leader individuals.
- 3.
- Exploration by Experienced Whales
- : random vectors with values in the interval [0, 1];
- : the lower and upper bounds of the search space.
2.3.2. Proposed IWMA
- Chaotic Mapping Mechanism
- 2.
- Elite Retention Mechanism
- : the mean position of the current leader individuals.
- : the position of the globally optimal individual.
- : random vectors within the range [0, 1] in D-dimensional space.
3. Results and Discussion
3.1. IWMA Performance Verification Experiments
3.1.1. Benchmark Functions
3.1.2. Ablation Analysis of the IWMA
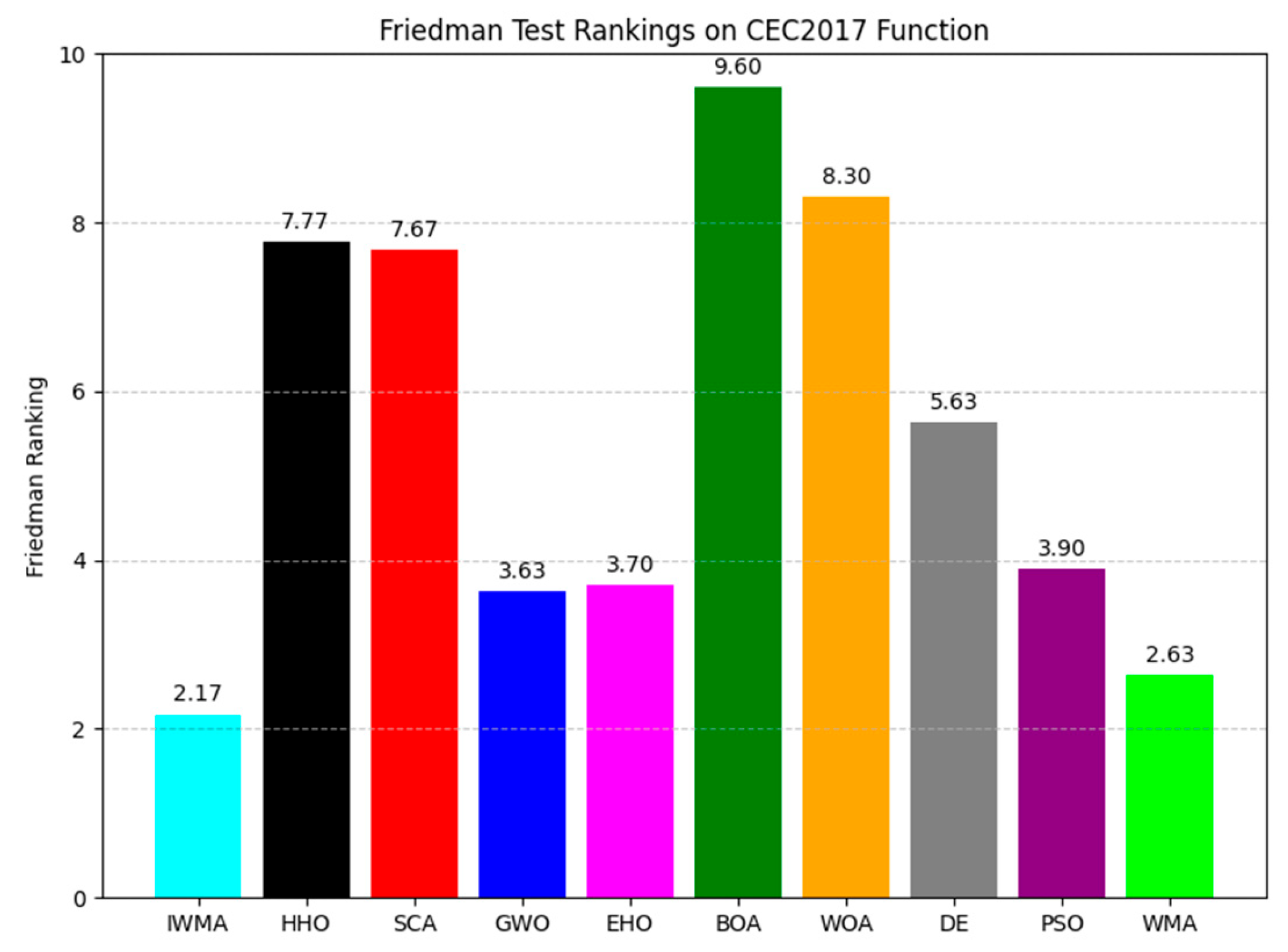
3.1.3. Comparison with Other Algorithms
- Harris hawks optimization (HHO) [38];
- Sine cosine algorithm (SCA) [39];
- Grey wolf optimization (GWO) [40];
- Elk herd optimization (EHO) [41];
- Butterfly optimization algorithm (BOA) [42];
- Whale optimization algorithm (WOA) [43];
- Particle swarm optimization (PSO) [44];
- Differential evolution (DE) [45].
3.2. VMD-IWMA-BiLSTM Framework for Rainfall Forecasting
3.2.1. Data Source and Missing Value Handling
3.2.2. VMD Decomposition
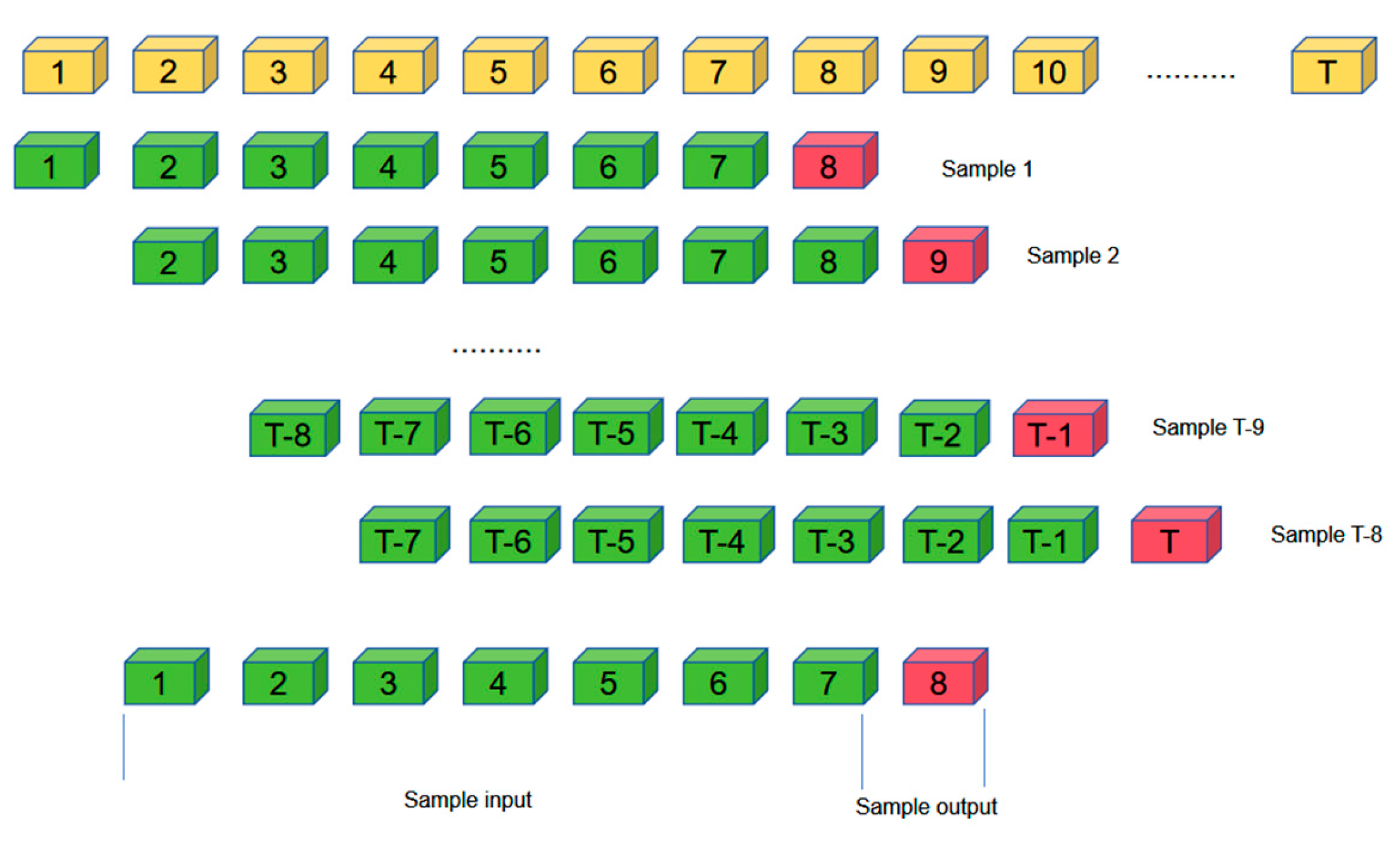
3.2.3. Sample Making
3.2.4. Data Normalization Processing
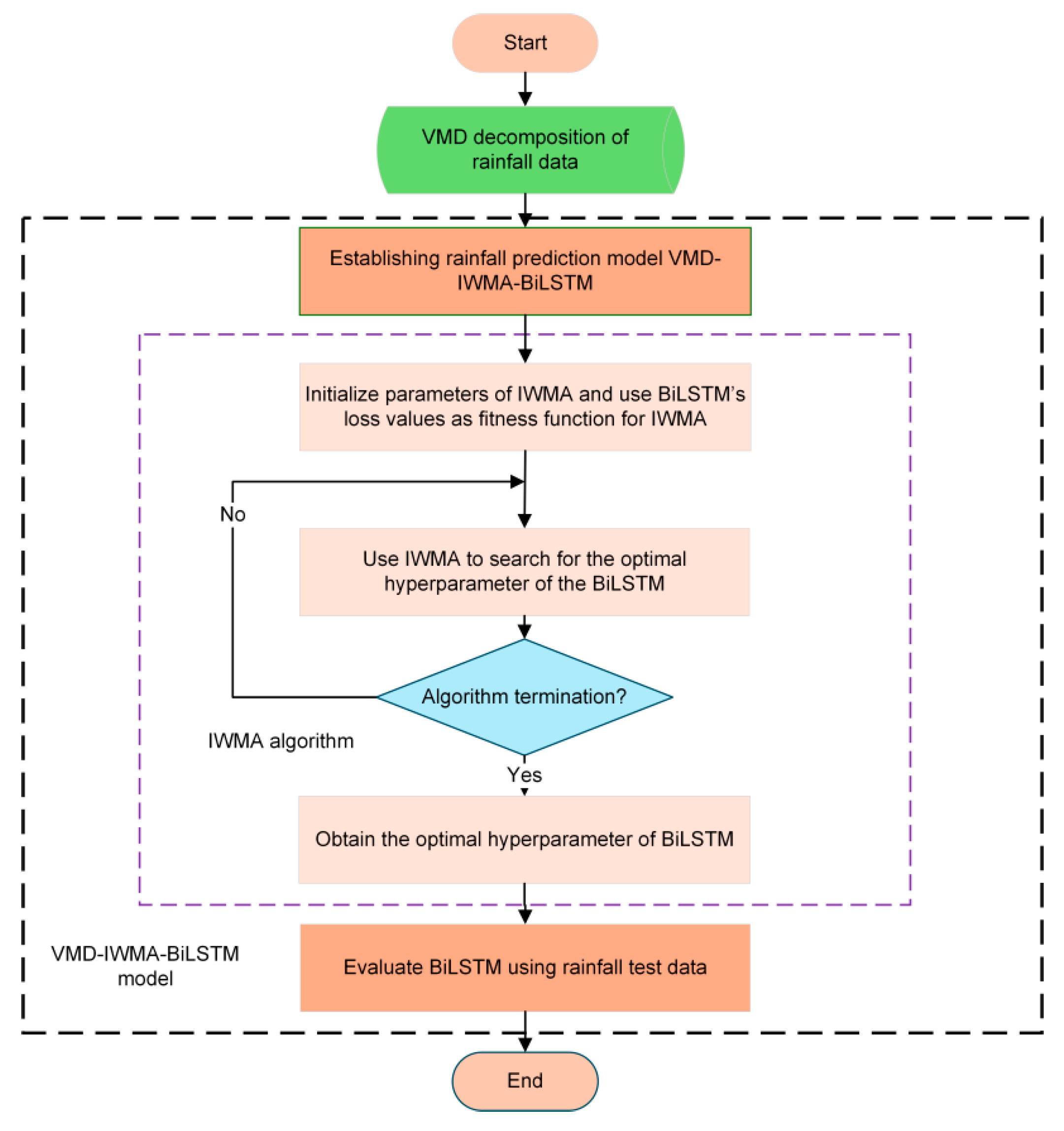
3.2.5. VMD-IWMA-BiLSTM Flowchart
3.2.6. Evaluation Metrics
3.2.7. Comparison of BiLSTM Optimized by Various Algorithms
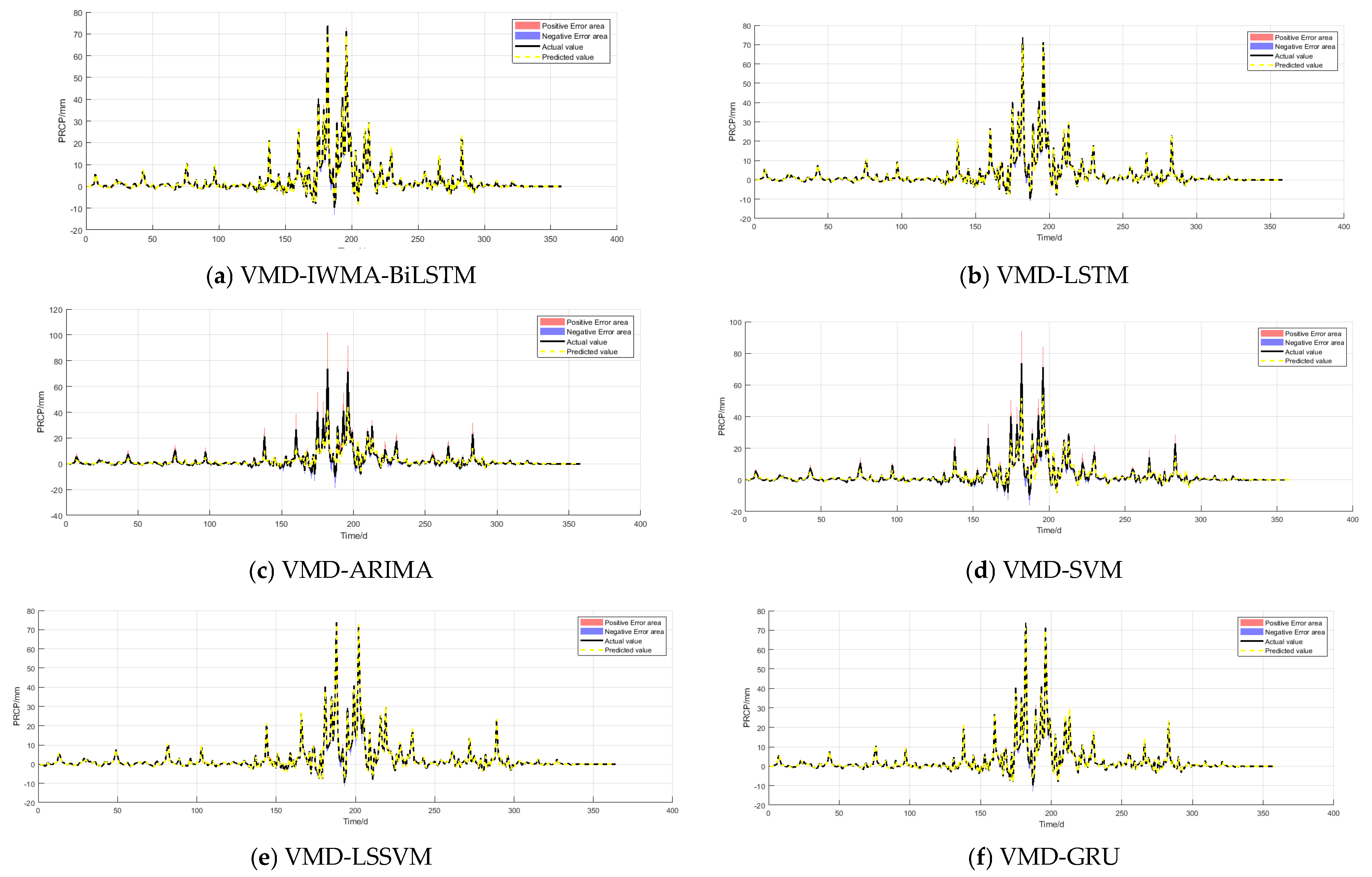
3.2.8. Comparison with Other Models
4. Conclusions
- To address the nonlinear characteristics of the sample data, this study introduces the Variational Mode Decomposition (VMD) method into the field of rainfall prediction. This approach effectively mitigates the non-stationarity problem of the original sequence, thereby improving modeling accuracy and predictive performance. It provides a novel perspective for modeling complex meteorological time series.
- This paper proposes a VMD-IWMA-BiLSTM framework for rainfall prediction and systematically verifies the superiority of the Improved Whale Migration Algorithm (IWMA) in hyperparameter optimization for deep learning models, as well as its significant enhancement of BiLSTM’s predictive ability.
- In comparative experiments with models such as ARIMA, SVM, LSSVM, RNN, and LSTM, the VMD-IWMA-BiLSTM model demonstrated the best performance in both modeling capability and prediction accuracy, significantly outperforming traditional machine learning and deep learning methods. The study further confirms the effectiveness of IWMA in hyperparameter optimization and the applicability of VMD in handling complex, non-stationary time series.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liker, J.K.; Augustyniak, S.; Duncan, G.J. Panel data and models of change: A comparison of first difference and conventional two-wave models. Soc. Sci. Res. 1985, 14, 80–101. [Google Scholar] [CrossRef]
- West, R.M. Best practice in statistics: The use of log transformation. Ann. Clin. Biochem. 2022, 59, 162–165. [Google Scholar] [CrossRef] [PubMed]
- De Livera, A.M.; Hyndman, R.J.; Snyder, R.D. Forecasting time series with complex seasonal patterns using exponential smoothing. J. Am. Stat. Assoc. 2011, 106, 1513–1527. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, E.H.; Zheng, Q.; Tung, C.C.; Liu, H.H. The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis. Proc. Roy. Soc. 1998, 454A, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Banjade, T.P.; Liu, J.; Li, H.; Ma, J. Enhancing earthquake signal based on variational mode decomposition and SG filter. J. Seismol. 2021, 25, 41–54. [Google Scholar] [CrossRef]
- Qin, Y.; Zhao, M.; Lin, Q.; Li, X.; Ji, J. Data-driven building energy consumption prediction model based on VMD-SA-DBN. Mathematics 2022, 10, 3058. [Google Scholar] [CrossRef]
- Masum, M.H.; Islam, R.; Hossen, M.A.; Akhie, A.A. Time series prediction of rainfall and temperature trend using ARIMA model. J. Sci. Res. 2022, 14, 215–227. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Kumar, D.N. Predictability of nonstationary time series using wavelet and EMD based ARMA models. J. Hydrol. 2013, 502, 103–119. [Google Scholar] [CrossRef]
- Hussein, E.; Ghaziasgar, M.; Thron, C. Regional rainfall prediction using support vector machine classification of large-scale precipitation maps. In Proceedings of the 2020 IEEE 23rd International Conference on Information Fusion (FUSION), Rustenburg, South Africa, 6–9 July 2020; IEEE: New York, NY, USA; pp. 1–8. [Google Scholar]
- Ma, M.; Zhao, G.; He, B.; Li, Q.; Dong, H.; Wang, S.; Wang, Z. XGBoost-based method for flash flood risk assessment. J. Hydrol. 2021, 598, 126382. [Google Scholar] [CrossRef]
- Reddy, P.C.S.; Yadala, S.; Goddumarri, S.N. Development of rainfall forecasting model using machine learning with singular spectrum analysis. IIUM Eng. J. 2022, 23, 172–186. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, H.; Liu, J. MM-RNN: A multimodal RNN for precipitation nowcasting. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4101914. [Google Scholar] [CrossRef]
- Poornima, S.; Pushpalatha, M. Prediction of rainfall using intensified LSTM based recurrent neural network with weighted linear units. Atmosphere 2019, 10, 668. [Google Scholar] [CrossRef]
- Salehin, I.; Talha, I.M.; Hasan, M.M.; Dip, S.T.; Saifuzzaman, M.; Moon, N.N. An artificial intelligence based rainfall prediction using LSTM and neural network. In Proceedings of the 2020 IEEE International Women in Engineering (WIE) Conference on Electrical and Computer Engineering (WIECON-ECE), Bhubaneswar, India, 26–27 December 2020; IEEE: New York, NY, USA; pp. 5–8. [Google Scholar]
- Xie, C.; Huang, C.; Zhang, D.; He, W. BiLSTM-I: A deep learning-based long interval gap-filling method for meteorological observation data. Int. J. Environ. Res. Public Health 2021, 18, 10321. [Google Scholar] [CrossRef]
- Siami-Namini, S.; Tavakoli, N.; Namin, A.S. The performance of LSTM and BiLSTM in forecasting time series. In Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), Los Angeles, CA, USA, 9–12 December 2019; IEEE: New York, NY, USA; pp. 3285–3292. [Google Scholar]
- Latifoğlu, L. A novel combined model for prediction of daily precipitation data using instantaneous frequency feature and bidirectional long short time memory networks. Environ. Sci. Pollut. Res. 2022, 29, 42899–42912. [Google Scholar] [CrossRef]
- Khalid, R.; Javaid, N. A survey on hyperparameters optimization algorithms of forecasting models in smart grid. Sustain. Cities Soc. 2020, 61, 102275. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the International Conference on Machine Learning, PMLR, Atlanta, GA, USA, 17–19 June 2013; pp. 115–123. [Google Scholar]
- Probst, P.; Boulesteix, A.L.; Bischl, B. Tunability: Importance of hyperparameters of machine learning algorithms. J. Mach. Learn. Res. 2019, 20, 1934–1965. [Google Scholar]
- El-Kenawy, E.S.M.; Abdelhamid, A.A.; Alrowais, F.; Abotaleb, M.; Ibrahim, A.; Khafaga, D.S. Al-Biruni Based Optimization of Rainfall Forecasting in Ethiopia. Comput. Syst. Sci. Eng. 2023, 46, 2885–2899. [Google Scholar] [CrossRef]
- Zoremsanga, C.; Hussain, J. Particle swarm optimized deep learning models for rainfall prediction: A case study in Aizawl, Mizoram. IEEE Access 2024, 12, 57172–57184. [Google Scholar] [CrossRef]
- Amini, A.; Dolatshahi, M.; Kerachian, R. Effects of automatic hyperparameter tuning on the performance of multi-Variate deep learning-based rainfall nowcasting. Water Resour. Res. 2023, 59, e2022WR032789. [Google Scholar] [CrossRef]
- Shawki, N.; Nunez, R.R.; Obeid, I.; Picone, J. On automating hyperparameter optimization for deep learning applications. In Proceedings of the 2021 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 4 December 2021; IEEE: New York, NY, USA; pp. 1–7. [Google Scholar]
- Belete, D.M.; Huchaiah, M.D. Grid search in hyperparameter optimization of machine learning models for prediction of HIV/AIDS test results. Int. J. Comput. Appl. 2022, 44, 875–886. [Google Scholar] [CrossRef]
- Alibrahim, H.; Ludwig, S.A. Hyperparameter optimization: Comparing genetic algorithm against grid search and bayesian optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Online, 28 June–1 July 2021; IEEE: New York, NY, USA; pp. 1551–1559. [Google Scholar]
- Du, L.; Gao, R.; Suganthan, P.N.; Wang, D.Z. Bayesian optimization based dynamic ensemble for time series forecasting. Inf. Sci. 2022, 591, 155–175. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Z. Ultra-short-term wind speed forecasting using an optimized artificial intelligence algorithm. Renew. Energy 2021, 171, 1418–1435. [Google Scholar] [CrossRef]
- Xu, M.; Cao, L.; Lu, D.; Hu, Z.; Yue, Y. Application of swarm intelligence optimization algorithms in image processing: A comprehensive review of analysis, synthesis, and optimization. Biomimetics 2023, 8, 235. [Google Scholar] [CrossRef]
- Venkatesh, C.; Prasad, B.V.V.S.; Khan, M.; Babu, J.C.; Dasu, M.V. An automatic diagnostic model for the detection and classification of cardiovascular diseases based on swarm intelligence technique. Heliyon 2024, 10, e25574. [Google Scholar] [CrossRef] [PubMed]
- Gaspar, A.; Oliva, D.; Cuevas, E.; Zaldívar, D.; Pérez, M.; Pajares, G. Hyperparameter optimization in a convolutional neural network using metaheuristic algorithms. In Metaheuristics in Machine Learning: Theory and Applications; Springer International Publishing: Cham, Switzerland, 2021; pp. 37–59. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Al-Betar, M.A.; Awadallah, M.A.; Braik, M.S.; Makhadmeh, S.; Doush, I.A. Elk herd optimizer: A novel nature-inspired metaheuristic algorithm. Artif. Intell. Rev. 2024, 57, 48. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Seyedali, M.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2015, 95, 51–67. [Google Scholar]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Joyce, T.; Herrmann, J.M. A review of no free lunch theorems, and their implications for metaheuristic optimisation. In Nature-Inspired Algorithms and Applied Optimization; Springer: Berlin/Heidelberg, Germany, 2017; pp. 27–51. [Google Scholar]
- Adam, S.P.; Alexandropoulos, S.A.N.; Pardalos, P.M.; Vrahatis, M.N. No free lunch theorem: A review. In Approximation and Optimization: Algorithms, Complexity and Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 57–82. [Google Scholar]
- Ghasemi, M.; Deriche, M.; Trojovský, P.; Mansor, Z.; Zare, M.; Trojovská, E.; Abualigah, L.; Ezugwu, A.E.; Mohammadi, S.K. An efficient bio-inspired algorithm based on humpback whale migration for constrained engineering optimization. Results Eng. 2025, 25, 104215. [Google Scholar] [CrossRef]
- Varol Altay, E.; Alatas, B. Bird swarm algorithms with chaotic mapping. Artif. Intell. Rev. 2020, 53, 1373–1414. [Google Scholar] [CrossRef]
- Wang, F.; Zhou, L.; Ren, H.; Liu, X. Search improvement process-chaotic optimization-particle swarm optimization-elite retention strategy and improved combined cooling-heating-power strategy based two-time scale multi-objective optimization model for stand-alone microgrid operation. Energies 2017, 10, 1936. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; National University of Defense Technology: Changsha, China; Kyungpook National University: Daegu, Republic of Korea; Nanyang Technological University: Singapore, 2017. [Google Scholar]
- Yang, Y.; Li, S.; Liu, H.; Guo, J. Carbon Dioxide Emission Forecasting Using BiLSTM Network Based on Variational Mode Decomposition and Improved Black-Winged Kite Algorithm. Mathematics 2025, 13, 1895. [Google Scholar] [CrossRef]





| Type | No. | Functions | Fi * = Fi (x*)1 |
|---|---|---|---|
| Unimodal Functions | 1 | Shifted and Rotated Bent Cigar Function | 100 |
| 3 | Shifted and Rotated Zakharov Function | 200 | |
| Simple Multimodal Functions | 4 | Shifted and Rotated Rosenbrock’s Function | 300 |
| 5 | Shifted and Rotated Rastrigin’s Function | 400 | |
| 6 | Shifted and Rotated Expanded Scaffer’s F6 Function | 500 | |
| 7 | Shifted and Rotated Lunacek Bi_Rastrigin Function | 600 | |
| 8 | Shifted and Rotated Non-Continuous Rastrigin’s Function | 700 | |
| 9 | Shifted and Rotated Levy Function | 800 | |
| 10 | Shifted and Rotated Schwefel’s Function | 900 | |
| Hybrid Functions | 11 | Hybrid Function 1 (N = 3) | 1000 |
| 12 | Hybrid Function 2 (N = 3) | 1100 | |
| 13 | Hybrid Function 3 (N = 3) | 1200 | |
| 14 | Hybrid Function 4 (N = 4) | 1300 | |
| 15 | Hybrid Function 5 (N = 4) | 1400 | |
| 16 | Hybrid Function 5 (N = 4) | 1500 | |
| 17 | Hybrid Function 6 (N = 5) | 1600 | |
| 18 | Hybrid Function 6 (N = 5) | 1700 | |
| 19 | Hybrid Function 6 (N = 5) | 1800 | |
| 20 | Hybrid Function 6 (N = 6) | 1900 | |
| Composition Functions | 21 | Composition Function 1 (N = 3) | 2000 |
| 22 | Composition Function 2 (N = 3) | 2100 | |
| 23 | Composition Function 3 (N = 4) | 2200 | |
| 24 | Composition Function 4 (N = 4) | 2300 | |
| 25 | Composition Function 5 (N = 5) | 2400 | |
| 26 | Composition Function 6 (N = 5) | 2500 | |
| 27 | Composition Function 7 (N = 6) | 2600 | |
| 28 | Composition Function 8 (N = 6) | 2700 | |
| 29 | Composition Function 9 (N = 3) | 2800 | |
| 30 | Composition Function 10 (N = 3) | 2900 |
| Model | CM 1 | ERM 2 |
|---|---|---|
| IWMA | 1 | 1 |
| CWMA | 1 | 0 |
| EWMA | 0 | 1 |
| WMA | 0 | 0 |
| Algorithm | Rank | +/−/= | Avg |
|---|---|---|---|
| IWMA | 1 | ~ | 2.3103 |
| CWMA | 2 | 13/12/1 | 2.3793 |
| EWMA | 3 | 12/16/1 | 2.6207 |
| WMA | 4 | 13/12/1 | 2.6897 |
| Algorithm | Parameter | Value |
|---|---|---|
| HHO | Escape energy (E), Random number (q, r) | E ∈ (−1–1); q, r ∈ (0,1) |
| SCA | Convergence parameter spiral factor (a) | a = 2 |
| GWO | Area vector (a), random vector (r1, r2) | A ∈ [0, 2], r1 ∈ [0, 1], r2 ∈ [0, 1] |
| EHO | Male ratio (br) | br ϵ (0–1) |
| BOA | Perception factor (c) | c ϵ (0.01–0.1) |
| WOA | Convergence factor decay rate (a) | a ϵ (2 → 0) |
| PSO | Population size of the particle swarm | α ϵ (20–1000) |
| DE | Scaling factor (F), Crossover probability (CR) | F ϵ (0–2], CR ϵ [0–1] |
| WMA | Population size (N), Number of leaders (NL) | N ϵ (20–100), NL ϵ (10–50) |
| Fun | F1 | F3 | F4 | |||
|---|---|---|---|---|---|---|
| Aver | Std | Aver | Std | Aver | Std | |
| IWMA | 3.8335E+03 | 4.2917E+03 | 4.5676E+04 | 1.3383E+04 | 4.9064E+02 | 2.1045E+01 |
| HHO | 4.6203E+08 | 2.8176E+08 | 5.6934E+04 | 7.3345E+03 | 6.8264E+02 | 7.5893E+01 |
| SCA | 2.0577E+10 | 3.1811E+09 | 8.7978E+04 | 2.0971E+04 | 3.5622E+03 | 1.2615E+03 |
| GWO | 2.3986E+09 | 1.5824E+09 | 6.3014E+04 | 1.2302E+04 | 7.1221E+02 | 3.0209E+02 |
| EHO | 2.7460E+04 | 6.2361E+04 | 2.2317E+08 | 1.3346E+05 | 5.1184E+02 | 4.2300E+01 |
| BOA | 3.6896E+10 | 7.5074E+09 | 1.4765E+05 | 4.8241E+04 | 1.2544E+04 | 2.6969E+03 |
| WOA | 6.5862E+09 | 2.8032E+09 | 2.7092E+05 | 6.0351E+04 | 1.3645E+03 | 3.8047E+02 |
| PSO | 9.6025E+08 | 1.1254E+09 | 6.6689E+04 | 3.0171E+04 | 6.9417E+02 | 3.3474E+02 |
| DE | 1.1514E+08 | 5.0998E+07 | 1.9832E+05 | 2.3148E+04 | 5.6293E+02 | 2.3962E+01 |
| WMA | 8.2757E+03 | 7.8386E+03 | 6.1679E+04 | 2.1791E+04 | 4.8691E+02 | 1.6544E+01 |
| F5 | F6 | F7 | ||||
| Aver | Std | Aver | Std | Aver | Std | |
| IWMA | 6.1811E+02 | 5.3252E+01 | 6.2289E+02 | 1.0344E+01 | 8.9391E+02 | 6.4040E+01 |
| HHO | 7.7268E+02 | 2.8107E+01 | 6.6673E+02 | 6.5391E+00 | 1.3244E+03 | 6.1795E+01 |
| SCA | 8.2804E+02 | 2.6270E+01 | 6.6291E+02 | 5.7395E+00 | 1.2241E+03 | 5.3127E+01 |
| GWO | 6.1629E+02 | 3.2591E+01 | 6.1262E+02 | 6.0461E+00 | 8.9891E+02 | 6.3787E+01 |
| EHO | 6.3614E+02 | 6.3391E+01 | 6.1997E+02 | 9.3679E+00 | 9.3030E+02 | 7.8652E+01 |
| BOA | 8.4816E+02 | 2.8787E+01 | 6.8019E+02 | 9.3301E+00 | 1.2631E+03 | 7.9684E+01 |
| WOA | 8.6193E+02 | 8.0098E+01 | 6.8101E+02 | 8.2975E+00 | 1.3248E+03 | 8.0341E+01 |
| PSO | 6.2439E+02 | 3.1687E+01 | 6.1707E+02 | 8.2960E+00 | 8.7893E+02 | 4.3155E+01 |
| DE | 7.3265E+02 | 1.7138E+01 | 6.0717E+02 | 1.0704E+00 | 9.8986E+02 | 1.7707E+01 |
| WMA | 6.1073E+02 | 5.1076E+01 | 6.2055E+02 | 6.7917E+00 | 9.2189E+02 | 5.9488E+01 |
| F8 | F9 | F10 | ||||
| Aver | Std | Aver | Std | Aver | Std | |
| IWMA | 9.2511E+02 | 5.0289E+01 | 3.1146E+03 | 1.4248E+03 | 6.6263E+03 | 1.4733E+03 |
| HHO | 9.8562E+02 | 2.1213E+01 | 8.5077E+03 | 1.1114E+03 | 6.1629E+03 | 7.8103E+02 |
| SCA | 1.1009E+03 | 2.3298E+01 | 8.1538E+03 | 1.4530E+03 | 8.9109E+03 | 3.7081E+02 |
| GWO | 8.9907E+02 | 1.9437E+01 | 2.6117E+03 | 9.8134E+02 | 5.7143E+03 | 1.5692E+03 |
| EHO | 9.2112E+02 | 5.4542E+01 | 4.6601E+03 | 2.6534E+03 | 8.1383E+03 | 1.6801E+03 |
| BOA | 1.0875E+03 | 3.4643E+01 | 8.4363E+03 | 1.8711E+03 | 8.2623E+03 | 2.6840E+02 |
| WOA | 1.0754E+03 | 4.6075E+01 | 1.1753E+04 | 3.9656E+03 | 7.6494E+03 | 7.5031E+02 |
| PSO | 9.1193E+02 | 2.3463E+01 | 3.5110E+03 | 2.2083E+03 | 4.4821E+03 | 7.2567E+02 |
| DE | 1.0397E+03 | 1.4250E+01 | 5.1060E+03 | 1.0360E+03 | 8.1185E+03 | 3.6845E+02 |
| WMA | 9.3006E+02 | 6.2443E+01 | 3.0402E+03 | 1.3284E+03 | 7.6698E+03 | 4.1130E+02 |
| F11 | F12 | F13 | ||||
| Aver | Std | Aver | Std | Aver | Std | |
| IWMA | 1.2482E+03 | 5.5580E+01 | 5.2486E+05 | 1.1992E+06 | 1.1842E+04 | 1.2110E+04 |
| HHO | 1.5881E+03 | 1.8010E+02 | 8.8699E+07 | 7.5546E+07 | 1.0541E+06 | 5.9189E+05 |
| SCA | 4.3086E+03 | 1.4446E+03 | 2.6397E+09 | 6.8462E+08 | 1.2108E+09 | 8.5282E+08 |
| GWO | 2.7959E+03 | 1.1159E+03 | 1.3578E+08 | 1.3592E+08 | 1.7521E+07 | 6.6045E+07 |
| EHO | 1.2920E+03 | 1.4219E+02 | 1.5906E+06 | 1.7021E+06 | 1.6083E+04 | 1.5214E+04 |
| BOA | 1.4092E+04 | 9.0656E+03 | 8.1566E+09 | 3.0805E+09 | 5.5045E+09 | 3.8426E+09 |
| WOA | 1.1471E+04 | 4.9141E+03 | 4.4957E+08 | 2.6414E+08 | 1.3698E+07 | 1.3192E+07 |
| PSO | 1.2856E+03 | 5.3667E+01 | 4.3042E+07 | 9.9985E+07 | 7.2437E+07 | 3.7998E+08 |
| DE | 1.8917E+03 | 2.3892E+02 | 1.4808E+08 | 5.4445E+07 | 8.2392E+06 | 2.9812E+06 |
| WMA | 1.2859E+03 | 5.2266E+01 | 3.1658E+05 | 3.2888E+05 | 2.0172E+04 | 1.8563E+04 |
| F14 | F15 | F16 | ||||
| Aver | Std | Aver | Std | Aver | Std | |
| IWMA | 2.5566E+04 | 2.4109E+04 | 5.3260E+03 | 4.2708E+03 | 2.6455E+03 | 3.7316E+02 |
| HHO | 1.4314E+06 | 1.7982E+06 | 1.2411E+05 | 5.5410E+04 | 3.7253E+03 | 5.0875E+02 |
| SCA | 9.4795E+05 | 9.1080E+05 | 5.5602E+07 | 3.2588E+07 | 4.0964E+03 | 2.2868E+02 |
| GWO | 6.4772E+05 | 6.3478E+05 | 2.6830E+06 | 6.9853E+06 | 2.6477E+03 | 2.7702E+02 |
| EHO | 5.1852E+04 | 7.4068E+04 | 9.3466E+03 | 1.0258E+04 | 3.3032E+03 | 6.4961E+02 |
| BOA | 5.5652E+06 | 5.7188E+06 | 1.0258E+04 | 1.0258E+04 | 5.1279E+03 | 1.0749E+03 |
| WOA | 2.5985E+06 | 2.0213E+06 | 4.6108E+06 | 4.0688E+06 | 4.3018E+03 | 6.1214E+02 |
| PSO | 4.5817E+04 | 4.9343E+04 | 9.3432E+03 | 9.9290E+03 | 2.7077E+03 | 2.6751E+02 |
| DE | 4.6123E+05 | 3.2696E+05 | 1.1444E+06 | 7.7283E+05 | 3.2785E+03 | 1.6600E+02 |
| WMA | 3.9975E+04 | 3.0426E+04 | 1.5217E+04 | 1.1414E+04 | 2.5404E+03 | 3.4748E+02 |
| F17 | F18 | F19 | ||||
| Aver | Std | Aver | Std | Aver | Std | |
| IWMA | 2.2747E+03 | 1.9667E+02 | 2.1521E+05 | 1.9037E+05 | 6.9415E+03 | 4.1947E+03 |
| HHO | 2.7611E+03 | 3.3641E+02 | 5.4493E+06 | 5.3706E+06 | 2.1051E+06 | 1.5549E+06 |
| SCA | 2.7980E+03 | 1.9634E+02 | 1.2451E+07 | 6.8237E+06 | 1.1225E+08 | 7.7834E+07 |
| GWO | 2.0944E+03 | 2.0920E+02 | 2.5848E+06 | 5.2115E+06 | 2.4152E+06 | 6.9286E+06 |
| EHO | 2.4811E+03 | 3.3588E+02 | 5.0061E+06 | 2.0602E+06 | 6.0849E+03 | 5.5869E+03 |
| BOA | 4.3826E+03 | 3.3059E+03 | 4.9864E+07 | 3.6979E+07 | 1.1974E+08 | 1.1917E+08 |
| WOA | 2.8598E+03 | 2.5644E+02 | 1.9953E+07 | 1.4790E+07 | 2.8107E+07 | 2.5189E+07 |
| PSO | 2.1635E+03 | 1.8680E+02 | 1.7294E+06 | 3.6252E+06 | 8.9578E+04 | 1.9737E+05 |
| DE | 2.3102E+03 | 1.2255E+02 | 6.1156E+06 | 3.9196E+06 | 2.8107E+07 | 2.8107E+07 |
| WMA | 2.2430E+03 | 2.2677E+02 | 3.2512E+05 | 3.1613E+05 | 1.5112E+04 | 1.4898E+04 |
| F20 | F21 | F22 | ||||
| Aver | Std | Aver | Std | Aver | Std | |
| IWMA | 2.4919E+03 | 1.6450E+02 | 2.4066E+03 | 3.8466E+01 | 2.5278E+03 | 1.2319E+03 |
| HHO | 2.7479E+03 | 1.8716E+02 | 2.6019E+03 | 4.9930E+01 | 7.2860E+03 | 1.6917E+03 |
| SCA | 2.9492E+03 | 1.1744E+02 | 2.5943E+03 | 2.2758E+01 | 9.9041E+03 | 1.3108E+03 |
| GWO | 2.4845E+03 | 1.4931E+02 | 2.4172E+03 | 4.2145E+01 | 5.5441E+03 | 2.3771E+03 |
| EHO | 2.8337E+03 | 4.7266E+02 | 2.4092E+03 | 4.8439E+01 | 6.4281E+03 | 3.6584E+03 |
| BOA | 2.8521E+03 | 1.4929E+02 | 2.6599E+03 | 3.9958E+01 | 7.4068E+03 | 2.1326E+03 |
| WOA | 2.9693E+03 | 2.0264E+02 | 2.6484E+03 | 5.0793E+01 | 8.2888E+03 | 1.5766E+03 |
| PSO | 2.5124E+03 | 2.4595E+02 | 2.4203E+03 | 3.0635E+01 | 3.7765E+03 | 1.7634E+03 |
| DE | 2.6176E+03 | 1.3078E+02 | 2.5281E+03 | 1.6652E+01 | 7.9579E+03 | 1.3318E+03 |
| WMA | 2.4771E+03 | 2.0009E+02 | 2.4228E+03 | 5.8878E+01 | 5.0660E+03 | 3.4448E+03 |
| F23 | F24 | F25 | ||||
| Aver | Std | Aver | Std | Aver | Std | |
| IWMA | 2.7823E+03 | 2.8817E+01 | 2.9334E+03 | 4.8514E+01 | 2.8938E+03 | 1.4374E+01 |
| HHO | 3.2580E+03 | 1.4151E+02 | 3.5244E+03 | 1.2935E+02 | 3.0032E+03 | 2.6020E+01 |
| SCA | 3.0910E+03 | 5.1821E+01 | 3.2525E+03 | 4.7233E+01 | 3.6980E+03 | 3.1486E+02 |
| GWO | 2.7746E+03 | 4.0570E+01 | 2.9816E+03 | 7.5686E+01 | 3.0228E+03 | 5.7992E+01 |
| EHO | 2.7803E+03 | 5.6466E+01 | 2.9535E+03 | 7.5145E+01 | 2.9141E+03 | 2.6943E+01 |
| BOA | 3.4089E+03 | 1.7738E+02 | 4.1588E+03 | 2.9684E+02 | 4.8421E+03 | 6.2663E+02 |
| WOA | 3.1917E+03 | 1.0472E+02 | 3.2791E+03 | 1.1495E+02 | 3.2267E+03 | 6.9736E+01 |
| PSO | 2.9199E+03 | 7.5239E+01 | 3.1152E+03 | 1.0319E+02 | 2.9113E+03 | 3.3957E+01 |
| DE | 2.8671E+03 | 1.1840E+01 | 3.0541E+03 | 1.2370E+01 | 2.9637E+03 | 2.0632E+01 |
| WMA | 2.7725E+03 | 3.1533E+01 | 2.9500E+03 | 5.7793E+01 | 2.8944E+03 | 1.5054E+01 |
| F26 | F27 | F28 | ||||
| Aver | Std | Aver | Std | Aver | Std | |
| IWMA | 4.9091E+03 | 1.1808E+03 | 3.2751E+03 | 4.7705E+01 | 3.2253E+03 | 3.1848E+01 |
| HHO | 8.1650E+03 | 9.1076E+02 | 3.5248E+03 | 1.2926E+02 | 3.4832E+03 | 8.7642E+01 |
| SCA | 8.0558E+03 | 4.9639E+02 | 3.5452E+03 | 9.1623E+01 | 4.5054E+03 | 3.6902E+02 |
| GWO | 4.9371E+03 | 5.2822E+02 | 3.2784E+03 | 3.4752E+01 | 3.5233E+03 | 2.5514E+02 |
| EHO | 5.2198E+03 | 7.3582E+02 | 3.2000E+03 | 5.9215E−05 | 3.3000E+03 | 6.4242E−05 |
| BOA | 9.8109E+03 | 7.4426E+02 | 4.2218E+03 | 3.4908E+02 | 6.6211E+03 | 6.9803E+02 |
| WOA | 8.5364E+03 | 1.0797E+03 | 3.4755E+03 | 1.3712E+02 | 3.8131E+03 | 2.5593E+02 |
| PSO | 5.2878E+03 | 1.2512E+03 | 3.2925E+03 | 5.9154E+01 | 3.3032E+03 | 1.2242E+02 |
| DE | 5.9038E+03 | 1.1456E+02 | 3.2437E+03 | 7.9643E+00 | 3.3778E+03 | 4.3239E+01 |
| WMA | 5.1406E+03 | 4.1734E+02 | 3.2840E+03 | 4.9737E+01 | 3.2314E+03 | 2.3790E+01 |
| F29 | F30 | |||||
| Aver | Std | Aver | Std | |||
| IWMA | 3.9872E+03 | 2.4230E+02 | 8.9112E+03 | 8.6313E+03 | ||
| HHO | 4.9993E+03 | 5.0915E+02 | 8.6770E+06 | 6.1255E+06 | ||
| SCA | 5.2185E+03 | 3.3745E+02 | 2.0164E+08 | 8.6977E+07 | ||
| GWO | 3.9589E+03 | 1.8399E+02 | 1.3657E+07 | 1.1548E+07 | ||
| EHO | 3.8611E+03 | 4.3740E+02 | 1.5969E+04 | 1.0573E+04 | ||
| BOA | 8.8982E+03 | 8.6935E+03 | 7.2774E+08 | 5.0417E+08 | ||
| WOA | 5.4822E+03 | 5.1093E+02 | 6.4434E+07 | 6.2238E+07 | ||
| PSO | 3.8672E+03 | 2.5080E+02 | 1.3000E+05 | 2.7154E+05 | ||
| DE | 4.5387E+03 | 1.6933E+02 | 1.0018E+06 | 4.5699E+05 | ||
| WMA | 4.0958E+03 | 2.5660E+02 | 1.6543E+04 | 9.0353E+03 | ||
| Fun | IWMA VS. HHO | IWMA VS. SCA | IWMA VS. GWO | IWMA VS. EHO | IWMA VS. BOA | IWMA VS. WOA | IWMA VS. PSO | IWMA VS. DE | IWMA VS. WMA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 2.71E−01 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 7.62E−01 |
| F3 | 1.68E−03 | 3.08E−08 | 5.56E−04 | 3.02E−11 | 3.69E−11 | 3.02E−11 | 5.56E−04 | 3.02E−11 | 8.50E−02 |
| F4 | 3.02E−11 | 3.02E−11 | 3.69E−11 | 6.74E−01 | 3.02E−11 | 3.02E−11 | 3.37E−05 | 3.02E−11 | 4.55E−01 |
| F5 | 1.33E−10 | 3.34E−11 | 5.40E−01 | 4.55E−01 | 3.02E−11 | 3.02E−11 | 9.94E−01 | 2.61E−10 | 8.77E−02 |
| F6 | 3.02E−11 | 3.02E−11 | 6.01E−08 | 9.33E−02 | 3.02E−11 | 3.02E−11 | 1.78E−04 | 5.49E−11 | 5.55E−02 |
| F7 | 3.02E−11 | 3.02E−11 | 5.37E−02 | 1.54E−01 | 3.02E−11 | 3.02E−11 | 4.84E−02 | 1.56E−08 | 4.97E−02 |
| F8 | 1.52E−03 | 3.02E−11 | 1.19E−01 | 3.48E−01 | 3.69E−11 | 1.33E−10 | 1.15E−01 | 9.76E−10 | 2.92E−02 |
| F9 | 3.02E−11 | 3.02E−11 | 3.51E−02 | 9.47E−01 | 3.02E−11 | 3.02E−11 | 9.05E−02 | 5.09E−06 | 7.06E−01 |
| F10 | 9.82E−01 | 4.20E−10 | 1.76E−02 | 6.77E−05 | 8.29E−06 | 3.15E−02 | 8.68E−03 | 8.88E−06 | 4.21E−02 |
| F11 | 4.62E−10 | 3.02E−11 | 3.69E−11 | 5.99E−01 | 3.02E−11 | 3.02E−11 | 2.46E−01 | 3.02E−11 | 1.62E−01 |
| F12 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 4.44E−07 | 3.02E−11 | 3.02E−11 | 1.87E−07 | 3.02E−11 | 8.19E−01 |
| F13 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 2.58E−01 | 3.02E−11 | 3.02E−11 | 1.20E−08 | 3.02E−11 | 6.10E−03 |
| F14 | 1.46E−10 | 3.34E−11 | 2.39E−08 | 1.75E−05 | 3.34E−11 | 3.34E−11 | 2.68E−06 | 3.69E−11 | 1.38E−02 |
| F15 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 9.33E−02 | 3.02E−11 | 3.02E−11 | 1.17E−03 | 3.02E−11 | 4.86E−03 |
| F16 | 4.62E−10 | 4.98E−11 | 7.98E−02 | 4.03E−03 | 3.02E−11 | 8.16E−11 | 2.97E−01 | 9.83E−08 | 4.83E−01 |
| F17 | 3.52E−07 | 1.41E−09 | 5.26E−04 | 7.39E−01 | 1.31E−08 | 6.01E−08 | 6.10E−01 | 1.67E−01 | 2.28E−01 |
| F18 | 3.20E−09 | 3.02E−11 | 1.07E−07 | 1.44E−03 | 3.34E−11 | 1.78E−10 | 5.86E−06 | 3.02E−11 | 2.71E−01 |
| F19 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 9.71E−01 | 3.02E−11 | 3.02E−11 | 4.83E−01 | 3.02E−11 | 2.61E−02 |
| F20 | 2.03E−09 | 2.15E−10 | 3.71E−01 | 1.03E−02 | 5.97E−09 | 4.99E−09 | 4.64E−01 | 4.46E−04 | 9.94E−01 |
| F21 | 1.78E−10 | 4.08E−11 | 4.38E−01 | 1.67E−01 | 4.50E−11 | 5.49E−11 | 2.92E−02 | 5.46E−09 | 2.17E−01 |
| F22 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 2.03E−07 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 9.03E−04 |
| F23 | 3.02E−11 | 3.02E−11 | 1.96E−01 | 5.69E−01 | 3.02E−11 | 3.69E−11 | 6.52E−09 | 1.87E−07 | 5.55E−02 |
| F24 | 3.02E−11 | 3.02E−11 | 5.75E−02 | 9.59E−01 | 3.02E−11 | 3.34E−11 | 4.20E−10 | 1.41E−09 | 6.95E−01 |
| F25 | 3.02E−11 | 3.02E−11 | 7.39E−11 | 2.24E−02 | 3.02E−11 | 3.02E−11 | 7.73E−02 | 1.96E−10 | 6.41E−01 |
| F26 | 3.02E−11 | 3.02E−11 | 8.42E−01 | 4.03E−03 | 3.02E−11 | 4.62E−10 | 2.92E−02 | 2.61E−10 | 2.81E−02 |
| F27 | 4.50E−11 | 3.02E−11 | 8.07E−01 | 3.02E−11 | 3.02E−11 | 7.38E−10 | 2.07E−02 | 3.92E−02 | 5.75E−02 |
| F28 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 4.08E−11 | 3.02E−11 | 3.37E−04 |
| F29 | 8.10E−10 | 3.34E−11 | 2.81E−02 | 6.20E−04 | 3.02E−11 | 4.08E−11 | 1.30E−03 | 3.08E−08 | 9.71E−01 |
| F30 | 3.02E−11 | 3.02E−11 | 3.02E−11 | 2.00E−05 | 3.02E−11 | 3.02E−11 | 4.43E−03 | 3.02E−11 | 7.17E−01 |
| Mode Number (K) | Penalty Factor (α) | Noise Tolerance (τ) | Convergence Tolerance (tol) | DC Component |
|---|---|---|---|---|
| 5 | 1800 | 0 | 1E−7 | 0 |
| Hyperparameter Name | Description | Lower Bounds | Upper Bounds |
|---|---|---|---|
| unit | The number of units in the BiLSTM layer | 50 | 300 |
| learning_rate | Parameter update step during model training | 0.001 | 0.01 |
| max_epochs | Maximum number of cycles for model training | 50 | 300 |
| Optimization Algorithm | Optimal Solution from the Optimization Algorithm | Evaluation Indicators | |||||
|---|---|---|---|---|---|---|---|
| Unit | lr | mp | MAE | RMSE | MAPE | PCC | |
| Grid Search | 300 | 0.0080 | 50 | 1.5159 | 3.4205 | 34.57% | 0.8823 |
| Random Search | 225 | 0.0031 | 298 | 1.1283 | 2.4464 | 28.59% | 0.8932 |
| Bayesian | 235 | 0.0037 | 287 | 1.2386 | 2.6226 | 25.82% | 0.8964 |
| HHO | 50 | 0.0010 | 50 | 0.5596 | 1.2178 | 9.95% | 0.9786 |
| SCA | 280 | 0.0085 | 50 | 0.3889 | 0.8383 | 6.23% | 0.9821 |
| GWO | 50 | 0.0068 | 172 | 0.4050 | 0.8899 | 6.82% | 0.9875 |
| EHO | 53 | 0.0011 | 64 | 0.4770 | 1.0798 | 7.99% | 0.9863 |
| BOA | 75 | 0.0073 | 286 | 0.4356 | 0.9960 | 7.56% | 0.9833 |
| WOA | 76 | 0.0054 | 114 | 0.3708 | 0.7956 | 6.14% | 0.9842 |
| PSO | 50 | 0.0064 | 177 | 0.3948 | 0.8560 | 6.90% | 0.9882 |
| DE | 71 | 0.0040 | 300 | 0.3785 | 0.8380 | 6.81% | 0.9898 |
| WMA | 300 | 0.0010 | 300 | 0.3427 | 0.7109 | 5.47% | 0.9932 |
| IWMA | 288 | 0.0010 | 258 | 0.2251 | 0.3896 | 3.76% | 0.9962 |
| Detection Station | Model | MAE | RMSE | MAPE | PCC | Rank |
|---|---|---|---|---|---|---|
| Aver (30 Times) | ||||||
| Xinzheng Testing Station, Zhengzhou City | ARIMA | 1.4898 | 3.5715 | 37.58% | 0.8912 | 6 |
| SVM | 1.1872 | 2.6111 | 26.91% | 0.9494 | 5 | |
| LSSVM | 0.4239 | 0.8162 | 5.19% | 0.9744 | 3 | |
| GRU | 0.3368 | 0.6939 | 5.09% | 0.9869 | 2 | |
| LSTM | 0.3632 | 0.7553 | 5.84% | 0.9861 | 4 | |
| BiLSTM | 0.2251 | 0.3896 | 3.76% | 0.9962 | 1 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Li, S.; Zhou, T.; Zhao, L.; Shi, X.; Du, B. Rainfall Forecasting Using a BiLSTM Model Optimized by an Improved Whale Migration Algorithm and Variational Mode Decomposition. Mathematics 2025, 13, 2483. https://doi.org/10.3390/math13152483
Yang Y, Li S, Zhou T, Zhao L, Shi X, Du B. Rainfall Forecasting Using a BiLSTM Model Optimized by an Improved Whale Migration Algorithm and Variational Mode Decomposition. Mathematics. 2025; 13(15):2483. https://doi.org/10.3390/math13152483
Chicago/Turabian StyleYang, Yueqiao, Shichuang Li, Ting Zhou, Liang Zhao, Xiao Shi, and Boni Du. 2025. "Rainfall Forecasting Using a BiLSTM Model Optimized by an Improved Whale Migration Algorithm and Variational Mode Decomposition" Mathematics 13, no. 15: 2483. https://doi.org/10.3390/math13152483
APA StyleYang, Y., Li, S., Zhou, T., Zhao, L., Shi, X., & Du, B. (2025). Rainfall Forecasting Using a BiLSTM Model Optimized by an Improved Whale Migration Algorithm and Variational Mode Decomposition. Mathematics, 13(15), 2483. https://doi.org/10.3390/math13152483





