Bidirectional Conservative–Dissipative Transitions in a Five-Dimensional Fractional Chaotic System
Abstract
1. Introduction
2. Fundamental Dynamics and Phenomena
2.1. Five-Dimensional System Construction and Analysis
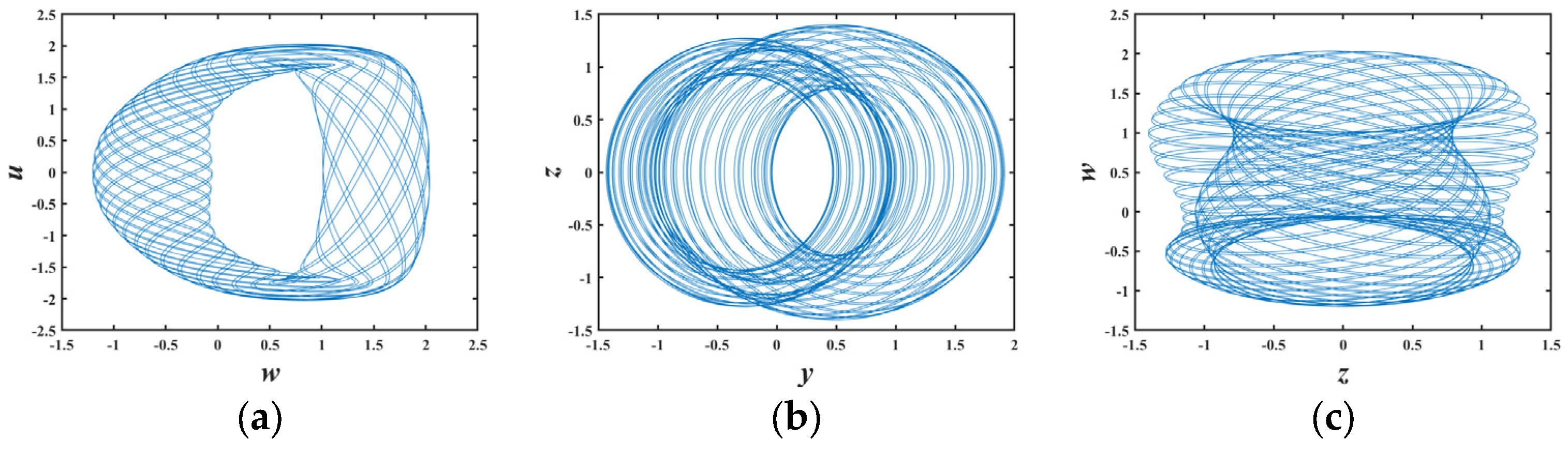
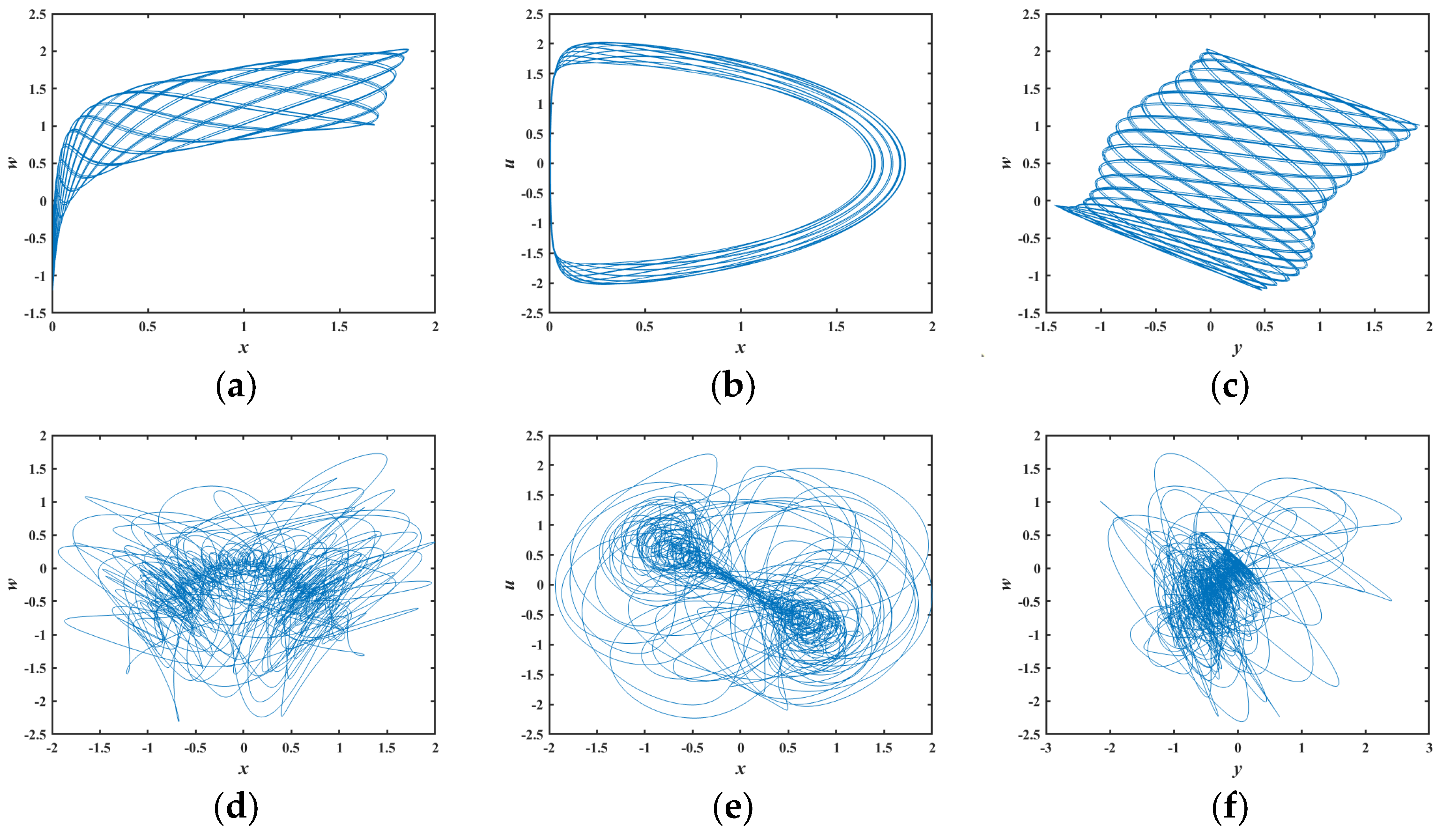
2.2. Phase Trajectory Diagram
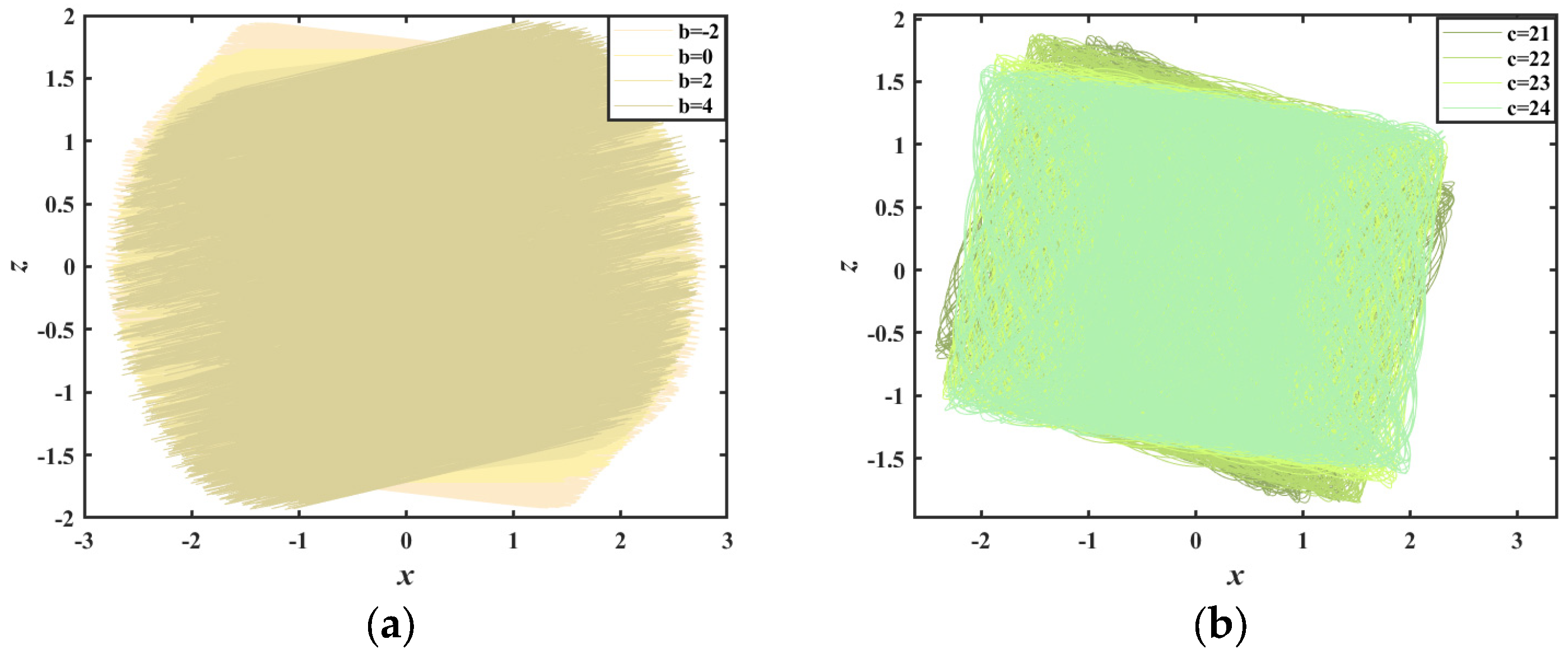
2.3. Offset Boost Behavior
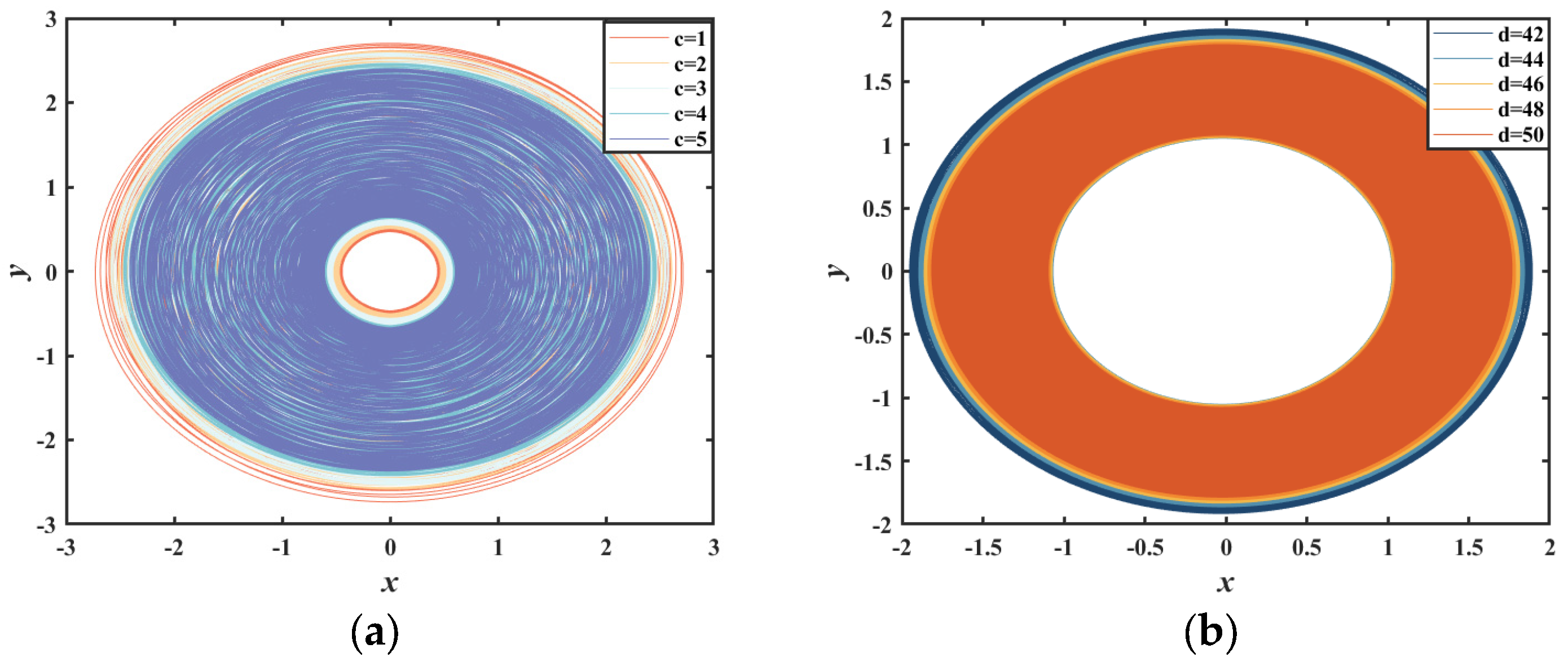
2.4. Rotational Behavior
2.5. Contraction Behavior
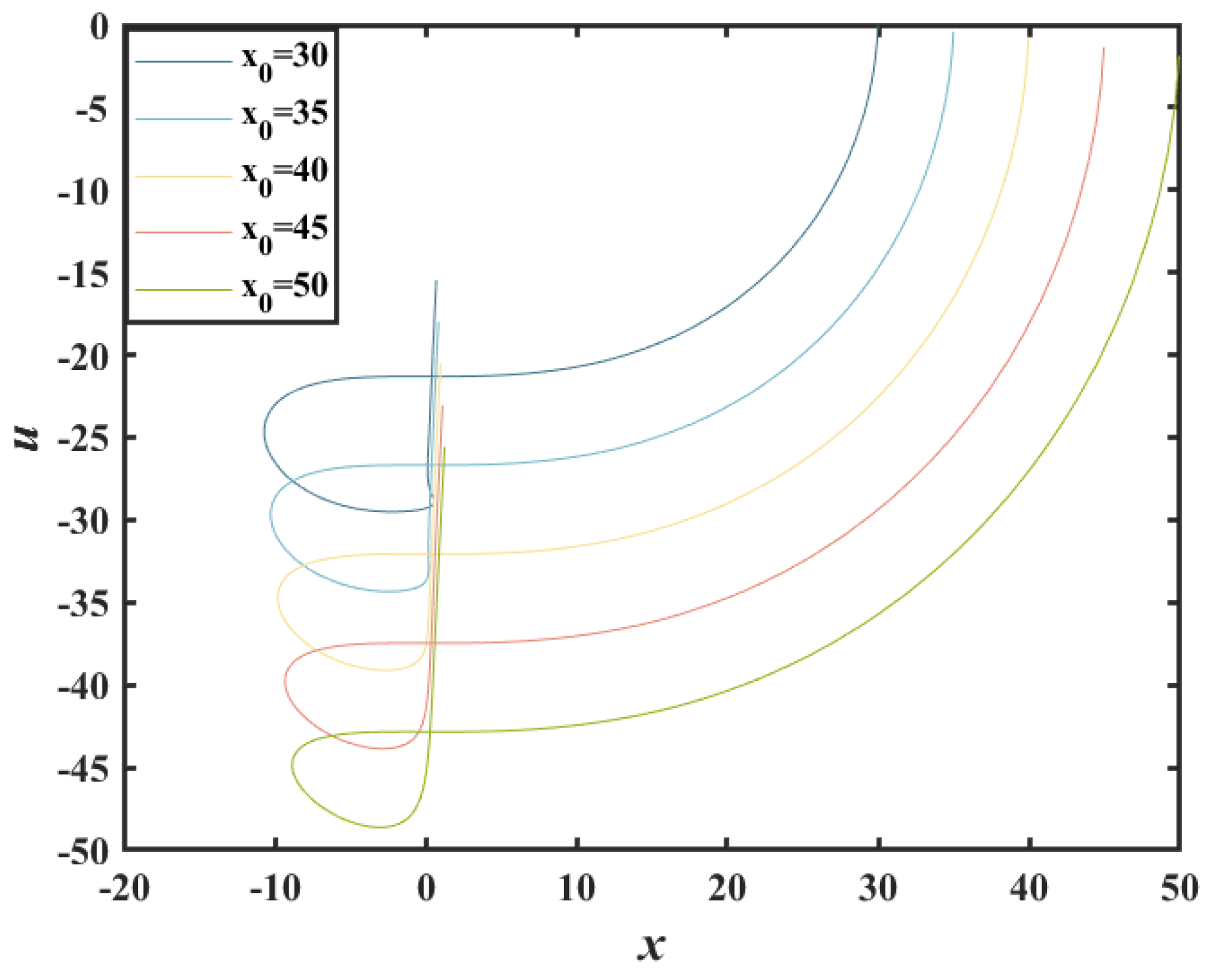
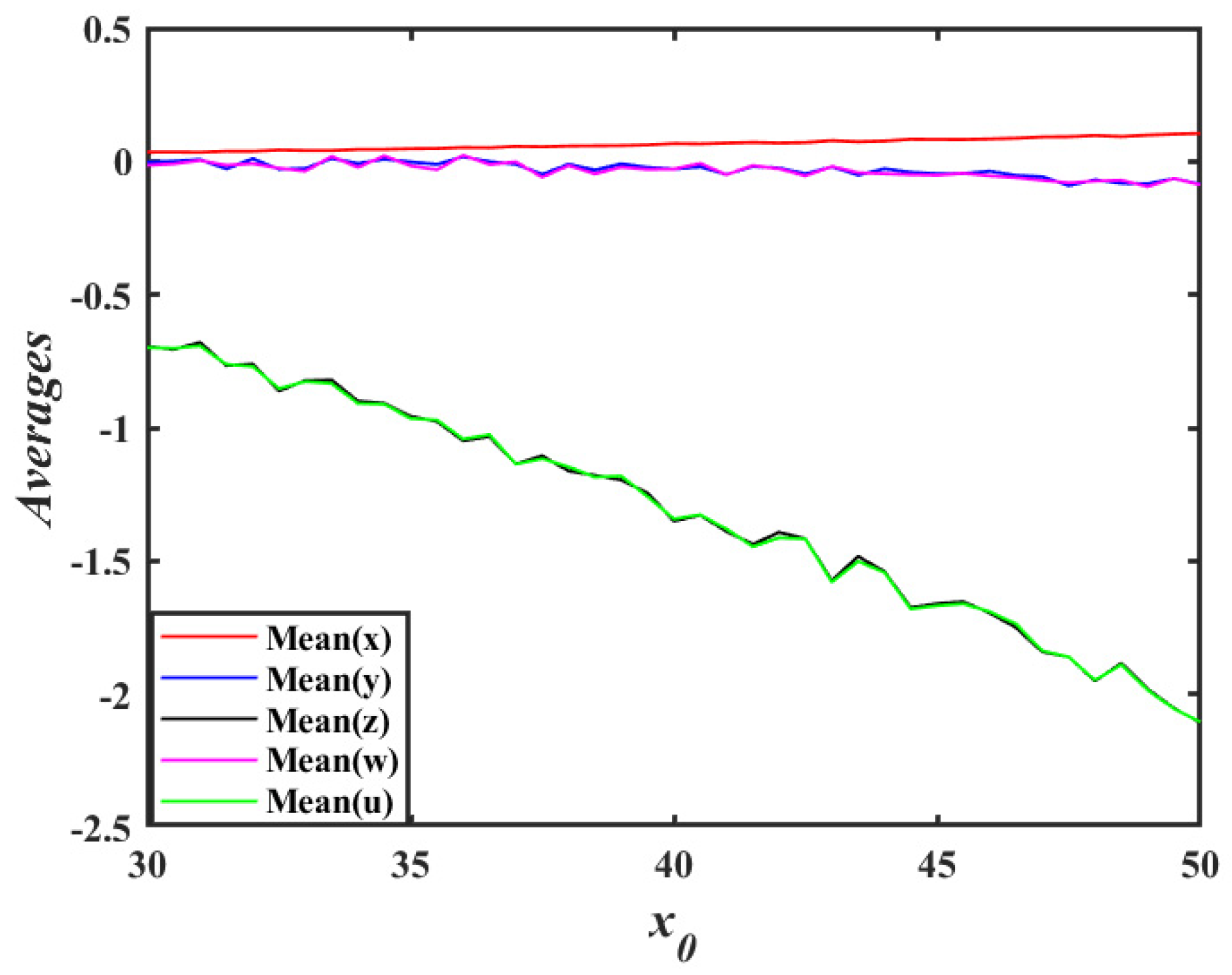
2.6. Phase Trajectory Reversal
3. Nonlinear Regime Analysis
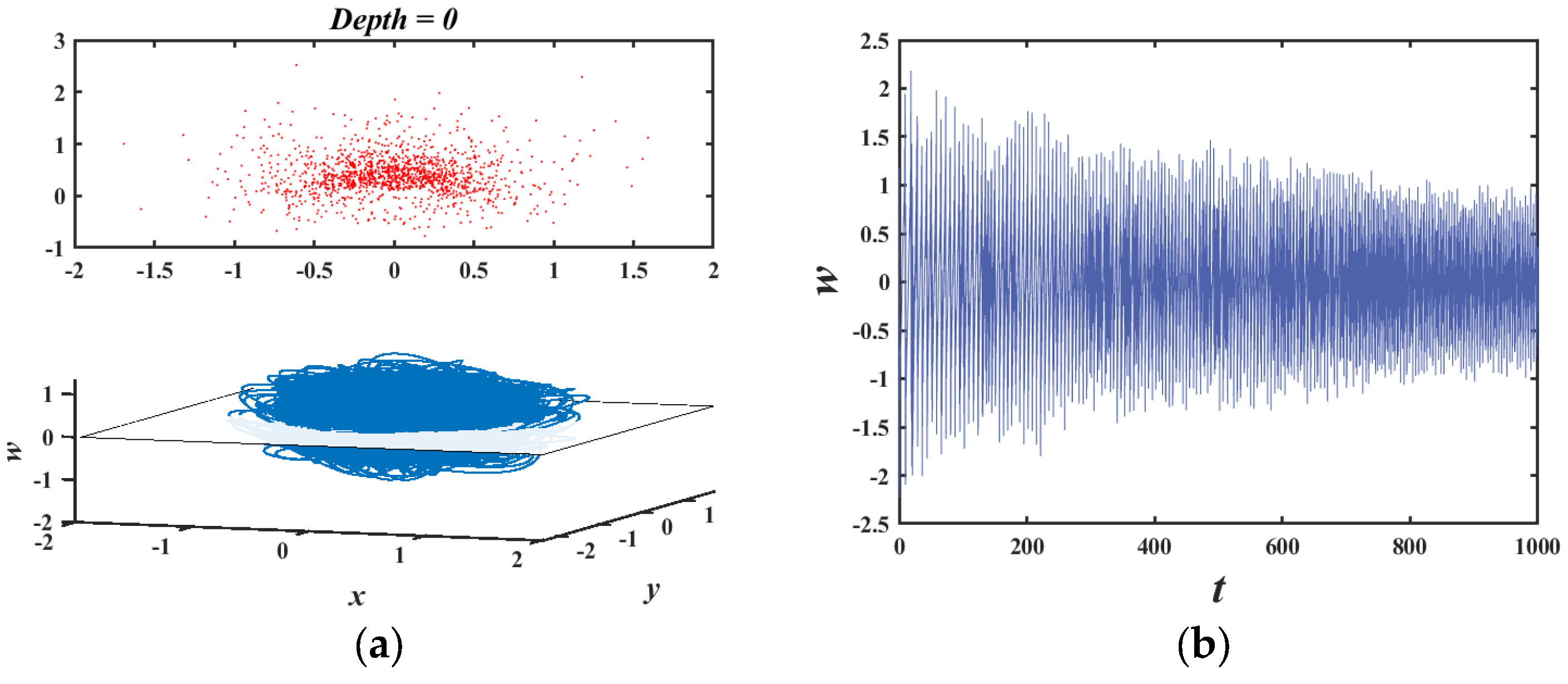
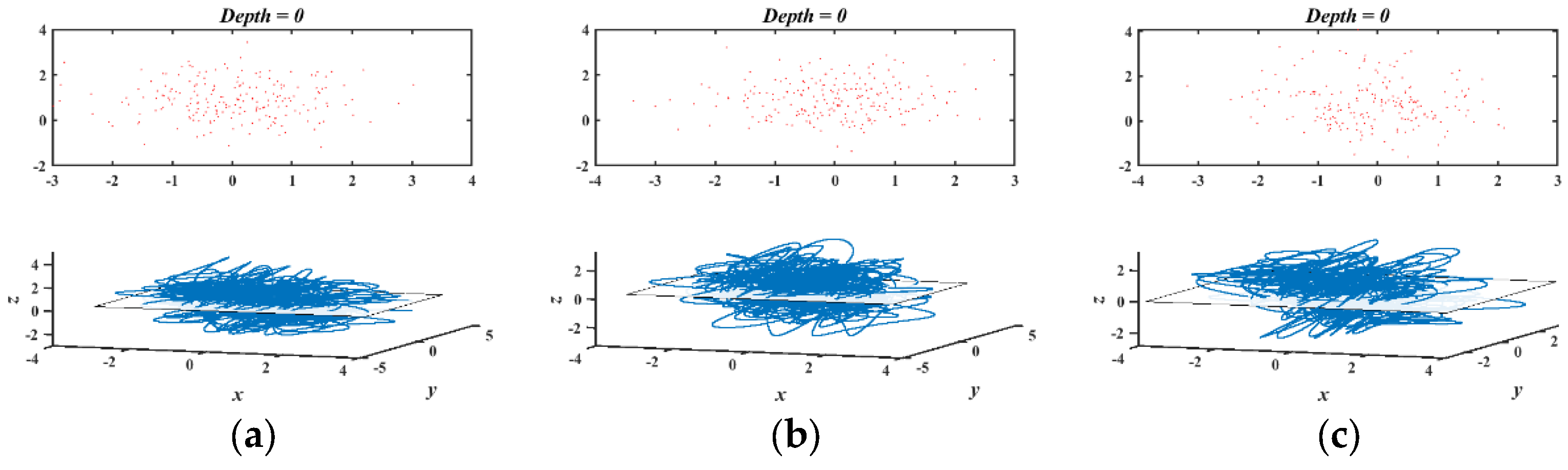
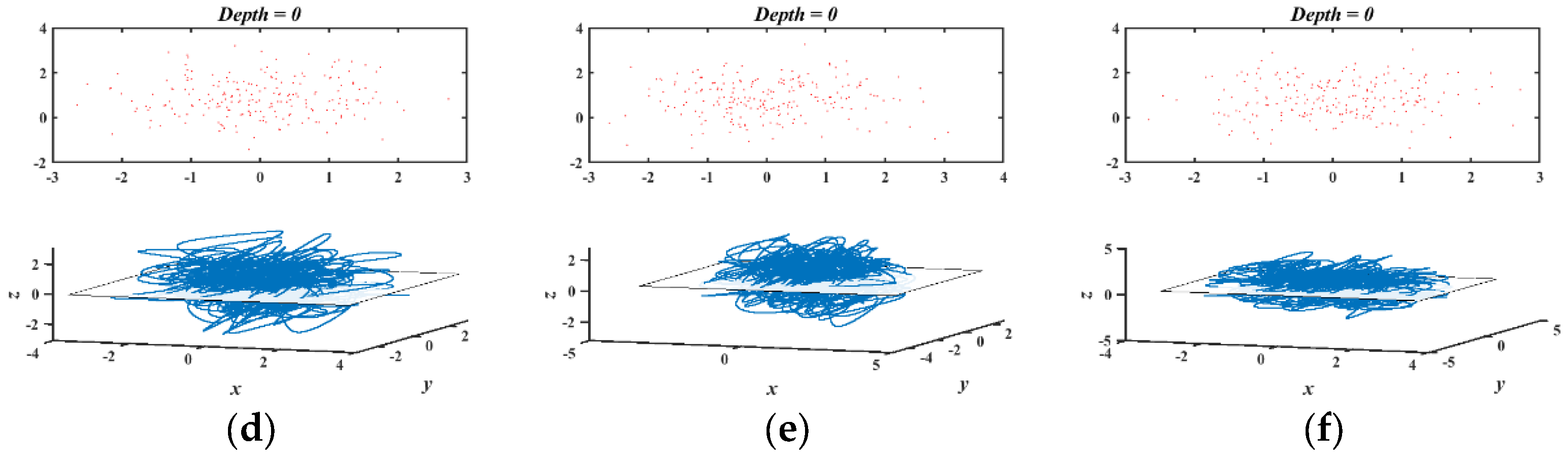
3.1. Large-Scale Hyperchaos Regions
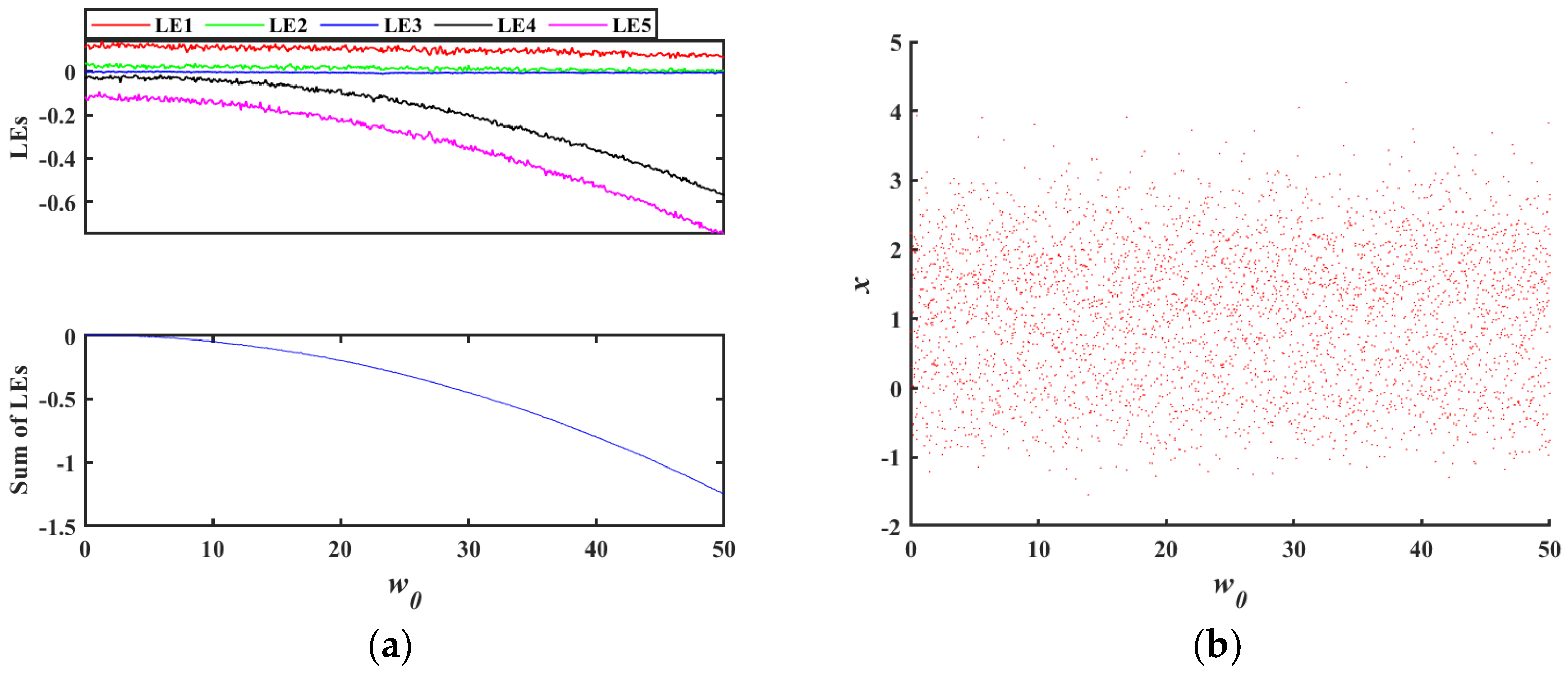
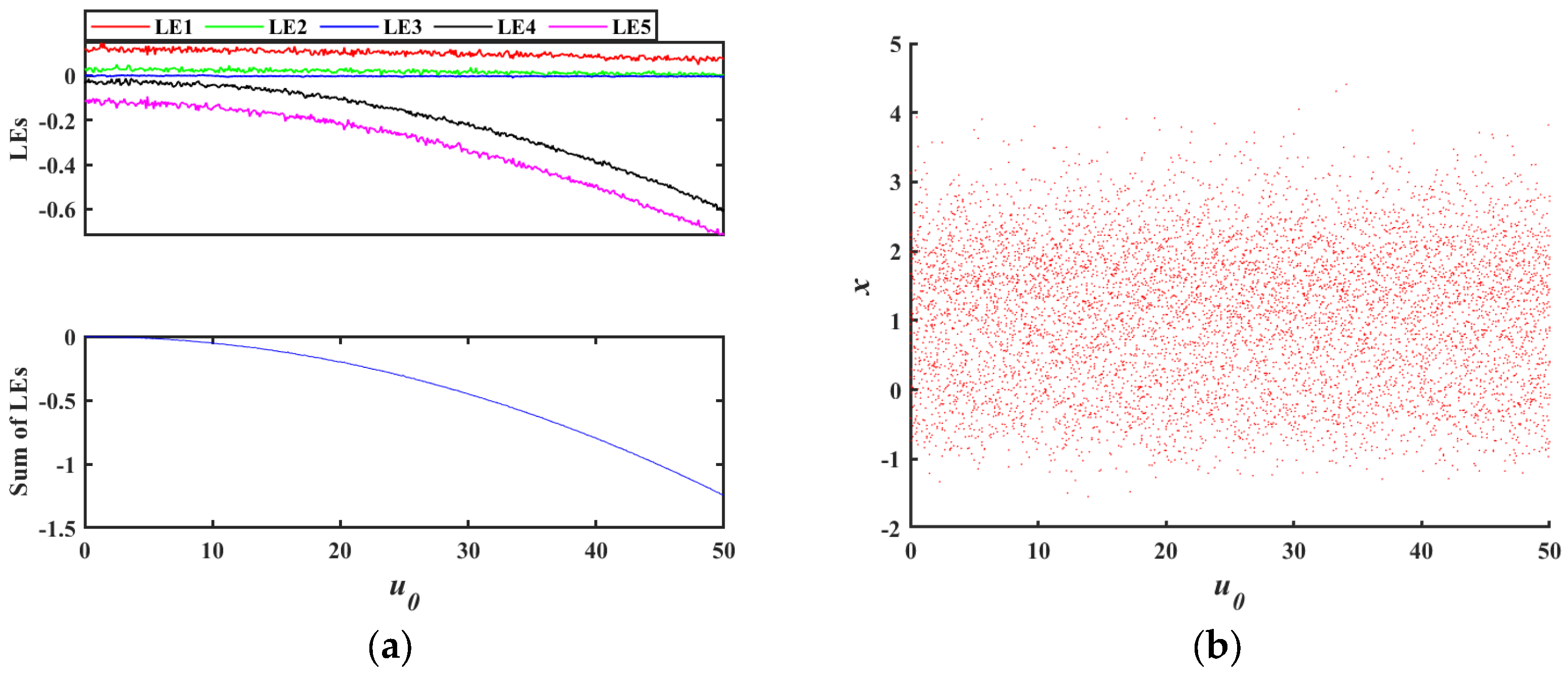
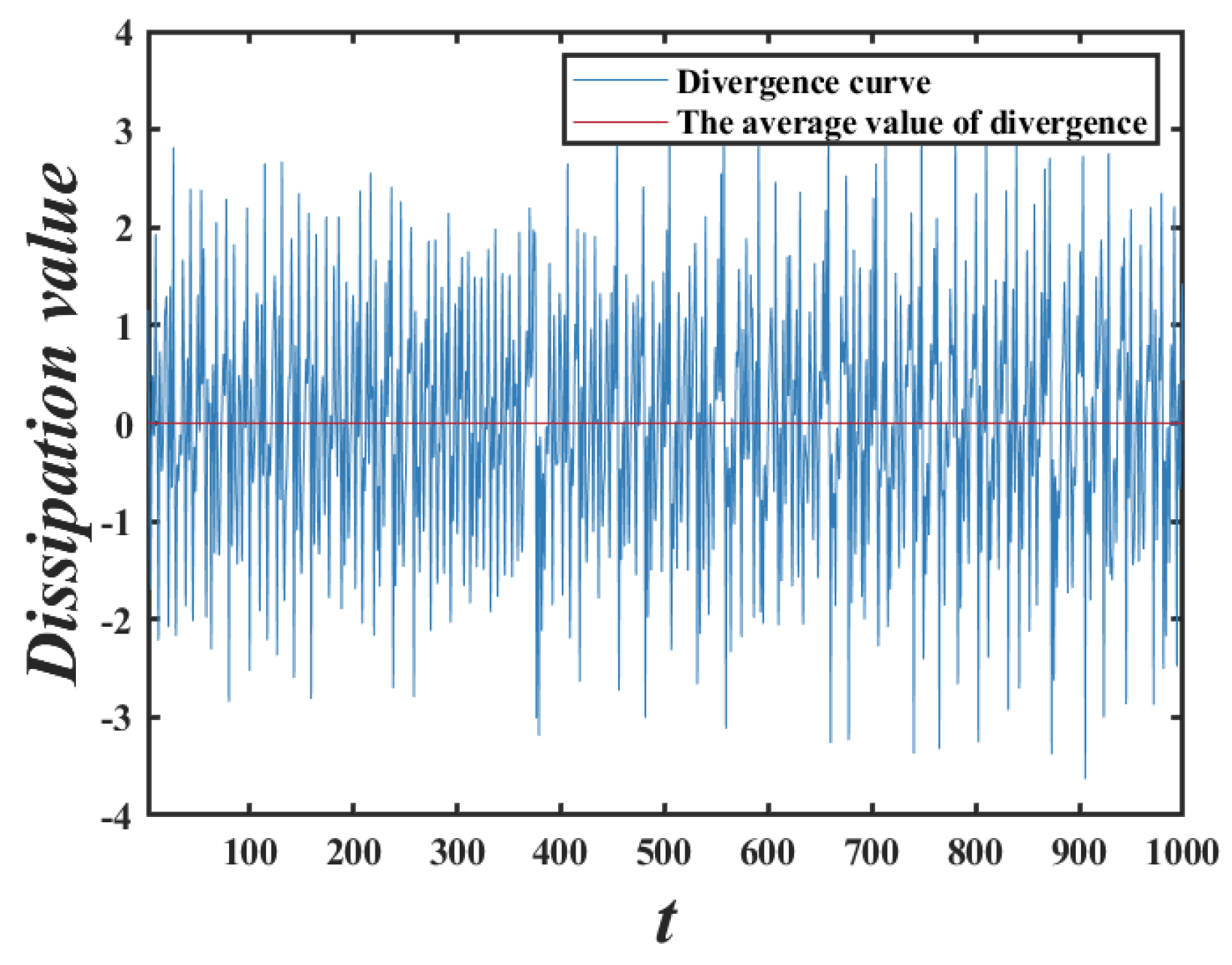
3.2. Transition from Conservative to Dissipative Behavior
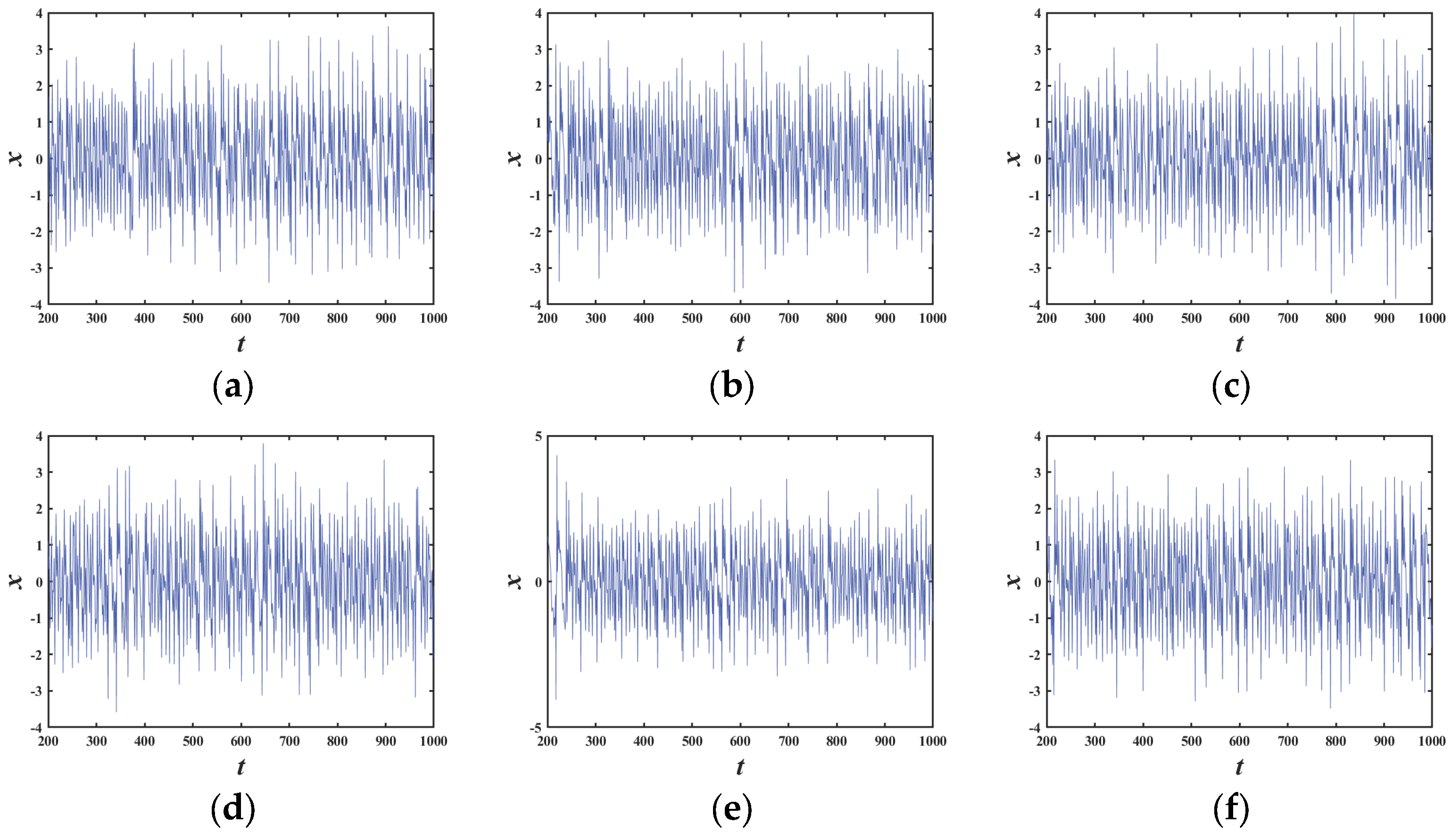
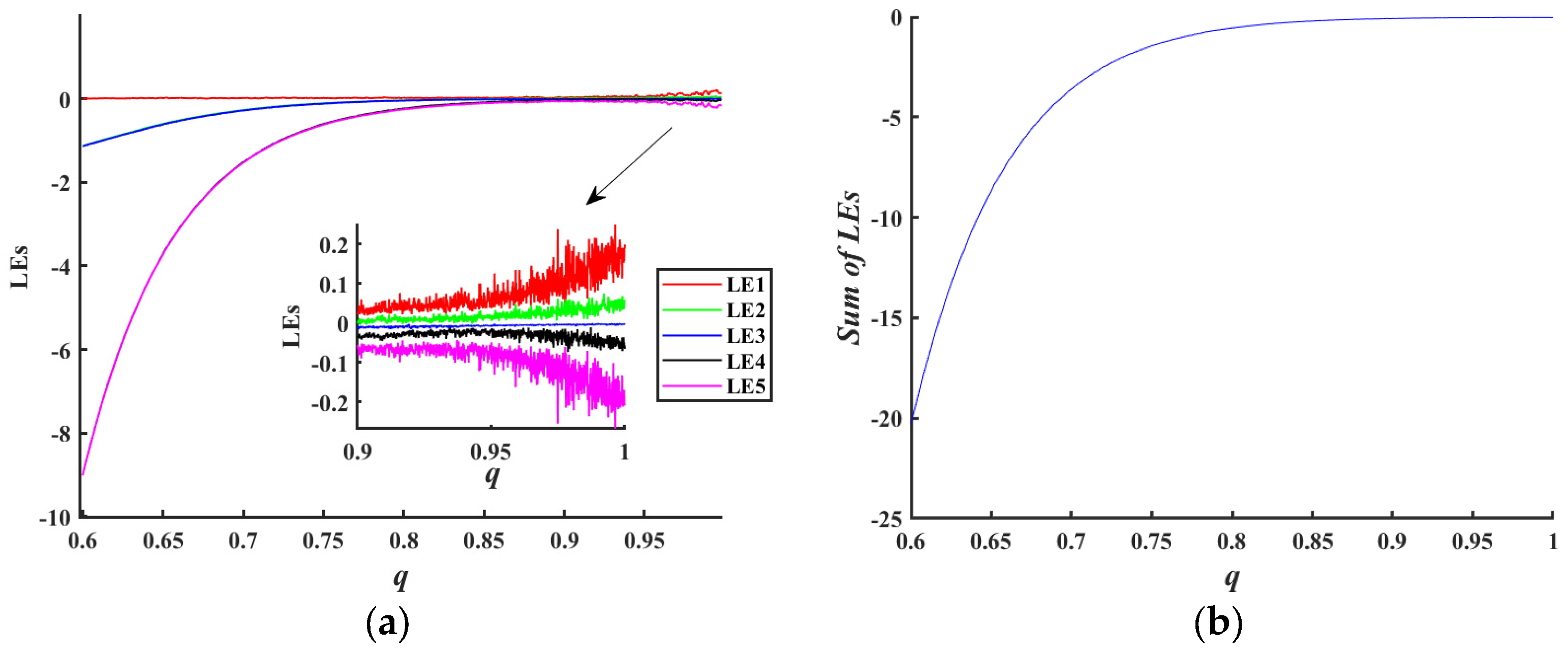
3.3. Fractional-Order Controlled Dynamics
4. DSP Verification
5. Conclusions
- (1)
- Conservative-to-dissipative transitions governed by initial conditions and dissipative-to-conservative transitions controlled by fractional order variations.
- (2)
- A unique chaotic-to-quasiperiodic transition occurring exclusively at low fractional orders.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, H.R.; Wang, C.H.; Tan, Y.M. Hidden Extreme Multistability with Hyperchaos and Transient Chaos in a Hopfield Neural Network Affected by Electromagnetic Radiation. Nonlinear Dyn. 2020, 99, 2369–2386. [Google Scholar] [CrossRef]
- Bao, H.; Liu, W.B.; Ma, J.; Wu, H.G. Memristor Initial-Offset Boosting in Memristive HR Neuron Model with Hidden Firing Patterns. Int. J. Bifurc. Chaos 2020, 30, 2030029. [Google Scholar] [CrossRef]
- Sajjadi, S.S.; Baleanu, D.; Jajarmi, A.; Pirouz, H.M. A New Adaptive Synchronization and Hyperchaos Control of a Biological Snap Oscillator. Chaos Solitons Fractals 2020, 138, 109919. [Google Scholar] [CrossRef]
- Karkaria, B.D.; Manhart, A.; Fedorec, A.J.K.; Barnes, C.P. Chaos in Synthetic Microbial Communities. PLoS Comput. Biol. 2022, 18, e1010548. [Google Scholar] [CrossRef]
- Signing, V.R.F.; Tegue, G.A.G.; Kountchou, M.; Njitacke, Z.T.; Tsafack, N.; Nkapkop, J.D.D.; Etoundi, C.M.L.; Kengne, J. A Cryptosystem Based on a Chameleon Chaotic System and Dynamic DNA Coding. Chaos Solitons Fractals 2022, 155, 111777. [Google Scholar] [CrossRef]
- Guler, H. Real-time Fuzzy-pid Synchronization of Memristor-based Chaotic Circuit Using Graphical Coded Algorithm in Secure Communication Applications. Phys. Scr. 2022, 97, 55212. [Google Scholar] [CrossRef]
- Nasrolahpour, H. Fractional Electromagnetic Metamaterials. Optik 2020, 203, 163969. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.F.; Yepez-Martínez, H.; Escobar-Jiménez, R.F.; Astorga-Zaragoza, C.M.; Morales-Mendoza, L.J.; González-Lee, M. Universal Character of the Fractional Space-time Electromagnetic Waves in Dielectric Media. J. Electromagn. Waves Appl. 2015, 29, 727–740. [Google Scholar] [CrossRef]
- Maurya, R.K.; Devi, V.; Singh, V.K. Multistep Schemes for One and Two Dimensional Electromagnetic Wave Models Based on Fractional Derivative Approximation. J. Comput. Appl. Math. 2020, 380, 112985. [Google Scholar] [CrossRef]
- El-Saka, H.A.A.; Lee, S.; Jang, B. Dynamic Analysis of Fractional-order Predator-prey Biological Economic System with Holling Type II Functional Response. Nonlinear Dyn. 2019, 96, 407–416. [Google Scholar] [CrossRef]
- Ramesh, P.; Sambath, M.; Mohd, H.M.; Krishnan, B. Stability Analysis of the Fractional-order Prey-predator Model with Infection. Int. J. Model. Simul. 2020, 41, 434–450. [Google Scholar] [CrossRef]
- Wang, J.; Lee, M.C.; Kim, J.H.; Kim, H.H. Fast Fractional-Order Terminal Sliding Mode Control for Seven-Axis Robot Manipulator. Appl. Sci. 2020, 10, 7757. [Google Scholar] [CrossRef]
- Saad, F.; Belafhal, A. Propagation Properties of Hollow Higher-order Cosh-Gaussian Beams in Quadratic Index Medium and Fractional Fourier Transform. Opt. Quantum Electron. 2021, 53, 28. [Google Scholar] [CrossRef]
- Mystkowski, A.; Zolotas, A. PLC-based Discrete Fractional-order Control Design for an Industrial-oriented Water Tank Volume System with Input Delay. Fract. Calc. Appl. Anal. 2018, 21, 1005–1026. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.P.; Tian, Y. Fractional-order Adaptive Controller for Chaotic Synchronization and Application to a Dual-channel Secure Communication System. Mod. Phys. Lett. B 2019, 33, 1950290. [Google Scholar] [CrossRef]
- Rivero, M.; Trujillo, J.J.; Vázquez, L.; Velasco, M.P. Fractional Dynamics of Populations. Appl. Math. Comput. 2011, 218, 1089–1095. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Pakiriswamy, S. A 3-D Novel Conservative Chaotic System and Its Generalized Projective Synchronization via Adaptive Control. J. Eng. Sci. Technol. Rev. 2014, 8, 52–60. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C. Analysis and Adaptive Control of a Novel 3-D Conservative No-equilibrium Chaotic System. Arch. Control Sci. 2015, 25, 333–353. [Google Scholar] [CrossRef]
- Cang, S.J.; Wu, A.G.; Wang, Z.H.; Chen, Z.Q. Four-dimensional Autonomous Dynamical Systems with Conservative Flows: Two-case Study. Nonlinear Dyn. 2017, 89, 2495–2508. [Google Scholar] [CrossRef]
- Jafari, S.; Nazarimehr, F.; Sprott, J.C.; Golpayegani, S.M.R.H. Limitation of Perpetual Points for Confirming Conservation in Dynamical Systems. Int. J. Bifurc. Chaos 2015, 25, 1550182. [Google Scholar] [CrossRef]
- Prasad, A. Existence of Perpetual Points in Nonlinear Dynamical Systems and Its Applications. Int. J. Bifurc. Chaos 2015, 25, 1530005. [Google Scholar] [CrossRef]
- Wu, A.G.; Cang, S.J.; Zhang, R.Y.; Wang, Z.; Chen, Z. Hyperchaos in a Conservative System with Nonhyperbolic Fixed Points. Complexity 2018, 2018, 9430637. [Google Scholar] [CrossRef]
- Cang, S.J.; Wu, A.G.; Zhang, R.Y.; Wang, Z.; Chen, Z. Conservative Chaos in a Class of Nonconservative Systems: Theoretical Analysis and Numerical Demonstrations. Int. J. Bifurc. Chaos 2018, 28, 1850087. [Google Scholar] [CrossRef]
- Singh, J.P.; Roy, B.K. Five New 4-D Autonomous Conservative Chaotic Systems with Various Type of Non-Hyperbolic and Lines of Equilibria. Chaos Solitons Fractals 2018, 114, 81–91. [Google Scholar] [CrossRef]
- Gu, S.Q.; Du, B.X.; Wan, Y.J. A New Four-Dimensional Non-Hamiltonian Conservative Hyperchaotic System. Int. J. Bifurc. Chaos 2020, 30, 2050242. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, L.; Liu, J.; Guo, Q.; Du, X. A new method of constructing cyclic symmetric conservative chaotic systems and improved offset boosting control. Chaos Solitons Fractals 2022, 158, 112103. [Google Scholar] [CrossRef]
- Ke, Y.Q.; Miao, C.F. Mittag-Leffler Stability of Fractional-order Lorenz and Lorenz-family Systems. Nonlinear Dyn. 2016, 83, 1237–1246. [Google Scholar] [CrossRef]
- Azil, S.; Odibat, Z.; Shawagfeh, N. Nonlinear Dynamics and Chaos in Caputo-Like Discrete Fractional Chen System. Phys. Scr. 2021, 96, 95219. [Google Scholar] [CrossRef]
- Odibat, Z.; Corson, N.; Aziz-Alaoui, M.A.; Alsaedi, A. Chaos in Fractional Order Cubic Chua System and Synchronization. Int. J. Bifurc. Chaos 2017, 27, 1750161. [Google Scholar] [CrossRef]
- Jia, H.Y.; Chen, Z.Q.; Qi, G.Y. Topological Horseshoe Analysis and Circuit Realization for a Fractional-Order Lü System. Nonlinear Dyn. 2013, 74, 203–212. [Google Scholar] [CrossRef]
- Xu, C.J.; Liao, M.X.; Li, P.L.; Yao, L.; Qin, Q.; Shang, Y. Chaos Control for a Fractional-Order Jerk System via Time Delay Feedback Controller and Mixed Controller. Fractal Fract. 2021, 5, 257. [Google Scholar] [CrossRef]
- Cafagna, D.; Grassi, G. Fractional-Order Systems without Equilibria: The First Example of Hyperchaos and Its Application to Synchronization. Chin. Phys. B 2015, 24, 80502. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.C.; Li, Z.J.; Zhou, C.Y. Hidden Extreme Multistability, Antimonotonicity and Offset Boosting Control in a Novel Fractional-Order Hyperchaotic System Without Equilibrium. Int. J. Bifurc. Chaos 2018, 28, 1850167. [Google Scholar] [CrossRef]
- Leng, X.; Gu, S.; Peng, Q.; Du, B. Study on a four-dimensional fractional-order system with dissipative and conservative properties. Chaos Solitons Fractals 2021, 150, 111185. [Google Scholar] [CrossRef]
- Tian, B.; Peng, Q.; Leng, X.; Du, B. A new 5D fractional-order conservative hyperchaos system. Phys. Scr. 2022, 98, 15207. [Google Scholar] [CrossRef]
- Leng, X.; Zhang, C.; Du, B. Modeling methods and characteristic analysis of new Hamiltonian and non-Hamiltonian conservative chaotic systems. AEU-Int. J. Electron. Commun. 2022, 152, 154242. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, C.H.; Zhang, X.; Yao, W. Various Attractors, Coexisting Attractors and Antimonotonicity in a Simple Fourth-Order Memristive Twin-T Oscillator. Int. J. Bifurc. Chaos 2018, 28, 1850050. [Google Scholar] [CrossRef]
- Leng, X.; Zhang, L.; Zhang, C.; Du, B. Modeling and complexity analysis of a fractional-order memristor conservative chaotic system. Phys. Scr. 2023, 98, 75206. [Google Scholar] [CrossRef]
- Lenka, B.K.; Upadhyay, R.K. New globally Lipschitz no-equilibrium fractional order systems and control of hidden memory chaotic attractors. J. Comput. Sci. 2025, 88, 102603. [Google Scholar] [CrossRef]
- Xiangxin, L.; Baoxiang, D.; Shuangquan, G.; He, S. Novel dynamical behaviors in fractional-order conservative hyperchaotic system and DSP implementation. Nonlinear Dyn. 2022, 109, 1167–1186. [Google Scholar] [CrossRef]
- Ye, X.L.; Wang, X.Y. Characteristic Analysis of a Simple Fractional-Order Chaotic System with Infinitely Many Coexisting Attractors and Its DSP Implementation. Phys. Scr. 2020, 95, 75212. [Google Scholar] [CrossRef]
- Fu, H.Y.; Lei, T.F. Adomian Decomposition, Dynamic Analysis and Circuit Implementation of a 5D Fractional-Order Hyperchaotic System. Symmetry 2022, 14, 484. [Google Scholar] [CrossRef]
- Rajagopal, K.; Nazarimehr, F.; Karthikeyan, A.; Srinivasan, A.; Jafari, S. CAMO: Self-Excited and Hidden Chaotic Flows. Int. J. Bifurc. Chaos 2019, 29, 1950143. [Google Scholar] [CrossRef]
- Li, G.H.; Zhang, X.Y.; Yang, H. Complexity Analysis and Synchronization Control of Fractional-Order Jafari-Sprott Chaotic System. IEEE Access 2020, 8, 53360–53373. [Google Scholar] [CrossRef]
- Yang, F.F.; Li, P. Characteristics Analysis of the Fractional-Order Chaotic Memristive Circuit Based on Chua’s Circuit. Mob. Netw. Appl. 2019, 26, 1862–1870. [Google Scholar] [CrossRef]
- He, S.B.; Sun, K.H.; Wang, H.H. Dynamics and Synchronization of Conformable Fractional-Order Hyperchaotic Systems Using the Homotopy Analysis Method. Commun. Nonlinear Sci. Numer. Simul. 2019, 73, 146–164. [Google Scholar] [CrossRef]
- Lenka, B.K.; Upadhyay, R.K. Hidden memory chaotic attractors in simple nonequilibrium fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2025, 150, 108970. [Google Scholar] [CrossRef]
- Fan, Z.; Zhang, C.; Wang, Y.; Du, B. Construction, dynamic analysis and DSP implementation of a novel 3D discrete memristive hyperchaotic map. Chaos Solitons Fractals 2023, 177, 114303. [Google Scholar] [CrossRef]
- Liu, B.; Ye, X.L.; Hu, G. Design of a New 3D Chaotic System Producing Infinitely Many Coexisting Attractors and Its Application to Weak Signal Detection. Int. J. Bifurc. Chaos 2021, 31, 2150235. [Google Scholar] [CrossRef]
- Yang, F.F.; Mou, J.; Ma, C.G.; Cao, Y.H. Dynamic Analysis of an Improper Fractional-Order Laser Chaotic System and Its Image Encryption Application. Opt. Lasers Eng. 2020, 129, 106031. [Google Scholar] [CrossRef]



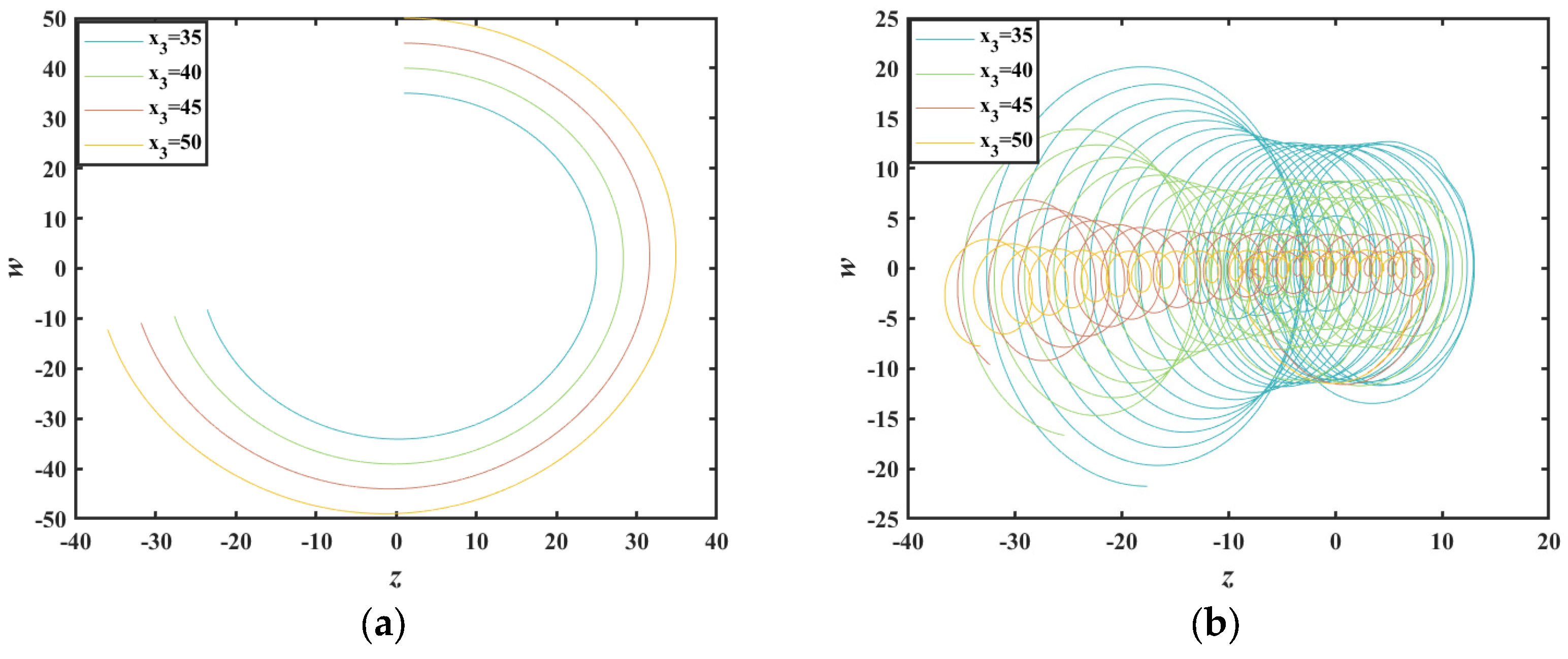
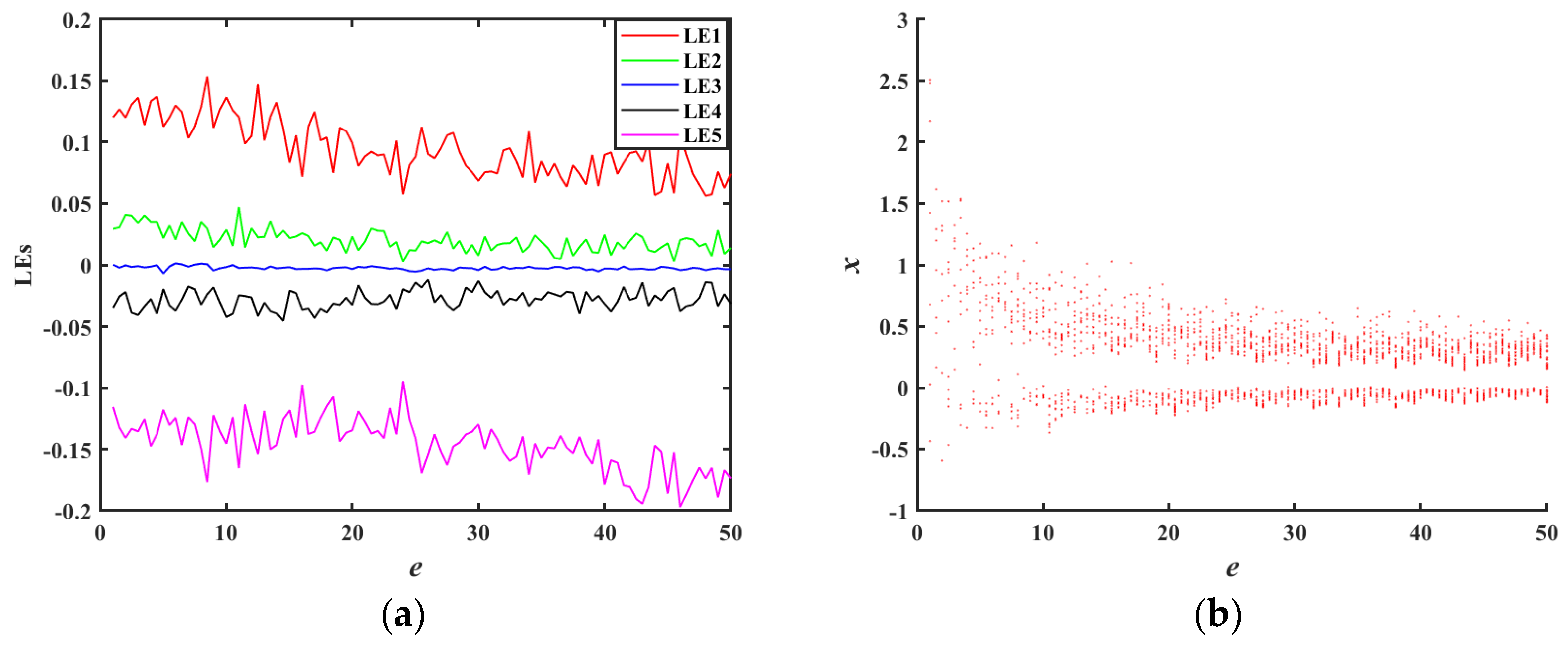
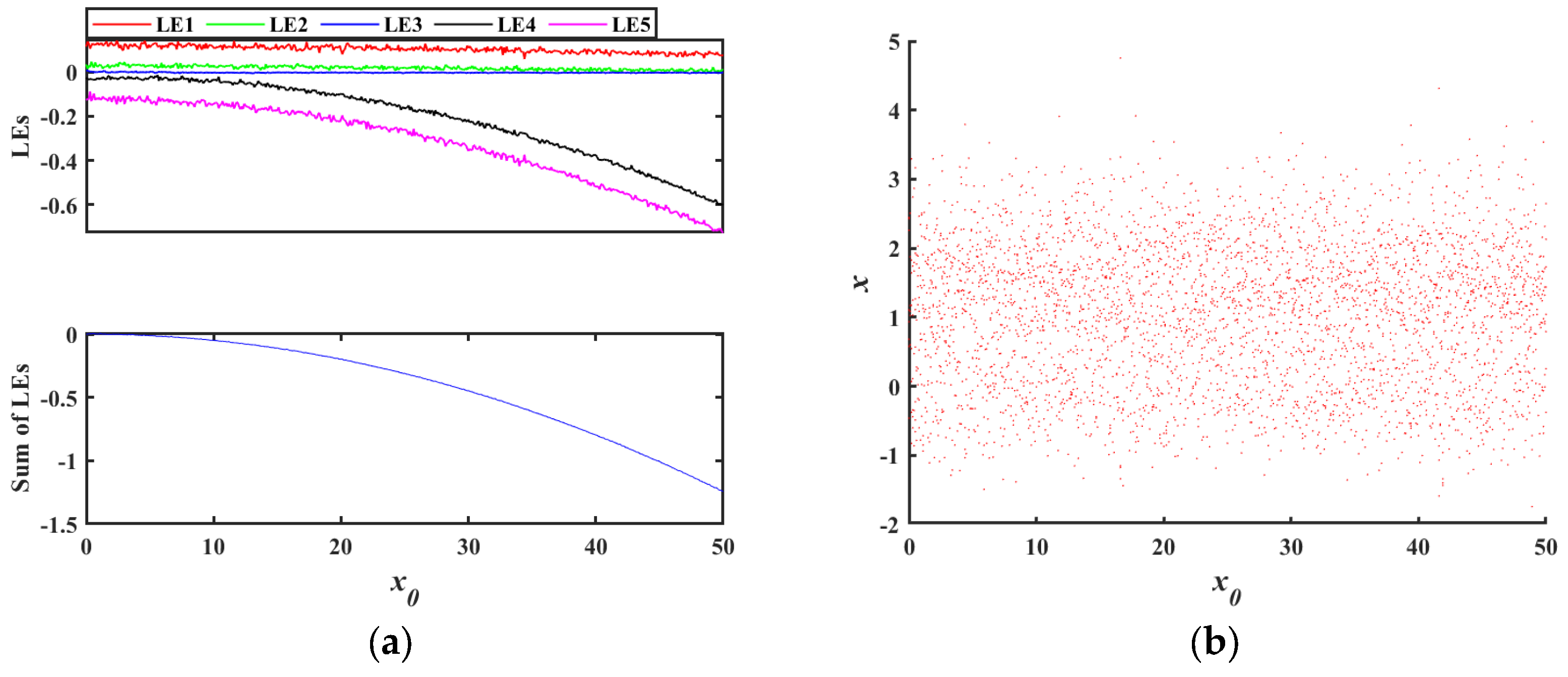

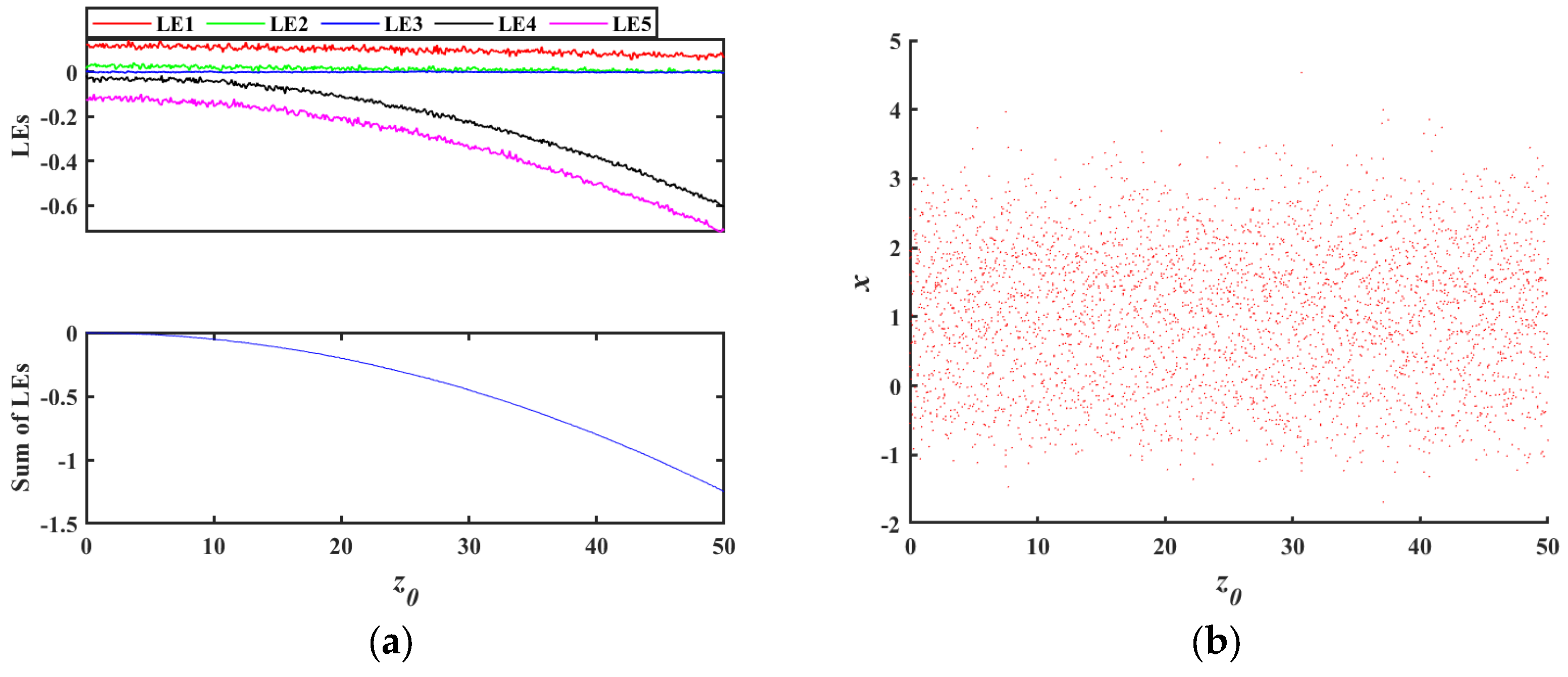






| Input: x0, h, q, a, b, c, d, e, nsteps: Output: xs, ys, zs, ws, us |
| 1: xs(1) = x0; ys(1) = y0; zs(1) = z0; us(1) = u0; vs(1) = v0; 2: for i = 1:nsteps-1 3: k1x = h*(-ays(i)+exs(i)vs(i)); 4: k1y = h(axs(i)+bzs(i)); 5: k1z = h*(-bys(i)+cus(i)); 6: k1u = h*(-czs(i)+dvs(i)); 7: k1v = h*(1-dus(i)-exs(i)^2); 8: k2x = h*(-a*(ys(i)+0.5k1y)+e(xs(i)+0.5k1x)(vs(i)+0.5k1v)); 9: k2y = h(a*(xs(i)+0.5k1x)+b(zs(i)+0.5k1z)); 10: k2z = h(-b*(ys(i)+0.5k1y)+c(us(i)+0.5k1u)); 11: k2u = h(-c*(zs(i)+0.5k1z)+d(vs(i)+0.5k1v)); 12: k2v = h(1-d*(us(i)+0.5k1u)-e(xs(i)+0.5k1x)^2); 13: k3x = h(-a*(ys(i)+0.5k2y)+e(xs(i)+0.5k2x)(vs(i)+0.5k2v)); 14: k3y = h(a*(xs(i)+0.5k2x)+b(zs(i)+0.5k2z)); 15: k3z = h(-b*(ys(i)+0.5k2y)+c(us(i)+0.5k2u)); 16: k3u = h(-c*(zs(i)+0.5k2z)+d(vs(i)+0.5k2v)); 17: k3v = h(1-d*(us(i)+0.5k2u)-e(xs(i)+0.5k2x)^2); 18: k4x = h(-a*(ys(i)+k3y)+e*(xs(i)+k3x)(vs(i)+k3v)); 19: k4y = h(a*(xs(i)+k3x)+b*(zs(i)+k3z)); 20: k4z = h*(-b*(ys(i)+k3y)+c*(us(i)+k3u)); 21: k4u = h*(-c*(zs(i)+k3z)+d*(vs(i)+k3v)); 22: k4v = h*(1-d*(us(i)+k3u)-e*(xs(i)+k3x)^2); 23: xs(i+1) = xs(i)+(k1x+2k2x+2k3x+k4x)/6; 24: ys(i+1) = ys(i)+(k1y+2k2y+2k3y+k4y)/6; 25: zs(i+1) = zs(i)+(k1z+2k2z+2k3z+k4z)/6; 26: us(i+1) = us(i)+(k1u+2k2u+2k3u+k4u)/6; 27: vs(i+1) = vs(i)+(k1v+2k2v+2k3v+k4v)/6; 28: end 29: return xs, ys, zs, ws, us |
| Lyapunov Exponent Sum | System Properties |
|---|---|
| Divergent | |
| Conservative | |
| Dissipative |
| Input: State variables x, y, z, w, u; system parameters a, b, c, d, e Output: Chaotic waveform |
| 1: Configure GPIO pins: GPIO35 as SPI chip select, GPIO36 as SPI clock, GPIO37 as SPI data line. Input initial state variables and parameters. 2: for i = 1 to time do 3: [x_new, y_new, z_new, w_new, u_new] = ADM_Solver (x, y, z, w, u, a, b, c, d, e, h)//Solve differential equations 4: DAC_Ch1 = (y_new + 20) * 500 //Data mapping 5: DAC_Ch2 = (w_new + 20) * 500 //Data mapping 6: SPI_Send(DAC_Ch1, GPIO35, GPIO36, GPIO37) //SPI output, send 24 bit data 7: SPI_Send(DAC_Ch2, GPIO35, GPIO36, GPIO37) //SPI output, send 24 bit data 8: x = x_new; y = y_new; z = z_new; w = w_new; u = u_new//Update state variables 9: end for |
| Input: DAC_Ch1, GPIO35, GPIO36, GPIO37 Output: Analog Signal |
| 1: CS = LOW //Enable chip select 2: for i = 23 down to 0 do //Send data 3: CLK = HIGH 4: MOSI = (data >> i) & 1 //Send current bit 5: CLK = LOW 6: end for 7: CS = HIGH //Release chip select |
| Input: x0, h, q, a, b, c, d, e Output: .x_new, y_new, z_new, w_new, u_new |
| 1: c10 = x; c20 = y; c30 =z; c40 = w; c50 = u; 2: c11 = −a* c20+e*c10*c50; 3: c21 = a*c10+b*c30; 4: c31 = −b*c20+c*c40; 5: c41 = −c*c30+d*c50; 6: c51 = 1−d*c40−e*c10*c10; 7: c12 = −a* c21+e*(c11*c50+c10*c51); 8: c22 = a*c11+b*c31; 9: c32 = −b*c21+c*c41; 10: c42 = −c*c31+d*c51; 11: c52 = 1−d*c41−2*e*c10*c11; 12: c13 = −a*c22+e*(c11*c51+c12*c50+c10*c51*(ᴦ(2q+1)/(ᴦ(q+1)^2))); 13: c23 = a*c12+b*c32; 14: c33 = −b*c22+c*c42; 15: c43 = −c*c32+d*c52; 16: c53 = 1−d*c42−e*(2*c10*c12+c11*c11*(ᴦ(2*q+1)/(ᴦ(q+1)^2))); 17: c14 = −a*c23+e*((c11*c52+c12*c51)*(ᴦ(3q+1)/(ᴦ(q+1)* ᴦ(2q+1)))+c10*c53+c13*c50); 18: c24 = a*c13+b*c33; 19: c34 = −b*c23+c*c43; 20: c44 = −c*c33+d*c53; 21: c54 = 1−d*c43−e*(2*c10*c13+2*c12*c11*(ᴦ(3*q+1)/(ᴦ(q+1)* ᴦ(2q+1)))); 22: c15 = −a* c24+e*((c11*c53+c13*c51)*(ᴦ(4q+1)/(ᴦ(q+1)* ᴦ(3q+1)))+c12*c52*(ᴦ(4q+1)/(ᴦ(2q+1)^2))+c10*c54+c14*c50); 23: c25 = a*c14+b*c34; 24: c35 = −b*c24+c*c44; 25: c45 = −c*c34+d*c54; 26: c55 = 1−d*c44−e*(2*c10*c14+2*c13*c11*(ᴦ(4q+1)/(ᴦ(q+1)* ᴦ(3q+1)))+c12*c12*(ᴦ(4q+1)/(ᴦ(2q+1)^2))); 27: x_new(1)= c10+c11*(h^q/ᴦ(q+1))+c12*h^(2*q)/ᴦ(2*q+1)+c13*h^(3*q)/ᴦ(3*q+1)+c14*h^(4*q)/ᴦ(4*q+1)+c15*h^(5*q)/ᴦ(5*q+1); 28: x_new(2)= c20+c21*(h^q/ᴦ(q+1))+c22*h^(2*q)/ᴦ(2*q+1)+c23*h^(3*q)/ᴦ(3*q+1)+c24*h^(4*q)/ᴦ(4*q+1)+c25*h^(5*q)ᴦ(5*q+1); 29: x_new(3)= c30+c31*(h^q/ᴦ(q+1))+c32*h^(2*q)/ᴦ(2*q+1)+c33*h^(3*q)/ᴦ(3*q+1)+c34*h^(4*q)/ᴦ(4*q+1)+c35*h^(5*q)/ᴦ(5*q+1); 30: x_new(4)= c40+c41*(h^q/ᴦ(q+1))+c42*h^(2*q)/ᴦ(2*q+1)+c43*h^(3*q)/ᴦ(3*q+1)+c44*h^(4*q)/ᴦ(4*q+1)+c45*h^(5*q)/ᴦ(5*q+1); 31: x_new(5)= c50+c51*(h^q/ᴦ(q+1))+c52*h^(2*q)/ᴦ(2*q+1)+c53*h^(3*q)/ᴦ(3*q+1)+c54*h^(4*q)/ᴦ(4*q+1)+c55*h^(5*q)/ᴦ(5*q+1); 32: return x_new, y_new, z_new, w_new, u_new |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Gao, F.; Zhu, M. Bidirectional Conservative–Dissipative Transitions in a Five-Dimensional Fractional Chaotic System. Mathematics 2025, 13, 2477. https://doi.org/10.3390/math13152477
Wang Y, Gao F, Zhu M. Bidirectional Conservative–Dissipative Transitions in a Five-Dimensional Fractional Chaotic System. Mathematics. 2025; 13(15):2477. https://doi.org/10.3390/math13152477
Chicago/Turabian StyleWang, Yiming, Fengjiao Gao, and Mingqing Zhu. 2025. "Bidirectional Conservative–Dissipative Transitions in a Five-Dimensional Fractional Chaotic System" Mathematics 13, no. 15: 2477. https://doi.org/10.3390/math13152477
APA StyleWang, Y., Gao, F., & Zhu, M. (2025). Bidirectional Conservative–Dissipative Transitions in a Five-Dimensional Fractional Chaotic System. Mathematics, 13(15), 2477. https://doi.org/10.3390/math13152477





