Extremal Values of Second Zagreb Index of Unicyclic Graphs Having Maximum Cycle Length: Two New Algorithms

Abstract

It is well-known that the necessary and sufficient condition for a connected graph to be unicyclic is that its omega invariant, a recently introduced graph invariant useful in combinatorial and topological calculations, is zero. This condition could be stated as the condition that the order and the size of the graph are equal. Using a recent result saying that the length of the unique cycle could be any integer between 1 and n − a₁ where a₁ is the number of pendant vertices in the graph, two explicit labeling algorithms are provided that attain these extremal values of the first and second Zagreb indices by means of an application of the well-known rearrangement inequality. When the cycle has the maximum length, we obtain the situation where all the pendant vertices are adjacent to the support vertices, the neighbors of the pendant vertices, which are placed only on the unique cycle. This makes it easy to calculate the second Zagreb index, as the contribution of the pendant edges to such indices is fixed, implying that we can only calculate these indices for the edges on the cycle.

1. Introduction

Throughout this paper, we let $G=(V,E)$ be a graph with the vertex set $V\left(G\right)=\{v_1,v_2,\cdots ,v_n\}$ and edge set $E\left(G\right)$. Let $\left|V\right(G\left)\right|=n$ and $\left|E\right(G\left)\right|=m$ be the order and the size of G. In that case, we use $G(n,m)$ in place of G to emphasize the order and size of G. By a simple graph, we mean that the graph has no loops or multiple edges. If $v_i$ and $v_j$ are adjacent vertices of G and if the edge e connects them, this situation will be denoted by $e=v_i{v}_j$. In such a case, the vertices $v_i$ and $v_j$ are called adjacent vertices and the edge e is said to be incident with $v_i$ and $v_j$. For any vertex $v\in V\left(G\right)$, we denote the degree of v by $d_G\left(v\right)$ or $d\left(v\right)$. The smallest and biggest vertex degrees in a graph will be denoted by $\delta$ and $\Delta$, respectively. If the degree of a vertex is 1, then this vertex is called a pendant vertex, and the edge incident to it is called a pendant edge. If the end vertices of an edge have degrees a and b, then this edge is said to be of type $\{a,b\}$. If there is at least one path between every pair of vertices of a graph, then the graph is said to be connected. Also, the set of all adjacent vertices of a vertex v in a graph G is called the neighborhood of v in G and is denoted by $N_G\left(v\right)$.

Topological indices, also called molecular descriptors by chemists, are the mathematical formulae giving us an invariant number as a result for all isomorphic graphs. The first such index is known as the Wiener index, defined by Wiener in 1947, to compare the boiling points of some alkane isomers. Since then, over 3000 such indices have taken their place in chemical databases for several applications. In this paper, we shall consider one of these indices, called the second Zagreb index, and calculate its extremal values for all connected unicyclic realizations of a given degree sequence such that the cycle length of the unique cycle in these realizations is maximum. We use the recently introduced graph invariant called omega invariant to determine unicyclicness condition obtained in [1] and the maximum cycle length formula obtained in [2] to obtain our results.

Of course, if the graphs are given, then the calculation of Zagreb or any other indices of graphs is very easy. But there is no general way of finding the values of any index for all the realizations of a given degree sequence. So here, not being able to calculate the second Zagreb index, we algorithmically find the extremal values of this index for unicyclic graphs with maximum cycle length. In the future, we believe that there will be follow-up papers for other graph classes and for other index types.

The first and second Zagreb indices of a graph G were defined by Gutman and Trinajstic in 1972 [3] by

$${\displaystyle M_1\left(G\right)=\sum _{e=uv\in E\left(G\right)}(d_u+d_v)\mathrm{and}{M}_2\left(G\right)=\sum _{e=uv\in E\left(G\right)}{d}_u{d}_v,}$$

respectively. The first Zagreb index is also formulated by ${\displaystyle M_1\left(G\right)=\sum _{v\in V\left(G\right)}{d}_v^2}$, alternatively. Some properties of these two indices are studied in [4,5,6,7,8,9,10].

The extremal values of topological indices are quite useful when we cannot obtain the exact values of them.

A recently defined graph invariant is called the omega invariant, see [2], which is defined for a degree sequence $D=\{1^{\left(a_1\right)},2^{\left(a_2\right)},\cdots ,{\Delta }^{\left(a_{\Delta }\right)}\}$ by $\Omega \left(D\right)={\sum }_{i=1}^{\Delta }{a}_i(i-2)$ where $a_i$’s are non-negative integers and $\Delta$ denotes the biggest vertex degree. Although it has a close relation with these two earlier graph parameters mentioned in [1,2,11], the omega invariant is still used in classifying several graph theoretical, topological and combinatorial properties, giving shorter proofs of the existing theorems such as Edmonds’ theorem which was proved in 1964 on the potential connectivity of realizations of a degree sequence and also in answering several open problems such as the connectivity of the realizations of a given degree sequence which was still an open problem before omega invariant was defined. The answer to this important open problem was given by the following statement: If $\Omega \left(D\right)\le -4$, then all the realizations are disconnected and cannot be drawn as a connected graph in any way. For all other values of $\Omega \left(D\right)$, the realizations could be connected or disconnected, which is briefly stated with the statement “potential connected”. Another example of open problems answered by the omega invariant is the cyclicness of the realizations of a degree sequence. In [1], the conditions for the cyclicness, in particular, acyclicness, unicyclicness, bicyclicness, tricyclicness, etc., are all stated in terms of omega invariant. There are over 60 papers, hundreds of conference papers, and at least five PhD theses on the omega invariant in the literature so far, and many graph parameters are related to the omega invariant, making it an invaluable tool for many calculations. In the remaining parts of this manuscript, we shall make use of some fundamental properties of the omega invariant, in particular, with the unicyclic realizations of D which are characterized by the statement that $\Omega \left(D\right)=0$. We could just use the word “unicyclic” for the realizations instead of using $\Omega \left(D\right)=0$, but as we leave some open problems for acyclic, bicyclic, tricyclic, etc., of the realizations as a generalization of the problem studied in this manuscript, we have to use omega invariant necessarily for this generalization possibility.

In many problems with graph parameters or topological graph indices, one cannot obtain the exact values of the required parameter or index. In such cases, we may go for the maximum and minimum values instead of the exact value. Similarly, we may be considering some property for a family of graphs that share a common property. Such problems are called extremal problems. A reasonable problem to consider would be the following:

Problem 1.

Find the extremal values of $M_1$ and $M_2$ for all connected unicyclic realizations of a given degree sequence D having maximum cycle length $n-a_1$.

Here, we answer this problem that we propose, and many similar results can be obtained for thousands of other graph indices. The methods that will be utilized could show slight changes from the ones here, according to the differences between topological graph indices.

One may wonder why we are dealing with the case of maximum cycle length. If we do not put this condition and the length of our unique cycle is shorter than $n-a_1$, say of length k, then $n-a_1-k$ vertices have to be placed outside the unique cycle. The only places are the ends of pendant edges. So the situation becomes more complicated and needs further assumptions. Without new assumptions, there is a large number of possible realizations, making the situation difficult to handle.

As the first Zagreb index can be reformulated as the sum of squares of all vertex degrees, for a given degree sequence D, all values of $M_1\left(G\right)$ where G is a realization of D will be the same. Therefore, the answer to our problem is quite obvious for the first Zagreb index:

Proposition 1.

$M_1\left(G\right)$ is fixed for all connected realizations G of a unicyclic degree sequence D having maximum cycle length $n-a_1$.

Hence, the minimum and maximum values of $M_1$ for this class of graphs are equal to each other. Therefore, we can only study the extremal values of the second Zagreb index for the same class of graph realizations.

2. Minimum Values of Second Zagreb Index of Unicyclic Graphs Having Maximum Cycle Length

Let $\Omega \left(D\right)=0$. In [2], it was shown that all connected realizations of D must be unicyclic and also the maximum cycle length can be $a_2+a_3+a_4+\cdots +a_{\Delta }=n-a_1$ in Theorem 3.3 in [2]. Let $G_i\left(k\right)$ be a unicyclic graph with cycle length k. By [2], $k=1,2,\cdots ,n-a_1$. As we are dealing with unicyclic graphs, which have the maximum cycle length, we shall take $k=n-a_1$. We want to determine the smallest second Zagreb index of all $G_i(n-a_1)$. In the case of maximum cycle length, all non-pendant vertices must be on the unique cycle. Also note that the placement of these vertices on the cycle does not affect the value of the second Zagreb index. We now have a useful result which will be needed later:

Observation 1.

Let $d_i\ge 3$. The contribution $d_i$ of a pendant edge $\{1,d_i\}$ to the second Zagreb index is the same for all realizations $G_i(n-a_1)$.

Therefore, we may omit the contributions of pendant edges when comparing the second Zagreb indices of all unicyclic realizations having the maximum value of the $M_2$. Henceforth, we shall denote the part of $M_2\left(G_i(n-a_1)\right)$ which is calculated only by means of non-pendant edges by $M_2^{*}\left(G_i(n-a_1)\right)$. Of course, this argument is only valid for connected unicyclic graphs.

In the following result, we calculate the total contribution of all pendant edges to the second Zagreb index by subtracting the contribution of non-pendant edges from the contribution of all edges:

Lemma 1.

Let G be a realization of a unicyclic degree sequence D with maximum cycle length. Then, the total contribution of all pendant edges to the second Zagreb index is

$${\displaystyle M_2\left(G\right)-M_2^{*}\left(G\right)=\sum _{i=3}^{\Delta }{a}_i\left(i^2-2i\right).}$$

Proof .

We know that the graph is unicyclic by [2]. The total contribution of all pendant edges to the second Zagreb index is $M_2\left(G\right)-M_2^{*}\left(G\right)$. Recall that there are $n-a_1$ non-pendant vertices which are placed on the unique cycle of the graph G. If these vertices have degrees $i\ge 2$, then there are $i-2$ pendant edges at each such vertex, as such a vertex is connected to two other neighboring vertices of the cycle, and as the graph is unicyclic. The contribution of each pendant edge, which will have vertex degrees 1 and i is $i·1=i$ and for each vertex, each of the $i-2$ pendant edges will contribute this much. Finally, there are $a_i$ times non-pendant vertices of degree i. For the vertices of degree 2 on the cycle, $i-2=0$ so no contribution is obtained from these vertices. So the sum is taken over all vertices of degree at least 3, and the required contribution is

$$\begin{array}{cc}\hfill M_2\left(G\right)-M_2^{*}\left(G\right)& {\displaystyle =\sum _{i=3}^{\Delta }(i-2)(i·1)a_i}\hfill \\ & {\displaystyle =\sum _{i=3}^{\Delta }{a}_i\left(i^2-2i\right).}\hfill \end{array}$$

□

We now give a useful result which will help us to prove our algorithm:

Lemma 2

((Rearrangement inequality) [12]). Let $r_1\le r_2\le \cdots \le r_n$ and $s_1\le s_2\le \cdots \le s_n$ be two sequences of integers. For any permutation $(t_1,t_2,\cdots ,t_n)$ of $(r_1,r_2,\cdots ,r_n)$, we have

$$r_1{s}_1+r_2{s}_2+\cdots +r_n{s}_n\ge s_1{t}_1+s_2{t}_2+\cdots +s_n{t}_n\ge r_n{s}_1\ge r_{n-1}{s}_2+\cdots +r_1{s}_n.$$

Note that the smallest value of the sum of the products of $r_i$’s and $s_i$’s appears when the larger values are multiplied by smaller values. This fact will be the key point in our algorithm.

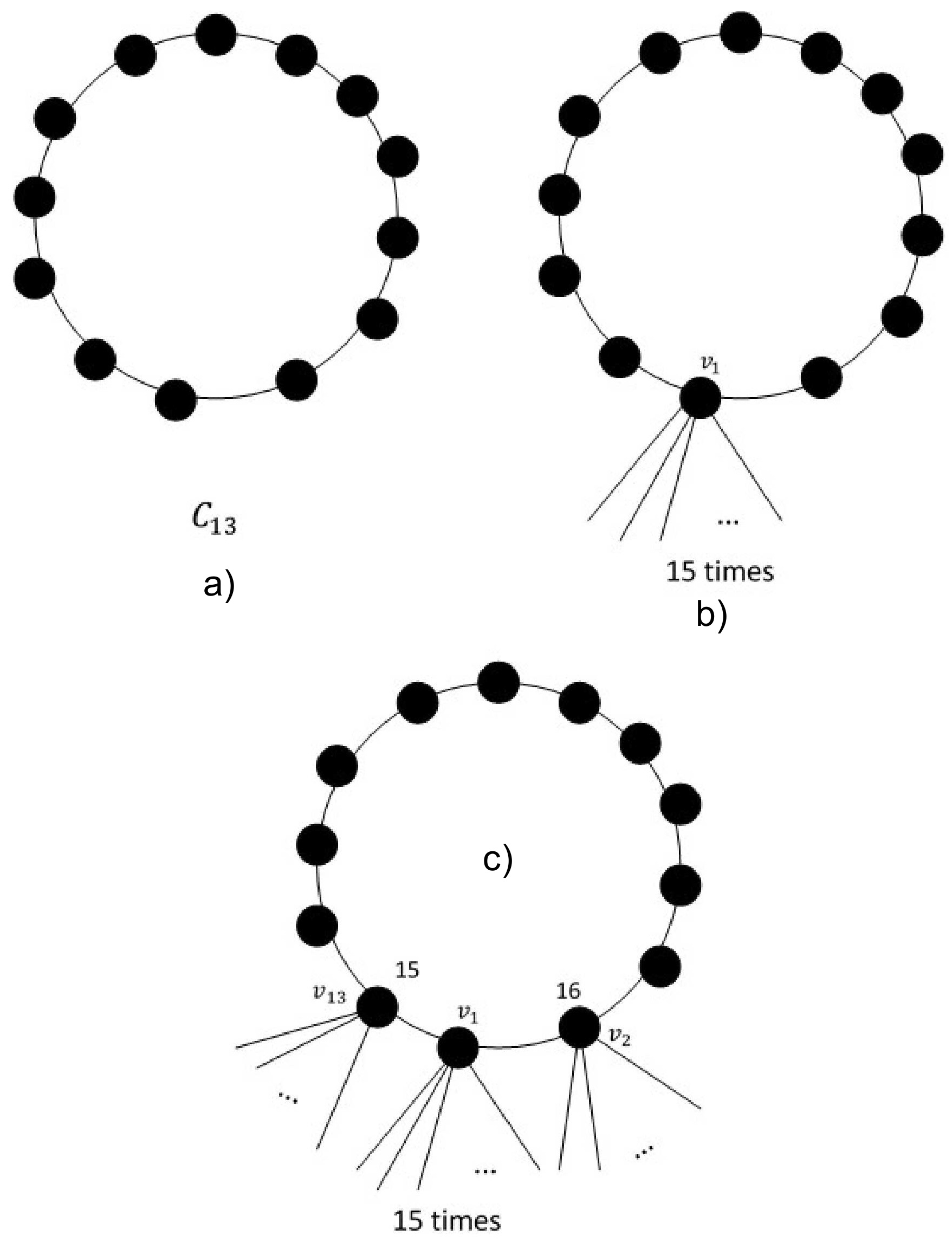
Let $D=\{1^{\left(a_1\right)},2^{\left(a_2\right)},\cdots ,{\Delta }^{\left(a_{\Delta }\right)}\}$ be a realizable degree sequence with $\Omega \left(D\right)=0$. Here $a_i\ge 0$ are integers and $\Delta$ is the biggest vertex degree. We relabel the vertex degrees that are greater than 1 by $d_1\ge d_2\ge \cdots \ge d_{n-a_1}$. The following algorithm gives us the realization of D with the minimum second Zagreb index.

Theorem 1 (Minimum second Zagreb index algorithm).

Consider a realization $G=G_i(n-a_1)$ of a unicyclic degree sequence D that has a maximum cycle length constructed as below. Then G has the minimum second Zagreb index amongst all unicyclic realizations of D having maximum cycle length.

• Label the vertices on the cycle by $v_1,v_2,\cdots ,v_{n-a_1}$ in rotating order (clockwise or anticlockwise). Wlog, we choose anticlockwise orientation. Assign the largest vertex degree $d_1$ to $v_1$.
• Assign the smallest vertex degree $d_{n-a_1}$ to $v_2$ and the next smallest vertex degree $d_{n-a_1-1}$ to $v_{n-a_1}$. That is, to both neighbors of the vertex with the largest vertex degree, we must place the two smallest vertex degrees.
• Assign the next largest vertex degree $d_2$ to $v_3$ and the remaining next biggest vertex degree $d_3$ to $v_{n-a_1-1}$.
• Repeat the last two steps until all vertices are labeled by the remaining vertex degrees. Note that when $n-a_1$ is odd, we have to label the last remaining vertex with that final degree, creating no new edge products.

Proof .

Our aim is to place $n-a_1$ positive integers to $n-a_1$ vertices on a cycle such that $M_2^{*}$ (and hence $M_2$) takes its minimum value. By the rearrangement inequality in Lemma 2, we must place two smallest degrees next to a large degree. So we start with the biggest degree $d_1$ and place the smallest two degrees to its adjacent vertices. At the next step, we must label the two adjacent vertices by the two largest degrees. The steps continue by placing the two largest and the two smallest degrees in a row, finishing the proof. □

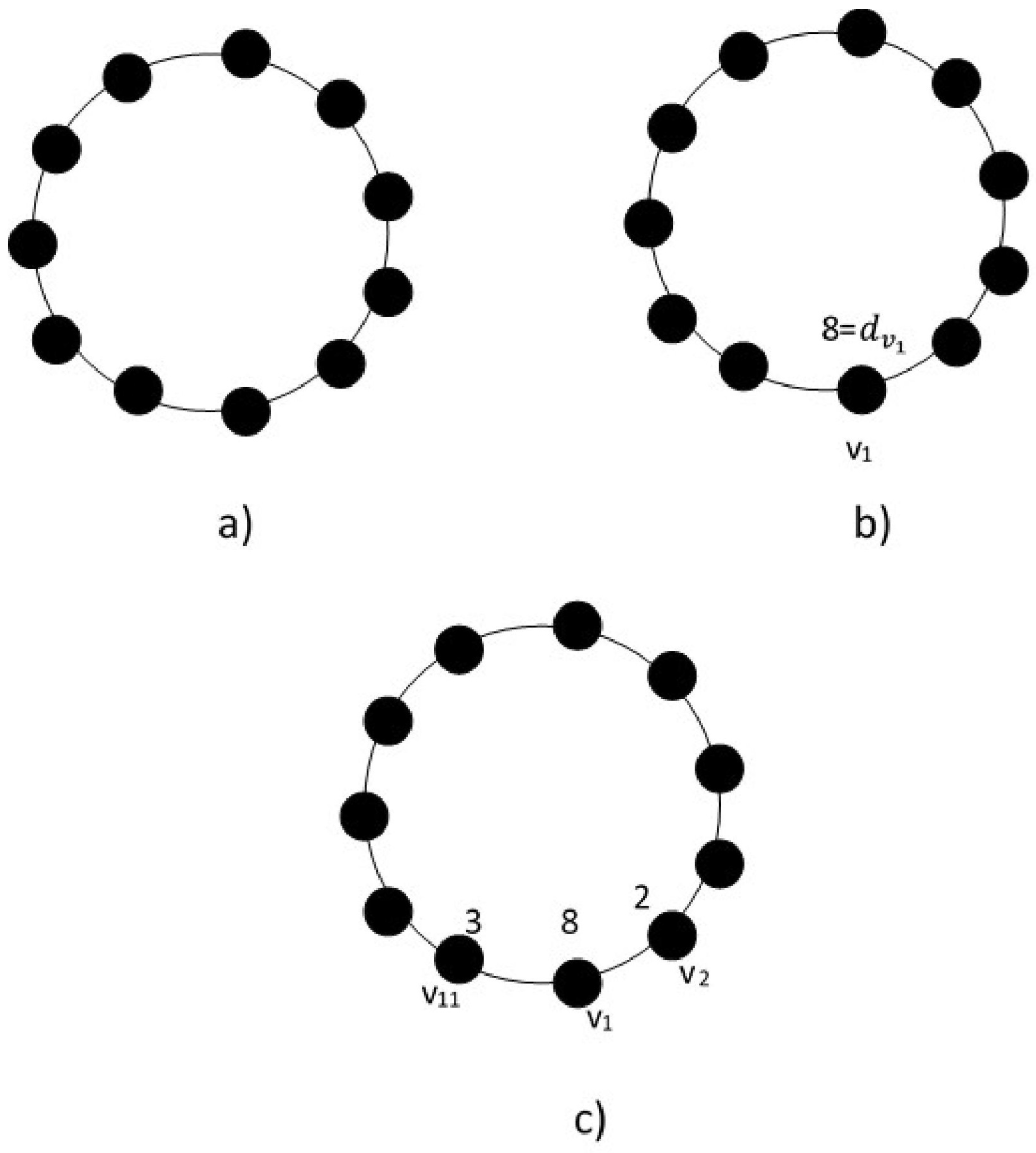
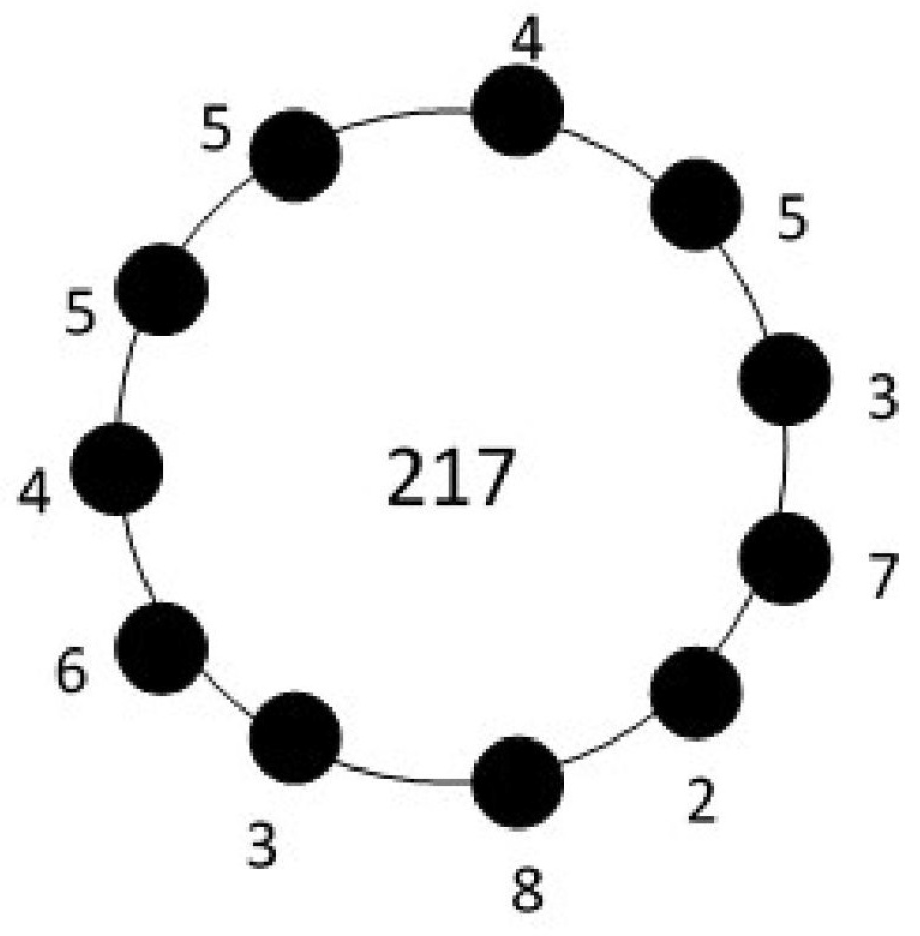
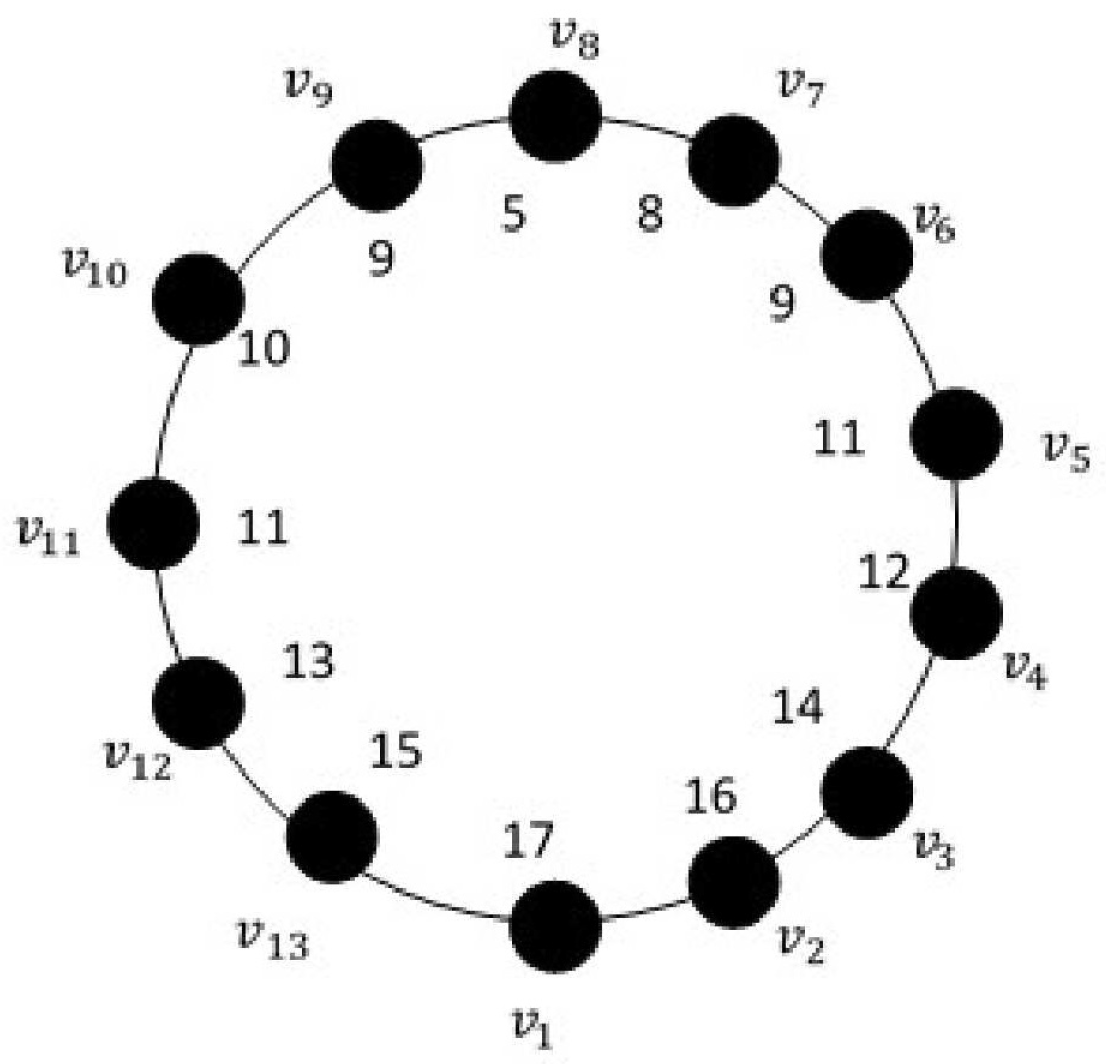
Example 1.

Let $D=\{1^{\left(30\right)},2^{\left(1\right)},3^{\left(2\right)},4^{\left(2\right)},5^{\left(3\right)},6^{\left(1\right)},7^{\left(1\right)},8^{\left(1\right)}\}$. Then, by the definition of omega invariant, we have $\Omega \left(D\right)=30(1-2)+1(2-2)+2(3-2)+2(4-2)+3(5-2)+1(6-2)+1(7-2)+1(8-2)=0$. We shall form several realizations of D as a connected unicyclic graph with maximum cycle length $n-a_1=11$ and observe that the realization obtained according to the final algorithm gives us the smallest second Zagreb index.

To apply our algorithm (Theorem 1), we start with a cycle graph $C_{n-a_1}=C_{11}$ and label its vertices as in Figure 1a. Then we label one of the vertices, say $v_1$ by the largest vertex degree, which is 8, see Figure 1b. At the second step, we pick up the smallest two degrees at non-pendant vertices, which are 2 and 3 and assign them to two adjacent vertices of $v_1$, say $v_2$ and $v_{n-a_1}=v_{11}$ as in Figure 1c. Then we follow the steps in the algorithm to reach the final labeling with minimum second Zagreb index, see Figure 2.

Here, the pendant edges are omitted in all figures as they do not affect the value of the second Zagreb index of all realizations, and they make the figures crowded. Therefore, for example, in Figure 1c, there are normally $3-2=1$ pendant edges at $v_{11}$ and $8-2=6$ pendant edges at $v_1$. But they are not drawn in the figures throughout the paper for the above reason. In Figure 3, three random examples of realizations are illustrated.

3. Maximum Values of Second Zagreb Index of Unicyclic Graphs Having Maximum Cycle Length

Secondly, we consider the problem of finding the maximum values of the second Zagreb index amongst all connected unicyclic realizations of some D having maximum cycle length. The following algorithm gives us the graph with this property:

Theorem 2 (Maximum second Zagreb index algorithm).

Let $D=\{1^{\left(a_1\right)},2^{\left(a_2\right)},\cdots ,{\Delta }^{\left(a_{\Delta }\right)}\}$ be a unicyclic degree sequence. Let $G=G_i(n-a_1)$ be a connected realization of D constructed by the following algorithm. Then, the maximum value of the second Zagreb index amongst all realizations of D with maximum cycle length is obtained for G:

• Assign the largest vertex degree to a vertex, say $v_1$.
• Assign the next largest vertex degree to one of the two vertices adjacent to $v_1$, say $v_2$ and assign the second largest vertex degree to the adjacent vertex with largest vertex degree so far, that is $v_1$. So let us call this vertex by $v_3$.
• For all the remaining vertex degrees, assign the largest value to the vertex that is adjacent to the larger of the two vertices at both ends of the labeled vertices. If any placement violates the alternating large/small rule, swapping the offending pair reduces the sum by the rearrangement inequality, hence our labeling is optimal.

Proof .

To obtain the largest value of the second Zagreb index amongst all connected unicyclic realizations of D having maximum cycle length, we must multiply the large values by large values. By Lemma 2, each swap strictly increases the local product. This proves the algorithm. □

The main idea that we utilize in this algorithm is very simple and depends on the rearrangement inequality: To obtain the larger values of the second Zagreb index amongst all connected unicyclic realizations of D having maximum cycle length, we have to select the correct ordering of the $n-a_1$ positive integers placed on a cycle graph so that the sum of all possible products of the successive pairs of those integers gives us the higher sums. Naturally, to obtain a higher sum, we must multiply large numbers by large numbers. Similarly, to obtain a higher sum, we must multiply large numbers by small numbers. We illustrate the algorithm in the following example:

Example 2.

Let $D=\{1^{\left(124\right)},5^{\left(1\right)},8^{\left(1\right)},9^{\left(2\right)},{10}^{\left(1\right)},{11}^{\left(2\right)},{12}^{\left(1\right)},{13}^{\left(1\right)},{14}^{\left(1\right)},{15}^{\left(1\right)},{16}^{\left(1\right)},{17}^{\left(1\right)}\}$ be a set. As $\Omega \left(D\right)=0$, all connected realizations of D will be unicyclic. Amongst those, the ones with maximum cycle length will have a cycle of length $n-a_1=13$. Now form a cycle graph $C_{13}$ as in Figure 4a. For each vertex degree $d_i$ in D that is greater than 2, we add $d_i-2$ pendant edges to the corresponding vertex. According to our algorithm, as the largest vertex degree in D is 17, say for the vertex $v_1$, we add $17-2=15$ pendant edges to $v_1$, see Figure 4b. At the end, we do this for all vertices with degree greater than 2 on the unique cycle. Figure 4c shows the beginning step of the algorithm where the successive vertices $v_2,v_1$ and $v_{13}$ are added the required numbers of pendant edges.

Figure 5 shows the completed labeling of the 13-cycle with the largest possible second Zagreb index 1845, where the pendant edges are also counted in the calculation of $M_2$. Once more, note that we start with the largest vertex degree, place the next largest two on both sides of the first vertex, and continue with the remaining largest vertex degree in the same fashion as explained in Theorem 2.

4. Conclusions

In [2], it was shown that the length of the unique cycle could be any integer between 1 and $n-a_1$ where $a_1$ is the number of pendant vertices in the graph. In the particular case where the cycle has the maximum length, we obtain the ideal situation where all the pendant vertices are adjacent to the support vertices lying only on the unique cycle. This makes it easy to calculate any index, as the contribution of the pendant edges to such indices is fixed, implying that we can only calculate these indices for the edges on the cycle. In this paper, two novel algorithms are introduced to find the extremal values of the second Zagreb index. Some potential extensions (acyclic, bicyclic, etc.) can also be studied, but one needs further hypotheses to study such graphs. As open problems, we propose the following questions: Could these algorithms be extended to all other degree-based indices and to all other topological indices? We believe that it would be possible to give several algorithms for acyclic, bicyclic, tricyclic and k-cyclic graphs to generalize the algorithmic approach given here. But the situation is different when the graph is unicyclic, that is, the omega invariant is zero. We are sure of what we have as possible realizations of such a degree sequence. In all other cases, one needs to know more information, which makes it much more difficult. In the future, we hope to find these conditions and have the general case.