Optical Frequency Comb-Based Continuous-Variable Quantum Secret Sharing Scheme

Abstract

Quantum secret sharing (QSS) faces inherent limitations in scaling to multi-user networks due to excess noise introduced by highly asymmetric beam splitters (HABSs) in chain-structured topologies. To overcome this challenge, we propose an optical frequency comb-based continuous-variable QSS (OFC CV-QSS) scheme that establishes parallel frequency channels between users and the dealer via OFC-generated multi-wavelength carriers. By replacing the chain-structured links with dedicated frequency channels and integrating the Chinese remainder theorem (CRT) with a decentralized architecture, our design eliminates excess noise from all users using HABS while providing mathematical- and physical-layer security. Simulation results demonstrate that the scheme achieves a more than 50% improvement in maximum transmission distance compared to chain-based QSS, with significantly slower performance degradation as users scale to 20. Numerical simulations confirm the feasibility of this theoretical framework for multi-user quantum networks, offering dual-layer confidentiality without compromising key rates.

1. Introduction

Quantum secret sharing (QSS) [1,2,3,4,5,6,7,8], as a multi-party secure quantum communication protocol, achieves dual-layer (quantum and physical) confidentiality by partitioning secrets among participants so that only authorized user groups can reconstruct the full information. In such a system, a designated dealer receives quantum states from multiple users through quantum channels and then distributes secrets and keys to ensure that no subset below the threshold can access the complete key information. Since the initial QSS proposal [1], numerous schemes have emerged [2,3,4]. In 2005, Christian Schmid et al. [5] introduced a single-qubit QSS with chain-structured transmission. Subsequently, Warren P. Grice and Bing Qi [6] developed continuous-variable QSS (CV-QSS) using similar architectures, followed by user-side and structural refinements [7,8]. Nevertheless, these works remain constrained by chain topologies, inevitably introducing excess noise through highly asymmetric couplers in multi-user quantum channels.

Meanwhile, optical frequency combs (OFCs) have gained attention as efficient WDM sources [9]. An OFC spectrum comprises equally spaced narrowband lines, $f_n=f_0+n·f_r$ where $f_0$ is the carrier-envelope offset frequency, $f_r$ is the repetition rate, and n is the mode index. Their advantages in spectral efficiency [10], receiver design [11,12,13,14], and signal processing [15,16,17] for WDM have motivated Lars Lundberg et al. [18] to implement OFC-based WDM transmission. Yijun Wang et al. [19] further leveraged OFCs for parallel transmission and coherent reception to boost CV-QKD key rates. While microresonator-based OFCs enable chip-scale integration [20,21], their phase noise (>100 rad/Hz^1/2 [22]) and line-spacing instability limit multi-user synchronization. We employ standard fiber-based OFCs due to their superior phase coherence (<10 rad/Hz^1/2 [19]) and precise frequency control, which are critical for parallel quantum channels requiring sub-Hz stability. Despite QSS’s greater need for parallel multi-user quantum channels, no theoretical or experimental OFC-based QSS studies exist. While recent experimental advances have demonstrated chip-based generation of photonic graph states for measurement-driven quantum processing [23], hyperentanglement-enhanced high-capacity quantum secure direct communication [24], and robust coherent-state QSS implementations tolerant of channel imperfections [25], these approaches fundamentally constrain scalability in multi-user secret sharing. Chip-integrated architectures lack wavelength-agile parallelism for dynamic user access; hyperentanglement systems incur prohibitive hardware complexity beyond a few-user scenarios; and existing CV-QSS experiments remain bound to chain-structured topologies that suffer from cumulative noise. Although microresonator soliton microcombs offer chip-scale advantages [26], this work employs fiber-based OFCs due to compatibility constraints with existing CV-QSS implementations and laboratory capabilities.

This work proposes an OFC-based CV-QSS scheme. Building on decentralized QSS architectures, we establish dedicated frequency channels between the dealer and individual users via OFCs, eliminating excess noise from chain couplers and removing idealistic assumptions (e.g., equidistant users). Consequently, we resolve the severe degradation of key rates and transmission distance that occurs with user scaling. Simultaneously, the Chinese remainder theorem (CRT) and decentralized structures ensure mathematical and architectural security, providing non-quantum layer protection.

This paper is organized as follows. In Section 2, we detail the mathematical foundations of the OFC-based CV-QSS scheme and describe the process of generating multi-frequency quantum states via OFCS for quantum transmission of our proposed OFC-based CV-QSS scheme. Additionally, we present the protocol design and implementation workflow. In Section 3, we firstly establish the classical (non-quantum) security through mathematical formalism and architectural analysis, then analyze the system security in terms of quantum aspects. Through numerical simulations, we evaluate the system performance, confirming the feasibility and superiority of the proposed scheme. The performance of the scheme is analyzed and verified via numerical simulations in Section 4. And we present our conclusions in Section 5.

2. Optical Frequency Comb-Based Continuous-Variable Quantum Secret Sharing Scheme

2.1. Preliminaries of the Chinese Remainder Theorem

The Chinese remainder theorem states: Let $m_1,m_2,\cdots ,m_k$ be k pairwise relatively prime positive integers. Then, for any integers $c_1,c_2,\cdots ,c_k$, there exists an integer x such that

$$\left\{\begin{array}{c}x\equiv c_1\left(\mathrm{mod}{m}_1\right)\hfill \\ x\equiv c_2\left(\mathrm{mod}{m}_2\right)\hfill \\ \cdots \hfill \\ x\equiv c_k\left(\mathrm{mod}{m}_k\right)\hfill \end{array}\right.$$

all of which hold. Moreover, in the sense of modulo $m_1{m}_2\cdots m_k$, the solution of the above system of congruence equations is unique and can be expressed as

$$x\equiv x_0(\mathrm{mod}{m}_1{m}_2\cdots m_k)$$

Here, $x_0$ can be determined as follows: Let $M_i={\displaystyle \frac{1}{m_i}}\left({\prod }_{j=1}^k{m}_j\right)$, $1⩽i⩽k$, and assume that $M_i^{-1}$ is the multiplicative inverse of $M_i$ modulo $m_i$. Then we can take

$$x_0=\sum _{j=1}^k{M}_j{M}_j^{-1}{c}_j$$

The proof of this theorem is straightforward. The integer x that satisfies the system of congruence equations can also be obtained in the following way: Let $x_1=c_1$, then $x_1$ satisfies the first equation. Consider the numbers $x_1+m_1,x_1+2m_1,\cdots ,x_1+m_2{m}_1$. Since $(m_1,m_2)=1$, they form a complete residue system modulo $m_2$. Therefore, there is an $x_2$ among them such that $x_2\equiv c_2\left(\mathrm{mod}{m}_2\right)$, and this $x_2$ satisfies the first two equations simultaneously. Then consider $x_2+m_2{m}_1,x_2+2m_2{m}_1,\cdots ,x_2+m_3{m}_2{m}_1$ and so on. By successive iteration, the integer $x_k$ that satisfies all the equations can be found.

If we do not know all the remainders of the congruence equations, taking the number of users as three as an example, given moduli $n_1=3$ and $n_2=5$ (pairwise coprime) with known remainders $x\equiv 2\left(\mathrm{mod}3\right)$ and $x\equiv 3\left(\mathrm{mod}5\right)$, the equations can be merged into $x\equiv 8\left(\mathrm{mod}15\right)$. However, if the remainder constraint for the third modulus $n_3=7$ is missing, the solution is not unique; substituting $x=15m+8$ and iterating m from 0 to 6 yields seven candidate solutions modulo 105 (i.e., $x=8, 23, 38, 53, 68, 83, 98$). All candidates satisfy the known equations, but the absence of the mod 7 constraint prevents the unique determination of x.

2.2. Optical Frequency Comb-Based Continuous-Variable Quantum Secret Sharing Scheme

This work presents a CV-QSS architecture that integrates phase-randomized optical frequency combs with displacement-driven quantum state modulation, enabling high-dimensional secure communication. The system leverages a multi-wavelength quantum source generated by the dealer, characterized by a central frequency $f_0^s$ and repetition rate $f_r^s$. The quantum field optical comb is mathematically expressed as follows:

$$\widehat{s}\left(t\right)=\sum _{n=n_{\min }}^{n_{\max }}\left(X_n^A+i{P}_n^A\right)exp\left\{j\left[-\phi \left(t\right)+2\pi \left(f_0^s+n{f}_r^s\right)t\right]\right\},$$

(1)

where $X_n^A$ and $P_n^A$ denote quadrature components following zero-mean Gaussian distributions with variance ${\sigma }^2$ (in shot-noise units), and $\phi \left(t\right)$ represents phase noise from laser fluctuations. Critically, each sub-comb branch is modulated with Rayleigh-distributed amplitudes $V_n\sim Ra\left(\sigma \right)$ and uniformly randomized phases ${\mathsf{\Phi }}_n\in [0,2\pi ]$, which collectively act as displacement operators $D\left({\alpha }_n\right)$ to coherently modulate the two-mode squeezed vacuum (TMSV) states transmitted by $Use{r}_j$, where $D\left({\alpha }_k\right)=\exp ({\alpha }_k{\widehat{a}}^{†}-{\alpha }_k^{*}\widehat{a})$ with ${\alpha }_k=V_k{e}^{j{\mathsf{\Phi }}_k}$ encodes classical randomness into TMSV states.

The dealer demultiplexes the optical comb into $N=n_{\max }-n_{\min }+1$ parallel sub-channels. For central sub-channels ($k=n_{\min }+1,\dots ,n_{\max }-1$), the displacement parameter ${\alpha }_k=V_k{e}^{j{\mathsf{\Phi }}_k}$ is generated through Rayleigh-amplitude and random-phase modulation. This displacement operation directly impresses classical randomness onto the quantum noise of $Use{r}_j$’s TMSV states, achieving quadrature-dependent encoding while preserving their inherent squeezing correlations. The exponential decay of the Rayleigh distribution inherently suppresses large-amplitude modulation events, confining excess noise near the shot-noise limit. Edge sub-channels ($r=n_{\min },n_{\max }$) encode fixed quadratures $X_r^A,P_r^A$ to facilitate phase drift compensation during detection.

At the receiver, $Use{r}_j$ employs a local optical frequency comb ($f_0^L=f_0^s,f_r^L=f_r^s$) to demultiplex the incoming signal into N frequency bins. Pilot tones are isolated for phase noise estimation via a phase-locked loop (PLL), while data-carrying sub-channels undergo adaptive homodyne detection. The pre-applied displacement modulation $D\left({\alpha }_k\right)$ reshapes the quadrature noise of the TMSV states, enabling direct measurement of their variances through $X/P$-basis homodyne detectors. Real-time phase modulation aligns measurement bases with the dealer’s encoding parameters, ensuring that the bases match for sifting.

Post-processing involves four key steps, as follows: (1) Basis sifting, where $Use{r}_j$ announces measurement bases and the dealer retains data from matched sub-channels; (2) parameter estimation, leveraging public disclosure of partial keys to evaluate channel transmittance $T_k$ and excess noise ${ϵ}_k$, with Rayleigh statistics enabling precise noise-floor calibration; (3) multi-mode reconciliation using rate-adaptive LDPC codes optimized by displacement correlation matrices; and (4) privacy amplification via universal hashing, where security proofs exploit the phase-space symmetry induced by displacement operations.

By unifying classical phase randomization with quantum displacement operations as in Figure 1, this architecture establishes a resource-efficient framework for large-scale quantum-secured networks. Figure 1 and Figure 2 depict the operational workflow of the proposed OFC CV-QSS scheme: (a) The dealer first determines the number of optical frequency comb (OFC) carrier pairs based on the user count. (b) Point-to-point quantum communication channels are established individually between the dealer and each user through dedicated OFC carriers. This process follows CV-QSS fairness protocols. (c) After all quantum links are established, the minimum key rate among the point-to-point connections defines the system key rate lower bound $R=min\{R_1,R_2,\dots ,R_n\}$. The final shared secret key is then derived through classical post-processing of quantum-measurement outcomes. The dealer’s optical comb not only serves as a multi-wavelength carrier but also physically enhances security through displacement-driven modulation of $Use{r}_j$’s TMSV states, ensuring compatibility with existing fiber-optic infrastructure and enabling high-rate, long-distance CV-QKD deployment.

Then, we present a secure CV-QSS scheme based on optical frequency combs, enabling the dealer to distribute a classical secret S to n participants via the CRT. The protocol consists of three phases [4].

2.2.1. Initialization

The dealer selects n primes $m^{U_1}=2$, $m^{U_2}=3$, …, $m^{U_n}$ (e.g., the first n primes), which are inherently coprime (i.e., $\gcd (m^{U_i},m^{U_j})=1$ for all $1\le i\ne j\le n$). The secret $S\in {\{0,1,\dots ,M\}}^L$, a checksum sequence $R\in {\{0,1,\dots ,M\}}^{L_1}$, and a unique pointer $P^{*}\in {\{0,1,\dots ,M\}}^{L_2}$ are generated, where $M={\prod }_{k=1}^n{m}^{U_k}-1$. The dealer put $P^{*}$ behind S and embeds them into R to form a sequence X as Figure 3, ensuring the uniqueness of $P^{*}$ (i.e., if a substring $T_j=P^{*}$, all other $T_k\ne P^{*}$). Shadows $X^{U_i}=X\mathrm{mod}{m}^{U_i}$ are computed for each participant $U_i$, and the parameters $\{m^{U_1},\dots ,m^{U_n}\}$, L, $L_1$, $L_2$, $P^{*}$, verification data V, and hash function $H\left(\right)$ are published.

2.2.2. Distribution

The dealer distributes $X^{U_i}$ to each user $U_i$ via optical frequency comb-based quantum channels: 1. State Preparation: Each $U_i$ prepares $L+L_1+L_2$ two-mode squeezed vacuum states, with quadratures derived from vacuum states ${\widehat{x}}_1^{\left(0\right)},{\widehat{p}}_1^{\left(0\right)}$ and ${\widehat{x}}_2^{\left(0\right)},{\widehat{p}}_2^{\left(0\right)}\sim N(0,1)$ with squeezing parameter r, satisfying:

$$\underset{r\to +\infty }{lim}{x}_1=x_2,\underset{r\to +\infty }{lim}{p}_1=-p_2.$$

2. Eavesdropping Detection: Users send the squeezed state $a_2$ and coherent states c to the dealer for error rate analysis. If anomalies are detected (e.g., excess error rate), communication is restarted. 3. Message Modulation: The dealer modulates received states with ${\alpha }_j\sim N(X^{U_i},{\sigma }^2)$ and returns the modulated state $a_4$ for decryption. 4. Joint Measurement: Users perform two-mode Bell measurements (using balanced beam splitters and homodyne detectors) on local state $a_1$ and received state $a_6$ to decrypt $X^{U_i}$.

2.2.3. Reconstruction

To securely recover S, all n users collaborate as shown in Figure 3: 1. Encryption & Exchange: Each $U_i$ generates a random sequence $U_i\in {\{0,\dots ,M\}}^{L+L_1+L_2}$, encrypts their shadow as $(X_j^{U_i}+U_{i,j})\mathrm{mod}(M+1)$, and exchanges encrypted messages. 2. Iterative Verification: Starting from $j=0$, users increment j, broadcast the j-th round keys $U_{1,j},U_{2,j},\dots ,U_{n,j}$, and decrypt $X_j^{U_i}=(M_{e_j}^{U_i}-U_{i,j})\mathrm{mod}(M+1)$. Using CRT, they recover $X_j$, compute $V_j^{\prime }=H(X_j+j(L+M))$, and abort if $V_j^{\prime }\ne V_j$. 3. Secret Extraction: When $j=L+L_2$, users check if the substring $T_j=X_{j-L_2+1},\dots ,X_j$ matches $P^{*}$. If matched, the secret $S=X_{j-L-L_2+1},\dots ,X_{j-L_2}$ is extracted; otherwise, the loop continues.

3. Security Analysis

In this section, we first conduct a security analysis of the proposed OFCQSS scheme. Additionally, since the quantum key distribution protocol serves as a security technique in this paper, we evaluate the performance of the scheme based on the security analysis of quantum key distribution. This evaluation primarily focuses on the performance metrics of the scheme, such as the secure key rate and noise.

3.1. Mathematical and Structural Security Analysis

3.1.1. Mathematical Security Proof Based on the Chinese Remainder Theorem

In the application of the Chinese remainder theorem, the secret S is decomposed into multiple remainders (shares), with each user holding only the remainder under a specific modulus. For example, in a two-user scheme, the secret S is decomposed into $X^{U_1}\equiv X\mathrm{mod}{m}^{U_1}$ and $X^{U_2}\equiv X\mathrm{mod}{m}^{U_2}$, where the moduli $m^{U_1}$ and $m^{U_2}$ are coprime. Only by possessing both $X^{U_1}$ and $X^{U_2}$ can the original message X be recovered through CRT, and the secret S be extracted accordingly.

The security guarantee mechanism of CRT is as follows [4]:

(1)

Mathematical irreversibility: Knowing a single remainder (e.g., $X^{U_1}$ or $X^{U_2}$) cannot uniquely determine the original value X. For instance, if $m^{U_1}=2$ and $X^{U_1}=0$, X could be 0, 2, 4, etc.; if $m^{U_2}=3$ and $X^{U_2}=0$, X could be 0, 3, 6, etc. Thus, the information entropy of a single remainder is much lower than that of the complete secret, making it impossible to effectively recover the secret through exhaustive enumeration or reverse calculation.

(2)

Information entropy separation: As analyzed in the paper, the information entropy of each share (e.g., $X^{U_1}$ or $X^{U_2}$) is 1 bit and ${log}_{2}3$ bits, respectively, while the entropy of the complete message X is ${log}_{2}6$ bits. The information contained in a single share is insufficient to cover the entropy of the complete secret, preventing participants from inferring the global secret through local information

(3)

Time complexity: If an attacker attempts to guess other participants’ shares through a single remainder, they need to enumerate all possible combinations. Since the product of the moduli grows exponentially with the number of participants, the complexity of exhaustive search is too high to be feasible.

The CRT—through its mathematical irreversibility and information entropy separation mechanism—ensures that the secret must be jointly recovered from multiple remainders. A single remainder provides only partial information and cannot be used to reverse-engineer the complete content. This characteristic completes the mathematical security proof of the system and eliminates the possibility that an attacker could guess other users’ information from partial shares.

3.1.2. Structural Security Proof Based on Decentralization

Fairness structure: The fairness mechanism of our proposed protocol, as illustrated in Figure 3, ensures that all participants either successfully reconstruct the secret simultaneously or fail together by progressively verifying messages in each recovery round, utilizing a hidden determination pointer to mark the end of the secret, and incorporating a sufficiently long random check sequence. Specifically, if cheating occurs before the secret’s position or after the pointer is fully revealed, it will either be detected immediately or render both parties unable to confirm the secret; if cheating occurs after the secret’s position but before the pointer is fully revealed, both parties still have a high probability of recovering the secret; the only scenario where a cheater could exclusively obtain the secret (cheating at the secret’s exact position) has an extremely low probability (inversely proportional to the check sequence length), and when the check sequence is sufficiently long, this unfairness becomes negligible [4].

Decentralized structure: Our system architecture employs a decentralized structure [7], where the traditional QSS scheme’s receiving parties (dealer and user) are granted equal status—each node can function either as a user for key distribution or as a dealer serving as the system receiver. This decentralized architecture eliminates the security risks and vulnerabilities inherent in centralized systems, while providing more flexible path selection options. The approach establishes a theoretical foundation for constructing and implementing multi-user network configurations.

3.2. Quantum Security

3.2.1. Quantum Security Analysis

As for the no-attack situation in Figure 2, we consider a three-user CV-QSS protocol where an honest dealer is selected among the participants, while users $U_1$ and $U_2$ prepare squeezed vacuum states $(a_1,a_2)$. Mode $a_2$ is transmitted to the dealer through a noisy quantum channel, resulting in mode $a_3$ characterized by the following [4]:

$$\begin{array}{cc}\hfill x_3& =\sqrt{{\eta }_1}{x}_2+\sqrt{1-{\eta }_1}{x}_{N1},\hfill \\ \hfill p_3& =\sqrt{{\eta }_1}{p}_2+\sqrt{1-{\eta }_1}{p}_{N1},\hfill \end{array}$$

(2)

where ${\eta }_1$ denotes channel transmissivity, and $x_{N1},p_{N1}\sim \mathcal{N}(0,{\mathsf{\Sigma }}_1^2)$ denotes model additive Gaussian noise. The dealer then performs displacement modulation on $a_3$ using the message $X^{A/B}$, generating mode $a_4$:

$$\begin{array}{cc}\hfill x_4& =x_3+X_k^A,\hfill \\ \hfill p_4& =p_3+P_k^A,\hfill \end{array}$$

(3)

With $X_k^A,P_k^A\sim \mathcal{N}(X^{(A/B)},{\sigma }^2)$ [19], the modulated state is sent back to $U_1$, undergoing channel noise to become $a_5$:

$$\begin{array}{cc}\hfill x_5& =\sqrt{{\eta }_2}{x}_4+\sqrt{1-{\eta }_2}{x}_{N2},\hfill \\ \hfill p_5& =\sqrt{{\eta }_2}{p}_4+\sqrt{1-{\eta }_2}{p}_{N2},\hfill \end{array}$$

(4)

where $x_{N2},p_{N2}\sim \mathcal{N}(0,{\mathsf{\Sigma }}_2^2)$ and ${\eta }_2$ is the reverse channel parameter. To compensate for channel loss, $a_5$ is amplified with gain $g=\sqrt{1/\left({\eta }_1{\eta }_2\right)}$:

$$x_6=g{x}_5.$$

(5)

A Bell measurement on $a_1$ and $a_6$ produces the following outcomes:

$$\begin{array}{cc}\hfill x_7& =\frac{1}{\sqrt{2}}(x_6+x_1),p_7=\frac{1}{\sqrt{2}}(p_6+p_1),\hfill \\ \hfill x_8& =\frac{1}{\sqrt{2}}(x_6-x_1),p_8=\frac{1}{\sqrt{2}}(p_6-p_1).\hfill \end{array}$$

(6)

For a squeezing parameter $r>0$, the $x_8$ quadrature follows a Gaussian distribution:

$$x_8={\displaystyle \frac{X_k^A}{\sqrt{2{\eta }_1}}}+{\displaystyle \frac{\sqrt{1-{\eta }_1}{x}_{N1}}{\sqrt{2{\eta }_1}}}+{\displaystyle \frac{\sqrt{1-{\eta }_2}{x}_{N2}}{\sqrt{2{\eta }_1{\eta }_2}}}-e^{-r}{\widehat{x}}_2^0.$$

(7)

The corresponding signal and noise variances are as follows:

$$V_s={\displaystyle \frac{{\sigma }^2}{2{\eta }_1}},$$

(8)

$$N_s={\displaystyle \frac{1-{\eta }_1}{2{\eta }_1}}{\mathsf{\Sigma }}_1^2+{\displaystyle \frac{1-{\eta }_2}{2{\eta }_1{\eta }_2}}{\mathsf{\Sigma }}_2^2-e^{-2r},$$

(9)

Yielding the signal-to-noise ratio $\gamma =V_s/N_s$, the mutual information is then:

$$I(S,R)={\displaystyle \frac{1}{2}}{log}_2(1+\gamma ).$$

(10)

Therefore, we can ensure that communication is reliable under certain conditions [4]. Similarly, we can also ensure that communication is reliable under internal attacks because the channel transmission efficiency $\eta$ is large enough [4,6,7]. This relies on the fact that each sub-channel between individual users and the dealer is generated through the frequency entanglement properties of an optical frequency comb. These sub-channels remain spectrally independent while maintaining phase locking via a common pump laser source. Consequently, multiplexed QSS signals can be simultaneously transmitted through a single optical fiber, thereby enhancing the system’s multi-user scalability.

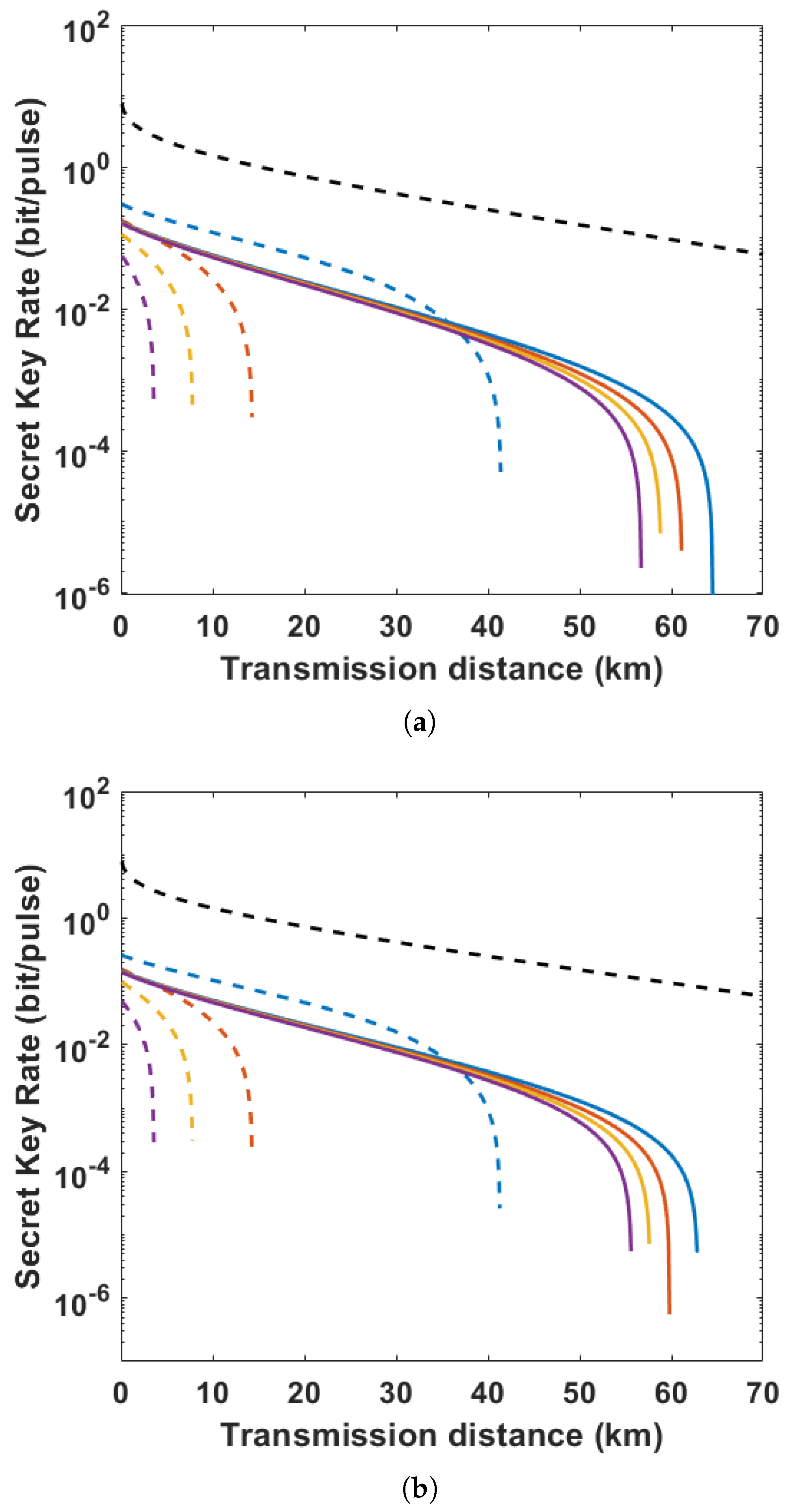
3.2.2. Numerical Simulation

The parameters in our experiment are as follows: The attenuation coefficient of a standard fiber link is $\delta$ = 0.2 dB/km; the detection efficiency and electronic noise of the imperfect heterodyne detector are $\mu$ = 0.6 and $v_{el}$ = 0.05; the reconciliation efficiency is $\beta$ = 0.98; and the system excess noise is ${\xi }_0$ = 0.001. The nonlinear coefficient is $\gamma$ = $1.3{\mathrm{W}}^{-1}{\mathrm{km}}^{-1}$; the dispersion parameter is $D=16\times {10}^{-6}\mathrm{s}/(\mathrm{m}·\mathrm{km})=16\mathrm{ps}/(\mathrm{nm}·\mathrm{km})$; the system repetition rate is $f_{\mathrm{rep}}=5\times {10}^7$ Hz, and the crosstalk coefficient is $\xi ={10}^{-R_e/10}$, where the extinction ratio is $R_e=40$ dB.

For the system’s maximum transmission distance and key rate [7], we first consider the point-to-point QKD key rate $R_i$ and transmission distance between each user $U_i$ and the designated dealer. The system key rate is given by $R=min\{R_1,R_2,\dots ,R_{d-1},R_{d+1},\dots ,R_n\}$, which reaches its minimum at the maximum transmission distance [6,7]. The asymptotic secret key rate lower bound for the QSS scheme is given by [27,28]:

$$R=\beta I_{\mathrm{UD}}-{\chi }_{\mathrm{DE}},$$

(11)

where $\beta$ is the reconciliation efficiency, $I_{\mathrm{UD}}$ is the mutual information between the user and dealer, and ${\chi }_{\mathrm{DE}}$ is the Holevo bound between Eve and the dealer.

However, because our system multiplexes multi-channel QSS signals in a single fiber via optical frequency comb technology, we must account for noise induced by frequency differences rather than noise from users $U_j$ coupled through highly asymmetric beam splitters (HABSs). On the one hand, when multiplexing multiple quantum signals through a single optical fiber, the generation of optical frequency combs (OFCs) in practical systems is fundamentally constrained by a finite extinction ratio $R_e$ [19], while inter-channel guard bands are intentionally incorporated during system design [18,29]. Consequently, we must account for inter-channel crosstalk noise (${\epsilon }_{\mathrm{cro}}$). On the other hand, since chromatic dispersion causes unavoidable phase deviations [18,19], it is necessary to consider the nonlinear noise (${\epsilon }_{\mathrm{non}}$) [30,31]. Therefore, the total excess noise can be expressed as follows:

$${\epsilon }_{\mathrm{total}}={\epsilon }_{\mathrm{cro}}+{\epsilon }_{\mathrm{non}}+{\epsilon }_0$$

(12)

where

$$\begin{array}{cc}\hfill {\epsilon }_{\mathrm{cro}}& =2(N-1)·\xi ·V_a,\hfill \\ \hfill {\epsilon }_{\mathrm{non}}& \propto {\gamma }^2{P}_{\mathrm{avg}}^2{L}_{\mathrm{eff}}^2{e}^{-\alpha L}{\displaystyle \frac{D{\lambda }^2}{c}}\Delta f^2\hfill \end{array}$$

(13)

where

• N is the total number of channels;
• $L_{\mathrm{eff}}$ is the effective length;
• $\Delta f$ is the channel spacing.

Then, the channel-added noise can be expressed as follows:

$${\chi }_{\mathrm{line}}={\displaystyle \frac{1}{T}}-1+{\epsilon }_{total}$$

(14)

and the noise between the dealer and user is given by the following:

$${\chi }_{\mathrm{het}}={\displaystyle \frac{2-\mu +2{\nu }_{\mathrm{el}}}{\mu }},$$

(15)

Then, the overall noise can be expressed as follows:

$${\chi }_{\mathrm{tot}}={\chi }_{\mathrm{line}}+{\displaystyle \frac{{\chi }_{\mathrm{het}}}{T}}.$$

(16)

The Shannon mutual information between the user and dealer is as follows:

$$I_{\mathrm{UD}}={log}_2\left({\displaystyle \frac{V+{\chi }_{\mathrm{tot}}}{1+{\chi }_{\mathrm{tot}}}}\right),$$

(17)

where $V=1+V_U$, and $V_U$ is the modulation variance at the user.

Assuming the loss and noise in Bob’s detector are trusted (inaccessible to eavesdroppers), the Holevo bound between Eve and the dealer is as follows:

$${\chi }_{\mathrm{DE}}=\sum _{j=1}^{2}G\left({\displaystyle \frac{{\lambda }_j-1}{2}}\right)-\sum _{j=3}^{5}G\left({\displaystyle \frac{{\lambda }_j-1}{2}}\right),$$

(18)

where $G\left(x\right)=(x+1){log}_2(x+1)-x{log}_{2}x$, and ${\lambda }_j$ are the symplectic eigenvalues derived from the covariance matrix:

$${\lambda }_{1,2}^2={\displaystyle \frac{1}{2}}\left[A\pm \sqrt{A^2-4B}\right],$$

(19)

where

$$A=V^2\left(1-2T\right)+2T+T^2{\left(V+{\chi }_{\mathrm{line}}\right)}^2$$

(20)

$$B=T^2{\left(V{\chi }_{\mathrm{line}}+1\right)}^2,$$

(21)

and

$${\lambda }_{3,4}^2={\displaystyle \frac{1}{2}}\left[C\pm \sqrt{C^2-4D}\right],$$

(22)

where

$$\begin{array}{cc}\hfill C=& {\displaystyle \frac{1}{T^2{\left(V+{\chi }_{\mathrm{tot}}\right)}^2}}\left\{A{\left({\chi }_{\mathrm{het}}\right)}^2+B+1\right.\hfill \\ \hfill & \left.+2{\chi }_{\mathrm{het}}\left[V\sqrt{B}+T\left(V+{\chi }_{\mathrm{line}}\right)+2T(V^2-1)\right]\right\},\hfill \end{array}$$

(23)

$$D={\left({\displaystyle \frac{V+\sqrt{B}{\chi }_{\mathrm{het}}}{T\left(V+{\chi }_{\mathrm{tot}}\right)}}\right)}^2,$$

(24)

$${\lambda }_5=1$$

(25)

Subsequently, we use the maximum likelihood estimation (MLE) mentioned in Appendix A to determine the channel parameters, thereby achieving a more precise estimation of the upper bound for the asymptotic key rate.

4. Performance Analysis and Discussion

In Figure 4, we compare the key rate and distance relationships between the traditional chain-structured DQSS scheme and the OFC-based CV-QSS scheme under different user scenarios. As shown in the results, under identical parameter conditions, the OFC-based CV-QSS scheme achieves a 50% improvement in maximum transmission distance compared with the traditional chain-structured DQSS scheme. Moreover, this performance gap widens as the number of users increases.

In other words, similar to other chain-structured CV-QSS schemes [6,7], the maximum transmission distance of chain-structured DQSS schemes decreases significantly with increasing user count. By contrast, the OFC-based QSS scheme exhibits a substantially smaller reduction in maximum transmission distance as the number of users grows.

This outcome aligns with our theoretical expectations. In traditional chain-structured QSS schemes, the channel-added noise is given by the following:

$${\chi }_{\mathrm{line}}={\displaystyle \frac{1}{T}}-1+\sum _{j=1}^n{\xi }_j,$$

(26)

where each ${\xi }_j$ increases with transmission distance, resulting in n-fold amplification. Conversely, in our proposed OFC-based CV-QSS scheme, an increase in distance or in the number of users causes only a single change in the variables ${\epsilon }_{\mathrm{cro}}$ and ${\epsilon }_{\mathrm{non}}$ in

$${\chi }_{\mathrm{line}}={\displaystyle \frac{1}{T}}-1+{\epsilon }_{total}=\mathrm{line}={\displaystyle \frac{1}{T}}-1+{\epsilon }_{\mathrm{cro}}+{\epsilon }_{\mathrm{non}}+{\epsilon }_0$$

(27)

At the system level, an inverse correlation constraint exists among key rate, transmission distance, and user capacity; enhancing any one of these parameters inevitably compromises the other two. This aligns with fundamental physical limits and constitutes an intrinsic characteristic of QSS schemes.

5. Conclusions

In this paper, we proposed an optical frequency comb-based continuous-variable quantum secret sharing (OFC CV-QSS) scheme that overcomes multi-user scalability limitations by replacing chain topologies with highly asymmetric beam splitters (HABSs) with OFC-generated parallel quantum channels. This eliminates the need to aggregate cumulative noise from sequential user couplings in system key rate calculations. Beyond inherent quantum-layer security, our solution establishes dual protection—the Chinese remainder theorem (CRT) ensures mathematical security for classical shadows through information-theoretic irreversibility, while decentralized architectures enforce structural security via distributed control and collaborative reconstruction. Numerical simulations confirm that the scheme achieves a substantially extended maximum transmission distance compared with chain-QSS, with significantly slower performance degradation as users scale, while maintaining full compatibility with existing fiber infrastructure. Future work will focus on experimental validation and OFC spectral optimization.