Abstract
Modeling and simulation of aneurysm formation, growth, and rupture plays an essential role in a wide spectrum of application scenarios, ranging from risk stratification to stability prediction, and from clinical decision-making to treatment innovation. Unfortunately, it remains a non-trivial task due to the difficulties imposed by the complex and under-researched pathophysiological mechanisms behind the different development stages of various aneurysms. In this paper, we present a novel computational method for aneurysm simulation using smoothed particle hydrodynamics (SPH). Firstly, we consider blood in a vessel as a kind of incompressible fluid and model its flow dynamics using the SPH method; and then, to simulate aneurysm growth and rupture, the relationship between the aneurysm development and the properties of fluid particles is established by solving the motion control equation. In view of the prevalence of aneurysms in bifurcation vessels, we further enhance the capability of the model by introducing a solution for bifurcation aneurysms simulation according to Murray’s law. In addition, a CUDA parallel computing scheme is also designed to speed up the simulation process. To evaluate the performance of the proposed method, we conduct extensive experiments with different physical parameters associated with morphological characteristics of an aneurysm. The experimental results demonstrate the effectiveness and efficiency of proposed method in modeling and simulating aneurysm formation, growth, and rupture.
Keywords:
aneurysm modeling and simulation; smoothed particle hydrodynamics; computational fluid dynamics MSC:
76M28; 92C35
1. Introduction
Aneurysms are the manifestation of localized expansion caused by the injury of arterial wall lesions. It has been estimated that the prevalence of unruptured aneurysms lies between 2% and 5% in the general population [1]. Despite its relatively lower incidence, the consequences of aneurysm rupture are generally catastrophic. A previous study suggested that aneurysm rupture has been associated with an approximate rate of 50% mortality and neurologic morbidity among the survivors [2,3]. In the past a few decades, numerous studies have been carried out to investigate the pathophysiological mechanisms behind the different development stages of aneurysms from the perspectives of biology (e.g., inflammatory pathways, genetics) and physics (e.g., geometry, flow patterns and dynamics) [3]. Among existing technical means for the understanding of aneurysms, computational aneurysm simulation is gaining increasing attention due to its significant roles in different kinds of application scenarios including risk stratification and prediction, clinical decision-making, treatment innovation, virtual surgery, medical education, and beyond.
In the field of computer graphics, various computational fluid simulation methods have been developed to generate realistic animations of fluids such as blood, smoke, and other substances [4,5,6]. Existing methods can be broadly classified into three categories: the mesh-based Euler method [7,8], particle-based Lagrange methods [9], and a combination of both methods, i.e., a hybrid method [10]. Despite the advancement, research efforts have scarcely been devoted to the development of effective computation aneurysm simulation solutions, and existing schemes cannot be directly applied to the simulation of aneurysms due to the intrinsic difference between these substances.
Among existing fluid simulation methods, blood flow simulation is a fluid simulation combined with a blood medical model to generate realistic physiological characteristics of simulated blood. The liquid–solid coupling dynamic simulation of blood and solid substances in the body, such as the interaction between blood and thrombus in thrombosis simulation [11,12], and the interaction between blood and arterial wall in aneurysmal lesion, can restore the real physiological phenomena and pathological process. Our simulation results qualitatively align with clinical observations, such as aneurysm expansion under hemodynamic stress, though future quantitative validation with patient-specific data is planned to enhance clinical applicability.However, due to the complex physiological characteristics of blood and the various liquid–solid coupling behaviors in different scenarios, existing methods do not fully consider the process of vascular blood flow diseases, and cannot simulate the process of specific disease through graphics fluid simulation technology effectively and efficiently. Combining blood characteristics with the physical characteristics of blood vessels, these liquid–solid coupling simulations based on fluid simulation methods (e.g., smoothed particle hydrodynamics (SPH)) can help clinical medical analysis and the prediction and diagnosis of various types of vascular diseases [13,14]. In this paper, we also use SPH to simulate blood flow dynamics in light of its great advantages [15] in complexity and computational efficiency, and introduce a novel method for the simulation of aneurysm formation, growth, and rupture.
The simulation of aneurysm growth and rupture includes two processes: the dilation of diseased artery wall caused by blood flow impact and the blood exudation caused by rupture of the aneurysm wall. They are mainly the result of the liquid–solid coupling between blood and diseased artery wall. The influence of blood on a diseased artery includes the plastic bulge and rupture of the artery wall, while the influence of artery on blood is mainly the turbulence phenomenon caused by the rebound of blood. For the growth and rupture of aneurysms, many studies are based on the numerical analysis of growth, rupture, or blood flow in the aneurysm [16,17,18,19]. Existing hematological modeling methods are complex, so that solving and simulating by computer will result in a large amount of calculation. At the same time, if the two processes of aneurysm growth and rupture are integrated, the efficiency of computation will be lower. It is the key to simplify the models and improve the efficiency of computation using the advantages of hardware, on the premise of ensuring the effectiveness of simulation.
Inspired by the biomedical models of aneurysm growth and rupture analysis, we introduce a novel aneurysm simulation method to model the growth and rupture of aneurysms and its interaction with blood flow. Firstly, combining with Laplace’s law, Poisson’s ratio, and differential properties, we establish the relationship model between aneurysm rupture threshold and physical properties to obtain the critical condition of rupture. Secondly, combining with the interaction of blood, elastin, collagen, and tissue fluid, we simulate the expansion of an aneurysm through the motion control equation using fluid particle properties. In order to reduce the complexity of calculation, the proposed method simplifies some unnecessary factors based on the existing biomedical models. Therefore, using the proposed method can ensure both effective and efficient simulation results.
The main contributions of this paper are summarized as follows: (1) we propose a novel SPH-based computational method for the simulation of aneurysm formation, growth, and rupture; (2) we conduct a parametric analysis to investigate the sensitivities of several physical parameters associated with aneurysms to meet the diverse needs in simulating aneurysms with different properties; and (3) we design a CUDA parallel computation scheme for real-time aneurysm simulation to satisfy the requirements of practical applications.
2. Related Work
In this section, we review relevant studies from two aspects, namely, SPH-based fluid simulation, and modeling and simulation of aneurysmal lesions and hemodynamics.
2.1. SPH-Based Fluid Simulation
The SPH method was first proposed in the field of astrophysics. As early as 2003, Muller et al. [15] applied it to the Navier–Stokes Equations [20] and used kernel function to solve fluid simulation problems. Since then, SPH has evolved into one of the most important methods for fluid simulation. In order to improve the incompressibility of fluid simulation, Becker et al. [21] proposed the weakly compressible SPH method (WCSPH) by changing a coefficient in the ideal gas equation of state. Although the simulated fluid achieves better incompressibility on the premise of not increasing the amount of calculation, it is difficult to simulate under the real-time conditions used in large-scale fluid particle simulation. To tackle this issue, Solenthaler et al. [9] proposed the PCISPH method, which can employ larger time steps in the simulation and speed up the simulation process by predicting the density error of the next time step in the calculation process. However, prior treatments of arbitrary solid boundaries do not reflect the correct cohesive behavior visible in many real-world scenarios. Thus, Schechter et al. [22] proposed the Ghost SPH scheme, which resolves this with a new particle sampling algorithm [23], in which a narrow layer of ghost particles is created in the surrounding air and solid with careful extrapolation and treatment of fluid variables to reflect the boundary conditions.
Errors in the reality of fluid simulation come not only from the divergence error but also from the density error. The continuity equation for incompressible flow also demands a divergence-free velocity field that is neglected by most methods. Although a few methods consider velocity divergence, they are either slow or have a perceivable density fluctuation. Macklin et al. [24] proposed similar incompressibility and convergence to modern SPH solvers, but their method inherits the stability of the geometric, position-based dynamics method, allowing large time steps suitable for real-time applications. Winchebach et al. [25] introduced a method for adaptive incompressible SPH simulations. Instead of using a number of fixed particle sizes or levels, this approach allows continuous particle sizes. Such a scheme guarantees low spatial variations in particle size, which is essential in order to achieve large adaptivity ratios for incompressible fluid simulations.
Ihmsen et al. [26] proposed the implicit incompressible SPH method (IISPH), which combines the pressure term of SPH with the discrete continuity equation to obtain the discrete pressure Poisson equation. Compared with previous methods, it has larger time steps and smaller errors. To further meet the incompressibility of fluid, Kang et al. [27] presented an SPH framework to simulate an incompressible fluid that satisfies both the divergence-free condition and the density-invariant condition based on the PBF method [24]. Bender et al. [28,29] proposed the DFSPH method to meet the conditions of divergence-free and density-invariant step by step, and achieved the condition of divergence-free by solving the stiffness coefficient. Different from previous SPH methods, DFSPH can be applied to large-scale fluid simulation. Therefore, their DFSPH approach is significantly faster and more stable than current state-of-the-art SPH methods for incompressible fluids. To further improve the efficiency and stability of simulation, unlike DFSPH, Wang et al. [30,31] proposed the CISPH method by coupling the two conditions of density-invariant and divergence-free, which achieves better performance in terms of simulation efficiency and stability.
In recent years, the SPH method has gained increasing attention in biomechanics, particularly for simulating complex phenomena in cardiovascular systems. For instance, Laha et al. [32] utilized GPU-accelerated SPH to model thrombus formation in cardiovascular systems, demonstrating the method’s capability to handle intricate biofluid dynamics efficiently. Similarly, Laha et al. [33] employed SPH for fluid–structure interaction (FSI) simulations of native and mechanical heart valves within a patient-specific aortic model, validating its effectiveness in capturing biomechanical interactions in cardiovascular flows. These studies underscore the versatility of SPH and provide a strong foundation for its application in the present work, where we simulate aneurysm rupture in arterial blood vessels.
In biomechanics, SPH has been applied to cardiovascular systems. Topalovic et al. [34] used SPH to simulate blood flow in coronary arteries, focusing on wall shear stress; however, their model did not address aneurysm growth or rupture. Laha et al. [33] employed SPH for microcirculation, emphasizing particle interactions but lacking fluid–solid coupling for arterial walls. Sigalotti et al. [35] developed an SPH framework for biofluids; however, the framework did not incorporate biomechanical models for aneurysm progression. In contrast, our method integrates SPH with Laplace’s law and Poisson’s ratio to model aneurysm growth and rupture, achieving real-time performance via CUDA parallelization, a unique contribution to computational mathematics in biomechanics.
2.2. Modeling and Simulation of Aneurysmal Lesions and Hemodynamics
In terms of the aneurysm growth and rupture mechanism, Hademenas et al. [17] constructed an elastic model for an ideal aneurysm with spherical and uniform wall thickness to study the rupture mechanism under the action of pressure only. Based on Laplace’s law, a nonlinear model between the tension and radius in the aneurysm was proposed to set forth the growth and rupture of cystic aneurysms. In contrast, Chitanvis et al. [18] considered that the stress of aneurysm before rupture may exceed its yield limit and produce plastic deformation, as well as the characteristics of material damage caused by voids in the material. The relationship between them was formulated as a nonlinear model. Chitanvis et al. [36] further proposed a nonlinear constitutive quasi-static model to achieve similar objectives. It is numerically solved by differential equations and applied to clinical data, while many aneurysm models based on Laplace’s law are the representation of static linear elastic sphere.
For the blood flow in an aneurysmal artery, Perktold et al. [19] studied the flow pattern and fluid particle path of a cystic aneurysm at the bifurcation of the bifurcation vessel by numerical method. They solved the governing equation of incompressible Newtonian fluid flow using the finite element method in order to analyze the flow characteristics of blood in aneurysms. Nieto and Torres [37] considered a nonlinear mathematical model to simulate the blood flow in an aneurysm, studied the important factors of aneurysm evolution, and provided some medical results that are helpful to understand the Willis ring aneurysm. Nikolov et al. [38] established a nonlinear mathematical model of blood flow through normal artery and serial aneurysm, and numerically solved and analyzed the model equation by a nonlinear dynamic method.
To explore the influence of the diameter change of artery on hemodynamics, Farnoush et al. [39] modeled arteries with different diameters and analyzed them with computational fluid dynamics (CFD), and used these models to evaluate the rupture of aneurysms through the morphological characteristics related to the formation of aneurysms. The studies mentioned above are all numerical. More computational models of the hemodynamics of aneurysms were reviewed by existing studies [40,41,42].
For the growth of aneurysms, Badgaish et al. [16] proposed a new mathematical model of the interaction between blood flow and the arterial wall surrounded by cerebrospinal fluid. Although most of the aforementioned studies have verified their biological significance through experiments, they are all numerical analyses, and fall short due to their high computational overhead for simulation.
Many current models struggle to accurately simulate aneurysm growth and rupture due to their high computational complexity and limited ability to handle complex geometries or fluid–structure interactions. For instance, while some models achieve reasonable agreement with idealized cases, their performance degrades when applied to real-world data with irregular vessel shapes. Our proposed SPH-based model addresses these shortcomings by improving computational efficiency and better capturing the dynamics of complex geometries, as demonstrated in our numerical experiments.
3. Proposed Method
In our method, the simulation of aneurysm progression consists of four aspects, namely SPH-based blood flow, aneurysm rupture, aneurysm growth, and bifurcation aneurysms.
3.1. SPH-Based Blood Flow Simulation
The general fluid obeys the Navier–Stokes equations and satisfies the law of conservation of mass [20]. The SPH method discretizes blood into particles and simulates the flow characteristics of incompressible fluids based on the Lagrangian approach. Blood flow adheres to the Navier–Stokes Equations (describing momentum conservation) and the law of mass conservation, ensuring the physical realism of the simulation, which can be expressed as:
and
respectively, where is the density of particles, is the flow velocity, t is time, is the gravitational acceleration, ∇ is the divergence, and is the Laplace operator. The three items on the right side of Equation (1) represent the gravity, viscosity force, and pressure acting on particles, respectively. Here, is the dynamic viscosity of the fluid.
In light of the fact that blood is a kind of incompressible fluid, we adopt the density-invariant and divergence-free method [30,31] to simulate blood flow based on SPH. That is, in addition to Equations (1) and (2), the model should also meet the following incompressible condition:
To calculate particles’ physical attributes, a common practice is to use the kernel method below:
where A represents a physical attribute, and are the positions of a particle and its neighboring particles, respectively, is the mass of a particle, is the density, is a kernel function, h is the effective radius of the kernel. When a particle is not within a pre-defined radius, will be 0. The density , pressure , and viscosity force are given by:
The intensity of pressure is calculated from the equation of state, where is the stiffness coefficient and is taken as 1 here, and is the constant density.
3.2. Simulation of Aneurysm Rupture
Generally, the arterial wall has three distinct layers, the tunica intima (inner layer), the tunica media (middle layer), and the tunica adventitia (outer layer). The middle and outer layers are made up of elastin and collagen, respectively, which give blood vessels their elasticity. Studies on histopathology and biomechanics have shown that aneurysmal lesions will impair the functions of elastin and collagen and damage the elasticity of arterial walls, making the aneurysm exist in a plastic state. As the aneurysm becomes larger, the aneurysm wall becomes thinner and may eventually rupture caused either by internal or external factors like abnormal blood pressure.
Inspired by [18,36], we first obtain the critical condition of aneurysm rupture. Laplace’s law, which defines the relationship between retraction force, tension, and radius, has been widely used for the analysis of the aneurysm rupture mechanism [17,18,36]. It can also be extended to the relationship with material thickness, that is:
where P is the pressure, R is the radius of an aneurysm, is the stress–strain on the artery wall, and h is the thickness of the aneurysm wall. Poisson’s ratio of aneurysm radius to aneurysm wall thickness is obtained from Poisson’s relationship of material deformation:
In light of the phenomenon that the fracture of molecular bonds results in the formation of internal voids of ductile materials, Chitanvis et al. [18,36] established their relationship and formulated it in a differential form:
where is porosity, and V is the volume of aneurysm wall. Assuming that the aneurysm is spherical, V can be approximately expressed as . Meanwhile, the nonlinear relationship between aneurysm wall stress and porosity is given by:
where Y is the yield limit of the stress–strain on the aneurysm wall. By combining (8)–(11), the differential relationship between the aneurysm radius and pressure on the aneurysm wall can be represented as:
According to the derivative property, when , the critical condition of aneurysm rupture can be estimated using Laplace’s law, which originates from the principle of force balance and describes the relationship between internal pressure P, radius R, wall thickness h, and wall tension in a thin-walled spherical vessel like an aneurysm. This law is essential for understanding how the arterial wall withstands blood flow pressure and for predicting rupture risk. Poisson’s ratio characterizes the material properties of the arterial wall by relating transverse to axial strain during deformation:
Since the porosity presents less variations during the growth of an aneurysm, it is regarded as a constant in our method.
The pressure on an artery wall causing aneurysm rupture mainly comes from blood flow, which in this paper, is simulated with discrete particles using the SPH method. For the sake of simplicity, we approximate the pressure with the force caused by the motion of particles located on the wall of an aneurysm. More specifically, the particles used to calculate the force are defined as those that exceed the boundary range before collision handling. For particle collision handling, some details are shown in Figure 1, which shows the collision handling mechanism for blood flow particles interacting with the aneurysm wall. In panel (a), the red particle represents a blood flow particle before collision, with its velocity direction indicated by the arrow. When a particle exceeds the boundary of the aneurysm wall, it is identified as a particle contributing to the pressure calculation on the wall. Panel (b) shows the update method, where the particle’s position and velocity are adjusted to simulate the rebound effect. Specifically, the particle’s velocity is reversed in the direction normal to the wall to mimic the elastic collision, while the tangential component remains unchanged. Finally, panel (c) depicts the particle’s position and velocity after handling, ensuring that the particle remains within the arterial domain and that the interaction with the wall is physically plausible. The red particle shown in Figure 1a is one of the particles involved in pressure calculation. The Impulse Momentum Calculator is given by:
where t is the time interval between two consecutive video frames, m and v are the mass and velocity of a particle, respectively. The impact force of a particle on the arterial wall thus can be represented as . Since v is the product of the acceleration a and time t, it is equivalent to write , where a calculated by the Navier–Stokes equation is given by:
In our method, the maximum impact force on the artery wall of all particles involved in the calculation is taken as the pressure on the wall of an aneurysm:
where S is the set of particles involved in the calculation. Hence, when the pressure on aneurysm wall exceeds the critical condition, i.e., , the aneurysm will rupture.
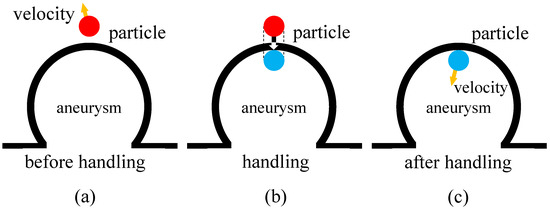

Figure 1.
Collision handling of particles beyond the boundary of aneurysm. (a) is the particle position and velocity direction before handling, (b) is the update method, and (c) is the particle position and velocity direction after handling.
3.3. Simulation of Aneurysm Growth
The forces on an artery wall come from not only the flow of blood and tissue fluid, but also the collagen and elastin contained in the artery wall. In an aneurysmal artery, elastin has a function of resisting the growth of aneurysm, while collagen can prevent the rupture of the aneurysm. All of these forces and interactions are essential for yielding a reasonable simulation model. Inspired by [16], we propose a new method for simulating the process of aneurysm growth by taking the aforementioned forces into account. The summation of forces acting on an artery wall gives:
where , and are the force of blood flow, tissue fluid flow, and the resistance of elastin and collagen, respectively. The sign of force in the equation refers to the direction of force. Figure 2 illustrates the force analysis of the aneurysm wall.
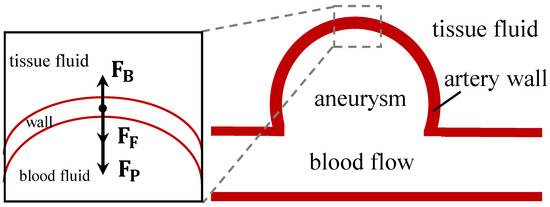
Figure 2.
Force analysis of the aneurysm wall. , , and are the force of blood flow, tissue fluid flow, and the resistance of elastin and collagen, respectively.
In contrast with previous method [16] in which a Fourier series is used to simulate the periodic change of blood pressure, we simply approximate with the pressure introduced in Section 3.2. This is because the particles involved in the calculation of in the SPH method change along with blood flow and thus have the characteristic of pulsatility.
For the calculation of the force , rather than using the SPH method, we directly employ a biomechanical method [16] in which tissue fluid is regarded as a kind of weakly compressible fluid and the simplified model of one-dimensional compressible inviscid Euler equation is used to formulate as the pressure and cross-sectional area acting on the aneurysm:
where is the density of tissue fluid, a and c are the cross-sectional area of tissue fluid acting on the aneurysm and the propagation velocity in the wave equation, respectively, and is the outward expansion speed of the aneurysm wall.
The resistance force of elastin and collagen is modeled using a particle system:
where is the scale factor, is the cross-sectional area, is stress, and the subscripts E and C stand for elastin and collagen, respectively. These parameters are derived from the biomechanical literature, with Young’s modulus values of 0.1–1 MPa for elastin and 100–1000 MPa for collagen [43]. Cross-sectional areas are estimated based on typical arterial wall thickness and composition [44]. These values are adjustable to accommodate patient-specific data or experimental measurements for enhanced accuracy.We represent the stress as according to the linear relationship between stress and strain. The relation between strain and the radius R of an aneurysm is given by [17]:
where is the increment of R.
Combining Equations (17)–(20), becomes:
where m is the mass of the aneurysm wall. The simulation of aneurysm growth can thus be achieved through the calculation of .
Since the risk of aneurysm rupture is related to not only the radius of aneurysm but also the thickness of aneurysm wall, which will decrease with the increase in aneurysm radius, we update the thickness of the aneurysm wall according to the Poisson relationship during the progression of aneurysm. The change of thickness is:
where and are the thickness of the aneurysm wall and the radius of the aneurysm at time t, respectively, and is the Poisson ratio.
Moreover, we manually set the upper limit of aneurysm size to indicate the complete development of aneurysms, and update the corresponding thickness of the aneurysm wall as:
where does not exceed 0.001, and represents the intensity coefficient of the relationship between aneurysm wall thickness and aneurysm radius.
3.4. Simulation of Bifurcation Aneurysms
Since many aneurysms occur at the bifurcation of arteries, we further extend the proposed model to bifurcation aneurysm simulation. Towards this end, we first develop a three-dimensional bifurcation artery model and then simulate aneurysm progression at the bifurcation.
The simulation uses a physical time step of 0.001 s, corresponding to a cardiac cycle period of 0.8 s, to model pulsatile blood flow. Each frame represents a time increment, with 3000 frames covering a 3 s simulation. This ensures physiological relevance in capturing blood flow dynamics and aneurysm progression.
For simplicity, we assume that the two daughter branches of an artery are symmetrical. That is, the deflection angles between the two branches and the main pipe are the same, and the radius of the two branches is also equal. According to Murray’s law [45], the radius of an artery and its bifurcation should satisfy:
where is the radius of the main pipe, and are the radii of the two branches. Furthermore, we also smooth the artery wall at the bifurcation to fix the problem caused by inconsistent radii of branch and main pipe in bifurcation artery.
The simulation efficiency of the SPH method has a strong positive correlation with the number of particles, which should be controlled within a proper range. In addition, since the blood simulation in an aneurysmal artery is only a small part of the human blood circulation system, it will cause the phenomenon that particles cannot be distributed and flow in the whole artery space if the blood particles flow directly in arteries without further handling. It will be inconsistent with the fact that the blood is full of flow in the artery, resulting in the unsatisfactory simulation effect. The effect of blood flow without filling the blood vessel is shown in Figure 3a.
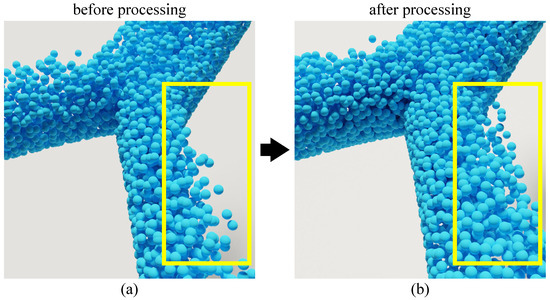
Figure 3.
Effect comparison of particle simulation in bifurcation artery before and after handling. (a) is the simulation effect before handling, and (b) is the simulation effect after handling.
This issue can be alleviated by controlling the flow of blood at the outlet and inlet of the artery. However, due to the limitation in the number of blood particles and the fact that the calculation of flow is related to too many physical quantities, the solution is infeasible in practice. To tackle this problem, we design a controller to reset the particles outside the action range in batch, and endow the particles with relatively stable velocity. To simulate realistic blood flow in the arterial domain, we designed a particle controller to manage the particles at the inlet and outlet of the artery. At the inlet, particles are continuously generated with an initial velocity that mimics the pulsatile nature of blood flow, as described by the velocity boundary condition in Section 3.5. At the outlet, particles that exit the simulation domain are removed and reintroduced at the inlet to maintain a constant number of particles and ensure that the artery remains filled with blood. This cyclic reintroduction of particles not only addresses the issue of particles not filling the entire arterial space but also provides a stable and periodic blood flow, which is crucial for accurately simulating the pressure exerted on the aneurysm wall. The effect of this controller is illustrated in Figure 3b, where the blood flow appears to fill the artery uniformly, in contrast to Figure 3a, which shows the simulation without the controller. In terms of blood flow control, we considered some characteristics in our simulation in that the lens collected in the simulation only accounts for a part of the environment and the particles beyond a certain range have no impact on the blood flow characteristics or the simulation of aneurysm lesion process. Figure 3b illustrates an instance of simulation using this method. Simulating the entire arterial system is computationally prohibitive due to the large number of particles required, which would significantly increase computational costs and hinder real-time performance. To address this, we focus on a localized segment of the artery containing the aneurysm while employing a particle reset mechanism. This mechanism reinitializes particles that exit the simulation domain, assigning them stable velocities to mimic continuous blood flow. This approach maintains the physiological realism of blood flow characteristics, such as pulsatile pressure changes, while optimizing computational efficiency by limiting the number of particles. As shown in Figure 3b, this method effectively simulates blood flow filling the vessel, consistent with physiological conditions, without the need for simulating the entire artery. This simulation method not only alleviates the issue that blood particles do not fill the blood vessels but also provides an approximately periodic and relatively stable blood pressure change, which is effectively consistent with the pressure calculation of blood flow on aneurysms. Meanwhile, the simulation efficiency can be improved without significantly affecting the simulation effect.
3.5. Boundary Conditions in Aneurysm Simulation
To enhance the accuracy and physiological relevance of our aneurysm simulation, we define specific boundary conditions for the computational domain. These conditions are crucial for modeling the interactions between blood flow and the vascular structures, including the inlet, outlet, vessel wall, and aneurysm wall. Below, we detail each boundary condition, their mathematical formulations, and their implementation within the SPH framework.
Inlet Boundary: The inlet region, where blood enters the vessel containing the aneurysm, is modeled using a velocity boundary condition to simulate pulsatile blood flow driven by the heartbeat. The velocity distribution at the inlet varies temporally and is defined as a sinusoidal function to reflect the periodic fluctuations observed under physiological conditions:
where is the peak velocity amplitude, t is time, and T is the cardiac cycle period. In the SPH method, this condition is enforced by assigning the prescribed velocity to fluid particles entering the domain.
Outlet Boundary: The outlet region, where blood exits the simulation domain, employs a pressure boundary condition to mimic the resistance of downstream vasculature. A constant pressure is applied:
where is a predefined pressure value. Within SPH, this is implemented by adjusting the pressure term of particles near the outlet to maintain the specified constant pressure.
Vessel Wall Boundary: The vessel wall is treated as a rigid, solid boundary with a no-slip condition, meaning the fluid velocity at the wall is zero:
In the SPH framework, this is achieved using the ghost particle method. Ghost particles are placed outside the vessel wall to enforce the no-slip condition, ensuring fluid particles do not penetrate the wall and their velocities align with the boundary constraint.
Aneurysm Wall Boundary: The aneurysm wall is modeled as a deformable boundary using an elastic wall model. The displacement of the aneurysm wall, , is governed by the balance between the fluid impact force and the elastic resistance:
where is the mass of the wall segment, is the force exerted by the fluid (calculated as in Equation (16)), and k is the elastic stiffness coefficient. If fluid exceeds a critical threshold (e.g., from Equation (13)), the wall ruptures, allowing fluid particles to pass through the breach. In SPH, this is implemented by dynamically updating the positions of boundary particles representing the aneurysm wall and removing them upon rupture.
These boundary conditions are integrated into the SPH simulation by modifying the particle interactions near the boundaries, ensuring that the physical behavior of blood flow and its interaction with vascular structures are accurately captured. This approach enhances the scientific rigor and credibility of our simulation results.
In SPH simulations, accurately handling open boundaries—such as the inlet and outlet of arterial blood vessels—is critical for modeling blood flow. To address this, we employ the ghost particle method for open boundary conditions. Ghost particles are virtual particles placed outside the fluid domain to enforce boundary conditions, such as no-slip, prescribed velocity, or pressure constraints. At the inlet, ghost particles simulate pulsatile blood flow by assigning them velocities that reflect cardiac-driven flow patterns, as defined by Equation (25). At the outlet, ghost particles maintain a constant pressure condition, as specified in Equation (26), to ensure stable outflow. These particles interact with fluid particles via the SPH kernel function, ensuring continuity and consistency of the flow field across the boundaries.
4. Experiments and Discussion
To evaluate the effectiveness and efficiency of proposed method, we carried out extensive experiments on a PC equipped with an Intel i5-9300H processor with 8 GB RAM, and running Windows 10 as its operating system.The proposed algorithm was implemented in C++ with Visual Studio 2015 integrated development environment. To facilitate simulation, CUDA was used to perform the parallel computing task. In addition, OpenGL 4.6 and Blender 4.1 were employed for real-time and offline rendering, respectively.
4.1. Subjective Effectiveness Evaluation of the Proposed Method in Simulating Aneurysm Progression
Subjective assessment is a common practice in the field of fluid simulation to evaluate the effectiveness of a method by investigating the realism of its simulation results. In this section, we conducted a subjective evaluation experiment to examine the visual effects of simulated aneurysm using the proposed method. To systematically validate our model, we simulated the growth and rupture of an aneurysm at the bifurcation of an artery. Without loss of generality, the experiment was tested with a set of pre-defined parameters involved in our model, which are summarized in Table 1. It is worth noting that these parameters can be flexibly adjusted to meet the diverse needs of real-world applications. A parametric analysis will be discussed in detail in Section 4.4.

Table 1.
Summary of the parameters involved in our experiment.
The simulation results of aneurysm growth and rupture using the proposed method are shown in Figure 4 (more details about the simulation can be found in the Supplementary Video S1). The figure consists of three columns, which correspond to three different stages of aneurysm progression, i.e., the original state (Frame 400, left), the growing state (Frame 2200, middle), and the rupture state (Frame 2400, right). Each column has two rows of frames that illustrate the particle state (top row) and fluid state (bottom row), respectively. As can been seen from the figure, the proposed method is capable of simulating aneurysm growth and rupture in a visually-realistic fashion. Simulation results demonstrate a high degree of consistency with actual physiological phenomena. For instance, fluctuations in the blood flow impact force reflect the pulsatile nature of blood flow driven by the heartbeat, a key physical driver of aneurysm growth and rupture. Additionally, the reduction in wall thickness h with increasing radius R aligns with the physical characteristics described by Poisson’s ratio, illustrating the material behavior of the arterial wall during expansion. These observations validate the physical accuracy of the simulation. To further demonstrate its efficacy, we provide two additional groups of simulation results in Figure 5. Likewise, the particle and fluid state of the simulation are presented separately in two rows. Each row of a group consists of four frames sampled from the resultant simulation video. We can see from Figure 5a,b that the proposed method is capable of simulating the progressions of aneurysm growth and rupture effectively.

Figure 4.
Simulation results of aneurysm growth and rupture. The two rows are particle state rendered online and fluid state rendered offline, respectively. (a,d) show the normal state of an arterial bifurcation at frame 400, (b,e) are the growing state of an aneurysm in the artery at frame 2200, and (c,f) are the rupture state at frame 2400.
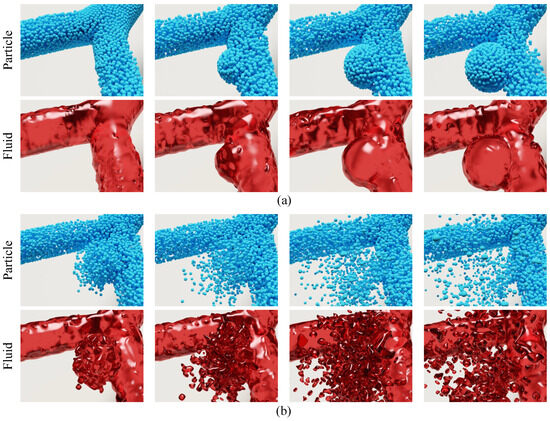
Figure 5.
Simulation results of aneurysm progression at the bifurcation of an artery. (a) Simulation of aneurysm growth, showing frames (from left): Frame 400, Frame 1000, Frame 1200, Frame 2200. (b) Simulation of aneurysm rupture, showing frames (from left): Frame 2200, Frame 2300, Frame 2400, Frame 2500. Each sub-figure illustrates four sample frames from the simulation video. The top row of each sub-figure (rendered with discrete blue spheroids) depicts the particle state, while the bottom row (rendered with translucent red material) corresponds to the fluid state.
4.2. Subjective Effectiveness Evaluation of the Proposed Method in Simulating Different Artery and Aneurysm Morphologies
Since the morphologies of arteries and aneurysms vary significantly in various simulation scenarios, we conducted two more experiments in this section to investigate the effectiveness of the proposed method in handling different types of arteries and aneurysms.
The first experiment was designed to examine the capability of the proposed method in simulating different morphologies of aneurysms. The hemodynamic parameters of an aneurysm are intimately related to its shape and size and that of the artery in which it occurs [40,46]. To verify whether the proposed method can handle different morphologies, we selected three common shapes of aneurysms, namely hemispherical, spherical and piriform. Their geometric parameters are summarized in Table 2. Figure 6 shows the simulation results of hemispherical, spherical, and piriform aneurysms in bifurcated arteries (see Supplementary Video S1 for more details). In this experiment, the bifurcation angle is set to . To analyze the hydrodynamic parameters of the three shapes, we used the aneurysm wall pressure and aneurysm wall thickness h as the indicators, and this is in line with relevant previous work [40,46].

Table 2.
The geometric parameters of three different shapes of aneurysms.
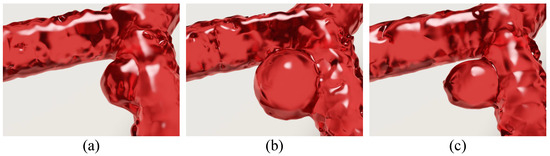
Figure 6.
Simulation of three different shapes of aneurysms occurring in the arterial bifurcation. (a) A hemispherical aneurysm; (b) a spherical aneurysm; and (c) a piriform aneurysm.
Figure 7 illustrates the hydrodynamic parameter changes of different aneurysm shapes from frame 400 to frame 3000. From the changes in the pressure on the aneurysm wall (Figure 7a) and those of the wall thickness of the aneurysm (Figure 7b), it can be seen that the fluctuations in the impact force of the blood flow in the aneurysm of different shapes are similar, and the change in thickness is related to the shapes of the aneurysms. In addition, the thickness changes of the hemispherical and spherical aneurysms are small, and the thickness of pear-shaped aneurysms tends to decrease relatively slowly, which is related to the growth rate of the aneurysms. Equation (16) reflects this phenomenon. In Figure 7b, the thickness change of the hemispherical aneurysm tends to change to 0 from about 1600 frames of the simulation. This is because the maximum size of the aneurysm can be set artificially in the implementation, while at this time, the hemispherical aneurysm has reached a fully developed state. Since the threshold of aneurysm rupture is related to the wall thickness and size of the aneurysm, we tracked the rupture pressure threshold of aneurysms of different shapes, as shown in Figure 7c. Before the aneurysm is fully developed, the pressure thresholds of spherical and hemispherical aneurysm ruptures are similar in magnitude, while that of piriform aneurysms is relatively small, and this is consistent with the relevant numerical analysis results summarized in the literature [40].
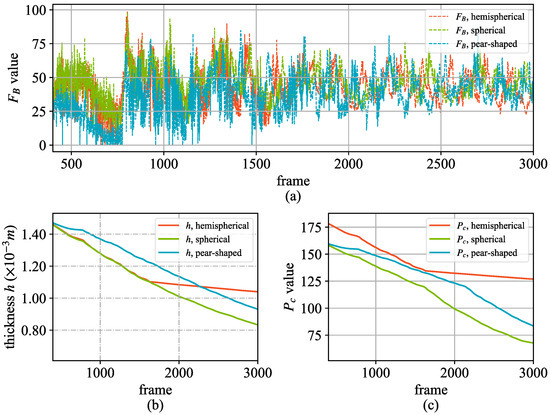
Figure 7.
Hydrodynamic parameter changes of the three different shapes. (a) The change in the blood flow impact force on the aneurysm wall; (b) The thickness change of the aneurysm wall; (c) The critical value of the rupture pressure of the aneurysm.
To validate the accuracy of our simulation, we compared the hemodynamic parameters, such as the pressure on the aneurysm wall and the wall thickness, with those reported in previous numerical studies [40,46]. For instance, our results show that the pressure threshold for rupture in spherical and hemispherical aneurysms is similar, while pear-shaped aneurysms exhibit a lower threshold, which aligns with the findings in [46]. Additionally, the simulated growth rates and rupture times for different aneurysm shapes are consistent with the expected behaviors based on their geometric characteristics. While direct comparison with real-life experiments is challenging due to ethical and practical constraints, our model incorporates key physical principles and parameters derived from biomedical literature, ensuring that the simulation reflects realistic physiological phenomena.
The second experiment was designed to examine the capability of the proposed method in simulating different morphologies of bifurcated arteries. This is based on the fact that blood flow varies with the shapes of bifurcated arteries. To verify the feasibility of the proposed simulation method, we created four different bifurcated arteries by setting the deflection angles to , , , and , respectively, and simulated blood flow with these angles accordingly. Figure 8 shows the simulation results under the test conditions (the Supplementary Video S1 provides more details about this experiment). From this figure, we can see that the proposed method is capable of simulating blood flow in different morphologies of bifurcated arteries.

Figure 8.
Simulation results under different bifurcation angles. The angles set in (a–d) are , , , and , respectively.
4.3. Efficiency Evaluation of the Proposed Method
The simulation approach we developed incorporates the SPH method with a hematology model, using CUDA parallel computation to boost simulation efficiency. We tested the real-time performance of our method via four sets of bifurcation blood flow simulations under diverse test conditions (TC). These experiments were designed to measure the algorithm’s runtime and assess the impact of particle quantity and aneurysm lesions on overall efficiency.
Table 3 displays the results of four test conditions, using frames per second (FPS) to evaluate performance. The proposed method achieves an FPS of 86.95 under TC1 with 5520 particles, utilizing CUDA. Performance declines as particle numbers rise. For example, under TC2 and TC4, with 15,456 and 40,296 particles, FPS values drop to 54.56 and 11.10, respectively. These results highlight the method’s effectiveness for real-time aneurysm simulation at moderate particle counts. Experiments suggest that a particle range of 10,000 to 20,000 strikes an optimal balance between simulation quality and performance. Additionally, a comparison of TC2 and TC3 reveals that simulating arterial blood flow with aneurysm lesions has minimal impact on efficiency.

Table 3.
Efficiency of the proposed method under four groups of test conditions.
4.4. Parametric Analysis of the Proposed Simulation Model
According to the analysis of aneurysm rupture pressure threshold calculated by (13) in Section 3.2, aneurysm radius R, wall thickness h, porosity , and Poisson’s ratio could have a great impact on the rupture threshold. Meanwhile, Poisson’s ratio is related to R, h and their increment. Therefore, in this subsection, we discuss the sensitivity of and to the change in rupture threshold and thickness by designing two experiments in which the progression of aneurysms is simulated with different parameters.It should be noted that the rupture threshold and aneurysm wall thickness values reported in this study are average values derived from multiple simulation runs. In our simulations, we chose three common shapes of aneurysms: hemispherical, spherical, and pear-shaped.
In the experiment, we fixed the bifurcation deflection angle to and to , and obtained the simulation results by setting to , , , , and , respectively. As can be seen from Figure 9, and are relatively abnormal in the first 100 frames of simulation process, which is caused by the preheating stage of the simulation. After this, on the aneurysm is relatively stable and has a regularity of pulsatility. Different Poisson’s ratio values have different maximum pressure thresholds . The smaller the value of , the greater the pressure threshold causing rupture and the longer the rupture occurs. Meanwhile, different values also have an impact on the speed at which the aneurysm wall thickness h decreases. The greater the value of , the faster the thickness decreases. Additionally, we conducted experiments to analyze the effect of porosity, , on the rupture threshold and wall thickness h. In the experiments, was fixed at 0.4, and was varied from to . The results, as shown in Table 4, indicate that an increase in leads to a decrease in the rupture threshold and a faster reduction in wall thickness h. This suggests that higher porosity can lead to earlier rupture and thinner aneurysm walls, corroborating previous discussions about the sensitivity of aneurysm rupture to and . In particular, when is set to and , the curves of pressure threshold and wall thickness exhibit two distinct patterns, so it can be seen that the aneurysms rupture only after they are fully developed. Comparing the results obtained with different , it can be seen that is sensitive to the simulation. Specifically, it takes longer to reach the critical point of aneurysm rupture. A key limitation of the current study is the absence of direct quantitative comparisons with real-world clinical or experimental data, primarily due to challenges in accessing real-time aneurysm progression data and ethical constraints. Our simulation results show qualitative consistency with clinical observations, such as aneurysm growth and rupture under elevated hemodynamic forces, as reported in studies like [3]. To address this, future work will involve collaborations with clinical researchers to validate and calibrate the model using patient-specific imaging data, enhancing its medical applicability and predictive accuracy.
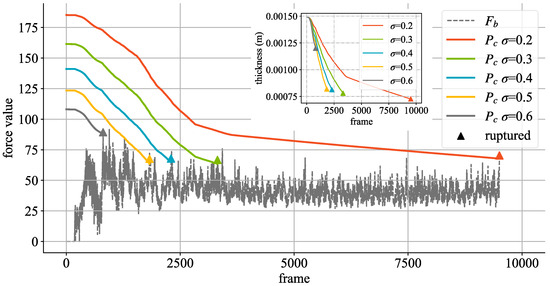
Figure 9.
Effects of different values on changes in aneurysm wall thickness and rupture threshold. is the impact force calculated by Equation (16) in Section 3.2. The triangular symbol represents the number of frames and the corresponding wall thickness and impact force when the aneurysm ruptures under the condition of corresponding values.

Table 4.
Effects of different and on the number of simulated aneurysm rupture frames.
Moreover, the value of involves aneurysm wall thickness (h), radius R, and , according to (22) in Section 3.3. In order to more intuitively observe the influence of on R and h, Figure 10 shows the effects of different values on the size of R and h when is fixed. From Figure 10, different values have the same law of decreasing thickness, and there is no obvious and sensitive change to its influence.
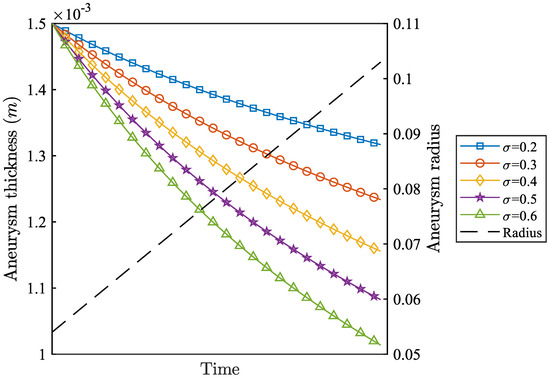
Figure 10.
Effects of different values on changes in radius (R) and thickness (h).
5. Conclusions
In this paper, we have proposed an SPH based method for aneurysm simulation. Based on the medical model of aneurysm growth and rupture, a blood flow particle model of aneurysm lesion is established. The simulation of aneurysm growth and rupture is implemented using the physical quantity calculation of the SPH method and controlling the size and thickness of the aneurysm. Experiment results show that the proposed method has good authenticity. Through parameter sensitivity analysis, the key parameters leading to aneurysm growth and rupture in the simulation model are identified. By adjusting different parameters, aneurysmal lesions in different physiological environments can be simulated. Using CUDA parallel computation, the real-time simulation of the proposed method is effectively guaranteed. The proposed SPH method successfully simulates the formation, growth, and rupture of aneurysms, validating the critical role of physical modeling in aneurysm simulation. Future research will focus on refining the physical models to incorporate additional biomechanical factors, such as the heterogeneity of the arterial wall and the non-Newtonian properties of blood, to further enhance simulation accuracy and clinical applicability. Our SPH-based method offers a significant advancement over existing approaches by enabling the real-time simulation of aneurysm formation, growth, and rupture while accounting for complex fluid–solid interactions. Unlike traditional methods, which often require extensive computational resources and time due to their complexity, our approach leverages CUDA parallel computation to achieve real-time performance with a moderate number of particles. This efficiency, combined with the method’s ability to simulate physiologically accurate blood flow and aneurysm dynamics, makes it uniquely suited for applications requiring rapid feedback, such as virtual surgery and medical education. Currently, no other method integrates these physical phenomena with such computational efficiency, positioning our approach as a valuable tool for both research and clinical applications.
Since porosity and Poisson’s ratio affect the maximum pressure threshold of aneurysms, as indicated by Equation (13), a higher results in a lower and a shorter time to rupture. In order to investigate the effect of on aneurysm rupture, we carried out another experiment, in which aneurysms were simulated with different values of and with bifurcation angle and values of and , respectively. Table 4 shows the corresponding frames of aneurysm rupture in the two groups of experiments corresponding to and under different values. The results demonstrate that higher porosity leads to quicker aneurysm rupture under the same conditions. This observation underscores the significant sensitivity of porosity in influencing the simulation outcomes.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/math13152439/s1.
Author Contributions
Conceptualization, Y.W. and F.W.; Methodology, Y.W. and F.W.; Software, Y.W., F.W. and Z.L.; Validation, X.S. and Z.L.; Formal analysis, X.S.; Investigation, Z.X.; Resources, Z.X. and T.Z.; Data curation, X.S. and M.Z.; Writing—original draft, Y.W. and F.W.; Writing—review & editing, X.S., Z.X., M.Z., B.Z. and T.Z.; Visualization, Z.L. and M.Z.; Supervision, B.Z. and T.Z.; Project administration, B.Z.; Funding acquisition, Y.W., F.W. and B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the Guangdong Provincial Science and Technology Innovation Strategy Special Project (“Big Project + Task List” Project) (STKJ2023069, STKJ202209003), Key Area Special Projects for General Colleges and Universities in Guangdong Province (2022ZDZX1007), Key Research Platforms and Projects of Guangdong Provincial Universities (Grant No. 2023KCXTD013), Key Research Platforms and Projects of Guangdong Provincial Universities (Grant No. 2022LSYS006).
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to thank all the participants and contributors for their valuable contributions and support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brisman, J.L.; Song, J.K.; Newell, D.W. Cerebral aneurysms. N. Engl. J. Med. 2006, 355, 928–939. [Google Scholar] [CrossRef]
- Rincon, F.; Rossenwasser, R.H.; Dumont, A. The epidemiology of admissions of nontraumatic subarachnoid hemorrhage in the United States. Neurosurgery 2013, 73, 217–223. [Google Scholar] [CrossRef] [PubMed]
- Texakalidis, P.; Sweid, A.; Mouchtouris, N.; Peterson, E.C.; Sioka, C.; Rangel-Castilla, L.; Reavey-Cantwell, J.; Jabbour, P. Aneurysm formation, growth, and rupture: The biology and physics of cerebral aneurysms. World Neurosurg. 2019, 130, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Chentanez, N.; Muller, M. Real-time eulerian water simulation using a restricted tall cell grid. ACM Siggraph 2011, 30, 82. [Google Scholar] [CrossRef]
- Wen, J.; Ma, H. Real-time smoke simulation based on vorticity preserving lattice Boltzmann method. Vis. Comput. 2019, 35, 1279–1292. [Google Scholar] [CrossRef]
- Hu, L.; Chen, M.; Liu, P.X.; Xu, S. A vortex method of 3D smoke simulation for virtual surgery. Comput. Methods Programs Biomed. 2021, 198, 105813. [Google Scholar] [CrossRef]
- Sequeira, A.; Bodnár, T. Blood Coagulation Simulations using a Viscoelastic Model. Math. Model. Nat. Phenom. 2014, 9, 34–45. [Google Scholar] [CrossRef]
- Leiderman, K.; Fogelson, A.L. Grow with the flow: A spatial-temporal model of platelet deposition and blood coagulation under flow. Math. Med. Biol. J. IMA 2011, 28, 47–84. [Google Scholar] [CrossRef] [PubMed]
- Solenthaler, B.; Pajarola, R. Predictive-corrective incompressible SPH. ACM Trans. Graph. 2009, 28, 40. [Google Scholar] [CrossRef]
- Foster, N.; Metaxas, D.N. Realistic Animation of Liquids. Graph. Model. Image Process. 1995, 58, 471–483. [Google Scholar] [CrossRef]
- Chen, X.; Wang, R.; Lin, S.; Wang, F.; Luo, X. Thrombus Clotting Simulation Method Based on the Gillespie Method. J. Comput.-Aided Des. Comput. Graph 2019, 31, 1301–1311. [Google Scholar] [CrossRef]
- Wang, F.; Xu, S.; Jiang, D.; Zhao, B.; Dong, X.; Zhou, T.; Luo, X. Particle hydrodynamic simulation of thrombus formation using velocity decay factor. Comput. Methods Programs Biomed. 2021, 207, 106173. [Google Scholar] [CrossRef]
- Faizal, W.; Ghazali, N.; Khor, C.; Badruddin, I.A.; Zainon, M.; Yazid, A.A.; Ibrahim, N.B.; Razi, R.M. Computational fluid dynamics modelling of human upper airway: A review. Comput. Methods Programs Biomed. 2020, 196, 105627. [Google Scholar] [CrossRef]
- Lopes, D.; Puga, H.; Teixeira, J.; Lima, R. Blood flow simulations in patient-specific geometries of the carotid artery: A systematic review. J. Biomech. 2020, 111, 110019. [Google Scholar] [CrossRef]
- Muller, M.; Charypar, D.; Gross, M. Particle-based fluid simulation for interactive applications. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 26–27 July 2003; pp. 154–159. [Google Scholar]
- Badgaish, M.; Lin, J.E.; Seshaiyer, P. Nonlinear Dynamics and Analysis of Intracranial Saccular Aneurysms with Growth and Remodeling. J. Nonlinear Dyn. 2016, 2016, 2869083. [Google Scholar] [CrossRef]
- Hademenos, G.; Massoud, T.; Valentino, D.; Duckwiler, G.; Viñuela, F. A nonlinear mathematical model for the development and rupture of intracranial saccular aneurysms. Neurol. Res. 1994, 16, 376–384. [Google Scholar] [CrossRef]
- Chitanvis, S.; Hademenos, G.; Powers, W. Hemodynamic assessment of the development and rupture of intracranial aneurysms using computational simulations. Neurol. Res. 1995, 17, 426–434. [Google Scholar] [CrossRef] [PubMed]
- Perktold, K.; Kenner, T.; Hilbert, D.; Spork, B.; Florian, H. Numerical blood flow analysis: Arterial bifurcation with a saccular aneurysm. Basic Res. Cardiol. 1988, 83, 24–31. [Google Scholar] [CrossRef] [PubMed]
- Bridson, R. Fluid Simulation for Computer Graphics, 2nd ed.; A K Peters/CRC Press: Natick, MA, USA, 2015; pp. 1–256. [Google Scholar]
- Becker, M.; Teschner, M. Weakly compressible SPH for free surface flows. In Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Diego, CA, USA, 2–4 August 2007; pp. 209–217. [Google Scholar]
- Schechter, H.; Bridson, R. Ghost SPH for animating water. ACM Trans. Graph. 2012, 31, 1–8. [Google Scholar] [CrossRef]
- Bridson, R. Fast Poisson Disk Sampling in Arbitrary Dimensions. In Proceedings of the ACM SIGGRAPH 2007 Sketches, SIGGRAPH ’07, San Diego, CA, USA, 5–9 August 2007; p. 22. [Google Scholar]
- Macklin, M.; Müller, M. Position Based Fluids. ACM Trans. Graph. 2013, 32, 104. [Google Scholar] [CrossRef]
- Winchenbach, R.; Hochstetter, H.; Kolb, A. Infinite continuous adaptivity for incompressible SPH. ACM Trans. Graph. 2017, 36, 102. [Google Scholar] [CrossRef]
- Ihmsen, M.; Cornelis, J.; Solenthaler, B.; Horvath, C.; Teschner, M. Implicit Incompressible SPH. IEEE Trans. Vis. Comput. Graph. 2014, 20, 426–435. [Google Scholar] [CrossRef]
- Kang, N.; Sagong, D. Incompressible SPH using the Divergence-Free Condition. Comput. Graph. Forum 2014, 33, 219–228. [Google Scholar] [CrossRef]
- Bender, J.; Koschier, D. Divergence-Free Smoothed Particle Hydrodynamics. In Proceedings of the SCA ’15, Los Angeles, CA, USA, 7–9 August 2015; pp. 147–155. [Google Scholar]
- Bender, J.; Koschier, D. Divergence-Free SPH for Incompressible and Viscous Fluids. IEEE Trans. Vis. Comput. Graph. 2017, 23, 1193–1206. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Lin, S.; Wang, R.; Li, Y.; Zhao, B.; Luo, X. Improving Incompressible SPH Simulation Efficiency by Integrating Density-Invariant and Divergence-Free Conditions. In Proceedings of the ACM SIGGRAPH 2018 Posters, SIGGRAPH ’18, Vancouver, BC, Canada, 12–16 August 2018. [Google Scholar]
- Wang, F.; Lin, S.; Luo, X.; Wang, R. Coupling Computation of Density-Invariant and Divergence-Free for Improving Incompressible SPH Efficiency. IEEE Access 2020, 8, 135912–135919. [Google Scholar] [CrossRef]
- Laha, S.; Fourtakas, G.; Das, P.K.; Keshmiri, A. Graphics processing unit accelerated modeling of thrombus formation in cardiovascular systems using smoothed particle hydrodynamics. Phys. Fluids 2025, 37, 021902. [Google Scholar] [CrossRef]
- Laha, S.; Fourtakas, G.; Das, P.K.; Keshmiri, A. Smoothed particle hydrodynamics based FSI simulation of the native and mechanical heart valves in a patient-specific aortic model. Sci. Rep. 2024, 14, 6762. [Google Scholar] [CrossRef]
- Topalovic, M.; Nikolic, A.; Milovanovic, V. Smoothed particle hydrodynamics for blood flow analysis: Development of particle lifecycle algorithm. Comput. Part. Mech. 2022, 9, 1119–1135. [Google Scholar] [CrossRef]
- Sigalotti, L.D.G.; Rendón, O.; Klapp, J.; Vargas, C.A.; Cruz, F. A new insight into the consistency of the SPH interpolation formula. Appl. Math. Comput. 2019, 356, 50–73. [Google Scholar] [CrossRef]
- Chitanvis, S.; Dewey, M.; Hademenos, G.; Powers, W.; Massoud, T. A nonlinear quasi-static model of intracranial aneurysms. Neurol. Res. 1997, 19, 489–496. [Google Scholar] [CrossRef]
- Nieto, J.J.; Torres, A. A nonlinear biomathematical model for the study of intracranial aneurysms. J. Neurol. Sci. 2000, 177, 18–23. [Google Scholar] [CrossRef]
- Nikolov, S.; Stoytchev, S.; Torres, A.; Nieto, J.J. Biomathematical modeling and analysis of blood flow in an intracranial aneurysm. Neurol. Res. 2003, 25, 497–504. [Google Scholar] [CrossRef]
- Farnoush, A.; Qian, Y.; Avolio, A. Effect of inflow on computational fluid dynamic simulation of cerebral bifurcation aneurysms. In Proceedings of the 33rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 1025–1028. [Google Scholar]
- Fu, C.; Yan, Z.; Zhang, H.; Ling, F. Advances in Numerical Simulations on the Hemodynamic of Intracranial Aneurysms and Their Rupture Mechanism. Adv. Mech. 2001, 31, 84–94. [Google Scholar]
- Chalouhi, N.; Hoh, B.L.; Hasan, D. Review of Cerebral Aneurysm Formation, Growth, and Rupture. Stroke 2013, 44, 3613–3622. [Google Scholar] [CrossRef]
- Zhang, M.; Shang, R.; Zhang, C.; Li, X.; Que, P.; Wei, X. Advances in hemodynamics of intracranial aneurysms. J. Mudanjiang Med. Univ. 2021, 42, 135–137. [Google Scholar]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering Science. Meccanica 2002, 37, 489–490. [Google Scholar] [CrossRef]
- Humphrey, J.D. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs; Springer: New York, NY, USA, 2002. [Google Scholar]
- Murray, C.D. The Physiological Principle of Minimum Work Applied to the Angle of Branching of Arteries. J. Gen. Physiol. 1926, 23, 835–841. [Google Scholar] [CrossRef] [PubMed]
- Burleson, A.C.; Strother, C.M.; Turitto, V.T. Computer modeling of intracranial saccular and lateral aneurysm for the study of their hemodynamics. Neurosurgery 1995, 37, 774–784. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).