Abstract
Aspect-based sentiment analysis (ABSA) aims at identifying the sentiment polarity for a particular aspect in a review. ABSA studies based on deep learning models have exploited the attention mechanism to detect aspect-related parts. Conventional softmax-based attention mechanisms generate dense distributions, which may limit performance in tasks that inherently require sparsity. Recent studies on sparse attention transformation functions have demonstrated their effectiveness over the conventional softmax function. However, these studies primarily focus on highly sparse tasks based on self-attention architectures, leaving their applicability to the ABSA domain unexplored. In addition, most ABSA research has focused on leveraging aspect terms despite the usefulness of aspect categories. To address these issues, we propose a sparse-attention-based residual joint network (SPA-RJ Net) for the aspect-category-based sentiment analysis (ACSA) task. SPA-RJ Net incorporates two aspect-guided sparse attentions—sparse aspect-category attention and sparse aspect-sentiment attention—that introduce sparsity in attention via a sparse distribution transformation function, enabling the model to selectively focus on aspect-related information. In addition, it employs a residual joint learning framework that connects the aspect category detection (ACD) task module and the ACSA task module via residual connections, enabling the ACSA module to receive explicit guidance on relevant aspect categories from the ACD module. Our experiment validates that SPA-RJ Net consistently outperforms existing models, demonstrating the effectiveness of sparse attention and residual joint learning for aspect category-based sentiment classification.
MSC:
68T01; 68T07; 68T50
1. Introduction
Aspect-based sentiment analysis (ABSA) is fine-grained sentiment analysis (SA) [1]. While traditional SA treats a review as a whole and assigns it a single sentiment label, ABSA aims at detecting the sentiment polarity corresponding to a particular aspect. Consider the sentence “pizza is good but sometimes service is so bad” as one of the common reviews about restaurants. It focuses on ‘pizza’ and ‘service’ as aspects of interest, each of which may have a different sentiment, e.g., positive for pizza and negative for service. ABSA, i.e., sentiment analysis pinpointing at the aspect level, will be useful to businesses and consumers who want valuable insights for decision-making from reviews. However, as reviews are generally written in an unstructured manner by individuals, the review texts vary in length, sentence structure, expression of aspect/sentiments, and other factors. Moreover, ABSA must handle multiple aspects, each potentially associated with different sentiment labels within a single review, which presents a significant challenge.
Recently, attention-based deep learning models have led to significant improvement in performance in ABSA by effectively identifying aspect-relevant words within an input review [2]. The conventional attention mechanism employs the softmax function to convert attention scores into a dense probability distribution, assigning positive weights to all input elements [3]. However, this property results in non-zero weights even for irrelevant elements, which can be a limitation in applications that benefit from sparsity [4,5,6]. A recent study by Google DeepMind [6] highlights the significance of exploring alternatives to softmax, pointing out its fundamental limitations in enabling robust reasoning over diverse inputs. Various methods have been introduced to address the sparsity issue in attention, such as regularization-based techniques [7,8,9] and temperature-scaled softmax variants [6,10,11]. However, these approaches still rely on the inherently dense nature of softmax, which restricts the level of sparsity achievable and hinders the model’s ability to distinguish sharply and filter out irrelevant input tokens. They often fail to fully capture the selective focus intended by attention mechanisms.
As an alternative to softmax, several studies have proposed the functions that directly transform logits into sparse probability distributions. Functions such as sparsemax [12] and entmax [13] explicitly assign zero weights to irrelevant tokens, thereby introducing sparsity into the attention mechanism. These methods have shown potential for improving interpretability, as their attention weights more clearly reflect which elements are considered important. Although sparse attention distributions have proven their effectiveness successfully in high-sparsity tasks, such as translation and summarization tasks, which are usually based on self-attention models such as Transformer [14] and BERT [15], their integration into the ABSA domain remains underexplored. In many ABSA studies, we observe that attention tends to be overly diffused across the entire review, which can negatively affect prediction accuracy. This issue becomes more pronounced when multiple aspects are present within a single sentence, where a sparse distribution could help the model focus more precisely on relevant information. Therefore, we believe that incorporating sparse attention into general ABSA frameworks presents a promising research direction.
On the other hand, most ABSA research has focused on aspect terms despite the practical utility of aspect categories. Aspects can be classified into aspect terms and aspect categories [1]. Aspect terms are explicitly mentioned in the text, providing clearer guidance to models, while aspect categories refer to high-level features that are often implicit, making aspect-category-based sentiment analysis (ACSA) more challenging. Nevertheless, the aspect-category-based approach offers advantages such as broader applicability and easier data collection [16]. In this paper, we focus on aspect-category-based sentiment analysis (ACSA), and hereafter, we use the term “aspect” to refer to aspect category.
To address these challenges, we propose SPA-RJ Net, a sparse-attention-based residual joint network. SPA-RJ Net provides two aspect-guided sparse attentions, i.e., sparse aspect-category attention and sparse aspect-sentiment attention. They incorporate sparse probability distribution into the attention mechanism by using the α-entmax function, which transforms attention scores into sparse distributions via Tsallis entropy. To evaluate the effect of sparse attention in ABSA, we adopt an aspect-guided attention model, a commonly used approach in this task, and apply varying degrees of sparsity by adjusting the sparsity parameter α. These sparse attentions enable the model to focus more effectively on aspect-related information. To the best of our knowledge, this is the first work to directly apply the sparse attention distribution to the ABSA task with benchmark datasets such as SemEval [17,18,19] and Multi-Aspect Multi-Sentiment (MAMS) [20].
Next, we adopt a joint learning framework that integrates ACD and ACSA, which enhances sentiment classification by providing explicit guidance on relevant aspect categories. In our joint learning setting [21], the ACD task module, as an auxiliary task, learns aspect-category-related features via sparse aspect-category attention and transfers this sparse attention information to the main ACSA task module. ACSA predicts sentimental polarity for each aspect through CNN-biLSTM layers and sparse aspect-sentiment attention. However, learning multiple tasks simultaneously can lead to information interference between tasks, which may result in unstable or suboptimal performance. To mitigate the problem, we propose to employ a residual connection [22] between ACD and ACSA and adjust a balancing hyperparameter to regulate the learning pace discrepancy between tasks. They help to promote more stable optimization and improve overall performance. Our experiments show that SPA-RJ Net outperforms existing models, particularly dense attention-based ones, demonstrating the effectiveness of sparse attention for ABSA.
In summary, the main contributions of this paper are as follows:
- We propose SPA-RJ Net to explore the effectiveness of sparse attention in ACSA. It employs two aspect-guided sparse attentions—aspect-category and aspect-sentiment attention—which introduce sparsity into attention via the α-entmax function. This enables the model to focus more effectively on a smaller number of aspect-specific elements, improving accuracy and interpretability.
- SPA-RJ Net adopts a residual joint learning framework with adjusting a balancing hyperparameter. The ACD module extracts aspect features by sparse aspect-category attention and transfers them to the main ACSA module via the residual pathway, which enhances final sentiment classification by providing explicit guidance on relevant aspect categories.
- Our experiments with ABSA benchmark datasets (SemEval and MAMS) validate the efficiency and the interpretability of SPA-RJ Net, which highlights the benefits of sparse attention and residual joint learning in the ABSA task domain.
The rest of the paper is designed as follows: The related work and background are described in Section 2 and Section 3. Then, our proposed model architecture is presented in Section 4. Section 5 presents our experimental setup and results, model analysis, and case study demonstrating the effectiveness of the proposed SPARJ-Net model. Lastly, this paper draws a conclusion and addresses research directions in Section 6.
2. Related Work
2.1. Attention-Based Deep Learning Models for ABSA
Deep learning techniques have demonstrated promising results in ABSA [2,23]. Deep learning models can automatically learn semantic representation from raw data without manual feature engineering [24,25]. Most models are based on a framework composed of task-independent word embedding and task-centric deep neural networks. Word embeddings become fundamental components in modern NLP tasks. Word2Vec [26] and GloVe [27] are popular pre-training models but focus on static word embeddings. Recently, BERT [15] introduced context-sensitive word representations by considering both left and right contexts of a word simultaneously. Its self-attention mechanism is effective at capturing the full context of a sentence.
For task-centric deep neural network models, RNN-based models and CNNs have been extensively utilized [28,29]. RNN-based models, such as long short-term memory (LSTM) [30] and gated recurrent units (GRUs) [31], are particularly effective at capturing sequential text information. BiLSTM enhanced performance of LSTM by allowing the model to access both prior and future context in a sequence, making it more effective in tasks requiring nuanced language understanding [32]. On the other hand, CNNs can efficiently detect patterns in shorter texts and contiguous words. The 2D-CNN can capture broader contextual information by transforming the text into a 2D image [33]. The BERT model also plays a role as the flexible and powerful post-training model when fine-tuned for specific tasks, including ABSA, by utilizing a multi-layer self-attention mechanism [34].
With the success of attention mechanisms in various tasks, such as machine translation [14,35] and emotion analysis [36], numerous attention-based deep learning models have been proposed for the ABSA task. Wang et al. [37] first introduced an LSTM model with a self-attention layer, known as ATAE-LSTM, which incorporates aspect embeddings into the attention mechanism. Tang et al. [38] proposed a deep memory network with multiple stacked computational layers, each containing an attention module. Building upon the HEAT network [39], Cheng et al. [40] developed an LSTM-based model that jointly learns to represent aspects and aspect-level sentiment information using two distinct attention mechanisms: aspect attention and sentiment attention. Ma et al. [41] presented the interactive attention network (IAN), which models the interactive attention between context word vectors and multi-word aspect term vectors. Huang et al. [42] proposed an attention-over-attention (AOA) neural network, which captures the interaction between aspects and context sentences by generating mutual attention representations. Xu et al. [43] introduced the multi-attentional network (MAN), which leverages both intra-level and inter-level attention to enhance the representation of aspect-specific sentiment.
Compared to previous models, hybrid learning models with attention, such as the LSTM-CNN with attention model, have shown improved performance because the hybrid model aims to compensate for the weaknesses of one model by leveraging the strengths of other models [44]. In ABSA where local context and sequential information are important, various attention-based hybrid models show their usefulness [45,46,47].
Currently, as another approach to effectively capture the dependency relation between aspect and context, graph convolution network (GCN) models are proposed [48,49,50]. However, since we aim to focus on the effectiveness of hierarchical sparse attention over the ABSA reviews in this work, we employ the model consisting of a BERT and a CNN-biLSTM for text processing.
2.2. Attention with Sparsity Constraints
The attention mechanism is known to improve both the accuracy and interpretability of models by assigning different weights to input elements based on their relevance. During the computation of attention, raw attention scores are transformed into a probability distribution that reflects the relative importance of each element [51]. Various functions have been proposed for this transformation, including sum-normalization [52], softmax [53], and spherical softmax [54], each of which maps vectors from Euclidean space to a probability simplex. Among these, softmax has become the standard choice for most attention implementations.
However, several studies have revealed the limitations of softmax in scenarios that benefit from sparsity. Luong et al. [55] reported that the dense attention distribution produced by softmax can degrade performance in long-sequence settings, particularly in machine translation tasks. Veličković et al. [6] further argued that softmax fundamentally fails to support robust reasoning across all input configurations. They validated this claim through empirical studies on tasks such as max-retrieval and CLRS-text, using Transformer-based architectures.
To address this issue, various methods have been proposed. Regularization-based approaches encourage sparsity by introducing constraints into the loss function, making them both flexible and easy to integrate into existing models [7,8]. However, these methods rely on indirect control over attention distributions, which can result in suboptimal sparsity levels and require careful tuning of the regularization strength. Instead of indirectly influencing the attention distribution, some researchers have proposed methods that directly induce sparsity. One such approach involves modifying the softmax function to suppress elements with lower attention scores [6,10,11]. Veličković et al. [6] introduced an adaptive temperature mechanism that adjusts based on the dataset, while Feng et al. [10] and Sun et al. [11] proposed techniques that retain only attention scores above a predefined threshold or select the top-k most relevant tokens using softmax variants. These methods were applied to tasks such as document classification, summarization, and question-answering; however, they have not yet been explored in the context of ABSA.
As an alternative line of research, several functions have been proposed to replace softmax in attention mechanisms. Since the introduction of sparsemax, a range of sparse transformation functions, such as sparsegen and entmax, have been developed to enable more selective and interpretable attention. The sparsemax function performs Euclidean projection onto the probability simplex, resulting in sparse attention distributions that improve interpretability [12]. It has shown promising empirical performance in tasks such as natural language inference and multi-label classification. Sparsegen, a generalization of sparsemax, offers greater flexibility in controlling the level of sparsity while retaining favorable optimization properties [56]. Entmax further generalizes both softmax and sparsemax by introducing a tunable parameter, α, which allows the dynamic adjustment of sparsity levels within a continuous range [13]. In this study, we adopt the entmax function to explore the effectiveness of sparse attention in the ABSA task, specifically investigating how varying degrees of sparsity influence model performance.
In the domain of ABSA, research on sparse attention remains relatively limited and has primarily focused on regularization-based methods [16,57,58]. Dhanith et al. [57] proposed a sparse-self-attention-based gated recurrent unit (SSA-GRU-AE), which applies L1 regularization to enforce sparsity in self-attention. Hu et al. [58] introduced two aspect-level regularization strategies: sparse regularization for individual aspects and orthogonal regularization across multiple aspects. In their subsequent work [16], they extended this approach by incorporating task-level regularization for ACD, forming a hybrid regularization framework. Although their model addressed the ACSA task using a multi-task learning setup similar to ours, it did not incorporate residual connections between tasks, and it required each input review to be accompanied by a predefined set of aspect categories. Furthermore, most existing studies have relied on self-attention architectures that naturally exhibit a high level of sparsity, which may limit the generality and adaptability of the learned representations. To the best of our knowledge, this study is the first to incorporate a sparse attention transformation function into the ABSA task within query-key attention architectures. We evaluate the effectiveness of sparse attention using widely adopted ABSA benchmark datasets, including SemEval and MAMS.
2.3. Joint Learning for ABSA
Joint learning has been increasingly adopted in ABSA to simultaneously optimize multiple related tasks, such as aspect term extraction (ATE), aspect category detection (ACD), and sentiment classification for target aspects. This multi-task paradigm, which is often used interchangeably with multi-task learning [21], leverages inter-task dependencies, thereby improving both generalization and overall model performance.
Previous ABSA studies exploring joint frameworks have primarily focused on the aspect-term-based sentiment analysis (ATSA) task, where the aspect term extraction (ATE) and sentiment classification tasks address the limitations of existing models that focus on a single task [46,59,60,61]. However, these approaches heavily rely on the accurate detection of aspect terms, which can significantly degrade sentiment classification performance.
There have also been studies in ACSA that utilize joint learning [62,63,64]. Schmitt et al. [62] proposed an end-to-end joint learning network, while Wang et al. [63] introduced the BERT-SAN model. Both employed ACD as an auxiliary task to guide sentiment prediction with explicit aspect category supervision. Pei et al. [64] proposed a multi-task joint learning framework to simultaneously solve the ACSA and ATSA tasks using BERT. However, prior works did not explicitly integrate the attention learned from ACD into the sentiment prediction module and did not incorporate residual learning to connect tasks. Our work introduces a residual joint learning architecture that enhances the information flow between ACD and ACSA through residual connections, while incorporating sparse attention to improve focus and interpretability.
3. Background
3.1. Attention Mechanism
To enhance the understanding of sparse attention, we first describe the general attention mechanism. It consists of four components: input features, query, attention computation, and output. The inputs of the attention model are the matrices of feature vectors and the query . The query tells the attention model which and how many input feature vectors to attend to the query.
To generate the attention, two different matrices are extracted from : the keys , and the values , where and are the dimensions of the key vectors and value vectors. The general way of obtaining and is through a linear transformation of using the weight matrices, and , respectively. and can be learned during training or previously predefined:
Attention computation is composed of three steps: attention score calculation, probability distribution transformation, and context vector construction, as presented in Figure 1.
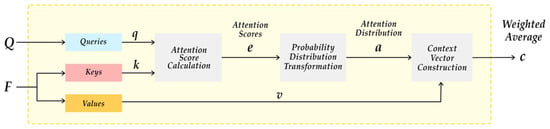
Figure 1.
General attention mechanism process.
Its goal is to produce some weighted vector(s) with vectors in . Each weight means a relative importance of each input feature vector according to a given query. These relative weights are obtained via attention score calculation and probability transformation.
At the step of attention score calculation, an attention score vector is produced with the query and the key matrix via some score function, :
The function can be defined as any function that measures the relatedness or similarity of the key and query, for example, dot product.
Then, in the probability transformation step, the attention scores are transformed into a probability distribution of [0, 1] by a probability transformation function. The probability transformation function allows the model to assign relative importance to different input elements while keeping the overall distribution balanced. There are various probability transformation functions, but current attention models typically use softmax. The softmax function converts a vector of weights to a vector that represents a posterior label probability, , where the sum of is 1, as follows:
Each element of the input vector is executed by the exponential function, and then the output values are normalized by dividing by the sum of the exponentials. The sum of the output vector is 1, satisfying the conditions of a probability distribution. The attention weights provide a rather intuitive interpretation for the attention module.
In the final weighted vector construction, a context vector is calculated as:
We observe that in the probability transformation step, softmax produces a dense probability distribution, assigning positive values to all elements due to its exponential operation. As a result, unrelated elements with positive weights can introduce noise that can degrade the model’s accuracy. It becomes particularly critical in multi-aspect presence.
3.2. Sparse Attention Distribution Transformation
Softmax is one of the possible transform functions that aim to map a given input onto the probability simplex in a differentiable manner. A simplex is a geometric structure in which vectors are constrained to be positive and sum to 1, as follows:
This forces the function to output a probability distribution that will lie on a corner of the probability simplex. Therefore, will be a binary vector with a 1 at the component of the highest value in , which leverages softmax (Equation (3)) to map onto the simplex, written in a differentiable approximation of the argmax operation:
where is the Gibz–Boltmann–Shannon entropy [65].
By changing the entropy, we can consistently describe other transformation functions. The sparsemax function can be defined with the Gini entropy :
This transformation can assign a zero value to low-attention-scoring elements, thereby generating a sparse attention distribution where only relevant elements have weights.
As a follow-up study, the α-entmax function was proposed [13]. Unlike sparsemax, α-entmax utilizes the Tsallis entropy [66] and controls the propensity of sparsity in probability distribution through the α parameter, defined as:
In Equation (8), is the positive part (ReLU) function, and τ: Rn → R is a normalizing function satisfying the constraint for any . As a result, entries with score get exactly zero probability and can be disregarded during computation.
As the value of α approaches 1, i.e., when becomes the Shannon entropy, the α-entmax function recovers the softmax function. For all α > 1, it produces continuously sparser output distributions. In particular, for α = 2, it recovers the sparsemax function.
Both sparsemax and α-entmax offer efficient and differentiable algorithms to generate sparse attention distributions, making them seamless alternatives to the softmax function. In this work, we use α-entmax to control sparsity in attention distributions based on the value of α.
3.3. Residual Learning
Residual learning, originally introduced in ResNet [67], is a widely adopted technique in deep neural networks, allowing layers to learn modifications (residuals) to the identity mapping, rather than learning the entire transformation. Instead of directly mapping the input feature to an output , the residual learning module reformulates the desired mapping as:
This skip connection to directly pass input information to subsequent layers can prevent vanishing gradients and accelerate network training.
In the context of multi-task learning and NLP, residual connections can be used to combine information from sub-tasks or earlier layers with downstream modules. This approach enables the model to support more stable learning and effective information transfer. By selectively adding refined signals rather than replacing input representations entirely, residual connections promote better generalization and interpretability in complex architectures.
4. Sparse-Attention-Based Residual Joint Network (SPA-RJ Net)
This section presents the SPA-RJNet architecture, as illustrated in Figure 2.
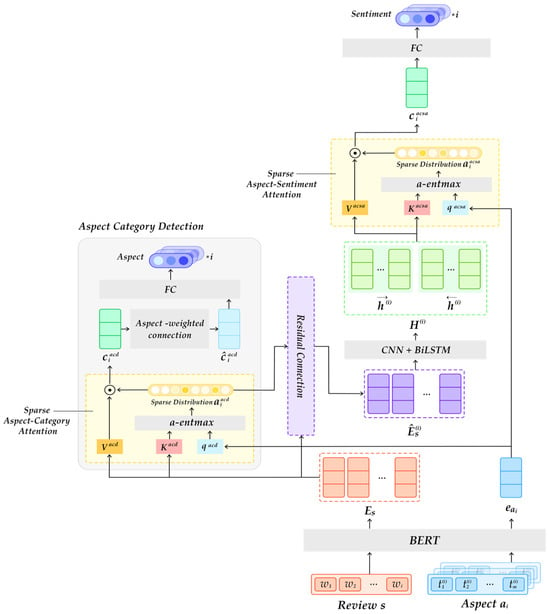
Figure 2.
SPA-RJ Net architecture.
4.1. Input Layer for Embedding
Given a review consisting of words, represented as , and a set of aspect categories where each aspect is a sequence of word tokens, SPA-RJ Net M predicts the sentiment polarity of with respect to :
Each word in the input sequence is initially mapped to a fixed d-dimensional (d = 768) vector, corresponding to the default hidden size of the pre-trained BERT base model. Thus, the input review is embedded into as follows:
Each aspect is first encoded by BERT at the token level. We apply mean pooling to obtain a fixed-length vector, which is then projected into a 1024-dimensional space via a linear transformation followed by a activation, as follows:
4.2. Sparse Aspect-Category Attention
The ACD module identifies which predefined aspect categories are present in a given review. To enhance precision and interpretability, it employs sparse aspect-category attention, which enables the model to selectively focus on the most informative words for each aspect. For aspect-category attention, the transformed aspect vector is used as the query , while serves as both the key and the value for the aspect , as follows:
To compute attention weights for ACD, we employ entmax in Equation (7), and then the attention score for the -th aspect is computed as follows:
where is the aspect-specific query, and is the key matrix projected from the input sequence .
Using , we obtain a context vector by a weighted sum over the value matrix:
To incorporate explicit aspect category information, we residually enhance the context vector by adding a linear transform of . Also, the resulting representation is then passed through a task-specific classifier to produce the ACD logit:
Since aspect category detection is formulated as a binary classification task for each aspect, we apply the binary cross-entropy loss with logits to supervise each logit against a binary ground-truth label . The overall ACD loss is defined as the average over all aspects:
4.3. Residual Connection from ACD to ACSA
To incorporate the attention signal generated during the ACD stage into the downstream ABSA task, we refine the original review representation by applying a residual connection. For an aspect , the attention distribution is used to reweigh the word-level input embeddings . This reweighting is performed via element-wise multiplication across the sequence length, allowing the model to amplify aspect-relevant features while attenuating irrelevant ones, as follows:
where denotes element-wise multiplication applied across the sequence length.
The residual connection ensures that the original semantic content captured by the pre-trained BERT encoder is preserved, while the attention weights selectively emphasize tokens that are informative for the aspect .
This fused representation serves as an enriched input for the subsequent ACSA-specific processing layers. By integrating attention-based reweighting with residual learning, the model benefits from both a targeted focus on aspect-relevant regions and retention of broader contextual meaning, which is critical for accurate sentiment classification.
4.4. Feature Extraction
At this stage, we encode the residual-enhanced review representation using a CNN-BiLSTM hybrid encoder, which captures both rich local and sequential features.
The aspect-enhanced review representation , obtained through residual integration, is then processed by a hybrid encoder consisting of a convolutional neural network (CNN) followed by a bidirectional long short-term memory (BiLSTM) network. The CNN layer captures local n-gram features by applying convolutions over the word sequence:
where is the number of output channels (feature maps).
This operation emphasizes localized patterns around each word, which are important for identifying sentiment-bearing phrases.
To model global dependencies beyond fixed local windows, the output is passed through a BiLSTM layer, which consists of two LSTM networks running in opposite directions. The forward LSTM processes the token sequence from the beginning to the end, capturing dependencies based on preceding context, while the backward LSTM traverses the sequence in reverse, modeling dependencies from future context. The outputs from both directions are concatenated at each timestep:
where = 2 × hidden_size denotes the dimensionality of the concatenated forward and backward hidden states.
The resulting representation provides rich, context-aware features for each token, which are used in the subsequent aspect-specific attention mechanism.
4.5. Sparse Aspect-Sentiment Attention
After obtaining the contextualized token representations from the BiLSTM encoder, we apply a second attention mechanism to aggregate aspect-relevant information for sentiment classification. This attention is guided by same transformed aspect vector , which is now projected into a new query vector , suitable for this stage. Like the first attention mechanism in ACD, the output sequence from the preceding BiLSTM layer serves as the source of both key and value representations for aspect-specific sentiment attention:
We then compute attention weights using the scaled dot product formulation, with sparsemax again employed to obtain a sparse, interpretable distribution over tokens:
Using these attention weights, we compute the final aspect-aware summary vector for the -th aspect, which serves as the input to the sentiment classification layer. The resulting context vector aggregates sentiment-relevant information over the entire sequence, weighted by the aspect-specific attention distribution, and serves as a compact yet informative representation for downstream classification:
The context vector , computed from the aspect-specific attention, is passed through a task-specific linear classifier to produce the sentiment logit for the -th aspect:
Here, , and denotes the number of sentiment classes (e.g., positive, neutral, and negative). The predicted sentiment is then supervised via the categorical cross-entropy loss with respect to the ground-truth label . The overall ABSA loss is computed as the mean over all aspects with valid labels:
This formulation enables the model to flexibly handle partial labels while still optimizing for fine-grained, aspect-specific sentiment prediction.
4.6. Loss Function for Joint Learning
To jointly optimize the ACD module and the ACSA module, we adopt a multi-task learning framework where the total loss is a weighted sum of the task-specific losses. The overall loss for a single instance is defined as:
where is a balancing hyperparameter that regulates the learning pace discrepancy between tasks.
This joint formulation allows the model to share and reinforce relevant representations across tasks. By jointly training both tasks within a unified architecture, the model benefits from mutual inductive bias: ACD helps guide attention toward sentiment-bearing phrases relevant to the identified aspect, while sentiment signals from ACSA serve to regularize and refine the identification of aspect categories.
Tasks in a joint learning framework often progress at different learning rates. In our experiments, the ACD task consistently converged more quickly than the ACSA task. When the loss functions are combined without adjusting a balancing parameter, the faster-learning task can dominate the optimization process, potentially hindering effective learning of the slower task and resulting in suboptimal performance. To mitigate this issue, we initialize the weighting coefficient γ to assign equal importance to both tasks, but as the ACD task stabilizes earlier on the validation set, γ is dynamically adjusted according to the following rule:
This adaptive scheduling strategy reflects the intuition that, once the ACD task reaches a reliable level of performance, the model should gradually shift its focus toward more effective sentiment polarity learning in the ACSA task. The threshold for this transition is determined empirically.
5. Experiment
5.1. Dataset Description
To validate the performance of the SPA-RJ Net, we ran experiments on four benchmark datasets in the experiments, including the restaurant domain from datasets from SemEval-2014 task4 [17], SemEval-2015 task 12 [18], SemEval-2016 task 5 [19], and the MAMS dataset [20]. Particularly, as most reviews in the MAMS dataset contain at least two different aspects with different sentiment polarities per review, our experiments effectively present the ability to handle multiple aspects.
We first removed any review instances that were not assigned to any aspect category and then categorized each aspect category into three sentiment labels: positive, negative, and neutral. To mitigate the effect of outliers, we excluded the top and bottom 5% of instances based on review length. The dataset was split into training and testing sets using an 80:20 ratio. Detailed statistics for the datasets are summarized in Table 1.

Table 1.
Sentiment-label distribution (train/test) for ABSA benchmark datasets.
Table 2 summarizes the per-aspect counts (food, service, ambience, and price) that fell into the training and test partitions of each dataset. We kept the split close to the customary 80:20 rule so that no category was under-represented in the held-out set.

Table 2.
Aspect category distribution (train/test) for ABSA benchmark datasets.
5.2. Evaluation Metrics
To evaluate the performance of our model, we selected accuracy and Macro-f1, both of which are widely used metrics. Accuracy offers an intuitive measure of the proportion of correctly predicted instances across the dataset. Macro-F1 is computed as the unweighted average of F1 scores across all classes, where F1 score is the harmonic mean of precision and recall. Precision measures the correctness of positive predictions, while recall reflects the model’s ability to capture all relevant instances. These metrics are defined as follows:
where TP, FP, and FN denote true positives, false positives, and false negatives, respectively:
By aggregating precision and recall per class and then averaging equally, Macro-F1 ensures that the model’s performance is not dominated by majority classes, offering a more balanced assessment. Therefore, we used accuracy and Macro-F1 as evaluation metrics in our experiments.
5.3. Comparison Models
We compared our model to existing attention-based deep learning models in the ABSA domain. They are built on LSTM, RNN, MemNet, and GNN models, each incorporating attention mechanisms in different ways:
- ATAE-LSTM [37]. The concatenations of an aspect embedding vector and each word embedding vector of the review are served as inputs to the LSTM model and an attention layer, allowing to selectively focus on aspect-relevant information.
- TD-LSTM [68]. TD-LSTM employs two target-dependent LSTMs that process the preceding part with the target term in both directions. Attention is applied to the concatenated hidden states, emphasizing words around the target.
- MemNet [38]. MemNet is a deep memory network with multiple computational layers, each of which includes an attention mechanism and explicit memory. Multi-hop attention enhances the ability to capture nuanced patterns by focusing on key context.
- IAN [41]. The interactive attention network (IAN) learns the interaction between aspect terms and words, generating separate representations for both, which effectively reflects the mutual influence between targets and contexts through two attention layers.
- AOA [42]. The attention-over-attention (AOA) jointly models the interaction between aspects and sentences, explicitly capturing the relationship between aspects and context, which enhances accuracy, particularly in complex multi-aspect contexts.
- ASGCN [48]. This model first uses GCN over the dependency tree to exploit syntactical information and word dependencies and to learn the aspect-specific representations.
- SAGCN [49]. SAGCN utilizes GCN to find correlation between the aspect and sentence using the dependency tree.
- DSMN [69]. DSMN uses the multi-hop attention guided by dynamically selected context memory. Then, it integrates the aspect information with the memory networks.
- CMA-MemNet [70]. The rich semantic information between the aspect and the sentence is extracted by this memory network. It uses multi-head self-attention to make up for the problem where it ignores the semantic information of the sequence itself.
- DualGCN [50]. This model uses two GCNs, SynGCN and SemGCN, that jointly consider the syntax structures and semantic correlations, with regularizers constraining attention scores in the SemGCN.
- MAT+2RO [16]. In a multi-task learning setting with ACD and ACSA, this LSTM-based model applies hybrid regularizations to the attention mechanism, combining aspect-level and task-level constraints to enhance performance.
5.4. Experiment Environment
All experiments were executed on a 64-bit workstation equipped with an Intel Core i9-10900X CPU (10 cores), 128 GB DDR4 RAM, and two NVIDIA GeForce RTX 3090 GPUs (24 GB GDDR6X VRAM each). The SPA-RJ Net was fine-tuned from BERT-base (12 layers, 768 hidden units) using the AdamW optimizer. We applied a learning rate of 2 × 10−5 to the encoder parameters and 1 × 10−4 to the newly added CNN-BiLSTM layers in the ACSA task. Training used a batch size of 32 and a maximum input length of 128 tokens. Dropout 0.1 was applied to all layers. Sparse attention for both ACD and ACSA tasks was implemented with entmax 2.0 (α = 2.0), and the threshold for the transition of balancing parameter was 0.92.
5.5. Experiment Result
We propose several variants of the SPA-RJ Net, distinguished along two dimensions: the sparsity of the attention mechanism—dense attention (DA) versus sparse attention (SPA)—and the learning framework—single-task learning (ST) versus residual joint learning (RJ). DA adopts the softmax function, while SPA employs the entmax function with a sparsity-controlling hyperparameter α. ST represents a single-task learning framework for the ACSA task, whereas RJ refers to a joint learning architecture that integrates ACD and ACSA through a residual connection. We evaluated SPA-RJ Net and its three variant models—DA-ST Net, SPA-ST Net, and DA-RJ Net—on four widely used ABSA benchmarks with three labels (positive, neutral, and negative): REST 14, REST 15, REST 16, and MAMS. We note that the sparse-attention-based learning models, i.e., SPA-ST Net and SPA-RJ Net, had the entmax sparsity parameter α set to 2.
Table 3 summarizes the performance comparison with a wide range of baseline models, including LSTM-based methods (e.g., ATAE-LSTM, IAN, and AOA), memory networks (e.g., MemNet, DSMN, and CMA-MemNet), and graph-based approaches (e.g., ASGCN and DualGCN). It is noteworthy in that DualGCN and MAT+2RO apply sparsity into attention using regularization techniques and MAT+2RO also adopts multi-task learning setting with ACD and ACSA. The baseline results are taken from the original and relevant papers, which used the same dataset under comparable settings. A summary table is provided in Appendix A.

Table 3.
Performance comparison on four datasets. The best performance is bold typed and unreported results are represented with a hyphen mark.
Based on the experimental results, our SPA-RJ Net and its variant models demonstrated superior performance across most of the ABSA datasets. Notably, SPA-RJ Net, which integrates sparse attention with a residual joint learning strategy, yielded the highest scores in all evaluation metrics except for the result on the REST 14 dataset. On the REST 14 dataset, SPA-ST Net—a variant of SPA-RJ Net that still incorporates sparse attention—achieved the highest accuracy, while DualGCN, which employs a regularization-based approach, obtained the highest F1 score. These results suggest that introducing sparsity into the attention mechanism can be effective for ABSA tasks.
Focusing on the impact of sparse attention, we analyzed its effectiveness by separately examining performance under single-task learning and multi-task joint learning settings. In the single-task learning setting, SPA-ST Net outperformed its counterpart, DA-ST Net. SPA-ST Net achieved higher Macro-F1 scores by 8.8% on REST 14, 10.0% on REST 15, 2.1% on REST 16, and 3.9% on MAMS. In terms of accuracy, it yielded improvements of 3–4% on REST 14, REST 15, and MAMS, and 1.4% on REST 16. In the residual joint learning setting, SPA-RJ Net using sparse attention outperformed its dense-attention counterpart DA-RJ Net. These gains confirm that a sparse probability simplex helps the model intensify aspect-relevant parts. We observed that DA-based models showed slightly lower accuracy but significantly worse F1 scores compared to SA-based models. These results suggest that the inherent tendency of dense attention to diffuse focus across all tokens may lead to poor recall for minority classes. In contrast, sparse attention selectively emphasizes important tokens, enhancing class-wise balance and improving overall F1 performance.
From the perspective of the learning framework (single-task learning vs. multi-task learning), SPA-ST Net and SPA-RJ Net—both of which utilize sparse attention but differ in their frameworks—demonstrated that residual joint learning led to improved performance, in addition to the benefits of sparse attention. SPA-RJ Net produced an additional 1.8% Macro-F1 on average and push accuracy above 94% on REST 16 and 79% on MAMS over SPA-ST Net.
Through the experiments, we observed that sparse attention played an important role in improving performance on the ABSA task. Using sparse attention instead of dense attention led to bigger improvements than switching the setting from single-task learning to residual joint learning. We also note that combining sparse attention with residual joint learning demonstrated a kind of synergistic effect, consistently improving both accuracy and Macro-F1 across various ABSA datasets. Therefore, we believe that this combination model, like SPA-RJ Net, is applicable to various kinds of applications and domains.
To complement overall accuracy and F1 results, we report class-wise precision and recall to better understand the model’s behavior across sentiment classes. Table 4 shows that SPA-RJ Net with sparsemax (α = 2) achieved strong and balanced performance. Positive and negative classes on both REST 16 and MAMS exhibited high precision and recall (e.g., ≥81% recall and ≥90% precision on REST 16), indicating effective detection of clear polarities. While the neutral class was more ambiguous than the others, the model still performed solidly (precision ≥ 72% and recall ≥ 78%) and avoided collapsing toward extremes. The small precision–recall gaps further suggested well-calibrated decision boundaries. These results support the model’s overall robustness across datasets and sentiment categories.

Table 4.
Class-wise precision and recall of SPA-RJ Net (sparsemax, α = 2).
Table 5 illustrates how the sparsity level of the attention distribution affected the performance of ACSA. We controlled the sparsity of the attention distribution by adjusting the value of , a parameter of the entmax function. As the value of increased from 1 (i.e., equivalent to softmax when α = 1 [13]) to 4, the attention distribution became sparser.

Table 5.
The effect of sparsity levels in the attention distribution. The best performance is bold typed.
In our experiments, every configuration that introduced sparsity (α > 1) outperformed dense attention across all four benchmark datasets. On all SemEval datasets, the optimal performance was observed at α = 2, whereas the best results on the MAMS dataset were achieved with α = 1.5. For instance, with α = 2.0, the model reached up to 94.44% accuracy and 88.26% Macro-F1 on REST 16, and with α = 1.5, the model achieved 81.00% accuracy and 80.67% Macro-F1 on MAMS. Then, beyond these values of α, performance gradually declined as α increased. This may result from dataset-specific characteristics in inherent sparsity, which can influence the optimal degree of attention sparsity for each dataset. Nevertheless, this result strongly highlights the limitations of relying on the conventional softmax function in the ABSA task and learning mode without a self-attention mechanism and suggests that sparse attention be actively considered as a viable alternative for achieving optimal performance.
5.6. Ablation Study
To investigate how individual components and task-specific sparsity settings influence performance, we conducted a series of ablation studies, as summarized in Table 5 and Table 6.

Table 6.
Ablation experiments on SPA-RJ Net. The best performance is bold typed.
In Table 6, we list several ablation models. SPA-RJ Net (with GloVe) denotes the model with pre-trained GloVe embedding vectors (*d = 300) instead of BERT to evaluate the impact of different input representations. The model using GloVe embeddings showed inferior performance compared to the original SPA-RJ Net (complete) using BERT. As GloVe provides static embeddings that assign a single representation to each word regardless of context, this limitation hinders the model’s ability to capture context-dependent meanings. This result underscores the effectiveness of contextualized embeddings like BERT for nuanced sentiment analysis in ABSA.
SPA-RJ Net (w/o ACD) ablates the ACD task, passing inputs only through a single sparse aspect-sentiment attention block for ACSA. Compared to the complete version (ACSA with ACD), SPA-RJ Net (w/o ACD) demonstrated overall lower performance. The performance gap was small on the SemEval 2014 dataset (less than 1%) but more significant on other datasets, with accuracy dropping by up to 5.13% and Macro-F1 by 9.8%. This underscores the critical role of the ACD module in providing explicit aspect-level guidance. To further explore the interaction between the ACD and ABSA attention mechanisms, we provide their respective attention maps in a case study.
Both SPA-RJ Net (w/o residual connection) and SPA-RJ Net (w/o balancing parameter) retain the two-task joint-learning framework. To examine the effect of residual connection from ACD to ACSA, we implemented SPA-RJ Net (w/o residual connection) by removing the residual learning submodule from SPA-RJ Net (complete). In this setting, only the ACD logits—without the refined, aspect-aware representations—are available to ACSA. This design restricts the transfer of aspect-aware context to the ACSA module, causing notable performance degradation—about 5% lower accuracy on REST 14 and MAMS, and nearly 10% lower Macro-F1 on REST 15. These findings suggest that the residual connection plays an essential role in capturing deeper semantic dependencies between ACD and ACSA by transferring semantically enriched information to the main task.
The performance difference between SPA-RJ Net (w/o balancing hyperparameter) and SPA-RJ Net (complete) reflects the effectiveness of the balancing hyperparameter. In our framework, which consists of separate ACD and ACSA tasks, the ACD task—being simpler than ACSA—generally learned significantly faster. Without adjusting the balancing hyperparameter, ACD may dominate the shared representation space, which can lead to suboptimal performance for the slower-learning ACSA task and hinder the convergence of both tasks. On average, SPA-RJ Net (complete) achieved 3.43% higher accuracy and a 5.69% gain in Macro-F1, highlighting the importance of controlling task imbalance during joint learning.
Table 7 explores the impact of different attention configurations in performance. In our model, there are two attention modules: the aspect-category attention in the ACD task and the aspect-sentiment attention in the ACSA task, applied sequentially in that order. We investigated how the type of attention distribution—sparse (SPA) or dense (DA)—in each attention affected the overall performance. For example, DA-SPA refers to a configuration where the aspect-category attention generates a dense attention distribution by using softmax, and the aspect-sentiment attention yields a sparse attention distribution by using entmax (α = 2). SPA-RJ Net adopts the SPA-SPA configuration, in which sparse attention distributions are applied in both attentions.

Table 7.
The effect of attention configuration on SPA-RJ Net. The best performance is bold typed.
Among the four configurations, SPA–SPA consistently achieved the best results across all datasets. For instance, it achieved an accuracy of 94.44% and a Macro-F1 score of 88.26 on REST 16, and 80.78% accuracy and 79.56 Macro-F1 on MAMS. In contrast, the DA–DA configuration, which applies dense attention in both modules, showed the lowest performance across most datasets, particularly in terms of Macro-F1 score, which demonstrates the limitations of dense attention in capturing fine-grained sentiment signals and the effectiveness of applying sparse attention in the domain of ACSA. The DA–SPA and SPA–DA configurations, each of which used a mix of sparse and dense attention, achieved intermediate results, suggesting that partial sparsity improved performance over fully dense configurations but did not outperform the fully sparse attention configuration.
The superior performance of the SPA–SPA setting suggests that sparse attention, by focusing on a limited number of informative tokens, is effective for both ACD and ACSA. In ACD, it highlights aspect-related cues while suppressing irrelevant information, leading to more accurate detection. In ACSA, it helps the model focus on sentiment-bearing expressions, reducing contextual noise. These results indicate that sparse attention offers a beneficial inductive bias for the task.
5.7. Case Study
In this section, we present a case study to examine how the proposed sparse attention in SPA-RJ Net operates during inference. We analyze several representative examples drawn from the MAMS dataset, which include review samples annotated with either a single aspect category (from case 1 to 4) or multiple aspect categories (from case 5 to 7).
As summarized in Table 8, these cases are selected to illustrate the model’s ability to focus on aspect-relevant words and to demonstrate how sparse attention enhances interpretability. For each review, the table presents the ground-truth labels provided by the dataset alongside the model’s predictions. Figure 3 visualizes the attention distributions under different settings (dense att. vs. sparse att.; ACD att. vs. ACSA att.) to provide an intuitive understanding of how the model allocates attention, with darker colors representing higher attention scores. Each distribution illustrates how various attention mechanisms or task settings influence the model’s focus on aspect-relevant words.

Table 8.
Case study on MAMS.

Figure 3.
The attention distribution of cases: (a) cases with a single aspect category and (b) cases with multiple aspect categories.
For cases with a single aspect category (cases 1 to 4), the model correctly predicts the sentiment polarity in cases 1 to 3. In particular, cases 1 and 2 offer direct visual comparisons between sparse and dense attention for the same aspect category (food), allowing us to examine their interpretability. As shown in Figure 3a, sparse attention assigns significantly higher weights to sentiment-relevant words, such as ‘dinner’, ‘meal’, and ‘great’ in case 1, resulting in a correct prediction. While case 1 involves a relatively simple sentence structure with clear aspect–opinion pairs, case 2 is more challenging due to the dispersed nature of aspect-related words. Nonetheless, sparse attention highlights key tokens like ‘noise’, ‘bad’, ‘people’, and ‘dinner’ more distinctly than dense attention, which tends to distribute weights more uniformly across tokens. These examples demonstrate that sparse attention offers better focus and interpretability, particularly in identifying opinion-bearing expressions critical for accurate sentiment analysis.
On the other hand, case 3 illustrates the distinct roles of aspect-category attention (ACD att.) and aspect-sentiment attention (ACSA att.) in SPA-RJ Net, where both are configured with sparse attention distributions. While the sparse aspect-category attention assigns high scores primarily to aspect targets, such as ‘atmosphere’, the sparse aspect-sentiment attention focuses not only on the same aspect targets but also on sentiment-bearing expressions like ‘enjoying’ and ‘having fun’.
However, our model makes a misprediction in case 4 where multiple aspect terms under the same aspect category express conflicting sentiment polarities. An analysis of two sparse attention distributions in SPA-JR Net reveals that the sparse aspect-category attention over-concentrates on the aspect target word ‘service’, while overlooking related terms such as ‘waiter’. This suggests that the strong focus of sparse attention on a few key words can lead to the omission of other important information. Therefore, it is important to consider how to apply sparsity appropriately to achieve a better balance between focus and contextual coverage.
In cases 5 to 7, which involve multiple aspect categories, we observe that different words within the same sentence receive distinct attention scores depending on the given aspect category. This provides an opportunity to examine the interpretability of sparse attention in more complex settings. In case 5 (Figure 3b), for instance, sparse attention distinctly highlights ‘food’ and ‘decent’ for the food category, while assigning higher attention to ‘server’, ‘no-where’, and ‘found’ for the service category. In contrast, the dense attention yields a near-uniform distribution, with much of the review text shaded in light red, making it difficult to distinguish sentiment-relevant tokens. This comparison visually demonstrates that sparse attention not only filters out irrelevant tokens but also adapts its focus based on the aspect category, offering more interpretable and fine-grained attention behavior.
Case 6 demonstrates that the two distinct attentions, as observed in case 3, also effectively fulfill their respective roles in multi-aspect scenarios. For the ambience aspect category, the sparse aspect-category attention (ACD att.) strongly focuses on the word ‘atmosphere’, which is closely related to the aspect, while the sparse aspect-sentiment attention (ACSA att.) additionally attends to the associated opinion expression ‘was amazing’. Although the review sentence remains the same, given the price aspect category, the ACD and ACSA attentions focus on different words compared to the ambience aspect category—namely, ‘price’ and ‘reasonable’, respectively. It indicates that even in multi-aspect scenarios, the ACD and ACSA attentions are able to correctly identify the aspect-relevant content based on the given aspect category.
On the other hand, case 7 produces an incorrect result for one of the two aspects. As shown in the sparse attention distribution for the price aspect category in case 7 of Figure 3b, the model fails to attend to the word ‘not’ in the opinion expression ‘not at all worth’ for the price aspect. As a result, it predicts the opposite sentiment label of the original negative. This outcome, like case 4, appears to result from excessively high attention sparsity, which causes the model to focus on too few words and miss a single critical term—ultimately leading to a reversal of sentiment polarity. This observation suggests the need to calibrate sparsity appropriately for the given dataset. Nevertheless, as demonstrated in the experiments from the previous section, the selective focus of sparse attention proved effective in many cases.
6. Discussion and Conclusions
In this paper, we proposed SPA-RJ Net to address the limitations of conventional dense attention generated by the softmax function and to explore the effectiveness of sparse attention in ACSA. SPA-RJ Net leverages two sparse attentions induced by the -entmax function and it also incorporates a residual joint learning framework between aspect category detection (ACD) and aspect category sentiment prediction (ACSA) tasks. This design enables our SPA-RJ Net to selectively focus on important words/context for the corresponding aspect category.
Our experiments empirically demonstrated the effectiveness of SPA-RJ Net, which largely outperformed a range of attention-based models, including those employing attention regularization or multi-task learning. In particular, the use of sparse attention led to meaningful performance gains, highlighting its value for ABSA tasks. The ablation study validated the contribution of each technical component, while case analysis illustrated the difference in sparse and dense attention distributions and clarified the roles of aspect-category and aspect-sentiment attentions. Overall, SPA-RJ Net improved both performance and interpretability in single- and multi-aspect ACSA scenarios.
We employed the entmax transformation function [13] to induce sparse attention, adjusting the α parameter in the range of 1.0 to 4.0. This allowed us to generate attention distributions with varying degrees of sparsity, including softmax (α = 1.0) and sparsemax (α = 2.0). Notably, we observed that the optimal α value varied across datasets, depending on their sparsity characteristics. For datasets with more concentrated opinion expressions, higher sparsity (larger α) led to better performance, whereas denser expressions favored lower α values. These results indicate that entmax provides a flexible and adaptive attention mechanism, capable of adjusting to the structure of different datasets rather than being limited to a specific domain or task.
While our experiments were conducted solely on the restaurant domain to align with prior works and ensure comparability, our model is designed to be domain-agnostic and can be easily applied to other domains. In future work, we plan to explore cross-domain and cross-lingual ABSA settings to validate the model’s effectiveness in transferring knowledge across diverse domains and languages, thereby providing broader insights into its generalizability and robustness.
Furthermore, we expect that SPA-RJ Net can be effectively applied to various downstream tasks, such as targeted summarization, question-answering, and the construction of explainable recommendation systems grounded in fine-grained opinion mining.
We plan to pursue future research in the following directions. First, we aim to dynamically learn sparsity-related parameters to adapt the level of attention sparsity to each dataset. By employing dataset-specific sparsity levels, we expect to achieve improved and more robust performance. In addition, we plan to extend our model by incorporating GNNs. Specifically, we aim to integrate sparse attention into GNNs, enabling each node to attend to its most relevant neighbors. This approach leverages syntactic dependencies while reducing noise, computational cost, and memory usage. We believe sparse attention inherently improves efficiency and scalability, and we plan to evaluate runtime and memory usage under varying dataset scales as part of future work, aiming to provide a more efficient solution for ABSA.
Author Contributions
Conceptualization, methodology, software, validation, J.K., H.K.; resources, data curation, J.K.; writingoriginal draft preparation, writing-review and editing, J.K., H.K.; visualization, J.K.; supervision, project administration, funding acquisition, H.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to data privacy.
Conflicts of Interest
All authors declare that the research was conducted without any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
We present a summary table of the baseline models used in our experiments. The table includes key implementation details, such as architectural characteristics, input format, and source of experiment results, enabling clearer comparison across various approaches.

Table A1.
Summary of the baseline models in the experiments.
Table A1.
Summary of the baseline models in the experiments.
| Model [#Ref] | Year | Architecture Characteristics | Input Format | Source of Experiment Result | |||
|---|---|---|---|---|---|---|---|
| REST 14 | REST 15 | REST 16 | MAMS | ||||
| ATAE-LSTM [37] | 2016 | Two LSTMs (left-to-aspect, aspect-to-right) | ⟨Left Context⟩, ⟨Right Context⟩, ⟨Aspect Term⟩ | [71] | [72] | ||
| TD-LSTM [68] | 2016 | LSTM over concatenated word-aspect embeddings with attention | ⟨[Word, Aspect Term]⟩ sequence | ||||
| MemNet [38] | 2015 | Multiple attention model over external memory | ⟨Context Words⟩, ⟨Aspect Term⟩ | ||||
| IAN [41] | 2017 | Two parallel LSTMs for aspect and context with interactive attention | ⟨Context Words⟩, ⟨Aspect Term⟩ | ||||
| AOA [42] | 2018 | Attention-over-attention mechanism | ⟨Context Words⟩, ⟨Aspect Term⟩ | ||||
| ASGCN [48] | 2021 | Aspect-specific graph convolutional network | ⟨Sentence⟩, ⟨Aspect Index⟩, ⟨Dependency Graph⟩ | [57] | - | ||
| SAGCN [49] | 2021 | Sparse attention-guided GCN | ⟨Sentence⟩, ⟨Aspect Term⟩, ⟨Dependency Graph⟩ | - | |||
| DSMN [69] | 2020 | Dynamic memory update with multiple reasoning hops | ⟨Context⟩, ⟨Aspect Term⟩ | - | |||
| CMA-MemNet [70] | 2021 | Dual memory modules (coarse-to-fine granularity) | ⟨Context⟩, ⟨Aspect Term⟩, ⟨Aspect Category⟩ | - | |||
| DualGCN [50] | 2022 | Dual GCNs (syntactic + semantic) fused via gating | ⟨Sentence⟩, ⟨Aspect Index⟩, ⟨Dependency Graph⟩, ⟨Semantic Graph⟩ | Original paper | - | ||
| MAT-2RO [16] | 2023 | Multi-level attention routing + hybrid regularization | ⟨Sentence⟩, ⟨Aspect Categories⟩ | Original paper | - | ||
References
- Zhang, W.; Li, X.; Deng, Y.; Bing, L.; Lam, W. A survey on avspect-based sentiment analysis: Tasks, methods, and challenges. IEEE Trans. Knowl. Data Eng. TKDE 2022, 35, 11019–11038. [Google Scholar] [CrossRef]
- Do, H.H.; Prasad, P.W.; Maag, A.; Alsadoon, A. Deep learning for aspect-based sentiment analysis: A comparative review. Expert Syst. Appl. 2019, 118, 272–299. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A review on the attention mechanism of deep learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Elfadel, I.M.; Wyatt, J.L., Jr. The “softmax” nonlinearity: Derivation using statistical mechanics and useful properties as a multiterminal analog circuit element. In Proceedings of the Advances in Neural Information Processing Systems, NIPS, Denver, CO, USA, 29 November–2 December 1993; Volume 6. [Google Scholar]
- Li, X.; Bing, L.; Lam, W.; Shi, B. Transformation Networks for Target-Oriented Sentiment Classification. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, ACL, Melbourne, Australia, 15–20 July 2018; pp. 946–956. [Google Scholar]
- Veličković, P.; Perivolaropoulos, C.; Barbero, F.; Pascanu, R. Softmax is not enough (for sharp out-of-distribution). In Proceedings of the First Workshop on System-2 Reasoning at Scale, NeurIPS, Vancouver, BC, Canada, 14 December 2024. [Google Scholar]
- Niculae, V.; Blondel, M. A regularized framework for sparse and structured neural attention. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NeurIPS, Long Beach, CA, USA, 4–9 December 2017; pp. 3340–3350. [Google Scholar]
- Liu, Y.; Liu, J.; Chen, L.; Lu, Y.; Feng, S.; Feng, Z.; Wang, H. Ernie-sparse: Learning hierarchical efficient transformer through regularized self-attention. arXiv 2022, arXiv:2203.12276. [Google Scholar]
- Li, Q. A comprehensive survey of sparse regularization: Fundamental, state-of-the-art methodologies and applications on fault diagnosis. Expert Syst. Appl. 2023, 229, 120517. [Google Scholar] [CrossRef]
- Feng, A.; Zhang, X.; Song, X. Unrestricted attention may not be all you need–masked attention mechanism focuses better on relevant parts in aspect-based sentiment analysis. IEEE Access 2022, 10, 8518–8528. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, Z.; Huang, B.; Lei, P.; Su, J.; Pan, S.; Cao, J. Sparse-softmax: A simpler and faster alternative softmax transformation. arXiv 2021, arXiv:2112.12433. [Google Scholar]
- Martins, A.T.; Astudillo, R.F. From softmax to sparsemax: A sparse model of attention and multi-label classification. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, ICML, New York, NY, USA, 20–22 June 2016; pp. 1614–1623. [Google Scholar]
- Blondel, M.; Martins, A.F.; Niculae, V. Learning with fenchel-young losses. J. Mach. Learn. Res. JMLR 2020, 21, 1–69. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Kenton, W.C.; Toutanova, L.K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, Minnesota, 2–7 June 2019; Volume 1, pp. 4171–4186. [Google Scholar]
- Hu, M.; Zhao, S.; Guo, H.; Su, Z. Hybrid regularizations for multi-aspect category sentiment analysis. IEEE Trans. Affect. Comput. 2023, 14, 3294–3304. [Google Scholar] [CrossRef]
- Kirange, D.; Deshmukh, R.R.; Kirange, M. Aspect based sentiment analysis semeval-2014 task 4. Asian J. Comput. Sci. Inf. Technol. 2014, 4, 72–75. [Google Scholar] [CrossRef]
- Pontiki, M.; Galanis, D.; Papageorgiou, H.; Manandhar, S.; Androutsopoulos, I. SemEval-2015 Task 12: Aspect Based Sentiment Analysis. In Proceedings of the 9th International Workshop on Semantic Evaluation, SemEval, Denver, CO, USA, 4–5 June 2015; pp. 486–495. [Google Scholar]
- Pontiki, M.; Galanis, D.; Papageorgiou, H.; Androutsopoulos, I.; Manandhar, S.; Al-Smadi, M.; Eryiğit, G. Semeval-2016 task 5: Aspect based sentiment analysis. In Proceedings of the International Workshop on Semantic Evaluation, San Diego, CA, USA, 16–17 June 2016; pp. 19–30. [Google Scholar]
- Jiang, Q.; Chen, L.; Xu, R.; Ao, X.; Yang, M. A challenge dataset and effective models for aspect-based sentiment analysis. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, EMNLP-IJCNLP, Miami, FL, USA, 12–16 November 2019; pp. 6280–6285. [Google Scholar]
- Chemmanam, A.J.; Jose, B.A. Joint learning for multitasking models. In Responsible Data Science; Springer Nature: Singapore, 2021; p. 155. [Google Scholar]
- Ebski, S.J.; Arpit, D.; Ballas, N.; Verma, V.; Che, T.; Bengio, Y. Residual connections encourage iterative inference. In Proceedings of the International Conference on Learning Representations, ICLR, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Liu, H.; Chatterjee, I.; Zhou, M.; Lu, X.S.; Busorrah, A. Aspect-based sentiment analysis: A survey of deep learning methods. IEEE Trans. Comput. Soc. Syst. 2020, 7, 1358–1375. [Google Scholar] [CrossRef]
- Vo, D.T.; Zhang, Y. Target-dependent twitter sentiment classification with rich automatic features. In Proceedings of the International Joint Conference on Artificial Intelligence, IJCAI, Buenos Aires, Argentina, 25–31 July 2015; pp. 1347–1453. [Google Scholar]
- Zhou, J.; Huang, J.X.; Chen, Q.; Hu, Q.V.; Wang, T.; He, L. Deep learning for aspect-level sentiment classification: Survey, vision, and challenges. IEEE Access 2019, 7, 78454–78483. [Google Scholar] [CrossRef]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. In Proceedings of the Advances in Neural Information Processing Systems, NIPS, Lake Tahoe, NA, USA, 5–8 December 2013; Volume 26, pp. 3111–3119. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global vectors for word representation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, EMNLP, Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Dong, L.; Wei, F.; Tan, C.; Tang, D.; Zhou, M.; Xu, K. Adaptive recursive neural network for target-dependent twitter sentiment classification. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, ACL, Baltimore, MD, USA, 22–27 June 2014; Volume 2, pp. 49–54. [Google Scholar]
- De Mulder, W.; Bethard, S.; Moens, M.F. A survey on the application of recurrent neural networks to statistical language modeling. Comput. Speech Lang. 2015, 30, 61–98. [Google Scholar] [CrossRef]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Graves, A.; Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Zhang, S.; Zheng, D.; Hu, X.; Yang, M. Bidirectional long short-term memory networks for relation classification. In Proceedings of the 29th Pacific Asia Conference on Language, Information and Computation, Shanghai, China, 30 October–1 November 2015; pp. 73–78. [Google Scholar]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef] [PubMed]
- Hoang, M.; Bihorac, O.A.; Rouces, J. Aspect-based sentiment analysis using bert. In Proceedings of the 22nd Nordic Conference on Computational Linguistics, Turku, Finland, 30 September–2 October 2019; pp. 187–196. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. In Proceedings of the International Conference on Learning Representations, ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Tang, D.; Qin, B.; Liu, T. Document modeling with gated recurrent neural network for sentiment classification. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, EMNLP, Lisbon, Portugal, 17–21 September 2015; pp. 1422–1432. [Google Scholar]
- Wang, Y.; Huang, M.; Zhu, X.; Zhao, L. Attention-based LSTM for aspect-level sentiment classification. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, EMNLP, Austin, TX, USA, 1–4 November 2016; pp. 606–615. [Google Scholar]
- Tang, D.; Qin, B.; Liu, T. Aspect Level Sentiment Classification with Deep Memory Network. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, EMNLP, Lisbon, Portugal, 17–21 September 2015; pp. 214–224. [Google Scholar]
- Yang, Z.; Yang, D.; Dyer, C.; He, X.; Smola, A.; Hovy, E. Hierarchical attention networks for document classification. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, San Diego, CA, USA, 12–17 June 2016; pp. 1480–1489. [Google Scholar]
- Cheng, J.; Zhao, S.; Zhang, J.; King, I.; Zhang, X.; Wang, H. Aspect-level sentiment classification with heat (hierarchical attention) network. In Proceedings of the ACM on Conference on Information and Knowledge Management, CIKM, Singapore, 6–10 November 2017; pp. 97–106. [Google Scholar]
- Ma, D.; Li, S.; Zhang, X.; Wang, H. Interactive Attention Networks for Aspect-Level Sentiment Classification. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, IJCAI, Melbourne, Australia, 19–25 August 2017; pp. 4068–4074. [Google Scholar]
- Huang, B.; Ou, Y.; Carley, K.M. Aspect level sentiment classification with attention-over-attention neural networks. In Proceedings of the Social, Cultural, and Behavioral Modeling: 11th International Conference, SBP-BRiMS, Washington, DC, USA, 10–13 July 2018; Volume 11, pp. 197–206. [Google Scholar]
- Xu, Q.; Zhu, L.; Dai, T.; Yan, C. Aspect-based sentiment classification with multi-attention network. Neurocomputing 2020, 388, 135–143. [Google Scholar] [CrossRef]
- Rhanoui, M.; Mikram, M.; Yousfi, S.; Barzali, S. A CNN-BiLSTM model for document-level sentiment analysis. Mach. Learn. Knowl. Extr. 2019, 1, 832–847. [Google Scholar] [CrossRef]
- Lin, J.; Najafabadi, M.K. Aspect level sentiment analysis with CNN Bi-LSTM and attention mechanism. In Proceedings of the IEEE/ACIS 8th International Conference on Big Data, Cloud Computing, and Data Science, BCD, Hochimin City, Vietnam, 14–16 December 2023; pp. 282–288. [Google Scholar]
- Ayetiran, E.F. Attention-based aspect sentiment classification using enhanced learning through CNN-BiLSTM networks. Knowl.-Based Syst. 2022, 252, 109409. [Google Scholar] [CrossRef]
- Lu, G.; Liu, Y.; Wang, J.; Wu, H. CNN-BiLSTM-Attention: A multi-label neural classifier for short texts with a small set of labels. Inf. Process. Manag. 2023, 60, 103320. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Q.; Song, D. Aspect-based sentiment classification with aspect-specific graph convolutional networks. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, EMNLP, Online, 16–20 November 2020; pp. 4568–4578. [Google Scholar]
- Hou, X.; Huang, J.; Wang, G.; Qi, P.; He, X.; Zhou, B. Selective Attention Based Graph Convolutional Networks for Aspect-Level Sentiment Classification. In Proceedings of the Fifteenth Workshop on Graph-Based Methods for Natural Language Processing (TextGraphs-15), Mexico City, Mexico, 11 June 2021; pp. 83–93. [Google Scholar]
- Li, R.; Chen, H.; Feng, F.; Ma, Z.; Wang, X.; Hovy, E. DualGCN: Exploring syntactic and semantic information for aspect-based sentiment analysis. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 7642–7656. [Google Scholar] [CrossRef]
- Brauwers, G.; Frasincar, F. A general survey on attention mechanisms in deep learning. IEEE Trans. Knowl. Data Eng. TKDE 2021, 35, 3279–3298. [Google Scholar] [CrossRef]
- Van Elteren, J.T.; Tennent, N.H.; Šelih, V.S. Multi-element quantification of ancient/historic glasses by laser ablation inductively coupled plasma mass spectrometry using sum normalization calibration. Anal. Chim. Acta 2009, 644, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Memisevic, R.; Zach, C.; Pollefeys, M.; Hinton, G.E. Gated softmax classification. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; Volume 23. [Google Scholar]
- Liu, W.; Zhang, Y.M.; Li, X.; Yu, Z.; Dai, B.; Zhao, T.; Song, L. Deep hyperspherical learning. In Proceedings of the Advances in Neural Information Processing Systems, NIPS, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Luong, T.; Pham, H.; Manning, C.D. Effective approaches to attention-based neural machine translation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, EMNLP, Lisbon, Portugal, 17–21 September 2015; pp. 1412–1421. [Google Scholar]
- Laha, A.; Chemmengath, S.A.; Agrawal, P.; Khapra, M.; Sankaranarayanan, K.; Ramaswamy, H.G. On controllable sparse alternatives to softmax. Adv. Neural Inf. Process. Syst. NIPS 2018, 31, 6423–6433. [Google Scholar]
- Dhanith, P.J.; Surendiran, B.; Rohith, G.; Kanmani, S.R.; Devi, K.V. A Sparse Self-Attention Enhanced Model for Aspect-Level Sentiment Classification. Neural Process. Lett. 2024, 56, 47. [Google Scholar] [CrossRef]
- Hu, M.; Zhao, S.; Zhang, L.; Cai, K.; Su, Z.; Cheng, R.; Shen, X. CAN: Constrained Attention Networks for Multi-Aspect Sentiment Analysis. In Proceedings of the Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing, EMNLP-IJCNLP, Hong Kong, China, 3–7 November 2019; pp. 4601–4610. [Google Scholar]
- Nguyen, H.; Shirai, K. A joint model of term extraction and polarity classification for aspect-based sentiment analysis. In Proceedings of the 2018 10th International Conference on Knowledge and Systems Engineering, KSE, Ho Chi Minh City, Vietnam, 1–3 November 2018; pp. 323–328. [Google Scholar]
- Zhao, G.; Luo, Y.; Chen, Q.; Qian, X. Aspect-based sentiment analysis via multitask learning for online reviews. Knowlege-Based Syst. 2023, 264, 110326. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, Z. A fine-grained sentiment analysis model based on multi-task learning. In Proceedings of the 2024 4th International Symposium on Computer Technology and Information Science, ISCTIS, Xi’an, China, 12–14 July 2024; pp. 157–161. [Google Scholar]
- Schmitt, M.; Steinheber, S.; Schreiber, K.; Roth, B. Joint aspect and polarity classification for aspect-based sentiment analysis with end-to-end neural networks. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, EMNLP, Brussels, Belgium, 31 October–4 November 2018; pp. 1109–1114. [Google Scholar]
- Pei, Y.; Wang, Y.; Wang, W.; Qi, J. Aspect-Based Sentiment Analysis with Multi-Task Learning. In Proceedings of the 2022 5th International Conference on Computing and Big Data, ICCBD, Shanghai, China, 16–18 December 2022; pp. 171–176. [Google Scholar]
- Wang, Y.; Chen, Q.; Wang, W. Multi-task bert for aspect-based sentiment analysis. In Proceedings of the IEEE International Conference on Smart Computing, SMARTCOMP, Irvine, CA, USA, 23–27 August 2021; pp. 383–385. [Google Scholar]
- Treumann, R.; Baumjohann, W. Beyond Gibbs-Boltzmann-Shannon: General entropies—The Gibbs-Lorentzian example. Front. Phys. 2014, 2, 49. [Google Scholar] [CrossRef]
- Anastasiadis, A. Tsallis entropy. Entropy 2012, 14, 174–176. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR, Las Vegas, NA, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Tang, D.; Qin, B.; Feng, X.; Liu, T. Effective LSTMs for Target-Dependent Sentiment Classification. In Proceedings of the COLING, Osaka, Japan, 11–16 December 2016; pp. 3298–3307. [Google Scholar]
- Lin, P.; Yang, M.; Lai, J. Deep selective memory network with selective attention and inter-aspect modeling for aspect level sentiment classification. IEEE/ACM Trans Audio Speech Lang Process 2021, 29, 1093–1106. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, B.; Zhao, T. Convolutional multi-head self-attention on memory for aspect sentiment classification. IEEE/CAA J. Autom. Sin. 2020, 7, 1038–1044. [Google Scholar] [CrossRef]
- Liu, H.; Wu, Y.; Li, Q.; Lu, W.; Li, X.; Wei, J.; Feng, J. Enhancing aspect-based sentiment analysis using a dual-gated graph convolutional network via contextual affective knowledge. Neurocomputing 2023, 553, 126526. [Google Scholar] [CrossRef]
- Deng, X.; Han, D.; Jiang, P. A Context-focused Attention Evolution Model for Aspect-based Sentiment Classification. ACM Trans. Asian Low-Resour. Lang. Inf. Process. 2023, 22, 1–14. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).