Convergence and Stability of the Truncated Stochastic Theta Method for McKean-Vlasov Stochastic Differential Equations Under Local Lipschitz Conditions

Abstract

This paper focuses on McKean-Vlasov stochastic differential equations under local Lipschitz conditions. We first introduce the stochastic interacting particle system and prove the propagation of chaos. Then we establish a truncated stochastic theta scheme to approximate the interacting particle system and obtain the strong convergence of the continuous-time truncated stochastic theta scheme to the non-interacting particle system. Furthermore, we study the asymptotical mean square stability of the interacting particle system and the truncated stochastic theta method. Finally, we give one numerical example to verify our theoretical results.

1. Introduction

McKean-Vlasov stochastic differential equations (MVSDEs) also known as distribution-dependent SDEs or mean-fields SDEs, are used to describe asymptotic behavior of an N-particle system with mean-field interaction. The coefficients of MVSDEs depend not only on the solutions but also on the law of the solutions which have received widespread attention and played increasingly important role in various fields. The well-posedness of MVSDEs with coefficients satisfying global Lipschitz condition has been well studied in [1,2,3,4]. By truncating the coefficients in both the space and the distribution variables, Liu and Ma [5] obtained the well-posedness of MVSDEs with coefficients satisfying local Lipschitz and linear growth conditions. Using an interpolated Euler-like sequence, Li et al. [6] established the well-posedness of MVSDEs under local one-sided Lipschitz and uniform linear growth conditions. We refer the reader to [7,8,9,10] and the references therein for more results on the well-posedness of MVSDEs under global and local Lipschitz conditions.

Compared to the well-posedness of MVSDEs, the research on the stability of MVSDEs is slightly lacking. In Bahlali et al. [1], they demonstrated various stability properties with respect to (w.r.t.) the initial data, the coefficients, and the driving processes by using the BDG inequality and the Gronwall lemma under an Osgood type condition. In Govindan and Ahmed [11], they investigated the exponential stability of the stochastic McKean-Vlasov evolution equation by using Lebesgue’s dominated convergence theorem and the Lyapunov function method under Lipschitz and linear growth conditions. In Ding and Qiao [12], they considered the mean square exponential stability of the MVSDE with non-Lipschitz coefficients and obtained the exponentially 2-ultimate boundedness of the solution by using the Lyapunov function method.

Most of MVSDEs cannot be solved explicitly, so numerical solutions are very important in practical applications. Compared with standard SDEs, the law in MVSDEs leads to the numerical simulation for MVSDEs always involving two steps: (1) approximating the law of MVSDE by the empirical distribution of interacting particle system, and (2) establishing a stable numerical method to solve the interacting particle system. The first study on the numerical method for MVSDEs was Bossy and Talay [13], in which they investigated the Euler-Maruyama (EM) scheme for MVSDEs under global Lipschitz condition. Furthermore, Budhiraja and Fan in [14] studied the explicit Euler scheme for a specific MVSDE under global Lipschitz condition. Dos Reis et al. [2] showed that the implicit Euler scheme is convergent for the MVSDEs with the drift term growing super-linearly under global Lipschitz condition. Bao et al. [15] derived the fully implementable first-order Milstein schemes for MVSDEs with a super-linearly growing drift term in the state component. More work on the numerical approximations for MVSDEs under global Lipschitz condition can be found in [6,16,17,18] and the references therein. Nevertheless, to our best knowledge, the stabilities of the numerical schemes for MVSDEs under local Lipschitz condition have not been studied yet. Accordingly, based on the stochastic particle method, this paper focuses on the numerical approximation for MVSDEs under local Lipschitz condition with the aim to establish the convergence and stability theorem.

This paper is organized as follows. In Section 2, we introduce some notations and assumptions. In Section 3, we describe the MVSDE under local Lipschitz conditions and the corresponding interacting particle system. In Section 4, we propose the truncated stochastic theta method and then obtain the convergence result. In Section 5, we impose an extra condition to study the stability result. Finally, we present a numerical example to confirm our theory results in Section 6.

2. Notations and Preliminaries

We first recall some notions and results. Denote by $A^T$ the transpose of $A\in {\mathbb{R}}^{d\times n}$, $tr(A)$ the trace of A, $|·|$ the Euclidean norm in ${\mathbb{R}}^d$, and $|A|=\sqrt{tr(A^{T}A)}$ the trace norm. Let $\lceil \alpha \rceil$ be the rounding upward of real constant $\alpha$.

Let $(\Omega ,\mathcal{F},\mathbb{P})$ be the complete probability space equipped with the filtrations ${({\mathcal{F}}_t)}_{t\ge 0}$ satisfying the usual conditions. Let $E(\xi )$ be the expectation of ${\mathbb{R}}^d$-valued random variable $\xi$ under $\mathbb{P}$ and ${\mathbb{L}}^p(\Omega ,{\mathbb{R}}^d)$$(p>0)$ be the set of all ${\mathbb{R}}^d$-valued random variables $\xi$ with ${E|\xi |}^p<\infty$. Denote by $\mathcal{P}({\mathbb{R}}^d)$ the set of all probability measures over $({\mathbb{R}}^d,\mathcal{B}({\mathbb{R}}^d))$ equipped with weak topology, where $\mathcal{B}({\mathbb{R}}^d)$ is the Borel $\sigma$-field over ${\mathbb{R}}^d$. In addition, ${\mathcal{P}}^2({\mathbb{R}}^d)=\left\{\mu \in \mathcal{P}({\mathbb{R}}^d):{\int }_{{\mathbb{R}}^d}{|x|}^2\mu (dx)<\infty \right\}$. For $q\ge 1,\mu ,v\in \mathcal{P}({\mathbb{R}}^d)$, define the q–Wasserstein distance ${\mathbb{W}}_q(\mu ,v)$ as

$$\begin{array}{c}\hfill {\mathbb{W}}_q(\mu ,v)={\left(\underset{\pi \in \Pi (\mu ,v)}{inf}{\int }_{{\mathbb{R}}^d\times {\mathbb{R}}^d}{|x-y|}^q\pi (dx,dy)\right)}^{\frac{1}{q}},\end{array}$$

where $\Pi (\mu ,v)$ is the set of couplings between $\mu$ and v on ${\mathbb{R}}^d\times {\mathbb{R}}^d$. In other words, $\pi \in \Pi (\mu ,v)$ is a probability measure on ${\mathbb{R}}^d\times {\mathbb{R}}^d$ such that $\pi (·\times {\mathbb{R}}^d)=\mu$ and $\pi ({\mathbb{R}}^d\times ·)=v$. In particular, if $\mu ={\mathbb{P}}_X$ and $v={\mathbb{P}}_Y$, then

$$\begin{array}{c}\hfill {\mathbb{W}}_1(\mu ,v)=\underset{\pi \in \Pi (\mu ,v)}{inf}{\int }_{{\mathbb{R}}^d\times {\mathbb{R}}^d}|x-y|\pi (dx,dy)\le {\int }_{{\mathbb{R}}^d\times {\mathbb{R}}^d}|x-y|d\left({\mathbb{P}}_{(X,Y)}(x,y)\right)=E|X-Y|,\end{array}$$

and

$$\begin{array}{c}\hfill {\mathbb{W}}_2^2(\mu ,v)=\underset{\pi \in \Pi (\mu ,v)}{inf}{\int }_{{\mathbb{R}}^d\times {\mathbb{R}}^d}{|x-y|}^2\pi (dx,dy)\le {\int }_{{\mathbb{R}}^d\times {\mathbb{R}}^d}{|x-y|}^{2}d\left({\mathbb{P}}_{(X,Y)}(x,y)\right)=E{|X-Y|}^2,\end{array}$$

where ${\mathbb{P}}_{(X,Y)}$ is the joint probability distribution of the random variables X and Y.

3. Stochastic Particle Method

Consider the following MVSDE

$$\left\{\begin{array}{cc}\hfill dZ(t)& =f(Z(t),{\mathcal{L}}_{Z(t)})dt+g(Z(t),{\mathcal{L}}_{Z(t)})d{B}_t,t\in (0,T],\hfill \\ \hfill Z(0)& =\xi ,\hfill \end{array}\right.$$

(1)

where $\xi$ is an ${\mathbb{R}}^d$-valued ${\mathcal{F}}_0$-measurable random variable, $f:{\mathbb{R}}^d\times {\mathcal{P}}^2({\mathbb{R}}^d)\to {\mathbb{R}}^d$ and $g:{\mathbb{R}}^d\times {\mathcal{P}}^2({\mathbb{R}}^d)\to {\mathbb{R}}^d\times {\mathbb{R}}^d$ are Borel measurable functions, $B_t$ is a d-dimensional Brownian motion, and ${\mathcal{L}}_{Z(t)}$ is the law of $Z(t)$. We impose some assumptions on f and g.

Assumption 1.

$f(x,\mu )$ is continuous in ${\mathbb{R}}^d\times {\mathcal{P}}^2({\mathbb{R}}^d)$. For each $R\ge 1$, there exist positive number a and $L_R\le alogR$ such that

$$\begin{array}{cc}\hfill {⟨x-y,f(x,\mu )-f(y,\mu )⟩\vee |g(x,\mu )-g(y,\mu )|}^2\le & L_R{(|x-y|}^2,\forall x,y\in {\mathbb{R}}^d,|x|\vee |y|\le R,\mu \in {\mathcal{P}}^2({\mathbb{R}}^d).\hfill \end{array}$$

Assumption 2.

There exists a positive constant L such that

$$\begin{array}{c}\hfill |f(x,\mu )-f(x,v)|\vee |g(x,\mu )-g(x,v)|\le L{\mathbb{W}}_1(\mu ,v),\forall x\in {\mathbb{R}}^d,\mu ,v\in {\mathcal{P}}^2({\mathbb{R}}^d).\end{array}$$

Assumption 3.

For any $x\in {\mathbb{R}}^d$ and $\mu \in {\mathcal{P}}^2({\mathbb{R}}^d)$, there exist positive constant M and $l>1$ such that

$$\begin{array}{c}\hfill ⟨x,f(x,\mu )⟩\le {M(1+|x|}^2+{\mathbb{W}}_2^2(\mu ,{\delta }_0)),|g(x,\mu )|\le M(|x|+{\mathbb{W}}_1(\mu ,{\delta }_0)),and|f(x,\mu ){|\le M(1+|x|}^l+{\mathbb{W}}_1(\mu ,{\delta }_0)),\end{array}$$

where ${\delta }_x$ denotes the Dirac measure concentrated on x.

Similar to Theorem 3.1 in [19], we may obtain the well-posedness of MVSDE (1).

Theorem 1.

Under Assumptions 1–3, if $\xi \in {\mathbb{L}}^r(\Omega ,{\mathbb{R}}^d)$ for any $r>0$, MVSDE (1) admits a unique solution ${\left\{Z(t)\right\}}_{0\le t\le T}$. For any $p>0$, there exists a constant $C>0$ such that

$$E\left(\underset{t\in [0,T]}{sup}{|Z(t)|}^p\right)<C.$$

Proof. 

This result is known well. So for brevity we only outline main steps.

• Uniqueness. Let $Z_1(t)$ and $Z_2(t)$ are solutions of (1) with the same initial value. Define $\overline{\Omega }(R)=\{\omega \in \Omega :{sup}_{0\le t\le T}|Z_1(t)|\vee {sup}_{0\le t\le T}|Z_2(t)|\ge R\}$. Then for any $p\ge 2l$, similar to the proof of Theorem 3.1 in [19], we have

  $$E\left(\underset{0\le t\le T}{sup}{|Z_1(t)-Z_2(t)|}^2\right)\le \frac{\widehat{C}}{\sqrt{R^p}}{R}^{\tilde{C}Ta},$$

  (2)

  where $\widehat{C}$ and $\tilde{C}$ are positive constants. Considering that p can be arbitrarily large, we choose $p>2\tilde{C}Ta$, such that the right-side of (2) converges to 0 when $R\to \infty$.
• Existence. Let $Z_t^0=Z(0)=\xi$, ${\mathcal{L}}_{Z_t^0}={\mathcal{L}}_{Z(0)}$. For any $n\ge 1$, let $Z_t^n$ solve the SDE

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{Z}_t^n=f(Z_t^n,{\mathcal{L}}_{Z_t^{n-1}})dt+g(Z_t^n,{\mathcal{L}}_{Z_t^{n-1}})d{B}_t,\hfill \\ Z_t^0=Z(0)=\xi .\hfill \end{array}\right.\end{array}$$

  Similar to the proof of Theorem 3.1 in [19], we can prove that $E\left({sup}_{0\le t\le T}{|Z_t^n|}^p\right)<C$ and $\left\{Z_t^n\right\}$ is a Cauchy sequence, and hence has a limit $Z_t$ in the space $C([0,T])$ as $n\to \infty$, which is a solution.

□

To approximate (1), we introduce an $N(\ge 1)$-dimensional system of interacting particles

$$\begin{array}{cc}\hfill d{Z}^{i,N}(t)=& f(Z^{i,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)})dt+g(Z^{i,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)})d{B}_t^i,i=1,2,\cdots ,N\hfill \end{array}$$

(3)

with the independent identical initial data $Z^{i,N}(0)={\xi }^i$, $i=1,2,\cdots ,N$, where ${(B_t^i)}_{1\le i\le N}$ are independent Brownian motion. As a bridge, we introduce the non-interacting particle system

$$d{Z}^i(t)=f(Z^i(t),{\mathcal{L}}_{Z^i(t)})dt+g(Z^i(t),{\mathcal{L}}_{Z^i(t)})d{B}_t^i$$

(4)

with initial value $Z^i(0)={\xi }^i$. It follows from Theorem 1 that ${\mathcal{L}}_{Z^i(t)}={\mathcal{L}}_{Z(t)}$ for all i.

Under Assumptions 1–3, we establish the well-posedness of the interacting particle system via the following lemma.

Lemma 1.

Assume that Assumptions 1–3 hold. Then for any $N\ge 2$ and $p>0$, the interacting particle system (3) admits a strong solution ${(Z^{i,N}(t))}_{0\le t\le T}$ and for $Z^{i,N}(0)={\xi }^i\in {\mathbb{L}}^p(\Omega ,{\mathbb{R}}^d)$ there exists a constant $C_p>0$ independent of i, such that

$$\begin{array}{c}\hfill \underset{1\le i\le N}{sup}E\left(\underset{t\in [0,T]}{sup}|Z^{i,N}(t){)|}^p\right)<C_p.\end{array}$$

(5)

Proof. 

Let

$$\tilde{Z}(t)={\left(Z^{1,N}(t),Z^{2,N}(t),\cdots ,Z^{N,N}(t)\right)}^T,B^N(t)={\left(B_t^1,B_t^2,\cdots ,B_t^N\right)}^T,$$

$$F(\tilde{Z}(t))={\left(f\left(Z^{1,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)}\right),f\left(Z^{2,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)}\right),\cdots ,f\left(Z^{N,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)}\right)\right)}^T,$$

$$G(\tilde{Z}(t))=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}{\left(g\left(Z^{1,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)}\right),g\left(Z^{2,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)}\right),\cdots ,g\left(Z^{N,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)}\right)\right)}^T.$$

Then, (3) can be rewritten as

$$\begin{array}{c}\hfill d\tilde{Z}(t)=F(\tilde{Z}(t))dt+G(\tilde{Z}(t))d{B}^N(t).\end{array}$$

(6)

Recalling the definition of ${\mathbb{W}}_1$, one has

$${\mathbb{W}}_1\left(\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)},\frac{1}{N}\sum _{i=1}^N{\delta }_{Y^{i,N}(t)}\right)\le \frac{1}{N}\sum _{i=1}^N|Z^{i,N}(t)-Y^{i,N}(t)|.$$

Then, for any $t\in [0,T]$ and $\tilde{Z}(t),\tilde{Y}(t)\in {\mathbf{R}}^{dN}$ with $|Z^{i,N}(t)|\vee |Y^{i,N}(t)|\le R$, it follows from Assumptions 1–3 that

$$\begin{array}{cc}\hfill ⟨\tilde{Z}(t)-\tilde{Y}(t),F(\tilde{Z}(t))-F(\tilde{Y}(t))⟩=& \sum _{i=1}^N⟨Z^{i,N}(t)-Y^{i,N}(t),f\left(Z^{i,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)}\right)-f\left(Y^{i,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Y^{i,N}(t)}\right)⟩\hfill \\ \hfill \le & L_R\sum _{i=1}^N|Z^{i,N}(t)-Y^{i,N}{(t)|}^2+L\sum _{i=1}^N|Z^{i,N}(t)-Y^{i,N}(t)|·{\mathbb{W}}_1\left(\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)},\frac{1}{N}\sum _{i=1}^N{\delta }_{Y^{i,N}(t)}\right)\hfill \\ \hfill \le & (L_R+L){|\tilde{Z}(t)-\tilde{Y}(t)|}^2,\hfill \end{array}$$

$$|G(\tilde{Z}(t))-G(\tilde{Y}(t)){|}^2\le 2L_R\sum _{i=1}^N{|Z^{i,N}(t)-Y^{i,N}(t)|}^2+\frac{2L^2}{N}\sum _{i=1}^N|Z^{i,N}(t)-Y^{i,N}(t){|}^2\le (2L_R+2L^2)|\tilde{Z}(t)-\tilde{Y}(t){|}^2,$$

$$|F(\tilde{Z}(t))|=\sum _{i=1}^N|f\left(Z^{i,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)}\right)|\le M\left(1+|\tilde{Z}{(t)|}^l+|\tilde{Z}(t)|\right),$$

$$|G(\tilde{Z}(t))|=\sum _{i=1}^N|g\left(Z^{i,N}(t),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)}\right)|\le M\sum _{i=1}^N\left(|Z^{i,N}(t)|+{\mathbb{W}}_1\left(\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(t)},{\delta }_0\right)\right)\le 2M|\tilde{Z}(t)|.$$

These together with the existence and uniqueness Lemma 4.1 in [6] imply that (6) has a unique solution on $[0,T]$ for any N.

For any $1\le i\le N$ and $R>0$, define the stopping time ${\tau }_R^i=inf\{t\in [0,T]:|Z^{i,N}(t)|\ge R\}$, by the growth condition, apply the Itô formula to ${[1+|x|]}^{\frac{p}{2}}$, we can prove (5), and so we omit it here. □

The following lemma describes the propagation of chaos for MVSDE under the local conditions.

Lemma 2.

Let Assumptions 1–3 hold. Then

$$\begin{array}{c}\hfill \underset{N\to \infty }{lim}\underset{1\le i\le N}{sup}E\left(\underset{t\in [0,T]}{sup}|Z^{i,N}(t)-Z^i(t){|}^2\right)=0,\end{array}$$

(7)

Proof. 

For any $1\le i\le N$ and $R>0$, let ${\tau }_R^i=inf\{t\in [0,T]:|Z^{i,N}(t)|\ge R\}$. Then, the Itô formula gives

$$\begin{array}{cc}\hfill & E\left[\underset{0\le r\le t\wedge {\tau }_R^i}{sup}|Z^{i,N}(r)-Z^i(r){|}^2\right]\hfill \\ \hfill & \le 2E\left[\underset{0\le r\le t\wedge {\tau }_R^i}{sup}{\int }_0^r⟨Z^{i,N}(s)-Z^i(s),f\left(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)-f\left(Z^i(s),{\mathcal{L}}_{Z^i(s)}\right)⟩ds\right]\hfill \\ \hfill & +2E\left[\underset{0\le r\le t\wedge {\tau }_R^i}{sup}{\int }_0^r⟨Z^{i,N}(s)-Z^i(s),g\left(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)-g\left(Z^i(s),{\mathcal{L}}_{Z^i(s)}\right)⟩d{B}_s^i\right]\hfill \\ \hfill & +E[\underset{0\le r\le t\wedge {\tau }_R^i}{sup}\left({\int }_0^r|g\left(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)-g\left(Z^i(s),{\mathcal{L}}_{Z^i(s)}\right){|}^{2}ds\right].\hfill \end{array}$$

(8)

Denote

$$\begin{array}{cc}\hfill & I_{1,R}^i(r)=2{\int }_0^r⟨Z^{i,N}(s)-Z^i(s),f\left(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)-f\left(Z^i(s),{\mathcal{L}}_{Z^i(s)}\right)⟩ds,\hfill \\ \hfill & I_{2,R}^i(r)=2{\int }_0^r⟨Z^{i,N}(s)-Z^i(s),g\left(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)-g\left(Z^i(s),{\mathcal{L}}_{Z^i(s)}\right)⟩d{B}_s^i,\hfill \\ \hfill & I_{3,R}^i(r)={\int }_0^r|g\left(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)-g\left(Z^i(s),{\mathcal{L}}_{Z^i(s)}\right){|}^{2}ds.\hfill \end{array}$$

It follows from Assumptions 1–3, the Hölder inequality, and the Schwarz inequality that

$$\begin{array}{cc}\hfill E\left[\underset{0\le r\le t\wedge {\tau }_R^i}{sup}{I}_{1,R}^i(r)\right]& \le 2E[\underset{0\le r\le t\wedge {\tau }_R^i}{sup}{\int }_0^t⟨Z^{i,N}(s)-Z^i(s),f\left(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)-f\left(Z^i(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)\hfill \\ \hfill & +f\left(Z^i(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)-f\left(Z^i(s),{\mathcal{L}}_{Z^i(s)}\right)⟩ds]\hfill \\ \hfill & \le (2L_R+1){\int }_0^{t}E{|Z^{i,N}(s\wedge {\tau }_R^i)-Z^i(s\wedge {\tau }_R^i)|}^{2}ds+L^2{\int }_0^{t}E|\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s\wedge {\tau }_R^i)}-{\mathcal{L}}_{Z^i(s\wedge {\tau }_R^i)}{|}^{2}ds.\hfill \end{array}$$

(9)

Combining Burkholder-Davis-Gundy (BDG) inequality and Assumption 2, we get

$$\begin{array}{cc}\hfill E\left[\underset{0\le r\le t\wedge {\tau }_R^i}{sup}{I}_{2,R}^i(r)\right]& \le 2E{\left({\int }_0^{t\wedge {\tau }_R^i}{|Z^{i,N}(s)-Z^i(s)|}^2|g\left(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)-g\left(Z^i(s),{\mathcal{L}}_{Z^i(s)}\right){|}^{2}ds\right)}^{\frac{1}{2}}\hfill \\ \hfill & \le \frac{1}{2}E\left[\underset{0\le s\le t}{sup}{|Z^{i,N}(s\wedge {\tau }_R^i)-Z^i(s\wedge {\tau }_R^i)|}^2\right]\hfill \\ \hfill & +2E{\int }_0^t|g\left(Z^{i,N}(s\wedge {\tau }_R^i),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s\wedge {\tau }_R^i)}\right)-g\left(Z^i(s\wedge {\tau }_R^i),{\mathcal{L}}_{Z^i(s\wedge {\tau }_R^i)}\right){|}^{2}ds\hfill \\ \hfill & \le \frac{1}{2}E\left[\underset{0\le s\le t}{sup}{|Z^{i,N}(s\wedge {\tau }_R^i)-Z^i(s\wedge {\tau }_R^i)|}^2\right]+4L_R{\int }_0^{t}E{|Z^{i,N}(s\wedge {\tau }_R^i)-Z^i(s\wedge {\tau }_R^i)|}^{2}ds\hfill \\ \hfill & +4L^2{\int }_0^{t}E|\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s\wedge {\tau }_R^i)}-{\mathcal{L}}_{Z^i(s\wedge {\tau }_R^i)}{|}^{2}ds\hfill \end{array}$$

(10)

Similarly,

$$\begin{array}{cc}\hfill E\left[\underset{0\le r\le t\wedge {\tau }_R^i}{sup}{I}_3^i(r)\right]& \le {\int }_0^{t\wedge {\tau }_R^i}E|g\left(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}\right)-g\left(Z^i(s),{\mathcal{L}}_{Z^i(t)}\right){|}^{2}ds\hfill \\ \hfill & \le 2L_R{\int }_0^{t}E{|Z^{i,N}(s\wedge {\tau }_R^i)-Z^i(s\wedge {\tau }_R^i)|}^{2}ds+2L^2{\int }_0^{t}E|\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s\wedge {\tau }_R^i)}-{\mathcal{L}}_{Z^i(s\wedge {\tau }_R^i)}{|}^{2}ds.\hfill \end{array}$$

(11)

Noting that

$$\begin{array}{cc}\hfill E|\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}-{\mathcal{L}}_{Z^i(t)}{|}^2& =E|\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}-\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^i(s)}+\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^i(s)}-{\mathcal{L}}_{Z^i(t)}{|}^2\hfill \\ \hfill & \le 2E|\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}-\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^i(s)}{|}^2+2E|\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^i(s)}-{\mathcal{L}}_{Z^i(t)}{|}^2.\hfill \end{array}$$

(12)

Considering the Glivenko-Cantelli lemma (Lemma 4.1 in [20] and Lemma 4.3 in [6]), we get that, for $q>2$ and $t\ge 0$,

$$E|\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^i(s)}-{\mathcal{L}}_{Z^i(t)}{|}^2\le C_{d,q}(E|Z^i(s){{|}^q)}^{\frac{2}{q}}\Phi (N),$$

where $C_{d,q}$ is a constant dependent of d, q, and

$$\begin{array}{c}\hfill \Phi (N):=\left\{\begin{array}{c}{N}^{-\frac{1}{2}}+N^{-\frac{q-2}{q}},d<4\mathrm{and}q\ne 4,\hfill \\ N^{-\frac{1}{2}}log(1+N)+N^{-\frac{q-2}{q}},d=4\mathrm{and}q\ne 4,\hfill \\ N^{-\frac{2}{d}}+N^{-\frac{q-2}{q}},d>4\mathrm{and}q\ne \frac{d}{d-2}.\hfill \end{array}\right.\end{array}$$

(13)

Substituting (9)–(13) into (8), we have

$$\begin{array}{cc}\hfill & E\left[\underset{0\le s\le t}{sup}{|Z^{i,N}(s\wedge {\tau }_R^i)-Z^i(s\wedge {\tau }_R^i)|}^2\right]\hfill \\ \hfill & \le 2(8L_R+14L^2+1){\int }_0^{t}E\left[\underset{0\le r\le s}{sup}{|Z^{i,N}(r\wedge {\tau }_R^i)-Z^i(r\wedge {\tau }_R^i)|}^2\right]ds+C\Phi (N),\hfill \end{array}$$

(14)

where C is a constant. Noting that R is independent of N and letting $N\to \infty$, the desired assertion can be obtained by using the Gronwall inequality. □

4. Truncated Stochastic Theta Method and Strong Convergence

In this section, we establish the truncated stochastic theta method for the stochastic interacting particle system, and then examine strong convergence of continuous-time truncated stochastic theta scheme to the non-interacting particle system.

4.1. Numerical Methods and Associated Moments

We introduce the stochastic theta method for the stochastic interacting particle system (3). We partition the time interval $[0,T]$ into n steps of size $\Delta =T/n$ with $\{t_k=k\Delta :k=0,1,\cdots ,n\}$. Let ${\tilde{Y}}_0^{i,N,n}={\xi }^i$ and

$$\begin{array}{c}\hfill {\tilde{Y}}_{k+1}^{i,N,n}={\tilde{Y}}_k^{i,N,n}+\theta f\left({\tilde{Y}}_{k+1}^{i,N,n},{\mu }_{k+1}^{\tilde{Y},N,n}\right)\Delta +(1-\theta )f\left({\tilde{Y}}_k^{i,N,n},{\mu }_k^{\tilde{Y},N,n}\right)\Delta +g\left({\tilde{Y}}_k^{i,N,n},{\mu }_k^{\tilde{Y},N,n}\right)\Delta B_k^i,\end{array}$$

(15)

where ${\mu }_k^{\tilde{Y},N,n}=\frac{1}{N}{\sum }_{i=1}^N{\delta }_{{\tilde{Y}}_k^{i,N,n}}$, and $\Delta B_k^i=B_{k+1}^i-B_k^i$. The parameter $\theta \in [0,1]$ decides the implicitness of the numerical scheme. $\theta =0$ implies the EM scheme, and $\theta =1$ implies the backward EM scheme. We should make sure an implicit scheme is well defined before we use it. To make sure the well-definedness, the drift term should satisfy

$$\begin{array}{c}\hfill ⟨x-y,f(x,\mu )-f(y,\mu )⟩\le {K|x-y|}^2,\end{array}$$

(16)

where K is a positive constant. We cannot relax this condition. From Assumption 1, $L_R$ may be ∞ as $R\to \infty$, which means that the stochastic theta method (15) may be not well-defined. So, we fall back on modifying the stochastic theta scheme by truncating it. Choose a strictly decreasing function $\kappa :(0,1)\to (0,\infty )$ such that

$$\begin{array}{c}\hfill \underset{\Delta \to 0}{lim}\kappa (\Delta )=\infty ,L_{\kappa (\Delta )}{e}^{L_{\kappa (\Delta )}}\Delta \le 1,\mathrm{and}\kappa (\Delta )\Delta \le 1.\end{array}$$

(17)

Such a function does exist. For example, let $\kappa (\Delta )=ln{\Delta }^{-\frac{1}{2}}$, then, $\kappa (\Delta )$ decreases strictly and tends to ∞ as $\Delta \to 0$. Define $L_{\kappa (\Delta )}=\kappa (\Delta )$, then $L_{\kappa (\Delta )}{e}^{L_{\kappa (\Delta )}}\Delta \le {\Delta }^{\frac{1}{2}}<1$ and $\kappa (\Delta )\Delta \le 1$.

We define a truncated function by

$$f_{\Delta }(y,·)=\left\{\begin{array}{c}f(y,·),\mathrm{for}|y|\le \kappa (\Delta ),\hfill \\ f\left(\kappa (\Delta )\frac{y}{|y|},·\right),\mathrm{for}|y|>\kappa (\Delta ).\hfill \end{array}\right.$$

It can be proved that the truncated function satisfies:

Lemma 3.

Under Assumptions 1–3, for any $y,z\in {\mathbb{R}}^d$ and $\mu \in {\mathcal{P}}^2({\mathbb{R}}^d)$, it holds that

$$\begin{array}{c}\hfill ⟨y-z,f_{\Delta }(y,\mu )-f_{\Delta }(z,\mu )⟩\le {\overline{L}}_{\kappa (\Delta )}{|y-z|}^2,\end{array}$$

(18)

where ${\overline{L}}_{\kappa (\Delta )}=2L_{\kappa (\Delta )}{+2M(1+|\kappa (\Delta )|}^l+|\kappa (\Delta )|)$.

Proof. 

The proof is similar to that of Lemma 2.3 in [21], so we omit the details here. □

For $\theta \in [0,1]$, we construct the truncated stochastic theta method for (3)

$$\begin{array}{c}\hfill Y_{k+1}^{i,N,n}=Y_k^{i,N,n}+\theta f_{\Delta }\left(Y_{k+1}^{i,N,n},{\mu }_{k+1}^{Y,N,n}\right)\Delta +(1-\theta )f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta +g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i,\end{array}$$

(19)

where ${\mu }_k^{Y,N,n}=\frac{1}{N}{\sum }_{i=1}^N{\delta }_{Y_k^{i,N,n}}$. By (17) and Lemma 3, the monotone operator implies that (19) is well defined (see discussion in Jentzen et al. [22]). Considering the implicitness of (19), we set $\theta \Delta <\frac{1}{2M}$, and M is defined in Assumption 3. Thus, we set ${\Delta }_1\in (0,\frac{1}{2\theta M})$ and choose $\Delta \in (0,{\Delta }_1]$. Now, we extend the discrete truncated stochastic theta method to a continuous form. Let $Y^{i,N}(t)$ be the continuous form of $Y_k^{i,N,n}$ such that $Y^{i,N}(0)=Y_0^{i,N,n}$, and for any $t\in [0,T]$,

$$\begin{array}{cc}\hfill {\int }_0^t\left[Y^{i,N}(s)-\theta f_{\Delta }\left(Y^{i,N}(s),{\mathcal{L}}_{Y^{i,N}(s)}\right)\right]ds& =(1-\theta ){\int }_0^t{f}_{\Delta }\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right)ds+{\int }_0^{t}g\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right)d{B}_s^i,\hfill \end{array}$$

(20)

where ${\widehat{Y}}^{i,N}(t)=Y_k^{i,N,n}$ and ${\mathcal{L}}_{{\overline{\widehat{Y}}}^N(t)}=\frac{1}{N}{\sum }_{i=1}^N{\delta }_{Y_{t_k}^{i,N,n}}$ for $t\in [t_k,t_{k+1}),k=0,1,\cdots ,n$.

Similarly, we can define ${\tilde{Y}}^{i,N}(t)$ as the continuous form of ${\tilde{Y}}_k^{i,N,n}$,

$$\begin{array}{cc}\hfill {\int }_0^t\left[{\tilde{Y}}^{i,N}(s)-\theta f\left({\tilde{Y}}^{i,N}(s),{\mathcal{L}}_{{\tilde{Y}}^{i,N}(s)}\right)\right]ds& =(1-\theta ){\int }_0^{t}f\left({\widehat{\tilde{Y}}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s)}\right)ds+{\int }_0^{t}g\left({\widehat{\tilde{Y}}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s)}\right)d{B}_s^i,\hfill \end{array}$$

${\widehat{\tilde{Y}}}^{i,N}(t)={\tilde{Y}}_k^{i,N,n}$ and ${\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(t)}=\frac{1}{N}{\sum }_{i=1}^N{\delta }_{{\tilde{Y}}_{t_k}^{i,N,n}}$ for $t\in [t_k,t_{k+1}),k=0,1,\cdots ,n$.

For denoting convenience, we use $C_i$, $i=0,2,\cdots ,39$ to denote different positive constants independent of $\Delta$ below, maybe some of $C_i$, $i=0,2,\cdots ,39$ are dependent of $n,T$ or p. Now, we proceed to estimate the pth moment of the numerical solution.

Lemma 4.

Let Assumption 3 hold. For $\theta \in [\frac{1}{2},1]$ and $p\ge 2$, it holds that

$$E\left(\underset{0\le k\le n}{sup}{|Y_k^{i,N,n}|}^p\right)\le C_0,$$

and

$$E\left(\underset{0\le k\le n}{sup}{|{\tilde{Y}}_k^{i,N,n}|}^p\right)\le C_1,$$

where $C_0$ and $C_1$ are positive constants.

Proof. 

Denote $Z_k^{i,N,n}=Y_k^{i,N,n}-\theta f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta$, by (19), we have

$$\begin{array}{cc}\hfill |Z_{k+1}^{i,N,n}{|}^2=& |Z_k^{i,N,n}{|}^2+2⟨Z_k^{i,N,n},f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta ⟩+|f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right){|}^2{\Delta }^2+|g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i{|}^2\hfill \\ \hfill & +2⟨Z_k^{i,N,n}+f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta ,g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i⟩\hfill \\ \hfill =& |Z_k^{i,N,n}{|}^2+2⟨Y_k^{i,N,n},f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta ⟩+(1-2\theta )|f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right){|}^2{\Delta }^2+|g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i{|}^2\hfill \\ \hfill & +2⟨Y_k^{i,N,n}+(1-\theta )f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta ,g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i⟩.\hfill \end{array}$$

(21)

Noting that $\theta \ge \frac{1}{2}$ and $f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta =\frac{1}{\theta }(Y_k^{i,N,n}-Z_k^{i,N,n})$, it follows from Assumption 3 that

$$\begin{array}{cc}\hfill |Z_{k+1}^{i,N,n}{|}^2\le & |Z_k^{i,N,n}{|}^2+2M\left(1+|Y_k^{i,N,n}{|}^2+{\mathbb{W}}_2^2({\mu }_k^{Y,N,n},{\delta }_0)\right)\Delta +|g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i{|}^2\hfill \\ \hfill & +\frac{2}{\theta }⟨Y_k^{i,N,n},g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i⟩-2\frac{1-\theta }{\theta }⟨Z_k^{i,N,n},g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i⟩.\hfill \end{array}$$

Summing both sides from 0 to k to give

$$\begin{array}{cc}\hfill |Z_{k+1}^{i,N,n}{|}^2\le & |Z_0^{i,N,n}{|}^2+2MT+2M\sum _{j=0}^k|Y_j^{i,N,n}{|}^2\Delta +2M\sum _{j=0}^k{\mathbb{W}}_2^2({\mu }_k^{Y,N,n},{\delta }_0)\Delta +\sum _{j=0}^k|g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right)\Delta B_j^i{|}^2\hfill \\ \hfill & +\frac{2}{\theta }\sum _{j=0}^k⟨Y_j^{i,N,n},g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right)\Delta B_j^i⟩-2\frac{1-\theta }{\theta }\sum _{j=0}^k⟨Z_j^{i,N,n},g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right)\Delta B_j^i⟩.\hfill \end{array}$$

For any $p\ge 1$, it follows from the elementary inequality that

$$\begin{array}{cc}\hfill & |Z_{k+1}^{i,N,n}{|}^{2p}\le 6^{p-1}{2}^p{M}^p{\left(\sum _{j=0}^k|Y_j^{i,N,n}{|}^2\right)}^p{\Delta }^p+6^{p-1}{2}^p{M}^p\left(\sum _{j=0}^k{\mathbb{W}}_2^2({\mu }_k^{Y,N,n},{\delta }_0)\right){\Delta }^p+6^{p-1}{\left(\sum _{j=0}^k|g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right)\Delta B_j^i{|}^2\right)}^p\hfill \\ \hfill & +6^{p-1}{4}^p|\sum _{j=0}^k⟨Y_j^{i,N,n},g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right)\Delta B_j^i⟩{|}^p+6^{p-1}{2}^p|\sum _{j=0}^k⟨Z_j^{i,N,n},g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right)\Delta B_j^i⟩{|}^p+6^{p-1}{\left(|Z_0^{i,N,n}{|}^2+2MT\right)}^p.\hfill \end{array}$$

(22)

Noting that ${\mathbb{W}}_2^2({\mu }_k^{Y,N,n},{\delta }_0)={\mathbb{W}}_2^2({\delta }_{Y_k^{i,N,n}},{\delta }_0)\le E{|Y_k^{i,N,n}|}^2$, for $0<s<n$, we have

$$\begin{array}{c}\hfill E\left[\underset{0\le k\le s}{sup}{\left(\sum _{j=0}^k|Y_j^{i,N,n}{|}^2\right)}^p\right]\le n^{p-1}\sum _{j=0}^{s}E|Y_j^{i,N,n}{|}^{2p},\end{array}$$

(23)

and by Assumption 3, we have

$$\begin{array}{cc}\hfill & E\left[\underset{0\le k\le s}{sup}{\left(\sum _{j=0}^k|g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right)\Delta B_j^i{|}^2\right)}^p\right]\le n^{p-1}E\left(\sum _{j=0}^s|g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right){|}^{2p}|\Delta B_j^i{|}^{2p}\right)\hfill \\ \hfill \le & (2p-1)!!n^{p-1}{M}^p{\Delta }^p\sum _{j=0}^{s}E{\left(|Y_j^{i,N,n}{|}^2+{\mathbb{W}}_2^2({\mu }_j^{Y,N,n},{\delta }_0)\right)}^p\le 4(2p-1)!!{(2n)}^{p-1}{M}^p{\Delta }^p\sum _{j=0}^{s}E|Y_j^{i,N,n}{|}^{2p}.\hfill \end{array}$$

(24)

Similarly, by Assumption 3 and the BDG inequality, we have

$$\begin{array}{cc}\hfill & E\left[\underset{0\le k\le s}{sup}|\sum _{j=0}^k⟨Y_j^{i,N,n},g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right)\Delta B_j^i⟩{|}^p\right]\le c_1(p)E{\left(\sum _{j=0}^s|Y_j^{i,N,n}{|}^2|g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right){|}^2\Delta \right)}^{\frac{p}{2}}\hfill \\ \hfill \le & c_1(p)n^{\frac{p}{2}-1}{M}^{\frac{p}{2}}{\Delta }^{\frac{p}{2}}E\sum _{j=0}^s|Y_j^{i,N,n}{|}^p{\left(|Y_j^{i,N,n}{|}^2+{\mathbb{W}}_2^2({\mu }_j^{Y,N,n},{\delta }_0)\right)}^{\frac{p}{2}}\le c_1(p)2^{p-1}{(2n)}^{\frac{p}{2}-1}{M}^{\frac{p}{2}}{\Delta }^{\frac{p}{2}}\sum _{j=0}^{s}E|Y_j^{i,N,n}{|}^{2p},\hfill \end{array}$$

(25)

and

$$\begin{array}{cc}\hfill & E\left[\underset{0\le k\le s}{sup}|\sum _{j=0}^k⟨Z_j^{i,N,n},g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right)\Delta B_j^i⟩{|}^p\right]\le c_1(p)E{\left(\sum _{j=0}^s|Z_j^{i,N,n}{|}^2|g\left(Y_j^{i,N,n},{\mu }_j^{Y,N,n}\right){|}^2\Delta \right)}^{\frac{p}{2}}\hfill \\ \hfill \le & c_1(p)n^{\frac{p}{2}-1}{M}^{\frac{p}{2}}{\Delta }^{\frac{p}{2}}E\left(\underset{0\le j\le s+1}{sup}|Z_j^{i,N,n}{|}^p\sum _{j=0}^s{\left(|Y_j^{i,N,n}{|}^2+{\mathbb{W}}_2^2({\mu }_j^{Y,N,n},{\delta }_0)\right)}^{\frac{p}{2}}\right)\le \frac{1}{2}E\left(\underset{0\le j\le s+1}{sup}|Z_j^{i,N,n}{|}^{2p}\right)+2c_1^2(p){(2n)}^{p-1}{M}^p{\Delta }^p\sum _{j=0}^{k}E|Y_j^{i,N,n}{|}^{2p},\hfill \end{array}$$

(26)

where $c_1(p)={\left[\frac{p^{p+1}}{2{(p-1)}^{p-1}}\right]}^{p/2}$. Substituting (23)–(26) into (22) to give

$$\begin{array}{c}\hfill E\left(\underset{0\le j\le s+1}{sup}|Z_j^{i,N,n}{|}^{2p}\right)\le C_2+C_3\sum _{j=0}^{s}E|Y_j^{i,N,n}{|}^{2p}.\end{array}$$

(27)

We derive from $Z_k^{i,N,n}=Y_k^{i,N,n}-\theta f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta$ and Lemma 3 that

$$\begin{array}{cc}\hfill |Z_k^{i,N,n}{|}^2& =|Y_k^{i,N,n}{|}^2-2⟨Y_k^{i,N,n},\theta f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta ⟩+|\theta f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {|}^2\hfill \\ \hfill & \ge |Y_k^{i,N,n}{|}^2-2M\theta \Delta \left(1+|Y_k^{i,N,n}{|}^2+{\mathbb{W}}_2^2({\mu }_k^{Y,N,n},{\delta }_0)\right)=(1-2M\theta \Delta )|Y_k^{i,N,n}{|}^2-2M\theta \Delta -2M\theta \Delta {\mathbb{W}}_2^2({\mu }_k^{Y,N,n},{\delta }_0).\hfill \end{array}$$

(28)

Thus,

$$\begin{array}{c}\hfill |Y_k^{i,N,n}{|}^2\le \frac{1}{1-2M\theta \Delta }\left(|Z_k^{i,N,n}{|}^2+2M\theta \Delta +2M\theta \Delta {\mathbb{W}}_2^2({\mu }_k^{Y,N,n},{\delta }_0)\right),\end{array}$$

which together with (27) yields

$$\begin{array}{c}\hfill E\left(\underset{0\le k\le n}{sup}{|Y_k^{i,N,n}|}^{2p}\right)\le C_4+C_5\sum _{k=0}^{n-1}E\left(\underset{0\le j\le k}{sup}{|Y_j^{i,N,n}|}^{2p}\right).\end{array}$$

Similarly, we can obtain

$$\begin{array}{c}\hfill E\left(\underset{0\le k\le n}{sup}{|{\tilde{Y}}_k^{i,N,n}|}^{2p}\right)\le C_6+C_7\sum _{k=0}^{n-1}E\left(\underset{0\le j\le k}{sup}{|{\tilde{Y}}_j^{i,N,n}|}^{2p}\right).\end{array}$$

By the discrete Gronwall inequality, the proof can be finished. □

Lemma 5.

Let Assumption 3 hold. Then for any $p\ge 2$, there exist two positive constants $C_8$ and $C_9$ such that

$$\begin{array}{c}\hfill E\left(\underset{0\le t\le T}{sup}{|Y^{i,N}(t)|}^p\right)\le C_8,\end{array}$$

(29)

and

$$\begin{array}{c}\hfill E\left(\underset{0\le k\le n-1}{sup}\underset{t_k\le t<t_{k+1}}{sup}{|Y^{i,N}(t)-Y^{i,N}(t_k)|}^p\right)\le C_9{\Delta }^{\frac{p}{2}},\end{array}$$

(30)

Proof. 

Let $V^{i,N}(t)=Y^{i,N}(t)-\theta f_{\Delta }\left(Y^{i,N}(t),{\mathcal{L}}_{Y^{i,N}(t)}\right)\Delta$, for any $p\ge 2$ and $t\in [0,T]$, it follows from (20), the elementary inequality, the Hölder inequality, the BDG inequality, and Lemma 4 that

$$\begin{array}{cc}\hfill E\left(\underset{0\le r\le t}{sup}{|V^{i,N}(r)|}^p\right)\le & 3^{p-1}E{|V^{i,N}(0)|}^p+3^{p-1}E(\underset{0\le r\le t}{sup}{\int }_0^r{\left(1-\theta )f_{\Delta }\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right)ds\right)}^p\hfill \\ \hfill & +3^{p-1}E{\left(\underset{0\le r\le t}{sup}{\int }_0^{r}g\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right)d{B}_s^i\right)}^p\hfill \\ \hfill \le & 3^{p-1}E{|V^{i,N}(0)|}^p+3^{p-1}{t}^{p-1}{(1-\theta )}^{p}E\left({\int }_0^t|f_{\Delta }\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right){|}^{p}ds\right)\hfill \\ \hfill & +3^{p-1}{c}_1(p)t^{\frac{p}{2}-1}E{\left({\int }_0^t|g\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right){|}^{2}ds\right)}^{\frac{p}{2}}\hfill \\ \hfill \le & C_{10}+C_{11}E\left({\int }_0^t\left(1+|{\widehat{Y}}^{i,N}{(s)|}^p+|{\widehat{Y}}^{i,N}{(s)|}^{lp}+E{|{\widehat{Y}}^{i,N}(s)|}^p\right)ds\right)\le C_{12},\hfill \end{array}$$

(31)

where $C_{10}$, $C_{11}$, $C_{12}$ are positive constants. Similar to (28), we have

$$\begin{array}{c}\hfill |Y^{i,N}(t){|}^2\le \frac{1}{1-2M\theta \Delta }\left(|V^{i,N}(t){|}^2+2M\theta \Delta +2M\theta \Delta {\mathbb{W}}_2^2({\mathcal{L}}_{Y^{i,N}(t)},{\delta }_0)\right),\end{array}$$

which together with (31) yields

$$\begin{array}{c}\hfill E\left(\underset{0\le t\le T}{sup}|Y^{i,N}(t){|}^2\right)\le C_{13}+C_{14}E\left(\underset{0\le t\le T}{sup}{|V^{i,N}(t)|}^p\right):=C_6,\end{array}$$

where $C_{11}$ and $C_{12}$ are positive constants.

Now we proceed to prove (30). By (20), the Hölder inequality, and the BDG inequality, we have

$$\begin{array}{cc}\hfill E\left(\underset{t_k\le t<t_{k+1}}{sup}|V^{i,N}(t)-V^{i,N}(t_k){|}^p\right)\le & 2^{p-1}E\left(\underset{t_k\le t<t_{k+1}}{sup}|{\int }_{t_k}^t(1-\theta )f_{\Delta }\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right)ds{|}^p\right)\hfill \\ \hfill & +2^{p-1}E\left(\underset{t_k\le t<t_{k+1}}{sup}|{\int }_{t_k}^{t}g\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right)d{B}_s^i{|}^p\right)\hfill \\ \hfill \le & 2^{p-1}{\Delta }^{p-1}E\left({\int }_{t_k}^{t_{k+1}}|(1-\theta )f_{\Delta }\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right){|}^{p}ds\right)\hfill \\ \hfill & +2^{p-1}{c}_1(p){\Delta }^{\frac{p}{2}-1}E\left({\int }_{t_k}^{t_{k+1}}|g\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right){|}^{p}ds\right)\hfill \\ \hfill \le & C_{15}{\Delta }^p+C_{16}{\Delta }^{\frac{p}{2}}\le C_{17}{\Delta }^{\frac{p}{2}},\hfill \end{array}$$

(32)

where $C_{15}$, $C_{16}$, $C_{17}$ are positive constants. By Lemma 4 and (32), we obtain

$$\begin{array}{cc}\hfill E\left(\underset{t_k\le t<t_{k+1}}{sup}|V^{i,N}(t)-Y^{i,N}(t_k){|}^p\right)\le & 2^{p-1}E\left(\underset{t_k\le t<t_{k+1}}{sup}|V^{i,N}(t)-V^{i,N}(t_k){|}^p\right)+2^{p-1}E|V^{i,N}(t_k)-Y^{i,N}(t_k){|}^p\hfill \\ \hfill \le & 2^{p-1}E\left(\underset{t_k\le t<t_{k+1}}{sup}|V^{i,N}(t)-V^{i,N}(t_k){|}^p\right)+2^{p-1}{\theta }^p{\Delta }^{p}E|f_{\Delta }\left(Y^{i,N}(t_k),{\mathcal{L}}_{Y^{i,N}(t_k)}\right){|}^p\hfill \\ \hfill \le & 2^{p-1}{C}_{17}{\Delta }^{\frac{p}{2}}+2^{p-1}{\theta }^p{\Delta }^{p}E|f_{\Delta }\left(Y^{i,N}(t_k),{\mathcal{L}}_{Y^{i,N}(t_k)}\right){|}^p\le C_{18}{\Delta }^{\frac{p}{2}},\hfill \end{array}$$

where $C_{18}$ ia a positive constant. Thus,

$$\begin{array}{cc}\hfill E\left(\underset{t_k\le t<t_{k+1}}{sup}|Y^{i,N}(t)-Y^{i,N}(t_k){|}^p\right)\le & E\left(\underset{t_k\le t<t_{k+1}}{sup}|Y^{i,N}(t)-V^{i,N}(t){|}^p\right)+E\left(\underset{t_k\le t<t_{k+1}}{sup}|V^{i,N}(t)-Y^{i,N}(t_k){|}^p\right)\hfill \\ \hfill \le & C_{19}{\Delta }^{\frac{p}{2}}.\hfill \end{array}$$

The desired assertion holds. □

Now, we turn to check the error of the solutions of solving (3) by the truncated stochastic theta method and the stochastic theta method.

Define

$${\widehat{\tau }}_{\Delta }^i=inf\{r\in [0,T]:|Y^{i,N}(r)|\ge \kappa (\Delta )\},{\tilde{\tau }}_{\Delta }^i=inf\{r\in [0,T]:|{\tilde{Y}}^{i,N}(r)|\ge \kappa (\Delta )\},{\tau }_{\Delta }^i={\widehat{\tau }}_{\Delta }^i\wedge {\tilde{\tau }}_{\Delta }^i.$$

Lemma 6.

Let Assumptions 1–3 hold. Then for any $T>0$ and $\theta \in [\frac{1}{2},1]$, it holds that

$$\mathbb{P}({\widehat{\tau }}_{\Delta }^i\le T)\le \frac{C_{20}}{{(\kappa (\Delta ))}^p},\mathbb{P}({\tilde{\tau }}_{\Delta }^i\le T)\le \frac{C_{21}}{{(\kappa (\Delta ))}^p},$$

where $C_{20}$ and $C_{21}$ are positive constants.

Proof. 

The proof can be finished by the Chebyshev inequality, so we omit it here. □

Lemma 7.

Under Assumptions 1–3, it holds that for $\theta \in [\frac{1}{2},1]$

$$\begin{array}{c}\hfill E\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(r\wedge {\tau }_{\Delta }^i)|}^2\right)\le C_{22}{e}^{{\overline{L}}_{\kappa (\Delta )}}{\Delta }^{\frac{1}{2}}.\end{array}$$

Proof. 

Denote ${\tilde{e}}^i(t)=Y^{i,N}(t)-{\tilde{Y}}^{i,N}(t)$. Applying the Itô formula to $|{\tilde{e}}^i(t\wedge {\tau }_{\Delta }^i){|}^2$ gives

$$\begin{array}{cc}\hfill |{\tilde{e}}^i(t\wedge {\tau }_{\Delta }^i){|}^2& \le 2{\int }_0^{t\wedge {\tau }_{\Delta }^i}\{⟨Y^{i,N}(s)-{\tilde{Y}}^{i,N}(s),(1-\theta )\left(f_{\Delta }\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right)-f\left({\widehat{\tilde{Y}}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s)}\right)\right)⟩\hfill \\ \hfill & +⟨Y^{i,N}(s)-{\tilde{Y}}^{i,N}(s),\theta \left(f_{\Delta }\left(Y^{i,N}(s),{\mathcal{L}}_{Y^{i,N}(s)}\right)-f\left({\tilde{Y}}^{i,N}(s),{\mathcal{L}}_{{\tilde{Y}}^{i,N}(s)}\right)\right)⟩\}ds\hfill \\ \hfill & +2{\int }_0^{t\wedge {\tau }_{\Delta }^i}⟨Y^{i,N}(s)-{\tilde{Y}}^{i,N}(s),g\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right)-g\left({\widehat{\tilde{Y}}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s)}\right)⟩d{B}_s^i\hfill \\ \hfill & +{\int }_0^{t\wedge {\tau }_{\Delta }^i}|g\left({\widehat{Y}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s)}\right)-g\left({\widehat{\tilde{Y}}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s)}\right){|}^{2}ds\hfill \\ \hfill & ={\Xi }_1^i(t)+{\Xi }_2^i(t)+{\Xi }_3^i(t).\hfill \end{array}$$

(33)

Note that $f_{\Delta }\left(Y^{i,N}(s)\right)=f\left(Y^{i,N}(s)\right)$ for $0\le s\le r\wedge {\tau }_{\Delta }^i$. By the Hölder inequality, Lemmas 3 and 5 we have

$$\begin{array}{cc}\hfill E\left(\underset{0\le r\le t}{sup}{\Xi }_1^i(r)\right)& \le 2E({\int }_0^t\{⟨Y^{i,N}(s\wedge {\tau }_{\Delta }^i)-{\widehat{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i)+{\widehat{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i)-{\widehat{\tilde{Y}}}^{i,N}(s\wedge {\tau }_{\Delta }^i)\hfill \\ \hfill & +{\widehat{\tilde{Y}}}^{i,N}(s\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i),(1-\theta )\left(f\left({\widehat{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s\wedge {\tau }_{\Delta }^i)}\right)-f\left({\widehat{\tilde{Y}}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s\wedge {\tau }_{\Delta }^i)}\right)\right)⟩\hfill \\ \hfill & +⟨Y^{i,N}(s\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i),\theta \left(f\left(Y^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{Y^{i,N}(s\wedge {\tau }_{\Delta }^i)}\right)-f\left({\tilde{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\tilde{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i)}\right)\right)⟩\}ds\hfill \\ \hfill & \le 2{\int }_0^t{\left(E|Y^{i,N}(s\wedge {\tau }_{\Delta }^i)-{\widehat{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i){|}^2\right)}^{\frac{1}{2}}{\left(E|f\left({\widehat{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s\wedge {\tau }_{\Delta }^i)}\right)-f\left({\widehat{\tilde{Y}}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s\wedge {\tau }_{\Delta }^i)}\right){|}^2\right)}^{\frac{1}{2}}ds\hfill \\ \hfill & +2{\int }_0^t{\left(E|{\widehat{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i){|}^2\right)}^{\frac{1}{2}}{\left(E|f\left({\widehat{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s\wedge {\tau }_{\Delta }^i)}\right)-f\left({\widehat{\tilde{Y}}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s\wedge {\tau }_{\Delta }^i)}\right){|}^2\right)}^{\frac{1}{2}}ds\hfill \\ \hfill & +C_{23}{\overline{L}}_{\kappa (\Delta )}{\int }_0^{t}E\left(\underset{0\le u\le s}{sup}|{\widehat{Y}}^{i,N}(u\wedge {\tau }_{\Delta }^i)-{\widehat{\tilde{Y}}}^{i,N}(u\wedge {\tau }_{\Delta }^i){|}^2\right)ds+C_{24}{\overline{L}}_{\kappa (\Delta )}{\int }_0^{t}E\left(\underset{0\le u\le s}{sup}|Y^{i,N}(u\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(u\wedge {\tau }_{\Delta }^i){|}^2\right)ds\hfill \\ \hfill & \le C_{25}{\Delta }^{\frac{1}{2}}+C_{26}{\overline{L}}_{\kappa (\Delta )}{\int }_0^{t}E\left(\underset{0\le u\le s}{sup}|Y^{i,N}(u\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(u\wedge {\tau }_{\Delta }^i){|}^2\right)ds.\hfill \end{array}$$

(34)

By the BDG inequality, the Cauchy-Schwarz inequality and Assumption 2, we have

$$\begin{array}{cc}\hfill E\left(\underset{0\le r\le t}{sup}{\Xi }_2^i(r)\right)& \le 8E{\left({\int }_0^t|Y^{i,N}(s\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i){|}^2|g\left({\widehat{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s\wedge {\tau }_{\Delta }^i)}\right)-g\left({\widehat{\tilde{Y}}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s\wedge {\tau }_{\Delta }^i)}\right){|}^{2}ds\right)}^{\frac{1}{2}}\hfill \\ \hfill & \le 8E{\left(\underset{0\le s\le t}{sup}|Y^{i,N}(s\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i){|}^2{\int }_0^t|g\left({\widehat{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{\widehat{Y}}}^N(s\wedge {\tau }_{\Delta }^i)}\right)-g\left({\widehat{\tilde{Y}}}^{i,N}(s),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s)}\right){|}^{2}ds\right)}^{\frac{1}{2}}\hfill \\ \hfill & \le \frac{1}{2}E\left(\underset{0\le s\le t}{sup}|Y^{i,N}(s\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i){|}^2\right)+128({\overline{L}}_{\kappa (\Delta )}+L^2){\int }_0^{t}E\left(\underset{0\le u\le s}{sup}|Y^{i,N}(u\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(u\wedge {\tau }_{\Delta }^i){|}^2\right)ds.\hfill \end{array}$$

(35)

Similarly,

$$\begin{array}{cc}\hfill E\left(\underset{0\le r\le t}{sup}{\Xi }_3^i(r)\right)& \le E\left({\int }_0^t|g\left({\widehat{Y}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{Y_1}}^N(s\wedge {\tau }_{\Delta }^i)}\right)-g\left({\widehat{\tilde{Y}}}^{i,N}(s\wedge {\tau }_{\Delta }^i),{\mathcal{L}}_{{\overline{\widehat{\tilde{Y}}}}^N(s\wedge {\tau }_{\Delta }^i)}\right){|}^{2}ds\right)\hfill \\ \hfill & \le 2({\overline{L}}_{\kappa (\Delta )}+L^2){\int }_0^{t}E\left(\underset{0\le u\le s}{sup}|Y^{i,N}(u\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(u\wedge {\tau }_{\Delta }^i){|}^2\right)ds.\hfill \end{array}$$

(36)

Combining (33)–(36) yields

$$\begin{array}{c}\hfill E\left(\underset{0\le r\le t}{sup}|Y^{i,N}(r\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(r\wedge {\tau }_{\Delta }^i){|}^2\right)\le C_{27}({\overline{L}}_{\kappa (\Delta )}+L^2){\int }_0^{t}E\left(\underset{0\le u\le s}{sup}|Y^{i,N}(u\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(u\wedge {\tau }_{\Delta }^i){|}^2\right)ds+C_{28}{\Delta }^{\frac{1}{2}}.\end{array}$$

(37)

The Gronwall inequality yields $E\left({sup}_{0\le r\le T}|Y^{i,N}(r\wedge {\tau }_{\Delta }^i)-{\tilde{Y}}^{i,N}(r\wedge {\tau }_{\Delta }^i){|}^2\right)\le$ $C_{29}{e}^{{\overline{L}}_{\kappa (\Delta )}+L^2}{\Delta }^{\frac{1}{2}}.$ This completes the proof. □

4.2. Strong Convergence

Define

$${\zeta }_{\Delta }^i=inf\{r\in [0,T]:|Z^{i,N}(r)|\ge \kappa (\Delta )\},{\widehat{\tau }}_{\Delta }^i=inf\{r\in [0,T]:|Y^{i,N}(r)|\ge \kappa (\Delta )\},v_{\Delta }^i={\zeta }_{\Delta }^i\wedge {\widehat{\tau }}_{\Delta }^i.$$

Lemma 8.

Under Assumptions 1–3, it holds that for any $T>0$ and $\theta \in [\frac{1}{2},1]$,

$$\mathbb{P}({\zeta }_{\Delta }^i\le T)\le \frac{C_{30}}{{(\kappa (\Delta ))}^p},\mathbb{P}({\widehat{\tau }}_{\Delta }^i\le T)\le \frac{C_{31}}{{(\kappa (\Delta ))}^p},$$

where $C_{30}$ and $C_{31}$ are positive constants.

Proof. 

The proof is similar to that of Lemma 6, so we omit the details here. □

Lemma 9.

Under Assumptions 1–3, it holds that for $\theta \in [\frac{1}{2},1]$

$$\begin{array}{c}\hfill E\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r\wedge v_{\Delta }^i)-Z^{i,N}(r\wedge v_{\Delta }^i)|}^2\right)\le C_{32}{e}^{{\overline{L}}_{\kappa (\Delta )}}\Delta ,\end{array}$$

where $C_{32}$ is a positive constant.

Proof. 

Denote $e^i(r)=Y^{i,N}(r)-Z^{i,N}(r)$. Applying the Itô formula to $|e^i(r\wedge v_{\Delta }^i){|}^2$, the rest of this proof is similar to that of Lemma 7, so we omit it here. □

Lemma 10.

Let Assumptions 1–3 hold. For any $ϵ>0$ and $\theta \in [\frac{1}{2},1]$, there exists a ${\Delta }^{*}$ such that for any $\Delta \in (0,{\Delta }^{*})$,

$$\begin{array}{c}\hfill E\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r)-Z^{i,N}(r)|}^2\right)<ϵ,.\end{array}$$

(38)

Proof. 

Recall the Young inequality,

$$Z^{q}Y\le \frac{q\eta Z^p}{p}+\frac{p-q}{p{\eta }^{\frac{q}{p-q}}}{Y}^{\frac{p}{p-q}},q<p,\eta >0,$$

for any $p>2$ and $\eta >0$, it has

$$\begin{array}{cc}\hfill E\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r)-Z^{i,N}(r)|}^2\right)& \le E\left({\mathbf{1}}_{\{{\zeta }_{\Delta }^i>T,{\widehat{\tau }}_{\Delta }^i>T\}}\underset{0\le r\le T}{sup}{|Y^{i,N}(r)-Z^{i,N}(r)|}^2\right)\hfill \\ \hfill & +\frac{2\eta }{p}E\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r)-Z^{i,N}(r)|}^p\right)+\frac{p-2}{p{\eta }^{\frac{2}{p-2}}}\mathbb{P}({\zeta }_{\Delta }^i\le T\mathrm{or}{\widehat{\tau }}_{\Delta }^i\le T),\hfill \end{array}$$

(39)

which, together with Lemmas 1, 5 and 9, yields

$$\begin{array}{cc}\hfill E\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r)-Z^{i,N}(r)|}^2\right)& \le E\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r\wedge v_{\Delta }^i)-Z^{i,N}(r\wedge v_{\Delta }^i)|}^2\right)+\frac{2\eta C_{33}}{p}+\frac{2(p-2)C_{34}}{p{\eta }^{\frac{2}{p-2}}{(\kappa (\Delta ))}^p}.\hfill \end{array}$$

For each $ϵ>0$, we can choose a sufficiently small $\eta$ to satisfy $\frac{2\eta C_{33}}{p}<\frac{ϵ}{3},$ and a sufficiently large $\kappa (\Delta )$ with $\Delta$ sufficiently small such that

$$\frac{2(p-2)C_{34}}{p{\eta }^{\frac{2}{p-2}}{(\kappa (\Delta ))}^p}<\frac{ϵ}{3},\mathrm{and}{C}_{32}{e}^{{\overline{L}}_{\kappa (\Delta )}}\Delta <\frac{ϵ}{3}.$$

Thus, the proof is finished. □

Theorem 2.

Let Assumptions 1–3 hold. For any $ϵ>0$ and $\theta \in [\frac{1}{2},1]$, there exists a ${\Delta }^{*}$ such that

$$\begin{array}{c}\hfill \underset{N\to \infty }{lim}\underset{0\le i\le N}{sup}E\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r)-Z^i(r)|}^2\right)=0.\end{array}$$

(40)

Proof. 

The proof can be finished by the triangle inequality, we omit the details here. □

Remark 1.

Compared to the standard SDEs, it is difficult to establish the rate of strong convergence of the numerical approximation for MVSDEs under local Lipschtiz drift coefficient due to that the stopping time technique cannot be directly applied to Mckean-Vlasov SDEs and thus the Gronwall inequality in the form of stopped process cannot be used. In Liu-Shi-Wu [19], they established the strong convergence of the numerical solution of Euler-Maruyama method for the MVSDEs whose drift and diffusion coefficients are dependent on the distribution and satisfies the local Lipschitz condition with Lipschitz constant $L_R=O(\sqrt{logR})$. They also showed that when the Lipschitz constant $L_R$ is independent of R, the order of convergence is $1/2$ under some polynomial growth conditions. Following their assertions in [19], we can obtain the convergence order of the truncated stochastic theta method, for example, we can choose sufficiently small Δ, η, and $\overline{L}$ such that $\frac{2\eta C_{33}}{p}<C_{35}\Delta$, $\frac{2(p-2)C_{34}}{p{\eta }^{\frac{2}{p-2}}\kappa {(\Delta )}^p}<C_{36}\Delta$, and $C_{32}{e}^{\overline{L}}\Delta <C_{37}\Delta$, thus,

$$\begin{array}{c}\hfill E\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r)-Z^i(r)|}^2\right)=E\left(\underset{0\le r\le T}{sup}{|Y^{i,N}(r)-Z^{i,N}(r)+Z^{i,N}(r)-Z^i(r)|}^2\right)\le C_{38}(N^{-1/2}+{\Delta }^{1/2})+C_{39}\Delta .\end{array}$$

This convergence order can be observed in our numerical simulation.

5. Stability of the Truncated Stochastic Theta Method

Having established the strong convergence of truncated stochastic theta method, we will proceed to the asymptotical mean square stability of both the underlying (3) and the truncated stochastic theta method. We suppose that $f(0,0)=0$, $g(0,0)=0$ and give the following two definitions of stability.

Definition 1.

The system of interacting particles (3) is said to be asymptotically stable in mean square, if

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}E{|Z^{i,N}(t)|}^2=0.\end{array}$$

(41)

Definition 2.

For a given step size $\Delta >0$, the truncated stochastic theta method is said to be asymptotically stable in mean square if for any initial value $Y_0^{i,N,n}=\xi \in {\mathbb{R}}^d$

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}E{|Y_k^{i,N,n}|}^2=0.\end{array}$$

(42)

We first recall a result on the stability of the exact solution for interacting particle system (3) and for which we need an extra assumption.

Assumption 4.

For any $x\in {\mathbb{R}}^d$ and $\mu \in {\mathcal{P}}^2({\mathbb{R}}^d)$, there exist positive constants $a_1$, $a_2$ such that

$$\begin{array}{c}\hfill 2⟨x,f(x,\mu )⟩+{|g(x,\mu )|}^2\le -a_1{|x|}^2+a_2{\mathbb{W}}_2^2(\mu ,{\delta }_0).\end{array}$$

This Lyapunov-type condition ensures a form of mean-square coercivity, which is crucial in proving stability of the system.

Theorem 3.

Let Assumptions 1–4 hold. If $a_1>a_2$, for any $i\in N$ and some $a\in (0,a_1-a_2)$, the solution $Z^{i,N}(t)$ to interacting particle system (3) satisfies

$$\underset{t\to \infty }{lim}\frac{1}{t}log(E|Z^{i,N}(t){|}^2)\le -a.$$

Proof. 

For any $i\in N$ and some $a\in (0,a_1-a_2)$, the Itô formula gives

$$\begin{array}{cc}\hfill e^{at}{|Z^{i,N}(t)|}^2=& |{\xi }_i{|}^2+{\int }_0^{t}a{e}^{as}{|Z^{i,N}(s)|}^{2}ds+2{\int }_0^t{e}^{as}⟨Z^{i,N}(s),f(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)})⟩ds\hfill \\ \hfill & +{\int }_0^t{e}^{as}|Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}{)|}^{2}ds+2{\int }_0^t{e}^{as}⟨Z^{i,N}(s),g(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)})⟩d{B}_s^i.\hfill \end{array}$$

(43)

Taking expectation on both sides of (43) and considering Assumption 4 to give

$$\begin{array}{cc}\hfill e^{at}E{|Z^{i,N}(t)|}^2=& E|{\xi }_i{|}^2+{\int }_0^{t}a{e}^{as}E{|Z^{i,N}(s)|}^{2}ds+2{\int }_0^t{e}^{as}E⟨Z^{i,N}(s),f(Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)})⟩ds\hfill \\ \hfill & +{\int }_0^t{e}^{as}E|Z^{i,N}(s),\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)}{)|}^{2}ds\hfill \\ \hfill \le & E|{\xi }_i{|}^2+{\int }_0^t{e}^{as}\left((a-a_1)E{|Z^{i,N}(s)|}^2+a_2{\mathbb{W}}_2^2(\frac{1}{N}\sum _{i=1}^N{\delta }_{Z^{i,N}(s)},{\delta }_0)\right)ds\hfill \\ \hfill \le & E|{\xi }_i{|}^2+{\int }_0^t{e}^{as}(a-a_1+a_2)E{|Z^{i,N}(s)|}^{2}ds,\hfill \end{array}$$

(44)

where we use a result of Wasserstein metric ${\mathbb{W}}_2^2(\frac{1}{N}{\sum }_{i=1}^N{\delta }_{Z^{i,N}(s)},{\delta }_0)\le E\left[\frac{1}{N}{\sum }_{j=1}^N{|Z^{j,N}(s)|}^2\right]$ and $E\left[\frac{1}{N}{\sum }_{j=1}^N{|Z^{j,N}(s)|}^2\right]=E{|Z^{i,N}(s)|}^2$. Thus, for $a\in (0,a_1-a_2)$, (44) gives

$$\begin{array}{c}\hfill E|Z^{i,N}{(t)|}^2\le e^{-at}E{|{\xi }_i|}^2,\end{array}$$

(45)

which means

$$\underset{t\to \infty }{lim}\frac{1}{t}log(E|Z^{i,N}(t){|}^2)\le -a.$$

□

Proposition 1.

(45) implies (41).

Next, we give a theorem on the asymptotical mean square stability of the truncated stochastic theta method. This theorem shows that under certain nonlinear conditions, for all step sizes $\Delta >0$, the truncated stochastic theta method with $\theta \in [\frac{1}{2},1]$ preserves the asymptotical mean square stability of the interacting particle system (3).

Theorem 4.

Let Assumptions 2–4 hold. If $\theta \in [\frac{1}{2},1]$, then the truncated stochastic theta method applied to interacting particle system (3) is asymptotically mean square stable for all $\Delta >0$.

Proof. 

Taking expectation on both-sides of (19), we have

$$\begin{array}{cc}\hfill E|Y_{k+1}^{i,N,n}-\theta f_{\Delta }\left(Y_{k+1}^{i,N,n},{\mu }_{k+1}^{Y,N,n}\right)\Delta {|}^2=& E|Y_k^{i,N,n}-\theta f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {|}^2+2E⟨Y_k^{i,N,n},f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta ⟩\hfill \\ \hfill & +(1-2\theta )E|f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right){|}^2{\Delta }^2+E|g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i{|}^2\hfill \\ \hfill & +2E⟨Y_k^{i,N,n}+(1-\theta )f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta ,g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta B_k^i⟩.\hfill \end{array}$$

(46)

Notice that, by definitions, $f\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)$ are measurable w.r.t. ${\mathcal{F}}_k=g\{B_t^i,0\le t\le k\Delta \}$, and ${\mathcal{F}}_k$ is independent of $B_{(k+1)\Delta }^i-B_{k\Delta }^i$. Thus by conditional on ${\mathcal{F}}_k$ and using the facts that

$$E\left[{(B_{(k+1)\Delta }^i-B_{k\Delta }^i)}^2\right]=\Delta \mathrm{and}E\left[B_{(k+1)\Delta }^i-B_{k\Delta }^i\right]=0,$$

(46) yields

$$\begin{array}{cc}\hfill E|Y_{k+1}^{i,N,n}-\theta f_{\Delta }\left(Y_{k+1}^{i,N,n},{\mu }_{k+1}^{Y,N,n}\right)\Delta {|}^2=& E|Y_k^{i,N,n}-\theta f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {|}^2+2\Delta E⟨Y_k^{i,N,n},f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)⟩\hfill \\ \hfill & +(1-2\theta ){\Delta }^{2}E|f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right){|}^2+\Delta E|g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right){|}^2.\hfill \end{array}$$

Set $I_k=E|Y_k^{i,N,n}-\theta f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)\Delta {|}^2$ and using Assumption 4, we have

$$\begin{array}{cc}\hfill I_{k+1}=& I_k+2\Delta E⟨Y_k^{i,N,n},f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right)⟩+\Delta E|g\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right){|}^2+(1-2\theta ){\Delta }^{2}E|f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right){|}^2\hfill \\ \hfill \le & I_k-a_{1}E{|Y_k^{i,N,n}|}^2+a_2{\mathbb{W}}_2^2({\mu }_k^{Y,N,n},{\delta }_0)+(1-2\theta ){\Delta }^{2}E|f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right){|}^2\hfill \\ \hfill \le & I_k-(a_1-a_2)E{|Y_k^{i,N,n}|}^2+(1-2\theta ){\Delta }^{2}E|f_{\Delta }\left(Y_k^{i,N,n},{\mu }_k^{Y,N,n}\right){|}^2,\hfill \end{array}$$

where we use a result of Wasserstein metric ${\mathbb{W}}_2^2({\mu }_k^{Y,N,n},{\delta }_0))\le E|Y_k^{i,N,n}{|}^2$.

By iteration, we have

$$\begin{array}{c}\hfill I_{k+1}\le I_0-(a_1-a_2)\sum _{l=0}^{k}E{|Y_l^{i,N,n}|}^2+(1-2\theta ){\Delta }^2\sum _{l=0}^{k}E|f_{\Delta }\left(Y_l^{i,N,n},{\mu }_l^{Y,N,n}\right){|}^2.\end{array}$$

(47)

In the case of $\theta \in [\frac{1}{2},1]$, $(1-2\theta )\le 0$ and $(1-2\theta ){\Delta }^2{\sum }_{l=0}^{k}E|f_{\Delta }\left(Y_l^{i,N,n},{\mu }_l^{Y,N,n}\right){|}^2$ is bounded. Since $(a_1-a_2)>0$, we can obtain from (47) that

$$\underset{k\to \infty }{lim}E{|Y_k^{i,N,n}|}^2=0,$$

i.e., the truncated stochastic theta method is asymptotically mean square stable for all $\Delta >0$. □

6. Numerical Example

Example 1.

Let $B(t)$ be a 1-dimensional Brownian motion and consider

$$\begin{array}{c}\hfill \left\{\begin{array}{c}dZ(t)=\left(-Z(t)-Z^3(t)+\frac{1}{4}EZ(t)\right)dt+\frac{1}{4}\left(Z(t)+EZ(t)\right)dB(t),t\in [0,1],\hfill \\ Z(0)=1,\hfill \end{array}\right.\end{array}$$

(48)

where $f(x,u)=-x-x^3+\frac{1}{4}{\int }_{\mathbb{R}}z\mu (dz)$, $g(x,u)=\frac{1}{4}(x+{\int }_{\mathbb{R}}z\mu (dz))$. For any integer $R\ge \sqrt{2}$ and $x,y,\mu \in \mathbf{R}$ with $|x|\vee |y|\le R$ and $a=42$,

$$\begin{array}{cc}\hfill ⟨x-y,f(x,\mu )-f(y,\mu )⟩& =⟨x-y,-x+y-x^3+y^3⟩\le 42logR{|x-y|}^2,\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill {|g(x,\mu )-g(y,\mu )|}^2& =\frac{1}{16}{|x-y|}^2.\hfill \end{array}$$

(50)

For $R\ge \sqrt{2}$ with $|x|\vee |y|\le R$ and $a=42$, we have ${|g(x,\mu )-g(y,\mu )|}^2=\frac{1}{16}{|x-y|}^2\le 42logR{|x-y|}^2$. Furthermore, For $x\in \mathbb{R}$ and $\mathbb{P}(·\times \mathbb{R})=\mu$, $\mathbb{P}(\mathbb{R}\times ·)=v$,

$$\begin{array}{c}\hfill |f(x,\mu )-f(x,v)|=\frac{1}{4}|{\int }_{\mathbb{R}}z\mu (dz)-{\int }_{\mathbb{R}}{z}^{\prime }v(d{z}^{\prime })|\le \frac{1}{4}|{\int }_{\mathbb{R}}|z-z^{\prime }|\mathbb{P}(dz,d{z}^{\prime })|\le \frac{1}{4}{\mathbb{W}}_1(\mu ,v),\end{array}$$

$$\begin{array}{c}\hfill |g(x,\mu )-g(x,v)|=\frac{1}{4}|{\int }_{\mathbb{R}}z\mu (dz)-{\int }_{\mathbb{R}}{z}^{\prime }v(d{z}^{\prime })|\le \frac{1}{4}|{\int }_{\mathbb{R}}|z-z^{\prime }|\mathbb{P}(dz,d{z}^{\prime })|\le \frac{1}{4}{\mathbb{W}}_1(\mu ,v).\end{array}$$

So, Assumptions 1 and 2 hold. For any $x\in \mathbb{R}$ and $\mu \in {\mathcal{P}}^2(\mathbb{R})$, by the Lyapunov inequality and the Young inequality, we have

$$\begin{array}{c}\hfill xf(x,\mu )=x\left(-x-x^3+\frac{1}{4}{\int }_{\mathbb{R}}z\mu (dz)\right)\le \frac{1}{4}\left(1+x^2+{\mathbb{W}}_2^2(\mu ,{\delta }_0)\right),|f(x,\mu )|=|-x-x^3+\frac{1}{4}{\int }_{\mathbb{R}}z\mu (dz)|\le 2\left(1+{|x|}^3+{\mathbb{W}}_1(\mu ,{\delta }_0)\right),\end{array}$$

and

$$\begin{array}{c}\hfill |g(x,\mu )|=|\frac{1}{4}\left(x+{\int }_{\mathbb{R}}z\mu (dz)\right)|\le \frac{1}{4}\left(|x|+{\mathbb{W}}_1(\mu ,{\delta }_0)\right),\end{array}$$

which means Assumption 3 holds. Thus Equation (48) admits a unique solution ${\left\{Z(t)\right\}}_{0\le t\le T}$. Furthermore, we can obtain

$$\begin{array}{c}\hfill xf(x,\mu )+\frac{1}{2}{|g(x,\mu )|}^2=x\left(-x-x^3+\frac{1}{4}{\int }_{\mathbb{R}}z\mu (dz)\right)+\frac{1}{32}|x+{\int }_{\mathbb{R}}{z\mu (dz)|}^2\le -\frac{1}{2}{|x|}^2+\frac{1}{4}{\mathbb{W}}_2^2(\mu ,{\delta }_0)),\end{array}$$

thus, Assumption 4 holds.

We have the interacting particle system,

$$\begin{array}{cc}\hfill d{Z}^{i,N}(t)=& \left(-Z^{i,N}(t)-{(Z^{i,N}(t))}^3+\frac{1}{4N}\sum _{i=1}^N{Z}^{i,N}(t)\right)dt+\left(\frac{1}{4}{Z}^{i,N}(t)+\frac{1}{4N}\sum _{i=1}^N{Z}^{i,N}(t)\right)d{B}^i(t),t\in [0,1],\hfill \end{array}$$

(51)

subject to $Z^{i,N}(0)=1$, $i=1,2,\cdots ,N$.

Let $\kappa (\Delta )=ln{\Delta }^{-\frac{1}{2}}$ and $\Delta =2^{-10}$. The truncated stochastic theta scheme for Equation (51) reads

$$Y_{k+1}^{i,N,n}=Y_k^{i,N,n}+\theta f_{\Delta }\left(Y_{k+1}^{i,N,n},\frac{1}{N}\sum _{i=1}^N{Y}_{k+1}^{i,N,n}\right)\Delta +(1-\theta )f_{\Delta }\left(Y_k^{i,N,n},+\frac{1}{N}\sum _{i=1}^N{Y}_k^{i,N,n}\right)\Delta +g\left(Y_k^{i,N,n},\frac{1}{N}\sum _{i=1}^N{Y}_k^{i,N,n}\right)\Delta B_k^i$$

with initial data $Y_0^{i,N,n}=1$. It is difficult to obtain the analytic solutions of Equation (48) and the interacting particle system, so we use the reference solution $\left\{Y^{i,N,n}(t_n^k)\right\}$ generated by the EM method with $n=2^{10}$. We use the maximum sample average ($N=100$) of the absolute error ${max}_{1\le k\le n}\frac{1}{N}{\sum }_{i=1}^N|Y^{i,N,n}(t_n^k)-Y_k^{i,N,n}|$ between the numerical solution $\left\{Y_k^{i,N,n}\right\}$ of the truncated stochastic theta scheme and the reference solution $\left\{Y^{i,N,n}(t_n^k)\right\}$ at time $t_n^k$ to denote the error and plot the numerical results in Figure 1 and Figure 2 and which verifies the convergence and asymptotical mean square stability of the proposed scheme.

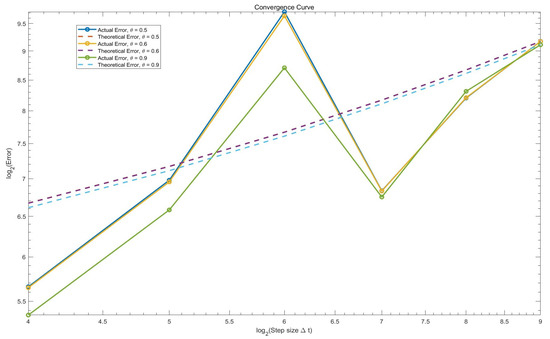
Figure 1. Convergence of the truncated stochastic theta method with different $\theta$ for (48).

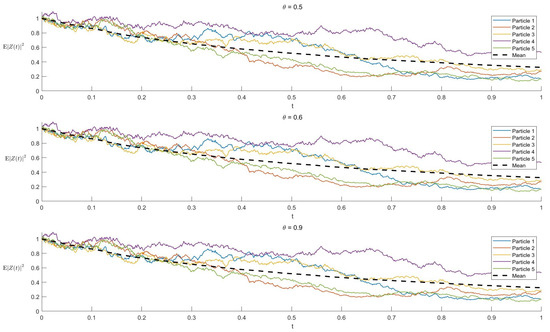
Figure 2. Asymptotical mean square stability of the truncated stochastic theta method with different $\theta$ for (48).

7. Conclusions

In this paper, we have focused the strong convergence and asymptotical mean square stability of the stochastic theta method for McKean-Vlasov stochastic differential equations (MVSDEs) under local Lipschitz condition. We have used the empirical distribution to represent the law and introduced the interacting particle system to approximate the MVSDE. We have introduced the truncated stochastic theta method and showed that the solution of the truncated stochastic theta scheme for the non-interacting particle system strongly converges to the exact solution. Moreover, we have studied the asymptotical mean square stability of MVSDE and the truncated stochastic theta scheme by adding an Lyapunov-type condition on the drift and diffusion coefficients and presented one example to check our theory results.