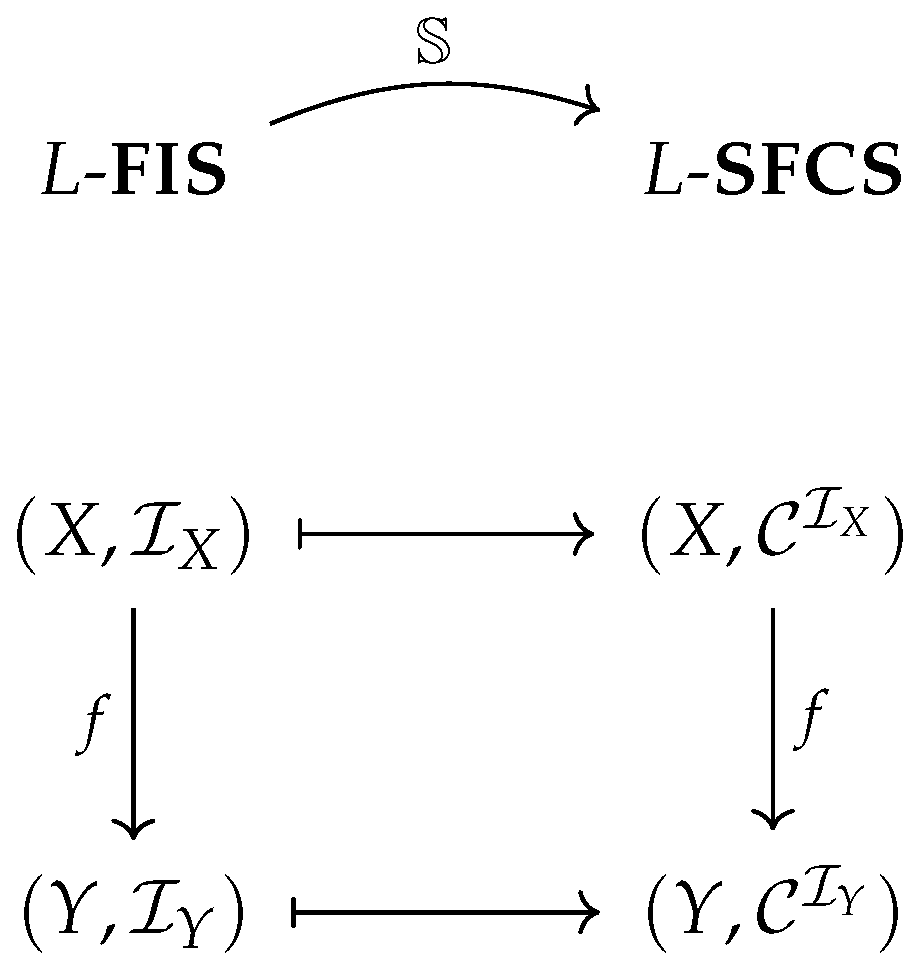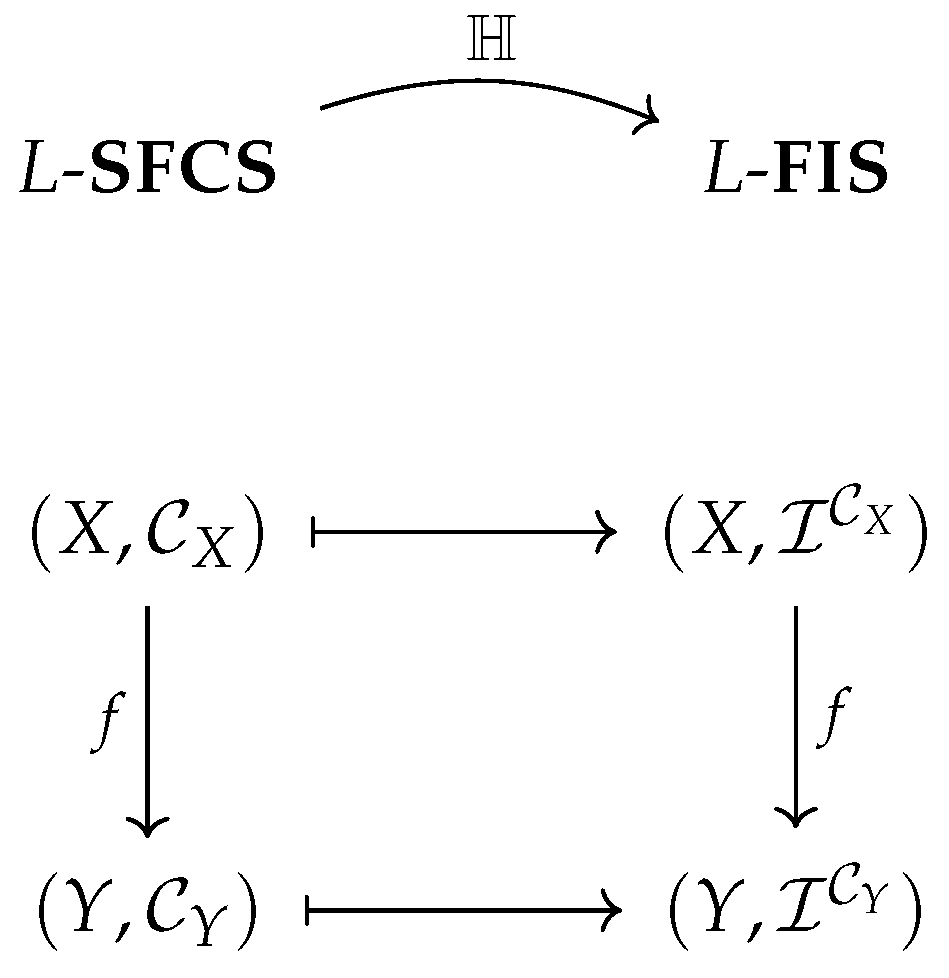Interval Operators and Preorders in Strong L-Fuzzy Convex Structures

Abstract

In this paper, the relationship between strong L-fuzzy convex structures and L-fuzzifying interval operators are investigated. It is proved that there is a Galois correspondence between the category of strong L-fuzzy convex spaces and that of L-fuzzifying interval spaces. Also, the concept of arity 2 strong L-fuzzy convex structures is presented, which can be reflectively embedded into the category of L-fuzzifying interval spaces. Finally, the ways of L-fuzzy preorders inducing strong L-fuzzy convex structures and strong L-fuzzy convex structures inducing L-fuzzy preorders are given. It is shown that a strong L-fuzzy convex structure generated by an L-fuzzy preorder is an arity 2 strong L-fuzzy convex structure.

1. Introduction

Convex structures play important roles in many research areas and have been widely used in many mathematical research areas, such as lattices [1,2], graphs [3,4], topological spaces [5,6], algebras [7,8], matroids [9], and so on. As we all know, ordered structures and topological structures are closely related [10,11]. As a topology-like structure, convex structures and ordered structures are also closely related [12]. Meanwhile, interval operators, as generalizations of intervals, provide a good method of describing convex structures. The purpose of this paper is to extend their relationship to a fuzzy setting.

Fuzzy set theory is an important mathematical tool to study uncertainty. The usefulness and versatility of this theory have amply been demonstrated by successful applications in a variety of problems [13,14,15,16,17,18,19,20,21]. With the development of fuzzy mathematics, convex structures have been interrelated to fuzzy set theory. In terms of applications, fuzzy convexity has been extensively studied due to its unique advantages in handling imprecise information and has demonstrated significant value across multiple fields. Research indicates that this theory has been successfully applied in practical scenarios such as industrial control [22], medical diagnosis [23], and decision analysis [24], fully showcasing its practicality and effectiveness in addressing complex real-world problems. While fuzzy convexity has proven valuable in practical domains, its theoretical foundations continue to be refined. Recent work has systematically investigated the relationships between lattice-valued interval operators, ordered structures, and convex structures [25,26,27,28,29,30]. These studies have primarily focused on completely distributive lattices with order-reversing involutions or commutative quantales, establishing important categorical relationships in these specialized settings. However, a significant gap remains in the more general framework of fuzzy convex structures: no study has investigated these relationships under the complete Heyting algebra setting, which occupies a crucial position between completely distributive lattices and general quantales in terms of both algebraic generality and logical expressiveness. This oversight limits the theoretical framework’s ability to model uncertainty in scenarios requiring intuitionistic logic features.

Motivated by this, we outline a more general theory of L-fuzzifying interval operators, L-fuzzy preorders and L-fuzzy convex structures using the structure of the complete Heyting algebra. To establish the relationships between these structures in this generalized environment, we employ Galois correspondence in category theory. This approach plays a significant role in establishing the relationships between different types of spatial structures, offering two fundamental advantages: (1) it can precisely characterize relationships between distinct spatial structures, and (2) the capacity for objects and morphisms in one category to bidirectionally derive or represent new information about the other.

Specifically, we focus on the relationship between L-fuzzifying interval operators and strong L-fuzzy convex structures via Galois correspondence. Additionally, we extend the classical concept of arity (a numerical feature indicating the ability of finite subsets to span the whole space via the hull operator) to the fuzzy setting. Specifically, within the lattice-valued environment of complete Heyting algebras, we establishes a precise definition for arity 2 strong L-fuzzy convex structures. Building upon this foundational definition, we investigate the relationship between arity 2 strong L-fuzzy convex structures and L-fuzzifying interval operators using Galois correspondence in category theory, aiming to establish a precise correspondence within this more general framework.

The structure of this paper is organized as follows. In Section 2, we recall some basic concepts and notations used in this paper. In Section 3, we investigate the categorical relationship between strong L-fuzzy convex spaces and L-fuzzifying interval spaces. In Section 4, we give the method of mutual induction between strong L-fuzzy convex structures and L-fuzzy preorders. In Section 5, we make a conclusion.

2. Preliminaries

Throughout this paper, L denotes a complete Heyting algebra, which means that L is a complete lattice, and for all $x,y_i(i\in I)\in L$ the following distributive law holds

$$x\wedge \underset{i\in I}{\bigvee }{y}_i=\underset{i\in I}{\bigvee }(x\wedge y_j).$$

The smallest element and the largest element in L are denoted by 0 and 1, respectively. For a complete Heyting algebra L, an implication operator $\to :L\times L⟶L$ as the right adjoint for the meet operator ∧ can be defined as

$$\forall x,y\in L,x\to y=\bigvee \{z\in L|x\wedge z\le y\}.$$

Thus, the pair $(\wedge ,\to )$ forms a Galois correspondence on L, that is,

$$\forall x,y,z\in L,x\wedge z\le y\iff x\le z\to y.$$

For a complete Heyting algebra L, the following properties of $(\wedge ,\to )$ hold: $\forall x,y,z\in L$, $x_i,y_i(i\in I)\in L,$

(1)

$x\to (x\wedge y)\ge y$, $x\wedge (x\to y)\le y$;

(2)

$1\to x=x$;

(3)

$x\le y⟺x\to y=1$;

(4)

$x\to {\bigwedge }_{i\in I}{y}_i={\bigwedge }_{i\in I}(x\to y_i)$;

(5)

${\bigvee }_{i\in I}{x}_i\to y={\bigwedge }_{i\in I}(x_i\to y)$;

(6)

$(x\wedge y)\to z=x\to (y\to z)=y\to (x\to z)$;

(7)

$y\le x\to y$;

(8)

$(x\to y)\wedge (y\to z)\le x\to z$.

For a nonempty set X, we denote the set of all L-subsets on X by $L^X$. All algebraic operations on L can be extended pointwise to $L^X$. The smallest element and the largest element in $L^X$ are denoted by $0_X$ and $1_X$, respectively. For any nonempty subset $A\subseteq X$, let ${\chi }_A$ denote the characteristic function of A. Clearly, ${\chi }_A$ can be regarded as an L-subset on X. For $a\in L$, the constant fuzzy set $a_X$ is given by $a_X\left(x\right)=a$ for all $x\in X$. The partial order and all algebraic operators on L can be extended to $L^X$ by pointwise order. For $a\in L$ and $A,B\in L^X$, write fuzzy sets $a\wedge A$, $a\to A$ and $A\to B$ by $(a\wedge A)\left(x\right)=a\wedge A\left(x\right)$, $(a\to A)\left(x\right)=a\to A\left(x\right)$ and $(A\to B)\left(x\right)=A\left(x\right)\to B\left(x\right)$ for all $x\in X$. We say a nonempty family ${\left\{A_i\right\}}_{i\in I}\subseteq L^X$ is a directed subset of $L^X$ if for each $A_{i1},A_{i2}\in {\left\{A_i\right\}}_{i\in I}$, there exists $A_{i3}\in {\left\{A_i\right\}}_{i\in I}$ such that $A_{i1},A_{i2}\le A_{i3}$.

Let $X,Y$ be nonempty sets and $f:X⟶Y$ be a mapping. Define $f^{\to }:L^X⟶L^Y$ and $f^{\leftarrow }:L^Y⟶L^X$ by $f^{\to }\left(A\right)\left(y\right)={\bigvee }_{f\left(x\right)=y}A\left(x\right)$ for $A\in L^X$ and $y\in Y$, and $f^{\leftarrow }\left(B\right)=B\left(f\left(x\right)\right)$ for $B\in L^Y$ and $x\in X$, respectively.

Lemma 1.

Let L be a complete Heyting algebra. For each directed subfamily ${\left\{A_i\right\}}_{i\in I}\subseteq L^X$, we have for each $x,y\in X$:

$$\underset{i\in I}{\bigvee }{A}_i\left(x\right)\wedge \underset{j\in I}{\bigvee }{A}_j\left(y\right)=\underset{i\in I}{\bigvee }(A_i\left(x\right)\wedge A_i\left(y\right)).$$

Proof. 

Obviously, ${\bigvee }_{i\in I}{A}_i\left(x\right)\wedge {\bigvee }_{j\in I}{A}_j\left(y\right)\ge {\bigvee }_{i\in I}(A_i\left(x\right)\wedge A_i\left(y\right)).$

Conversely,

$$\begin{array}{cc}& \underset{i\in I}{\bigvee }{A}_i\left(x\right)\wedge \underset{j\in I}{\bigvee }{A}_j\left(y\right)\hfill \\ \hfill & =\underset{i\in I}{\bigvee }\underset{j\in I}{\bigvee }(A_i\left(x\right)\wedge A_j\left(y\right))\left(\mathrm{distributive}\mathrm{law}\right)\hfill \\ \hfill & \le \underset{i\in I}{\bigvee }(A_i\left(x\right)\wedge A_i\left(y\right))(\mathrm{since}{\left\{A_i\right\}}_{i\in I}\subseteq L^X\mathrm{is}\mathrm{directed})\hfill \end{array}$$

Hence, ${\bigvee }_{i\in I}{A}_i\left(x\right)\wedge {\bigvee }_{j\in I}{A}_j\left(y\right)={\bigvee }_{i\in I}(A_i\left(x\right)\wedge A_i\left(y\right)).$ □

For each $A,B\in L^X$, the subsethood degree [31] of A in B is defined by

$$\mathcal{S}(A,B)=\underset{x\in X}{\bigwedge }(A\left(x\right)\to B\left(x\right)).$$

Now, we collect some properties of the subsethood degree in the following lemma.

Lemma 2

([31,32]). Let $A,B,C,A_j,B_j(j\in J)\in L^X$ and $a\in L$. Then,

(1)

$\mathcal{S}(A,B)=1⟺A\le B$;

(2)

$\mathcal{S}\left(A,{\bigwedge }_{j\in J}{B}_j\right)={\bigwedge }_{j\in J}\mathcal{S}(A,B_j)$;

(3)

$\mathcal{S}\left({\bigvee }_{j\in J}{A}_j,B\right)={\bigwedge }_{j\in J}\mathcal{S}(A_j,B)$;

(4)

$\mathcal{S}(A,B)\wedge \mathcal{S}(B,C)\le \mathcal{S}(A,C)$;

(5)

$\mathcal{S}(A,B)\to B\left(x\right)\ge A\left(x\right);$

(6)

$\mathcal{S}(A,a\to B)=a\to \mathcal{S}(A,B)$;

(7)

$\mathcal{S}(f^{\to }\left(A\right),B)=\mathcal{S}(A,f^{\leftarrow }\left(B\right))$.

Notions related to category theory used this paper can be found in [33].

Definition 1

([34]). A subset $\mathcal{C}$ of $2^X$ is called a convex structure on X if it satisfies the following conditions:

(C1)

$\varnothing ,X\in \mathcal{C}$;

(C2)

If ${\left\{A_i\right\}}_{i\in I}\subseteq \mathcal{C}$ is nonempty, then ${\bigcap }_{i\in I}{A}_i\in \mathcal{C}$;

(C3)

If ${\left\{A_i\right\}}_{i\in I}\subseteq \mathcal{C}$ is directed, then ${\bigcup }_{i\in I}{A}_i\in \mathcal{C}$.

If $\mathcal{C}$ is a convex structure on X, then the pair $(X,\mathcal{C})$ is called a convex space.

Definition 2

([34]). The hull operator $c{o}_{\mathcal{C}}:2^X⟶2^X$ (briefly, $co$) of a convex space $(X,\mathcal{C})$ is defined by:

$$\forall A\in 2^X,co\left(A\right)=\bigcap \{B:A\subseteq B\in \mathcal{C}\}$$

Definition 3

([34]). A convex structure $\mathcal{C}$ on X is said to be of arity n, where $n\in \mathbb{N}$ and $\mathbb{N}$ is the set of all positive natural numbers, if

$$\mathcal{C}=\{A\in 2^X:\forall F\subseteq A,|F|⩽n,co\left(F\right)\subseteq A\},$$

where $\left|F\right|$ is the cardinality of F. In particular, if $n=2$, then we say $\mathcal{C}$ is of arity 2

Definition 4

([25,27]). An L-fuzzifying interval operator $\mathcal{I}$ on X is a mapping $\mathcal{I}:X\times X⟶L^X$ if it satisfies the following conditions: for any $x,y\in X$,

(LFT1)

$\mathcal{I}(x,y)\left(x\right)=\mathcal{I}(x,y)\left(y\right)=1$;

(LFT2)

$\mathcal{I}(x,y)=\mathcal{I}(y,x)$.

For an L-fuzzifying interval operator $\mathcal{I}$ on X, the pair $(X,\mathcal{I})$ is called an L-fuzzifying interval space.

A mapping $f:(X,{\mathcal{I}}_X)⟶(Y,{\mathcal{I}}_Y)$ between L-fuzzifying interval spaces is called L-fuzzifying-interval-preserving (L-FIP for short) provided that $\forall x,y\in X$, $f^{\to }\left({\mathcal{I}}_X(x,y)\right)\le {\mathcal{I}}_Y(f\left(x\right),f\left(y\right))$.

The category whose objects are L-fuzzifying interval spaces and whose morphisms are L-FIP mappings will be denoted by $L\text{-}\mathbf{FIS}$.

Definition 5

([35]). A strong L-fuzzy convex structure $\mathcal{C}$ on X is a mapping $\mathcal{C}:L^X⟶L$ which satisfies the following conditions:

(LFC1)

$\mathcal{C}\left(0_X\right)=\mathcal{C}\left(1_X\right)=1$;

(LFC2)

if ${\left\{A_i\right\}}_{i\in I}\subseteq L^X$ is nonempty, then $\mathcal{C}\left({\bigwedge }_{i\in I}{A}_i\right)\ge {\bigwedge }_{i\in I}\mathcal{C}\left(A_i\right)$;

(LFC3)

if ${\left\{A_i\right\}}_{i\in I}\subseteq L^X$ is directed, then $\mathcal{C}\left({\bigvee }_{i\in I}{A}_i\right)\ge {\bigwedge }_{i\in I}\mathcal{C}\left(A_i\right)$;

(LFC4)

for each $a\in L$ and $A\in L^X$, $a\to \mathcal{C}\left(A\right)\le \mathcal{C}(a\to A)$.

For a strong L-fuzzy convex structure $\mathcal{C}$ on X, the pair $(X,\mathcal{C})$ is called a strong L-fuzzy convex space.

A mapping $f:(X,{\mathcal{C}}_X)⟶(Y,{\mathcal{C}}_Y)$ between strong L-fuzzy convex spaces is called L-fuzzy-convexity-preserving (L-FCP for short), provided that $\forall B\in L^Y$, ${\mathcal{C}}_Y\left(B\right)\le {\mathcal{C}}_X\left(f^{\leftarrow }\left(B\right)\right)$.

The category whose objects are strong L-fuzzy convex spaces and whose morphisms are L-FCP mappings will be denoted by $L\text{-}\mathbf{SFCS}$.

Remark 1.

Definition 5 is a generalization of the definition of strong L-convex structures introduced by Pang in [32].

Definition 6

([36,37]). An L-fuzzy relation on X is a mapping $\mathcal{R}:X\times X⟶L.$ An L-fuzzy relation $\mathcal{R}$ on X is called an L-fuzzy preorder if it satisfies:

(LFR1)

reflexive if $\mathcal{R}(x,x)=1$ for any $x\in X$;

(LFR2)

transitive if $\mathcal{R}(x,y)\wedge \mathcal{R}(y,z)\le \mathcal{R}(x,z)$ for any $x,y,z\in X$.

For an L-fuzzy preorder $\mathcal{R}$ on X, the pair $(X,\mathcal{R})$ is called an L-fuzzy preordered set.

A mapping $f:(X,{\mathcal{R}}_X)⟶(Y,{\mathcal{R}}_Y)$ between L-fuzzy preordered sets is called L-fuzzy-preorder-preserving (L-FRP for short) provided that $\forall x,y\in X$, ${\mathcal{R}}_X(x,y)\le {\mathcal{R}}_Y(f\left(x\right),f\left(y\right))$.

The category whose objects are L-fuzzy preordered sets and whose morphisms are L-FRP mappings will be denoted by $L-\mathbf{FRS}$.

3. L-Fuzzifying Interval Operators and Strong L-Fuzzy Convex Structures

In this section, we will discuss the relationship between categories $L-\mathbf{SFCS}$ and $L-\mathbf{FIS}$. Also, we will present the concept of arity 2 strong L-fuzzy convex structures and study its relationship with L-fuzzifying interval operators in a categorical sense.

Next, we study the relationship between categories L-SFCS and L-FIS.

Proposition 1.

Let $(X,\mathcal{I})$ be an L-fuzzifying interval space and define ${\mathcal{C}}^{\mathcal{I}}:L^X⟶L$ by

$$\forall A\in L^X,{\mathcal{C}}^{\mathcal{I}}\left(A\right)=\underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y\left)\right)\to \mathcal{S}\left(\mathcal{I}\right(x,y),A)\right).$$

Then ${\mathcal{C}}^{\mathcal{I}}$ is a strong L-fuzzy convex structure on X.

Proof. 

It suffices to verify that ${\mathcal{C}}^{\mathcal{I}}$ satisfies (LFC1)–(LFC4). Indeed,

(LFC1) Obviously.

(LFC2) Take any $\{A_i:i\in I\}\subseteq L^X$. Then,

$$\begin{array}{cc}\hfill {\mathcal{C}}^{\mathcal{I}}\left(\underset{i\in I}{\bigwedge }{A}_i\right)& =\underset{x,y\in X}{\bigwedge }\left(\left(\underset{i\in I}{\bigwedge }{A}_i\left(x\right)\wedge \underset{i\in I}{\bigwedge }{A}_i\left(y\right)\right)\to \mathcal{S}\left(\mathcal{I}(x,y),\underset{i\in I}{\bigwedge }{A}_i\right)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left(\underset{i\in I}{\bigwedge }(A_i\left(x\right)\wedge A_i\left(y\right))\to \underset{i\in I}{\bigwedge }\mathcal{S}(\mathcal{I}(x,y),A_i)\right)\hfill \\ \hfill & \ge \underset{i\in I}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left((A_i\left(x\right)\wedge A_i\left(y\right))\to \mathcal{S}(\mathcal{I}(x,y),A_i)\right)\hfill \\ \hfill & =\underset{i\in I}{\bigwedge }{\mathcal{C}}^{\mathcal{I}}\left(A_i\right).\hfill \end{array}$$

(LFC3) Take each directed subfamily $\{A_i:i\in I\}\subseteq L^X$. Then,

$$\begin{array}{cc}\hfill {\mathcal{C}}^{\mathcal{I}}\left(\underset{i\in I}{\bigvee }{A}_i\right)& =\underset{x,y\in X}{\bigwedge }\left(\left(\underset{i\in I}{\bigvee }{A}_i\left(x\right)\wedge \underset{i\in I}{\bigvee }{A}_i\left(y\right)\right)\to \mathcal{S}\left(\mathcal{I}(x,y),\underset{i\in I}{\bigvee }{A}_i\right)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left(\underset{i\in I}{\bigvee }(A_i\left(x\right)\wedge A_i\left(y\right))\to \mathcal{S}\left(\mathcal{I}(x,y),\underset{i\in I}{\bigvee }{A}_i\right)\right)\left(\mathrm{by}\mathrm{Lemma}1\right)\hfill \\ \hfill & \ge \underset{x,y\in X}{\bigwedge }\left(\underset{i\in I}{\bigvee }(A_i\left(x\right)\wedge A_i\left(y\right))\to \underset{i\in I}{\bigvee }\mathcal{S}(\mathcal{I}(x,y),A_i)\right)\hfill \\ \hfill & \ge \underset{i\in I}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left((A_i\left(x\right)\wedge A_i\left(y\right))\to \mathcal{S}(\mathcal{I}(x,y),A_i)\right)\hfill \\ \hfill & =\underset{i\in I}{\bigwedge }{\mathcal{C}}^{\mathcal{I}}\left(A_i\right).\hfill \end{array}$$

(LFC4) Take each $a\in L$ and $A\in L^X$. Then,

$$\begin{array}{cc}\hfill {\mathcal{C}}^{\mathcal{I}}(a\to A)& =\underset{x,y\in X}{\bigwedge }\left(\left((a\to A)\left(x\right)\wedge (a\to A)\left(y\right)\right)\to \mathcal{S}(\mathcal{I}(x,y),a\to A)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left(\left((a\to A(x\left)\right)\wedge (a\to A(y\left)\right)\right)\to \left(a\to \mathcal{S}\left(\mathcal{I}\right(x,y),A)\right)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left(\left(a\to \left(A\right(x)\wedge A(y\left)\right)\right)\to \left(a\to \mathcal{S}\left(\mathcal{I}\right(x,y),A)\right)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left(\left(a\to \left(A\right(x)\wedge A(y\left)\right)\right)\to \left(a\wedge a\to \mathcal{S}\left(\mathcal{I}\right(x,y),A)\right)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left(\left(a\to \left(A\right(x)\wedge A(y\left)\right)\right)\to \left(a\to (a\to \mathcal{S}(\mathcal{I}(x,y),A\left)\right)\right)\right)\hfill \\ \hfill & \ge \underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y\left)\right)\to (a\to \mathcal{S}(\mathcal{I}(x,y),A\left)\right)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left(a\to \left(\left(A\right(x)\wedge A(y\left)\right)\to \mathcal{S}\left(\mathcal{I}\right(x,y),A)\right)\right)\hfill \\ \hfill & =a\to \underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y\left)\right)\to \mathcal{S}\left(\mathcal{I}\right(x,y),A)\right)\hfill \\ \hfill & =a\to {\mathcal{C}}^{\mathcal{I}}\left(A\right).\hfill \end{array}$$

Hence, ${\mathcal{C}}^{\mathcal{I}}$ is a strong L-fuzzy convex structure on X. □

Example 1.

Let $X=\{x,y\}$ and $L=[0,1]$ be the unit interval, with the implication defined by

$$x\to y=\left\{\begin{array}{cc}1,\hfill & x\le y;\hfill \\ y,\hfill & x>y.\hfill \end{array}\right.$$

Define $\mathcal{I}:X\times X⟶L^X$ as follows (

Table 1. Example of L-fuzzifying interval operator $\mathcal{I}$ on $X=\{x,y\}$.

	$\mathcal{I}$(x, x)	$\mathcal{I}$(x, y)	$\mathcal{I}$(y, y)	$\mathcal{I}$(y, x)
x	1	1	1	1
y	1	1	1	1

):

Then, it is easy to verify that $\mathcal{I}$ is an L-fuzzifying interval operator on X. Further, define a mapping ${\mathcal{C}}^{\mathcal{I}}:L^X⟶L$ by

$$\forall A\in L^X,{\mathcal{C}}^{\mathcal{I}}\left(A\right)=\underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y\left)\right)\to \mathcal{S}\left(\mathcal{I}\right(x,y),A)\right).$$

For convenience, let $A\left(x\right)=a$ and $A\left(y\right)=b$ for any $\in L^X$, where $a,b\in L$. Through calculation, we obtain the following formulas:

$$\begin{array}{cc}\hfill {\mathcal{C}}^{\mathcal{I}}\left(A\right)& =\underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y\left)\right)\to \mathcal{S}\left(\mathcal{I}\right(x,y),A)\right)\hfill \\ \hfill & =\left(a\to \left(\right(1\to a)\wedge (1\to b\left)\right)\right)\wedge \left(b\to \left(\right(1\to a)\wedge (1\to b\left)\right)\right)\wedge 1\wedge 1\hfill \\ \hfill & =\left(a\to (a\wedge b)\right)\wedge \left(b\to (a\wedge b)\right)\hfill \\ \hfill & =\left((a\vee b)\to (a\wedge b)\right).\hfill \end{array}$$

Then, it is easy to verify that ${\mathcal{C}}^{\mathcal{I}}$ is a strong L-fuzzy convex structure on X.

Proposition 2.

If $f:(X,{\mathcal{I}}_X)⟶(Y,{\mathcal{I}}_Y)$ is L-FIP, then $f:(X,{\mathcal{C}}^{{\mathcal{I}}_X})⟶(Y,{\mathcal{C}}^{{\mathcal{I}}_Y})$ is L-FCP.

Proof. 

Since $f:(X,{\mathcal{I}}_X)⟶(Y,{\mathcal{I}}_Y)$ is L-FIP, it follows that

$$\forall x,y\in X,f^{\to }\left({\mathcal{I}}_X(x,y)\right)\le {\mathcal{I}}_Y(f\left(x\right),f\left(y\right)).$$

Take each $B\in L^Y$. Then

$$\begin{array}{cc}\hfill {\mathcal{C}}^{{\mathcal{I}}_X}\left(f^{\leftarrow }\left(B\right)\right)& =\underset{x,y\in X}{\bigwedge }\left((f^{\leftarrow }\left(B\right)\left(x\right)\wedge f^{\leftarrow }\left(B\right)\left(y\right))\to \mathcal{S}({\mathcal{I}}_X(x,y),f^{\leftarrow }\left(B\right))\right)\hfill \\ \hfill & =\underset{f\left(x\right),f\left(y\right)\in Y}{\bigwedge }\left((f^{\leftarrow }\left(B\right)\left(x\right)\wedge f^{\leftarrow }\left(B\right)\left(y\right))\to \mathcal{S}({\mathcal{I}}_X(x,y),f^{\leftarrow }\left(B\right))\right)\hfill \\ \hfill & =\underset{f\left(x\right),f\left(y\right)\in Y}{\bigwedge }\left((B\left(f\left(x\right)\right)\wedge B\left(f\left(y\right)\right))\to \mathcal{S}(f^{\to }\left({\mathcal{I}}_X(x,y)\right),B)\right)\hfill \\ \hfill & \ge \underset{f\left(x\right),f\left(y\right)\in Y}{\bigwedge }\left((B\left(f\left(x\right)\right)\wedge B\left(f\left(y\right)\right))\to \mathcal{S}({\mathcal{I}}_Y(f\left(x\right),f\left(y\right)),B)\right)\hfill \\ \hfill & \ge \underset{m,n\in Y}{\bigwedge }\left((B\left(m\right)\wedge B\left(n\right))\to \mathcal{S}({\mathcal{I}}_Y(m,n),B)\right)\hfill \\ \hfill & ={\mathcal{C}}^{{\mathcal{I}}_Y}\left(B\right).\hfill \end{array}$$

This implies that $f:(X,{\mathcal{C}}^{{\mathcal{I}}_X})⟶(Y,{\mathcal{C}}^{{\mathcal{I}}_Y})$ is L-FCP. □

By Propositions 1 and 2, we obtain a functor $\mathbb{S}:L-\mathbf{FIS}⟶L-\mathbf{SFCS}$ by

$$\mathbb{S}:(X,\mathcal{I})⟼(X,{\mathcal{C}}^{\mathcal{I}})andf⟼f.$$

The action of functor $\mathbb{S}$ is illustrated in the following commutative diagram (Figure 1):

Proposition 3.

Let $(X,\mathcal{C})$ be a strong L-fuzzy convex space and define ${\mathcal{I}}^{\mathcal{C}}:X\times X⟶L^X$ by

$$\forall x,y\in X,{\mathcal{I}}^{\mathcal{C}}(x,y)\left(z\right)=\underset{B\in L^X}{\bigwedge }\left(\left(B\right(x)\wedge B(y)\wedge \mathcal{C}(B\left)\right)\to B\left(z\right)\right).$$

Then ${\mathcal{I}}^{\mathcal{C}}$ is an L-fuzzifying interval operator on X.

Proof. 

(LFT1) and (LFT2) are trivial. □

Proposition 4.

If $f:(X,{\mathcal{C}}_X)⟶(Y,{\mathcal{C}}_Y)$ is L-FCP, then $f:(X,{\mathcal{I}}^{{\mathcal{C}}_X})⟶(Y,{\mathcal{I}}^{{\mathcal{C}}_Y})$ is L-FIP.

Proof. 

Since $f:(X,{\mathcal{C}}_X)⟶(Y,{\mathcal{C}}_Y)$ is L-FCP, it follows that

$$\forall B\in L^Y,{\mathcal{C}}_Y\left(B\right)\le {\mathcal{C}}_X\left(f^{\leftarrow }\left(B\right)\right).$$

Take each $x,y\in X$. Then,

$$\begin{array}{cc}\hfill f^{\leftarrow }\left({\mathcal{I}}^{{\mathcal{C}}_Y}(f\left(x\right),f\left(y\right))\right)\left(z\right)& ={\mathcal{I}}^{{\mathcal{C}}_Y}(f\left(x\right),f\left(y\right))\left(f\left(z\right)\right)\hfill \\ \hfill & =\underset{B\in L^Y}{\bigwedge }\left((B\left(f\left(x\right)\right)\wedge B\left(f\left(y\right)\right)\wedge {\mathcal{C}}_Y\left(B\right))\to B\left(f\left(z\right)\right)\right)\hfill \\ \hfill & =\underset{B\in L^Y}{\bigwedge }\left((f^{\leftarrow }\left(B\right)\left(x\right)\wedge f^{\leftarrow }\left(B\right)\left(y\right)\wedge {\mathcal{C}}_Y\left(B\right))\to f^{\leftarrow }\left(B\right)\left(z\right)\right)\hfill \\ \hfill & \ge \underset{B\in L^Y}{\bigwedge }\left((f^{\leftarrow }\left(B\right)\left(x\right)\wedge f^{\leftarrow }\left(B\right)\left(y\right)\wedge {\mathcal{C}}_X\left(f^{\leftarrow }\left(B\right)\right))\to f^{\leftarrow }\left(B\right)\left(z\right)\right)\hfill \\ \hfill & \ge \underset{A\in L^X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right)\wedge {\mathcal{C}}_X\left(A\right))\to A\left(z\right)\right)\hfill \\ \hfill & ={\mathcal{I}}^{{\mathcal{C}}_X}(x,y)\left(z\right).\hfill \end{array}$$

This implies that $f^{\to }\left({\mathcal{I}}^{{\mathcal{C}}_X}(x,y)\right)\le {\mathcal{I}}^{{\mathcal{C}}_Y}(f\left(x\right),f\left(y\right)),$ as desired. □

By Propositions 3 and 4, we obtain a functor $\mathbb{H}:L-\mathbf{SFCS}⟶L-\mathbf{FIS}$ by

$$\mathbb{H}:(X,\mathcal{C})⟼(X,{\mathcal{I}}^{\mathcal{C}})andf⟼f.$$

The action of functor $\mathbb{H}$ is illustrated in the following commutative diagram (Figure 2):

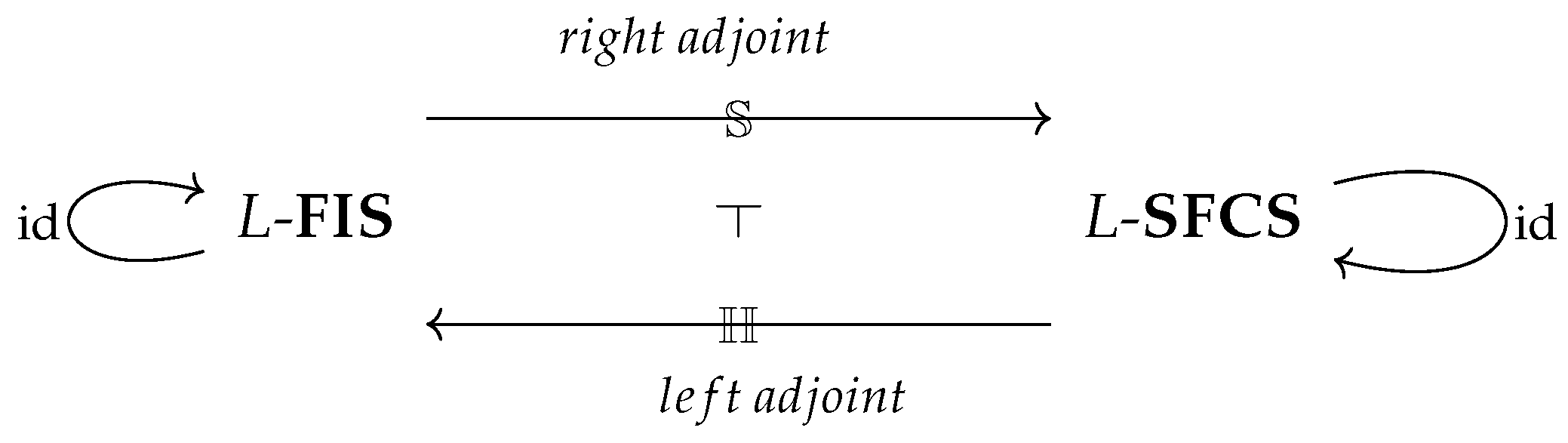
Theorem 1.

$(\mathbb{H},\mathbb{S})$ is a Galois correspondence.

Proof. 

It suffices to prove that $\mathbb{H}\circ \mathbb{S}{\ge }_{\mathcal{I}}{\mathbb{I}}_{L-\mathbf{FIS}}$ and $\mathbb{S}\circ \mathbb{H}{\le }_{\mathcal{C}}{\mathbb{I}}_{L-\mathbf{SFCS}}$. That is to say, we only need to verify (1) ${\mathcal{I}}^{{\mathcal{C}}^{\mathcal{I}}}{\ge }_{\mathcal{I}}\mathcal{I}(\mathrm{i}.\mathrm{e}.,{\mathcal{I}}^{{\mathcal{C}}^{\mathcal{I}}}\ge \mathcal{I});$ (2) ${\mathcal{C}}^{{\mathcal{I}}^{\mathcal{C}}}{\le }_{\mathcal{C}}\mathcal{C}(\mathrm{i}.\mathrm{e}.,\mathcal{C}\le {\mathcal{C}}^{{\mathcal{I}}^{\mathcal{C}}}).$

For (1), take each $x,y\in X$. Then

$$\begin{array}{cc}\hfill {\mathcal{I}}^{{\mathcal{C}}^{\mathcal{I}}}(x,y)\left(z\right)& =\underset{B\in L^X}{\bigwedge }\left((B\left(x\right)\wedge B\left(y\right)\wedge {\mathcal{C}}^{\mathcal{I}}\left(B\right))\to B\left(z\right)\right)\hfill \\ \hfill & =\underset{B\in L^X}{\bigwedge }\left(\left(B\left(x\right)\wedge B\left(y\right)\wedge \underset{m,n\in X}{\bigwedge }(B\left(m\right)\wedge B\left(n\right)\to \mathcal{S}(\mathcal{I}(m,n),B))\right)\to B\left(z\right)\right)\hfill \\ \hfill & \ge \underset{B\in L^X}{\bigwedge }\left(\left(B\left(x\right)\wedge B\left(y\right)\wedge \left(B\right(x)\wedge B(y)\to \mathcal{S}(\mathcal{I}(x,y),B\left)\right)\right)\to B\left(z\right)\right)\hfill \\ \hfill & \ge \underset{B\in L^X}{\bigwedge }(\mathcal{S}(\mathcal{I}(x,y),B)\to B\left(z\right))\hfill \\ \hfill & \ge \mathcal{I}(x,y)\left(z\right).\hfill \end{array}$$

This means that ${\mathcal{I}}^{{\mathcal{C}}^{\mathcal{I}}}{\ge }_{\mathcal{I}}\mathcal{I}.$

For (2), take each $A\in L^X$. Then

$$\begin{array}{cc}\hfill {\mathcal{C}}^{{\mathcal{I}}^{\mathcal{C}}}\left(A\right)& =\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \mathcal{S}({\mathcal{I}}^{\mathcal{C}}(x,y),A)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \underset{z\in X}{\bigwedge }({\mathcal{I}}^{\mathcal{C}}(x,y)\left(z\right)\to A\left(z\right))\right)\hfill \\ \hfill & =\underset{z\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to ({\mathcal{I}}^{\mathcal{C}}(x,y)\left(z\right)\to A\left(z\right))\right)\hfill \\ \hfill & =\underset{z\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \left(\underset{B\in L^X}{\bigwedge }\left(\left(B\right(x)\wedge B(y)\wedge \mathcal{C}(B\left)\right)\to B\left(z\right)\right)\to A\left(z\right)\right)\right)\hfill \\ \hfill & \ge \underset{z\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \left(\left(\right(A\left(x\right)\wedge A\left(y\right)\wedge \mathcal{C}\left(A\right))\to A(z\left)\right)\to A\left(z\right)\right)\right)\hfill \\ \hfill & \ge \underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y\left)\right)\to \left(A\right(x)\wedge A(y)\wedge \mathcal{C}(A\left)\right)\right)\hfill \\ \hfill & \ge \mathcal{C}\left(A\right).\hfill \end{array}$$

This shows that ${\mathcal{C}}^{{\mathcal{I}}^{\mathcal{C}}}{\le }_{\mathcal{C}}\mathcal{C},$ as desired. □

This adjunction $\mathbb{H}⊣\mathbb{S}$ is represented diagrammatically as follows (Figure 3):

Next, based on the result in Theorem 1, we will further study the embedding and reflective properties with the categories $L-\mathbf{SFCS}$ and $L-\mathbf{FIS}$ by using the properties of Galois correspondence.

Definition 7

([35]). Let $(X,\mathcal{C})$ be a strong L-fuzzy convex space and define $c{o}^{\mathcal{C}}:L^X⟶L^X$ by

$$\forall A\in L^X,c{o}^{\mathcal{C}}\left(A\right)=\underset{B\in L^X}{\bigwedge }\left(\left(\mathcal{S}\right(A,B)\wedge \mathcal{C}(B\left)\right)\to B\right).$$

Then $c{o}^{\mathcal{C}}$ is an L-ordered hull operator on X.

Lemma 3.

Let $(X,\mathcal{C})$ be a strong L-fuzzy convex space and $c{o}^{\mathcal{C}}$ be defined as in Definition 7. Then

$$c{o}^{\mathcal{C}}\left({\chi }_{\{x,y\}}\right)=\underset{B\in L^X}{\bigwedge }\left(\left(B\right(x)\wedge B(y)\wedge \mathcal{C}(B\left)\right)\to B\right).$$

Proof. 

From Definition 7, we have

$$\begin{array}{cc}\hfill c{o}^{\mathcal{C}}\left({\chi }_{\{x,y\}}\right)& =\underset{B\in L^X}{\bigwedge }\left((\mathcal{S}({\chi }_{\{x,y\}},B)\wedge \mathcal{C}\left(B\right))\to B\right)\hfill \\ \hfill & =\underset{B\in L^X}{\bigwedge }\left(\left(\underset{z\in X}{\bigwedge }({\chi }_{\{x,y\}}\left(z\right)\to B\left(z\right))\wedge \mathcal{C}\left(B\right)\right)\to B\right)\hfill \\ \hfill & =\underset{B\in L^X}{\bigwedge }\left(\left(B\right(x)\wedge B(y)\wedge \mathcal{C}(B\left)\right)\to B\right),\hfill \end{array}$$

as desired. □

Definition 8.

A strong L-fuzzy convex structure $\mathcal{C}$ on X is called arity 2 if it satisfies:

(LFA)

$\forall A\in L^X,\mathcal{C}\left(A\right)={\bigwedge }_{x,y\in X}\left((A\left(x\right)\wedge A\left(y\right))\to \mathcal{S}(c{o}^{\mathcal{C}}\left({\chi }_{\{x,y\}}\right),A)\right).$

For an arity 2 strong L-fuzzy convex structure $\mathcal{C}$ on X, the pair $(X,\mathcal{C})$ is called an arity 2 strong L-fuzzy convex space. The full subcategory of L-SFCS with arity 2 strong L-fuzzy convex spaces as objects is denoted by L-SFCS(2).

Remark 2.

When $L=\{0,1\}$, Definitions 7 and 8 are in agreement with the classical concepts given by Van De Vel in [34], respectively.

Example 2.

Let $X=\{x,y\}$ and $L=[0,1]$ be the unit interval, the corresponding implication is defined by

$$x\to y=\left\{\begin{array}{cc}1,\hfill & x\le y;\hfill \\ y,\hfill & x>y.\hfill \end{array}\right.$$

Define $\mathcal{C}:L^X⟶L$ as follows:

$$\mathcal{C}\left(A\right)=\left\{\begin{array}{cc}1,\hfill & A\left(x\right)=A\left(y\right);\hfill \\ A\left(x\right)\wedge A\left(y\right),\hfill & otherwise.\hfill \end{array}\right.$$

Then, it is easy to verify that $\mathcal{C}$ is an arity 2 strong L-fuzzy convex structure on X.

Next, we study the relationship between categories L-SFCS(2) and L-FIS.

Proposition 5.

Let $(X,\mathcal{I})$ be an L-fuzzifying interval space and define ${\mathcal{C}}^{\mathcal{I}}:L^X⟶L$ by

$$\forall A\in L^X,{\mathcal{C}}^{\mathcal{I}}\left(A\right)=\underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y\left)\right)\to \mathcal{S}\left(\mathcal{I}\right(x,y),A)\right).$$

Then ${\mathcal{C}}^{\mathcal{I}}$ is an arity 2 strong L-fuzzy convex structure on X.

Proof. 

By Proposition 1, we only need to prove that ${\mathcal{C}}^{\mathcal{I}}$ satisfies (LFA), i.e.,

$$\forall A\in L^X,{\mathcal{C}}^{\mathcal{I}}\left(A\right)=\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \mathcal{S}(c{o}^{{\mathcal{C}}^{\mathcal{I}}}\left({\chi }_{\{x,y\}}\right),A)\right).$$

We first prove $\mathcal{I}(x,y)\le c{o}^{{\mathcal{C}}^{\mathcal{I}}}\left({\chi }_{\{x,y\}}\right)$ for each $x,y\in X.$

• Take each $x,y,z\in X.$ Then,

  $$\begin{array}{cc}\hfill c{o}^{{\mathcal{C}}^{\mathcal{I}}}\left({\chi }_{\{x,y\}}\right)\left(z\right)& =\underset{B\in L^X}{\bigwedge }\left((B\left(x\right)\wedge B\left(y\right)\wedge {\mathcal{C}}^{\mathcal{I}}\left(B\right))\to B\left(z\right)\right)\hfill \\ \hfill & =\underset{B\in L^X}{\bigwedge }\left(\left(B\left(x\right)\wedge B\left(y\right)\wedge \underset{m,n\in X}{\bigwedge }((B\left(m\right)\wedge B\left(n\right))\to \mathcal{S}(\mathcal{I}(m,n),B))\right)\to B\left(z\right)\right)\hfill \\ \hfill & \ge \underset{B\in L^X}{\bigwedge }\left(\left(B\left(x\right)\wedge B\left(y\right)\wedge \left(\right(B\left(x\right)\wedge B\left(y\right))\to \mathcal{S}(\mathcal{I}(x,y),B\left)\right)\right)\to B\left(z\right)\right)\hfill \\ \hfill & \ge \underset{B\in L^X}{\bigwedge }(\mathcal{S}(\mathcal{I}(x,y),B)\to B\left(z\right))\hfill \\ \hfill & \ge \mathcal{I}(x,y)\left(z\right).\left(\mathrm{by}\left(\mathrm{S}5\right)\right)\hfill \end{array}$$

It follows that

$$\begin{array}{cc}\hfill & \underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \mathcal{S}(c{o}^{{\mathcal{C}}^{\mathcal{I}}}({\chi }_{\{x,y\}},A)\right)\hfill \\ \hfill & \le \underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y\left)\right)\to \mathcal{S}\left(\mathcal{I}\right(x,y),A)\right)\hfill \\ & ={\mathcal{C}}^{\mathcal{I}}\left(A\right).\hfill \end{array}$$

Conversely,

$$\begin{array}{cc}\hfill & \underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \mathcal{S}(c{o}^{{\mathcal{C}}^{\mathcal{I}}}\left({\chi }_{\{x,y\}}\right),A)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \left(\underset{B\in L^X}{\bigwedge }(B\left(x\right)\wedge B\left(y\right)\wedge {\mathcal{C}}^{\mathcal{I}}\left(B\right)\to B)\to A\right)\right)\hfill \\ \hfill & \ge \underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \left(\left(A\left(x\right)\wedge A\left(y\right)\wedge {\mathcal{C}}^{\mathcal{I}}\left(A\right)\to A\right)\to A\right)\right)\hfill \\ \hfill & \ge \underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to (A\left(x\right)\wedge A\left(y\right)\wedge {\mathcal{C}}^{\mathcal{I}}\left(A\right))\right)\hfill \\ & \ge {\mathcal{C}}^{\mathcal{I}}\left(A\right).\hfill \end{array}$$

Hence, ${\mathcal{C}}^{\mathcal{I}}\left(A\right)={\bigwedge }_{x,y\in X}(A\left(x\right)\wedge A\left(y\right)\to \mathcal{S}(c{o}^{{\mathcal{C}}^{\mathcal{I}}}\left({\chi }_{\{x,y\}}\right),A)),$ as desired. □

By Propositions 2, 3, 4, and 5, we know ${\mathbb{H}}^{★}\stackrel{\Delta }{=}{\mathbb{H}|}_{L-\mathbf{SFCS}\left(\mathbf{2}\right)}:L-\mathbf{SFCS}\left(\mathbf{2}\right)⟶L\mathbf{FIS}$ and ${\mathbb{S}}^{★}\stackrel{\Delta }{=}\mathbb{S}:L-\mathbf{FIS}⟶L-\mathbf{SFCS}\left(\mathbf{2}\right)$ are still functors. Then, we obtain the following result.

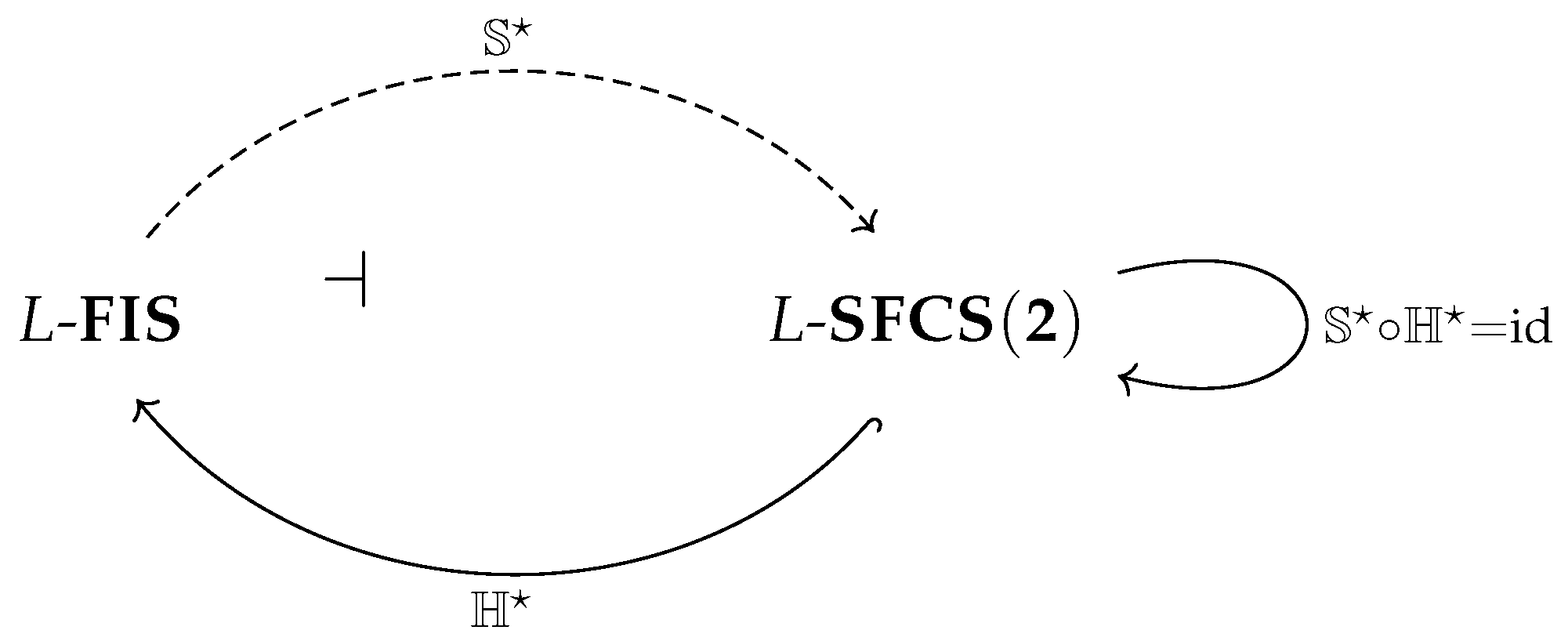
Theorem 2.

$({\mathbb{S}}^{★},{\mathbb{H}}^{★})$ is a Galois correspondence. Moreover, ${\mathbb{S}}^{★}$ is a left inverse of ${\mathbb{H}}^{★}$.

Proof. 

It is sufficient to prove that ${\mathbb{H}}^{★}\circ {\mathbb{S}}^{★}\left(\mathcal{I}\right){\ge }_{\mathcal{I}}\mathcal{I}$ for any $(X,\mathcal{I})\in L-\mathbf{FIS}$ and ${\mathbb{S}}^{★}\circ {\mathbb{H}}^{★}\left(\mathcal{C}\right)=\mathcal{C}$ for any $(X,\mathcal{C})\in L-\mathbf{SFCS}\left(\mathbf{2}\right)$. Indeed, it follows from Theorem 1, we only need to prove that ${\mathbb{S}}^{★}\circ {\mathbb{H}}^{★}\left(\mathcal{C}\right)=\mathcal{C}(i.e.,{\mathcal{C}}^{{\mathcal{I}}^{\mathcal{C}}}=\mathcal{C})$ for any $(X,\mathcal{C})\in L-\mathbf{SFCS}\left(\mathbf{2}\right).$

Firstly, by Proposition 3 and Lemma 3, we have $c{o}^{\mathcal{C}}\left({\chi }_{\{x,y\}}\right)\left(z\right)={\mathcal{I}}^{\mathcal{C}}(x,y)\left(z\right)$ for each $z\in X$. This implies that

$$\begin{array}{cc}\hfill {\mathcal{C}}^{{\mathcal{I}}^{\mathcal{C}}}\left(A\right)& =\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \mathcal{S}({\mathcal{I}}^{\mathcal{C}}(x,y),A)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \mathcal{S}(c{o}^{\mathcal{C}}\left({\chi }_{\{x,y\}}\right),A)\right)\hfill \\ \hfill & =\mathcal{C}\left(A\right).\left(\mathrm{by}\left(\mathrm{LFA}\right)\right)\hfill \end{array}$$

This shows that $\mathcal{C}={\mathcal{C}}^{{\mathcal{I}}^{\mathcal{C}}},$ as desired. □

Corollary 1.

The category L-SFCS(2)can be embedded in the category L-FISas a reflective subcategory.

This reflective subcategory structure is captured in the following diagram, which visualizes the adjunction ${\mathbb{S}}^{★}⊣{\mathbb{H}}^{★}$ and the left inverse property (Figure 4):

4. Strong $\mathit{L}$-Fuzzy Convex Structures and $\mathit{L}$-Fuzzy Preorders

In this section, we will discuss the connection between strong L-fuzzy convex structures and L-fuzzy preorders.

Now, we give a way of mutual construction of strong L-fuzzy convex structures and L-fuzzy preorders.

Proposition 6.

Let $(X,\mathcal{R})$ be an L-fuzzy preordered set and define ${\mathcal{C}}^{\mathcal{R}}:L^X⟶L$ by

$$\forall A\in L^X,{\mathcal{C}}^{\mathcal{R}}\left(A\right)=\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }(A\left(x\right)\wedge A\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y))\to A\left(u\right)\right).$$

Then ${\mathcal{C}}^{\mathcal{R}}$ is a strong L-fuzzy convex structure on X.

Proof. 

It suffices to verify that ${\mathcal{C}}^{\mathcal{R}}$ satisfies (LFC1)–(LFC4). Indeed,

(LFC1) it is clear that ${\mathcal{C}}^{\mathcal{R}}\left(1_X\right)={\mathcal{C}}^{\mathcal{R}}\left(0_X\right)=1.$

(LFC2) Take any $\{A_i:i\in I\}\subseteq L^X$. Then,

$$\begin{array}{cc}\hfill {\mathcal{C}}^{\mathcal{R}}\left(\underset{i\in I}{\bigwedge }{A}_i\right)& =\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }\left(\underset{i\in I}{\bigwedge }{A}_i\left(x\right)\wedge \underset{i\in I}{\bigwedge }{A}_i\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y)\right)\to \underset{i\in I}{\bigwedge }{A}_i\left(u\right)\right)\hfill \\ \hfill & =\underset{i\in I}{\bigwedge }\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }\left(\underset{i\in I}{\bigwedge }(A_i\left(x\right)\wedge A_i\left(y\right))\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y)\right)\to A_i\left(u\right)\right)\hfill \\ \hfill & \ge \underset{i\in I}{\bigwedge }\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }(A_i\left(x\right)\wedge A_i\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y))\to A_i\left(u\right)\right)\hfill \\ \hfill & =\underset{i\in I}{\bigwedge }{\mathcal{C}}^{\mathcal{R}}\left(A_i\right).\hfill \end{array}$$

(LFC3) Take each directed subfamily $\{A_i:i\in I\}\subseteq L^X$. Then,

$$\begin{array}{cc}\hfill {\mathcal{C}}^{\mathcal{R}}\left(\underset{i\in I}{\bigvee }{A}_i\right)& =\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }\left(\underset{i\in I}{\bigvee }{A}_i\left(x\right)\wedge \underset{i\in I}{\bigvee }{A}_i\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y)\right)\to \underset{i\in I}{\bigvee }{A}_i\left(u\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }\left(\underset{i\in I}{\bigvee }(A_i\left(x\right)\wedge A_i\left(y\right))\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y)\right)\to \underset{i\in I}{\bigvee }{A}_i\left(u\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }\left(\underset{i\in I}{\bigvee }(A_i\left(x\right)\wedge A_i\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y))\right)\to \underset{i\in I}{\bigvee }{A}_i\left(u\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\left(\underset{i\in I}{\bigvee }\underset{x,y\in X}{\bigvee }(A_i\left(x\right)\wedge A_i\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y))\to \underset{i\in I}{\bigvee }{A}_i\left(u\right)\right)\hfill \\ \hfill & \ge \underset{i\in I}{\bigwedge }\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }(A_i\left(x\right)\wedge A_i\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y))\to A_i\left(u\right)\right)\hfill \\ \hfill & =\underset{i\in I}{\bigwedge }{\mathcal{C}}^{\mathcal{R}}\left(A_i\right).\hfill \end{array}$$

(LFC4) Take each $a\in L$ and $A\in L^X$. Then,

$$\begin{array}{cc}\hfill {\mathcal{C}}^{\mathcal{R}}(a\to A)& =\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }((a\to A)\left(x\right)\wedge (a\to A)\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y))\to (a\to A)\left(u\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(\right(a\to A\left(x\right))\wedge (a\to A\left(y\right))\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y\left)\right)\to (a\to A(u\left)\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(\right(a\to A\left(x\right))\wedge (a\to A\left(y\right))\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y\left)\right)\to (a\wedge a\to A(u\left)\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(\right(a\to A\left(x\right))\wedge (a\to A\left(y\right))\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y\left)\right)\to (a\to (a\to A\left(u\right)\left)\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(\right(a\to \left(A\right(x)\wedge A(y\left)\right))\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y\left)\right)\to (a\to (a\to A\left(u\right)\left)\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left((a\wedge (a\to \left(A\right(x)\wedge A(y\left)\right))\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y\left)\right)\to (a\to A(u\left)\right)\right)\hfill \\ \hfill & \ge \underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y\left)\right)\to (a\to A(u\left)\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(a\to \left(\right(A\left(x\right)\wedge A\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y))\to A(u\left)\right)\right)\hfill \\ \hfill & =a\to \underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y\left)\right)\to A\left(u\right)\right)\hfill \\ \hfill & =a\to \underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }(A\left(x\right)\wedge A\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y))\to A\left(u\right)\right)\hfill \\ \hfill & =a\to {\mathcal{C}}^{\mathcal{R}}\left(A\right).\hfill \end{array}$$

Hence ${\mathcal{C}}^{\mathcal{R}}$ is a strong L-fuzzy convex structure on X. □

Proposition 7.

If $f:(X,{\mathcal{R}}_X)⟶(Y,{\mathcal{R}}_Y)$ is L-FRP, then $f:(X,{\mathcal{C}}^{{\mathcal{R}}_X})⟶(Y,{\mathcal{C}}^{{\mathcal{R}}_Y})$ is L-FCP.

Proof. 

Since $f:(X,{\mathcal{R}}_X)⟶(Y,{\mathcal{R}}_Y)$ is L-FRP, it follows that

$$\forall x,y\in X,{\mathcal{R}}_X(x,y)\le {\mathcal{R}}_Y(f\left(x\right),f\left(y\right)).$$

Take each $B\in L^Y$. Then,

$$\begin{array}{cc}\hfill {\mathcal{C}}^{{\mathcal{R}}_X}\left(f^{\leftarrow }\left(B\right)\right)& =\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }(f^{\leftarrow }\left(B\right)\left(x\right)\wedge f^{\leftarrow }\left(B\right)\left(y\right)\wedge {\mathcal{R}}_X(x,u)\wedge {\mathcal{R}}_X(u,y))\to f^{\leftarrow }\left(B\right)\left(u\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\left(\underset{f\left(x\right),f\left(y\right)\in Y}{\bigvee }(f^{\leftarrow }\left(B\right)\left(x\right)\wedge f^{\leftarrow }\left(B\right)\left(y\right)\wedge {\mathcal{R}}_X(x,u)\wedge {\mathcal{R}}_X(u,y))\to f^{\leftarrow }\left(B\right)\left(u\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\left(\underset{f\left(x\right),f\left(y\right)\in Y}{\bigvee }(B\left(f\left(x\right)\right)\wedge B\left(f\left(y\right)\right)\wedge {\mathcal{R}}_X(x,u)\wedge {\mathcal{R}}_X(u,y))\to B\left(f\left(u\right)\right)\right)\hfill \\ \hfill & \ge \underset{u\in X}{\bigwedge }\left(\underset{f\left(x\right),f\left(y\right)\in Y}{\bigvee }(B\left(f\left(x\right)\right)\wedge B\left(f\left(y\right)\right)\wedge {\mathcal{R}}_Y(f\left(x\right),f\left(u\right))\wedge {\mathcal{R}}_Y(f\left(u\right),f\left(y\right)))\to B\left(f\left(u\right)\right)\right)\hfill \\ \hfill & \ge \underset{u\in X}{\bigwedge }\left(\underset{m,n\in Y}{\bigvee }(B\left(m\right)\wedge B\left(n\right)\wedge {\mathcal{R}}_Y(m,f\left(u\right))\wedge {\mathcal{R}}_Y(f\left(u\right),n))\to B\left(f\left(u\right)\right)\right)\hfill \\ \hfill & \ge \underset{z\in Y}{\bigwedge }\left(\underset{m,n\in Y}{\bigvee }(B\left(m\right)\wedge B\left(n\right)\wedge {\mathcal{R}}_Y(m,z)\wedge {\mathcal{R}}_Y(z,n))\to B\left(z\right)\right)\hfill \\ \hfill & ={\mathcal{C}}^{{\mathcal{R}}_Y}\left(B\right).\hfill \end{array}$$

This means that $f:(X,{\mathcal{C}}^{{\mathcal{R}}_X})⟶(Y,{\mathcal{C}}^{{\mathcal{R}}_Y})$ is L-FCP. □

Proposition 8.

Let $(X,\mathcal{C})$ be a strong L-fuzzy convex space and define ${\mathcal{R}}^{\mathcal{C}}:X\times X⟶L$ by

$$\forall x,y\in X,{\mathcal{R}}^{\mathcal{C}}(x,y)=\underset{B\in L^X}{\bigwedge }(\mathcal{C}\left(B\right)\to (B\left(y\right)\to B\left(x\right))).$$

Then ${\mathcal{R}}^{\mathcal{C}}$ is an L-fuzzy preorder on X.

Proof. 

It is clear that ${\mathcal{R}}^{\mathcal{C}}(x,x)=1.$

(LFR2) Take each $x,y,z\in X$. Then,

$$\begin{array}{cc}\hfill {\mathcal{R}}^{\mathcal{C}}(x,y)\wedge {\mathcal{R}}^{\mathcal{C}}(y,z)& =\underset{B\in L^X}{\bigwedge }(\mathcal{C}\left(B\right)\to (B\left(y\right)\to B\left(x\right)))\wedge \underset{A\in L^X}{\bigwedge }(\mathcal{C}\left(A\right)\to (A\left(z\right)\to A\left(y\right)))\hfill \\ \hfill & =\underset{B\in L^X}{\bigwedge }\underset{A\in L^X}{\bigwedge }\left(\left(\mathcal{C}\right(B)\to (B\left(y\right)\to B\left(x\right)\left)\right)\wedge \left(\mathcal{C}\right(A)\to (A\left(z\right)\to A\left(y\right)\left)\right)\right)\hfill \\ \hfill & \le \underset{B\in L^X}{\bigwedge }\left(\left(\mathcal{C}\right(B)\to (B\left(y\right)\to B\left(x\right)\left)\right)\wedge \left(\mathcal{C}\right(B)\to (B\left(z\right)\to B\left(y\right)\left)\right)\right)\hfill \\ \hfill & =\underset{B\in L^X}{\bigwedge }\left(\mathcal{C}\left(B\right)\to \left(\left(B\right(y)\to B(x\left)\right)\wedge \left(B\right(z)\to B(y\left)\right)\right)\right)\hfill \\ \hfill & \le \underset{B\in L^X}{\bigwedge }(\mathcal{C}\left(B\right)\to (B\left(z\right)\to B\left(x\right)))\hfill \\ \hfill & ={\mathcal{R}}^{\mathcal{C}}(x,z).\hfill \end{array}$$

Hence ${\mathcal{R}}^{\mathcal{C}}$ is an L-fuzzy preorder on X. □

Proposition 9.

If $f:(X,{\mathcal{C}}_X)⟶(Y,{\mathcal{C}}_Y)$ is L-FCP, then $f:(X,{\mathcal{R}}^{{\mathcal{C}}_X})⟶(Y,{\mathcal{R}}^{{\mathcal{C}}_Y})$ is L-FRP.

Proof. 

Since $f:(X,{\mathcal{C}}_X)⟶(Y,{\mathcal{C}}_Y)$ is L-FCP, it follows that

$$\forall B\in L^Y,{\mathcal{C}}_Y\left(B\right)\le {\mathcal{C}}_X\left(f^{\leftarrow }\left(B\right)\right).$$

Take each $x,y\in X$. Then,

$$\begin{array}{cc}\hfill {\mathcal{R}}^{{\mathcal{C}}_Y}(f\left(x\right),f\left(y\right))& =\underset{B\in L^Y}{\bigwedge }\left({\mathcal{C}}_Y\left(B\right)\to (B\left(f\left(y\right)\right)\to B\left(f\left(x\right)\right))\right)\hfill \\ \hfill & =\underset{B\in L^Y}{\bigwedge }\left({\mathcal{C}}_Y\left(B\right)\to (f^{\leftarrow }\left(B\right)\left(y\right)\to f^{\leftarrow }\left(B\right)\left(x\right))\right)\hfill \\ \hfill & \ge \underset{B\in L^Y}{\bigwedge }\left({\mathcal{C}}_X\left(f^{\leftarrow }\left(B\right)\right)\to (f^{\leftarrow }\left(B\right)\left(y\right)\to f^{\leftarrow }\left(B\right)\left(x\right))\right)\hfill \\ \hfill & \ge \underset{A\in L^X}{\bigwedge }({\mathcal{C}}_X\left(A\right)\to (A\left(y\right)\to A\left(x\right)))\hfill \\ \hfill & ={\mathcal{R}}^{{\mathcal{C}}_X}(x,y).\hfill \end{array}$$

This implies that $f:(X,{\mathcal{R}}^{{\mathcal{C}}_X})⟶(Y,{\mathcal{R}}^{{\mathcal{C}}_Y})$ is L-FRP. □

Proposition 10.

Let $(X,\mathcal{C})$ be a strong L-fuzzy convex space. Then ${\mathcal{C}}^{{\mathcal{R}}^{\mathcal{C}}}\ge \mathcal{C}.$

Proof. 

Take each $A\in L^X$. Then,

$$\begin{array}{cc}\hfill & {\mathcal{C}}^{{\mathcal{R}}^{\mathcal{C}}}\left(A\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }(A\left(x\right)\wedge A\left(y\right)\wedge {\mathcal{R}}^{\mathcal{C}}(x,u)\wedge {\mathcal{R}}^{\mathcal{C}}(u,y))\to A\left(u\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }\left(A\left(x\right)\wedge A\left(y\right)\wedge \underset{B\in L^X}{\bigwedge }(\mathcal{C}\left(B\right)\to (B\left(u\right)\to B\left(x\right)))\wedge \underset{D\in L^X}{\bigwedge }(\mathcal{C}\left(D\right)\to (D\left(y\right)\to D\left(u\right)))\right)\to A\left(u\right)\right)\hfill \\ \hfill & \ge \underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }\left(A\left(x\right)\wedge A\left(y\right)\wedge \left(\mathcal{C}\right(A)\to (A\left(u\right)\to A\left(x\right)\left)\right)\wedge \left(\mathcal{C}\right(A)\to (A\left(y\right)\to A\left(u\right)\left)\right)\right)\to A\left(u\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(A\left(x\right)\wedge A\left(y\right)\wedge \left(\mathcal{C}\right(A)\to (A\left(u\right)\to A\left(x\right)\left)\right)\wedge \left(\mathcal{C}\right(A)\to (A\left(y\right)\to A\left(u\right)\left)\right)\right)\to A\left(u\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(A\left(x\right)\wedge A\left(y\right)\wedge \left(\mathcal{C}\right(A)\to (A\left(u\right)\to A\left(x\right)\left)\right)\right)\to \left(\left(\mathcal{C}\right(A)\to (A\left(y\right)\to A\left(u\right)\left)\right)\to A\left(u\right)\right)\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(A\left(x\right)\wedge A\left(y\right)\wedge \left(\mathcal{C}\right(A)\to (A\left(u\right)\to A\left(x\right)\left)\right)\right)\to \left(\left(\right(\mathcal{C}\left(A\right)\wedge A\left(y\right))\to A(u\left)\right)\to A\left(u\right)\right)\right)\hfill \\ \hfill & \ge \underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(A\left(x\right)\wedge A\left(y\right)\wedge \left(\mathcal{C}\right(A)\to (A\left(u\right)\to A\left(x\right)\left)\right)\right)\to (\mathcal{C}\left(A\right)\wedge A\left(y\right))\right)\hfill \\ \hfill & =\underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(A\left(x\right)\wedge \left(\mathcal{C}\right(A)\to (A\left(u\right)\to A\left(x\right)\left)\right)\right)\to \left(A\left(y\right)\to \left(\mathcal{C}\right(A)\wedge A(y\left)\right)\right)\right)\hfill \\ \hfill & \ge \underset{u\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(A\left(x\right)\wedge \left(\mathcal{C}\right(A)\to (A\left(u\right)\to A\left(x\right)\left)\right)\right)\to \mathcal{C}\left(A\right)\right)\hfill \\ & \ge \mathcal{C}\left(A\right).\hfill \end{array}$$

It means that ${\mathcal{C}}^{{\mathcal{R}}^{\mathcal{C}}}\ge \mathcal{C},$ as desired. □

Finally, we shall show that a strong L-fuzzy convex structure generated by an L-fuzzy preorder is an arity 2 strong L-fuzzy convex structure.

Proposition 11.

Let $(X,\mathcal{R})$ be an L-fuzzy preordered set and define ${\mathcal{C}}^{\mathcal{R}}:L^X⟶L$ by

$$\forall A\in L^X,{\mathcal{C}}^{\mathcal{R}}\left(A\right)=\underset{u\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }(A\left(x\right)\wedge A\left(y\right)\wedge \mathcal{R}(x,u)\wedge \mathcal{R}(u,y))\to A\left(u\right)\right).$$

Then, ${\mathcal{C}}^{\mathcal{R}}$ is an arity 2 strong L-fuzzy convex structure on X.

Proof. 

By Proposition 6, we only need to prove that ${\mathcal{C}}^{\mathcal{R}}$ satisfies (LFA), i.e.,

$$\forall A\in L^X,{\mathcal{C}}^{\mathcal{R}}\left(A\right)=\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \mathcal{S}(c{o}^{{\mathcal{C}}^{\mathcal{R}}}\left({\chi }_{\{x,y\}}\right),A)\right).$$

We first prove $\mathcal{R}(x,z)\wedge \mathcal{R}(z,y)\le c{o}^{{\mathcal{C}}^{\mathcal{R}}}\left({\chi }_{\{x,y\}}\right)\left(z\right)$ for each $x,y\in X.$

• Take each $x,y\in X.$ Then,

  $$\begin{array}{cc}\hfill & c{o}^{{\mathcal{C}}^{\mathcal{R}}}\left({\chi }_{\{x,y\}}\right)\left(z\right)\hfill \\ \hfill & =\underset{B\in L^X}{\bigwedge }((B\left(x\right)\wedge B\left(y\right)\wedge {\mathcal{C}}^{\mathcal{R}}\left(B\right))\to B\left(z\right))\hfill \\ \hfill & =\underset{B\in L^X}{\bigwedge }\left(\left(B\left(x\right)\wedge B\left(y\right)\wedge \underset{u\in X}{\bigwedge }\left(\underset{m,n\in X}{\bigvee }(B\left(m\right)\wedge B\left(n\right)\wedge \mathcal{R}(m,u)\wedge \mathcal{R}(u,n))\to B\left(u\right)\right)\right)\to B\left(z\right)\right)\hfill \\ \hfill & \ge \underset{B\in L^X}{\bigwedge }\left(\left(B\left(x\right)\wedge B\left(y\right)\wedge \left(\underset{m,n\in X}{\bigvee }(B\left(m\right)\wedge B\left(n\right)\wedge \mathcal{R}(m,z)\wedge \mathcal{R}(z,n))\to B\left(z\right)\right)\right)\to B\left(z\right)\right)\hfill \\ \hfill & =\underset{B\in L^X}{\bigwedge }\left((B\left(x\right)\wedge B\left(y\right))\to \left(\left(\underset{m,n\in X}{\bigvee }(B\left(m\right)\wedge B\left(n\right)\wedge \mathcal{R}(m,z)\wedge \mathcal{R}(z,n))\to B\left(z\right)\right)\to B\left(z\right)\right)\right)\hfill \\ \hfill & \ge \underset{B\in L^X}{\bigwedge }\left((B\left(x\right)\wedge B\left(y\right))\to \underset{m,n\in X}{\bigvee }(B\left(m\right)\wedge B\left(n\right)\wedge \mathcal{R}(m,z)\wedge \mathcal{R}(z,n))\right)\hfill \\ \hfill & \ge \underset{B\in L^X}{\bigwedge }\left(\left(B\right(x)\wedge B(y\left)\right)\to \left(B\right(x)\wedge B(y)\wedge \mathcal{R}(x,z)\wedge \mathcal{R}(z,y\left)\right)\right)\hfill \\ \hfill & \ge \mathcal{R}(x,z)\wedge \mathcal{R}(z,y).\hfill \end{array}$$

It follows that

$$\begin{array}{cc}\hfill & \underset{x,y\in X}{\bigwedge }((A\left(x\right)\wedge A\left(y\right))\to \mathcal{S}\left(c{o}^{{\mathcal{C}}^{\mathcal{R}}}({\chi }_{\{x,y\}},A)\right)\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \underset{z\in X}{\bigwedge }(c{o}^{{\mathcal{C}}^{\mathcal{R}}}\left({\chi }_{\{x,y\}}\right)\left(z\right)\to A\left(z\right))\right)\hfill \\ \hfill & =\underset{z\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to (c{o}^{{\mathcal{C}}^{\mathcal{R}}}\left({\chi }_{\{x,y\}}\right)\left(z\right)\to A\left(z\right))\right)\hfill \\ \hfill & =\underset{z\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right)\wedge c{o}^{{\mathcal{C}}^{\mathcal{R}}}\left({\chi }_{\{x,y\}}\right)\left(z\right))\to A\left(z\right)\right)\hfill \\ \hfill & \le \underset{z\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left(\left(A\right(x)\wedge A(y)\wedge \mathcal{R}(x,z)\wedge \mathcal{R}(z,y\left)\right)\to A\left(z\right)\right)\hfill \\ \hfill & =\underset{z\in X}{\bigwedge }\left(\underset{x,y\in X}{\bigvee }(A\left(x\right)\wedge A\left(y\right)\wedge \mathcal{R}(x,z)\wedge \mathcal{R}(z,y))\to A\left(z\right)\right)\hfill \\ \hfill & ={\mathcal{C}}^{\mathcal{R}}\left(A\right).\hfill \end{array}$$

Conversely,

$$\begin{array}{cc}\hfill & \underset{x,y\in X}{\bigwedge }((A\left(x\right)\wedge A\left(y\right))\to \mathcal{S}(c{o}^{{\mathcal{C}}^{\mathcal{R}}}\left({\chi }_{\{x,y\}}\right),A))\hfill \\ \hfill & =\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \underset{z\in X}{\bigwedge }(c{o}^{{\mathcal{C}}^{\mathcal{R}}}\left({\chi }_{\{x,y\}}\right)\left(z\right)\to A\left(z\right))\right)\hfill \\ \hfill & =\underset{z\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \left(\underset{B\in L^X}{\bigwedge }(B\left(x\right)\wedge B\left(y\right)\wedge {\mathcal{C}}^{\mathcal{R}}\left(B\right)\to B\left(z\right))\to A\left(z\right)\right)\right)\hfill \\ \hfill & \ge \underset{z\in X}{\bigwedge }\underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to \left((A\left(x\right)\wedge A\left(y\right)\wedge {\mathcal{C}}^{\mathcal{R}}\left(A\right)\to A\left(z\right))\to A\left(z\right)\right)\right)\hfill \\ \hfill & \ge \underset{x,y\in X}{\bigwedge }\left((A\left(x\right)\wedge A\left(y\right))\to (A\left(x\right)\wedge A\left(y\right)\wedge {\mathcal{C}}^{\mathcal{R}}\left(A\right))\right)\hfill \\ \hfill & \ge {\mathcal{C}}^{\mathcal{R}}\left(A\right).\hfill \end{array}$$

Hence, ${\mathcal{C}}^{\mathcal{R}}\left(A\right)={\bigwedge }_{x,y\in X}(A\left(x\right)\wedge A\left(y\right)\to \mathcal{S}(c{o}^{{\mathcal{C}}^{\mathcal{R}}}\left({\chi }_{\{x,y\}}\right),A)),$ as desired. □

5. Conclusions

In this paper, we showed that there is a Galois correspondence between the category of strong L-fuzzy convex spaces and that of L-fuzzifying interval spaces. Further, we presented the concept of arity 2 strong L-fuzzy convex structures and proved that the category of arity 2 strong L-fuzzy convex spaces can be reflectively embedded into that of L-fuzzifying interval spaces. Finally, we investigated the relationship between strong L-fuzzy convex structures and L-fuzzy preorders. While these results lay a solid foundation within the framework of complete Heyting algebras, we acknowledge certain limitations and outline promising avenues for future research to broaden the scope and impact of this work:

• Limitation:

The current study assumes L to be a complete Heyting algebra. More general algebraic structures (e.g., residuated lattices or quantales) may be necessary for wider practical applications, particularly in domains like advanced fuzzy logic.

• Future Direction 1: In addition to interval operators, there are many mathematical structures closely related to convex structures that are worth studying. We will also consider the fuzzy forms of other mathematical structures related to convex structures and study their relationships in lattice-valued environments through Galois correspondence in category theory.
• Future Direction 2: Inspired by classical convex spaces and convex preference models in economics, we will define a convexity degree for preference relations using the $\alpha$-cut method and investigate the properties of fuzzy convex preferences under various fuzzy convex structures.