Offline Magnetometer Calibration Using Enhanced Particle Swarm Optimization

Abstract

To address the decline in measurement accuracy of magnetometers due to process errors and environmental interference, as well as the insufficient robustness of traditional calibration algorithms under strong interference conditions, this paper proposes an ellipsoid fitting algorithm based on Dynamic Adaptive Elite Particle Swarm Optimization (DAEPSO). The proposed algorithm integrates three enhancement mechanisms: dynamic stratified elite guidance, adaptive inertia weight adjustment, and inferior particle relearning via Lévy flight, aiming to improve convergence speed, solution accuracy, and noise resistance. First, a magnetometer calibration model is established. Second, the DAEPSO algorithm is employed to fit the ellipsoid parameters. Finally, error calibration is performed based on the optimized ellipsoid parameters. Our simulation experiments demonstrate that compared with the traditional Least Squares Method (LSM) the proposed method reduces the standard deviation of the total magnetic field intensity by 54.73%, effectively improving calibration precision in the presence of outliers. Furthermore, when compared to PSO, TSLPSO, MPSO, and AWPSO, the sum of the absolute distances from the simulation data to the fitted ellipsoidal surface decreases by 53.60%, 41.96%, 53.01%, and 27.40%, respectively. The results from 60 independent experiments show that DAEPSO achieves lower median errors and smaller interquartile ranges than comparative algorithms. In summary, the DAEPSO-based ellipsoid fitting algorithm exhibits high fitting accuracy and strong robustness in environments with intense interference noise, providing reliable theoretical support for practical engineering applications.

1. Introduction

In modern warfare, offensive weapons face stringent demands for precision strikes and rapid response. Guided munitions, with their high-accuracy target engagement and tactical flexibility, have become indispensable assets [1,2]. Their precision strike capability relies on accurate projectile attitude acquisition, where geomagnetic measurement—as a passive, all-weather, and globally applicable technology—is widely adopted for projectile navigation and attitude determination. As the core sensor, the magnetometer’s accuracy directly impacts attitude solution reliability and guidance stability. However, in practical applications, magnetometer readings are susceptible to various systematic errors caused by sensor manufacturing imperfections and environmental interference. Specifically, these errors can be categorized into (1) fabrication-induced errors such as sensitivity deviations, non-orthogonality, and zero-offset bias, and (2) environmental interference errors caused by hard-iron and soft-iron effects [3]. Thus, pre-launch calibration is essential to enhance measurement accuracy and ensure reliable attitude data.

Traditional calibration methods such as the Least Squares Method (LSM) and ellipsoid fitting have been widely adopted. For instance, Fang Xu et al. [4], Zhi Zuwei et al. [5], and Peng Jiabao et al. [6] all constructed models based on LSM to solve error parameters. However, LSM exhibits high sensitivity to outliers. Larger residuals become significantly amplified during squaring operations, causing model deviation from actual conditions. Moreover, such methods typically rely on matrix inversion or pseudo-inverse operations, resulting in poor numerical stability. Li Zhimin et al. [7] proposed an improved least squares ellipsoid fitting method based on Random Sample Consensus (RANSAC). Although this approach enhances robustness against abnormal data, RANSAC’s random sampling mechanism remains vulnerable to noise interference. Overall, traditional methods demonstrate insufficient noise resistance, failing to ensure calibration accuracy and stability.

To overcome these limitations, researchers have turned to intelligent optimization algorithms for magnetometer error calibration. For example, algorithms such as the artificial fish swarm algorithm [8], the dragonfly algorithm [9], the beetle swarm antenna search algorithm [10], the genetic algorithm [11], differential evolution [12], improved Particle Swarm Optimization (PSO) [13,14], the gray wolf optimizer algorithm [15,16], the dung beetle optimizer [17], and the moth–flame algorithm [18] have been applied to enhance accuracy and robustness. While these methods perform well in specific scenarios, they still exhibit robustness and efficiency shortcomings in complex environments. Consequently, developing high-precision, robust, and efficient calibration algorithms remains a critical research priority.

To address these challenges, this paper proposes a Dynamic Adaptive Elite Particle Swarm Optimization (DAEPSO)-based ellipsoid fitting algorithm, targeting high-precision triaxial magnetometer calibration in complex magnetic interference environments. Specifically, DAEPSO first performs ellipsoid fitting on raw magnetometer measurements. Then, an error compensation model is constructed using the optimized ellipsoid parameters, and, finally, the raw geomagnetic data is corrected via the calibrated model. The proposed method aims to enhance calibration accuracy, robustness, and convergence efficiency compared to the existing methods.

2. Calibration Model and Ellipsoid Fitting Method

2.1. Magnetometer Calibration Model

For triaxial magnetometer errors caused by manufacturing imperfections and environmental interference, the relationship between measured values and true values is expressed by Equation (1) [19]:

$$H_m=K_{si}{K}_n\left(K_s{H}_r+H_h\right)+H_0$$

(1)

where $H_m$ is the actual measured value, $H_r$ is the ideal output value, $K_{si}$ is the sensitivity error matrix, $K_n$ is the non-orthogonal error matrix, $K_s$ is the soft-iron error matrix, $H_h$ is the hard-iron error vector, and $H_0$ is the zero-offset error vector. Equation (1) can be further simplified as

$$H_m=K{H}_r+H$$

(2)

where $K=K_{si}{K}_n{K}_s$, $H=K_{si}{K}_n{H}_h+H_0$. Based on Equation (2), the magnetometer error compensation model is derived as

$$H_r=K^{-1}\left(H_m-H\right)$$

(3)

Under ideal conditions, the total geomagnetic field intensity measured by a triaxial magnetometer is constant $\left|\right|H_b\left|\right|$, with measurements distributed on a sphere of radius $\left|\right|H_b\left|\right|$. Based on Equation (3), the total intensity is

$${\parallel H_b\parallel }^2={\left(H_r\right)}^T{H}_r={\left(H_m-H\right)}^T{\left(K^{-1}\right)}^T{K}^{-1}\left(H_m-H\right);$$

(4)

that is

$${\left(H_m-H\right)}^T{\displaystyle \frac{{\left(K^{-1}\right)}^T{K}^{-1}}{{\parallel H_b\parallel }^2}}\left(H_m-H\right)=1$$

(5)

2.2. Ellipsoid Fitting Method

In practical measurements, influenced by measurement errors, triaxial magnetometer output data typically distributes on an ellipsoidal surface with an off-origin center. A well-defined mathematical correspondence exists between this ellipsoid’s parameters and the magnetometer error model coefficients. Consequently, geomagnetic error calibration parameters can be obtained by solving ellipsoidal parameters [20].

As a specific type of quadric surface, the standard ellipsoid equation is expressed as

$$F\left(\xi ,z\right)={\xi }^{T}z=a{x}^2+b{y}^2+c{z}^2+2dxy+2exz+2fyz+2px+2qy+2rz+g=0$$

(6)

where $z={\left[x^2,y^2,z^2,2xy,2xz,2yz,2x,2y,2z,1\right]}^T$ is the combined vector formed by the measured triaxial geomagnetic data, while $\xi ={\left[a,b,c,d,e,f,p,q,r,g\right]}^T$ is the ellipsoidal parameter vector.

An ellipsoid fitting model is established based on the least squares criterion [21]:

$$\underset{\xi }{min}{\parallel F(\xi ,z)\parallel }^2=\underset{\xi }{min}{\xi }^T{D}^{T}D\xi$$

(7)

where D is the measurement data matrix, defined as

$$D=\left[\begin{array}{cccccccccc}{x}_1^2& y_1^2& z_1^2& 2x_1{y}_1& 2x_1{z}_1& 2y_1{z}_1& 2x_1& 2y_1& 2z_1& 1\\ x_2^2& y_2^2& z_2^2& 2x_2{y}_2& 2x_2{z}_2& 2y_2{z}_2& 2x_2& 2y_2& 2z_2& 1\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ x_n^2& y_n^2& z_n^2& 2x_n{y}_n& 2x_n{z}_n& 2y_n{z}_n& 2x_n& 2y_n& 2z_n& 1\end{array}\right]$$

(8)

We rewrite the ellipsoid Equation (6) in vector form:

$${\left(X-X_0\right)}^{T}A\left(X-X_0\right)=1$$

(9)

where $A=\left[\begin{array}{ccc}a& d& e\\ d& b& f\\ e& f& c\end{array}\right]$ is the ellipsoid shape parameter matrix, while $X_0=-A^{-1}\left[\begin{array}{c}p\\ q\\ r\end{array}\right]$ is the ellipsoid center coordinates.

Combining Equations (5) and (9), the parameter transformation relationship is derived:

$$\left\{\begin{array}{c}{\displaystyle \frac{{\left(K^{-1}\right)}^T{K}^{-1}}{{\parallel H_b\parallel }^2}}=G^{T}G=A\hfill \\ H=X_0\hfill \end{array}\right.$$

(10)

where G and $K^{-1}$ can be obtained by the following equation [22]:

$$\left\{\begin{array}{c}{K}^{-1}=\left|\right|H_b\left|\right|G\hfill \\ G=VD{V}^{-1}\hfill \end{array}\right.$$

(11)

where G is a diagonal matrix whose elements are the square roots of the eigenvalues of A, and where V is the matrix composed of the eigenvectors of A. After determining the error correction $K^{-1}$ and bias vector H, magnetometer calibration is performed using Equation (3).

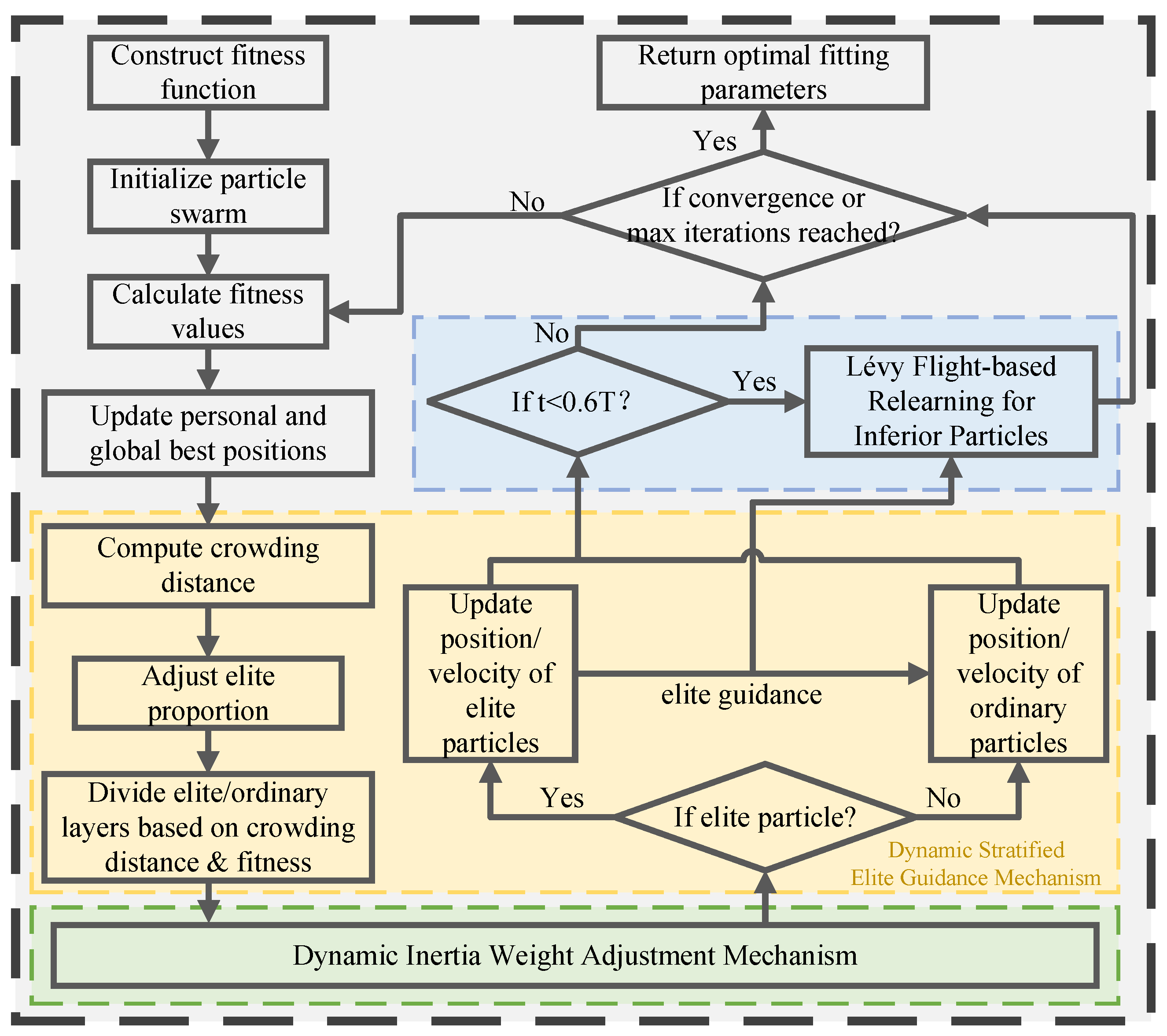
3. DAEPSO-Based Ellipsoid Fitting Algorithm

3.1. Standard PSO

The Particle Swarm Optimization (PSO) algorithm is a metaheuristic technique inspired by collective biological behavior, drawing on the collaborative exploration observed in bird flock foraging. In PSO, each particle represents a candidate solution in the search space, characterized by a position vector x and velocity vector v. Particles iteratively adjust their velocities by leveraging their personal best position $pbest$ and the swarm’s global best position $gbest$, guiding the search toward optimal regions [23]. The velocity and position update equations in standard PSO are expressed as follows:

$$\left\{\begin{array}{c}{v}_i^{t+1}=\omega ·v_i^t+c_1·r_1(pbes{t}_i^t-x_i^t)+c_2·r_2(gbes{t}^t-x_i^t)\hfill \\ x_i^{t+1}=x_i^t+v_i^{t+1}\hfill \end{array}\right.$$

(12)

where $v_i^t$ and $x_i^t$ denote the velocity vector and position vector of particle i at iteration t, w is the inertia weight controlling particle momentum retention, $c_1$ and $c_2$ are acceleration factors weighting individual and social cognition, $pbes{t}_i^t$ represents the historical best position of particle i at iteration t, $gbes{t}^t$ indicates the global best position of the swarm through iteration t, and $r_1$, $r_2$ denotes uniformly distributed random variables.

3.2. Improvement Strategies of DAEPSO Algorithm

During particle swarm optimization, balancing “exploration” of the solution space and “exploitation” of potential high-quality solutions is critical for enhancing global optimization capability. To efficiently search for global optima, the algorithm must dynamically balance exploration and exploitation across different phases: maintaining sufficient population diversity to broaden the search scope in the early stages, while focusing on promising regions to improve convergence precision in later phases. However, traditional PSO often lacks adaptive control mechanisms for this balance when handling complex problems, leading to local optima entrapment and limited search performance. To address this, this paper proposes a Dynamic Adaptive Elite Particle Swarm Optimization (DAEPSO) algorithm, which significantly enhances optimization through three core mechanisms:

(1)

Dynamic stratified elite guidance: Dynamically divides particles into elite and ordinary layers based on individual fitness and crowding distance, utilizing elite particles’ search experience to guide ordinary particles’ exploration direction.

(2)

Dynamic inertia weight adjustment: Adaptively adjusts inertia weight according to iteration progress.

(3)

Lévy flight-based relearning for inferior particles: Implements Lévy flight for resampling particles trapped in low-quality regions, guiding escape from local optima.

3.2.1. Dynamic Stratified Elite Guidance Mechanism

(1)

Elite Measurement and Dynamic Stratification

In each iteration, the algorithm evaluates particles based on fitness values and crowding distance. The particles are sorted in descending order by the product of these two metrics, with the top $E_r·NP$ particles forming the elite layer and the remainder forming the ordinary layer, as shown in Equation (13):

$$\left\{\begin{array}{c}X=sort\left(f·d\right)\hfill \\ E_p=\left\{x_i\in X|i=1,2,\dots ,E_r·NP\right\}\hfill \\ N_p=\left\{x_i\in X|i=E_r·NP,\dots ,NP\right\}\hfill \end{array}\right.$$

(13)

where X denotes the set of particles sorted according to the product of fitness value and crowding distance, $N_P$ denotes the population size of the particle swarm, $E_p$ denotes the elite particle set, $N_p$ represents the ordinary particle set, $E_r$ indicates the elite proportion, argmax sorts particles by fitness-crowding distance product, f is the fitness value, and d is the crowding distance, calculated as

$$d_i={\displaystyle \frac{f_{i+1}-f_{i-1}}{f_{min}-f_{max}}}$$

(14)

where $f_{max}$ and $f_{min}$ refer to the maximum and minimum fitness values in the current iteration, respectively. Subsequently, the elite proportion is dynamically adjusted based on the swarm’s average crowding distance to balance exploration and exploitation needs throughout the search. The adjustment function is designed as

$$E_r=r_{min}+(r_{max}-r_{min}){\displaystyle \frac{d_{mean}-d_{min}}{d_{max}-d_{min}}}$$

(15)

where $r_{min}$ and $r_{max}$ are the lower/upper bounds of the elite proportion, $d_{min}$ and $d_{max}$ are the lower/upper bounds of the crowding distance, and $d_{mean}$ is the average crowding distance at the current iteration.

(2)

Differentiated Updates for Elite and Ordinary Layers

During particle updates, the algorithm applies distinct update strategies based on particle stratification.

Elite Layer:

Elite particles locate in promising regions, primarily performing local exploitation. Their updates follow standard PSO (Equation (12)), but with the individual learning factor $c_{1e}=2.0$ and the social learning factor $c_{2e}=1.5$ to intensify historical best utilization for refined searching.

Ordinary Layer:

As exploration agents, ordinary particles incorporate elite guidance to enhance convergence toward high-quality regions. Their update formula is

$$\left\{\begin{array}{c}{v}_i^{t+1}=w·v_i^t+c_{1n}·r_1(pbes{t}_i^t-x_i^t)+c_{2n}·r_2(gbes{t}_i^t-x_i^t)+c_{3n}·r_3·e_{guide}\hfill \\ x_i^{t+1}=x_i^t+v_i^{t+1}\hfill \end{array}\right.$$

(16)

where $c_{1n}$, $c_{2n}$, $c_{3n}$ denote the learning factors for personal best, global best, and elite guidance, with values of 1.5, 2.0, and 0.2, respectively, while $e_{guide}$ is the elite guidance term defined as the mean positional difference between the current particle and the randomly selected elites:

$$e_{guide}={\displaystyle \frac{1}{k}}\sum _{j\in {\epsilon }_k}\left(x_j-x_i\right)$$

(17)

where ${\epsilon }_k$ represents a random subset (20% of elite particles) from $E_p$.

3.2.2. Dynamic Inertia Weight Adjustment Mechanism

Inertia weight is a key parameter in PSO that balances particle search scope and convergence speed. This paper employs a dynamic adjustment method based on a cosine annealing strategy. This approach enables smooth decay of inertia weight, enhancing global search capability in the early stages while gradually transitioning to local exploitation later, effectively avoiding premature convergence and improving final precision. The adjustment formula is

$$w={w_{min}+{\displaystyle \frac{1}{2}}\left(w_{min}-w_{max}\left[1+cos\left(\pi ·{\displaystyle \frac{t}{T}}\right)\right]\right)}_{min}$$

(18)

where $w_{min}$ and $w_{max}$ denote the minimum and maximum inertia weights, t represents the current iteration count, and T indicates the maximum iteration count.

3.2.3. Lévy Flight-Based Relearning for Inferior Particles

To further enhance global exploration in complex search spaces, this paper introduces a Lévy flight-based relearning mechanism for inferior particles based on dynamic stratified elite guidance, directing disadvantaged individuals to escape local optima.

The specific procedure is as follows: First, sort particles by fitness and select the bottom 10% as the inferior particle set. Unlike random re-initialization or undirected perturbation, this mechanism incorporates precomputed elite guidance with Lévy flight disturbance during updates:

$$x_{new}^{t+1}=e_{guide}+Levy$$

(19)

This mechanism combines a Lévy flight’s long-jump capability with elite-guided directional constraints, enhancing escape from local optima while increasing perturbation effectiveness and reducing futile exploration, thereby strengthening algorithm robustness and diversity.

Figure 1 illustrates the complete DAEPSO algorithm workflow.

The detailed process of the proposed DAEPSO algorithm is illustrated in Algorithm 1 as pseudocode.

Algorithm 1: Pseudocode of DAEPSO.

3.3. DAEPSO-Based Ellipsoid Fitting Algorithm

Traditional ellipsoid fitting methods use least squares to fit data points to an ellipsoidal model, but their sensitivity to noise and outliers often causes fitting deviations. To address this, this paper proposes a DAEPSO-based ellipsoid fitting algorithm that leverages a particle swarm cooperative search for global optimization to achieve high-precision ellipsoid parameter estimation.

3.3.1. Fitness Function

The core objective is to accurately fit optimal ellipsoid parameters $\xi$, using DAEPSO. To evaluate the fitting quality, the sum of the squared distances from the data points to the ellipsoidal surface is adopted as the fitness function, given by Equation (20):

$$L\left(\xi \right)=\sum _{i=1}^N{\left(f\left(x_i,y_i,z_i\right)\right)}^2$$

(20)

where N denotes the total number of sampling points,

$$f(x,y,z)=a{x}^2+b{y}^2+c{z}^2+2dxy+2exz+2fyz+2px+2qy+2rz+g$$

(21)

3.3.2. DAEPSO Parameter Initialization

The initial parameters for DAEPSO are listed in

Table 1. Initialization parameter settings for DAEPSO.

Parameter	Symbol	Value/Range
Population size	$NP$	100
Parameter dimension	$dim$	10
Maximum iterations	T	500
Inertia weight	${\omega }_{min},{\omega }_{max}$	0.5, 0.7

. These values are set based on preliminary experiments and common practices in the literature to ensure a balance between convergence speed and solution quality.

4. Simulation Experiment Verification

4.1. Simulated Data Generation and Experimental Setup

To validate the effectiveness and robustness of the proposed DAEPSO-based ellipsoid fitting algorithm under complex magnetic interference, a numerical simulation environment was constructed based on the attitude resolution model of triaxial magnetometers [24]. The simulation experiments were conducted on a personal computer equipped with an AMD Ryzen 7 8845H processor, 24 GB of RAM, and MATLAB R2022b. One thousand sets of randomly generated ideal triaxial geomagnetic data were used, with the total geomagnetic field intensity set to 50 µT. To simulate practical error interference, five typical errors were introduced: hard-iron, soft-iron, sensitivity, non-orthogonal, and zero-offset errors. The parameter settings for each error are listed in

Table 2. Parameters for magnetometer simulation model.

Name	Value
Geomagnetic intensity/µT	50
Magnetic declination/∘	$-5.8$
Magnetic inclination/∘	$49.0$
Sensitivity coefficients	$\left[1.1130.9041.107\right]$
Non-orthogonal angles	$\left[0.00280.00260.0035\right]$
Zero-offset error/µT	${[2.0-3.04.0]}^T$
Soft-iron error	$\left[\begin{array}{ccc}0.84& -0.053& 0.026\\ 0.082& 0.72& -0.012\\ -0.016& 0.034& 0.83\end{array}\right]$
Hard-iron error/µT	${[10.030.0-10.0]}^T$

[25].

Based on this data, multiple comparative experiments were designed to comprehensively evaluate DAEPSO’s performance. First, geomagnetic data correction was performed, using both DAEPSO-based ellipsoid fitting and LSM-based ellipsoid fitting algorithms, with detailed comparative analysis. Second, to further demonstrate DAEPSO’s superiority, standard PSO [26], Two-Swarm Learning Particle Swarm Optimization (TSLPSO) [27], Modified Particle Swarm Optimization (MPSO) using adaptive strategy [28], and a novel sigmoid-function-based Adaptive Weighted Particle Swarm Optimizer (AWPSO) [29] were integrated with ellipsoid fitting. Systematic analysis of the algorithmic differences was conducted by comparing the optimization results.

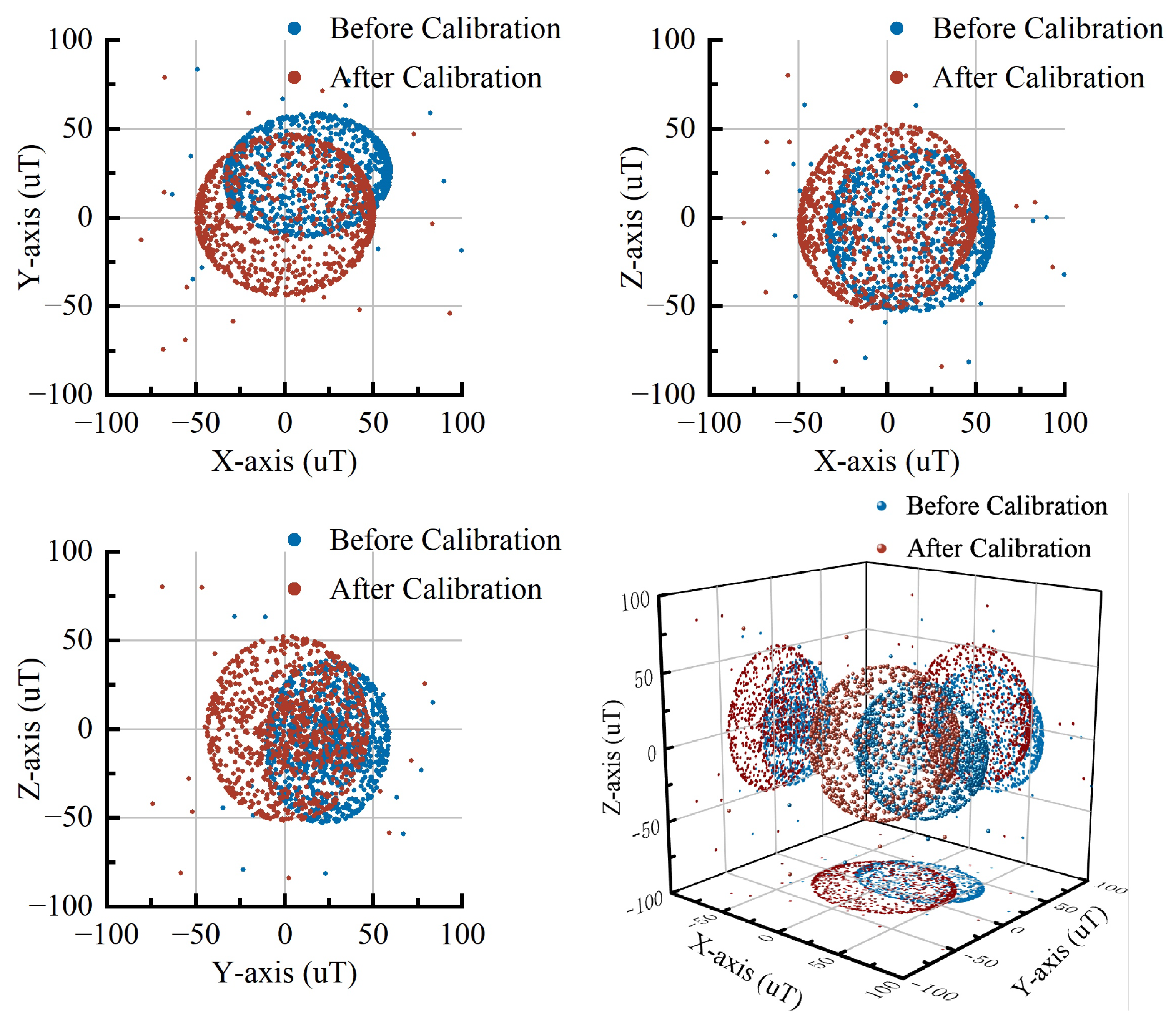
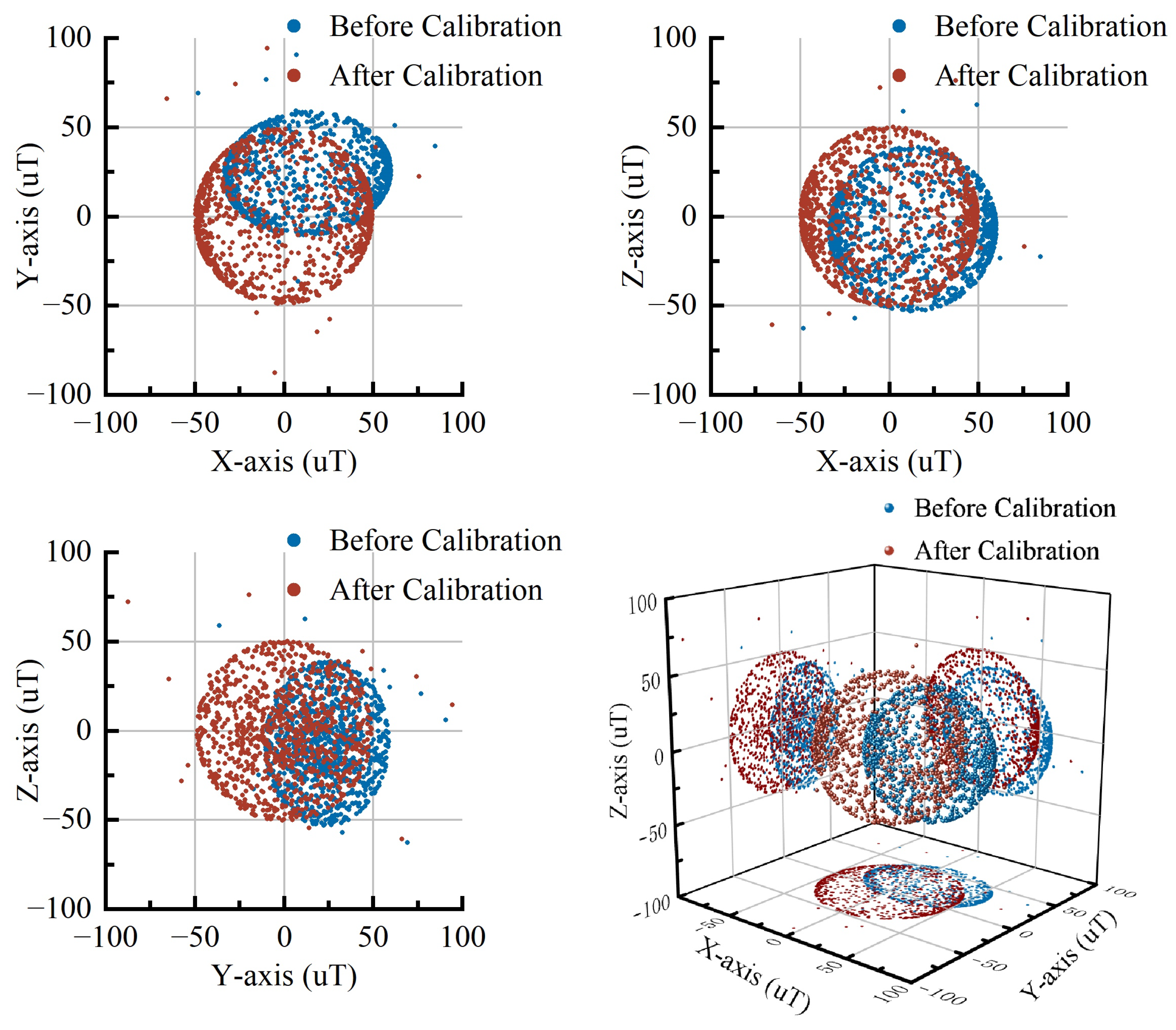
4.2. Comparison with LSM

To verify the robustness of DAEPSO in handling outlier-contaminated data, 2% outlier noise was introduced to the standard dataset to simulate extreme measurement errors. Comparative experiments with LSM-based ellipsoid fitting were conducted to evaluate fitting stability under outlier interference.

Figure 2 and Figure 3 display geomagnetic data distributions before and after calibration for both algorithms with outliers. Our observations show that LSM’s sensitivity to outliers causes corrected results to significantly deviate from ideal spherical topology in 3D space. In contrast, DAEPSO maintains smooth geometric structure and distribution despite outlier noise, demonstrating notable robustness.

For quantitative assessment of the fitting effects, Figure 4 shows variations in the total magnetic field intensity before and after correction. Before correction, affected by errors, the total intensity exhibited significant fluctuations; excluding the outlier data, its standard deviation reached 11.70 µT. After calibration by LSM-based ellipsoid fitting, the standard deviation decreased to 1.48 µT, yet the results still deviated from the ideal values. In contrast, the DAEPSO-based ellipsoid fitting substantially improved the calibration accuracy, with the corrected total intensity converging closer to the theoretical values and the standard deviation further reduced to 0.67 µT, achieving a 54.73% reduction compared to the LSM.

These results confirm DAEPSO’s stronger anti-interference capability with outlier-contaminated data. Compared to the LSM, DAEPSO effectively suppresses outlier impact, delivering more stable and reliable fitting models.

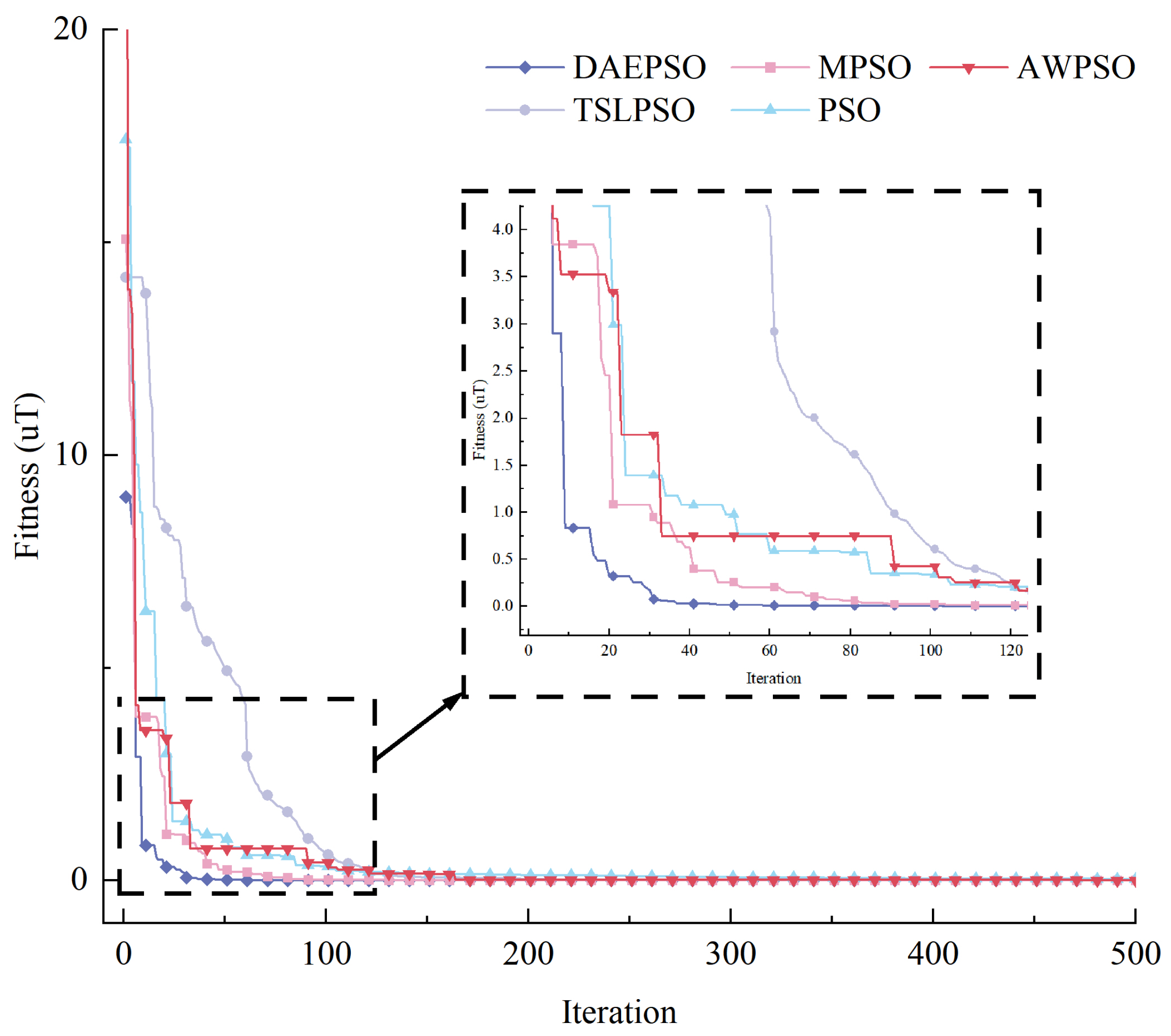
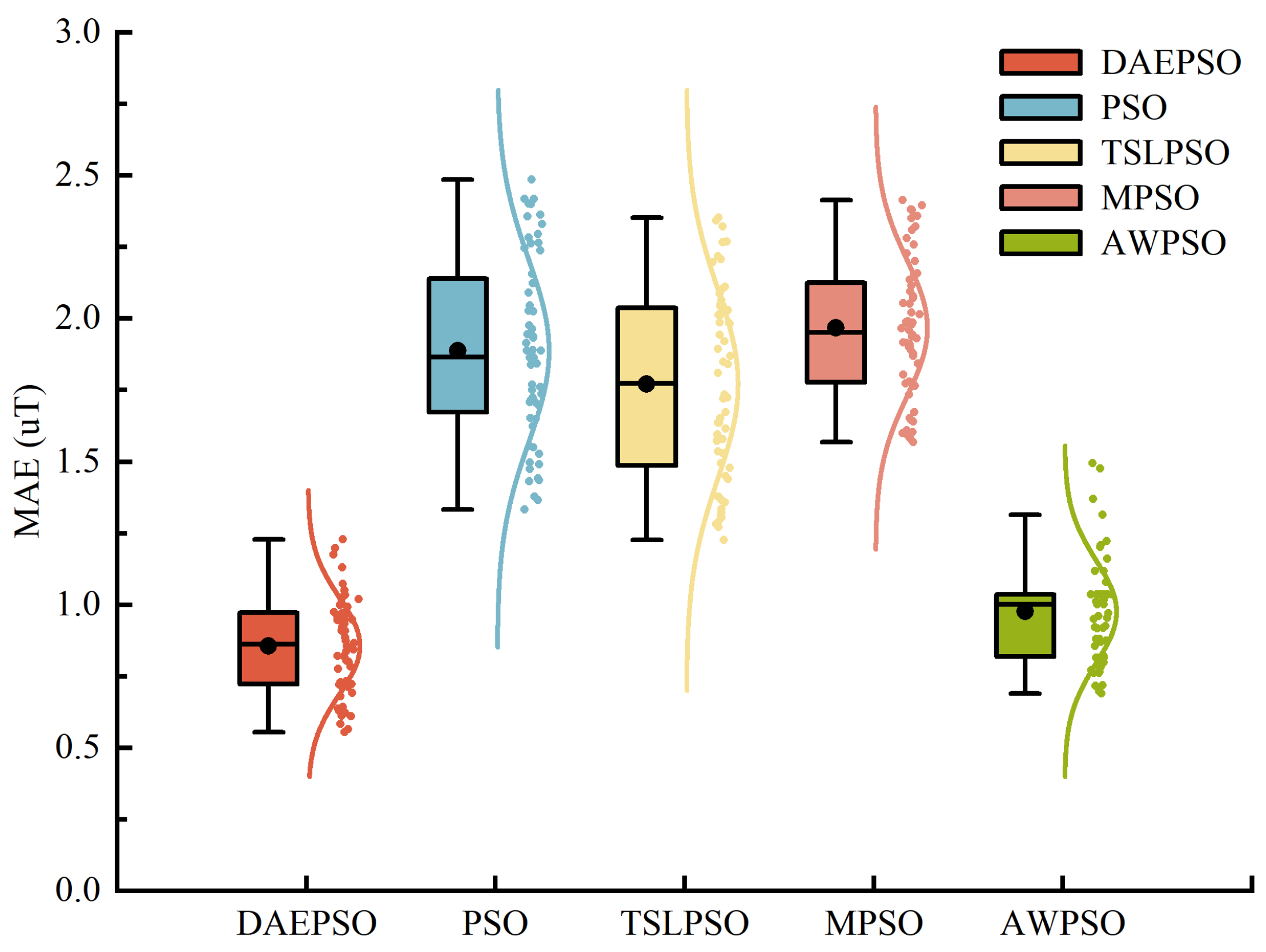
4.3. Comparison with PSO Variants

To further verify the performance advantages of DAEPSO, comparative analysis was conducted against traditional PSO, TSLPSO, MPSO, and AWPSO. The key parameters for each algorithm are listed in

Table 3. Optimization algorithm parameters.

Algorithm	Parameters
PSO	$c_1=1.5,c_2=2.5,w:0.7\sim 0.5$
TSLPSO	$c_1=c_2=1.5,c_3:0.5\sim 2.5,w:0.9\sim 0.4$
MPSO	$c_1=c_2=2,w:0.9\sim 0.4$
AWPSO	$w:0.9\sim 0.5,a=0.000035·m,b=0.5,c=0,d=1.5$

.

For the quantitative fitting performance analysis (excluding outliers), the sum of the absolute distances from the data points to the fitted ellipsoidal surface served as the evaluation metric. Figure 5 shows the performance differences under this metric. The results indicate that DAEPSO achieved the sum of 700.91 µT—reducing by 53.60% versus traditional PSO (1510.66 µT). Superiority remained significant against variants: 41.96% reduction versus TSLPSO (1207.58 µT), 53.01% versus MPSO (1491.66 µT), and 27.40% versus AWPSO (965.42 µT). This confirms DAEPSO’s enhanced search capability.

Figure 6 illustrates the fitness convergence curves of different algorithms during the optimization process, enabling a comparative analysis of their convergence performance. As shown in the figure, the proposed DAEPSO algorithm exhibited a faster reduction in fitness values during the early iterations and achieved convergence with fewer iterations compared to the benchmark algorithms, including PSO, TSLPSO, MPSO, and AWPSO. These results confirm the superior global search efficiency of DAEPSO.

To further evaluate stability, 60 independent trials per algorithm were executed. The Mean Absolute Error (MAE) between the simulated data and the fitted ellipsoid was statistically analyzed via boxplots (Figure 7). DAEPSO yielded a median error of 0.84 µT, significantly lower than PSO (1.86 µT), TSLPSO (1.77 µT), MPSO (1.95 µT), and AWPSO (1.00 µT). Its Interquartile Range (IQR) of 0.21 µT also outperformed the others: PSO (0.45 µT), TSLPSO (0.54 µT), MPSO (0.34 µT), AWPSO (0.22 µT).

In summary, DAEPSO not only surpassed the existing PSO variants in optimal solution accuracy but also maintained higher consistency and smaller fluctuation ranges across repeated trials, robustly validating its reliability in complex environments.

5. Conclusions

This paper proposes an enhanced Particle Swarm Optimization algorithm (DAEPSO) that integrates dynamic stratified elite guidance, adaptive inertia weight adjustment, and Lévy flight-based relearning for inferior particles, aimed at high-precision triaxial magnetometer calibration. Applied to ellipsoid fitting, the method effectively addresses the limitations of conventional approaches under strong interference and outlier conditions. Comparative analysis with the LSM, traditional PSO, TSLPSO, MPSO, and AWPSO validates the method’s effectiveness, yielding the following key conclusions:

(1)

Compared to the LSM, DAEPSO-based ellipsoid fitting demonstrates superior anti-interference capability and higher precision when processing outlier-contaminated data, effectively mitigating outlier impact while maintaining stability.

(2)

Compared to traditional PSO, TSLPSO, MPSO, and AWPSO, DAEPSO more efficiently locates global optima in ellipsoid fitting and exhibits enhanced reliability and consistency across repeated trials.

In summary, the proposed DAEPSO-based ellipsoid fitting algorithm shows advantages in interference resistance, convergence efficiency, and robustness, offering a promising and scalable calibration solution for magnetometers and potentially other sensors.

Future research will focus on two main directions: First, the development of a real-time dynamic calibration method based on DAEPSO to address the variations and interferences encountered by magnetometers in practical applications, ensuring precise calibration in rapidly changing environments. Second, further optimization of the DAEPSO algorithm will be pursued to enhance its convergence speed and global search capability, exploring more efficient heuristic strategies and adaptive adjustment mechanisms. These improvements will enhance the real-time performance and robustness of DAEPSO, expanding its applicability in real-world engineering scenarios.