Finite-Time Tracking Control in Robotic Arm with Physical Constraints Under Disturbances
Abstract
1. Introduction
- In contrast to [1,3,11,12,13,14,15,16,17,18,19], this study employs a specific class of NP functions (also called nonlinear transformations) to design the control law, which deals with the asymmetric yet time-varying position and velocity constraints without involving feasibility conditions. Compared with traditional methods [8,9,10], the states are always within the given constraints, without solving complex optimization problems. The states can approach the constraint boundaries arbitrarily.
- NP is also used in the framework of finite time control to ensure the given tracking quality. The transient and steady-state performance of the tracking errors are improved. Meanwhile, the other system signals converge within a finite time under different initial conditions.
2. Preliminaries and Problem Formulation
2.1. Notations and Key Lemmas
- is Euclidean space of dimension with norm .
- denotes the space of real matrices with the Frobenius norm .
- denotes the zero matrix (of the corresponding dimension).
- For quadratic matrices means that is a positive-definite matrix (negative-definite matrix).
- or represents the maximum or minimum singular value of matrix.
- is the trace of matrix.
2.2. Problem Formulation
3. Main Results
3.1. DOB Design via RBFNNs
3.2. Nonlinear Mapping
- (a).
- for all ;
- (b).
- is a continuously differentiable function and
- (c).
- is bounded function on for all .
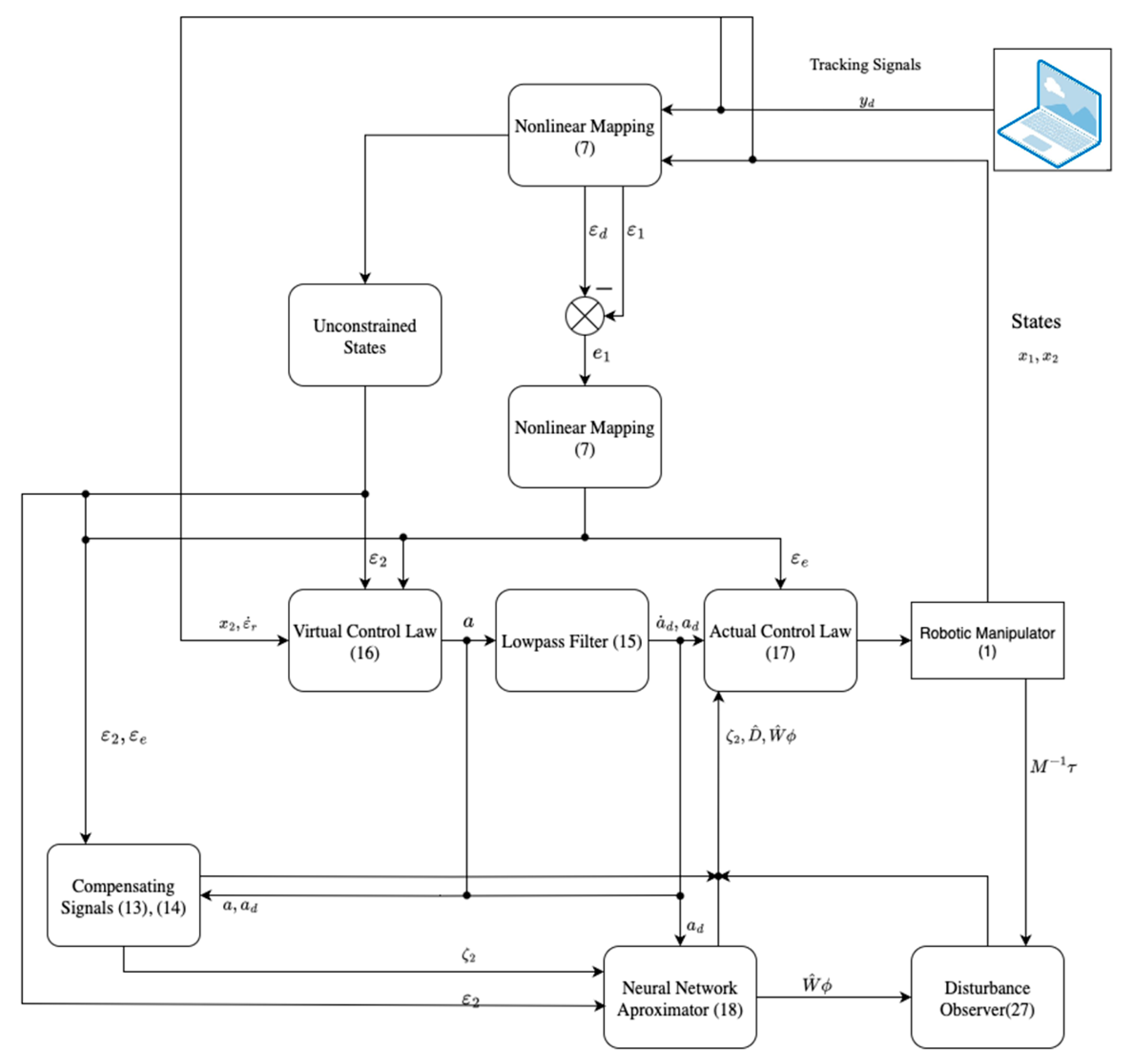
3.3. Control Design for Uncertain Robotic Manipulators
3.4. Stability Analysis
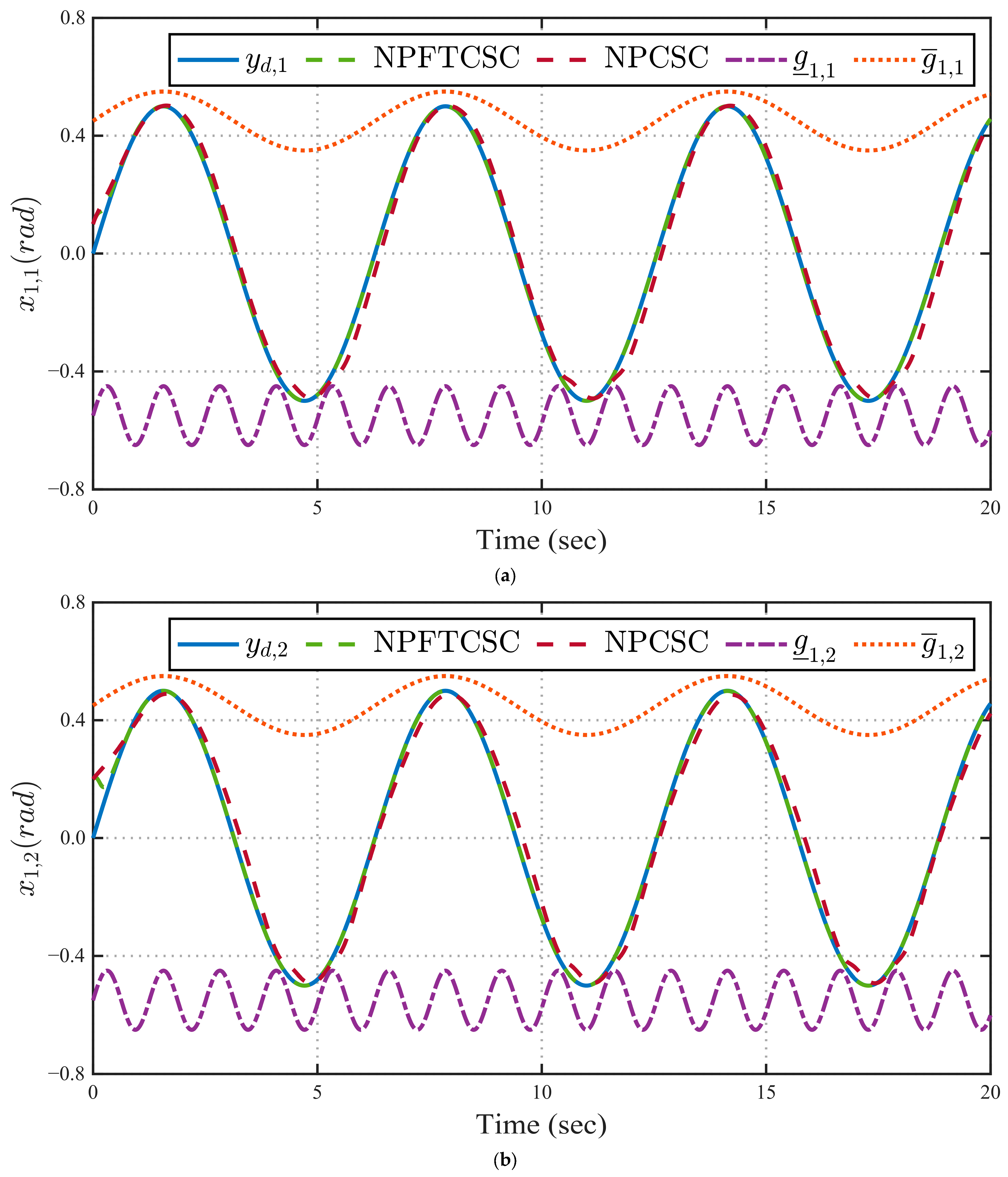
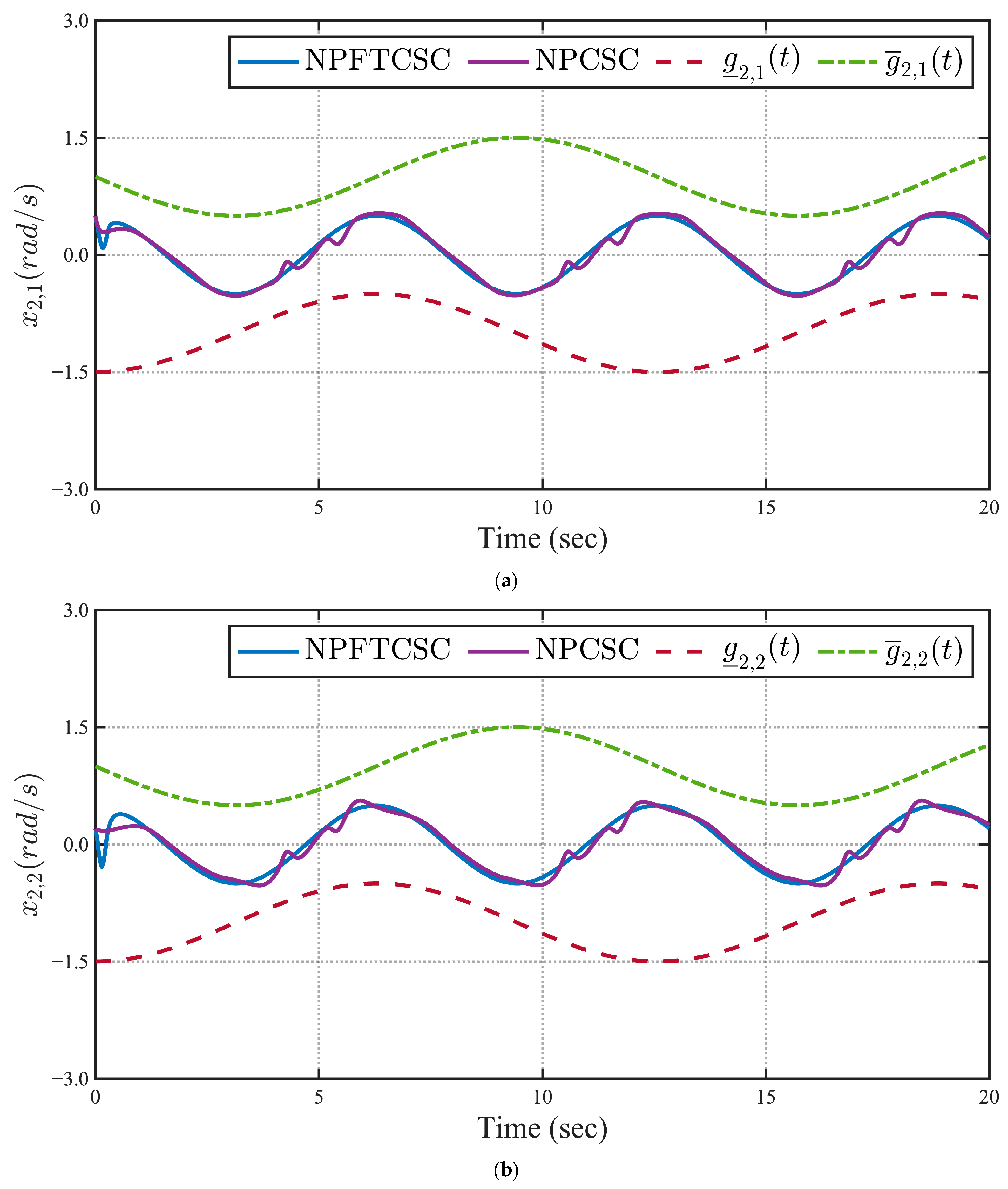
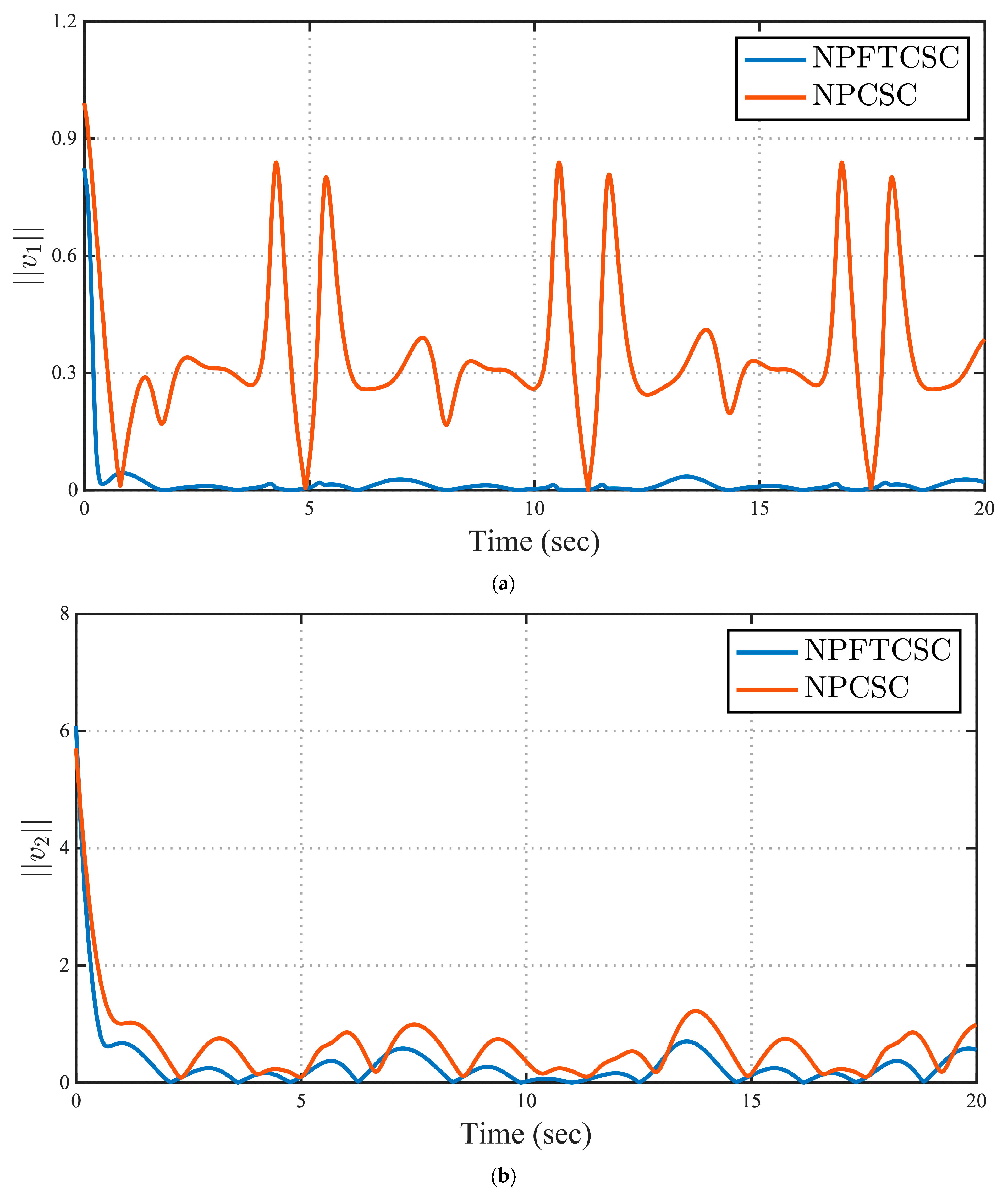
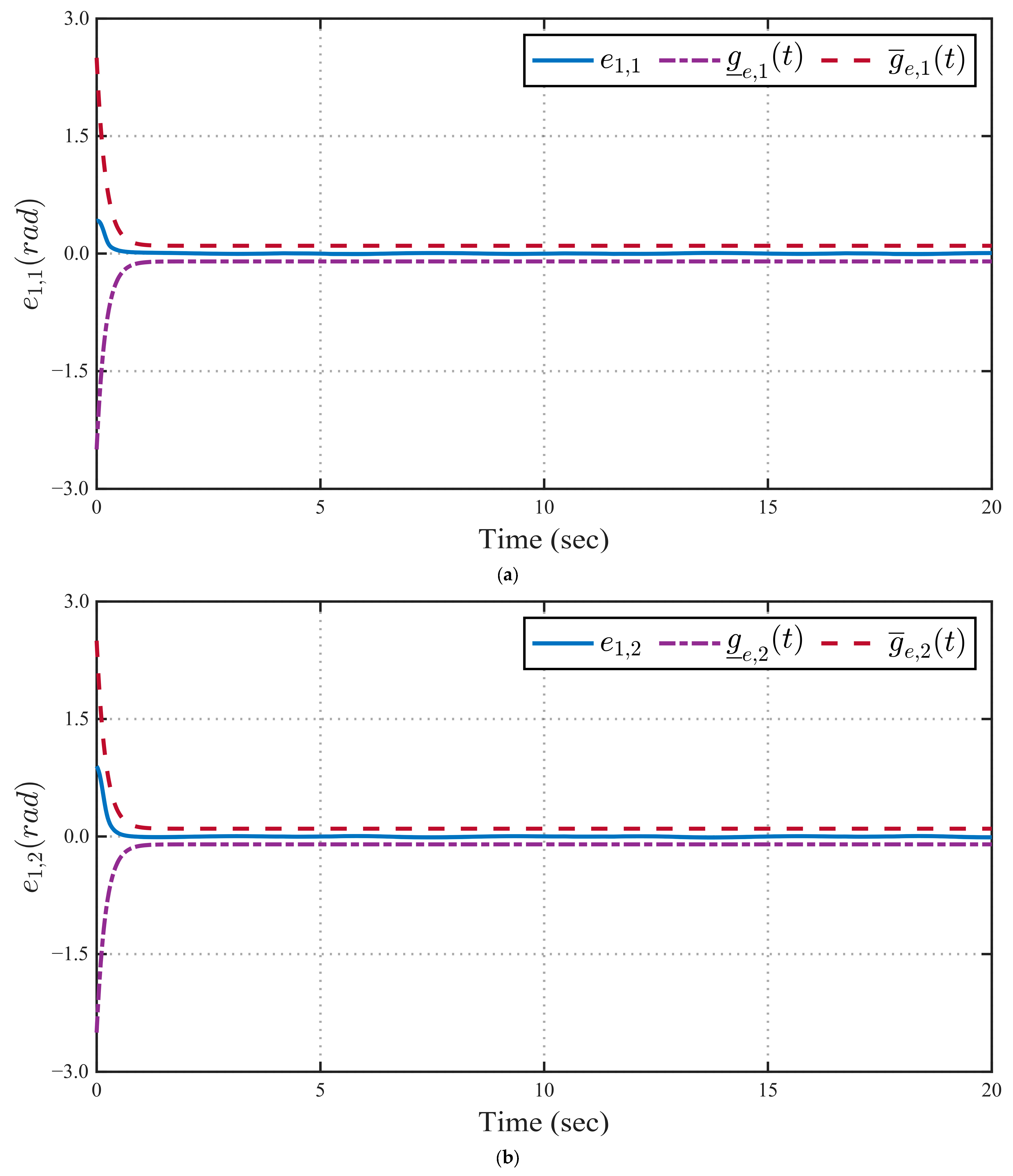
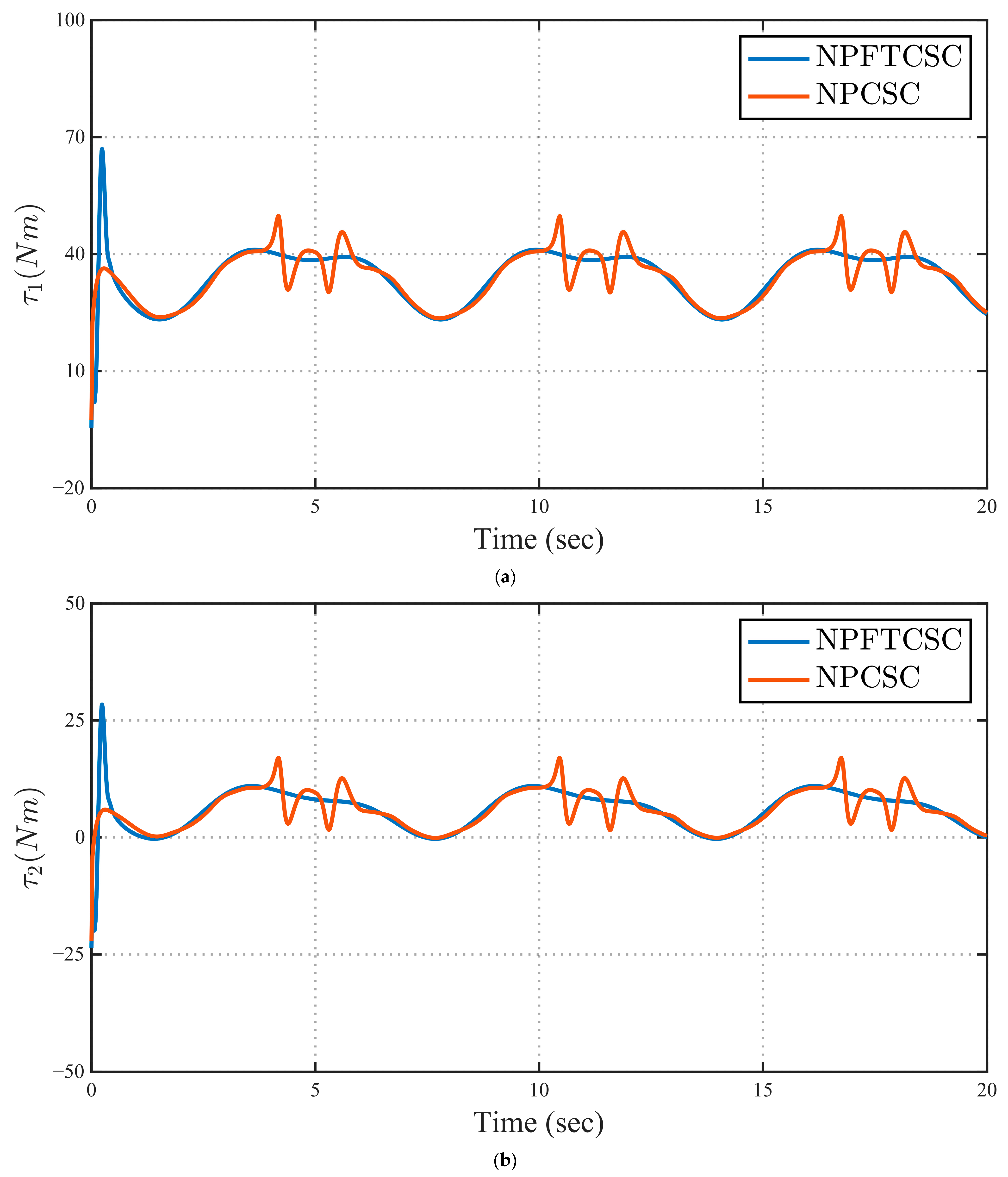
4. Simulations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qi, R.; Lam, H.-K.; Liu, J.; Yu, J. Adaptive Fuzzy Finite-Time Singular Perturbation Control for Flexible Joint Manipulators with State Constraints. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 7521–7527. [Google Scholar] [CrossRef]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Liu, Q.; Zhang, Z.; Li, J.; Bu, X.; Hanajima, N. Adaptive Neural Network Iterative Learning Control of Long-Stroke Hybrid Robots with Initial Errors and Full State Constraints. Meas. Control 2024, 58, 128–144. [Google Scholar] [CrossRef]
- Lu, S.M.; Li, D.P.; Liu, Y.J. Adaptive Neural Network Control for Uncertain Time-Varying State Constrained Robotics Systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 2511–2518. [Google Scholar] [CrossRef]
- Luo, X.; Mu, D.; Wang, Z.; Ning, P.; Hua, C. Adaptive Full-State Constrained Tracking Control for Mobile Robotic System with Unknown Dead-Zone Input. Neurocomputing 2023, 524, 31–42. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y.D.; Shen, Z.X. Neuroadaptive Fault-Tolerant Control of Nonlinear Systems under Output Constraints and Actuation Faults. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 286–298. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Song, Y.D.; Ma, T.; He, L. Prescribed Performance Control of Uncertain Euler–Lagrange Systems Subject to Full-State Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3478–3489. [Google Scholar] [PubMed]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained Model Predictive Control: Stability and Optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Bemporad, A. Reference Governor for Constrained Nonlinear Systems. IEEE Trans. Autom. Control 1998, 43, 415–419. [Google Scholar] [CrossRef]
- Dehaan, D.; Guay, M. Extremum-Seeking Control of State-Constrained Nonlinear Systems. Automatica 2005, 41, 1567–1574. [Google Scholar] [CrossRef]
- He, W.; Chen, Y.; Yin, Z. Adaptive Neural Network Control of an Uncertain Robot with Full-State Constraints. IEEE Trans. Cybern. 2016, 46, 620–629. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Zhao, L.; Xu, Z. Finite-Time Adaptive Event-Triggered Control for Robot Manipulators with Output Constraints. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3824–3828. [Google Scholar] [CrossRef]
- Fang, X.; Fan, H.; Liu, L.; Wang, B. Adaptive Fixed-Time Fault-Tolerant Control of Saturated MIMO Nonlinear Systems with Time-Varying State Constraints. Nonlinear Dyn. 2022, 110, 3463–3483. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, C.; Xia, J.; Shen, H.; Xie, X. Dynamic Event-Triggered-Based Adaptive Fuzzy Optimized Control for Slowly Switched Nonlinear System with Intermittent State Constraints. Inf. Sci. 2024, 674, 120717. [Google Scholar] [CrossRef]
- Li, D.P.; Liu, Y.J.; Tong, S.; Chen, C. Neural Networks-Based Adaptive Control for Nonlinear State Constrained Systems with Input Delay. IEEE Trans. Cybern. 2018, 49, 1249–1258. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Xie, X.-J. Robust Adaptive Control for State-Constrained Nonlinear Systems with Input Saturation and Unknown Control Direction. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 1192–1202. [Google Scholar] [CrossRef]
- Cui, B.; Xia, Y.; Liu, K.; Shen, G. Finite-Time Tracking Control for a Class of Uncertain Strict-Feedback Nonlinear Systems with State Constraints: A Smooth Control Approach. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4920–4932. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Su, S.F.; Wu, Y.Q.; Xia, J.W.; Nguyen, V.T. Adaptive Fuzzy Control with High-Order Barrier Lyapunov Functions for High-Order Uncertain Nonlinear Systems with Full-State Constraints. IEEE Trans. Cybern. 2020, 50, 3424–3432. [Google Scholar] [CrossRef] [PubMed]
- Phan, V.D.; Truong, H.; Le, V.C.; Ho, S.P.; Ahn, K.K. Adaptive Neural Observer-Based Output Feedback Anti-Actuator Fault Control of a Non-Linear Electro-Hydraulic System with Full State Constraints. Sci. Rep. 2025, 15, 3044. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.; Huang, H.; Chen, C.; Wu, L.; Xiao, J. Neuro-Adaptive Command-Filtered Backstepping Control of Uncertain Flexible-Joint Manipulators with Input Saturation via Output. Sci. Rep. 2025, 15, 17254. [Google Scholar] [CrossRef] [PubMed]
- Sui, S.; Chen, C.L.P.; Tong, S. Command Filter-Based Predefined Time Adaptive Control for Nonlinear Systems. IEEE Trans. Autom. Control 2024, 69, 7863–7870. [Google Scholar] [CrossRef]
- Farrell, J.A.; Polycarpou, M.; Sharma, M.; Dong, W. Command Filtered Backstepping. IEEE Trans. Autom. Control 2009, 54, 1391–1395. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y. Neuroadaptive Robotic Control under Time-Varying Asymmetric Motion Constraints: A Feasibility-Condition-Free Approach. IEEE Trans. Cybern. 2018, 50, 15–24. [Google Scholar] [CrossRef] [PubMed]
- Ji, Q.; Chen, G.; He, Q. Neural Network-Based Distributed Finite-Time Tracking Control of Uncertain Multi-Agent Systems with Full State Constraints. IEEE Access 2020, 8, 174365–174374. [Google Scholar] [CrossRef]
- Zhang, T.; Xia, M.; Yi, Y.; Shen, Q. Adaptive Neural Dynamic Surface Control of Pure-Feedback Nonlinear Systems with Full State Constraints and Dynamic Uncertainties. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2378–2387. [Google Scholar] [CrossRef]
- Guo, T.; Wu, X. Backstepping Control for Output-Constrained Nonlinear Systems Based on Nonlinear Mapping. Neural Comput. Appl. 2014, 25, 1665–1674. [Google Scholar] [CrossRef]
- Ning, P.; Mu, D.; Hua, C. Global Prescribed-Time Tracking Control Mobile Robot Systems with Performance Constraints. IEEE Trans. Circuits Syst. II Express Briefs 2023, 71, 181–185. [Google Scholar]
- Gao, J.; Tan, Z.; Li, L.; Jia, G.; Liu, P.X. A Novel Finite-Time Non-Singular Robust Control for Robotic Manipulators. Chaos Solitons Fractals 2025, 194, 116266. [Google Scholar] [CrossRef]
- Dang, V.T.; Nguyen, X.B.; Tran, T.D.T.; Le, D.T.; Nguyen, T.L. Finite-Time Velocity Sensorless Integral Sliding Mode Control for Roll-to-Roll Systems under Matched Disturbances. ISA Trans. 2025. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Song, Y.; Krstic, M.; Wen, C. Fault-tolerant finite time consensus for multiple uncertain nonlinear mechanical systems under single-way directed communication interactions and actuation failures. Automatica 2016, 63, 374–383. [Google Scholar] [CrossRef]
- Yu, J.; Shi, P.; Zhao, L. Finite-Time Command Filtered Backstepping Control for a Class of Nonlinear Systems. Automatica 2018, 92, 173–180. [Google Scholar] [CrossRef]
- Sanner, R.M.; Slotine, J.J.E. Gaussian Networks for Direct Adaptive Control. In Proceedings of the 1991 American Control Conference, Boston, MA, USA, 26–28 June 1991; IEEE: Boston, MA, USA, 1991; pp. 2153–2159. [Google Scholar]
- Park, J.; Sandberg, I.W. Universal Approximation Using Radial-Basis-Function Networks. Neural Comput. 1991, 3, 246–257. [Google Scholar] [CrossRef] [PubMed]
- Nikiforov, V.; Gerasimov, D. Adaptive Regulation; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar]
- Furtat, I.; Gushchin, P. Nonlinear Feedback Control Providing Plant Output in Given Set. Int. J. Control 2022, 95, 1533–1542. [Google Scholar] [CrossRef]
- Nguyen, B.H.; Furtat, I.B. Output Stabilization of Linear Systems in Given Set. Mathematics 2023, 11, 3542. [Google Scholar] [CrossRef]
- Zuo, Z.; Tie, L. A New Class of Finite-Time Nonlinear Consensus Protocols for Multi-Agent Systems. Int. J. Control 2013, 87, 363–370. [Google Scholar] [CrossRef]
- Lewis, F.L.; Liu, K.; Yesildirek, A. Neural Net Robot Controller with Guaranteed Tracking Performance. IEEE Trans. Neural Netw. 1995, 6, 703–715. [Google Scholar] [CrossRef] [PubMed]
- Venkaiah, P.; Sarkar, B.K.; Chatterjee, A. Harris Hawks Optimization Tuned Exponential Reaching Law Based Integral SMC for Pitch Control of Linear Hydraulic Actuated Wind Turbines. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 238, 1855–1873. [Google Scholar] [CrossRef]
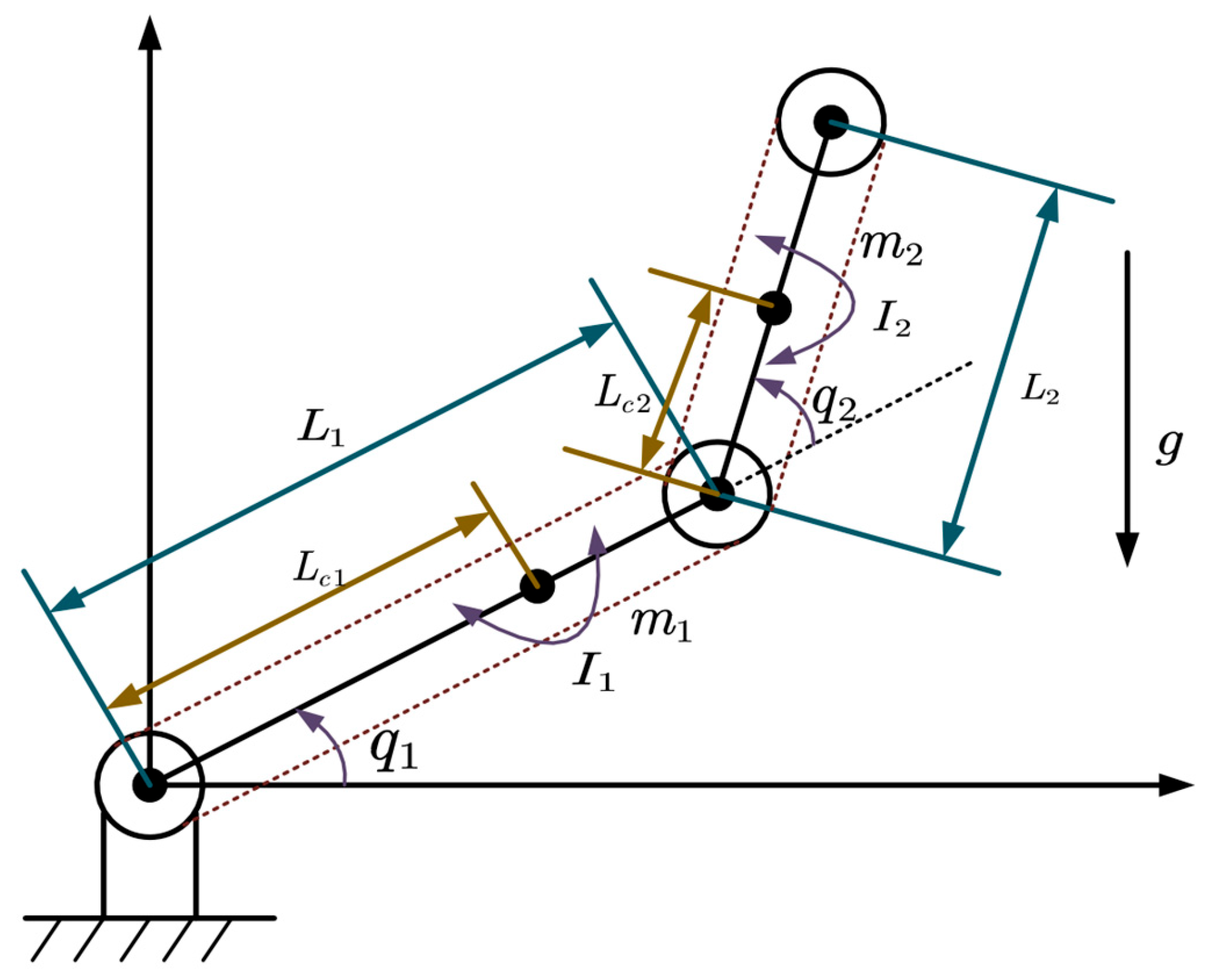

| Symbol | Description | Unit |
|---|---|---|
| Angular positions of links 1 and 2 | rad | |
| Masses of links 1 and 2 | kg | |
| Link lengths | ||
| Centroid offset distances from joints | ||
| Linear momenta of links | ||
| Gravity acceleration |
| Performance Evaluation Metrics | IAE | ISE | CE | |
|---|---|---|---|---|
| Control Scheme | ||||
| NPCSC | 1.571 | 0.107 | 6.107 | |
| NPFTCSC | 0.368 | 0.056 | 6.348 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lou, J.; Wen, X.; Shavetov, S. Finite-Time Tracking Control in Robotic Arm with Physical Constraints Under Disturbances. Mathematics 2025, 13, 2336. https://doi.org/10.3390/math13152336
Lou J, Wen X, Shavetov S. Finite-Time Tracking Control in Robotic Arm with Physical Constraints Under Disturbances. Mathematics. 2025; 13(15):2336. https://doi.org/10.3390/math13152336
Chicago/Turabian StyleLou, Jiacheng, Xuecheng Wen, and Sergei Shavetov. 2025. "Finite-Time Tracking Control in Robotic Arm with Physical Constraints Under Disturbances" Mathematics 13, no. 15: 2336. https://doi.org/10.3390/math13152336
APA StyleLou, J., Wen, X., & Shavetov, S. (2025). Finite-Time Tracking Control in Robotic Arm with Physical Constraints Under Disturbances. Mathematics, 13(15), 2336. https://doi.org/10.3390/math13152336






