An Exponentially Delayed Feedback Chaotic Model Resistant to Dynamic Degradation and Its Application
Abstract
1. Introduction
2. A New Feedback Method to Improve Chaos Map Performance
3. Exponential Feedback Digital Logistic Map Numerical Simulation
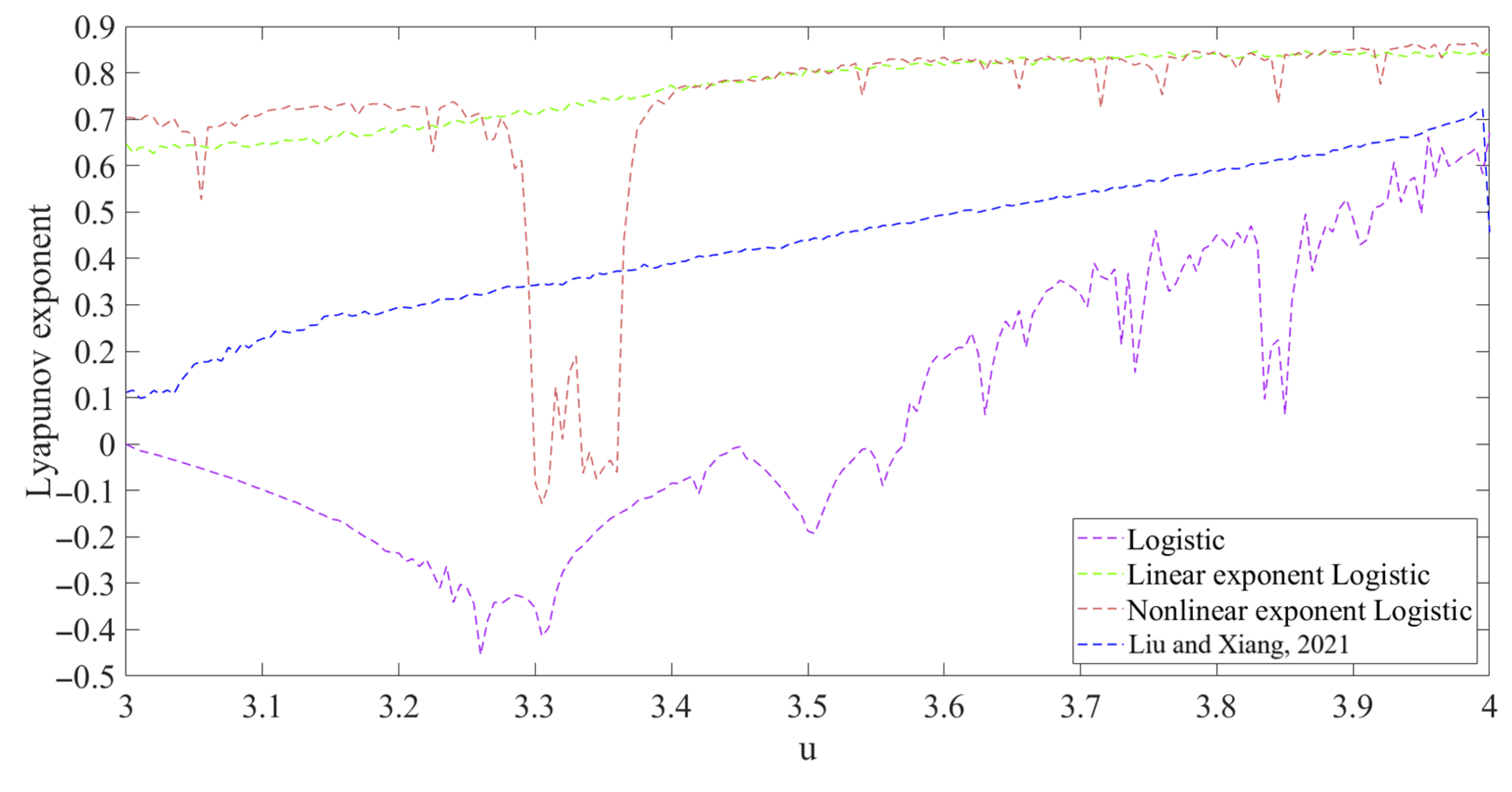
3.1. Maximum Lyapunov Exponent
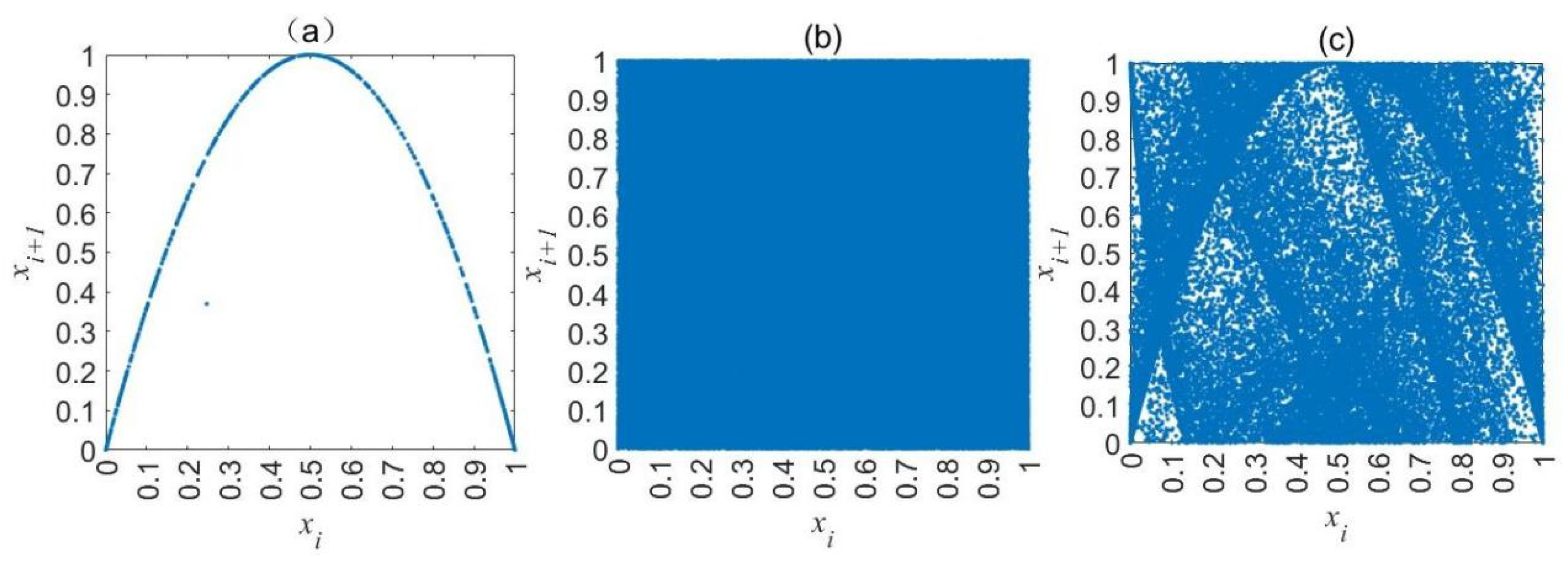
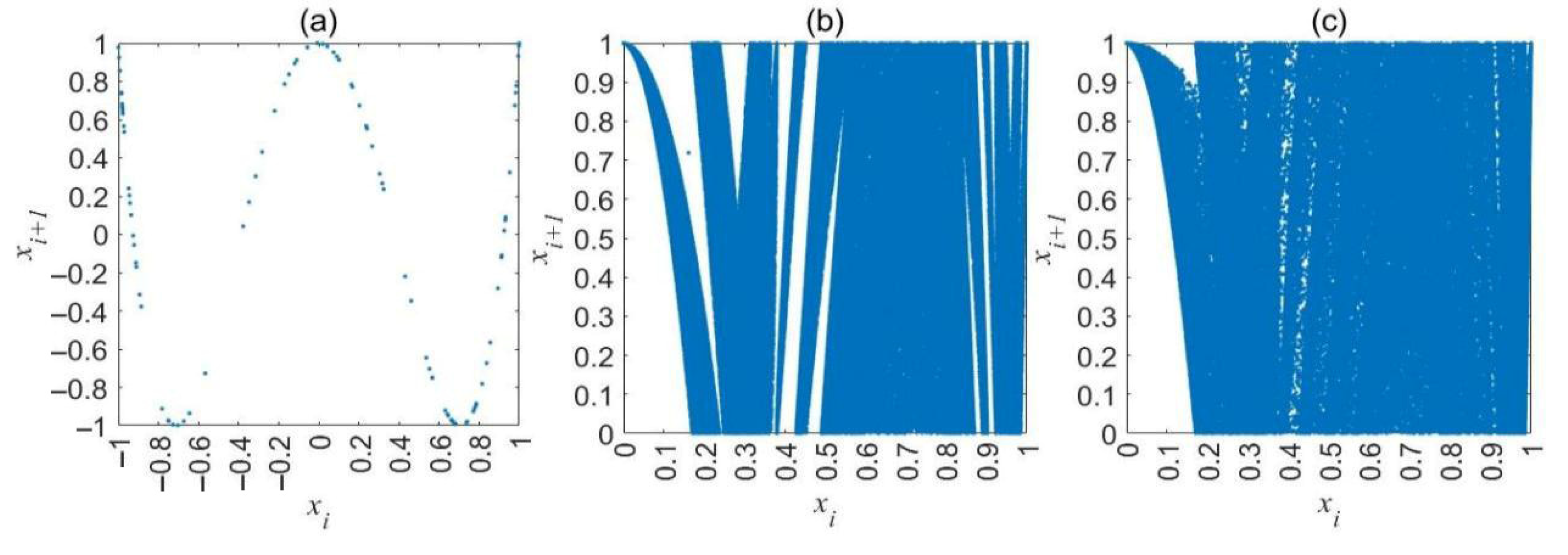
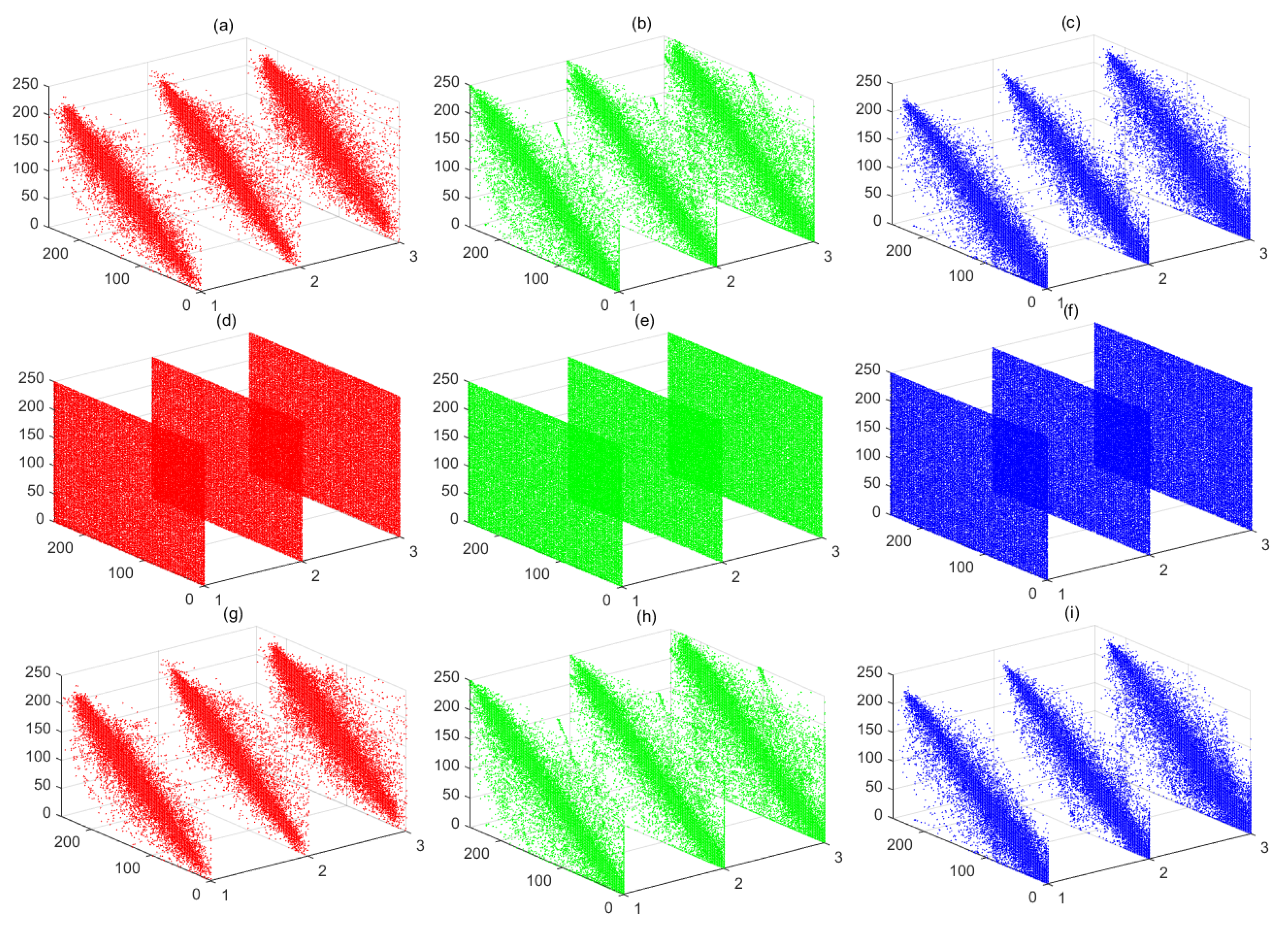
3.2. Trajectory and Phase Diagrams
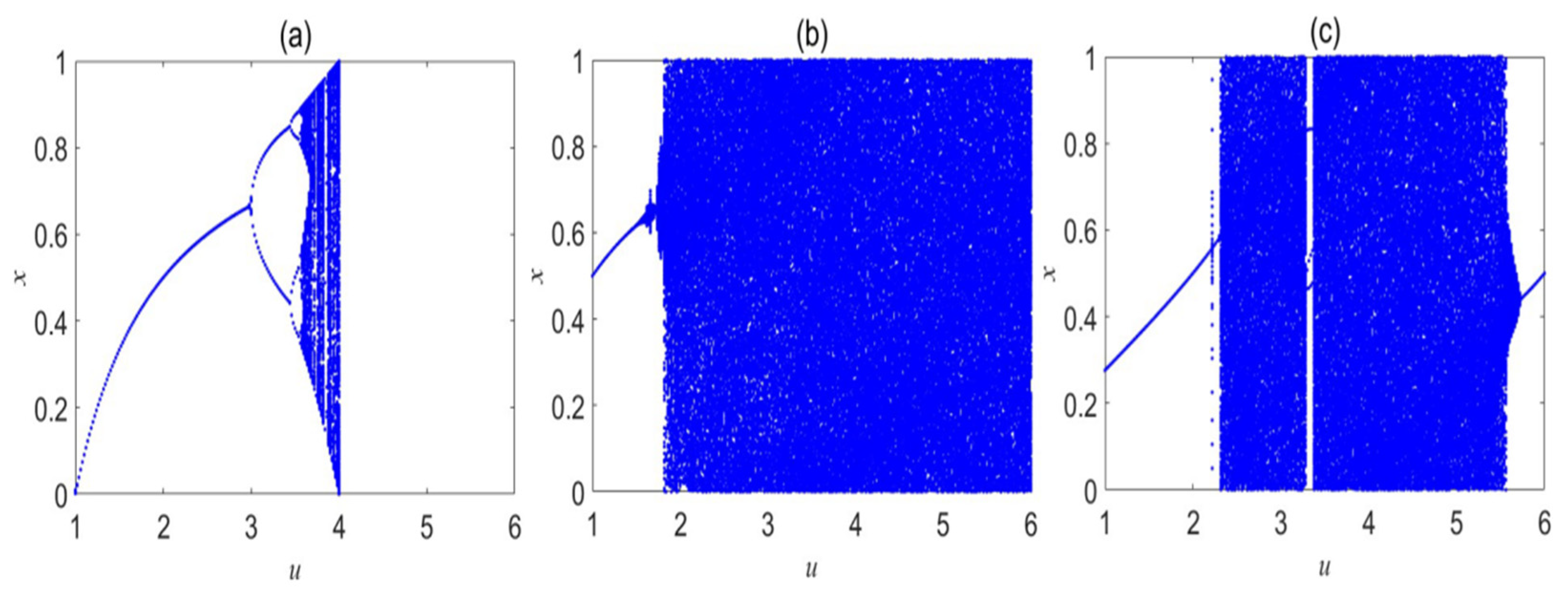
3.3. Bifurcation Diagram
3.4. Period Analysis
3.5. Correlation Dimension Analysis
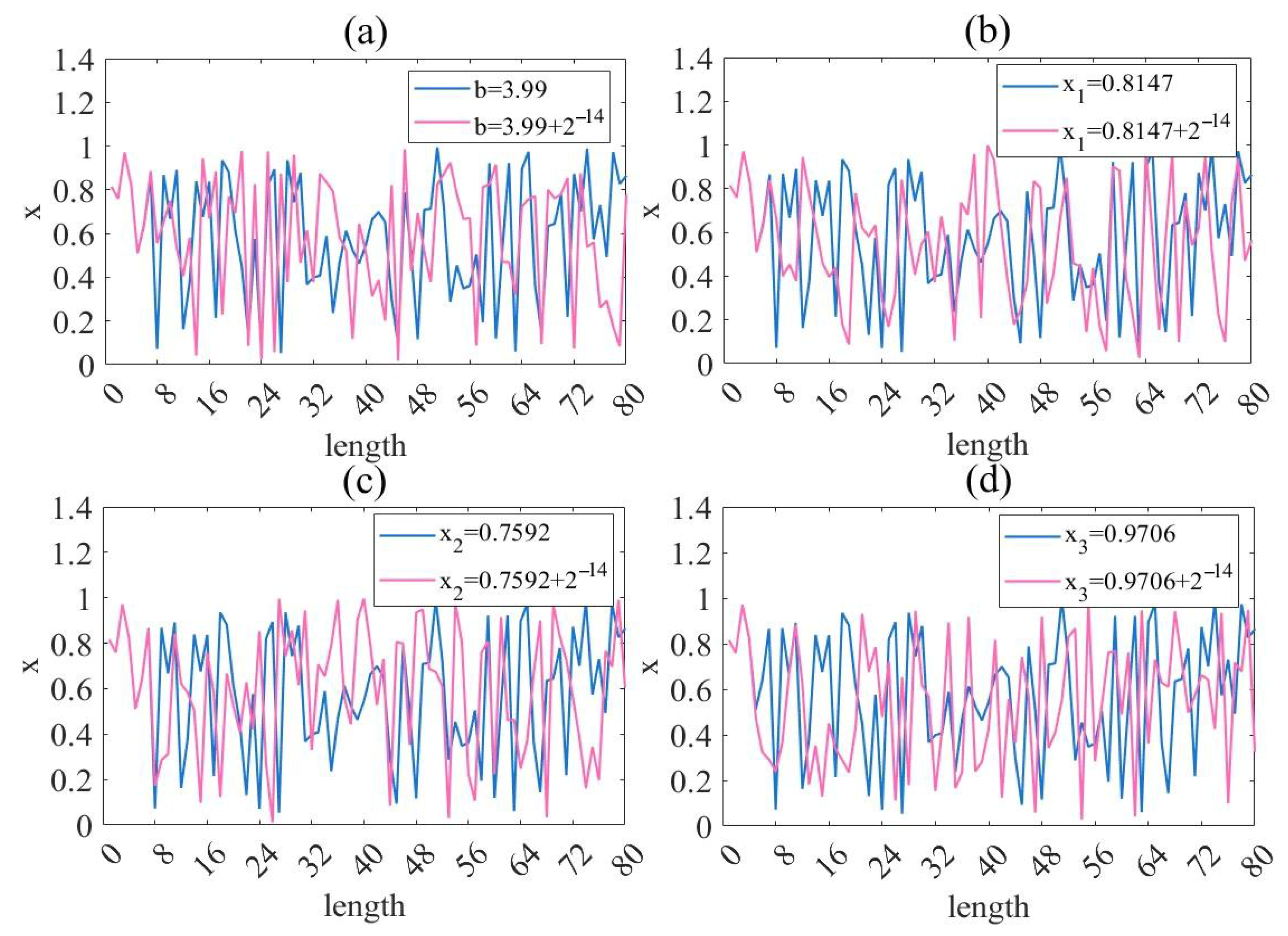
3.6. Sensitivity Analysis of Initial Condition
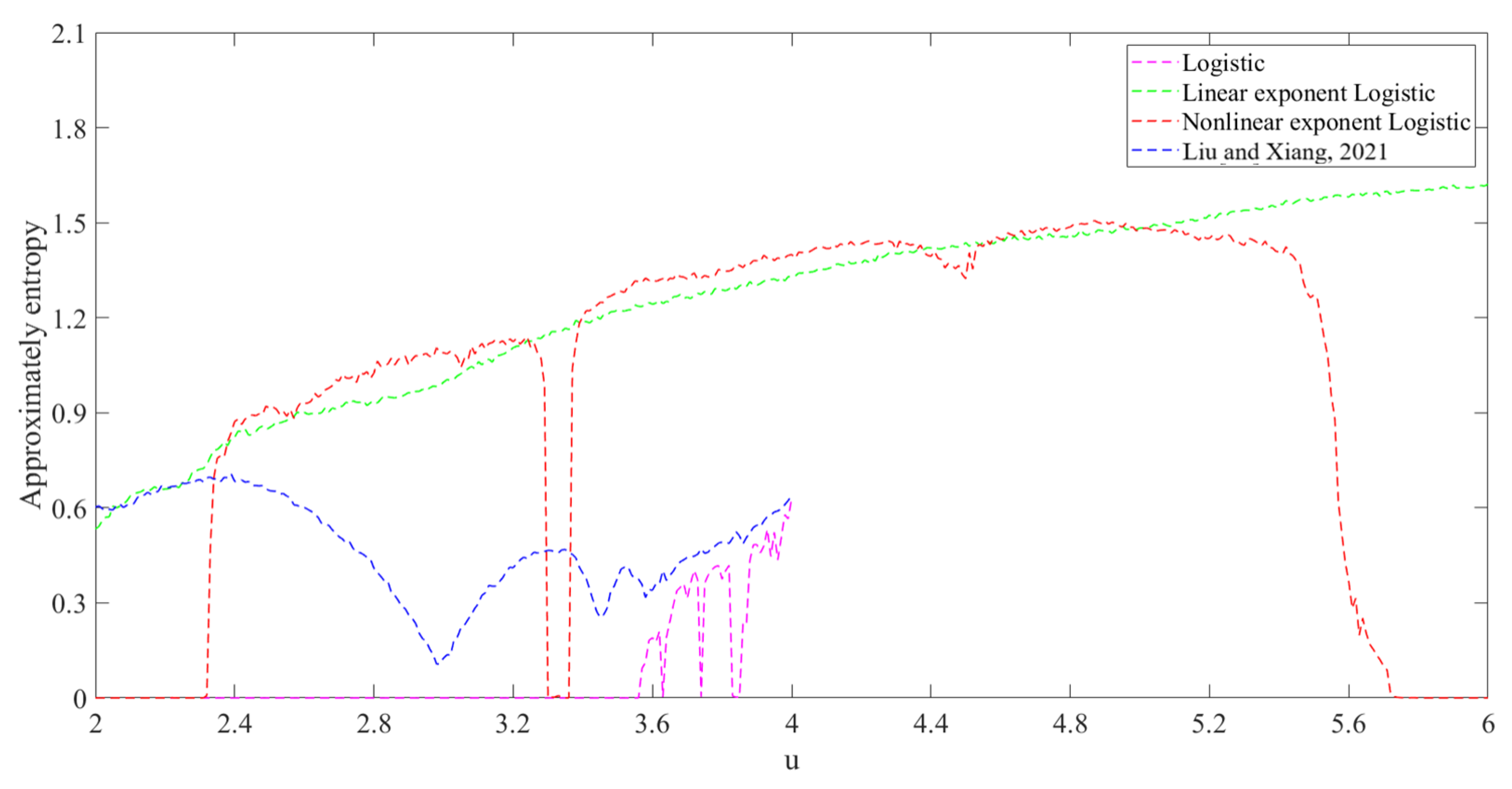
3.7. Approximate Entropy Analysis
3.8. Permutation Entropy Analysis
4. Exponential Feedback Digital Chebyshev Map Numerical Simulation
4.1. Trajectory and Phase Diagrams
4.2. Period Analysis
4.3. Sensitivity Analysis
4.4. Correlation Dimension Analysis
4.5. Approximate Entropy Analysis
4.6. Permutation Entropy Analysis
5. Application of Image Encryption Algorithm
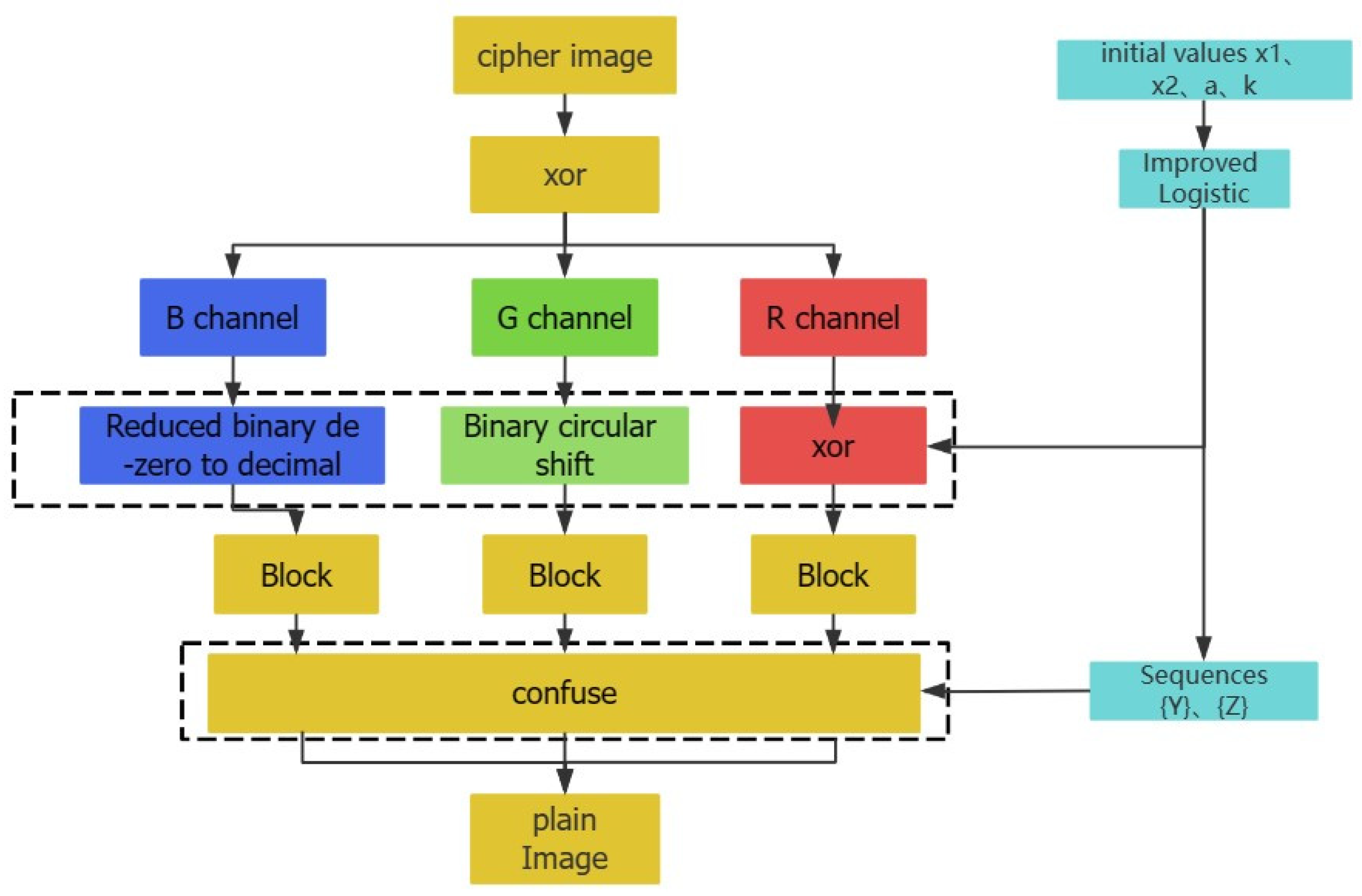
5.1. Image Encryption Algorithm Based on Linear Exponential Delayed Feedback Logstic
5.2. Security Analysis
5.2.1. Encryption and Decryption Analysis
5.2.2. Key Sensitivity Analysis
5.2.3. Key Space Analysis
5.2.4. Histogram Analysis
5.2.5. Pixel Correlation Analysis
5.2.6. Robustness Analysis
5.2.7. Resistance to Differential Attacks
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alexan, W.; Elkandoz, M.; Mashaly, M.; Azab, E.; Aboshousha, A. Color image encryption through chaos and KAA map. IEEE Access 2023, 11, 11541–11554. [Google Scholar] [CrossRef]
- ErkErkan, U.; Toktas, A.; Lai, Q. 2D hyperchaotic system based on Schaffer function for image encryption. Expert Syst. Appl. 2022, 213, 119076. [Google Scholar] [CrossRef]
- Li, S.; Chen, G.; Mou, X. On the dynamical degradation of digital piecewise linear chaotic maps. Int. J. Bifurc. Chaos 2005, 15, 3119–3151. [Google Scholar] [CrossRef]
- Liu, L.; Wang, J. A shift coupling digital chaotic model with counteracting dynamical degradation. Nonlinear Dyn. 2023, 111, 19459–19486. [Google Scholar] [CrossRef]
- Xiang, H.; Liu, L. An improved digital logistic map and its application in image encryption. Multimed. Tools Appl. 2020, 79, 30329–30355. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, L.; Giesl, P. An iteration-time combination method to reduce the dynamic degradation of digital chaotic maps. Complexity 2020, 2020, 5707983. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, C.; Xu, Y.; Lin, J.; Pang, Y.; Liu, Z.; Shen, J. Mathematical exploration on control of bifurcation for a 3D predator-prey model with delay. AIMS Math. 2024, 9, 29883–29915. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L. A novel chaos-based image encryption using magic square scrambling and octree diffusing. Mathematics 2022, 10, 457. [Google Scholar] [CrossRef]
- Iskakova, K.; Alam, M.M.; Ahmad, S.; Saifullah, S.; Akgül, A.; Yılmaz, G. Dynamical study of a novel 4D hyperchaotic system: An integer and fractional order analysis. Math. Comput. Simul. 2023, 208, 219–245. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, C.; Sun, J.; Yu, F. A chaotic image encryption method based on the artificial fish swarms algorithm and the DNA coding. Mathematics 2023, 11, 767. [Google Scholar] [CrossRef]
- Huang, X.; Dong, Y.; Ye, G.; Shi, Y. Meaningful image encryption algorithm based on compressive sensing and integer wavelet transform. Front. Comput. Sci. 2023, 17, 173804. [Google Scholar] [CrossRef]
- Zhu, S.; Deng, X.; Zhang, W.; Zhu, C. Image encryption scheme based on newly designed chaotic map and parallel DNA coding. Mathematics 2023, 11, 231. [Google Scholar] [CrossRef]
- Zhao, H.; Gong, Z.; Gan, K.; Gan, Y.; Xing, H.; Wang, S. Supervised kernel principal component analysis-polynomial chaos-Kriging for high-dimensional surrogate modelling and optimization. Knowl.-Based Syst. 2024, 305, 112617. [Google Scholar] [CrossRef]
- Chen, Y.; Li, H.; Song, Y.; Zhu, X. Recoding hybrid stochastic numbers for preventing bit width accumulation and fault tolerance. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 72, 1243–1255. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Z.; Wang, G.; Zhang, Q.; Xia, S.; Wu, D.; Liu, Y. Constructing three-way decision with fuzzy granular-ball rough sets based on uncertainty invariance. IEEE Trans. Fuzzy Syst. 2025, 33, 1781–1792. [Google Scholar] [CrossRef]
- Khan, J.S.; Ahmad, J. Chaos based efficient selective image encryption. Multidimens. Syst. Signal Process. 2019, 30, 943–961. [Google Scholar] [CrossRef]
- Zhu, H.; Dai, L.; Liu, Y.; Wu, L. A three-dimensional bit-level image encryption algorithm with Rubik’s cube method. Math. Comput. Simul. 2021, 185, 754–770. [Google Scholar] [CrossRef]
- Liu, L.; Xiang, H.; Li, X. A novel perturbation method to reduce the dynamical degradation of digital chaotic maps. Nonlinear Dyn. 2021, 103, 1099–1115. [Google Scholar] [CrossRef]
- Ren, Q.; Teng, L.; Jiang, D.; Si, R.; Wang, X. Visual image encryption algorithm based on compressed sensing and 2D cosine-type logistic map. Phys. Scr. 2023, 98, 095212. [Google Scholar] [CrossRef]
- Shukla, V.K.; Joshi, M.C.; Mishra, P.K.; Xu, C. Mechanical analysis and function matrix projective synchronization of El-Nino chaotic system. Phys. Scr. 2024, 100, 015255. [Google Scholar] [CrossRef]
- Shukla, V.K.; Joshi, M.C.; Mishra, P.K.; Xu, C. Adaptive fixed-time difference synchronization for different classes of chaotic dynamical systems. Phys. Scr. 2024, 99, 095264. [Google Scholar] [CrossRef]
- Han, C. An image encryption algorithm based on modified logistic chaotic map. Optik 2019, 181, 779–785. [Google Scholar] [CrossRef]
- Liu, L.; Liu, B.; Hu, H.; Miao, S. Reducing the dynamical degradation by bi-coupling digital chaotic maps. IntInt. J. Bifurc. Chaos 2018, 28, 1850059. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. Delay-introducing method to improve the dynamical degradation of a digital chaotic map. Inf. Sci. 2017, 396, 1–13. [Google Scholar] [CrossRef]
- Liu, J.; Liang, Z.; Luo, Y.; Cao, L.; Zhang, S.; Wang, Y.; Yang, S. A hardware pseudo-random number generator using stochastic computing and logistic map. Micromachines 2020, 12, 31. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Xiang, H.; Liu, L. A new perturbation-feedback hybrid control method for reducing the dynamic degradation of digital chaotic systems and its application in image encryption. Multimed. Tools Appl. 2021, 80, 19237–19261. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, B.; Zhou, N. A novel image compression—Encryption hybrid algorithm based on the analysis sparse representation. Opt. Commun. 2017, 392, 223–233. [Google Scholar] [CrossRef]
- Chen, C.; Sun, K.H.; Peng, Y.X.; Alamodi, A. A novel control method to counteract the dynamical degradation of a digital chaotic sequence. Eur. Phys. J. Plus 2019, 134, 31. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Liao, X.; Wu, J. Cryptanalysis and enhancement of an image encryption scheme based on a 1-D coupled Sine map. Nonlinear Dyn. 2020, 100, 2917–2931. [Google Scholar] [CrossRef]
- Zhang, Y.-Q.; Huang, H.-F.; Wang, X.-Y.; Huang, X.-H. A secure image encryption scheme based on genetic mutation and MLNCML chaotic system. Multimed. Tools Appl. 2021, 80, 19291–19305. [Google Scholar] [CrossRef]
- Jithin, K.; Sankar, S. Colour image encryption algorithm combining Arnold map, DNA sequence operation, and a Mandelbrot set. J. Inf. Secur. Appl. 2020, 50, 102428. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, B.; Wu, Z. Research on color image encryption algorithm based on bit-plane and Chen Chaotic System. Entropy 2022, 24, 186. [Google Scholar] [CrossRef]
- Alexan, W.; ElBeltagy, M.; Aboshousha, A. RGB image encryption through cellular automata, S-box and the Lorenz system. Symmetry 2022, 14, 443. [Google Scholar] [CrossRef]












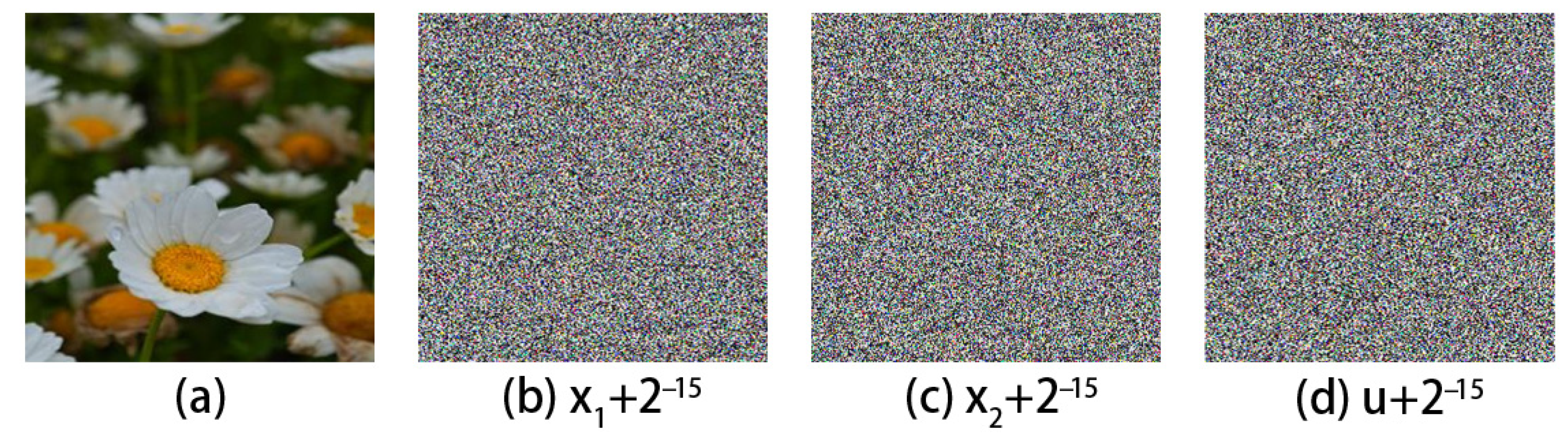



| Precision | Period of Equation (5) | Period of Equation (7) | Period of Equation (8) | Number of Iterations When Entering a Cycle (Equation (5)) | Number of Iterations When Entering a Cycle (Equation (7)) | Number of Iterations When Entering a Cycle (Equation (8)) |
|---|---|---|---|---|---|---|
| 4 | 1 | 98 | 20 | 194 | 63 | |
| 7 | 1 | 1 | 17 | 801 | 30 | |
| 3 | 200 | 362 | 22 | 1656 | 203 | |
| 6 | 329 | 1 | 13 | 1352 | 83 | |
| 9 | 5424 | 312 | 82 | 2730 | 305 | |
| 42 | 1 | 1032 | 15 | 2006 | 1839 | |
| 63 | 1 | 1013 | 82 | 3606 | 256 | |
| 91 | 1 | 32 | 47 | 6204 | 3513 | |
| 79 | 1 | 10,931 | 77 | 87,639 | 3357 | |
| 199 | 125,271 | 1 | 8 | 47,014 | 17,407 | |
| 588 | N | 1902 | 75 | N | 43,628 | |
| 656 | 1 | 6662 | 63 | 96,865 | 10,636 | |
| 451 | N | 33,071 | 52 | N | 19,982 | |
| 311 | N | N | 301 | N | N | |
| 931 | N | N | 596 | N | N | |
| 771 | N | N | 786 | N | N | |
| 993 | N | N | 1791 | N | N |
| Presicion | Equation (7) | Equation (8) | Ref. [24] | Ref. [25] |
|---|---|---|---|---|
| 194 | 63 | 11 | 15 | |
| 801 | 30 | 32 | 6 | |
| 1656 | 203 | 39 | 18 | |
| 1352 | 83 | 6 | 34 | |
| 2730 | 305 | 6 | 34 | |
| 2006 | 1839 | 81 | 48 | |
| 3606 | 256 | 6 | 29 | |
| 6204 | 3513 | 63 | 52 |
| Precision | Period of Equation (9) | Period of Equation (11) | Period of Equation (12) | Number of Iterations When Entering a Cycle (Equation (9)) | Number of Iterations When Entering a Cycle (Equation (11)) | Number of Iterations When Entering a Cycle (Equation (12)) |
|---|---|---|---|---|---|---|
| 7 | 6 | 22 | 6 | 198 | 21 | |
| 7 | 342 | 244 | 26 | 381 | 26 | |
| 57 | 2490 | 80 | 7 | 403 | 95 | |
| 35 | 2107 | 59 | 13 | 1235 | 665 | |
| 28 | 257 | 864 | 9 | 7047 | 151 | |
| 40 | 20,734 | 2095 | 150 | 2532 | 3537 | |
| 134 | 19,359 | 4466 | 9 | 11,007 | 6205 | |
| 285 | 56,084 | 1960 | 34 | 19,559 | 10,172 | |
| 40 | N | 898 | 354 | N | 14,857 | |
| 196 | N | 9589 | 117 | N | 14,877 | |
| 30 | N | 70,591 | 66 | N | 89,621 | |
| 364 | N | N | 351 | N | N | |
| 1341 | N | N | 342 | N | N | |
| 1144 | N | N | 558 | N | N | |
| 528 | N | N | 36 | N | N | |
| 378 | N | N | 629 | N | N | |
| 1585 | N | N | 1353 | N | N |
| Algorithm | Key Space |
|---|---|
| Proposed | 2186 |
| Ref. [28] | 2176 |
| Ref. [29] | 2160 |
| Ref. [30] | 2139 |
| Ref. [31] | 2186 |
| Ref. [32] | 2186 |
| Image | Derection | Cipher Image | ||
|---|---|---|---|---|
| R | G | B | ||
| Flowers | Horizontal | 0.0020 | 0.0015 | −0.0017 |
| Vertical | −0.0016 | 0.0031 | −0.0020 | |
| Diagonal | 0.0017 | −0.0021 | −0.0025 | |
| Boats | Horizontal | 0.0013 | 0.0029 | −0.0029 |
| Vertical | 0.0031 | 0.0022 | −0.0032 | |
| Diagonal | 0.0021 | −0.0019 | −0.0011 | |
| Gorilla | Horizontal | 0.0019 | −0.0025 | 0.0022 |
| Vertical | 0.0023 | −0.0035 | −0.0011 | |
| Diagonal | −0.0039 | −0.0027 | 0.0014 | |
| Peppers | Horizontal | −0.0013 | 0.0014 | 0.0019 |
| Vertical | 0.0015 | 0.0024 | −0.0023 | |
| Diagonal | −0.0018 | 0.0016 | 0.0044 | |
| Ref. [33] | Horizontal | −0.004 | −0.0042 | −0.0009 |
| Vertical | −0.0007 | 0.0012 | −0.0069 | |
| Diagonal | −0.0019 | 0.0021 | −0.0041 | |
| Ref. [34] | Horizontal | −0.0104 | 0.0180 | 0.0087 |
| Vertical | 0.0178 | 0.0006 | −0.0063 | |
| Diagonal | −0.0049 | −0.000015 | 0.0003 | |
| Images | Channel | NPCR | UACI |
|---|---|---|---|
| Flowers | R | 0.9962 | 0.3350 |
| G | 0.9961 | 0.3344 | |
| B | 0.9961 | 0.3345 | |
| Boats | R | 0.9960 | 0.3345 |
| G | 0.9959 | 0.3340 | |
| B | 0.9960 | 0.3345 | |
| Gorilla | R | 0.9961 | 0.3345 |
| G | 0.9959 | 0.3344 | |
| B | 0.9960 | 0.3344 | |
| Peppers | R | 0.9960 | 0.3350 |
| G | 0.9962 | 0.3343 | |
| B | 0.9963 | 0.3346 | |
| Ref. [34] | R | 0.9959 | 0.3355 |
| G | 0.9961 | 0.3335 | |
| B | 0.9961 | 0.3343 | |
| Ref. [35] | R | 0.9960 | 0.3335 |
| G | 0.9960 | 0.3347 | |
| B | 0.9938 | 0.3344 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Song, J.; Jiang, N.; Wang, Z. An Exponentially Delayed Feedback Chaotic Model Resistant to Dynamic Degradation and Its Application. Mathematics 2025, 13, 2324. https://doi.org/10.3390/math13142324
Liu B, Song J, Jiang N, Wang Z. An Exponentially Delayed Feedback Chaotic Model Resistant to Dynamic Degradation and Its Application. Mathematics. 2025; 13(14):2324. https://doi.org/10.3390/math13142324
Chicago/Turabian StyleLiu, Bocheng, Jian Song, Niande Jiang, and Zhuo Wang. 2025. "An Exponentially Delayed Feedback Chaotic Model Resistant to Dynamic Degradation and Its Application" Mathematics 13, no. 14: 2324. https://doi.org/10.3390/math13142324
APA StyleLiu, B., Song, J., Jiang, N., & Wang, Z. (2025). An Exponentially Delayed Feedback Chaotic Model Resistant to Dynamic Degradation and Its Application. Mathematics, 13(14), 2324. https://doi.org/10.3390/math13142324





