Symmetry and Quantum Calculus in Defining New Classes of Analytic Functions

Abstract

This paper introduces a novel class of analytic functions that integrates q-calculus, Janowski-type functions, and (a, b)-symmetrical functions. By exploring convolution operations and quantum calculus, we establish essential convolution conditions that lay the groundwork for subsequent research. Building on a new conceptual framework, we also define analogous neighborhoods for the classes ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$ and investigate related neighborhood properties. These developments provide a deeper understanding of the structural and analytical behavior of these functions, opening up avenues for future study.

1. Introduction

An $(a,b)$-symmetrical function is a type of function that remains invariant under specific transformations involving two parameters, a and b. These functions exhibit symmetrical properties that can simplify complex mathematical problems, making them particularly useful in geometric function theory (GFT).

In GFT, $(a,b)$-symmetrical functions play a critical role in analyzing and mapping geometric properties, especially in the study of conformal mappings, univalent functions, and quasi conformal mappings. By leveraging their symmetry, researchers can explore relationships between geometric objects and solve boundary value problems more effectively. These functions also provide a framework for constructing and characterizing classes of functions that adhere to specific symmetry constraints, enabling a deeper understanding of their geometric and analytical behaviors.

In their seminal 1995 study, Liczberski and Polubinski [1] introduced the framework of $(a,b)$-symmetrical functions, where a and b are integers such that $a\in \{0,1,2,\dots ,b-1\}$ and $b\ge 2$. Let $\tilde{U}$ denote a domain with b-fold rotational symmetry, and let a be an integer within the specified range. A function $h:\tilde{U}\to \mathbb{C}$ is classified as $(a,b)$-symmetrical if it satisfies the following condition for every $z\in \tilde{U}$:

$$h\left(\epsilon z\right)={\epsilon }^{a}h\left(z\right),$$

where $\epsilon =e^{\frac{2\pi i}{b}}$ represents the b-th root of unity, corresponding to the symmetry operation associated with the b-fold structure of $\tilde{U}$. The set of all $(a,b)$-symmetrical functions is denoted by ${\overline{\mathcal{G}}}_a^b$. Specific cases include ${\overline{\mathcal{G}}}_2^0$, which corresponds to the class of even functions, ${\overline{\mathcal{G}}}_2^1$, representing the class of odd functions, and ${\overline{\mathcal{G}}}_a^1$, which includes functions symmetric under a-fold rotational operations. We define the set of all functions that are analytic within the open unit disk, denoted by $\Delta =\{z\in \mathbb{C};|z|<1\}$, as $\overline{\mathcal{G}}$, which consists of functions expressible in the following power series form:

$$h\left(z\right)=z+\sum _{v=2}^{\infty }{c}_v{z}^v.$$

(1)

Let $h,g\in \overline{\mathcal{G}}$ be two analytic functions, where h is defined by (1) and $g\left(z\right)=z+{\sum }_{v=2}^{\infty }{d}_v{z}^v$. The convolution, also referred to as the Hadamard product, of h and g, denoted by $h\ast g$, is given by

$$(h\ast g)\left(z\right)=z+\sum _{v=2}^{\infty }{c}_v{d}_v{z}^v.$$

A key result from Liczberski and Polubinski’s [1] decomposition theorem asserts that any function $h:\Delta \to \mathbb{C}$ defined on a domain $\Delta$ with b-fold symmetry can be uniquely decomposed into its $(a,b)$-symmetrical components:

$$h\left(z\right)=\sum _{a=0}^{b-1}{h}_{a,b}\left(z\right),h_{a,b}\left(z\right)={\displaystyle \frac{1}{b}}\sum _{r=0}^{b-1}{\epsilon }^{-ra}h\left({\epsilon }^{r}z\right),\forall z\in \Delta .$$

(2)

Equivalently, this decomposition can be expressed in terms of series expansion:

$$h_{a,b}\left(z\right)=\sum _{v=1}^{\infty }{\delta }_a^v{c}_v{z}^v,\mathrm{where}{\delta }_a^v=\left\{\begin{array}{cc}1,\hfill & v=lb+a,\hfill \\ 0,\hfill & v\ne lb+a.\hfill \end{array}\right.$$

(3)

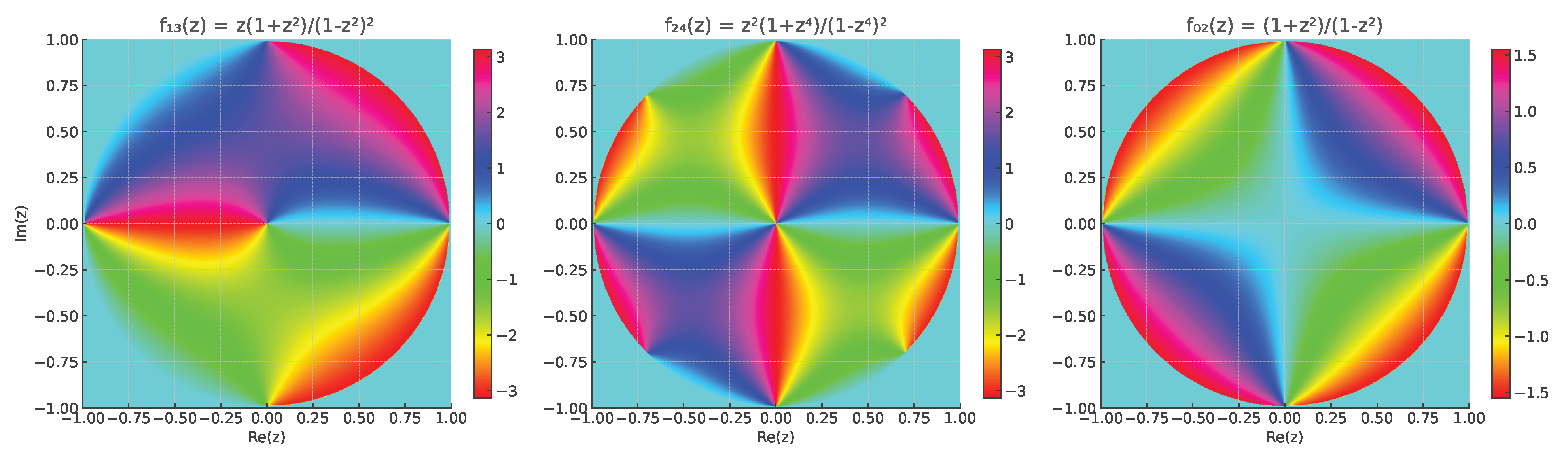
Three examples of $(a,b)$-symmetrical functions were plotted within the open unit disk:

$h_{1,3}\left(z\right)={\displaystyle \frac{z(1+z^2)}{{(1-z^2)}^2}}$, $h_{2,4}\left(z\right)={\displaystyle \frac{z^2(1+z^4)}{{(1-z^4)}^2}}$ and $h_{0,2}\left(z\right)={\displaystyle \frac{1+z^2}{1-z^2}}$. The geometric behavior of the functions is shown in Figure 1.

The phase portraits (color-coded by the argument of $h\left(z\right)$) provide a clear visualization of the angular behavior and symmetrical properties of each function within the unit disk.

The class $\mathcal{SC}$ of Schwarz functions is defined as

$$\mathcal{SC}:=\left\{w\in \overline{\mathcal{G}}\mid w\left(0\right)=0,\left|w\left(z\right)\right|<1\right\}\mathrm{for}\mathrm{all}z\in \Delta .$$

For two analytic functions $h\left(z\right)$ and $g\left(z\right)$ defined in the domain $\Delta$, we say that $h\left(z\right)$ is subordinate to $g\left(z\right)$, denoted $h\left(z\right)\prec g\left(z\right)$ if there exists an analytic function $w\left(z\right)\in \mathcal{SC}$ such that $h\left(z\right)=g\left(w\right(z\left)\right)$ for all $z\in \Delta$.

When $g\left(z\right)$ is univalent in $\Delta$, this subordination is equivalent to the conditions $h\left(0\right)=g\left(0\right)$ and $h(\Delta )\subseteq g(\Delta )$, as discussed in [2].

Definition 1.

Let $\mathcal{P}$ represent the class of functions $p\in \overline{\mathcal{G}}$ that satisfy $p\left(0\right)=1$ and $Rep\left(z\right)>0$ for all $z\in \Delta$. Alternatively, a function $p\in \mathcal{P}$ can be expressed as

$$p\left(z\right)={\displaystyle \frac{1+w\left(z\right)}{1-w\left(z\right)}},$$

where $w\in \mathcal{SC}$, as described in [3].

Janowski [4] extended this concept to define the class $\mathcal{P}[F,H]$, where $-1\le H<F\le 1$. A function h is said to belong to $\mathcal{P}[F,H]$ if it satisfies either of the following equivalent conditions:

$$h\left(z\right)\prec {\displaystyle \frac{1+Fz}{1+Hz}},\mathrm{or}h\left(z\right)={\displaystyle \frac{1+Fw\left(z\right)}{1+Hw\left(z\right)}},\mathrm{for}\mathrm{some}w\left(z\right)\in \mathcal{SC}.$$

To introduce a novel class of q-Janowski symmetrical functions within the domain $\Delta$, it is essential to revisit the foundational principles of quantum calculus, also known as q-calculus. This framework provides a powerful extension of classical calculus, enabling new analytical tools and insights.

In [5,6], Jackson introduced and examined the q-derivative operator ${\partial }_{q}h\left(z\right)$, which is defined as follows:

$${\partial }_{q}h\left(z\right)=\left\{\begin{array}{cc}{h}^{\prime }\left(z\right),\hfill & q=1.\hfill \\ {\displaystyle \frac{h\left(z\right)-h\left(qz\right)}{z(1-q)}},\hfill & z\ne 0,0<q<1,\hfill \\ h^{\prime }\left(0\right),\hfill & z=0.\hfill \end{array}\right.$$

(4)

Equivalently, Equation (4) can be rewritten as

$${\partial }_{q}h\left(z\right)=1+\sum _{v=2}^{\infty }{\left[v\right]}_q{c}_v{z}^{v-1}z\ne 0,$$

where

$${\left[v\right]}_q={\displaystyle \frac{1-q^v}{1-q}}=1+q+q^2+...+q^{v-1}.$$

(5)

Quantum calculus has become a pivotal framework for addressing mathematical challenges in discrete and quantum systems. By leveraging the unique properties of the parameter q, it extends traditional calculus and introduces innovative approaches to problem-solving. The use of the q-derivative, in particular, has paved the way for significant advancements in geometric function theory.

Ismail et al. [7] were among the first to highlight the connection between quantum calculus and geometric function theory, providing foundational insights. Building on this, researchers like Srivastava et al. [8] have applied q-calculus to explore distortion bounds, radii of univalence, and starlikeness for various subclasses of q-starlike functions. Similarly, Naeem et al. [9] investigated q-convex function subfamilies tied to Janowski functions and q-conic domains. Further contributions include the study by Mohammed and Darus [10], who analyzed approximation techniques and geometric properties of q-operators for certain analytic function subclasses within a compact disk. Other researchers [11,12] have expanded the scope of q-calculus, introducing new classes and methodologies. For example, in [13], the symmetric q-derivative operator was employed to define a novel subclass of analytic and bi-univalent functions. Notable advancements have also been achieved by Bulboacă, Frasin, and collaborators [14,15], who utilized the concept of $(j,k)$-symmetrical functions in conjunction with q-derivatives to derive results across diverse functional classes. Additionally, Srivastava [16] has published a comprehensive review that serves as an essential resource for researchers exploring this dynamic and rapidly developing area of study.

To develop the main results, we defined a new class of analytic functions characterized by $(\lambda ,\gamma )$-symmetry. This class is constructed using quantum calculus techniques and generalized Janowski-type subordination, providing a broader framework for function theoretic analysis.

Definition 2.

For arbitrary fixed numbers $q,F$, and H, $0<q<1,$ $-1\le H<F\le 1$. Let $h\in \overline{\mathcal{G}}$ and ${\partial }_{q}h$ be defined on a q-geometric such that

$${\displaystyle \frac{z{\partial }_{q}h\left(z\right)}{h_{a,b}\left(z\right)}}\prec {\displaystyle \frac{2+\left[F\right(1+q)+(1-q\left)\right]z}{2+\left[H\right(1+q)+(1-q\left)\right]z}},$$

(6)

then $h\left(z\right)\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)$, where $h_{a,b}$ is defined in (2).

In particular cases defined by the parameters a, b, q, F, and H, the class ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$ encompasses several well-established subclasses of $\overline{\mathcal{G}}$. For instance,

• When ${\overline{\mathcal{F}}}_q^{0,1}(F,H):={\tilde{\mathcal{S}}}_q(F,H)$, it reduces to the class described by Srivastava et al. [17].
• The subclass ${\overline{\mathcal{F}}}_1^{a,b}(F,H):={\tilde{\mathcal{S}}}^{a,b}(F,H)$ introduced by Latha et al. [18].
• ${\overline{\mathcal{F}}}_1^{1,b}(F,H):={\tilde{\mathcal{S}}}_a(F,H)$, as developed by the authors Latha and Darus [19], are notable extensions.
• ${\overline{\mathcal{F}}}_q^{1,1}(1-2\lambda ,-1)={\tilde{\mathcal{S}}}_q\left(\lambda \right)$, which was introduced by Agrawal and Sahoo [20].
• ${\overline{\mathcal{F}}}_1^{1,1}(1-2\lambda ,-1)=\tilde{\mathcal{S}}\left(\lambda \right)$, which is the class of starlike functions of order $\lambda$ first studied by Robertson [21].
• Additional important subclasses include ${\overline{\mathcal{F}}}_1^{1,b}(1,-1):={\tilde{\mathcal{S}}}_k$, inspired by Sakaguchi [22].
• ${\overline{\mathcal{F}}}_q^{1,1}(1,-1)={\tilde{\mathcal{S}}}_q$, which was introduced by Ismail et al. [7].
• ${\overline{\mathcal{F}}}_1^{1,1}(F,H):=\tilde{\mathcal{S}}[F,H]$, which simplifies to the Janowski class [4].
• ${\overline{\mathcal{F}}}_1^{1,1}(1,-1)={\tilde{\mathcal{S}}}^{\ast }$ represents the class of starlike functions, which was introduced by Nevanlinna [23].

These examples underscore the versatility and foundational significance of the class ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$ in encompassing and extending classical results in geometric function theory.

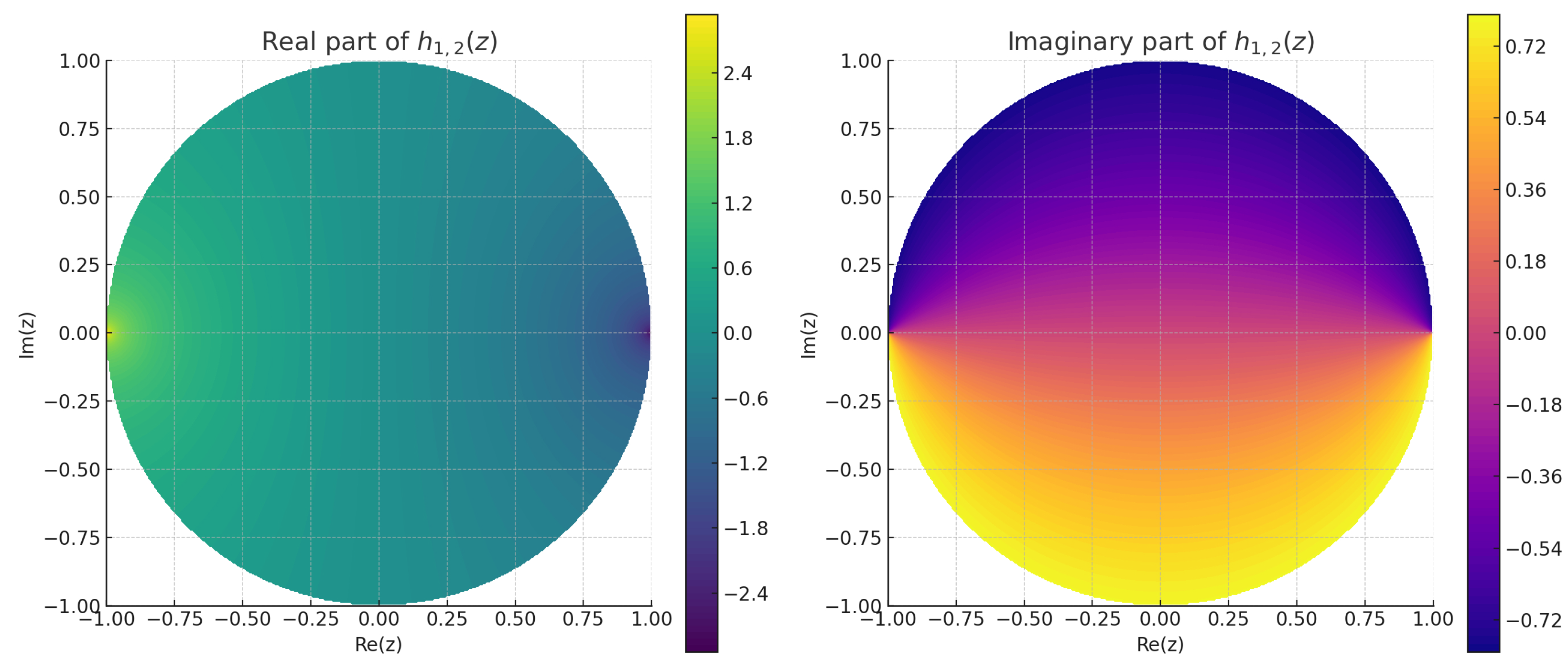
Example 1.

Consider the function

$$h\left(z\right)=log\left({\displaystyle \frac{1}{1-z}}\right)=z+{\displaystyle \frac{z^2}{2}}+{\displaystyle \frac{z^3}{3}}+\dots ,$$

which is analytic in the open unit disk $\Delta =\{z\in \mathbb{C}:|z|<1\}$.

For $b=2$ and $a=1$, the $(a,b)$-symmetric component $h_{1,2}\left(z\right)$ is defined as

$$h_{1,2}\left(z\right)={\displaystyle \frac{1}{2}}\left[h\left(z\right)-h(-z)\right].$$

Substituting $h\left(z\right)$, we have

$$h_{1,2}\left(z\right)={\displaystyle \frac{1}{2}}\left[log\left({\displaystyle \frac{1}{1-z}}\right)-log\left({\displaystyle \frac{1}{1+z}}\right)\right].$$

Simplifying the expression, this becomes

$$h_{1,2}\left(z\right)={\displaystyle \frac{1}{2}}log\left({\displaystyle \frac{1-z}{z+1}}\right).$$

Verification of Starlikeness

The function $h_{1,2}\left(z\right)$ satisfies the condition for starlike functions:

$$Re\left({\displaystyle \frac{z{h}^{\prime }\left(z\right)}{h\left(z\right)}}\right)>0,forallz\in \Delta .$$

Additionally, the q-derivative of $h\left(z\right)$ is given by

$${\partial }_{q}h\left(z\right)=1+{\left[2\right]}_{q}z+{\displaystyle \frac{{\left[3\right]}_q}{3}}{z}^2+\dots ,$$

where ${\left[v\right]}_q=1+q+q^2+\dots +q^{v-1}$ is the q-analog of the integer v.

The symmetric function $h_{1,2}\left(z\right)$ satisfies the subordination condition:

$${\displaystyle \frac{z{\partial }_{q}h\left(z\right)}{h_{1,2}\left(z\right)}}\prec {\displaystyle \frac{2+\left[F\right(1+q)+(1-q\left)\right]z}{2+\left[H\right(1+q)+(1-q\left)\right]z}},$$

for suitable choices of $F,H,\mathit{and}q$. Thus, $h_{1,2}\left(z\right)\in {\overline{\mathcal{F}}}_q^{1,2}(F,H)$.

The plot in Figure 2 demonstrates the real and imaginary parts of the $(1,2)$-symmetric function $h_{1,2}\left(z\right)$ in the unit disk $\Delta$. The symmetry with respect to the origin confirms the $(a,b)$ structure for $a=1$ and $b=2$. This supports the function’s inclusion in the class ${\overline{\mathcal{F}}}_q^{1,2}(F,H)$ under suitable conditions.

It is essential to revisit the concept of neighborhoods initially introduced by Goodman [24] and later refined by Ruscheweyh [25].

Definition 3.

For any $h\in \overline{\mathcal{G}}$, the ϱ-neighborhood of the function h is defined as

$${\mathcal{N}}_{\varrho }\left(h\right)=\left\{g\in \overline{\mathcal{G}}:g\left(z\right)=z+\sum _{v=2}^{\infty }{d}_v{z}^v,\sum _{v=2}^{\infty }v|c_v-d_v|\le \varrho \right\}.$$

(7)

For $e\left(z\right)=z$, we can see that

$${\mathcal{N}}_{\varrho }\left(e\right)=\left\{g\in \overline{\mathcal{G}}:g\left(z\right)=z+\sum _{v=2}^{\infty }{d}_v{z}^v,\sum _{v=2}^{\infty }v\left|d_v\right|\le \varrho \right\}.$$

(8)

Ruscheweyh [25] showed that for all $\sigma \in \mathbb{C}$ with $\left|\sigma \right|<\varrho$, among other results,

$${\displaystyle \frac{h\left(z\right)+\sigma z}{1+\sigma }}\in {\mathcal{S}}^{\ast }\Rightarrow {\mathcal{N}}_{\varrho }\left(h\right)\subset {\mathcal{S}}^{\ast }.$$

In this study, the main objective is to introduce and explore a new class of analytic functions that combine three distinct mathematical concepts, namely q-calculus, Janowski-type functions, and $(a,b)$-symmetrical functions. The key goals are

• Integration of Mathematical Concepts: We aim to merge q-calculus, Janowski-type functions, and $(a,b)$-symmetry to create a new class of functions with potentially rich properties.
• Examine Convolution Conditions: Using convolution and quantum calculus, we aim to investigate the convolution conditions for these functions. These conditions are essential for understanding the interactions between these mathematical structures and will provide a foundation for future theoretical developments.
• Neighborhood Definitions: Inspired by a novel conceptual framework, we define analogous neighborhoods for the classes ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$. This will help in characterizing the behavior of these functions and exploring their properties in a more structured way.

2. Main Results

Theorem 1.

A function $h\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)$ if and only if

$${\displaystyle \frac{1}{z}}\left[h\ast \left({\displaystyle \frac{(2+[H(1+q)+(1-q)]e^{i\varphi })z}{(1-z)(1-qz)}}-{\displaystyle \frac{(2+[F(1+q)+(1-q)]e^{i\varphi })z}{1-{\delta }_a^{1}z}}\right)\right]\ne 0,\left|z\right|<1,$$

(9)

where $0<q<1,$ $-1\le H<F\le 1,0\le \varphi <2\pi$.

Proof. 

We have $h\in {\overline{\mathcal{S}}}_q^{a,b}(F,H)$ if and only if

$${\displaystyle \frac{z{\partial }_{q}h\left(z\right)}{h_{a,b}\left(z\right)}}\ne {\displaystyle \frac{2+[F(1+q)+(1-q)]e^{i\varphi }}{2+[H(1+q)+(1-q)]e^{i\varphi }}},\left|z\right|<R,$$

This condition reflects that the q-derivative of h, normalized by the generalized $(a,b)$-symmetrical transform $h_{a,b}\left(z\right)$, must avoid a specific complex value determined by the parameters F, H, and $\varphi$. It is analogous to certain subordination conditions in classical geometric function theory.

This implies

$$z{\partial }_{q}h\left(z\right)\{2+[H(1+q)+(1-q)]e^{i\varphi }\}-h_{a,b}\left(z\right)\{2+[F(1+q)+(1-q)]e^{i\varphi }\}\ne 0.$$

(10)

Setting $h\left(z\right)=z+{\sum }_{v=2}^{\infty }{c}_v{z}^v$, we have

$$z{\partial }_{q}h\left(z\right)=z+\sum _{v=2}^{\infty }{\left[v\right]}_q{c}_v{z}^v=h\ast {\displaystyle \frac{1}{(1-z)(1-qz)}}.$$

(11)

Here, the expression for $z{\partial }_{q}h\left(z\right)$ is rewritten as a Hadamard (coefficient-wise) convolution between h and a known generating function. This step simplifies the manipulation of the operator form and is helpful in subsequent analysis.

$$h_{a,b}\left(z\right)=\sum _{v=1}^{\infty }{\delta }_a^v{c}_v{z}^v=h\ast {\displaystyle \frac{1}{(1-{\delta }_a^{1}z)}}.$$

(12)

Similarly, $h_{a,b}\left(z\right)$ is also expressed via convolution. This parallel representation allows us to combine terms under the same framework.

Substituting (11) and (12) into (10), we get

$${\displaystyle \frac{1}{z}}\left[h\ast \left({\displaystyle \frac{(2+[H(1+q)+(1-q)]e^{i\varphi })z}{(1-z)(1-qz)}}-{\displaystyle \frac{(2+[F(1+q)+(1-q)]e^{i\varphi })z}{1-{\delta }_a^{1}z}}\right)\right].$$

This final expression transforms the condition into a single convolution operator involving a known kernel. The non-vanishing of this form provides a powerful analytic condition for class membership and is especially useful in deriving bounds and constructing examples, as seen later.

Thus, the result follows from Theorem 1.  □

From Theorem 1, the equivalent condition for a function h to belong to the class ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$ can be derived straightforwardly, as stated in the following corollary:

Corollary 1.

$h\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)$ if and only if

$${\displaystyle \frac{(h\ast T)\left(z\right)}{z}}\ne 0,$$

(13)

where $T\left(z\right)$ has the form

$$\begin{array}{cc}\hfill T\left(z\right)=z+\sum _{v=2}^{\infty }{t}_v{z}^v,& \\ \hfill t_v={\displaystyle \frac{2({\delta }_a^v-{\left[v\right]}_q)+((H+1){\left[v\right]}_q-(F+1){\delta }_a^v)e^{i\varphi }}{(H-F)e^{i\varphi }}}.\end{array}$$

(14)

The functions belonging to the class ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$ possess structural properties that make them suitable candidates as kernel functions in the solution of certain q-deformed differential equations arising in quantum mechanics. In particular, the presence of the q-derivative aligns naturally with models in quantum calculus that describe systems with discrete energy levels or non-classical symmetries.

Such systems are often governed by q-differential equations of the form

$${\partial }_{q}h\left(z\right)+V\left(z\right)h\left(z\right)=0,$$

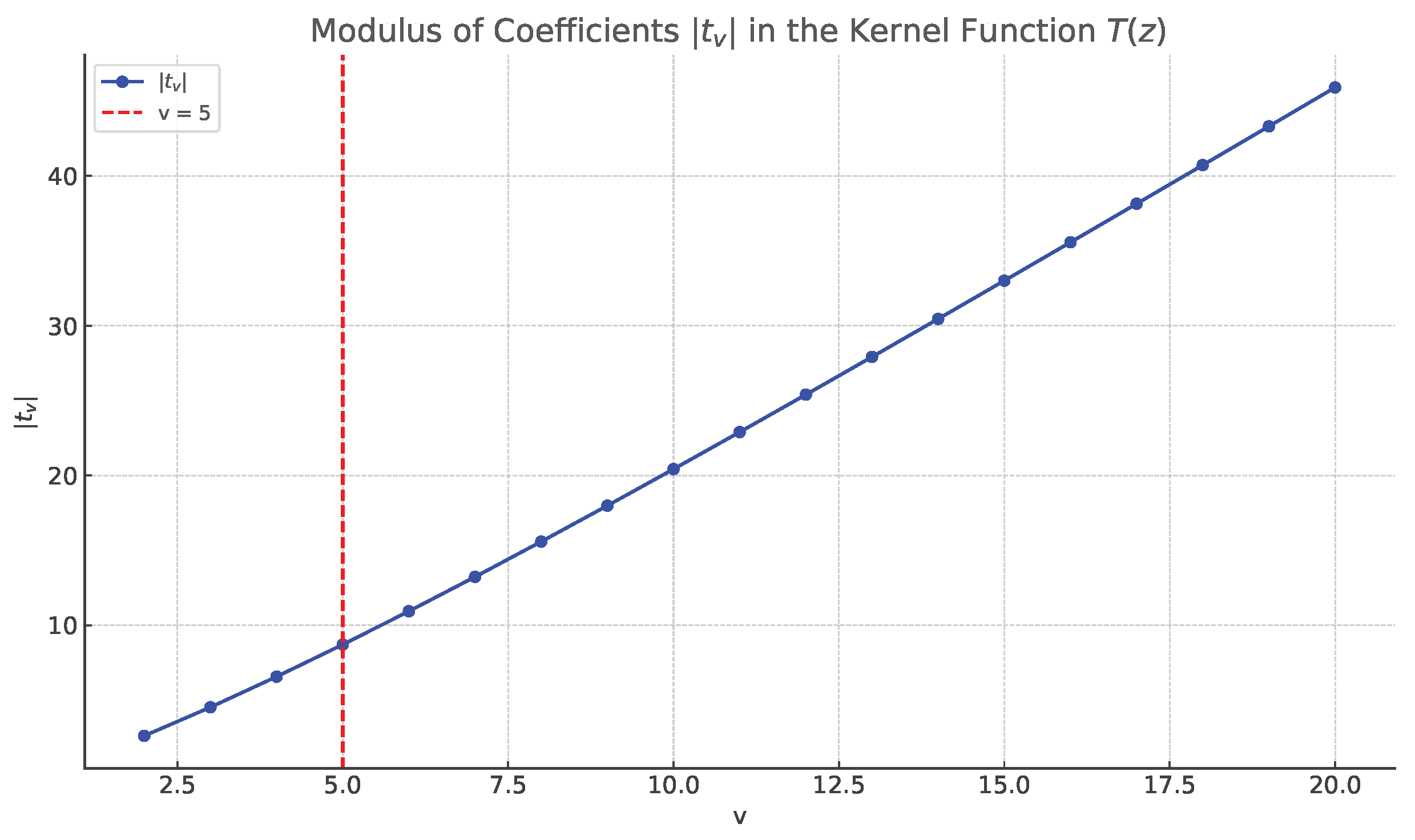
where ${\partial }_q$ is the Jackson q-derivative and $V\left(z\right)$ denotes a complex-valued potential function. Due to the convolution-based definition and parameter-controlled symmetry in ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$, functions in this class can serve as analytic models for wave functions or Green’s functions under q-deformation. These coefficients govern the behavior of the convolution condition as in Figure 3, used to define the class ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$. The plotted values demonstrate how the magnitude of $t_v$ evolves with v, which is important in estimating bounds and convergence in applications.

Theorem 2.

Let $f\left(z\right)=z+\zeta z^v,v\ge 2$, then $f\left(z\right)\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)$ if and only if

$$\left|\zeta \right|\le {\displaystyle \frac{|F-H|}{2({\delta }_a^v-{\left[v\right]}_q)+|(H+1){\left[v\right]}_q-(F+1){\delta }_a^v|}}.$$

(15)

Proof. 

Let $f\left(z\right)=z+\zeta z^v,$ which satisfies inequality (15).

Let T given in Corollary 1 and

$$\left|{\displaystyle \frac{(f\ast T)\left(z\right)}{z}}\right|\ge 1-\sum _{v=2}^{\infty }\left|\zeta \right||t_v{\left|\right|z|}^{v-1}>1-\left|z\right|>0,z\in \Delta .$$

By applying Theorem 1, we obtain $f\left(z\right)\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)$. Conversely, suppose $f\left(z\right)\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)$ and consider

$$\left|T\left(z\right)\right|=\left|z\right|+\sum _{v=2}^{\infty }{\displaystyle \frac{2({\delta }_a^v-{\left[v\right]}_q)+|(H+1){\left[v\right]}_q-(F+1){\delta }_a^v|}{|H-F|}}{\left|z\right|}^v.$$

Then, using Theorem 1, we obtain

$${\displaystyle \frac{(f\ast T)\left(z\right)}{z}}=1+\zeta {\displaystyle \frac{2({\delta }_a^v-{\left[v\right]}_q)+|(H+1){\left[v\right]}_q-(F+1){\delta }_a^v|}{|H-F|}}{z}^{v-1}\ne 0.$$

Let $\left|\zeta \right|>{\displaystyle \frac{|F-H|}{2({\delta }_a^v-{\left[v\right]}_q)+|(H+1){\left[v\right]}_q-(F+1){\delta }_a^v|}}$, then there exists $\tau \in \Delta$ such that

$${\displaystyle \frac{(f\ast T)\left(\tau \right)}{\tau }}=0$$

which is a contradiction. Hence, $\left|\zeta \right|\le {\displaystyle \frac{|H-F|}{2({\delta }_a^v-{\left[v\right]}_q)+|(H+1){\left[v\right]}_q-(F+1){\delta }_a^v|}}.$  □

To derive neighborhood results analogous to those obtained by Ruscheweyh [25] for the classes, we introduce the following neighborhood concepts:

Definition 4.

For any $h\in \overline{\mathcal{G}}$, the ϱ-neighborhood of the function h is defined as follows:

$${\mathcal{N}}_{\alpha ,\varrho }\left(h\right)=\left\{g\in \overline{\mathcal{G}}:g\left(z\right)=z+\sum _{v=2}^{\infty }{d}_v{z}^v,\sum _{v=2}^{\infty }{\alpha }_v|c_v-d_v|\le \varrho \right\},(\varrho \ge 0).$$

(16)

For $e\left(z\right)=z$, we can see that

$${\mathcal{N}}_{\alpha ,\varrho }\left(e\right)=\left\{g\in \overline{\mathcal{G}}:g\left(z\right)=z+\sum _{v=2}^{\infty }{d}_v{z}^v,\sum _{v=2}^{\infty }{\alpha }_v\left|d_v\right|\le \varrho \right\},(\varrho \ge 0),$$

(17)

where ${\left[v\right]}_q$ is given by Equation (5).

Remark 1.

• For ${\alpha }_v=v$ in Definition 4 we get Definition 3.
• For ${\alpha }_v={\left[v\right]}_q$ in Definition 4, we obtain the definition of the neighborhood with the q-derivative ${\mathcal{N}}_{q,\varrho }\left(h\right),{\mathcal{N}}_{q,\varrho }\left(e\right)$.
• For ${\alpha }_v=\left|t_v\right|$ given by (14) in Definition 4, we obtain the definition of the neighborhood for the class ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$, which is ${\mathcal{N}}_{q,\varrho }^{a,b}(F,H;h)$.

 

Theorem 3.

Let $h\in \overline{\mathcal{F}}$, and for all complex numbers η, with $\left|\sigma \right|<\varrho$, if

$${\displaystyle \frac{h\left(z\right)+\sigma z}{1+\sigma }}\in {\overline{\mathcal{F}}}_q^{a,b}(F,H).$$

(18)

Then

$${\mathcal{N}}_{q,{\varrho }_1}^{a,b}(F,H;h)\subset {\overline{\mathcal{F}}}_q^{a,b}(F,H).$$

where ${\varrho }_1={\displaystyle \frac{\varrho |H-F|}{2(1+|H\left|\right)}}$.

Proof. 

Given a function f defined by $f\left(z\right)=z+{\sum }_{v=2}^{\infty }{d}_v{z}^v$, we posit that it belongs to the class ${\mathcal{N}}_{q,{\varrho }_1}^{a,b}(F,H;h)$. To establish this, we are required to demonstrate that f is within the class ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$. This proof is structured into three distinct steps, leveraging Theorem 1 as a foundational element, $f\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)$. We would prove this claim using Corollary 1, in which we have

$$h\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)\iff {\displaystyle \frac{1}{z}}\left[\left((h\ast T)\left(z\right)\right)\right]\ne 0,z\in \Delta ,$$

(19)

where

$$T\left(z\right)=z+\sum _{v=2}^{\infty }{\displaystyle \frac{2({\delta }_a^v-{\left[v\right]}_q)+((H+1){\left[v\right]}_q-(F+1){\delta }_a^v)e^{i\varphi }}{(H-F)e^{i\varphi }}}{z}^v,$$

where $0\le \varphi <2\pi , -1\le H<F\le 1$. We can write $T\left(z\right)=z+{\sum }_{v=2}^{\infty }{t}_v{z}^v$ so that $|t_v|\le {\displaystyle \frac{2{\left[v\right]}_q(1+|H\left|\right)}{|H-F|}}.$

Secondly, we determine that (18) is equivalent to

$$\left|{\displaystyle \frac{h\left(z\right)\ast T\left(z\right)}{z}}\right|\ge \varrho ,$$

(20)

because if $h\left(z\right)=z+{\sum }_{v=2}^{\infty }{c}_v{z}^v\in \mathcal{F}$ and satisfies (18), then (19) is equivalent to

$$T\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)\iff {\displaystyle \frac{1}{z}}\left[{\displaystyle \frac{h\left(z\right)\ast T\left(z\right)}{1+\sigma }}\right]\ne 0,\left|\sigma \right|<\varrho .$$

Thirdly, letting $f\left(z\right)=z+{\sum }_{v=2}^{\infty }{d}_v{z}^v$, we notice that

$$\left|{\displaystyle \frac{f\left(z\right)\ast T\left(z\right)}{z}}\right|=\left|{\displaystyle \frac{h\left(z\right)\ast T\left(z\right)}{z}}+{\displaystyle \frac{\left(f\right(z)-h(z\left)\right)\ast T\left(z\right)}{z}}\right|$$

$$\ge \varrho -\left|{\displaystyle \frac{\left(f\right(z)-h(z\left)\right)\ast T\left(z\right)}{z}}\right|,(\mathrm{by}\mathrm{using}(20))$$

$$=\varrho -\left|\sum _{v=2}^{\infty }(d_v-c_v)t_v{z}^v\right|,$$

$$\ge \varrho -\left|z\right|\sum _{v=2}^{\infty }{\displaystyle \frac{2{\left[v\right]}_q(1+|H\left|\right)}{|H-F|}}|d_v-c_v|$$

$$\ge \varrho -\varrho \left|z\right|>0.$$

This is to establish the non-vanishing property of the expression

$${\displaystyle \frac{(f\ast T)\left(z\right)}{z}}\ne 0,z\in \Delta .$$

We employ the insights gained from our previous observations, specifically (19). This analysis leads us to the conclusion that the function f belongs to the set ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$. Thus, we have demonstrated that f satisfies the required conditions, completing the proof of the theorem.  □

As $q\to 1^{-}$, with $a=F=b=1$ and $H=-1$, the above theorem yields the well-known result proved by Ruscheweyh in [25].

Theorem 4.

Let $h\left(z\right)=z+{\sum }_{v=2}^{\infty }{c}_v{z}^v$ in the class ${\mathcal{N}}_{q,1}\left(e\right)$, then

$$\left|{\displaystyle \frac{z{\partial }_{q}h\left(z\right)}{h_{a,b}\left(z\right)}}-1\right|<1,$$

(21)

where $0<q<1,z\in \Delta .$

Proof. 

Setting $h\left(z\right)=z+{\sum }_{v=2}^{\infty }{c}_v{z}^v$, we have

$$z{\partial }_{q}h\left(z\right)=z+\sum _{v=2}^{\infty }{\left[v\right]}_q{c}_v{z}^v\mathrm{and}{h}_{a,b}\left(z\right)=\sum _{v=1}^{\infty }{\delta }_a^v{c}_v{z}^v.$$

(22)

Consider

$$|z{\partial }_{q}h\left(z\right)-h_{a,b}\left(z\right)|=\left|\sum _{v=2}^{\infty }({\left[v\right]}_q-{\delta }_a^v)c_v{z}^{v-1}\right|$$

$$\begin{array}{c}\hfill <\left|\varpi \right|\sum _{v=2}^{\infty }{\left[v\right]}_q|c_m|-\sum _{v=2}^{\infty }{\delta }_a^v|c_v{\left|\right|z|}^{v-1}\\ \hfill =\left|\varpi \right|-\sum _{v=2}^{\infty }{\delta }_a^v|c_v{\left|\right|z|}^{v-1}\\ \hfill \le |h_{a,b}\left(z\right)|,z\in \Delta . \end{array}$$

This concludes the proof.  □

Theorem 5.

Let $h\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)$ for ${\varrho }_1<k$. Then

$${\mathcal{N}}_{q,{\varrho }_1}^{a,b}(F,H;h)\subset {\overline{\mathcal{F}}}_q^{a,b}(F,H).$$

where k is a non-zero real number with $k\le \left|{\displaystyle \frac{(h\ast T)\left(z\right)}{z}}\right|,z\in \Delta$ and T is defined in Corollary 1.

Proof. 

Let $f\left(z\right)=z+{\sum }_{v=2}^{\infty }{d}_v{z}^v\in {\mathcal{N}}_{q,{\varrho }_1}^{a,b}(F,H;h)$. For the proof of Theorem 5, it suffices to show that ${\displaystyle \frac{(f\ast T)\left(z\right)}{z}}\ne 0$ where T is given by (14). Consider

$$\left|{\displaystyle \frac{f\left(z\right)\ast T\left(z\right)}{z}}\right|\ge \left|{\displaystyle \frac{h\left(z\right)\ast T\left(z\right)}{z}}\right|-\left|{\displaystyle \frac{\left(f\right(z)-h(z\left)\right)\ast T\left(z\right)}{z}}\right|.$$

(23)

since $h\in {\overline{\mathcal{F}}}_q^{a,b}(F,H)$ if and only if ${\displaystyle \frac{(h\ast T)\left(z\right)}{z}}\ne 0$. Using (14), we get

$$\left|{\displaystyle \frac{(h\ast T)\left(z\right)}{z}}\right|\ge 1-\sum _{v=2}^{\infty }{\displaystyle \frac{2({\delta }_a^v-{\left[v\right]}_q)+|(H+1){\left[v\right]}_q-(F+1){\delta }_a^v|}{|F-H|}}|c_v{||z|}^{v-1}>0,z\in \Delta .$$

Therefore,

$$\left|{\displaystyle \frac{(h\ast T)\left(z\right)}{z}}\right|\ge k,$$

(24)

where k is a non-zero real number and $z\in \Delta$. Now

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{\left(f\right(z)-h(z\left)\right)\ast T\left(z\right)}{z}}\right|=\left|\sum _{v=2}^{\infty }(d_v-c_v)t_v{z}^v\right|\\ \hfill \le \sum _{v=2}^{\infty }{\displaystyle \frac{2({\delta }_a^v-{\left[v\right]}_q)+|(H+1){\left[v\right]}_q-(F+1){\delta }_a^v|}{|F-H|}}|d_v-c_v|\\ \hfill \le \sum _{v=2}^{\infty }{\displaystyle \frac{2{\left[v\right]}_q(1+|H\left|\right)}{|H-F|}}|d_v-c_v|\\ \hfill \le {\displaystyle \frac{\varrho |H-F|}{2{\left[v\right]}_q(1+|H\left|\right)}}={\varrho }_1, \end{array}$$

(25)

By substituting (24) and (25) into (23), we arrive at

$$\left|{\displaystyle \frac{f\left(z\right)\ast T\left(z\right)}{z}}\right|\ge k-{\varrho }_1>0,$$

with the condition that ${\varrho }_1<k$. This conclusion finalizes the proof.  □

3. Conclusions

This paper introduces a novel class of analytic functions that integrates q-calculus, Janowski-type functions, and $(a,b)$-symmetrical functions. Through the examination of convolution conditions and quantum calculus, we established foundational results that enhance the understanding of these functions’ geometric and analytical properties. Additionally, by defining analogous neighborhoods for the classes ${\overline{\mathcal{F}}}_q^{a,b}(F,H)$, we further explored their structural behaviors. These contributions provide a solid foundation for future research and applications in areas such as geometric function theory, complex analysis, and boundary value problems.