A Note on Rigidity and Vanishing Theorems for Translating Solitons

Abstract

In this short note, we focus on complete translating solitons with a bounded $L_f^n$-norm of the second fundamental form and obtain two results. First, based on a Sobolev-type inequality and a Simons-type inequality, we establish a rigidity theorem of complete translating solitons. Second, based on the same Sobolev-type inequality and a Bochner-type inequality, a vanishing theorem regarding $L_f^p$ weighted harmonic 1-forms is proved.

1. Introduction

Let $X:M^n\to {\mathbb{R}}^{n+k}$ be an n-dimensional smooth submanifold isometrically immersed in ${\mathbb{R}}^{n+k}$. A family of immersions $X_t=X(·,t):M\to {\mathbb{R}}^{n+k}$ is called a mean curvature flow [1] of M in ${\mathbb{R}}^{n+k}$ if it satisfies

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial X(x,t)}{\partial t}}=H(x,t),x\in M,\hfill \\ X(x,0)=X\left(x\right),\hfill \end{array}\right.$$

(1)

where $H(x,t)$ is the mean curvature vector of $X_t\left(M\right)$ in ${\mathbb{R}}^{n+k}$.

We call $X:M^n\to {\mathbb{R}}^{n+k}$ a translating soliton [2] in ${\mathbb{R}}^{n+k}$ if it satisfies

$$H=V^N,$$

where V is a unit constant vector in ${\mathbb{R}}^{n+k}$ and $V^N$ denotes the orthonormal projection of V onto the normal bundle of M. A translating soliton is a special solution to (1) that moves by translation in the direction of V in ${\mathbb{R}}^{n+k}$.

Translating solitons, which frequently arise in physical systems, exhibit fundamentally different behavior in Minkowski spacetime compared to Euclidean space. The existence, uniqueness, and asymptotic properties of rotationally symmetric translating solitons under mean curvature flow in Minkowski spacetime were first studied by Jian [3] in 2006. Subsequent work by Lawn and Ortega [4] introduced new classes of translating solitons, with particular emphasis on Minkowski spacetime. Their approach employed manifolds that admit submersions and cohomogeneity-one isometric group actions on suitable open subsets, thereby generalizing the classical Euclidean framework. Within this setting, they achieved a complete classification of time-like, invariant translating solitons generated by rotations and boosts in Minkowski spacetime.

In the 1910s, Bernstein proved that any solution to the minimal surface equation defined on the entire plane must be an affine linear function, implying that its graph is a plane. Various generalizations of this celebrated result form what is now known as the Bernstein-type problem. A central theme in this area is the rigidity of minimal submanifolds of arbitrary codimension, that is, determining the conditions under which such submanifolds must be affine linear. Building on an important observation by Ilmanen (see [5]), a translating soliton can be viewed as a minimal submanifold under a conformal change of the ambient space. This insight naturally motivates the study of the rigidity properties of translating solitons. In the codimension-one case, Bao and Shi [6] established a rigidity theorem in 2014: if the image of the Gauss map of a translating soliton lies within a compact subset of an open hemisphere of the standard sphere ${\mathbb{S}}^n$, then the soliton must be affine linear. For higher codimensions, one may consider the slope function w, which measures the inclination of the soliton relative to a fixed plane. When $w>0$, the function $v=w^{-1}$ represents the volume element of the soliton and satisfies $v\ge 1$ in general. In 2015, Kunikawa [7] proved that any complete translating soliton $M^n$ with a flat normal bundle in ${\mathbb{R}}^{n+k}$ must be an affine subspace if $w>0$ and $v=o\left(R^{1/2}\right)$. Around the same time, Xin [8], using local estimates of the second fundamental form in terms of the v-function, showed that if $v\le v_1<v_0={\displaystyle \frac{2·3^{2/3}}{1+3^{2/3}}}$, then any complete translating soliton $M^n$ in ${\mathbb{R}}^{n+k}$ (for $k\ge 2$) must also be affine linear. Further improvements in this direction—specifically, enlarging the upper bound $v_0$—can be found in a series of recent works [9,10,11,12,13]. Another important approach to rigidity involves imposing integrability conditions on the (trace-free) second fundamental form, particularly in terms of certain (weighted) Lebesgue norms. For developments in this direction, we refer to [8,14,15,16] and the references therein. Notably, in [14], Dung–Dung–Huy not only proved two rigidity theorems, but also established a vanishing theorem for $L_f^p$-weighted harmonic 1-forms on hypersurface translating solitons. Around the same time, Nam–Pyo [17] proved a similar vanishing theorem for $L_f^2$-weighted harmonic 1-forms on translating solitons of arbitrary codimension, under different assumptions. The analysis and geometry of translating solitons have been the subject of extensive study; see [2,3,8,10,11,12,13,14,18,19,20,21,22,23,24,25,26] and the references therein.

In this paper, we focus on the general codimension setting and present both a rigidity theorem and a vanishing theorem for $L_f^p$-weighted harmonic 1-forms. To precisely formulate and prove our results, we begin by fixing some notations. Let $X:M^n\to {\mathbb{R}}^{n+k}$ be a translating soliton. Let H and A denote the mean curvature vector field and second fundamental form of M, respectively. Let V be a fixed unit vector in ${\mathbb{R}}^{n+m}$ such that the normal component of V satisfies $V^N=H$. Let $f=-⟨V,X⟩$, and it is well known that the weighted Hodge Laplacian [27] is given by

$${\Delta }_f=\Delta -L_{\nabla f}=-(d\delta +\delta d)-d{\iota }_{\nabla f}-{\iota }_{\nabla f}d=-(d{\delta }_f+{\delta }_{f}d),$$

where L is the Lie derivative, $\delta$ is the co-differential, $\iota$ is the interior product, and ${\delta }_f:=\delta +{\iota }_{\nabla f}$. A q-form $\omega$ on M is referred to as the $L_f^p$ weighted harmonic q-form if

$${\Delta }_f\omega =0,{\int }_M{|\omega |}^p{e}^{-f}\mathrm{d}v<\infty ,$$

and referred to as the weighted harmonic q-form when $\omega$ only satisfies the former condition. The trace-free second fundamental form is given by

$$\mathsf{\Phi }=A-{\displaystyle \frac{1}{n}}g\otimes H,$$

where g is the induced metric on M. It is well known that

$$|\mathsf{\Phi }{|}^2={|A|}^2-{\displaystyle \frac{1}{n}}{|H|}^2.$$

Given two q-forms $\omega$ and $\theta$ on $M,$ we define a pointwise inner product

$$⟨\omega ,\theta ⟩=\sum _{i_1,\cdots ,i_q=1}^n\omega \left(e_{i_1},\cdots ,e_{i_q}\right)\theta \left(e_{i_1},\cdots ,e_{i_q}\right),$$

where ${\left\{e_i\right\}}_{i=1}^n$ is a local orthonormal frame field of M. Observe that we are omitting the normalizing factor $1/q!$.

We employ the mathematical technique of cut-off functions. This approach ensures that our results hold not only locally but also extend to complete translating solitons. Specifically, if we define the scaled cut-off function on M as

$${\eta }_R\left(x\right)=\eta \left({\displaystyle \frac{x}{R}}\right),R>0,$$

then the following key properties hold:

(i)

Uniform derivative bounds:

$$|{\nabla }^k{\eta }_R|\le {\displaystyle \frac{C_k}{R^k}},\forall k\in \mathbb{N},$$

(ii)

Asymptotic vanishing of gradient terms:

$$\underset{R\to \infty }{\lim }{\int }_M|\nabla {\eta }_R{|}^2|\varphi |dv=0.$$

where $\varphi$ is a function on $M.$

In addition, to obtain our results, we need to impose a condition on the translating soliton. For the convenience of description, we write this condition separately as follows:

$${\int }_M⟨V,X⟩e^{⟨V,X⟩}\mathrm{d}v\ge 0.$$

(2)

We will explain this condition in Section 2. Finally, throughout this paper, the volume of the n-dimensional Euclidean unit ball is denoted by ${\omega }_n$. Now, we present the two main theorems of this paper.

Theorem 1 (Rigidity theorem).

Let $M^n(n\ge 3)$ be a complete translating soliton in ${\mathbb{R}}^{n+k}$ that satisfies condition (2). If the second fundamental form A of M satisfies

$${\left({\int }_M{|A|}^n{e}^{-f}\mathrm{d}v\right)}^{{\displaystyle \frac{1}{n}}}<G\left(n\right):=\sqrt{{\displaystyle \frac{(n-1){(n-2)}^2{\omega }_n^{\frac{2}{n}}}{2·{25}^n{n}^4}}},$$

(3)

then M is a linear subspace.

Theorem 2 (Vanishing theorem).

Let $M^n(n\ge 3)$ be a complete translating soliton in ${\mathbb{R}}^{n+k}$ that satisfies condition (2). For $p\ge 2$, suppose that the second fundamental form A of M satisfies

$${\left({\int }_M{|A|}^n{e}^{-f}\mathrm{d}v\right)}^{{\displaystyle \frac{1}{n}}}<\sqrt{{\displaystyle \frac{(p-1){(n-2)}^2{\omega }_n^{\frac{2}{n}}}{{25}^n{n}^2{p}^2}}}.$$

Then M admits no nontrivial $L_f^p$ weighted harmonic 1-forms.

Remark 1.

Compared with [14], Theorem 1 presents rigidity under different conditions. Compared with [14,17], Theorem 2 obtains a vanishing result for $L_f^p$ weighted harmonic 1-forms. Owing to the exponential terms in the denominator, the constants in the two theorems are smaller than the two ones of [14,17] with increasing dimensionality, respectively.

2. Some Lemmas

To prove Theorems 1 and 2, this section presents some preliminary lemmas and illustrative examples.

First of all, we state that an important inequality can be obtained under the condition (2). Actually, in [28], Alves de Medeiros provided a weighted Michael–Simon–Sobolev-type inequality that says if $X:M^n\to ({\mathbb{R}}^{n+k},g_{\mathrm{can}},e^{-\phi }\mathrm{d}v)$ is a submanifold of weighted Euclidean space and

$$\begin{array}{c}\hfill {\int }_M⟨X,\overline{\nabla }\phi ⟩e^{-\phi }\mathrm{d}v\le 0\mathrm{on}M,\end{array}$$

(4)

then inequality

$${\left({\int }_M{u}^{{\displaystyle \frac{n}{n-1}}}{e}^{-\phi }\mathrm{d}v\right)}^{{\displaystyle \frac{n-1}{n}}}\le C_n{\int }_M\left(|\nabla u|+u|H_{\phi }|\right)e^{-\phi }\mathrm{d}v,$$

(5)

holds for any positive Lipschitz function u with compact support on M, where $C_n={\displaystyle \frac{n}{n-1}}{\displaystyle \frac{5^n}{{\omega }_n^{1/n}}}$ and $H_{\phi }=H+{\left(\overline{\nabla }\phi \right)}^N$ is the so-called $\phi$-mean curvature vector field. When $M^n$ is a translating soliton in ${\mathbb{R}}^{n+k}$ and the weight function $\phi =-⟨V,X⟩=:f$, it is easy to see that $H_f=0$ and $⟨X,\overline{\nabla }f⟩=-⟨V,X⟩$, and then the condition (4) becomes to the condition (2). If we select the direction vector is $V=(0,\cdots ,0,1)\in {\mathbb{R}}^{n+k}$, the condition (2) implies that the angle between its position vector and the direction vector is acute, which results in its entire image lying above the hyperplane orthogonal to direction vector V. In our setting, the above result reduces to

Lemma 1.

Let $M^n$ be a translating soliton in ${\mathbb{R}}^{n+k}$ that satisfies the condition (2). Then, for any positive Lipschitz function u with compact support on M, we have

$${\left({\int }_M{z}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right)}^{{\displaystyle \frac{n-2}{n}}}\le D_n{\int }_M{|\nabla z|}^2{e}^{-f}\mathrm{d}v,$$

(6)

where $D_n={\displaystyle \frac{4·{25}^n{n}^2}{{(n-2)}^2{\omega }_n^{2/n}}}$.

Proof. 

The proof is obvious by setting $u=z^{{\displaystyle \frac{2(n-1)}{n-2}}}$ in inequality (5) and using the Cauchy–Schwarz inequality on the right-hand side. □

Here, we provide two examples of translating solitons that satisfies the condition (2).

Example 1

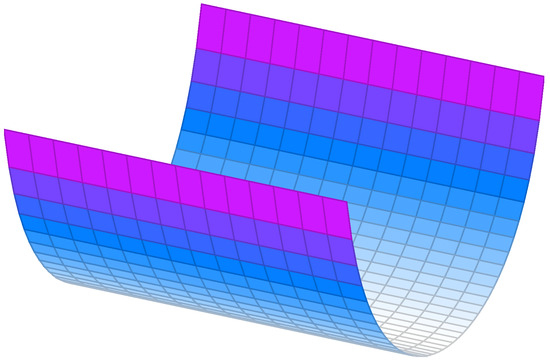
(Grim reaper cylinders; see [29]). Let Γ is the grim reaper and its function is

$$r\left(t\right)=-\log \cos t,t\in \left(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right).$$

Set $M^n=\Gamma \times {\mathbb{R}}^{n-1}$ and the position vector $X:M^n\to {\mathbb{R}}^{n+1}$ is given by

$$X(t,q)=(q,r\left(t\right))\in {\mathbb{R}}^{n+1},$$

where $q\in {\mathbb{R}}^{n-1}\subset {\mathbb{R}}^n$ and $t\in \left(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right)$. Then the submanifold $X\left(M^n\right)\subset {\mathbb{R}}^{n+1}$ is translating soliton with the direction $V=(0,\cdots ,0,1)\in {\mathbb{R}}^{n+1}$. From this, it is easy to get

$$⟨X,\overline{\nabla }f⟩=-⟨X,V⟩=-r\left(t\right)\le 0,$$

where $t\in \left(-{\displaystyle \frac{\pi }{2}},{\displaystyle \frac{\pi }{2}}\right)$, so $M^n$ satisfies the condition (2). For immediate geometric apprehension, we suppose $n=2$; then, the grim reaper cylinder [29] is depicted in Figure 1.

Figure 1. A 2-dimensional grim reaper cylinder: the surface $z=-\log \left(\cos x\right)$ extended along the y-axis.

Example 2

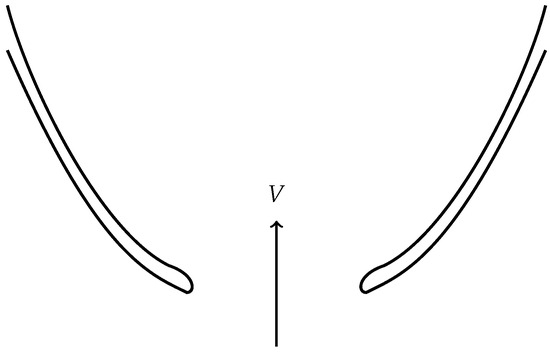
(The case of arbitrary codimension; see [29]). Let $N^{n-1}$ be any complete minimal submanifold of the unit sphere ${\mathbb{S}}^{m-2}\subset {\mathbb{R}}^{m-1}$ and $r\left(t\right):{\mathbb{R}}_{+}\to \mathbb{R}$ be a function satisfying the ODE

$$\ddot{r}\left(t\right)=\left(1+\dot{r}{\left(t\right)}^2\right)\left(1-{\displaystyle \frac{(n-1)\dot{r}\left(t\right)}{t}}\right).$$

Set $M^n={\mathbb{R}}_{+}\times N^{n-1}$ and the position vector $X:M^n\to {\mathbb{R}}^m$ by

$$X(t,q)=(tq,r\left(t\right))\in {\mathbb{R}}^m,$$

where $q\in N^{n-1}\subset {\mathbb{S}}^{m-2}\subset {\mathbb{R}}^{m-1}$ and $t\in {\mathbb{R}}_{+}$. Then, the submanifold $X\left(M^n\right)\subset {\mathbb{R}}^m$ is a translating soliton with the direction $V=(0,\cdots ,0,1)\in {\mathbb{R}}^m$. We say that the condition (2) is satisfied on M. In fact, the solution to the above ODE has the following asymptotic expansion:

$$r\left(t\right)={\displaystyle \frac{t^2}{n-1}}-\ln t+O\left({\displaystyle \frac{1}{t}}\right).$$

It follows that $r\left(t\right)\sim t^2(|t|\to \infty )$. So it is easy to get

$${\int }_M⟨X,\overline{\nabla }f⟩e^{-f}\mathrm{d}v=-{\int }_M⟨V,X⟩e^{⟨V,X⟩}\mathrm{d}v=-{\int }_{M}r\left(t\right)e^{r\left(t\right)}<0$$

as long as $|t|\ge L$ for some sufficiently large positive number L.

As a special example [29], we select a complete minimal submanifold $N^{n-1}\subset {\mathbb{S}}^{m-2}$ and Wing-like curve (see Figure 2), so

$$X(t,q)=(tq,W\left(t\right))\in {\mathbb{R}}^m$$

is a translating soliton in an arbitrary codimension.

Figure 2. Wing-like curve.

Secondly, to prove Theorem 1, we need the following Simons-type inequality.

Lemma 2

(see [16]). If $M^n$ is a translating soliton in ${\mathbb{R}}^{n+k}$, then we have

$$\begin{array}{c}\hfill {\Delta }_f|\mathsf{\Phi }{|}^2\ge |\nabla \mathsf{\Phi }{|}^2-\tau |\mathsf{\Phi }{|}^4-{\displaystyle \frac{2}{n}}{|H|}^2|\mathsf{\Phi }{|}^2,\end{array}$$

(7)

where

$$\begin{array}{c}\hfill \tau =\left\{\begin{array}{cc}2,\hfill & ifk=1,\hfill \\ 4,\hfill & ifk\ge 2.\hfill \end{array}\right.\end{array}$$

Finally, in order to prove Theorem 2, we need to establish the following lemma, which is a Bochner-type inequality for weighted harmonic 1-forms.

Lemma 3

(see [14]). Let $M^n$ be a translating soliton in ${\mathbb{R}}^{n+k}$ and let ω be a weighted harmonic 1-form on M. Then, we have

$$|\omega |{\Delta }_f|\omega |\ge -{|A|}^2{|\omega |}^2.$$

3. Proofs of Theorems 1 and 2

With the preparations in Section 2, we can now prove our main theorems.

Proof of Theorem 1.

Let $\eta$ be a smooth function with compact support on M. We multiply both sides of inequality (7) by $|\mathsf{\Phi }{|}^{n-2}{\eta }^2$ and integrate with respect to the measure $e^{-f}\mathrm{d}v$ on M, obtaining

$$\begin{array}{cc}\hfill 0\ge & 2{\int }_M|\nabla |\mathsf{\Phi }|{|}^2|\mathsf{\Phi }{|}^{n-2}{\eta }^2{e}^{-f}\mathrm{d}v-\tau {\int }_M|\mathsf{\Phi }{|}^{n+2}{\eta }^2{e}^{-f}\mathrm{d}v\hfill \\ & -{\displaystyle \frac{2}{n}}{\int }_M|\mathsf{\Phi }{|}^n{|H|}^2{\eta }^2{e}^{-f}\mathrm{d}v-{\int }_M|\mathsf{\Phi }{|}^{n-2}{\eta }^2{\Delta }_f|\mathsf{\Phi }{|}^2{e}^{-f}\mathrm{d}v.\hfill \end{array}$$

(8)

Since $\eta$ has compact support on M, the divergence theorem gives

$$\begin{array}{cc}\hfill -{\int }_M|\mathsf{\Phi }{|}^{n-2}{\eta }^2{\Delta }_f|\mathsf{\Phi }{|}^2{e}^{-f}\mathrm{d}v=& -{\int }_M|\mathsf{\Phi }{|}^{n-2}{\eta }^2\mathrm{div}\left(\nabla |\mathsf{\Phi }{|}^2{e}^{-f}\right)\mathrm{d}v\hfill \\ \hfill =& 2{\int }_M|\mathsf{\Phi }|\left(\nabla \left({|\mathsf{\Phi }|}^{n-2}{\eta }^2\right)·\nabla |\mathsf{\Phi }|\right)e^{-f}\mathrm{d}v\hfill \\ \hfill =& 4\left({\displaystyle \frac{n}{2}}-1\right){\int }_M{|\nabla |\mathsf{\Phi }\parallel }^2|\mathsf{\Phi }{|}^{n-2}{\eta }^2{e}^{-f}\mathrm{d}v\hfill \\ & +4{\int }_M(\nabla |\mathsf{\Phi }|·\nabla \eta )|\mathsf{\Phi }{|}^{n-1}\eta e^{-f}\mathrm{d}v.\hfill \end{array}$$

(9)

Combining (8) and (9), we get

$$\begin{array}{cc}\hfill 0\ge & 4\left({\displaystyle \frac{n}{2}}-{\displaystyle \frac{1}{2}}\right){\int }_M{|\nabla |\mathsf{\Phi }||}^2|\mathsf{\Phi }{|}^{n-2}{\eta }^2{e}^{-f}\mathrm{d}v-\tau {\int }_M|\mathsf{\Phi }{|}^{n+2}{\eta }^2{e}^{-f}\mathrm{d}v\hfill \\ & -{\displaystyle \frac{2}{n}}{\int }_M|\mathsf{\Phi }{|}^n{|H|}^2{\eta }^2{e}^{-f}\mathrm{d}v+4{\int }_M(\nabla |\mathsf{\Phi }|·\nabla \eta )|\mathsf{\Phi }{|}^{n-1}\eta e^{-f}\mathrm{d}v.\hfill \end{array}$$

For $0<\epsilon <{\displaystyle \frac{n}{2}}-{\displaystyle \frac{1}{2}}$, we apply the Cauchy–Schwarz inequality to the last term on the right-hand side of this inequality and therefore get

$$\begin{array}{cc}& 4\left({\displaystyle \frac{n}{2}}-{\displaystyle \frac{1}{2}}-\epsilon \right){\int }_M|\nabla |\mathsf{\Phi }{||}^2|\mathsf{\Phi }{|}^{n-2}{\eta }^2{e}^{-f}\mathrm{d}v\hfill \\ \hfill \le & \tau {\int }_M|\mathsf{\Phi }{|}^{n+2}{\eta }^2{e}^{-f}\mathrm{d}v+{\displaystyle \frac{2}{n}}{\int }_M|\mathsf{\Phi }{|}^n{|H|}^2{\eta }^2{e}^{-f}\mathrm{d}v+{\displaystyle \frac{1}{\epsilon }}{\int }_M|\mathsf{\Phi }{|}^n{|\nabla \eta |}^2{e}^{-f}\mathrm{d}v.\hfill \end{array}$$

(10)

Taking $z={|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta$ in inequality (6) and applying the Cauchy–Schwarz inequality, we have

$$\begin{array}{cc}& {\left[{\int }_M{\left({|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta \right)}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right]}^{{\displaystyle \frac{n-2}{n}}}\hfill \\ \hfill \le & D_n{\int }_M{\left|\nabla \left({|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta \right)\right|}^2{e}^{-f}\mathrm{d}v\hfill \\ \hfill =& D_n\left({\displaystyle \frac{n^2}{4}}{\int }_M{|\nabla |\mathsf{\Phi }||}^2|\mathsf{\Phi }{|}^{n-2}{\eta }^2{e}^{-f}\mathrm{d}v+n{\int }_M|\mathsf{\Phi }{|}^{n-1}\eta \left(\nabla |\mathsf{\Phi }|·\nabla \eta \right)e^{-f}\mathrm{d}v\right)\hfill \\ & +D_n{\int }_M|\mathsf{\Phi }{|}^n{|\nabla \eta |}^2{e}^{-f}\mathrm{d}v\hfill \\ \hfill \le & D_n\left({\displaystyle \frac{n^2(1+\delta )}{4}}{\int }_M{|\nabla |\mathsf{\Phi }||}^2|\mathsf{\Phi }{|}^{n-2}{\eta }^2{e}^{-f}\mathrm{d}v+\left(1+{\displaystyle \frac{1}{\delta }}\right){\int }_M|\mathsf{\Phi }{|}^n{|\nabla \eta |}^2{e}^{-f}\mathrm{d}v\right),\hfill \end{array}$$

where $\delta >0$. Substituting (10) into the above inequality and noting that $\tau \le 4$, we have

$$\begin{array}{cc}& D_n^{-1}{\left[{\int }_M{\left({|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta \right)}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right]}^{{\displaystyle \frac{n-2}{n}}}\hfill \\ \hfill \le & {\displaystyle \frac{\frac{n^2}{4}(1+\delta )}{\frac{n}{2}-\frac{1}{2}-\epsilon }}\left({\int }_M|\mathsf{\Phi }{|}^{n+2}{\eta }^2{e}^{-f}\mathrm{d}v+{\displaystyle \frac{1}{n}}{\int }_M|\mathsf{\Phi }{|}^n{|H|}^2{\eta }^2{e}^{-f}\mathrm{d}v\right)\hfill \\ & +{\displaystyle \frac{\frac{n^2}{4}(1+\delta )}{\frac{n}{2}-\frac{1}{2}-\epsilon }}·{\displaystyle \frac{1}{4\epsilon }}{\int }_M|\mathsf{\Phi }{|}^n{|\nabla \eta |}^2{e}^{-f}\mathrm{d}v+\left(1+{\displaystyle \frac{1}{\delta }}\right){\int }_M|\mathsf{\Phi }{|}^n{|\nabla \eta |}^2{e}^{-f}\mathrm{d}v,\hfill \end{array}$$

By the fact that ${|A|}^2={|\mathsf{\Phi }|}^2+{\displaystyle \frac{1}{n}}{|H|}^2$, we can rewrite the above inequality as

$$\begin{array}{cc}& D_n^{-1}{\left[{\int }_M{\left({|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta \right)}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right]}^{{\displaystyle \frac{n-2}{n}}}\hfill \\ \hfill \le & {\displaystyle \frac{n^2(1+\delta )}{4\left(\frac{n}{2}-\frac{1}{2}-\epsilon \right)}}{\int }_M|\mathsf{\Phi }{|}^n{|A|}^2{\eta }^2{e}^{-f}\mathrm{d}v+C(n,\delta ,\epsilon ){\int }_M|\mathsf{\Phi }{|}^n{|\nabla \eta |}^2{e}^{-f}\mathrm{d}v,\hfill \end{array}$$

where $C(n,\delta ,\epsilon )$ is a positive constant depending on $n,\delta$ and $\epsilon$. By the Hölder’s inequality and noting that $|\mathsf{\Phi }|\le |A|$, we have

$$\begin{array}{cc}& D_n^{-1}{\left[{\int }_M{\left({|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta \right)}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right]}^{{\displaystyle \frac{n-2}{n}}}\hfill \\ \hfill \le & {\displaystyle \frac{n^2(1+\delta )}{4\left(\frac{n}{2}-\frac{1}{2}-\epsilon \right)}}{\left({\int }_M{|A|}^n{e}^{-f}\mathrm{d}v\right)}^{{\displaystyle \frac{2}{n}}}{\left({\int }_M{\left({|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta \right)}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right)}^{{\displaystyle \frac{n-2}{n}}}\hfill \\ & +C(n,\delta ,\epsilon ){\int }_M{|A|}^n{|\nabla \eta |}^2{e}^{-f}\mathrm{d}v.\hfill \end{array}$$

(11)

Setting $G(n,\delta ,\epsilon )=\sqrt{{\displaystyle \frac{4\left(\frac{n}{2}-\frac{1}{2}-\epsilon \right)}{n^2(1+\delta )D_n}}}$, then we obtain $\underset{\delta >0,0<\epsilon <{\displaystyle \frac{n}{2}}-{\displaystyle \frac{1}{2}}}{\sup }G(n,\delta ,\epsilon )=G\left(n\right)$. Combined with the assumption (3), there exists a positive constant G, ${\delta }_0>0$ and ${\epsilon }_0\in \left(0,{\displaystyle \frac{n}{2}}-{\displaystyle \frac{1}{2}}\right)$ such that

$${\left({\int }_M{|A|}^n{e}^{-f}\mathrm{d}v\right)}^{{\displaystyle \frac{1}{n}}}<G<G(n,{\delta }_0,{\epsilon }_0)<G\left(n\right).$$

(12)

By inequalities (11) and (12), there exists $0<\xi <1$ such that

$$\begin{array}{cc}\hfill D_n^{-1}{\left[{\int }_M{\left({|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta \right)}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right]}^{{\displaystyle \frac{n-2}{n}}}\le & D_n^{-1}{\displaystyle \frac{G^2}{G{(n,{\delta }_0,{\epsilon }_0)}^2}}{\left({\int }_M{\left({|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta \right)}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right)}^{{\displaystyle \frac{n-2}{n}}}\hfill \\ & +C(n,{\delta }_0,{\epsilon }_0){\int }_M{|A|}^n{|\nabla \eta |}^2{e}^{-f}\mathrm{d}v\hfill \\ \hfill \le & {\displaystyle \frac{1-\xi }{D_n}}{\left({\int }_M{\left({|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta \right)}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right)}^{{\displaystyle \frac{n-2}{n}}}\hfill \\ & +C(n,{\delta }_0,{\epsilon }_0){\int }_M{|A|}^n{|\nabla \eta |}^2{e}^{-f}\mathrm{d}v,\hfill \end{array}$$

which is equivalent to

$${\left[{\int }_M{\left({|\mathsf{\Phi }|}^{{\displaystyle \frac{n}{2}}}\eta \right)}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right]}^{{\displaystyle \frac{n-2}{n}}}\le C(n,{\delta }_0,{\epsilon }_0){\displaystyle \frac{D_n}{\xi }}{\int }_M{|A|}^n{|\nabla \eta |}^2{e}^{-f}\mathrm{d}v.$$

(13)

Now let $o\in M$ be a fixed point and let $B_R\left(o\right)$ be the geodesic ball centered at o with radius R. Choose a cut-off function $\eta$ on M such that $0\le \eta \le 1$ and

(i)

$\eta =1$ on $B_{R/2}\left(o\right)$ and $\eta =0$ outside $B_R\left(o\right)$;

(ii)

$\left|\nabla \eta \right|\le {\displaystyle \frac{2}{R}}$.

By substituting this test function $\eta$ into inequality (13), we can obtain

$${\left[{\int }_{B_{R/2}\left(o\right)}{|\mathsf{\Phi }|}^{{\displaystyle \frac{n^2}{n-2}}}{e}^{-f}\mathrm{d}v\right]}^{{\displaystyle \frac{n-2}{n}}}\le C(n,{\delta }_0,{\epsilon }_0){\displaystyle \frac{D_n}{\xi }}{\displaystyle \frac{4}{R^2}}{\int }_{B_{R/2}\left(o\right)}{|A|}^n{e}^{-f}\mathrm{d}v.$$

Let $R\to \infty$ in this inequality. Then, by making use of assumption (3) again, we can immediately determine that $|\mathsf{\Phi }|\equiv 0$. Furthermore, following [16], M is a linear subspace. □

Proof of Theorem 2.

Lemma 3 gives

$$|\omega |{\Delta }_f|\omega |\ge -{|A|}^2{|\omega |}^2.$$

Let $\eta$ be a smooth compactly supported function on M. By multiplying both sides of the above inequality by ${\eta }^2{|\omega |}^{p-2}$ and then integrating the obtained result with respect to the measure $e^{-f}\mathrm{d}v$, we arrive at

$$\begin{array}{c}\hfill {\int }_M{\eta }^2{\left|\omega \right|}^{p-1}{\Delta }_f\left|\omega \right|e^{-f}\mathrm{d}v\ge -{\int }_M{\left|A\right|}^2{\left|\omega \right|}^p{\eta }^2{e}^{-f}\mathrm{d}v.\end{array}$$

(14)

Since $\eta$ has compact support on M, the divergence theorem gives

$$\begin{array}{cc}\hfill {\int }_M{\eta }^2{\left|\omega \right|}^{p-1}{\Delta }_f\left|\omega \right|e^{-f}\mathrm{d}v=& -{\int }_M\left(\nabla \left({\eta }^2{\left|\omega \right|}^{p-1}\right)·\nabla \left|\omega \right|\right)e^{-f}\mathrm{d}v\hfill \\ \hfill =& -2{\int }_M{\left|\omega \right|}^{p-1}\left(\nabla \eta ·\nabla \left|\omega \right|\right)\eta e^{-f}\mathrm{d}v\hfill \\ & -(p-1){\int }_M{\eta }^2{\left|\omega \right|}^{p-2}{\left|\nabla \left|\omega \right|\right|}^2{e}^{-f}\mathrm{d}v.\hfill \end{array}$$

This equation and (14) imply

$$\begin{array}{cc}\hfill (p-1){\int }_M{\eta }^2{\left|\omega \right|}^{p-2}{\left|\nabla \left|\omega \right|\right|}^2{e}^{-f}\mathrm{d}v\le & -2{\int }_M{\left|\omega \right|}^{p-1}\left(\nabla \eta ·\nabla \left|\omega \right|\right)\eta e^{-f}\mathrm{d}v\hfill \\ & +{\int }_M{\left|A\right|}^2{\left|\omega \right|}^p{\eta }^2{e}^{-f}\mathrm{d}v.\hfill \end{array}$$

(15)

For the first term on the right-hand side of inequality (15), we have for any $\epsilon >0$,

$$\begin{array}{cc}& -2{\int }_M{\left|\omega \right|}^{p-1}\left(\nabla \eta ·\nabla \left|\omega \right|\right)\eta e^{-f}\mathrm{d}v\hfill \\ \hfill \le & 2{\int }_M{\left|\omega \right|}^{p-1}\left|\left(\nabla \eta ·\nabla \left|\omega \right|\right)\right|\left|\eta \right|e^{-f}\mathrm{d}v\hfill \\ \hfill \le & {\displaystyle \frac{1}{\epsilon }}{\int }_M{\left|\nabla \eta \right|}^2{\left|\omega \right|}^p{e}^{-f}\mathrm{d}v+\epsilon {\int }_M{\left|\omega \right|}^{p-2}{\left|\nabla \left|\omega \right|\right|}^2{\eta }^2{e}^{-f}\mathrm{d}v.\hfill \end{array}$$

(16)

Apply the Hölder’s inequality to the second term on the right-hand side of the above inequality. Then, apply Lemma 1 to the second factor of the resulting expression for $z={|\omega |}^{{\displaystyle \frac{p}{2}}}\eta$, and we obtain

$$\begin{array}{cc}& {\int }_M{\left|A\right|}^2{\left|\omega \right|}^p{\eta }^2{e}^{-f}\mathrm{d}v\hfill \\ \hfill \le & {\left({\int }_M{|A|}^n{e}^{-f}\mathrm{d}v\right)}^{{\displaystyle \frac{2}{n}}}{\left({\int }_M{(\eta |\omega |}^{{\displaystyle \frac{p}{2}}}{)}^{{\displaystyle \frac{2n}{n-2}}}{e}^{-f}\mathrm{d}v\right)}^{{\displaystyle \frac{n-2}{n}}}\hfill \\ \hfill \le & D_n{∥A∥}_{n,f}^2{\int }_M{\left|\nabla \left(\eta {\left|\omega \right|}^{{\displaystyle \frac{p}{2}}}\right)\right|}^2{e}^{-f}\mathrm{d}v\hfill \\ \hfill =& D_n{∥A∥}_{n,f}^2{\int }_M\left({\left|\omega \right|}^p{\left|\nabla \eta \right|}^2+p\eta {\left|\omega \right|}^{p-1}\nabla \left|\omega \right|·\nabla \eta +{\displaystyle \frac{p^2}{4}}{\left|\omega \right|}^{p-2}{\eta }^2{\left|\nabla \left|\omega \right|\right|}^2\right)e^{-f}\mathrm{d}v.\hfill \end{array}$$

(17)

For the above $\epsilon$, the AM–GM inequality gives

$$\begin{array}{c}\hfill p\eta {\left|\omega \right|}^{p-1}\nabla \left|\omega \right|·\nabla \eta \le {\displaystyle \frac{{\left|\nabla \eta \right|}^2{\left|\omega \right|}^p}{\epsilon }}+{\displaystyle \frac{\epsilon p^2}{4}}{\left|\omega \right|}^{p-2}{\eta }^2{\left|\nabla \left|\omega \right|\right|}^2.\end{array}$$

This inequality together with (17) implies

$$\begin{array}{cc}& {\int }_M{\left|A\right|}^2{\left|\omega \right|}^p{\eta }^2{e}^{-f}\mathrm{d}v\hfill \\ \hfill \le & D_n{∥A∥}_{n,f}^2\left[\left(1+{\displaystyle \frac{1}{\epsilon }}\right){\int }_M{\left|\omega \right|}^p{\left|\nabla \eta \right|}^2{e}^{-f}\mathrm{d}v+{\displaystyle \frac{(1+\epsilon )p^2}{4}}{\int }_M{\left|\omega \right|}^{p-2}{\eta }^2{\left|\nabla \left|\omega \right|\right|}^2{e}^{-f}\mathrm{d}v\right].\hfill \end{array}$$

(18)

Combining (15), (16), and (18), we get

$$\begin{array}{cc}& \left[p-1-{\displaystyle \frac{p^2}{4}}{D}_n{∥A∥}_{n,f}^2-{\displaystyle \frac{\epsilon p^2}{4}}{D}_n{∥A∥}_{n,f}^2+\epsilon \right]{\int }_M{\eta }^2{\left|\omega \right|}^{p-2}{\left|\nabla \left|\omega \right|\right|}^2{e}^{-f}\mathrm{d}v\hfill \\ \hfill \le & \left[\left(1+{\displaystyle \frac{1}{\epsilon }}\right)D_n{∥A∥}_{n,f}^2+{\displaystyle \frac{1}{\epsilon }}\right]{\int }_M{\left|\omega \right|}^p{\left|\nabla \eta \right|}^2{e}^{-f}\mathrm{d}v.\hfill \end{array}$$

For a sufficiently small $\epsilon >0,$ the above inequality implies that there is constant $C>0$ such that

$$\begin{array}{cc}\hfill {\int }_M{\left|\omega \right|}^{p-2}{\left|\nabla \left|\omega \right|\right|}^2{\eta }^2{e}^{-f}\mathrm{d}v\le & C{\int }_M{\left|\omega \right|}^p{\left|\nabla \eta \right|}^2{e}^{-f}\mathrm{d}v,\hfill \end{array}$$

(19)

provided that

$$\begin{array}{c}\hfill p-1-{\displaystyle \frac{p^2}{4}}{D}_n{∥A∥}_{n,f}^2>0,\end{array}$$

or namely,

$$\begin{array}{c}\hfill {∥A∥}_{n,f}^2<{\displaystyle \frac{4\left(p-1\right)}{p^2{D}_n}}={\displaystyle \frac{\left(p-1\right){\left(n-2\right)}^2{\omega }_n^{\frac{2}{n}}}{{25}^n{n}^2{p}^2}}.\end{array}$$

Let $o\in M$ be a fixed point and let $B_r\left(o\right)$ be the geodesic ball centered at o with radius R. Apply the same cut-off function $\eta$ as used in the proof of Theorem 1 to (19), we get

$$\begin{array}{c}\hfill {\int }_{B_{R/2}\left(o\right)}{\left|\omega \right|}^{p-2}{\left|\nabla \left|\omega \right|\right|}^2{e}^{-f}\mathrm{d}v\le {\displaystyle \frac{4C}{R^2}}{\int }_{B_{R/2}\left(o\right)}{\left|\omega \right|}^p{e}^{-f}\mathrm{d}v.\end{array}$$

Letting R tend to ∞ in the above inequality and note that $\omega \in L_f^p,$ we conclude that $\nabla \left|\omega \right|=0$, which shows that $\left|\omega \right|$ is a constant. Moreover, since ${\int }_M{|\omega |}^p{e}^{-f}v<\infty$ and the weighted volume of M is infinite, we finally get $\omega =0$. The proof is completed. □

4. Conclusions

This paper focuses on translating solitons in Euclidean space and investigates their rigidity (Bernstein property) as well as the vanishing of weighted harmonic 1-forms. On one hand, under the assumption that the $L_f^n$-norm of the second fundamental form is bounded, we established the vanishing of the second fundamental form, hence the linearity of the translating soliton, by employing a weighted Sobolev inequality, a Simons-type inequality, suitably chosen cut-off functions, and a series of analytical estimates. On the other hand, under similar assumptions, we also proved the nonexistence of nontrivial $L_f^p$ weighted harmonic 1-forms on translating solitons. The proof follows a similar strategy, except that the Simons type inequality is replaced by a Bochner-type inequality for weighted harmonic 1-forms.

In future work, we hope to further weaken the assumptions, for example, by improving the bounds on the $L_f^n$-norm of the second fundamental form or by establishing a new and sharper weighted Sobolev inequality. In addition, regarding vanishing theorems on translating solitons, we aim to investigate the vanishing of general weighted harmonic q-forms for $q\ge 1$, which will rely on developing a Bochner-type inequality tailored to weighted harmonic q-forms. Ultimately, we also hope to apply our results and/or methods to other problems in the geometry and topology of submanifolds.