Robust Variable Selection via Bayesian LASSO-Composite Quantile Regression with Empirical Likelihood: A Hybrid Sampling Approach
Abstract
1. Introduction
2. Modeling and Sparse Optimization Framework
2.1. BEL Variable Selection Algorithm Based on Spike-and-Slab Prior
- (1)
- Let t = 0 and the initial value ;
- (2)
- Given , generate from , where , ;
- (3)
- Get from ;
- (4)
- From the proposed distribution comes , obeys the normal distribution, and the acceptance probability of is as follows:
- (5)
- Repeat (2) to (4) until the Markov chain is smooth. The Gibbs sampler and Metropolis–Hastings algorithm construct a Markov chain whose stationary distribution converges to the target posterior distribution. Steps (2)–(4) are repeated until the chain reaches stationarity.
2.2. Empirical Likelihood Variable Selection Algorithm Based on Bayesian LASSO
- (1)
- Let t = 0, initial value , given , ;
- (2)
- Update , which converges after q iterations using the EM algorithm to obtain the following:where can be estimated using the sample means obtained from the first q − 1 iterations of the EM algorithm;
- (3)
- Update : from gamma (, );
- (4)
- M-H algorithm update :The multivariate normal distribution is chosen as the proposed distribution, and the new parameter is drawn from the proposed distribution to calculate the following:where ;The M-H algorithm is quite sensitive to the choice of the scaling parameter in the proposal distribution . When is too large, most candidate points will be rejected, resulting in low algorithm efficiency. If is too small, almost all candidate points will be accepted, also resulting in low efficiency. Therefore, in practical applications, we need to appropriately adjust the scale parameter to monitor the acceptance rate, generally keeping it within [0.15, 0.5] [49].
- (5)
- Generate a random number from a uniform distribution , if , then accept and have otherwise ;
- (6)
- Repeat (2)–(5) until a steady-state is reached.
3. Simulation Study
3.1. No Outlier Scenario Simulation
- (1)
- The mean of the mean absolute deviation (MMAD):
- (2)
- The mean of True Variable Selection (TV) quantifies the average number of correctly identified non-zero parameters among the truly non-zero coefficients. Specifically, it counts the variables for which both the estimated coefficient by the model and the corresponding true coefficient are non-zero. A higher TV value indicates a superior performance of the estimation method, reflecting its effectiveness in pinpointing relevant variables within the regression model.
- (3)
- The mean of False Variable Selection (FV) measures the average number of incorrectly identified non-zero parameters among the truly zero coefficients. It captures the variables whose coefficients are estimated as non-zero by the model, while their true values are actually zero. A lower FV value is indicative of a more accurate estimation method, as it suggests fewer false positives in the variable selection process and, consequently, a better alignment with the true underlying model structure.
- Scenario I: Setting
- Scenario II: Settings
3.2. Simulation of Outlier-Containing Scenarios
- (1)
- A random 5% outlier is added to the response variable;
- (2)
- Add a random 10% outlier to the response variable.
4. Demonstration of Actual Data
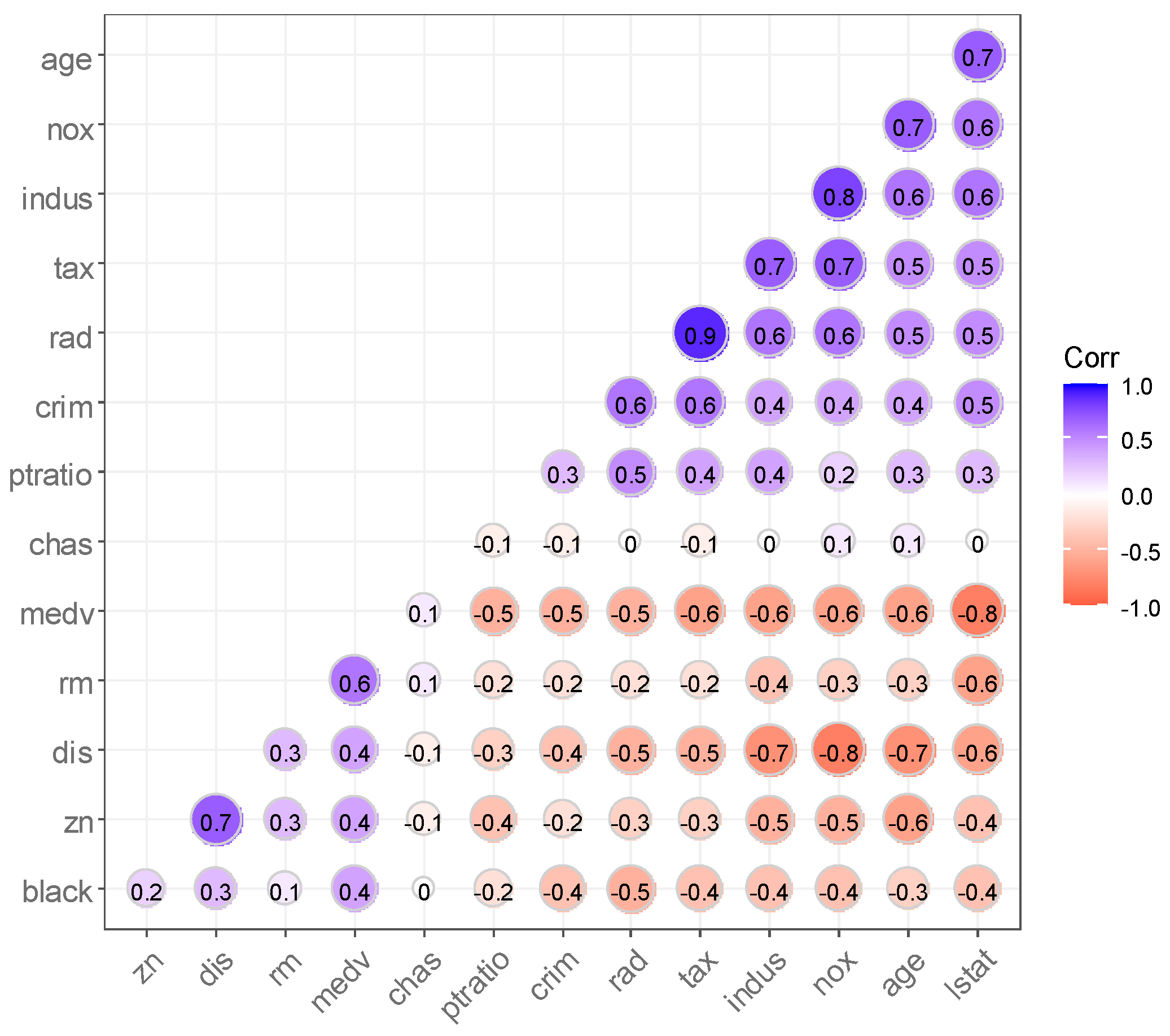
4.1. Data Analysis of House Prices in Boston Suburbs, USA
4.2. Analysis of Iowa Home Price Data
- (1)
- Missing Value Handling:
- Variables with missing data exceeding 10% were removed to maintain data integrity.
- For numerical variables, missing values were imputed using the column mean.
- Categorical variables with missing values were filled with the mode (most frequent category).
- (2)
- Data Normalization:
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zou, H.; Yuan, M. Composite Quantile Regression and the Oracle Model Selection Theory. Ann. Stat. 2008, 36, 1108–1126. [Google Scholar] [CrossRef]
- Huang, H.; Chen, Z. Bayesian composite quantile regression. J. Stat. Comput. Simul. 2015, 85, 3744–3754. [Google Scholar] [CrossRef]
- Wang, J.F.; Fan, G.L.; Wen, L.M. Compound quantile regression estimation of regression functions under random missingness of censored indicators. Syst. Sci. Math. 2018, 38, 1347–1362. [Google Scholar]
- Liu, H.; Yang, H.; Peng, C. Weighted composite quantile regression for single index model with missing covariates at random. Comput. Stat. 2019, 34, 1711–1747. [Google Scholar] [CrossRef]
- Art, O. Empirical likelihood for linear models. Ann. Stat. 2007, 19, 1725–1747. [Google Scholar]
- Art, O. Empirical likelihood ratio confidence regions. Ann. Stat. 2007, 18, 90–120. [Google Scholar]
- Owen, B.A.; Cox, D.; Reid, N. Empirical Likelihood; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Zhao, P.; Zhou, X.; Lin, L. Empirical likelihood for composite quantile regression modeling. J. Appl. Math. Comput. 2015, 48, 321–333. [Google Scholar] [CrossRef]
- Lazar, A.N. Bayesian Empirical Likelihood. Biometrika 2003, 90, 319–326. [Google Scholar] [CrossRef]
- Fang, K.; Mukerjee, R. Empirical-Type Likelihoods Allowing Posterior Credible Sets with Frequentist Validity: Higher-Order Asymptotics. Biometrika 2006, 93, 723–733. [Google Scholar] [CrossRef]
- Yang, Y.; He, X. Bayesian empirical likelihood for quantile regression. Ann. Stat. 2012, 40, 1102–1131. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, N. Bayesian empirical likelihood estimation of quantile structural equation models. J. Syst. Sci. Complex. 2017, 30, 122–138. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Mondal, D.; Yin, T. Hamiltonian Monte Carlo sampling in Bayesian empirical likelihood computation. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2017, 79, 293–320. [Google Scholar] [CrossRef]
- Vexler, A.; Yu, J.; Lazar, N. Bayesian empirical likelihood methods for quantile comparisons. J. Korean Stat. Soc. 2017, 46, 518–538. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Ghosh, M.; Rao, K.N.J.; Wu, C. Bayesian empirical likelihood inference with complex survey data. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2020, 82, 155–174. [Google Scholar] [CrossRef]
- Dong, X.G.; Liu, X.R.; Wang, C.J. Bayesian empirical likelihood for accelerated failure time models under right-censored data. J. Math. Stat. Manag. 2020, 39, 838–844. [Google Scholar]
- Bedoui, A.; Lazar, A.N. Bayesian empirical likelihood for ridge and lasso regressions. Comput. Stat. Data Anal. 2020, 145, 106917. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, D.H. Bayesian empirical likelihood inference for the generalized binomial AR(1) model. J. Korean Stat. Soc. 2022, 51, 977–1004. [Google Scholar] [CrossRef]
- Sheng, C.L.; Ying, H.L. Bayesian empirical likelihood of quantile regression with missing observations. Metrika 2022, 86, 285–313. [Google Scholar] [CrossRef]
- Tibshirani, R.J. Regression Shrinkage and Selection via the LASSO. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable Selection via Non-concave Penalized Likelihood and Its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zou, H. The Adaptive LASSO and Its Oracle Properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Mitchell, T.J.; Beauchamp, J.J. Bayesian variable selection in linear regression. J. Am. Stat. Assoc. 1988, 83, 1023–1032. [Google Scholar] [CrossRef]
- Nardi, Y.; Rinaldo, A. Autoregressive process modeling via the lasso procedure. J. Multivar. Anal. 2011, 102, 528–549. [Google Scholar] [CrossRef]
- Schmidt, D.F.; Makalic, E. Estimation of stationary autoregressive models with the Bayesian lasso. J. Time Ser. Anal. 2013, 34, 517–531. [Google Scholar] [CrossRef]
- Kwon, S.; Lee, S.; Na, O. Tuning parameter selection for the adaptive Lasso in the autoregressive model. J. Korean Stat. Soc. 2017, 46, 285–297. [Google Scholar] [CrossRef]
- Ishwaran, H.; Rao, J.S. Spike and Slab Variable Selection: Frequentist and Bayesian Strategies. Ann. Stat. 2005, 33, 730–773. [Google Scholar] [CrossRef]
- Malsiner-Walli, G.; Wagner, H. Comparing spike and slab priors for Bayesian variable selection. Austrian J. Stat. 2011, 40, 241–264. [Google Scholar] [CrossRef]
- Narisetty, N.N.; He, X. Bayesian variable selection with shrinking and diffusing priors. Ann. Stat. 2014, 42, 789–817. [Google Scholar] [CrossRef]
- Luo, Y.X.; Li, H.F. Research on random effects quantile regression model based on double adaptive Lasso penalty. J. Quant. Econ. Tech. Econ. Res. 2017, 34, 136–148. [Google Scholar]
- Luo, Y.X.; Li, H.F. Simulation study on dimension reduction algorithm for longitudinal data quantile regression model. Stat. Decis. 2018, 34, 5–9. [Google Scholar]
- Xu, Y.J.; Luo, Y.X. Principal component Lasso dimension reduction algorithm and simulation based on variable clustering. Stat. Decis. 2021, 37, 31–36. [Google Scholar]
- George, E.I.; Mcculloch, R.E. Variable selection via Gibbs sampling. J. Am. Stat. Assoc. 1993, 88, 881–889. [Google Scholar] [CrossRef]
- Nascimento, M.G.L.; Gonçalves, K.C.M. Bayesian variable selection in quantile regression with random effects: An application to Municipal Human Development Index. J. Appl. Stat. 2022, 49, 3436–3450. [Google Scholar] [CrossRef] [PubMed]
- Priya, K.; Damitri, K.; Kiranmoy, D.A. Bayesian variable selection approach to longitudinal quantile regression. Stat. Methods Appl. 2022, 32, 149–168. [Google Scholar] [CrossRef]
- Taddy, A.M.; Kottas, A. A Bayesian nonparametric approach to inference for quantile regression. J. Bus. Econ. Stat. Econ. Stat. 2010, 28, 357–369. [Google Scholar] [CrossRef]
- Androulakis, E.; Koukouvinos, C.; Vonta, F. Estimation and variable selection via frailty models with penalized likelihood. Stat. Med. 2012, 31, 2223–2239. [Google Scholar] [CrossRef] [PubMed]
- Li, C.J.; Zhao, H.M.; Dong, X.G. Bayesian empirical likelihood and variable selection for censored linear model with applications to acute myelogenous leukemia data. Int. J. Biomath. 2019, 12, 799–813. [Google Scholar] [CrossRef]
- Xi, R.; Li, Y.; Hu, Y. Bayesian quantile regression based on the empirical likelihood with spike and slab priors. Bayesian Anal. 2016, 11, 821–855. [Google Scholar] [CrossRef]
- Li, C.J. Bayesian Empirical Likelihood Statistical Inference for Regression Models Under Censored Data. Ph.D. Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Tang, Y.C.; Leng, C. Penalized high-dimensional empirical likelihood. Biometrika 2010, 97, 905–919. [Google Scholar] [CrossRef]
- Lahiri, N.S.; Mukhopadhyay, S. A penalized empirical likelihood method in higah dimensions. Ann. Stat. 2012, 40, 2511–2540. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, X. Variable selection using penalized empirical likelihood. Sci. China Math. 2011, 54, 1829–1845. [Google Scholar] [CrossRef]
- Bayati, M.; Ghoreishi, K.S.; Wu, J. Bayesian analysis of restricted penalized empirical likelihood. Comput. Stat. 2021, 36, 1321–1339. [Google Scholar] [CrossRef]
- Moon, C.; Bedoui, A. Bayesian elastic net based on empirical likelihood. J. Stat. Comput. Simul. 2023, 93, 1669–1693. [Google Scholar] [CrossRef]
- Liya, F.; Shuwen, H.; Jiaqi, L. Robust penalized empirical likelihood in high dimensional longitudinal data analysis. J. Stat. Plan. Inference 2024, 228, 11–22. [Google Scholar]
- Park, T.; Casella, G. The Bayesian LASSO. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Gilks, W.; Richardson, S.; Spiegelhalter, D. Markov Chain Monte Carlo in Practice; Chapman and Hall: New York, NY, USA, 1996. [Google Scholar]



| n | LASSO | SCAD | BEL | BLEL | |
|---|---|---|---|---|---|
| 50 | MMAD | 0.072 | 0.087 | 0.042 | 0.028 |
| TV | 2.89 | 2.94 | 2.77 | 2.97 | |
| FV | 0.02 | 0.04 | 0.05 | 0.01 | |
| 100 | MMAD | 0.065 | 0.079 | 0.033 | 0.026 |
| TV | 2.92 | 2.98 | 2.91 | 3 | |
| FV | 0.01 | 0.02 | 0.02 | 0 | |
| 200 | MMAD | 0.047 | 0.039 | 0.027 | 0.015 |
| TV | 3 | 3 | 2.96 | 3 | |
| FV | 0 | 0 | 0 | 0 |
| n | LASSO | SCAD | BEL | BLEL | |
|---|---|---|---|---|---|
| 50 | MMAD | 0.113 | 0.261 | 0.036 | 0.019 |
| TV | 3.92 | 3.86 | 3.79 | 3.95 | |
| FV | 0.04 | 0.03 | 0.05 | 0.02 | |
| 100 | MMAD | 0.084 | 0.197 | 0.029 | 0.023 |
| TV | 3.94 | 3.97 | 3.95 | 3.99 | |
| FV | 0.02 | 0.01 | 0.03 | 0 | |
| 200 | MMAD | 0.067 | 0.155 | 0.016 | 0.012 |
| TV | 3.99 | 4 | 4 | 4 | |
| FV | 0.01 | 0 | 0 | 0 |
| n | LASSO | SCAD | BEL | BLEL | |
|---|---|---|---|---|---|
| 50 | MMAD | 0.769 | 0.802 | 1.107 | 0.346 |
| TV | 2.46 | 2.19 | 3.2 | 4.54 | |
| FV | 0.09 | 3.4 | 1.5 | 0.28 | |
| 100 | MMAD | 0.725 | 0.836 | 0.186 | 0.112 |
| TV | 3.83 | 2.71 | 4.86 | 5 | |
| FV | 0.05 | 3.25 | 0.05 | 0 | |
| 200 | MMAD | 1.416 | 0.947 | 0.052 | 0.037 |
| TV | 4.55 | 2.95 | 4.99 | 5 | |
| FV | 0 | 2.96 | 0 | 0 |
| n | LASSO | SCAD | BEL | BLEL | |
|---|---|---|---|---|---|
| 50 | MMAD | 0.969 | 1.261 | 1.693 | 0.506 |
| TV | 1.72 | 1.89 | 2.7 | 3.84 | |
| FV | 0.14 | 2.32 | 1.87 | 0.37 | |
| 100 | MMAD | 0.902 | 0.978 | 0.202 | 0.134 |
| TV | 3.54 | 2.57 | 4.79 | 4.96 | |
| FV | 0.06 | 3.51 | 0.07 | 0 | |
| 200 | MMAD | 0.877 | 0.708 | 0.147 | 0.086 |
| TV | 4.33 | 2.91 | 4.88 | 5 | |
| FV | 0.02 | 3.16 | 0.04 | 0 |
| Variant | Name (of a Thing) | Variable Interpretation |
|---|---|---|
| Y | medv | Median value of owner-occupied dwellings (in USD 1000 increments) |
| X1 | crim | Per capita urban crime rate |
| X2 | zn | Percentage of residential lots on parcels over 25,000 square feet |
| X3 | indus | Percentage of non-retail business space per town |
| X4 | chas | 1—along the river, 0—other |
| X5 | nox | NOx concentration (ppm) |
| X6 | rm | Average number of rooms per dwelling |
| X7 | age | Proportion of owner-occupied housing built before 1940 |
| X8 | dis | Weighted average of distances to five Boston job centers |
| X9 | rad | Radial road accessibility index |
| X10 | tax | Full-value property tax rate on a per USD 10,000 basis |
| X11 | ptratio | Teacher–student ratio in towns and cities |
| X12 | black | Calculated from , where is the percentage of urban blacks |
| X13 | lstat | Percentage of population in the lower classes (%) |
| VARIAN | NAME | LASSO | SCAD | BEL | BLEL |
|---|---|---|---|---|---|
| X1 | crim | −0.026 | −0.108 | 0 | 0 |
| X2 | zn | 0.001 | 0.046 | 0 | 0 |
| X3 | indus | 0 | 0 | 0.15 | 0 |
| X4 | chas | 2.084 | 2.718 | 0 | 0.474 |
| X5 | nox | −5.538 | −17.38 | −0.467 | 0 |
| X6 | rm | 4.271 | 3.801 | 0 | 0.314 |
| X7 | age | 0 | 0 | −0.34 | 0 |
| X8 | dis | −0.467 | −1.493 | −0.82 | 0 |
| X9 | rad | 0 | 0.299 | 0.665 | 0.401 |
| X10 | tax | 0 | −0.012 | −0.427 | −0.332 |
| X11 | ptratio | −0.811 | −0.946 | −0.297 | −0.297 |
| X12 | black | 0.006 | 0.009 | 0 | −0.158 |
| X13 | lstat | −0.519 | −0.523 | −0.897 | −0.829 |
| Variant | Name (of a Thing) | LASSO | SCAD | BEL | BLEL |
|---|---|---|---|---|---|
| X1 | crim | −0.372 | −0.84 | 0 | 0 |
| X2 | zn | 0.117 | 0.85 | 0.178 | 0 |
| X3 | indus | −0.309 | −0.025 | −0.379 | 0 |
| X4 | chas | 0.165 | −0.253 | 0 | 0 |
| X5 | nox | −0.66 | −1.398 | −0.199 | −0.487 |
| X6 | rm | 1.175 | 1.085 | 0.068 | 0.231 |
| X7 | age | −0.21 | −0.556 | 0 | 0 |
| X8 | dis | −0.056 | −2.159 | −0.29 | −0.003 |
| X9 | rad | 0 | 2.012 | 0.569 | 0.386 |
| X10 | tax | −0.35 | −2.032 | −0.511 | −0.501 |
| X11 | ptratio | −1.278 | 1.441 | −0.128 | −0.443 |
| X12 | black | 0.54 | 0.69 | 0 | −0.111 |
| X13 | lstat | −2.671 | −2.613 | −0.47 | −0.042 |
| Number of Individuals | Factor | |
|---|---|---|
| LASSO | 16 | LotArea, OverallQual, OverallCond, YearBuilt, YearRemodAdd, BsmtFinSF1, TotalBsmtSF, X1stFlrSF, GrLivArea, BsmtFullBath, KitchenAbvGr, Fireplaces, GarageCars, GarageArea, WoodDeckSF, ScreenPorch |
| SCAD | 27 | LotArea, OverallQual, OverallCond, YearBuilt, YearRemodAdd, BsmtFinSF1, BsmtFinSF2, BsmtUnfSF, TotalBsmtSF, LowQualFinSF, GrLivArea, BsmtFullBath, FullBath, HalfBath, BedroomAbvGr, KitchenAbvGr, TotRmsAbvGrd, Fireplaces, GarageCars, GarageArea, WoodDeckSF, EnclosedPorch, X3SsnPorch, ScreenPorch, PoolArea, MiscVal, YrSold |
| BEL | 24 | MSSubClass, LotFrontage, LotArea, OverallQual, OverallCond, YearBuilt, YearRemodAdd, BsmtFinSF1, BsmtUnfSF, TotalBsmtSF, X1stFlrSF, GrLivArea, BsmtFullBath, FullBath, HalfBath, KitchenAbvGr, TotRmsAbvGrd, GarageCars, GarageArea, OpenPorchSF, X3SsnPorch, ScreenPorch, MiscVal |
| BEL LASSO | 16 | LotArea, OverallQual, OverallCond, YearBuilt, YearRemodAdd, BsmtFinSF1, TotalBsmtSF, X1stFlrSF, GrLivArea, BsmtHalfBath, BedroomAbvGr, TotRmsAbvGrd, Fireplaces, GarageCars, MiscVal, MoSold |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nan, R.; Wang, J.; Li, H.; Luo, Y. Robust Variable Selection via Bayesian LASSO-Composite Quantile Regression with Empirical Likelihood: A Hybrid Sampling Approach. Mathematics 2025, 13, 2287. https://doi.org/10.3390/math13142287
Nan R, Wang J, Li H, Luo Y. Robust Variable Selection via Bayesian LASSO-Composite Quantile Regression with Empirical Likelihood: A Hybrid Sampling Approach. Mathematics. 2025; 13(14):2287. https://doi.org/10.3390/math13142287
Chicago/Turabian StyleNan, Ruisi, Jingwei Wang, Hanfang Li, and Youxi Luo. 2025. "Robust Variable Selection via Bayesian LASSO-Composite Quantile Regression with Empirical Likelihood: A Hybrid Sampling Approach" Mathematics 13, no. 14: 2287. https://doi.org/10.3390/math13142287
APA StyleNan, R., Wang, J., Li, H., & Luo, Y. (2025). Robust Variable Selection via Bayesian LASSO-Composite Quantile Regression with Empirical Likelihood: A Hybrid Sampling Approach. Mathematics, 13(14), 2287. https://doi.org/10.3390/math13142287





