Abstract
Most image forgery localization methods rely on supervised learning, requiring large labeled datasets for training. Recently, several unsupervised approaches based on the variational autoencoder (VAE) framework have been proposed for forged pixel detection. In these approaches, the latent space is built by a simple Gaussian distribution or a Gaussian Mixture Model. Despite their success, there are still some limitations: (1) A simple Gaussian distribution assumption in the latent space constrains performance due to the diverse distribution of forged images. (2) Gaussian Mixture Models (GMMs) introduce non-convex log-sum-exp functions in the Kullback–Leibler (KL) divergence term, leading to gradient instability and convergence issues during training. (3) Estimating GMM mixing coefficients typically involves either the expectation-maximization (EM) algorithm before VAE training or a multilayer perceptron (MLP), both of which increase computational complexity. To address these limitations, we propose the Deep ViT-VAE-GMM (DVVG) framework. First, we employ Jensen’s inequality to simplify the KL divergence computation, reducing gradient instability and improving training stability. Second, we introduce convolutional neural networks (CNNs) to adaptively estimate the mixing coefficients, enabling an end-to-end architecture while significantly lowering computational costs. Experimental results on benchmark datasets demonstrate that DVVG not only enhances VAE performance but also improves efficiency in modeling complex latent distributions. Our method effectively balances performance and computational feasibility, making it a practical solution for real-world image forgery localization.
MSC:
68U10
1. Introduction
With the rapid advancement of digital image processing technologies and the widespread availability of image editing software, image manipulation has become increasingly accessible, leading to a proliferation of deceptive visual content. Such manipulations compromise the authenticity of images and pose significant risks to various sectors, particularly journalism and legal forensics. Consequently, robust models for detecting image tampering have become a critical issue in digital image security. Image-manipulation techniques can generally be categorized into the following types: image retouching, copy–move, splicing, and removal [1].
Existing image manipulation localization (IML) research [2,3,4,5] has focused primarily on detecting and localizing these forms of manipulation. Copy–move operations involve duplicating a region within an image, optionally applying transformations such as scaling, and pasting it elsewhere in the same image. In contrast, splicing involves incorporating external elements into an image, making it a more detectable form of tampering. The removal operation deletes a selected region and fills the void with surrounding pixel information. Like splicing, this operation introduces new elements into the image. Given the diversity of forgery techniques, detecting manipulated content remains a significant challenge.
In the field of image manipulation localization (IML), traditional methods primarily rely on passive forensics techniques, such as Scale-Invariant Feature Transform (SIFT) [6], Speeded-Up Robust Features (SURF) [7], overlapping patch strategies [8], pattern noise analysis [9], Camera Filter Array (CFA) features [10], and statistical feature analysis [11]. While effective for specific types of manipulation, these approaches struggle to address complex and multi-modal tampering due to the increasing sophistication of forgery techniques, thereby limiting their real-world applicability.
Recently, deep neural networks (DNNs) have achieved remarkable success in dense prediction tasks within computer vision (CV), such as object detection and semantic segmentation, which align closely with the goals of IML—accurate identification and localization of manipulated regions. Consequently, computer vision techniques have been increasingly incorporated into IML. Notably, methods based on convolutional neural networks (CNNs) [12], object detection frameworks [13], semantic segmentation architectures [14], and Vision Transformers (ViTs) [15] have driven significant progress in this domain.
The emergence of ViT-based models in CV has further motivated researchers to explore their potential in IML, as demonstrated in studies such as those of Lin et al. [16] and Xiang et al. [17]. However, despite their strong performance in CV tasks, the core objectives of DNNs and ViTs—such as object recognition, semantic segmentation, and pose estimation—do not fully align with the unique challenges of IML. Traditional CV tasks typically involve targets with well-defined shapes, boundaries, and semantic content, whereas IML often deals with manipulated regions that exhibit irregular geometries and vague or ambiguous semantics. This discrepancy hampers the direct transferability of existing CV techniques to the IML domain.
The Vision Transformer Variational Autoencoder (ViT-VAE) [18] integrates ViT to encode forged images, reconstruct them based on latent distributions, and identify forged pixels through reconstruction errors. These methods assume that small forged regions differ significantly from surrounding pristine areas, treating these anomalies as forged pixels. Unlike conventional methods, ViT-VAEs do not require large pre-training datasets and can detect forged pixels using a single image. However, their performance degrades when processing complex forged images due to the simplified Gaussian assumption in the latent space.
Some researchers have attempted to improve vanilla VAE performance by incorporating Gaussian Mixture Models (GMMs), demonstrating that GMMs enhance VAE effectiveness. The Unified Unsupervised Gaussian Mixture Variational Autoencoder (UUGMVAE) [19] employs a GMM to model the latent distribution but relies on the expectation-maximization (EM) algorithm to estimate mixing coefficients, increasing computational complexity. To overcome this limitation, the Gaussian Mixture Variational Autoencoder (GMVAE) [20] and the Deep Autoencoding Gaussian Mixture Model (DAGMM) [21] replace the EM algorithm with a neural network for coefficient estimation. The DVAEGMM [22] combines GMMs with a Generative Adversarial Network (GAN) to approximate latent representation densities, while the CGMVAE [23] introduces a Dirichlet conjugate loss as a regularization term to prevent the GMM estimator from degenerating into a few Gaussians. However, these models have complex objective functions with high computational costs and are prone to gradient instability, such as gradient explosion, when computing the log-sum-exp function of the Kullback–Leibler (KL) term.
To address these challenges, we propose an adaptive GMM-VAE framework to reduce the computational complexity of GMM-based VAEs. Our key contributions are as follows:
- To mitigate gradient instability, such as gradient explosion, we analyze the KL term in VAEs with GMMs and apply Jensen’s inequality to eliminate mixing coefficients and log-sum-exp functions, thereby reducing computational complexity.
- To optimize the estimation of GMM mixing coefficients in existing GMM-VAEs, we replace the multilayer perceptron (MLP) with a one-dimensional convolutional neural network (1D CNN). This substitution enhances computational efficiency and improves adaptability for image datasets.
- We evaluate DVVG on several benchmark datasets, demonstrating that our model achieves superior performance with lower computational complexity compared to other GMM-based VAE methods.
2. Related Works
Many forged images have been widely used in various fields due to the convenience of image editing software. The manipulation of image content poses significant social risks, particularly in journalism and forensic investigations. Detecting and localizing forged pixels in forged images is a crucial task. Therefore, numerous methods have been proposed to detect image forgery [24,25]. These methods can mainly be categorized into reference-based image forgery detection and blind image forgery detection. Reference-based forgery detection is the process of identifying image manipulations by comparing a suspicious image with a known, authentic reference image. This approach relies on the explicit differences between the two images, utilizing techniques such as hashing, watermark verification, or structural similarity measurements. Blind image forgery detection refers to the process of identifying manipulated or forged images without requiring access to the original, unaltered version of the image. This method relies on intrinsic statistical, physical, or deep learning-based features to detect inconsistencies or artifacts introduced by forgery operations such as copy–move, splicing, or image enhancement. ManTra-Net [26] integrates the concept of multi-task learning to simultaneously perform tampering detection and boundary localization. It is a tampering detection and localization network that combines multi-task learning with anomaly feature detection. Although its performance may be influenced by various factors, it exhibits certain advantages in handling multiple known and unknown types of tampering. CAT-Net [27] is an end-to-end fully convolutional neural network that combines RGB and DCT streams to jointly learn the forensic features of compression artifacts in both RGB and DCT domains. It employs a multi-resolution feature fusion approach. The primary function of this network is to detect and localize image-splicing regions by capturing and analyzing compression artifacts, thereby improving the accuracy of image forensics. MVSS-Net [28] is a multi-view, multi-scale supervised image tampering detection model that captures tampering features through two branches: edge supervision and noise supervision. The model has achieved outstanding detection results on multiple public datasets and has demonstrated its ability to detect various types of tampering operations. However, its sensitivity to certain specific tampering operations, such as copy–move manipulation, may require further improvement. DFCN [2] is a dual-branch, fully convolutional network specifically designed for image-splicing detection. Combining the advantages of global and local features, it enhances the accuracy of splicing detection. The fully convolutional network design allows it to handle input images of arbitrary sizes. It exhibits good generalization capabilities and can adapt to different types of splicing operations. However, the model requires a large amount of annotated data for training, and its detection capability may be limited for complex splicing operations, such as deepfakes or highly realistic spliced images. OSN [29] is a tampering detection method that is robust to the interference that images may suffer from during social media transmission (such as JPEG compression, Gaussian blur, etc.). This method effectively copes with damage to image quality caused by transmission by using an anti-interference feature extraction strategy, thereby maintaining high accuracy in cross-platform detection.
The performance of supervised learning typically relies heavily on several key factors, including the availability of large-scale datasets and the necessity of annotated data. Larger datasets generally lead to better generalization performance, as models can learn more complex patterns and features from the data. However, collecting and annotating large-scale datasets can be time-consuming, costly, and sometimes impractical.
Blind methods are more promising and practical. NOI [9] is a blind image forensics method based on noise inconsistency. It leverages the statistical differences in images across different frequency bands and reveals tampering traces by analyzing noise characteristics in the image. Splicebuster [30] is a feature-based algorithm capable of computing local features from the cooccurrence residuals of an image and extracting synthetic feature parameters using these features. It assumes that spliced images and host images have different parameters. By leveraging the expectation-maximization algorithm, Splicebuster learns the distinct parameters of spliced and host images and uses a segmentation algorithm to divide the image into authentic and spliced regions. Noiseprint [31] employs a convolutional neural network (CNN) to extract and identify camera model fingerprints from digital images. Different camera models introduce unique noise patterns during the imaging process, which can serve as “fingerprints” to distinguish between cameras. This capability makes Noiseprint applicable for tasks such as image source authentication, tampering detection, and camera model identification.
ForSim [32] incorporates a forensic similarity metric for digital images. It utilizes a convolutional neural network (CNN)-based feature extractor to capture subtle tampering traces in images. A similarity network is employed to compute the forensic feature distance between image pairs and evaluate their similarity. The method adopts weakly supervised learning to reduce reliance on extensive, precise annotations, thereby reducing labeling costs and improving the model’s generalization ability. MPC [33] enhances tampered-region segmentation by modeling pixel relationships via supervised contrastive learning. ViT-VAE [18] uses a ViT to encode forged images, reconstruct them from latent distributions, and detect forged pixels via reconstruction errors. Unlike traditional methods, it operates without large pre-training datasets and detects forgeries from a single image. However, its performance declines on complex forgeries due to the simplified Gaussian assumption in the latent space.
3. Preliminaries
To facilitate the subsequent discussion, we introduce the following definitions.
Definition 1.
Input image tensor : The input image can be denoted as the tensor , where W and H are the width and height of the image, and C is the channel. In this study, for the RGB channel since we focus on detecting colorful image forgery. Also, we denote by the reconstructed image tensor by the VAE framework.
Definition 2.
The latent variable : The latent variable can be denoted as . In this study, the one-dimensional latent variable is adopted for simplification. means that the latent variable conforms to the standard Gaussian distribution, where is the identity matrix. In another case, we denote if the latent variable follows a different Gaussian distribution, where and . Additionally, we assume that the covariance matrix is a diagonal matrix to simplify the calculation. Thus, the corresponding i-th latent dimension is .
Definition 3.
The forgery indication matrix : The ground-truth forgery indication matrix can be denoted as , where represents the forged pixel and represents the non-forged pixel. Correspondingly, the predicted forgery indication matrix by the output of the CNN can be denoted as .
In this paper, blind image forgery detection can be formulated as follows:
The objective is to infer forged pixels based on the latent distribution of the image. Given an input image tensor , the function is learned to approximate the latent distribution of the forged image and reconstruct the image as using a neural network. By analyzing the discrepancy between the input and reconstructed images, forged pixels can be detected using a predefined threshold.
It is important to distinguish between anomaly detection and forgery detection as two different concepts. However, in this study, we aim to identify forged pixels by detecting outliers inferred from the latent distribution. Accordingly, the detection of anomalous pixels can be regarded as equivalent to identifying tampered pixels in this context.
4. Methodology
The overall framework of DVVG is illustrated in Figure 1. First, we generate Noiseprint feature maps, high-pass filtering residual maps, and Laplacian edge maps, following the approach in [18]. These different feature maps are concatenated to form multi-modal representations. The multi-modal maps are then divided into small cliques using a stride size of S. Each clique, denoted as , is fed into a linear neural network and projected onto a lower-dimensional space.
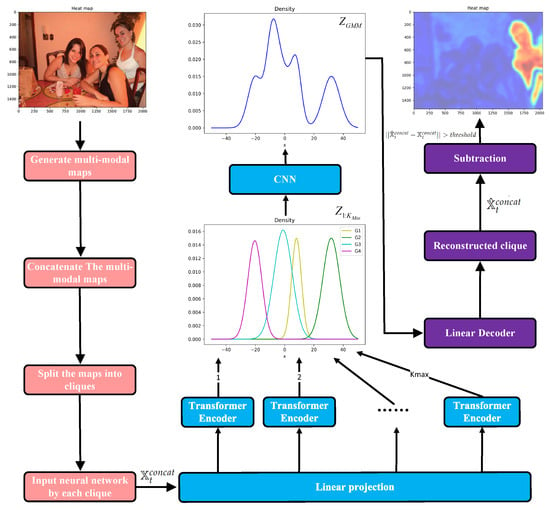
Figure 1.
Framework of DVVG. The framework generates multi-modal feature maps (Noiseprint, high-pass residual, and Laplacian edge maps), which are divided into small cliques and processed through a linear neural network. A Vision Transformer (ViT) computes the Gaussian distribution parameters, and a CNN estimates the mixing coefficients. During decoding, cliques are reconstructed, and forged pixels are identified by comparing the reconstructed and original images.
Next, the Vision Transformer (ViT) module [15] is applied to compute the mean and covariance of the Gaussian posterior distribution. The Gaussian distributions are then concatenated, and a CNN is employed to adaptively estimate the mixing coefficients of each Gaussian distribution. During the decoding stage, we sample from the learned distribution and reconstruct each clique using linear neural network layers. Forged pixels are identified by computing the difference between the reconstructed and original images. A pixel is classified as a forgery if this difference exceeds a predefined threshold.
It is important to note that not all forgery patterns are equally detectable as anomalies, particularly if they closely resemble the normal distribution. However, many unsupervised or semi-supervised anomaly detection methods, including those based on generative models or statistical approaches, can be adapted for forgery detection, as such manipulations often introduce detectable deviations from the normal data distribution. Following the baseline of the VAE [18], we leverage larger reconstruction errors as indicators of forgery to effectively identify manipulated regions in an image.
4.1. Vanilla VAE Framework
The VAE is a powerful generative artificial neural network designed to learn a latent representation of data and is commonly used for anomaly detection. Originally developed for unsupervised learning, the VAE differs from traditional autoencoders by mapping the input data to a probabilistic rather than a deterministic latent space. Specifically, it assumes that the latent variables follow a prior distribution, typically a Gaussian distribution, and employs a neural network to approximate the corresponding posterior distribution. The formulation of the VAE can be derived as follows:
where is learned by a neural network and aims to approximate the true posterior distribution . In vanilla VAEs, it is commonly assumed that the posterior distribution follows a Gaussian distribution, i.e., . Based on the Evidence Lower Bound (ELBO), the model optimizes the lower bound of the marginal likelihood as follows:
where represents the expectation with respect to and denotes the Kullback–Leibler (KL) divergence. Typically, the standard Gaussian distribution is applied to approximate the prior distribution as . Following this baseline, the VAE is designed to reconstruct the input image. The reconstruction loss, which quantifies how well the decoder reconstructs the input data, is incorporated into Equation (3). Consequently, the objective function of the VAE can be reformulated as follows:
In Equation (4), the framework of the vanilla VAE consists of encoder and decoder stages with the learning parameters . Since our task is to perform pixel-wise forgery localization in images, a Vision Transformer (ViT) is used as the encoder, while two linear layers, each followed by batch normalization and a GeLU activation function [34], serve as the decoder structure. Meanwhile, to make the model trainable using backpropagation, the VAE employs the reparameterization trick expressed as , where is sampled from standard noise . Therefore, the minimized objective function in Equation (4) can be reformulated as
where represents the reconstructed tensor of the image. From this derivation, the image is constrained to a single Gaussian distribution. However, as the number and patterns of images are unknown, even a non-forged image does not always follow a Gaussian distribution. As a result, this vanilla VAE approach is inherently limited in real-world applications.
4.2. Gaussian Mixture Model
A Gaussian Mixture Model (GMM) [35] is a probabilistic model that represents a dataset as a combination of multiple Gaussian distributions. It is commonly used for clustering, density estimation, and as a generative model. A GMM can approximate any complex density estimation in theory, and it can be formulated as [36]
where is the mixing coefficient for the i-th component of the GMM and K is the total number of Gaussian components in the GMM. To obtain the accurate , the expectation-maximization (EM) algorithm is often applied. However, the time complexity of the EM algorithm can reach if we do not assume a diagonal variance matrix for when applying the standard EM algorithm to image data of shape (W, H, C). During the E-step, for each of the WH pixels (data points), the algorithm computes the likelihoods for K Gaussian components. Each likelihood involves evaluating a multivariate Gaussian, which costs due to the quadratic form with covariance . Hence, the total cost is per iteration. Even with diagonal covariances, the cost remains high for large images. The DVAEGMM [22] attempts to estimate the mixing coefficients for each Gaussian component using a multi-layered model. An estimation network predicts the mixing coefficients to sustain the end-to-end learning framework of VAE. However, the time complexity of this approach remains in theory. Moreover, these methods are prone to encountering gradient instability or convergence problems due to the KL term when directly replacing the prior Gaussian distribution with a Gaussian Mixture Model (GMM). Also, choosing a suitable value for the hyperparameter K is still a major problem, since each forged image has its own distribution, and a simple method such as grid search increases the training time. We discuss these problems in the next section.
4.3. VAE Enhanced by a GMM
To enhance the performance of the vanilla VAE, some researchers combine it with a Gaussian Mixture Model (GMM) to approximate the posterior distribution , instead of relying on a simple single Gaussian distribution, making it more feasible for real applications [19,20,21,22,23]. The authors of [19] substituted with a GMM, as shown in Equations (4) and (6). This substitution results in the following new objective function:
When a single Gaussian distribution is replaced with a Gaussian Mixture Model (GMM) in the variational distribution , the KL term becomes more complex and intractable due to the log-sum-exp operation. This replacement transforms the convex KL term into a non-convex function, which can lead to gradient instability or convergence issues during training.
In this study, we revisit the problem from a theoretical perspective and aim to reduce the time complexity of Equation (7). First, we apply Jensen’s inequality to the KL term in Equation (7), as follows:
By applying Jensen’s inequality, we not only simplify the calculation by excluding from the KL term but also mitigate gradient instability caused by the exponential function by moving the summation outside the logarithm. Consequently, the updated objective function can be formulated as
Then, by applying the reparameterization trick to the single Gaussian distribution to the objective function, we obtain
where , and represent the mean, covariance, and standard Gaussian noise for the i-th entry of the j-th GMM component, and ⊙ denotes the Hadamard product. Although Jensen’s inequality simplifies the KL term, the computational complexity of estimating the mixing coefficients remains high. Additionally, selecting an appropriate value for the hyperparameter K remains a significant challenge.
Rather than relying on the EM or MLP and determining the K value by grid searching, we choose a sufficiently large through grid search. We then set to a sufficiently large value and concatenate the estimated means and covariances as and . Finally, instead of using an MLP, we employ a 1D CNN with batch normalization (BN) to estimate the posterior distribution, making our approach more adaptive. Consequently, the final objective function can be formulated as
Through this approach, we can reduce the time complexity from for the EM algorithm to , where denotes the kernel size of the 1D CNN. The corresponding pseudocode is provided in Algorithm 1.
| Algorithm 1: ViT-VAE with GMM algorithm |
 |
5. Experiments
5.1. Datasets
To verify the performance and effectiveness of the proposed model, we used three benchmark datasets, including COVERAGE [37], DSO [38], CASIA V1 [39], and NIST2016 [40]:
- COVERAGE: The COVERAGE [37] dataset is a novel benchmark designed specifically for evaluating copy–move forgery detection techniques. It consists of high-resolution images that include realistic forgeries created through various copy–move operations. These manipulations involve copying a region within an image and pasting it elsewhere in the same image, often with transformations such as rotation, scaling, or color adjustments to make the forgery less conspicuous. COVERAGE provides annotations for both the original and tampered regions, enabling precise evaluation of detection algorithms. COVERAGE contains 100 original–forged image pairs, where each original contains similar-but-genuine objects (SGOs), making the discrimination of forged from genuine objects highly challenging.
- DSO [38]: The DSO dataset is a specialized resource for image forgery detection and tampering localization, featuring a variety of forged and original images with corresponding pixel-level ground-truth masks, and contains 100 images. It encompasses common forgery types like splicing, copy–move, and post-processing effects (e.g., blurring and noise addition) to simulate realistic manipulation scenarios. With diverse content in terms of lighting, resolution, and image subjects, the dataset is widely used in training and benchmarking deep learning models for forgery detection and tampered-region localization. It serves as a critical tool in advancing research in digital forensics and image integrity verification.
- CASIA V1 [39]: The CASIA V1 dataset is a publicly available image dataset commonly used in research on image forgery detection. It contains 920 tampered images. The forgeries in this dataset were created using various manipulation techniques, such as copy–move and splicing, making it a valuable resource for developing and evaluating image forensic algorithms. The dataset covers diverse scenes and objects, contributing to its robustness for generalizing forgery detection models. Researchers often use CASIA V1 as a benchmark for assessing the effectiveness of different image authenticity verification methods.
- NIST2016 [40]: The NIST2016 dataset is a publicly available dataset designed for research on image and video forensics. It was developed as part of the Nimble Challenge to support the detection and localization of manipulations in visual media. The dataset contains 1124 images, including 560 authentic and 564 forged images, with forgery types such as splicing, copy–move, and content removal. It provides a standardized benchmark for evaluating forensic algorithms in tasks like image authenticity verification and provenance analysis.
5.2. Experimental Settings
Our model was implemented in PyTorch 1.7 and executed on a Linux server with the following specifications: a CPU (Intel(R) Core(TM) i7-11800H @ 2.30 GHz), a GPU (NVIDIA GeForce RTX 3080), and 16 GB of memory. The GMM hyperparameter was set to 5, while the number of CNN kernels for calculating the mixing coefficient was set to . The values of other hyperparameters followed those of the ViT-VAE model. Additionally, the projected dimension M and the threshold value were set to 10 and 0.4. The DVVG code is available at https://github.com/yhc141/DVVG (accessed on 1 June 2025).
5.3. Baseline
In this study, we compare our method with baseline blind approaches, including ViT-VAE [18], NOI [9], ForSim [32], Splicebuster [30], and Noiseprint [31], as well as non-blind methods such as Mantra-Net [26], CAT-Net [27], MVSS-Net [28], DFCN [2], and OSN [29], utilizing ground-truth data for supervised learning:
- NOI [9] utilizes the wavelet transform, and the wavelet coefficients of the tampered region are compared with those of the background region, thereby identifying the tampered area.
- ForSim [32] utilizes a novel forensic similarity metric to assess the similarity between digital images, aiming to detect tampering and forgery in images.
- Splicebuster [30] is a new blind image-splicing detector capable of detecting splicing forgeries in images without relying on prior information.
- Noiseprint [31] uses a CNN-based method for extracting camera model fingerprints, which can be used for source camera identification and tampering detection in image forensics.
- Mantra-Net [26] is a method for detecting and localizing forgeries in images, with a particular focus on identifying anomalous features.
- CAT-Net [27] is a method for detecting and localizing compression artifacts in image splicing, improving accuracy in image forensics.
- MVSS-Net [28] is a multi-view steganalysis and segmentation network for forgery detection, enabling localization of tampered regions in images.
- DFCN [2] uses a dual-branch fully convolutional network for image-splicing detection, effectively capturing features of tampered regions.
- OSN [29] builds a baseline detector. Through a systematic analysis of the introduced noise, the noise is decoupled into two types of independent modeling: predictable noise and unknown noise.
- ViT-VAE [18] is a Vision Transformer-based variational autoencoder for image anomaly detection, effectively capturing abnormal patterns in images.
5.4. Metrics
We used the following metrics:
- Area Under the Curve (AUC): The AUC represents the area under the Receiver Operating Characteristic (ROC) curve, which plots the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings. It provides a comprehensive measure of a model’s performance across all classification thresholds, where a higher AUC indicates better discrimination capability.
- F1 Score: The F1 score is the harmonic mean of precision and recall, defined aswhere precision measures the proportion of true positive predictions out of all positive predictions, and recall measures the proportion of true positive predictions out of all actual positives. The F1 score balances precision and recall, making it a useful metric in cases of imbalanced datasets.
- Intersection over Union (IoU): IoU, also known as the Jaccard Index, is a metric used to evaluate the overlap between two regions and is commonly used in object detection and segmentation tasks. It is calculated aswhere the intersection area is the common region between the predicted and ground-truth bounding boxes or masks, and the union area is the total area covered by both. An IoU closer to 1 indicates better overlap.
5.5. Results
The results of forgery detection and localization across three datasets are presented in Table 1. Our proposed method achieved superior performance, outperforming most blind detection approaches across multiple datasets. Moreover, it remained competitive compared to non-blind or supervised deep learning methods. Notably, our approach attained enhanced results without relying on any external preprocessing.

Table 1.
Performance comparison on benchmark datasets.
In comparison to ViT-VAE, our model yielded a higher Intersection over Union (IoU), as it more effectively approximated complex latent distributions than the single Gaussian distribution employed by ViT-VAE. Consequently, our method provided a more precise localization of forged pixels at a higher resolution.
To ensure a clear evaluation of our proposed model and the ViT-VAE model, we selected representative images and plotted the precision–recall (PR) curve for comparison. As shown in Figure 2, our proposed algorithm demonstrated superior performance compared to ViT-VAE, attributable to its more effective estimation of the latent space distribution.
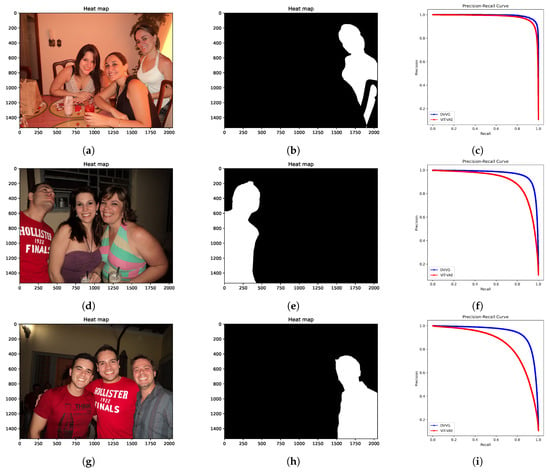
Figure 2.
Precision-Recall (PR) curves for three test images. Columns (from left to right): (a,d,g) original images; (b,e,h) ground-truth forgery localization masks; (c,f,i) PR curves generated by the ViT-VAE model and our proposed DVVG model.
To evaluate the performance of our proposed model, we plot the heatmap and the forgery mask in Figure 3. The results show that our model achieves a clearer contour of the ground-truth mask and a more continuous representation of the image compared to the ViT-VAE model, which demonstrates the effectiveness of the latent distribution of the image.
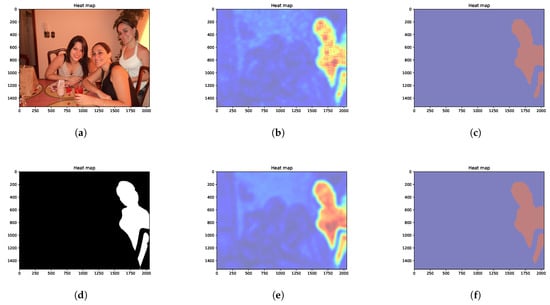
Figure 3.
Comparison of the ViT-VAE model and our proposed model: (a) Original image. (b) Difference between the original and reconstructed images from the ViT-VAE model. (c) Predicted mask from the ViT-VAE model. (d) Ground-truth mask. (e) Difference between the original and reconstructed images from our proposed model. (f) Predicted mask from our proposed model.
5.6. Latent Distribution Representation
To analyze the distribution of the latent space, we visualize the latent representations of images in Figure 3, obtained using both the ViT-VAE model and our proposed approach. The corresponding results are presented in Figure 4. Since the latent space is high-dimensional with , direct visualization is not feasible. Instead, we computed the average of the mean vector and the variance across the 10 dimensions, reducing the representation to a single dimension for visualization purposes. As shown in Figure 4, the latent distribution of forged images exhibits greater complexity than a single Gaussian distribution can capture. In contrast, the GMM provides a more accurate approximation of the latent space, effectively capturing its intricate structure beyond the limitations of a single Gaussian distribution.
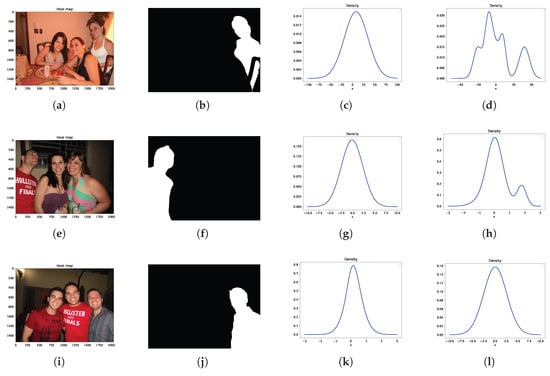
Figure 4.
Visualization of the latent distributions of the ViT-VAE model and our proposed DVVG model on selected images. Columns (from left to right): (a,e,i) original images; (b,f,j) ground-truth forgery localization masks; (c,g,k) latent probability density functions (PDFs) generated by the ViT-VAE model; (d,h,l) latent PDFs produced by the proposed DVVG model.
5.7. Time and Space Complexity Analysis
To evaluate the computational efficiency of our model in comparison with other VAE models incorporating GMMs, we conducted time complexity experiments. The results are presented in Table 2. As shown in Table 2, our model achieved the best time complexity both theoretically and in real-time execution, highlighting its effectiveness in the theoretical derivation of the KL term and the utilization of CNNs.

Table 2.
Time complexity analysis of different models.
In addition to time complexity, we analyzed the space complexity by comparing the number of trainable parameters. Using the torchsummary tool with an input size of [1536 × 2048], DVVG had approximately 268.8 million parameters (≈1025.2 MB), while ViT-VAE had about 64.0 million (≈244.2 MB). The higher parameter count in DVVG aligns with its design, which incorporates multiple latent components . Thus, the increased memory usage is reasonable given the model’s greater representational capacity.
5.8. Ablation Study and Parameter Sensitivity Analysis
To verify the effectiveness of our model and determine the optimal parameters for the GMM, we conducted an ablation study and parameter sensitivity analysis on the DSO dataset. The results are presented in Table 3. The autoencoder (AE) model was limited in accuracy due to its projection of data onto a deterministic representation in the latent space. In contrast, the variational autoencoder (VAE) achieved higher accuracy by employing a probabilistic distribution in the latent space, making it more suitable for generative tasks. The Vision Transformer (ViT) in the encoder stage outperformed the convolutional neural network (CNN) approach, resulting in superior accuracy. Meanwhile, we employed the conventional EM algorithm to estimate the mixing coefficients of the GMM prior to training the VAE framework, denoted as ViT-VAE + EM. However, this approach failed to achieve superior performance compared to the standard ViT-VAE, as it disrupted the end-to-end learning architecture and compromised the model’s adaptability, unlike our proposed DVVG method. Our Gaussian Mixture Model (GMM) enhanced forgery detection performance by replacing a single Gaussian distribution with a combination of multiple Gaussian distributions. This adaptation allowed for a more accurate approximation of the complex latent distribution of forged images, thereby achieving optimal performance.

Table 3.
Results of the ablation study and parameter sensitivity analysis on the DSO dataset.
Notably, in the absence of a GMM in the latent representation, the model became equivalent to ViT-VAE. As shown in Table 3, incorporating the GMM significantly enhanced the performance of ViT-VAE. Additionally, the parameter had a considerable impact on the model when its value was small. However, increasing beyond a certain value did not further improve performance, indicating the presence of a complex latent distribution that could not be adequately captured by a single Gaussian distribution. The sensitivity analysis of the CNN kernel size, presented in Table 3, revealed that optimal performance was achieved with = 3.
6. Discussion and Conclusions
In this paper, we propose an innovative DVVG framework for image forgery detection and localization. The encoder stage incorporates a linear projection and a ViT. A GMM is then used to represent the latent space distribution. Unlike other VAE models that integrate GMMs, we apply the ELBO to the KL term to eliminate gradient instability and convergence issues during training caused by log-sum-exp operations. From the theoretical derivation, the mixing coefficient can be removed to reduce time complexity. Furthermore, instead of using the EM algorithm or an MLP, we employ a CNN to compute the mixing coefficient in the reconstruction term of the objective function. Finally, two linear layers are used to reconstruct the image from the latent variables. By reconstructing the image, our model enables the detection and localization of potentially forged pixels. Experimental results show the superior accuracy and computational efficiency of our model, even when trained on a single image, making it more feasible for real-world applications. While the proposed framework demonstrates strong performance in unsupervised forgery localization, its effectiveness is inherently limited by the distinguishability of latent distribution differences between authentic and forged regions. The image-specific processing paradigm, although allowing flexible single-image analysis, incurs higher computational costs than batch-based alternatives. In future work, we plan to improve the model’s ability to detect sophisticated forgeries by developing more advanced latent representation learning techniques, while also enhancing computational efficiency through lightweight architectural designs.
Author Contributions
Conceptualization, H.Y. and K.U.; Investigation H.Y. and W.M.; Writing-Original Draft, H.Y.; Methodology, K.U.; Writing-Review & Editing, K.U. and J.W.; Software, J.W.; Validation, J.W.; Formal Analysis, W.M.; Visualization, W.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are openly available in https://github.com/yhc141/DVVG. accessed on 1 June 2025.
Conflicts of Interest
Author Jing Wang was employed by the company CEPREI Certification Body. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Chennamma, H.; Madhushree, B. A comprehensive survey on image authentication for tamper detection with localization. Multimed. Tools Appl. 2023, 82, 1873–1904. [Google Scholar] [CrossRef]
- Zhuang, P.; Li, H.; Tan, S.; Li, B.; Huang, J. Image Tampering Localization Using a Dense Fully Convolutional Network. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2986–2999. [Google Scholar] [CrossRef]
- Bayar, B.; Stamm, M.C. Constrained convolutional neural networks: A new approach towards general purpose image manipulation detection. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2691–2706. [Google Scholar] [CrossRef]
- Bappy, J.H.; Roy-Chowdhury, A.K.; Bunk, J.; Nataraj, L.; Manjunath, B. Exploiting spatial structure for localizing manipulated image regions. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 4970–4979. [Google Scholar]
- Chen, X.; Dong, C.; Ji, J.; Cao, J.; Li, X. Image manipulation detection by multi-view multi-scale supervision. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 14185–14193. [Google Scholar]
- Amerini, I.; Ballan, L.; Caldelli, R.; Del Bimbo, A.; Serra, G. A sift-based forensic method for copy–move attack detection and transformation recovery. IEEE Trans. Inf. Forensics Secur. 2011, 6, 1099–1110. [Google Scholar] [CrossRef]
- Pandey, R.C.; Singh, S.K.; Shukla, K.K.; Agrawal, R. Fast and robust passive copy-move forgery detection using SURF and SIFT image features. In Proceedings of the 2014 9th International Conference on Industrial and Information Systems (ICIIS), Gwalior, India, 15–17 December 2014; pp. 1–6. [Google Scholar]
- Farid, H.; Lyu, S. Higher-order wavelet statistics and their application to digital forensics. In Proceedings of the 2003 Conference on Computer Vision and Pattern Recognition Workshop, Madison, WI, USA, 16–22 June 2003; Volume 8, p. 94. [Google Scholar]
- Mahdian, B.; Saic, S. Using noise inconsistencies for blind image forensics. Image Vis. Comput. 2009, 27, 1497–1503. [Google Scholar] [CrossRef]
- Popescu, A.C.; Farid, H. Exposing digital forgeries in color filter array interpolated images. IEEE Trans. Signal Process. 2005, 53, 3948–3959. [Google Scholar] [CrossRef]
- Stamm, M.C.; Liu, K.R. Forensic detection of image manipulation using statistical intrinsic fingerprints. IEEE Trans. Inf. Forensics Secur. 2010, 5, 492–506. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhao, K.; Yin, H. SCCA-Net: A Novel Network for Image Manipulation Localization Using Split-Channel Contextual Attention. In Proceedings of the Asian Conference on Computer Vision (ACCV), Hanoi, Vietnam, 8–12 December 2024; pp. 4473–4487. [Google Scholar]
- Li, S.; Xu, S.; Ma, W.; Zong, Q. Image Manipulation Localization Using Attentional Cross-Domain CNN Features. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 5614–5628. [Google Scholar] [CrossRef]
- Xu, D.; Shen, X.; Shi, Z.; Ta, N. Semantic-agnostic progressive subtractive network for image manipulation detection and localization. Neurocomputing 2023, 543, 126263. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Lin, X.; Wang, S.; Deng, J.; Fu, Y.; Bai, X.; Chen, X.; Qu, X.; Tang, W. Image manipulation detection by multiple tampering traces and edge artifact enhancement. Pattern Recognit. 2023, 133, 109026. [Google Scholar] [CrossRef]
- Xiang, Y.; Yuan, X.; Zhao, K.; Liu, T.; Xie, Z.; Huang, G.; Li, J. Image Manipulation Localization Using Dual-Shallow Feature Pyramid Fusion and Boundary Contextual Incoherence Enhancement. IEEE Trans. Emerg. Top. Comput. Intell. 2024, 1–11. [Google Scholar] [CrossRef]
- Chen, T.; Li, B.; Zeng, J. Learning traces by yourself: Blind image forgery localization via anomaly detection with ViT-VAE. IEEE Signal Process. Lett. 2023, 30, 150–154. [Google Scholar] [CrossRef]
- Liao, W.; Guo, Y.; Chen, X.; Li, P. A unified unsupervised gaussian mixture variational autoencoder for high dimensional outlier detection. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 1208–1217. [Google Scholar]
- Zhou, C.; Ban, H.; Zhang, J.; Li, Q.; Zhang, Y. Gaussian mixture variational autoencoder for semi-supervised topic modeling. IEEE Access 2020, 8, 106843–106854. [Google Scholar] [CrossRef]
- Zong, B.; Song, Q.; Min, M.R.; Cheng, W.; Lumezanu, C.; Cho, D.; Chen, H. Deep autoencoding gaussian mixture model for unsupervised anomaly detection. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Khan, W.; Haroon, M.; Khan, A.N.; Hasan, M.K.; Khan, A.; Mokhtar, U.A.; Islam, S. Dvaegmm: Dual variational autoencoder with gaussian mixture model for anomaly detection on attributed networks. IEEE Access 2022, 10, 91160–91176. [Google Scholar] [CrossRef]
- Gu, C.; Xie, H.; Lu, X.; Zhang, C. Cgmvae: Coupling gmm prior and gmm estimator for unsupervised clustering and disentanglement. IEEE Access 2021, 9, 65140–65149. [Google Scholar] [CrossRef]
- Kumari, R.; Garg, H. Image splicing forgery detection: A review. Multimed. Tools Appl. 2025, 84, 4163–4201. [Google Scholar] [CrossRef]
- Pham, N.T.; Park, C.S. Toward deep-learning-based methods in image forgery detection: A survey. IEEE Access 2023, 11, 11224–11237. [Google Scholar] [CrossRef]
- Wu, Y.; AbdAlmageed, W.; Natarajan, P. Mantra-net: Manipulation tracing network for detection and localization of image forgeries with anomalous features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9543–9552. [Google Scholar]
- Kwon, M.J.; Yu, I.J.; Nam, S.H.; Lee, H.K. CAT-Net: Compression Artifact Tracing Network for Detection and Localization of Image Splicing. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Virtual, 5–9 January 2021; pp. 375–384. [Google Scholar]
- Dong, C.; Chen, X.; Hu, R.; Cao, J.; Li, X. Mvss-net: Multi-view multi-scale supervised networks for image manipulation detection. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 3539–3553. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, J.; Tian, J.; Liu, J.; Qiao, Y. Robust image forgery detection against transmission over online social networks. IEEE Trans. Inf. Forensics Secur. 2022, 17, 443–456. [Google Scholar] [CrossRef]
- Cozzolino, D.; Poggi, G.; Verdoliva, L. Splicebuster: A new blind image splicing detector. In Proceedings of the 2015 IEEE International Workshop on Information Forensics and Security (WIFS), Rome, Italy, 16–19 November 2015; pp. 1–6. [Google Scholar]
- Cozzolino, D.; Verdoliva, L. Noiseprint: A CNN-based camera model fingerprint. IEEE Trans. Inf. Forensics Secur. 2019, 15, 144–159. [Google Scholar] [CrossRef]
- Mayer, O.; Stamm, M.C. Forensic Similarity for Digital Images. IEEE Trans. Inf. Forensics Secur. 2019, 15, 1331–1346. [Google Scholar] [CrossRef]
- Lou, Z.; Cao, G.; Guo, K.; Yu, L.; Weng, S. Exploring Multi-View Pixel Contrast for General and Robust Image Forgery Localization. IEEE Trans. Inf. Forensics Secur. 2025, 20, 2329–2341. [Google Scholar] [CrossRef]
- Şahinuç, F.; Koç, A. Fractional Fourier transform meets transformer encoder. IEEE Signal Process. Lett. 2022, 29, 2258–2262. [Google Scholar] [CrossRef]
- Bouguila, N.; Fan, W. Mixture models and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Liang, G.; U, K.; Chen, J.; Jiang, Z. Real-time traffic anomaly detection based on gaussian mixture model and hidden markov model. Concurr. Comput. Pract. Exp. 2021, e6714. [Google Scholar] [CrossRef]
- Wen, B.; Zhu, Y.; Subramanian, R.; Ng, T.T.; Shen, X.; Winkler, S. COVERAGE—A novel database for copy-move forgery detection. In Proceedings of the 2016 IEEE international conference on image processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 161–165. [Google Scholar]
- Carvalho, T.J.D.; Riess, C.; Angelopoulou, E.; Pedrini, H.; de Rezende Rocha, A. Exposing digital image forgeries by illumination color classification. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1182–1194. [Google Scholar] [CrossRef]
- Dong, J.; Wang, W.; Tan, T. Casia image tampering detection evaluation database. In Proceedings of the 2013 IEEE China Summit and International Conference on Signal and Information Processing, Beijing, China, 6–10 July 2013; pp. 422–426. [Google Scholar]
- NIST Nimble 2016 Datasets. Online. 2016. Available online: https://www.nist.gov/itl/iad/mig/ (accessed on 23 January 2022).
- Cozzolino, D.; Verdoliva, L. Single-image splicing localization through autoencoder-based anomaly detection. In Proceedings of the 2016 IEEE International Workshop on Information Forensics and Security (WIFS), Abu Dhabi, United Arab Emirates, 4–7 December 2016; pp. 1–6. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).