An Integrated Implementation Framework for Warehouse 4.0 Based on Inbound and Outbound Operations
Abstract
1. Introduction
- (1)
- An integrated implementation framework is proposed to use swarm intelligence and joint scheduling strategies to address inbound and outbound operations. This optimizes warehouse processes, reduces error rates and operational costs, and enhances the overall supply chain’s responsiveness and competitiveness.
- (2)
- An allocation algorithm for goods locations is proposed, which can assign goods locations based on order goods information. This improves the operational efficiency of goods location allocation, effectively reduces the operation time of automated warehouses, and enhances the efficiency of goods inbound and outbound processes. The implementation of this algorithm requires collaboration with hardware and software to achieve autonomous storage location allocation.
- (3)
- A combined warehousing order picking and distribution operation is proposed, which performs batch order picking and rational distribution route planning. This improves the inefficiency of the First-In-First-Out (FIFO) model, enhances overall order fulfillment efficiency, optimizes warehouse resources, and ensures the efficient operation of the intelligent warehouse cloud service system.
2. Literature Review
3. Problem Description and Its Implementation Framework
3.1. Problem Description
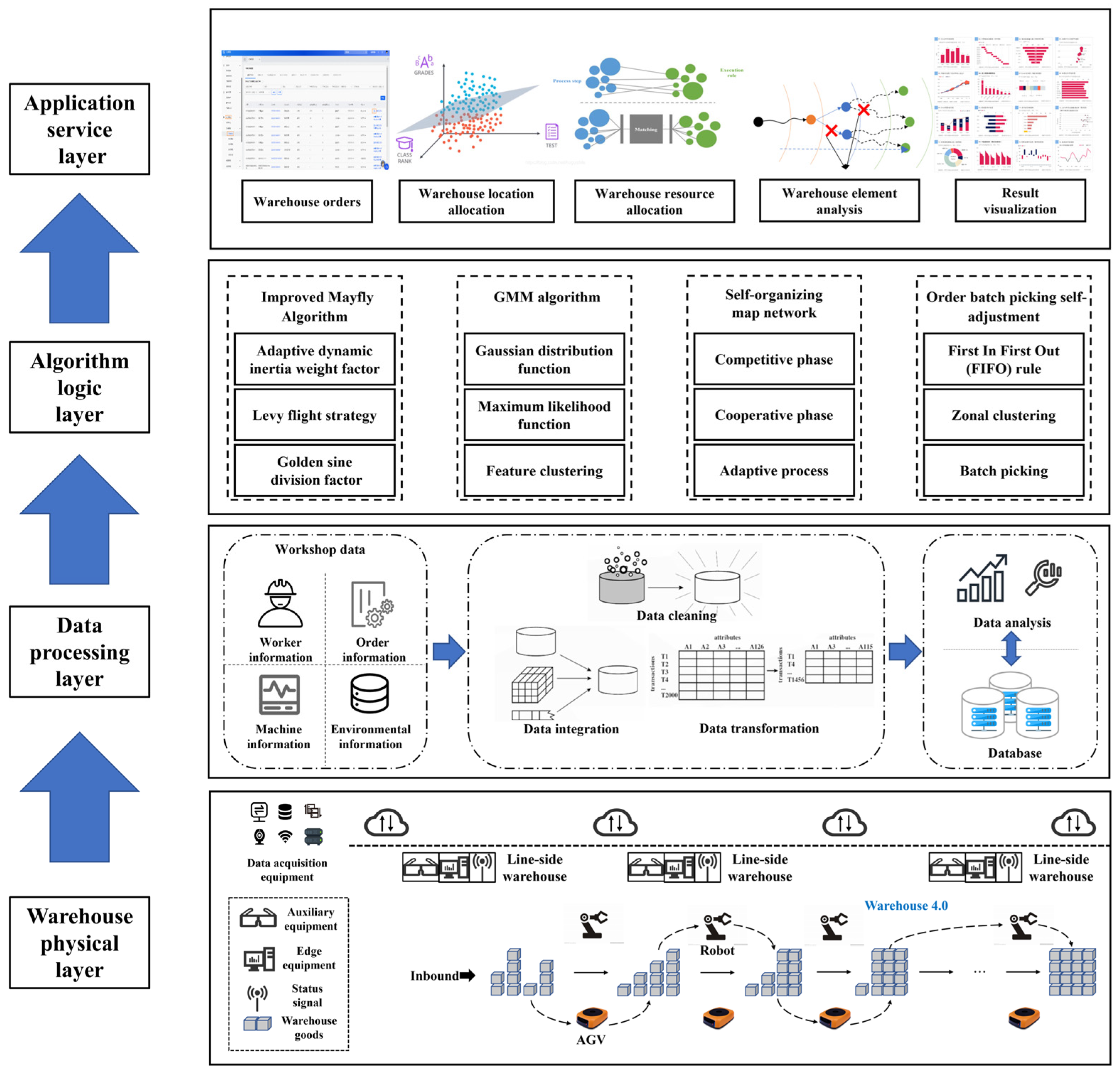
3.2. Integrated Implementation Framework for Warehouse 4.0-Based Inbound and Outbound Operations
3.3. Process of Inbound and Outbound Operations
4. Inbound Storage Location Allocation Based on Improved Mayfly Algorithm
4.1. Mathematical Model for Storage Location Allocation
4.1.1. Objective Function
- (1)
- Goods are stored in containers, which are placed at the center of the pallets in storage bays;
- (2)
- Each storage bay within the high-rise racking system is of the same size, and only one container can be stored in each bay;
- (3)
- The initial position of the aisle stacker crane is at the I/O port. It moves at a constant speed both horizontally and vertically, and the time required for receiving signals, turning, and picking up goods is neglected;
- (4)
- Goods are accessed while placed on pallets;
- (5)
- The waiting time for goods to be stored in the warehouse is ignored;
- (6)
- Each storage location stores only one type of commodity, taking into account the volume of the commodity and the storage space of the location, i.e., zoning based on volume;
- (7)
- In the storage location allocation scenario during storage operations, on a rack where several storage bays are already occupied, a reasonable storage location is allocated for the goods from the vacant bays.
- 1.
- Depending on whether the rack is in an odd or even row, the formula for the conveyor transport distance varies, and the floor function is used to represent the conveyor transport distance [13]. The operational time of the conveyor can be expressed as follows:where is the time consumed by the conveyor for horizontal transportation of the slot, is the distance traveled by the conveyor in the horizontal direction, is the speed of the conveyor, and L is the length and width value of the slot.
- 2.
- The second objective function aims to minimize the sum of the products of the weights of all goods and the levels of their respective assigned positions.where denotes the weight of goods i.
4.1.2. Constraints
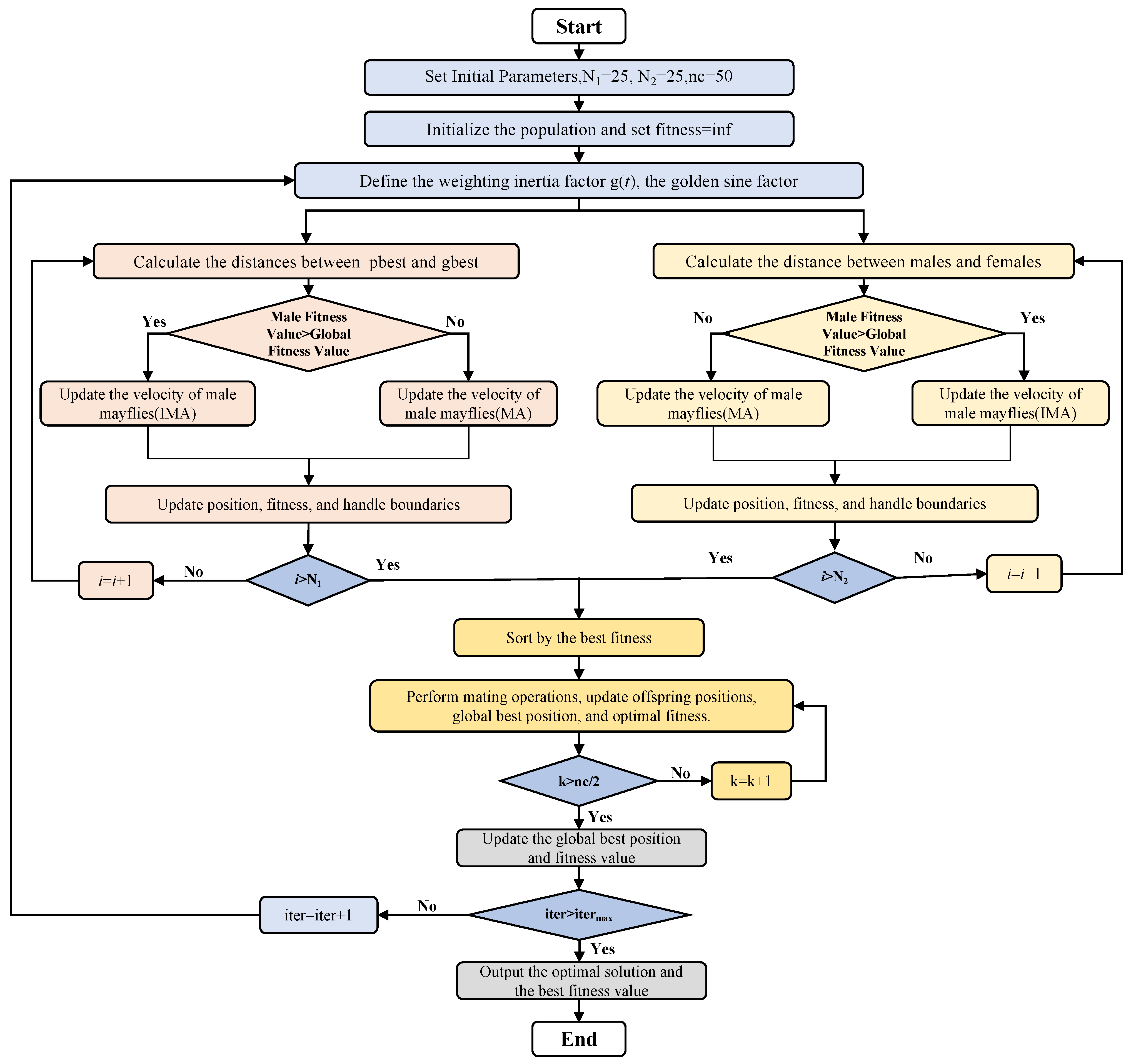
4.2. Autonomous Location Allocation Based on Improved Mayfly Algorithm
- (1)
- Introduction of the Adaptive Dynamic Inertia Weight Factor
- (2)
- Introduction of the Lévy Flight Strategy
- (3)
- Introduction of the Golden Sine Division Factor
5. Joint Scheduling of Outbound Order Picking and Distribution Based on a Three-Stage Algorithm
5.1. Mathematical Model for Joint Scheduling of Outbound Order Picking and Distribution
5.1.1. Objective Function
- (1)
- All distribution vehicles are identical, possessing a fixed capacity, and there is no limit on the number of vehicles.
- (2)
- Upon the vehicle’s arrival at the customer’s location, a fixed service time is required for each customer.
- (3)
- Once the distribution vehicle is fully loaded, it immediately begins distribution without any delay.
- (4)
- The initial position of the picking stacker is at the I/O port, and its horizontal and vertical movements are uniform, disregarding the time required for receiving signals, turning, and picking up goods.
- (5)
- Goods are stored and retrieved on pallets.
- (6)
- The time required for product verification and packaging during outbound operations is disregarded.
5.1.2. Constraints
5.2. Joint Scheduling Optimization Based on Three-Stage Algorithm
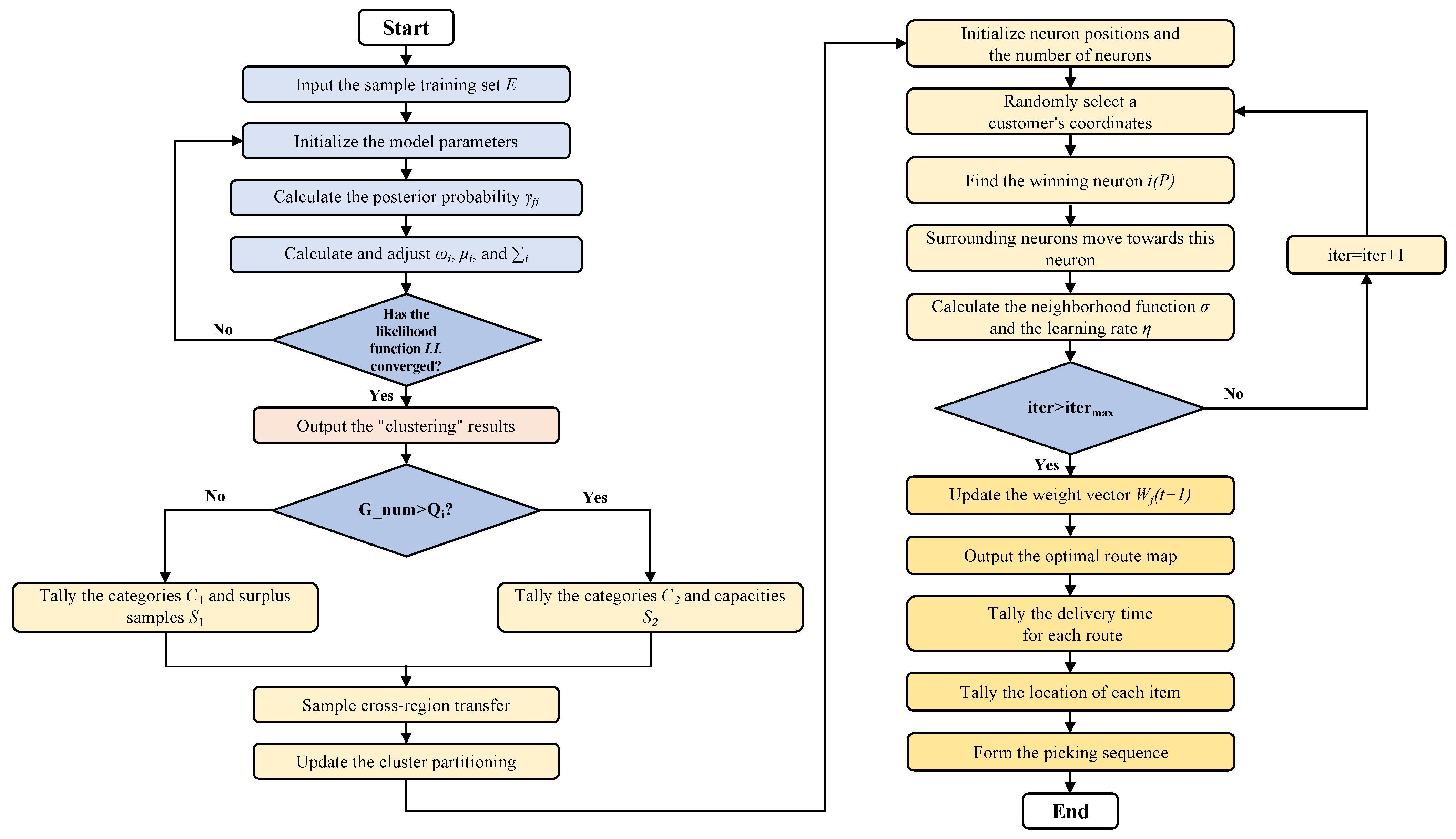
5.2.1. Constrained Outbound Order GMM Clustering
5.2.2. Partitioned Distribution Path Planning Based on Self-Organizing Map (SOM) Network
- (1)
- The maximum value of the topological neighborhood defined at is symmetric, ensuring that the winning neuron i reaches its maximum at .
- (2)
- The magnitude of the topological neighborhood monotonically decreases as increases, and , satisfying the convergence condition of the SOM network.
5.2.3. Autonomous Adjustment of Order Batch Picking Based on Distribution Duration
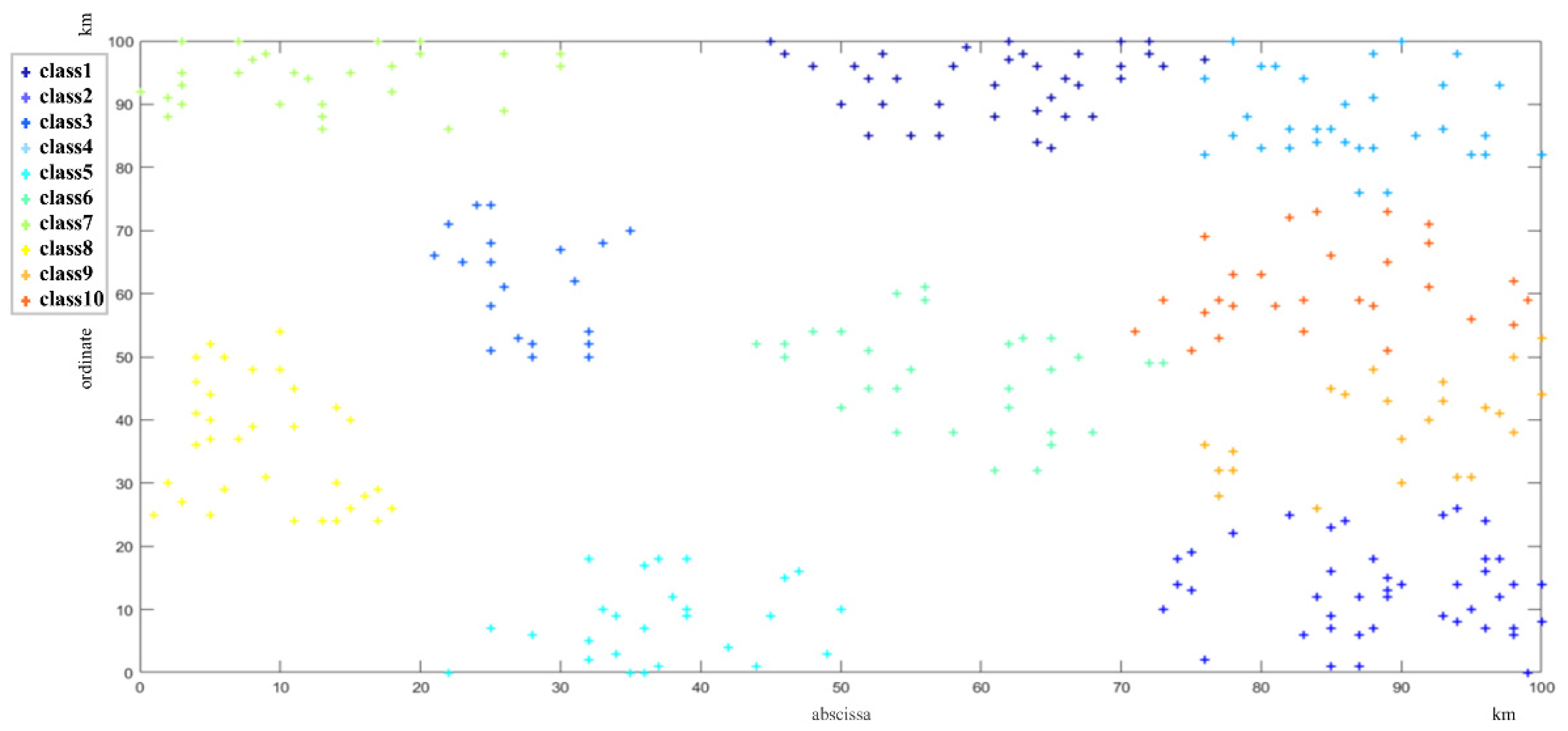
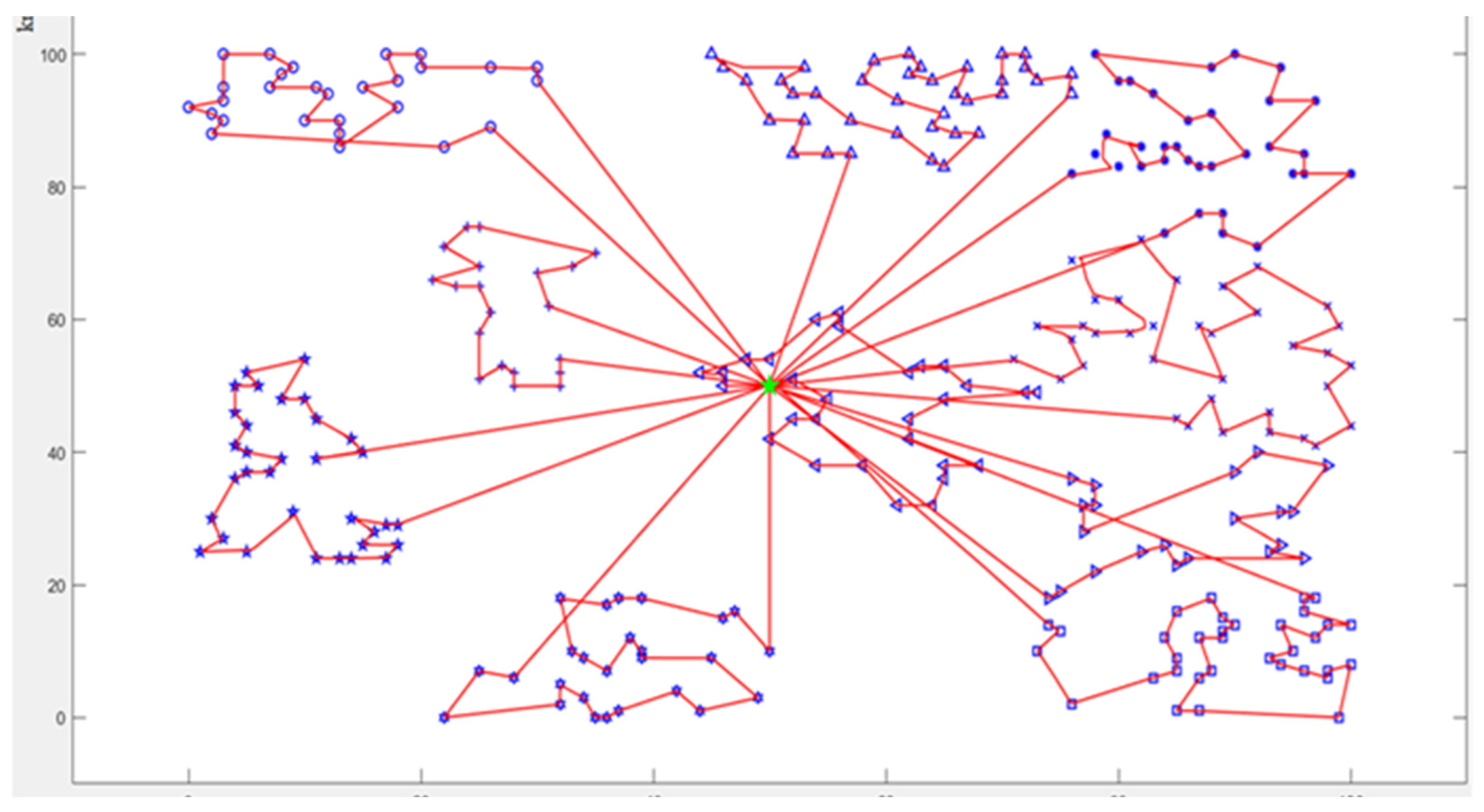
6. Case Study
6.1. Storage Location Allocation of Inbound Operation
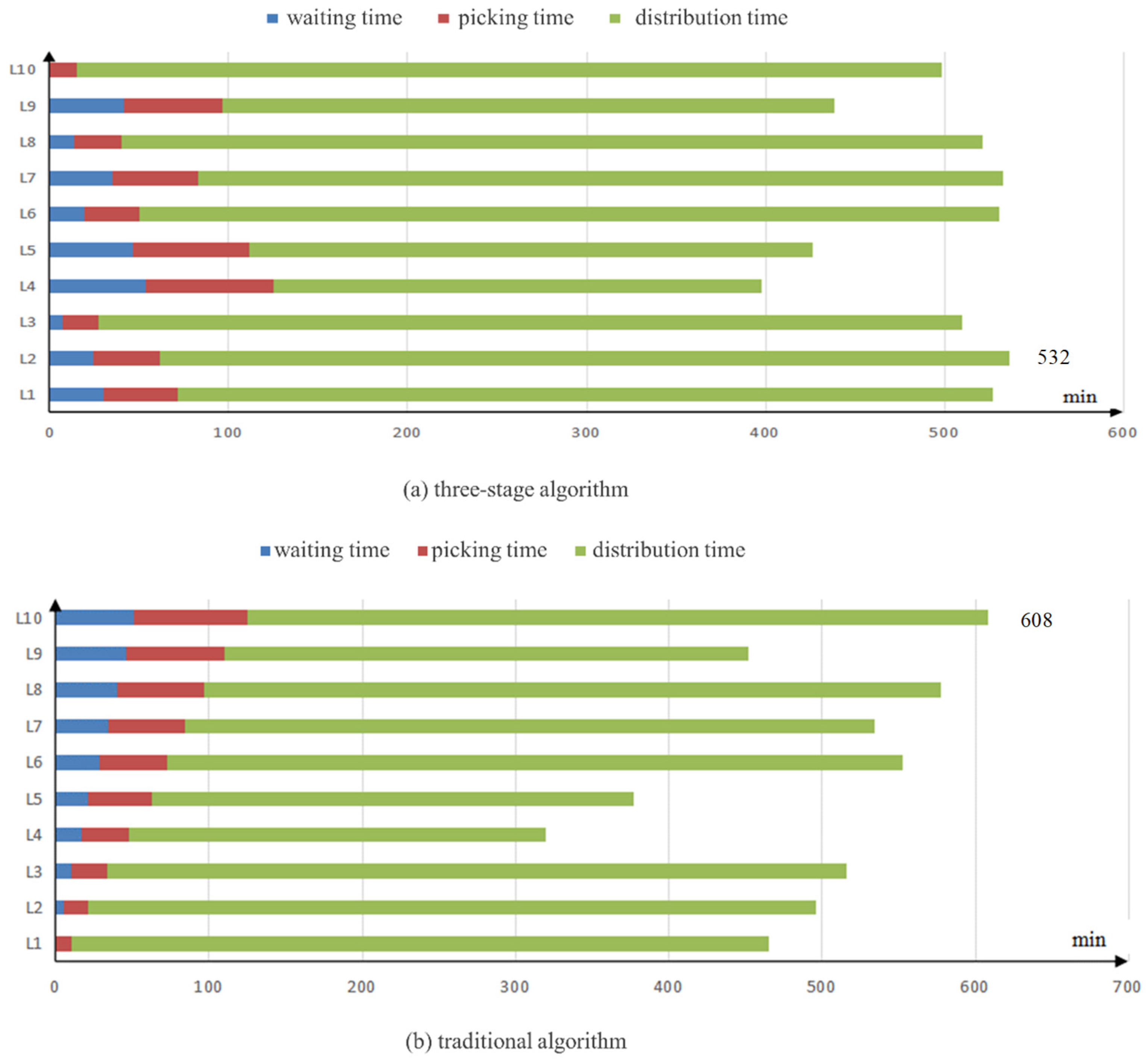
6.2. Joint Scheduling of Picking and Distribution for Outbound Operation
7. Conclusions
- (1)
- An improved mayfly algorithm (IMA) incorporating adaptive dynamic inertia weight factors, Lévy flight strategies, and golden sine factors is developed for parallel stacker crane scenarios. Simulations demonstrate that IMA achieves 64.5%, 65.5%, and 74.5% faster convergence speeds compared to PSO, GA, and MA, respectively, with fitness values reduced by 23.3%, 24.7%, and 20.1%.
- (2)
- A three-stage algorithm integrates Gaussian clustering for customer analysis, self-organizing neural networks for route planning, and operation-duration-based picking sequence optimization. Case studies verify a 12% reduction in order fulfillment time and a 1.8% improvement in average processing efficiency compared to traditional FIFO methods.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leng, J.W.; Jiang, P.Y.; Xu, K.L.; Liu, Q.; Zhao, J.L.; Bian, Y.Y.; Shi, R. Makerchain: A Blockchain with Chemical Signature for Self-Organizing Process in Social Manufacturing. J. Clean. Prod. 2019, 234, 767–778. [Google Scholar] [CrossRef]
- Tubis, A.A.; Rohman, J. Intelligent Warehouse in Industry 4.0-Systematic Literature Review. Sensors 2023, 23, 4105. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.L.; Leng, J.W.; Zhao, L.; Zhou, X.L.; Yuan, Y.; Lu, Y.Q.; Mourtzis, D.; Qi, Q.L.; Huang, S.H.; Song, X.G.; et al. Industrial metaverse towards Industry 5.0: Connotation, architecture, enablers, and challenges. J. Manuf. Syst. 2024, 76, 25–42. [Google Scholar] [CrossRef]
- Leng, J.W.; Zhou, M.; Xiao, Y.X.; Zhang, H.; Liu, Q.; Shen, W.M.; Su, Q.Y.; Li, L.Z. Digital Twins-based Remote Semi-Physical Commissioning of Flow-Type Smart Manufacturing Systems. J. Clean. Prod. 2021, 306, 127278. [Google Scholar] [CrossRef]
- Leng, J.W.; Guo, J.W.; Xie, J.X.; Zhou, X.L.; Liu, A.; Gu, X.; Mourtzis, D.; Qi, Q.L.; Liu, Q.; Shen, W.M.; et al. Review of manufacturing system design in the interplay of Industry 4.0 and Industry 5.0 (Part I): Design thinking and modeling methods. J. Manuf. Syst. 2024, 76, 158–187. [Google Scholar] [CrossRef]
- Leng, J.W.; Zhong, Y.W.; Lin, Z.S.; Xu, K.L.; Mourtzis, D.; Zhou, X.L.; Zheng, P.; Liu, Q.; Zhao, J.L.; Shen, W.M. Towards resilience in Industry 5.0: A decentralized autonomous manufacturing paradigm. J. Manuf. Syst. 2023, 71, 95–114. [Google Scholar] [CrossRef]
- Leng, J.W.; Sha, W.N.; Lin, Z.S.; Jing, J.B.; Liu, Q.; Chen, X. Blockchained smart contract pyramid-driven multi-agent autonomous process control for resilient individualised manufacturing towards Industry 5.0. Int. J. Prod. Res. 2023, 61, 4302–4321. [Google Scholar] [CrossRef]
- Tsou, M.C. Online analysis process on Automatic Identification System data warehouse for application in vessel traffic service. Proc. Inst. Mech. Eng. Part M-J. Eng. Marit. Environ. 2016, 230, 199–215. [Google Scholar] [CrossRef]
- Liu, J.M.; Liao, H.T.; White, J.A. Stochastic analysis of an automated storage and retrieval system with multiple in-the-aisle pick positions. Nav. Res. Logist. 2021, 68, 454–470. [Google Scholar] [CrossRef]
- Shoaee, M.; Samouei, P. Clusters of floor locations-allocation of stores to cross-docking warehouse considering satisfaction and space using MOGWO and NSGA-II algorithms. Flex. Serv. Manuf. J. 2024, 36, 315–342. [Google Scholar] [CrossRef]
- Wan, Y.C.; Wang, S.D.; Hu, Y.J.; Xie, Y.Y. Multiobjective Optimization of the Storage Location Allocation of a Retail E-commerce Picking Zone in a Picker-to-parts Warehouse. Eng. Lett. 2023, 31, 232023. [Google Scholar]
- Gao, J.; Xie, W.D.; Shi, D.K.; Wu, J.; Wang, R. Synchronized optimization of the logistics system of a tobacco high-bay warehouse under production task fluctuations. Eng. Res. Express. 2024, 6, 045580. [Google Scholar] [CrossRef]
- Ma, Q.L.; Xu, L.L.; Zhu, L.; Jia, P. Research on storage location allocation in three-dimensional automated warehouse based on cargo damage control. Int. J. Ind. Eng. Comput. 2025, 16, 177–196. [Google Scholar] [CrossRef]
- Islam, M.S.; Uddin, M.K. An efficient correlation-based storage location assignment heuristic for multi-block multi-aisle warehouses. Int. J. Ind. Eng. Manag. 2024, 15, 125–139. [Google Scholar] [CrossRef]
- Rungjaroenporn, C.; Setthawong, R. Multiobjective Optimization Using Flower Pollination Algorithm for Storage Location Assignment at Lazada Thailand Warehouse. In Proceedings of the 13th International Conference on Knowledge and Smart Technology (KST), Bangsaen, Thailand, 21–24 January 2021. [Google Scholar]
- Xu, X.B.; Ren, C.H. Research on Dynamic Storage Location Assignment of Picker-to-Parts Picking Systems under Traversing Routing Method. Complexity 2020, 2020, 1621828. [Google Scholar] [CrossRef]
- Zhang, S.W.; Fu, L.P.; Chen, R.; Mei, Y. Optimizing the Cargo Location Assignment of Retail E-Commerce Based on an Artificial Fish Swarm Algorithm. Math. Probl. Eng. 2020, 2020, 1621828. [Google Scholar] [CrossRef]
- De Puiseau, C.W.; Nanfack, D.T.; Tercan, H.; Löbbert-Plattfaut, J.; Meisen, T. Dynamic Storage Location Assignment in Warehouses Using Deep Reinforcement Learning. Technologies 2023, 10, 129. [Google Scholar] [CrossRef]
- Leng, J.W.; Yan, D.X.; Liu, Q.; Zhang, H.; Zhao, G.G.; Wei, L.J.; Zhang, D.; Yu, A.L.; Chen, X. Digital twin-driven joint optimisation of packing and storage assignment in large-scale automated high-rise warehouse product-service system. Int. J. Comput. Integr. Manuf. 2021, 34, 783–800. [Google Scholar] [CrossRef]
- Gao, S.; Qi, L.; Lei, L. Integrated batch production and distribution scheduling with limited vehicle capacity. Int. J. Prod. Econ. 2015, 160, 13–25. [Google Scholar] [CrossRef]
- Li, K.; Zhou, C.; Leung, J.Y.T.; Ma, Y. Integrated production and delivery with single machine and multiple vehicles. Expert Syst. Appl. 2016, 57, 12–20. [Google Scholar] [CrossRef]
- Rasti-Barzoki, M.; Hejazi, S.R. Pseudo-polynomial dynamic programming for an integrated due date assignment, resource allocation, production, and distribution scheduling model in supply chain scheduling. Appl. Math. Model. 2015, 39, 3280–3289. [Google Scholar] [CrossRef]
- Suppini, C.; Lysova, N.; Bocelli, M.; Solari, F.; Tebaldi, L.; Volpi, A.; Montanari, R. From Single Orders to Batches: A Sensitivity Analysis of Warehouse Picking Efficiency. Sustainability 2024, 16, 8231. [Google Scholar] [CrossRef]
- Schumann, D.; Cevirgen, C.; Becker, J.; Arian, O.; Nyhuis, P. Development of a Procedure Model to Compare the Picking Performance of Different Layouts in a Distribution Center. In Proceedings of the 8th International Conference on Competitive Manufacturing (COMA), Stellenbosch, South Africa, 9–11 March 2022. [Google Scholar]
- Modenov, A.; Boboshko, A.; Durandina, A.; Kharchenko, O. A New Mathematical Model for Joint Production and Distribution Optimization in a Multi-Echelon Supply Chain. Ind. Eng. Manag. Syst. 2021, 20, 349–355. [Google Scholar] [CrossRef]
- Han, D.Y.; Yang, Y.J.; Wang, D.J.; Cheng, T.C.E.; Yin, Y.Q. Integrated production, inventory, and outbound distribution operations with fixed departure times in a three-stage supply chain. Transp. Res. Part E-Logist. Transp. Rev. 2019, 125, 334–347. [Google Scholar] [CrossRef]
- Czerniachowska, K.; Wichniarek, R.; Zywicki, K. Matheuristics for the Order-picking Problem with Sequence-dependant Constraints in a Logistic Center with a One-directional Conveyor Between Buffers. Manag. Prod. Eng. Rev. 2024, 15, 140–160. [Google Scholar] [CrossRef]
- Czerniachowska, K.; Wichniarek, R.; Zywicki, K. A Model for an Order-Picking Problem with a One-Directional Conveyor and Buffer. Sustainability 2023, 15, 13731. [Google Scholar] [CrossRef]
- Tsang, Y.P.; Wu, C.H.; Lam, H.Y.; Choy, K.L.; Ho, G.T.S. Integrating Internet of Things and multi-temperature delivery planning for perishable food E-commerce logistics: A model and application. Int. J. Prod. Res. 2021, 59, 1534–1556. [Google Scholar] [CrossRef]
- Mukherjee, T.; Sangal, I.; Sarkar, B.; Alkadash, T.M.; Almaamari, Q. Pallet Distribution Affecting a Machine’s Utilization Level and Picking Time. Mathematics 2023, 11, 2956. [Google Scholar] [CrossRef]
- Zhang, F.Q.; Xu, F.L.; Zhou, X.L.; Ding, K.; Shao, S.J.; Du, C.; Leng, J.W. Data-driven and Knowledge-guided Prediction Model of Milling Tool Life Grade. Int. J. Comput. Integr. Manuf. 2024, 37, 669–684. [Google Scholar] [CrossRef]



| Algorithm | Description | Advantages | Disadvantages |
|---|---|---|---|
| GA | An optimization algorithm that simulates natural selection and genetic mechanisms | High robustness | Complexity in encoding and decoding processes |
| PSO | Swarm intelligence-based optimization algorithm that searches for optimal solutions through collaboration and competition among particles | Strong global search capability | Sensitivity to parameter settings |
| MA | An optimization algorithm inspired by the biological behaviors of mayflies | Simple and easy to understand | Slower convergence speed |
| IMA | Introduces adaptive dynamic inertia weight factor, Lévy flight strategy, and golden sine division factor | Faster convergence speed, high randomness, and stability of solutions | Relatively higher algorithm complexity, and potentially complex parameter tuning |
| Name | Function |
|---|---|
| the goods’ name | |
| the supplier’s name | |
| B | the carton specifications |
| the inbound time | |
| R | the outbound frequency |
| W | the weight of the goods |
| K | the type of goods |
| N | the quantity of goods |
| the customer information | |
| the goods information | |
| the distribution vehicle information | |
| the customer’s name | |
| the customer’s contact information | |
| the customer’s location | |
| the quantity of goods ordered by the customer | |
| the name of the goods | |
| the code of the goods | |
| the coordinates of the goods on the shelf | |
| the code of the distribution vehicle | |
| the state of the distribution vehicle | |
| the maximum capacity of the distribution vehicle |
| Parameters | Offspring | Male | Female | Iterations |
| Value | 50 | 25 | 25 | 500 |
| Parameter | Wedding Dance Coefficient | Wedding Dance Decay Parameter | Population Learning Coefficient | Individual Learning Coefficient |
| Value | 0.1 | 0.8 | 1.5 | 1 |
| Parameter | Visibility Coefficient | Mutation Rate | Random Flight Coefficient | Random Flight Decay Parameter |
| Value | 2 | 0.01 | 0.1 | 0.99 |
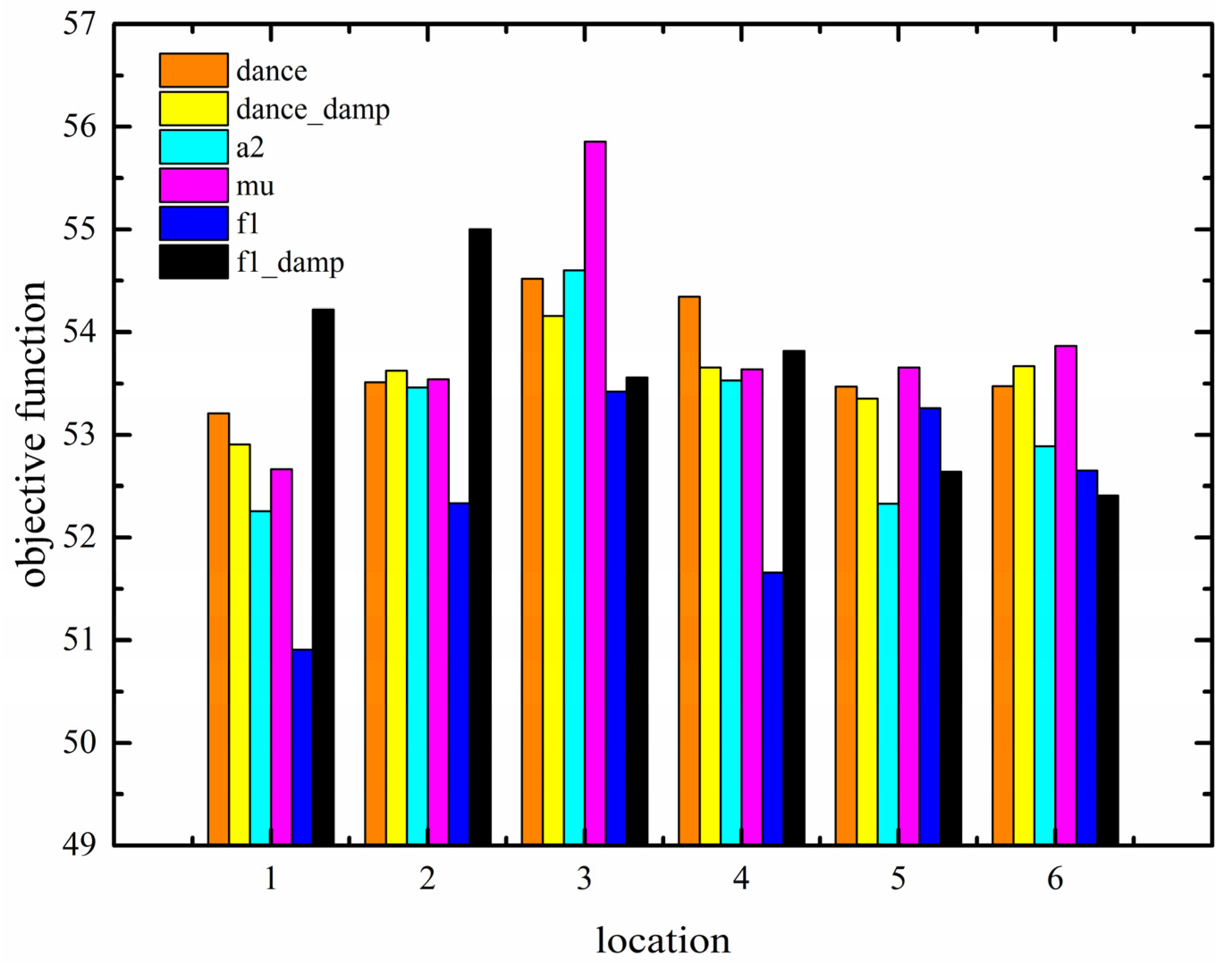
| Location | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Parameter | ||||||
| pc | 0.45 | 0.55 | 0.65 | 0.75 | 0.85 | 0.95 |
| pm | 0.01 | 0.02 | 0.04 | 0.06 | 0.08 | 0.10 |
| w | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.90 |
| c1 | 1.30 | 1.40 | 1.50 | 1.60 | 1.70 | 1.80 |
| c2 | 1.30 | 1.40 | 1.50 | 1.60 | 1.70 | 1.80 |
| dance | 0.10 | 0.14 | 0.18 | 0.22 | 0.26 | 0.30 |
| dance_damp | 0.80 | 0.84 | 0.88 | 0.92 | 0.96 | 0.99 |
| a2 | 1.50 | 1.60 | 1.70 | 1.80 | 1.90 | 2.00 |
| mu | 0.01 | 0.03 | 0.05 | 0.07 | 0.09 | 0.10 |
| f1 | 0.10 | 0.14 | 0.18 | 0.22 | 0.26 | 0.30 |
| fl_damp | 0.80 | 0.84 | 0.88 | 0.92 | 0.96 | 0.99 |
| ID | Shipper Name | Goods Name | Container Specifications | Shipper Level | Weight (kg) | Storage Period (Days) | Turnover Rate | Allocated Storage Location |
|---|---|---|---|---|---|---|---|---|
| 1 | A1 | Deep Groove Ball Bearing | 5 | 1 | 15 | 30 | 0.24 | (2, 2, 3) |
| 2 | B1 | Cylindrical Gear | 5 | 2 | 10 | 35 | 0.32 | (1, 2, 4) |
| 3 | A3 | M10 Bolt | 4 | 1 | 70 | 40 | 0.15 | (4, 1, 3) |
| 4 | C1 | Gear Coupling | 1 | 3 | 100 | 10 | 0.5 | (1, 4, 1) |
| 5 | B2 | Worm Gear | 3 | 2 | 80 | 360 | 0.52 | (3, 2, 1) |
| 6 | B2 | Jaw Clutch | 4 | 2 | 25 | 120 | 0.19 | (3, 1, 4) |
| 7 | B2 | V-Belt | 4 | 2 | 30 | 90 | 0.23 | (2, 1, 2) |
| 8 | B2 | Chain | 3 | 2 | 5 | 90 | 0.12 | (4, 4, 4) |
| 9 | A2 | M20 Bolt | 5 | 1 | 35 | 90 | 0.42 | (2, 5, 1) |
| 10 | A2 | Double-Ended Stud | 3 | 1 | 10 | 90 | 0.82 | (2, 2, 4) |
| 11 | A2 | Lock Nut | 2 | 1 | 28 | 120 | 0.32 | (3, 2, 2) |
| 12 | A1 | Washer | 5 | 1 | 10 | 150 | 0.54 | (3, 1, 3) |
| 13 | A1 | Spring | 5 | 1 | 26 | 150 | 0.2 | (4, 3, 3) |
| 14 | A1 | Helical Gear | 4 | 1 | 60 | 90 | 0.28 | (3, 1, 2) |
| 15 | A1 | Bevel Gear | 1 | 1 | 50 | 90 | 0.74 | (1, 1, 1) |
| 16 | A1 | Spur Gear | 1 | 1 | 22 | 100 | 0.74 | (1, 2, 2) |
| 17 | A1 | Herringbone Gear | 1 | 1 | 30 | 60 | 0.74 | (1, 3, 1) |
| 18 | A1 | Overflow Valve | 1 | 1 | 30 | 100 | 0.74 | (2, 3, 1) |
| Algorithm | Best | Worst | Average | |||
|---|---|---|---|---|---|---|
| Fitness Value | Convergence Count | Fitness Value | Convergence Count | Fitness Value | Convergence Count | |
| IMA | 45.98 | 18 | 53.95 | 286 | 48.11 | 109 |
| MA | 59.46 | 385 | 61.56 | 450 | 60.23 | 428 |
| PSO | 60.79 | 280 | 64.13 | 422 | 62.73 | 307 |
| GA | 61.86 | 291 | 65.32 | 356 | 63.86 | 316 |
| Algorithm | Theoretical Complexity | Measured Time (n = 1000) |
|---|---|---|
| IMA | O(mn) | 8 s |
| MA | O(mn logn) | 14 s |
| PSO | O(m2n) | 10 s |
| GA | O(mn2) | 12 s |
| Three-Stage Algorithm | Traditional FIFO Algorithm | ||||||
|---|---|---|---|---|---|---|---|
| Area | Distribution Time (min) | Picking Start Time (min) | Picking Time (min) | Distribution End Time (min) | Picking Start Time (min) | Picking Time (min) | Distribution End Time (min) |
| L1 | 455 | 30 | 41 | 526 | 0 | 10 | 465 |
| L2 | 475 | 24 | 36 | 536 | 4 | 16 | 496 |
| L3 | 482 | 7 | 19 | 509 | 10 | 23 | 515 |
| L4 | 272 | 53 | 71 | 397 | 16 | 30 | 319 |
| L5 | 314 | 46 | 65 | 426 | 21 | 40 | 376 |
| L6 | 480 | 19 | 30 | 530 | 28 | 43 | 552 |
| L7 | 450 | 35 | 47 | 532 | 34 | 49 | 533 |
| L8 | 481 | 13 | 26 | 520 | 40 | 56 | 577 |
| L9 | 342 | 41 | 55 | 438 | 46 | 64 | 452 |
| L10 | 483 | 0 | 15 | 498 | 51 | 73 | 608 |
| Fulfillment Time | 536 | 608 | |||||
| Average Fulfillment Time | 491 | 500 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hui, J.; Zhi, S.; Liu, W.; Chu, C.; Zhang, F. An Integrated Implementation Framework for Warehouse 4.0 Based on Inbound and Outbound Operations. Mathematics 2025, 13, 2276. https://doi.org/10.3390/math13142276
Hui J, Zhi S, Liu W, Chu C, Zhang F. An Integrated Implementation Framework for Warehouse 4.0 Based on Inbound and Outbound Operations. Mathematics. 2025; 13(14):2276. https://doi.org/10.3390/math13142276
Chicago/Turabian StyleHui, Jizhuang, Shaowei Zhi, Weichen Liu, Changhao Chu, and Fuqiang Zhang. 2025. "An Integrated Implementation Framework for Warehouse 4.0 Based on Inbound and Outbound Operations" Mathematics 13, no. 14: 2276. https://doi.org/10.3390/math13142276
APA StyleHui, J., Zhi, S., Liu, W., Chu, C., & Zhang, F. (2025). An Integrated Implementation Framework for Warehouse 4.0 Based on Inbound and Outbound Operations. Mathematics, 13(14), 2276. https://doi.org/10.3390/math13142276






