Abstract
For systems such as the van der Pol and van der Pol–Duffing oscillators, the study of their oscillation is currently a very active area of research. Many authors have used the bifurcation method to try to determine oscillatory behavior. But when the system involves n separate delays, the equations for bifurcation become quite complex and difficult to deal with. In this paper, the existence of periodic oscillatory behavior was studied for a system consisting of n coupled equations with multiple delays. The method begins by rewriting the second-order system of differential equations as a larger first-order system. Then, the nonlinear system of first-order equations is linearized by disregarding higher-degree terms that are locally small. The instability of the trivial solution to the linearized equations implies the instability of the nonlinear equations. Periodic behavior often occurs when the system is unstable and bounded, so this paper also studied the boundedness here. It follows from previous work on the subject that the conditions here did result in periodic oscillatory behavior, and this is illustrated in the graphs of computer simulations.
MSC:
34K13
1. Introduction
Periodic oscillation is one of the key characteristics in a general class of nonlinear systems, and in coupled van der Pol-like systems in particular. Bifurcation can arise as a periodic solution. Therefore, many researchers have investigated various models of van der Pol or van der Pol-like oscillators by means of bifurcation or other methods. For example, Torres et al. [1] studied a triplet of mechanical oscillators equipped with a van der Pol term and having a Huygens coupling. These have a special coordinated motion. A transformation was used to reduce the system. Then, the system was analyzed using Poincare’s perturbation method. In [2], accurate analytical solutions were obtained for a system of three coupled van der Pol–Duffing oscillators. In [3], there was a system of four mixed-mode vibration types with a pitchfork bifurcation delay phenomenon. In [4], the oscillations of a hybrid van der Pol–Duffing–Rayleigh system were studied, both numerically and theoretically. In [5], bursting oscillations were analyzed in a complex coupled four-dimensional Mathieu–van der Pol oscillator. In [6], sufficient conditions were obtained for the exponential input-to-state stability of a coupled van der Pol system using graph theory and Kirchoff’s matrix-tree theorem. In [7], fold bifurcation and Hopf bifurcation were studied using the formal adjoin theory, the center manifold theorem, and the normal form method for a neutral differential–difference equation of the van der Pol type. In [8], Ghosh et al. studied zones of stability for a delayed Duffing–van der Pol system, which gave rise to a variety of synchronization channels. In [9], the original system was transformed into a three-dimensional system, and then all of the Darboux polynomials of a Mathieu–van der Pol–Duffing system were characterized and a complete system of rational first integrals was obtained. In [10], Sysoev proposed a method involving multivariate time series for the reconstruction of nonlinear coupling functions for all elements of ensembles of coupled van der Pol systems. In [11], Hoskoti et al. proposed a reduced-order method to study the oscillatory nature of wake dynamics caused by vortex shedding. This used a spring-mounted airfoil coupled with a van der Pol oscillator. In [12], a chaotic system of van der Pol oscillators coupled to linear oscillators was stabilized using adaptive control and synchronization. The authors of [13] investigated the stability and dynamic behavior of the simultaneous primary and super-harmonic resonance of a van der Pol oscillator. The authors of [14] investigated bifurcation structures in a van der Pol–Mathieu oscillator with external excitation. In [15], modulated motion and bifurcation were studied for two van der Pol oscillators that were nonlinearly coupled and parametrically excited. The authors of [16] studied the dynamic behavior of a van der Pol biorhythmic oscillator subjected to both colored noise and harmonic excitation. The authors of [17] conducted a systematic search of the parameter space for bi-rhythmic and tri-rhythmic families of van der Pol and Rayleigh oscillators and their higher-order variants using a numerical simulation. The authors of [18,19] studied the bifurcation characteristics of a van der Pol–Duffing oscillator subjected to white noise excitation and adaptive synchronization. They identified parameters for chaos to occur. In [20], the lateral oscillations of a pedestrian walking on a periodically moving floor were modeled by a modified van der Pol–Rayleigh oscillator. The authors of [21] studied voltage oscillations in a Bonhoeffer–van der Pol oscillator with a non-ideal capacitor. In 2011, Zhang et al. discussed the dynamic behavior of the following symmetric system [22]:
The dynamics of System (1) were carried out using a symmetric Hopf bifurcation result. Some important results about the spontaneous bifurcations of multiple branches of periodic solutions and their spatiotemporal patterns were obtained. Recently, Liu and Zhang extended Model (1) to four coupled van der Pol oscillators:
where , , , and are constants. By means of the symmetric Hopf bifurcation theory, the normal form of the system on the central manifold, the multiple periodic solutions of spatiotemporal patterns of the system were obtained and the bifurcating periodic solutions were also derived [23]. On the other hand, Nganso et al. considered the van der Pol oscillator with extended nonlinearity described by the following system:
where represents the strength of the coupling and and are the interaction parameters. A phenomenon of coupling-induced multi-stability was found in Model (3). A large limit cycle and a smaller quasi-periodic-like attractor were discussed [24]. Ji and Zhang discussed a van der Pol–Duffing oscillator:
Hopf bifurcation and a quasi-periodic solution to Model (4) were investigated [25]. Motivated by the above models, in this paper, we studied the following n-coupled nonlinear differential system:
where all the parameters are real numbers, , and the time delays are . We were concerned with the existence of periodic oscillatory solutions to Model (5). It is known that periodic solutions can arise from bifurcation. However, if time delays involve several different numbers, the bifurcation method is hard to carry out in Model (5) due to the complexity of the bifurcation equations. In the present paper, the method of mathematical analysis was used to deal with the question of oscillatory solutions to this model.
2. Preliminaries
System (5) can be expressed in the following equivalent form:
where . System (6) can be expressed as the following:
The matrix form of System (7) is as follows:
where , , and are both matrices, and is a -by-1 vector:
where The linearized System (8) is as follows:
Lemma 1.
If matrixis a nonsingular matrix for selected parameters, then there exists a unique equilibrium point for System (7) (or (8)).
Proof of Lemma 1.
Assume that is an equilibrium point of System (7); then, we have the following algebraic equations:
Lemma 2.
All solutions to System (6) (or (7)) are bounded, assuming that
Proof of Lemma 2.
To prove the boundedness of the solutions in System (6), we constructed a Lyapunov function By calculating the derivative of through System (6), we have
3. The Existence of Oscillatory Solutions
Theorem 1.
Assume that System (7) (or (8)) has the unique trivial equilibrium point for selected parameter values. Let
and 0, be characteristic values of matrix and matrix , respectively. Assume that Re() > 0 (), or there exists a characteristic value, say , and Re(with Re(; then, the unique trivial solution to System (7) is unstable, implying that there exists an oscillatory solution in System (7).
Proof of Theorem 1.
Obviously, if the trivial solution to System (9) is unstable, then the trivial solution to System (7) (or (8)) is also unstable. Therefore, to discuss the instability of the trivial solution to System (7), we only need to deal with the instability of the trivial solution to System (9). The characteristic equation associated with System (9) is the following:
where is the identity matrix of 2 by 2. Noting that 0, are characteristic values of matrix , from (13), we have
Thus, we are led to an investigation of the nature of the roots for some }:
or
For Equation (15), if Re() > 0, this implies that there is a positive real part characteristic value. So, the trivial solution to System (9) is unstable. Equation (16) is a transcendental equation for which it is hard to find all the solutions. However, we showed that the trivial solution to System (9) is unstable under the assumption of Theorem 1. Let where respectively. By separating the real part and imaginary part of Equation (16), we obtain the following:
From the assumptions, there exists one , and Re() > 0 with ; we showed that Equation (17) has a positive real part root. Let
Obviously, is a continuous function of . Noting that then Since as there exists a suitably large , say , such that □
According to the intermediate value theorem, there exists a say (0, ), such that implying that there is a positive real part characteristic value of Equation (17). This means that the trivial solution to System (9) is unstable. Note that of System (8) is a higher-order infinitesimal as Therefore, the instability of the trivial solution to System (9) implies the instability of the trivial solution to nonlinear System (8). This suggests that the unique trivial equilibrium point of System (7) is unstable. This instability of the unique trivial equilibrium point, together with the boundedness of the solutions, will force System (7) (or (8)) to generate an oscillatory solution [26,27].
Now we adopt the following norms of the vector and matrix [28]:
Note that ; thus, and we have the following:
Theorem 2.
Assume that the conditions of Lemma 1 and Lemma 2 hold. Determine if the following inequality is satisfied:
where If so, then the trivial solution to System (9) is unstable, implying that System (7) (or (8)) has an oscillatory solution.
Proof of Theorem 2.
To prove the instability of the trivial solution to System (9), let Therefore, and
Specifically, consider a scalar equation:
According to the comparison theory of differential equations, we have If the trivial solution to Equation (22) is unstable, then the trivial solution to (21) is still unstable. The characteristic equation associated with Equation (22) is given by
If the trivial solution to Equation (22) is stable, then Equation (23) must have a real negative root, say , and from (23), we have
One can prove that the inequality holds. So, we have
A contradiction with Inequality (20) implies that the trivial solution to Equation (22) is unstable. This suggests that the trivial solution to Equation (21) is unstable, implying that the trivial solution to System (8) is unstable. Similar to Theorem 1, System (7) (or (8)) generates an oscillatory solution. The proof is completed. □
4. Simulation Result
Firstly, consider in System (6) as the following:
The parameter values are shown in Table 1.

Table 1.
The parameter values in System (26).
Then, the characteristic values of matrices and in System (26) are 0.0022 0.9747 0.0022 0.9592 0.0023 0.9899 0.0024 0.9798 and 0.0446, 1.4635, 0.5417 1.2873 0, 0, 0, 0, 0, respectively. The time delays are selected as 1.15, .16, and , respectively. All the characteristic values of matrix are complex numbers, and the real parts are greater than zero. Matrix has a characteristic value of zero; thus the conditions of Theorem 1 are satisfied. There exists an oscillatory solution to System (26) (see Figure 1 and Figure 2). From Figure 1 and Figure 2, the curves of , , , , and are smooth and the amplitude of is only 4.0743. However, the curves of , , , , and are jagged due to the higher order of variables in their equations. The amplitude of curve is 14.1072. The oscillation frequency slows down as the time delay increases.
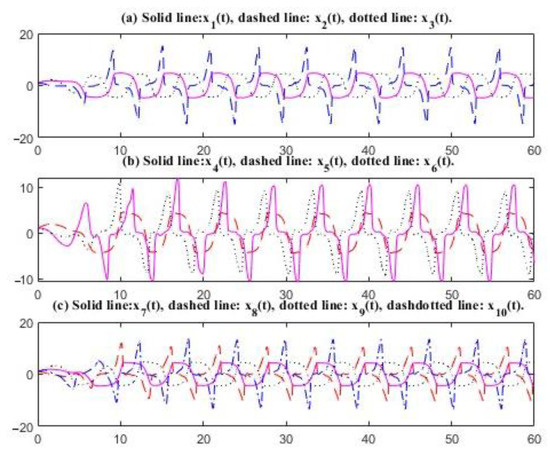
Figure 1.
Oscillations of the solutions; delays: 1.15, 1.16, 1.25, 1.18, and 1.12.
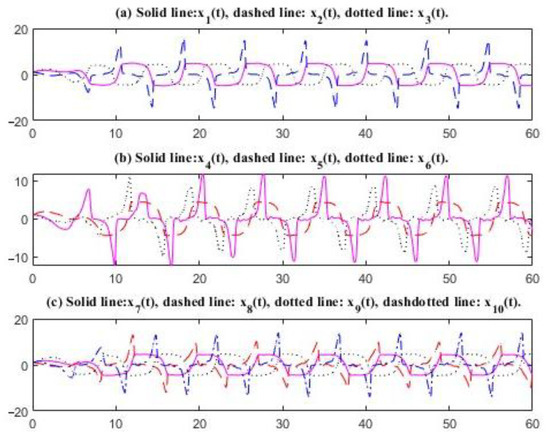
Figure 2.
Oscillations of the solutions; delays: 1.65, 1.66, 1.75, 1.68, and 1.62.
Then, consider in System (6) as the following:
The parameters are shown in Table 2.

Table 2.
The parameter values in System (27).
It is easy to see that 1.0148 and 4.74 in System (27). The time delays are selected as 0.75, .78, and , respectively. Then, and Thus, and The conditions of Theorem 2 are satisfied. There exists an oscillatory solution to System (27) (see Figure 3 and Figure 4). From Figure 3 and Figure 4, the curves for odd subscripts are even and almost the same shapes, and the amplitude of is 2.4018. The curves for even subscripts are steep and uneven, and the amplitude of is 10.1625. The amplitude of the less-even curves is greater than that of the smooth curves. When the time delays increase, the oscillation frequencies decrease slightly.
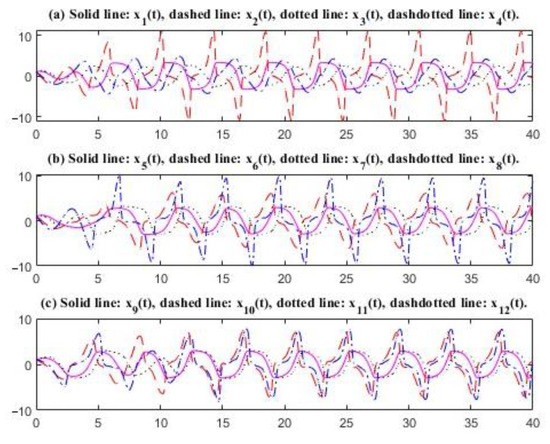
Figure 3.
Oscillations of the solutions; delays: 0.75, 0.78, 0.74, 0.72, 0.73, and 0.77.
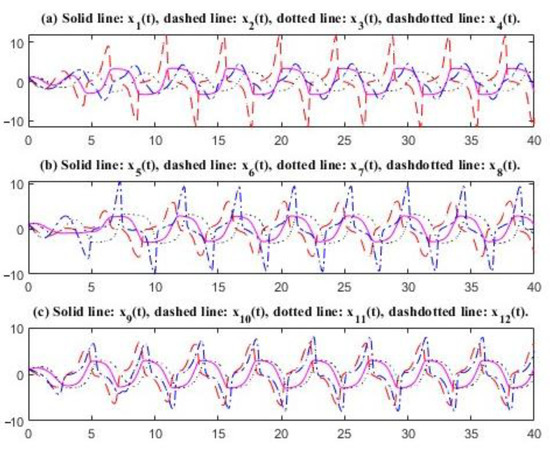
Figure 4.
Oscillations of the solutions; delays: 1.05, 1.08, 1.04, 1.02, 1.03, and 1.07.
Then, consider in System (6) as the following:
The parameters are shown in Table 3.

Table 3.
The parameter values in System (28).
The characteristic values of matrices and in System (28) are and respectively. The time delays are selected as 0.75, .78, and respectively. It is easy to see that the conditions of Theorem 1 are satisfied. There exists an oscillatory solution to System (28) (see Figure 5 and Figure 6). The curves for odd subscripts are even and the curves for even subscripts are uneven. In Figure 5, the amplitude of is just 3.3591, but that for is 12.6238. Figure 5 and Figure 6 indicate that the time delay affects the oscillation frequency. A change in the time delays will cause a change in the oscillatory frequency.
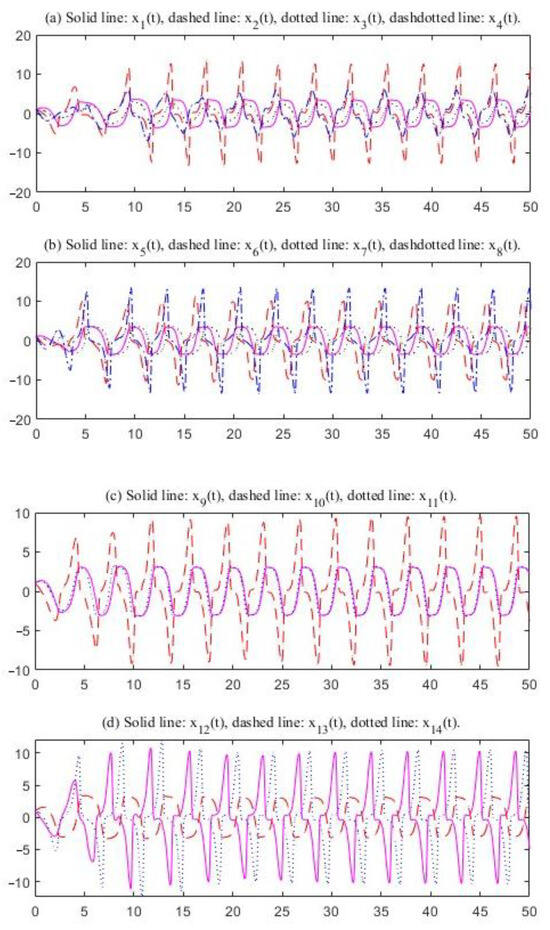
Figure 5.
Oscillations of the solutions; delays: 0.75, 0.78, 0.80, 0.76, 0.74, 0.77, and 0.72.
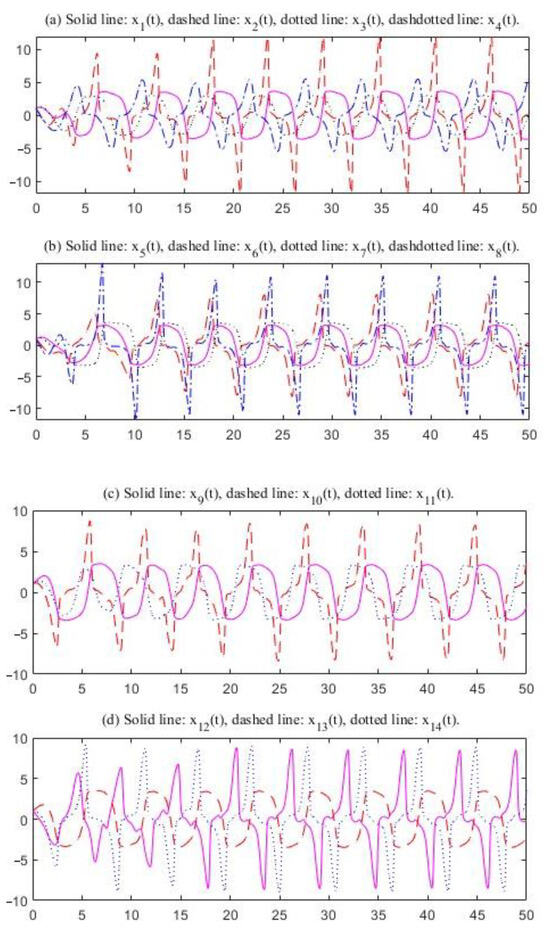
Figure 6.
Oscillations of the solutions; delays: 0.85, 0.88, 0.90, 0.86, 0.84, 0.87, and 0.82.
Finally, we considered in System (6) as the following:
From Table 4, 1.0019 and 7.65. The time delays are selected as 0.38, .40, 0.39, Thus, The conditions of Theorem 2 are satisfied. There exists an oscillatory solution to System (29) (see Figure 7 and Figure 8). Figure 7 and Figure 8 indicate that the values of affect the oscillation frequency. The parameters in the two figures are almost the same. In Figure 8, only the parameters are less than the values of in Figure 7. The oscillation frequencies are different from each other.

Table 4.
The parameter values in System (29).
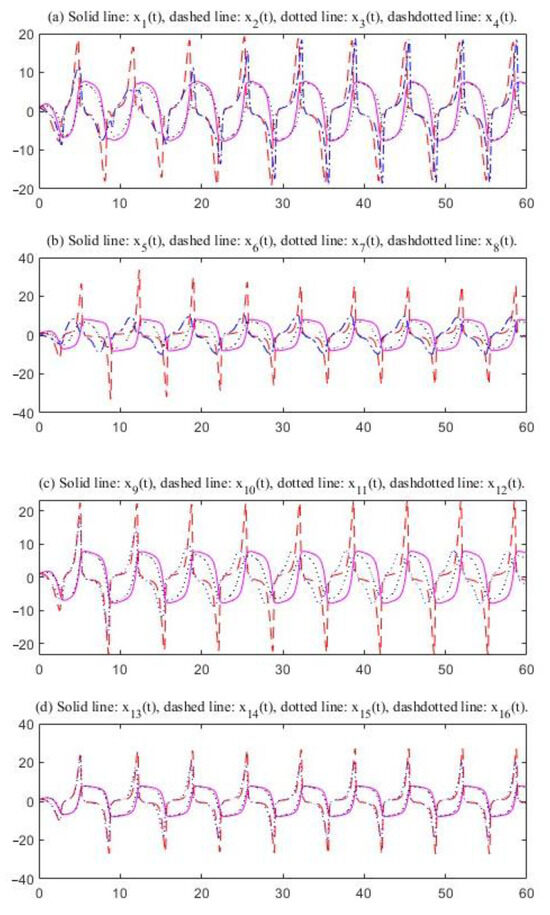
Figure 7.
Oscillations of the solutions; delays: 0.38, 0.40, 0.42, 0.43, 0.36, 0.36, 0.41, and 0.39.
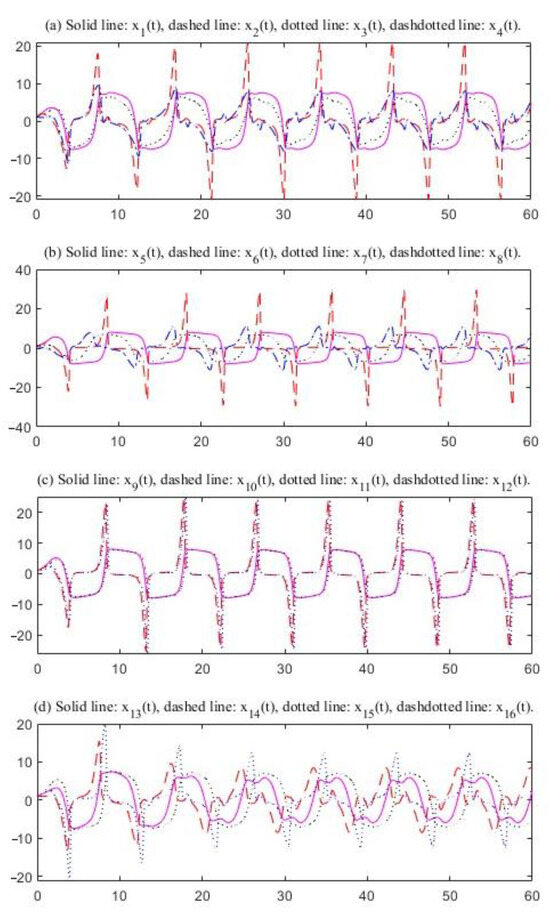
Figure 8.
Oscillations of the solutions; delays: 0.38, 0.40, 0.42, 0.43, 0.36, 0.36, 0.41, and 0.39.
The values of
The values of
5. Discussion
The present criteria only determine the existence of oscillatory solutions. They cannot provide the bifurcation values about the delays. It is pointed out that it is difficult to deal with the present models using the bifurcation method. Even if for the bifurcation equation will be the following:
where is a ten-order polynomial, are nine-order polynomials about , and is a constant. If are different real numbers, then are different variables. Equation (30) is a transcendental equation with five different variables. Theoretically, one can use Ruan’s method to find the bifurcation values [29]. However, finding the bifurcating values from Equation (30) is not easy work.
6. Conclusions
Gap differential equations of types related to the van der Pol and van der Pol–Duffing equations are difficult to study directly from the bifurcation conditions when the system involves many gaps. In this paper, it was shown that, alternatively, a study of these systems can be effective with a method of reduction to first-order, linearization, and the determination of the instability of the trivial solution, together with boundedness. This is shown by the periodic appearance of the graphs for simulations with randomly chosen parameters. Two theorems are proved in this paper that provide sufficient conditions.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Torres, J.A.; Ramirez, J.P.; Nijmeijer, H. Coordination of oscillators driven by non-identical van der Pol excitation interacting via Huygens’ coupling. IFAC Pap. 2024, 58, 34–39. [Google Scholar] [CrossRef]
- Qian, Y.H.; Chen, S.M. Accurate approximate analytical solutions for multi-degree-of-freedom coupled van der Pol-Duffing oscillators by homotopy analysis method. Commun. Nonlinear Sci. Numer. Simulat. 2010, 15, 3113–3130. [Google Scholar] [CrossRef]
- Ma, X.D.; Yu, Y.; Wang, L.F. Complex mixed-mode vibration types triggered by the pitchfork bifurcation delay in a driven van der Pol-Duffing oscillator. App. Math. Comput. 2021, 411, 126522. [Google Scholar] [CrossRef]
- Ma, X.D.; Zhang, Z. Symmetric and asymmetric bursting oscillations in a hybrid van der Pol-Duffing-Rayleigh system. Chaos Solitons Fractals 2024, 186, 115310. [Google Scholar] [CrossRef]
- Jiang, Y.D.; Zhang, W.; Zhang, Y.F.; Bi, Q.S. Bursting oscillations in coupling Mathieu-van der Pol oscillator under parametric excitation. Chaos Solitons Fractals 2024, 178, 114279. [Google Scholar] [CrossRef]
- Liu, H.Y.; Ai, X.H. Exponential input-to-state stability for coupled Van der Pol system driven by a second-order process. Commun. Nonlinear Sci. Numer. Simulat. 2025, 141, 108480. [Google Scholar] [CrossRef]
- Niu, B.; Jiang, W.H. Multiple bifurcation analysis in a NDDE arising from van der Pol’s equation with extended delay feedback. Nonlinear Anal. RWA 2013, 14, 699–717. [Google Scholar] [CrossRef]
- Ghosh, D.; Chowdhury, A.R.; Saha, P. On the various kinds of synchronization in delayed Duffing-Van der Pol system. Commun. Nonlinear Sci. Numer. Simulat. 2008, 13, 790–803. [Google Scholar] [CrossRef]
- Cen, Z.H.; Xie, F. Darboux integrability of a Mathieu-van der Pol-Duffing oscillator. Nonlinear Anal. RWA 2023, 70, 103785. [Google Scholar] [CrossRef]
- Sysoev, I.V. Reconstruction of ensembles of generalized Van der Pol oscillators from vector time series. Phys. D Nonlinear Phenom. 2018, 384–385, 1–11. [Google Scholar] [CrossRef]
- Hoskoti, L.; Aravinth, D.; Misra, A.; Sucheendran, M.M. Frequency lock-in during nonlinear vibration of an airfoil coupled with van der Pol oscillator. J. Fluids Struct. 2020, 92, 102776. [Google Scholar] [CrossRef]
- Fotsin, H.; Bowong, S. Adaptive control and synchronization of chaotic systems consisting of van der Pol oscillators coupled to linear oscillators. Chaos Solitons Fractals 2006, 27, 822–835. [Google Scholar] [CrossRef]
- Cai, C.C.; Shen, Y.J.; Wen, S.F. Primary and super-harmonic simultaneous resonance of van der Pol oscillator. Int. J. Non-Linear Mech. 2022, 147, 104237. [Google Scholar] [CrossRef]
- Ma, X.D.; Jiang, W.A.; Yu, Y. Periodic bursting behaviors induced by pulse-shaped explosion or non-pulse-shaped explosion in a van der Pol-Mathieu oscillator with external excitation. Commun. Nonlinear Sci. Numer. Simulat. 2021, 103, 105959. [Google Scholar] [CrossRef]
- Maccari, A. Modulated motion and infinite-period bifurcation for two non-linearly coupled and parametrically excited van der Pol oscillators. Int. J. Non-Linear Mech. 2001, 36, 335–347. [Google Scholar] [CrossRef]
- Yonkeu, R.M.; Yamapi, R.; Filatrella, G.; Tchawoua, C. Effects of a periodic drive and correlated noise on birhythmic van der Pol systems. Phys. A Stat. Mech. Appl. 2017, 466, 552–569. [Google Scholar] [CrossRef]
- Saha, S.; Gangopadhyay, G.; Ray, D.S. Systematic designing of bi-rhythmic and tri-rhythmic models in families of Van der Pol and Rayleigh oscillators. Commun. Nonlinear Sci. Numer. Simulat. 2020, 85, 105234. [Google Scholar] [CrossRef]
- Kumar, P.; Narayanan, S.; Gupta, S. Investigations on the bifurcation of a noisy Duffing–Van der Pol oscillator. Probabilistic Eng. Mech. 2016, 75, 70–86. [Google Scholar] [CrossRef]
- Fotsin, H.B.; Woafo, P. Adaptive synchronization of a modified and uncertain chaotic Van der Pol-Duffing oscillator based on parameter identification. Chaos Solitons Fractals 2005, 24, 1363–1371. [Google Scholar] [CrossRef]
- Erlicher, S.; Trovato, A.; Argoul, P. A modified hybrid Van der Pol/Rayleigh model for the lateral pedestrian force on a periodically moving floor. Mech. Syst. Signal Process. 2013, 41, 485–501. [Google Scholar] [CrossRef]
- Brechtl, J.; Xie, X.; Liaw, P.K. Investigation of chaos and memory effects in the Bonhoeffer-van der Pol oscillator with a non-ideal capacitor. Commun. Nonlinear Sci. Numer. Simulat. 2019, 73, 195–216. [Google Scholar] [CrossRef]
- Zhang, C.R.; Zheng, B.D.; Wang, L.C. Multiple Hopf bifurcations of three coupled van der Pol oscillators with delay. Appl. Math. Comput. 2011, 217, 7155–7166. [Google Scholar] [CrossRef]
- Liu, L.Q.; Zhang, C.R. Multiple Hopf bifurcations of four coupled van der Pol oscillators with delay. Mathematics 2023, 11, 4831. [Google Scholar] [CrossRef]
- Nganso, E.N.; Ngueuteu, M.S.; Yamapi, R.; Filatrella, G.; Kurths, J. Two-attractor chimera and solitary states in a network of nonlocally coupled birhythmic van der Pol oscillators. Chaos Solitons Fractals 2023, 169, 113235. [Google Scholar] [CrossRef]
- Ji, J.C.; Zhang, N. Additive resonances of a controlled van der Pol–Duffing oscillator. J. Sound. Vibrat. 2008, 315, 22–33. [Google Scholar] [CrossRef]
- Chafee, N.A. Bifurcation problem for a functional differential equation of finite retarded type. J. Math. Anal. Appl. 1971, 35, 312–348. [Google Scholar] [CrossRef]
- Feng, C. Oscillatory behavior of the solutions for a Parkinson’s disease model with discrete and distributed delays. Axioms 2024, 13, 75. [Google Scholar] [CrossRef]
- Gopalsamy, K. Stability and Oscillations in Delay Differential Equations of Population Dynamics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Ruan, S.G.; Wei, J.J. On the zero of some transcendental function with applications to stability of delay differential equations with two delays. Dyn. Contin. Impuls. Syst. 2003, 10, 863–874. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).