Abstract
In this paper, we present a new space-time Galerkin-like method, where we treat the discretization of spatial and temporal domains simultaneously. This method utilizes a mixed formulation of the tensor-train (TT) and quantized tensor-train (QTT) (please see Section Tensor-Train Decomposition), designed for the finite element discretization (Q1-FEM) of the time-dependent convection–diffusion–reaction (CDR) equation. We reformulate the assembly process of the finite element discretized CDR to enhance its compatibility with tensor operations and introduce a low-rank tensor structure for the finite element operators. Recognizing the banded structure inherent in the finite element framework’s discrete operators, we further exploit the QTT format of the CDR to achieve greater speed and compression. Additionally, we present a comprehensive approach for integrating variable coefficients of CDR into the global discrete operators within the TT/QTT framework. The effectiveness of the proposed method, in terms of memory efficiency and computational complexity, is demonstrated through a series of numerical experiments, including a semi-linear example.
Keywords:
space-time finite element; tensor network approach; time-dependent problem; convection–diffusion–reaction equation; variable coefficients MSC:
15A69; 35Q79; 65M70
1. Introduction
1.1. Time-Dependent 3D Convection–Diffusion–Reaction Problem
This paper develops a space-time finite element method for tensor network low-rank numerical solution of the time-dependent 3D convection–diffusion–reaction (CDR) equation with Dirichlet boundary conditions of the type
where , , and are the linear coefficients of t and , and . The computational domain in space is a three-dimensional cube, which is a Cartesian product of three intervals, and T is the final time-point. We considered inhomogeneous boundary conditions and a nonzero initial value of (1) and developed tensor-train space-time formats for coefficients that are either constant or separable. Subsequently, we extended the approach to accommodate a more general class of variable coefficients.
1.2. Classical Methods for Solving CDR
Finite element method (FEM) is a powerful technique for solving CDR with high accuracy [1,2,3,4,5]. Discontinuous Galerkin [6,7] and Petrov–Galerkin [8,9] methods are widely used for solving CDR, particularly in spectral methods and virtual element methods [10,11,12,13]. These methods involve approximating the partial differential equation (PDE) solution by projecting it onto a finite-dimensional subspace of trial functions. The key idea is to ensure that the residual error is orthogonal to the chosen subspace of test functions.
In the Galerkin approach, the continuous problem is discretized by selecting a finite number of trial functions to approximate the solution. These functions are typically chosen from a function space like polynomials or piecewise-defined functions. In the classical (Bubnov–Galerkin) method, the same set of functions is used for both the trial (approximation of the solution) and test (weighting) functions, which ensures that the residual error is orthogonal to the space spanned by the trial functions. The PDE is transformed into its weak (integral) form by multiplying it by a test function and integrating over the domain. The weak form allows handling problems with lower regularity solutions and dealing with complex geometries.
The Petrov–Galerkin (PG) method generalizes the Bubnov–Galerkin method by allowing test and trial spaces to differ. This added flexibility allows for improved stability and accuracy, especially for convection-dominated problems or where numerical instability is a concern. By selecting appropriate test functions, the Petrov–Galerkin method can introduce stabilization mechanisms, such as upwinding in convection-dominated problems, thereby reducing oscillations or instabilities. In the present work, we do not apply such stabilization mechanisms since our underlying problem is a diffusion-dominated problem. In fact, we employ the same discrete basis for both test and trial functions. Our method follows the Petrov–Galerkin framework because the underlying continuous function spaces differ, specifically in the norms employed; our stability analysis depends on this difference, and it is based on an inf-sup condition [14,15]. A survey of space-time discretization of parabolic evolution equations deals with finite element [16,17,18], discontinuous Galerkin approach [19], virtual element method [20,21], spectral collocation methods [12,22].
Space-time discretizations treat the discretization of spatial and temporal domains simultaneously. Treating space and time together requires more computational resources, particularly due to the memory needed to represent the solution across a time slab. However, this approach offers greater flexibility in temporal discretization, enabling spatially localized refinement in time. Space-time methods can also be easier to analyze and may achieve higher accuracy than traditional time-marching schemes. Our current numerical examples serve as proofs of concept for the new space-time tensor method.
1.3. Mitigating the Curse of Dimensionality
The CDR equations model a wide range of phenomena in physics, chemistry, and engineering, which often demand substantial computational resources due to the need for fine spatial and temporal discretizations. Traditional approaches to solving such problems often lead to prohibitively large systems of equations, making them impractical for many real-world applications, since the number of grid points grows exponentially with the number of dimensions. In real-life applications modeled by time-dependent PDEs, such as full waveform inversion problems, the number of grid points required for solving the PDE can be as large as per time step. With a large number of time steps , one must store a total of floating-point numbers [23].
This phenomenon is known as the curse of dimensionality [24]. The curse of dimensionality leads to poor computational scaling in numerical algorithms and poses the main challenge in multidimensional numerical computations, irrespective of the specific problem. Notably, even exascale high-performance computing, with its optimization strategies, cannot overcome the curse of dimensionality. This phenomenon forces algorithm developers to make hard choices—either to reduce the fidelity of the model using, e.g., reduced-order models (ROMs) or to repeat computation using checkpointing-type strategies. ROMs focus on creating a reduced form of the PDE operator and are an excellent solution in some cases. However, they are often tailored to specific models and demand significant domain expertise. Furthermore, ROMs can be incompatible with legacy codes as they often require invasive modification of the simulation software. ROM development is an active area of research and can work well for solving certain classes of problems [25,26].
As an alternative, tensor network techniques have shown promise in alleviating the curse of dimensionality associated with high-dimensional problems. Among these, the tensor-train (TT) format, introduced by Oseledets and Tyrtyshnikov [27], has gained particular attention due to its ability to represent high-dimensional data efficiently while maintaining computational tractability.
Here, we present a novel approach that combines the high accuracy of space-time finite element methods with the computational efficiency of TT decomposition for solving time-dependent CDR equations in three spatial dimensions. Our method exploits the inherent low-rank structure often present in the solutions of such equations to dramatically reduce the computational complexity and storage requirements. Moreover, given that the finite element discrete operators have banded structures, we further exploit the quantized tensor-train (QTT) format for more economical and efficient solvers [28]. Specifically, we develop a mixed TT/QTT decomposition of the four-dimensional (three space plus time) space-time finite element Galerkin discretization, and demonstrate how to construct the TT and QTT representations of the finite element discretization. While Kornev et al. [29] also explore QTT-based FEM, their work focuses on stationary 2D problems with time-stepping, whereas our approach addresses fully time-dependent 3D problems in a unified space-time framework. Our results show that this TT/QTT-FEM-PG approach can achieve high accuracy while dramatically reducing the computational resources required, making it possible to solve previously intractable problems in CDR systems.
The remainder of this paper is organized as follows. In Section 2, we derive the weak formulation of (1), review some basic concepts for space-time finite element methods, and introduce the discretization and its matrix formulation. Section 3 reviews the tensor notations and definitions of the TT format, the TT-matrix format, the QTT format, and the TT-cross interpolation technique. In Section 4, we detail the low-rank structure of the discrete formulation of the model problem. Section 5 describes the assembly process that leads to the global linear system. We have reformulated this process to be more compatible with tensor operations. This reformulation is particularly important as it simplifies and optimizes the tensorization process. In Section 6, we present our mixed TT/QTT design of the numerical solution of the CDR equation and introduce our algorithms in TT/QTT format. Section 7 generalizes the proposed technique for arbitrary order. In Section 8, we present our numerical results and assess the performance of our method. In Section 9, we offer our final remarks and discuss possible future work. Additional details on the CDR tensorization approach are provided in Appendix A, Appendix B, Appendix C, Appendix D and Appendix E.
2. Space-Time Finite Element Formulation of CDR
The numerical approximation of partial differential equations (PDEs) is essential in many scientific and engineering fields, especially when dealing with complex geometries and singular solutions. Finite element methods (FEMs) are renowned for their robustness and accuracy in addressing such problems. However, as the problem size and complexity grow, the computational cost of FEM increases substantially, making high-resolution simulations computationally prohibitive. This challenge motivates the development of a space-time tensor network approach, which aims to preserve the accuracy and convergence order of the original method while significantly reducing the computational cost.
In this section, we provide the background details of the FEM used throughout the text. We employ the following notations: denote fixed intervals of , while . The time interval is denoted by , and our space-time domain is .
In FEM, the domain is broken into smaller, simple “elements”, and we approximate the solution u using simple functions on the elements. This is done by first transforming the PDE into its weak formulation. The domain is divided into elements for defining basis functions. The weak formulation is then discretized in terms of the basis functions, from which the mass and stiffness matrices are computed. The resulting linear system is then formulated and solved. Space-time FEM is formulated over the entire space-time domain . In this subsection, we detail the FEM for the 3D CRD in Equation (1).
2.1. Space-Time Weak Formulation
We let denote the set of infinitely differentiable functions with compact support within open set , while and denote the set of (equivalence classes of) square-integrable and essentially bounded functions over , respectively. Given a multi-index consisting of non-negative integers, and a function , we let denote the th partial derivative of :
where . If u is a (locally) integrable function, then we let denote the th partial derivative of u in the weak sense. That is, if there exists a (locally integrable) function v such that
for all , then we assign . We let denote the Sobolev space consisting of all square-integrable functions that are differentiable in the weak sense up to the first order. We equip with the norm
where is the standard norm. The space denotes the special subspace of , consisting of functions that vanish on the boundary in the weak sense, and thus satisfy homogeneous boundary conditions. By , we mean the dual space of , i.e., the space of all bounded linear functionals on . We give the standard operator norm:
where denotes the duality between and . Given a function space X with the associated norm , the Bochner space consists of (equivalence classes of) functions u such that for almost all . We equip this space with the norm
Similarly, we define the space as the space of all functions whose weak time derivatives are in ; we equip it with the norm
These spaces, especially with and , define the appropriate function spaces for posing the weak formulation of CRD. The space ensures that a function is square-integrable in time, and each time slice has square-integrable first-spatial derivatives. Similarly, the space ensures that a function has a first-order time derivative that is weakly square-integrable in time. We define the trial space associated with the norm , and the test space . Integrating by parts, we obtain the weak formulation of the model problem (1) with homogeneous boundary conditions and a zero initial guess, as finding a function such that
where . Throughout, we assume that , and that the coefficients satisfy
for almost every . We define the bilinear forms
and
Note that the assumption on the coefficients of (2) leads us to the continuity of , i.e., there exists a constant
Furthermore, to prove the inf-sup condition, we need the following two assumptions:
Assumption 1.
(a) There exists a positive constant , so
(b) There exist positive constants and , such that
for almost all .
These two assumptions allow us to prove the following inf-sup Theorem:
Theorem 1.
Proof.
To prove (8), we use [16] (Assumption 2.1), which requires two ingredients. First, for , we define a mapping such that
where denotes the inner product, i.e., the spatial integration only. Next, under assumption (6), we conclude that
We also deduce that
Borrowing the same arguments as [30], we prove the thesis. □
Now, we are in a position to state the unique solvability of (2):
Theorem 2.
Proof.
We will briefly state the proof of the theorem. Since, satisfies the inf-sup condition, we can write
□
Interested readers may refer to [14,15] (Theorem 3.7) for a detailed proof of Theorem 2. In the weak formulation of the CDR in Equation (2), the solution u and test function v are chosen from appropriate function spaces to account for both the spatial and temporal regularities. Contrast this against the (Bubnov–Galerkin) methods, where we pick the same function space for the trial and test functions, which may cause instability. For example, when the velocity field is strong (i.e., large convection), the convective term can cause steep gradients or sharp layers to appear in the solution, which the standard Galerkin method fails to resolve properly. In the Galerkin approach, the test function v can come from a different space than the trial function.
Equation (2) is the weak formulation corresponding to (1) with homogeneous boundary conditions [20,30,31]. The weak formulation corresponding to the inhomogeneous boundary conditions can be obtained by following the standard technique of decomposing the solution of (1) as , where is the unknown solution of (1) with homogeneous Dirichlet boundary conditions, and satisfies the boundary conditions on , and is different from zero only on the boundaries. In the weak formulation, this simply results in a modified loading term, . We refer to [20] (Remark 1) for a detailed proof of the inhomogeneous initial and boundary conditions.
2.2. Finite Element Approximation
We will now describe the finite element approximation of Equation (2). This is done by picking finite-dimensional subspaces and specified by chosen bases described below. Let be the basis for , and be the basis for . Then any approximate solution can be written as
and each test function is written as
Substituting and into the weak form in Equation (2) and approximating the coefficients with Lagrange interpolation results in a discrete system. We now describe this system for a particular choice of linear basis functions.
First, the domain is discretized into a set of hypercubes that overlap only on their boundaries. The hypercube elements are defined by dividing each axis into smaller intervals:
The resulting hypercubes are of the form . Throughout, we adopt a uniform mesh on with for all . Furthermore, we assume so that there is a total of total nodes along each dimension, and N intervals. We let denote the index for the nodes in each of the one-dimensional spaces. There is a total of total space-time nodes in . We denote these elements by , which are raster-ordered with X before Y before Z before T. The bijection between the linear element index l and the individual element indices is then given by
Local Estimates
Throughout, we make use of local interpolation, which we describe here. Each 4D element, , consists of two nodes per dimension for a total of 16 nodes. For a fixed element, each node can be indexed by four indices, , with the zero index corresponding to the lower value in the interval. The local index for each element is given by
Along each dimension, we define the standard piecewise linear hat functions defined on the one-dimensional elements. For example, on the interval
Clearly, the have derivatives defined almost everywhere:
We similarly define . Using the local index notation associated with element , the local space-time basis functions are defined as the tensor products of the 1D hat functions:
where we use the correspondence between the element l and interval index (12), and the local index i with node index (13). For completeness, we note that the 16 functions are nonzero only on the cell .
2.3. Local and Global Interpolation Operators
Now we will define the global and local Lagrange interpolation operators, and , respectively. For cell and local index i, we let denote the node at index i in cell l. We define the local interpolation operator at , , as
In other words, approximates the solution locally using the hat functions defined on the vertices of the finite element with index l. The global interpolation operator is defined as
The global interpolation operator combines the contributions from all elements of the mesh. These operators may be applied to the solution u, as well as the coefficient and forcing functions. In fact, we deduce the following standard approximation property of [5] from (17) as follows:
where and . Let denote the finite-dimensional subspace spanned by a set of linearly independent functions . Substituting the approximate solution and a test function into the weak form Equation (2) leads to our discrete system of equations. Specifically, the Galerkin discretization of the variational problem seeks to find such that
While can have lower regularity than the basis for , in practice, we will consecutively use each local space-time Lagrange basis function, , as the test function, , in Equation (19). We denote each term of Equation (19) by . The goal of this paper is to provide a tensor representation for all terms in Equation (19). Furthermore, for , , we denote the discrete bilinear form as
and
Hence, (19) reduces to finding such that
The discrete inf-sup condition of is discussed below in Theorem 3:
Theorem 3.
Let , and be the discrete spaces satisfying , and we assume that (6) is satisfied. Then the following discrete stability condition holds:
where C is a positive constant that depends on the regularity of , , and , but is independent of the mesh size h.
denotes the norm in the discrete space , which is defined in (A29). The proof can be completed by following the arguments in Theorem 3.1 in [30] and using the approximation property of the interpolation operator discussed in (18). By adding and subtracting to (19) and employing the approximation property of , we can prove the discrete inf-sup condition for sufficiently small values h of the mesh size. Hence, (19) is well-posed, i.e., it has a unique solution (see [30], section 3). In Appendix D, we provide a detailed proof of Theorem 3. Moreover, we highlight that the Galerkin orthogonality is not satisfied, i.e.,
where u and satisfy (2) and (19), respectively. We refer to (23) as an inconsistency error in the discrete scheme. In fact, the error estimate depends on the bound given in (23) as derived below.
Theorem 4.
Proof.
The proof is a consequence of the discrete inf-sup condition stated in Theorem 3. For arbitrary , we split the error as . Since , we use the discrete inf-sup condition, and the required result follows directly. In Appendix E, we provide a detailed proof. □
3. Tensor-Train Decomposition
In this section, we introduce the TT format [32], as well as the representation of linear operators in the so-called TT-matrix format, the cross-interpolation method, and the QTT format. All these methods are fundamental in the tensorization of our finite element discretization of the CDR equation.
3.1. Tensor-Train
The TT format, introduced by Oseledets in 2011 [32], represents a sequential chain of matrix products involving both two-dimensional matrices and three-dimensional tensors, referred to as TT-cores. We can visualize this chain as in Figure 1.
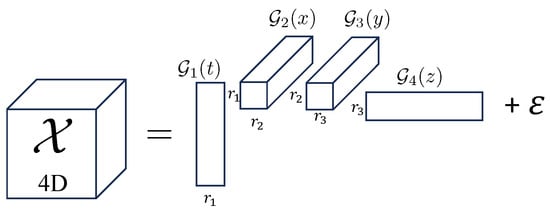
Figure 1.
TT format of a 4D tensor with TT ranks and approximation error , in accordance with Equation (25).
Given that tensors in our formulation are, at most, four-dimensional (one temporal and three spatial dimensions), we consider the tensor-train format in the context of 4D tensors. Specifically, the TT approximation of a four-dimensional tensor is a tensor with elements
Here, we have where the error, , is a tensor with the same dimensions as . The elements of the array are the TT-ranks, which quantify the compression effectiveness of the TT approximation. Since each TT-core, , only depends on a single index of the full tensor, , the TT format effectively embodies a discrete separation of variables [33]. In Figure 1, we show a four-dimensional array , decomposed in the TT format.
3.2. Linear Operators in the TT-Matrix Format
Suppose the approximate solution of the CDR equation is a 4D tensor , the linear operator acting on that solution is represented as an 8D tensor. The transformation is defined as follows:
The tensor can be related to a matrix operator via
We can construct the tensor by suitably reshaping and permuting the dimensions of the matrix . The linear operator can be further represented in a variant of the TT format, called the TT-matrix, cf. [34]. The component-wise TT-matrix is defined as follows:
where are 4D TT-cores. Figure 2 shows the process of transforming a matrix operator to its tensor format, , and, finally, to its TT-matrix format, .
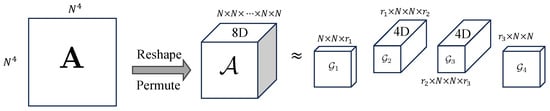
Figure 2.
Representation of a linear matrix in the TT-matrix format. First, we reshape the operation matrix and permute its indices to create the tensor . Then, we factorize the tensor in the tensor-train matrix format according to Equation (27) to obtain .
The Kronecker product ⊗ of two matrices is an operation that produces a larger matrix, while the tensor product ∘ produces a higher-dimensional tensor (see the Appendix A.2). We can further simplify the TT-matrix representations of the matrix if it is a Kronecker product of matrices, i.e., . Based on the relationship defined in Equation (26), the tensor can be constructed using the tensor product as . This implies that the internal ranks of the TT format of in (27) are all equal to 1. In such a case, all summations in Equation (27) reduce to a sequence of single matrix–matrix multiplications, and the TT format of becomes the tensor product of d matrices:
This specific structure appears quite often in the matrix discretization, and will be exploited in the tensorization to construct the efficient TT format.
3.3. TT-Cross Interpolation
The original TT algorithm is based on consecutive applications of singular-value decompositions (SVDs) on the unfoldings of a tensor [32]. Although known for its efficiency, the TT algorithm requires access to the full tensor, which is impractical and even impossible for extra-large tensors. To address this challenge, the cross-interpolation algorithm, TT-cross, has been developed [27]. The idea behind TT-cross is essentially to replace the SVD in the TT algorithm with an approximate version of the skeleton/CUR decomposition [35,36]. CUR decomposition approximates a matrix by selecting a few of its columns , a few of its rows , and a matrix that connects them, as shown in Figure 3.
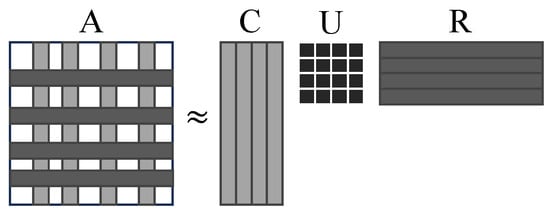
Figure 3.
CUR matrix decomposition.
Mathematically, the CUR decomposition finds an approximation for a matrix , as . The TT-cross algorithm utilizes the maximum volume principle (maxvol algorithm) [37,38] to determine . The maxvol algorithm chooses a few columns, , and rows, , of such that the intersection matrix has maximum volume [39].
TT-cross interpolation and its variants can be seen as a heuristic generalization of the CUR decomposition to tensors [40,41]. TT-cross utilizes the maximum volume algorithm iteratively, often beginning with a few randomly chosen fibers, to select an optimal number of specific tensor fibers that capture essential information of the tensor [42]. These fibers are used to construct a lower-rank TT representation. The naive generalization of CUR is proven to be expensive, which has led to the development of various heuristic optimization techniques, such as TT-ALS [43], DMRG [39,44], and AMEN [45]. Another active direction for further reducing the computational cost of TT-cross interpolation is the development of parallel algorithms to enhance efficiency and scalability [46].
3.4. Quantized Tensor-Train Format
When the TT-cores of linear operators in the tensor-train (TT) format exhibit specific tensor structures, they can undergo further compression to enhance computational efficiency. One such advanced compression technique is the quantized tensor-train (QTT) format, which extends the standard TT decomposition by leveraging hidden low-rank structures in exponentially large spaces.
In a traditional TT decomposition, a high-dimensional tensor is factorized into a sequence of smaller, lower-dimensional tensors (TT-cores). This reduces storage complexity and makes computations more manageable. However, when dealing with extremely large tensors—such as those arising from discretizations with many degrees of freedom—even the standard TT decomposition may become computationally intensive.
To address this, the QTT format introduces an additional layer of compression by applying the TT decomposition recursively. The key idea behind QTT is to reshape the original tensor into a higher-dimensional structure by performing a dyadic (power-of-two) partitioning of its modes. Once reshaped, the resulting smaller tensors are then factorized using the TT format. This hierarchical approach significantly reduces both storage requirements and computational costs, particularly when working with structured tensors that exhibit self-similar patterns across multiple scales. A notable advantage of the QTT format is its ability to efficiently represent structured operators, such as those with Toeplitz structures, which inherently possess low-rank QTT representations [47,48,49,50]. For instance, in the context of solving the CDR equations, the TT-cores of the corresponding linear operators exhibit such structures, making them ideal candidates for QTT-based compression.
Thus, to achieve higher compression and improved computational efficiency, we further transform these TT-cores into the QTT format. We then solve a mixed TT/QTT version of the problem using an appropriate TT optimization technique.
4. Tensorization of the FEM
In this section, we detail the tensorization of the FEM for the space-time CDR equation. We will begin by deriving the local mass, stiffness, and time derivative matrices associated with the system (2). From there, the Galerkin approximation will be written in terms of a sum of Kronecker products of the local matrices. This will then be used to assemble global matrices for the system. This ultimately leads to the tensorization of the discrete form of the CDR (19).
4.1. Local One-Dimensional Mass, Stiffness, and Time-Derivative Matrices
We now define the local mass (time derivative) and stiffness (diffusion) matrices. Since test functions and local basis functions are tensor products of 1D hat functions, these matrices can be described as Kronecker products of local 1D mass and stiffness matrices. From Equations (14) and (15), we see that the local 1D mass and stiffness matrices at index k for the variable x is given by
The matrices for other space-intervals, are defined in a similar way. For the local time derivative matrix, , we have the following expression:
Importantly, since we are using a uniform space-time grid, the defined mass and stiffness matrices are the same for each four-dimensional hypercube and do not depend on the index k.
4.2. Local Discretization of the Variational Form
Using these local matrices, we detail the discretization and matricization of each of the bilinear forms in Equation (19). Throughout, we will pick the local basis functions for our test functions .
4.2.1. Discretization of the Time-Derivative Term, , on a Local Four-Dimensional Hypercube
The discrete approximation of the time-derivative term, on the local four-dimensional hypercube, , is
where . For simplification, we suppress the local element index l from the basis functions and afterward, unless otherwise specified. Using the properties of multiple integrals on the Cartesian product mesh and the fact that the space-time local functions are expressed as products of one-dimensional functions, the expression can be compactly expressed using one-dimensional mass, stiffness, and time-derivative matrices via the Kronecker product. When we consecutively use—for —every one of the 16 space-time functions defined on the hypercube , Equation (31) yields 16 equations with 16 unknowns, which, in matrix notation, can be expressed as follows:
where is a column vector containing the unknown components of on .
4.2.2. Discretization of the Diffusion Term, , on the Four-Dimensional Hypercube, with a Constant Diffusion Coefficient,
In this section, we derive the matricization of with , so that the term reduces to . By using (16), and , we can explicitly write locally on as
This result in 16 expressions with 16 unknowns, which in the matrix notation becomes
4.2.3. Discretization of the Diffusion Term, , on the Four-Dimensional Hypercube, with a Non-Constant Diffusion Function
For the variable diffusion coefficient, , we employ the Lagrange interpolation operator defined in (16). Assuming that is well-defined at the nodes of , and once again using , we derive the matricization of as
where are the values of the diffusion function at the nodes of . Here, in contrast to (33), each one-dimensional integration involves the product of one basis function and the gradients of two basis functions. To formulate this in a way that is structurally similar to (34), for each dimension, we introduce the following modified mass and stiffness matrices:
where the index p assumes two values, namely, 0 and 1. For , Equation (35) reduces to a matrix–vector product, where the associated matrix can be constructed by using one-dimensional matrices introduced in (36). Using the properties of multiple integrals on the Cartesian product mesh, and the fact that the space-time local functions are products of one-dimensional functions, we explicitly have
Here, we employ local index m for each element as defined in (13).
4.2.4. Discretization of the Convection Term, , on the Four-Dimensional Hypercube, with a Non-Constant Convection Function
In this section, we derive the matricization of the convection term with variable coefficients. Following the same approach as in (35), using (17) and , becomes
To derive the matrix structure of (38), we introduce the following one-dimensional local space-derivative matrix for each dimension. On the interval , we define
where . By using (39) and (36), we find that
4.2.5. Discretization of the Reaction Term, , on the Four-Dimensional Hypercube
In this section, we build the matricization of the reaction term, , with the variable reaction coefficient. We should note that for a constant reaction coefficient and , the matrix associated with reduces to the mass matrix. In this case, it follows from (29) that
For the variable reaction coefficient, we discretize the reaction term using the Lagrange interpolation operator (16). Again, taking , becomes
Using (36), we derive
4.2.6. Discretization of the Loading Term, , on the Four-Dimensional Hypercube
5. Assembly of Global Matrices
5.1. Assembly for Terms with Constant Coefficients
The local matrix structures of , and can easily be extended to similar global structures when the diffusion, convection, and reaction coefficients are constants. To achieve this, we need to construct the global mass, stiffness, and time-derivative matrices using the local ones for each variable.
First, we construct from (30) the following block matrix, , for the temporal variable. Recall that the time interval is decomposed using uniform intervals . We define
where is defined as in Equation (30). To achieve the proper global assembly of the 1D time derivative matrix, we need to take into account the common boundary points of each interval. This can be accomplished with the help of the binary matrix, :
Then, the global time-derivative matrix, , can be determined as
In a similar fashion, using , we can build the global one-dimensional mass matrices , and . Finally, we obtain the following for :
here, is a global column solution vector of size . Similarly, we build the term :
where is the column load vector of size .
5.2. Assembly for Terms with Variable Coefficients
5.2.1. Assembly of , When the Diffusion Coefficient Depends on Space-Time Variables, but Enables a Separation of Variables
First, let us assume that
, , , and denote the separation of variables of the function , then locally, we have the following (37):
To assemble the global matrix in the x-dimension, let us define the following pairs of local one-dimensional coefficient matrices. For each interval, , we have
and similarly for , and t dimensions. By evaluating at all points of , we define the following pair of global block coefficient matrices in the x-dimension:
Using (39), we construct the global pair of stiffness block matrices as follows:
By using (45), (52)–(54), we construct the global stiffness matrices corresponding to the variable x:
and similarly, the global stiffness matrices , , , and . Now, we focus on the construction of block matrices and , whose diagonal positions consist of local mass matrices (35) as follows:
By using (45), (52), (53), (57), and (58), we construct the global mass matrices corresponding to the variable x as follows:
and similarly for the remaining dimensions. By using the above matrices, we construct the global space-time matricization for the diffusion term as follows:
Furthermore, we highlight that we use the same notation for the global mass and stiffness matrices corresponding to the diffusion, convection, and reaction terms, unless otherwise specified.
5.3. Assembly for the Convection Term , on the Four-Dimensional Hypercube
The coefficient matrices corresponding to the convective part can be constructed following the analogous technique as described in the previous section. First, we write
Moreover, we assume that each component for satisfies the separation of variable conditions. Thus, we have
where denote the separation of variables of the function for each i. Then, we have
We define the following pairs of local one-dimensional coefficient matrices to assemble the global matrix in the x-dimension corresponding to the convective term. On each interval , we have
We follow the same constriction for the y, z, and t dimensions. Using (62),
Using (39), we construct the global pair of derivative block matrices as follows:
The construction of the block matrices consisting of local mass matrices and , follows the same techniques as in Section 5.2.1 (Equations (57) and (58)). Using (45) and (63)–(65), we construct the global derivative matrices corresponding to the x variable as follows:
The matrices , , and are constructed following the same structure as (67). Furthermore, we construct the global mass matrix as (59)
The construction of the mass matrices for the other variables, such as y, z, and t, follows the same techniques as in (68). By using these global matrices corresponding to the variables x,y,z, and t, we derive the low-rank structure of the convective term as follows:
5.4. Assembly for the Reaction Term on the Four-Dimensional Hypercube
5.5. The Global System
Throughout, we assume that , , and c are rank one functions in order to derive expressions for , and . In a general case, we utilize the cross-interpolation technique [51] to approximate the TT format of general functions, which can be interpreted as an approximation in separated-variable form. Hence, the techniques described above can be used to construct the global matrices. Taking into account all expressions , and results in the following system of equations:
Finally, to deal with boundary conditions, we reformulate the system in Equation (71) to only include interior nodes:
where is the boundary term incorporating the boundary and initial conditions. To implement the boundary conditions in the TT format, we reduce the linear system to hold only for interior nodes, while the boundary conditions are imposed on the boundary nodes, and the corresponding columns in (71) are subtracted from the right-hand side of the equation. As a result, the load vector is modified to account for the boundary conditions. This standard approach is implemented in the TT format via matrix–vector multiplication [34]. More details of this formulation are described in [12] (Section 2.2.4).
6. Tensorization of the Weak-Form of CDR
6.1. Transformation of the CDR Discretization into TT and QTT Formats
To solve the CDR equation with coefficients , , and , along with boundary conditions, initial conditions, and loading functions that do not allow separation of variables, we use TT-cross to construct the TT format directly from these inputs. The space-time discretization process leads to the formulation of a linear system for all interior nodes, as outlined in Equation (72). For simplicity, we will omit part of the indices and refer to this equation as follows: , where represents the operator matrix, is the solution vector, is the loading term, and accounts for the boundary and initial conditions. In the following section, we will provide a detailed explanation of how to construct the TT and QTT formats for each component of this linear system, utilizing the following three steps:
where and are formulated using , and loading terms such as , which are expressed in and tensor formats.
6.2. Construction of the TT Format for Linear System Components
Given that the operators in their matrix representations exhibit the Kronecker product structures, as derived in Section 2, their TT formats can be constructed by employing component matrices as TT-cores; see Equation (28). To construct the TT format of the operators acting on the interior nodes, we first need to define some sets of indices:
- TT format of , : From the formulation in Equation (47), the global temporal operator in the TT-matrix format acting only on the interior nodes is constructed as follows:where the tensor product operator ∘ is defined in Appendix A.
- TT format of , : From the formulation in Equation (60), the diffusion operator in the TT-matrix format is constructed as follows:
- TT format of , : Following the formulation in Equation (69), the convection operator in the TT-matrix format is constructed as follows:
- TT format of , : Following the formulation in Equation (70), the reaction term is constructed as follows:
- TT format of , : From Equation (48), the loading term is constructed as follows:The TT format of the loading term is approximated by the cross-interpolation algorithm [52].
- TT format of the boundary term, : The boundary and initial conditions are enforced by the boundary term, which will map from all nodes to only interior nodes. In fact, we constructed a map that enforces the boundary condition in each equation of the system only corresponding to the interior nodes. This approach is very convenient for the TT modification, as it only requires matrix–vector multiplication. The detailed construction of is included in Appendix B.
6.3. Construction of the QTT Format for Linear System Components
Given the banded structure of the component matrices, they can be further compressed through transformation into the QTT format [28]. We will proceed with the construction of the QTT format. The idea is to first convert the component matrices into QTT format and then link them together, as in the case of the TT format. This algorithm is described in [34] (Algorithm 1).
At this point, we have completed constructing the TT format and QTT format of the linear system in Equation (73). To solve the TT/QTT linear system using tensor network optimization techniques, we employed the MATLAB TT-Toolbox [52].
7. Extension of the Method to Higher Orders and Dimensions
In this section, we briefly show how the proposed technique can be extended to arbitrary order and arbitrary dimension d. We define the set of basis functions on the interval as follows:
where each for is a polynomial of degree , and satisfies the property on each node on . For simplification, we avoid specifying the interval k. On , we define the mass and stiffness matrices corresponding to a single variable, x, as follows:
By using (80), we generate the discretization of as follows:
where and are the mass and stiffness matrices corresponding to the variable for . denotes a column vector of size on each cell containing the components of on . Similarly, we construct the matrix corresponding to the inner-product on , i.e., as follows:
In fact, we can extend the tensorization of various terms, including the variable coefficients, adopting the same technique. Thus, we emphasize that our method is very convenient for the simulation of multi-dimensional PDEs. Moreover, the equalities (81) and (82) are exact, and the practical implementation of these terms involves only quadrature error, which can be minimized by selecting an appropriate quadrature rule. However, for higher-order quadrilateral elements, the interpolation matrix associated with Lagrange basis functions can become ill-conditioned, leading to numerical instability in solving the resulting systems of equations, especially for large-scale problems. Preconditioning techniques can help mitigate these issues. Furthermore, in [53], the authors discussed the QTT-FEM for the wave equation by employing a hierarchical basis. However, the system becomes ill-conditioned for higher-order approximation. They used preconditioning to demonstrate that the system is uniformly well-conditioned. This technique could be helpful for higher-order approximations in our methods and will be explored in future work.
8. Numerical Experiments
In this section, we discuss a series of numerical experiments to assess the performance of our proposed tensor-network space-time finite element method in both the TT and QTT formats. All simulations were conducted using MATLAB R2022b software running on a Linux operating system equipped with a 2.1 GHz Intel Gold 6152 processor. Moreover, in all numerical experiments, we chose a TT truncation tolerance smaller than the approximation error in the TT construction. We compared the performance of TT and QTT solvers against the full-grid solver, which performed calculations on full tensors. Furthermore, we computed the relative error in the norm for all numerical experiments. We report the error quantity as follows:
We used linear polynomials for all experiments; consequently, we have observed a quadratic order of convergence ([20], Figure 3). Furthermore, we highlight that in Theorem 4, we proved the convergence estimate in the norm. The theory does not cover convergence analysis in the norm. However, from the interpolation estimate (18), we expect an optimal order of convergence in the norm.
8.1. TT-Ranks of the Diffusion Operator
Here, we explore how the TT-ranks of the diffusion operator in the TT format vary with four different coefficient functions . We chose to conduct this investigation because the TT-ranks of the diffusion operator might not be expected to remain low, given the complex assembly process described in Equation (75). The chosen coefficient functions have varying TT-ranks to illustrate their impact on the TT-ranks of the diffusion operator. Moreover, these functions possess exact TT-ranks that are independent of the grid size. The function , however, demonstrates more complex behavior, with TT-ranks that vary depending on the selected TT truncation tolerance, while still remaining independent of the grid size.
The results from Table 1 show that when the coefficient function is simply , the TT-ranks of the global diffusion operator are surprisingly low at across three discretization grid sizes. Despite the complex assembly process in FEM, this demonstrates that the global diffusion operator itself possesses a low-rank structure, which depends on the rank of the diffusion function and its rank. In general, we observe that the TT-ranks of the diffusion operator increase at a rate that is, at most, twice the TT-ranks of the coefficient function . Moreover, the number of elements per dimension does not affect the TT-ranks, which will lead to better compression on a larger grid. This result suggests a relationship between the complexity of the coefficient function and the rank of the resulting global diffusion operator in the TT format.

Table 1.
TT-ranks of the diffusion operator. The results show the connection between the TT-ranks of the diffusion coefficient function —calculated via TT-cross interpolation with a truncation error (TT-tol)—and the TT-ranks of the diffusion operator (i.e., the operator on the left-hand side of Equation (83) in discrete form). Here, the number of elements is , and each element, , has nodes.
8.2. Three-Dimensional Poisson Equation
Next, we demonstrate the performance of the TT and QTT solvers on the 3D Poisson equation:
and with the manufactured solution on the computational domain with -rank 1, and . The loading term and the boundary conditions are computed in a way to enforce the manufactured solution. We compute the solutions with three different solvers, namely, the full-grid solver, TT solver, and QTT solver.
The performance of the three solvers is shown in Table 2 and Figure 4, with the convergence analysis in the left panel, the computational cost in the middle panel, and the compression ratios of the TT and QTT formats in the right panel. Figure 4 (left) illustrates that both the TT and QTT formats maintain the same level of accuracy, with second-order convergence, as the full-grid solver up to a grid size of 33 elements per dimension. Beyond this point, the full-grid solver requires more memory than is available. Both the TT and QTT solvers were able to run simulations on finer grids while successfully maintaining the convergence rate.

Table 2.
Comparison of the relative numerical error, execution time, and compression ratio for the 3D Poisson problem using the full grid, TT, and QTT solvers. Full grid reports error and time only, while TT and QTT include operator compression ratios (defined as the storage size relative to the full tensor).
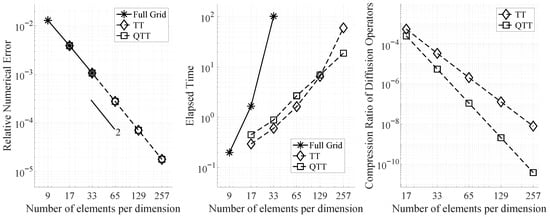
Figure 4.
Performance of the full-grid, TT, and QTT solvers on the 3D Poisson equation.
Figure 4 (middle) illustrates the computational time required by all three solvers. As expected, the full-grid solver is the most computationally expensive, with much steeper scaling compared to the TT and QTT solvers. When comparing the TT and QTT solvers, the TT solver is slightly faster for smaller grids, but begins to show steeper scaling compared to the QTT solver at grid sizes of 129 and 257 elements per dimension.
Figure 4 (right) displays the compression ratio of the diffusion operators in TT and QTT formats across different grid sizes. The compression ratio is defined as the ratio of the number of elements in the TT or QTT formats to the number of elements in the full tensor. The plot indicates that the QTT format becomes increasingly efficient compared to the TT format as the grid size grows. For smaller grids, the compression achieved by the QTT format is similar to that of the TT format, which explains why the QTT solver is slightly slower than the TT solver at these grid sizes. This is because, at similar levels of compression, the QTT format involves calculations with more dimensions, making it more computationally demanding than the TT algorithm. However, as the compression advantage of the QTT format becomes more pronounced (about 2 orders of magnitude better at the grid size of 129), its computational efficiency starts to outweigh that of the TT format, reflected in the reduced computational time.
Furthermore, the performance crossover between TT and QTT formats is primarily due to the scaling behavior of compression and arithmetic complexity. At small grid sizes, the TT format is faster because it involves fewer dimensions (four cores for space-time), resulting in less overhead during construction and computation. In contrast, the QTT format introduces more TT-cores due to binary decomposition, which increases setup costs at small scales. However, as the number of elements increases, QTT exhibits significantly better compression ratios because it captures hierarchical and structured patterns more effectively, especially for operators with regular banded structures (e.g., stiffness matrices). This leads to much lower TT-ranks in QTT format for large problems, reducing both memory and computational costs. Furthermore, QTT operations scale logarithmically with the problem size compared to polynomial scaling in standard TT. As a result, at larger scales, the benefits of deeper compression and lower ranks outweigh the initial overhead, making QTT more efficient than TT.
8.3. Three-Dimensional CDR Equation
In this experiment, we investigate the performance of TT and QTT solvers in solving a 3D convection–diffusion–reaction equation with inhomogeneous boundary conditions.
where , , and . Here, it is clear that the convective field satisfies the divergence-free condition, i.e., , and therefore, (see (6)). The manufactured solution is with -rank 2 and the space-time computational domain is .
The performance of three solvers (full grid, TT, and QTT) is presented in Table 3 and Figure 5, with convergence shown in the left panel, computational cost in the middle panel, and compression ratios in the TT and QTT formats displayed in the right panel.

Table 3.
Performance comparison for Test Case 2: Time-dependent convection–diffusion–reaction (CDR) equation in three spatial dimensions. The table reports the relative numerical error, runtime, and compression ratio of the diffusion operator for the full grid, TT, and QTT solvers. The TT and QTT methods show improved scalability through low-rank tensor representations, while full grid results are shown where computationally feasible.
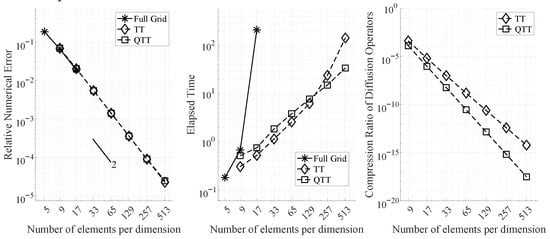
Figure 5.
Performance of the full-grid, TT, and QTT solvers on the 3D CDR equation with the manufactured solution.
Figure 5 (left) demonstrates that both the TT and QTT formats maintain a similar level of accuracy as the full-grid solver, with second-order convergence, consistent with the findings from the first experiment. Up to a grid size of 17 elements per dimension, all solvers perform comparably. However, beyond this point, the full-grid solver becomes infeasible due to memory limitations. In contrast, both the TT and QTT solvers continue to perform on finer grids, preserving the convergence rate even at higher resolutions.
Figure 5 (middle) shows the computational time required by the three solvers. The full-grid solver is the most expensive, exhibiting significantly steeper scaling with increasing grid size. When comparing the TT and QTT solvers, they initially perform comparably on smaller grids. However, as the grid size increases to 257 and 513 elements per dimension, the QTT solver’s scaling becomes less steep, eventually overtaking the TT solver in computational efficiency.
Figure 5 (right) illustrates the behavior of the diffusion operators in TT and QTT formats across different grid sizes. The results show that the QTT format becomes increasingly more effective as the grid size increases. For example, at the grid size of 513 elements per dimension, the compression of the QTT format is 4 orders of magnitude lower compared to the compression of the TT format.
Given that this is a 4D problem, the TT and QTT solvers show superior efficiency compared to the full-grid solver, which potentially allows for much faster and more accurate simulations at much higher resolutions. Furthermore, we highlight that the space-time scheme provides a better numerical approximation than the time-stepping scheme. Interested readers may refer to [12,54] for a comparison between the space-time scheme and the time-stepping scheme.
8.4. Three-Dimensional CDR Equation with a Nonlinear Loading Term
In this section, we present numerical results for a simplified semiconductor problem, where the drift-diffusion physics is replaced with a Poisson–Boltzmann equation approximation [55]. In this example, we benchmark the performance of the TT and QTT solvers on a three-dimensional nonlinear equation:
with the computational domain , and the manufactured solution,
with -rank 2. The output of the discretization process is a nonlinear equation in TT format, given as follows:
where and . The QTT format of this equation can be achieved by using the process described above in Section 6.3.
The nonlinear TT/QTT equation is solved using the step truncation TT-Newton method developed in [22] (Algorithm 1), with the loss function defined as follows:
The Jacobian of this matrix function is explicitly computable. Figure 6 compares three solvers for this nonlinear problem, showing convergence (left panel), the computational cost (middle panel), and the number of Newton iterations (right panel). The data is shown in Table 4. The diffusion operator compression for the TT and QTT solvers is not shown, as it is similar to that in the third experiment.
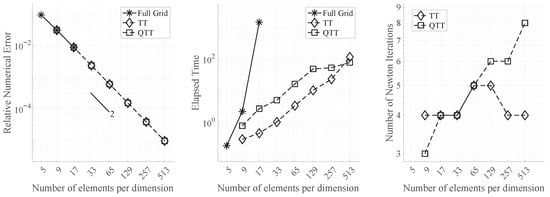
Figure 6.
Performance of the full-grid, TT, and QTT solvers on the 3D nonlinear equation with the manufactured solution.

Table 4.
Performance comparison for Test Case 3: nonlinear 3D time-dependent equation solved using the full grid, TT, and QTT solvers. The table reports the relative numerical error, runtime, and number of Newton iterations. The full grid results are shown only for smaller sizes due to memory limitations.
Figure 6 (left) demonstrates that both TT and QTT maintain accuracy comparable to the full-grid solver up to 17 elements per dimension, beyond which the full-grid solver becomes memory-infeasible. As expected, the TT and QTT solvers efficiently handle finer grids and preserve second-order convergence rates.
Figure 6 (middle) presents the computational time, where the full-grid solver is the most expensive. The TT solver is initially faster for smaller grids, but QTT shows better scaling at larger grid sizes (257 and 513 elements per dimension).
However, as shown in Figure 6 (right), at larger grid sizes (257 and 513), the QTT solver requires a greater number of Newton iterations to converge. For example, at a grid size of 513, QTT requires 8 iterations compared to 4 iterations for the TT solver. This results in QTT being twice as fast in terms of computational time per Newton iteration at this grid size. The results suggest that QTT and TT solvers may take distinct paths to convergence, which is intriguing and likely linked to the choice of truncation errors in these formats. This relationship is particularly important, as prior research has demonstrated that the selection of TT truncation errors significantly influences both the efficiency and accuracy of TT-format PDE solvers [22,56,57,58,59]. This observed difference in solver behavior certainly deserves a more detailed investigation and thorough analysis.
9. Conclusions
In conclusion, we developed a Galerkin TT/QTT space-time formulation specifically tailored to the finite element discretization of convection–diffusion–reaction equations. This approach includes a detailed construction of finite element discrete operators in both TT and QTT formats, accommodating general coefficient functions. By leveraging the QTT format, we have effectively compressed the discrete operators while addressing the banded structure, leading to enhanced computational efficiency. Our numerical experiments demonstrate that our mixed approach not only achieves significant speedup but also significantly reduces memory usage, enabling high-resolution simulations to be conducted in a much shorter time. These advancements highlight the potential of our approach to tackle more complex and large-scale problems efficiently. Moving forward, future work will focus on extending this framework to address nonlinear partial differential equations and adapting it for application to more complex domains, thereby broadening the scope and impact of this method in computational science and engineering.
We also plan to develop a discontinuous Petrov–Galerkin (DPG) formulation—of the type introduced by Demkowicz and Gopalakrishnan [60,61]—by employing the so-called mixed formulation of DPG (see Roberts et al. [62], Appendix A.5.1). The mixed formulation will enable the application of TT formats by preserving the tensor-product structure of the basis functions; the mixed formulation avoids explicit computation of DPG’s optimal test functions and computes an explicit error-representation function, which can be used to evaluate the accuracy of the solution. In the TT context, the latter could enable an iterative refinement approach, whereby error estimates are used to determine the placement of refined elements in the appropriate 1D mesh components. DPG has previously been applied to steady convection–diffusion–reaction problems [8], and to space-time convection [63] and convection–reaction problems [64]. A DPG-based TT formulation of space-time convection–diffusion–reaction can be expected to provide excellent stability properties, even on coarse meshes and for challenging problems.
Author Contributions
Conceptualization, D.A., D.P.T., R.V., S.D., D.D., N.V.R., K.Ø.R. and B.S.A.; methodology, D.A., D.P.T., R.V., S.D., D.D., N.V.R., K.Ø.R. and B.S.A.; writing—original draft, D.A., D.P.T., R.V., S.D., D. D., N.V.R., K.Ø.R. and B.S.A.; writing—review and editing, D.A., D.P.T., R.V., S.D., D.D., N.V.R., K.Ø.R. and B.S.A.; supervision, K.Ø.R. and B.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Laboratory Directed Research and Development (LDRD) project number 20230067DR.
Data Availability Statement
The data that support the findings of this research are available from the corresponding author upon reasonable request.
Acknowledgments
The authors gratefully acknowledge the support of the Laboratory Directed Research and Development (LDRD) program of Los Alamos National Laboratory under project number 20230067DR. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (contract no. 89233218CNA000001). The authors gratefully acknowledge the support of the Laboratory Directed Research and Development (LDRD) program of Sandia. Sandia National Laboratories is a multimission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government. This article has been authored by an employee of National Technology & Engineering Solutions of Sandia, LLC under Contract No. DE-NA0003525 with the U.S. Department of Energy (DOE). The employee owns all right, title and interest in and to the article and is solely responsible for its contents. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this article or allow others to do so, for United States Government purposes. The DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (https://www.energy.gov/downloads/doe-public-access-plan, accessed on 8 July 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Notations and Definitions
Appendix A.1. Notation Table

Table A1.
Summary of notation.
Table A1.
Summary of notation.
| Symbol | Description |
|---|---|
| Spatial domain in | |
| or | Time interval |
| Space-time domain | |
| U | Trial space: |
| V | Test space: |
| Discrete projection operator | |
| Nodal basis functions | |
| TT | Tensor-Train format |
| QTT | Quantized Tensor-Train format |
| TT-core tensor in TT decomposition | |
| TT-rank between the k-th and -th TT-core | |
| norm | |
| TT Tensor format of solution | |
| QTT Tensor format of solution | |
| Lagrange interpolation operator | |
| Loss function in TT-Newton method | |
| Partial derivative of u with respect to time t |
Appendix A.2. Kronecker Product
The Kronecker product ⨂ of matrix and matrix is the matrix of size , defined as follows:
Equivalently, it holds that , where , , with , , , and .
Appendix A.3. The Tensor Product
The tensor product of matrix and matrix produces the four-dimensional tensor of size , with the following elements:
for , , , .
Appendix B. TT Format Construction of the Boundary Term F bd,TT
The boundary term is computed as
where
Next, we will show how to construct each component We redefine the sets of indices and where N is the number of elements per dimension. Then the TT format of each component is constructed as follows:
Next, we describe the construction of the tensor . The full grid tensor is a tensor, where only the initial and boundary elements are nonzero, with all other elements being zeros. The tensor in TT format is then constructed using the cross-interpolation technique.
Finally, the TT format of the boundary term is computed as .
Appendix C. QTT Format Construction
Appendix D. Discrete Inf-Sup Condition
This appendix establishes the discrete inf-sup condition for the finite element discretization of the time-dependent CDR equation. Namely, we establish the mesh-independence result of Theorem 3. Recall that , , and , are the finite-dimensional subspaces specified by the finite elements. The goal is to show that the following discrete stability condition holds:
where C is a positive constant that depends on the regularity of , , and , but independent of mesh size h. As in the text, we define
for and . We assume the coefficients , and c satisfy the conditions ensuring coercivity and continuity. In the continuous case, the coercivity constant can be expressed as follows:
Indeed, using the identity , we can write the following:
The continuous variational problem
is then well defined. The projection operator is defined by , where and z satisfy,
By assumption of coercivity and continuity, is well defined and bounded by the Lax–Milgram theorem [5].
Appendix D.1. Construction of Approximate Projection Operator
For , recall is defined as
where is the Lagrange interpolation operator defined in (16). We also recall Definition (20)
We define the approximate projection operator, [65] by , where and satisfy the following:
To prove that the definition (A20) is well-defined, we first will prove that is coercive.
Lemma A1.
The discrete bilinear form, is coercive, that is, there exists a positive constant , such that
Moreover, this constant is independent of mesh size h for all sufficiently small h.
Proof.
The proof will follow the set of steps outlined in Equation (A16). Notice that we have
Previously, at the continuous level, integration by parts was applied to the diffusive term to write the whole expression in terms of and . In this discrete case, we instead need to perform some approximations. We write
By assumption, and . Therefore, . Hence, we get
We now provide bounds for the other two integral terms. To this end, note that applying the Cauchy–Schwarz inequality yields
From the approximation property of in norm [66] (Corollary (4.4.24)), we get
where the second inequality comes from Poincaré’s inequality. Similarly, we observe that
Letting , we therefore have
This holds for every h. Hence, for sufficiently small h, we can pick a constant so that . This completes the proof. □
Appendix D.2. Proof of Theorem 3
We now provide the Proof of the inf-sup condition. First, we recall the mesh dependent norm
Theorem A1.
Let , and be the discrete space satisfying , and we assume that (6) is satisfied. Then the following discrete stability condition holds
where C is a positive constant that depends on the regularity of , , and , but independent of mesh size h.
Proof.
For each , we use the projection operator, , defined in (A20),
That is, for all . Since , we conclude that . We will show that there is a test function such that , so that the inf-sup stability condition holds. Since , it follows from Lemma A1 that
Note that is bounded. Specifically for and we have
For simplicity, we denote
Using the definition of , the coercivity of , as well as (A33), we derive that
Next, by using Young’s inequality (), and using ; ; and , we have
Hence, we have
Now, we can put it all together. Breaking up the bilinear form and using (A32) and (A37), we get
Dropping the positive term yields
Furthermore, using the expressions of and , (A15) and (A34), we can assume that for specific , and , we can choose, . For this choice, we obtain
This completes the proof of the discrete inf-sup condition. □
In the above proof, we have made the constant appearing in the discrete inf-sup condition positive for sufficiently small values of mesh size h. This technique is quite standard since implies a small value. Thus, we conclude that our proposed scheme is discrete inf-sup stable and has a unique solution. In the discrete scheme, we have considered the interpolation of the coefficients instead of direct computation. This technique is well known in finite elements and virtual elements for the analysis of nonlinear PDEs [67,68], and is referred to as the finite element method/virtual element method with interpolated coefficients.
Appendix E. Convergence Analysis (Proof of Theorem 4)
In this section, we will estimate the error . To do that, we need the following result:
Lemma A2.
Let be a given function with a homogeneous boundary condition and , and let be the interpolation operator as defined in (17). Then the following estimate holds:
where C is a positive constant independent of h.
Proof.
The proof is followed by discrete inf-sup conditions and the discrete continuity property of the stationary part of (2). For detailed proof, we refer [20] (Theorem 4.4). □
Next, we start the main proof of Theorem 4.
Proof.
Let , since , by using the discrete inf-sup condition (Theorem 3), we have
By using (19), we write
Now, we bound the differences and on the right-hand side of (A42). By using the approximation property of , we bound the term as follows
Now, we focus on constructing a suitable Ritz-type projection operator [30] (Theorem 3.3), by
Since satisfies the discrete inf-sup condition, and is a bounded functional on , (A45) is well defined. By using the approximation property of the Lagrange interpolation operator (Lemma A2), we derive that
By choosing in (24), where is the elliptic projection operator as defined in (A45), and boundedness of , we conclude that
where u, and are the continuous and discrete solutions satisfying (2), and (19) respectively. Upon using , we split the error as follows
From Equation (A29), we have
By setting , and using (A43), (A48), we deduce from (A41) that
By inserting (A46), and (A49) in (A47), we derive that
By the definition of in (A45) and the choice of , we have . This completes the proof. □
References
- John, V.; Schmeyer, E. Finite element methods for time-dependent convection–diffusion–reaction equations with small diffusion. Comput. Methods Appl. Mech. Eng. 2008, 198, 475–494. [Google Scholar] [CrossRef]
- John, V.; Novo, J. Error analysis of the SUPG finite element discretization of evolutionary convection-diffusion-reaction equations. SIAM J. Numer. Anal. 2011, 49, 1149–1176. [Google Scholar] [CrossRef]
- Roos, H.G. Robust Numerical Methods for Singularly Perturbed Differential Equations; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Knobloch, P.; Tobiska, L. The P 1 mod element: A new nonconforming finite element for convection-diffusion problems. SIAM J. Numer. Anal. 2003, 41, 436–456. [Google Scholar] [CrossRef]
- Ciarlet, P.G. The Finite Element Method for Elliptic Problems; SIAM: Philadelphia, PA, USA, 2002. [Google Scholar]
- Shu, C.W. Discontinuous Galerkin methods: General approach and stability. Numer. Solut. Partial Differ. Equ. 2009, 201, 149–201. [Google Scholar]
- Ayuso, B.; Marini, L.D. Discontinuous Galerkin methods for advection-diffusion-reaction problems. SIAM J. Numer. Anal. 2009, 47, 1391–1420. [Google Scholar] [CrossRef]
- Bui-Thanh, T.; Demkowicz, L.; Ghattas, O. A unified discontinuous Petrov–Galerkin method and its analysis for Friedrichs’ systems. SIAM J. Numer. Anal. 2013, 51, 1933–1958. [Google Scholar] [CrossRef]
- Houston, P.; Roggendorf, S.; van der Zee, K.G. Eliminating Gibbs phenomena: A non-linear Petrov–Galerkin method for the convection–diffusion–reaction equation. Comput. Math. Appl. 2020, 80, 851–873. [Google Scholar] [CrossRef]
- da Veiga, L.B.; Dassi, F.; Lovadina, C.; Vacca, G. SUPG-stabilized virtual elements for diffusion-convection problems: A robustness analysis. ESAIM Math. Model. Numer. Anal. 2021, 55, 2233–2258. [Google Scholar] [CrossRef]
- Gharibi, Z.; Dehghan, M. Convergence analysis of weak Galerkin flux-based mixed finite element method for solving singularly perturbed convection-diffusion-reaction problem. Appl. Numer. Math. 2021, 163, 303–316. [Google Scholar] [CrossRef]
- Adak, D.; Truong, D.P.; Manzini, G.; Rasmussen, K.O.; Alexandrov, B.S. Tensor Network Space-Time Spectral Collocation Method for Time Dependent Convection-Diffusion-Reaction Equations. arXiv 2024, arXiv:2402.18073. [Google Scholar] [CrossRef]
- Arrutselvi, M.; Natarajan, E.; Natarajan, S. Virtual element method for the quasilinear convection-diffusion-reaction equation on polygonal meshes. Adv. Comput. Math. 2022, 48, 78. [Google Scholar] [CrossRef]
- Boffi, D.; Brezzi, F.; Fortin, M. Mixed Finite Element Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2013; Volume 44. [Google Scholar]
- Steinbach, O. Numerical Approximation Methods for Elliptic Boundary Value Problems: Finite and Boundary Elements; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Andreev, R. Stability of sparse space–time finite element discretizations of linear parabolic evolution equations. IMA J. Numer. Anal. 2013, 33, 242–260. [Google Scholar] [CrossRef]
- Stevenson, R.; Westerdiep, J. Stability of Galerkin discretizations of a mixed space–time variational formulation of parabolic evolution equations. IMA J. Numer. Anal. 2021, 41, 28–47. [Google Scholar] [CrossRef]
- Langer, U.; Steinbach, O.; Tröltzsch, F.; Yang, H. Space-time finite element discretization of parabolic optimal control problems with energy regularization. SIAM J. Numer. Anal. 2021, 59, 675–695. [Google Scholar] [CrossRef]
- Cangiani, A.; Dong, Z.; Georgoulis, E.H. hp-version space-time discontinuous Galerkin methods for parabolic problems on prismatic meshes. SIAM J. Sci. Comput. 2017, 39, A1251–A1279. [Google Scholar] [CrossRef]
- Gomez, S.; Mascotto, L.; Moiola, A.; Perugia, I. Space-time virtual elements for the heat equation. SIAM J. Numer. Anal. 2024, 62, 199–228. [Google Scholar] [CrossRef]
- Gómez, S.; Mascotto, L.; Perugia, I. Design and performance of a space-time virtual element method for the heat equation on prismatic meshes. Comput. Methods Appl. Mech. Eng. 2024, 418, 116491. [Google Scholar] [CrossRef]
- Adak, D.; Danis, M.; Truong, D.P.; Rasmussen, K.Ø.; Alexandrov, B.S. Tensor Network Space-Time Spectral Collocation Method for Solving the Nonlinear Convection Diffusion Equation. arXiv 2024, arXiv:2406.02505. [Google Scholar]
- Krebs, J.R.; Anderson, J.E.; Hinkley, D.; Neelamani, R.; Lee, S.; Baumstein, A.; Lacasse, M.D. Fast full-wavefield seismic inversion using encoded sources. Geophysics 2009, 74, WCC177–WCC188. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Leugering, G.; Benner, P.; Engell, S.; Griewank, A.; Harbrecht, H.; Hinze, M.; Rannacher, R.; Ulbrich, S. Trends in PDE Constrained Optimization; Springer: Cham, Switzerland, 2014; Volume 165. [Google Scholar]
- Gunzburger, M.D.; Peterson, J.S.; Shadid, J.N. Reduced-order modeling of time-dependent PDEs with multiple parameters in the boundary data. Comput. Methods Appl. Mech. Eng. 2007, 196, 1030–1047. [Google Scholar] [CrossRef]
- Oseledets, I.; Tyrtyshnikov, E. TT-cross approximation for multidimensional arrays. Linear Algebra Its Appl. 2010, 432, 70–88. [Google Scholar] [CrossRef]
- Kazeev, V.A.; Khoromskij, B.N.; Tyrtyshnikov, E.E. Multilevel Toeplitz matrices generated by tensor-structured vectors and convolution with logarithmic complexity. SIAM J. Sci. Comput. 2013, 35, A1511–A1536. [Google Scholar] [CrossRef]
- Kornev, E.; Dolgov, S.; Perelshtein, M.; Melnikov, A. TetraFEM: Numerical Solution of Partial Differential Equations Using Tensor Train Finite Element Method. Mathematics 2024, 12, 3277. [Google Scholar] [CrossRef]
- Steinbach, O. Space-time finite element methods for parabolic problems. Comput. Methods Appl. Mat. 2015, 15, 551–566. [Google Scholar] [CrossRef]
- Schwab, C.; Stevenson, R. Space-time adaptive wavelet methods for parabolic evolution problems. Math. Comput. 2009, 78, 1293–1318. [Google Scholar] [CrossRef]
- Oseledets, I.V. Tensor-train decomposition. SIAM J. Sci. Comput. 2011, 33, 2295–2317. [Google Scholar] [CrossRef]
- Bachmayr, M.; Schneider, R.; Uschmajew, A. Tensor networks and hierarchical tensors for the solution of high-dimensional partial differential equations. Found. Comput. Math. 2016, 16, 1423–1472. [Google Scholar] [CrossRef]
- Truong, D.P.; Ortega, M.I.; Boureima, I.; Manzini, G.; Rasmussen, K.O.; Alexandrov, B.S. Tensor networks for solving the time-independent Boltzmann neutron transport equation. J. Comput. Phys. 2024, 507, 112943. [Google Scholar] [CrossRef]
- Goreinov, S.A.; Tyrtyshnikov, E.E.; Zamarashkin, N.L. A theory of pseudoskeleton approximations. Linear Algebra Appl. 1997, 261, 1–21. [Google Scholar] [CrossRef]
- Mahoney, M.W.; Drineas, P. CUR matrix decompositions for improved data analysis. Proc. Natl. Acad. Sci. USA 2009, 106, 697–702. [Google Scholar] [CrossRef] [PubMed]
- Goreinov, S.A.; Oseledets, I.V.; Savostyanov, D.V.; Tyrtyshnikov, E.E.; Zamarashkin, N.L. How to find a good submatrix. In Matrix Methods: Theory, Algorithms and Applications: Dedicated to the Memory of Gene Golub; World Scientific: Singapore, 2010; pp. 247–256. [Google Scholar]
- Mikhalev, A.; Oseledets, I.V. Rectangular maximum-volume submatrices and their applications. Linear Algebra Appl. 2018, 538, 187–211. [Google Scholar] [CrossRef]
- Savostyanov, D.; Oseledets, I. Fast adaptive interpolation of multi-dimensional arrays in tensor train format. In Proceedings of the The 2011 International Workshop on Multidimensional (nD) Systems, Poitiers, France, 5–7 September 2011; pp. 1–8. [Google Scholar]
- Oseledets, I.V.; Savostianov, D.V.; Tyrtyshnikov, E.E. Tucker dimensionality reduction of three-dimensional arrays in linear time. SIAM J. Matrix Anal. Appl. 2008, 30, 939–956. [Google Scholar] [CrossRef]
- Sozykin, K.; Chertkov, A.; Schutski, R.; Phan, A.H.; Cichoki, A.S.; Oseledets, I. TTOpt: A maximum volume quantized tensor train-based optimization and its application to reinforcement learning. Adv. Neural. Inf. Process Syst. 2022, 35, 26052–26065. [Google Scholar]
- Savostyanov, D.V. Quasioptimality of maximum-volume cross interpolation of tensors. Linear Algebra Its Appl. 2014, 458, 217–244. [Google Scholar] [CrossRef]
- Holtz, S.; Rohwedder, T.; Schneider, R. The alternating linear scheme for tensor optimization in the tensor train format. SIAM J. Sci. Comput. 2012, 34, A683–A713. [Google Scholar] [CrossRef]
- Oseledets, I.V.; Dolgov, S.V. Solution of linear systems and matrix inversion in the TT-format. SIAM J. Sci. Comput. 2012, 34, A2718–A2739. [Google Scholar] [CrossRef]
- Dolgov, S.V.; Savostyanov, D.V. Alternating minimal energy methods for linear systems in higher dimensions. SIAM J. Sci. Comput. 2014, 36, A2248–A2271. [Google Scholar] [CrossRef]
- Dolgov, S.; Savostyanov, D. Parallel cross interpolation for high-precision calculation of high-dimensional integrals. Comput. Phys. Commun. 2019, 246, 106869. [Google Scholar] [CrossRef]
- Kazeev, V.; Reichmann, O.; Schwab, C. Low-rank tensor structure of linear diffusion operators in the TT and QTT formats. Linear Algebra Its Appl. 2013, 438, 4204–4221. [Google Scholar] [CrossRef]
- Khoromskij, B.N.; Oseledets, I.V. QTT approximation of elliptic solution operators in higher dimensions. Russ. J. Numer. Anal. Math. Model. 2011, 26, 303–322. [Google Scholar] [CrossRef]
- Vysotsky, L.; Rakhuba, M. Tensor rank bounds and explicit QTT representations for the inverses of circulant matrices. Numer. Linear Algebra Appl. 2023, 30, e2461. [Google Scholar] [CrossRef]
- Kazeev, V.A.; Khoromskij, B.N. Low-rank explicit QTT representation of the Laplace operator and its inverse. SIAM J. Matrix Anal. Appl. 2012, 33, 742–758. [Google Scholar] [CrossRef]
- Oseledets, I.V. Approximation of 2d × 2d matrices using tensor decomposition. SIAM J. Matrix Anal. Appl. 2010, 31, 2130–2145. [Google Scholar] [CrossRef]
- Oseledets, I. TT-Toolbox, Version 2.2. 2023. Available online: https://github.com/oseledets/TT-Toolbox (accessed on 8 July 2025).
- Fraschini, S.; Kazeev, V.; Perugia, I. Symplectic QTT-FEM solution of the one-dimensional acoustic wave equation in the time domain. arXiv 2024, arXiv:2411.11321. [Google Scholar]
- Dolgov, S.V.; Khoromskij, B.N.; Oseledets, I.V. Fast solution of parabolic problems in the tensor train/quantized tensor train format with initial application to the Fokker–Planck equation. SIAM J. Sci. Comput. 2012, 34, A3016–A3038. [Google Scholar] [CrossRef]
- Holst, M.J. Multilevel Methods for the Poisson-Boltzmann Equation. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 1993. [Google Scholar]
- Rodgers, A.; Dektor, A.; Venturi, D. Adaptive integration of nonlinear evolution equations on tensor manifolds. J. Sci. Comput. 2022, 92, 39. [Google Scholar] [CrossRef]
- Rodgers, A.; Venturi, D. Implicit integration of nonlinear evolution equations on tensor manifolds. J. Sci. Comput. 2023, 97, 33. [Google Scholar] [CrossRef]
- Danis, M.E.; Truong, D.; Boureima, I.; Korobkin, O.; Rasmussen, K.; Alexandrov, B. Tensor-Train WENO Scheme for Compressible Flows. arXiv 2024, arXiv:2405.12301. [Google Scholar] [CrossRef]
- Danis, M.E.; Truong, D.P.; DeSantis, D.; Petersen, M.; Rasmussen, K.O.; Alexandrov, B.S. High-order Tensor-Train Finite Volume Method for Shallow Water Equations. arXiv 2024, arXiv:2408.03483. [Google Scholar] [CrossRef]
- Demkowicz, L.; Gopalakrishnan, J. A Class of Discontinuous Petrov-Galerkin Methods. Part I: The Transport Equation. Comput. Methods Appl. Mech. Eng. 2010, 199, 1558–1572. [Google Scholar] [CrossRef]
- Demkowicz, L.; Gopalakrishnan, J. A class of discontinuous Petrov–Galerkin methods. Part II: Optimal test functions. Numer. Methods Partial Differ. Equ. 2011, 27, 70–105. [Google Scholar] [CrossRef]
- Roberts, N.V.; Miller, S.T.; Bond, S.D.; Cyr, E.C. An implicit-in-time DPG formulation of the 1D1V Vlasov-Poisson equations. Comput. Math. Appl. 2024, 154, 103–119. [Google Scholar] [CrossRef]
- Broersen, D.; Dahmen, W.; Stevenson, R.P. On the Stability of DPG Formulations of Transport Equations. Math. Comput. 2018, 87, 1051–1082. [Google Scholar] [CrossRef]
- Demkowicz, L.F.; Roberts, N.V.; Matute, J.M. The DPG Method for the Convection-Reaction Problem, Revisited. Comput. Methods Appl. Math. 2023, 23, 93–125. [Google Scholar] [CrossRef]
- Sande, E.; Manni, C.; Speleers, H. Explicit error estimates for spline approximation of arbitrary smoothness in isogeometric analysis. Numer. Math. 2020, 144, 889–929. [Google Scholar] [CrossRef]
- Brenner, S.C. The Mathematical Theory of Finite Element Methods; Springer: New York, NY, USA, 2008. [Google Scholar]
- Chen, C.M.; Larsson, S.; Zhang, N.Y. Error estimates of optimal order for finite element methods with interpolated coefficients for the nonlinear heat equation. IMA J. Numer. Anal. 1989, 9, 507–524. [Google Scholar] [CrossRef]
- Adak, D.; Natarajan, S. Virtual element method for semilinear sine–Gordon equation over polygonal mesh using product approximation technique. Math. Comput. Simul. 2020, 172, 224–243. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).