Unveiling Hidden Dynamics in Air Traffic Networks: An Additional-Symmetry-Inspired Framework for Flight Delay Prediction

Abstract

Flight delays pose a significant challenge to the modern aviation industry, with prediction difficulties arising from the need to accurately model spatio-temporal dependencies and uncertainties within complex air traffic networks. To address this challenge, this study proposes a novel hybrid predictive framework named DenseNet-LSTM-FBLS. The framework first employs a DenseNet-LSTM module for deep spatio-temporal feature extraction, where DenseNet captures the intricate spatial correlations between airports, and LSTM models the temporal evolution of delays and meteorological conditions. In a key innovation, the extracted features are fed into a Fuzzy Broad Learning System (FBLS)—marking the first application of this method in the field of flight delay prediction. The FBLS component effectively handles data uncertainty through its fuzzy logic, while its “broad” architecture offers greater computational efficiency compared to traditional deep networks. Validated on a large-scale dataset of 198,970 real-world European flights, the proposed model achieves a prediction accuracy of 92.71%, significantly outperforming various baseline models. The results demonstrate that the DenseNet-LSTM-FBLS framework provides a highly accurate and efficient solution for flight delay forecasting, highlighting the considerable potential of Fuzzy Broad Learning Systems for tackling complex real-world prediction tasks.

1. Introduction

The inherent interconnectedness of modern aviation networks means that initial, localized disruptions can cascade through the system, leading to widespread, systemic delays. Consequently, delay propagation models, which analyze how these disturbances spread, have become a cornerstone of flight delay research [1,2,3]. Methodologies for predicting flight delays using learning algorithms have evolved significantly and can be broadly categorized into two main paradigms: approaches based on traditional machine learning algorithms [4,5], and leveraging advanced deep learning neural networks [6,7].

Within the domain of traditional machine learning, early research often focused on network-based analysis, frequently simplifying complex external variables under idealized conditions. For instance, Ahmadbeygi et al. [8] pioneered a network model that optimized flight operations by systematically adjusting the slack time within flight queues, thereby enhancing the network’s resilience to initial delays. Subsequently, Pyrgiotis et al. [9] introduced an approximate network delay model grounded in delay propagation algorithms and queuing theory. The significance of this model lay in its ability to reduce computational complexity, which greatly improved its applicability for analyzing large-scale, real-world air traffic systems. In a novel approach, Baspinar et al. [10] employed an epidemiological model, drawing an analogy between the spread of a disease and a flight delay. This framework allowed them to calculate delay propagation and recovery rates between flights and airports, revealing critical insights into the underlying patterns of how delays are transmitted and absorbed across the network. Furthering the use of real-world data, Moreira et al. [11] constructed a comprehensive dataset for delay prediction by merging the publicly available VRA dataset from the Brazilian National Civil Aviation Agency with meteorological data scraped from Weather Underground, applying various machine learning models to forecast delays.

However, a primary limitation of these traditional algorithms is their often-suboptimal generalization performance when confronted with new or anomalous data, as they can be overly sensitive to the statistical properties of the training set [12,13]. Furthermore, the feature engineering and training processes can be time-consuming. In response to these challenges, advanced deep learning neural network algorithms have emerged as a more powerful and efficient choice for flight delay prediction. Yazdi et al. [14] proposed a sophisticated model based on deep learning (DL) that utilized stacked denoising autoencoders (SDA) in conjunction with the Levenberg-Marquardt (LM) algorithm to refine prediction accuracy. Their comparative study demonstrated that the SDA-LM architecture consistently outperformed other models across key metrics, including precision, accuracy, and F-measure, on both imbalanced and balanced datasets.

More recently, the field has seen the rise of models that explicitly account for the network structure of airports. Cai et al. [15] introduced a method based on graph convolutional neural networks, which combined temporal convolution blocks with adaptive graph convolution blocks. This architecture proved highly effective, capturing not only the temporal evolution of delays but also their spatial dependencies across the airport network, leading to superior performance over benchmark methods. Addressing the needs of strategic planning, Wang et al. [16] developed a machine learning method specifically for predicting the *distribution* of flight delays, providing airport and airline managers with a valuable tool for long-term operational forecasting, which they validated using empirical data from Guangzhou Baiyun International Airport. Pushing the boundaries of accuracy and transparency, Wu et al. [17] proposed a spatio-temporal propagation network (STPN). This model integrates spatially and temporally separable graph convolution networks with a multi-head self-attention mechanism, which not only improved prediction accuracy beyond state-of-the-art methods but also generated interpretable patterns of delay propagation. Similarly, Kim et al. [18] adopted a comprehensive data-driven approach, analyzing a decade of data from major international airports to validate the effectiveness of various machine learning and deep learning models for long-term departure delay prediction with high accuracy.

In recent years, the trend of applying advanced computational models to solve complex system problems across various domains has become increasingly prominent, providing valuable interdisciplinary insights for prediction and optimization research in fields such as air transportation. For instance, in bio-manufacturing, researchers have begun to utilize machine learning-enhanced soft robotic systems to investigate complex biological functions [19]. In industrial engineering, cutting-edge techniques like cognitive computing are also being employed to predict the “flow status” within complex equipment such as flexible rectifiers [20]. These studies indicate that a core challenge, whether in biological or industrial systems, lies in accurately capturing and predicting nonlinear dynamic behaviors [21]. This paradigm even extends to the field of human-computer interaction, where advanced artificial muscles and sensing technologies are used to build wearable devices that simulate and reproduce complex haptic sensations [22]. Collectively, this cross-disciplinary research reveals a powerful trend: leveraging data-driven and intelligent algorithms to unveil the underlying dynamics of complex systems has become a robust paradigm. This inspires our own study to apply a novel hybrid intelligent model to tackle the equally complex problem of flight delay prediction within air traffic networks.

Despite these significant advancements in improving predictive accuracy, many of these innovative approaches still fall short of adequately modeling the complex, intertwined temporal and spatial correlations inherent in aviation data. A persistent challenge is to simultaneously capture the static airport network topology (spatial correlation) and the dynamic evolution of flight schedules and delays (temporal correlation). Moreover, the substantial computational resources and time required by many deep learning algorithms pose a significant barrier to their deployment in real-time prediction systems, which demand rapid and continuous updates [23]. To address these prevailing challenges, this paper proposes a novel hybrid architecture, the DenseNet-LSTM-FBLS model. The selection of this specific combination is deliberate and synergistic.

First, the DenseNet-LSTM component is designed as a powerful feature extractor for the complex, coupled dynamics of aviation networks. DenseNet, with its densely connected structure, is exceptionally suited for capturing the hierarchical spatial correlations between airports (e.g., how congestion at a hub airport propagates outwards), while LSTM effectively models the temporal evolution of delays and sequential data like weather patterns.

Second, this paper marks the first introduction of a Fuzzy Broad Learning System (FBLS) to the domain of flight delay research. The FBLS serves two critical functions: (1) its fuzzy-logic-based frontend adeptly handles the inherent uncertainty and ambiguity in aviation data (e.g., imprecise weather impacts, vague definitions of ‘minor’ vs. ‘moderate’ delay), improving model robustness; (2) its “broad” learning architecture offers a computationally efficient alternative to deep networks, enabling rapid training and adaptation, which is crucial for real-time applications. By integrating these components, our model aims to achieve a superior balance of predictive accuracy, robustness against uncertainty, and computational efficiency.

The empirical foundation of this study is a large-scale, real-world dataset encompassing all flight data from 123 airports under the jurisdiction of the European Aviation Safety Agency (EASA) over a three-year period, from January 2016 to December 2018. The core of our methodology begins with a sophisticated feature extraction framework. We employ a DenseNet-LSTM structure specifically designed to capture the intricate, intertwined nature of flight delays. The Densely Connected Convolutional Network (DenseNet) component excels at extracting complex spatial hierarchies and dependencies from the airport network, while the Long Short-Term Memory (LSTM) network component effectively models the temporal evolution of delays and sequential patterns in flight operations.

These extracted spatio-temporal features are then augmented with critical external factors (such as adverse weather conditions, air traffic control regulations, and airport-specific operational characteristics) to form a comprehensive and high-dimensional feature vector. This vector serves as the input to the novel prediction engine of our model: the Fuzzy Broad Learning System (FBLS) [24,25]. The FBLS is uniquely suited to this task for two key reasons. First, it leverages fuzzy logic to generate a series of interpretable fuzzy rules, which allows the model to adeptly handle the inherent uncertainty, vagueness, and ambiguity present in real-world aviation data [26,27]. These rules establish a robust, non-linear relationship between the input features and the predicted delay.

Second, by employing a Broad Learning algorithm, the FBLS can process this large set of input features with remarkable efficiency. Unlike traditional deep learning models that rely on time-consuming, iterative backpropagation through many layers, Broad Learning Systems offer superior adaptability and significantly reduced computational complexity by reshaping the network architecture into a wide, incrementally learnable structure [28,29]. Once the model is trained, test data is processed by the FBLS, which generates final, high-accuracy flight delay predictions based on the learned fuzzy rules and complex feature relationships.

2. Theoretical Background: DenseNet-LSTM-FBLS

This paper details the specific implementation steps of the proposed DenseNet-LSTM-FBLS model, which processes complex aviation data through a multi-stage feature engineering pipeline.

First, to independently capture the dynamic temporal impact of meteorological conditions on flight delays, we employed a Long Short-Term Memory (LSTM) framework. Leveraging LSTM’s inherent strengths in processing time-series data and capturing long-term dependencies, this module takes historical weather data (e.g., temperature, wind speed) as input to generate a temporal feature vector representing weather effects.

Next, to extract the more complex spatio-temporal correlations within the airport network, we designed a hybrid DenseNet-LSTM-based framework. The core of this framework involves first utilizing a Dense Convolutional Network (DenseNet) unit to capture the spatial dependencies and hierarchical structures of airport states, such as delays and congestion. Subsequently, the spatial feature maps extracted by DenseNet are fed into an LSTM unit to further capture the dynamic evolution of these spatial patterns over time—that is, the delay propagation process.

Finally, in the feature fusion and prediction stage, we concatenate the outputs from the preceding stages—the temporal feature vector from weather and the spatio-temporal feature vector from airport dynamics—with a set of static external features (such as airline information and air traffic control regulations) to form a comprehensive, high-dimensional feature vector. This final vector is then fed into the Fuzzy Broad Learning System (FBLS), which serves as the prediction engine to perform the final classification of the flight delay status. The detailed architecture and data flow of the entire model are illustrated in Figure 1.

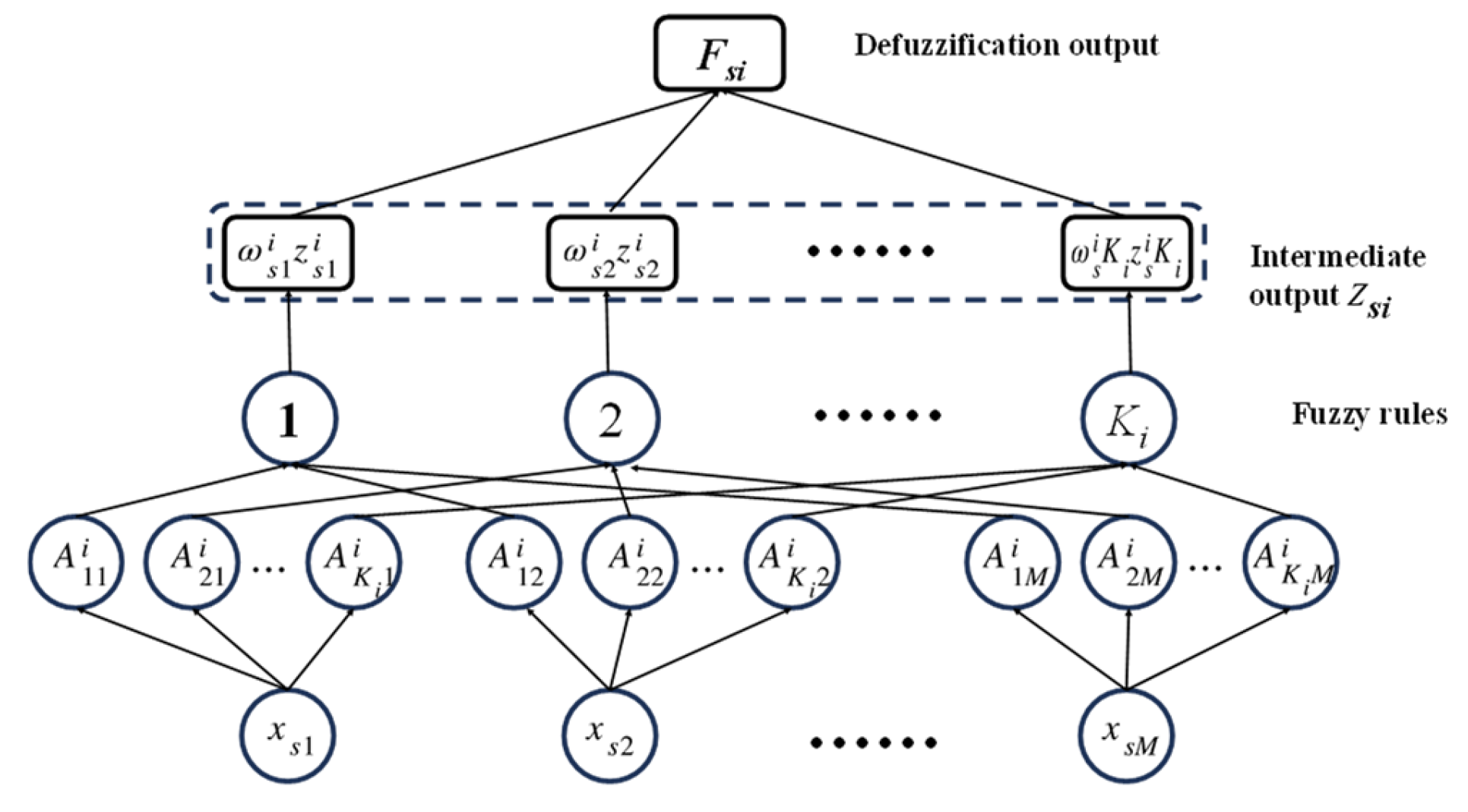
2.1. Fuzzy Broad Learning System (FBLS)

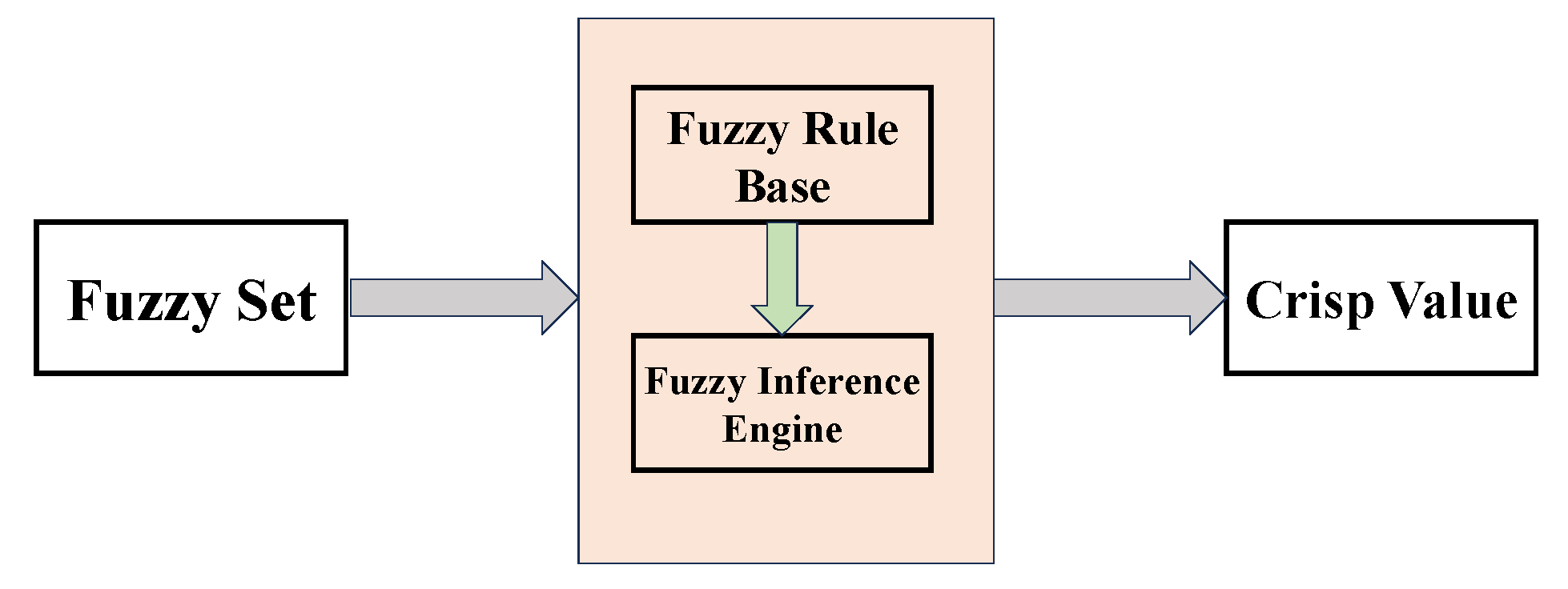
2.1.1. TSK Fuzzy System

The TSK fuzzy system is one of the most popular approaches in fuzzy theory, known for its outstanding performance across a wide range of real-world applications [30]. Recently, it has been widely recognized as an effective component in constructing numerous fuzzy and neuro-fuzzy frameworks. The key characteristic of the TSK fuzzy system lies in the THEN (consequent) part of its fuzzy rules, which is represented by a function of the input variables, typically a polynomial. Specifically, given an input vector $x=(x_1,x_2,\dots ,x_M)$, the k-th fuzzy rule in the TSK fuzzy system can be expressed as follows:

$$\begin{array}{l}\mathrm{If} x_{1}is{A}_{k1}\Lambda x_{2}is{A}_{k2}\Lambda \dots \Lambda x_{m}isA\\ {\mathrm{then}}_k={\displaystyle {\int }_k(x)},k=1,2,\dots ,K\end{array}$$

(1)

where $A_n^m$ represents the feature mapping nodes and enhancement nodes in the initial network. $A_{kj}$ represents a fuzzy subset defined over the input discourse, $f_k(x)$ is a polynomial of the input variables, and K denotes the number of fuzzy rules. Typically, $f_k(x)$ is set as either a constant or a linear combination of the components of x, corresponding to a zero-order or first-order TSK fuzzy system. The output is expressed as follows:

$$\widehat{y}={\displaystyle \frac{{\displaystyle \sum _{K=1}^K{\displaystyle \prod _{j=1}^M{\mu }_{kj}}}(x_j)f_k(x)}{{\displaystyle \sum _{K=1}^K{\displaystyle \prod _{j=1}^M{\mu }_{kj}}}(x_j)}}={\displaystyle \frac{{\displaystyle \sum _{K=1}^K{\mu }_k}(x)z_k}{{\displaystyle \sum _{K=1}^K{\mu }_k}(x)}}$$

(2)

In this case, $u_{kj}(x)$ refers to the membership function associated with the fuzzy subset $A_{kj}(x)$, while ${\mu }_k(x)={\displaystyle \prod _{j=1}^M{\mu }_{kj}}(x_j)$ represents the firing strength (activation level) of the k-th fuzzy rule.

However, as long as it accurately describes the output within the domain specified by the fuzzy rule premise, f_k can be any function. Such a fuzzy system is called a first-order TS fuzzy model when f_k is a first-order polynomial. Another common model is the zero-order TS fuzzy model. The zero-order TS model can be viewed as a special case of another widely used fuzzy system—the Mamdani fuzzy system—where the conclusion of each rule is represented by a fuzzy singleton (or a defuzzified outcome). A schematic diagram of the TS model is shown in Figure 2.

In a typical TSK fuzzy system, it is necessary to compute the parameters of the membership function A (such as the center and width of a Gaussian membership function) as well as the coefficients. In this process, to ensure the fuzzy rules are empirically grounded in the dataset’s natural structure, a K-means clustering algorithm was applied directly to the departure delay time variable (Δt) within the training set. The centroids of the resulting clusters, which represent the natural data groupings of delay severity, were then used to define the centers of the Gaussian membership functions for the corresponding fuzzy sets. This procedure calibrates the fuzzy subsystem to the specific statistical distribution of aviation delays observed in the data.

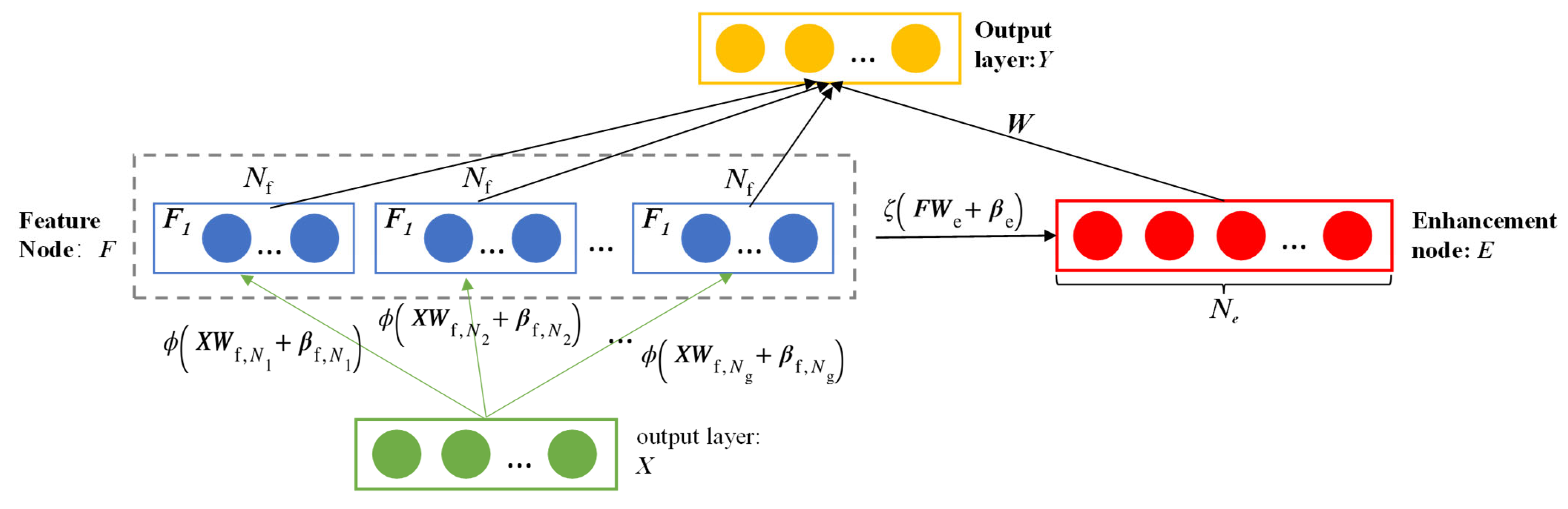
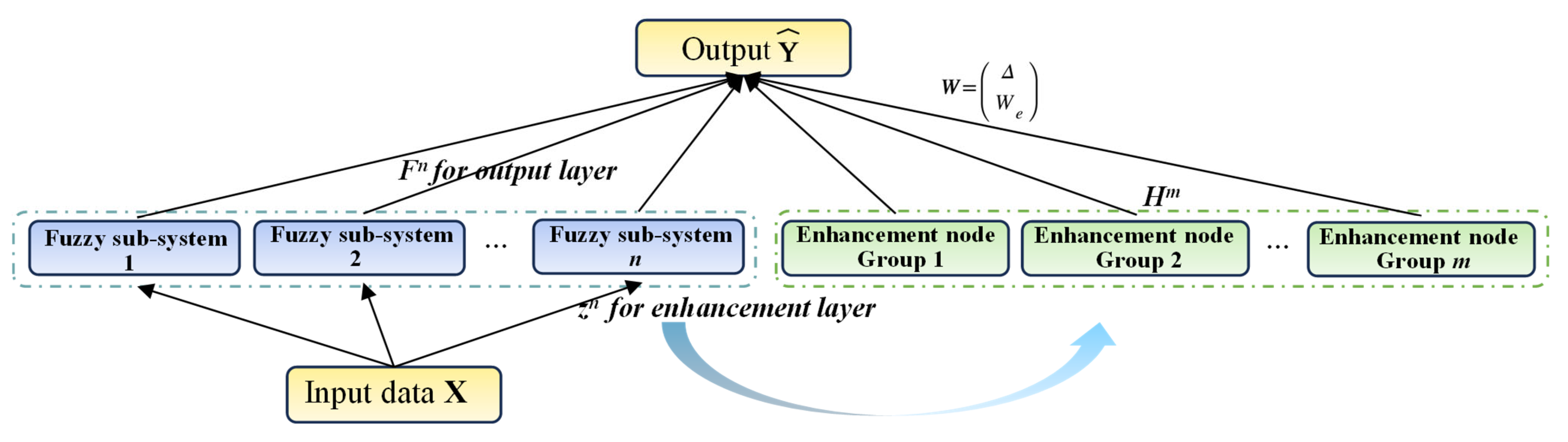
2.1.2. Broad Learning System (BLS)

Due to the large number of parameters and complex structure of deep networks, they are often time-consuming to train. To address this, Chen et al. proposed a novel Broad Learning System (BLS), which adds direct connections from the input layer to the output layer, as well as nonlinear transformations from the input layer to an enhancement layer, within a single-layer feedforward network. The algorithm proposed in this paper primarily relies on the principles of BLS to achieve human-machine interaction classification. In the equation, X, Y, n, and m represent the input data, output results, feature nodes, and enhancement nodes, respectively. ${\varphi }_i$ and ${\xi }_{\mathrm{j}}$ are activation functions, while $W_{ei}$, $W_{h_j}$, and ${\beta }_{ei}$ ${\beta }_{hj}$ denote the randomly generated weights and biases. The i-th mapped feature is expressed as:

$$N_i={\varphi }_{i}X{W}_{e_i}+{\beta }_{ei},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}i=1,..,n$$

(3)

All mapped features are represented as follows, where the $N^n=[N_1\hspace{0.33em},\dots ,N_n]\hspace{0.33em}$ enhancement node is expressed as:

$$M_j={\xi }_{\mathrm{j}}(N^n{W}_{h_j}+{\beta }_{h_j}),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}j=1,\dots ,m$$

(4)

All enhancement nodes are denoted as $M^m=[M_1\hspace{0.33em},\dots ,M_m]\hspace{0.33em}$. Therefore, the structure of the BLS network can be expressed by the following function:

$$Y=[N_1,\hspace{0.33em}{N}_2\hspace{0.33em}\dots ,\hspace{0.33em}{N}_n\hspace{0.33em},M_1,\hspace{0.33em}{M}_2\hspace{0.33em}\dots ,M_m]\hspace{0.33em}{W}^m=[N_n,M_m]\hspace{0.33em}{W}^m$$

(5)

The overall framework of the network using the broad learning algorithm is illustrated in Figure 3. In this network, new input samples are used as training samples for the next iteration, which significantly reduces training time. The formula for dynamically updating the coefficients is as follows:

$$N_{new}^n={\left[\varphi \left(X_a{W}_{e_i}+\beta \overleftrightarrow{\mathbb{S}},\dots ,\varphi \left(X_a{W}_{e_n}+{\beta }_n\right)\right)\right]}_1$$

(6)

$$A_{\mathrm{new}}=\left[\begin{array}{c}\varphi \left(X_a{W}_{e1}+{\beta }_1\right),\dots ,\varphi \left(X_a{W}_{e_n}+{\beta }_n\right),\\ \xi \left(N_{new}^n{W}_{h_1}+{\beta }_{h_1}\right),\dots ,\xi \left(N_{new}^n{W}_{h_m}+{\beta }_h\right)\end{array}\right]$$

(7)

where $A_n^m$ represents the feature mapping nodes and enhancement nodes in the initial network.

The weights of the output layer are given as follows:

$${}^{new}W_{\mathrm{n}}^{\mathrm{m}}=W_n^m+\left(\begin{array}{c}{Y}_A^T-{\Lambda }_{\mathrm{new}}^T{W}_n^m\end{array}\right)B$$

(8)

$$\left({}^{new}A_{\mathrm{n}}^{\mathrm{m}}\right)+={\left[\left(A_n^m\right)+-B{D}^T|B\right]}_4$$

(9)

$$D^T=A_{\mathrm{ncw}}^T{A}_n^{m+}$$

(10)

$$C=A_{new}^T-D^T{A}_{n\le }^m$$

(11)

$$BT=\left\{\begin{array}{ll}{C}^{+}\hfill & if\mathrm{C}\ne 0\hfill \\ (1+DTD)-1(Amn)+D\hfill & if\mathrm{C}=0\hfill \end{array}\right.$$

(12)

2.1.3. FBLS

The Fuzzy Broad Learning System is a novel machine learning model that combines the Broad Learning System with the TSK fuzzy system. By integrating the TSK fuzzy model with the broad neural network, the feature data of flight delays are first processed through the TSK model for fuzzification. The fuzzified output is then used as input to the broad neural network for training. Through supervised learning and pseudoinverse computation, the final weight vector is obtained. The overall network structure is illustrated in Figure 4.

To reduce the complexity of its network structure, the Fuzzy Broad Learning System replaces the autoencoder used for coefficient learning in the original Broad Learning System with a fuzzy subsystem. This optimization enhances the model’s robustness and generalization ability, ultimately improving its predictive performance and interpretability, while streamlining the overall model structure. The structure of the i-th fuzzy subsystem is shown in Figure 5.

2.1.4. Algorithm Flow

The Fuzzy Broad Learning Model constructed in this paper initializes the optimal accuracy and result set each time a new dataset is loaded to ensure that the output accuracy is always the best possible. Additionally, before running the code, the search ranges for the number of fuzzy rules, the number of fuzzy subsystems, and the number of enhancement nodes are predefined. During model iteration, these parameters are automatically updated within the specified search range, which significantly reduces training time and simplifies the model structure. The algorithm for the Fuzzy Broad Learning Model is outlined in Algorithm 1.

Algorithm 1. FBLS Training Algorithm

Input: Training samples (X,Y) ∈RN×(M+C), numbers of fuzzy rules Ki, enhancement nodes Lj, fuzzy subsystems n and enhancement node groups m.

Output: Training time T1, and maximum allowed training time

1. Set a standard deviation of 1, which will be used to calculate the parameters of the fuzzy subsystem function.

2. Start the timer to measure the code execution time.

3. Standardize the training data.

4. Define a vector to store information about the training data, where the vector consists of all fuzzy rules from the i-th fuzzy subsystem.

5. Store the training data in the predefined vector.

6. Create a zero matrix y, which will be used to store the fuzzy outputs.

7. Begin a loop, with the number of iterations determined by the number of fuzzy rules in the input variable, aimed at searching for the optimal number of fuzzy systems.

8. Perform the fuzzy subsystem design, including the layout of the fuzzy system

9. Use the K-means algorithm to cluster the training data and obtain the cluster centers.

10. Calculate the fuzzy rules and the membership functions according to the predefined settings of the fuzzy subsystems.

11. Apply standardization to the membership functions, ensuring they are in the range [0, 1].

12. Use the output of the system T1 and the corresponding feature values to calculate the final hierarchical output.

13. Use the pseudoinverse to calculate the final weight matrix and apply the Jacobian matrix to derive the final output Y

14. Continue this process by optimizing the system’s structure to minimize the error.

15. Calculate the difference between the current output and the target output from the previous iteration. If the difference is less than the threshold, stop the training.

16. Output the final model’s accuracy and training time.

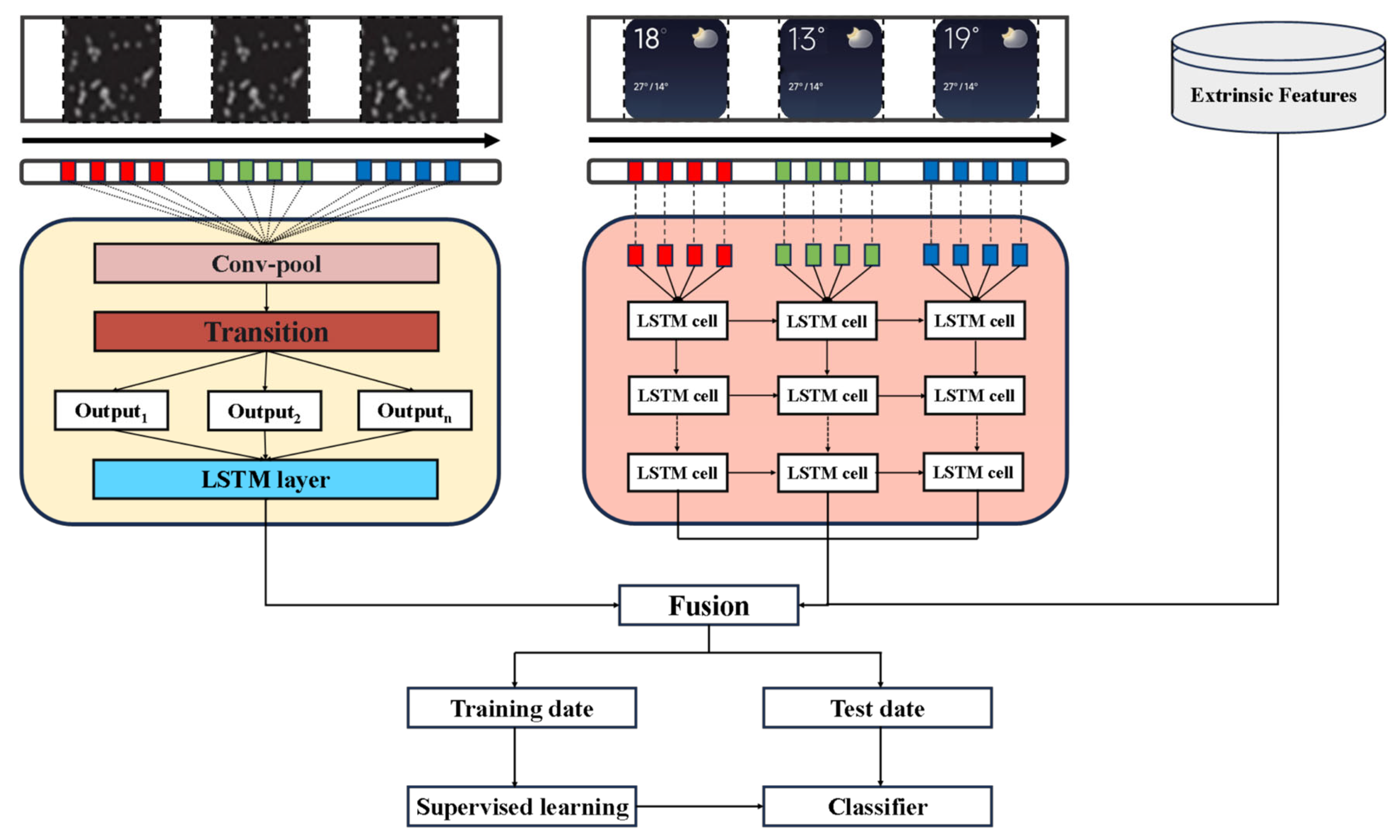
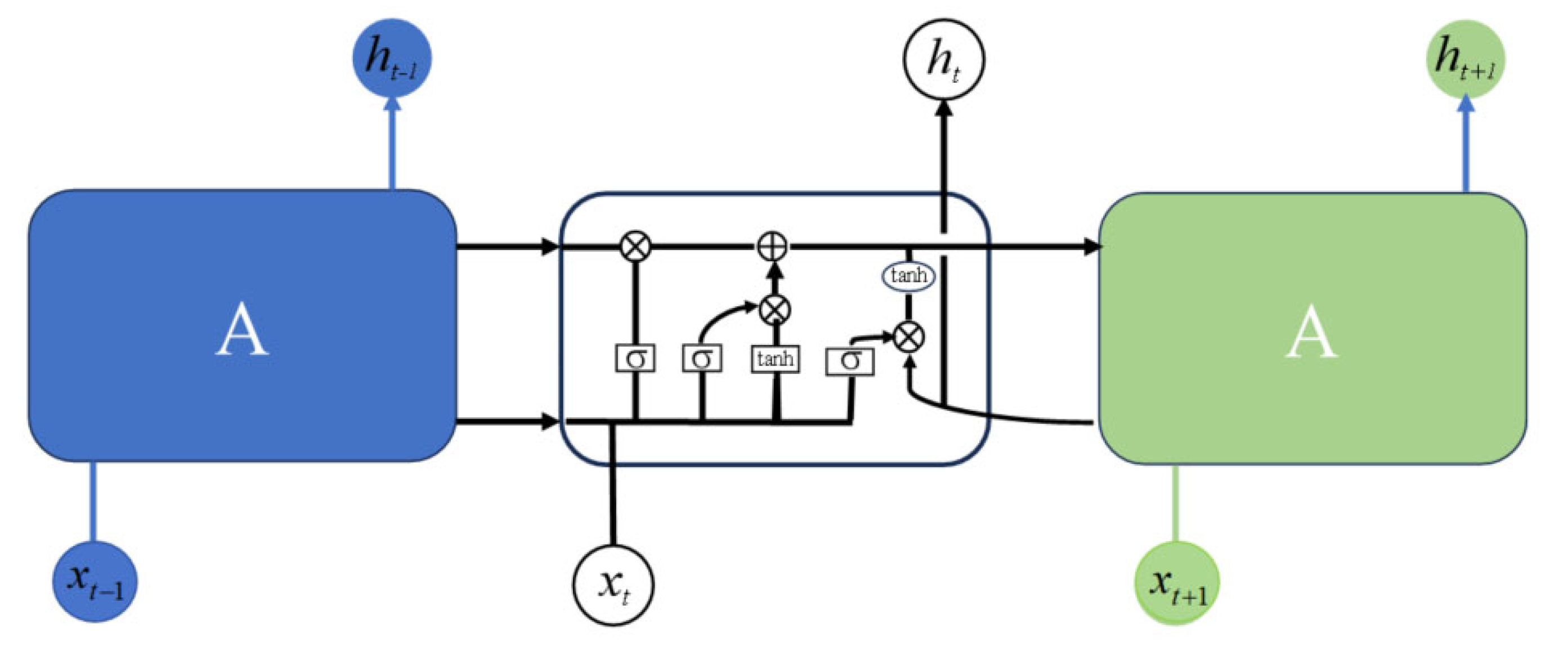
2.2. DenseNet-LSTM

2.2.1. Temporal Feature Extraction

To capture the temporal impact of weather conditions on flight delays, we employed the LSTM model [31]. Long Short-Term Memory (LSTM) networks are a type of recurrent neural network (RNN) specifically designed to overcome the vanishing and exploding gradient problems that commonly affect traditional RNN models.

In this study, historical weather data over a specific time period were used as input, including information such as temperature, wind speed, and humidity. The time interval was set to track weather conditions at several hours, leading up to the current time ttt, such as t, t − 1h, t − 2h, …, t − nht.

$$I_w=\left[W_{t-nh},W_{t-(n-1)h},\dots ,W_t\right]$$

(13)

where W represents the weather features, including temperature, wind speed, humidity, and other related factors.

As shown in Figure 6, Long Short-Term Memory (LSTM) networks introduce gated units to effectively learn and retain long-term dependencies, making them more efficient in handling time-series data. Unlike traditional Recurrent Neural Networks (RNNs), LSTM replaces the single structure of RNNs with four interacting layers [32]. This design enables LSTM networks to flexibly manage time-series data, overcoming the vanishing gradient problem commonly seen in traditional RNNs and providing an effective solution for capturing long-term dependencies. The LSTM model is expressed as follows:

$$i_t=\sigma \left({\displaystyle \sum w_{xi}}{x}_t+{\displaystyle \sum w_{hi}}{x}_{t-1}+{\displaystyle \sum w_{ci}}{x}_{t-1}+b_i\right)$$

(14)

$$f_t=\sigma \left({\displaystyle \sum W_{xf}}{x}_t+{\displaystyle \sum W_{hf}}{x}_{t-1}+{\displaystyle \sum W_{cf}}{x}_{t-1}+b_f\right)$$

(15)

$$o_t=\sigma \left({\displaystyle \sum W_{xo}}{x}_t+{\displaystyle \sum W_{ho}}{x}_{t-1}+{\displaystyle \sum W_{co}}{x}_{t-1}+b_o\right)$$

(16)

$$o_t=\sigma \left({\displaystyle \sum W_{xo}}{x}_t+{\displaystyle \sum W_{ho}}{x}_{t-1}+{\displaystyle \sum W_{co}}{x}_{t-1}+b_o\right),$$

(17)

$$c_t=f_t{c}_{t-1}+i_t\tanh \left({\displaystyle \sum W_{xc}}{x}_t+{\displaystyle \sum W_{hc}}{x}_{t-1}+b_c\right)$$

(18)

$$h_t=o_t°\tanh (c_t)$$

(19)

where f_t is the output of the forget gate, a is the Sigmoid function, W_f is the weight matrix, h_t−1 is the hidden state from the previous time step, x_t is the input at the current time step, and b_f is the bias term. i_t represents the output of the input gate, while ${\tilde{C}}_t$ denotes the new candidate memory value.

During the training process, we input historical weather data into the LSTM model, which learns the impact of weather changes on flight delays through its memory and update mechanisms. The feature output from the LSTM model is represented as:

$$X_t=\mathrm{LSTM}(I_w)$$

(20)

where ${\widehat{X}}_t$ represents the temporal impact of the captured weather features.

Through the aforementioned approach, we effectively capture the temporal correlations of weather features, thereby improving the accuracy of flight delay predictions. The use of the LSTM model allows us to account for both past and current weather conditions’ ongoing impact on flight delays, incorporating this information into subsequent prediction models [33,34].

2.2.2. Method for Extracting Spatial Correlations Using DenseNet

In aviation operations, aircraft connect various airports, resulting in significant spatial correlations between neighboring regions, including issues such as airport delays and congestion [35,36]. In the current study, Convolutional Neural Networks (CNNs) are effective in addressing these spatial dependency problems [37]. However, traditional CNNs struggle to match the performance of DenseNet due to limitations in feature propagation, gradient vanishing, parameter redundancy, and network depth.

Therefore, this paper employs DenseNet [24] (Dense Convolutional Network) to extract features through densely connected convolutional layers, as illustrated in Figure 7.

The specific process is as follows: First, as shown in Figure 8, the airport map is divided into 20 × 26 regions based on geographical location, with each region representing an airport. The formula is expressed as follows:

$$M={\left\{r_{ij}\right\}}_{H\times W}$$

(21)

where H and W represent the height and width of the map, respectively, with each spatial region denoted as $r_{ij}$.

Next, for each region, we define the number of flights operating within a given time interval and the average departure delay time, which represent airport congestion and delay, respectively. The formulas are expressed as follows:

$$B_{t-nh,t}(ij)={\displaystyle \sum _{T=t-nh}^{\otimes }{f}_{Tij}}$$

(22)

$$F_{t-nh,t}(ij)={\displaystyle \frac{{\displaystyle \sum _{T=t-nh}^{t}D}{F}_{Tij}}{N}}$$

(23)

where $f_{Tij}$ represents the number of flights within the time interval, $D{F}_{Tij}$ denotes the departure delay time, and N is the total number of flights. These features are then combined to form the input matrix:

$$I_s={\left[\begin{array}{cc}{B}_{t-nh,t}(ij)& F_{t-nh,t}(ij)\end{array}\right]}_{24\times 26}\in {ℝ}^{24\times 26\times 24}$$

(24)

In the DenseNet model, the input matrix undergoes multiple convolutional operations to extract local spatial features. DenseNet utilizes dense connections between layers, where the output of each layer is used as input for subsequent layers, allowing it to capture more comprehensive features. The core formula of DenseNet is as follows:

$$x_l=H_l\left(\left[\begin{array}{c}{x}_0,x_1,\dots ,x_{l-1}\end{array}\right]\right)$$

(25)

where $H_l$ represents the nonlinear transformation function of the l-th layer, and $\left[\begin{array}{c}{x}_0,x_1,\dots ,x_{l-1}\end{array}\right]$ denotes the concatenation of all feature maps from the preceding layers. The extracted spatial features are then fed into the LSTM model to capture the temporal dependencies of airport delays and congestion.

By combining the spatial features extracted by DenseNet with the temporal features captured by LSTM, we gain a more comprehensive understanding of the dynamic changes in airport congestion and delays, thereby improving the accuracy and efficiency of flight delay prediction [38]. The integration of DenseNet and LSTM enables the model to simultaneously capture both spatial and temporal correlations, providing a richer informational foundation for prediction [39,40].

2.2.3. Training of the DenseNet-LSTM-FBLS Model

In this work, the flight data were randomly divided into two batches, with 70% used for training and 30% for testing. The training data were then subjected to 10-fold cross-validation. The training process of the DenseNet-LSTM-FBLS model is outlined in Algorithm 2:

Algorithm 2: DenseNet-LSTM-FBLS for Flight Delay Prediction

Input: D: {d1, d2, …, dm, Y}, dataset containing flight data    Iw: time-series data of weather attributes {Wt, W{t-1}, …, W{t-n}}    Ist: time-series data of flight delays and airport congestion    XExt: external features {x1, x2, …, xn}

Output: The class of flight delays (on-time or delay)

For i in range(epochs) do

N = spatial feature information

For attribute value Ist in Ist do

N = FDenseNet(Ist)

N += N

end

T = temporal feature information

T = FLSTM(Iw)

ALL = N + T + XExt

Ŷ = FFBLS(ALL)

params_grad = evaluate_gradient (loss_function = (Ŷ − Y)^2)

Update_model(params_grad)

end

Ypred = FFBLS*predict(ALL, Y)

3. Experimental Results

3.1. Experimental Environment

The experimental hardware configuration includes an Intel64 Family 6 Model 183 Stepping 1 GenuineIntel ~3400 MHz processor, 32 GB of RAM, and a 13th Gen Intel(R) Core(TM) i7-13700K GPU. The graphics card used is the NVIDIA RTX 4060 Ti. The software environment was set up on a 64-bit Windows 10 operating system, running MATLAB 2023b.

3.2. Data and Processing

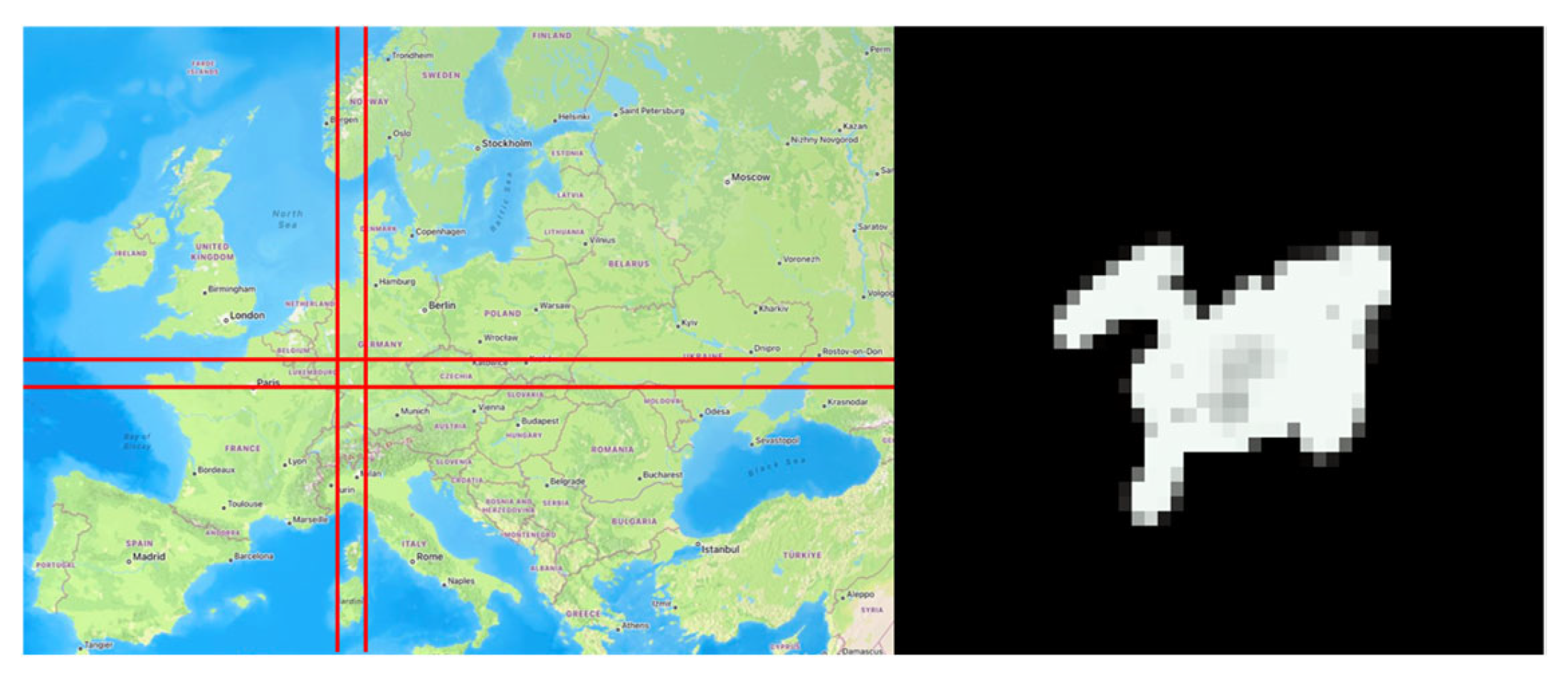
3.2.1. Source of Data

This study utilizes flight data from 123 airports under the management of the European Aviation Safety Agency (EASA) between January 2016 and December 2018. The dataset includes 198,970 individual samples, each containing 34 features, as shown in

Table 1. Data Feature Summary.

Feature Names
origin_airport
scheduled_departure_year
scheduled_departure_month
scheduled_departure_day
scheduled_departure_hour
scheduled_departure_minute
take_off_year
take_off_month
take_off_day
take_off_hour
take_off_minute
Advance Flight Arrival year
Advance Flight Arrival month
Advance Flight Arrival day
Advance Flight Arrival hour
Advance Flight Arrival minute
scheduled_arrival_year
scheduled_arrival_month
scheduled_arrival_day
scheduled_arrival_hour
scheduled_arrival_minute
origin_air_temperature
origin_wind_direction
origin_wind_speed
origin_visibility
origin_cloud_height_lvl_1
destination_air_temperature
destination_wind_direction
destination_wind_speed
destination_visibility
destination_cloud_height_lvl_1
origin_cloud_coverage1
destination_cloud_coverage1
aircraft_type_code0
origin_cloud_height_lvl_1

. These features include, but are not limited to, the departure and destination airports, airline, aircraft tail number, scheduled and actual departure/arrival times, weather conditions, and flight delay durations. The wide range of features in this dataset allows for an in-depth analysis of various factors affecting flight delays.

The choice of the 2016–2018 timeframe is intentional. This period represents a phase of stable and high-volume air traffic operations in Europe prior to the unprecedented disruptions caused by the COVID-19 pandemic starting in 2020. By using this pre-pandemic dataset, we aim to build a model based on typical, systemic operational patterns rather than the anomalous and highly volatile dynamics observed during the global health crisis. This provides a more robust baseline for understanding fundamental delay propagation mechanisms. We acknowledge that the model’s performance on more recent, post-pandemic data is a crucial next step, which we outline in our future work.

3.2.2. Data Preprocessing

• Missing value handling

In the data preprocessing process for air traffic flow prediction, handling missing and outlier values is a critical task, as these issues often arise from recording errors or unpredictable events [41,42]. The presence of missing or abnormal values can severely affect the accuracy and predictive power of the model, especially in forecasting future trends [43]. The strategy employed in this study to identify these values involves assessing whether data points deviate abnormally from their neighboring values [44].

Addressing these data issues involves a variety of complex strategies, considering multiple potential causes, such as system errors, recording mistakes, adverse weather conditions, or technical failures. In this study, we adopted the interpolation method to correct missing and outlier values. This method was chosen based on its effectiveness in data recovery and maintaining data integrity. Interpolation works by analyzing and calculating values from surrounding data points to recover missing information, thus enhancing the dataset’s completeness and coherence. The specific interpolation method can be defined by the following formula:

$$f\left(x\right)={\displaystyle \frac{f\left(x_1\right)+f\left(x_2\right)}{2}}$$

(26)

where $f\left(x\right)$ represents the missing value to be predicted and filled, while $f\left(x_1\right)$ and $f\left(x_2\right)$ represent the real air traffic flow values immediately before and after the missing value, respectively.

• feature code

In the dataset used in this study, there are numerous categorical features. To facilitate subsequent calculations and modeling, these features must first be encoded. Since some features have a large number of categories, applying the traditional one-hot encoding method would significantly expand the feature space, increasing the risk of dimensionality issues. Therefore, categorical features were transformed into numerical data to simplify the model’s complexity and improve processing efficiency. The feature encoding is shown in

Table 2. Feature Code.

Feature	Data Type
Scheduled Departure Year	Int32
Scheduled departure month	Int32
Scheduled departure day	Int32
Scheduled departure hour	Int32
scheduled_departure_minute	Int32
……	……
Aircraft type code0	Int32
Origin airport	Int32
Origin air temperature	Float64
Destination air temperature	Float64
Origin wind speed	Float64
Destination wind speed	Float64
Origin visibility	Float64
Destination visibility	Float64
Origin cloud height lvl 1	Float64
Destination cloud height lvl 1	Float64

.

3.2.3. Imbalance Handling

In this study, the severity of flight delays is classified into five levels, based on the duration of departure delays. The classification method is shown in

Table 3. Classification of Flight Delays.

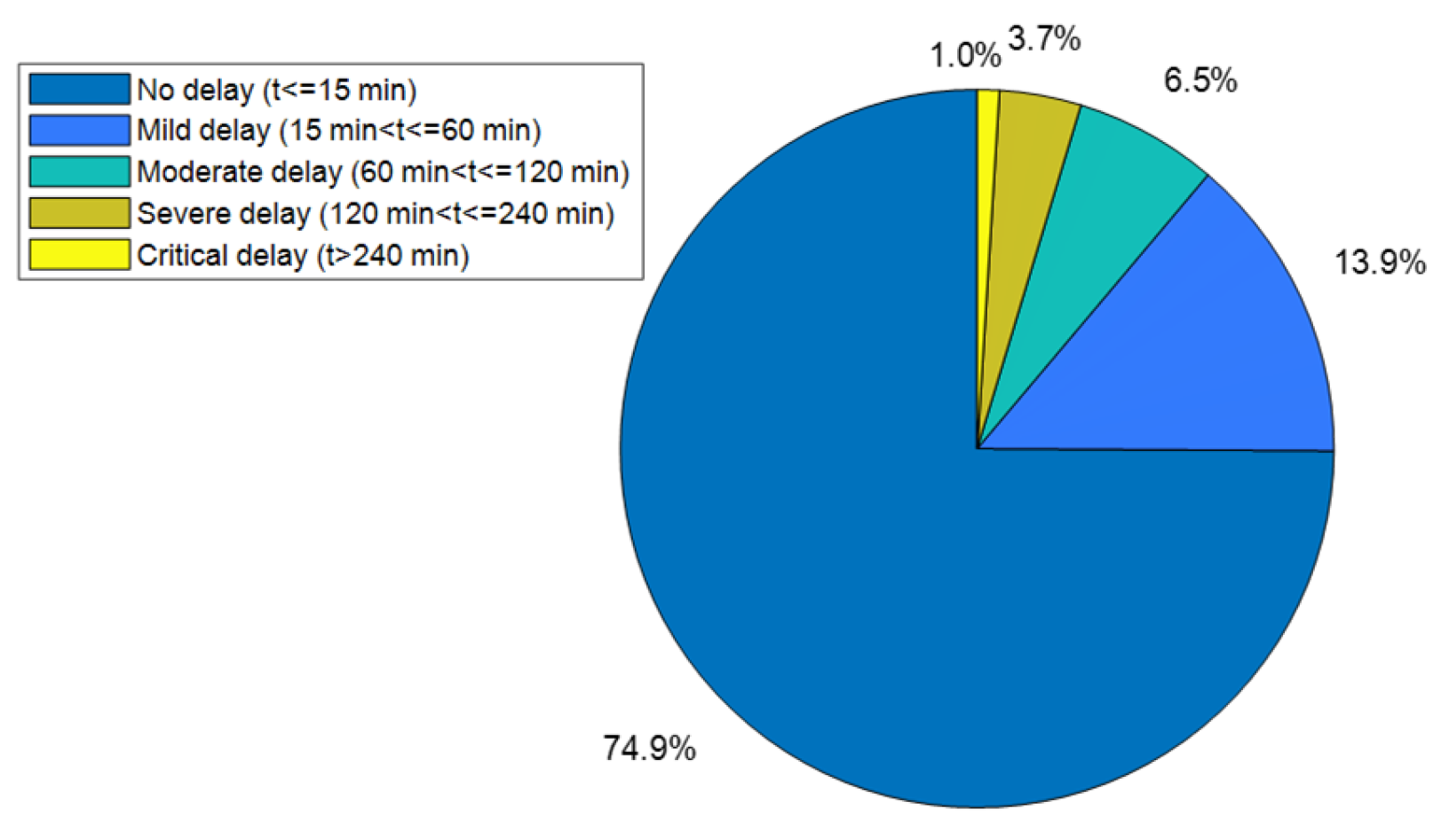
Level of Delay	Grade Meaning	Slippage Time (At/min)
1	No delayed	At ≤ 15
2	Mild Delay	15 < At ≤ 60
3	Moderate Delay	60 < At ≤ 120
4	Severe Delay	120 < At ≤ 240
5	Critical Delay	240 < At

, where t represents the difference between the actual departure time and the scheduled departure time.

The proportion of each sample category relative to the total dataset is shown in Figure 9. As seen in Figure 9, the number of non-delayed flights accounts for nearly three-quarters of the total flights, which is approximately 75 times more than the severely delayed flights, the category with the smallest proportion. If predictions are made directly on such an imbalanced dataset, the model is likely to overfit the majority class, leading to underfitting for the minority classes. As a result, the model would be biased towards predicting flights as “non-delayed” and fail to accurately predict the severity of delays.

To address the issue of imbalanced data, resampling methods are applied to adjust the number of samples in each class, making the class distribution relatively balanced. This study employs the SMOTE-Tomek combined sampling method. First, the Synthetic Minority Oversampling Technique (SMOTE) algorithm [45] is used to generate new samples by randomly selecting the nearest neighbors of the minority class. Then, Tomek links are removed from the data to maintain clear classification boundaries. After processing, the distribution of each delay level is shown in Figure 10.

3.3. Experimental Setup

3.3.1. Parameter Settings

The flight dataset used in this experiment consists of 198,970 individual samples, with a feature dimension of 34. Additionally, since the proportion of non-delayed flights is significantly larger in real-world scenarios, the distribution of samples across different classes in the dataset is imbalanced. During the training phase, a batch sampling strategy based on the data balancing method proposed in literatures [46] was applied to compensate for the uneven class distribution while maintaining classification standards. To systematically determine the optimal hyperparameters for the FBLS model and avoid the limitations of manual grid searches, this study employed a Bayesian Optimization approach [47]. This method iteratively builds a probabilistic surrogate model of the objective function and uses an acquisition function to intelligently select the most promising hyperparameter set for the next evaluation. The optimized hyperparameters included the number of fuzzy rules (r), the number of fuzzy subsystems (s), and the number of enhancement nodes (e).

3.3.2. Evaluation Indicators

In the flight delay prediction model presented in this paper, the primary metrics used to evaluate its performance are accuracy, precision, recall, and F1 score. Accuracy represents the proportion of correctly predicted samples out of the total samples, reflecting the overall predictive accuracy of the model on the dataset. Precision refers to the proportion of true positive samples among all samples predicted as positive, indicating the model’s accuracy in predicting positive instances. Recall measures the proportion of true positive samples correctly identified out of all actual positive samples, representing the model’s ability to capture positive instances. The F1 score is the harmonic mean of precision and recall, providing a balanced evaluation of model performance. The definitions for accuracy, precision, recall, and F1 score are as follows:

$$A={\displaystyle \frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{TN}+\mathrm{FP}+\mathrm{FN}}}$$

(27)

$$P={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}}$$

(28)

where A represents accuracy and P represents precision.

In the case of imbalanced data, using only accuracy to evaluate the model is insufficient. When the number of positive samples is far smaller than the number of negative samples, a model could achieve high accuracy by predicting all samples as negative. However, such a model would fail to identify the positive samples. Therefore, in this situation, recall becomes an important metric to consider. Recall represents the proportion of actual positive samples that are correctly predicted as positive, reflecting the model’s ability to capture minority class instances. In the context of flight delay prediction, this indicates the model’s ability to detect delayed flights. Thus, in the case of imbalanced data, both accuracy and recall should be considered together for a comprehensive evaluation of the model’s performance. The formula for recall is as follows:

$$R={\displaystyle \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}}$$

(29)

The F1 score can be understood as the harmonic mean of precision and recall, providing a comprehensive evaluation of the model’s performance. The F1 score ranges from 0 to 1, with values closer to 1 indicating better model performance. The formula for the F1 score is as follows:

$${\displaystyle \frac{2}{F}}={\displaystyle \frac{1}{P}}+{\displaystyle \frac{1}{R}}$$

(30)

$$P_{\mathrm{Macro}}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{P}_i}$$

(31)

$$R_{\mathrm{Macro}}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{R}_i}$$

(32)

$$F_{\mathrm{Macro}}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{F}_i}$$

(33)

$$F_{\mathrm{Macro}}={\displaystyle \frac{2\times P_{\mathrm{Macro}}\times R_{\mathrm{Macro}}}{P_{\mathrm{Macro}}+R_{\mathrm{Macro}}}}$$

(34)

It is important to note that the traditional formulas for precision, recall, and F1 score are primarily designed for binary classification models. However, since this study employs a multi-class model, different methods are required for evaluation. To more accurately assess the performance of the model, this study adopts the macro-average approach. The macro-average method calculates the precision, recall, and F1 score for each class individually, and then averages these scores to obtain an overall performance metric. This method provides a more comprehensive evaluation in a multi-class setting, allowing for a better understanding of the model’s performance across different classes. The definitions of accuracy, precision, recall, and F1 score for multi-class classification are as follows:

3.4. Projected Results

After the data preprocessing described earlier, this study resulted in a dataset containing 34 variables and 198,970 records. For building the flight delay classification model, the “label” variable was used as the target classification label, while the other variables were used as classification features. A random split method was applied to the dataset, dividing it into a training set and a testing set in a 7:3 ratio to construct a classification model.

To improve model performance, three different activation functions were tested on the Fuzzy Broad Learning System (FBLS). The regularization parameters, fuzzy rules, fuzzy subsystems, and enhancement nodes were all set within the same range. The model was evaluated on multiple datasets, such as Wbc and Wine, to calculate the average accuracy. As shown in

Table 4. Comparison of Different Activation Functions.

Activation Function	Logsig		Softmax		Tansig
Data Set	Training	Testing	Training	Testing	Training	Testing
Wbc	99.71	98.62	98.67	97.52	96.57	99.29
Balance	98.31	98.02	95.41	93.51	97.82	96.83
Iris	98.62	98.14	96.36	95.13	97.26	96.42
Glass	91.26	89.32	96.81	95.41	98.41	97.67
Pageblocks	90.23	88.42	97.52	96.38	93.45	92.26
Segment	86.51	85.13	97.42	95.61	95.62	94.29
Texture	83.47	82.87	94.79	93.26	87.27	86.41
Pendigits	81.26	80.10	93.51	92.64	90.17	89.26

, the results were compared with well-established and representative machine learning models to determine the optimal activation function.

As shown in Table 4, the Fuzzy Broad Learning System can improve the test accuracy by using different types of activation functions when handling binary and multi-class classification problems. For binary classification tasks, such as the Wbc dataset, the Logsig activation function delivers the best results. However, its performance declines for more complex multi-class classification tasks. For multi-class problems, such as the Glass dataset, the Softmax activation function performs better. The Tansig activation function demonstrates more balanced performance across tasks. Therefore, in this study, we selected the Softmax activation function for the model.

In this study, the Bayesian Optimization process was executed to tune the FBLS parameters, converging on the optimal configuration presented in

Table 5. Characteristic Importance and Prediction Error.

Parameter Settings	FBLS
Parameters	r	s	e
	110	110	40

, which was subsequently used for the final model training and evaluation. The feature importance and prediction errors are presented in Table 5.

Where e represents the number of enhancement nodes, r denotes the number of fuzzy rules, and s refers to the number of fuzzy subsystems.

The confusion matrix for the model is as follows (Figure 11):

3.5. Experimental Results and Analysis

To further evaluate the multi-class flight delay prediction performance of the proposed algorithm, we compared the results of the improved model with several baseline models, including BP Neural Network, Convolutional Neural Network (CNN), K-Nearest Neighbors (KNN), Long Short-Term Memory (LSTM), Support Vector Machine (SVM), Naive Bayes, Radial Basis Function Neural Network (RBF), Extreme Learning Machine (ELM), and Random Forest (RF). As shown in

Table 6. Comparison of Data Across Models.

Modek	Training Set/%	Test Set/%	Accuracy/%	Recall Rate/%	F1	Time/s
ELM	17.5469	16.5545	16.4435	16.5425	0.1645	10.6226
Bayes	40.0934	35.6783	35.6673	35.6648	0.3567	6.6554
RBF	100	67.9148	67.9012	67.8495	0.6779	80.6415
KNN	88.5271	81.9906	81.9852	81.9915	0.8243	1004.5215
BP	88.0743	88.0334	88.0235	88.0256	0.8802	65.2154
SVM	90.2562	88.2513	88.2655	88.3457	0.8837	85.2155
LSTM	89.5419	88.5446	88.4562	88.4454	0.8850	70.2524
CNN	92.5348	90.5348	90.5298	90.5302	0.9053	1260.5138
RF	100	92.6337	92.5821	92.5962	0.9260	61.2544
LightGBM	91.5462	90.3325	90.3015	90.3154	0.9024	136.4562
Xgboost	84.8545	82.6514	82.6545	82.6351	0.822 9	391.5559
GBDT	76.4321	72.7536	71.4545	72.4524	0.7213	879.3654
Bls	80.2762	79.4621	79.2346	79.3166	0.7834	0.0234
Fbls	97.6652	89.8242	89.7643	89.1346	0.89134	50.1345
Bp + Bls	94.5415	91.5626	91.5654	91.5662	0.9155	70.4563
Rf + bls	91.5469	90.3248	90.2365	90.2436	0.9024	72.2563
Cnn + Bls	96.5424	92.3658	92.3668	92.3754	0.9238	1500.1349
Cnn + fbls	98.3164	91.6542	91.6525	91.6564	0.9165	1608.4304
Bp + fbls	95.4454	91.3556	91.3541	91.3561	0.9136	72.5546
DenseNet-LSTM-FBLS	93.7651	92.7141	92.7145	0.9271	86.1246	86.1246

, the proposed DenseNet-LSTM-FBLS model achieves a test set accuracy of 92.71%, which is the highest among all 18 baseline and hybrid models compared. This result strongly validates the effectiveness of our proposed architecture. Discussion on Performance and Runtime. The superiority of our model can be attributed to its synergistic design. Compared to standalone models like LSTM (88.54%) or CNN (90.53%), our integrated framework shows a significant performance boost, confirming that simultaneously modeling spatial and temporal features is crucial. Furthermore, the model’s computational efficiency was evaluated. As shown in the training time, our model (86.12 s) demonstrates a remarkable balance. While a precise FLOPS (Floating-Point Operations per Second) comparison is complex due to the varied architectures of the baseline models, a theoretical analysis supports the efficiency of the FBLS architecture. Unlike traditional deep networks that rely on computationally expensive, iterative backpropagation through many layers, the FBLS primarily depends on pseudoinverse calculations, which are non-iterative and significantly faster. This structural advantage leads to a substantially lower computational load compared to other high-performing deep learning hybrids like CNN+BLS (1500.13 s), making the proposed model highly suitable for scenarios requiring periodic retraining with new data. This highlights the efficiency of the FBLS architecture compared to traditional deep, layered training paradigms, making our model more suitable for scenarios requiring periodic retraining with new data. The comparison with earlier works, such as the graph-based methods, suggests that our framework provides a competitive alternative, particularly excelling in its ability to handle data uncertainty and reduce computational overhead through the novel use of FBLS.

The analysis acknowledges that the feature concatenation mechanism inherent in DenseNet’s dense connectivity pattern results in a higher computational overhead compared to standard CNNs. However, this architectural choice is a deliberate trade-off, justified by the model’s enhanced ability to capture complex spatial hierarchies, which leads to a significant accuracy improvement as validated by the ablation study.

To further dissect the contribution of each key component within our proposed framework, we conducted a series of ablation studies. We compared our full model (DenseNet-LSTM-FBLS) against three degraded variants:

CNN-LSTM-FBLS: Replaces the DenseNet block with a standard Convolutional Neural Network (CNN) to evaluate the effectiveness of the dense-connectivity pattern for spatial feature extraction.

LSTM-FBLS: Removes the spatial feature extraction component entirely to isolate the contribution of modeling spatial correlations.

DenseNet-LSTM-BLS: Replaces the Fuzzy Broad Learning System (FBLS) with a standard Broad Learning System (BLS) to assess the impact of the fuzzy subsystem in handling data uncertainty.

As shown in

Table 7. Ablation Study of Model Components.

Model	Accuracy/%	Precision/%	Recall/%	F1-Score
LSTM-FBLS (No Spatial)	89.15	89.08	89.05	0.8906
CNN-LSTM-FBLS	91.24	91.22	91.23	0.9122
DenseNet-LSTM-BLS (No Fuzzy)	91.88	91.85	91.86	0.9185
DenseNet-LSTM-FBLS (Full Model)	92.71	92.71	92.71	0.9271

, the results of the ablation study clearly demonstrate the value of each component. The performance drops from 92.71% to 89.15% when the spatial feature extractor is removed (LSTM-FBLS), underscoring the importance of modeling airport network dependencies. Using DenseNet (92.71%) provides a clear advantage over a standard CNN (91.24%), confirming its superior ability to capture complex spatial hierarchies. Finally, the use of FBLS (92.71%) over a standard BLS (91.88%) leads to a notable improvement, validating our hypothesis that the fuzzy component effectively enhances the model’s ability to handle the inherent uncertainties in the data, leading to higher predictive accuracy. This marginal accuracy gain of 0.83 percentage points (92.71% vs. 91.88%), while numerically moderate, is significant in the context of complex systems prediction. This improvement, coupled with the FBLS’s theoretical advantage in mitigating uncertainty through fuzzy logic, demonstrates a favorable accuracy-efficiency trade-off and strongly justifies its integration into the proposed architecture.

4. Conclusions

This study addressed two persistent challenges in the field of flight delay prediction: the accurate modeling of complex, intertwined spatio-temporal dependencies and the high computational demands of conventional deep learning models that hinder real-time application. To overcome these hurdles, we designed, implemented, and validated a novel hybrid architecture, the DenseNet-LSTM-FBLS model.

Our primary contribution lies in the synergistic integration of three powerful components. First, we leveraged a DenseNet-LSTM framework to effectively extract critical features from the high-dimensional flight data. The DenseNet component adeptly captured the complex spatial correlations between airports, such as cascading congestion, while the LSTM component modeled the temporal evolution of delays and the impact of time-series variables like weather. This dual approach ensures that the model learns from both the network topology and the sequential nature of flight operations.

Second, while a Bayesian Optimization approach was employed for hyperparameter tuning, future work could explore the comparative performance of other heuristic algorithms (e.g., genetic algorithms, particle swarm optimization) or expand the optimization search space to include parameters from the DenseNet-LSTM feature extractor itself.

The proposed model was rigorously tested on a large-scale, real-world dataset comprising 198,970 flights across 123 European airports. The experimental results unequivocally demonstrate the superiority of our approach. The DenseNet-LSTM-FBLS model achieved a predictive accuracy of 92.71%, outperforming a comprehensive suite of 18 baseline models, including individual components (LSTM, CNN, BLS), established machine learning algorithms (SVM, RF), and other hybrid models (BP+FBLS, CNN+FBLS). This confirms that our integrated architecture is more effective than its constituent parts, successfully capturing the complex patterns that other models miss.

The significance of these findings is twofold. From a technical standpoint, we have shown that combining deep feature extraction with broad, fuzzy learning systems is a highly effective strategy for complex predictive tasks. From a practical standpoint, a model with this level of accuracy and efficiency offers tangible value to the aviation industry. It can empower airlines and airport authorities with a more reliable tool for proactive decision-making, leading to optimized resource allocation, improved operational efficiency, and ultimately, a better travel experience for passengers.

While the results are promising, we acknowledge several limitations that open avenues for future research. First, this study was conducted exclusively on a European dataset from a pre-pandemic period. Future work should validate the framework’s generalizability by testing it on air traffic networks from other regions (e.g., North America, Asia) and on more recent, post-pandemic data to assess its robustness to different operational environments and structural shifts in traffic patterns. Second, the parameters of the FBLS were set based on a predefined search range. Employing systematic hyperparameter optimization techniques, such as Bayesian optimization, could potentially unlock further performance gains and reduce model complexity. Third, while the FBLS component is inherently more interpretable than “black box” models, future research could focus on extracting and analyzing the learned fuzzy rules to provide human-readable insights into the key drivers of flight delays. Finally, integrating additional real-time data sources, such as air traffic control directives or social media data on emergent disruptions, could further enhance the model’s predictive power. The success of this hybrid framework also suggests its potential for adaptation to other complex network-based prediction problems, such as in public transportation or logistics management.