Deep Reinforcement Learning for Real-Time Airport Emergency Evacuation Using Asynchronous Advantage Actor–Critic (A3C) Algorithm

Abstract

Emergencies can occur unexpectedly and require immediate action, especially in aviation, where time pressure and uncertainty are high. This study focused on improving emergency evacuation in airport and aircraft scenarios using real-time decision-making support. A system based on the Asynchronous Advantage Actor–Critic (A3C) algorithm, an advanced deep reinforcement learning method, was developed to generate faster and more efficient evacuation routes compared to traditional models. The A3C model was tested in various scenarios, including different environmental conditions and numbers of agents, and its performance was compared with the Deep Q-Network (DQN) algorithm. The results showed that A3C achieved evacuations 43.86% faster on average and converged in fewer episodes (100 vs. 250 for DQN). In dynamic environments with moving threats, A3C also outperformed DQN in maintaining agent safety and adapting routes in real time. As the number of agents increased, A3C maintained high levels of efficiency and robustness. These findings demonstrate A3C’s strong potential to enhance evacuation planning through improved speed, adaptability, and scalability. The study concludes by highlighting the practical benefits of applying such models in real-world emergency response systems, including significantly faster evacuation times, real-time adaptability to evolving threats, and enhanced scalability for managing large crowds in high-density environments including airport terminals. The A3C-based model offers a cost-effective alternative to full-scale evacuation drills by enabling virtual scenario testing, supports proactive safety planning through predictive modeling, and contributes to the development of intelligent decision-support tools that improve coordination and reduce response time during emergencies.

1. Introduction

Emergencies in aviation settings demand rapid, informed decision-making under conditions of uncertainty, high population density, and constrained infrastructure. As passenger volumes increase and airport operations grow more complex, even localized disruptions, fires, mechanical failures, or security threats can escalate rapidly, endangering lives and straining existing emergency response systems. Although aircraft evacuations follow stringent time-based regulations, most notably the Federal Aviation Administration (FAA)’s 90 s rule, which mandates that all passengers and crew must be able to evacuate the aircraft within 90 s using only half the available exits during certification tests, no comparable standard exists for evacuations in airport terminals. Terminal evacuations must contend with a broader range of variables, including architectural variability, unpredictable threat dynamics, and diverse passenger behavior [1,2,3].

Conventional evacuation planning strategies often rely on static models or pre-scripted procedures that fail to adapt to evolving threats or complex human behaviors. Numerous studies have explored the use of agent-based simulations to evaluate evacuation strategies in airports and large crowd settings [4,5,6], emphasizing factors such as exit placement, group movement, and accessibility. However, these models often lack adaptability and scalability. Notably, efforts to simulate diverse populations, including individuals with disabilities, are limited, despite their heightened vulnerability during evacuations [7,8].

Recent advances in machine learning and artificial intelligence (AI) offer promising alternatives to traditional models by enabling dynamic, data-driven decision-making. Machine learning has been used to predict passenger flow [9,10] and enhance threat detection using computer vision [11,12], but these applications focus primarily on pre-incident stages of emergency management. More recent developments in reinforcement learning present an opportunity to optimize decision-making during evacuations themselves. Reinforcement learning agents can learn and refine strategies in real time by interacting with their environment and receiving feedback, making reinforcement learning particularly well-suited for high-stakes, uncertain conditions [13].

Among the reinforcement learning approaches, the Asynchronous Advantage Actor–Critic (A3C) algorithm has shown considerable advantages over earlier methods like Deep Q-Networks (DQN), particularly in terms of training speed, policy convergence, and scalability in multi-agent systems [14,15,16]. While A3C has demonstrated promise in theoretical and constrained settings, its application to realistic airport evacuations remains limited in the existing literature. Studies integrating social force models and reinforcement learning [17,18], as well as multi-agent simulation frameworks [19,20,21] suggest the potential for improved coordination and decision-making among agents. However, few efforts have directly compared A3C to DQN within complex, dynamic airport environments, particularly under varied agent densities and evolving threat scenarios. In addition, behavioral and psychological responses to emergencies remain a critical but underrepresented aspect of modeling. As Vorst [22] and Wang et al. [23] note, panic, group cohesion, and decision inertia can significantly affect evacuation timelines. Integrating such behavioral insights into evacuation algorithms can enhance their realism and usability, yet many current models assume ideal or fully rational agent behavior, overlooking critical human factors.

This study addresses these gaps by developing a real-time, simulation-based evacuation model that compares the performance of A3C and DQN algorithms under diverse emergency scenarios. Built within a custom airport environment using OpenAI’s Gym toolkit, version 0.26.2, the model tests algorithmic performance across single- and multi-agent configurations and in both static and dynamically evolving threat contexts. The study’s core objectives are threefold: (1) assess the ability of each algorithm to generate efficient and adaptive evacuation routes; (2) evaluate responsiveness to dynamic threat conditions such as fire spread or moving hazards; and (3) examine coordination and performance in multi-agent environments where emergent behavior and congestion effects are likely to occur. By testing algorithm performance across varying threat types and agent configurations, the model provides a deeper understanding of how intelligent systems can support timely and adaptive evacuation decisions. This approach extends beyond static planning by incorporating dynamic threat evolution, agent interactions, and realistic spatial constraints. The findings offer practical implications for the development of AI-assisted evacuation support tools, with the potential to enhance operational resilience and safety outcomes in high-density transportation environments.

2. Materials and Methods

This study utilized two advanced reinforcement learning algorithms, A3C and DQN, to develop a simulation-based decision-making model tailored for emergency evacuation scenarios in airport environments. By modeling realistic agent behaviors and environmental threats, the study aimed to assess the performance of both algorithms in navigating dynamic, constrained spaces under high-pressure conditions.

2.1. Asynchronous Advantage Actor–Critic (A3C) Algorithm

The A3C algorithm is a powerful reinforcement learning method designed to address the limitations of traditional, synchronous learning models. In the context of emergency evacuations, especially in dynamic environments such as airports, rapid and effective decision-making is critical. This study employed A3C to simulate and optimize evacuation strategies, aiming to improve both speed and efficiency under unpredictable conditions. A3C offers key advantages by allowing multiple agents (actors) to interact with separate copies of the environment in parallel (Figure 1). This structure accelerates learning and reduces redundancy across training episodes, making A3C well-suited for time-sensitive applications like evacuation planning.

The A3C algorithm utilizes a dual-component framework composed of an actor and a critic, which together implement the actor–critic architecture. The actor defines the policy function, which is discussed in further detail below, and determines the probability of selecting each action based on the current state of the environment. Its primary role is to guide agents toward optimal decisions to maximize long-term rewards. In contrast, the critic evaluates the performance of the actor by estimating the value function of the current policy, computing an advantage score that helps refine the actor’s decision-making strategy. By leveraging both components, A3C effectively integrates the strengths of policy-based and value-based reinforcement learning approaches. Policy-based methods offer the flexibility to directly optimize behavior by mapping states to actions, which is particularly useful in high-dimensional or continuous action spaces. Meanwhile, value-based methods generally provide more stable and lower-variance estimates, although they may be less efficient in complex environments [13]. A3C’s hybrid structure capitalizes on the benefits of both strategies, making it well-suited for a broad range of reinforcement learning problems.

In this framework, the policy parameter θ guides agent actions, while the value function parameter θᵥ assesses the quality of those actions. Both θ and θᵥ are implemented using CNNs with shared parameters, excluding their output layers. A softmax function is applied to θ to produce a probability distribution over possible actions, while θᵥ uses a linear layer to output a scalar value representing the estimated return.

At the beginning of the algorithm, the global shared counter T is initialized to zero, and the local thread step counter is set to one. The algorithm defines two types of parameter vectors: global shared parameters θ and θv, and thread-specific parameters θ′ and θ’v. At each iteration, the thread-specific parameters θ′ and θ’v are synchronized with the global parameters. The system then interacts with the environment, selecting an action a_t based on the current state St and the policy π (a_t∣St; θ′). Upon executing the action, the agent receives a reward rt a and observes the next state St + 1. This process continues until a terminal state is reached or the number of steps taken exceeds t − t_start.

If the episode terminates, indicating the end of the agent’s trajectory, the expected return R is set to zero since no additional rewards are available. If the episode ends at a non-terminal state, the return is estimated using the value function: R = V (st, θ′v). The algorithm then backpropagates through time from step t − 1 to t_start, calculating the return and the gradients with respect to θ′ and θ′v. The return $R_t$ is computed as the sum of discounted rewards from time t to the end of the episode:

$$R_t=r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\dots +{\gamma }^{T-t}{r}_T$$

(1)

In Equation (1), shown above, r_t; represents the reward at time t, and γ is the discount factor (ranging from 0 to 1) that determines the importance of future rewards. A smaller γ places more emphasis on immediate rewards, while a value closer to 1 prioritizes long-term outcomes. In this study, γ was set to 0.99 to reflect the critical importance of long-term decision-making in successful airport evacuations, such as avoiding delayed threats or navigating congested paths. While a value of 1 technically maximizes the weight of future rewards, it can lead to unstable learning due to the absence of discounting, especially in environments with noisy or non-stationary dynamics. Setting γ to 0.99 strikes a practical balance: it emphasizes long-term outcomes while maintaining numerical stability and facilitating more consistent policy convergence. Through hyperparameter tuning, 0.99 was identified as the most effective setting for this domain, offering improved learning stability without sacrificing the algorithm’s ability to plan for long-term goals.

The A3C algorithm belongs to the policy gradient family and uses the temporal difference (TD) error as a critic to evaluate the actor’s performance. The empirical estimate of the policy gradient for reinforcement learning problems is given by

$${\nabla }_{\mathsf{\theta }}{R}_{\mathsf{\theta }}\approx {\displaystyle \frac{1}{N}}{\displaystyle \sum _{n=1}^N}{\displaystyle \sum _{t=1}^{T_n}}\begin{array}{c}\left({\displaystyle \sum _{t^{\prime }=t}^{T_n}}{\mathsf{\gamma }}^{t^{\prime }-t}{r}_{t^{\prime }}^n-b\right){\nabla }_{\mathsf{\theta }}\mathrm{l}\mathrm{o}\mathrm{g}{\mathsf{\pi }}_{\mathsf{\theta }}\left(a_t^n|s_t^n\right)\end{array}$$

(2)

In this equation, N denotes the number of trajectories (or episodes), and T_n is the number of time steps in the n-th trajectory. The discount factor γ, set to 0.99 in this study, emphasizes the importance of long-term rewards. The inner summation computes the cumulative discounted return from time step t onward, while b represents a baseline, typically an estimate from the critic’s value function, to reduce variance in the gradient estimate. The policy ${\mathsf{\pi }}_{\mathsf{\theta }}\left(a_t^n|s_t^n\right)$defines the probability of selecting action $a_t^n$ given state $s_t^n$ under the current policy parameters θ. The gradient of the log-policy ${\nabla }_{\mathsf{\theta }}\mathrm{l}\mathrm{o}\mathrm{g}{\mathsf{\pi }}_{\mathsf{\theta }}\left(a_t^n|s_t^n\right)$is scaled by the advantage, guiding the update of the policy toward actions that yield higher-than-expected returns. This formulation enables stable and efficient learning in complex, high-dimensional environments such as airport evacuations. This approach enhances both the stability and convergence properties of policy gradient methods.

A key feature in A3C is the advantage function, which captures the difference between the expected return of taking a particular action in each state and the expected value of following the current policy in that same state. The basic form is

$${Advantage(A}_t)=R_t-V\left(s_t\right)$$

(3)

where $R_t$ is the cumulative discounted return from time t, and $V\left(s_t\right)$ is the critic’s estimate of the state value. The advantage function quantifies how much better (or worse) an action performed compared to the policy’s expected outcome. More specifically, the advantage can be computed as follows:

$$A\left(s_t,a_t\right)=r_t+\mathsf{\gamma }{V}^{\mathsf{\pi }}\left(s_{t+1}\right)-V^{\mathsf{\pi }}\left(s_t\right)$$

(4)

Here, $r_t$ is the immediate reward, $V^{\pi }\left(s_{t+1}\right)$ is the estimated value of the next state, and $V^{\pi }\left(s_t\right)$ is the estimated value of the current state. This expression captures the temporal difference between the observed reward and the expected value. To update the policy parameters based on this advantage, the A3C algorithm uses the following policy gradient update rule:

$${\nabla }_{\mathsf{\theta }}J\left(\mathsf{\theta }\right)\approx {\nabla }_{\mathsf{\theta }}\log {\mathsf{\pi }}_{\mathsf{\theta }}\left(a_t|s_t\right)A\left(s_t,a_t\right)$$

(5)

In this expression, ${\mathsf{\pi }}_{\mathsf{\theta }}\left(a_t|s_t\right)$represents the probability of selecting action $a_t$given state $a_t$ under the current policy parameterized by θ. The A3C algorithm is built on an actor–critic architecture, which consists of two components: the actor and the critic. The actor defines the policy function, ${\mathsf{\pi }}_{\mathsf{\theta }}\left(a_t|s\right),$which models a probability distribution over possible actions based on the current state. In this study, the policy is implemented using a convolutional neural network (CNN), with shared layers between the actor and critic except for their respective output layers. The actor’s output passes through a softmax activation function to produce a normalized distribution across all actions, allowing the agent to select actions stochastically during training and thereby promote exploration. During learning, the gradient of the expected return is scaled by the advantage function, guiding the policy updates to increase the likelihood of actions that perform better than expected under the current value estimates.

In practical applications, the A3C algorithm enhances learning performance by incorporating an entropy regularization term, which serves to promote exploration throughout the training process. This mechanism encourages the agent to occasionally select actions with less certainty or prior knowledge rather than strictly exploiting known strategies. By doing so, the agent interacts more broadly with the environment and learns from a wider range of experiences. This approach helps address one of the core challenges in reinforcement learning: the exploration–exploitation trade-off, where the agent must balance immediate gains from known actions with the potential long-term benefits of discovering new ones (Figure 2).

To effectively manage this trade-off, the overall loss function used in A3C combines three key components: the policy gradient loss, the value function loss, and the entropy regularization term. The complete objective function optimized during training can be expressed as follows:

$$L\left(\mathsf{\theta }\right)=-\log {\mathsf{\pi }}_{\mathsf{\theta }}\left(a_t|s_t\right)A\left(s_t,a_t\right)+\mathsf{\lambda }{\left(V\left(s_t\right)-\widehat{V}\left(s_t\right)\right)}^2-\mathsf{\beta }\sum _a{\mathsf{\pi }}_{\mathsf{\theta }}\left(a|s_t\right)\log {\mathsf{\pi }}_{\mathsf{\theta }}\left(a|s_t\right)$$

(6)

The first term in this equation, $-\log {\mathsf{\pi }}_{\mathsf{\theta }}\left(a_t|s_t\right)A\left(s_t,a_t\right)$, represents the policy gradient loss. This term directs the learning process by increasing the probability of actions that lead to higher-than-expected returns, as determined by the advantage function $A\left(s_t,a_t\right)$. Conversely, actions resulting in lower-than-expected outcomes are discouraged, thereby refining the policy toward more effective decision-making.

The second term, $\mathsf{\lambda }{\left(V\left(s_t\right)-\widehat{V}\left(s_t\right)\right)}^2$, corresponds to the value function loss. It uses a mean-squared error to penalize inaccuracies in the agent’s predicted value of the current state. The current estimate $V\left(s_t\right)$ is compared to a target value $\widehat{V}$, which is calculated using bootstrapped returns. Ensuring the accuracy of this value function is essential for the reliable computation of advantage values and, in turn, for guiding efficient policy updates.

The final term, $-\mathsf{\beta }{\sum }_a{\mathsf{\pi }}_{\mathsf{\theta }}\left(a|s_t\right)\log {\mathsf{\pi }}_{\mathsf{\theta }}\left(a|s_t\right)$, is the entropy regularization term. It promotes exploratory behavior by discouraging the policy from becoming overly deterministic. This encourages the agent to continue exploring a variety of possible actions, rather than prematurely converging on a narrow set of choices. The coefficient β controls the strength of this regularization. A higher β value encourages greater exploration by increasing the penalty for low-entropy (i.e., predictable) policies, while a lower β value allows the agent to focus more on exploiting known high-reward actions. In this study, β was set to 0.01 based on hyperparameter tuning, striking a balance between adequate exploration and stable policy convergence. Such exploration is critical for long-term performance, especially in complex or dynamic environments. As the training process seeks to minimize this composite loss function, both the policy and the value function parameters are refined simultaneously. This joint optimization allows the A3C algorithm to steadily improve the agent’s strategy over time, enabling it to make increasingly effective decisions while maintaining a balance between exploiting known information and exploring new possibilities.

2.2. Deep Q-Network (DQN) Algorithm

To evaluate efficiency in terms of time and learning performance, this study utilized the Q-learning algorithm, implemented through DQN, to simulate airport evacuation procedures. DQN was selected as the primary baseline model due to its widespread use in reinforcement learning research, including evacuation and other simulation-based environments. As one of the earliest and most influential deep reinforcement learning algorithms, DQN demonstrated that neural networks could effectively approximate Q-values in high-dimensional state spaces. This strength makes DQN well-suited for handling the complexity of airport evacuation scenarios and provides a reliable benchmark for comparing the performance of the A3C algorithm.

Q-learning, the underlying algorithm of DQN, is a value-based reinforcement learning method that aims to learn the optimal value of an action in each state to maximize cumulative reward. The Q-learning algorithm serves as the core foundation of the DQN, which was used in this study to simulate airport evacuation scenarios. At the start of training, Q-values are initialized arbitrarily, providing a baseline from which the learning process begins. These Q-values represent the estimated utility of taking a specific action in a given state. As the agent interacts with the environment, these estimates are updated iteratively based on observed outcomes. Each training episode starts with the initialization of the environment’s state, such as the initial positions of agents within the airport terminal.

Throughout each episode, actions are selected using an ε-greedy policy. This strategy promotes a balance between exploitation and exploration. With a probability of 1 − ε, the agent selects the action with the highest current Q-value, exploiting known information. With a probability of ε, it chooses an action at random, allowing for the exploration of alternative strategies. This trade-off helps the agent avoid premature convergence to suboptimal policies and improves its adaptability over time.

Once an action is taken, the agent receives an immediate reward and transitions to a new state. The Q-value is then updated using the Bellman equation, which integrates the current estimate, the observed reward, and the discounted estimate of future rewards. The update rule is expressed as follows:

$$Q\left(s,a\right)\leftarrow Q\left(s,a\right)+\alpha \left[r+\gamma \max \left(over a^{\prime }\right)Q\left(s^{\prime },a^{\prime }\right)-Q\left(s,a\right)\right]$$

(7)

In this formula, $Q\left(s, a\right)$ is the current value estimate for taking action α in state s, α is the learning rate that determines how quickly the model adapts to new information, $r$is the reward received, and γ is the discount factor that weighs the importance of future rewards. The agent continues this process step by step until a terminal state is reached, marking the end of an episode. This iterative learning process allows the agent to develop increasingly effective evacuation strategies in response to dynamic challenges.

DQN enhances classical Q-learning by incorporating a deep neural network to estimate the Q-value function, which is particularly useful for managing complex, high-dimensional environments such as airports. In addition, DQN leverages experience replay, a mechanism that stores past transitions in a memory buffer. During training, random samples from this buffer are used to update the neural network. This approach helps reduce the correlation between sequential experiences, prevents overfitting to recent events, and improves overall training stability. Over time, the DQN algorithm refines its Q-value estimates, allowing it to identify optimal evacuation strategies that adapt to changing conditions and agent behaviors.

The application of the DQN algorithm in this study provided an effective platform for simulating airport evacuations and offers a solid benchmark for evaluating the performance of more advanced methods, such as the A3C. By comparing DQN and A3C within the same simulation framework, this research highlighted their respective strengths and limitations. DQN’s effectiveness in handling complex decision-making and its capacity for gradual improvement make it a reliable standard. However, the comparison also reveals potential advantages of A3C in areas such as learning efficiency, scalability, and responsiveness to dynamic environments. This comparative analysis provided deeper insight into the practical application of reinforcement learning algorithms for real-world emergency management challenges.

2.3. Hyperparameter Selection and Fairness Comparison

To ensure a fair and rigorous comparison between the A3C and DQN algorithms, both models were implemented using the same CNN architecture, which included two convolutional layers followed by a fully connected layer. In the A3C model, both the actor and critic shared this CNN backbone, but each had its own output layer. The actor’s output layer used a softmax activation function to produce a probability distribution over all possible actions, allowing the agent to make stochastic decisions during training. The critic’s output produced a single scalar value that estimated the expected cumulative future reward from a given state. This estimate was learned by comparing the critic’s prediction with the actual reward outcomes over a short sequence of steps and adjusting its predictions to better match observed returns. The critic, in essence, served to evaluate how well the actor’s decisions were performing and provided feedback to improve the policy.

In contrast, the DQN model used the same CNN structure to estimate the value of each possible action in a given state. These values, known as Q-values, were updated by comparing the current prediction with the reward received and the predicted value of the next state. To ensure stability during training, DQN used a separate target network and a replay memory buffer, which stored past experiences and allowed the model to learn from them in batches.

For hyperparameters, A3C used a learning rate of 0.0007, an entropy regularization coefficient of 0.01 to encourage exploration, a discount factor of 0.99 to prioritize future rewards, and the RMSProp optimizer. It also implemented gradient clipping to prevent instability and used four parallel training threads to accelerate learning. The DQN model was tuned with a learning rate of 0.0005, the same discount factor of 0.99, a replay buffer that could store 10,000 experiences, a batch size of 64 for training, and a target network that was updated every 1000 steps. Exploration in DQN was guided by an epsilon-greedy strategy, where the chance of choosing random actions gradually decreased from full exploration to more exploitative behavior.

These hyperparameters were selected through a combination of grid search, review of prior literature [24,25,26], and validation in smaller test environments before applying them to the full simulation. This method ensured that both models were tuned for optimal performance under comparable conditions, supporting a reliable and meaningful evaluation of their learning stability, efficiency, and evacuation capabilities.

2.4. Custom Gym Environment

The simulation environment used in this study was developed entirely using the OpenAI Gym toolkit [27]. Rather than relying on pre-existing Gym environments, a custom model was created to replicate the layout and operational flow of a real-world airport. This customized environment allowed reinforcement learning agents to interact under conditions resembling actual evacuation scenarios.

The Gym environment was structured around five main components: environment space, agents, observation, reward system, and episodes. The environment space consisted of a 50 × 50 grid representing a realistic airport floor plan. The environment’s 50 × 50 grid map was selected to match realistic scale, based on average human step length, approximately 2.2 to 2.5 feet (0.67 to 0.76 m) per step [28], allowing the simulation to reflect real-world movement rates during evacuation. Based on this step length, each cell in the grid corresponds to roughly 0.7 m, making the full environment approximately 35 m by 35 m, or 1225 square meters in area. This scale reflects the dimensions of a typical airport terminal section, such as a concourse or gate area [3], enabling more realistic modeling of agent behavior, movement, and congestion dynamics during simulated emergencies.

Within this space, agents could choose from nine possible actions: four cardinal directions, four diagonal directions, or remain stationary. The state space recorded the agent’s current location, while the action space defined all valid movement choices. Observations and scalar rewards provided feedback on actions, guiding agents toward optimal evacuation policies over time.

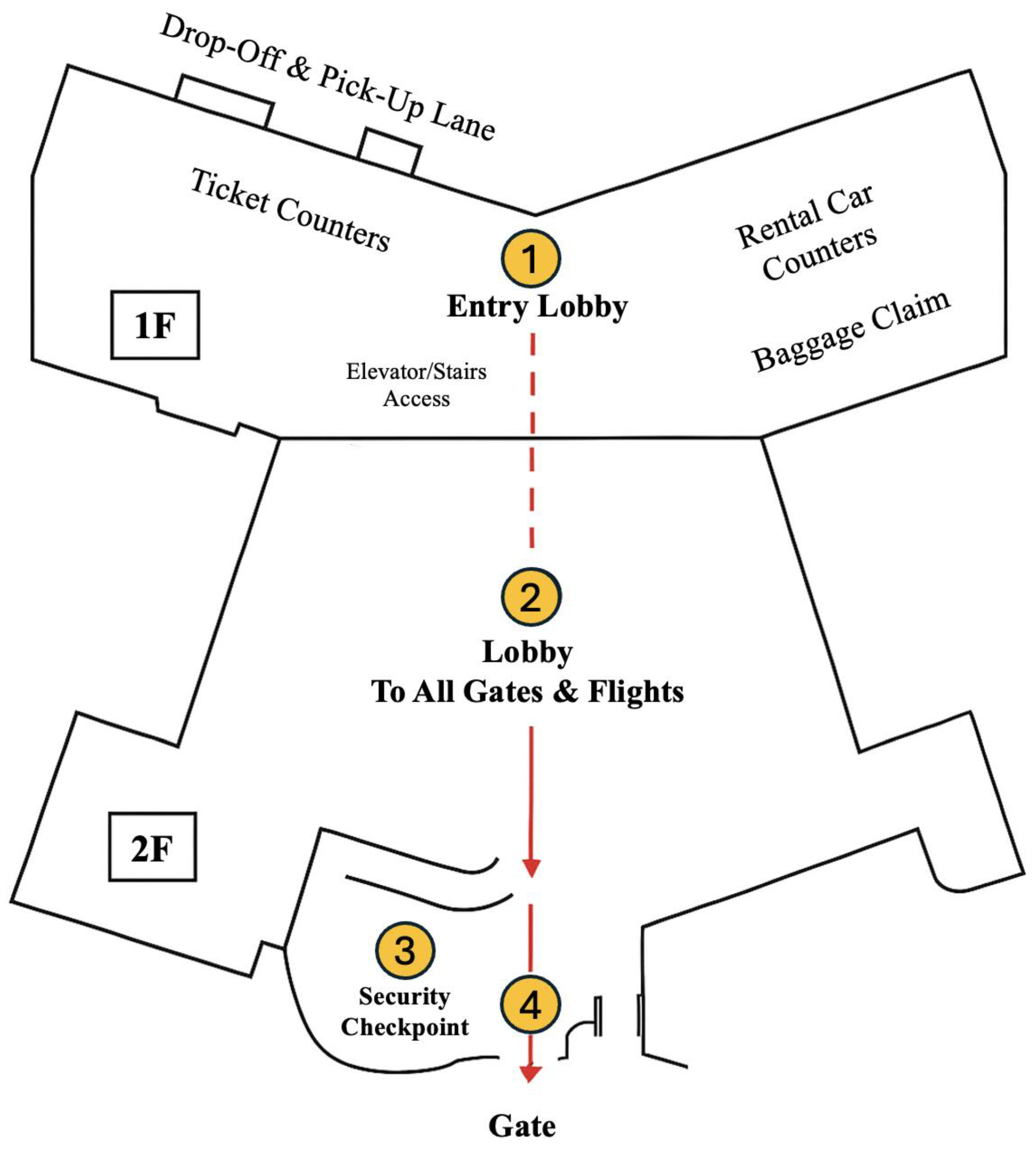
A realistic airport map was used as the base for this simulation (Figure 3), with an emphasis on the ground floor where check-in and security procedures take place (Figure 4). These phases were selected due to their higher risk of emergency incidents, such as bomb threats or fires. Other airport zones, like boarding gates, were excluded to maintain simulation focus and reduce complexity.

The custom map (Figure 4) included structural features such as walls, ticket counters, and baggage claim areas. A NumPy array was used to define wall positions, ensuring agents could not move through obstacles. The red arrows on the map indicate the path for departing passengers from check-in to boarding, while the red dotted line shows vertical movement from the 1F check-in area to the 3F departure lobby via elevator or escalator.

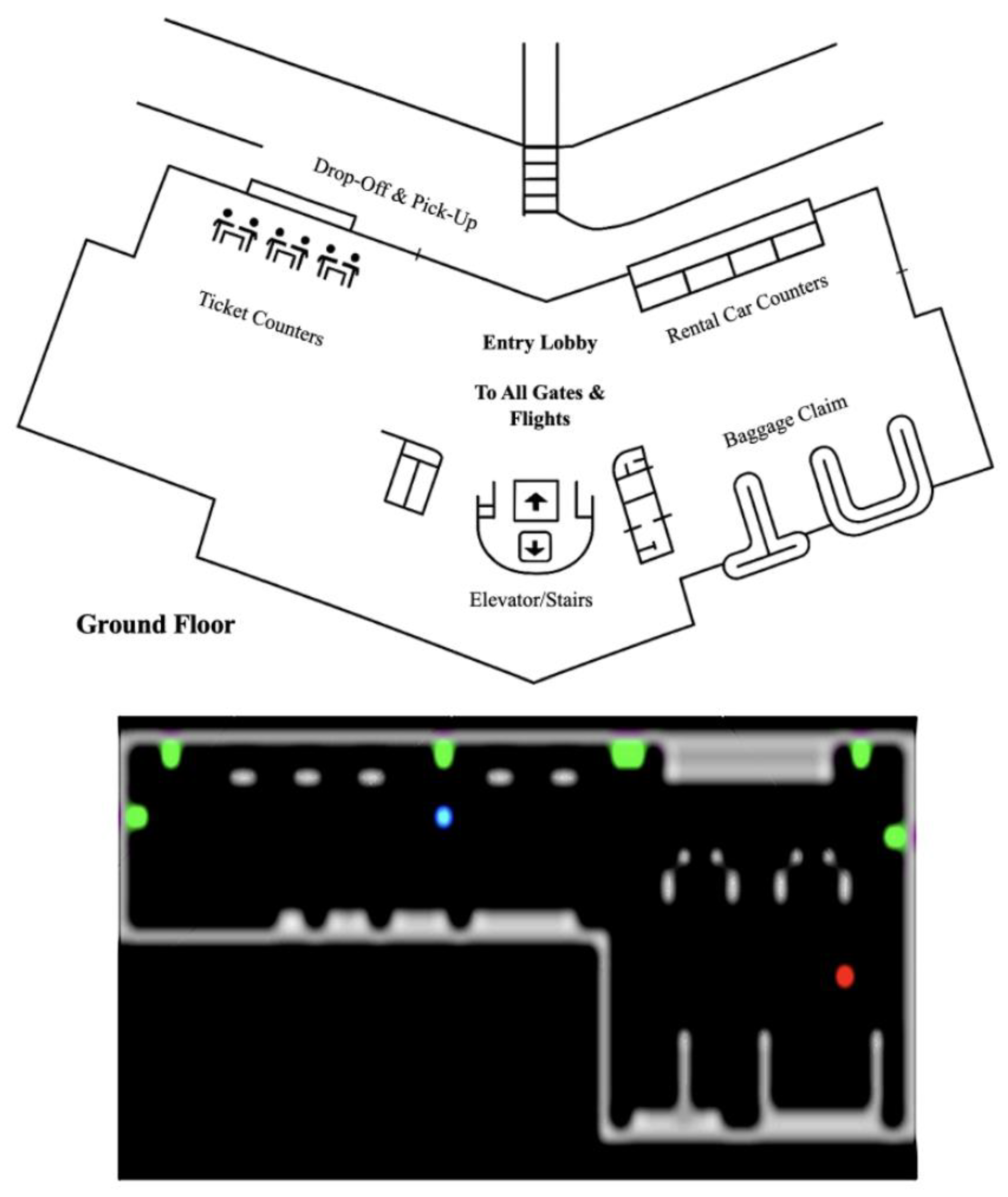
To simplify the layout within the custom Gym environment’s constraints, the airport floor was split into two sections and joined into a rectangular shape (Figure 5). This helped avoid angled hallways and upper-level rooms that would add simulation noise. The environment retained essential features, including emergency exits, rental counters, and threats, such as a bomb near the baggage claim. Figure 5 illustrates the terminal layout and its simulation representation. The red numbers (1–7) mark entry doors from the drop-off and pick-up lane into various sections of the terminal. Doors 1–3 lead to the ticket counters, doors 4–5 provide access to the main entry lobby, and doors 6–7 open near the rental car counters and baggage claim area. Green circles highlight the physical locations of these entry points. The blue-shaded area represents the terminal interior, while the red dot indicates a designated target or goal location. In the simulation map below, black areas denote walls or obstacles, gray areas are walkable paths, green squares indicate entry points, and the blue square marks a key element such as an agent or checkpoint.

This robust setup provided a consistent platform to evaluate different reinforcement learning algorithms, including DQN and A3C, under identical emergency conditions. Agents trained in this environment learned to recognize threat zones, avoid obstacles, and identify the fastest and safest exits.

2.5. Scenario Design

To evaluate agent behavior and algorithm performance under different emergency conditions, four distinct evacuation scenarios were designed within the custom Gym environment. The first scenario, the single-agent static threat environment, featured a lone agent navigating an airport space while avoiding a fixed-position threat, such as a bomb. With no interference from other agents, the simulation allowed the agent to freely explore the environment and develop an optimal evacuation route. This scenario served as a baseline, enabling focused analysis of learning efficiency without added complexity from crowd dynamics. Figure 6 illustrates the scenario layout and threat positioning.

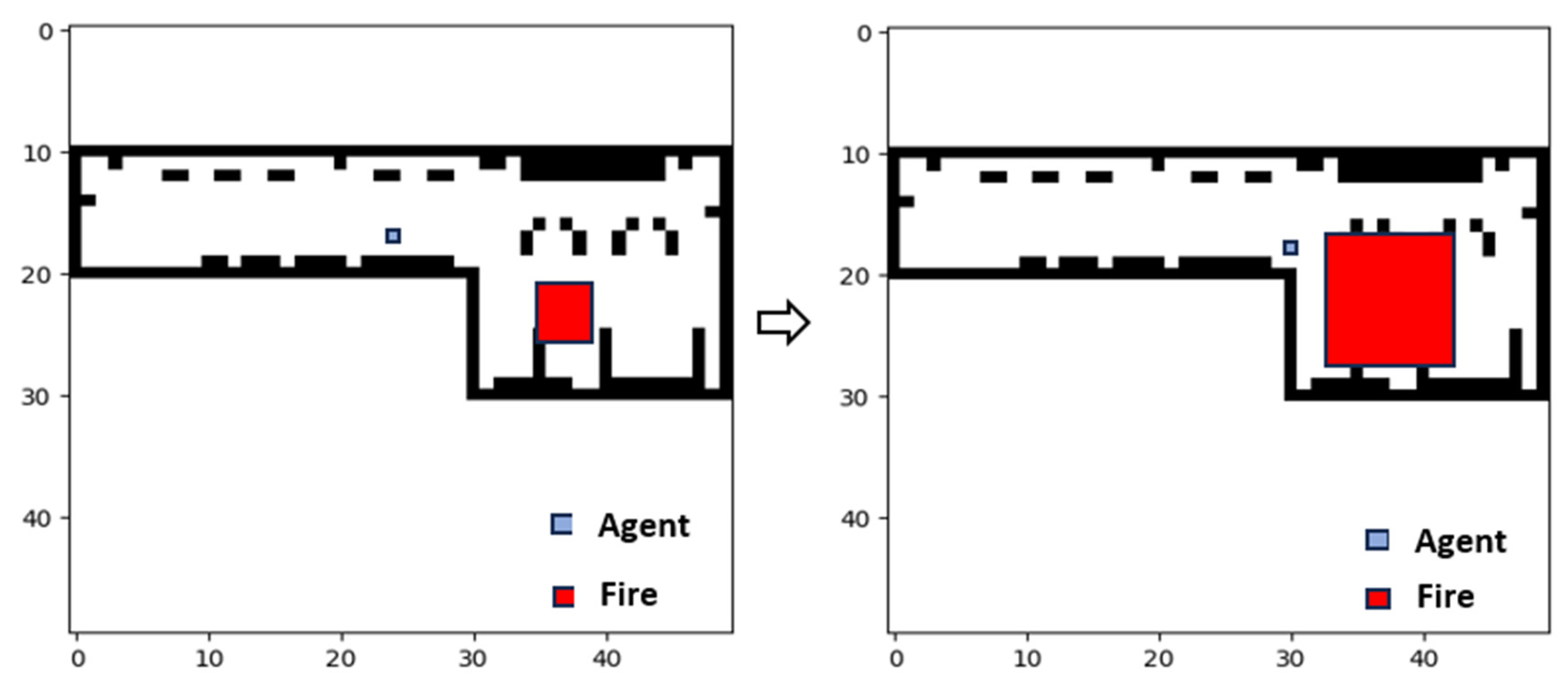
The second scenario introduced a single agent facing a dynamic hazard: a spreading fire. Replacing the static threat with a moving one added complexity, requiring the agent to continuously adapt its route in response to environmental changes. The fire’s behavior was modeled using a stochastic spread algorithm adapted from Martin [29], originally developed to simulate forest fires on an n × n grid. In this model, each burning cell evaluates its Moore neighborhood, comprising the eight surrounding cells, and attempts to ignite each neighbor based on a fixed ignition probability p, introducing localized randomness into the fire’s expansion. This stochastic behavior simulates the unpredictability of real-world fire dynamics, where the spread is influenced by environmental conditions and spatial variability.

To adapt the model for airport environments, two key modifications were made. First, fire spread was decoupled from the presence of specific “flammable” content, allowing the hazard to propagate across any unburned cell regardless of its occupancy status, representing the open-plan nature of terminal floors. Second, the fire’s spread was constrained by static obstacles such as walls or barriers; cells marked as obstacles in the environment grid were excluded from the ignition process, effectively blocking propagation. These changes increased the realism and challenge of the simulation, creating a dynamic, non-deterministic hazard that required the agent to navigate around evolving threats in a confined, structured space (Figure 7).

The third scenario, the multi-agent static threat environment, added multiple agents into the simulation while retaining the fixed-position bomb. This design tested the agents’ ability to coordinate and navigate through shared spaces without conflict or congestion. It also enabled the observation of emergent behaviors such as clustering or suboptimal decision-making due to blocked paths.

Finally, the most complex scenario combined multiple agents with a moving fire threat. In this setting, agents had to simultaneously avoid each other and dynamically adjust to a spreading hazard. This high-stakes simulation mimicked real-world emergency evacuations involving dense crowds and evolving threats, presenting a challenging benchmark for evaluating the adaptability and scalability of the learning algorithms.

Each scenario was executed within the same environment framework to ensure consistent benchmarking of the DQN and A3C algorithms. Threats were positioned near key areas such as baggage claim, mimicking likely emergency locations. The consistent layout across scenarios enabled fair comparison while capturing a broad range of realistic emergency conditions.

Overall, the scenario design paired with the custom environment provided a comprehensive and realistic testing ground for evaluating reinforcement learning models in emergency evacuation tasks. These varied settings facilitated a deeper understanding of individual and collective agent behavior under both static and dynamic threat conditions.

2.6. Simulation Setup

Simulations were executed on a high-performance workstation featuring an AMD Ryzen 5600X CPU, NVIDIA GeForce RTX 3060 Ti GPU, and 16 GB of RAM. Each training run consisted of 1000 episodes, and for each configuration, the entire training process was repeated across at least 50 independent trials. In this context, a trial refers to a full training run of 1000 episodes from random initialization to completion. This repetition ensured statistical reliability by accounting for variance due to stochastic elements in the environment and learning process. Metrics collected included cumulative reward per episode, average steps to evacuation, threat contact rate, and exit path usage frequency. This setup provided sufficient computational resources to capture performance trends and facilitated the robust comparison of algorithm behavior under identical environmental conditions.

2.7. Reward Function Design

The reward function was designed to guide agent behavior toward efficient and safe evacuation while penalizing undesirable outcomes. At each time step during an episode, agents received a step-wise penalty to encourage faster evacuation and discourage aimless wandering. Specifically, a small negative reward (e.g., −0.01) was assigned per time step to minimize the duration of the evacuation.

When an agent successfully reached an exit, it received a positive terminal reward, reinforcing the goal of efficient escape. Conversely, if the agent collided with a threat (such as fire or other hazards) or failed to evacuate within the episode limit, it received a large negative reward, representing a failure to complete the objective safely.

In multi-agent environments, if agents collided with each other, an additional penalty was applied to simulate realistic congestion and to promote decentralized coordination and collision avoidance behavior. This reward structure helped balance both individual agent safety and group movement efficiency.

The cumulative discounted rewards collected during each episode were used to compute the advantage function, which in turn informed policy updates during training. The design of the reward system thus reinforced both short-term efficiency and long-term survival, aligning with the real-world goals of minimizing evacuation time while avoiding hazards.

2.8. Reward Tuning

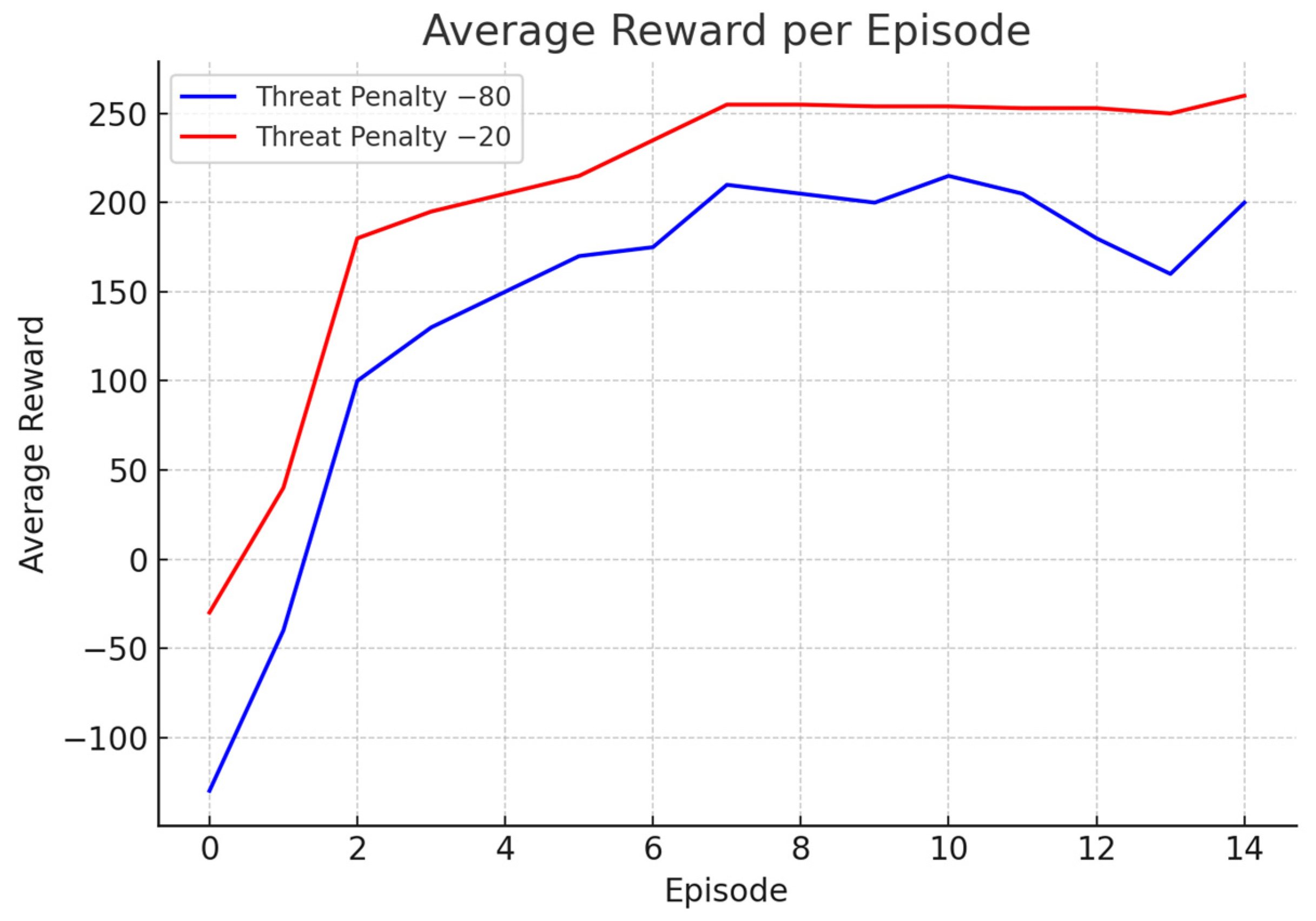
To fine-tune agent behavior, different threat penalty values were analyzed. As shown in Figure 8 and Figure 9, a penalty of −20 led to smoother and faster convergence, while a harsher penalty of −80 introduced volatility in the learning curve. This behavior indicated overly cautious exploration, with agents avoiding risk even when it meant bypassing optimal paths. The final reward structure, +200 for successful evacuation, −20 for threat contact, and −0.1 per step, was selected to balance safety, urgency, and learning efficiency. These values helped shape a strategy where agents could confidently explore the environment, learn optimal evacuation routes, and adapt to dynamic hazards without being overly deterred by risk.

3. Results

To assess and summarize the evacuation outcomes across varying conditions, the results were categorized into three distinct scenarios: a single-agent static threat environment, a single-agent moving threat environment, and a multi-agent environment. Within each scenario, evacuation simulations were executed using two algorithms, A3C and DQN, to evaluate their relative performance. The comparison focused on two key metrics: the time required for each successful evacuation (measured in seconds) and the cumulative rewards earned per episode, which reflected the learning efficiency of each algorithm. These metrics enabled the consistent evaluation of both algorithms under equivalent environmental conditions.

3.1. Static Threat Environment

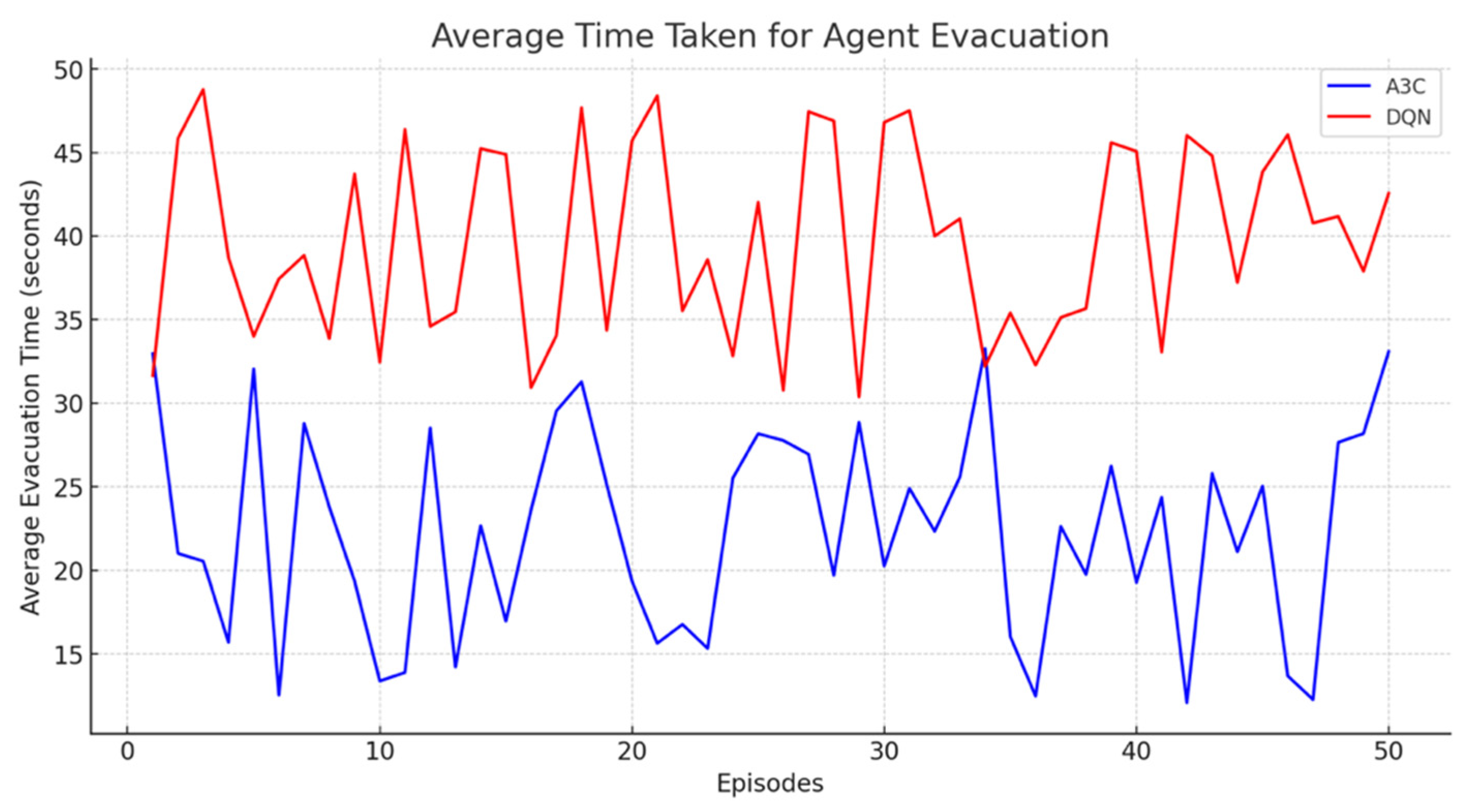
Efficiency was evaluated based on the average evacuation time (in seconds) required for a single agent to escape from a static threat environment. A3C outperformed DQN in this scenario. Figure 10 further highlights A3C’s superior performance (shown in blue), consistently achieving faster evacuation times than DQN (shown in red) across all episodes. The graph plots the number of episodes on the x-axis and the average evacuation time on the y-axis. Specifically, the average evacuation time for A3C was approximately 22.32 s, while DQN averaged around 39.75 s, indicating that A3C was about 43.86% more efficient.

This notable performance gap can largely be attributed to A3C’s asynchronous learning approach. Unlike DQN, which updates its strategy only after completing each episode, A3C utilizes multiple parallel threads to learn and update policies concurrently. This parallelism enables faster exploration and more efficient policy optimization. Additionally, the learning curves reveal differences in the number of episodes required for each algorithm to reach a stable evacuation strategy. A “stable evacuation strategy” was defined based on the convergence of both the average cumulative reward per episode and the average evacuation time, measured within a ±5% threshold over a moving window of 50 episodes. This ensured that convergence reflected not only consistent policy learning but also operational performance. A3C typically reached this stability between episodes 100 and 200, while DQN required 200–300 episodes (Figure 11). This discrepancy may be attributed to DQN’s learning structure, which typically demands more iterations to fully recognize and adapt to the environmental dynamics in this setting.

This analysis provides a detailed comparison of how A3C and DQN adapt and optimize their behaviors in response to environmental challenges. In the single-agent static threat environment, both A3C and DQN exhibited similar learning curve patterns, benefiting from the predictability of the threat to quickly develop effective strategies. However, A3C demonstrated a slight advantage in optimizing its strategy more rapidly, as evidenced by a steeper learning curve during the early episodes.

3.2. Moving Threat Environment

In the single-agent moving threat environment, the learning curves reveal significant differences in how each algorithm handles dynamic hazards. A3C demonstrated a faster learning rate, with a sharp reduction in the evacuation time as the agent quickly learned to anticipate and avoid the moving threat. In contrast, DQN required more time to adapt, exhibiting a slower progression toward a stable evacuation strategy, as reflected by the more gradual slope of its learning curve (Figure 12).

Compared to the relatively smooth and stable learning curves observed in the static threat environment, the results from the moving threat scenario were notably more volatile. Both A3C and DQN exhibited pronounced fluctuations across episodes, reflecting the ongoing challenge of adapting to a dynamic threat modeled as a spreading fire. These periodic variations in performance highlight the continuous cycle of learning and re-learning required to cope with the evolving hazard. A3C demonstrated a strong capacity for real-time adjustment, with its agent quickly recalibrating its strategy in response to the shifting threat. This adaptability stems from A3C’s asynchronous, multi-threaded learning framework, which enables rapid policy updates but can also lead to temporary performance dips as new behaviors are explored and integrated. Overall, the fluctuating curves underscore A3C’s robustness in managing complex, unpredictable environments through continual refinement and adaptation.

3.3. Multi-Agent Environment

In the multi-agent environment, simulations were limited to static threats, as moving threats failed to reach convergence. This limitation primarily arose from the rule-based collision avoidance mechanism implemented for agent interactions. Specifically, while the reinforcement learning agent learned evacuation strategies based on environmental observations and reward signals, the rule-based system operated as a hard-coded safety layer to prevent direct collisions between agents. This system overrode the reinforcement learning policy only in situations where agent trajectories would otherwise result in overlap or unsafe proximity. While this ensured a baseline level of realism and safety during training, it also introduced constraints that could limit the agent’s ability to learn more adaptive, cooperative strategies. As a result, the interaction between the learned policy and the rule-based system was semi-independent: the reinforcement learning agent guided strategic movement, while the rule-based logic enforced local separation. This separation of responsibilities contributed to stable training under static threat conditions but restricted the scalability of the model in more dynamic environments. Simulating realistic multi-agent behavior with moving threats would require not only extended training durations and more sophisticated neural network architectures but also an integrated policy that learns both threat avoidance and inter-agent coordination, potentially eliminating the need for rigid rule-based overrides.

The implementation of inter-agent collision avoidance further complicates the learning process. As the agent density increases, so does the unpredictability of emergent behaviors. For example, agents may begin to cluster in zones perceived as safe, inadvertently adopting suboptimal strategies that would not translate well to real evacuation scenarios. Effective evacuation under these conditions demands that agents learn cooperative behaviors, balancing individual threat avoidance with collective movement efficiency. This intricate interplay between individual decision-making and group dynamics significantly increases the learning burden on reinforcement learning models.

In static threat scenarios, however, the asynchronous nature of A3C demonstrated clear benefits, particularly in multi-agent settings. A3C’s design allows agents to learn concurrently and update shared policies, resulting in accelerated and more efficient convergence, as seen in the steeper learning curves. While DQN was able to support some level of cooperative behavior, its convergence was noticeably slower, underscoring its limitations in managing parallel learning processes typical of multi-agent systems.

A3C’s advantage lies in its ability to parallelize learning across agents. Each agent explores the environment independently but contributes to a shared policy update, enabling faster emergence of cooperative strategies. This structure is well-suited for complex evacuation scenarios, as demonstrated by the experimental outcomes in Figure 13, where A3C facilitated quicker coordination and improved policy performance.

In contrast, DQN’s sequential and centralized learning structure restricts its ability to process simultaneous experiences from multiple agents. This limitation results in slower policy refinement and reduces its effectiveness in adapting to dynamic, multi-agent environments. Consequently, DQN is less capable of supporting rapid coordination and mutual adaptation, key requirements for successful evacuation in high-stakes, multi-agent contexts.

A detailed analysis of exit selection patterns indicates that the A3C algorithm identifies more optimal evacuation routes than DQN. As illustrated in Figure 14, A3C results in a more evenly distributed use of available exits, demonstrating its superior ability to explore the environment thoroughly. This comprehensive exploration allows agents to select routes that align more closely with their starting positions, leading to shorter travel distances and quicker evacuations.

This performance advantage is largely due to A3C’s asynchronous, parallel learning architecture, which enables agents to adapt and coordinate efficiently in complex, dynamic environments. This capacity for real-time responsiveness is especially valuable in multi-agent contexts, such as collaborative robotics or crowd simulations, where rapid strategy formation and adaptation are critical. In scenarios like airport evacuations, where agents (e.g., passengers) must continually adjust to shifting threats and environmental changes, A3C’s flexibility and responsiveness offer a significant advantage. Its ability to continuously integrate new information and update decision-making strategies in real time makes it well-suited for high-stakes, real-world applications.

Overall, the results reveal a clear performance gap between A3C and DQN across various scenarios, including static threats, moving threats, and multi-agent configurations. In every case, A3C exhibited faster and more consistent learning, outperforming DQN in both route optimization and evacuation efficiency. This can be attributed to A3C’s strength in handling asynchronous updates and its superior adaptability to complex and evolving environments. While DQN performs reasonably well under simpler conditions, such as single-agent scenarios with static threats, it struggles to keep pace in environments that require simultaneous learning, rapid adaptation, and cooperative agent behavior, areas where A3C consistently excels.

4. Discussions

This study addressed a critical gap in the integration of simulation modeling, behavioral analysis, and reinforcement learning to enhance emergency evacuation outcomes in complex, high-stakes environments. By evaluating the A3C and DQN algorithms in realistic airport evacuation scenarios, this research extends current understanding of how adaptive decision-making models can support real-time emergency response.

Consistently with findings by Ding et al. [14], the results confirm A3C’s advantage in learning efficiency, adaptability, and responsiveness in dynamic environments. A3C outperformed DQN in all tested conditions, achieving faster convergence, smoother evacuation flows, and improved route selection. These results also align with Yao et al. [30], who demonstrated the utility of reinforcement learning in evacuation modeling under uncertainty. However, unlike single-layer models or group-based simulations, the present study applied A3C in multi-agent environments with evolving hazards, leveraging its parallel learning architecture to enhance coordination and scalability.

Beyond human behavioral considerations, specific challenges in aviation emergency scenarios include spatial constraints, time-critical operations, infrastructure complexity, and the coordination of heterogeneous agents, such as passengers with mobility limitations, security personnel, and autonomous systems. These physical and procedural constraints can significantly influence evacuation strategies and demand that decision-making models account for fixed obstacles, dynamic hazard propagation, communication delays, and security protocols unique to airport environments [31,32]. These factors complicate the learning environment and necessitate models that can generalize across rapidly changing and highly structured spatial conditions [33].

The results also underscore the feasibility and performance limitations of current reinforcement learning techniques in real-time emergency response. For instance, A3C required approximately 22.32 s on average to reach a solution, while DQN required 39.75 s. In real-world scenarios, such as an active fire or explosion, these timeframes may be impractical due to the rapidly deteriorating conditions. A delay of even 20 s could drastically alter the environment and jeopardize the validity of the learned policy [34]. To address this, hybrid approaches are recommended. These include using pre-trained models for rapid policy retrieval, deploying distributed edge computing for faster local inference, and integrating reinforcement learning agents with rule-based contingency protocols to account for abrupt, high-risk transitions. Moreover, real-time constraints could be addressed by leveraging transfer learning from previously simulated environments and periodically updating policies based on streaming sensor data, enabling models to adapt to changing scenarios without full retraining.

Although A3C demonstrated strong performance with static and semi-dynamic threats, the inability to achieve convergence with moving threats in the multi-agent environment presents a significant limitation. Real-world emergencies will involve numerous humans responding unpredictably to dynamic hazards such as fire, smoke, and hostile actors. The current reliance on static threat modeling limits the model’s ability to fully simulate stochastic interactions and emergent behaviors. This limitation stems from the challenges posed by the rule-based collision avoidance system, which constrained the agents’ learning by overriding RL-generated actions to prevent collisions. As a result, the interaction between the learned policy and the deterministic safety rules reduced the flexibility of learning under dynamic conditions.

To bridge this gap, future models should incorporate curriculum learning strategies where environments incrementally introduce complexity, e.g., transitioning from static to moving threats and increasing the agent density, to support convergence. Additionally, more advanced neural architectures such as attention mechanisms or graph neural networks may improve spatial reasoning and inter-agent coordination. Another promising direction involves multi-agent reinforcement learning (MARL) with centralized training and decentralized execution, which can enable agents to cooperatively learn shared policies without requiring full global awareness.

While A3C and DQN provide foundational insights into the application of reinforcement learning in aviation evacuation modeling, their practical use in real-world operations remains limited by computational demands, threat generalizability, and the unpredictability of human behavior. Nevertheless, the modular nature of reinforcement learning systems enables incremental improvement, allowing these models to be refined and adapted for real-world use as sensor networks, computing infrastructure, and simulation environments continue to evolve.

5. Conclusions

The results of this study highlight A3C’s potential as a powerful tool for simulating and managing emergency evacuations in complex environments. Compared to DQN, A3C consistently demonstrated superior performance in optimizing evacuation routes, reducing travel time, and dynamically adapting to environmental changes, particularly in multi-agent scenarios. These advantages reflect the importance of selecting reinforcement learning models tailored to the behavioral and spatial complexities of the operational environment. From a practical standpoint, A3C offers a compelling framework for integrating machine learning into transportation emergency protocols, where its adaptability and learning efficiency can support more effective, real-time decision-making. Policymakers and emergency planners may benefit from A3C-based simulations to evaluate, test, and enhance evacuation strategies with improved speed, safety, and scalability.

Despite these contributions, several limitations must be acknowledged. Real-world evacuations are shaped by a range of unpredictable human behaviors, such as panic, group cohesion, and hesitation, that were not modeled in this study. Psychological and social factors, including emotional response, cognitive load, and decision delays, were outside the scope of the simulation, limiting behavioral realism. Similarly, demographic variables such as age, physical ability, and body dimensions were not incorporated, though they play a significant role in evacuation performance and equity. Future work should integrate these elements to improve population representation and the ecological validity of outcomes.

The simulation framework also involved technical limitations. Although A3C demonstrated robust performance in multi-agent settings, its implementation required substantial computational resources, posing challenges for real-time deployment in resource-constrained environments. Moreover, the rule-based collision avoidance mechanism, while essential for preventing agent–agent collisions, sometimes interfered with the reinforcement learning agent’s capacity to learn optimal cooperative behaviors. The exclusion of moving hazards in the multi-agent configuration, due to convergence difficulties, further restricts the generalizability of findings to fully dynamic, high-density evacuation scenarios.

To address these limitations, future research should focus on optimizing training strategies and network architectures to facilitate convergence under complex, dynamic conditions. Expanding the model to incorporate behavior variability, environmental uncertainty, and architectural detail, such as physical constraints or signage, would greatly enhance realism. The integration of social force modeling and psychological behavior layers could improve the responsiveness to human factors. Finally, exploring reward function design and penalty structures in greater depth may help refine agent learning outcomes and encourage more naturalistic decision-making. With continued development, the simulation framework presented here has strong potential to support safer, more resilient evacuation planning in aviation and broader transportation domains.