A Goodness-of-Fit Test for Log-Linearity in Cox Proportional Hazards Model Under Monotonic Covariate Effects

Abstract

The Cox proportional hazards (PH) model is widely used because it models the covariates to the hazard through a log-linear effect. However, exploring flexible effects becomes desirable within the Cox PH framework when only a monotonic relationship between covariates and the hazard is assumed. This work proposes a partial-likelihood-based goodness-of-fit (GOF) test to assess the log-linear effect assumption in a univariate Cox PH model. Rejection of log-linearity suggests the need to incorporate monotonic and non-log-linear covariate effects on the hazard. Our simulation studies show that the proposed GOF test controls type I error rates and exhibits consistency across various scenarios. We illustrate the proposed GOF test with two datasets, breast cancer data and lung cancer data, to assess the presence of log-linear effects in the Cox PH model.

1. Introduction

The Cox proportional hazards (PH) model [1,2] is one of the most commonly applied survival analysis models since it effectively associates the covariates with the survival time through a hazard function. Since the hazard function is also known as the instantaneous risk of experiencing an event of interest, such as death, disease, or failure, given that the individual has survived to that point, the Cox PH model is also widely used in many areas, such as biology, medicine, and the social sciences.

The hazard function in the Cox PH model with time-independent covariates has the following functional form:

$$\begin{array}{c}\hfill \lambda \left(t\right|Z)={\lambda }_0\left(t\right)exp\left(Z^{\top }\beta \right),\end{array}$$

(1)

where Z is a $p\times 1$ vector of covariates, $\beta$ is a $p\times 1$ coefficient vector, and ${\lambda }_0\left(t\right)$ is a baseline hazard function. In (1), the proportional hazard and the log-linearity hazard are two key assumptions of practical interest. The proportional hazard suggests that the hazard ratio for different individuals only depends on the value of covariates and the model coefficient $\beta$. On the other hand, taking the logarithm of (1),

$$\begin{array}{c}\hfill log\lambda \left(t\right|Z)=log{\lambda }_0\left(t\right)+Z^{\top }\beta .\end{array}$$

The log-linearity hazard enables researchers to analyze the linear effect of every unit change in the covariate on the log of the hazard function.

While most of the existing literature focuses on testing the proportional hazards assumption [3,4], our primary focus is on validating the log-linearity assumption. This assumption is critical, as assessing its validity provides a foundation for exploring alternative monotonic effects when the log-linear effect may not hold. To this end, we propose a goodness-of-fit (GOF) test designed to evaluate the log-linearity assumption in the Cox PH model.

In the literature, martingale-based residual methods have been widely used to investigate and test the GOF for log-linearity. Therneau et al. [5] introduced a graphical approach using smoothed martingale residuals to examine the functional form of covariate effects. Lin et al. [6] proposed an analytical test for log-linearity based on partial cumulative sums of martingale residuals, providing asymptotic properties, such as the limiting Gaussian process of the residuals and the null distribution of the test statistics. However, the existing literature has not explicitly addressed testing log-linearity against monotonic effects.

In this work, we consider a univariate covariate Z and a monotonic function $\varphi$ to explore the monotonic effect. Relaxing $exp\left(Z\beta \right)$ in the Cox PH model to $\varphi \left(Z\right)$, Chung et al. [7] considered the isotonic PH model with a hazard function

$$\begin{array}{c}\hfill \lambda \left(t\right|Z)={\lambda }_0\left(t\right)exp\left\{\varphi \left(Z\right)\right\},\end{array}$$

which maintains the proportional hazard assumption. Similar to the estimation process in the traditional Cox PH model, Chung et al. [7] developed nonparametric partial-likelihood-based estimation for $\varphi$. Therefore, a ratio of partial likelihoods from the Cox and isotonic PH models is a natural test statistic for checking log-linearity. Inspired by Xu et al. [8], we propose a bootstrapping method conditional on covariates and censoring time to determine the critical values.

The remaining sections are organized as follows. Section 2 reviews the estimations in the Cox PH model and the isotonic proportional hazards models for a univariate time-independent covariate. In Section 3, we propose the GOF test for the Cox PH model under monotonicity constraints. We provide a numerical study in Section 4 to evaluate the performance of the GOF test. Lastly, in Section 5, we apply the proposed GOF test in two data examples, including a lung cancer study conducted by the North Central Cancer Treatment Group [9] and a breast cancer study conducted by the German Breast Cancer Study Group in the R package survival. All the R codes are available on GitHub https://github.com/cftang9/LLGOF_UniCoxPH, accessed on 30 June 2025.

2. Partial Likelihood Estimators

We assume that the survival time $T_i$ follows a continuous distribution $F\left(t\right|Z_i)$ associating with a covariate $Z_i\in \mathbb{R}$ for $t\ge 0$, for $i=1,\dots ,n$. Let $C_i$ denote the censoring time. We observe that $X_i=min\{T_i,C_i\}$ with the censoring indicator ${\Delta }_i=I(T_i\le C_i)$, where I is an indicator function. We assume that $T_i$ and $C_i$ are independent and that $C_i$ follows a distribution G. Thus, the observed data consist of triplets ${\left\{(X_i,{\Delta }_i,Z_i)\right\}}_{i=1}^n$.

A univariate Cox PH model relates the hazard of $T_i$ and the covariate $Z_i$ as follows:

$$\begin{array}{c}\hfill \lambda \left(t\right|Z_i)={\lambda }_0\left(t\right)exp\left(Z_i\beta \right),\end{array}$$

(2)

where $\beta \in \mathbb{R}$ is a vector of coefficients and ${\lambda }_0\left(t\right)$ is a baseline hazard function invariant of covariates. The parameter $\beta$ is estimated by maximizing the partial likelihood $L_{Cox}$, given by

$$L_{Cox}\left(\beta \right)=\prod _{i=1}^n\prod _{t\ge 0}{\left[{\displaystyle \frac{exp\left(Z_i\beta \right)}{{\sum }_{j=1}^n{Y}_j\left(t\right)exp\left(Z_j\beta \right)}}\right]}^{d{N}_i\left(t\right)},$$

(3)

where $N_i\left(t\right)=I(X_i\le t,{\Delta }_i=1)$ are the counting processes indicating that the event of interest occurs at or before time t, and $Y_i\left(t\right)=I(X_i\ge t)$ are the at-risk processes that no events of interest or censoring occurs before time t. The log-partial-likelihood, denoted by ${\mathsf{\ell }}_{Cox}\left(\beta \right)$, is given by

$$\begin{array}{cc}\hfill {\mathsf{\ell }}_{Cox}\left(\beta \right)=& \sum _{i=1}^n{\int }_0^{\infty }\{Z_i\beta -log\sum _{j=1}^n{Y}_j\left(u\right)exp(Z_j\beta )\}d{N}_i\left(u\right).\hfill \end{array}$$

(4)

The maximum partial likelihood estimator (MPLE) is denoted by $\widehat{\beta }=arg{max}_{\beta \in \mathbb{R}}{\mathsf{\ell }}_{Cox}\left(\beta \right)$ and can be obtained numerically by the Newton–Raphson method.

When a monotonic covariate effect is preferable to a log-linearity effect in (2), it is natural to relax from $exp\left(Z_i\beta \right)$ to $\varphi \left(Z_i\right)$, where $\varphi$ is monotonic. Hence, $\lambda \left(t\right|Z_i)$ can be relaxed to

$$\begin{array}{c}\hfill \lambda \left(t\right|Z_i)={\lambda }_0\left(t\right)exp\left\{\varphi \left(Z_i\right)\right\}\end{array}$$

(5)

which is also known as the isotonic PH model [7]. Without loss of generality, we assume that $\varphi (·)$ is a non-decreasing function. Under the isotonic PH model, the partial likelihood is slightly different. Define $Z_{\left(i\right)}^{\star }$ as the ith-order statistic of $Z_i^{\star }$. Given a monotonic function $\varphi$, define ${\varphi }_i^{\star }=\varphi \left(Z_{\left(i\right)}^{\star }\right)$ as the value of $\varphi$ at $Z_{\left(i\right)}^{\star }$ for $i=1,\dots ,n^{\star }$, where $n^{\star }$ is the number of uncensored subjects, so that ${\varphi }_1^{\star }\le \dots \le {\varphi }_{n^{\star }}^{\star }$. We further denote ${\varphi }^{\star }={({\varphi }_1^{\star },\dots ,{\varphi }_{n^{\star }}^{\star })}^{\top }$ as the vector of parameters ${\varphi }_i^{\star }$ and $I_i^{\star }=[Z_{\left(i\right)}^{\star },Z_{(i+1)}^{\star })$ for $i=1,\dots ,n^{\star }-1$ and $I_{n^{\star }}^{\star }=[Z_{\left(n^{\star }\right)}^{\star },\infty )$, which are the intervals formed by order statistics $Z_{\left(i\right)}^{*}$. Chung et al. [7] proposed the partial likelihood for the isotonic PH model (5) as

$$L_{Iso}\left({\varphi }^{\star }\right)=\prod _{i=1}^{n^{\star }}\prod _{t\ge 0}{\left[{\displaystyle \frac{exp\left({\varphi }_i^{\star }\right)}{{\sum }_{j=1}^{n^{\star }}{Y}_j^{\star }\left(t\right)exp\left({\varphi }_j^{\star }\right)}}\right]}^{d{N}_i^{\star }\left(t\right)},$$

(6)

where the counting process $N_i^{\star }\left(t\right)={\sum }_{i=1}^{n}I(Z_{\left(i\right)}^{\star }\le t)$ and the at-risk process $Y_j^{\star }\left(t\right)={\sum }_{h\in R_j}{Y}_h\left(t\right)$, where $R_j=\{h:Z_h\in I_j^{\star },h=1,...,n\}$. Hence, the log partial likelihood can be defined accordingly as

$$\begin{array}{c}\hfill {\mathsf{\ell }}_{Iso}\left({\varphi }^{\star }\right)=\sum _{i=1}^{n^{\star }}{\int }_0^{\infty }\left\{{\varphi }_i^{\star }-log\sum _{j=1}^{n^{\star }}{Y}_j^{\star }\left(u\right)exp\left({\varphi }_j^{\star }\right)\right\}d{N}_i^{\star }\left(u\right).\end{array}$$

(7)

Note that ${\mathsf{\ell }}_{Iso}\left({\varphi }^{\star }\right)={\mathsf{\ell }}_{Iso}({\varphi }^{\star }+c)$ for any constant c. Due to the identifiability issue, restricting the monotonic function $\varphi$ satisfying $\varphi \left(Z_K\right)=0$ for some $Z_K$ suffices. In this work, we consider $Z_K$ as the median of the covariates $Z_i$ as in Chung et al. [7]. They also developed a computationally efficient pseudo-iterative convex minorant algorithm to obtain the MPLE, denoted by ${\widehat{\varphi }}^{\star }$.

3. Goodness-of-Fit Test

Here, we propose a GOF test for the log-linearity in the Cox PH model (2) under the isotonic PH model (5). The null and alternative hypotheses, $H_0$ and $H_1$, respectively, are defined as follows:

$$\begin{array}{c}\hfill \begin{array}{c}{H}_0:\varphi \left(Z\right)=Z\beta , \mathrm{for} \mathrm{some} \beta \ge 0;\hfill \\ H_1:\varphi \left(Z\right) \mathrm{is} \mathrm{increasing} \mathrm{in} Z, \mathrm{but} \mathrm{not} H_0.\hfill \end{array}\end{array}$$

(8)

Given a sample ${\left\{(X_i,{\Delta }_i,Z_i)\right\}}_{i=1}^n$, we have MPLEs $\widehat{\beta }$ and ${\widehat{\varphi }}^{\star }$ of partial likelihood (4) and (6) under the Cox PH model (2) and isotonic PH model (5), respectively. Under $H_0$, it is natural to consider a restricted MPLE ${\widehat{\beta }}_{+}=max\{\widehat{\beta },0\}$. Plugging in the MPLEs into their corresponding partial likelihoods, we propose a partial-likelihood-based test statistic

$${\mathcal{T}}_n={\mathsf{\ell }}_{Iso}\left({\widehat{\varphi }}^{\star }\right)-{\mathsf{\ell }}_{Cox}\left({\widehat{\beta }}_{+}\right).$$

(9)

Since the linear relationship $Z\beta$ with $\beta \ge 0$ under $H_0$ is a special case of a monotone relationship $\varphi \left(Z\right)$ under $H_0\cup H_1$, it is expected that ${\mathsf{\ell }}_{Iso}\left({\widehat{\varphi }}^{\star }\right)\ge {\mathsf{\ell }}_{Cox}\left({\widehat{\beta }}_{+}\right)$ and ${\mathcal{T}}_n\ge 0$. Therefore, large values of ${\mathcal{T}}_n$ suggest rejecting $H_0$. On the other hand, if $\varphi$ in (8) is decreasing in Z, the restricted MPLE ${\widehat{\beta }}_{+}$ can be replaced by a restricted MPLE ${\widehat{\beta }}_{-}=min\{0,\widehat{\beta }\}$ and ${\widehat{\varphi }}^{\star }$ under ${\varphi }_1\ge \dots \ge {\varphi }_{n^{\star }}$. Then, the test statistic is obtained by ${\mathsf{\ell }}_{Iso}\left({\widehat{\varphi }}^{\star }\right)-{\mathsf{\ell }}_{Cox}\left({\widehat{\beta }}_{-}\right)$ and the log-linearity is rejected when ${\mathcal{T}}_n$ is too small.

We propose a bootstrap method to determine a critical value for ${\mathcal{T}}_n$ to reject $H_0$. Inspired by Xu et al. [8], we consider a bootstrapping approach conditional on covariates and censoring times under the null hypothesis $H_0$. To generate survival time in the bootstrap samples, we apply the traditional inverse of the distribution function method to generate the bootstrap survival time. Note that a survival function defined by $S\left(t\right|Z_i)=1-F\left(t\right|Z_i)$ of the Cox PH model is $S\left(t\right|Z_i)=exp\{-{\Lambda }_0\left(t\right)exp\left(Z_i\beta \right)\},$ where ${\Lambda }_0\left(t\right)={\int }_0^t{\lambda }_0\left(u\right)du$ is the cumulative baseline hazard function. Therefore, provided by existences, an inverse of $S\left(t\right|Z)$ is given by $S^{-1}\left(u\right|Z_i)={\Lambda }_0^{-1}\{-log\left(u\right)exp(-Z_i\beta )\}$ for $u\in [0,1]$, where ${\Lambda }_0^{-1}\left(t\right)$ is the inverse of ${\Lambda }_0\left(t\right)$.

Since the estimators of ${\Lambda }_0$ and $\beta$ are required when estimating $S^{-1}\left(u\right|Z_i)$, we first consider the Breslow-type estimator [10]

$${\widehat{\Lambda }}_0\left(t\right)=\sum _{i=1}^n{\int }_0^t{\displaystyle \frac{d{N}_i\left(u\right)}{{\sum }_{j=1}^n{Y}_j\left(u\right)exp\left(Z_j{\widehat{\beta }}_{+}\right)}},$$

and the corresponding inverse defined by ${\widehat{\Lambda }}_0^{-1}\left(v\right)=inf\{t:{\widehat{\Lambda }}_0\left(t\right)\ge v\},$ for $0\le v<\infty$. Note that ${\widehat{\Lambda }}_0^{-1}$ is a step function such that the bootstrapped survival times generated from it may contain ties, potentially reducing the efficiency and stability of the proposed test. To address this issue, we consider a continuous and piecewise linear version of ${\widehat{\Lambda }}_0$, denoted by ${\tilde{\Lambda }}_0\left(t\right)$, to smooth ${\widehat{\Lambda }}_0$ and avoid ties of the bootstrapped survival times and enhance the performance of the test. Specifically, denote $t_0=0$, and $0<t_1<\dots <t_m<\infty$ are the locations of jump points of ${\widehat{\Lambda }}_0$ such that ${lim}_{\delta \to 0^{+}}{\widehat{\Lambda }}_0(t_i-\delta )<{\widehat{\Lambda }}_0\left(t_i\right)$ for $1\le i\le m$. Then, we define ${\tilde{\Lambda }}_0\left(t\right)={\displaystyle \frac{{\widehat{\Lambda }}_0\left(t_i\right)-{\widehat{\Lambda }}_0\left(t_{i-1}\right)}{t_i-t_{i-1}}}(t-t_{i-1})+{\widehat{\Lambda }}_0\left(t_{i-1}\right)$ for $t\in [t_{i-1},t_i)$, $i=1,\dots ,m$, and ${\tilde{\Lambda }}_0\left(t\right)={\widehat{\Lambda }}_0\left(t_m\right)$ for $t\in [t_m,\infty )$. The corresponding inverse is defined by

$$\begin{array}{cc}\hfill {\tilde{\Lambda }}_0^{-1}\left(w\right)=& \left\{\begin{array}{cc}{\displaystyle \frac{(t_i-t_{i-1})(w-{\widehat{\Lambda }}_0\left(t_{i-1}\right)}{{\widehat{\Lambda }}_0\left(t_i\right)-{\widehat{\Lambda }}_0\left(t_{i-1}\right)}}+t_{i-1},& w\in ({\widehat{\Lambda }}_0\left(t_{i-1}\right),{\widehat{\Lambda }}_0\left(t_i\right)],i=1,\dots ,m;\hfill \\ t_m,& w\in ({\widehat{\Lambda }}_0\left(t_m\right),\infty ).\hfill \end{array}\right.\hfill \end{array}$$

Therefore, in the bth bootstrapped sample, we generate the survival times

$$\begin{array}{c}\hfill T_i^b={\tilde{\Lambda }}_0^{-1}\{-log\left(U_i^b\right)exp(-Z_i{\widehat{\beta }}_{+})\},\end{array}$$

(10)

for the $i=1,\dots ,n$, where $U_i^b$ are random variables independently and identically generated from a univariate uniform distribution with support $(0,1)$, denoted by $\mathcal{U}(0,1)$.

Based on the censoring status ${\Delta }_i$, we generate the bootstrapped censoring time for the ith subject in the bth bootstrapped sample, denoted by $C_i^b$. If the survival time is censored (${\Delta }_i=0$), obtain the bootstrapped censoring time as the original censoring time with $C_i^b=C_i$. If the survival time is observed (${\Delta }_i=1$), we again apply the inverse distribution method from the estimated censoring distribution G. We approximate G by the traditional Kaplan–Meier estimator, denoted by $\widehat{G}$, with modified data ${\left\{(X_i,1-{\Delta }_i)\right\}}_{i=1}^n$. Similar to bootstrapped survival times, to generate bootstrapped censoring times, we smooth and interpolate $\widehat{G}$ linearly and obtain $\tilde{G}$. Then, we obtain the corresponding inverse

$$\begin{array}{cc}\hfill {\tilde{G}}^{-1}\left(u\right)=& \left\{\begin{array}{cc}{\displaystyle \frac{(c_i-c_{i-1})(u-\widehat{G}\left(t_{i-1}\right)}{\widehat{G}\left(t_i\right)-\widehat{G}\left(t_{i-1}\right)}}+c_{i-1},& u\in (\widehat{G}\left(c_{i-1}\right),\widehat{G}\left(c_i\right)],i=1,\dots ,m^{\prime };\hfill \\ c_{m^{\prime }},& u\in (\widehat{G}\left(c_{m^{\prime }}\right),1),\hfill \end{array}\right.\hfill \end{array}$$

where $c_0=0$, $0<c_1<\dots <c_{m^{\prime }}<\infty$ are the locations of jump points of $\widehat{G}$ such that ${lim}_{\delta \to 0^{+}}\widehat{G}(c_i-\delta )<\widehat{G}\left(c_i\right)$ for $1\le i\le m^{\prime }$. Hence, we obtain

$$\begin{array}{c}\hfill C_i^b={\tilde{G}}^{-1}\left(V_i^b\right)I({\Delta }_i=1)+C_{i}I({\Delta }_i=0),\end{array}$$

(11)

where $V_i^b$ is independently and identically generated from $\mathcal{U}(0,1)$ and is independent from $U_i^b$.

In summary, given data ${\left\{(X_i,{\Delta }_i,Z_i)\right\}}_{i=1}^n$, we independently generate B bootstrapped survival and censoring times, $T_i^b$ and $C_i^b$, from (10) and (11), respectively, and obtain $X_i^b=min\{T_i^b,C_i^b\}$ and ${\Delta }_i^b=I(T_i^b\le C_i^b)$ for $b=1,\dots ,B$. Using each bootstrapped sample, ${\left\{(X_i^b,{\Delta }_i^b,Z_i)\right\}}_{i=1}^n$, we calculate the bootstrapped test statistic ${\mathcal{T}}_n^b$. The critical value, denoted by $c_{\alpha }$, is approximated by the αth upper quantile of ${\left\{{\mathcal{T}}_n^b\right\}}_{b=1}^B$. We reject the null hypothesis when ${\mathcal{T}}_n>c_{\alpha }$.

4. Simulation

4.1. Size and Power Study

We set a significant level of $\alpha =0.05$ for Section 4 and Section 5. To evaluate the size and power of the proposed GOF test, we consider seven different functions $\varphi \left(Z\right)$ over $Z\in (0.1,2)$ in the isotonic PH model in (5) with the constant baseline hazard ${\lambda }_0\left(t\right)=1$. Three effect functions are linear—$\varphi \left(Z\right)=0,Z$, and $5Z$, satisfying $H_0$—and the remaining four correspond to nonlinear increasing functions: $\varphi \left(Z\right)=Z^2,exp\left(Z\right)$, $log\left(Z\right)$, and $6\sqrt{Z}$, satisfying $H_1$. The covariates $Z_i$ were independently generated from scaled and shifted beta distributions over the support $(0.1,2)$ with densities proportional to ${\{(u-0.1)/1.9\}}^a{\{1-(u-0.1)/1.9\}}^b$ for $u\in (0.1,2)$, with $a,b>0$. We consider three covariate distribution scenarios, denoted by $C_{\mathrm{c}}$, $C_{\mathrm{u}}$, and $C_{\mathrm{b}}$, corresponding to parameter pairs $(a,b)=(2,2),(1,1)$, and $(0.5,0.5)$, respectively. In scenario $C_{\mathrm{c}}$, covariate values are concentrated near the center of the support. In contrast, scenario $C_{\mathrm{b}}$ emphasizes values near the boundaries, while scenario $C_{\mathrm{u}}$ results in a uniform distribution of covariates across the support.

For each scenario, 500 Monte Carlo samples were generated to approximate the probabilities of rejecting $H_0$. We consider $n=\{50,100,200,500,1000\}$ to assess the effect of sample size on test performance. Censoring times are drawn from a uniform distribution $\mathcal{U}(0,\theta )$ with $\theta >0$ such that the censoring rate is about $30\%$. For each sample, critical values for the proposed GOF test are computed using $B=500$ bootstrap replications conditional on covariates and censoring times. We compare the proposed GOF test with the commonly applied residual-based GOF test proposed by Lin et al. [6], denoted by ${\mathcal{R}}_n$, which does not rely on the isotonic PH assumption.

Under $H_0$, according to the results in Table 1, all the type-I error probabilities are below $0.075$ and do not significantly exceed the nominal level $\alpha =0.05$, with a margin of error of $0.025\approx z_{0.995}\times \sqrt{0.05(1-0.05)/500}$ for 500 Monte Carlo samples at a confidence level of $99\%$, where $z_{0.995}$ is the 99.5th quantile of the standard normal distribution. Regarding the proposed test ${\mathcal{T}}_n$, the case with $\varphi \left(Z\right)=Z$ generally exhibits slightly larger type I error probabilities compared to $\varphi \left(Z\right)=0$ and $5Z$. Conversely, ${\mathcal{R}}_n$ does not exhibit systematic patterns. Furthermore, neither ${\mathcal{T}}_n$ nor ${\mathcal{R}}_n$ demonstrates notable differences across the covariate distributions considered.

Table 1. Rejection rates for the GOF tests ${\mathcal{T}}_n$ and ${\mathcal{R}}_n$ with covariate distributions $C_{\mathrm{c}}$, $C_{\mathrm{u}}$, and $C_{\mathrm{b}}$.

			$\varphi \left(Z\right)$ Under $H_0$			$\varphi \left(Z\right)$ Under $H_1$
n			0	Z	$5Z$	$Z^2$	$\exp \left(Z\right)$	$log\left(Z\right)$	$6\sqrt{Z}$
50	$C_{\mathrm{c}}$	${\mathcal{T}}_n$	0.018	0.056	0.044	0.092	0.140	0.074	0.056
		${\mathcal{R}}_n$	0.044	0.040	0.038	0.044	0.080	0.062	0.070
	$C_{\mathrm{u}}$	${\mathcal{T}}_n$	0.026	0.060	0.022	0.130	0.216	0.098	0.058
		${\mathcal{R}}_n$	0.054	0.062	0.046	0.102	0.134	0.072	0.062
	$C_{\mathrm{b}}$	${\mathcal{T}}_n$	0.026	0.046	0.028	0.148	0.254	0.190	0.066
		${\mathcal{R}}_n$	0.042	0.032	0.038	0.108	0.166	0.144	0.112
100	$C_{\mathrm{c}}$	${\mathcal{T}}_n$	0.028	0.052	0.026	0.222	0.276	0.102	0.070
		${\mathcal{R}}_n$	0.042	0.060	0.040	0.124	0.186	0.090	0.088
	$C_{\mathrm{u}}$	${\mathcal{T}}_n$	0.030	0.058	0.028	0.222	0.428	0.202	0.100
		${\mathcal{R}}_n$	0.040	0.050	0.052	0.238	0.372	0.150	0.138
	$C_{\mathrm{b}}$	${\mathcal{T}}_n$	0.038	0.060	0.022	0.278	0.534	0.364	0.148
		${\mathcal{R}}_n$	0.060	0.040	0.032	0.332	0.586	0.304	0.138
200	$C_{\mathrm{c}}$	${\mathcal{T}}_n$	0.024	0.056	0.018	0.406	0.470	0.152	0.114
		${\mathcal{R}}_n$	0.042	0.044	0.054	0.232	0.408	0.138	0.136
	$C_{\mathrm{u}}$	${\mathcal{T}}_n$	0.022	0.050	0.022	0.406	0.782	0.346	0.204
		${\mathcal{R}}_n$	0.052	0.040	0.038	0.512	0.792	0.342	0.266
	$C_{\mathrm{b}}$	${\mathcal{T}}_n$	0.038	0.040	0.028	0.602	0.910	0.614	0.342
		${\mathcal{R}}_n$	0.040	0.044	0.038	0.748	0.938	0.596	0.426
500	$C_{\mathrm{c}}$	${\mathcal{T}}_n$	0.034	0.060	0.038	0.870	0.886	0.316	0.282
		${\mathcal{R}}_n$	0.038	0.040	0.054	0.570	0.874	0.286	0.314
	$C_{\mathrm{u}}$	${\mathcal{T}}_n$	0.046	0.068	0.026	0.870	0.998	0.730	0.508
		${\mathcal{R}}_n$	0.048	0.034	0.026	0.944	0.998	0.684	0.630
	$C_{\mathrm{b}}$	${\mathcal{T}}_n$	0.038	0.068	0.030	0.948	1.000	0.950	0.812
		${\mathcal{R}}_n$	0.072	0.068	0.064	0.980	1.000	0.964	0.870
1000	$C_{\mathrm{c}}$	${\mathcal{T}}_n$	0.030	0.066	0.046	0.994	0.998	0.624	0.500
		${\mathcal{R}}_n$	0.062	0.064	0.042	0.904	0.998	0.554	0.554
	$C_u$	${\mathcal{T}}_n$	0.018	0.052	0.032	0.994	1.000	0.962	0.856
		${\mathcal{R}}_n$	0.054	0.062	0.046	1.000	1.000	0.974	0.928
	$C_{\mathrm{b}}$	${\mathcal{T}}_n$	0.026	0.050	0.022	1.000	1.000	1.000	0.986
		${\mathcal{R}}_n$	0.042	0.046	0.044	1.000	1.000	1.000	0.992

Under $H_1$, both ${\mathcal{T}}_n$ and ${\mathcal{R}}_n$ exhibit powers approaching 1 as sample size n increases, suggesting that both tests are capable of detecting deviations from log-linearity in the hazard function with high probability for large sample sizes. Among the considered covariate distributions, $C_b$ generally leads to the highest power, followed by $C_u$ and then $C_c$, since there is greater curvature near the boundaries, which aligns well with the boundary-focused distribution $C_b$. Notably, ${\mathcal{T}}_n$ shows greater power for small sample sizes $n=50$ for $\varphi \left(Z\right)=Z^2$, $exp\left(Z\right)$, and $log\left(Z\right)$. When the sample size grows, ${\mathcal{T}}_n$ continues to outperform under $C_c$ when the covariates focus more around the center of the support, where $\varphi$ is not as curved around boundaries. Conversely, ${\mathcal{R}}_n$ demonstrates higher power under $C_b$, while, under $C_u$, the performances of ${\mathcal{T}}_n$ and ${\mathcal{R}}_n$ are generally comparable, with neither test consistently dominating. Lastly, for $\varphi \left(Z\right)=6\sqrt{Z}$, although the power of ${\mathcal{T}}_n$ tends to be lower than ${\mathcal{R}}_n$, it remains competitive across most of the covariate distributions and sample sizes.

4.2. Evaluation of Robustness Across Baseline Hazards

We evaluate the robustness of the tests ${\mathcal{T}}_n$ and ${\mathcal{R}}_n$ under different baseline hazard functions, using the effect functions $\varphi$ and uniform covariate distribution $C_u$ as in Section 4.1. Specifically, we consider baseline hazards generated from Gompertz distributions, denoted by G$(\eta ,b)$, with shape parameter $\eta$ and scale parameter b. Two Gompertz models are used: G$(1,2)$ and G$(2,0.5)$. In contrast to the constant baseline hazard from the exponential distribution with mean 1, both G$(1,2)$ and G$(2,0.5)$ have increasing hazard functions, while G$(2,0.5)$ increases faster. The distinct shapes of these hazard functions are illustrated in Figure 1.

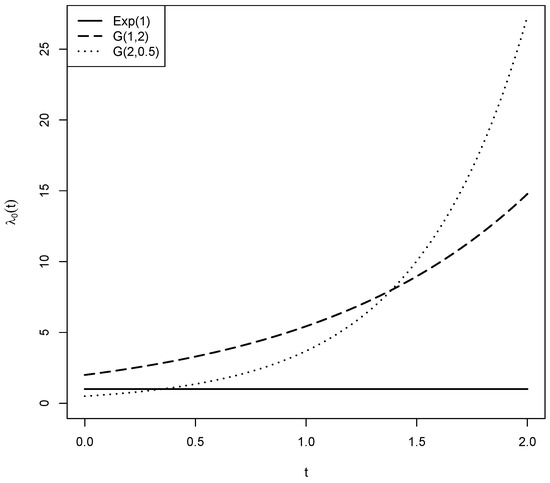
Figure 1. Hazard functions for the exponential distribution with mean 1 and the Gompertz distributions G$(1,2)$ and G$(2,0.5)$.

Under $H_0$, Table 2 shows that both ${\mathcal{T}}_n$ and ${\mathcal{R}}_n$ have similar type I error probabilities lower than $0.075$, maintaining well-controlled type-I error rates, as shown in the size study in Section 4.1. Under $H_1$, the test ${\mathcal{T}}_n$ demonstrates robustness between different baseline hazard functions, with most power differences between G$(1,2)$ and G$(2,0.5)$ remaining below $0.05$. In contrast, ${\mathcal{R}}_n$ is more sensitive to the changes in the baseline hazards, with power differences up to $0.168$ and $0.166$ when $\varphi \left(Z\right)=6\sqrt{Z}$ with $n=500$ and 1000, respectively.

Table 2. Rejection rates for the GOF tests ${\mathcal{T}}_n$ and ${\mathcal{R}}_n$ under baseline hazards G$(1,2)$ and G$(2,0.5)$. Power differences of at least 0.05 between the two settings are indicated with an asterisk (*), and differences exceeding 0.12 are further marked with a dagger (^†).

			$\varphi \left(Z\right)$ Under $H_0$			$\varphi \left(Z\right)$ Under $H_1$
n			0	Z	$5Z$	$Z^2$	$\exp \left(Z\right)$	$log\left(Z\right)$	$6\sqrt{Z}$
50	${\mathcal{T}}_n$	G$(1,2)$	0.028	0.058	0.020	0.146	0.214	0.118	0.062
		G$(2,0.5)$	0.030	0.056	0.020	0.150	0.230	0.132	0.058
	${\mathcal{R}}_n$	G$(1,2)$	0.030	0.034	0.034	0.114	0.142	0.078	0.058
		G$(2,0.5)$	0.032	0.030	0.040	0.090	0.102	0.060	0.058
100	${\mathcal{T}}_n$	G$(1,2)$	0.026	0.068	0.028	0.234	0.440	0.240	0.094
		G$(2,0.5)$	0.026	0.058	0.020	0.240	0.430	0.262	0.100
	${\mathcal{R}}_n$	G$(1,2)$	0.042	0.054	0.052	0.230	0.362 *	0.148	0.132
		G$(2,0.5)$	0.040	0.040	0.052	0.206	0.274 *	0.128	0.110
200	${\mathcal{T}}_n$	G$(1,2)$	0.020	0.054	0.022	0.420	0.782	0.380	0.206
		G$(2,0.5)$	0.020	0.060	0.024	0.436	0.776	0.414	0.198
	${\mathcal{R}}_n$	G$(1,2)$	0.046	0.056	0.038	0.492 *	0.800 †	0.352	0.272 *
		G$(2,0.5)$	0.052	0.038	0.040	0.384 *	0.672 †	0.312	0.222 *
500	${\mathcal{T}}_n$	G$(1,2)$	0.044	0.074	0.032	0.886	0.998	0.746	0.508
		G$(2,0.5)$	0.044	0.068	0.034	0.892	1.000	0.794	0.508
	${\mathcal{R}}_n$	G$(1,2)$	0.050	0.036	0.024	0.948 *	0.996	0.710	0.662 †
		G$(2,0.5)$	0.048	0.054	0.032	0.880 *	0.996	0.676	0.494 †
1000	${\mathcal{T}}_n$	G$(1,2)$	0.024	0.052	0.030	0.994	1.000	0.968	0.872
		G$(2,0.5)$	0.024	0.046	0.032	0.992	1.000	0.974	0.868
	${\mathcal{R}}_n$	G$(1,2)$	0.048	0.060	0.052	1.000	1.000	0.980	0.932 †
		G$(2,0.5)$	0.054	0.042	0.040	0.994	1.000	0.974	0.766 †

5. Illustrations with Real Data

5.1. German Breast Cancer Study

Breast cancer is the most common cancer among women worldwide, and although it predominantly affects women, men can also develop breast cancer. It can profoundly impact a person’s life, but with advances in medical research and treatment, the prognosis for many patients has improved significantly. Early detection, comprehensive treatment plans, and ongoing support can help individuals and their families manage the challenges posed by breast cancer and improve their overall quality of life.

Here, we analyze the gbsg dataset in the R package survival, which is also known as the German Breast Cancer Study Group (GBSG) dataset. It comes from a clinical trial conducted by the German Breast Cancer Study Group. The dataset contains information on 686 patients with primary node-positive breast cancer who were treated at 17 centers in Germany between 1984 and 1989. In the dataset, 387 of 686 patients were censored, so the censoring rate is $56.4\%$. Except for the survival time and status of whether a patient is censored, the dataset includes several variables, such as age, tumor size, and the number of positive lymph nodes.

Here, we wish to test the log-linearity assumption for an important prognostic factor in breast cancer: the number of positive lymph nodes. As suggested by Fitzgibbons et al. [11], a higher number of positive lymph nodes is associated with an increased risk of breast cancer recurrence and a higher risk of death from the disease. We assume the monotonicity constraints to be satisfied and conduct the GOF test with hypotheses

$$\begin{array}{cc}\hfill & H_0:\lambda \left(t\right|Z)={\lambda }_0\left(t\right)\exp \left(Z\beta \right) \mathrm{for} \mathrm{some} \beta \ge 0,\hfill \\ \hfill & H_1:\lambda \left(t\right|Z)={\lambda }_0\left(t\right)\exp \left\{\varphi \left(Z\right)\right\} \mathrm{for} \mathrm{some} \mathrm{increasing} \mathrm{function} \varphi , \mathrm{but} \mathrm{not} H_0,\hfill \end{array}$$

where Z is the number of positive lymph nodes. For the estimation of $\varphi$, we choose $Z_K=2$ such that $\widehat{\varphi }\left(Z_K\right)=0$. With the bootstrap sample size of 500, we obtain the test statistic ${\mathcal{T}}_n=18.215$ and bootstrap critical value $c_{\alpha }=9.288$. We reject the null hypothesis that the log-linearity of the hazard associated with the number of positive lymph nodes is satisfied.

In Figure 2, we present shifted log-hazard effect $(Z-Z_K){\widehat{\beta }}_{+}$ and $\widehat{\varphi }\left(Z\right)$, so $(Z-Z_K){\widehat{\beta }}_{+}=\widehat{\varphi }\left(Z\right)=0$ at $Z=Z_K$. This normalization mitigates identifiability issues and facilitates clearer graphical comparisons. From Figure 2, $\varphi \left(Z\right)$ from the isotonic PH model reveals a faster increase in hazard for a smaller number of positive nodes and deviates from the log-linear effect $Z{\widehat{\beta }}_{+}$ with constant slope ${\widehat{\beta }}_{+}$. In addition, the shape of estimate $\widehat{\varphi }\left(Z\right)$ motivates a square-root transformed covariate $\sqrt{Z}$ in the Cox PH model with hazard $\lambda \left(t\right|Z)={\lambda }_0\left(t\right)exp\left(\sqrt{Z}{\beta }^{*}\right)$ for some ${\beta }^{*}\ge 0$. For comparisons, we added $(\sqrt{Z}-\sqrt{Z_K}){\tilde{\beta }}_{+}$, where ${\tilde{\beta }}_{+}$ is the corresponding restricted MPLE of ${\beta }^{*}$, in Figure 2. Compared with $(Z-Z_K){\widehat{\beta }}_{+}$, the square-root transformed $(\sqrt{Z}-\sqrt{Z_K}){\tilde{\beta }}_{+}$ captures the faster increase in hazard for a smaller number of positive nodes but a slower increase for a larger number of positive nodes. To further evaluate the square-root transformation, we apply the proposed GOF test with the following hypotheses:

$$\begin{array}{cc}\hfill & H_0^{*}:\lambda \left(t\right|Z)={\lambda }_0\left(t\right)exp\left(\sqrt{Z}{\beta }^{*}\right) \mathrm{for} \mathrm{some} {\beta }^{*}\ge 0,\hfill \\ \hfill & H_1^{*}:\lambda \left(t\right|Z)={\lambda }_0\left(t\right)exp\left\{{\varphi }^{*}\left(\sqrt{Z}\right)\right\} \mathrm{for} \mathrm{some} \mathrm{increasing} \mathrm{function} {\varphi }^{*}, \mathrm{but} \mathrm{not} H_0^{*}.\hfill \end{array}$$

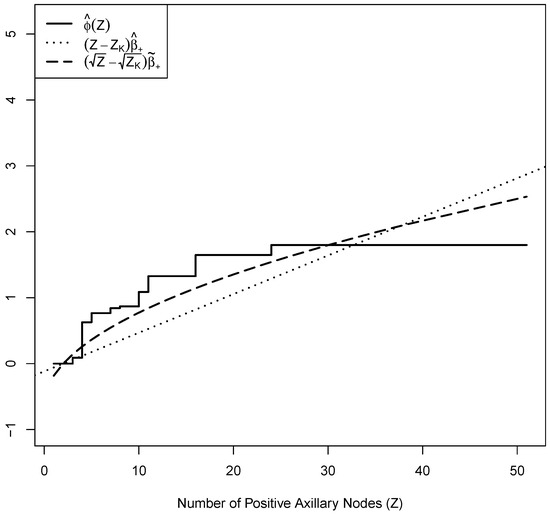
Figure 2. Shifted log-hazard effect estimates for the breast cancer dataset. The plot includes $(Z-Z_K){\widehat{\beta }}_{+}$ from a Cox PH model, $\widehat{\varphi }\left(Z\right)$ from the isotonic PH model, and $(\sqrt{Z}-\sqrt{Z_K}){\tilde{\beta }}_{+}$ from a Cox PH model with the square-root transformed covariate $\sqrt{Z}$.

With test statistic ${\mathcal{T}}_n=8.413$ and an estimated critical value $c_{\alpha }=9.703$ from $B=500$ bootstrapped samples, the evidence is not strong enough to reject $H_0^{*}$ and support the appropriateness of $\sqrt{Z}$ in the Cox PH model. This finding is consistent with the approach of Royston and Altman [12], which performed a square-root transformation on the number of nodes when applying the Cox PH model.

5.2. NCCTG Lung Cancer Data

While progress has been made in recent years, particularly in the areas of early detection, targeted therapies, and immunotherapies, lung cancer remains a challenging problem. Lung cancer holds the top position in cancer-related deaths across the globe, resulting in a higher number of fatalities than the sum of breast, prostate, and colorectal cancer deaths. Compared to early-stage lung cancer, advanced lung cancer, which refers to lung cancer that has progressed to a stage where it has spread beyond the lungs to other parts of the body or has become locally extensive, affecting nearby tissues and structures, typically has a poorer prognosis.

Here, we analyze the cancer dataset in the R package survival, which is collected from a study conducted by the North Central Cancer Treatment Group (NCCTG) on patients with advanced lung cancer. As mentioned by Loprinzi et al. [9], this study aimed to assess if the prognostic information gathered from a patient-completed questionnaire could offer independent insights beyond those already obtained by the patient’s physician through descriptive data. The Karnofsky Performance Score (KPS), rated by patients, assesses a patient’s ability to perform routine daily tasks and activities. The KPS was developed by Karnofsky [13] as a method for evaluating a patient’s functional status, particularly in assessing the response to chemotherapeutic agents in cancer treatment. The score ranges from 0 to 100, with higher scores indicating better functional ability. We consider the relationship between the hazard of failure and the KPS to be decreasing. Therefore, we can apply the GOF test for the Cox PH model to check if the log-linearity assumption is satisfied for the KPS. The hypotheses are as follows:

$$\begin{array}{cc}\hfill & H_0:\lambda \left(t\right|Z)={\lambda }_0\left(t\right)exp\left(Z\beta \right) \mathrm{for} \mathrm{some} \beta \le 0,\hfill \\ \hfill & H_1:\lambda \left(t\right|Z)={\lambda }_0\left(t\right)exp\left\{\varphi \left(Z\right)\right\} \mathrm{for} \mathrm{some} \mathrm{increasing} \mathrm{function} \varphi \left(Z\right), \mathrm{but} \mathrm{not} H_0,\hfill \end{array}$$

where Z represents the KPS rated by the patient. In the dataset, 63 of the 225 patients were censored after removing the records with missing values. Here, we choose $Z_K=70$ such that $\widehat{\varphi }\left(Z_K\right)=0$. With the bootstrap sample size of 500, we obtain the test statistic ${\mathcal{T}}_n=1.308$ and bootstrap critical value $c_{\alpha }=4.671$. We fail to reject the null hypothesis that the log-linearity assumption between the hazard of death and the Karnofsky Performance Score is satisfied. The shifted log-linear hazard effect $(Z-Z_K){\widehat{\beta }}_{-}$ and log-monotonic hazard effect $\widehat{\varphi }\left(Z\right)$ are presented in Figure 3. These two log-hazard effects are close overall, also suggesting that the Cox PH model is a reasonable choice for studying the hazard through the patients’ self-rated KPS.

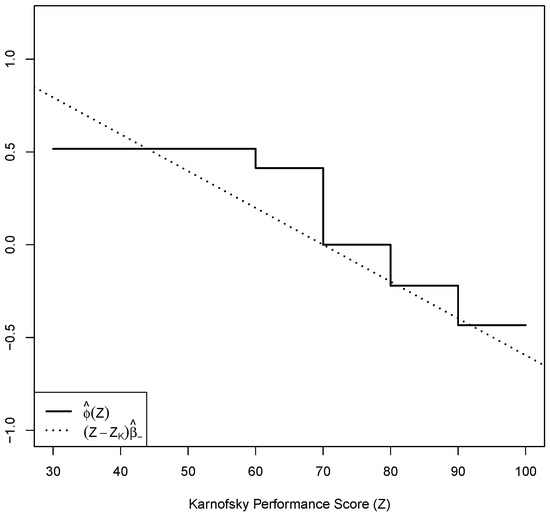
Figure 3. Shifted log-hazard effect estimates for the NCCTG lung cancer data. The plot includes $(Z-Z_K){\widehat{\beta }}_{+}$ from a Cox PH model and $\widehat{\varphi }\left(Z\right)$ from the isotonic PH model, and $(\sqrt{Z}-\sqrt{Z_K}){\tilde{\beta }}_{+}$ from a Cox PH model with the square-root transformed covariate $\sqrt{Z}$.

6. Discussion

In this work, we propose a GOF test for evaluating the log-linearity effect of a univariate covariate in the traditional Cox PH model framed within the isotonic PH model. The bootstrapped critical values used in the test demonstrate well-controlled type I error rates and strong power for detecting deviations from log-linearity. In addition, when the proposed GOF test rejects the log-linearity, from the estimated $\widehat{\varphi }\left(Z\right)$ plot, one can propose a transformation $g\left(Z\right)$ and perform the GOF test for

$$\begin{array}{cc}\hfill & H_0^{*}:\lambda \left(t\right|Z)={\lambda }_0\left(t\right)exp\left(g\left(Z\right){\beta }^{*}\right) \mathrm{for} \mathrm{some} {\beta }^{*}\ge 0,\hfill \\ \hfill & H_1^{*}:\lambda \left(t\right|Z)={\lambda }_0\left(t\right)exp\left[{\varphi }^{*}\left\{g\left(Z\right)\right\}\right] \mathrm{for} \mathrm{some} \mathrm{increasing} \mathrm{function} {\varphi }^{*}, \mathrm{but} \mathrm{not} H_0^{*},\hfill \end{array}$$

to check if the transformed $g\left(Z\right)$ is appropriate or further monotonic transformation is needed.

As shown in Section 4.1, the proposed test appears to be conservative, indicating potential for improvement. In addition to the robustness assessment in Section 4.2, we further provide more numerical results for a higher censoring rate of $50\%$ and discrete censoring distributions in the Supplementary Material. As expected, a higher censoring rate leads to more conservative tests; however, the tests remain valid since the power approaches 1 as the sample size increases. On the other hand, we observe that a uniform discrete censoring distribution that mildly discretizes the continuous uniform censoring distribution has a minor impact on the rejection rates. In addition, exploring the asymptotic properties and theoretical justifications is crucial for improving our understanding of the test statistic’s distribution and refining the choice of critical values. Investigating how the shape of the monotonic function affects power could also yield valuable insights guided by these theoretical advancements.

Despite these challenges, extending the proposed partial-likelihood-based GOF test to handle multiple covariates or a partial linear PH model with monotonic effects [7] is a natural and promising direction. However, such extensions require careful consideration and warrant further investigation. Finally, resolving the open problem of understanding the distribution of the log partial likelihood in (7), even for univariate covariates, remains a challenging and necessary task.