A Quasi-Convex RKPM for 3D Steady-State Thermomechanical Coupling Problems
Abstract
1. Introduction
2. A Brief Review of QCRK Approximation
3. QCRKPM for Steady-State Heat Conduction Problems
4. QCRKPM for Sequential Thermal Stress Problems
5. Numerical Examples
5.1. Steady-State Heat Conduction Problems in the Three-Dimensional Central Hollow Sphere
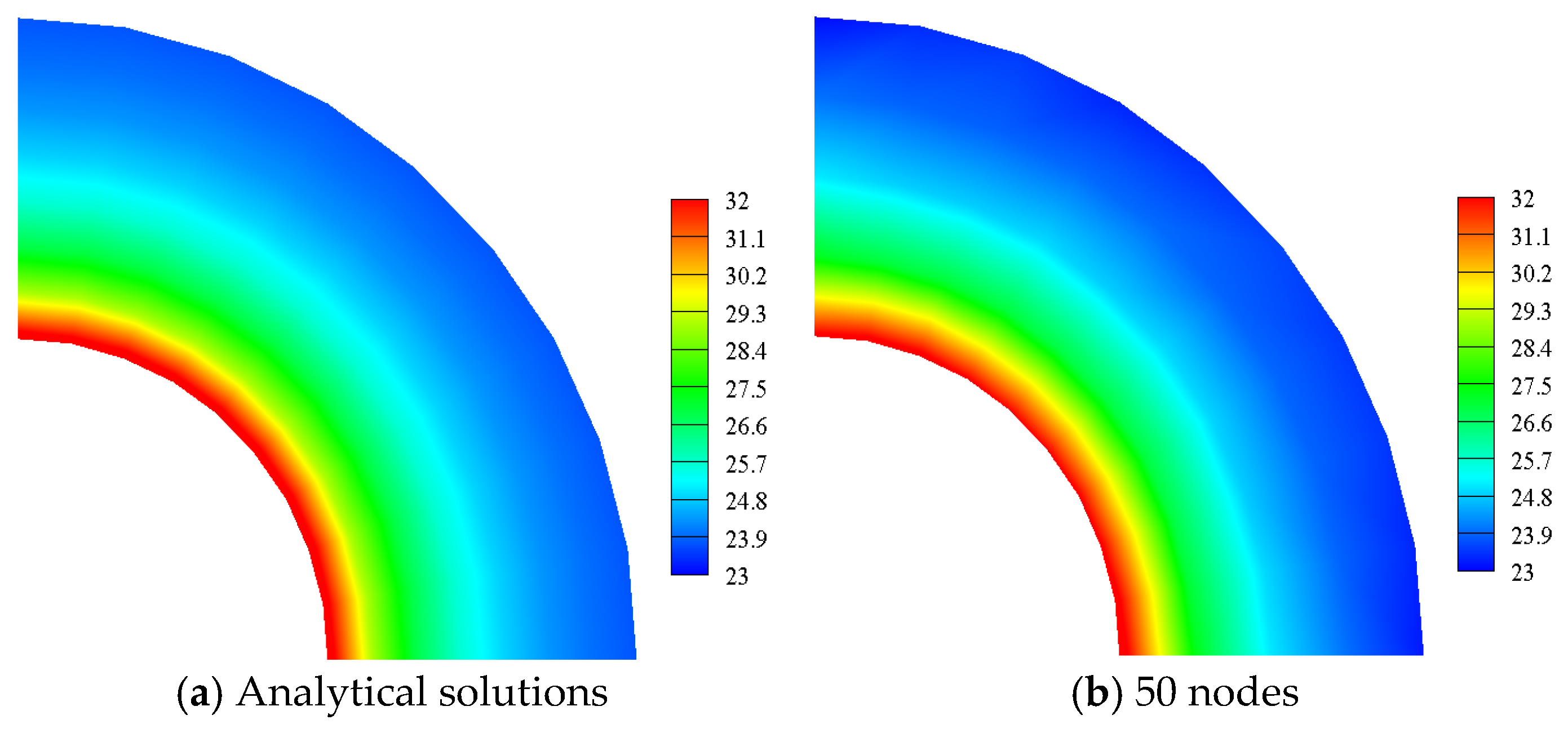
5.1.1. Results of Uniform Node Distribution of 1/4 Central Hollow Sphere
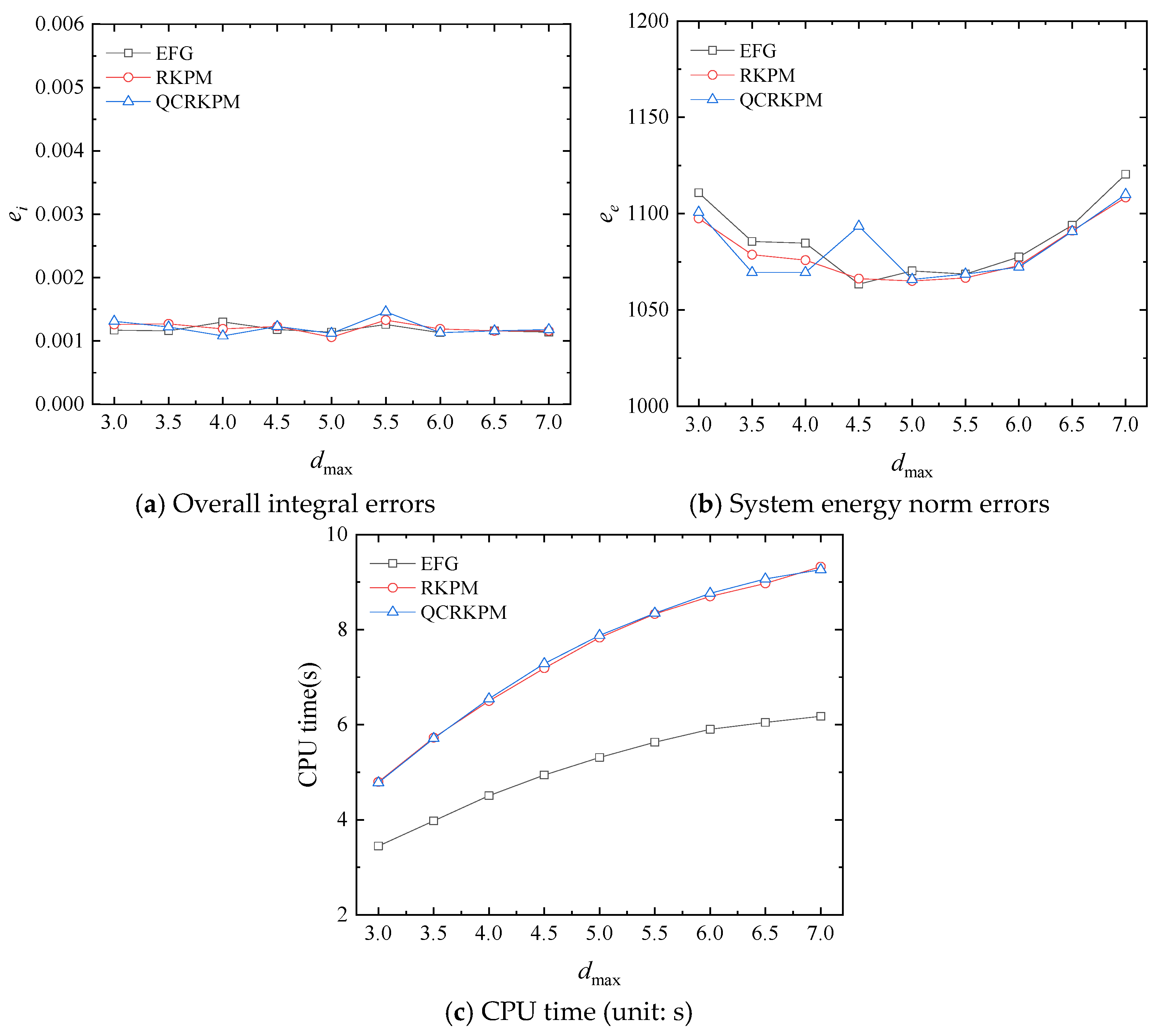
5.1.2. Convergence Study of the Calculation Parameters and Node Distribution of 1/4 Central Hollow Sphere
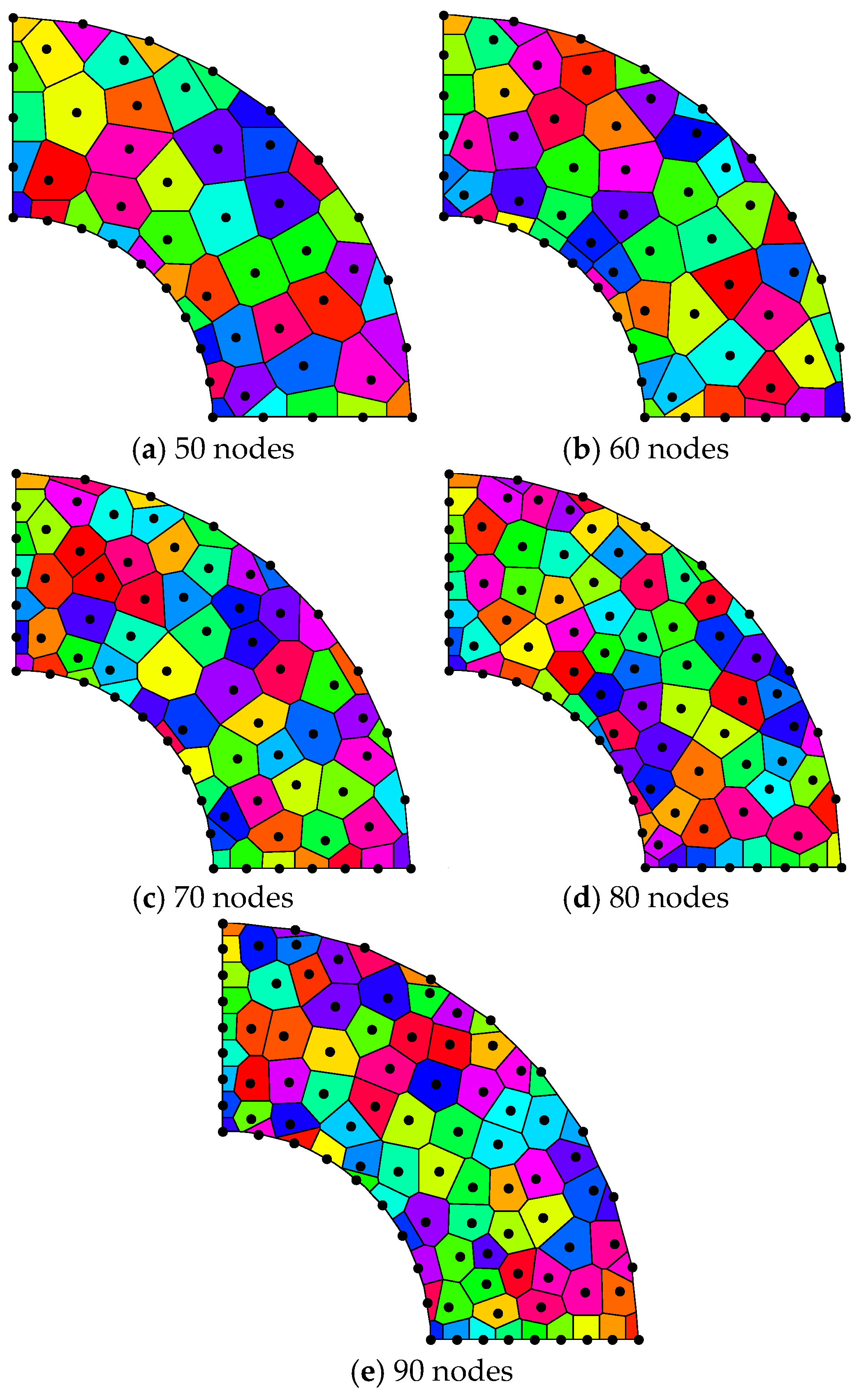
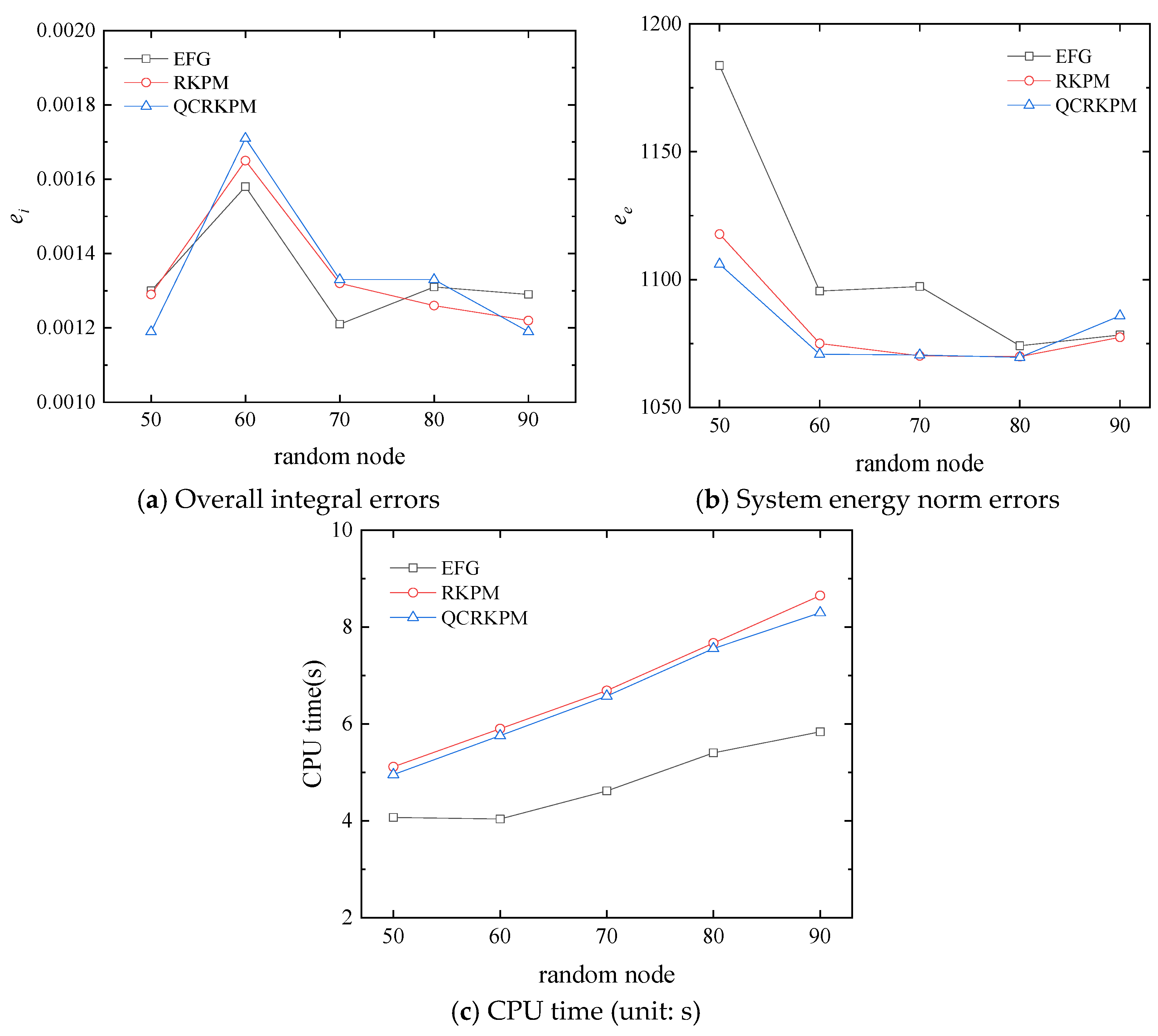
5.1.3. Effects of Random Node Distribution of 1/4 Central Hollow Sphere
5.2. Steady-State Thermomechanical Coupling Problems on Circular Ring Under Distributed Loads from Inside and Outside
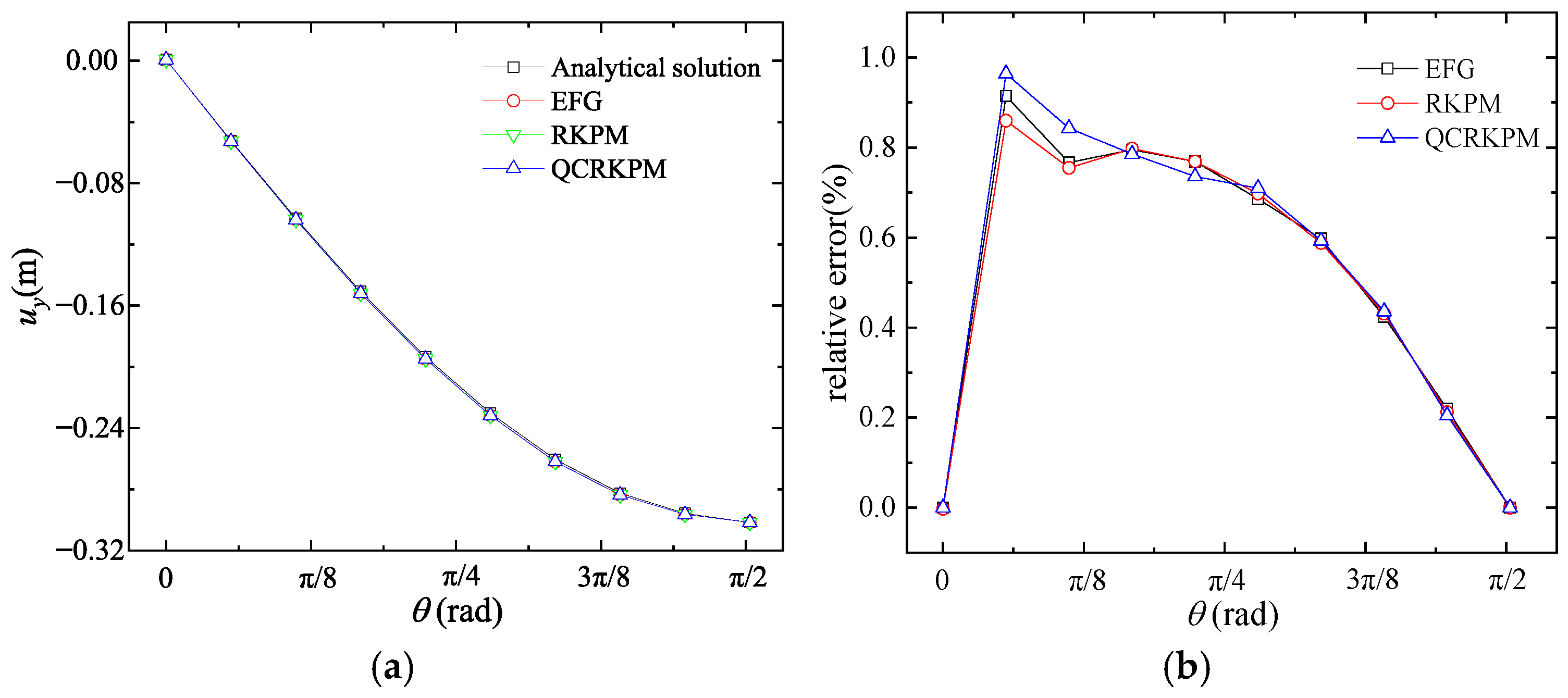
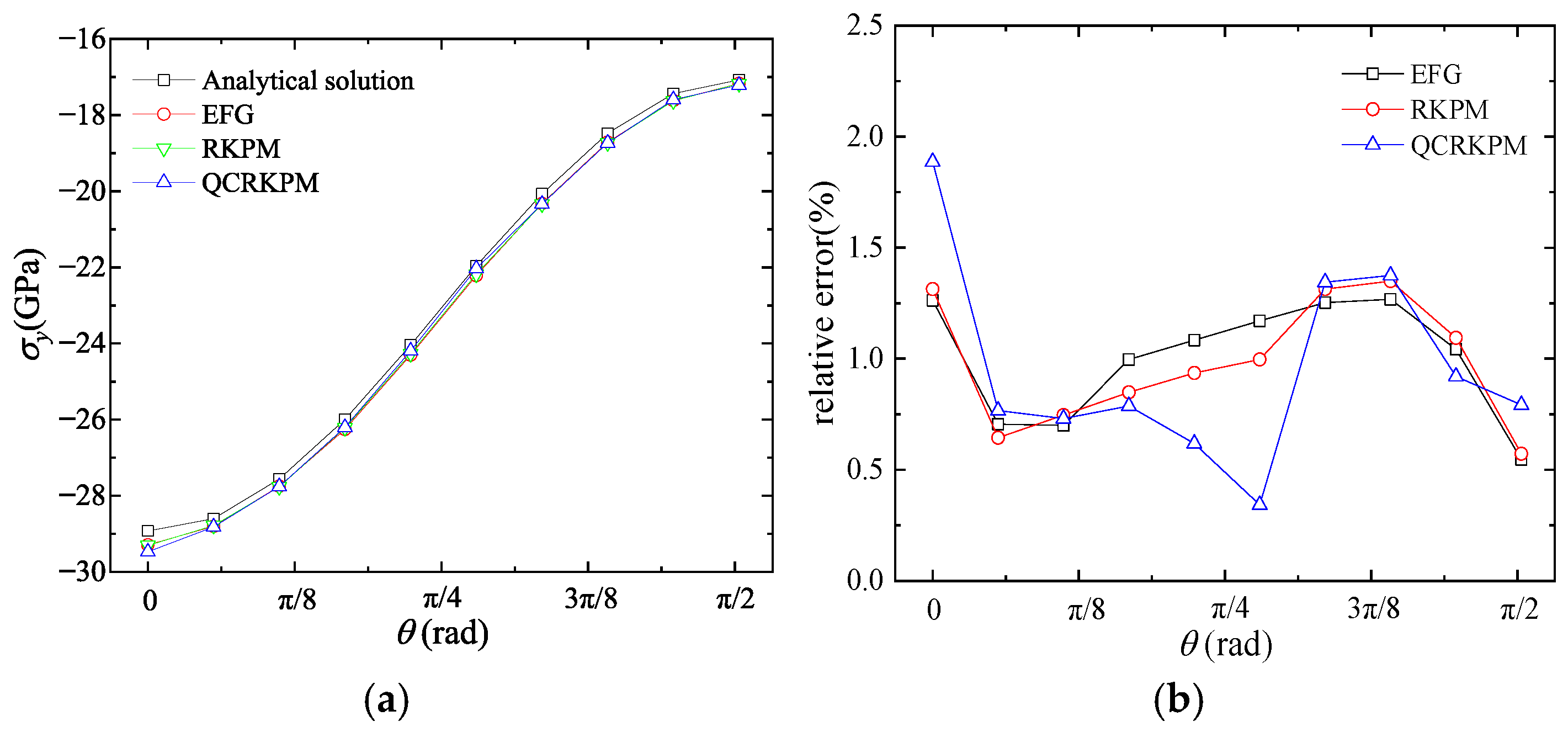
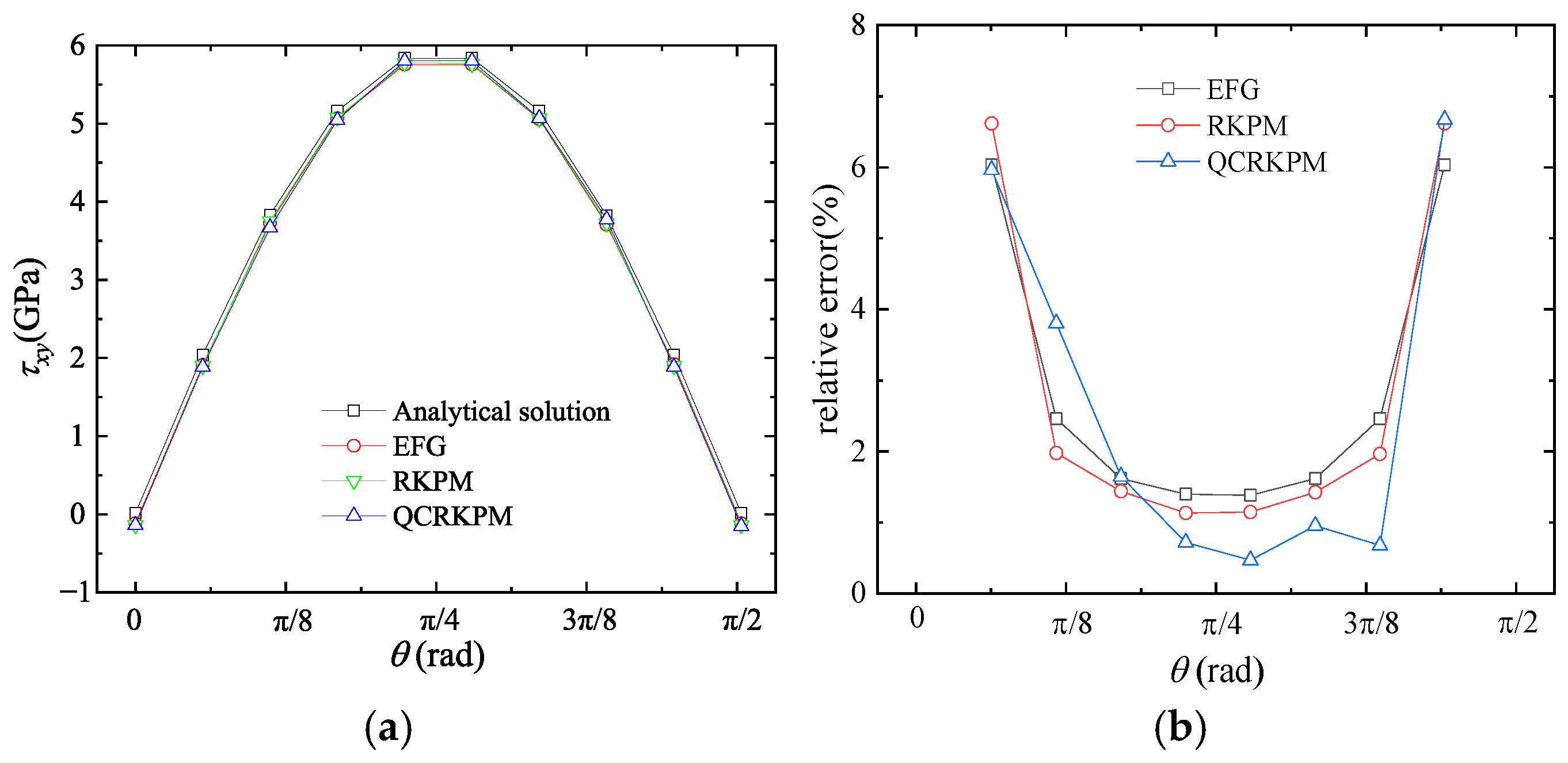
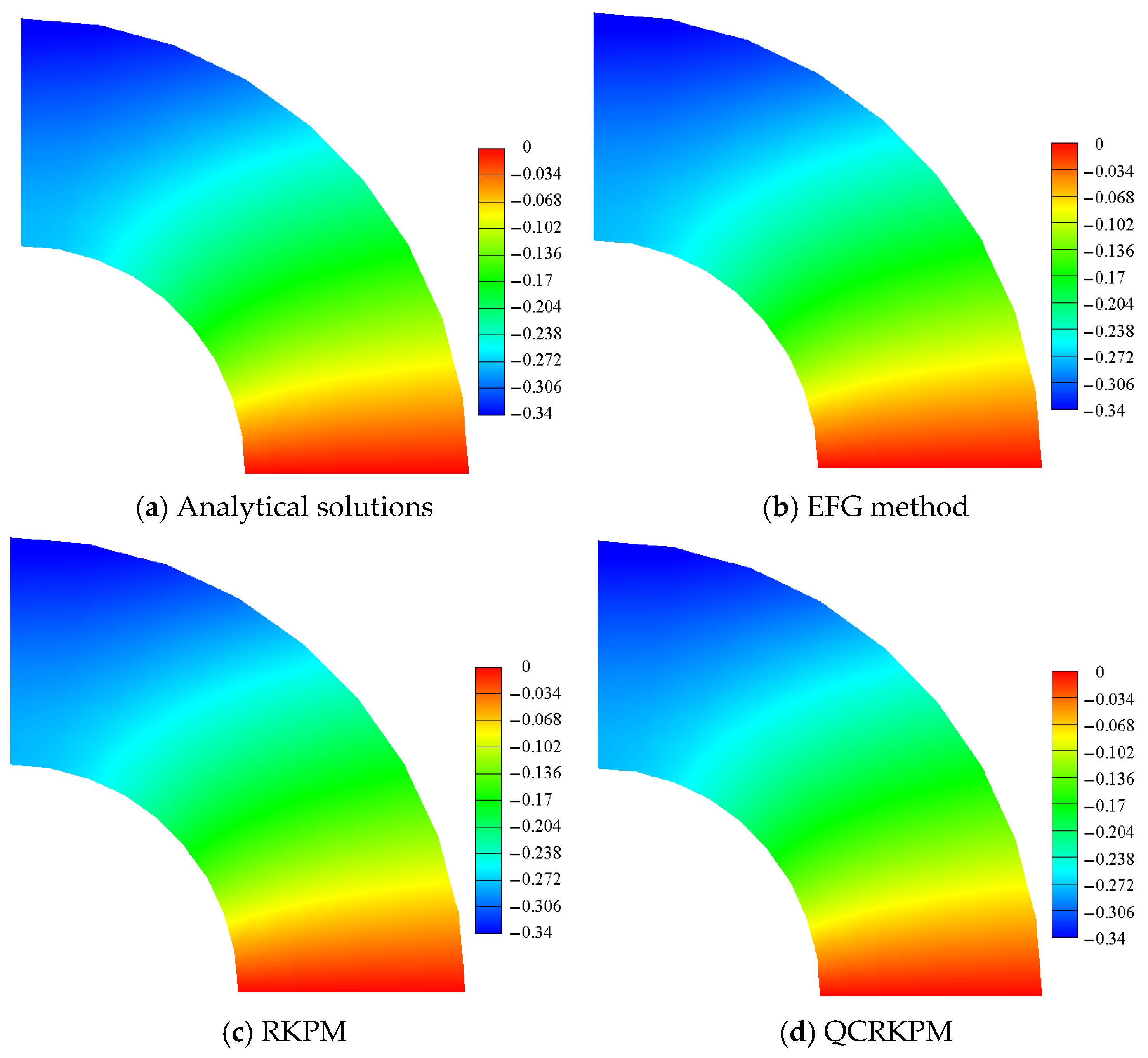
5.2.1. Results of Uniform Node Distribution of 1/4 Circular Ring
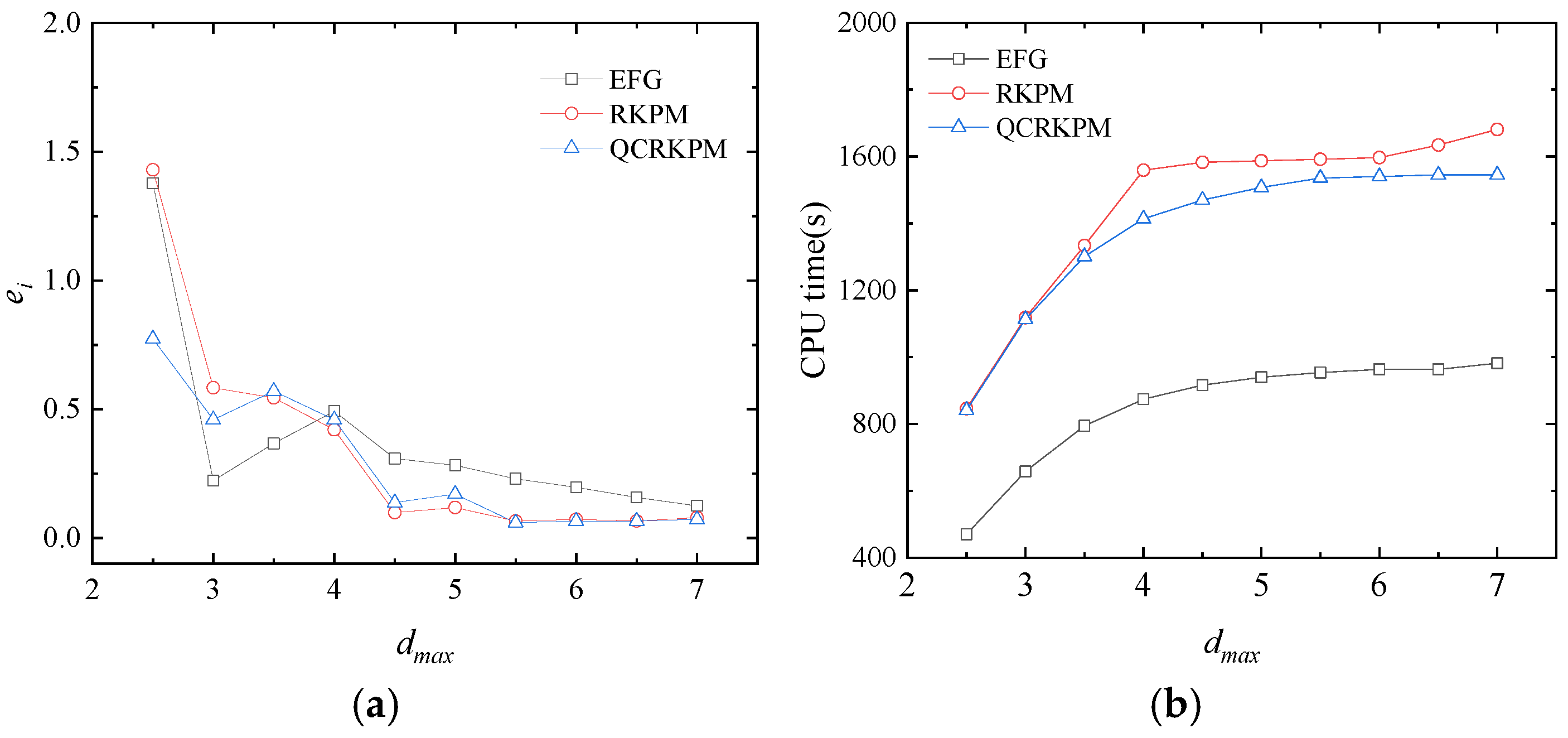
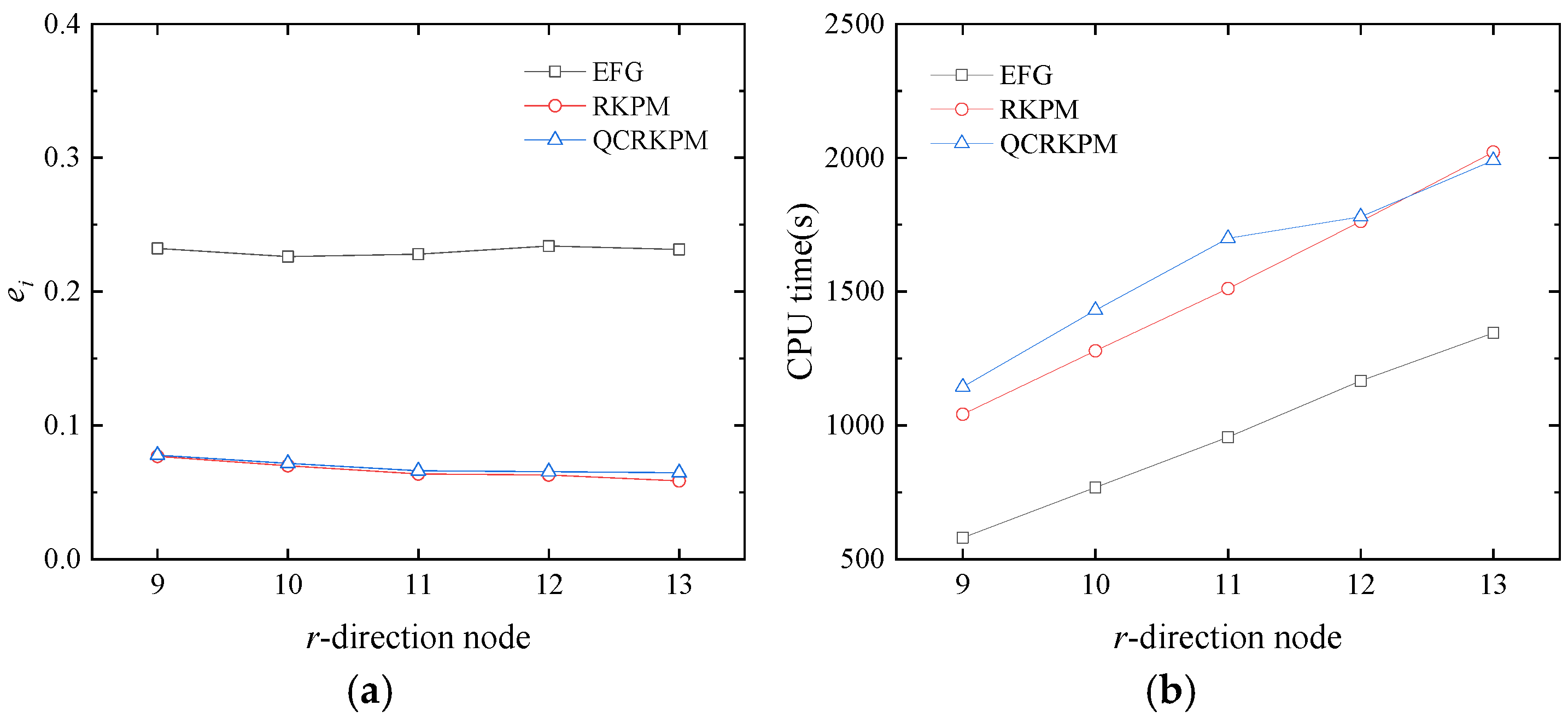
5.2.2. Convergence Study of the Calculation Parameters and Node Distribution in 1/4 Circular Ring
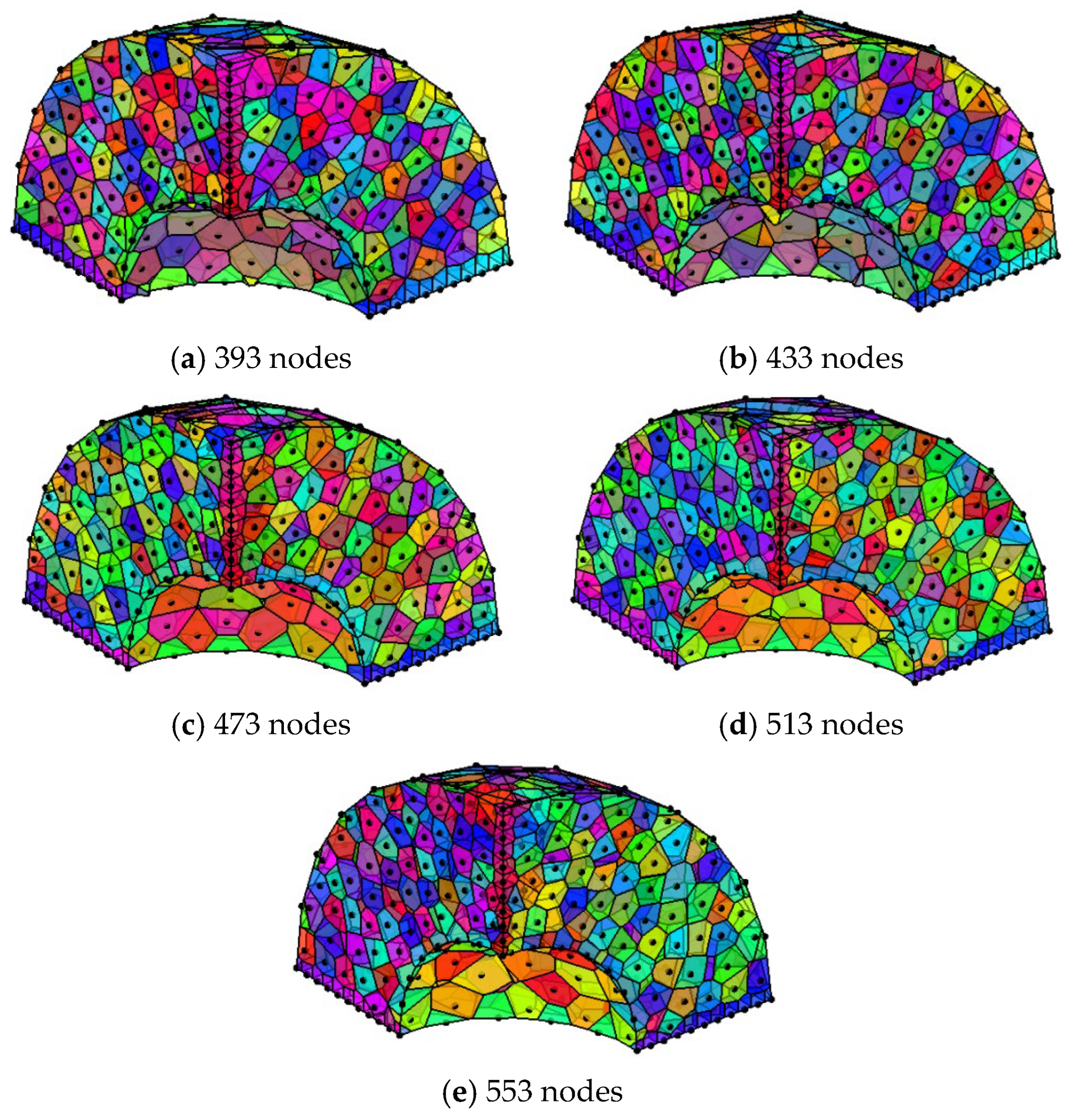
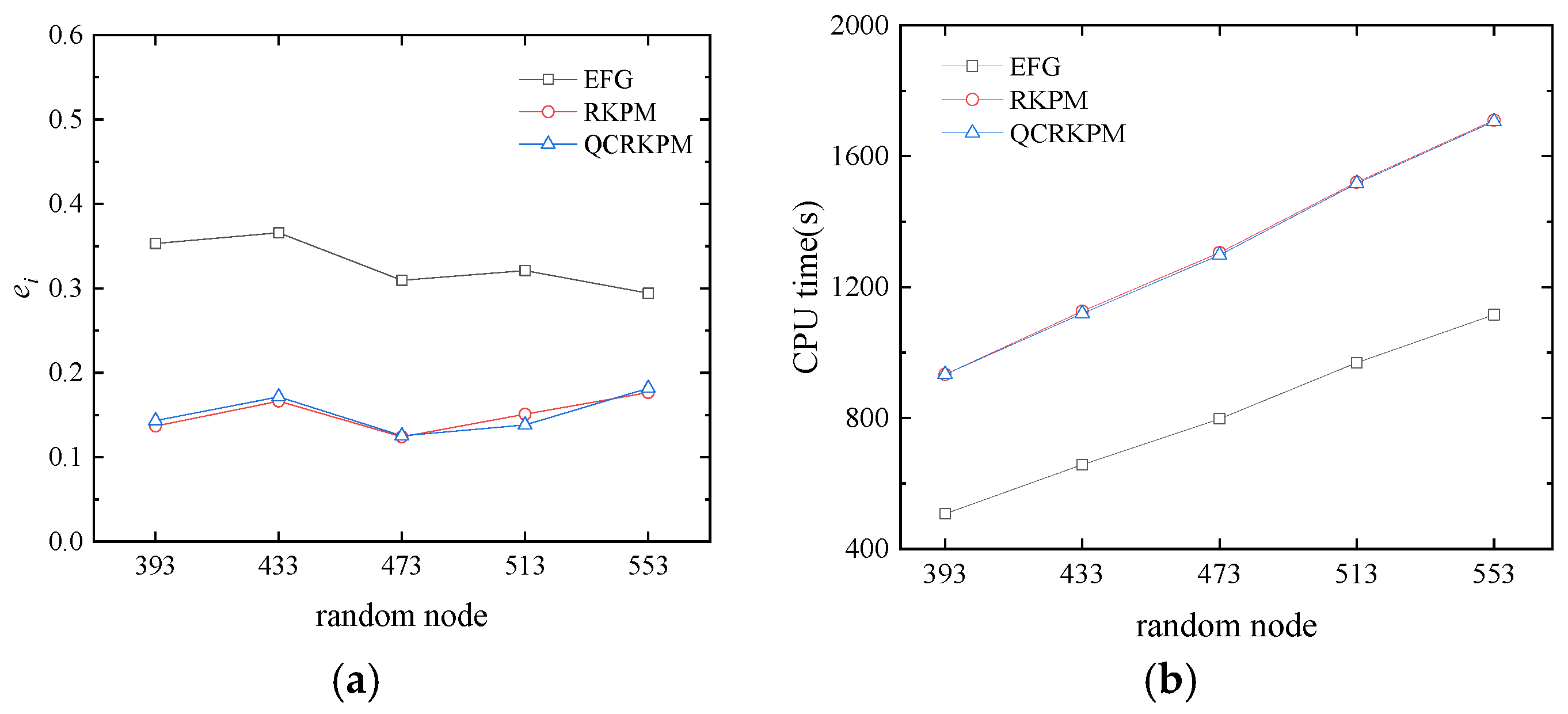
5.2.3. Effects of Random Node Distribution of 1/4 Circular Ring
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deng, Y.B.; Wu, Y.W.; Zhang, D.L.; Lu, Q.; Tian, W.X.; Qiu, S.; Su, G.H. Thermal-mechanical coupling behavior analysis on metal-matrix dispersed plate-type fuel. Prog. Nucl. Energy 2017, 95, 8–22. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, J.H.; Wu, X.Q.; Zhuang, C. Digital twin-based dynamic prediction of thermomechanical coupling for skiving process. Int. J. Adv. Manuf. Technol. 2012, 131, 5471–5488. [Google Scholar] [CrossRef]
- Li, Y.; Cui, X.F.; Tan, N.; Li, Q. Evolution of microstructure and performance of plasma cladding coating and interface with thermomechanical coupling effects. Surf. Eng. 2010, 36, 695–705. [Google Scholar] [CrossRef]
- Ghasemi, M.A.; Falahatgar, S.R.; Mostof, T.M. Mechanical and thermomechanical mesoscale analysis of multiple surface cracks in ceramic coatings based on the DEM-FEM coupling method. Int. J. Solids Struct. 2012, 236, 111336. [Google Scholar] [CrossRef]
- Joulin, C.; Xiang, J.S.; Latham, J.P. A novel thermo-mechanical coupling approach for thermal fracturing of rocks in the three-dimensional FDEM. Comput. Part. Mech. 2010, 7, 935–946. [Google Scholar] [CrossRef]
- Zhao, S.W.; Zhao, J.D.; Lai, Y.M. Multiscale modeling of thermo-mechanical responses of granular materials: A hierarchical continuum–discrete coupling approach. Comput. Methods Appl. Mech. Eng. 2010, 367, 113100. [Google Scholar] [CrossRef]
- Belytschko, T.; Kronggauz, Y.; Organ, D.; Fleming, M. Meshless methods: An overview and recent developments. Comput. Methods Appl. Mech. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef]
- Liu, G.R. Mesh Free Methods: Moving Beyond the Finite Element Method, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Nayroles, B.; Touzot, G.; Villon, P. Generalizing the finite element method: Diffuse approximation and diffuse elements. Comput. Mech. 1992, 10, 307–318. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Atluri, S.N.; Zhu, T. A new meshless local Petrov-Galerkin (MLPG) approach in computational mechanics. Comput. Mech. 1998, 22, 117–127. [Google Scholar] [CrossRef]
- Wang, J.G.; Liu, G.R. A point interpolation meshless method based on radial basis functions. Int. J. Numer. Methods Eng. 2012, 54, 1623–1648. [Google Scholar] [CrossRef]
- Gu, L. Moving kriging interpolation and element-free Galerkin method. Int. J. Numer. Methods Eng. 2013, 56, 1–11. [Google Scholar] [CrossRef]
- Chen, J.S.; Hu, W.; Hu, H.Y. Reproducing kernel enhanced local radial basis collocation method. Int. J. Numer. Methods Eng. 2018, 75, 600–627. [Google Scholar] [CrossRef]
- Sukumar, N. Construction of polygonal interpolants: A maximum entropy approach. Int. J. Numer. Methods Eng. 2014, 61, 2159–2181. [Google Scholar] [CrossRef]
- Li, D.; Bai, F.N.; Cheng, Y.M.; Liew, K.M. A novel complex variable element-free Galerkin method for two-dimensional large deformation problems. Comput. Methods Appl. Mech. Eng. 2012, 233–236, 1–10. [Google Scholar] [CrossRef]
- Wang, D.D.; Chen, P.J. Quasi-convex reproducing kernel meshfree method. Comput. Mech. 2014, 54, 689–709. [Google Scholar] [CrossRef]
- Li, D.M.; Zhang, L.W.; Liew, K.M. A three-dimensional element-free framework for coupled mechanical-diffusion induced nonlinear deformation of polymeric gels using the IMLS-Ritz method. Comput. Methods Appl. Mech. Eng. 2015, 296, 232–247. [Google Scholar] [CrossRef]
- Chen, J.S.; Pan, C.; Wu, C.T.; Liu, W.K. Reproducing Kernel Particle Methods for large deformation analysis of non-linear structures. Comput. Methods Appl. Mech. Eng. 1996, 139, 195–227. [Google Scholar] [CrossRef]
- Li, S.; Hao, W.; Liu, W.K. Mesh-free simulations of shear banding in large deformation. Int. J. Solids Struct. 2010, 37, 7185–7206. [Google Scholar] [CrossRef]
- Liew, K.M.; Ng, T.Y.; Wu, Y.C. Meshfree method for large deformation analysis–A reproducing kernel particle approach. Eng. Struct. 2012, 24, 543–551. [Google Scholar] [CrossRef]
- Li, D.M.; Zhang, Z.; Liew, K.M. A numerical framework for two-dimensional large deformation of inhomogeneous swelling of gels using the improved complex variable element-free Galerkin method. Comput. Methods Appl. Mech. Eng. 2014, 274, 84–102. [Google Scholar] [CrossRef]
- Li, D.M.; Liew, K.M.; Cheng, Y.M. An improved complex variable element-free Galerkin method for two-dimensional large deformation elastoplasticity problems. Comput. Methods Appl. Mech. Eng. 2014, 269, 72–86. [Google Scholar] [CrossRef]
- Li, D.M.; Kong, L.H.; Liu, J.H. A generalized decoupling numerical framework for polymeric gels and its element-free implementation. Int. J. Numer. Methods Eng. 2010, 121, 2701–2726. [Google Scholar] [CrossRef]
- Li, D.M.; Featherston, C.A.; Wu, Z. An element-free study of variable stiffness composite plates with cutouts for enhanced buckling and post-buckling performance. Comput. Methods Appl. Mech. Eng. 2010, 371, 113314. [Google Scholar] [CrossRef]
- Fleming, M.; Chu, Y.A.; Moran, B.; Belytschko, T. Enriched element-free Galerkin methods for crack tip fields. Int. J. Numer. Methods Eng. 1997, 40, 1483–1504. [Google Scholar] [CrossRef]
- Rao, B.N.; Rahman, S. An efficient meshless method for fracture analysis of cracks. Comput. Mech. 2010, 26, 398–408. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T. Cracking particles: A simplified meshfree method for arbitrary evolving cracks. Int. J. Numer. Methods Eng. 2014, 61, 2316–2343. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, Y.G.; Liew, K.M. A mesh-free simulation of cracking and failure using the cohesive segments method. Int. J. Eng. Sci. 2017, 45, 541–553. [Google Scholar] [CrossRef]
- Peng, Y.X.; Zhang, A.M.; Ming, F.R. A 3D meshfree crack propagation algorithm for the dynamic fracture in arbitrary curved shell. Comput. Methods Appl. Mech. Eng. 2010, 367, 113139. [Google Scholar] [CrossRef]
- Li, D.M.; Liu, J.H.; Nie, F.H.; Featherston, C.A.; Wu, Z. On tracking arbitrary crack path with complex variable meshless methods. Comput. Methods Appl. Mech. Eng. 2012, 399, 115402. [Google Scholar] [CrossRef]
- Pan, J.H.; Li, D.M.; Luo, X.B.; Zhu, W. An enriched improved complex variable element-free Galerkin method for efficient fracture analysis of orthotropic materials. Theor. Appl. Fract. Mech. 2012, 121, 103488. [Google Scholar] [CrossRef]
- Pan, J.H.; Li, D.M.; Cai, S.; Luo, X.B. A pure complex variable enrichment method for modeling progressive fracture of orthotropic functionally gradient materials. Eng. Fract. Mech. 2013, 277, 108984. [Google Scholar] [CrossRef]
- Zhang, G.M.; Batra, R.C. Modified smoothed particle hydrodynamics method and its application to transient problems. Comput. Mech. 2014, 34, 137–146. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Lu, M.W. A meshless method based on least-squares approach for steady- and unsteady-state heat conduction problems. Numer. Heat Transf. Part B Fundam. 2015, 47, 257–275. [Google Scholar] [CrossRef]
- Qian, L.; Batra, R. Three-Dimensional transient heat conduction in a functionally graded thick plate with a higher-order plate theory and a meshless local Petrov-Galerkin method. Comput. Mech. 2015, 35, 214–226. [Google Scholar] [CrossRef]
- Singh, A.; Singh, I.V.; Prakash, R. Meshless element free Galerkin method for unsteady nonlinear heat transfer problems. Int. J. Heat Mass Transf. 2017, 50, 1212–1219. [Google Scholar] [CrossRef]
- Nakonieczny, K.; Sadowski, T. Modelling of thermal shocks in composite materials using a meshfree FEM. Comput. Mater. Sci. 2019, 44, 1307–1311. [Google Scholar] [CrossRef]
- Cheng, R.; Liew, K.M. The reproducing kernel particle method for two-dimensional unsteady heat conduction problems. Comput. Mech. 2019, 45, 1–10. [Google Scholar] [CrossRef]
- Cao, L.; Qin, Q.H.; Zhao, N. An RBF-MFS model for analysing thermal behavior of skin tissues. Int. J. Heat Mass Transf. 2010, 53, 1298–1307. [Google Scholar] [CrossRef]
- Tang, J.D.; He, Z.H.; Liu, H.; Dong, S.K.; Tan, H.P. Reproducing kernel particle method for coupled conduction-radiation phase-change heat transfer. Int. J. Heat Mass Transf. 2018, 120, 387–398. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Zhan, J.; Liu, S.; Guan, Y.; Naceur, H.; Coutellier, D.; Lin, J. Meshless SPH analysis for transient heat conduction in the functionally graded structures. Compos. Commun. 2011, 24, 100664. [Google Scholar] [CrossRef]
- Guan, Y.; Atluri, S.N. Meshless fragile points methods based on Petrov-Galerkin weak-forms for transient heat conduction problems in complex anisotropic nonhomogeneous media. Int. J. Numer. Methods Eng. 2011, 122, 4055–4092. [Google Scholar] [CrossRef]
- Sládek, J.; Sládek, V.; Atluri, S.N. A pure contour formulation for the meshless local boundary integral equation method in thermoelasticity. Cmes-Comput. Model. Eng. Sci. 2011, 2, 423–434. [Google Scholar]
- Bobaru, F.; Mukherjee, S. Meshless approach to shape optimization of linear thermoelastic solids. Int. J. Numer. Methods Eng. 2012, 53, 765–796. [Google Scholar] [CrossRef]
- Qian, L.F.; Batra, R.C.; Chen, L.M. Analysis of cylindrical bending thermoelastic deformations of functionally graded plates by a meshless local Petrov-Galerkin method. Comput. Mech. 2014, 33, 263–273. [Google Scholar] [CrossRef]
- Qian, L.F.; Batra, R.C. Transient thermoelastic deformations of a thick functionally graded plate. J. Therm. Stress. 2014, 27, 705–740. [Google Scholar] [CrossRef]
- Chen, J. Determination of thermal stress intensity factors for an interface crack in a graded orthotropic coating- substrate structure. Int. J. Fract. 2015, 133, 303–328. [Google Scholar] [CrossRef]
- Ching, H.K.; Yen, S.C. Meshless local Petrov-Galerkin analysis for 2D functionally graded elastic solids under mechanical and thermal loads. Compos. Part B Eng. 2015, 36, 223–240. [Google Scholar] [CrossRef]
- Ching, H.K.; Yen, S.C. Transient thermoelastic deformations of 2-D functionally graded beams under nonuniformly convective heat supply. Compos. Struct. 2016, 73, 381–393. [Google Scholar] [CrossRef]
- Wang, H.; Qin, Q.H. Meshless approach for thermo-mechanical analysis of functionally graded materials. Eng. Anal. Bound. Elem. 2018, 32, 704–712. [Google Scholar] [CrossRef]
- Zheng, B.J.; Gao, X.W.; Yang, K.; Zhang, C.Z. A novel meshless local Petrov-Galerkin method for dynamic coupled thermoelasticity analysis under thermal and mechanical shock loading. Eng. Anal. Bound. Elem. 2015, 60, 154–161. [Google Scholar] [CrossRef]
- Vaghefi, R.; Hematiyan, M.R.; Nayebi, A. Three-dimensional thermo-elastoplastic analysis of thick functionally graded plates using the meshless local Petrov-Galerkin method. Eng. Anal. Bound. Elem. 2016, 71, 34–49. [Google Scholar] [CrossRef]
- Memari, A.; Azar, M.R.K. Thermo-mechanical shock fracture analysis by meshless method. Theor. Appl. Fract. Mech. 2019, 102, 171–192. [Google Scholar] [CrossRef]
- Khosravifard, A.; Hematiyan, M.R.; Ghiasi, N. A meshfree method with dynamic node reconfiguration for analysis of thermo-elastic problems with moving concentrated heat sources. Appl. Math. Model. 2010, 79, 624–638. [Google Scholar] [CrossRef]
- Hillman, M.; Lin, K.C. Nodally integrated thermomechanical RKPM: Part I—Thermoelasticity. Comput. Mech. 2011, 68, 795–820. [Google Scholar] [CrossRef]
- Hillman, M.; Lin, K.C. Nodally integrated thermomechanical RKPM: Part II—Generalized thermoelasticity and hyperbolic finite-strain thermoplasticity. Comput. Mech. 2011, 68, 821–844. [Google Scholar] [CrossRef]
- Reséndiz-Flores, E.O.; Saucedo-Zendejo, F.R.; Jiménez-Villalpando, A.V. Fully coupled meshfree numerical approach based on the finite pointset method for static linear thermoelasticity problems. Comput. Part. Mech. 2012, 9, 237–250. [Google Scholar] [CrossRef]
- Saucedo-Zendejo, F.R.; Reséndiz-Flores, E.O. Meshfree numerical approach based on the finite pointset method for two-way coupled transient linear thermoelasticity. Comput. Part. Mech. 2013, 10, 289–302. [Google Scholar] [CrossRef]
- Shukla, V.; Singh, J. Thermo-mechanical stability analysis of angle-ply plates using meshless method. Appl. Math. Comput. 2012, 413, 126644. [Google Scholar] [CrossRef]
- Wu, C.T.; Park, C.K.; Chen, J.S. A generalized approximation for the meshfree analysis of solids. Int. J. Numer. Methods Eng. 2011, 85, 693–722. [Google Scholar] [CrossRef]
- Arroyo, M.; Ortiz, M. Local maximum-entropy approximation schemes: A seamless bridge between finite elements and meshfree methods. Int. J. Numer. Methods Eng. 2016, 65, 2167–2202. [Google Scholar] [CrossRef]
- Zhang, H.J.; Wang, D.D. An isogeometric enriched quasi-convex meshfree formulation with application to material interface modeling. Eng. Anal. Bound. Elem. 2015, 60, 37–50. [Google Scholar] [CrossRef]
- Zhang, H.J.; Wu, J.Z.; Wang, D.D. Free vibration analysis of cracked thin plates by quasi-convex coupled isogeometric-meshfree method. Front. Struct. Civ. Eng. 2015, 9, 405–419. [Google Scholar] [CrossRef]
- Wang, F.J.; Chen, W.; Qu, W.Z.; Gu, Y. A BEM formulation in conjunction with parametric equation approach for three-dimensional Cauchy problems of steady heat conduction. Eng. Anal. Bound. Elem. 2016, 63, 1–14. [Google Scholar] [CrossRef]
- Marin, L.; Karageorghis, A. The MFS-MPS for two-dimensional steady-state thermoelasticity problems. Eng. Anal. Bound. Elem. 2013, 37, 1004–1020. [Google Scholar] [CrossRef]


















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Li, D.M.; Liao, C.-Y.; Tian, L.-R. A Quasi-Convex RKPM for 3D Steady-State Thermomechanical Coupling Problems. Mathematics 2025, 13, 2259. https://doi.org/10.3390/math13142259
Zhang L, Li DM, Liao C-Y, Tian L-R. A Quasi-Convex RKPM for 3D Steady-State Thermomechanical Coupling Problems. Mathematics. 2025; 13(14):2259. https://doi.org/10.3390/math13142259
Chicago/Turabian StyleZhang, Lin, D. M. Li, Cen-Ying Liao, and Li-Rui Tian. 2025. "A Quasi-Convex RKPM for 3D Steady-State Thermomechanical Coupling Problems" Mathematics 13, no. 14: 2259. https://doi.org/10.3390/math13142259
APA StyleZhang, L., Li, D. M., Liao, C.-Y., & Tian, L.-R. (2025). A Quasi-Convex RKPM for 3D Steady-State Thermomechanical Coupling Problems. Mathematics, 13(14), 2259. https://doi.org/10.3390/math13142259






