An Improvement of Least Squares Theory: Theory of Least p-Variances Approximation and p-Uncorrelated Functions

Abstract

We establish a theory whose structure is based on a fixed variable and an algebraic inequality and which improves the well-known least squares theory. The mentioned fixed variable plays a basic role in creating such a theory. In this direction, some new concepts, such as p-covariances with respect to a fixed variable, p-correlation coefficients with respect to a fixed variable, and p-uncorrelatedness with respect to a fixed variable, are defined in order to establish least p-variance approximations. We then obtain a specific system, called the p-covariances linear system, and apply the p-uncorrelatedness condition on its elements to find a general representation for p-uncorrelated variables. Afterwards, we apply the concept of p-uncorrelatedness for continuous functions, particularly for polynomial sequences, and we find some new sequences, such as a generic two-parameter hypergeometric polynomial of the ${}_{4}F_3$ type that satisfies a p-uncorrelatedness property. In the sequel, we obtain an upper bound for 1-covariances, an improvement to the approximate solutions of over-determined systems and an improvement to the Bessel inequality and Parseval identity. Finally, we generalize the concept of least p-variance approximations based on several fixed orthogonal variables.

1. Introduction

Least squares theory is known in the literature as an essential tool for optimal approximations and regression analysis, and it has found extensive applications in mathematics, statistics, physics and engineering [1,2,3,4]. Some important parts of this theory include the following: the best linear unbiased estimator, Gauss–Markov theorem, the moving least squares method and its improvements [5,6,7], least-squares spectral analysis, orthogonal projections and least squares function and polynomial approximations [8]. See also [9] for synergy interval partial least squares algorithms. It was officially discovered and published by A. M. Legendre [10] in 1805, though it is also co-credited to C. F. Gauss, who contributed significant theoretical advances to the method and may have previously used it in his work in 1795 [11]. The base of this theory is to minimize the sum of the squares of the residuals, which are the difference between observed values and the fitted values provided via an approximate linear (or nonlinear) model. In many linear models [12], in order to reduce the influence of errors in the derived observations, one would like to use a greater number of samplings than the number of unknown parameters in the model, which leads to so-called overdetermined linear systems. In other words, let $b\in {\mathbf{R}}^m$ be a given vector and $A\in {\mathbf{R}}^{m\times n}$ for $m>n$ a given matrix. The problem is to find a vector, $x\in {\mathbf{R}}^n$, such that $Ax$ is the best approximation to b. There are many possible ways of defining the best solution; see [13]. A very common choice is to let x be a solution of the minimization problem $\underset{x}{min}{∥Ax-b∥}_2^2$, where ${\Vert .\Vert }_2$ denotes the Euclidean vector norm. Now, if one refers to $r=b-Ax$ as the residual vector, a least squares solution in fact minimizes ${∥r∥}_2^2={\displaystyle \sum _{i=1}^m}{r}_i^2$. In linear statistical models, one assumes that the vector $b\in {\mathbf{R}}^m$ of observations is related to the unknown parameter vector $x\in {\mathbf{R}}^n$ through a linear relation

$$Ax=b+e,$$

(1)

where $A\in {\mathbf{R}}^{m\times n}$ is a predetermined matrix of rank n, and e denotes a vector of random errors. In the standard linear model, the following conditions are known as the basic conditions of Gauss–Markov theorem:

$$E\left(e\right)=0\mathrm{and}\mathrm{var}\left(e\right)={\sigma }^2{I}_n,$$

(2)

i.e., the random errors, $e_i$, are uncorrelated and all have zero means with the same variance, in which ${\sigma }^2$ is the true error variance. In summary, the Gauss–Markov theorem expresses that, if the linear model (1) is available, where e is a random vector with mean and variance given by (2), then the optimal solution of (1) is the least squares estimator, obtained by minimizing the sum of squares ${∥Ax-b-e∥}_2^2$. Furthermore, $E\left(s^2\right)={\sigma }^2$, where $s^2={\displaystyle \frac{1}{m-n}}{∥b-Ax-Ae∥}_2^2$. Similar to other approximate techniques, the least squares method contains some constrains and limitations, just like in the above-mentioned theorem, such that the conditions (2) are necessary. In this research, we introduce a new fixed variable in the minimization problem to somehow miniaturize the primitive quantity associated with sampling errors. For this purpose, we begin with a basic identity which gives rise to an important algebraic inequality, too. Let $\mathbf{S}$ denote an inner product space. Knowing that the elements of $\mathbf{S}$ satisfy four properties of linearity, symmetry, homogeneity and positivity, there is an identity in this space that is directly related to the definition of the projection of two arbitrary elements of $\mathbf{S}$, i.e.,

$$\mathrm{pro}{\mathrm{j}}_{x_2}{x}_1={\displaystyle \frac{⟨x_1,x_2⟩}{⟨x_2,x_2⟩}}{x}_2,$$

(3)

where $⟨x_1,x_2⟩$ indicates the inner product of $x_1$ and $x_2$ and $⟨x_2,x_2⟩={∥x_2∥}^2\ge 0$ denotes the norm square value of $x_2$. In other words, suppose that $x,y,z$ are three specific elements of $\mathbf{S}$, and $p\in [0,1]$ is a free parameter. Noting (3), the following identity holds true:

$$⟨x-(1-\sqrt{1-p})\mathrm{pro}{\mathrm{j}}_{z}x,y-(1-\sqrt{1-p})\mathrm{pro}{\mathrm{j}}_{z}y⟩=⟨x,y⟩-p{\displaystyle \frac{⟨x,z⟩⟨y,z⟩}{⟨z,z⟩}},$$

(4)

and, naturally, for $y=x$, it leads to the Schwarz inequality

$$⟨x,x⟩-p{\displaystyle \frac{{⟨x,z⟩}^2}{⟨z,z⟩}}\ge 0,\forall p\in [0,1].$$

(5)

This identity can also be considered in mathematical statistics. Essentially, as the content of this research is about the least variance of an approximation based on a fixed variable, if we equivalently use the expected value symbol $E(.)$ instead of the inner product symbol $⟨.⟩$, though there is no difference between them for use, we will get to a new definition of covariance concept, as follows:

Definition 1.

p-Covariances with respect to a fixed variable.

Let $X,Y$ and Z be three random variables and $p\in [0,1]$. With reference to (4), we correspondingly define

$$\begin{array}{cc}\hfill {\mathrm{cov}}_p(X,Y;Z)& =E\left(\left(X-(1-\sqrt{1-p}){\displaystyle \frac{E\left(XZ\right)}{E\left(Z^2\right)}}Z\right)\left(Y-(1-\sqrt{1-p}){\displaystyle \frac{E\left(YZ\right)}{E\left(Z^2\right)}}Z\right)\right)\hfill \\ \hfill & =E\left(XY\right)-p{\displaystyle \frac{E\left(XZ\right)E\left(YZ\right)}{E\left(Z^2\right)}},\hfill \end{array}$$

(6)

and call it “p-covariance of X and Y with respect to the fixed variable Z”.

Note, in (6), that

$${\displaystyle \frac{E\left(XZ\right)}{E\left(Z^2\right)}}Z=\mathrm{pro}{\mathrm{j}}_{Z}X,$$

and, therefore, e.g., for $p=1$,

$${\mathrm{cov}}_1(X,Y;Z)=E\left(\left(X-\mathrm{pro}{\mathrm{j}}_{Z}X\right)\left(Y-\mathrm{pro}{\mathrm{j}}_{Z}Y\right)\right).$$

If $p=1$ and Z follows a constant distribution, say $Z=c^{*}$, where $c^{*}\ne 0$, then (6) will reduce to an ordinary covariance as follows:

$${\mathrm{cov}}_1(X,Y;c^{*})=E\left(XY\right)-E\left(X\right)E\left(Y\right)=\mathrm{cov}(X,Y).$$

Also, for $p=0$, it follows that the fixed variable Z has no effect on Definition (6).

For $Y=X$ in (6), an extended definition of the ordinary variance is concluded as

$${\mathrm{var}}_p(X;Z)={\mathrm{cov}}_p(X,X;Z)=E\left(X^2\right)-p{\displaystyle \frac{E^2\left(XZ\right)}{E\left(Z^2\right)}}\ge 0,$$

(7)

where $E\left(Z^2\right)$ is always to be positive.

Moreover, for any fixed variable Z and $p\in [0,1]$, we have

$$0\le {\mathrm{var}}_1(X;Z)\le {\mathrm{var}}_p(X;Z)\le {\mathrm{var}}_0(X;Z)=E\left(X^2\right),$$

(8)

which is equivalent to

$$\begin{array}{c}0\le ⟨x-{\displaystyle \frac{⟨x,z⟩}{⟨z,z⟩}}z,x-{\displaystyle \frac{⟨x,z⟩}{⟨z,z⟩}}z⟩\hfill \\ \hfill \le ⟨x-(1-\sqrt{1-p}){\displaystyle \frac{⟨x,z⟩}{⟨z,z⟩}}z,x-(1-\sqrt{1-p}){\displaystyle \frac{⟨x,z⟩}{⟨z,z⟩}}z⟩\le ⟨x,x⟩\forall z\in \mathbf{S},\end{array}$$

in an inner product space. Note that, after simplification, the second part of the latter inequality is in the same form as (5). Although inequality (8) shows that the best option is $p=1$, we prefer to apply the parametric case $p\in [0,1]$ throughout this paper. The reasons for making such a decision will be revealed in forthcoming sections (see the illustrative Section 2.4 in this regard). The following properties hold true for Definitions (6) and (7):

(a1)${\mathrm{cov}}_p(X,Y;Z)={\mathrm{cov}}_p(Y,X;Z).$

(a2)${\mathrm{cov}}_p(\alpha X,\beta Y;Z)=\alpha \beta {\mathrm{cov}}_p(X,Y;Z)(\alpha ,\beta \in \mathbb{R}).$

(a3)$$\begin{gathered} {\mathrm{cov}}_p(X+\alpha ,Y+\beta ;Z)= \\ {\mathrm{cov}}_p(X,Y;Z)+\alpha {\mathrm{cov}}_p(1,Y;Z)+\beta {\mathrm{cov}}_p(X,1;Z)+\alpha \beta {\mathrm{cov}}_p(1,1;Z). \end{gathered}$$

(a4) ${\mathrm{var}}_p(X;Z)=0\mathrm{if}p=1\mathrm{and}Z=c^{*}X(c^{*}\ne 0).$

(a5) ${\mathrm{cov}}_p(X,Y;c^{*}X)={\mathrm{cov}}_p(X,Y;c^{*}Y)=(1-p)E\left(XY\right)(c^{*}\ne 0).$

(a6) ${\mathrm{cov}}_p\left({\displaystyle \sum _{k=0}^n}{c}_k{X}_k,X_m;Z\right)={\displaystyle \sum _{k=0}^n}{c}_k{\mathrm{cov}}_p(X_k,X_m;Z)({\left\{c_k\right\}}_{k=0}^n\in \mathbb{R}).$

• and

  $${\mathrm{var}}_p(\alpha X+\beta Y;Z)={\alpha }^2{\mathrm{var}}_p(X;Z)+{\beta }^2{\mathrm{var}}_p(Y;Z)+2\alpha \beta {\mathrm{cov}}_p(X,Y;Z).$$

  (9)

Definition 2.

p-Correlation coefficient with respect to a fixed variable.

Based on relations (6) and (7), we can define a generalization of the Pearson correlation coefficient as

$${\rho }_p(X,Y;Z)={\displaystyle \frac{{\mathrm{cov}}_p(X,Y;Z)}{\sqrt{{\mathrm{var}}_p(X;Z){\mathrm{var}}_p(Y;Z)}}},$$

(10)

and call it “p-correlation coefficient of X and Y with respect to the fixed variable Z”.

It is straightforward to observe that ${\rho }_p(X,Y;Z)\in [-1,1]$, because, if the values

$$U=X-(1-\sqrt{1-p}){\displaystyle \frac{E\left(XZ\right)}{E\left(Z^2\right)}}Z\mathrm{and}V=Y-(1-\sqrt{1-p}){\displaystyle \frac{E\left(YZ\right)}{E\left(Z^2\right)}}Z,$$

are replaced in the Cauchy–Schwarz inequality [14]

$$E^2\left(UV\right)\le E\left(U^2\right)E\left(V^2\right),$$

(11)

then ${\mathrm{cov}}_p^2(X,Y;Z)\le {\mathrm{var}}_p(X;Z){\mathrm{var}}_p(Y;Z)$. In this sense, note that

$$E\left(UZ\right)=\sqrt{1-p}E\left(XZ\right)\mathrm{and}E\left(VZ\right)=\sqrt{1-p}E\left(YZ\right),$$

which are equal to zero only for the case $p=1$.

Definition 3.

p-Normal standard variable with respect to a fixed variable.

Noting the Definitions (10) and (6), since

$${\rho }_p(X,Y;Z)=E\left(\left({\displaystyle \frac{X-(1-\sqrt{1-p})\mathrm{pro}{\mathrm{j}}_{Z}X}{\sqrt{{\mathrm{var}}_p(X;Z)}}}\right)\left({\displaystyle \frac{Y-(1-\sqrt{1-p})\mathrm{pro}{\mathrm{j}}_{Z}Y}{\sqrt{{\mathrm{var}}_p(Y;Z)}}}\right)\right),$$

a p-Normal standard variable, say $N_p(X;Z)$ can be defined with respect to the fixed variable Z as

$$N_p(X;Z)={\displaystyle \frac{X-(1-\sqrt{1-p})\mathrm{pro}{\mathrm{j}}_{Z}X}{\sqrt{{\mathrm{var}}_p(X;Z)}}}.$$

For instance, we have $N_1(X;Z=c^{*})={\displaystyle \frac{X-E\left(X\right)}{\sqrt{\mathrm{var}\left(X\right)}}}.$

Definition 4.

p-Uncorrelatedness with respect to a fixed variable.

If, in (10)${\rho }_p(X,Y;Z)=0$, which is equivalent to the condition

$$pE\left(XZ\right)E\left(YZ\right)=E\left(XY\right)E\left(Z^2\right),$$

then we say that X and Y are p-uncorrelated with respect to the fixed variable Z.

Such a definition can be expressed in an inner product space, too. We say that two elements, $x,y\in \mathbf{S}$, are p-uncorrelated with respect to the fixed element $z\in \mathbf{S}$ if

$$\left(x-(1-\sqrt{1-p})\mathrm{pro}{\mathrm{j}}_{z}x\right)\perp \left(y-(1-\sqrt{1-p})\mathrm{pro}{\mathrm{j}}_{z}y\right),$$

(12)

or, equivalently,

$$p⟨x,z⟩⟨y,z⟩=⟨x,y⟩⟨z,z⟩.$$

As (12) shows, $p=0$ gives rise to the well-known orthogonality property. In summary, 0-uncorrelatedness gives the orthogonality notion, $p=1$ results in complete uncorrelatedness and $p\in (0,1)$ leads to incomplete uncorrelatedness. We will use the phrase “complete uncorrelated” instead of 1-uncorrelated.

The aforesaid definition can similarly be expressed in a probability space. We say that two events, A and B, are p-independent with respect to the event C if

$$p{P}_r\left(\left.A\right|C\right)P_r\left(\left.B\right|C\right)=P_r(A\cap B),$$

which is equivalent to

$$p{P}_r(A\cap C)P_r(B\cap C)=P_r(A\cap B)P_r^2\left(C\right).$$

Hence, e.g., 1-independent means a complete independent with respect to the event C.

2. Least p-Variances Approximation Based on a Fixed Variable

Let ${\left\{X_k\right\}}_{k=0}^n$ and Y be arbitrary random variables, and consider the following approximation in the sequel

$$Y\cong {\displaystyle \sum _{k=0}^n}{c}_k{X}_k,$$

(13)

in which ${\left\{c_k\right\}}_{k=0}^n$ are unknown coefficients to be appropriately determined.

According to (7), the p-variance of the remaining term

$$R(c_0,c_1,\dots ,c_n)={\displaystyle \sum _{k=0}^n}{c}_k{X}_k-Y,$$

(14)

is defined with respect to the fixed variable Z as follows:

$$\begin{array}{c}{\mathrm{var}}_p\left(R(c_0,\dots ,c_n);Z\right)=E\left({\left(R(c_0,\dots ,c_n)-(1-\sqrt{1-p}){\displaystyle \frac{E\left(ZR(c_0,\dots ,c_n)\right)}{E\left(Z^2\right)}}Z\right)}^2\right)\hfill \\ \hfill =E\left({\left({\displaystyle \sum _{k=0}^n}{c}_k\left(X_k-(1-\sqrt{1-p}){\displaystyle \frac{E\left(Z{X}_k\right)}{E\left(Z^2\right)}}Z\right)-(Y-(1-\sqrt{1-p}){\displaystyle \frac{E\left(ZY\right)}{E\left(Z^2\right)}}Z)\right)}^2\right),\end{array}$$

(15)

where ${\displaystyle \frac{E\left(ZR(c_0,\dots ,c_n)\right)}{E\left(Z^2\right)}}Z$ shows the projection of the error term (14) on the fixed variable Z and ${\displaystyle \frac{E\left(Z{X}_k\right)}{E\left(Z^2\right)}}Z$ the projection of each elements on Z. For the special case $p=1$, we have in fact considered (15) as

$${\mathrm{var}}_1\left(R(c_0,\dots ,c_n);Z\right)=E\left({\left(R(c_0,\dots ,c_n)-\mathrm{pro}{\mathrm{j}}_{z}R(c_0,\dots ,c_n)\right)}^2\right).$$

We wish to find the unknown coefficients ${\left\{c_k\right\}}_{k=0}^n$ in (15), such that ${\mathrm{var}}_p\left(R(c_0,\dots ,c_n);Z\right)$ is minimized. In this direction, it is important to point out that, according to inequality (8), the following inequalities always hold for any arbitrary variable Z:

$$0\le {\mathrm{var}}_1\left(R(c_0,\dots ,c_n);Z\right)\le {\mathrm{var}}_p\left(R(c_0,\dots ,c_n);Z\right)\le {\mathrm{var}}_0\left(R(c_0,\dots ,c_n);Z\right)=E\left(R^2(c_0,\dots ,c_n)\right).$$

(16)

This means that inequalities (16) are valid for any free selection of ${\left\{c_k\right\}}_{k=0}^n$, especially when they minimize the quantity (15). In other words, we have

$$\underset{c_0,\dots ,c_n}{min}{\mathrm{var}}_1\left(R(c_0,\dots ,c_n);Z\right)\le \underset{c_0,\dots ,c_n}{min}{\mathrm{var}}_p\left(R(c_0,\dots ,c_n);Z\right)\le \underset{c_0,\dots ,c_n}{min}E\left(R^2(c_0,\dots ,c_n)\right),$$

which shows the superiority of the present theory with respect to the ordinary least squares theory (see Section 2.4 and Section 3 in this regard).

To minimize (15), for every $j=0,1,\dots ,n$ we have

$$\begin{array}{c}{\displaystyle \frac{\partial {\mathrm{var}}_p(R(c_0,\dots ,c_n);Z)}{\partial c_j}}=0\Rightarrow 2E\left((X_j-(1-\sqrt{1-p}){\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z)\right.\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\left.\left({\displaystyle \sum _{k=0}^n}{c}_k\left(X_k-(1-\sqrt{1-p}){\displaystyle \frac{E\left(X_{k}Z\right)}{E\left(Z^2\right)}}Z\right)-(Y-(1-\sqrt{1-p}){\displaystyle \frac{E\left(YZ\right)}{E\left(Z^2\right)}}Z)\right)\right)=0,\end{array}$$

(17)

leading to the linear system

$$\begin{array}{cc}\hfill & \left[\begin{array}{cccc}\begin{array}{c}{\mathrm{var}}_p(X_0;Z)\\ {\mathrm{cov}}_p(X_1,X_0;Z)\\ ⋮\\ {\mathrm{cov}}_p(X_n,X_0;Z)\end{array}& \begin{array}{c}{\mathrm{cov}}_p(X_0,X_1;Z)\\ {\mathrm{var}}_p(X_1;Z)\\ ⋮\\ {\mathrm{cov}}_p(X_n,X_1;Z)\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}{\mathrm{cov}}_p(X_0,X_n;Z)\\ {\mathrm{cov}}_p(X_1,X_n;Z)\\ ⋮\\ {\mathrm{var}}_p(X_n;Z)\end{array}\end{array}\right]\left[\begin{array}{c}{c}_0\\ c_1\\ ⋮\\ c_n\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}{\mathrm{cov}}_p(X_0,Y;Z)\\ {\mathrm{cov}}_p(X_1,Y;Z)\\ ⋮\\ {\mathrm{cov}}_p(X_n,Y;Z)\end{array}\right].\hfill \end{array}$$

(18)

Notice that only finding the analytical solution of the above system is sufficient to guarantee that ${\mathrm{var}}_p\left(R(c_0,\dots ,c_n);Z\right)$ is minimized, because we automatically have

$${\left\{{\displaystyle \frac{{\partial }^2{\mathrm{var}}_p(R(c_0,\dots ,c_n);Z)}{\partial {c_j}^2}}\right\}}_{j=0}^n\ge 0.$$

For instance, after solving (2.6) for $n=1$, the approximation (13) takes the form

$$\begin{array}{c}Y\cong {\displaystyle \frac{{\mathrm{var}}_p(X_1;Z){\mathrm{cov}}_p(X_0,Y;Z)-{\mathrm{cov}}_p(X_0,X_1;Z){\mathrm{cov}}_p(X_1,Y;Z)}{{\mathrm{var}}_p(X_1;Z){\mathrm{var}}_p(X_0;Z)-{\mathrm{cov}}_p^2(X_0,X_1;Z)}}{X}_0\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{{\mathrm{var}}_p(X_0;Z){\mathrm{cov}}_p(X_1,Y;Z)-{\mathrm{cov}}_p(X_0,X_1;Z){\mathrm{cov}}_p(X_0,Y;Z)}{{\mathrm{var}}_p(X_1;Z){\mathrm{var}}_p(X_0;Z)-{\mathrm{cov}}_p^2(X_0,X_1;Z)}}{X}_1.\end{array}$$

In general, two continuous and discrete cases can be considered for the system (18), which we call from now on a “p-covariances linear system with respect to the fixed variable Z”.

2.1. Continuous Case of p-Covariances Linear System

If ${\left\{X_k={\Phi }_k\left(x\right)\right\}}_{k=0}^n$, $Y=f\left(x\right)$ and $Z=z\left(x\right)$ are defined in a continuous space with a probability density function as $P_r\left(X=x\right)={\displaystyle \frac{w\left(x\right)}{{\int }_a^{b}w\left(x\right)dx}}$, for any arbitrary function $w\left(x\right)$ positive on the interval $[a,b]$, then the components of the linear system (18) appear as

$$\begin{array}{l}{\mathrm{cov}}_p\left({\Phi }_i\left(x\right),{\Phi }_j\left(x\right);z\left(x\right)\right)=\hfill \\ {\displaystyle \frac{1}{{\int }_a^{b}w\left(x\right)dx}}\left({\int }_a^{b}w\left(x\right){\Phi }_i\left(x\right){\Phi }_j\left(x\right)dx-p{\displaystyle \frac{{\int }_a^{b}w\left(x\right){\Phi }_i\left(x\right)z\left(x\right)dx{\int }_a^{b}w\left(x\right){\Phi }_j\left(x\right)z\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}}\right),\hfill \end{array}$$

(19)

where ${\int }_a^{b}w\left(x\right)z^2\left(x\right)dx>0$.

2.2. Discrete Case of p-Covariances Linear System

If the above-mentioned variables are defined on a counter set, say $A^{*}={\left\{x_k\right\}}_{k=0}^m$ with a discrete probability density function as $P_r\left(X=x\right)={\displaystyle \frac{j\left(x\right)}{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right)}}$, for any arbitrary function $j\left(x\right)$ positive on $x\in A^{*}$, then

$$\begin{array}{c}{\mathrm{cov}}_p\left({\Phi }_i\left(x\right),{\Phi }_j\left(x\right);z\left(x\right)\right)=\hfill \\ \hspace{1em}\hspace{1em}{\displaystyle \frac{1}{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right)}}\left(\sum _{x\in A^{*}}j\left(x\right){\Phi }_i\left(x\right){\Phi }_j\left(x\right)-p{\displaystyle \frac{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right){\Phi }_i\left(x\right)z\left(x\right){\displaystyle \sum _{x\in A^{*}}}j\left(x\right){\Phi }_j\left(x\right)z\left(x\right)}{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right)z^2\left(x\right)}}\right),\hfill \end{array}$$

(20)

where ${\displaystyle \sum _{x\in A^{*}}}j\left(x\right)z^2\left(x\right)>0$.

One of the important cases of the approximation (13) is when ${\left\{X_k={\Phi }_k\left(x\right)=x^k\right\}}_{k=0}^n$ has a constant distribution function, which leads to the Hilbert problem [13,15] in a continuous space and to the polynomial type regression in a discrete space. In other words, if ${\left\{X_k=x^k\right\}}_{k=0}^n$, $Y=f\left(x\right)$, $Z=z\left(x\right)$ and $w\left(x\right)=1$ for $x\in [0,1]$ are substituted into (18), then

$${\mathrm{cov}}_p(x^i,x^j;z\left(x\right))={\displaystyle \frac{1}{i+j+1}}-p{\displaystyle \frac{{\int }_0^1{x}^{i}z\left(x\right)dx{\int }_0^1{x}^{j}z\left(x\right)dx}{{\int }_0^1{z}^2\left(x\right)dx}}\mathrm{for}i,j=0,1,\dots ,n,$$

and

$${\mathrm{cov}}_p(x^j,f\left(x\right);z\left(x\right))={\int }_0^1{x}^{j}f\left(x\right)dx-p{\displaystyle \frac{{\int }_0^1{x}^{j}z\left(x\right)dx{\int }_0^{1}f\left(x\right)z\left(x\right)dx}{{\int }_0^1{z}^2\left(x\right)dx}}\mathrm{for}j=0,1,\dots ,n.$$

For $p=0$, we clearly encounter with the Hilbert problem.

Similarly, if in a discrete space ${\left\{X_k=x^k\right\}}_{k=0}^n$, $A^{*}={\left\{x_k\right\}}_{k=1}^m$, $Y=f\left(x\right)$ where $f\left(x_k\right)=y_k$, $Z=z\left(x\right)$ and $j\left(x\right)=1$, the entries of the system (18), respectively, take the forms

$${\mathrm{cov}}_p(x^i,x^j;z\left(x\right))={\displaystyle \frac{1}{m}}{\displaystyle \sum _{k=1}^m}{\left(x_k\right)}^{i+j}-{\displaystyle \frac{p}{m}}{\displaystyle \frac{{\displaystyle \sum _{k=1}^m}{\left(x_k\right)}^{i}z\left(x_k\right){\displaystyle \sum _{k=1}^m}{\left(x_k\right)}^{j}z\left(x_k\right)}{{\displaystyle \sum _{k=1}^m}{z}^2\left(x_k\right)}}\mathrm{for}i,j=0,1,\dots ,n,$$

and

$${\mathrm{cov}}_p(x^j,f\left(x\right);z\left(x\right))={\displaystyle \frac{1}{m}}{\displaystyle \sum _{k=1}^m}{y}_k{\left(x_k\right)}^j-{\displaystyle \frac{p}{m}}{\displaystyle \frac{{\displaystyle \sum _{k=1}^m}{\left(x_k\right)}^{j}z\left(x_k\right){\displaystyle \sum _{k=1}^m}{y}_{k}z\left(x_k\right)}{{\displaystyle \sum _{k=1}^m}{z}^2\left(x_k\right)}}\mathrm{for}j=0,1,\dots ,n.$$

As a particular sample, the system corresponding to the linear regression $Y=c_0{X}_0+c_1{X}_1=c_0+c_{1}x$ with respect to the fixed variable $Z=z\left(x\right)$ appears as

$$\begin{array}{c}\left[\begin{array}{cc}m{\displaystyle \sum _{k=1}^m}{z}^2\left(x_k\right)-p({\displaystyle \sum _{k=1}^m}z\left(x_k\right){)}^2,& {\displaystyle \sum _{k=1}^m}{x}_k{\displaystyle \sum _{k=1}^m}{z}^2\left(x_k\right)-p{\displaystyle \sum _{k=1}^m}z\left(x_k\right){\displaystyle \sum _{k=1}^m}{x}_{k}z\left(x_k\right)\\ {\displaystyle \sum _{k=1}^m}{x}_k{\displaystyle \sum _{k=1}^m}{z}^2\left(x_k\right)-p{\displaystyle \sum _{k=1}^m}z\left(x_k\right){\displaystyle \sum _{k=1}^m}{x}_{k}z\left(x_k\right),& {\displaystyle \sum _{k=1}^m}{x}_k^2{\displaystyle \sum _{k=1}^m}{z}^2\left(x_k\right)-p({\displaystyle \sum _{k=1}^m}{x}_{k}z\left(x_k\right){)}^2\end{array}\right]\hfill \\ \hfill \times \left[\begin{array}{c}{c}_0\\ c_1\end{array}\right]=\left[\begin{array}{c}{\displaystyle \sum _{k=1}^m}{y}_k{\displaystyle \sum _{k=1}^m}{z}^2\left(x_k\right)-p{\displaystyle \sum _{k=1}^m}z\left(x_k\right){\displaystyle \sum _{k=1}^m}{y}_{k}z\left(x_k\right)\\ {\displaystyle \sum _{k=1}^m}{x}_k{y}_k{\displaystyle \sum _{k=1}^m}{z}^2\left(x_k\right)-p{\displaystyle \sum _{k=1}^m}{x}_{k}z\left(x_k\right){\displaystyle \sum _{k=1}^m}{y}_{k}z\left(x_k\right)\end{array}\right].\end{array}$$

It is interesting to know that, if $z\left(x\right)=c^{*}\ne 0$ is substituted into the above partially system for $p\ne 1$, the output gives the well-known result

$$Y={\displaystyle \frac{{\displaystyle \sum _{k=1}^m}{x}_k^2{\displaystyle \sum _{k=1}^m}{y}_k-{\displaystyle \sum _{k=1}^m}{x}_k{\displaystyle \sum _{k=1}^m}{x}_k{y}_k}{m{\displaystyle \sum _{k=1}^m}{x}_k^2-{({\displaystyle \sum _{k=1}^m}{x}_k)}^2}}+{\displaystyle \frac{m{\displaystyle \sum _{k=1}^m}{x}_k{y}_k-{\displaystyle \sum _{k=1}^m}{x}_k{\displaystyle \sum _{k=1}^m}{y}_k}{m{\displaystyle \sum _{k=1}^m}{x}_k^2-{({\displaystyle \sum _{k=1}^m}{x}_k)}^2}}x,$$

i.e., $p\ne 1$ has been automatically deleted. In this sense, if the only case $p=1$ is substituted into the above mentioned system for $z\left(x\right)=c^{*}\ne 0$ as

$$\left[\begin{array}{cc}0,& 0\\ 0,& m{\displaystyle \sum _{k=1}^m}{x}_k^2-{\left({\displaystyle \sum _{k=1}^m}{x}_k\right)}^2\end{array}\right]\left[\begin{array}{c}{c}_0\\ c_1\end{array}\right]=\left[\begin{array}{c}0\\ m{\displaystyle \sum _{k=1}^m}{x}_k{y}_k-{\displaystyle \sum _{k=1}^m}{x}_k{\displaystyle \sum _{k=1}^m}{y}_k\end{array}\right],$$

the output gives the result $Y=c_0+{\displaystyle \frac{m{\displaystyle \sum _{k=1}^m}{x}_k{y}_k-{\displaystyle \sum _{k=1}^m}{x}_k{\displaystyle \sum _{k=1}^m}{y}_k}{m{\displaystyle \sum _{k=1}^m}{x}_k^2-{\left({\displaystyle \sum _{k=1}^m}{x}_k\right)}^2}}x$, where $c_0$ is a free parameter.

In the next section, we show why $c_0$ became a free parameter when $z\left(x\right)=c^{*}\ne 0$ and $p=1$.

2.3. Some Reducible Cases of the p-Covariances Linear System

2.3.1. First Case

Suppose there exists a specific distribution for the fixed variable Z, such that

$$E\left(Z{X}_k\right)=0\mathrm{for}\mathrm{every}k=0,1,\dots ,n.$$

(21)

Then, the p-covariances system (18) reduces to the well-known normal equations system

$$\left[\begin{array}{cccc}\begin{array}{c}E\left(X_0^2\right)\\ E\left(X_1{X}_0\right)\\ ⋮\\ E\left(X_n{X}_0\right)\end{array}& \begin{array}{c}E\left(X_0{X}_1\right)\\ E\left(X_1^2\right)\\ ⋮\\ E\left(X_n{X}_1\right)\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}E\left(X_0{X}_n\right)\\ E\left(X_1{X}_n\right)\\ ⋮\\ E\left(X_n^2\right)\end{array}\end{array}\right]\left[\begin{array}{c}{c}_0\\ c_1\\ ⋮\\ c_n\end{array}\right]=\left[\begin{array}{c}E\left(X_{0}Y\right)\\ E\left(X_{1}Y\right)\\ ⋮\\ E\left(X_{n}Y\right)\end{array}\right],$$

(22)

and

$$\underset{c_0,\dots ,c_n}{min}{\mathrm{var}}_p\left(R(c_0,\dots ,c_n);Z|{\left\{E\left(Z{X}_k\right)\right\}}_{k=0}^n=0\right)=\underset{c_0,\dots ,c_n}{min}E\left(R^2(c_0,\dots ,c_n)\right).$$

(23)

Also, it is obvious for $p=0$ that

$$\underset{c_0,\dots ,c_n}{min}{\mathrm{var}}_0\left(R(c_0,\dots ,c_n);Z\right)=\underset{c_0,\dots ,c_n}{min}E\left(R^2(c_0,\dots ,c_n)\right).$$

2.3.2. Second Case

If Z follows a constant distribution (say $Z=c^{*}\ne 0$) and $X_0=1$, the condition (21) is no longer valid for $k=0$ because $c^{*}E\left(1\right)\ne 0$. Therefore, noting the fact that ${\mathrm{cov}}_p(X,Y;c^{*})=E\left(XY\right)-pE\left(X\right)E\left(Y\right)$, the linear system (18) reduces to

$$\begin{array}{cc}\hfill & \left[\begin{array}{cccc}\begin{array}{c}1-p\\ (1-p)E\left(X_1\right)\\ ⋮\\ (1-p)E\left(X_n\right)\end{array}& \begin{array}{c}(1-p)E\left(X_1\right)\\ E\left(X_1^2\right)-p{E}^2\left(X_1\right)\\ ⋮\\ E\left(X_n{X}_1\right)-pE\left(X_n\right)E\left(X_1\right)\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}(1-p)E\left(X_n\right)\\ E\left(X_1{X}_n\right)-pE\left(X_1\right)E\left(X_n\right)\\ ⋮\\ E\left(X_n^2\right)-p{E}^2\left(X_n\right)\end{array}\end{array}\right]\hfill \\ \hfill & \times \left[\begin{array}{c}{c}_0\\ c_1\\ ⋮\\ c_n\end{array}\right]=\left[\begin{array}{c}(1-p)E\left(Y\right)\\ E\left(X_{1}Y\right)-pE\left(X_1\right)E\left(Y\right)\\ ⋮\\ E\left(X_{n}Y\right)-pE\left(X_n\right)E\left(Y\right)\end{array}\right],\hfill \end{array}$$

(24)

Relation (24) shows that for $p=1$, $c_0$ is a free parameter. For $X_0=1$, the approximation (13) takes the simplified form $Y\cong c_0+{\displaystyle \sum _{k=1}^n}{c}_k{X}_k$, and replacing it in the normal system (22) yields

$$\left[\begin{array}{cccc}\begin{array}{c}1\\ E\left(X_1\right)\\ ⋮\\ E\left(X_n\right)\end{array}& \begin{array}{c}E\left(X_1\right)\\ E\left(X_1^2\right)\\ ⋮\\ E\left(X_n{X}_1\right)\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}E\left(X_n\right)\\ E\left(X_1{X}_n\right)\\ ⋮\\ E\left(X_n^2\right)\end{array}\end{array}\right]\left[\begin{array}{c}{c}_0\\ c_1\\ ⋮\\ c_n\end{array}\right]=\left[\begin{array}{c}E\left(Y\right)\\ E\left(X_{1}Y\right)\\ ⋮\\ E\left(X_{n}Y\right)\end{array}\right].$$

(25)

Now, the important point is that, after some elementary operations, the system (25) will exactly be transformed into the linear system (24). This means that, for any arbitrary $p\in [0,1]$, we have

$$\begin{array}{c}\underset{c_1,\dots ,c_n}{min}{\mathrm{var}}_p\left(R(c_0,\dots ,c_n);Z|Z=c^{*}\mathrm{and}{X}_0=1\right)\hfill \\ \hfill =\underset{c_1,\dots ,c_n}{min}E\left(R^2(c_0,\dots ,c_n)|X_0=1\mathrm{and}{c}_0=E\left(Y\right)-{\displaystyle \sum _{k=1}^n}{c}_{k}E\left(X_k\right)\right).\end{array}$$

(26)

Such a result in (26) can similarly be proved for every $Z=X_k$ where $k=1,2,\dots ,n$, as the following example proves.

2.4. An Illustrative Example and the Role of the Fixed Variable in It

The previous Section 2.1, Section 2.2 and Section 2.3 affirm that the fixed variable Z plays a basic role in the theory of least p-variances. Here, we present an illustrative example to show the importance of such a fixed function in constituting the initial approximation (13). Let $Y=\sqrt{1-x}$ be defined on $[0,1]$ together with the probability density function $w\left(x\right)=1$ and the fixed function $z\left(x\right)=x^{\lambda }$, where $\lambda >-1/2$ because ${\int }_0^{1}w\left(x\right)z^2\left(x\right)dx={\displaystyle \frac{1}{2\lambda +1}}$. For the basis functions ${\left\{X_k=x^k\right\}}_{k=0}^2$, the initial approximation (13) takes the form

$$\sqrt{1-x}\cong c_0(\lambda ,p)+c_1(\lambda ,p)x+c_2(\lambda ,p)x^2={\mathbf{A}}_2(x;\lambda ,p),$$

(27)

in which the unknown coefficients satisfy the following linear system according to (18):

$$\begin{array}{cc}\hfill & \left[\begin{array}{ccc}1-{\displaystyle \frac{2\lambda +1}{{(\lambda +1)}^2}}p,& {\displaystyle \frac{1}{2}}-{\displaystyle \frac{2\lambda +1}{(\lambda +1)(\lambda +2)}}p,& {\displaystyle \frac{1}{3}}-{\displaystyle \frac{2\lambda +1}{(\lambda +1)(\lambda +3)}}p\\ {\displaystyle \frac{1}{2}}-{\displaystyle \frac{2\lambda +1}{(\lambda +1)(\lambda +2)}}p,& {\displaystyle \frac{1}{3}}-{\displaystyle \frac{2\lambda +1}{{(\lambda +2)}^2}}p,& {\displaystyle \frac{1}{4}}-{\displaystyle \frac{2\lambda +1}{(\lambda +2)(\lambda +3)}}p\\ {\displaystyle \frac{1}{3}}-{\displaystyle \frac{2\lambda +1}{(\lambda +1)(\lambda +3)}}p,& {\displaystyle \frac{1}{4}}-{\displaystyle \frac{2\lambda +1}{(\lambda +2)(\lambda +3)}}p,& {\displaystyle \frac{1}{5}}-{\displaystyle \frac{2\lambda +1}{{(\lambda +3)}^2}}p\end{array}\right]\left[\begin{array}{c}{c}_0(\lambda ,p)\\ c_1(\lambda ,p)\\ c_2(\lambda ,p)\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}{\displaystyle \frac{2}{3}}-{\displaystyle \frac{2\lambda +1}{\lambda +1}}B(\lambda +1,{\displaystyle \frac{3}{2}})p\\ {\displaystyle \frac{4}{15}}-{\displaystyle \frac{2\lambda +1}{\lambda +2}}B(\lambda +1,{\displaystyle \frac{3}{2}})p\\ {\displaystyle \frac{16}{105}}-{\displaystyle \frac{2\lambda +1}{\lambda +3}}B(\lambda +1,{\displaystyle \frac{3}{2}})p\end{array}\right],\hfill \end{array}$$

(28)

where

$$B(a,b)={\int }_0^1{x}^{a-1}{(1-x)}^{b-1}dx={\displaystyle \frac{\Gamma \left(a\right)\Gamma \left(b\right)}{\Gamma (a+b)}}(a,b>0).$$

After solving (28), ${\mathbf{A}}_2(x;\lambda ,p)$ will be determined, and since the remaining term of (27) is defined as

$${\mathbf{R}}_2(x;\lambda ,p)={\mathbf{A}}_2(x;\lambda ,p)-\sqrt{1-x},$$

so

$${\mathrm{var}}_p\left({\mathbf{R}}_2(x;\lambda ,p);x^{\lambda }\right)=E\left({\left({\mathbf{R}}_2(x;\lambda ,p)\right)}^2\right)-p(2\lambda +1)E^2\left(x^{\lambda }{\mathbf{R}}_2(x;\lambda ,p)\right).$$

However, there are two different cases for the parameter $\lambda >-1/2$, which should be studied separately.

2.4.1. First Case

If $\lambda =0,1,2$, then the fixed functions $z\left(x\right)=1,x,x^2$ coincide, respectively, with the first, second, and third basis functions in (27), and the system (28) is simplified for $\lambda =0$ as

$$\left[\begin{array}{ccc}1-p,& {\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}p,& {\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{3}}p\\ {\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}p,& {\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{4}}p,& {\displaystyle \frac{1}{4}}-{\displaystyle \frac{1}{6}}p\\ {\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{3}}p,& {\displaystyle \frac{1}{4}}-{\displaystyle \frac{1}{6}}p,& {\displaystyle \frac{1}{5}}-{\displaystyle \frac{1}{9}}p\end{array}\right]\left[\begin{array}{c}{c}_0(0,p)\\ c_1(0,p)\\ c_2(0,p)\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{2}{3}}-{\displaystyle \frac{2}{3}}p\\ {\displaystyle \frac{4}{15}}-{\displaystyle \frac{1}{3}}p\\ {\displaystyle \frac{16}{105}}-{\displaystyle \frac{2}{9}}p\end{array}\right],$$

and for $\lambda =1$ as

$$\left[\begin{array}{ccc}1-{\displaystyle \frac{3}{4}}p,& {\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}p,& {\displaystyle \frac{1}{3}}-{\displaystyle \frac{3}{8}}p\\ {\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}p,& {\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{3}}p,& {\displaystyle \frac{1}{4}}-{\displaystyle \frac{1}{4}}p\\ {\displaystyle \frac{1}{3}}-{\displaystyle \frac{3}{8}}p,& {\displaystyle \frac{1}{4}}-{\displaystyle \frac{1}{4}}p,& {\displaystyle \frac{1}{5}}-{\displaystyle \frac{3}{16}}p\end{array}\right]\left[\begin{array}{c}{c}_0(1,p)\\ c_1(1,p)\\ c_2(1,p)\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{2}{3}}-{\displaystyle \frac{2}{5}}p\\ {\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{15}}p\\ {\displaystyle \frac{16}{105}}-{\displaystyle \frac{1}{5}}p\end{array}\right],$$

and finally for $\lambda =2$ as

$$\left[\begin{array}{ccc}1-{\displaystyle \frac{5}{9}}p,& {\displaystyle \frac{1}{2}}-{\displaystyle \frac{5}{12}}p,& {\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{3}}p\\ {\displaystyle \frac{1}{2}}-{\displaystyle \frac{5}{12}}p,& {\displaystyle \frac{1}{3}}-{\displaystyle \frac{5}{16}}p,& {\displaystyle \frac{1}{4}}-{\displaystyle \frac{1}{4}}p\\ {\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{3}}p,& {\displaystyle \frac{1}{4}}-{\displaystyle \frac{1}{4}}p,& {\displaystyle \frac{1}{5}}-{\displaystyle \frac{1}{5}}p\end{array}\right]\left[\begin{array}{c}{c}_0(2,p)\\ c_1(2,p)\\ c_2(2,p)\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{2}{3}}-{\displaystyle \frac{16}{63}}p\\ {\displaystyle \frac{4}{15}}-{\displaystyle \frac{4}{21}}p\\ {\displaystyle \frac{16}{105}}-{\displaystyle \frac{16}{105}}p\end{array}\right].$$

According to the result (26), the solutions of all above systems must be the same and independent of p so that, in the final form, we have

$${\mathbf{A}}_2(x;0,p)={\mathbf{A}}_2(x;1,p)={\mathbf{A}}_2(x;2,p)={\mathbf{A}}_2(x;\lambda ,0)=-{\displaystyle \frac{4}{7}}{x}^2-{\displaystyle \frac{8}{35}}x+{\displaystyle \frac{34}{35}}.$$

Note for $p=1$, after solving (28), we get

$${\mathbf{A}}_2(x;0,1)=-{\displaystyle \frac{4}{7}}{x}^2-{\displaystyle \frac{8}{35}}x+c_0(0,1),$$

in which $c_0(0,1)=E\left(\sqrt{1-x}\right)+{\displaystyle \frac{4}{7}}E\left(x^2\right)+{\displaystyle \frac{8}{35}}E\left(x\right)={\displaystyle \frac{34}{35}}$ according to (26) again.

In this sense, $E\left({\mathbf{R}}_2(x;0,1)\right)=E\left({\mathbf{A}}_2(x;0,1)-\sqrt{1-x}\right)=0$, implies that

$$\begin{array}{c}{\mathrm{var}}_1\left({\mathbf{R}}_2(x;0,1);z\left(x\right)=1\right)=E\left({\left({\mathbf{R}}_2(x;0,1)\right)}^2\right)\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\int }_0^1{\left(-{\displaystyle \frac{4}{7}}{x}^2-{\displaystyle \frac{8}{35}}x+{\displaystyle \frac{34}{35}}-\sqrt{1-x}\right)}^{2}dx={\displaystyle \frac{1}{2450}}\cong 0.000408.\end{array}$$

2.4.2. Second Case

Any assumption other than $\lambda =0,1,2$ causes the system (28) to have a unique solution. For example, $\lambda =1/2$ simplifies (28) in the form

$$\left[\begin{array}{ccc}1-{\displaystyle \frac{8}{9}}p,& {\displaystyle \frac{1}{2}}-{\displaystyle \frac{8}{15}}p,& {\displaystyle \frac{1}{3}}-{\displaystyle \frac{8}{21}}p\\ {\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}p,& {\displaystyle \frac{1}{3}}-{\displaystyle \frac{8}{25}}p,& {\displaystyle \frac{1}{4}}-{\displaystyle \frac{8}{35}}p\\ {\displaystyle \frac{1}{3}}-{\displaystyle \frac{1}{3}}p,& {\displaystyle \frac{1}{4}}-{\displaystyle \frac{8}{35}}p,& {\displaystyle \frac{1}{5}}-{\displaystyle \frac{8}{49}}p\end{array}\right]\left[\begin{array}{c}{c}_0({\displaystyle \frac{1}{2}},p)\\ c_1({\displaystyle \frac{1}{2}},p)\\ c_2({\displaystyle \frac{1}{2}},p)\end{array}\right]=\left[\begin{array}{c}{\displaystyle \frac{2}{3}}-{\displaystyle \frac{1}{6}}\pi p\\ {\displaystyle \frac{4}{15}}-{\displaystyle \frac{1}{10}}\pi p\\ {\displaystyle \frac{16}{105}}-{\displaystyle \frac{1}{14}}\pi p\end{array}\right].$$

(29)

After solving the system (29), we obtain

$${\mathbf{A}}_2(x;{\displaystyle \frac{1}{2}},p)=-{\displaystyle \frac{7}{3}}{\displaystyle \frac{(75\pi +64)p-300}{1224p-1225}}{x}^2+20{\displaystyle \frac{(21\pi -80)p+14}{1224p-1225}}x+{\displaystyle \frac{1}{2}}{\displaystyle \frac{(105\pi +2048)p-2380}{1224p-1225}}.$$

For the special case $p=1$, i.e.,

$${\mathbf{A}}_2(x;{\displaystyle \frac{1}{2}},1)=-({\displaystyle \frac{1652}{3}}-175\pi )x^2+(1320-420\pi )x+166-{\displaystyle \frac{105}{2}}\pi ,$$

we have

$$E\left(x^{{\displaystyle \frac{1}{2}}}{\mathbf{R}}_2(x;{\displaystyle \frac{1}{2}},1)\right)=-{\displaystyle \frac{2}{7}}({\displaystyle \frac{1652}{3}}-175\pi )+{\displaystyle \frac{2}{5}}(1320-420\pi )+{\displaystyle \frac{2}{3}}(166-{\displaystyle \frac{105}{2}}\pi )-{\displaystyle \frac{\pi }{8}},$$

and consequently

$${\mathrm{var}}_1\left({\mathbf{R}}_2(x;{\displaystyle \frac{1}{2}},1);x^{{\displaystyle \frac{1}{2}}}\right)=E\left({\left({\mathbf{R}}_2(x;{\displaystyle \frac{1}{2}},1)\right)}^2\right)-2E^2\left(x^{{\displaystyle \frac{1}{2}}}{\mathbf{R}}_2(x;{\displaystyle \frac{1}{2}},1)\right)\cong 0.000388.$$

As we observe

$${\mathrm{var}}_1\left({\mathbf{R}}_2(x;{\displaystyle \frac{1}{2}},1);x^{{\displaystyle \frac{1}{2}}}\right)<{\mathrm{var}}_1\left({\mathbf{R}}_2(x;0,1);1\right)=E\left({\left({\mathbf{R}}_2(x;0,1)\right)}^2\right),$$

which clearly shows the role of the fixed function in the obtained approximations.

2.5. How to Choose a Suitable Option for the Fixed Variable: A Geometric Interpretation

Although inequality (28) holds for any arbitrary variable Z, our wish is to determine some conditions to find a suitable option for the fixed variable Z, such that

$${\mathrm{var}}_1(X;Z)\ll E\left(X^2\right),$$

(30)

and/or

$${\displaystyle \frac{E^2\left(XZ\right)}{E\left(Z^2\right)}}\gg 0.$$

(31)

Various states can be considered for the above-mentioned goal. For example, replacing $Z=c^{*}\ne 0$ in (31) yields $E^2\left(X\right)\gg 0$ which means that, if the magnitude of the mean value $E\left(X\right)\ne 0$ is very big, we expect that the presented theory based on the fixed variable $Z=c^{*}\ne 0$ acts much better than the ordinary least squares theory. Another approach is to directly minimize the value ${\mathrm{var}}_1(X;Z)$ in (30), such that $X-{\displaystyle \frac{E\left(XZ\right)}{E\left(Z^2\right)}}Z\to 0$. The Figure 1 describes our aim in a vector space.

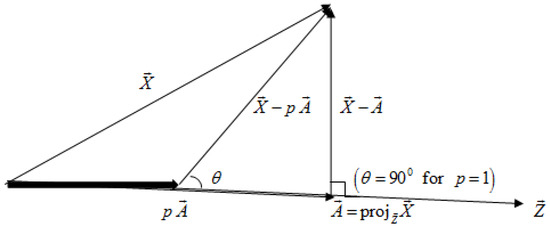
Figure 1. Least p-variances based on the fixed vector $\overrightarrow{Z}$ and the role of p from 0 to 1.

In this figure, ${∥\overrightarrow{X}∥}_2^2={\displaystyle \sum _{k=1}^m}{x}_k^2$ leads to the same as ordinary least squares for $p=0$, ${∥\overrightarrow{X}-\overrightarrow{A}∥}_2^2={∥\overrightarrow{X}-\mathrm{pro}{\mathrm{j}}_{\overrightarrow{Z}}\overrightarrow{X}∥}_2^2$ leads to the complete type of least variances based on $\overrightarrow{Z}$ and $p=1$, and finally, ${∥\overrightarrow{X}-p\overrightarrow{A}∥}_2^2$ leads to the least p-variances based on $\overrightarrow{Z}$ and $p\in [0,1]$.

3. p-Uncorrelatedness Condition on the p-Covariances Linear System and Its Consequences

Since the coefficients matrix of the system (18) is symmetric and all its diagonal entries are positive, the aforesaid system is solvable, and its unknown coefficients are computable. However, as we observed in the previous example, analytically solving such linear systems is difficult from a computational point of view. To resolve this problem, we can impose the condition

$${\mathrm{cov}}_p(X_i,X_j;Z)={\mathrm{var}}_p(X_j;Z){\delta }_{i,j}\mathrm{for}\mathrm{every}i,j=0,1,\dots ,n\mathrm{with}{\delta }_{i,j}=\left\{\begin{array}{c}0(i\ne j),\hfill \\ 1(i=j),\hfill \end{array}\right.$$

(32)

on the elements of the system (18) to easily obtain the unknown coefficients in the form

$$c_k={\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}.$$

In this case,

$$Y\cong {\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k,$$

(33)

would be the best approximation in the sense of least p-variance of the error with respect to the fixed variable Z.

Theorem 1.

Any finite set of random variables satisfying the p-uncorrelatedness condition (32) is linearly independent.

Proof. 

Assume that ${\displaystyle \sum _{k=0}^n}{a}_k{X}_k=0$, where ${\left\{a_k\right\}}_{k=0}^n$ are not all zero, and ${\left\{X_k\right\}}_{k=0}^n$ are p-uncorrelated variables satisfying (32). Then, applying ${\mathrm{cov}}_p(.,X_j;Z)$ on both sides of this assumption yields

$$0={\mathrm{cov}}_p\left({\displaystyle \sum _{k=0}^n}{a}_k{X}_k,X_j;Z\right)={\displaystyle \sum _{k=0}^n}{a}_k{\mathrm{cov}}_p(X_k,X_j;Z)=a_j{\mathrm{var}}_p(X_j;Z),$$

which implies that $a_j=0$ for $j=0,1,\dots ,n$, i.e., a contradiction. □

The question is now how to find linear combinations that are p-uncorrelated with respect to the variable Z. There is a basic theorem in this direction similar to the Gram–Schmidt orthogonalization theorem [16].

Theorem 2.

Let ${\left\{V_k\right\}}_{k=0}^n$ be a finite or infinite sequence of random variables, such that any finite number of elements, ${\left\{V_k\right\}}_{k=0}^n$, are linearly independent. One can find constants $\left\{a_{i,j}\right\}$, such that the elements

$$\begin{array}{c}{X}_0=V_0,\hfill \\ X_1=V_1+a_{12}{V}_0,\hfill \\ X_2=V_2+a_{22}{V}_1+a_{23}{V}_0,\hfill \\ ⋮\hfill \\ X_n=V_n+a_{n2}{V}_{n-1}+\cdots +a_{n,n+1}{V}_0,\hfill \end{array}$$

(34)

are mutually p-uncorrelated with respect to the fixed variable Z

Proof. 

Let us set, recursively,

$$\begin{array}{c}{X}_0=V_0,\hfill \\ X_1=V_1-{\displaystyle \frac{{\mathrm{cov}}_p(X_0,V_1;Z)}{{\mathrm{var}}_p(X_0;Z)}}{X}_0,\hfill \\ ⋮\hfill \\ X_n=V_n-{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,V_n;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k.\hfill \end{array}$$

(35)

Since relations (35) show that $X_n$ is a linear combination of ${\left\{V_k\right\}}_{k=0}^n$, it is just enough to show that $X_n$ is p-uncorrelated to ${\left\{X_j\right\}}_{j=0}^{n-1}$ with respect to the variable Z. For $j=0,1,\dots ,n-1$ we have

$$\begin{array}{cc}\hfill {\mathrm{cov}}_p(X_n,X_j;Z)& ={\mathrm{cov}}_p\left(V_n-{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,V_n;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k,X_j;Z\right)\hfill \\ \hfill & ={\mathrm{cov}}_p(V_n,X_j;Z)-{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,V_n;Z)}{{\mathrm{var}}_p(X_k;Z)}}{\mathrm{cov}}_p(X_k,X_j;Z)\hfill \\ \hfill & ={\mathrm{cov}}_p(V_n,X_j;Z)-{\mathrm{cov}}_p(X_j,V_n;Z)=0.\hspace{1em}\square \hfill \end{array}$$

In fact, Theorem 2 is a generalization of the Gram–Schmidt orthogonalization process when $p=0$ or the condition $E\left(Z{V}_k\right)=0$ holds for every $k=0,1,\dots ,n$.

Theorem 3.

The reverse proposition of the previous theorem is as follows: There are constants, $\left\{b_{i,j}\right\}$, such that

$$\begin{array}{c}{V}_0=X_0,\hfill \\ V_1=X_1+b_{12}{X}_0,\hfill \\ V_2=X_2+b_{22}{X}_1+b_{23}{X}_0,\hfill \\ ⋮\hfill \\ V_n=X_n+b_{n2}{X}_{n-1}+\cdots +b_{n,n+1}{X}_0,\hfill \end{array}$$

(36)

and

$${\mathrm{cov}}_p(X_n,V_k;Z)=0\mathrm{for}k=0,1,\dots ,n-1,$$

provided that

$${\mathrm{cov}}_p(X_i,X_j;Z)=0\mathrm{for}i\ne j.$$

(37)

Proof. 

By virtue of the fact that the system (34) is invertible, the general element of (36) in the form

$$V_k=X_k+b_{k2}{X}_{k-1}+\cdots +b_{k,k+1}{X}_0,$$

yields

$$\begin{array}{cc}\hfill {\mathrm{cov}}_p(X_n,V_k;Z)& ={\mathrm{cov}}_p(X_n,X_k+{\displaystyle \sum _{j=2}^{k+1}}{b}_{k,j}{X}_{k+1-j};Z)\hfill \\ \hfill & ={\mathrm{cov}}_p(X_n,X_k;Z)+{\displaystyle \sum _{j=2}^{k+1}}{b}_{k,j}{\mathrm{cov}}_p(X_n,X_{k+1-j};Z)=0,\hfill \end{array}$$

which is valid for every $k=0,1,\dots ,n-1$, according to the condition (37). □

A General Representation for p-Uncorrelated Variables

Both previous theorems, Theorems 2 and 3, help us now obtain a general representation for p-uncorrelated variables with respect to the variable Z. Assume that ${\left\{V_k\right\}}_{k=0}^n$ is an arbitrary, independent sequence of random variables, and ${\left\{X_k\right\}}_{k=0}^n$ satisfy the condition (32) as before. Noting the last row of (35) and this fact from (34) that $X_n={\displaystyle \sum _{k=0}^n}{a}_{n,n+1-k}{V}_k$ where $a_{n,1}=1$, for $m\le n$, we have

$$\begin{array}{cc}\hfill & {\mathrm{cov}}_p(X_n,X_m;Z)={\mathrm{cov}}_p\left(X_n,V_m-{\displaystyle \sum _{j=0}^{m-1}}{\displaystyle \frac{{\mathrm{cov}}_p(X_j,V_m;Z)}{{\mathrm{var}}_p(X_j;Z)}}{X}_j;Z\right)\hfill \\ \hfill & ={\mathrm{cov}}_p(X_n,V_m;Z)-{\displaystyle \sum _{j=0}^{m-1}}{\displaystyle \frac{{\mathrm{cov}}_p(X_j,V_m;Z)}{{\mathrm{var}}_p(X_j;Z)}}{\mathrm{cov}}_p\left(X_n,X_j;Z\right)={\mathrm{cov}}_p(V_m,X_n;Z)\hfill \\ \hfill & ={\mathrm{cov}}_p(V_m,{\displaystyle \sum _{k=0}^n}{a}_{n,n+1-k}{V}_k;Z)={\displaystyle \sum _{k=0}^n}{a}_{n,n+1-k}{\mathrm{cov}}_p\left(V_m,V_k;Z\right)={\mathrm{var}}_p(X_n;Z){\delta }_{m,n}.\hfill \end{array}$$

(38)

For $m=0,1,\dots ,n$, relation (38) leads eventually to the linear system

$$\begin{array}{cc}\hfill & \left[\begin{array}{cccc}\begin{array}{c}{\mathrm{var}}_p(V_0;Z)\\ {\mathrm{cov}}_p(V_1,V_0;Z)\\ ⋮\\ {\mathrm{cov}}_p(V_n,V_0;Z)\end{array}& \begin{array}{c}{\mathrm{cov}}_p(V_0,V_1;Z)\\ {\mathrm{var}}_p(V_1;Z)\\ ⋮\\ {\mathrm{cov}}_p(V_n,V_1;Z)\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}{\mathrm{cov}}_p(V_0,V_n;Z)\\ {\mathrm{cov}}_p(V_1,V_n;Z)\\ ⋮\\ {\mathrm{var}}_p(V_n;Z)\end{array}\end{array}\right]\left[\begin{array}{c}{a}_{n,n+1}\\ a_{n,n}\\ ⋮\\ a_{n,1}\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}0\\ 0\\ ⋮\\ {\mathrm{var}}_p(X_n;Z)\end{array}\right].\hfill \end{array}$$

(39)

If the determinant

$${\Delta }_n^{\left(p\right)}\left({\left\{V_k\right\}}_{k=0}^n;Z\right)=\left|\begin{array}{cccc}\begin{array}{c}{\mathrm{var}}_p(V_0;Z)\\ {\mathrm{cov}}_p(V_1,V_0;Z)\\ ⋮\\ {\mathrm{cov}}_p(V_n,V_0;Z)\end{array}& \begin{array}{c}{\mathrm{cov}}_p(V_0,V_1;Z)\\ {\mathrm{var}}_p(V_1;Z)\\ ⋮\\ {\mathrm{cov}}_p(V_n,V_1;Z)\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}{\mathrm{cov}}_p(V_0,V_n;Z)\\ {\mathrm{cov}}_p(V_1,V_n;Z)\\ ⋮\\ {\mathrm{var}}_p(V_n;Z)\end{array}\end{array}\right|,$$

(40)

is defined with ${\Delta }_{-1}^{\left(p\right)}(.)=1$, the first result of solving the system (39) is that the value ${\mathrm{var}}_p(X_n;Z)$ can be computed in terms of the determinant (40) as

$${\mathrm{var}}_p(X_n;Z)={\displaystyle \frac{{\Delta }_n^{\left(p\right)}\left({\left\{V_k\right\}}_{k=0}^n;Z\right)}{{\Delta }_{n-1}^{\left(p\right)}\left({\left\{V_k\right\}}_{k=0}^{n-1};Z\right)}}.$$

(41)

On the other side, it follows from (41) as a first-order equation that

$${\Delta }_n^{\left(p\right)}\left({\left\{V_k\right\}}_{k=0}^n;Z\right)={\displaystyle \prod _{k=0}^n}{\mathrm{var}}_p(X_k;Z)\ge 0.$$

(42)

The second result of solving (39) is to derive a general representation for $X_n$ as

$$\begin{array}{c}{\Delta }_{n-1}^{\left(p\right)}\left({\left\{V_k\right\}}_{k=0}^{n-1};Z\right)X_n\hfill \\ \hfill =\left|\begin{array}{c}\begin{array}{cccc}\begin{array}{c}{\mathrm{var}}_p(V_0;Z)\\ {\mathrm{cov}}_p(V_1,V_0;Z)\\ ⋮\\ {\mathrm{cov}}_p(V_{n-1},V_0;Z)\\ V_0\end{array}& \begin{array}{c}{\mathrm{cov}}_p(V_0,V_1;Z)\\ {\mathrm{var}}_p(V_1;Z)\\ ⋮\\ {\mathrm{cov}}_p(V_{n-1},V_1;Z)\\ V_1\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \\ \cdots \end{array}& \begin{array}{c}{\mathrm{cov}}_p(V_0,V_n;Z)\\ {\mathrm{cov}}_p(V_1,V_n;Z)\\ ⋮\\ {\mathrm{cov}}_p(V_{n-1},V_n;Z)\\ V_n\end{array}\end{array}\hfill \end{array}\right|,\end{array}$$

(43)

where we have exploited (41) to derive it.

Inequality (42) reveals that the determinant of the coefficients matrix of the system (18) is always non-negative. Moreover, if $p=0$ or $E\left(Z{X}_k\right)=0$, for every $k=0,1,\dots ,n$ in (43), it gives the same as the Gram–Schmidt orthogonalization process. For instance, the expanded forms of (43) for $n=0,1,2$ are

$$\begin{array}{cc}\hfill X_0& =V_0,\hfill \\ \hfill X_1& =V_1-{\displaystyle \frac{{\mathrm{cov}}_p(V_0,V_1;Z)}{{\mathrm{var}}_p(V_0;Z)}}{V}_0,\hfill \\ \hfill X_2& =V_2-{\displaystyle \frac{{\mathrm{var}}_p(V_0;Z){\mathrm{cov}}_p(V_1,V_2;Z)-{\mathrm{cov}}_p(V_0,V_1;Z){\mathrm{cov}}_p(V_0,V_2;Z)}{{\mathrm{var}}_p(V_0;Z){\mathrm{var}}_p(V_1;Z)-{\mathrm{cov}}_p^2(V_0,V_1;Z)}}{V}_1\hfill \\ \hfill & -{\displaystyle \frac{{\mathrm{var}}_p(V_1;Z){\mathrm{cov}}_p(V_0,V_2;Z)-{\mathrm{cov}}_p(V_0,V_1;Z){\mathrm{cov}}_p(V_1,V_2;Z)}{{\mathrm{var}}_p(V_0;Z){\mathrm{var}}_p(V_1;Z)-{\mathrm{cov}}_p^2(V_0,V_1;Z)}}{V}_0,\hfill \end{array}$$

satisfying the conditions

$${\mathrm{cov}}_p(X_0,X_1;Z)={\mathrm{cov}}_p(X_0,X_2;Z)={\mathrm{cov}}_p(X_1,X_2;Z)=0.$$

Notice that, although the general representation (43) is computationally slower than the recursive algorithm described in Theorem 2, it is of theoretical interest, as we have used it to find new sequences of p-uncorrelated functions (see examples of Section 7, Section 8, Section 9 and Section 10).

4. p-Uncorrelated Expansions with Respect to a Fixed Variable

Let ${\left\{X_k\right\}}_{k=0}^n$ be a sequence of p-uncorrelated variables with respect to the variable Z. If $n\to \infty$ in approximation (33), the series

$${\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k,$$

is called a p-uncorrelated expansion with respect to Z for Y, and then we write

$$Y\sim {\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k.$$

(44)

In the case where n is finite, there is a separate theorem, as follows.

Theorem 4.

Let ${\left\{V_k\right\}}_{k=0}^n$ be linearly independent variables, and let ${\left\{X_k\right\}}_{k=0}^n$ be their corresponding p-uncorrelated elements generated via ${\left\{V_k\right\}}_{k=0}^n$ in Theorem 2. If ${\displaystyle \sum _{k=0}^n}{a}_k{V}_k=W_n$, and then

$$W_n={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,W_n;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k.$$

(45)

Proof. 

First from Theorem 3 and relation (36), we have

$$\begin{array}{cc}\hfill & W_n={\displaystyle \sum _{k=0}^n}{a}_k{V}_k=a_0\left(X_0\right)+a_1(X_1+b_{12}{X}_0)+\cdots +a_n(X_n+b_{n2}{X}_{n-1}+\cdots +b_{n,n+1}{X}_0)\hfill \\ \hfill & =c_0{X}_0+c_1{X}_1+\cdots +c_n{X}_n.\hfill \end{array}$$

(46)

Now, for $k=0,1,\dots ,n$, apply ${\mathrm{cov}}_p(.,X_k;Z)$ on both sides of (46) to get

$${\mathrm{cov}}_p(W_n,X_k;Z)={\mathrm{cov}}_p({\displaystyle \sum _{j=0}^n}{c}_j{X}_j,X_k;Z)={\displaystyle \sum _{j=0}^n}{c}_j{\mathrm{cov}}_p(X_j,X_k;Z)=c_k{\mathrm{var}}_p(X_k;Z),$$

which yields

$$c_k={\displaystyle \frac{{\mathrm{cov}}_p(W_n,X_k;Z)}{{\mathrm{var}}_p(X_k;Z)}},$$

and (45) is, therefore, proven. □

Remark 1.

There is an important point in Theorem 4. Let us reconsider $n+1$ mutually p-uncorrelated elements ${\left\{X_k\right\}}_{k=0}^n$, satisfying the condition

$${\mathrm{cov}}_p(X_i,X_j;Z)={\mathrm{var}}_p(X_j;Z){\delta }_{i,j}.$$

(47)

Since

$${\mathrm{cov}}_p(X_i,X_j;Z)=E\left(\left(X_i-(1-\sqrt{1-p}){\displaystyle \frac{E\left(X_{i}Z\right)}{E\left(Z^2\right)}}Z\right)\left(X_j-(1-\sqrt{1-p}){\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z\right)\right),$$

by defining the variable

$$T_{j,p}\left(Z\right)=X_j-(1-\sqrt{1-p}){\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z=X_j-(1-\sqrt{1-p})\mathrm{pro}{\mathrm{j}}_Z{X}_j,$$

(48)

we observe in (47) that

$$E\left(T_{i,p}\left(Z\right)T_{j,p}\left(Z\right)\right)=E\left(T_{j,p}^2\left(Z\right)\right){\delta }_{i,j}.$$

(49)

Now notice that the orthogonal sequence ${\left\{T_{j,p}\left(Z\right)\right\}}_{j=0}^n$ in (48) is created only when we have already created the uncorrelated sequence ${\left\{X_j\right\}}_{j=0}^n$ because of the term ${\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z$; otherwise, generating such orthogonal sequences is impossible. This means that uncorrelatedness would always lead to orthogonality, but its reverse is not possible when ${\left\{E\left(Z{X}_k\right)\right\}}_{k=0}^n\ne 0$. Also, note that the original shape of these two sequences is quite different, so their corresponding approximations are different, such that the approximation corresponding to the orthogonal base ${\left\{T_{j,p}\left(Z\right)\right\}}_{j=0}^n$ is optimized in the sense of ordinary least squares, while the approximation corresponding to the uncorrelated base ${\left\{X_j\right\}}_{j=0}^n$ is optimized in the sense of least p-variances. Referring to (48) and (49), let us now consider the following orthogonal approximation sum for the same variable $W_n$, as stated in (45),

$$S_n={\displaystyle \sum _{j=0}^n}{\displaystyle \frac{E\left(W_n{T}_{j,p}\left(Z\right)\right)}{E\left(T_{j,p}^2\left(Z\right)\right)}}{T}_{j,p}\left(Z\right).$$

(50)

Since, in (50),

$$E\left(W_n{T}_{j,p}\left(Z\right)\right)=E\left(W_n\left(X_j-(1-\sqrt{1-p}){\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z\right)\right)={\mathrm{cov}}_p(X_j,W_n;Z),$$

and

$$E\left(T_{j,p}^2\left(Z\right)\right)=E\left({\left(X_j-(1-\sqrt{1-p}){\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z\right)}^2\right)={\mathrm{var}}_p(X_j;Z),$$

the aforesaid sum is simplified as

$$\begin{array}{cc}\hfill S_n& ={\displaystyle \sum _{j=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_j,W_n;Z)}{{\mathrm{var}}_p(X_j;Z)}}\left(X_j-(1-\sqrt{1-p}){\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z\right)\hfill \\ \hfill & =W_n-(1-\sqrt{1-p}){\displaystyle \frac{Z}{E\left(Z^2\right)}}{\displaystyle \sum _{j=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_j,W_n;Z)E\left(X_{j}Z\right)}{{\mathrm{var}}_p(X_j;Z)}}.\hfill \end{array}$$

(51)

The main point is now here: if, in (51), $p=0$ or ${\left\{E\left(X_{j}Z\right)=0\right\}}_{j=0}^n$ (see Section 2.3.1) and/or the limit condition

$${\displaystyle \sum _{j=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p(X_j,W_n;Z)E\left(X_{j}Z\right)}{{\mathrm{var}}_p(X_j;Z)}}=0,$$

(52)

is satisfied, then $\underset{n\to \infty }{lim}{S}_n=\underset{n\to \infty }{lim}{W}_n=W^{*}$, and subsequently

$${\displaystyle \sum _{j=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p(X_j,W^{*};Z)}{{\mathrm{var}}_p(X_j;Z)}}{X}_j={\displaystyle \sum _{j=0}^{\infty }}{\displaystyle \frac{E\left(W^{*}{T}_{j,p}\left(Z\right)\right)}{E\left(T_{j,p}^2\left(Z\right)\right)}}{T}_{j,p}\left(Z\right).$$

(53)

This means that the two aforesaid expansions in (53) coincide with each other only if the condition (52) holds. However, in many cases, this condition will not occur independently, as $W_n$ is distinct for each choice, especially in continuous spaces; see Corollary 9 in this regard. We finally add that, in a general case, we have

$$\begin{array}{cc}\hfill {\displaystyle \sum _{j=0}^n}{C}_j{T}_{j,p}\left(Z\right)& ={\displaystyle \sum _{j=0}^n}{C}_j\left(X_j-(1-\sqrt{1-p}){\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z\right)\hfill \\ \hfill & ={\displaystyle \sum _{j=0}^n}{C}_j{X}_j-(1-\sqrt{1-p}){\displaystyle \frac{Z}{E\left(Z^2\right)}}E\left(Z{\displaystyle \sum _{j=0}^n}{C}_j{X}_j\right)\hfill \\ \hfill & ={\displaystyle \sum _{j=0}^n}{C}_j{X}_j-(1-\sqrt{1-p})\mathrm{pro}{\mathrm{j}}_Z\left({\displaystyle \sum _{j=0}^n}{C}_j{X}_j\right).\hfill \end{array}$$

4.1. A Biorthogonality Property

Let ${\left\{X_k\right\}}_{k=0}$ be a sequence of complete uncorrelated variables satisfying the condition

$${\mathrm{cov}}_1(X_k,X_j;Z)={\mathrm{var}}_1(X_j;Z){\delta }_{k,j}.$$

Since

$$E\left(X_k\left(X_j-{\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z\right)\right)={\mathrm{cov}}_1(X_k,X_j;Z),$$

so the relation

$$E\left(X_k\left(X_j-{\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z\right)\right)={\mathrm{var}}_1(X_j;Z){\delta }_{k,j}.$$

implies that the sequence ${\left\{X_k\right\}}_{k=0}$ is biorthogonal with respect to the sequence ${\left\{X_j-{\displaystyle \frac{E\left(X_{j}Z\right)}{E\left(Z^2\right)}}Z\right\}}_{j=0}$. This means that every complete uncorrelated sequence can be biorthogonal, but its reverse proposition is not true. See also Corollary 7. To study the topic of biorthogonality, we refer the readers to [17,18].

Theorem 5.

Let ${\left\{X_k\right\}}_{k=0}$ be p-uncorrelated variables satisfying the condition (47), and let Y be arbitrary. Then,

$${\mathrm{var}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k;Z\right)\le {\mathrm{var}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\alpha }_k{X}_k;Z\right),$$

(54)

for any selection of constants ${\left\{{\alpha }_k\right\}}_{k=0}^n$.

Proof. 

According to (9), we first have

$$\begin{array}{cc}\hfill & {\mathrm{var}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\alpha }_k{X}_k;Z\right)={\mathrm{var}}_p\left(Y;Z\right)+{\mathrm{var}}_p\left({\displaystyle \sum _{k=0}^n}{\alpha }_k{X}_k;Z\right)-2{\mathrm{cov}}_p\left({\displaystyle \sum _{k=0}^n}{\alpha }_k{X}_k,Y;Z\right)\hfill \\ \hfill & ={\mathrm{var}}_p\left(Y;Z\right)+{\displaystyle \sum _{k=0}^n}{\alpha }_k^2{\mathrm{var}}_p\left(X_k;Z\right)-2{\displaystyle \sum _{k=0}^n}{\alpha }_k{\mathrm{cov}}_p\left(X_k,Y;Z\right)\hfill \\ \hfill & ={\mathrm{var}}_p\left(Y;Z\right)+{\displaystyle \sum _{k=0}^n}{\left({\alpha }_k\sqrt{{\mathrm{var}}_p\left(X_k;Z\right)}-{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{\sqrt{{\mathrm{var}}_p\left(X_k;Z\right)}}}\right)}^2-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p^2(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}},\hfill \end{array}$$

(55)

in which the following identity has been used:

$${\mathrm{var}}_p\left({\displaystyle \sum _{k=0}^n}{a}_k{X}_k;Z\right)={\displaystyle \sum _{k=0}^n}{a}_k^2{\mathrm{var}}_p\left(X_k;Z\right)\iff {\mathrm{cov}}_p\left(X_i,X_j;Z\right)=0\mathrm{for}i\ne j.$$

Since ${\mathrm{var}}_p\left(Y;Z\right)-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p^2(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}$ is independent of ${\left\{{\alpha }_k\right\}}_{k=0}^n$ in the last equality of (55), the minimum of ${\mathrm{var}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\alpha }_k{X}_k;Z\right)$ is, therefore, achieved only when

$${\alpha }_k\sqrt{{\mathrm{var}}_p\left(X_k;Z\right)}-{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{\sqrt{{\mathrm{var}}_p\left(X_k;Z\right)}}}=0,$$

(56)

which results in the left side of inequality (54). □

With reference to (8), inequality (54) can be completed as follows

$${\mathrm{var}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k;Z\right)\le {\mathrm{var}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\alpha }_k{X}_k;Z\right)\le E\left({\left(Y-{\displaystyle \sum _{k=0}^n}{\alpha }_k{X}_k\right)}^2\right),$$

(57)

where ${\left\{{\alpha }_k\right\}}_{k=0}^n$ are arbitrary.

Again, inequality (57) shows the superiority of p-uncorrelated approximations (33) with respect to any approximation that is made using the least square method (in particular orthogonal approximations). See Example 3 in this regard.

Corollary 1.

Let ${\left\{V_k\right\}}_{k=0}^n$ be an independent set of random variables. The problem of finding that linear combination of $V_0,V_1,\dots ,V_n$, which minimizes ${\mathrm{var}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\beta }_k{V}_k;Z\right)$, for any selection of constants ${\left\{{\beta }_k\right\}}_{k=0}^n$ is solved using ${\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k$ where ${\left\{X_k\right\}}_{k=0}^n$ are mutually p-uncorrelated with respect to the variable Z. This corollary tells us that every least p-variance problem with respect to a fixed variable is solved by an appropriate truncated p-uncorrelated expansion of type (44).

Corollary 2.

Substituting (56) into (55) gives

$$\begin{array}{c}{\mathrm{var}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k;Z\right)={\mathrm{var}}_p(Y;Z)-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p^2(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\mathrm{var}}_p(Y;Z)\left(1-{\displaystyle \sum _{k=0}^n}{\rho }_p^2(X_k,Y;Z)\right).\hfill \end{array}$$

(58)

On the other hand, the positivity of a p-variance in (58) implies that

$${\displaystyle \sum _{k=0}^n}{\rho }_p^2(X_k,Y;Z)\le 1,$$

where ${\left\{X_k\right\}}_{k=0}^n$ satisfy (47). Also, if ${\left\{X_k\right\}}_{k=0}^{\infty }$ is an infinite sequence of p-uncorrelated variables, then the latter inequality changes to

$${\displaystyle \sum _{k=0}^{\infty }}{\rho }_p^2(X_k,Y;Z)\le 1\mathrm{or}{\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p^2(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}\le {\mathrm{var}}_p(Y;Z).$$

(59)

Finally, convergence in the series (59) causes

$$\underset{k\to \infty }{lim}{\rho }_p^2(X_k,Y;Z)=0\mathrm{or}\underset{k\to \infty }{lim}{\displaystyle \frac{{\mathrm{cov}}_p^2(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}=0.$$

Definition 5.

Convergence in p-variance with respect to a fixed variable

• Reconsider the approximation (13), and form the p-variance of its error just like in relation (15). If

  $$\underset{n\to \infty }{lim}{\mathrm{var}}_p\left(R(c_0,\dots ,c_n);Z\right)=0,$$

  (60)

we call the limit relation (60) “Convergence in p-variance with respect to the fixed variable Z”. In this sense, by noting identity (58) if

$$0=\underset{n\to \infty }{lim}{\mathrm{var}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k;Z\right)={\mathrm{var}}_p(Y;Z)\underset{n\to \infty }{lim}\left(1-{\displaystyle \sum _{k=0}^n}{\rho }_p^2(X_k,Y;Z)\right),$$

and then

$${\displaystyle \sum _{k=0}^{\infty }}{\rho }_p^2(X_k,Y;Z)=1\mathrm{or}{\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p^2(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}={\mathrm{var}}_p(Y;Z),$$

provided that ${\left\{X_k\right\}}_{k=0}$ are mutually p-uncorrelated.

Theorem 6.

Let ${\left\{V_k\right\}}_{k=0}^n$ be linearly independent variables, and let ${\left\{X_k\right\}}_{k=0}^n$ be their corresponding p-uncorrelated elements generated via ${\left\{V_k\right\}}_{k=0}^n$ in Theorem 2. Then, for any selection of constants ${\left\{{\lambda }_k\right\}}_{k=0}^{n-1}$, we have

$${\mathrm{var}}_p\left(X_n;Z\right)\le {\mathrm{var}}_p\left(V_n+{\displaystyle \sum _{k=0}^{n-1}}{\lambda }_k{V}_k;Z\right).$$

(61)

Proof. 

First, suppose in (54) that $n\to n-1$, and then take $Y=V_n$. Noting the last equality of (35) gives

$${\mathrm{var}}_p\left(V_n-{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,V_n;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k;Z\right)={\mathrm{var}}_p\left(X_n;Z\right)\le {\mathrm{var}}_p\left(V_n-{\displaystyle \sum _{k=0}^{n-1}}{\alpha }_k{X}_k;Z\right).$$

(62)

On the other hand, according to relations (34), there exists an arbitrary sequence, say ${\left\{{\lambda }_k\right\}}_{k=0}^{n-1}$, such that $-{\displaystyle \sum _{k=0}^{n-1}}{\alpha }_k{X}_k={\displaystyle \sum _{k=0}^{n-1}}{\lambda }_k{V}_k$ in (62) which completes the proof of (61). □

Corollary 3.

Let ${\left\{X_k\right\}}_{k=0}^n$ be a p-uncorrelated variables with respect to the fixed variable Z. Then, for any variable Y and every $j=0,1,\dots ,n$, we have

$$\begin{array}{cc}\hfill & {\mathrm{cov}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}{X}_k,X_j;Z\right)\hfill \\ \hfill & ={\mathrm{cov}}_p\left(Y,X_j;Z\right)-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;Z)}{{\mathrm{var}}_p(X_k;Z)}}{\mathrm{cov}}_p\left(X_k,X_j;Z\right)\hfill \\ \hfill & ={\mathrm{cov}}_p\left(Y,X_j;Z\right)-{\mathrm{cov}}_p\left(X_j,Y;Z\right)=0.\hfill \end{array}$$

Here is a suitable position for studying the p-uncorrelatedness topic practically and introducing new sequences of functions in continuous and discrete spaces.

5. p-Uncorrelated Functions with Respect to a Fixed Function

Let ${\left\{{\Phi }_k\left(x\right)\right\}}_{k=0}$ be a sequence of continuous functions defined on $[a,b]$, and let $w\left(x\right)$ be positive on this interval. Also let $z\left(x\right)$ be a continuous function, such that ${\int }_a^{b}w\left(x\right)z^2\left(x\right)dx>0$. Referring to (19), we say that ${\left\{{\Phi }_k\left(x\right)\right\}}_{k=0}^{\infty }$ are (weighted) p-uncorrelated functions with respect to the fixed function $z\left(x\right)$ if they satisfy the condition

$$\begin{array}{c}{\int }_a^{b}w\left(x\right){\Phi }_m\left(x\right){\Phi }_n\left(x\right)dx-p{\displaystyle \frac{{\int }_a^{b}w\left(x\right){\Phi }_m\left(x\right)z\left(x\right)dx{\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right)z\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left({\int }_a^{b}w\left(x\right){\Phi }_n^2\left(x\right)dx-p{\displaystyle \frac{{\left({\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right)z\left(x\right)dx\right)}^2}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}}\right){\delta }_{m,n}.\hfill \end{array}$$

(63)

Especially when $w\left(x\right)z\left(x\right)=v\left(x\right)$, (63) becomes

$$\begin{array}{c}{\int }_a^{b}w\left(x\right){\Phi }_m\left(x\right){\Phi }_n\left(x\right)dx-{\lambda }_p^2{\int }_a^{b}v\left(x\right){\Phi }_m\left(x\right)dx{\int }_a^{b}v\left(x\right){\Phi }_n\left(x\right)dx\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left({\int }_a^{b}w\left(x\right){\Phi }_n^2\left(x\right)dx-{\lambda }_p^2{\left({\int }_a^{b}v\left(x\right){\Phi }_n\left(x\right)dx\right)}^2\right){\delta }_{m,n},\hfill \end{array}$$

where ${\lambda }_p^2=p/{\int }_a^b{\displaystyle \frac{v^2\left(x\right)}{w\left(x\right)}}dx$ (e.g., see relation (225)).

• Noting (20), such a definition in (63) can similarly be considered for discrete functions as

  $$\begin{array}{c}\sum _{x\in A^{*}}j\left(x\right){\Phi }_m\left(x\right){\Phi }_n\left(x\right)-p{\displaystyle \frac{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right){\Phi }_m\left(x\right)z\left(x\right){\displaystyle \sum _{x\in A^{*}}}j\left(x\right){\Phi }_n\left(x\right)z\left(x\right)}{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right)z^2\left(x\right)}}\hfill \\ \hfill =\left(\sum _{x\in A^{*}}j\left(x\right){\Phi }_n^2\left(x\right)-p{\displaystyle \frac{{\left({\displaystyle \sum _{x\in A^{*}}}j\left(x\right){\Phi }_n\left(x\right)z\left(x\right)\right)}^2}{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right)z^2\left(x\right)}}\right){\delta }_{m,n}.\end{array}$$

Remark 2.

Relation (63) clarifies that, after deriving p-uncorrelated functions, one will be able to define a sequence of orthogonal functions in the form

$${\Phi }_n\left(x\right)-(1-\sqrt{1-p}){\displaystyle \frac{{\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right)z\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}}z\left(x\right)=G_n(x;p),$$

(64)

having the orthogonality property

$$\begin{array}{cc}\hfill {\int }_a^{b}w\left(x\right)G_m(x;p)G_n(x;p)dx& =\left({\int }_a^{b}w\left(x\right)G_n^2(x;p)dx\right){\delta }_{m,n}\hfill \\ \hfill & =\left({\int }_a^{b}w\left(x\right)dx\right)\left({\mathrm{var}}_p({\Phi }_n\left(x\right);z\left(x\right))\right){\delta }_{m,n},\hfill \end{array}$$

whereas its reverse proposition is not feasible when ${\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right)z\left(x\right)dx\ne 0$ or $p\ne 0$ in (64). Thus, p-uncorrelated functions cannot be directly derived from orthogonal sequences, as they are an extension of orthogonal functions for $p=0$, while, from p-uncorrelated functions, the aforesaid aim is always possible.

There are essentially two classifications for deriving (weighted) p-uncorrelated functions with respect to a fixed function.

5.1. Two Classifications for Deriving p-Uncorrelated Functions

5.1.1. First Classification

If the weight function in (63) is non-classical, i.e., not belonging to the Pearson distributions family and its symmetric analogue [19,20], the procedure to derive p-uncorrelated functions will lead to the same as generalized Gram–Schmidt process presented in Theorem 2 or equivalently in the representation (43). In this sense, there are ten classical sequences of real polynomials [20] that are orthogonal with respect to the Pearson distributions family

$$W\left(\left.\begin{array}{c}\begin{array}{cc}d,& e\end{array}\\ a,b,c\end{array}\right|x\right)=exp\left(\int {\displaystyle \frac{dx+e}{a{x}^2+bx+c}}dx\right)(a,b,c,d,e\in \mathbb{R}),$$

and its symmetric analogue [19]

$$W^{*}\left(\left.\begin{array}{cc}r,& s\\ p,& q\end{array}\right|x\right)=exp\left(\int {\displaystyle \frac{r{x}^2+s}{x(p{x}^2+q)}}dx\right)(p,q,r,s\in \mathbb{R}).$$

Five of them are infinitely orthogonal with respect to particular cases of the two above-mentioned distributions and five other ones are finitely orthogonal which are limited to some parametric constraints. For other applications of orthogonal polynomials, see, e.g., [21,22,23,24]. Table 1 shows the main characteristics of these sequences, where

$$S_n\left(\left.\begin{array}{cc}r,& s\\ p,& q\end{array}\right|x\right)={\displaystyle \sum _{k=0}^{[n/2]}}\left(\begin{array}{c}[n/2]\\ k\end{array}\right){\displaystyle \prod _{i=0}^{[n/2]-(k+1)}}{\displaystyle \frac{\left(2i+{(-1)}^{n+1}+2[n/2]\right)p+r}{\left(2i+{(-1)}^{n+1}+2\right)q+s}}{x}^{n-2k}=S_n\left(x\right),$$

is a four-parametric sequence of symmetric orthogonal polynomials [19] that satisfies the second-order differential equation

$$x^2(p{x}^2+q)S_n^{″}\left(x\right)+x(r{x}^2+s)S_n^{\prime }\left(x\right)-\left(n(r+(n-1)p)x^2+(1-{(-1)}^n)s/2\right)S_n\left(x\right)=0.$$

Table 1. Characteristics of ten sequences of classical orthogonal polynomials.

Symbol	Weight Function	Kind, Interval & Parameters Constraint
$P_n^{(u,v)}\left(x\right)$	$W\left(\left.\begin{array}{c}\begin{array}{cc}-u-v,& -u+v\end{array}\\ \begin{array}{ccc}-1,& 0,& 1\end{array}\end{array}\right|x\right)={(1-x)}^u{(1+x)}^v$	Infinite, $[-1,1]$ $u>-1,v>-1$
$L_n^{\left(u\right)}\left(x\right)$	$W\left(\left.\begin{array}{c}\begin{array}{cc}-1,& u\end{array}\\ \begin{array}{ccc}0,& 1,& 0\end{array}\end{array}\right|x\right)=x^{u}exp(-x)$	$\mathrm{Infinite},[0,\infty )$ $u>-1$
$H_n\left(x\right)$	$W\left(\left.\begin{array}{c}\begin{array}{cc}-2,& 0\end{array}\\ \begin{array}{ccc}0,& 0,& 1\end{array}\end{array}\right|x\right)=exp(-x^2)$	$\mathrm{Infinite},(-\infty ,\infty )$ -
$J_n^{(u,v)}\left(x\right)$	$W\left(\left.\begin{array}{c}\begin{array}{cc}-2u,& v\end{array}\\ \begin{array}{ccc}1,& 0,& 1\end{array}\end{array}\right|x\right)={(1+x^2)}^{-u}exp(varctanx)$	$\mathrm{Finite},(-\infty ,\infty )$ $maxn<(u-1)/2$
$M_n^{(u,v)}\left(x\right)$	$W\left(\left.\begin{array}{c}\begin{array}{cc}-u,& v\end{array}\\ \begin{array}{ccc}1,& 1,& 0\end{array}\end{array}\right|x\right)=x^v{(x+1)}^{-(u+v)}$	$\mathrm{Finite},[0,\infty )$ $\begin{array}{c}maxn<(u-1)/2,\hfill \\ v>-1\hfill \end{array}$
$N_n^{\left(u\right)}\left(x\right)$	$W\left(\left.\begin{array}{c}\begin{array}{cc}-u,& 1\end{array}\\ \begin{array}{ccc}1,& 0,& 0\end{array}\end{array}\right|x\right)=x^{-u}exp(-1/x)$	$\mathrm{Finite},[0,\infty )$ $maxn<(u-1)/2$
$S_n\left(\left.\begin{array}{cc}-2u-2v-2,& 2u\\ -1,& 1\end{array}\right|x\right)$	$W^{*}\left(\left.\begin{array}{cc}-2u-2v,& 2u\\ -1,& 1\end{array}\right|x\right)=x^{2u}{(1-x^2)}^v$	$\mathrm{Infinite},[-1,1]$ $u>-1/2,v>-1$
$S_n\left(\left.\begin{array}{cc}-2,& 2u\\ 0,& 1\end{array}\right|x\right)$	$W^{*}\left(\left.\begin{array}{cc}-2,& 2u\\ 0,& 1\end{array}\right|x\right)=x^{2u}exp(-x^2)$	$\mathrm{Infinite},(-\infty ,\infty )$ $u>-1/2$
$S_n\left(\left.\begin{array}{cc}-2u-2v+2,& -2u\\ 1,& 1\end{array}\right|x\right)$	$W^{*}\left(\left.\begin{array}{cc}-2u-2v,& -2u\\ 1,& 1\end{array}\right|x\right)=x^{-2u}{(1+x^2)}^{-v}$	$\mathrm{Finite},(-\infty ,\infty )$ $\begin{array}{c}n<u+v-1/2,\hfill \\ u<1/2,v>0\hfill \end{array}$
$S_n\left(\left.\begin{array}{cc}-2u+2,& 2\\ 1,& 0\end{array}\right|x\right)$	$W^{*}\left(\left.\begin{array}{cc}-2u,& 2\\ 1,& 0\end{array}\right|x\right)=x^{-2u}\exp (-1/x^2)$	$\mathrm{Finite},(-\infty ,\infty )$ $maxn<u-1/2$

5.1.2. Second Classification

If the weight function belongs to the family of distributions presented in Table 1, there is an analogue theorem below for p-uncorrelated functions similar to the well-known Sturm–Liouville theorem for orthogonal functions [20].

Theorem 7.

Let $a\left(x\right),b\left(x\right),u\left(x\right)$ and $v\left(x\right)$ be four given functions continuous on the interval $[a,b]$ and $p\in [0,1]$. If

$$w\left(x\right)=u\left(x\right)exp\left(\int {\displaystyle \frac{b\left(x\right)-a^{\prime }\left(x\right)}{a\left(x\right)}}dx\right),$$

is a positive function on $[a,b]$ and the sequence ${\left\{{\Phi }_n\left(x\right)\right\}}_{n=0}^{\infty }$ with the corresponding eigenvalues $\left\{{\lambda }_n\right\}$ satisfies an integro-differential equation of the form

$$\begin{array}{cc}a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+({\lambda }_{n}u\left(x\right)\hfill & +v\left(x\right)){\Phi }_n\left(x\right)\hfill \\ & =p\left({\lambda }_n+A_z\right)u\left(x\right)z\left(x\right){\displaystyle \frac{{\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right)z\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}},\hfill \end{array}$$

(65)

such that the function $z\left(x\right)$ satisfies the equation

$${\displaystyle \frac{a\left(x\right)z^{″}\left(x\right)+b\left(x\right)z^{\prime }\left(x\right)+v\left(x\right)z\left(x\right)}{u\left(x\right)z\left(x\right)}}=A_z,$$

(66)

where $A_z$ is a constant value, and also

$$\begin{array}{c}{\alpha }_1{\Phi }_n\left(a\right)+{\beta }_1{\Phi }_n^{\prime }\left(a\right)=0,\hfill \\ {\alpha }_2{\Phi }_n\left(b\right)+{\beta }_2{\Phi }_n^{\prime }\left(b\right)=0,\hfill \end{array}$$

(67)

are two initial conditions where ${\alpha }_1,{\beta }_1,{\alpha }_2$ and ${\beta }_2$ are given constants, then ${\left\{{\Phi }_n\left(x\right)\right\}}_{n=0}^{\infty }$ are (weighted) p-uncorrelated functions with respect to the fixed function $z\left(x\right)$.

Proof. 

For the sake of simplicity, we assume in (65) that ${\displaystyle \frac{{\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right)z\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}}={\beta }_n^{*}$. Then, Equation (65) can be written in the self-adjoint form

$${\left(r\left(x\right){\Phi }_n^{\prime }\left(x\right)\right)}^{\prime }+\left({\lambda }_{n}w\left(x\right)+q\left(x\right)\right){\Phi }_n\left(x\right)=p\left({\lambda }_n+A_z\right){\beta }_n^{*}w\left(x\right)z\left(x\right),$$

(68)

and for the index m as

$${\left(r\left(x\right){\Phi }_m^{\prime }\left(x\right)\right)}^{\prime }+\left({\lambda }_{m}w\left(x\right)+q\left(x\right)\right){\Phi }_m\left(x\right)=p\left({\lambda }_m+A_z\right){\beta }_m^{*}w\left(x\right)z\left(x\right),$$

(69)

in which

$$r\left(x\right)=a\left(x\right)exp\left(\int {\displaystyle \frac{b\left(x\right)-a^{\prime }\left(x\right)}{a\left(x\right)}}dx\right),$$

and

$$q\left(x\right)=v\left(x\right)exp\left(\int {\displaystyle \frac{b\left(x\right)-a^{\prime }\left(x\right)}{a\left(x\right)}}dx\right).$$

On multiplying by ${\Phi }_m\left(x\right)$ and ${\Phi }_n\left(x\right)$ in, respectively, (68) and (69) and subtracting, we get

$$\begin{array}{c}{\left[r\left(x\right)\left({\Phi }_m\left(x\right){\Phi }_n^{\prime }\left(x\right)-{\Phi }_n\left(x\right){\Phi }_m^{\prime }\left(x\right)\right)\right]}_a^b+\left({\lambda }_n-{\lambda }_m\right){\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx\hfill \\ =p\left({\lambda }_n+A_z\right){\beta }_n^{*}{\int }_a^{b}w\left(x\right){\Phi }_m\left(x\right)z\left(x\right)dx-p\left({\lambda }_m+A_z\right){\beta }_m^{*}{\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right)z\left(x\right)dx\\ \hfill =p\left({\lambda }_n-{\lambda }_m\right){\displaystyle \frac{{\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right)z\left(x\right)dx{\int }_a^{b}w\left(x\right){\Phi }_m\left(x\right)z\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}},\end{array}$$

which results in

$$\begin{array}{c}\left({\lambda }_n-{\lambda }_m\right)\left({\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx-p{\displaystyle \frac{{\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right)z\left(x\right)dx{\int }_a^{b}w\left(x\right){\Phi }_m\left(x\right)z\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}}\right)\hfill \\ \hfill =-{\left[r\left(x\right)\left({\Phi }_m\left(x\right){\Phi }_n^{\prime }\left(x\right)-{\Phi }_n\left(x\right){\Phi }_m^{\prime }\left(x\right)\right)\right]}_a^b=0\iff n\ne m.\hspace{1em}\square \end{array}$$

It is important to mention that the integro-differential equation (65) can be transformed into a fourth-order equation using (66). First of all, without a loss in generality, we can assume in (65) that $u\left(x\right)=1$ because it is just enough to divide both side of (65) by $u\left(x\right)$. In this case, substituting

$$z\left(x\right)={\displaystyle \frac{1}{p\left({\lambda }_n+A_z\right){\beta }_n^{*}}}\left(a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+\left({\lambda }_n+v\left(x\right)\right){\Phi }_n\left(x\right)\right)$$

into the equation

$$a\left(x\right)z^{″}\left(x\right)+b\left(x\right)z^{\prime }\left(x\right)+\left(v\left(x\right)-A_z\right)z\left(x\right)=0,$$

yields

$$\begin{array}{c}{a}^2\left(x\right){\Phi }_n^{\left(4\right)}\left(x\right)+2a\left(x\right)\left(a^{\prime }\left(x\right)+b\left(x\right)\right){\Phi }_n^{\left(3\right)}\left(x\right)+\hfill \\ \hspace{1em}\hspace{1em}\left(a\left(x\right)\left(a^{″}\left(x\right)+2b^{\prime }\left(x\right)+2v\left(x\right)+{\lambda }_n-A_z\right)+b\left(x\right)\left(a^{\prime }\left(x\right)+b\left(x\right)\right)\right){\Phi }_n^{″}\left(x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}+\left(a\left(x\right)\left(b^{″}\left(x\right)+2v^{\prime }\left(x\right)\right)+b\left(x\right)\left(b^{\prime }\left(x\right)+2v\left(x\right)+{\lambda }_n-A_z\right)\right){\Phi }_n^{\prime }\left(x\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left(a\left(x\right)v^{″}\left(x\right)+b\left(x\right)v^{\prime }\left(x\right)+v^2\left(x\right)+({\lambda }_n-A_z)v\left(x\right)-A_z{\lambda }_n\right){\Phi }_n\left(x\right)=0,\end{array}$$

having four independent basis solutions.

5.2. A Generalized Theorem with an Important Remark

5.2.1. An Extension of the Previous Theorem

This time, let us assume in the right side of (65) that the function $u\left(x\right)z\left(x\right)=h\left(x\right)$ satisfies a second-order differential equation of the form

$$p\left(x\right)h^{″}\left(x\right)+q\left(x\right)h^{\prime }\left(x\right)+r\left(x\right)h\left(x\right)=0,$$

instead of satisfying the Equation (66), where $p\left(x\right),q\left(x\right)$ and $r\left(x\right)$ are all known functions. Then, Equation (65) will be transformed into the fourth-order equation

$$\begin{array}{c}p\left(x\right){\left(a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+\left({\lambda }_{n}u\left(x\right)+v\left(x\right)\right){\Phi }_n\left(x\right)\right)}^{″}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}+q\left(x\right){\left(a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+\left({\lambda }_{n}u\left(x\right)+v\left(x\right)\right){\Phi }_n\left(x\right)\right)}^{\prime }\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+r\left(x\right)\left(a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+\left({\lambda }_{n}u\left(x\right)+v\left(x\right)\right){\Phi }_n\left(x\right)\right)=0,\end{array}$$

which is equivalent to

$$\begin{array}{cc}\hfill & p\left(x\right)a\left(x\right){\Phi }_n^{\left(4\right)}\left(x\right)+\left(p\left(x\right)\left(2a^{\prime }\left(x\right)+b\left(x\right)\right)+q\left(x\right)a\left(x\right)\right){\Phi }_n^{\left(3\right)}\left(x\right)\hfill \\ \hfill & +\left(p\left(x\right)u\left(x\right){\lambda }_n+p\left(x\right)\left(a^{″}\left(x\right)+2b^{\prime }\left(x\right)+v\left(x\right)\right)+q\left(x\right)\left(a^{\prime }\left(x\right)+b\left(x\right)\right)+r\left(x\right)a\left(x\right)\right){\Phi }_n^{″}\left(x\right)\hfill \\ \hfill & +\left(\left(2p\left(x\right)u^{\prime }\left(x\right)+q\left(x\right)u\left(x\right)\right){\lambda }_n+p\left(x\right)\left(b^{″}\left(x\right)+2v^{\prime }\left(x\right)\right)+q\left(x\right)\left(b^{\prime }\left(x\right)+v\left(x\right)\right)+r\left(x\right)b\left(x\right)\right){\Phi }_n^{\prime }\left(x\right)\hfill \\ \hfill & +\left(\left(p\left(x\right)u^{″}\left(x\right)+q\left(x\right)u^{\prime }\left(x\right)+r\left(x\right)u\left(x\right)\right){\lambda }_n+p\left(x\right)v^{″}\left(x\right)+q\left(x\right)v^{\prime }\left(x\right)+r\left(x\right)v\left(x\right)\right){\Phi }_n\left(x\right)=0.\hfill \end{array}$$

(70)

Noting the above-mentioned comments, Equation (65) can now be generalized as

$$a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+\left({\lambda }_{n}u\left(x\right)+v\left(x\right)\right){\Phi }_n\left(x\right)=R_n\left(x\right),$$

whose self-adjoint form

$${\left(r\left(x\right){\Phi }_n^{\prime }\left(x\right)\right)}^{\prime }+\left({\lambda }_{n}w\left(x\right)+q\left(x\right)\right){\Phi }_n\left(x\right)={\displaystyle \frac{w\left(x\right)}{u\left(x\right)}}{R}_n\left(x\right),$$

yields

$$\begin{array}{c}{\left[r\left(x\right)\left({\Phi }_m\left(x\right){\Phi }_n^{\prime }\left(x\right)-{\Phi }_n\left(x\right){\Phi }_m^{\prime }\left(x\right)\right)\right]}_a^b+\left({\lambda }_n-{\lambda }_m\right){\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx\hfill \\ \hfill ={\int }_a^b{\displaystyle \frac{w\left(x\right)}{u\left(x\right)}}\left(R_n\left(x\right){\Phi }_m\left(x\right)-R_m\left(x\right){\Phi }_n\left(x\right)\right)dx.\end{array}$$

(71)

Now, if in (71), we set

$$R_n\left(x\right)=p\left({\lambda }_n+A_z\right){\displaystyle \frac{{\int }_a^{b}w\left(x\right)z\left(x\right){\Phi }_n\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}}u\left(x\right)z\left(x\right),$$

we directly get to Theorem 7.

5.2.2. Remark

The previous section shows that Equation (65) is, in fact, a non-homogeneous second-order differential equation whose general solution for $p=1$ reads as

$${\Phi }_n\left(x\right)=c_1{y}_{1,n}\left(x\right)+c_2{y}_{2,n}\left(x\right)+{\lambda }^{*}z\left(x\right)(c_1,c_2,{\lambda }^{*}\in \mathbb{R}),$$

(72)

where $c_1{y}_{1,n}\left(x\right)+c_2{y}_{2,n}\left(x\right)$ is the solution of the homogeneous equation

$$a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+\left({\lambda }_{n}p\left(x\right)+q\left(x\right)\right){\Phi }_n\left(x\right)=0,$$

with two independent solutions, $y_{1,n}\left(x\right)$ and $y_{2,n}\left(x\right)$, respectively.

Hence, substituting (72) into (65) for $p=1$ simplifies the general solution as

$${\Phi }_n\left(x\right)=c_1\left(y_{1,n}\left(x\right)-{\displaystyle \frac{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{1,n}\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx}}{y}_{2,n}\left(x\right)\right)+{\lambda }^{*}z\left(x\right),$$

(73)

provided that ${\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx\ne 0(\forall n\notin {\mathbb{Z}}^{+})$. On the other hand, since, in (73),

$${\int }_a^b{\Phi }_n\left(x\right)w\left(x\right)z\left(x\right)dx={\lambda }^{*}{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx,$$

the uncorrelated condition (63) for $p=1$ is simplified as

$$\begin{array}{c}{\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx-{{\lambda }^{*}}^2{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx\hfill \\ \hfill =\left({\int }_a^{b}w\left(x\right){\Phi }_n^2\left(x\right)dx-{{\lambda }^{*}}^2{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx\right){\delta }_{m,n},\end{array}$$

leading to the “simple type of p-uncorrelated variables” to be defined and studied in detail in the next Section 6. In this sense, note that

$$\begin{array}{c}{\displaystyle \frac{1}{c_1^2}}\left({\int }_a^{b}w\left(x\right){\Phi }_n^2\left(x\right)dx-{{\lambda }^{*}}^2{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx\right)={\int }_a^{b}w\left(x\right)y_{1,n}^2\left(x\right)dx\hfill \\ +{\displaystyle \frac{{\left({\int }_a^{b}w\left(x\right)z\left(x\right)y_{1,n}\left(x\right)dx\right)}^2}{{\left({\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx\right)}^2}}{\int }_a^{b}w\left(x\right)y_{2,n}^2\left(x\right)dx\\ -2{\displaystyle \frac{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{1,n}\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx}}{\int }_a^{b}w\left(x\right)y_{1,n}\left(x\right)y_{2,n}\left(x\right)dx,\end{array}$$

i.e., the aforementioned 1-variance value is always independent of ${\lambda }^{*}$.

Example 1.

Consider the following integro-differential equation

$${\Phi }_n^{″}\left(x\right)+n^2{\Phi }_n\left(x\right)=(n^2+A)z\left(x\right){\displaystyle \frac{{\int }_0^{\pi }{\Phi }_n\left(x\right)z\left(x\right)dx}{{\int }_0^{\pi }{z}^2\left(x\right)dx}},$$

(74)

in which $z\left(x\right)$ satisfies the equation

$${\displaystyle \frac{z^{″}\left(x\right)}{z\left(x\right)}}=A.$$

(75)

Noting (70), the equivalent form of (74), together with (75), is

$${\Phi }_n^{\left(4\right)}\left(x\right)+\left(n^2-A\right){\Phi }_n^{″}\left(x\right)-A{n}^2{\Phi }_n\left(x\right)=(D^2+n^2)(D^2-A){\Phi }_n\left(x\right)=0,$$

having the general solution

$${\Phi }_n\left(x\right)=c_{1}sinnx+c_{2}cosnx+{\lambda }^{*}z\left(x\right)\mathrm{where}(D^2-A)z\left(x\right)=0.$$

(76)

According to (73), the solution (76) changes to

$${\Phi }_n\left(x\right)=c_1\left(sinnx-{\displaystyle \frac{{\int }_0^{\pi }z\left(x\right)sinnxdx}{{\int }_0^{\pi }z\left(x\right)cosnxdx}}cosnx\right)+{\lambda }^{*}z\left(x\right),$$

(77)

satisfying the relation

$${\int }_0^{\pi }{\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx-{{\lambda }^{*}}^2{\int }_0^{\pi }{z}^2\left(x\right)dx=c_1^2{\displaystyle \frac{\pi }{2}}\left(1+{\displaystyle \frac{{\left({\int }_0^{\pi }z\left(x\right)sinnxdx\right)}^2}{{\left({\int }_0^{\pi }z\left(x\right)cosnxdx\right)}^2}}\right){\delta }_{m,n}.$$

In this regard, notice that the two sub-sequences

$${\Phi }_{2n}\left(x\right)=c_1\left(sin2nx-{\displaystyle \frac{{\int }_0^{\pi }z\left(x\right)sin2nxdx}{{\int }_0^{\pi }z\left(x\right)cos2nxdx}}cos2nx\right)+{\lambda }^{*}z\left(x\right),$$

and

$${\Phi }_{2n+1}\left(x\right)=c_1\left(sin(2n+1)x-{\displaystyle \frac{{\int }_0^{\pi }z\left(x\right)sin(2n+1)xdx}{{\int }_0^{\pi }z\left(x\right)cos(2n+1)xdx}}cos(2n+1)x\right)+{\lambda }^{*}z\left(x\right),$$

in (77) are automatically uncorrelated (without any constraint) with respect to every fixed function, $z\left(x\right)$, that satisfies (75).

In total, three cases can occur for the constant value A in (75).

• (i) If $A={\alpha }^2(\alpha \ne 0)$, the solution of equation (75) is as $z\left(x\right)=a_1{e}^{\alpha x}+a_2{e}^{-\alpha x}$, and subsequently, (76) takes the form

  $${\Phi }_n\left(x\right)=c_{1}sinnx+c_{2}cosnx+a_1{e}^{\alpha x}+a_2{e}^{-\alpha x}.$$
• (ii) If $A=-{\alpha }^2(\alpha \ne 0)$, then $z\left(x\right)=b_{1}cos\left(\alpha x\right)+b_{2}sin\left(\alpha x\right)$ and

  $${\Phi }_n\left(x\right)=c_{1}sinnx+c_{2}cosnx+b_{1}cos\left(\alpha x\right)+b_{2}sin\left(\alpha x\right).$$
• (iii) If $A=0$, then $z\left(x\right)=c_{3}x+c_4$ and

  $${\Phi }_n\left(x\right)=c_{1}sinnx+c_{2}cosnx+c_{3}x+c_4.$$

For instance, if $z\left(x\right)=e^x$ is chosen from the above mentioned options, the general solution of the equation

$${\Phi }_n^{″}\left(x\right)+n^2{\Phi }_n\left(x\right)={\displaystyle \frac{2(n^2+1)}{e^{2\pi }-1}}{e}^x{\int }_0^{\pi }{\Phi }_n\left(x\right)e^{x}dx,$$

is, according to (77), as

$${\Phi }_n\left(x\right)=c_1\left(sinnx-{\displaystyle \frac{{\int }_0^{\pi }{e}^{x}sinnxdx}{{\int }_0^{\pi }{e}^{x}cosnxdx}}cosnx\right)+{\lambda }^{*}{e}^x.$$

(78)

On the other hand,

$${\int }_0^{\pi }{e}^{x}sinnxdx=-{\displaystyle \frac{n}{n^2+1}}({(-1)}^n{e}^{\pi }-1)\mathrm{and}{\int }_0^{\pi }{e}^{x}cosnxdx={\displaystyle \frac{1}{n^2+1}}({(-1)}^n{e}^{\pi }-1),$$

imply that (78) takes the final form

$${\Phi }_n\left(x\right)=c_1\left(sinnx+ncosnx\right)+{\lambda }^{*}{e}^x,$$

(79)

where $c_1,{\lambda }^{*}\in \mathbb{R}$. Note that, since in (79),

$${\Phi }_n\left(0\right)={\Phi }_n^{\prime }\left(0\right)\mathrm{and}{\Phi }_n\left(\pi \right)={\Phi }_n^{\prime }\left(\pi \right),$$

so

$${\left[{\Phi }_m\left(x\right){\Phi }_n^{\prime }\left(x\right)-{\Phi }_n\left(x\right){\Phi }_m^{\prime }\left(x\right)\right]}_0^{\pi }=0.$$

However, for other choices of $z\left(x\right)$, we may have to determine the values $c_1$ and ${\lambda }^{*}$ uniquely. Also, for $n=m$, we obtain

$$\pi {\mathrm{var}}_1({\Phi }_n\left(x\right);e^x)={\int }_0^{\pi }{\Phi }_n^2\left(x\right)dx-{{\lambda }^{*}}^2{\displaystyle \frac{e^{2\pi }-1}{2}}=c_1^2{\displaystyle \frac{\pi }{2}}(n^2+1)(\forall n\in \mathbb{N}).$$

Finally, according to Remark 2, the sequence

$${\Phi }_n\left(x\right)-{\lambda }^{*}{e}^x=c_1\left(\sin nx+ncosnx\right),$$

must be orthogonal with respect to the constant weight function on $[0,\pi ]$, i.e.,

$$\begin{array}{c}{\int }_0^{\pi }\left(\sin (n+1)x+(n+1)\cos (n+1)x\right)\left(\sin (m+1)x+(m+1)\cos (m+1)x\right)dx\hfill \\ \hfill ={\displaystyle \frac{\pi }{2}}(n^2+2n+2){\delta }_{n,m},\end{array}$$

in which

$$\sin (n+1)x+(n+1)\cos (n+1)x=\sqrt{n^2+2n+2}\sin \left((n+1)x+\arctan (n+1)\right),$$

having the explicit roots

$$x_k={\displaystyle \frac{k\pi -arctan(n+1)}{n+1}}\mathrm{for}k=1,2,\dots ,n+1.$$

The important Section 5.2.2 and its subsequent example imply that we study and investigate a specific type of p-uncorrelated variables in the next section.

6. Simple p-Uncorrelated Variables and Their Relationship with Orthogonal Sequences

Instead of applying previous statistical concepts, in this section, we focus on an inner product space and study a special case that extends the orthogonality concept and leads to defining a simple type of p-uncorrelated variables. As before, assuming that $⟨u,v⟩$ indicates the inner product of two free elements and $⟨u,u⟩={∥u∥}^2\ge 0$ denotes the norm square value, suppose that ${\left\{x_k\right\}}_{k=0}^n$ and y are arbitrary variables, and consider the approximation

$$y\cong {\displaystyle \sum _{k=0}^n}{c}_k{x}_k,$$

(80)

together with its remaining term

$$R(c_0,\dots ,c_n)={\displaystyle \sum _{k=0}^n}{c}_k{x}_k-y,$$

(81)

where ${\left\{c_k\right\}}_{k=0}^n$ are unknown coefficients to be appropriately determined.

It is well known that minimizing the value

$${∥R(c_0,\dots ,c_n)∥}^2=⟨{\displaystyle \sum _{k=0}^n}{c}_k{x}_k-y,{\displaystyle \sum _{k=0}^n}{c}_k{x}_k-y⟩,$$

(82)

will lead to the normal equations system [13,17],

$$\left[\begin{array}{cccc}\begin{array}{c}⟨x_0,x_0⟩\\ ⟨x_1,x_0⟩\\ ⋮\\ ⟨x_n,x_0⟩\end{array}& \begin{array}{c}⟨x_0,x_1⟩\\ ⟨x_1,x_1⟩\\ ⋮\\ ⟨x_n,x_1⟩\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}⟨x_0,x_n⟩\\ ⟨x_1,x_n⟩\\ ⋮\\ ⟨x_n,x_n⟩\end{array}\end{array}\right]\left[\begin{array}{c}{c}_0\\ c_1\\ ⋮\\ c_n\end{array}\right]=\left[\begin{array}{c}⟨x_0,y⟩\\ ⟨x_1,y⟩\\ ⋮\\ ⟨x_n,y⟩\end{array}\right].$$

(83)

It is also known that applying the orthogonality condition

$$⟨x_m,x_n⟩=⟨x_n,x_n⟩{\delta }_{m,n},$$

(84)

on the components of the above linear system eventually gives the explicit solutions

$${\left\{c_k={\displaystyle \frac{⟨x_k,y⟩}{⟨x_k,x_k⟩}}\right\}}_{k=0}^n.$$

Hence, the orthogonal approximation

$$y\cong {\displaystyle \sum _{k=0}^n}{\displaystyle \frac{⟨x_k,y⟩}{⟨x_k,x_k⟩}}{x}_k,$$

(85)

is derived as the optimal case in the sense of ordinary least squares.

By repeating the steps (80) to (83), instead of considering the orthogonality condition (84), we consider the generalized condition

$$⟨x_m,x_n⟩=\left\{\begin{array}{c}\lambda (m\ne n),\hfill \\ ⟨x_n,x_n⟩(m=n),\hfill \end{array}\right.$$

(86)

where the non-negative parameter $\lambda$ is independent of the indices $m,n$.

As we mentioned in the preceding sections, the random variables ${\left\{X_k\right\}}_{k=0}^n$ are said to be p-uncorrelated with respect to the fixed variable Z if, for every $m\ne n$:

$${cov}_p(X_m,X_n;Z)=E\left(X_m{X}_n\right)-p{\displaystyle \frac{E\left(X_{m}Z\right)E\left(X_{n}Z\right)}{E\left(Z^2\right)}}=0.$$

(87)

In addition to the condition (87), if we now add another condition as

$$E\left(X_{k}Z\right)=r^{2}E\left(Z^2\right)>0\mathrm{for}\mathrm{every}k=0,1,\dots ,n,$$

(88)

where r is independent of k, then we say that ${\left\{X_k\right\}}_{k=0}^n$ are simple p-uncorrelated variables. In this case, both conditions (87) and (88) imply that

$$E\left(X_m{X}_n\right)=\left\{\begin{array}{c}p{r}^{4}E\left(Z^2\right)(m\ne n),\hfill \\ E\left(X_n^2\right)(m=n).\hfill \end{array}\right.$$

(89)

Furthermore, replacing the extra condition (88) in the condition (87) for $p=r=1$ leads to the orthogonality condition

$$E\left((X_m-Z)(X_n-Z)\right)=0.$$

Note in (89) that the parameter p has no effect on simple p-uncorrelated variables. Hence, throughout this section, we assume that $p=1$. The definition (88) can similarly be applied in an inner product space. We say that $x_k$ is a simple uncorrelated variable if the condition (86) holds, and also,

$$⟨x_k,1⟩=r^2⟨1,1⟩>0\mathrm{for}\mathrm{every}k=0,1,\dots ,n.$$

In this case, if the sequence ${\{y_k=x_k-r\}}_{k=0}^n$ is orthogonal, then, for every $m\ne n$ the orthogonality condition

$$⟨x_m-r,x_n-r⟩=⟨x_m,x_n⟩-r⟨x_m,1⟩-r⟨1,x_n⟩+r^2⟨1,1⟩=⟨x_m,x_n⟩-r^2⟨1,1⟩=0,$$

would be equivalent to (86) for $\lambda =r^2⟨1,1⟩$. Moreover, according to the Schwarz inequality, ${⟨x_m,x_n⟩}^2\le ⟨x_m,x_m⟩⟨x_n,x_n⟩$, (86) implies that $⟨x_m,x_m⟩⟨x_n,x_n⟩\ge {\lambda }^2\iff m\ne n$.

Noting the above-mentioned definition, now suppose that ${\left\{x_k\right\}}_{k=0}^n$ are simple uncorrelated variables, and then substitute (86) into the normal system (83) to arrive at

$$\left[\begin{array}{cccc}\begin{array}{c}⟨x_0,x_0⟩\\ \lambda \\ ⋮\\ \lambda \end{array}& \begin{array}{c}\lambda \\ ⟨x_1,x_1⟩\\ ⋮\\ \lambda \end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}\lambda \\ \lambda \\ ⋮\\ ⟨x_n,x_n⟩\end{array}\end{array}\right]\left[\begin{array}{c}{c}_0\\ c_1\\ ⋮\\ c_n\end{array}\right]=\left[\begin{array}{c}⟨x_0,y⟩\\ ⟨x_1,y⟩\\ ⋮\\ ⟨x_n,y⟩\end{array}\right].$$

(90)

An interesting point is that the above system is explicitly solvable. In fact, there is even a more general case that can be solved analytically according to the following theorem.

Theorem 8.

Given the real numbers ${\left\{a_{jj}\right\}}_{j=0}^n,{\left\{{\lambda }_j\right\}}_{j=0}^n\mathrm{and}{\left\{b_j\right\}}_{j=0}^n$, the general solution of the linear system

$$\left[\begin{array}{cccc}\begin{array}{c}{a}_{00}\\ {\lambda }_0\\ ⋮\\ {\lambda }_0\end{array}& \begin{array}{c}{\lambda }_1\\ a_{11}\\ ⋮\\ {\lambda }_1\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}{\lambda }_n\\ {\lambda }_n\\ ⋮\\ a_{nn}\end{array}\end{array}\right]\left[\begin{array}{c}{c}_0\\ c_1\\ ⋮\\ c_n\end{array}\right]=\left[\begin{array}{c}{b}_0\\ b_1\\ ⋮\\ b_n\end{array}\right],$$

(91)

is (for every $j=0,1,\dots ,n$) given by

$$c_j={\displaystyle \frac{b_j\left(1+{\displaystyle \sum _{k=0}^n}\frac{{\lambda }_k}{a_{kk}-{\lambda }_k}\right)-{\displaystyle \sum _{k=0}^n}\frac{{\lambda }_k{b}_k}{a_{kk}-{\lambda }_k}}{\left(a_{jj}-{\lambda }_j\right)\left(1+{\displaystyle \sum _{k=0}^n}\frac{{\lambda }_k}{a_{kk}-{\lambda }_k}\right)}}={\displaystyle \frac{b_j-S_n\left({\left\{{\lambda }_k;a_{kk},b_k\right\}}_{k=0}^n\right)}{a_{jj}-{\lambda }_j}},$$

(92)

where

$$S_n\left({\left\{{\lambda }_k;a_{kk},b_k\right\}}_{k=0}^n\right)={\displaystyle \frac{{\displaystyle \sum _{k=0}^n}{\lambda }_k{b}_k{\displaystyle \prod _{\genfrac{}{}{0pt}{}{j=0\hfill }{j\ne k\hfill }}^n}(a_{jj}-{\lambda }_j)}{{\displaystyle \prod _{j=0}^n}(a_{jj}-{\lambda }_j)+{\displaystyle \sum _{k=0}^n}{\lambda }_k{\displaystyle \prod _{\genfrac{}{}{0pt}{}{j=0\hfill }{j\ne k\hfill }}^n}(a_{jj}-{\lambda }_j)}}.$$

Proof. 

First, the system (91) can be rewritten as follows:

$$\left\{\begin{array}{c}{\displaystyle \sum _{k=0}^n}{\lambda }_k{c}_k=b_0-\left(a_{00}-{\lambda }_0\right)c_0,\hfill \\ {\displaystyle \sum _{k=0}^n}{\lambda }_k{c}_k=b_1-\left(a_{11}-{\lambda }_1\right)c_1,\hfill \\ ⋮\hfill \\ {\displaystyle \sum _{k=0}^n}{\lambda }_k{c}_k=b_n-\left(a_{nn}-{\lambda }_n\right)c_n.\hfill \end{array}\right.$$

(93)

Comparing the first two rows of (93) yields

$$c_1={\displaystyle \frac{b_1-b_0}{a_{11}-{\lambda }_1}}+{\displaystyle \frac{a_{00}-{\lambda }_0}{a_{11}-{\lambda }_1}}{c}_0.$$

As well, comparing the first row of (93) with other rows gives, generally,

$$c_k={\displaystyle \frac{b_k-b_0}{a_{kk}-{\lambda }_k}}+{\displaystyle \frac{a_{00}-{\lambda }_0}{a_{kk}-{\lambda }_k}}{c}_0.$$

(94)

By replacing (94) in the first row of (93) as

$${\displaystyle \sum _{k=0}^n}{\lambda }_k\left({\displaystyle \frac{b_k-b_0}{a_{kk}-{\lambda }_k}}+{\displaystyle \frac{a_{00}-{\lambda }_0}{a_{kk}-{\lambda }_k}}{c}_0\right)=b_0-\left(a_{00}-{\lambda }_0\right)c_0,$$

we finally obtain

$$c_0={\displaystyle \frac{b_0-{\displaystyle \sum _{k=0}^n}{\lambda }_k\frac{b_k-b_0}{a_{kk}-{\lambda }_k}}{a_{00}-{\lambda }_0+{\displaystyle \sum _{k=0}^n}{\lambda }_k\frac{a_{00}-{\lambda }_0}{a_{kk}-{\lambda }_k}}}={\displaystyle \frac{b_0-S_n\left({\left\{{\lambda }_k;a_{kk},b_k\right\}}_{k=0}^n\right)}{a_{00}-{\lambda }_0}}.$$

Following the above-mentioned approach for other unknown coefficients, ${\left\{c_j\right\}}_{j=1}^n$ are derived as

$$c_j={\displaystyle \frac{b_j-{\displaystyle \sum _{\genfrac{}{}{0pt}{}{k=0\hfill }{k\ne j\hfill }}^n}{\lambda }_k\frac{b_k-b_j}{a_{kk}-{\lambda }_k}}{a_{jj}+{\displaystyle \sum _{\genfrac{}{}{0pt}{}{k=0\hfill }{k\ne j\hfill }}^n}{\lambda }_k\frac{a_{jj}-{\lambda }_j}{a_{kk}-{\lambda }_k}}}={\displaystyle \frac{b_j-{\displaystyle \sum _{k=0}^n}{\lambda }_k\frac{b_k-b_j}{a_{kk}-{\lambda }_k}}{a_{jj}-{\lambda }_j+{\displaystyle \sum _{k=0}^n}{\lambda }_k\frac{a_{jj}-{\lambda }_j}{a_{kk}-{\lambda }_k}}}={\displaystyle \frac{b_j-S_n\left({\left\{{\lambda }_k;a_{kk},b_k\right\}}_{k=0}^n\right)}{a_{jj}-{\lambda }_j}}.\hspace{1em}\square$$

A particular case of the system (91) arises when ${\lambda }_0={\lambda }_1=\cdots ={\lambda }_n=\lambda$. In this case, the general solution (92) is simplified as

$$c_j={\displaystyle \frac{b_j\left(1+\lambda {\displaystyle \sum _{k=0}^n}\frac{1}{a_{kk}-\lambda }\right)-\lambda {\displaystyle \sum _{k=0}^n}\frac{b_k}{a_{kk}-\lambda }}{\left(a_{jj}-\lambda \right)\left(1+\lambda {\displaystyle \sum _{k=0}^n}\frac{1}{a_{kk}-\lambda }\right)}}={\displaystyle \frac{b_j-S_n\left(\lambda ;{\left\{a_{kk},b_k\right\}}_{k=0}^n\right)}{a_{jj}-\lambda }},$$

(95)

where

$$S_n\left(\lambda ;{\left\{a_{kk},b_k\right\}}_{k=0}^n\right)={\displaystyle \frac{\lambda {\displaystyle \sum _{k=0}^n}{b}_k{\displaystyle \prod _{\genfrac{}{}{0pt}{}{j=0\hfill }{j\ne k\hfill }}^n}(a_{jj}-\lambda )}{{\displaystyle \prod _{j=0}^n}(a_{jj}-\lambda )+\lambda {\displaystyle \sum _{k=0}^n}{\displaystyle \prod _{\genfrac{}{}{0pt}{}{j=0\hfill }{j\ne k\hfill }}^n}(a_{jj}-\lambda )}}.$$

(96)

From (95) and (96), one can conclude that

$$\left|\begin{array}{cccc}\begin{array}{c}{a}_{00}\\ \lambda \\ ⋮\\ \lambda \end{array}& \begin{array}{c}\lambda \\ a_{11}\\ ⋮\\ \lambda \end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}\lambda \\ \lambda \\ ⋮\\ a_{nn}\end{array}\end{array}\right|={\displaystyle \prod _{j=0}^n}(a_{jj}-\lambda )\left(1+\lambda {\displaystyle \sum _{k=0}^n}{\displaystyle \frac{1}{a_{kk}-\lambda }}\right).$$

We can now apply the solution of type (95) for the linear system (90).

Corollary 4.

If the condition (86) is satisfied for the elements of the approximation (80), then

$$y\cong {\displaystyle \sum _{j=0}^n}{\displaystyle \frac{⟨x_j,y⟩-S_n\left(\lambda \right)}{⟨x_j,x_j⟩-\lambda }}{x}_j,$$

(97)

in which $S_n\left(\lambda \right)=S_n\left(\lambda ;{\left\{⟨x_k,x_k⟩,⟨x_k,y⟩\right\}}_{k=0}^n\right)={\displaystyle \frac{\lambda {\displaystyle \sum _{k=0}^n}\frac{⟨x_k,y⟩}{⟨x_k,x_k⟩-\lambda }}{1+\lambda {\displaystyle \sum _{k=0}^n}\frac{1}{⟨x_k,x_k⟩-\lambda }}}$, is the best approximation in the sense of ordinary least squares, such that

$${∥{\displaystyle \sum _{j=0}^n}{\displaystyle \frac{⟨x_j,y⟩-S_n\left(\lambda \right)}{⟨x_j,x_j⟩-\lambda }}{x}_j-y∥}^2\le {∥{\displaystyle \sum _{j=0}^n}{\alpha }_j{x}_j-y∥}^2(\forall {\left\{{\alpha }_j\right\}}_{j=0}^n\in \mathbb{R}).$$

When it is noted that (97) is a generalization of the orthogonal approximation (85) for $\lambda =0$, substituting $n=0,1,2$, respectively, gives

$$\begin{array}{c}y\cong {\displaystyle \frac{⟨x_0,y⟩}{⟨x_0,x_0⟩}}{x}_0,\hfill \\ y\cong {\displaystyle \frac{⟨x_0,y⟩⟨x_1,x_1⟩-\lambda ⟨x_1,y⟩}{⟨x_0,x_0⟩⟨x_1,x_1⟩-{\lambda }^2}}{x}_0+{\displaystyle \frac{⟨x_1,y⟩⟨x_0,x_0⟩-\lambda ⟨x_0,y⟩}{⟨x_0,x_0⟩⟨x_1,x_1⟩-{\lambda }^2}}{x}_1,\hfill \end{array}$$

and

$$\begin{array}{c}y\cong {\displaystyle \frac{⟨x_0,y⟩⟨x_1,x_1⟩⟨x_2,x_2⟩-{\lambda }^2⟨x_0-x_1-x_2,y⟩-\lambda \left(⟨x_1,y⟩⟨x_2,x_2⟩+⟨x_2,y⟩⟨x_1,x_1⟩\right)}{⟨x_0,x_0⟩⟨x_1,x_1⟩⟨x_2,x_2⟩-{\lambda }^2\left(⟨x_0,x_0⟩+⟨x_1,x_1⟩+⟨x_2,x_2⟩-2\lambda \right)}}{x}_0\hfill \\ +{\displaystyle \frac{⟨x_1,y⟩⟨x_0,x_0⟩⟨x_2,x_2⟩-{\lambda }^2⟨x_1-x_0-x_2,y⟩-\lambda \left(⟨x_0,y⟩⟨x_2,x_2⟩+⟨x_2,y⟩⟨x_0,x_0⟩\right)}{⟨x_0,x_0⟩⟨x_1,x_1⟩⟨x_2,x_2⟩-{\lambda }^2\left(⟨x_0,x_0⟩+⟨x_1,x_1⟩+⟨x_2,x_2⟩-2\lambda \right)}}{x}_1\hfill \\ +{\displaystyle \frac{⟨x_2,y⟩⟨x_0,x_0⟩⟨x_1,x_1⟩-{\lambda }^2⟨x_2-x_1-x_0,y⟩-\lambda \left(⟨x_0,y⟩⟨x_1,x_1⟩+⟨x_1,y⟩⟨x_0,x_0⟩\right)}{⟨x_0,x_0⟩⟨x_1,x_1⟩⟨x_2,x_2⟩-{\lambda }^2\left(⟨x_0,x_0⟩+⟨x_1,x_1⟩+⟨x_2,x_2⟩-2\lambda \right)}}{x}_2.\hfill \end{array}$$

The question is now how to find the elements ${\left\{x_k\right\}}_{k=0}^n$, such that they satisfy the generalized condition (86).

Theorem 9.

Let ${\left\{v_k\right\}}_{k=0}$ be a finite or infinite sequence of variables defined in an inner product space, such that any finite number of elements ${\left\{v_k\right\}}_{k=0}^n$ are linearly independent. One can find constants $\left\{a_{i,j}\right\}$, such that the elements

$$\begin{array}{c}{x}_0=v_0,\hfill \\ x_1=v_1+a_{12}{v}_0,\hfill \\ x_2=v_2+a_{22}{v}_1+a_{23}{v}_0,\hfill \\ ⋮\hfill \\ x_n=v_n+a_{n2}{v}_{n-1}+\cdots +a_{n,n+1}{v}_0,\hfill \end{array}$$

(98)

satisfy the condition (86).

Proof. 

Referring to (96), we first assume, only for simplicity, that

$$\begin{array}{cc}\hfill S_{n-1}^{*}\left(\lambda \right)& =\lambda -S_{n-1}\left(\lambda ;{\left\{⟨x_k,x_k⟩,\lambda -⟨x_k,v_n⟩\right\}}_{k=0}^{n-1}\right)\hfill \\ \hfill & =\lambda \left(1+{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩}{⟨x_k,x_k⟩-\lambda }}\right){\displaystyle /\phantom{\left(1+{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩}{⟨x_k,x_k⟩-\lambda }}\right)\left(1+{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{\lambda }{⟨x_k,x_k⟩-\lambda }}\right)}}\left(1+{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{\lambda }{⟨x_k,x_k⟩-\lambda }}\right),\hfill \end{array}$$

(99)

with $S_{-1}^{*}\left(\lambda \right)=\lambda$. Then, set recursively,

$$\begin{array}{c}{x}_0=v_0,\hfill \\ x_1=v_1-{\displaystyle \frac{⟨x_0,v_1⟩-S_0^{*}\left(\lambda \right)}{⟨x_0,x_0⟩-\lambda }}{x}_0,\hfill \\ ⋮\hfill \\ x_n=v_n-{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_k,x_k⟩-\lambda }}{x}_k.\hfill \end{array}$$

(100)

Since the final shape of $x_n$ is a linear combination of ${\left\{v_k\right\}}_{k=0}^n$ in (100), it is enough to show that $⟨x_n,x_j⟩=\lambda$ for every $j=0,1,\dots ,n-1$. For this purpose, applying $⟨.,x_j⟩$ on both sides of the last equality of (100) gives

$$\begin{array}{c}\lambda =⟨x_n,x_j⟩=⟨v_n-{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_k,x_k⟩-\lambda }}{x}_k,x_j⟩\hfill \\ =⟨v_n,x_j⟩-{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_k,x_k⟩-\lambda }}⟨x_k,x_j⟩.\hfill \end{array}$$

Therefore, we have to prove that

$${\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_k,x_k⟩-\lambda }}⟨x_k,x_j⟩=⟨v_n,x_j⟩-\lambda .$$

(101)

We first simplify the left side of equality (101) as follows:

$$\begin{array}{c}\lambda {\displaystyle \sum _{\genfrac{}{}{0pt}{}{k=0\hfill }{k\ne j\hfill }}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_k,x_k⟩-\lambda }}+{\displaystyle \frac{⟨x_j,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_j,x_j⟩-\lambda }}⟨x_j,x_j⟩\hfill \\ =\lambda {\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_k,x_k⟩-\lambda }}-\lambda {\displaystyle \frac{⟨x_j,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_j,x_j⟩-\lambda }}+{\displaystyle \frac{⟨x_j,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_j,x_j⟩-\lambda }}⟨x_j,x_j⟩\hfill \\ =\lambda {\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_k,x_k⟩-\lambda }}+⟨x_j,v_n⟩-S_{n-1}^{*}\left(\lambda \right).\hfill \end{array}$$

(102)

It is now sufficient to use (99) and replace

$$\lambda \left(1+{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩}{⟨x_k,x_k⟩-\lambda }}\right)=\left(1+{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{\lambda }{⟨x_k,x_k⟩-\lambda }}\right)S_{n-1}^{*}\left(\lambda \right),$$

in the last equality of (102) to complete the proof of (101). □

Here, one may ask how we could find relations (100). The answer is as follows:

Since ${\left\{v_k\right\}}_{k=0}^n$ are assumed to be linearly independent, there are constants ${\left\{q_k\right\}}_{k=0}^{n-1}$, such that the general element in (98) can be rewritten as $x_n=v_n+{\displaystyle \sum _{k=0}^{n-1}}{q}_k{x}_k$. For $j=0,1,\dots ,n-1$, apply $⟨.,x_j⟩$ on both sides of the later assumption to get

$$⟨x_n,x_j⟩=⟨v_n,x_j⟩+{\displaystyle \sum _{k=0}^{n-1}}{q}_k⟨x_k,x_j⟩,$$

which leads to the familiar linear system:

$$\left[\begin{array}{cccc}\begin{array}{c}⟨x_0,x_0⟩\\ \lambda \\ ⋮\\ \lambda \end{array}& \begin{array}{c}\lambda \\ ⟨x_1,x_1⟩\\ ⋮\\ \lambda \end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}\lambda \\ \lambda \\ ⋮\\ ⟨x_{n-1},x_{n-1}⟩\end{array}\end{array}\right]\left[\begin{array}{c}{q}_0\\ q_1\\ ⋮\\ q_{n-1}\end{array}\right]=\left[\begin{array}{c}\lambda -⟨x_0,v_n⟩\\ \lambda -⟨x_1,v_n⟩\\ ⋮\\ \lambda -⟨x_{n-1},v_n⟩\end{array}\right],$$

having the explicit solutions

$$q_k=-{\displaystyle \frac{⟨x_k,v_n⟩-S_{n-1}^{*}\left(\lambda \right)}{⟨x_k,x_k⟩-\lambda }}.$$

Note that the procedure will be simplified if the initial data are orthogonal. In other words, let ${\left\{v_k\right\}}_{k=0}^n$ be mutually orthogonal, i.e., $⟨v_n,v_m⟩=⟨v_n,v_n⟩{\delta }_{n,m}$. Also, let ${\left\{x_k\right\}}_{k=0}^n$ satisfy the condition (86) as before. Noting the last row of (100) and this fact from (98) that $x_n={\displaystyle \sum _{k=0}^n}{a}_{n,n+1-k}{v}_k$ where $a_{n,1}=1$, for $m\le n$, we have

$$\begin{array}{c}⟨x_n,x_m⟩=⟨x_n,v_m-{\displaystyle \sum _{j=0}^{m-1}}{\displaystyle \frac{⟨x_j,v_m⟩-S_{m-1}^{*}\left(\lambda \right)}{⟨x_j,x_j⟩-\lambda }}{x}_j⟩\hfill \\ =⟨x_n,v_m⟩-\lambda {\displaystyle \sum _{j=0}^{m-1}}{\displaystyle \frac{⟨x_j,v_m⟩-S_{m-1}^{*}\left(\lambda \right)}{⟨x_j,x_j⟩-\lambda }}=⟨v_m,{\displaystyle \sum _{k=0}^n}{a}_{n,n+1-k}{v}_k⟩+\lambda -S_{m-1}^{*}\left(\lambda \right)\hfill \\ ={\displaystyle \sum _{k=0}^n}{a}_{n,n+1-k}⟨v_m,v_k⟩+\lambda -S_{m-1}^{*}\left(\lambda \right)=\left\{\begin{array}{c}\lambda (m\ne n),\hfill \\ ⟨x_n,x_n⟩(m=n),\hfill \end{array}\right.\hfill \end{array}$$

(103)

where we have used the following equality from (99):

$$-\lambda {\displaystyle \sum _{j=0}^{m-1}}{\displaystyle \frac{⟨x_j,v_m⟩-S_{m-1}^{*}\left(\lambda \right)}{⟨x_j,x_j⟩-\lambda }}=\lambda -S_{m-1}^{*}\left(\lambda \right).$$

For $m=0,1,\dots ,n$, relation (103) leads eventually to the linear system

$$\left[\begin{array}{cccc}\begin{array}{c}⟨v_0,v_0⟩\\ ⟨v_1,v_0⟩\\ ⋮\\ ⟨v_n,v_0⟩\end{array}& \begin{array}{c}⟨v_0,v_1⟩\\ ⟨v_1,v_1⟩\\ ⋮\\ ⟨v_n,v_1⟩\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}⟨v_0,v_n⟩\\ ⟨v_1,v_n⟩\\ ⋮\\ ⟨v_n,v_n⟩\end{array}\end{array}\right]\left[\begin{array}{c}{a}_{n,n+1}\\ a_{n,n}\\ ⋮\\ a_{n,1}\end{array}\right]=\left[\begin{array}{c}\lambda \\ S_0^{*}\left(\lambda \right)\\ ⋮\\ \begin{array}{c}{S}_{n-2}^{*}\left(\lambda \right)\hfill \\ ⟨x_n,x_n⟩-\lambda +S_{n-1}^{*}\left(\lambda \right)\hfill \end{array}\end{array}\right].$$

(104)

Now, applying the orthogonality condition $⟨v_n,v_m⟩=⟨v_n,v_n⟩{\delta }_{n,m}$ on the components of the coefficients matrix (104) gives

$$a_{n,n+1-k}={\displaystyle \frac{S_{k-1}^{*}\left(\lambda \right)}{⟨v_k,v_k⟩}}\mathrm{and}⟨x_n,x_n⟩=⟨v_n,v_n⟩+\lambda -S_{n-1}^{*}\left(\lambda \right).$$

Noting the identity

$$\lambda -S_{m-1}^{*}\left(\lambda \right)=-\lambda \left({\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-\lambda }{⟨x_k,x_k⟩-\lambda }}\right){\displaystyle /\phantom{\left({\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-\lambda }{⟨x_k,x_k⟩-\lambda }}\right)\left(1+{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{\lambda }{⟨x_k,x_k⟩-\lambda }}\right)}}\left(1+{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{\lambda }{⟨x_k,x_k⟩-\lambda }}\right),$$

we respectively obtain

$$x_n=v_n+{\displaystyle \sum _{m=0}^{n-1}}{\displaystyle \frac{\lambda }{⟨v_m,v_m⟩}}{\displaystyle \frac{1+{\displaystyle \sum _{j=0}^{m-1}}\frac{⟨x_j,v_m⟩}{⟨x_j,x_j⟩-\lambda }}{1+{\displaystyle \sum _{j=0}^{m-1}}\frac{\lambda }{⟨x_j,x_j⟩-\lambda }}}{v}_m,$$

(105)

and

$$⟨x_n,x_n⟩=⟨v_n,v_n⟩-\lambda \left({\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-\lambda }{⟨x_k,x_k⟩-\lambda }}\right){\displaystyle /\phantom{\left({\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{⟨x_k,v_n⟩-\lambda }{⟨x_k,x_k⟩-\lambda }}\right)\left(1+{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{\lambda }{⟨x_k,x_k⟩-\lambda }}\right)}}\left(1+{\displaystyle \sum _{k=0}^{n-1}}{\displaystyle \frac{\lambda }{⟨x_k,x_k⟩-\lambda }}\right).$$

On the other hand, for every $j=0,1,\dots ,m-1$, since

$$⟨x_j,v_m⟩=⟨{\displaystyle \sum _{k=0}^j}{p}_k{v}_k,v_m⟩={\displaystyle \sum _{k=0}^j}{p}_k⟨v_k,v_m⟩=0,$$

so

$$x_n=v_n+{\displaystyle \sum _{m=0}^{n-1}}{\displaystyle \frac{\lambda }{⟨v_m,v_m⟩\left(1+{\displaystyle \sum _{j=0}^{m-1}}\frac{\lambda }{⟨x_j,x_j⟩-\lambda }\right)}}{v}_m,$$

and

$${\displaystyle \frac{\lambda }{1+{\displaystyle \sum _{k=0}^{n-1}}\frac{\lambda }{⟨x_k,x_k⟩-\lambda }}}=⟨v_n,v_n⟩+\lambda -⟨x_n,x_n⟩,$$

which finally simplifies (105) as

$$x_n=v_n+{\displaystyle \sum _{m=0}^{n-1}}{\displaystyle \frac{⟨v_m,v_m⟩+\lambda -⟨x_m,x_m⟩}{⟨v_m,v_m⟩}}{v}_m.$$

(106)

There is a simple recurrence relation for the final result (106) if $n\to n+1$. We have

$$x_{n+1}-v_{n+1}=x_n-v_n+{\displaystyle \frac{⟨v_n,v_n⟩+\lambda -⟨x_n,x_n⟩}{⟨v_n,v_n⟩}}{v}_n,$$

which can be rewritten as

$$x_{n+1}=x_n+v_{n+1}+{\displaystyle \frac{\lambda -⟨x_n,x_n⟩}{⟨v_n,v_n⟩}}{v}_n.$$

(107)

For instance, the expanded forms of (106) or, equivalently, (107) for $n=0,1,2,3$ are

$$\begin{array}{c}{x}_0=v_0,\hfill \\ x_1=v_1+\lambda {\displaystyle \frac{v_0}{⟨v_0,v_0⟩}},\hfill \\ x_2=v_2+\lambda \left(1-{\displaystyle \frac{\lambda }{⟨v_0,v_0⟩}}\right){\displaystyle \frac{v_1}{⟨v_1,v_1⟩}}+\lambda {\displaystyle \frac{v_0}{⟨v_0,v_0⟩}},\hfill \end{array}$$

(108)

and

$$x_3=v_3+\lambda \left(1-{\displaystyle \frac{\lambda }{⟨v_0,v_0⟩}}-{\displaystyle \frac{\lambda {\left(⟨v_0,v_0⟩-\lambda \right)}^2}{{⟨v_0,v_0⟩}^2⟨v_1,v_1⟩}}\right){\displaystyle \frac{v_2}{⟨v_2,v_2⟩}}+\lambda \left(1-{\displaystyle \frac{\lambda }{⟨v_0,v_0⟩}}\right){\displaystyle \frac{v_1}{⟨v_1,v_1⟩}}+\lambda {\displaystyle \frac{v_0}{⟨v_0,v_0⟩}},$$

satisfying the conditions

$$⟨x_0,x_1⟩=⟨x_0,x_2⟩=⟨x_0,x_3⟩=⟨x_1,x_2⟩=⟨x_1,x_3⟩=⟨x_2,x_3⟩=\lambda .$$

Let us consider an illustrative example here. The shifted Legendre polynomials

$$P_{n,+}\left(x\right)={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+1)}_k}{{\left(1\right)}_k}}{\displaystyle \frac{x^k}{k!}},$$

where ${\left(a\right)}_k=a(a+1)\dots (a+k-1),$ satisfy the orthogonal relation

$${\int }_0^1{P}_{n,+}\left(x\right)P_{m,+}\left(x\right)dx={\displaystyle \frac{1}{2n+1}}{\delta }_{n,m}.$$

Since $P_{0,+}\left(x\right)=1,P_{1,+}\left(x\right)=-2x+1,P_{2,+}\left(x\right)=6x^2-6x+1,$ and $P_{3,+}\left(x\right)=-20x^3+30x^2-12x+1$, replacing them in (108) eventually yields

$$\begin{array}{c}{P}_{0,+}(x;\lambda )=1,\hfill \\ P_{1,+}(x;\lambda )=-2x+\lambda +1,\hfill \\ P_{2,+}(x;\lambda )=6x^2+6\left({\lambda }^2-\lambda -1\right)x-3{\lambda }^2+4\lambda +1,\hfill \end{array}$$

and

$$\begin{array}{c}{P}_{3,+}(x;\lambda )=-20x^3+30\left(-3{\lambda }^4+6{\lambda }^3-4{\lambda }^2+\lambda +1\right)x^2\hfill \\ +6\left(15{\lambda }^4-30{\lambda }^3+21{\lambda }^2-6\lambda -2\right)x-15{\lambda }^4+30{\lambda }^3-23{\lambda }^2+9\lambda +1,\hfill \end{array}$$

satisfying the simple uncorrelatedness condition

$${\int }_0^1{P}_{n,+}(x;\lambda )P_{m,+}(x;\lambda )dx=\lambda \iff m\ne n\mathrm{and}m,n=0,1,2,3.$$

Remark 3.

A very obvious case is when $\lambda =⟨v_0,v_0⟩$ as (106) or (107) takes the simple form $x_n=v_n+v_0$ and, for $m\ne n$, we therefore have

$$⟨x_n,x_m⟩=⟨v_n+v_0,v_m+v_0⟩=⟨v_n,v_m⟩+⟨v_n,v_0⟩+⟨v_0,v_m⟩+⟨v_0,v_0⟩=⟨v_0,v_0⟩.$$

In this sense, for the above-mentioned example, since $\lambda =⟨P_{0,+}\left(x\right),P_{0,+}\left(x\right)⟩=1$, so $P_{n,+}(x;1)=P_{n,+}\left(x\right)+1.$ See also Section 9 in this regard.

6.1. A Biorthogonality Property

Reconsider the condition (86), and let $x_r$ be a fixed variable. Since

$$⟨x_m,x_n⟩=\lambda \mathrm{for}m\ne n\mathrm{and}⟨x_m,x_r⟩=\lambda \mathrm{for}m\ne r,$$

it follows that $⟨x_m,x_n-x_r⟩=0\mathrm{for}m\ne n,r$. This means that the sequence ${\left\{x_m\right\}}_{m=0}$ is biorthogonal with respect to the sequence ${\left\{x_n^{*}=x_n-x_r\right\}}_{n=0}$, particularly when $r=0$.

6.2. A Basic Remark

Theorem 9 and analytically solving the linear system (91) in Theorem 8 show that we can apply the aforesaid approach for any functional type of linear approximations. In other words, consider the approximation

$$f\left(x\right)\cong {\displaystyle \sum _{k=0}^n}{c}_k{\Phi }_k\left(x\right),$$

(109)

in which ${\left\{c_k\right\}}_{k=0}^n$ are unknown coefficients and ${\left\{{\Phi }_k\left(x\right)\right\}}_{k=0}^n$ are known basis functions. Applying the linear functionals ${\left\{L_j\right\}}_{j=0}^n$ on both sides of (109) one by one will lead to the following linear system:

$$\left[\begin{array}{cccc}\begin{array}{c}{L}_0\left({\Phi }_0\left(x\right)\right)\\ L_1\left({\Phi }_0\left(x\right)\right)\\ ⋮\\ L_n\left({\Phi }_0\left(x\right)\right)\end{array}& \begin{array}{c}{L}_0\left({\Phi }_1\left(x\right)\right)\\ L_1\left({\Phi }_1\left(x\right)\right)\\ ⋮\\ L_n\left({\Phi }_1\left(x\right)\right)\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}{L}_0\left({\Phi }_n\left(x\right)\right)\\ L_1\left({\Phi }_n\left(x\right)\right)\\ ⋮\\ L_n\left({\Phi }_n\left(x\right)\right)\end{array}\end{array}\right]\left[\begin{array}{c}{c}_0\\ c_1\\ ⋮\\ c_n\end{array}\right]=\left[\begin{array}{c}{L}_0\left(f\left(x\right)\right)\\ L_1\left(f\left(x\right)\right)\\ ⋮\\ L_n\left(f\left(x\right)\right)\end{array}\right].$$

Now, if the uncorrelatedness condition

$$L_m\left({\Phi }_n\left(x\right)\right)=\left\{\begin{array}{c}\lambda \ge 0(m\ne n),\hfill \\ L_n\left({\Phi }_n\left(x\right)\right)(m=n),\hfill \end{array}\right.$$

is employed on the components of the above linear system, we will reach the same solution as in Theorem 8. The concepts presented in the preceding subsections help us now derive some orthogonal sequences of continuous functions in the next section.

6.3. Simple Uncorrelated Functions of Classical Type

Noting Theorem 7, again, let $a\left(x\right),b\left(x\right),u\left(x\right)$ and $v\left(x\right)$ be four given functions continuous on the interval $[a,b]$, and let $\left\{{\lambda }_n\right\}$ be a sequence of eigenvalues. A Sturm–Liouville problem is a second-order linear differential equation of the form

$$a\left(x\right)y_n^{″}\left(x\right)+b\left(x\right)y_n^{\prime }\left(x\right)+\left({\lambda }_{n}u\left(x\right)+v\left(x\right)\right)y_n\left(x\right)=L\left(y_n\right)+{\lambda }_{n}w\left(x\right)y_n=0,$$

(110)

where

$$L\left(y_n\right)={\displaystyle \frac{d}{dx}}\left(r\left(x\right)y_n^{\prime }\left(x\right)\right)+q\left(x\right)y_n\left(x\right),$$

in which

$$r\left(x\right)=a\left(x\right)exp\left(\int {\displaystyle \frac{b\left(x\right)-a^{\prime }\left(x\right)}{a\left(x\right)}}dx\right),q\left(x\right)=v\left(x\right)exp\left(\int {\displaystyle \frac{b\left(x\right)-a^{\prime }\left(x\right)}{a\left(x\right)}}dx\right),$$

and $w\left(x\right)=u\left(x\right)exp\left(\int {\displaystyle \frac{b\left(x\right)-a^{\prime }\left(x\right)}{a\left(x\right)}}dx\right)>0,\forall x\in (a,b)$.

Equation (110) should be considered on an open interval, say $(a,b)$, with boundary conditions ${\alpha }_1{y}_n\left(a\right)+{\beta }_1{y}_n^{\prime }\left(a\right)=0$ and ${\alpha }_2{y}_n\left(b\right)+{\beta }_2{y}_n^{\prime }\left(b\right)=0$, where ${\alpha }_1,{\alpha }_2$ and ${\beta }_1,{\beta }_2$ are given constants and $r\left(x\right),r^{\prime }\left(x\right),q\left(x\right)$ and $w\left(x\right)$ are to be assumed continuous for $x\in [a,b]$.

Suppose that $y_n\left(x\right)$ and $y_m\left(x\right)$ are two eigenfunctions of Equation (110). According to Sturm–Liouville theory [21], they are orthogonal with respect to the weight function $w\left(x\right)$ on $(a,b)$ under the given conditions, such that

$${\int }_a^{b}w\left(x\right)y_n\left(x\right)y_m\left(x\right)dx=\left({\int }_a^{b}w\left(x\right)y_n^2\left(x\right)dx\right){\delta }_{n,m}.$$

(111)

Now if, in (111), there exists a specific function, say $z\left(x\right)$, such that

$$y_n\left(x\right)={\Phi }_n\left(x\right)-z\left(x\right),$$

(112)

then substituting (112) into (111) yields

$$\begin{array}{cc}\hfill & {\int }_a^{b}w\left(x\right)\left({\Phi }_n\left(x\right)-z\left(x\right)\right)\left({\Phi }_m\left(x\right)-z\left(x\right)\right)dx\hfill \\ \hfill & ={\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx-{\int }_a^{b}w\left(x\right)z\left(x\right){\Phi }_n\left(x\right)dx-{\int }_a^{b}w\left(x\right)z\left(x\right){\Phi }_m\left(x\right)dx\hfill \\ \hfill & +{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx=\left({\int }_a^{b}w\left(x\right){\left({\Phi }_n\left(x\right)-z\left(x\right)\right)}^{2}dx\right){\delta }_{n,m}.\hfill \end{array}$$

(113)

On the other hand, the sequence of functions ${\left\{{\Phi }_n\left(x\right)\right\}}_{n=0}^{\infty }$ is said to be simply uncorrelated if, for the known specific function $v\left(x\right)$ and for every n, we have

$${\int }_a^{b}v\left(x\right){\Phi }_n\left(x\right)dx=\lambda \ge 0,$$

where the non-negative parameter $\lambda$ is independent of n.

Based on this definition, if ${\left\{{\Phi }_n\left(x\right)\right\}}_{n=0}^{\infty }$ in (112) is a sequence of real functions, such that

$${\int }_a^{b}w\left(x\right)z\left(x\right){\Phi }_n\left(x\right)dx={\int }_a^{b}w\left(x\right)z^2\left(x\right)dx\ge 0,$$

(114)

then (113) will be simplified as

$$\begin{array}{c}{\int }_a^{b}w\left(x\right)\left({\Phi }_n\left(x\right)-z\left(x\right)\right)\left({\Phi }_m\left(x\right)-z\left(x\right)\right)dx={\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx-{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx\hfill \\ \hfill =\left({\int }_a^{b}w\left(x\right){\Phi }_n^2\left(x\right)dx-{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx\right){\delta }_{n,m}.\end{array}$$

(115)

Moreover, replacing (112) in (110) gives the inhomogeneous differential equation

$$\begin{array}{c}a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+\left({\lambda }_{n}u\left(x\right)+v\left(x\right)\right){\Phi }_n\left(x\right)\hfill \\ =a\left(x\right)z^{″}\left(x\right)+b\left(x\right)z^{\prime }\left(x\right)+\left({\lambda }_{n}u\left(x\right)+v\left(x\right)\right)z\left(x\right).\hfill \end{array}$$

(116)

Let us impose an extra condition on Equation (116) for the function $z\left(x\right)$ as follows:

$$a\left(x\right)z^{″}\left(x\right)+b\left(x\right)z^{\prime }\left(x\right)+v\left(x\right)z\left(x\right)=A_z^{*}u\left(x\right)z\left(x\right),$$

(117)

where $A_z^{*}$ is a constant value independent of x. Using relations (114), (115) and Equations (116) and (117), we can extract a remarkable result for inhomogeneous type of Sturm–Liouville equations.

Theorem 10.

Let $a\left(x\right),b\left(x\right),u\left(x\right)$ and $v\left(x\right)$ be four given functions continuous on $[a,b]$. If

$$w\left(x\right)=u\left(x\right)exp\left(\int {\displaystyle \frac{b\left(x\right)-a^{\prime }\left(x\right)}{a\left(x\right)}}dx\right),$$

(118)

is positive on $(a,b)$ and the sequence ${\left\{{\Phi }_n\left(x\right)\right\}}_{n=0}^{\infty }$ with the corresponding eigenvalues $\left\{{\lambda }_n\right\}$ satisfies an inhomogeneous differential equation of the form

$$a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+\left({\lambda }_{n}u\left(x\right)+v\left(x\right)\right){\Phi }_n\left(x\right)=\left({\lambda }_n+A_z^{*}\right)u\left(x\right)z\left(x\right),$$

(119)

such that

$${\int }_a^{b}w\left(x\right)z\left(x\right){\Phi }_n\left(x\right)dx={\int }_a^{b}w\left(x\right)z^2\left(x\right)dx,$$

and

$${\displaystyle \frac{a\left(x\right)z^{″}\left(x\right)+b\left(x\right)z^{\prime }\left(x\right)+v\left(x\right)z\left(x\right)}{u\left(x\right)z\left(x\right)}}=A_z^{*},$$

where $A_z^{*}$ is constant, and also ${\alpha }_1{\Phi }_n\left(a\right)+{\beta }_1{\Phi }_n^{\prime }\left(a\right)=0$ and ${\alpha }_2{\Phi }_n\left(b\right)+{\beta }_2{\Phi }_n^{\prime }\left(b\right)=0$ are two initial conditions where ${\alpha }_1,{\beta }_1,{\alpha }_2\mathrm{and}{\beta }_2$ are given constants, then the sequence of functions in the form

$$G_n\left(x\right)=y_{1,n}\left(x\right)-{\displaystyle \frac{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{1,n}\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx}}{y}_{2,n}\left(x\right),$$

(120)

is orthogonal with respect to the weight function (118) on $[a,b]$ provided that

$${\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx\ne 0(\forall n\notin {\mathbb{Z}}^{+}).$$

Proof. 

First, write Equation (119) in the self-adjoint form

$${\left(r\left(x\right){\Phi }_n^{\prime }\left(x\right)\right)}^{\prime }+\left({\lambda }_{n}w\left(x\right)+q\left(x\right)\right){\Phi }_n\left(x\right)=\left({\lambda }_n+A_z^{*}\right)w\left(x\right)z\left(x\right),$$

(121)

and, for the index m, as

$${\left(r\left(x\right){\Phi }_m^{\prime }\left(x\right)\right)}^{\prime }+\left({\lambda }_{m}w\left(x\right)+q\left(x\right)\right){\Phi }_m\left(x\right)=\left({\lambda }_m+A_z^{*}\right)w\left(x\right)z\left(x\right),$$

(122)

in which $r\left(x\right)=a\left(x\right)exp\left(\int {\displaystyle \frac{b\left(x\right)-a^{\prime }\left(x\right)}{a\left(x\right)}}dx\right)$, and $q\left(x\right)=v\left(x\right)exp\left(\int {\displaystyle \frac{b\left(x\right)-a^{\prime }\left(x\right)}{a\left(x\right)}}dx\right)$.

• On multiplying by ${\Phi }_m\left(x\right)$ and ${\Phi }_n\left(x\right)$ in, respectively, (121) and (122) and subtracting, we get

$$\begin{array}{c}{\left[r\left(x\right)\left({\Phi }_m\left(x\right){\Phi }_n^{\prime }\left(x\right)-{\Phi }_n\left(x\right){\Phi }_m^{\prime }\left(x\right)\right)\right]}_a^b+\left({\lambda }_n-{\lambda }_m\right){\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx\hfill \\ =\left({\lambda }_n+A_z^{*}\right){\int }_a^{b}w\left(x\right)z\left(x\right){\Phi }_m\left(x\right)dx-\left({\lambda }_m+A_z^{*}\right){\int }_a^{b}w\left(x\right)z\left(x\right){\Phi }_n\left(x\right)dx\hfill \\ =\left({\lambda }_n-{\lambda }_m\right){\int }_a^{b}w\left(x\right)z^2\left(x\right)dx,\hfill \end{array}$$

which results in

$$\begin{array}{c}\left({\lambda }_n-{\lambda }_m\right)\left({\int }_a^{b}w\left(x\right){\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx-{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx\right)\hfill \\ =-{\left[r\left(x\right)\left({\Phi }_m\left(x\right){\Phi }_n^{\prime }\left(x\right)-{\Phi }_n\left(x\right){\Phi }_m^{\prime }\left(x\right)\right)\right]}_a^b=0\iff n\ne m.\hfill \end{array}$$

But on the other hand, Equation (119) is inhomogeneous, and its general solution takes the form

$${\Phi }_n\left(x\right)=c_1{y}_{1,n}\left(x\right)+c_2{y}_{2,n}\left(x\right)+z\left(x\right)(c_1,c_2\in \mathbb{R}),$$

(123)

where $c_1{y}_{1,n}\left(x\right)+c_2{y}_{2,n}\left(x\right)$ is the solution of the homogeneous equation

$$a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+\left({\lambda }_{n}p\left(x\right)+q\left(x\right)\right){\Phi }_n\left(x\right)=0,$$

with two independent solutions, $y_{1,n}\left(x\right)$ and $y_{2,n}\left(x\right)$, respectively. So, substituting (123) into (114) simplifies the solution as

$${\Phi }_n\left(x\right)=c_1\left(y_{1,n}\left(x\right)-{\displaystyle \frac{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{1,n}\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx}}{y}_{2,n}\left(x\right)\right)+z\left(x\right),$$

(124)

provided that ${\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx\ne 0$ for every $n\notin {\mathbb{Z}}^{+}$. Finally, for $c_1=1$, the sequence

$${\Phi }_n\left(x\right)-z\left(x\right)=y_{1,n}\left(x\right)-{\displaystyle \frac{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{1,n}\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx}}{y}_{2,n}\left(x\right),$$

would be orthogonal with respect to the weight function $w\left(x\right)$ in (118) on $[a,b]$ according to the relation (115). □

Remark 4.

The given condition ${\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx\ne 0$ in (124) reveals the importance of the role of $z\left(x\right)\ne 0$ in the above-mentioned theorem. Moreover, if it is a constant function, say $z\left(x\right)=1$, we will not be able anymore to use the theorem because $\left\{y_{1,n}\left(x\right)\right\}$ is orthogonal, and we have (especially for orthogonal polynomial sequences) the case in which ${\int }_a^{b}w\left(x\right)y_{1,n}\left(x\right)dx=0$.

• In other words, for $z\left(x\right)=1$, the sequence $G_n\left(x\right)$ in (120) will be reduced to the single case $G_n\left(x\right)=y_{1,n}\left(x\right)$.

Finally, when it is noted in (124) that ${\int }_a^{b}w\left(x\right)z\left(x\right){\Phi }_n\left(x\right)dx={\int }_a^{b}w\left(x\right)z^2\left(x\right)dx$, the norm square value is explicitly computed as follows:

$$\begin{array}{c}{\int }_a^{b}w\left(x\right)G_n^2\left(x\right)dx={\int }_a^{b}w\left(x\right)y_{1,n}^2\left(x\right)dx+{\left({\displaystyle \frac{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{1,n}\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx}}\right)}^2{\int }_a^{b}w\left(x\right)y_{2,n}^2\left(x\right)dx\hfill \\ -2{\displaystyle \frac{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{1,n}\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z\left(x\right)y_{2,n}\left(x\right)dx}}{\int }_a^{b}w\left(x\right)y_{1,n}\left(x\right)y_{2,n}\left(x\right)dx.\hfill \end{array}$$

6.3.1. New Classes of Orthogonal Functions

In order to introduce some new sequences of orthogonal functions using Theorem 10, we first recall some comments available in the literature. A generalized hypergeometric series of order $(p,q)$ is defined as

$${}_{p}F_q\left(\left.\begin{array}{c}{a}_1,\dots ,a_p\\ b_1,\dots ,b_q\end{array}\right|x\right)={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(a_1\right)}_k\dots {\left(a_p\right)}_k}{{\left(b_1\right)}_k\dots {\left(b_q\right)}_k}}{\displaystyle \frac{x^k}{k!}},$$

(125)

where ${\left(a\right)}_k={\displaystyle \frac{\Gamma (a+k)}{\Gamma \left(a\right)}}=a(a+1)\dots (a+k-1)$ denotes the Pochhammer symbol, and $\Gamma \left(x\right)={\int }_0^{\infty }{t}^{x-1}{e}^{-t}dt,(\mathrm{Re}\left(x\right)>0),$ is the well-known gamma function.

There are two special cases of the series (125) arising in many physics and engineering problems [20,25]. The first case is the Gauss hypergeometric function whose integral representation

$${}_{2}F_1\left(\left.\begin{array}{c}\begin{array}{cc}a,& b\end{array}\\ c\end{array}\right|x\right)={\displaystyle \frac{\Gamma \left(c\right)}{\Gamma \left(a\right)\Gamma (c-a)}}{\int }_0^1{t}^{a-1}{(1-t)}^{c-a-1}{(1-xt)}^{-b}dt(c>a>0),$$

(126)

satisfies the differential equation

$$x(1-x)y^{″}\left(x\right)+(c-(a+b+1)x)y^{\prime }\left(x\right)-aby\left(x\right)=0,$$

(127)

with the general solution

$$y=c_1{}_{2}F_1\left(\left.\begin{array}{c}a,b\\ c\end{array}\right|x\right)+c_2{x}^{1-c}{}_{2}F_1\left(\left.\begin{array}{c}a+1-c,b+1-c\\ 2-c\end{array}\right|x\right).$$

(128)

When the well-known beta integral is noted, substituting $x=1$ into (126) gives

$${}_{2}F_1\left(\left.\begin{array}{c}a,b\\ c\end{array}\right|1\right)={\displaystyle \frac{\Gamma \left(c\right)\Gamma (c-a-b)}{\Gamma (c-a)\Gamma (c-b)}}.$$

The second case is known in the literature as the confluent hypergeometric function with the integral representation

$${}_{1}F_1\left(\left.\begin{array}{c}a\\ c\end{array}\right|x\right)={\displaystyle \frac{\Gamma \left(c\right)}{\Gamma \left(a\right)\Gamma (c-a)}}{\int }_0^1{t}^{a-1}{(1-t)}^{c-a-1}{e}^{xt}dt(c>a>0),$$

satisfying the equation

$$x{y}^{″}\left(x\right)+(c-x)y^{\prime }\left(x\right)-ay\left(x\right)=0,$$

(129)

whose general solution is given by

$$y=b_1{}_{1}F_1\left(\left.\begin{array}{c}a\\ c\end{array}\right|x\right)+b_2{x}^{1-c}{}_{1}F_1\left(\left.\begin{array}{c}a+1-c\\ 2-c\end{array}\right|x\right).$$

(130)

In this sense, there are two sequences of classical orthogonal polynomials that can be represented in terms of Gauss and confluent hypergeometric series. The first sequence is the shifted monic Jacobi polynomials

$${\overline{P}}_{n,+}^{(\alpha ,\beta )}\left(x\right)={\displaystyle \frac{{(-1)}^n{(\beta +1)}_n}{{(n+\alpha +\beta +1)}_n}}{}_{2}F_1\left(\left.\begin{array}{c}-n,n+\alpha +\beta +1\\ \beta +1\end{array}\right|x\right),$$

(131)

that are orthogonal with respect to the weight function ${(1-x)}^{\alpha }{x}^{\beta }$ on $[0,1]$ as

$${\int }_0^1{(1-x)}^{\alpha }{x}^{\beta }{\overline{P}}_{m,+}^{(\alpha ,\beta )}\left(x\right){\overline{P}}_{n,+}^{(\alpha ,\beta )}\left(x\right)dx=n!2^{2n}{\displaystyle \frac{\Gamma (n+\alpha +\beta +1)\Gamma (n+\alpha +1)\Gamma (n+\beta +1)}{\Gamma (2n+\alpha +\beta +1)\Gamma (2n+\alpha +\beta +2)}}{\delta }_{n,m},$$

and the second sequence is the monic (generalized) Laguerre polynomials

$${\overline{L}}_n^{\left(\alpha \right)}\left(x\right)={(-1)}^n{(\alpha +1)}_n{}_{1}F_1\left(\left.\begin{array}{c}-n\\ \alpha +1\end{array}\right|x\right),$$

(132)

that are orthogonal with respect to the weight function $x^{\alpha }{e}^{-x}$ on $[0,\infty )$ as

$${\int }_0^{\infty }{x}^{\alpha }{e}^{-x}{\overline{L}}_m^{\left(\alpha \right)}\left(x\right){\overline{L}}_n^{\left(\alpha \right)}\left(x\right)dx=n!\Gamma (n+\alpha +1){\delta }_{n,m}.$$

We can now introduce some sequences of orthogonal functions by means of Theorem 10.

First Sequence

With reference to the Gauss hypergeometric Equation (127), consider the differential equation

$$\begin{array}{c}x(1-x){{\Phi }^{″}}_n\left(x\right)+(c-(d+1)x){{\Phi }^{\prime }}_n\left(x\right)+n(n+d){\Phi }_n\left(x\right)\hfill \\ =x(1-x)z^{″}\left(x\right)+(c-(d+1)x)z^{\prime }\left(x\right)+n(n+d)z\left(x\right),\hfill \end{array}$$

(133)

with the general solution

$$\begin{array}{cc}\hfill {\Phi }_n\left(x\right)& =c_1{}_{2}F_1\left(\left.\begin{array}{c}-n,n+d\\ c\end{array}\right|x\right)\hfill \\ \hfill & +c_2{x}^{1-c}{}_{2}F_1\left(\left.\begin{array}{c}-n+1-c,n+d+1-c\\ 2-c\end{array}\right|x\right)+z\left(x\right).\hfill \end{array}$$

(134)

For a known parameter e, assume in (133) that

$$x(1-x)z^{″}\left(x\right)+(c-(d+1)x)z^{\prime }\left(x\right)=-e(e+d)z\left(x\right),$$

(135)

which has a general solution, according to (127) and (128), as

$$\begin{array}{cc}\hfill z\left(x\right)& =z\left(x;A,B,c,d,e\right)\hfill \\ \hfill & =A{}_{2}F_1\left(\left.\begin{array}{c}-e,e+d\\ c\end{array}\right|x\right)+B{x}^{1-c}{}_{2}F_1\left(\left.\begin{array}{c}-e+1-c,e+d+1-c\\ 2-c\end{array}\right|x\right),\hfill \end{array}$$

(136)

in which $A,B$ are two free parameters. It turns out from (133) to (136) that the general solution of the equation

$$\begin{array}{c}x(1-x){\Phi }_n^{″}\left(x\right)+(c-(d+1)x){\Phi }_n^{\prime }\left(x\right)+n(n+d){\Phi }_n\left(x\right)=\left(n(n+d)-e(e+d)\right)\hfill \\ \times \left(A{}_{2}F_1\left(\left.\begin{array}{c}-e,e+d\\ c\end{array}\right|x\right)+B{x}^{1-c}{}_{2}F_1\left(\left.\begin{array}{c}-e+1-c,e+d+1-c\\ 2-c\end{array}\right|x\right)\right),\hfill \end{array}$$

(137)

is as

$$\begin{array}{c}{\Phi }_n\left(x\right)=c_1{}_{2}F_1\left(\left.\begin{array}{c}-n,n+d\\ c\end{array}\right|x\right)+c_2{x}^{1-c}{}_{2}F_1\left(\left.\begin{array}{c}-n+1-c,n+d+1-c\\ 2-c\end{array}\right|x\right)\hfill \\ +A{}_{2}F_1\left(\left.\begin{array}{c}-e,e+d\\ c\end{array}\right|x\right)+B{x}^{1-c}{}_{2}F_1\left(\left.\begin{array}{c}-e+1-c,e+d+1-c\\ 2-c\end{array}\right|x\right).\hfill \end{array}$$

(138)

Note that the sequence (138) is also the general solution of the fourth-order equation

$$\begin{array}{c}x(1-x){\left(x(1-x){\Phi }_n^{″}\left(x\right)+(c-(d+1)x){\Phi }_n^{\prime }\left(x\right)+n(n+d){\Phi }_n\left(x\right)\right)}^{″}\hfill \\ +(c-(d+1)x){\left(x(1-x){\Phi }_n^{″}\left(x\right)+(c-(d+1)x){\Phi }_n^{\prime }\left(x\right)+n(n+d){\Phi }_n\left(x\right)\right)}^{\prime }\hfill \\ +e(e+d)\left(x(1-x){\Phi }_n^{″}\left(x\right)+(c-(d+1)x){\Phi }_n^{\prime }\left(x\right)+n(n+d){\Phi }_n\left(x\right)\right)=0.\hfill \end{array}$$

Considering that there are five parameters for $z\left(x;A,B,c,d,e\right)$ in (136) and the well-known identity ${}_{2}F_1(a,c;c;x)={(1-x)}^{-a}$, various cases can be considered for Equation (137) and its solution in (138). Here, we introduce four orthogonal subsequences of (138).

(i) 

First subsequence. For two given parameters $p,q\in \mathbb{R}$, if

$$\left(A,B,c,d,e\right)=\left(0,1,1+p,1+p+q,-p-q\right),$$

are replaced in (137) as

$$\begin{array}{c}x(1-x){\Phi }_n^{″}\left(x\right)-((p+q+2)x-p-1){\Phi }_n^{\prime }\left(x\right)+n(n+p+q+1){\Phi }_n\left(x\right)\hfill \\ \hfill =(n+1)(n+p+q)x^{-p}{(1-x)}^{-q},\end{array}$$

(139)

its general solution, according to (138), reads as

$$\begin{array}{cc}\hfill {\Phi }_n\left(x\right)& =c_1{}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)\hfill \\ \hfill & +c_2{x}^{-p}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right)+x^{-p}{(1-x)}^{-q}.\hfill \end{array}$$

(140)

As the weight function corresponding to the self adjoint form of Equation (139) is $w(x;p,q)=x^p{(1-x)}^q$ and $z\left(x\right)=x^{-p}{(1-x)}^{-q}$, applying the condition (114) on the solution (140) gives

$$c_1{\int }_0^1{}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)dx+c_2{\int }_0^1{x}^{-p}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right)dx=0.$$

(141)

Since in (141),

$$\begin{array}{c}{\int }_0^1{}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)dx={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+p+q+1)}_k}{{(p+1)}_{k}k!}}{\displaystyle \frac{1}{1+k}}\hfill \\ ={}_{3}F_2\left(\left.\begin{array}{c}-n,n+p+q+1,1\\ p+1,2\end{array}\right|1\right)={\displaystyle \frac{p}{(n+1)(n+p+q)}}\left(1+{(-1)}^n{\displaystyle \frac{{\left(q\right)}_{n+1}}{{\left(p\right)}_{n+1}}}\right),\hfill \end{array}$$

(142)

and

$$\begin{array}{c}{\int }_0^1{x}^{-p}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right)dx={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n-p)}_k{(n+1+q)}_k}{{(1-p)}_{k}k!}}{\displaystyle \frac{1}{1-p+k}}\hfill \\ ={\displaystyle \frac{1}{1-p}}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 2-p\end{array}\right|1\right)={\displaystyle \frac{{(-1)}^n{(p+q)}_n}{(n+1)!}}\mathrm{B}(1-p,1-q),\hfill \end{array}$$

the first orthogonal subsequence appears as

$$\begin{array}{c}{G}_n^{\left(1\right)}(x;p,q)={}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)\hfill \\ -{\displaystyle \frac{n!\left({(-1)}^n{\left(p\right)}_{n+1}+{\left(q\right)}_{n+1}\right)}{\mathrm{B}(1-p,1-q){(p+q)}_{n+1}{(p+1)}_n}}{x}^{-p}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right),\hfill \end{array}$$

(143)

which is orthogonal with respect to the weight function $w(x;p,q)=x^p{(1-x)}^q$ on $[0,1]$ if and only if $p,q\in (-1,0)$, because ${\Phi }_n\left(x\right)$ must be convergent at the points $x=0,1$ in (140).

• To derive (142), we have used the identity

$${}_{3}F_2\left(\left.\begin{array}{c}{a}_1,a_2,1\\ b_1,2\end{array}\right|1\right)={\displaystyle \frac{b_1-1}{(a_1-1)(a_2-1)}}\left({}_{2}F_1\left(\left.\begin{array}{c}{a}_1-1,a_2-1\\ b_1-1\end{array}\right|1\right)-1\right).$$

Also, notice that the first term of (143) is the same as shifted Jacobi polynomials $P_{n,+}^{(q,p)}\left(x\right)$ defined in (131).

(ii) 

Second subsequence. If $\left(A,B,c,d,e\right)=\left(0,1,1+p,1+p+q,-p\right)$ are replaced in (137) as

$$\begin{array}{c}x(1-x){\Phi }_n^{″}\left(x\right)-((p+q+2)x-p-1){\Phi }_n^{\prime }\left(x\right)+n(n+p+q+1){\Phi }_n\left(x\right)\hfill \\ \hfill =(n+1)(n+q+1)x^{-p},\end{array}$$

(144)

its general solution, according to (138), is as

$${\Phi }_n\left(x\right)=c_1{}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)+c_2{x}^{-p}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right)+x^{-p}.$$

(145)

As $z\left(x\right)=x^{-p}$ in (144), applying the condition (114) on the solution (145) gives

$$\begin{array}{c}{c}_1{\int }_0^1{(1-x)}^q{}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)dx\hfill \\ \hfill +c_2{\int }_0^1{x}^{-p}{(1-x)}^q{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right)dx=0.\end{array}$$

(146)

Since in (146),

$$\begin{array}{c}{\int }_0^1{(1-x)}^q{}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)dx={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+p+q+1)}_k}{{(p+1)}_{k}k!}}{\displaystyle \frac{{\left(1\right)}_k}{(q+1){(q+2)}_k}}\hfill \\ ={\displaystyle \frac{1}{q+1}}{}_{3}F_2\left(\left.\begin{array}{c}-n,n+p+q+1,1\\ p+1,q+2\end{array}\right|1\right)={\displaystyle \frac{p}{(p+n)(q+1+n)}},\hfill \end{array}$$

(147)

and

$$\begin{array}{c}{\int }_0^1{x}^{-p}{(1-x)}^q{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right)dx\hfill \\ ={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n-p)}_k{(n+1+q)}_k}{{(1-p)}_{k}k!}}B(k+1-p,q+1)\hfill \\ =B(1-p,q+1){}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 2-p+q\end{array}\right|1\right)={\displaystyle \frac{{(-1)}^n{\left(p\right)}_n}{(q+1){(q+2)}_n}},\hfill \end{array}$$

the second subsequence is finally derived as

$$\begin{array}{cc}\hfill G_n^{\left(2\right)}(x;p,q)& ={}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)\hfill \\ \hfill & -{(-1)}^n{\displaystyle \frac{{(q+1)}_n}{{(p+1)}_n}}{x}^{-p}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right),\hfill \end{array}$$

(148)

which is orthogonal with respect to the weight function $w(x;p,q)=x^p{(1-x)}^q$ on $[0,1]$ for $p\in (-1,0)$ and $q>-1$. To derive (147), we have used the Pfaff–Saalschutz summation theorem [26]

$${}_{3}F_2\left(\left.\begin{array}{c}-n,a,b\\ d,e\end{array}\right|1\right)={\displaystyle \frac{{(d-a)}_n{(d-b)}_n}{{\left(d\right)}_n{(d-a-b)}_n}}\iff -n+a+b+1=d+e.$$

(iii) 

Third subsequence. If $\left(A,B,c,d,e\right)=\left(1,0,1+p,1+p+q,-q\right)$ are replaced as

$$\begin{array}{c}x(1-x){\Phi }_n^{″}\left(x\right)-((p+q+2)x-p-1){\Phi }_n^{\prime }\left(x\right)+n(n+p+q+1){\Phi }_n\left(x\right)\hfill \\ \hfill =(n+q)(n+p+1){(1-x)}^{-q},\end{array}$$

(149)

its general solution reads as

$$\begin{array}{cc}\hfill {\Phi }_n\left(x\right)& =c_1{}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)\hfill \\ \hfill & +c_2{x}^{-p}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right)+{(1-x)}^{-q}.\hfill \end{array}$$

(150)

As $z\left(x\right)={(1-x)}^{-q}$ in (149), applying the condition (114) on the solution (150) yields

$$\begin{array}{c}{c}_1{\int }_0^1{x}^p{}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)dx\hfill \\ \hfill +c_2{\int }_0^1{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right)dx=0.\end{array}$$

(151)

Since in (151),

$$\begin{array}{c}{\int }_0^1{x}^p{}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)dx={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+p+q+1)}_k}{{(p+1)}_{k}k!}}{\displaystyle \frac{1}{p+1+k}}\hfill \\ ={\displaystyle \frac{1}{p+1}}{}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+2\end{array}\right|1\right)={\displaystyle \frac{{(-1)}^n{\left(q\right)}_n}{{(p+1)}_{n+1}}},\hfill \end{array}$$

and

$$\begin{array}{c}{\int }_0^1{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right)dx={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n-p)}_k{(n+1+q)}_k}{{(1-p)}_{k}k!}}{\displaystyle \frac{{\left(1\right)}_k}{{\left(2\right)}_k}}\hfill \\ ={}_{3}F_2\left(\left.\begin{array}{c}-n-p,n+q+1,1\\ 1-p,2\end{array}\right|1\right)\hfill \\ ={\displaystyle \frac{-p}{(n+p+1)(n+q)}}\left(1+{\displaystyle \frac{{(-1)}^{n}qB(-p,-q){(p+q+1)}_n}{n!}}\right),\hfill \end{array}$$

the third subsequence appears as

$$\begin{array}{c}{G}_n^{\left(3\right)}(x;p,q)={}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)\hfill \\ +{\displaystyle \frac{{(-1)}^{n}n!{\left(q\right)}_{n+1}{x}^{-p}}{{\left(p\right)}_{n+1}\left(n!+{(-1)}^{n}B(-p,-q){(p+q+1)}_n\right)}}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right),\hfill \end{array}$$

(152)

which is orthogonal with respect to the weight $x^p{(1-x)}^q$ on $[0,1]$ for $-1<p,q<0$.

From (143), (148) and (152), we can conclude that, in fact,

$$G_n^{\left(k\right)}(x;p,q)={}_{2}F_1\left(\left.\begin{array}{c}-n,n+p+q+1\\ p+1\end{array}\right|x\right)+{\lambda }_n^{\left(k\right)}(p,q)x^{-p}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+q\\ 1-p\end{array}\right|x\right),$$

where

$$\begin{array}{c}{\lambda }_n^{\left(1\right)}(p,q)=-{\displaystyle \frac{n!\left({(-1)}^n{\left(p\right)}_{n+1}+{\left(q\right)}_{n+1}\right)}{\mathrm{B}(1-p,1-q){(p+q)}_{n+1}{(p+1)}_n}},\hfill \\ {\lambda }_n^{\left(2\right)}(p,q)=-{(-1)}^n{\displaystyle \frac{{(q+1)}_n}{{(p+1)}_n}},\hfill \end{array}$$

and

$${\lambda }_n^{\left(3\right)}(p,q)={\displaystyle \frac{{(-1)}^{n}n!{\left(q\right)}_{n+1}}{{\left(p\right)}_{n+1}\left(n!+{(-1)}^{n}B(-p,-q){(p+q+1)}_n\right)}}.$$

However, as we pointed out, there are also other orthogonal sequences that are different from the above-mentioned general form. We consider one case here.

(iv) 

Fourth subsequence. If $\left(A,B,c,d,e\right)=\left(A,B,1+p,1+2p,-p\right)$, where $A,B$ are two free parameters, are replaced in (137) as

$$\begin{array}{c}\hfill x(1-x){\Phi }_n^{″}\left(x\right)+(p+1-(2p+2)x){\Phi }_n^{\prime }\left(x\right)+n(n+2p+1){\Phi }_n\left(x\right)\\ \hfill =(n+p)(n+p+1)\left(A{(1-x)}^{-p}+B{x}^{-p}\right),\end{array}$$

(153)

its general solution is

$$\begin{array}{cc}\hfill {\Phi }_n\left(x\right)& =c_1{}_{2}F_1\left(\left.\begin{array}{c}-n,n+2p+1\\ p+1\end{array}\right|x\right)\hfill \\ \hfill & +c_2{x}^{-p}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+1+p\\ 1-p\end{array}\right|x\right)+A{(1-x)}^{-p}+B{x}^{-p}.\hfill \end{array}$$

(154)

As $z\left(x\right)=A{(1-x)}^{-p}+B{x}^{-p}$ in (153), applying (114) to the solution (154) gives

$$\begin{array}{c}{c}_1{\int }_0^1\left(A{x}^p+B{(1-x)}^p\right){}_{2}F_1\left(\left.\begin{array}{c}-n,n+2p+1\\ p+1\end{array}\right|x\right)dx\hfill \\ +c_2{\int }_0^1\left(A+B{x}^{-p}{(1-x)}^p\right){}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+p+1\\ 1-p\end{array}\right|x\right)dx=0.\hfill \end{array}$$

(155)

Since, in (155),

$${\int }_0^1\left(A{x}^p+B{(1-x)}^p\right){}_{2}F_1\left(\left.\begin{array}{c}-n,n+2p+1\\ p+1\end{array}\right|x\right)dx=\left({(-1)}^{n}A+B\right){\displaystyle \frac{p}{(n+p)(n+p+1)}},$$

and

$$\begin{array}{c}{\int }_0^1\left(A+B{x}^{-p}{(1-x)}^p\right){}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+p+1\\ 1-p\end{array}\right|x\right)dx\hfill \\ ={\displaystyle \frac{p}{(n+p)(n+p+1)}}\left(-A\left(1+{\displaystyle \frac{{(-1)}^{n}pB(-p,-q){(2p+1)}_n}{n!}}\right)+{(-1)}^{n}B\right),\hfill \end{array}$$

the fourth subsequence appears as

$$\begin{array}{c}{G}_n^{\left(4\right)}(x;p)={}_{2}F_1\left(\left.\begin{array}{c}-n,n+2p+1\\ p+1\end{array}\right|x\right)\hfill \\ +{\displaystyle \frac{\left({(-1)}^{n}A+B\right)x^{-p}}{\left({(-1)}^n+\frac{p}{n!}B(-p,-p){(2p+1)}_n\right)A-B}}{}_{2}F_1\left(\left.\begin{array}{c}-n-p,n+p+1\\ 1-p\end{array}\right|x\right),\hfill \end{array}$$

(156)

which is orthogonal with respect to the weight function $w(x;p)=x^p{(1-x)}^p$ on $[0,1]$ for $-1<p<0$.

Second Sequence

Noting the confluent hypergeometric Equation (129), this time, we consider the differential equation

$$x{\Phi }_n^{″}\left(x\right)+(c-x){\Phi }_n^{\prime }\left(x\right)+n{\Phi }_n\left(x\right)=x{z}^{″}\left(x\right)+(c-x)z^{\prime }\left(x\right)+nz\left(x\right),$$

(157)

with the general solution

$${\Phi }_n\left(x\right)=b_1{}_{1}F_1\left(\left.\begin{array}{c}-n\\ c\end{array}\right|x\right)+b_2{x}^{1-c}{}_{1}F_1\left(\left.\begin{array}{c}-n+1-c\\ 2-c\end{array}\right|x\right)+z\left(x\right).$$

(158)

For a known parameter e, assume in (157) that

$$x{z}^{″}\left(x\right)+(c-x)z^{\prime }\left(x\right)=-ez\left(x\right),$$

(159)

having a general solution, according to (129) and (130), as

$$z\left(x\right)=z\left(x;A^{*},B^{*},c,e\right)=A^{*}{}_{1}F_1\left(\left.\begin{array}{c}-e\\ c\end{array}\right|x\right)+B^{*}{x}^{1-c}{}_{1}F_1\left(\left.\begin{array}{c}-e+1-c\\ 2-c\end{array}\right|x\right),$$

(160)

in which $A^{*},B^{*}$ are free parameters. Consequently, from (157) to (160), we can conclude that the general solution of the equation

$$\begin{array}{c}x{\Phi }_n^{″}\left(x\right)+(c-x){\Phi }_n^{\prime }\left(x\right)+n{\Phi }_n\left(x\right)\hfill \\ \hfill =\left(n-e\right)\left(A^{*}{}_{1}F_1\left(\left.\begin{array}{c}-e\\ c\end{array}\right|x\right)+B^{*}{x}^{1-c}{}_{1}F_1\left(\left.\begin{array}{c}-e+1-c\\ 2-c\end{array}\right|x\right)\right),\end{array}$$

(161)

is

$$\begin{array}{c}{\Phi }_n\left(x\right)=b_1{}_{1}F_1\left(\left.\begin{array}{c}-n\\ c\end{array}\right|x\right)+b_2{x}^{1-c}{}_{1}F_1\left(\left.\begin{array}{c}-n+1-c\\ 2-c\end{array}\right|x\right)\hfill \\ +A^{*}{}_{1}F_1\left(\left.\begin{array}{c}-e\\ c\end{array}\right|x\right)+B^{*}{x}^{1-c}{}_{1}F_1\left(\left.\begin{array}{c}-e+1-c\\ 2-c\end{array}\right|x\right).\end{array}$$

(162)

Note that (162) is also the general solution of the fourth-order equation

$$\begin{array}{cc}\hfill & x{\left(x{\Phi }_n^{″}\left(x\right)+(c-x){\Phi }_n^{\prime }\left(x\right)+n{\Phi }_n\left(x\right)\right)}^{″}+(c-x){\left(x{\Phi }_n^{″}\left(x\right)+(c-x){\Phi }_n^{\prime }\left(x\right)+n{\Phi }_n\left(x\right)\right)}^{\prime }\hfill \\ \hfill & +e\left(x{\Phi }_n^{″}\left(x\right)+(c-x){\Phi }_n^{\prime }\left(x\right)+n{\Phi }_n\left(x\right)\right)=0.\hfill \end{array}$$

Similar to the preceding First Sequence Section, there are various subcases for the sequence (162). Here, we consider one case. For the given parameters $p\in \mathbb{R}$, if

$$\left(A^{*},B^{*},c,e\right)=\left(0,1,1+p,-p\right),$$

are replaced in (161) as

$$x{\Phi }_n^{″}\left(x\right)+(p+1-x){\Phi }_n^{\prime }\left(x\right)+n{\Phi }_n\left(x\right)=(n+p)x^{-p},$$

(163)

then its general solution reads as

$${\Phi }_n(x;p)=b_1{}_{1}F_1\left(\left.\begin{array}{c}-n\\ p+1\end{array}\right|x\right)+b_2{x}^{-p}{}_{1}F_1\left(\left.\begin{array}{c}-n-p\\ 1-p\end{array}\right|x\right)+x^{-p}.$$

(164)

As the weight function corresponding to the self adjoint form of Equation (163) is $w(x;p)=x^p{e}^{-x}$ defined on $[0,\infty )$ and $z\left(x\right)=x^{-p}$, applying the condition (114) on the solution (164) gives

$$b_1{\int }_0^{\infty }{e}^{-x}{}_{1}F_1\left(\left.\begin{array}{c}-n\\ p+1\end{array}\right|x\right)dx+b_2{\int }_0^{\infty }{x}^{-p}{e}^{-x}{}_{1}F_1\left(\left.\begin{array}{c}-n-p\\ 1-p\end{array}\right|x\right)dx=0.$$

(165)

But since in (165),

$${\int }_0^{\infty }{x}^{-p}{e}^{-x}{}_{1}F_1\left(\left.\begin{array}{c}-n-p\\ 1-p\end{array}\right|x\right)dx=\Gamma (1-p){\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n-p)}_k}{k!}}=0,$$

and

$$\begin{array}{c}{\int }_0^{\infty }{e}^{-x}{}_{1}F_1\left(\left.\begin{array}{c}-n\\ p+1\end{array}\right|x\right)dx={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{\left(1\right)}_k}{{(p+1)}_{k}k!}}={}_{2}F_1\left(\left.\begin{array}{c}-n,1\\ p+1\end{array}\right|1\right)={\displaystyle \frac{p}{p+n}}\ne 0\hfill \\ \hfill \mathrm{for}p\ne 0,\end{array}$$

choosing $b_1=0$ in (164) eventually yields

$$G_n(x;p)=x^{-p}{}_{1}F_1\left(\left.\begin{array}{c}-n-p\\ 1-p\end{array}\right|x\right),$$

which is orthogonal with respect to the weight $x^p{e}^{-x}$ on $[0,\infty )$ if and only if $p\in (-1,1)$. Let us prove this latter result via its differential equation, too. If equation (163) is written in the self-adjoint form

$${\left(x^{p+1}{e}^{-x}{\Phi }_n^{\prime }\left(x\right)\right)}^{\prime }+n{x}^p{e}^{-x}{\Phi }_n\left(x\right)=(n+p)e^{-x},$$

and for the index m as

$${\left(x^{p+1}{e}^{-x}{\Phi }_m^{\prime }\left(x\right)\right)}^{\prime }+m{x}^p{e}^{-x}{\Phi }_m\left(x\right)=(m+p)e^{-x},$$

we get

$$\begin{array}{c}{\left[x^{p+1}{e}^{-x}\left({\Phi }_m\left(x\right){\Phi }_n^{\prime }\left(x\right)-{\Phi }_n\left(x\right){\Phi }_m^{\prime }\left(x\right)\right)\right]}_0^{\infty }+\left(n-m\right){\int }_0^{\infty }{x}^p{e}^{-x}{\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx\hfill \\ =\left(n+p\right){\int }_0^{\infty }{e}^{-x}{\Phi }_m\left(x\right)dx-\left(m+p\right){\int }_0^{\infty }{e}^{-x}{\Phi }_n\left(x\right)dx=\left(n-m\right)\Gamma (1-p),\hfill \end{array}$$

which results in

$$\begin{array}{c}\left(n-m\right)\left({\int }_0^{\infty }{x}^p{e}^{-x}{\Phi }_n\left(x\right){\Phi }_m\left(x\right)dx-\Gamma (1-p)\right)\hfill \\ =-{\left[x^{p+1}{e}^{-x}\left({\Phi }_m\left(x\right){\Phi }_n^{\prime }\left(x\right)-{\Phi }_n\left(x\right){\Phi }_m^{\prime }\left(x\right)\right)\right]}_0^{\infty }=0\iff n\ne m,-1<p<1.\hfill \end{array}$$

Finally, since

$${\int }_0^{\infty }{x}^p{e}^{-x}{G}_n(x;p)G_m(x;p)dx={\int }_0^{\infty }{x}^{-p}{e}^{-x}{}_{1}F_1\left(\left.\begin{array}{c}-n-p\\ 1-p\end{array}\right|x\right){}_{1}F_1\left(\left.\begin{array}{c}-m-p\\ 1-p\end{array}\right|x\right)dx,$$

the simplified sequence $G_n^{*}(x;p)={}_{1}F_1\left(\left.\begin{array}{c}-n+p\\ 1+p\end{array}\right|x\right)$ is orthogonal with respect to the weight function $x^p{e}^{-x}$ on $[0,\infty )$ if $-1<p<1$.

7. p-Uncorrelated Polynomials Sequence (p-UPS)

As the most important part of p-uncorrelated functions is the class of p-uncorrelated polynomials, we prefer to study them in a separate section and consider their monic form ( i.e., with leading coefficient equal to 1generality) in a continuous space. With reference to Theorem 2 (or representation (43)) and using the initial monomial data ${\{V_k=x^k\}}_{k=0}^n$, a monic type of p-UPS with respect to $z\left(x\right)$, say ${\overline{P}}_n\left(x,p;z\left(x\right)\right)$, can be generated, so that

$${\mathrm{cov}}_p\left({\overline{P}}_n\left(x,p;z\left(x\right)\right),{\overline{P}}_m\left(x,p;z\left(x\right)\right);z\left(x\right)\right)=0\iff n\ne m.$$

(166)

In a weighted continuous space, the condition (166) is equivalent to

$$\begin{array}{c}{\int }_a^{b}w\left(x\right){\overline{P}}_n\left(x,p;z\left(x\right)\right){\overline{P}}_m\left(x,p;z\left(x\right)\right)dx\hfill \\ -p{\displaystyle \frac{{\int }_a^{b}w\left(x\right)z\left(x\right){\overline{P}}_n\left(x,p;z\left(x\right)\right)dx{\int }_a^{b}w\left(x\right)z\left(x\right){\overline{P}}_m\left(x,p;z\left(x\right)\right)dx}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}}\\ \hfill =\left({\int }_a^{b}w\left(x\right){\overline{P}}_n^2\left(x,p;z\left(x\right)\right)dx-p{\displaystyle \frac{{\left({\int }_a^{b}w\left(x\right)z\left(x\right){\overline{P}}_n\left(x,p;z\left(x\right)\right)dx\right)}^2}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}}\right){\delta }_{n,m},\end{array}$$

(167)

where $w\left(x\right)>0$ and $z\left(x\right)$ are two continuous functions, such that ${\int }_a^{b}w\left(x\right)z^2\left(x\right)dx>0$.

The existence of relation (167) is when the integrals ${\int }_a^{b}w\left(x\right)x^{n}z\left(x\right)dx$ all exist and are bounded for every $n=0,1,\dots$. In this section, we deal with such spaces of type (167) as the role of $z\left(x\right)$ would be undeniable. Let us recall that a hypergeometric polynomial as a particular case of the generalized hypergeometric series

$${}_{p}F_q\left(\left.\begin{array}{c}{a}_1,\dots ,a_p\\ b_1,\dots ,b_q\end{array}\right|x\right)={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\left(a_1\right)}_k\dots {\left(a_p\right)}_k}{{\left(b_1\right)}_k\dots {\left(b_q\right)}_k}}{\displaystyle \frac{x^k}{k!}},$$

where $b_1,\dots ,b_q\ne 0,-1,-2,\dots$ and ${\left(a\right)}_k=a(a+1)\dots (a+k-1)$, appears when one of the values ${\left\{a_k\right\}}_{k=1}^p$ is a negative integer. Also, we recall that the aforesaid series is convergent for all x if $p<q+1$, convergent for $x\in (-1,1)$ if $p=q+1$, and it is divergent for all $x\ne 0$ if $p>q+1$, while, if one of ${\left\{a_k\right\}}_{k=1}^p$ is a negative integer, it will reduce to a hypergeometric polynomial that is convergent for all real x.

Theorem 11.

Let $\left\{{\overline{P}}_n(x,p;z\left(x\right))\right\}$ be a monic p-UPS with respect to the fixed function $z\left(x\right)$, and let ${\overline{Q}}_m\left(x\right)$ be an arbitrary monic polynomial of degree $m\le n$. Then,

$${\mathrm{cov}}_p\left({\overline{Q}}_m\left(x\right),{\overline{P}}_n(x,p;z\left(x\right));z\left(x\right)\right)={\mathrm{var}}_p\left({\overline{P}}_n(x,p;z\left(x\right));z\left(x\right)\right){\delta }_{m,n}.$$

Proof. 

Since ${\overline{P}}_n\left(x,p;z\left(x\right)\right)$ is a p-UPS, its elements are linearly independent according to Theorem 1. Hence, ${\left\{{\overline{P}}_k(x,p;z\left(x\right))\right\}}_{k=0}^m$ is a basis for all polynomials of degree at most m and, for any arbitrary monic polynomial of degree m, say ${\overline{Q}}_m\left(x\right)$, there exist constants $\left\{b_k\right\}$, such that

$${\overline{Q}}_m\left(x\right)={\displaystyle \sum _{k=0}^m}{b}_k{\overline{P}}_k(x,p;z\left(x\right))\mathrm{with}{b}_m=1.$$

By the linearity of p-covariances with respect to $z\left(x\right)$ and using (166), we get

$$\begin{array}{cc}\hfill {\mathrm{cov}}_p\left({\overline{Q}}_m\left(x\right),{\overline{P}}_n(x,p;z\left(x\right));z\left(x\right)\right)& ={\displaystyle \sum _{k=0}^m}{b}_k{\mathrm{cov}}_p\left({\overline{P}}_k(x,p;z\left(x\right)),{\overline{P}}_n(x,p;z\left(x\right));z\left(x\right)\right)\hfill \\ \hfill & =\left\{\begin{array}{c}0\mathrm{if}m<n,\hfill \\ {\mathrm{var}}_p\left({\overline{P}}_n(x,p;z\left(x\right));z\left(x\right)\right)\mathrm{if}m=n.\hfill \end{array}\right.\hspace{1em}\square \hfill \end{array}$$

(168)

For the monomial basis ${\left\{V_k=x^k\right\}}_{k=0}^n$, the elements of the main determinant (40), i.e.,

$${\Delta }_n^{\left(p\right)}\left({\left\{x^k\right\}}_{k=0}^n;z\left(x\right)\right)=\left|\begin{array}{cccc}\begin{array}{c}{\mathrm{var}}_p(1;z\left(x\right))\\ {\mathrm{cov}}_p(x,1;z\left(x\right))\\ ⋮\\ {\mathrm{cov}}_p(x^n,1;z\left(x\right))\end{array}& \begin{array}{c}{\mathrm{cov}}_p(1,x;z\left(x\right))\\ {\mathrm{var}}_p(x;z\left(x\right))\\ ⋮\\ {\mathrm{cov}}_p(x^n,x;z\left(x\right))\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}{\mathrm{cov}}_p(1,x^n;z\left(x\right))\\ {\mathrm{cov}}_p(x,x^n;z\left(x\right))\\ ⋮\\ {\mathrm{var}}_p(x^n;z\left(x\right))\end{array}\end{array}\right|,$$

(169)

can be expressed in terms of a special case of moments that are related to $z\left(x\right)$ directly. In other words, if we define

$${\mu }_n\left(z\left(x\right)\right)=\left({\int }_a^{b}w\left(x\right)dx\right)E\left(x^{n}z\left(x\right)\right)={\int }_a^{b}w\left(x\right)x^{n}z\left(x\right)dx,$$

(170)

then the entries of (169) can be represented in terms of definition (170) as follows

$${\mathrm{cov}}_p\left(x^i,x^j;z\left(x\right)\right)={\displaystyle \frac{{\mu }_{i+j}\left(1\right)}{{\mu }_0\left(1\right)}}-p{\displaystyle \frac{{\mu }_i\left(z\left(x\right)\right){\mu }_j\left(z\left(x\right)\right)}{{\mu }_0\left(1\right){\mu }_0\left(z^2\left(x\right)\right)}}.$$

Theorem 12.

A necessary condition for the existence of a monic p-UPS with respect to the function $z\left(x\right)$ is that ${\Delta }_n^{\left(p\right)}\left({\left\{x^k\right\}}_{k=0}^n;z\left(x\right)\right)\ne 0$.

Proof. 

Suppose ${\overline{P}}_n(x,p;z\left(x\right))={\displaystyle \sum _{k=0}^n}{c}_k^{\left(n\right)}\left(p\right)x^k$ is a monic p-UPS with $c_n^{\left(n\right)}\left(p\right)=1$. Referring to (168), for $m\le n$ and ${\overline{Q}}_m\left(x\right)=x^m$, we observe that the relations

$${\mathrm{cov}}_p\left(x^m,{\overline{P}}_n(x,p;z\left(x\right));z\left(x\right)\right)={\displaystyle \sum _{k=0}^n}{c}_k^{\left(n\right)}\left(p\right){\mathrm{cov}}_p\left(x^m,x^k;z\left(x\right)\right)={\mathrm{var}}_p\left({\overline{P}}_n(x,p;z\left(x\right));z\left(x\right)\right){\delta }_{m,n},$$

will at last lead to the following solvable linear system:

$$\begin{array}{cc}\hfill & \left[\begin{array}{cccc}\begin{array}{c}{\mathrm{var}}_p(1;z\left(x\right))\\ {\mathrm{cov}}_p(x,1;z\left(x\right))\\ ⋮\\ {\mathrm{cov}}_p(x^n,1;z\left(x\right))\end{array}& \begin{array}{c}{\mathrm{cov}}_p(1,x;z\left(x\right))\\ {\mathrm{var}}_p(x;z\left(x\right))\\ ⋮\\ {\mathrm{cov}}_p(x^n,x;z\left(x\right))\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}{\mathrm{cov}}_p(1,x^n;z\left(x\right))\\ {\mathrm{cov}}_p(x,x^n;z\left(x\right))\\ ⋮\\ {\mathrm{var}}_p(x^n;z\left(x\right))\end{array}\end{array}\right]\left[\begin{array}{c}{c}_0^{\left(n\right)}\left(p\right)\\ c_1^{\left(n\right)}\left(p\right)\\ ⋮\\ c_n^{\left(n\right)}\left(p\right)\end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{c}0\\ 0\\ ⋮\\ {\mathrm{var}}_p\left({\overline{P}}_n(x,p;z\left(x\right));z\left(x\right)\right)\end{array}\right],\hfill \end{array}$$

which obviously implies that ${\Delta }_n^{\left(p\right)}\left({\left\{x^k\right\}}_{k=0}^n;z\left(x\right)\right)\ne 0$. □

One of the consequences of solving the above system is that

$${\mathrm{var}}_p\left({\overline{P}}_n(x,p;z\left(x\right));z\left(x\right)\right)={\displaystyle \frac{{\Delta }_n^{\left(p\right)}\left({\left\{x^k\right\}}_{k=0}^n;z\left(x\right)\right)}{{\Delta }_{n-1}^{\left(p\right)}\left({\left\{x^k\right\}}_{k=0}^n;z\left(x\right)\right)}}(n\ge 1),$$

(171)

which is valid for $n=0$ if we set ${\Delta }_{-1}^{\left(p\right)}(.)=1$.

Another consequence is a general representation for the non-monic case of uncorrelated polynomials as

$$P_n\left(x,p;z\left(x\right)\right)=\left|\begin{array}{cccc}{\mathrm{var}}_p(1;z\left(x\right))& {\mathrm{cov}}_p(1,x;z\left(x\right))& \cdots & {\mathrm{cov}}_p(1,x^n;z\left(x\right))\\ {\mathrm{cov}}_p(x,1;z\left(x\right))& {\mathrm{var}}_p(x;z\left(x\right))& \cdots & {\mathrm{cov}}_p(x,x^n;z\left(x\right))\\ ⋮& ⋮& ⋮& ⋮\\ {\mathrm{cov}}_p(x^{n-1},1;z\left(x\right))& {\mathrm{cov}}_p(x^{n-1},x;z\left(x\right))& \cdots & {\mathrm{cov}}_p(x^{n-1},x^n;z\left(x\right))\\ 1& x& \cdots & x^n\end{array}\right|$$

(172)

Remark 5.

For $p=1$ and $z\left(x\right)=x^{\lambda }$, since

$${\mathrm{cov}}_1(x^i,x^j;x^{\lambda })=0\iff \lambda =i\mathrm{or}\lambda =j,$$

the rows of determinant (172) show that $z\left(x\right)$ should conditionally be chosen as a member of the monomial basis ${\left\{x^k\right\}}_{k=0}$. For example, if $\lambda =5$, the finite polynomial set ${\left\{P_n(x,1;x^5)\right\}}_{n=0}^5$ is finitely 1-uncorrelated with respect to $z\left(x\right)=x^5$. The determinant (172) also shows that for the monic type of the polynomials we always have ${\overline{P}}_n(x,1;x^n)=x^n$, e.g., ${\overline{P}}_5(x,1;x^5)=x^5$.

Theorem 13.

Let $\left\{P_n(x,p;z\left(x\right))\right\}$ be a (weighted) p-UPS with respect to the function $z\left(x\right)$. For any arbitrary polynomial $Q_n\left(x\right)={\displaystyle \sum _{k=0}^n}{q}_k{x}^k$ of degree n, we have

$$\begin{array}{cc}\hfill {\mathrm{cov}}_p\left(Q_n\left(x\right),P_n\left(x,p;z\left(x\right)\right);z\left(x\right)\right)& =q_n{\mathrm{cov}}_p\left(x^n,P_n\left(x,p;z\left(x\right)\right);z\left(x\right)\right)\hfill \\ \hfill & =q_n{c}_n^{\left(n\right)}\left(p\right){\displaystyle \frac{{\Delta }_n^{\left(p\right)}\left({\left\{x^k\right\}}_{k=0}^n;z\left(x\right)\right)}{{\Delta }_{n-1}^{\left(p\right)}\left({\left\{x^k\right\}}_{k=0}^n;z\left(x\right)\right)}},\hfill \end{array}$$

where $c_n^{\left(n\right)}\left(p\right)$ denotes the leading coefficient of $P_n(x,p;z\left(x\right))$.

Proof. 

Suppose $Q_n\left(x\right)=q_n{x}^n+Q_{n-1}^{*}\left(x\right)$, in which $Q_{n-1}^{*}\left(x\right)$ is a polynomial of degree at most $n-1$. In this case,

$$\begin{array}{cc}\hfill & {\mathrm{cov}}_p\left(Q_n\left(x\right),P_n\left(x,p;z\left(x\right)\right);z\left(x\right)\right)=q_n{\mathrm{cov}}_p\left(x^n,P_n\left(x,p;z\left(x\right)\right);z\left(x\right)\right)\hfill \\ \hfill & +{\mathrm{cov}}_p\left(Q_{n-1}^{*}\left(x\right),P_n\left(x,p;z\left(x\right)\right);z\left(x\right)\right)=q_n{\mathrm{cov}}_p\left(x^n,P_n\left(x,p;z\left(x\right)\right);z\left(x\right)\right),\hfill \end{array}$$

and the proof is completed by noting (171) and Theorem 12. □

7.1. A Generic Recurrence Relation for p-UPS

Let ${\overline{Q}}_m\left(x\right)$ be an arbitrary monic polynomial of degree m, and let $\left\{{\overline{P}}_n(x,p;z\left(x\right))\right\}$ be a monic p-UPS with respect to the function $z\left(x\right)$. According to Theorem 11 and relation (168), we have

$${\overline{Q}}_m\left(x\right)={\displaystyle \sum _{k=0}^m}{\displaystyle \frac{{\mathrm{cov}}_p\left({\overline{Q}}_m\left(x\right),{\overline{P}}_k(x,p;z\left(x\right));z\left(x\right)\right)}{{\mathrm{var}}_p\left({\overline{P}}_k(x,p;z\left(x\right));z\left(x\right)\right)}}{\overline{P}}_k(x,p;z\left(x\right)).$$

(173)

Now, replacing $m=n+1$ and ${\overline{Q}}_{n+1}\left(x\right)=x{\overline{P}}_n\left(x,p;z\left(x\right)\right)$ in (173) as

$$x{\overline{P}}_n(x,p;z\left(x\right))={\displaystyle \sum _{k=0}^{n+1}}{\displaystyle \frac{{\mathrm{cov}}_p\left(x{\overline{P}}_n(x,p;z\left(x\right)),{\overline{P}}_k(x,p;z\left(x\right));z\left(x\right)\right)}{{\mathrm{var}}_p\left({\overline{P}}_k(x,p;z\left(x\right));z\left(x\right)\right)}}{\overline{P}}_k(x,p;z\left(x\right)),$$

(174)

gives a $n+2$ term recurrence relation for the sequence $\left\{{\overline{P}}_n(x,p;z\left(x\right))\right\}$.

In general, since

$$\begin{array}{c}{\mathrm{cov}}_p\left(f\left(x\right)h\left(x\right),g\left(x\right);z\left(x\right)\right)={\mathrm{cov}}_p\left(f\left(x\right),h\left(x\right)g\left(x\right);z\left(x\right)\right)\hfill \\ \hfill +p{\displaystyle \frac{E\left(f\left(x\right)z\left(x\right)\right)E\left(h\left(x\right)g\left(x\right)z\left(x\right)\right)-E\left(g\left(x\right)z\left(x\right)\right)E\left(f\left(x\right)h\left(x\right)z\left(x\right)\right)}{E\left(z^2\left(x\right)\right)}},\end{array}$$

the coefficients of (174) can be changed in the form

$$\begin{array}{cc}\hfill & {\mathrm{cov}}_p\left(x{\overline{P}}_n(x,p;z\left(x\right)),{\overline{P}}_k(x,p;z\left(x\right));z\left(x\right)\right)={\mathrm{cov}}_p\left({\overline{P}}_n(x,p;z\left(x\right)),x{\overline{P}}_k(x,p;z\left(x\right));z\left(x\right)\right)\hfill \\ \hfill & +p{\displaystyle \frac{E\left(x{\overline{P}}_k(x,p;z\left(x\right))z\left(x\right)\right)E\left({\overline{P}}_n(x,p;z\left(x\right))z\left(x\right)\right)-E\left(x{\overline{P}}_n(x,p;z\left(x\right))z\left(x\right)\right)E\left({\overline{P}}_k(x,p;z\left(x\right))z\left(x\right)\right)}{E\left(z^2\left(x\right)\right)}}.\hfill \end{array}$$

Note in the above formula that

$${\mathrm{cov}}_p\left({\overline{P}}_n(x,p;z\left(x\right)),x{\overline{P}}_k(x,p;z\left(x\right));z\left(x\right)\right)=0\iff k+1<n.$$

Accordingly, if $p=0$ or $E\left(z\left(x\right){\overline{P}}_k(x,p;z\left(x\right))\right)=0$ in (174), it will reduce to the same as celebrated three term recurrence relation of monic orthogonal polynomials [25]. See also relations (201) and (202) in this regard.

7.2. A Complete Uncorrelated Sequence of Hypergeometric Polynomials of ${}_{4}F_3$ Type

In this section, we introduce a complete uncorrelated hypergeometric polynomial that reveals the importance of the role of a non-constant fixed function. Let $w\left(x\right)=1$ be defined on $[0,1]$ and $z\left(x\right)=x^r$ for $r>-1/2$ as ${\int }_0^{1}w\left(x\right)z^2\left(x\right)dx={\displaystyle \frac{1}{2r+1}}$. Then, the components of determinant (172) are explicitly computed as

$$\begin{array}{c}{\mathrm{cov}}_p\left(x^i,x^j;x^r\right)={\displaystyle \frac{(r+i+1)(r+j+1)-p(2r+1)(i+j+1)}{(r+i+1)(r+j+1)(i+j+1)}}\hfill \\ \hfill \mathrm{for}i=0,1,\dots ,n-1\mathrm{and}j=0,1,\dots ,n.\end{array}$$

(175)

A few samples of the monic type of the corresponding p-uncorrelated polynomials are

$$\begin{array}{cc}\hfill {\overline{P}}_0(x,p;x^r)& =1,\hfill \\ \hfill {\overline{P}}_1(x,p;x^r)& =x-{\displaystyle \frac{r+1}{2(r+2)}}{\displaystyle \frac{(r+1)(r+2)-2p(2r+1)}{{(r+1)}^2-p(2r+1)}},\hfill \\ \hfill {\overline{P}}_2(x,p;x^r)& =x^2-{\displaystyle \frac{r+2}{r+3}}{\displaystyle \frac{{(r+1)}^2(r+2)(r+3)-p(2r+1)(5r^2+5r+6)}{{(r+1)}^2{(r+2)}^2-4p(2r+1)(r^2+r+1)}}x\hfill \\ \hfill & +{\displaystyle \frac{r+1}{6(r+3)}}{\displaystyle \frac{(r+1){(r+2)}^2(r+3)-6p(2r+1)(r^2+r+2)}{{(r+1)}^2{(r+2)}^2-4p(2r+1)(r^2+r+1)}},\hfill \end{array}$$

satisfying the uncorrelatedness condition

$${\int }_0^1{\overline{P}}_n(x,p;x^r){\overline{P}}_m(x,p;x^r)dx=p(2r+1){\int }_0^1{x}^r{\overline{P}}_n(x,p;x^r)dx{\int }_0^1{x}^r{\overline{P}}_m(x,p;x^r)dx\iff n\ne m.$$

For $p=0$, the above samples are in fact the monic type of the well-known shifted Legendre polynomials $P_n(x,0;x^r)=P_{n,+}\left(x\right)={}_{2}F_1\left(\left.\begin{array}{c}-n,n+1\\ 1\end{array}\right|x\right)$, having the orthogonal property [25] ${\int }_0^1{P}_{n,+}\left(x\right)P_{m,+}\left(x\right)dx={\displaystyle \frac{1}{2n+1}}{\delta }_{n,m},$ while, for the optimized case $p=1$, relation (175) is first simplified as

$$\begin{array}{c}{\mathrm{cov}}_1\left(x^i,x^j;x^r\right)={\displaystyle \frac{(r-i)(r-j)}{(r+i+1)(r+j+1)(i+j+1)}}\hfill \\ \hfill \mathrm{for}i=0,1,\dots ,n-1\mathrm{and}j=0,1,\dots ,n.\end{array}$$

(176)

If (176) is directly substituted into (172), with the aid of advanced mathematical software, see, e.g., [26,27], we can eventually find the explicit form of the polynomials as

$$P_n(x,1;x^r)={}_{4}F_3\left(\left.\begin{array}{c}-n,n+1,-r,r+2\\ 1,-r+1,r+1\end{array}\right|x\right),$$

(177)

satisfying the complete uncorrelatedness condition

$$\begin{array}{c}{\int }_0^1{P}_n(x,1;x^r)P_m(x,1;x^r)dx-(2r+1){\int }_0^1{x}^r{P}_n(x,1;x^r)dx{\int }_0^1{x}^r{P}_m(x,1;x^r)dx\hfill \\ \hfill =\left({\int }_0^1{P}_n^2(x,1;x^r)dx-(2r+1){\left({\int }_0^1{x}^r{P}_n(x,1;x^r)dx\right)}^2\right){\delta }_{m,n},\end{array}$$

(178)

where

$$\begin{array}{cc}\hfill {\int }_0^1{x}^r{P}_n(x,1;x^r)dx& ={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+1)}_k{(-r)}_k{(r+2)}_k}{{\left(1\right)}_k{(-r+1)}_k{(r+1)}_{k}k!(r+1+k)}}\hfill \\ \hfill & ={\displaystyle \frac{1}{r+1}}{}_{2}F_3\left(\left.\begin{array}{c}-n,n+1,-r\\ 1,-r+1\end{array}\right|1\right)={\displaystyle \frac{1}{r+1}}{\displaystyle \frac{{(1+r)}_n}{{(1-r)}_n}},\hfill \end{array}$$

(179)

and

$$\begin{array}{c}{\int }_0^1{P}_n(x,1;x^r)P_m(x,1;x^r)dx\hfill \\ \hfill ={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+1)}_k{(-r)}_k{(r+2)}_k}{{\left(2\right)}_k{(-r+1)}_k{(r+1)}_{k}k!}}{}_{5}F_4\left(\left.\begin{array}{c}-m,m+1,-r,r+2,k+1\\ 1,-r+1,r+1,k+2\end{array}\right|1\right),\end{array}$$

which simplifies the left side of (178) as

$$\begin{array}{cc}\hfill & {\int }_0^1{P}_n(x,1;x^r)P_m(x,1;x^r)dx-(2r+1){\int }_0^1{x}^r{P}_n(x,1;x^r)dx{\int }_0^1{x}^r{P}_m(x,1;x^r)dx\hfill \\ \hfill & ={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+1)}_k{(-r)}_k{(r+2)}_k}{{\left(2\right)}_k{(-r+1)}_k{(r+1)}_{k}k!}}{}_{5}F_4\left(\left.\begin{array}{c}-m,m+1,-r,r+2,k+1\\ 1,-r+1,r+1,k+2\end{array}\right|1\right)\hfill \\ \hfill & -{\displaystyle \frac{2r+1}{{(r+1)}^2}}{\displaystyle \frac{{(1+r)}_n{(1+r)}_m}{{(1-r)}_n{(1-r)}_m}}.\hfill \end{array}$$

(180)

Of course, the result of (179) has been derived using the following technique. Since

$$H\left(n\right)={}_{3}F_2\left(\left.\begin{array}{c}-n,n+1,-r\\ 1,-r+1\end{array}\right|1\right),$$

satisfies the first order recurrence equation

$$H(n+1)={\displaystyle \frac{n+1+r}{n+1-r}}H\left(n\right),$$

so

$${}_{3}F_2\left(\left.\begin{array}{c}-n,n+1,-r\\ 1,-r+1\end{array}\right|1\right)={\displaystyle \frac{{(1+r)}_n}{{(1-r)}_n}}.$$

This technique can similarly be used to obtain ${}_{5}F_4(.)$ in (180). First, we can find out that the sequence

$$S\left(m\right)={}_{5}F_4\left(\left.\begin{array}{c}-m,m+1,-r,r+2,k+1\\ 1,-r+1,r+1,k+2\end{array}\right|1\right),$$

satisfies the second-order recurrence equation

$$\begin{array}{c}(m+1)(m+2-r)(m+3+k)S(m+2)\hfill \\ \hfill -(2m+3)\left((m+1)(m+2)+r(k+1)\right)S(m+1)+(m+2)(m+1+r)(m-k)S\left(m\right)=0,\end{array}$$

having two independent solutions

$$S_1\left(m\right)={\displaystyle \frac{(m+r){\left(r\right)}_m}{(m-r){(-r)}_m}}\mathrm{and}{S}_2\left(m\right)={\displaystyle \frac{{(-k)}_m}{(k+m+1)(k+m){\left(k\right)}_m}}.$$

It is clear that

$$S\left(m\right)=A{S}_1\left(m\right)+B{S}_2\left(m\right).$$

(181)

To compute the unknown coefficients A and B, it is sufficient to replace $m=0,1$, respectively, in (181) to finally get

$$\begin{array}{c}{}_{5}F_4\left(\left.\begin{array}{c}-m,m+1,-r,r+2,k+1\\ 1,-r+1,r+1,k+2\end{array}\right|1\right)\hfill \\ \hfill =-{\displaystyle \frac{k+1}{(k+r+1)(r+1)}}\left({\displaystyle \frac{(2r+1)(m+r){\left(r\right)}_m}{(m-r){(-r)}_m}}+{\displaystyle \frac{rk(k-r){(-k)}_m}{(k+m+1)(k+m){\left(k\right)}_m}}\right).\end{array}$$

(182)

Thus, in order to compute

$${\mathrm{var}}_1\left(P_n(x,1;x^r);x^r\right)={\int }_0^1{P}_n^2(x,1;x^r)dx-(2r+1){\left({\int }_0^1{x}^r{P}_n(x,1;x^r)dx\right)}^2,$$

we first suppose in (180) that $m=n$ and then refer to (182) to arrive at

$$\begin{array}{c}{S}^{*}={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+1)}_k{(-r)}_k{(r+2)}_k}{{\left(2\right)}_k{(-r+1)}_k{(r+1)}_{k}k!}}{}_{5}F_4\left(\left.\begin{array}{c}-n,n+1,-r,r+2,k+1\\ 1,-r+1,r+1,k+2\end{array}\right|1\right)\hfill \\ =-{\displaystyle \frac{(2r+1)(n+r){\left(r\right)}_n}{(r+1)(n-r){(-r)}_n}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+1)}_k{(-r)}_k{(r+2)}_k}{{\left(2\right)}_k{(-r+1)}_k{(r+1)}_{k}k!}}{\displaystyle \frac{k+1}{k+r+1}}\\ \hfill -{\displaystyle \frac{r}{r+1}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+1)}_k{(-r)}_k{(r+2)}_k}{{\left(2\right)}_k{(-r+1)}_k{(r+1)}_{k}k!}}{\displaystyle \frac{k+1}{k+r+1}}{\displaystyle \frac{k(k-r){(-k)}_n}{(k+n+1)(k+n){\left(k\right)}_n}}.\end{array}$$

(183)

Since, in general,

$${\displaystyle \frac{{\left(a\right)}_k}{{(a+1)}_k}}={\displaystyle \frac{a}{a+k}},$$

relation (183) is simplified as

$$\begin{array}{cc}\hfill S^{*}& =-{\displaystyle \frac{(2r+1)(n+r){\left(r\right)}_n}{{(r+1)}^2(n-r){(-r)}_n}}{\displaystyle \frac{{(1+r)}_n}{{(1-r)}_n}}+{\displaystyle \frac{r^2}{{(r+1)}^2(n+1)!}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-k)}_n{(n+1)}_k{(-n)}_k}{{\left(1\right)}_k{(n+2)}_k}}\hfill \\ \hfill & =-{\displaystyle \frac{(2r+1)(n+r){\left(r\right)}_n}{{(r+1)}^2(n-r){(-r)}_n}}{\displaystyle \frac{{(1+r)}_n}{{(1-r)}_n}}+{\displaystyle \frac{r^2}{{(r+1)}^2(n+1)!}}{\displaystyle \frac{n!{(n+1)}_n}{{(n+2)}_n}}.\hfill \end{array}$$

(184)

Noting that ${(-k)}_n=0$ for any $k<n$ in (184), the following final result will be derived.

Corollary 5.

If $r>-1/2$ and $r\notin {\mathbb{Z}}^{+}$, then

$${\int }_0^1{P}_n^2(x,1;x^r)dx-(2r+1){\left({\int }_0^1{x}^r{P}_n(x,1;x^r)dx\right)}^2={\displaystyle \frac{r^2}{{(r+1)}^2}}{\displaystyle \frac{1}{2n+1}}.$$

Moreover, (180) is simplified as

$$\begin{array}{c}{\int }_0^1{P}_n(x,1;x^r)P_m(x,1;x^r)dx-(2r+1){\int }_0^1{x}^r{P}_n(x,1;x^r)dx{\int }_0^1{x}^r{P}_m(x,1;x^r)dx\hfill \\ \hfill ={\displaystyle \frac{r^2}{{(r+1)}^2(m+1)!}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(n+1)}_k{(-n)}_k}{{(m+2)}_k}}{\displaystyle \frac{{(-k)}_m}{k!}}=0\iff m\ne n,\end{array}$$

which means

$${\displaystyle \sum _{k=m}^n}{\displaystyle \frac{{(n+1)}_k{(-n)}_k}{{(m+2)}_k}}{\displaystyle \frac{{(-k)}_m}{k!}}={\displaystyle \frac{(n+1)!}{2n+1}}{\delta }_{n,m}.$$

Remark 6.

It is interesting to know that

$$\underset{r\to \infty }{lim}{P}_n(x,1;x^r)=\underset{r\to \infty }{lim}{}_{4}F_3\left(\left.\begin{array}{c}-n,n+1,-r,r+2\\ 1,-r+1,r+1\end{array}\right|x\right)={}_{2}F_1\left(\left.\begin{array}{c}-n,n+1\\ 1\end{array}\right|x\right)=P_{n,+}\left(x\right),$$

and from Corollary 5, we subsequently conclude that

$$\begin{array}{c}\underset{r\to \infty }{lim}{\displaystyle \frac{r^2}{{(r+1)}^2}}{\displaystyle \frac{1}{2n+1}}=\underset{r\to \infty }{lim}\left({\int }_0^1{P}_n^2(x,1;x^r)dx-(2r+1){\left({\int }_0^1{x}^r{P}_n(x,1;x^r)dx\right)}^2\right)\hfill \\ \hfill ={\int }_0^1\underset{r\to \infty }{lim}{P}_n^2(x,1;x^r)dx-\underset{r\to \infty }{lim}(2r+1){\left({\displaystyle \frac{1}{r+1}}{\displaystyle \frac{{(1+r)}_n}{{(1-r)}_n}}\right)}^2={\int }_0^1{P}_{n,+}^2\left(x\right)dx={\displaystyle \frac{1}{2n+1}}.\end{array}$$

Remark 7.

Instead of $z\left(x\right)=x^r$, if we take $z\left(x\right)={(1-x)}^r$ defined on $[0,1]$, (178) changes to

$$\begin{array}{cc}\hfill & {\int }_0^1{P}_n\left(1-x,1;{(1-x)}^r\right)P_m\left(1-x,1;{(1-x)}^r\right)dx\hfill \\ \hfill & -(2r+1){\int }_0^1{(1-x)}^r{P}_n\left(1-x,1;{(1-x)}^r\right)dx{\int }_0^1{(1-x)}^r{P}_m\left(1-x,1;{(1-x)}^r\right)dx\hfill \\ \hfill & ={\displaystyle \frac{r^2}{{(r+1)}^2}}{\displaystyle \frac{1}{2n+1}}{\delta }_{m,n}.\hfill \end{array}$$

Using Corollary 5, we can now establish an optimized approximation (or expansion as $n\to \infty$) of polynomial type for any expandable function, say $f\left(x\right)$, as follows:

$$f\left(x\right)\cong {\displaystyle \frac{{(r+1)}^2}{r^2}}{\displaystyle \sum _{k=0}^n}(2k+1){\mathrm{cov}}_1\left(f\left(x\right),P_k(x,1;x^r);x^r\right)P_k(x,1;x^r),$$

whose error 1-variance is minimized with respect to the fixed function $z\left(x\right)=x^r$ on $[0,1]$.

Furthermore, if $f\left(x\right)$ is of a polynomial type, the approximate operator in the above relation will change to an equality according to the finite type Theorem 4 and its important consequences in Remark 1. For example, since $P_0(x,1;x^r)=1$, $P_1(x,1;x^r)=-2{\displaystyle \frac{r(r+2)}{r^2-1}}x+1$ and $P_2(x,1;x^r)=6{\displaystyle \frac{r(r+3)}{(r-2)(r+1)}}{x}^2-6{\displaystyle \frac{r(r+2)}{r^2-1}}x+1,$ every arbitrary polynomial of degree 2, say $a{x}^2+bx+c$, can be expanded in terms of the above samples as follows:

$$\begin{array}{c}a{x}^2+bx+c={\displaystyle \frac{{(r+1)}^2}{r^2}}{\mathrm{cov}}_1\left(a{x}^2+bx+c,P_0(x,1;x^r);x^r\right)\hfill \\ +3{\displaystyle \frac{{(r+1)}^2}{r^2}}{\mathrm{cov}}_1\left(a{x}^2+bx+c,P_1(x,1;x^r);x^r\right)\left(-2{\displaystyle \frac{r(r+2)}{r^2-1}}x+1\right)\\ \hfill +5{\displaystyle \frac{{(r+1)}^2}{r^2}}{\mathrm{cov}}_1\left(a{x}^2+bx+c,P_2(x,1;x^r);x^r\right)\left(6{\displaystyle \frac{r(r+3)}{(r-2)(r+1)}}{x}^2-6{\displaystyle \frac{r(r+2)}{r^2-1}}x+1\right),\end{array}$$

where

$$\begin{array}{c}{\mathrm{cov}}_1\left(a{x}^2+bx+c,P_0(x,1;x^r);x^r\right)={\displaystyle \frac{1}{3}}{\displaystyle \frac{r(r-2)}{(r+1)(r+3)}}a+{\displaystyle \frac{1}{2}}{\displaystyle \frac{r(r-1)}{(r+1)(r+2)}}b+{\displaystyle \frac{r^2}{{(r+1)}^2}}c,\hfill \\ \hfill {\mathrm{cov}}_1\left(a{x}^2+bx+c,P_1(x,1;x^r);x^r\right)=-{\displaystyle \frac{1}{6}}{\displaystyle \frac{r(r-2)}{(r+1)(r+3)}}a-{\displaystyle \frac{1}{6}}{\displaystyle \frac{r(r-1)}{(r+1)(r+2)}}b,\end{array}$$

and

$${\mathrm{cov}}_1\left(a{x}^2+bx+c,P_2(x,1;x^r);x^r\right)={\displaystyle \frac{1}{30}}{\displaystyle \frac{r(r-2)}{(r+1)(r+3)}}a.$$

According to Remark 2, since the uncorrelated polynomials (177) are now explicitly known, a new sequence of orthogonal functions can be constructed as follows:

$$G_n(x,1;r)={}_{4}F_3\left(\left.\begin{array}{c}-n,n+1,-r,r+2\\ 1,-r+1,r+1\end{array}\right|x\right)-{\displaystyle \frac{2r+1}{r+1}}{\displaystyle \frac{{(1+r)}_n}{{(1-r)}_n}}{x}^r,$$

satisfying the orthogonality relation

$${\int }_0^1{G}_n(x,1;r)G_m(x,1;r)dx={\displaystyle \frac{r^2}{{(r+1)}^2}}{\displaystyle \frac{1}{2n+1}}{\delta }_{n,m}.$$

The above orthogonality is valid for every n if and only if $r>-1/2$ and $r\notin {\mathbb{Z}}^{+}$. However, if $r=m\in \mathbb{N}$, the polynomial set ${\left\{G_n(x,1;m)\right\}}_{n=0}^{m-1}$ will be finitely orthogonal on $[0,1]$ according to Remark 5. For instance, for $m=3$ the elements of the finite set

$${\left\{G_n(x,1;3)\right\}}_{n=0}^2=\{-{\displaystyle \frac{7}{4}}{x}^3+1,{\displaystyle \frac{7}{2}}{x}^3-{\displaystyle \frac{15}{4}}x+1,-{\displaystyle \frac{35}{2}}{x}^3+27x^2-{\displaystyle \frac{45}{4}}x+1\},$$

are mutually orthogonal with respect to the constant weight function $w\left(x\right)=1$ on $[0,1]$ having the norm square value ${\displaystyle \frac{9}{16}}{\left\{{\displaystyle \frac{1}{2n+1}}\right\}}_{n=0}^2$.

8. On the Ordinary Case of p-Covariances

When $Z=c^{*}\ne 0$ and $p=1$, we have ${\mathrm{cov}}_1(X,Y;c^{*})=\mathrm{cov}(X,Y)$. Replacing these assumptions in (43) as

$$X_n=\left|\begin{array}{cccc}\mathrm{var}\left(V_0\right)& \mathrm{cov}(V_0,V_1)& \cdots & \mathrm{cov}(V_0,V_n)\\ \mathrm{cov}(V_1,V_0)& \mathrm{var}\left(V_1\right)& \cdots & \mathrm{cov}(V_1,V_n)\\ ⋮& ⋮& ⋮& ⋮\\ \mathrm{cov}(V_{n-1},V_0)& \mathrm{cov}(V_{n-1},V_1)& \cdots & \mathrm{cov}(V_{n-1},V_n)\\ V_0& V_1& \cdots & V_n\end{array}\right|,$$

(185)

generates an ordinary uncorrelated element. Note that the leading coefficient in (43) has no effect on being uncorrelated, and we have therefore ignored it in the above determinant.

There are, in total, two cases for the initial value $V_0$ in (185), i.e., when $V_0$ is a constant value (preferably $V_0=1$) or it is not constant. As we have shown in Section 2.3.2, the first case leads to the approved result (26), whereas the non-constant case contains some novel results. The next subsection describes one of them.

Another Uncorrelated Sequence of Hypergeometric Polynomials of ${}_{4}F_3$ Type

Let $w\left(x\right)=1$ be defined on $[0,1]$, and consider the initial data ${\{V_k=x^{r+k}\}}_{k=0}^n$ for $r\ne 0$ because $V_0\ne 1$. In this case, the components corresponding to (185) are computed as

$$\begin{array}{c}\mathrm{cov}(x^{r+i},x^{r+j})={\displaystyle \frac{(r+i)(r+j)}{(r+i+1)(r+j+1)(2r+i+j+1)}}\hfill \\ \hfill \mathrm{for}i=0,1,\dots ,n-1\mathrm{and}j=0,1,\dots ,n.\end{array}$$

(186)

Since $\mathrm{var}\left(x^{r+j}\right)={\displaystyle \frac{{(r+j)}^2}{{(r+j+1)}^2(2r+1+2j)}}>0,$ for $j=0$, we must also add the condition $2r+1>0$. If (186) is directly substituted into (185), with the aid of advanced mathematical software, we can again find the explicit form of the functions, say $X_n=f_{r+n}(x;r)$, as

$$f_{r+n}(x;r)=x^r{Q}_n(x;r)=x^r{}_{4}F_3\left(\left.\begin{array}{c}-n,n+2r+1,r,r+2\\ 2r+1,r+1,r+1\end{array}\right|x\right),$$

(187)

satisfying the ordinary uncorrelatedness condition

$$\begin{array}{c}{\int }_0^1{f}_{r+n}(x;r)f_{r+m}(x;r)dx-{\int }_0^1{f}_{r+n}(x;r)dx{\int }_0^1{f}_{r+m}(x;r)dx\hfill \\ \hfill =\left({\int }_0^1{f}_{r+n}^2(x;r)dx-{\left({\int }_0^1{f}_{r+n}(x;r)dx\right)}^2\right){\delta }_{m,n},\end{array}$$

which is equivalent to

$$\begin{array}{c}{\int }_0^1{x}^{2r}{Q}_n(x;r)Q_m(x;r)dx-{\int }_0^1{x}^r{Q}_n(x;r)dx{\int }_0^1{x}^r{Q}_m(x;r)dx\hfill \\ \hfill =\left({\int }_0^1{x}^{2r}{Q}_n^2(x;r)dx-{\left({\int }_0^1{x}^r{Q}_n(x;r)dx\right)}^2\right){\delta }_{m,n}.\end{array}$$

(188)

Remark 8.

If, in general, $P_r(X=x)=u\left(x\right)/{\int }_a^{b}u\left(x\right)dx$, one can find a relationship between ordinary covariances and 1-covariances as follows:

$$\begin{array}{c}\left({\int }_a^{b}w\left(x\right)dx\right){\left.\mathrm{cov}\left(z\left(x\right)f\left(x\right),z\left(x\right)g\left(x\right)\right)\right|}_{u\left(x\right)=w\left(x\right)}\hfill \\ \hfill =\left({\int }_a^{b}w\left(x\right)z^2\left(x\right)dx\right){\left.{\mathrm{cov}}_1\left(f\left(x\right),g\left(x\right);{\displaystyle \frac{1}{z\left(x\right)}}\right)\right|}_{u\left(x\right)=w\left(x\right)z^2\left(x\right)}.\end{array}$$

(189)

Hence, (188) shows that, if $z\left(x\right)=x^r$ and $w\left(x\right)=1$ are replaced in (189), then

$${\left.\mathrm{cov}\left(x^r{Q}_n(x;r),x^r{Q}_m(x;r)\right)\right|}_{u\left(x\right)=1}={\displaystyle \frac{1}{2r+1}}{\left.{\mathrm{cov}}_1\left(Q_n(x;r),Q_m(x;r);x^{-r}\right)\right|}_{u\left(x\right)=x^{2r}}.$$

In the sequel, in (188),

$$\begin{array}{cc}\hfill {\int }_0^1{x}^r{Q}_n(x;r)dx& ={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+2r+1)}_k{\left(r\right)}_k{(r+2)}_k}{{(2r+1)}_k{(r+1)}_k{(r+1)}_{k}k!(r+1+k)}}\hfill \\ \hfill & ={\displaystyle \frac{1}{r+1}}{}_{3}F_2\left(\left.\begin{array}{c}-n,n+2r+1,r\\ 2r+1,r+1\end{array}\right|1\right)={\displaystyle \frac{1}{r+1}}{\displaystyle \frac{n!}{{(2r+1)}_n}},\hfill \end{array}$$

(190)

and

$$\begin{array}{c}{\int }_0^1{x}^{2r}{Q}_n(x;r)Q_m(x;r)dx\hfill \\ \hfill ={\displaystyle \frac{1}{2r+1}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+2r+1)}_k{\left(r\right)}_k{(r+2)}_k}{{(2r+2)}_k{(r+1)}_k{(r+1)}_{k}k!}}{}_{5}F_4\left(\left.\begin{array}{c}-m,m+2r+1,r,r+2,2r+1+k\\ 2r+1,r+1,r+1,2r+2+k\end{array}\right|1\right),\end{array}$$

yielding

$$\begin{array}{c}{\int }_0^1{x}^{2r}{Q}_n(x;r)Q_m(x;r)dx-{\int }_0^1{x}^r{Q}_n(x;r)dx{\int }_0^1{x}^r{Q}_m(x;r)dx\hfill \\ ={\displaystyle \frac{1}{2r+1}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+2r+1)}_k{\left(r\right)}_k{(r+2)}_k}{{(2r+2)}_k{(r+1)}_k{(r+1)}_{k}k!}}{}_{5}F_4\left(\left.\begin{array}{c}-m,m+2r+1,r,r+2,2r+1+k\\ 2r+1,r+1,r+1,2r+2+k\end{array}\right|1\right)\hfill \\ \hfill -{\displaystyle \frac{1}{{(r+1)}^2}}{\displaystyle \frac{n!m!}{{(2r+1)}_n{(2r+1)}_m}}.\end{array}$$

(191)

To derive (190), we have used a similar computational technique as follows. Since

$$A\left(n\right)={}_{3}F_2\left(\left.\begin{array}{c}-n,n+2r+1,r\\ 2r+1,r+1\end{array}\right|1\right),$$

satisfies the first-order equation

$$A(n+1)={\displaystyle \frac{n+1}{n+1+2r}}A\left(n\right),$$

so

$${}_{3}F_2\left(\left.\begin{array}{c}-n,n+2r+1,r\\ 2r+1,r+1\end{array}\right|1\right)={\displaystyle \frac{n!}{{(2r+1)}_n}}.$$

Also, to compute the hypergeometric term in (191), since

$$B\left(m\right)={}_{5}F_4\left(\left.\begin{array}{c}-m,m+2r+1,r,r+2,2r+1+k\\ 2r+1,r+1,r+1,2r+2+k\end{array}\right|1\right),$$

satisfies the recurrence relation

$$\begin{array}{c}-(m+2r+1)(m+2r+2)(m+2r+3+k)B(m+2)\hfill \\ \hfill +(m+2)(2m+2r+3)(m+2r+1)B(m+1)+(m+1)(m+2)(k-m)B\left(m\right)=0,\end{array}$$

having two independent solutions

$$B_1\left(m\right)={\displaystyle \frac{m!}{{(2r+1)}_m}}\mathrm{and}{B}_2\left(m\right)={\displaystyle \frac{m!{(-k)}_m}{{(2r+1)}_m{(2r+k+2)}_m}},$$

so

$$B\left(m\right)=c_1{B}_1\left(m\right)+c_2{B}_2\left(m\right),$$

which finally results in

$$\begin{array}{c}{}_{5}F_4\left(\left.\begin{array}{c}-m,m+2r+1,r,r+2,2r+1+k\\ 2r+1,r+1,r+1,2r+2+k\end{array}\right|1\right)\hfill \\ \hfill ={\displaystyle \frac{1}{(r+1)(r+1+k)}}{\displaystyle \frac{m!}{{(2r+1)}_m}}\left(2r+1+k+r(r+k){\displaystyle \frac{{(-k)}_m}{{(2r+2+k)}_m}}\right).\end{array}$$

(192)

In order to compute

$$\mathrm{var}\left(f_{r+n}(x,r)\right)={\int }_0^1{x}^{2r}{Q}_n^2(x;r)dx-{\left({\int }_0^1{x}^r{Q}_n(x;r)dx\right)}^2,$$

it is enough to take $m=n$ in (191) and then use (192) to arrive at

$$\begin{array}{c}{B}^{*}={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+2r+1)}_k{\left(r\right)}_k{(r+2)}_k}{{(2r+2)}_k{(r+1)}_k{(r+1)}_{k}k!}}{}_{5}F_4\left(\left.\begin{array}{c}-n,n+2r+1,r,r+2,2r+1+k\\ 2r+1,r+1,r+1,2r+2+k\end{array}\right|1\right)\hfill \\ ={\displaystyle \frac{n!}{{(2r+1)}_n}}{\displaystyle \frac{2r+1}{{(r+1)}^2}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+2r+1)}_k{\left(r\right)}_k}{{\left(2\right)}_k{(-r+1)}_k{(r+1)}_{k}k!}}\\ \hfill +{\displaystyle \frac{n!}{{(2r+1)}_n}}{\displaystyle \frac{r^2}{{(r+1)}^2{(2r+2)}_n}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+2r+1)}_k{(-k)}_n}{{(n+2r+2)}_{k}k!}},\end{array}$$

which is finally simplified as

$$B^{*}={\displaystyle \frac{2r+1}{{(r+1)}^2}}{\displaystyle \frac{{(n!)}^2}{{(2r+1)}_n{(2r+1)}_n}}+{\displaystyle \frac{r^2}{{(r+1)}^2}}{\displaystyle \frac{{(n!)}^2{(n+2r+1)}_n}{{(2r+1)}_n{(2r+2)}_n{(n+2r+2)}_n}}.$$

Corollary 6.

If $r>-1/2$ and $r\ne 0$, then

$${\int }_0^1{x}^{2r}{Q}_n^2(x;r)dx-{\left({\int }_0^1{x}^r{Q}_n(x;r)dx\right)}^2={\displaystyle \frac{1}{2n+2r+1}}{\left({\displaystyle \frac{rn!}{(r+1){(2r+1)}_n}}\right)}^2.$$

Moreover, (191) is simplified as

$$\begin{array}{c}{\int }_0^1{x}^{2r}{Q}_n(x;r)Q_m(x;r)dx-{\int }_0^1{x}^r{Q}_n(x;r)dx{\int }_0^1{x}^r{Q}_m(x;r)dx\hfill \\ \hfill ={\displaystyle \frac{r^{2}m!}{{(r+1)}^2(2r+1){(2r+1)}_m{(2r+2)}_m}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(n+2r+1)}_k{(-n)}_k}{{(m+2r+2)}_k}}{\displaystyle \frac{{(-k)}_m}{k!}}=0\iff m\ne n.\end{array}$$

Therefore,

$${\displaystyle \sum _{k=m}^n}{\displaystyle \frac{{(n+2r+1)}_k{(-n)}_k}{{(m+2r+2)}_k}}{\displaystyle \frac{{(-k)}_m}{k!}}=n!{\displaystyle \frac{n+2r+1}{2n+2r+1}}{\delta }_{n,m},$$

(193)

which is a generalization of the second result of Corollary 5 for $r=0$.

In Section 10, we will prove that both polynomials obtained in Section 7 and Section 8 are particular cases of a two-parametric sequence of uncorrelated polynomials.

9. A Class of Uncorrelated Polynomials Based on a Predetermined Orthogonal Polynomial

In this section, we introduce a class of uncorrelated polynomials which is constructed through a predetermined sequence of orthogonal polynomials, and then we study its general properties in detail. In order to clarify the subject, we also present two hypergeometric examples based on Jacobi and Laguerre polynomials. First of all, we should raise two important points. Let ${\left\{{\Phi }_n\left(x\right)\right\}}_{n=0}$ (with ${\Phi }_0\left(x\right)=1$ valid especially for polynomial sequences) be a sequence of real functions orthogonal with respect to $w\left(x\right)$ on $[a,b]$, i.e.,

$${\left.E\left({\Phi }_m\left(x\right){\Phi }_n\left(x\right)\right)\right|}_{w\left(x\right)}={\left.E\left({\Phi }_n^2\left(x\right)\right)\right|}_{w\left(x\right)}{\delta }_{m,n},$$

(194)

where ${\left.(.)\right|}_{w\left(x\right)}$ means $P_r(X=x)={\displaystyle \frac{w\left(x\right)}{{\int }_a^{b}w\left(x\right)dx}}$, as before.

The first point is that, if the mentioned sequence has the special form

$${\Phi }_n\left(x\right)=\theta \left(x\right)g_n\left(x\right)+{\beta }_n(\mathrm{with}{\Phi }_0\left(x\right)=1),$$

in which $\theta \left(x\right)$ is a function independent of n, and $\left\{{\beta }_n\right\}$ is an arbitrary numeric sequence, then noting (194) and (189) in Remark 8, we have

$$\begin{array}{cc}\hfill & {\left.cov\left({\Phi }_m\left(x\right),{\Phi }_n\left(x\right)\right)\right|}_{w\left(x\right)}\hfill \\ \hfill & ={\left.E\left({\Phi }_m\left(x\right){\Phi }_n\left(x\right)\right)\right|}_{w\left(x\right)}-{\left.E\left({\Phi }_m\left(x\right){\Phi }_0\left(x\right)\right)\right|}_{w\left(x\right)}{\left.E\left({\Phi }_n\left(x\right){\Phi }_0\left(x\right)\right)\right|}_{w\left(x\right)}\hfill \\ \hfill & ={\left.E\left({\Phi }_n^2\left(x\right)\right)\right|}_{w\left(x\right)}{\delta }_{m,n}={\left.cov\left(\theta \left(x\right)g_m\left(x\right)+{\beta }_m,\theta \left(x\right)g_n\left(x\right)+{\beta }_n\right)\right|}_{w\left(x\right)}\hfill \\ \hfill & ={\left.cov\left(\theta \left(x\right)g_m\left(x\right),\theta \left(x\right)g_n\left(x\right)\right)\right|}_{w\left(x\right)}\hfill \\ \hfill & ={\displaystyle \frac{{\int }_a^{b}w\left(x\right){\theta }^2\left(x\right)dx}{{\int }_a^{b}w\left(x\right)dx}}{\left.{cov}_1\left(g_m\left(x\right),g_n\left(x\right);{\displaystyle \frac{1}{\theta \left(x\right)}}\right)\right|}_{w\left(x\right){\theta }^2\left(x\right)},\hfill \end{array}$$

(195)

leading to the following biorthogonality relation according to the Section 4.1,

$${\left.E\left(g_m\left(x\right)\left(g_n\left(x\right)-{\displaystyle \frac{E\left(g_n\left(x\right)/\theta \left(x\right)\right)}{E\left(1/{\theta }^2\left(x\right)\right)}}{\displaystyle \frac{1}{\theta \left(x\right)}}\right)\right)\right|}_{w\left(x\right){\theta }^2\left(x\right)}={\displaystyle \frac{{\int }_a^{b}w\left(x\right)dx}{{\int }_a^{b}w\left(x\right){\theta }^2\left(x\right)dx}}{\left.E\left({\Phi }_n^2\left(x\right)\right)\right|}_{w\left(x\right)}{\delta }_{m,n}.$$

Also, if it satisfies a second-order equation as

$$a\left(x\right){\Phi }_n^{″}\left(x\right)+b\left(x\right){\Phi }_n^{\prime }\left(x\right)+{\lambda }_{n}u\left(x\right){\Phi }_n\left(x\right)=0,$$

then ${\left\{g_n\left(x\right)\right\}}_{n=0}$ will satisfy the equation

$$\begin{array}{c}\left(a\left(x\right)\theta \left(x\right)\right)g_n^{″}\left(x\right)+\left(2a\left(x\right){\theta }^{\prime }\left(x\right)+b\left(x\right)\theta \left(x\right)\right)g_n^{\prime }\left(x\right)\hfill \\ \hfill +\left(a\left(x\right){\theta }^{″}\left(x\right)+b\left(x\right){\theta }^{\prime }\left(x\right)+{\lambda }_{n}u\left(x\right)\theta \left(x\right)\right)g_n\left(x\right)=-{\lambda }_n{\beta }_{n}u\left(x\right).\end{array}$$

(196)

In this sense, the second point is that the relation

$${\displaystyle \frac{{\int }_a^{b}w\left(x\right)\theta \left(x\right)g_n\left(x\right)dx}{{\int }_a^{b}w\left(x\right)dx}}={\displaystyle \frac{{\int }_a^{b}w\left(x\right)\left({\Phi }_n\left(x\right)-{\beta }_n\right)dx}{{\int }_a^{b}w\left(x\right)dx}}=-{\beta }_n,$$

will change Equation (196) to

$$\begin{array}{c}\left(a\left(x\right)\theta \left(x\right)\right)g_n^{″}\left(x\right)+\left(2a\left(x\right){\theta }^{\prime }\left(x\right)+b\left(x\right)\theta \left(x\right)\right)g_n^{\prime }\left(x\right)\hfill \\ \hfill +\left(a\left(x\right){\theta }^{″}\left(x\right)+b\left(x\right){\theta }^{\prime }\left(x\right)+{\lambda }_{n}u\left(x\right)\theta \left(x\right)\right)g_n\left(x\right)={\lambda }_{n}u\left(x\right){\displaystyle \frac{{\int }_a^{b}w\left(x\right)\theta \left(x\right)g_n\left(x\right)dx}{{\int }_a^{b}w\left(x\right)dx}},\end{array}$$

which is a particular case of Equation (65) in Theorem 7.

Now, noting the two above-mentioned points, for a real parameter $\lambda$ let

$${\left\{P_n(x;\lambda )={\displaystyle \sum _{k=0}^n}{a}_k^{\left(n\right)}{(x-\lambda )}^k\right\}}_{n=0},$$

be a sequence of polynomials orthogonal with respect to $w\left(x\right)$ on $[a,b]$, such that

$${\left.E\left(P_m(x;\lambda )P_n(x;\lambda )\right)\right|}_{w\left(x\right)}={\left.E\left(P_n^2(x;\lambda )\right)\right|}_{w\left(x\right)}{\delta }_{m,n}.$$

(197)

It can be verified that the sequence

$$Q_n(x;\lambda )={\displaystyle \frac{P_{n+1}(x;\lambda )-P_{n+1}(\lambda ;\lambda )}{x-\lambda }}={\displaystyle \sum _{k=0}^n}{a}_{k+1}^{(n+1)}{(x-\lambda )}^k,$$

(198)

is also a polynomial of degree n. With reference to (195) and (197), the following relations hold for the polynomial sequence (198),

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{\int }_a^{b}w\left(x\right){(x-\lambda )}^{2}dx}{{\int }_a^{b}w\left(x\right)dx}}{\left.{\mathrm{cov}}_1\left(Q_m(x;\lambda ),Q_n(x;\lambda );{\displaystyle \frac{1}{x-\lambda }}\right)\right|}_{w\left(x\right){(x-\lambda )}^2}\hfill \\ \hfill & ={\left.\mathrm{cov}\left((x-\lambda )Q_m(x;\lambda ),(x-\lambda )Q_n(x;\lambda )\right)\right|}_{w\left(x\right)}\hfill \\ \hfill & ={\left.\mathrm{cov}\left(P_{m+1}(x;\lambda )-P_{m+1}(\lambda ;\lambda ),P_{n+1}(x;\lambda )-P_{n+1}(\lambda ;\lambda )\right)\right|}_{w\left(x\right)}\hfill \\ \hfill & ={\left.\mathrm{cov}\left(P_{m+1}(x;\lambda ),P_{n+1}(x;\lambda )\right)\right|}_{w\left(x\right)}={\left.E\left(P_{n+1}^2(x;\lambda )\right)\right|}_{w\left(x\right)}{\delta }_{m,n}.\hfill \end{array}$$

(199)

Corollary 7.

From (199), the relation

$${\left.{\mathrm{cov}}_1\left(Q_m(x;\lambda ),Q_n(x;\lambda );{\displaystyle \frac{1}{x-\lambda }}\right)\right|}_{w\left(x\right){(x-\lambda )}^2}={\displaystyle \frac{{\int }_a^{b}w\left(x\right)P_{n+1}^2(x;\lambda )dx}{{\int }_a^{b}w\left(x\right){(x-\lambda )}^{2}dx}}{\delta }_{m,n},$$

shows that the polynomial set ${\left\{Q_n(x;\lambda )\right\}}_{n=0}$ is a complete uncorrelated sequence with respect to the fixed function $z\left(x\right)={\displaystyle \frac{1}{x-\lambda }}$ and the probability function $P_r(X=x)={\displaystyle \frac{w\left(x\right){(x-\lambda )}^2}{{\int }_a^{b}w\left(x\right){(x-\lambda )}^{2}dx}}$, respectively. Also, relation (199) shows that the two defined sequences

$${\left\{P_n(x;\lambda )={\displaystyle \sum _{k=0}^n}{a}_k^{\left(n\right)}{(x-\lambda )}^k\right\}}_{n=0}\mathit{and}{\left\{Q_n(x;\lambda )={\displaystyle \sum _{k=0}^n}{a}_{k+1}^{(n+1)}{(x-\lambda )}^k\right\}}_{n=0}$$

are biorthogonal with respect to the weight function $(x-\lambda )w\left(x\right)$ on $[a,b]$, as we have

$$\begin{array}{c}{\left.{\mathrm{cov}}_1\left(Q_m(x;\lambda ),Q_n(x;\lambda );{\displaystyle \frac{1}{x-\lambda }}\right)\right|}_{w\left(x\right){(x-\lambda )}^2}\hfill \\ \hfill =E{\left.\left(Q_m(x;\lambda )\left(Q_n(x;\lambda )-{\displaystyle \frac{E\left(Q_n(x;\lambda )/(x-\lambda )\right)}{E\left(1/{(x-\lambda )}^2\right)}}{\displaystyle \frac{1}{x-\lambda }}\right)\right)\right|}_{w\left(x\right){(x-\lambda )}^2},\end{array}$$

where

$$Q_n(x;\lambda )-{\displaystyle \frac{E\left(Q_n(x;\lambda )/(x-\lambda )\right)}{E\left(1/{(x-\lambda )}^2\right)}}{\displaystyle \frac{1}{x-\lambda }}={\displaystyle \frac{P_{n+1}(x;\lambda )}{x-\lambda }}.$$

There is a direct proof for this result in an inner product space, too. If we suppose

$${⟨P_m(x;\lambda ),P_n(x;\lambda )⟩}_{w\left(x\right)}={⟨P_n(x;\lambda ),P_n(x;\lambda )⟩}_{w\left(x\right)}{\delta }_{m,n},$$

then, for every $m\in \mathbb{N}$, we have

$$\begin{array}{cc}\hfill & {⟨Q_n(x;\lambda ),P_m(x;\lambda )⟩}_{(x-\lambda )w\left(x\right)}={⟨{\displaystyle \frac{P_{n+1}(x;\lambda )-P_{n+1}(\lambda ;\lambda )}{x-\lambda }},P_m(x;\lambda )⟩}_{(x-\lambda )w\left(x\right)}\hfill \\ \hfill & ={⟨P_{n+1}(x;\lambda ),P_m(x;\lambda )⟩}_{w\left(x\right)}-P_{n+1}(\lambda ;\lambda ){⟨1,P_m(x;\lambda )⟩}_{w\left(x\right)}\hfill \\ \hfill & ={⟨P_{n+1}(x;\lambda ),P_{n+1}(x;\lambda )⟩}_{w\left(x\right)}{\delta }_{n+1,m}.\hfill \end{array}$$

(200)

Using (200), one can create a biorthogonal approximation (or expansion as $n\to \infty$) for any appropriate function, say $f\left(x\right)$, in terms of the uncorrelated polynomials ${\left\{Q_k(x;\lambda )\right\}}_{k=0}$ as follows:

$$f\left(x\right)\cong {\displaystyle \sum _{k=0}^n}{c}_k{Q}_k(x;\lambda )={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{⟨f\left(x\right),P_{k+1}(x;\lambda )⟩}_{(x-\lambda )w\left(x\right)}}{{⟨P_{k+1}(x;\lambda ),P_{k+1}(x;\lambda )⟩}_{w\left(x\right)}}}{\displaystyle \frac{P_{k+1}(x;\lambda )-P_{k+1}(\lambda ;\lambda )}{x-\lambda }},$$

whose error is clearly minimized with respect to the fixed function $z\left(x\right)={\displaystyle \frac{1}{x-\lambda }}$ in the sense of least 1-variances. In the sequel, since ${\left\{P_n(x;\lambda )\right\}}_{n=0}$ was assumed to be orthogonal, its monic type must satisfy a three term recurrence relation [25] of the form

$${\overline{P}}_{n+1}(x;\lambda )=(x-B_n){\overline{P}}_n(x;\lambda )-C_n{\overline{P}}_{n-1}(x;\lambda )\mathrm{with}{\overline{P}}_0(x;\lambda )=1\mathrm{and}{\overline{P}}_1(x;\lambda )=x-B_1.$$

(201)

After doing some computations are performed in hand, substituting (198) into (201) gives

$${\overline{Q}}_{n+1}(x;\lambda )=(x-B_{n+1}){\overline{Q}}_n(x;\lambda )-C_{n+1}{\overline{Q}}_{n-1}(x;\lambda )+{\overline{P}}_{n+1}(\lambda ;\lambda )\mathrm{with}{\overline{Q}}_0(x;\lambda )=1.$$

(202)

This type of recurrence relation in (202) helps us obtain an analogue of the well-known Christoffel–Darboux identity [25] as follows. We have, respectively, in (202),

$$\begin{array}{c}\left(x{\overline{Q}}_n(x;\lambda )+{\overline{P}}_{n+1}(\lambda ;\lambda )\right){\overline{Q}}_n(t;\lambda )={\overline{Q}}_{n+1}(x;\lambda ){\overline{Q}}_n(t;\lambda )\hfill \\ \hfill +B_{n+1}{\overline{Q}}_n(x;\lambda ){\overline{Q}}_n(t;\lambda )+C_{n+1}{\overline{Q}}_{n-1}(x;\lambda ){\overline{Q}}_n(t;\lambda ),\end{array}$$

and

$$\begin{array}{c}\left(t{\overline{Q}}_n(t;\lambda )+{\overline{P}}_{n+1}(\lambda ;\lambda )\right){\overline{Q}}_n(x;\lambda )={\overline{Q}}_{n+1}(t;\lambda ){\overline{Q}}_n(x;\lambda )\hfill \\ \hfill +B_{n+1}{\overline{Q}}_n(t;\lambda ){\overline{Q}}_n(x;\lambda )+C_{n+1}{\overline{Q}}_{n-1}(t;\lambda ){\overline{Q}}_n(x;\lambda ).\end{array}$$

Therefore, by defining the kernel

$$G_n(x,t)={\displaystyle \frac{1}{{\displaystyle \prod _{j=1}^{n+1}}{C}_j}}{\displaystyle \frac{{\overline{Q}}_{n+1}(x;\lambda ){\overline{Q}}_n(t;\lambda )-{\overline{Q}}_{n+1}(t;\lambda ){\overline{Q}}_n(x;\lambda )}{x-t}},$$

we eventually obtain

$$\begin{array}{c}{\displaystyle \sum _{n=0}^m}{\displaystyle \frac{1}{{\displaystyle \prod _{j=1}^{n+1}}{C}_j}}\left({\overline{Q}}_n(x;\lambda ){\overline{Q}}_n(t;\lambda )-{\overline{P}}_{n+1}(\lambda ;\lambda ){\displaystyle \frac{{\overline{Q}}_n(x;\lambda )-{\overline{Q}}_n(t;\lambda )}{x-t}}\right)\hfill \\ \hfill ={\displaystyle \sum _{n=0}^m}{G}_n(x,t)-G_{n-1}(x,t)={\displaystyle \frac{1}{{\displaystyle \prod _{j=1}^{m+1}}{C}_j}}{\displaystyle \frac{{\overline{Q}}_{m+1}(x;\lambda ){\overline{Q}}_m(t;\lambda )-{\overline{Q}}_{m+1}(t;\lambda ){\overline{Q}}_m(x;\lambda )}{x-t}}.\end{array}$$

(203)

We now introduce two uncorrelated polynomials of the hypergeometric type that are constructed based on Jacobi and Laguerre polynomials, and then we apply all the above-mentioned results on them.

9.1. An Uncorrelated Sequence of Hypergeometric Polynomials of ${}_{3}F_2$ Type

The monic type of Jacobi polynomials [20]

$${\overline{P}}_n^{(\alpha ,\beta )}\left(x\right)={\displaystyle \frac{2^n{(\alpha +1)}_n}{{(n+\alpha +\beta +1)}_n}}{}_{2}F_1\left(\left.\begin{array}{c}-n,n+\alpha +\beta +1\\ \alpha +1\end{array}\right|{\displaystyle \frac{1-x}{2}}\right),$$

(204)

satisfy the equation

$$(1-x^2){\displaystyle \frac{d^2}{d{x}^2}}{\overline{P}}_n^{(\alpha ,\beta )}\left(x\right)-\left((\alpha +\beta +2)x+\alpha -\beta \right){\displaystyle \frac{d}{dx}}{\overline{P}}_n^{(\alpha ,\beta )}\left(x\right)+n(n+\alpha +\beta +1){\overline{P}}_n^{(\alpha ,\beta )}\left(x\right)=0,$$

(205)

and are orthogonal with respect to the weight function ${(1-x)}^{\alpha }{(1+x)}^{\beta }$ on $[-1,1]$ as

$$\begin{array}{c}{\int }_{-1}^1{(1-x)}^{\alpha }{(1+x)}^{\beta }{\overline{P}}_m^{(\alpha ,\beta )}\left(x\right){\overline{P}}_n^{(\alpha ,\beta )}\left(x\right)dx\hfill \\ \hfill =n!2^{2n+\alpha +\beta +1}{\displaystyle \frac{\Gamma (n+\alpha +\beta +1)\Gamma (n+\alpha +1)\Gamma (n+\beta +1)}{\Gamma (2n+\alpha +\beta +1)\Gamma (2n+\alpha +\beta +2)}}{\delta }_{n,m}.\end{array}$$

(206)

Since ${\overline{P}}_n^{(\alpha ,\beta )}(-x)={(-1)}^n{\overline{P}}_n^{(\beta ,\alpha )}\left(x\right)$, another representation of these polynomials is as

$${\overline{P}}_n^{(\alpha ,\beta )}\left(x\right)={\displaystyle \frac{{(-1)}^n{2}^n{(\beta +1)}_n}{{(n+\alpha +\beta +1)}_n}}{}_{2}F_1\left(\left.\begin{array}{c}-n,n+\alpha +\beta +1\\ \beta +1\end{array}\right|{\displaystyle \frac{1+x}{2}}\right).$$

(207)

They also satisfy a three term recurrence relation in the form

$$\begin{array}{c}{\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(x\right)=\left(x-{\displaystyle \frac{{\beta }^2-{\alpha }^2}{(2n+\alpha +\beta )(2n+\alpha +\beta +2)}}\right){\overline{P}}_n^{(\alpha ,\beta )}\left(x\right)\hfill \\ \hfill -4{\displaystyle \frac{n(n+\alpha )(n+\beta )(n+\alpha +\beta )}{(2n+\alpha +\beta +1){(2n+\alpha +\beta )}^2(2n+\alpha +\beta -1)}}{\overline{P}}_{n-1}^{(\alpha ,\beta )}\left(x\right).\end{array}$$

(208)

Representations (204) and (207) show that there are two specific values for $\lambda$ in (198), i.e., $\lambda =1$ and $\lambda =-1$. Noting that ${\overline{P}}_n^{(\alpha ,\beta )}\left(1\right)={\displaystyle \frac{2^n{(\alpha +1)}_n}{{(n+\alpha +\beta +1)}_n}},$ the first kind of uncorrelated polynomials is defined as

$$\begin{array}{c}{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)={\displaystyle \frac{{\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(1\right)-{\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(x\right)}{1-x}}\hfill \\ \hfill ={\displaystyle \frac{(n+1)2^n{(\alpha +2)}_n}{{(n+\alpha +\beta +3)}_n}}{}_{3}F_2\left(\left.\begin{array}{c}-n,n+\alpha +\beta +3,1\\ \alpha +2,2\end{array}\right|{\displaystyle \frac{1-x}{2}}\right).\end{array}$$

(209)

Also, for $\lambda =-1$ the second kind is defined by

$$\begin{array}{c}{\overline{Q}}_n^{(\alpha ,\beta )}(x;-1)={\displaystyle \frac{{\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(x\right)-{\overline{P}}_{n+1}^{(\alpha ,\beta )}(-1)}{x+1}}={\displaystyle \frac{{(-1)}^{n+1}{\overline{P}}_{n+1}^{(\beta ,\alpha )}(-x)-{(-1)}^{n+1}{\overline{P}}_{n+1}^{(\beta ,\alpha )}\left(1\right)}{1-(-x)}}\hfill \\ \hfill ={(-1)}^n{\overline{Q}}_n^{(\beta ,\alpha )}(-x;1)={\displaystyle \frac{(n+1){(-2)}^n{(\beta +2)}_n}{{(n+\alpha +\beta +3)}_n}}{}_{3}F_2\left(\left.\begin{array}{c}-n,n+\alpha +\beta +3,1\\ \beta +2,2\end{array}\right|{\displaystyle \frac{1+x}{2}}\right).\end{array}$$

(210)

Relation (210) reveals that we, in fact, deal with only one value, i.e., $\lambda =1$.

If in (209), ${\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(x\right)=(x-1){\overline{Q}}_n^{(\alpha ,\beta )}(x;1)+{\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(1\right)$ is substituted into the differential Equation (205), we obtain

$$\begin{array}{c}{(1-x)}^2(1+x){\displaystyle \frac{d^2}{d{x}^2}}{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)-(1-x)\left((\alpha +\beta +4)x+\alpha -\beta +2\right){\displaystyle \frac{d}{dx}}{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)\hfill \\ +\left(n(n+\alpha +\beta +3)(1-x)+2\alpha +2\right){\overline{Q}}_n^{(\alpha ,\beta )}(x;1)\\ \hfill =(n+1)(n+\alpha +\beta +2){\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(1\right)={\displaystyle \frac{(n+1)(n+\alpha +\beta +2)2^n{(\alpha +1)}_n}{{(n+\alpha +\beta +1)}_n}}.\end{array}$$

(211)

On the other hand,

$$\begin{array}{c}{\int }_{-1}^1{(1-x)}^{\alpha +1}{(1+x)}^{\beta }{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)dx={\int }_{-1}^1{(1-x)}^{\alpha }{(1+x)}^{\beta }\left({\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(1\right)-{\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(x\right)\right)dx\hfill \\ \hfill ={\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(1\right){\int }_{-1}^1{(1-x)}^{\alpha }{(1+x)}^{\beta }dx={\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(1\right)2^{\alpha +\beta +1}{\displaystyle \frac{\Gamma (\alpha +1)\Gamma (\beta +1)}{\Gamma (\alpha +\beta +2)}},\end{array}$$

changes Equation (211) to

$$\begin{array}{c}{(1-x)}^2(1+x){\displaystyle \frac{d^2}{d{x}^2}}{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)-(1-x)\left((\alpha +\beta +4)x+\alpha -\beta +2\right){\displaystyle \frac{d}{dx}}{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)\hfill \\ +\left({\gamma }_n^{*}(1-x)+2\alpha +2\right){\overline{Q}}_n^{(\alpha ,\beta )}(x;1)\\ \hfill ={\displaystyle \frac{\Gamma (\alpha +\beta +2)({\gamma }_n^{*}+\alpha +\beta +2)}{2^{\alpha +\beta +1}\Gamma (\alpha +1)\Gamma (\beta +1)}}{\int }_{-1}^1{(1-x)}^{\alpha +1}{(1+x)}^{\beta }{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)dx,\end{array}$$

(212)

in which ${\gamma }_n^{*}=n(n+\alpha +\beta +3)$.

Theorem 14.

For any $\alpha ,\beta >-1$, we have

$$\begin{array}{c}{\left.{\mathrm{cov}}_1\left({\overline{Q}}_m^{(\alpha ,\beta )}(x;1),{\overline{Q}}_n^{(\alpha ,\beta )}(x;1);{\displaystyle \frac{1}{1-x}}\right)\right|}_{{(1-x)}^{\alpha +2}{(1+x)}^{\beta }}\hfill \\ \hfill =n!2^{2n-2}{\displaystyle \frac{\Gamma (\alpha +\beta +4)\Gamma (n+\alpha +\beta +1)\Gamma (n+\alpha +1)\Gamma (n+\beta +1)}{\Gamma (\alpha +3)\Gamma (\beta +1)\Gamma (2n+\alpha +\beta +1)\Gamma (2n+\alpha +\beta +2)}}{\delta }_{m,n}.\end{array}$$

Proof. 

We would like to prove this theorem via differential Equation (212) so that, if it is written in the self-adjoint form

$$\begin{array}{c}{\displaystyle \frac{d}{dx}}\left({(1-x)}^{\alpha +3}{(1+x)}^{\beta +1}{\displaystyle \frac{d}{dx}}{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)\right)\hfill \\ +\left({\gamma }_n^{*}{(1-x)}^{\alpha +2}{(1+x)}^{\beta }+\left(2\alpha +2\right){(1-x)}^{\alpha +1}{(1+x)}^{\beta }\right){\overline{Q}}_n^{(\alpha ,\beta )}(x;1)\hfill \\ ={\displaystyle \frac{\Gamma (\alpha +\beta +2)({\gamma }_n^{*}+\alpha +\beta +2)}{2^{\alpha +\beta +1}\Gamma (\alpha +1)\Gamma (\beta +1)}}\left({\int }_{-1}^1{(1-x)}^{\alpha +1}{(1+x)}^{\beta }{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)dx\right){(1-x)}^{\alpha +1}{(1+x)}^{\beta },\hfill \end{array}$$

then

$$\begin{array}{c}{\left[{(1-x)}^{\alpha +3}{(1+x)}^{\beta +1}\left({\overline{Q}}_m^{(\alpha ,\beta )}(x;1){\displaystyle \frac{d}{dx}}{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)-{\overline{Q}}_n^{(\alpha ,\beta )}(x;1){\displaystyle \frac{d}{dx}}{\overline{Q}}_m^{(\alpha ,\beta )}(x;1)\right)\right]}_{-1}^1\hfill \\ +\left({\gamma }_n^{*}-{\gamma }_m^{*}\right){\int }_{-1}^1{(1-x)}^{\alpha +2}{(1+x)}^{\beta }{\overline{Q}}_n^{(\alpha ,\beta )}(x;1){\overline{Q}}_m^{(\alpha ,\beta )}(x;1)dx\\ ={\displaystyle \frac{\Gamma (\alpha +\beta +2)}{2^{\alpha +\beta +1}\Gamma (\alpha +1)\Gamma (\beta +1)}}\left({\gamma }_n^{*}-{\gamma }_m^{*}\right)\\ \hfill \times \left({\int }_{-1}^1{(1-x)}^{\alpha +1}{(1+x)}^{\beta }{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)dx\right)\left({\int }_{-1}^1{(1-x)}^{\alpha +1}{(1+x)}^{\beta }{\overline{Q}}_m^{(\alpha ,\beta )}(x;1)dx\right),\end{array}$$

leading to the result

$$\begin{array}{c}{\int }_{-1}^1{(1-x)}^{\alpha +2}{(1+x)}^{\beta }{\overline{Q}}_n^{(\alpha ,\beta )}(x;1){\overline{Q}}_m^{(\alpha ,\beta )}(x;1)dx\hfill \\ ={\displaystyle \frac{\left({\int }_{-1}^1{(1-x)}^{\alpha +1}{(1+x)}^{\beta }{\overline{Q}}_n^{(\alpha ,\beta )}(x;1)dx\right)\left({\int }_{-1}^1{(1-x)}^{\alpha +1}{(1+x)}^{\beta }{\overline{Q}}_m^{(\alpha ,\beta )}(x;1)dx\right)}{{\int }_{-1}^1{(1-x)}^{\alpha }{(1+x)}^{\beta }dx}}\\ ={\overline{P}}_{n+1}^{(\alpha ,\beta )}\left(1\right){\overline{P}}_{m+1}^{(\alpha ,\beta )}\left(1\right){\int }_{-1}^1{(1-x)}^{\alpha }{(1+x)}^{\beta }dx\\ \hfill =2^{n+m+\alpha +\beta +1}{\displaystyle \frac{\Gamma (\alpha +1)\Gamma (\beta +1)}{\Gamma (\alpha +\beta +2)}}{\displaystyle \frac{{(\alpha +1)}_n{(\alpha +1)}_m}{{(n+\alpha +\beta +1)}_n{(m+\alpha +\beta +1)}_m}}\iff n\ne m,\end{array}$$

(213)

which proves the first part. To obtain the variance value, i.e., for $n=m$ in (213), it is enough to refer to Corollary 7 and then apply relation (206). □

Note that, in (208), $C_j={\displaystyle \frac{1}{4}}{\displaystyle \frac{j(j+\alpha )(j+\beta )(j+\alpha +\beta )}{(j+\frac{\alpha +\beta +1}{2}){(j+\frac{\alpha +\beta }{2})}^2(j+\frac{\alpha +\beta -1}{2})}},$ we have

$${\displaystyle \prod _{j=1}^{m+1}}{C}_j={\displaystyle \frac{1}{4^{m+1}}}{\displaystyle \frac{{\left(1\right)}_{m+1}{(\alpha +1)}_{m+1}{(\beta +1)}_{m+1}{(\alpha +\beta +1)}_{m+1}}{{\left(\frac{\alpha +\beta +3}{2}\right)}_{m+1}{\left(\frac{\alpha +\beta +2}{2}\right)}_{m+1}^2{\left(\frac{\alpha +\beta +1}{2}\right)}_{m+1}}}.$$

Hence, the identity (203) can be applied straightforwardly.

Some Particular Trigonometric Cases

There are four trigonometric cases of Jacobi polynomials that are known in the literature as the Chebyshev polynomials of the first, second, third, and fourth kinds. The main advantage of these trigonometric polynomials is that their roots are explicitly known [25]; see also [28]. Their monic forms are represented, respectively, as follows:

$$\begin{array}{cc}\hfill {\overline{T}}_n\left(x\right)& ={\overline{P}}_n^{(-{\displaystyle \frac{1}{2}},-{\displaystyle \frac{1}{2}})}\left(x\right)={\displaystyle \frac{1}{2^{n-1}}}cos\left(narccosx\right)={\displaystyle \prod _{k=1}^n}(x-cos{\displaystyle \frac{(2k-1)\pi }{2n}}),\hfill \\ \hfill {\overline{U}}_n\left(x\right)& ={\overline{P}}_n^{({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})}\left(x\right)={\displaystyle \frac{1}{2^n\sqrt{1-x^2}}}sin\left((n+1)arccosx\right)={\displaystyle \prod _{k=1}^n}(x-cos{\displaystyle \frac{k\pi }{n+1}}),\hfill \\ \hfill {\overline{V}}_n\left(x\right)& ={\overline{P}}_n^{(-{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})}\left(x\right)={\displaystyle \frac{1}{2^n}}\sqrt{{\displaystyle \frac{2}{1+x}}}cos((n+{\displaystyle \frac{1}{2}})arccosx)={\displaystyle \prod _{k=1}^n}(x-cos{\displaystyle \frac{(2k-1)\pi }{2n+1}}),\hfill \\ \hfill {\overline{W}}_n\left(x\right)& ={\overline{P}}_n^{({\displaystyle \frac{1}{2}},-{\displaystyle \frac{1}{2}})}\left(x\right)={\displaystyle \frac{1}{2^n}}\sqrt{{\displaystyle \frac{2}{1-x}}}sin((n+{\displaystyle \frac{1}{2}})arccosx)={\displaystyle \prod _{k=1}^n}(x-cos{\displaystyle \frac{2k\pi }{2n+1}}).\hfill \end{array}$$

(214)

When it is noted that

$$T_n\left(x\right)=2^{n-1}{\overline{T}}_n\left(x\right),U_n\left(x\right)=2^n{\overline{U}}_n\left(x\right),V_n\left(x\right)=2^n{\overline{V}}_n\left(x\right)\mathrm{and}{W}_n\left(x\right)=2^n{\overline{W}}_n\left(x\right),$$

they also satisfy the following orthogonality relations:

$$\begin{array}{cc}\hfill & {\int }_{-1}^1{T}_n\left(x\right)T_m\left(x\right){\displaystyle \frac{1}{\sqrt{1-x^2}}}dx=\left\{\begin{array}{c}{\displaystyle \frac{\pi }{2}}{\delta }_{n,m},\hfill \\ \pi \mathrm{if}n=m=0,\hfill \end{array}\right.\hfill \\ \hfill & {\int }_{-1}^1{U}_n\left(x\right)U_m\left(x\right)\sqrt{1-x^2}dx={\displaystyle \frac{\pi }{2}}{\delta }_{n,m},\hfill \\ \hfill & {\int }_{-1}^1{V}_n\left(x\right)V_m\left(x\right)\sqrt{{\displaystyle \frac{1+x}{1-x}}}dx=\pi {\delta }_{n,m},\hfill \\ \hfill & {\int }_{-1}^1{W}_n\left(x\right)W_m\left(x\right)\sqrt{{\displaystyle \frac{1-x}{1+x}}}dx=\pi {\delta }_{n,m}.\hfill \end{array}$$

(215)

Now, we can employ relations (214) and define four trigonometric uncorrelated sequences, according to the main definition (209), as follows:

$$\begin{array}{c}{\overline{T}}_n(x;1)={\overline{Q}}_n^{(-{\displaystyle \frac{1}{2}},-{\displaystyle \frac{1}{2}})}(x;1)={\displaystyle \frac{1-{\overline{T}}_{n+1}\left(x\right)}{1-x}}\hfill \\ \hfill ={\displaystyle \frac{(n+1)2^n{(3/2)}_n}{{(n+2)}_n}}{}_{3}F_2\left(\left.\begin{array}{c}-n,n+2,1\\ 3/2,2\end{array}\right|{\displaystyle \frac{1-x}{2}}\right)={\displaystyle \prod _{k=1}^n}(x-cos{\displaystyle \frac{2k\pi }{n+1}}),\end{array}$$

(216)

$$\begin{array}{c}{\overline{U}}_n(x;1)={\overline{Q}}_n^{({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})}(x;1)={\displaystyle \frac{n+2-{\overline{U}}_{n+1}\left(x\right)}{1-x}}\hfill \\ \hfill ={\displaystyle \frac{(n+1)2^n{(5/2)}_n}{{(n+4)}_n}}{}_{3}F_2\left(\left.\begin{array}{c}-n,n+4,1\\ 5/2,2\end{array}\right|{\displaystyle \frac{1-x}{2}}\right),\end{array}$$

$$\begin{array}{c}{\overline{V}}_n(x;1)={\overline{Q}}_n^{(-{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}})}(x;1)={\displaystyle \frac{1-{\overline{V}}_{n+1}\left(x\right)}{1-x}}\hfill \\ \hfill ={\displaystyle \frac{(n+1)2^n{(3/2)}_n}{{(n+3)}_n}}{}_{3}F_2\left(\left.\begin{array}{c}-n,n+3,1\\ 3/2,2\end{array}\right|{\displaystyle \frac{1-x}{2}}\right)={\displaystyle \prod _{k=1}^n}(x-cos{\displaystyle \frac{2k\pi }{n}}),\end{array}$$

(217)

$$\begin{array}{c}{\overline{W}}_n(x;1)={\overline{Q}}_n^{({\displaystyle \frac{1}{2}},-{\displaystyle \frac{1}{2}})}(x;1)={\displaystyle \frac{2n+3-{\overline{W}}_{n+1}\left(x\right)}{1-x}}\hfill \\ \hfill ={\displaystyle \frac{(n+1)2^n{(5/2)}_n}{{(n+3)}_n}}{}_{3}F_2\left(\left.\begin{array}{c}-n,n+3,1\\ 5/2,2\end{array}\right|{\displaystyle \frac{1-x}{2}}\right).\end{array}$$

As we observe, only relations (216) and (217) are decomposable having multiple roots. In this direction, it is worth mentioning that there is a generic decomposable sequence,

$$T_n(x;\lambda )={\displaystyle \frac{T_{n+1}\left(x\right)-T_{n+1}\left(\lambda \right)}{x-\lambda }}=2^n{\displaystyle \prod _{k=1}^n}x-\left(\lambda cos{\displaystyle \frac{2k\pi }{n+1}}-\sqrt{1-{\lambda }^2}sin{\displaystyle \frac{2k\pi }{n+1}}\right),$$

satisfying the non-homogeneous differential equation

$$\begin{array}{c}(x-\lambda )(1-x^2){\displaystyle \frac{d^2}{d{x}^2}}{T}_n(x;\lambda )+\left(-3x^2+\lambda x+2\right){\displaystyle \frac{d}{dx}}{T}_n(x;\lambda )\hfill \\ \hfill +\left({(n+1)}^2(x-\lambda )-x\right)T_n(x;\lambda )=-{(n+1)}^{2}cos((n+1)arccos\lambda ),\end{array}$$

and the recurrence relation

$$T_{n+1}(x;\lambda )=2x{T}_n(x;\lambda )-T_{n-1}(x;\lambda )+2cos(narccos\lambda ).$$

For instance,

$$T_n(x;0)={\displaystyle \frac{T_{n+1}\left(x\right)-T_{n+1}\left(0\right)}{x}}=2^n{\displaystyle \prod _{k=1}^n}(x+sin{\displaystyle \frac{2k\pi }{n+1}}),$$

is an uncorrelated polynomial with respect to the fixed function $z\left(x\right)=x^{-1}$ so that according to Corollary 7 and relation (215), we have

$${\int }_{-1}^1{\displaystyle \frac{T_{n+1}^2\left(x\right)}{\sqrt{1-x^2}}}dx={\int }_{-1}^1{\displaystyle \frac{x^2}{\sqrt{1-x^2}}}dx={\displaystyle \frac{\pi }{2}},$$

and as a result,

$$\begin{array}{c}{\left.{\mathrm{cov}}_1\left(T_m(x;0),T_n(x;0);{\displaystyle \frac{1}{x}}\right)\right|}_{{\displaystyle \frac{x^2}{\sqrt{1-x^2}}}}={\int }_{-1}^1{\displaystyle \frac{x^2}{\sqrt{1-x^2}}}{T}_m(x;0)T_n(x;0)dx\hfill \\ \hfill -{\displaystyle \frac{1}{\pi }}{\int }_{-1}^1{\displaystyle \frac{x}{\sqrt{1-x^2}}}{T}_m(x;0)dx{\int }_{-1}^1{\displaystyle \frac{x}{\sqrt{1-x^2}}}{T}_n(x;0)dx={\delta }_{m,n}.\end{array}$$

9.2. An Uncorrelated Sequence of Hypergeometric Polynomials of ${}_{2}F_2$ Type

At this turn, we consider the monic type of the (generalized) Laguerre polynomials [20,25]

$${\overline{L}}_n^{\left(\alpha \right)}\left(x\right)={(-1)}^n{(\alpha +1)}_n{}_{1}F_1\left(\left.\begin{array}{c}-n\\ \alpha +1\end{array}\right|x\right),$$

satisfying the equation

$$x{\displaystyle \frac{d^2}{d{x}^2}}{\overline{L}}_n^{\left(\alpha \right)}\left(x\right)+\left(\alpha +1-x\right){\displaystyle \frac{d}{dx}}{\overline{L}}_n^{\left(\alpha \right)}\left(x\right)+n{\overline{L}}_n^{\left(\alpha \right)}\left(x\right)=0.$$

They also satisfy the recurrence relation

$${\overline{L}}_{n+1}^{\left(\alpha \right)}\left(x\right)=\left(x-2n-\alpha -1\right){\overline{L}}_n^{\left(\alpha \right)}\left(x\right)-n(n+\alpha ){\overline{L}}_{n-1}^{\left(\alpha \right)}\left(x\right).$$

Noting that ${\overline{L}}_n^{\left(\alpha \right)}\left(0\right)={(-1)}^n{(\alpha +1)}_n,$ the uncorrelated polynomials based on Laguerre polynomials is defined as

$${\overline{Q}}_n^{\left(\alpha \right)}(x;0)={\displaystyle \frac{{\overline{L}}_{n+1}^{\left(\alpha \right)}\left(x\right)-{\overline{L}}_{n+1}^{\left(\alpha \right)}\left(0\right)}{x}}={(-1)}^n(n+1){(\alpha +2)}_n{}_{4}F_2\left(\left.\begin{array}{c}-n,1\\ \alpha +2,2\end{array}\right|x\right).$$

(218)

Similar to the previous example, for $\alpha >-1$, we can prove that

$${\left.{\mathrm{cov}}_1\left({\overline{Q}}_m^{\left(\alpha \right)}(x;0),{\overline{Q}}_n^{\left(\alpha \right)}(x;0);{\displaystyle \frac{1}{x}}\right)\right|}_{x^{\alpha +2}{e}^{-x}}={\displaystyle \frac{n!\Gamma (n+\alpha +1)}{\Gamma (\alpha +3)}}{\delta }_{m,n}.$$

10. A Unified Approach for the Polynomials Obtained in Section 7, Section 8 and Section 9

According to the distributions given in Table 1, only beta and gamma weight functions can be considered for the non-symmetric infinite cases of uncorrelated polynomials, as the normal distribution is somehow connected to a special case of gamma distribution. In this direction, the general properties of two polynomials, (177) and (187), reveal that the most general case of complete uncorrelated polynomials relevant to the beta weight function is when $w\left(x\right)=x^a{(1-x)}^b$ and $w\left(x\right)z\left(x\right)=x^c{(1-x)}^d$, i.e., $z\left(x\right)=x^{c-a}{(1-x)}^{d-b}$ where $a,b,c,d\in \mathbb{R}$ and $x\in [0,1]$. Hence, if the corresponding uncorrelated polynomial is indicated as ${\mathbf{P}}_n(x;a,b,c,d)$, we have

$$\begin{array}{cc}\hfill & {\int }_0^1{x}^a{(1-x)}^b{\mathbf{P}}_n(x;a,b,c,d){\mathbf{P}}_m(x;a,b,c,d)dx\hfill \\ \hfill & -{\displaystyle \frac{\Gamma (2c+2d-a-b+2)}{\Gamma (2c-a+1)\Gamma (2d-b+1)}}{\int }_0^1{x}^c{(1-x)}^d{\mathbf{P}}_n(x;a,b,c,d)dx{\int }_0^1{x}^c{(1-x)}^d{\mathbf{P}}_m(x;a,b,c,d)dx\hfill \\ \hfill & =\left({\int }_0^1{x}^a{(1-x)}^b{\mathbf{P}}_n^2(x;a,b,c,d)dx-{\displaystyle \frac{\Gamma (2c+2d-a-b+2)}{\Gamma (2c-a+1)\Gamma (2d-b+1)}}{\left({\int }_0^1{x}^c{(1-x)}^d{\mathbf{P}}_n(x;a,b,c,d)dx\right)}^2\right){\delta }_{m,n},\hfill \end{array}$$

(219)

provided that $2c-a+1>0,2d-b+1>0\mathrm{and}b,d>-1.$

The components of the determinant (172) corresponding to this generic polynomial are computed as follows

$$\begin{array}{c}{\left.{\mathrm{cov}}_1\left(x^i,x^j;x^{c-a}{(1-x)}^{d-b}\right)\right|}_{w\left(x\right)=x^a{(1-x)}^b}=\Gamma (b+1){\displaystyle \frac{\Gamma (a+i+j+1)}{\Gamma (a+b+i+j+2)}}\hfill \\ \hfill -{\displaystyle \frac{\Gamma (2c+2d-a-b+2){\Gamma }^2(d+1)}{\Gamma (2c-a+1)\Gamma (2d-b+1)}}{\displaystyle \frac{\Gamma (c+i+1)\Gamma (c+j+1)}{\Gamma (c+d+i+2)\Gamma (c+d+j+2)}},\end{array}$$

(220)

in which $2c-a+1>0,2d-b+1>0$ and $b,d>-1$.

According to the preceding information, the polynomials (177) can be represented as

$${}_{4}F_3\left(\left.\begin{array}{c}-n,n+1,-r,r+2\\ 1,-r+1,r+1\end{array}\right|x\right)={\mathbf{P}}_n(x;0,0,r,0),$$

(221)

and the polynomials (187) as

$${}_{4}F_3\left(\left.\begin{array}{c}-n,n+2r+1,r,r+2\\ 2r+1,r+1,r+1\end{array}\right|x\right)={\mathbf{P}}_n(x;2r,0,r,0),$$

(222)

and noting (213), since

$$\begin{array}{c}{\int }_0^1{x}^{\alpha +2}{(1-x)}^{\beta }{}_{3}F_2\left(\left.\begin{array}{c}-n,n+\alpha +\beta +3,1\\ \alpha +2,2\end{array}\right|x\right){}_{3}F_2\left(\left.\begin{array}{c}-m,m+\alpha +\beta +3,1\\ \alpha +2,2\end{array}\right|x\right)dx\hfill \\ ={\displaystyle \frac{1}{{\int }_0^1{x}^{\alpha }{(1-x)}^{\beta }dx}}\left({\int }_0^1{x}^{\alpha +1}{(1-x)}^{\beta }{}_{3}F_2\left(\left.\begin{array}{c}-n,n+\alpha +\beta +3,1\\ \alpha +2,2\end{array}\right|x\right)dx\right)\hfill \\ \times \left({\int }_0^1{x}^{\alpha +1}{(1-x)}^{\beta }{}_{3}F_2\left(\left.\begin{array}{c}-m,m+\alpha +\beta +3,1\\ \alpha +2,2\end{array}\right|x\right)dx\right)\iff n\ne m,\hfill \end{array}$$

the shifted polynomials (210) on $[0,1]$ are represented as

$${}_{3}F_2\left(\left.\begin{array}{c}-n,n+\alpha +\beta +3,1\\ \alpha +2,2\end{array}\right|x\right)={\mathbf{P}}_n(x;\alpha +2,\beta ,\alpha +1,\beta ).$$

Similarly, the most general case of complete uncorrelated polynomials relevant to the gamma weight function is when $w\left(x\right)=x^a{e}^{-bx}$ and $w\left(x\right)z\left(x\right)=x^c{e}^{-dx}$, i.e., $z\left(x\right)=x^{c-a}{e}^{-(d-b)x}$ where $a,b,c,d\in \mathbb{R}$ and $x\in {\mathbb{R}}^{+}$. Therefore, if the corresponding uncorrelated polynomial is indicated as ${\mathbf{Q}}_n(x;a,b,c,d)$, then

$$\begin{array}{c}{\int }_0^{\infty }{x}^a{e}^{-bx}{\mathbf{Q}}_n(x;a,b,c,d){\mathbf{Q}}_m(x;a,b,c,d)dx\hfill \\ -{\displaystyle \frac{{(2d-b)}^{2c-a+1}}{\Gamma (2c-a+1)}}{\int }_0^{\infty }{x}^c{e}^{-dx}{\mathbf{Q}}_n(x;a,b,c,d)dx{\int }_0^{\infty }{x}^c{e}^{-dx}{\mathbf{Q}}_m(x;a,b,c,d)dx\hfill \\ \hfill =\left({\int }_0^{\infty }{x}^a{e}^{-bx}{\mathbf{Q}}_n^2(x;a,b,c,d)dx-{\displaystyle \frac{{(2d-b)}^{2c-a+1}}{\Gamma (2c-a+1)}}{\left({\int }_0^{\infty }{x}^c{e}^{-dx}{\mathbf{Q}}_n(x;a,b,c,d)dx\right)}^2\right){\delta }_{m,n},\end{array}$$

provided that $2c-a+1>0,2d-b>0\mathrm{and}b,d>0.$

The components of the determinant (172) corresponding to this second generic polynomial are computed as

$$\begin{array}{c}{\left.{\mathrm{cov}}_1\left(x^i,x^j;x^{c-a}{e}^{-(d-b)x}\right)\right|}_{w\left(x\right)=x^a{e}^{-bx}}\hfill \\ \hfill ={\displaystyle \frac{\Gamma (a+i+j+1)}{b^{a+i+j+1}}}-{\displaystyle \frac{{(2d-b)}^{2c-a+1}}{\Gamma (2c-a+1)}}{\displaystyle \frac{\Gamma (c+i+1)\Gamma (c+j+1)}{d^{2c+i+j+2}}},\end{array}$$

in which $2c-a+1>0,2d-b>0\mathrm{and}b,d>0$.

As a sample, the polynomials (218) can be represented as

$${}_{2}F_2\left(\left.\begin{array}{c}-n,1\\ \alpha +2,2\end{array}\right|x\right)={\mathbf{Q}}_n(x;\alpha +2,1,\alpha +1,1).$$

A Basic Example of Uncorrelated Hypergeometric Polynomials of ${}_{4}F_3$ Type

In this section, we are going to obtain the explicit form of ${\mathbf{P}}_n(x;a,0,c,0)$ using an interesting technique. Since $b=d=0$, $w\left(x\right)=x^a$ and $z\left(x\right)=x^{c-a}$ defined on $[0,1]$. In the first step, we simplify (220) for $b=d=0$ as follows:

$${\left.{\mathrm{cov}}_1\left(x^i,x^j;x^{c-a}\right)\right|}_{w\left(x\right)=x^a}={\displaystyle \frac{(c-a-i)(c-a-j)}{(i+c+1)(j+c+1)(i+j+a+1)}},$$

where $2c-a+1>0,a\ne c\mathrm{and}a,c>-1$.

Referring to the results (221) and (222) and the fact that ${\mathbf{P}}_n(x;a,0,c,0)$ is a generalization of both of them, we can imagine that it is of the ${}_{4}F_3$ type without a loss in generality.

Since, in a ${}_{4}F_3$-type polynomial of the form

$${}_{4}F_3\left(\left.\begin{array}{c}-n,a_2,a_3,a_4\\ b_1,b_2,b_3\end{array}\right|x\right)={\displaystyle \sum _{k=0}^n}{u}_k{x}^k\mathrm{where}{u}_k={\displaystyle \frac{{(-n)}_k{\left(a_2\right)}_k{\left(a_3\right)}_k{\left(a_4\right)}_k}{{\left(b_1\right)}_k{\left(b_2\right)}_k{\left(b_3\right)}_{k}k!}},$$

we have

$${\displaystyle \frac{u_{n-1}}{u_n}}=-{\displaystyle \frac{n(n+b_1-1)(n+b_2-1)(n+b_3-1)}{(n+a_2-1)(n+a_3-1)(n+a_4-1)}},$$

(223)

which is to be equal to the minus of the coefficient of $x^{n-1}$ in the determinant of the monic polynomial ${\overline{\mathbf{P}}}_n(x;a,0,c,0)$ in (172), if, for simplicity, we set

$$a_{i,j}={\displaystyle \frac{(c-a-i)(c-a-j)}{(i+c+1)(j+c+1)(i+j+a+1)}}\mathrm{for}i=0,1,\dots ,n-1\mathrm{and}j=0,1,\dots ,n,$$

to achieve our goal, we should, therefore, compute the two following determinants (according to the main determinant (172)),

$$M_n=\left|\begin{array}{ccccc}{a}_{0,0}& a_{0,1}& \cdots & a_{0,n-2}& a_{0,n-1}\\ a_{1,0}& a_{1,1}& \cdots & a_{1,n-2}& a_{1,n-1}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ a_{n-1,0}& a_{n-1,1}& \cdots & a_{n-1,n-2}& a_{n-1,n-1}\end{array}\right|,$$

and

$$N_n=\left|\begin{array}{ccccc}{a}_{0,0}& a_{0,1}& \cdots & a_{0,n-2}& a_{0,n}\\ a_{1,0}& a_{1,1}& \cdots & a_{1,n-2}& a_{1,n}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ a_{n-1,0}& a_{n-1,1}& \cdots & a_{n-1,n-2}& a_{n-1,n}\end{array}\right|,$$

and then obtain the quotient $-N_n/M_n$ (with the aid of advanced mathematical software) as

$$-{\displaystyle \frac{N_n}{M_n}}=-{\displaystyle \frac{n(n+a)(n+a-c)(n+c)}{(2n+a)(n+a-c-1)(n+c+1)}},$$

and compare it with (223) to finally obtain the explicit form of the polynomials as

$${\mathbf{P}}_n(x;a,0,c,0)={}_{4}F_3\left(\left.\begin{array}{c}-n,n+a+1,a-c,c+2\\ a+1,a-c+1,c+1\end{array}\right|x\right),$$

(224)

satisfying the uncorrelatedness condition (219) with $b=d=0$, i.e.,

$$\begin{array}{c}{\int }_0^1{x}^a{\mathbf{P}}_n(x;a,0,c,0){\mathbf{P}}_m(x;a,0,c,0)dx\hfill \\ -(2c-a+1){\int }_0^1{x}^c{\mathbf{P}}_n(x;a,0,c,0)dx{\int }_0^1{x}^c{\mathbf{P}}_m(x;a,0,c,0)dx\\ =\left({\int }_0^1{x}^a{\mathbf{P}}_n^2(x;a,0,c,0)dx-(2c-a+1){\left({\int }_0^1{x}^c{\mathbf{P}}_n(x;a,0,c,0)dx\right)}^2\right){\delta }_{m,n}\\ \hfill \iff 2c-a+1>0,a\ne c\mathrm{and}a,c>-1.\end{array}$$

(225)

For the limit case $2c-a+1=0$ in (225), the polynomials (224) would reduce to the well-known special case of shifted Jacobi polynomials defined on $[0,1]$, i.e.,

$${\mathbf{P}}_n(x;a,0,{\displaystyle \frac{a-1}{2}},0)=P_{n,+}^{(0,a)}\left(x\right)={}_{2}F_1\left(\left.\begin{array}{c}-n,n+a+1\\ a+1\end{array}\right|x\right)(a>-1).$$

Also, we have

$$\begin{array}{cc}\hfill \underset{c\to \infty }{lim}{\mathbf{P}}_n(x;a,0,c,0)& =\underset{c\to \infty }{lim}{}_{4}F_3\left(\left.\begin{array}{c}-n,n+a+1,a-c,c+2\\ a+1,a-c+1,c+1\end{array}\right|x\right)\hfill \\ \hfill & ={}_{2}F_1\left(\left.\begin{array}{c}-n,n+a+1\\ a+1\end{array}\right|x\right)=P_{n,+}^{(0,a)}\left(x\right),\hfill \end{array}$$

and

$$\underset{a\to \infty }{lim}{\mathbf{P}}_n(x;a,0,c,0)={}_{2}F_1\left(\left.\begin{array}{c}-n,c+2\\ c+1\end{array}\right|x\right)(c>-1).$$

As we mentioned, the polynomials (224) are a generalization of (177) or (221) for $(a,c)=(0,r)$ and a generalization of (187) or (222) for $(a,c)=(2r,r)$. In order to evaluate the existing integrals in (225), we first have

$$\begin{array}{c}{\int }_0^1{x}^c{\mathbf{P}}_n(x;a,0,c,0)dx={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+a+1)}_k{(a-c)}_k{(c+2)}_k}{{(a+1)}_k{(a-c+1)}_k{(c+1)}_{k}k!(c+1+k)}}\hfill \\ \hfill ={\displaystyle \frac{1}{c+1}}{}_{3}F_2\left(\left.\begin{array}{c}-n,n+a+1,a-c\\ a+1,a-c+1\end{array}\right|1\right)={\displaystyle \frac{1}{c+1}}{\displaystyle \frac{n!{(c+1)}_n}{{(a+1)}_n{(a+1-c)}_n}},\end{array}$$

(226)

and

$$\begin{array}{c}{\int }_0^1{x}^a{\mathbf{P}}_n(x;a,0,c,0){\mathbf{P}}_m(x;a,0,c,0)dx={\displaystyle \frac{1}{a+1}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+a+1)}_k{(a-c)}_k{(c+2)}_k}{{(a+2)}_k{(a-c+1)}_k{(c+1)}_{k}k!}}\hfill \\ \hfill \times {}_{5}F_4\left(\left.\begin{array}{c}-m,m+a+1,a-c,c+2,a+1+k\\ a+1,a-c+1,c+1,a+2+k\end{array}\right|1\right),\end{array}$$

(227)

which simplifies the left side of (225) as

$$\begin{array}{cc}\hfill & {\int }_0^1{x}^a{\mathbf{P}}_n(x;a,0,c,0){\mathbf{P}}_m(x;a,0,c,0)dx\hfill \\ \hfill & -(2c-a+1){\int }_0^1{x}^c{\mathbf{P}}_n(x;a,0,c,0)dx{\int }_0^1{x}^c{\mathbf{P}}_m(x;a,0,c,0)dx\hfill \\ \hfill & ={\displaystyle \frac{1}{a+1}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+a+1)}_k{(a-c)}_k{(c+2)}_k}{{(a+2)}_k{(a-c+1)}_k{(c+1)}_{k}k!}}\hfill \\ \hfill & \times {}_{5}F_4\left(\left.\begin{array}{c}-m,m+a+1,a-c,c+2,a+1+k\\ a+1,a-c+1,c+1,a+2+k\end{array}\right|1\right)\hfill \\ \hfill & -{\displaystyle \frac{2c-a+1}{{(c+1)}^2}}{\displaystyle \frac{n!{(c+1)}_n}{{(a+1)}_n{(a+1-c)}_n}}{\displaystyle \frac{m!{(c+1)}_m}{{(a+1)}_m{(a+1-c)}_m}}.\hfill \end{array}$$

(228)

To evaluate (226), we have again used the recurrence relations technique. Since

$$N\left(n\right)={}_{3}F_2\left(\left.\begin{array}{c}-n,n+a+1,a-c\\ a+1,a-c+1\end{array}\right|1\right),$$

satisfies the first-order relation

$$N(n+1)={\displaystyle \frac{(n+1)(n+c+1)}{(n+a+1)(n+a-c+1)}}N\left(n\right),$$

so

$${}_{3}F_2\left(\left.\begin{array}{c}-n,n+a+1,a-c\\ a+1,a-c+1\end{array}\right|1\right)={\displaystyle \frac{n!{(c+1)}_n}{{(a+1)}_n{(a+1-c)}_n}}.$$

However, note that all results obtained in (226), (190) and (179) could also be derived using the Pfaff-Saalschutz summation theorem employed to derive (147). Similarly, to evaluate ${}_{5}F_4(.)$ in (227), we can apply a recurrence technique as follows. Since

$$M\left(m\right)={}_{5}F_4\left(\left.\begin{array}{c}-m,m+a+1,a-c,c+2,a+1+k\\ a+1,a-c+1,c+1,a+2+k\end{array}\right|1\right),$$

satisfies the second-order equation

$$\begin{array}{c}(2m+a+2)(m+a+2)(m+a+1)(m+a+2-c)(m+a+3+k)M(m+2)\hfill \\ -(2m+a+3)(m+a+1)(m+2)\left(2m(m+a+3)+(2c-a)k+(a+2)(c+2)\right)M(m+1)\\ \hfill +(2m+a+4)(m+2)(m+1)(m+1+c)(m-k)M\left(m\right)=0,\end{array}$$

having two independent solutions

$$M_1\left(m\right)={\displaystyle \frac{m!{(c+1)}_m}{{(a+1)}_m{(a+1-c)}_m}},\mathrm{and}{M}_2\left(m\right)={\displaystyle \frac{m!{(-k)}_m}{{(a+1)}_m{(a+2+k)}_m}},$$

so,

$$\begin{array}{cc}\hfill & {}_{5}F_4\left(\left.\begin{array}{c}-m,m+a+1,a-c,c+2,a+1+k\\ a+1,a-c+1,c+1,a+2+k\end{array}\right|1\right)={\displaystyle \frac{m!}{(c+1)(c+1+k){(a+1)}_m}}\hfill \\ \hfill & \times \left((2c-a+1)(a+1+k){\displaystyle \frac{{(c+1)}_m}{{(a+1-c)}_m}}+(a-c)(a-c+k){\displaystyle \frac{{(-k)}_m}{{(a+2+k)}_m}}\right).\hfill \end{array}$$

(229)

Hence, in order to compute

$$\begin{array}{c}{\mathrm{var}}_1\left({\mathbf{P}}_n(x;a,0,c,0);x^{c-a}\right)\hfill \\ \hfill ={\int }_0^1{x}^a{\mathbf{P}}_n^2(x;a,0,c,0)dx-(2c-a+1){\left({\int }_0^1{x}^c{\mathbf{P}}_n(x;a,0,c,0)dx\right)}^2,\end{array}$$

we first suppose in (228) that $m=n$, and then we refer to (229) to arrive at

$$\begin{array}{cc}\hfill \left(a+1\right)M^{*}& ={\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+a+1)}_k{(a-c)}_k{(c+2)}_k}{{(a+2)}_k{(a-c+1)}_k{(c+1)}_{k}k!}}\hfill \\ \hfill & \times {}_{5}F_4\left(\left.\begin{array}{c}-n,n+a+1,a-c,c+2,a+1+k\\ a+1,a-c+1,c+1,a+2+k\end{array}\right|1\right)\hfill \\ \hfill & ={\displaystyle \frac{(a+1)(2c-a+1)}{{(c+1)}^2}}{\displaystyle \frac{{(n!)}^2{(c+1)}_n^2}{{(a+1)}_n^2{(a-c+1)}_n^2}}\hfill \\ \hfill & +{\displaystyle \frac{(a+1){(a-c)}^2}{{(c+1)}^2}}{\displaystyle \frac{n!}{(n+a+1){(a+1)}_n^2}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(-n)}_k{(n+a+1)}_k{(-k)}_n}{{(n+a+2)}_{k}k!}}.\hfill \end{array}$$

Again, when it is noted that ${(-k)}_n=0$ for every $k<n$, the following final result will be derived.

Corollary 8.

If $2c-a+1>0,a\ne c\mathrm{and}a,c>-1$, then

$${\int }_0^1{x}^a{\mathbf{P}}_n^2(x;a,0,c,0)dx-(2c-a+1){\left({\int }_0^1{x}^c{\mathbf{P}}_n(x;a,0,c,0)dx\right)}^2={\displaystyle \frac{1}{2n+a+1}}{\left({\displaystyle \frac{(a-c)n!}{(c+1){(a+1)}_n}}\right)}^2.$$

Moreover, (228) is simplified as

$$\begin{array}{c}{\int }_0^1{x}^a{\mathbf{P}}_n(x;a,0,c,0){\mathbf{P}}_m(x;a,0,c,0)dx\hfill \\ -(2c-a+1){\int }_0^1{x}^c{\mathbf{P}}_n(x;a,0,c,0)dx{\int }_0^1{x}^c{\mathbf{P}}_m(x;a,0,c,0)dx\\ \hfill ={\displaystyle \frac{{(a-c)}^2}{{(c+1)}^2}}{\displaystyle \frac{m!}{(m+a+1){(a+1)}_m^2}}{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{(n+a+1)}_k{(-n)}_k}{{(m+a+2)}_k}}{\displaystyle \frac{{(-k)}_m}{k!}}=0\iff m\ne n,\end{array}$$

leading to the same as relation (193) for $2r=\alpha >-1$.

Corollary 9.

Using the latter corollary, we can now construct an optimized polynomial approximation (or expansion as $n\to \infty$) for $f\left(x\right)$, whose error 1-variance is minimized as follows:

$$f\left(x\right)\cong {\displaystyle \sum _{k=0}^n}{\displaystyle \frac{A_k}{B_k}}{}_{4}F_3\left(\left.\begin{array}{c}-k,k+a+1,a-c,c+2\\ a+1,a-c+1,c+1\end{array}\right|x\right),$$

(230)

in which

$$\begin{array}{cc}\hfill A_k& ={\int }_0^1{x}^{a}f\left(x\right){}_{4}F_3\left(\left.\begin{array}{c}-k,k+a+1,a-c,c+2\\ a+1,a-c+1,c+1\end{array}\right|x\right)dx\hfill \\ \hfill & -\left(2c-a+1\right){\int }_0^1{x}^{c}f\left(x\right)dx{\int }_0^1{x}^c{}_{4}F_3\left(\left.\begin{array}{c}-k,k+a+1,a-c,c+2\\ a+1,a-c+1,c+1\end{array}\right|x\right)dx\hfill \\ \hfill & ={\displaystyle \sum _{j=0}^k}{\displaystyle \frac{{(-k)}_j{(k+a+1)}_j{(a-c)}_j{(c+2)}_j}{{(a+1)}_j{(a-c+1)}_j{(c+1)}_{j}j!}}{\int }_0^1{x}^{a+j}f\left(x\right)dx-{\displaystyle \frac{2c-a+1}{{(c+1)}^2}}{\displaystyle \frac{k!{(c+1)}_k}{{(a+1)}_k{(a+1-c)}_k}}{\int }_0^1{x}^{c}f\left(x\right)dx,\hfill \end{array}$$

(231)

and

$$B_k={\displaystyle \frac{1}{2k+a+1}}{\left({\displaystyle \frac{(a-c)k!}{(c+1){(a+1)}_k}}\right)}^2.$$

(232)

We clearly observe in the polynomial-type approximation (230) that its basis do not satisfy an orthogonal condition but a complete uncorrelatedness condition. However, if we define the non-polynomial sequence

$$\begin{array}{c}{\mathbf{G}}_n(x;a,c)\hfill \\ \hfill ={}_{4}F_3\left(\left.\begin{array}{c}-n,n+a+1,a-c,c+2\\ a+1,a-c+1,c+1\end{array}\right|x\right)-{\displaystyle \frac{2c-a+1}{c+1}}{\displaystyle \frac{n!{(c+1)}_n}{{(a+1)}_n{(a+1-c)}_n}}{x}^{c-a},\end{array}$$

(233)

satisfying the orthogonality condition

$$\begin{array}{c}{\int }_0^1{x}^a{\mathbf{G}}_n(x;a,c){\mathbf{G}}_m(x;a,c)dx={\displaystyle \frac{1}{2n+a+1}}{\left({\displaystyle \frac{(a-c)n!}{(c+1){(a+1)}_n}}\right)}^2{\delta }_{m,n}\hfill \\ \hfill \iff 2c-a+1>0,a\ne c\mathrm{and}a,c>-1,\end{array}$$

(234)

we then obtain a non-polynomial type approximation (or expansion) as follows:

$$f\left(x\right)\cong {\displaystyle \sum _{k=0}^n}{\displaystyle \frac{A_k^{*}}{B_k^{*}}}{\mathbf{G}}_k(x;a,c),$$

(235)

in which $A_k^{*}=A_k\mathrm{and}{B}_k^{*}=B_k$ according to the important Remark 1 and relation (53), i.e., as the same forms as (231) and (232). Once again, the orthogonal sequence (233) is generated only when the uncorrelated polynomial sequence (224) has been already generated. Also, the non-polynomial approximation (235) is optimized in the sense of ordinary least squares, while the polynomial-type approximation (230) is optimized in the sense of least 1-variances.

11. p-Uncorrelated Vectors with Respect to a Fixed Vector

The concept of p-uncorrelatedness can similarly be employed in vector spaces. Let ${\overrightarrow{A}}_m=(a_1,a_2,\dots ,a_m)$ and ${\overrightarrow{B}}_m=(b_1,b_2,\dots ,b_m)$ be two arbitrary vectors, and let ${\overrightarrow{I}}_m=(1,1,\dots ,1)$ denote a unit vector. Also, let ${\overrightarrow{Z}}_m=(z_1,z_2,\dots ,z_m)$ be a fixed and predetermined vector. When the definition of the inner product of two vectors is recalled as ${\overrightarrow{A}}_m.{\overrightarrow{B}}_m={\displaystyle \sum _{k=1}^m}{a}_k{b}_k,$ it is not difficult to verify that

$$\begin{array}{cc}\hfill & \left({\overrightarrow{A}}_m-(1-\sqrt{1-p}){\displaystyle \frac{{\overrightarrow{A}}_m.{\overrightarrow{Z}}_m}{{\overrightarrow{Z}}_m.{\overrightarrow{Z}}_m}}{\overrightarrow{Z}}_m\right).\left({\overrightarrow{B}}_m-(1-\sqrt{1-p}){\displaystyle \frac{{\overrightarrow{B}}_m.{\overrightarrow{Z}}_m}{{\overrightarrow{Z}}_m.{\overrightarrow{Z}}_m}}{\overrightarrow{Z}}_m\right)\hfill \\ \hfill & ={\overrightarrow{A}}_m.{\overrightarrow{B}}_m-p{\displaystyle \frac{({\overrightarrow{A}}_m.{\overrightarrow{Z}}_m)({\overrightarrow{B}}_m.{\overrightarrow{Z}}_m)}{{\overrightarrow{Z}}_m.{\overrightarrow{Z}}_m}}.\hfill \end{array}$$

(236)

For instance, if ${\overrightarrow{Z}}_m={\overrightarrow{I}}_m$, then

$$\begin{array}{cc}\hfill & \left({\overrightarrow{A}}_m-(1-\sqrt{1-p}){\displaystyle \frac{{\overrightarrow{A}}_m.{\overrightarrow{I}}_m}{m}}{\overrightarrow{I}}_m\right).\left({\overrightarrow{B}}_m-(1-\sqrt{1-p}){\displaystyle \frac{{\overrightarrow{B}}_m.{\overrightarrow{I}}_m}{m}}{\overrightarrow{I}}_m\right)\hfill \\ \hfill & ={\overrightarrow{A}}_m.{\overrightarrow{B}}_m-{\displaystyle \frac{p}{m}}({\overrightarrow{A}}_m.{\overrightarrow{I}}_m)({\overrightarrow{B}}_m.{\overrightarrow{I}}_m),\hfill \end{array}$$

where ${\overrightarrow{I}}_m.{\overrightarrow{I}}_m=m$ and $p\in [0,1]$. Relation (236) shows that the two vectors ${\overrightarrow{A}}_m\mathrm{and}{\overrightarrow{B}}_m$ are p-uncorrelated with respect to the fixed vector ${\overrightarrow{Z}}_m$ if $p({\overrightarrow{A}}_m.{\overrightarrow{Z}}_m)({\overrightarrow{B}}_m.{\overrightarrow{Z}}_m)=({\overrightarrow{A}}_m.{\overrightarrow{B}}_m)({\overrightarrow{Z}}_m.{\overrightarrow{Z}}_m).$

• Also, the notions of p-covariance and p-variance can be defined for these two vectors (with respect to ${\overrightarrow{Z}}_m$) as follows:

$${\mathrm{cov}}_p({\overrightarrow{A}}_m,{\overrightarrow{B}}_m;{\overrightarrow{Z}}_m)={\displaystyle \frac{1}{m}}\left({\overrightarrow{A}}_m.{\overrightarrow{B}}_m-p{\displaystyle \frac{({\overrightarrow{A}}_m.{\overrightarrow{Z}}_m)({\overrightarrow{B}}_m.{\overrightarrow{Z}}_m)}{{\overrightarrow{Z}}_m.{\overrightarrow{Z}}_m}}\right),$$

(237)

and

$${\mathrm{var}}_p({\overrightarrow{A}}_m;{\overrightarrow{Z}}_m)={\displaystyle \frac{1}{m}}\left({\overrightarrow{A}}_m.{\overrightarrow{A}}_m-p{\displaystyle \frac{{({\overrightarrow{A}}_m.{\overrightarrow{Z}}_m)}^2}{{\overrightarrow{Z}}_m.{\overrightarrow{Z}}_m}}\right)\ge 0.$$

(238)

Referring to the basic representation (43) and definitions (237) and (238), we can establish a set of p-uncorrelated vectors in terms of the parameter $p\in [0,1]$ if and only if $m=n+1$ and the finite set of initial vectors are linearly independent.

Example 2.

For $m=3$, given three initial orthogonal vectors

$${\overrightarrow{V}}_{0,3}(1,0,0),{\overrightarrow{V}}_{1,3}(0,1,0),{\overrightarrow{V}}_{2,3}(0,0,1),$$

together with the fixed vector ${\overrightarrow{Z}}_3(1,2,3)$. Substituting them into (43) eventually yields

$${\overrightarrow{X}}_{0,3}\left(p\right)=(1,0,0),{\overrightarrow{X}}_{1,3}\left(p\right)=({\displaystyle \frac{2p}{14-p}},1,0),{\overrightarrow{X}}_{2,3}\left(p\right)=({\displaystyle \frac{3p}{14-5p}},{\displaystyle \frac{6p}{14-5p}},1),$$

(239)

which satisfy the conditions

$${\mathrm{cov}}_p\left({\overrightarrow{X}}_{0,3}\left(p\right),{\overrightarrow{X}}_{1,3}\left(p\right);{\overrightarrow{Z}}_3\right)={\mathrm{cov}}_p\left({\overrightarrow{X}}_{0,3}\left(p\right),{\overrightarrow{X}}_{2,3}\left(p\right);{\overrightarrow{Z}}_3\right)={\mathrm{cov}}_p\left({\overrightarrow{X}}_{1,3}\left(p\right),{\overrightarrow{X}}_{2,3}\left(p\right);{\overrightarrow{Z}}_3\right)=0.$$

According to Theorem 4, every arbitrary vector of dimension 3 can be expanded in terms of the above vectors so that we have

$$\begin{array}{c}\overrightarrow{A}=(a,b,c)={\displaystyle \frac{{\mathrm{cov}}_p({\overrightarrow{X}}_{0,3}\left(p\right),\overrightarrow{A};{\overrightarrow{Z}}_3)}{{\mathrm{var}}_p({\overrightarrow{X}}_{0,3}\left(p\right);{\overrightarrow{Z}}_3)}}(1,0,0)+{\displaystyle \frac{{\mathrm{cov}}_p({\overrightarrow{X}}_{1,3}\left(p\right),\overrightarrow{A};{\overrightarrow{Z}}_3)}{{\mathrm{var}}_p({\overrightarrow{X}}_{1,3}\left(p\right);{\overrightarrow{Z}}_3)}}({\displaystyle \frac{2p}{14-p}},1,0)\hfill \\ \hfill +{\displaystyle \frac{{\mathrm{cov}}_p({\overrightarrow{X}}_{2,3}\left(p\right),\overrightarrow{A};{\overrightarrow{Z}}_3)}{{\mathrm{var}}_p({\overrightarrow{X}}_{2,3}\left(p\right);{\overrightarrow{Z}}_3)}}({\displaystyle \frac{3p}{14-5p}},{\displaystyle \frac{6p}{14-5p}},1),\end{array}$$

(240)

in which

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{\mathrm{cov}}_p({\overrightarrow{X}}_{0,3}\left(p\right),\overrightarrow{A};{\overrightarrow{Z}}_3)}{{\mathrm{var}}_p({\overrightarrow{X}}_{0,3}\left(p\right);{\overrightarrow{Z}}_3)}}=a-{\displaystyle \frac{2p}{14-p}}b-{\displaystyle \frac{3p}{14-p}}c,\hfill \\ \hfill & {\displaystyle \frac{{\mathrm{cov}}_p({\overrightarrow{X}}_{1,3}\left(p\right),\overrightarrow{A};{\overrightarrow{Z}}_3)}{{\mathrm{var}}_p({\overrightarrow{X}}_{1,3}\left(p\right);{\overrightarrow{Z}}_3)}}=b-{\displaystyle \frac{6p}{14-5p}}c,\mathrm{and}{\displaystyle \frac{{\mathrm{cov}}_p({\overrightarrow{X}}_{2,3}\left(p\right),\overrightarrow{A};{\overrightarrow{Z}}_3)}{{\mathrm{var}}_p({\overrightarrow{X}}_{2,3}\left(p\right);{\overrightarrow{Z}}_3)}}=c.\hfill \end{array}$$

(241)

For $p=0$, the finite expansion (240) would reduce to an ordinary orthogonal expansion, while there is an important point for the case $p=1$. We observe that replacing $p=1$ in the last item of (239) gives

$${\overrightarrow{X}}_{2,3}\left(1\right)={\displaystyle \frac{1}{3}}(1,2,3)={\displaystyle \frac{1}{3}}{\overrightarrow{Z}}_3.$$

Hence, in (240) (and subsequently (241)),

$${\mathrm{cov}}_1({\overrightarrow{X}}_{2,3}\left(1\right),\overrightarrow{A};{\overrightarrow{Z}}_3)={\mathrm{cov}}_1({\overrightarrow{X}}_{2,3}\left(1\right),\overrightarrow{A};3{\overrightarrow{X}}_{2,3}\left(1\right))=0,$$

and

$${\mathrm{var}}_1({\overrightarrow{X}}_{2,3}\left(1\right);{\overrightarrow{Z}}_3)={\mathrm{var}}_1({\displaystyle \frac{1}{3}}{\overrightarrow{Z}}_3;{\overrightarrow{Z}}_3)=0,$$

which shows that the finite expansion (240) is not valid for the sole case $p=1$, although it is valid for any other $p\in [0,1)$. This is one of the reasons why we have considered this theory for every arbitrary parameter $p\in [0,1]$. For a better analysis, see Figure 1 again. In general, we conjecture that

$${\overrightarrow{X}}_{n,m}\left(1\right)={\displaystyle \frac{det({\overrightarrow{V}}_{0,m},{\overrightarrow{V}}_{1,m},\dots ,{\overrightarrow{V}}_{n-1,m},{\overrightarrow{V}}_{n,m})}{det({\overrightarrow{V}}_{0,m},{\overrightarrow{V}}_{1,m},\dots ,{\overrightarrow{V}}_{n-1,m},{\overrightarrow{Z}}_m)}}{\overrightarrow{Z}}_m(m=n+1),$$

(242)

as for the above-mentioned example

$$det({\overrightarrow{V}}_{0,3},{\overrightarrow{V}}_{1,3},{\overrightarrow{V}}_{2,3})=\left|\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right|=1\mathrm{and}det({\overrightarrow{V}}_{0,3},{\overrightarrow{V}}_{1,3},{\overrightarrow{Z}}_3)=\left|\begin{array}{ccc}1& 0& 1\\ 0& 1& 2\\ 0& 0& 3\end{array}\right|=3.$$

We symbolically examined such a conjecture (242) for the particular cases $n=2,3$, and the results were true. Now that the explicit forms of the p-uncorrelated vectors (239) are available, we can make three parametric orthogonal vectors based on them as follows:

$$\begin{array}{cc}\hfill {\overrightarrow{V}}_{0,3}\left(p\right)& ={\overrightarrow{X}}_{0,3}\left(p\right)-(1-\sqrt{1-p}){\displaystyle \frac{{\overrightarrow{X}}_{0,3}\left(p\right).{\overrightarrow{Z}}_3}{{\overrightarrow{Z}}_3.{\overrightarrow{Z}}_3}}{\overrightarrow{Z}}_3\hfill \\ \hfill & ={\displaystyle \frac{1}{14}}(13+\sqrt{1-p},-2+2\sqrt{1-p},-3+3\sqrt{1-p}),\hfill \\ \hfill {\overrightarrow{V}}_{1,3}\left(p\right)& ={\displaystyle \frac{1}{14-p}}(2p-2+2\sqrt{1-p},-p+10+4\sqrt{1-p},-6+6\sqrt{1-p}),\hfill \\ \hfill {\overrightarrow{V}}_{2,3}\left(p\right)& ={\displaystyle \frac{1}{14-5p}}(3p-3+3\sqrt{1-p},6p-6+6\sqrt{1-p},-5p+5+9\sqrt{1-p}).\hfill \end{array}$$

(243)

Note in the above vectors that

$${\overrightarrow{V}}_{0,3}\left(0\right)={\overrightarrow{V}}_{0,3},{\overrightarrow{V}}_{1,3}\left(0\right)={\overrightarrow{V}}_{1,3}\mathrm{and}{\overrightarrow{V}}_{2,3}\left(0\right)={\overrightarrow{V}}_{2,3},$$

while for $p=1$ we have

$${\overrightarrow{V}}_{0,3}\left(1\right)={\displaystyle \frac{1}{14}}(13,-2,-3),{\overrightarrow{V}}_{1,3}\left(1\right)={\displaystyle \frac{3}{13}}(0,3,-2)\mathrm{and}{\overrightarrow{V}}_{2,3}\left(1\right)=(0,0,0),$$

which confirms that it is not valid for choosing in the orthogonal vectors (243).

12. An Upper Bound for 1-Covariances

As the optimized case is $p=1$, in this part, we are going to obtain an upper bound for ${\mathrm{cov}}_1(X,Y;Z)$. Let $m_X,m_Y,M_X$ and $M_Y$ be real numbers, such that

$$m_{X}Z\le X\le M_{X}Z\mathrm{and}{m}_{Y}Z\le Y\le M_{Y}Z.$$

(244)

It can be verified that the following identity holds true:

$${\mathrm{var}}_1(X;Z)={\displaystyle \frac{1}{E\left(Z^2\right)}}\left(M_{X}E\left(Z^2\right)-E\left(XZ\right)\right)\left(E\left(XZ\right)-m_{X}E\left(Z^2\right)\right)-E\left(\left(M_{X}Z-X\right)\left(X-m_{X}Z\right)\right).$$

(245)

Noting the conditions (244) and this fact that

$$E\left(\left(M_{X}Z-X\right)\left(X-m_{X}Z\right)\right)\ge 0,$$

equality (245) leads to the inequality

$$\begin{array}{c}{\mathrm{var}}_1(X;Z)\le {\displaystyle \frac{1}{E\left(Z^2\right)}}\left(M_{X}E\left(Z^2\right)-E\left(XZ\right)\right)\left(E\left(XZ\right)-m_{X}E\left(Z^2\right)\right)\hfill \\ \hfill \le {\displaystyle \frac{1}{4E\left(Z^2\right)}}{\left(M_{X}E\left(Z^2\right)-m_{X}E\left(Z^2\right)\right)}^2={\displaystyle \frac{E\left(Z^2\right)}{4}}{\left(M_X-m_X\right)}^2.\end{array}$$

(246)

On the other hand, following (246) in the well-known inequality

$${\mathrm{cov}}_1^2(X,Y;Z)\le {\mathrm{var}}_1(X;Z){\mathrm{var}}_1(Y;Z),$$

gives

$$\begin{array}{cc}\hfill {\mathrm{cov}}_1^2(X,Y;Z)& \le {\displaystyle \frac{1}{E^2\left(Z^2\right)}}\left(M_{X}E\left(Z^2\right)-E\left(XZ\right)\right)\left(E\left(XZ\right)-m_{X}E\left(Z^2\right)\right)\hfill \\ \hfill & \times \left(M_{Y}E\left(Z^2\right)-E\left(YZ\right)\right)\left(E\left(YZ\right)-m_{Y}E\left(Z^2\right)\right)\hfill \\ \hfill & \le {\displaystyle \frac{E^2\left(Z^2\right)}{16}}{\left(M_X-m_X\right)}^2{\left(M_Y-m_Y\right)}^2.\hfill \end{array}$$

(247)

One of the direct consequences of (247) is that

$$\left|{\mathrm{cov}}_1(X,Y;Z)\right|\le {\displaystyle \frac{E\left(Z^2\right)}{4}}\left(M_X-m_X\right)\left(M_Y-m_Y\right),$$

(248)

where the constant $1/4$ in (248) is the best possible number in the sense that it cannot be replaced with a smaller quantity. As a particular case, if, in (248), we take

$$P_r(X=x)={\displaystyle \frac{w\left(x\right)}{{\int }_{\alpha }^{\beta }w\left(x\right)dx}},X=f\left(x\right),Y=g\left(x\right)\mathrm{and}Z=z\left(x\right)=1,$$

it will reduce to the weighted Grüss inequality [29,30]

$$\left|{\displaystyle \frac{{\int }_{\alpha }^{\beta }w\left(x\right)f\left(x\right)g\left(x\right)dx}{{\int }_{\alpha }^{\beta }w\left(x\right)dx}}-{\displaystyle \frac{\left({\int }_{\alpha }^{\beta }w\left(x\right)f\left(x\right)dx\right)\left({\int }_{\alpha }^{\beta }w\left(x\right)g\left(x\right)dx\right)}{{\left({\int }_{\alpha }^{\beta }w\left(x\right)dx\right)}^2}}\right|\le {\displaystyle \frac{1}{4}}(M_f-m_f)(M_g-m_g),$$

in which

$$m_f\le f\left(x\right)\le M_f\mathrm{and}{m}_g\le g\left(x\right)\le M_g\mathrm{for}\mathrm{all}x\in [\alpha ,\beta ].$$

13. An Improvement to the Approximate Solutions of Over-Determined Systems

For $n>m$, consider the linear system of equations

$${\displaystyle \sum _{j=1}^m}{a}_{i,j}{x}_j=b_i(i=1,2,\dots ,n),$$

(249)

whose matrix representation is as $A_{n\times m}{X}_{m\times 1}=B_{n\times 1}$ where

$$A=\left[\begin{array}{cccc}\begin{array}{c}{a}_{11}\\ a_{21}\\ ⋮\\ a_{n1}\end{array}& \begin{array}{c}{a}_{12}\\ a_{22}\\ ⋮\\ a_{n1}\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}{a}_{1m}\\ a_{2m}\\ ⋮\\ a_{nm}\end{array}\end{array}\right],X=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_m\end{array}\right]\mathrm{and}B=\left[\begin{array}{c}{b}_1\\ b_2\\ ⋮\\ b_n\end{array}\right].$$

As we mentioned in the introduction, the linear system (249) is called an over-determined system since the number of equations is more than the number of unknowns.

Such systems usually have no exact solution, and the goal is instead to find an approximate solution for the unknowns ${\left\{x_j\right\}}_{j=1}^m$ that fit equations in the sense of solving the problem

$$\underset{\left\{x_j\right\}}{min}{E}_{m,n}(x_1,\dots ,x_m)=\underset{\left\{x_j\right\}}{min}{\displaystyle \sum _{i=1}^n}{\left({\displaystyle \sum _{j=1}^m}{a}_{i,j}{x}_j-b_i\right)}^2.$$

(250)

It has been proven [13] that the minimization problem (250) has a unique vector solution, provided that the m columns of the matrix A are linearly independent, which is given by solving the normal equations $A^{T}A\tilde{X}=A^{T}b,$ where $A^T$ indicates the matrix transpose of A, and $\tilde{X}$ is the approximate solution of the least squares type expressed by $\tilde{X}={\left(A^{T}A\right)}^{-1}{A}^{T}b.$

Instead of considering the problem (250), we would like now to consider the minimization problem

$$\underset{\left\{x_j\right\}}{min}{V}_{m,n}\left(\left.x_1,\dots ,x_m\right|{\left\{z_i\right\}}_{i=1}^n\right)=\underset{\left\{x_j\right\}}{min}{\displaystyle \sum _{i=1}^n}{\left({\displaystyle \sum _{j=1}^m}{a}_{i,j}{x}_j-b_i\right)}^2-{\displaystyle \frac{p}{{\displaystyle \sum _{i=1}^n}{z}_i^2}}{\left({\displaystyle \sum _{i=1}^n}{z}_i({\displaystyle \sum _{j=1}^m}{a}_{i,j}{x}_j-b_i)\right)}^2,$$

(251)

based on the fixed vector $Z_{1\times n}^T=[z_1,z_2,\dots ,z_n]$, where the quantity (251) is clearly smaller than the quantity (250) for any arbitrary selection of ${\left\{z_i\right\}}_{i=1}^n$. In this direction,

$$\begin{array}{c}{\displaystyle \frac{\partial V_{m,n}\left(\left.x_1,\dots ,x_m\right|{\left\{z_i\right\}}_{i=1}^n\right)}{\partial x_k}}\hfill \\ \hfill =2{\displaystyle \sum _{i=1}^n}{a}_{i,k}({\displaystyle \sum _{j=1}^m}{a}_{i,j}{x}_j-b_i)-{\displaystyle \frac{2p}{{\displaystyle \sum _{i=1}^n}{z}_i^2}}\left({\displaystyle \sum _{i=1}^n}{a}_{i,k}{z}_i\right)\left({\displaystyle \sum _{i=1}^n}{z}_i({\displaystyle \sum _{j=1}^m}{a}_{i,j}{x}_j-b_i)\right)=0,\end{array}$$

leads to the linear system

$${\displaystyle \sum _{j=1}^m}\left({\displaystyle \sum _{i=1}^n}{a}_{i,k}{a}_{i,j}-p{\displaystyle \frac{{\displaystyle \sum _{i=1}^n}{a}_{i,k}{z}_i{\displaystyle \sum _{i=1}^n}{a}_{i,j}{z}_i}{{\displaystyle \sum _{i=1}^n}{z}_i^2}}\right)x_j={\displaystyle \sum _{i=1}^n}{a}_{i,k}{b}_i-p{\displaystyle \frac{{\displaystyle \sum _{i=1}^n}{a}_{i,k}{z}_i{\displaystyle \sum _{i=1}^n}{b}_i{z}_i}{{\displaystyle \sum _{i=1}^n}{z}_i^2}}(k=1,2,\dots ,m),$$

(252)

which can also be represented as the matrix form

$$\left(A^{T}A-{\displaystyle \frac{p}{Z^{T}Z}}{A}^{T}Z{Z}^{T}A\right){\tilde{X}}_{p,Z}=A^{T}B-{\displaystyle \frac{p}{Z^{T}Z}}{A}^{T}Z{Z}^{T}B,$$

with the solution

$${\tilde{X}}_{p,Z}={\left(A^{T}A-{\displaystyle \frac{p}{Z^{T}Z}}{A}^{T}Z{Z}^{T}A\right)}^{-1}\left(A^{T}B-{\displaystyle \frac{p}{Z^{T}Z}}{A}^{T}Z{Z}^{T}B\right).$$

(253)

A simple case of the approximate solution (253) is when $Z_{1\times n}^T=I_n=[1,1,\dots ,1]$ and $p=1$, i.e., an ordinary least variance problem such that (253) becomes

$${\tilde{X}}_{1,I_n}={\left(A^{T}A-{\displaystyle \frac{1}{n}}{A}^T{I}_n^T{I}_{n}A\right)}^{-1}\left(A^{T}B-{\displaystyle \frac{1}{n}}{A}^T{I}_n^T{I}_{n}B\right).$$

Example 3.

Suppose $m=2$, $Z_{1\times n}^T=I_n=[1,1,\dots ,1]$ and $p=1$. Then, the corresponding over-determined system takes the simple form

$$a_{i,1}{x}_1+a_{i,2}{x}_2=b_i(i=1,2,\dots ,n>2),$$

and the problem (251) reduces to

$$\underset{\{x_1,x_2\}}{min}{V}_{2,n}\left(\left.x_1,x_2\right|I_n\right)=\underset{\{x_1,x_2\}}{min}{\displaystyle \sum _{i=1}^n}{(a_{i,1}{x}_1+a_{i,2}{x}_2-b_i)}^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle \sum _{i=1}^n}(a_{i,1}{x}_1+a_{i,2}{x}_2-b_i)\right)}^2.$$

(254)

Hence, the explicit solutions of the system (252), i.e.,

$$\left\{\begin{array}{c}\left({\displaystyle \sum _{i=1}^n}{\left(a_{i,1}\right)}^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}\right)}^2\right)x_1+\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{a}_{i,2}-{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{a}_{i,1}{\displaystyle \sum _{i=1}^n}{a}_{i,2}\right)x_2\hfill \\ ={\displaystyle \sum _{i=1}^n}{a}_{i,1}{b}_i-{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{a}_{i,1}{\displaystyle \sum _{i=1}^n}{b}_i,\hfill \\ \left({\displaystyle \sum _{i=1}^n}{a}_{i,2}{a}_{i,1}-{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{a}_{i,2}{\displaystyle \sum _{i=1}^n}{a}_{i,1}\right)x_1+\left({\displaystyle \sum _{i=1}^n}{\left(a_{i,2}\right)}^2-{\displaystyle \frac{1}{n}}{\left({\displaystyle \sum _{i=1}^n}{a}_{i,2}\right)}^2\right)x_2\hfill \\ ={\displaystyle \sum _{i=1}^n}{a}_{i,2}{b}_i-{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{a}_{i,2}{\displaystyle \sum _{i=1}^n}{b}_i,\hfill \end{array}\right.$$

are, respectively,

$$x_1={\displaystyle \frac{\begin{array}{c}\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{b}_i-\frac{1}{n}{\displaystyle \sum _{i=1}^n}{a}_{i,1}{\displaystyle \sum _{i=1}^n}{b}_i\right)\left({\displaystyle \sum _{i=1}^n}{\left(a_{i,2}\right)}^2-\frac{1}{n}{\left({\displaystyle \sum _{i=1}^n}{a}_{i,2}\right)}^2\right)\hfill \\ -\left({\displaystyle \sum _{i=1}^n}{a}_{i,2}{b}_i-\frac{1}{n}{\displaystyle \sum _{i=1}^n}{a}_{i,2}{\displaystyle \sum _{i=1}^n}{b}_i\right)\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{a}_{i,2}-\frac{1}{n}{\displaystyle \sum _{i=1}^n}{a}_{i,1}{\displaystyle \sum _{i=1}^n}{a}_{i,2}\right)\hfill \end{array}}{\begin{array}{c}\left({\displaystyle \sum _{i=1}^n}{\left(a_{i,1}\right)}^2-\frac{1}{n}{\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}\right)}^2\right)\left({\displaystyle \sum _{i=1}^n}{\left(a_{i,2}\right)}^2-\frac{1}{n}{\left({\displaystyle \sum _{i=1}^n}{a}_{i,2}\right)}^2\right)\hfill \\ -{\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{a}_{i,2}-\frac{1}{n}{\displaystyle \sum _{i=1}^n}{a}_{i,1}{\displaystyle \sum _{i=1}^n}{a}_{i,2}\right)}^2\hfill \end{array}}},$$

and

$$x_2={\displaystyle \frac{\begin{array}{c}\left({\displaystyle \sum _{i=1}^n}{a}_{i,2}{b}_i-\frac{1}{n}{\displaystyle \sum _{i=1}^n}{a}_{i,2}{\displaystyle \sum _{i=1}^n}{b}_i\right)\left({\displaystyle \sum _{i=1}^n}{\left(a_{i,1}\right)}^2-\frac{1}{n}{\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}\right)}^2\right)\hfill \\ -\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{b}_i-\frac{1}{n}{\displaystyle \sum _{i=1}^n}{a}_{i,1}{\displaystyle \sum _{i=1}^n}{b}_i\right)\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{a}_{i,2}-\frac{1}{n}{\displaystyle \sum _{i=1}^n}{a}_{i,1}{\displaystyle \sum _{i=1}^n}{a}_{i,2}\right)\hfill \end{array}}{\begin{array}{c}\left({\displaystyle \sum _{i=1}^n}{\left(a_{i,1}\right)}^2-\frac{1}{n}{\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}\right)}^2\right)\left({\displaystyle \sum _{i=1}^n}{\left(a_{i,2}\right)}^2-\frac{1}{n}{\left({\displaystyle \sum _{i=1}^n}{a}_{i,2}\right)}^2\right)\hfill \\ -{\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{a}_{i,2}-\frac{1}{n}{\displaystyle \sum _{i=1}^n}{a}_{i,1}{\displaystyle \sum _{i=1}^n}{a}_{i,2}\right)}^2\hfill \end{array}}},$$

while the approximate solutions corresponding to the well-known problem (250) are

$${\tilde{x}}_1={\displaystyle \frac{\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{b}_i\right){\displaystyle \sum _{i=1}^n}{\left(a_{i,2}\right)}^2-\left({\displaystyle \sum _{i=1}^n}{a}_{i,2}{b}_i\right){\displaystyle \sum _{i=1}^n}{a}_{i,1}{a}_{i,2}}{{\displaystyle \sum _{i=1}^n}{\left(a_{i,1}\right)}^2{\displaystyle \sum _{i=1}^n}{\left(a_{i,2}\right)}^2-{\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{a}_{i,2}\right)}^2}},$$

and

$${\tilde{x}}_2={\displaystyle \frac{\left({\displaystyle \sum _{i=1}^n}{a}_{i,2}{b}_i\right){\displaystyle \sum _{i=1}^n}{\left(a_{i,1}\right)}^2-\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{b}_i\right){\displaystyle \sum _{i=1}^n}{a}_{i,1}{a}_{i,2}}{{\displaystyle \sum _{i=1}^n}{\left(a_{i,1}\right)}^2{\displaystyle \sum _{i=1}^n}{\left(a_{i,2}\right)}^2-{\left({\displaystyle \sum _{i=1}^n}{a}_{i,1}{a}_{i,2}\right)}^2}}.$$

Let us compare these two series of solutions for a particular numerical case. If, for instance,

$$A_{4\times 2}=\left[\begin{array}{cc}\begin{array}{c}-1\\ 2\\ 1\\ -1\end{array}& \begin{array}{c}1\\ -1\\ -2\\ 2\end{array}\end{array}\right],X_{2\times 1}=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]\mathrm{and}{B}_{4\times 1}=\left[\begin{array}{c}1\\ 2\\ 3\\ 4\end{array}\right],$$

then the solutions of the ordinary least squares problem are $({\tilde{x}}_1,{\tilde{x}}_2)=({\displaystyle \frac{9}{7}},1),$ while the solutions corresponding to the minimization problem (254) are

$$\left(x_1(p=1;I_4),x_2(p=1;I_4)\right)=({\displaystyle \frac{8}{74}},{\displaystyle \frac{13}{74}}).$$

By substituting such values into the remaining term

$$V_{2,4}\left(\left.x_1,x_2\right|I_4\right)={\displaystyle \sum _{i=1}^4}{(a_{i,1}{x}_1+a_{i,2}{x}_2-b_i)}^2-{\displaystyle \frac{1}{4}}{\left({\displaystyle \sum _{i=1}^4}(a_{i,1}{x}_1+a_{i,2}{x}_2-b_i)\right)}^2,$$

we observe that

$$V_{2,4}\left(\left.{\displaystyle \frac{9}{7}},1\right|I_4\right)={\displaystyle \frac{53983}{7252}}\cong 7.4438,$$

whereas

$$V_{2,4}\left(\left.{\displaystyle \frac{8}{74}},{\displaystyle \frac{13}{74}}\right|I_4\right)={\displaystyle \frac{35378}{7252}}\cong 4.8783.$$

On the other hand, for the well-known remaining term

$$E_{2,4}(x_1,x_2)={\displaystyle \sum _{i=1}^4}{(a_{i,1}{x}_1+a_{i,2}{x}_2-b_i)}^2,$$

we observe that

$$E_{2,4}\left({\displaystyle \frac{9}{7}},1\right)={\displaystyle \frac{185}{7}}\cong 26.4285,$$

whereas

$$E_{2,4}\left({\displaystyle \frac{8}{74}},{\displaystyle \frac{13}{74}}\right)={\displaystyle \frac{80335}{2738}}\cong 29.3407.$$

In conclusion,

$$V_{2,4}\left(\left.{\displaystyle \frac{8}{74}},{\displaystyle \frac{13}{74}}\right|I_4\right)<V_{2,4}\left(\left.{\displaystyle \frac{9}{7}},1\right|I_4\right)<E_{2,4}\left({\displaystyle \frac{9}{7}},1\right),$$

which confirms inequality (16).

14. An Improvement of the Bessel Inequality and Parseval Identity

In general, two cases can be considered for this purpose.

14.1. First Type of Improvement

Let ${\left\{{\Phi }_k\left(x\right)\right\}}_{k=0}^{\infty }$ be a sequence of continuous functions which are p-uncorrelated with respect to the fixed function $z\left(x\right)$ and the probability density function $w\left(x\right)/{\int }_a^{b}w\left(x\right)dx$ on $[a,b]$ as before. Then, according to (44),

$$f\left(x\right)\sim {\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p\left({\Phi }_k\left(x\right),f\left(x\right);z\left(x\right)\right)}{{\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right)}}{\Phi }_k\left(x\right),$$

(255)

denotes a p-uncorrelated expansion for $f\left(x\right)$ in which

$$\begin{array}{c}{\displaystyle \frac{{\mathrm{cov}}_p\left({\Phi }_k\left(x\right),f\left(x\right);z\left(x\right)\right)}{{\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right)}}=\hfill \\ \hfill {\displaystyle \frac{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx{\int }_a^{b}w\left(x\right){\Phi }_k\left(x\right)f\left(x\right)dx-p{\int }_a^{b}w\left(x\right){\Phi }_k\left(x\right)z\left(x\right)dx{\int }_a^{b}w\left(x\right)f\left(x\right)z\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx{\int }_a^{b}w\left(x\right){\Phi }_k^2\left(x\right)dx-p{\left({\int }_a^{b}w\left(x\right){\Phi }_k\left(x\right)z\left(x\right)dx\right)}^2}}.\end{array}$$

Referring to Corollary 2 and relation (59), the following inequality holds true for the expansion (255):

$$0\le {\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p^2\left({\Phi }_k\left(x\right),f\left(x\right);z\left(x\right)\right)}{{\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right)}}\le {\mathrm{var}}_p\left(f\left(x\right);z\left(x\right)\right).$$

(256)

Also, according to the definition of convergence in p-variance, inequality (256) will be transformed to an equality if

$$\underset{n\to \infty }{lim}{\mathrm{var}}_p\left(f\left(x\right)-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p\left({\Phi }_k\left(x\right),f\left(x\right);z\left(x\right)\right)}{{\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right)}}{\Phi }_k\left(x\right)\right)=0,$$

(257)

which results in

$${\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p^2\left({\Phi }_k\left(x\right),f\left(x\right);z\left(x\right)\right)}{{\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right)}}={\mathrm{var}}_p\left(f\left(x\right);z\left(x\right)\right).$$

(258)

If (257) or, equivalently, (258) is satisfied, the p-uncorrelated sequence ${\left\{{\Phi }_k\left(x\right)\right\}}_{k=0}^{\infty }$ is said to be “complete” with respect to the fixed function $z\left(x\right)$, and the symbol “∼” in (255) will change to the equality. Noting the above comments, now let $f,g$ be two expandable functions of type (255), and let ${\left\{{\Phi }_k\left(x\right)\right\}}_{k=0}^{\infty }$ be a “complete” p-uncorrelated sequence. Since

$$f\left(x\right)={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p\left({\Phi }_k\left(x\right),f\left(x\right);z\left(x\right)\right)}{{\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right)}}{\Phi }_k\left(x\right),$$

and

$$g\left(x\right)={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p\left({\Phi }_k\left(x\right),g\left(x\right);z\left(x\right)\right)}{{\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right)}}{\Phi }_k\left(x\right),$$

thanks to the general identity

$${\mathrm{cov}}_p\left({\displaystyle \sum _{k=0}^n}{a}_k{\Phi }_k\left(x\right),{\displaystyle \sum _{j=0}^m}{b}_j{\Phi }_j\left(x\right);z\left(x\right)\right)={\displaystyle \sum _{k=0}^n}{\displaystyle \sum _{j=0}^m}{a}_k{b}_j{\mathrm{cov}}_p\left({\Phi }_k\left(x\right),{\Phi }_j\left(x\right);z\left(x\right)\right),$$

and the fact that ${\mathrm{cov}}_p\left({\Phi }_k\left(x\right),{\Phi }_j\left(x\right);z\left(x\right)\right)={\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right){\delta }_{k,j},$ we obtain

$$\begin{array}{c}{\mathrm{cov}}_p\left(f\left(x\right),g\left(x\right);z\left(x\right)\right)=\hfill \\ {\mathrm{cov}}_p\left(\left({\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p\left({\Phi }_k\left(x\right),f\left(x\right);z\left(x\right)\right)}{{\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right)}}{\Phi }_k\left(x\right)\right),\left({\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p\left({\Phi }_k\left(x\right),g\left(x\right);z\left(x\right)\right)}{{\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right)}}{\Phi }_k\left(x\right)\right);z\left(x\right)\right)\\ \hfill ={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{\mathrm{cov}}_p\left({\Phi }_k\left(x\right),f\left(x\right);z\left(x\right)\right){\mathrm{cov}}_p\left({\Phi }_k\left(x\right),g\left(x\right);z\left(x\right)\right)}{{\mathrm{var}}_p\left({\Phi }_k\left(x\right);z\left(x\right)\right)}}.\end{array}$$

(259)

which is an extension of the identity (258) for $f\left(x\right)=g\left(x\right)$. Also, for $p=0$, this important identity leads to the generalized Parseval identity [16]

$$E\left(f\left(x\right)g\left(x\right)\right)={\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{E\left(f\left(x\right){\Phi }_k\left(x\right)\right)E\left(g\left(x\right){\Phi }_k\left(x\right)\right)}{E\left({\Phi }_k^2\left(x\right)\right)}}.$$

(260)

The finite type of (259) occurs when $f,g$ and ${\left\{{\Phi }_k\left(x\right)\right\}}_{k=0}^{\infty }$ are all polynomial functions. For example, let ${\Phi }_k\left(x\right)={\mathbf{P}}_k(x;a,0,c,0)$ denote the same as polynomials (224) satisfying

$$\begin{array}{c}{\int }_0^1{x}^a{\mathbf{P}}_n(x;a,0,c,0){\mathbf{P}}_m(x;a,0,c,0)dx\hfill \\ -(2c-a+1){\int }_0^1{x}^c{\mathbf{P}}_n(x;a,0,c,0)dx{\int }_0^1{x}^c{\mathbf{P}}_m(x;a,0,c,0)dx\\ \hfill ={\displaystyle \frac{1}{2n+a+1}}{\left({\displaystyle \frac{(a-c)n!}{(c+1){(a+1)}_n}}\right)}^2{\delta }_{m,n}\iff 2c-a+1>0,a\ne c\mathrm{and}a,c>-1.\end{array}$$

Also let $Q_m\left(x\right)={\displaystyle \sum _{k=0}^m}{q}_k{x}^k\mathrm{and}{R}_m\left(x\right)={\displaystyle \sum _{k=0}^m}{r}_k{x}^k,$ be two arbitrary polynomials of the same degree. Since

$$\begin{array}{c}{Q}_m\left(x\right)={\displaystyle \sum _{k=0}^m}(2k+a+1){\left({\displaystyle \frac{(c+1){(a+1)}_k}{(a-c)k!}}\right)}^2\hfill \\ \hfill \times {\mathrm{cov}}_1\left({\mathbf{P}}_k(x;a,0,c,0),Q_m\left(x\right);x^{c-a}\right){\mathbf{P}}_k(x;a,0,c,0),\end{array}$$

and

$$\begin{array}{c}{R}_m\left(x\right)={\displaystyle \sum _{k=0}^m}(2k+a+1){\left({\displaystyle \frac{(c+1){(a+1)}_k}{(a-c)k!}}\right)}^2\hfill \\ \hfill \times {\mathrm{cov}}_1\left({\mathbf{P}}_k(x;a,0,c,0),R_m\left(x\right);x^{c-a}\right){\mathbf{P}}_k(x;a,0,c,0),\end{array}$$

according to (259), we have

$$\begin{array}{c}{\mathrm{cov}}_1\left(Q_m\left(x\right),R_m\left(x\right);x^{c-a}\right)={\displaystyle \sum _{k=0}^m}(2k+a+1){\left({\displaystyle \frac{(c+1){(a+1)}_k}{(a-c)k!}}\right)}^2\hfill \\ \hfill \times {\mathrm{cov}}_1\left({\mathbf{P}}_k(x;a,0,c,0),Q_m\left(x\right);x^{c-a}\right){\mathrm{cov}}_1\left({\mathbf{P}}_k(x;a,0,c,0),R_m\left(x\right);x^{c-a}\right).\end{array}$$

14.2. Second Type of Improvement

As inequality (57) is valid for any arbitrary selection of the coefficients ${\left\{{\alpha }_k\right\}}_{k=0}^n$, i.e.,

$$0\le {\mathrm{var}}_p\left(Y-{\displaystyle \sum _{k=0}^n}{\alpha }_k{X}_k;Z\right)\le E\left({\left(Y-{\displaystyle \sum _{k=0}^n}{\alpha }_k{X}_k\right)}^2\right),$$

(261)

such kind of inequalities can be applied for orthogonal expansions. Suppose that ${\left\{{\Phi }_k\left(x\right)\right\}}_{k=0}^{\infty }$ is a sequence of continuous functions orthogonal with respect to the weight function $w\left(x\right)$ on $[a,b]$. If $f\left(x\right)$ is a piecewise continuous function, then

$$f\left(x\right)\sim {\displaystyle \sum _{k=0}^{\infty }}{\alpha }_k{\Phi }_k\left(x\right)\mathrm{with}{\alpha }_k={\displaystyle \frac{{⟨f,{\Phi }_k⟩}_w}{{⟨{\Phi }_k,{\Phi }_k⟩}_w}},$$

is known as its corresponding orthogonal expansion in which ${⟨f,g⟩}_w={\int }_a^{b}w\left(x\right)f\left(x\right)g\left(x\right)dx$. The positive quantity

$$S_n={\int }_a^{b}w\left(x\right){\left({\displaystyle \sum _{k=0}^n}{\alpha }_k{\Phi }_k\left(x\right)-f\left(x\right)\right)}^{2}dx,$$

(262)

will eventually lead to the Bessel inequality [15]

$$0\le S_n={⟨f,f⟩}_w-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{⟨f,{\Phi }_k⟩}_w^2}{{⟨{\Phi }_k,{\Phi }_k⟩}_w}}.$$

Now, noting (261) and (262), instead of $S_n$, we define the following positive quantity:

$$\begin{array}{cc}\hfill & V_n(p;z\left(x\right))=S_n-R_n^2(p;z\left(x\right))\hfill \\ \hfill & ={\int }_a^{b}w\left(x\right){\left({\displaystyle \sum _{k=0}^n}{\alpha }_k{\Phi }_k\left(x\right)-f\left(x\right)\right)}^{2}dx-{\displaystyle \frac{p}{{\int }_a^{b}w\left(x\right)z^2\left(x\right)dx}}{\left({\int }_a^{b}w\left(x\right)z\left(x\right)\left({\displaystyle \sum _{k=0}^n}{\alpha }_k{\Phi }_k\left(x\right)-f\left(x\right)\right)dx\right)}^2.\hfill \end{array}$$

It is clear that

$$0\le V_n(p;z\left(x\right))\le S_n.$$

(263)

Therefore,

$$\begin{array}{c}0\le V_n(p;z\left(x\right))={⟨f,f⟩}_w-{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{⟨f,{\Phi }_k⟩}_w^2}{{⟨{\Phi }_k,{\Phi }_k⟩}_w}}\hfill \\ \hfill -{\displaystyle \frac{p}{{⟨z,z⟩}_w}}\left({\left({\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{⟨f,{\Phi }_k⟩}_w{⟨z,{\Phi }_k⟩}_w}{{⟨{\Phi }_k,{\Phi }_k⟩}_w}}\right)}^2+{⟨f,z⟩}_w^2-2{⟨f,z⟩}_w{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{⟨f,{\Phi }_k⟩}_w{⟨z,{\Phi }_k⟩}_w}{{⟨{\Phi }_k,{\Phi }_k⟩}_w}}\right),\end{array}$$

can be rewritten as

$$\begin{array}{c}{⟨z,z⟩}_w{⟨f,f⟩}_w-p{⟨f,z⟩}_w^2\ge {⟨z,z⟩}_w{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{⟨f,{\Phi }_k⟩}_w^2}{{⟨{\Phi }_k,{\Phi }_k⟩}_w}}+p{\left({\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{⟨f,{\Phi }_k⟩}_w{⟨z,{\Phi }_k⟩}_w}{{⟨{\Phi }_k,{\Phi }_k⟩}_w}}\right)}^2\hfill \\ \hfill -2p{⟨f,z⟩}_w{\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{⟨f,{\Phi }_k⟩}_w{⟨z,{\Phi }_k⟩}_w}{{⟨{\Phi }_k,{\Phi }_k⟩}_w}}.\end{array}$$

(264)

Inequality (264) is an improvement of the well-known Bessel inequality for every $p\in [0,1]$ with respect to the fixed function $z\left(x\right)$. For example, if ${\Phi }_k\left(x\right)=sin(k+1)x$ for $x\in [0,\pi ]$ and $w\left(x\right)=z\left(x\right)=1$ are replaced in (264), the Bessel inequality of the Fourier sine expansion will be improved as follows

$$\begin{array}{c}{\int }_0^{\pi }{f}^2\left(x\right)dx-{\displaystyle \frac{p}{\pi }}{\left({\int }_0^{\pi }f\left(x\right)dx\right)}^2\ge {\displaystyle \frac{2}{\pi }}{\displaystyle \sum _{k=0}^n}{\left({\int }_0^{\pi }f\left(x\right)sin(k+1)xdx\right)}^2\hfill \\ +{\displaystyle \frac{4p}{{\pi }^3}}{\left({\displaystyle \sum _{k=0}^n}{\displaystyle \frac{1+{(-1)}^k}{k+1}}{\int }_0^{\pi }f\left(x\right)sin(k+1)xdx\right)}^2\\ \hfill -{\displaystyle \frac{4p}{{\pi }^2}}\left({\int }_0^{\pi }f\left(x\right)dx\right){\displaystyle \sum _{k=0}^n}{\displaystyle \frac{1+{(-1)}^k}{k+1}}{\int }_0^{\pi }f\left(x\right)sin(k+1)xdx.\end{array}$$

Obviously (264) will remain an inequality if the sequence ${\left\{{\Phi }_k\left(x\right)\right\}}_{k=0}$ does not form a complete orthogonal system. On the other side, if they are a complete orthogonal set, inequality (264) becomes an equality when $n\to \infty$. In other words, suppose ${\left\{{\Phi }_k\left(x\right)\right\}}_{k=0}$ is a complete orthogonal set. Since

$$\underset{n\to \infty }{lim}{S}_n=\underset{n\to \infty }{lim}{\int }_a^{b}w\left(x\right){\left({\displaystyle \sum _{k=0}^n}{\alpha }_k{\Phi }_k\left(x\right)-f\left(x\right)\right)}^{2}dx=0,$$

we directly conclude from (263) that

$$0\le \underset{n\to \infty }{lim}{V}_n(p;z\left(x\right))\le \underset{n\to \infty }{lim}{S}_n=0,$$

and, therefore,

$$\underset{n\to \infty }{lim}{S}_n-R_n^2(p;z\left(x\right))=\underset{n\to \infty }{lim}{\left({\int }_a^{b}w\left(x\right)z\left(x\right)\left({\displaystyle \sum _{k=0}^n}{\alpha }_k{\Phi }_k\left(x\right)-f\left(x\right)\right)dx\right)}^2=0,$$

eventually yields

$${\displaystyle \sum _{k=0}^{\infty }}{\displaystyle \frac{{⟨f,{\Phi }_k⟩}_w{⟨z,{\Phi }_k⟩}_w}{{⟨{\Phi }_k,{\Phi }_k⟩}_w}}={⟨f,z⟩}_w,$$

which is known in the literature as the inner product form of the generalized Parseval identity (260). In the next section, we will refer to the above-mentioned results in order to extend the presented theory in terms of a set of fixed mutually orthogonal variables.

15. Least p-Variances with Respect to Fixed Orthogonal Variables

Since parts of this section are somewhat similar to the previous ones, we just state basic concepts. Suppose $x,y$ and ${\left\{z_k\right\}}_{k=1}^m$ are elements of an inner product space $\mathbf{S}$, such that ${\left\{z_k\right\}}_{k=1}^m$ are mutually orthogonal as

$$⟨z_i,z_j⟩=⟨z_j,z_j⟩{\delta }_{i,j}.$$

(265)

Due to the orthogonality property (265), the following identity holds true

$$\begin{array}{cc}\hfill & ⟨x-(1-\sqrt{1-p}){\displaystyle \sum _{k=1}^m}{\displaystyle \frac{⟨x,z_k⟩}{⟨z_k,z_k⟩}}{z}_k,y-(1-\sqrt{1-p}){\displaystyle \sum _{k=1}^m}{\displaystyle \frac{⟨y,z_k⟩}{⟨z_k,z_k⟩}}{z}_k⟩\hfill \\ \hfill & =⟨x,y⟩-p{\displaystyle \sum _{k=1}^m}{\displaystyle \frac{⟨x,z_k⟩⟨y,z_k⟩}{⟨z_k,z_k⟩}},\hfill \end{array}$$

(266)

and, for $y=x$, it gives

$$⟨x,x⟩-p{\displaystyle \sum _{k=1}^m}{\displaystyle \frac{{⟨x,z_k⟩}^2}{⟨z_k,z_k⟩}}\ge 0\forall p\in [0,1].$$

(267)

The identity (266) and inequality (267) can again be employed in mathematical statistics concepts.

Definition 6.

Let $X,Y$ and ${\left\{Z_k\right\}}_{k=1}^m$ be arbitrary random variables, such that ${\left\{Z_k\right\}}_{k=1}^m$ are mutually orthogonal, i.e.,

$$E\left(Z_i{Z}_j\right)=E\left(Z_j^2\right){\delta }_{i,j},i,j=1,2,\dots ,m.$$

(268)

Corresponding to (266), we define

$$\begin{array}{cc}\hfill & {\mathrm{cov}}_p(X,Y;{\left\{Z_k\right\}}_{k=1}^m)\hfill \\ \hfill & =E\left(\left(X-(1-\sqrt{1-p}){\displaystyle \sum _{k=1}^m}{\displaystyle \frac{E\left(X{Z}_k\right)}{E\left(Z_k^2\right)}}{Z}_k\right)\left(Y-(1-\sqrt{1-p}){\displaystyle \sum _{k=1}^m}{\displaystyle \frac{E\left(Y{Z}_k\right)}{E\left(Z_k^2\right)}}{Z}_k\right)\right)\hfill \\ \hfill & =E\left(XY\right)-p{\displaystyle \sum _{k=1}^m}{\displaystyle \frac{E\left(X{Z}_k\right)E\left(Y{Z}_k\right)}{E\left(Z_k^2\right)}},\hfill \end{array}$$

(269)

and call it the “p-covariance of X and Y with respect to the fixed orthogonal variables ${\left\{Z_k\right\}}_{k=1}^m$”.

For $Y=X$, (269) changes to

$$\begin{array}{cc}\hfill {\mathrm{var}}_p(X;{\left\{Z_k\right\}}_{k=1}^m)& =E\left({\left(X-(1-\sqrt{1-p}){\displaystyle \sum _{k=1}^m}{\displaystyle \frac{E\left(X{Z}_k\right)}{E\left(Z_k^2\right)}}{Z}_k\right)}^2\right)\hfill \\ \hfill & =E\left(X^2\right)-p{\displaystyle \sum _{k=1}^m}{\displaystyle \frac{E^2\left(X{Z}_k\right)}{E\left(Z_k^2\right)}}\ge 0,\hfill \end{array}$$

(270)

where ${\left\{E\left(Z_k^2\right)\right\}}_{k=1}^m$ are all positive. Note in (269) that

$${\displaystyle \sum _{k=1}^m}{\displaystyle \frac{E\left(X{Z}_k\right)}{E\left(Z_k^2\right)}}{Z}_k={\displaystyle \sum _{k=1}^m}\mathrm{pro}{\mathrm{j}}_{Z_k}X,$$

and, therefore, e.g., for $p=1$,

$${\mathrm{cov}}_1(X,Y;{\left\{Z_k\right\}}_{k=1}^m)=E\left((X-{\displaystyle \sum _{k=1}^m}\mathrm{pro}{\mathrm{j}}_{Z_k}X)(Y-{\displaystyle \sum _{k=1}^m}\mathrm{pro}{\mathrm{j}}_{Z_k}Y)\right).$$

Moreover, for orthogonal variables ${\left\{Z_k\right\}}_{k=1}^m$ and $p\in [0,1]$, we have

$$0\le {\mathrm{var}}_1(X;{\left\{Z_k\right\}}_{k=1}^m)\le {\mathrm{var}}_p(X;{\left\{Z_k\right\}}_{k=1}^m)\le {\mathrm{var}}_0(X;{\left\{Z_k\right\}}_{k=1}^m)=E\left(X^2\right).$$

(271)

A remarkable point in (271) is that, if $m,n$ are two natural numbers, such that $n>m$, then

$$0\le {\mathrm{var}}_p(X;{\left\{Z_k\right\}}_{k=1}^n)\le {\mathrm{var}}_p(X;{\left\{Z_k\right\}}_{k=1}^m),$$

which can be proved directly via (270). For instance, if $n=2$ and $m=1$, then

$$0\le {\mathrm{var}}_1(X;Z_1,Z_2)\le {\mathrm{var}}_p(X;Z_1,Z_2)\le {\mathrm{var}}_p(X;Z_1)\le {\mathrm{var}}_0(X;Z_1)=E\left(X^2\right),$$

in which $E\left(Z_1{Z}_2\right)=0.$

The following properties hold true for definitions (269) and (270), provided that the orthogonal condition (268) is satisfied:

$$\begin{array}{cc}\hfill \left(b1\right)& {\mathrm{cov}}_p(X,Y;{\left\{Z_k\right\}}_{k=1}^m)={\mathrm{cov}}_p(Y,X;{\left\{Z_k\right\}}_{k=1}^m).\hfill \\ \hfill \left(b2\right)& {\mathrm{cov}}_p(\alpha X,\beta Y;{\left\{Z_k\right\}}_{k=1}^m)=\alpha \beta {\mathrm{cov}}_p(X,Y;{\left\{Z_k\right\}}_{k=1}^m)(\alpha ,\beta \in \mathbb{R}).\hfill \\ \hfill \left(b3\right)& \begin{array}{c}{\mathrm{cov}}_p(X+\alpha ,Y+\beta ;{\left\{Z_k\right\}}_{k=1}^m)={\mathrm{cov}}_p(X,Y;{\left\{Z_k\right\}}_{k=1}^m)+\alpha {\mathrm{cov}}_p(1,Y;{\left\{Z_k\right\}}_{k=1}^m)\hfill \\ +\beta {\mathrm{cov}}_p(X,1;{\left\{Z_k\right\}}_{k=1}^m)+\alpha \beta {\mathrm{cov}}_p(1,1;{\left\{Z_k\right\}}_{k=1}^m).\hfill \end{array}\hfill \\ \hfill \left(b4\right)& {\mathrm{cov}}_p\left({\displaystyle \sum _{k=0}^n}{c}_k{X}_k,X_j;{\left\{Z_k\right\}}_{k=1}^m\right)={\displaystyle \sum _{k=0}^n}{c}_k{\mathrm{cov}}_p(X_k,X_j;{\left\{Z_k\right\}}_{k=1}^m)({\left\{c_k\right\}}_{k=0}^n\in \mathbb{R}).\hfill \\ \hfill \left(b5\right)& \begin{array}{c}{\mathrm{var}}_p(\alpha X+\beta Y;{\left\{Z_k\right\}}_{k=1}^m)={\alpha }^2{\mathrm{var}}_p(X;{\left\{Z_k\right\}}_{k=1}^m)+{\beta }^2{\mathrm{var}}_p(Y;{\left\{Z_k\right\}}_{k=1}^m)\hfill \\ +2\alpha \beta {\mathrm{cov}}_p(X,Y;{\left\{Z_k\right\}}_{k=1}^m).\hfill \end{array}\hfill \end{array}$$

Definition 7.

Based on definitions (269) and (270) and the orthogonality condition (268), we define

$${\rho }_p(X,Y;{\left\{Z_k\right\}}_{k=1}^m)={\displaystyle \frac{{\mathrm{cov}}_p(X,Y;{\left\{Z_k\right\}}_{k=1}^m)}{\sqrt{{\mathrm{var}}_p(X;{\left\{Z_k\right\}}_{k=1}^m){\mathrm{var}}_p(Y;{\left\{Z_k\right\}}_{k=1}^m)}}},$$

(272)

and call it “p-correlation coefficient of X and Y with respect to the fixed orthogonal variables ${\left\{Z_k\right\}}_{k=1}^m$”. Clearly,

$${\rho }_p(X,Y;{\left\{Z_k\right\}}_{k=1}^m)\in [-1,1],$$

because, if

$$U=X-(1-\sqrt{1-p}){\displaystyle \sum _{k=1}^m}{\displaystyle \frac{E\left(X{Z}_k\right)}{E\left(Z_k^2\right)}}{Z}_k\mathrm{and}V=Y-(1-\sqrt{1-p}){\displaystyle \sum _{k=1}^m}{\displaystyle \frac{E\left(Y{Z}_k\right)}{E\left(Z_k^2\right)}}{Z}_k,$$

are replaced in the Cauchy–Schwarz inequality (11), then

$${\mathrm{cov}}_p^2(X,Y;{\left\{Z_k\right\}}_{k=1}^m)\le {\mathrm{var}}_p(X;{\left\{Z_k\right\}}_{k=1}^m){\mathrm{var}}_p(Y;{\left\{Z_k\right\}}_{k=1}^m).$$

Definition 8.

If ${\rho }_p(X,Y;{\left\{Z_k\right\}}_{k=1}^m)=0$ in (272), we say that X and Y are p-uncorrelated with respect to ${\left\{Z_k\right\}}_{k=1}^m$, and we have

$$E\left(XY\right)=p{\displaystyle \sum _{k=1}^m}{\displaystyle \frac{E\left(X{Z}_k\right)E\left(Y{Z}_k\right)}{E\left(Z_k^2\right)}}.$$

15.1. Least p-Variances Approximation Based on Fixed Orthogonal Variables

Again, consider the approximation (13), $Y\cong {\displaystyle \sum _{k=0}^n}{c}_k{X}_k,$ and define the p-variance of the remaining term $R(c_0,c_1,\dots ,c_n)={\displaystyle \sum _{k=0}^n}{c}_k{X}_k-Y,$ with respect to the orthogonal variables ${\left\{Z_k\right\}}_{k=1}^m$ as follows:

$$\begin{array}{c}{\mathrm{var}}_p\left(R(c_0,\dots ,c_n);{\left\{Z_k\right\}}_{k=1}^m\right)\hfill \\ \hfill =E\left({\left(R(c_0,\dots ,c_n)-(1-\sqrt{1-p}){\displaystyle \sum _{k=1}^m}{\displaystyle \frac{E\left(Z_{k}R(c_0,\dots ,c_n)\right)}{E\left(Z_k^2\right)}}{Z}_k\right)}^2\right).\end{array}$$

(273)

To minimize (273), the relations

$${\displaystyle \frac{\partial {\mathrm{var}}_p\left(R(c_0,\dots ,c_n);{\left\{Z_k\right\}}_{k=1}^m\right)}{\partial c_j}}=0\mathrm{for}j=0,1,\dots ,n,$$

eventually lead to the following linear system:

$$\begin{array}{cc}\hfill & \left[\begin{array}{cccc}\begin{array}{c}{\mathrm{var}}_p(X_0;{\left\{Z_k\right\}}_{k=1}^m)\\ {\mathrm{cov}}_p(X_1,X_0;{\left\{Z_k\right\}}_{k=1}^m)\\ ⋮\\ {\mathrm{cov}}_p(X_n,X_0;{\left\{Z_k\right\}}_{k=1}^m)\end{array}& \begin{array}{c}{\mathrm{cov}}_p(X_0,X_1;{\left\{Z_k\right\}}_{k=1}^m)\\ {\mathrm{var}}_p(X_1;{\left\{Z_k\right\}}_{k=1}^m)\\ ⋮\\ {\mathrm{cov}}_p(X_n,X_1;{\left\{Z_k\right\}}_{k=1}^m)\end{array}& \begin{array}{c}\cdots \\ \cdots \\ ⋮\\ \cdots \end{array}& \begin{array}{c}{\mathrm{cov}}_p(X_0,X_n;{\left\{Z_k\right\}}_{k=1}^m)\\ {\mathrm{cov}}_p(X_1,X_n;{\left\{Z_k\right\}}_{k=1}^m)\\ ⋮\\ {\mathrm{var}}_p(X_n;{\left\{Z_k\right\}}_{k=1}^m)\end{array}\end{array}\right]\hfill \\ \hfill & \times \left[\begin{array}{c}{c}_0\\ c_1\\ ⋮\\ c_n\end{array}\right]=\left[\begin{array}{c}{\mathrm{cov}}_p(X_0,Y;{\left\{Z_k\right\}}_{k=1}^m)\\ {\mathrm{cov}}_p(X_1,Y;{\left\{Z_k\right\}}_{k=1}^m)\\ ⋮\\ {\mathrm{cov}}_p(X_n,Y;{\left\{Z_k\right\}}_{k=1}^m)\end{array}\right].\hfill \end{array}$$

(274)

Two continuous and discrete spaces can be considered for the system (274).

15.1.1. First Case

If ${\left\{X_k={\Phi }_k\left(x\right)\right\}}_{k=0}^n$, $Y=f\left(x\right)$ and the orthogonal set ${\left\{Z_k=z_k\left(x\right)\right\}}_{k=1}^m$ are defined in a continuous space with a probability density function as $P_r\left(X=x\right)={\displaystyle \frac{w\left(x\right)}{{\int }_a^{b}w\left(x\right)dx}},$ the elements of the system (274) appear as

$$\begin{array}{c}{\mathrm{cov}}_p\left({\Phi }_i\left(x\right),{\Phi }_j\left(x\right);{\left\{z_k\left(x\right)\right\}}_{k=1}^m\right)=\hfill \\ \hfill {\displaystyle \frac{1}{{\int }_a^{b}w\left(x\right)dx}}\left({\int }_a^{b}w\left(x\right){\Phi }_i\left(x\right){\Phi }_j\left(x\right)dx-p{\displaystyle \sum _{k=1}^m}{\displaystyle \frac{{\int }_a^{b}w\left(x\right){\Phi }_i\left(x\right)z_k\left(x\right)dx{\int }_a^{b}w\left(x\right){\Phi }_j\left(x\right)z_k\left(x\right)dx}{{\int }_a^{b}w\left(x\right)z_k^2\left(x\right)dx}}\right),\end{array}$$

if only if

$${\int }_a^{b}w\left(x\right)z_i\left(x\right)z_j\left(x\right)dx=\left({\int }_a^{b}w\left(x\right)z_j^2\left(x\right)dx\right){\delta }_{i,j}.$$

15.1.2. Second Case

If the above-mentioned variables are defined on a counter set, say $A^{*}={\left\{x_k\right\}}_{k=0}^m$, with a discrete probability density function as $P_r\left(X=x\right)={\displaystyle \frac{j\left(x\right)}{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right)}},$ then

$$\begin{array}{c}{\mathrm{cov}}_p\left({\Phi }_i\left(x\right),{\Phi }_j\left(x\right);{\left\{z_k\left(x\right)\right\}}_{k=1}^m\right)=\hfill \\ \hfill {\displaystyle \frac{1}{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right)}}\left({\displaystyle \sum _{x\in A^{*}}}j\left(x\right){\Phi }_i\left(x\right){\Phi }_j\left(x\right)-p{\displaystyle \sum _{k=1}^m}{\displaystyle \frac{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right){\Phi }_i\left(x\right)z_k\left(x\right){\displaystyle \sum _{x\in A^{*}}}j\left(x\right){\Phi }_j\left(x\right)z_k\left(x\right)}{{\displaystyle \sum _{x\in A^{*}}}j\left(x\right)z_k^2\left(x\right)}}\right),\end{array}$$

only if

$$\sum _{x\in A^{*}}j\left(x\right)z_i\left(x\right)z_j\left(x\right)=\left(\sum _{x\in A^{*}}j\left(x\right)z_i^2\left(x\right)\right){\delta }_{i,j}.$$

Let us consider a particular example. Suppose that $m=2$, $x\in [0,\pi ]$ and $P_r\left(X=x\right)={\displaystyle \frac{1}{\pi }}$. In this case, it is well known that, if we take $z_1\left(x\right)=sinx$ and $z_2\left(x\right)=cosx$, then

$$E\left(z_1\left(x\right)z_2\left(x\right)\right)={\displaystyle \frac{1}{\pi }}{\int }_0^{\pi }sinxcosxdx=0,$$

and, therefore,

$$\begin{array}{c}{\mathrm{cov}}_p\left({\Phi }_i\left(x\right),{\Phi }_j\left(x\right);sinx,cosx\right)={\displaystyle \frac{1}{\pi }}{\int }_0^{\pi }{\Phi }_i\left(x\right){\Phi }_j\left(x\right)dx\hfill \\ \hfill -{\displaystyle \frac{2p}{{\pi }^2}}\left({\int }_0^{\pi }{\Phi }_i\left(x\right)sinxdx{\int }_0^{\pi }{\Phi }_j\left(x\right)sinxdx+{\int }_0^{\pi }{\Phi }_i\left(x\right)cosxdx{\int }_0^{\pi }{\Phi }_j\left(x\right)cosxdx\right).\end{array}$$

The weighted version of the above example can be considered in various cases. For example, if $w\left(x\right)=e^x,z_1\left(x\right)=e^{-x}sinx$ and $z_2\left(x\right)=cosx$ all defined on $[0,\pi ]$, then

$$E\left(z_1\left(x\right)z_2\left(x\right)\right)={\displaystyle \frac{1}{e^{\pi }-1}}{\int }_0^{\pi }sinxcosxdx=0,$$

and consequently the corresponding space is defined as

$$\begin{array}{c}\left(e^{\pi }-1\right){\mathrm{cov}}_p\left({\Phi }_i\left(x\right),{\Phi }_j\left(x\right);sinx,cosx\right)={\int }_0^{\pi }{e}^x{\Phi }_i\left(x\right){\Phi }_j\left(x\right)dx\hfill \\ \hfill -p\left({\displaystyle \frac{{\int }_0^{\pi }{\Phi }_i\left(x\right)sinxdx{\int }_0^{\pi }{\Phi }_j\left(x\right)sinxdx}{{\int }_0^{\pi }{e}^{-x}{sin}^{2}xdx}}+{\displaystyle \frac{{\int }_0^{\pi }{\Phi }_i\left(x\right)e^{x}cosxdx{\int }_0^{\pi }{\Phi }_j\left(x\right)e^{x}cosxdx}{{\int }_0^{\pi }{e}^x{cos}^{2}xdx}}\right),\end{array}$$

where

$${\int }_0^{\pi }{e}^{-x}{sin}^{2}xdx={\displaystyle \frac{2}{5}}(1-e^{-\pi })\mathrm{and}{\int }_0^{\pi }{e}^x{cos}^{2}xdx={\displaystyle \frac{3}{5}}(e^{\pi }-1).$$

In the sequel, applying the uncorrelatedness condition

$${\mathrm{cov}}_p(X_i,X_j;{\left\{Z_k\right\}}_{k=1}^m)={\mathrm{var}}_p(X_j;{\left\{Z_k\right\}}_{k=1}^m){\delta }_{i,j}\mathrm{for}\mathrm{every}i,j=0,1,\dots ,n,$$

(275)

on the elements of the linear system (274), we can obtain the unknown coefficients as

$$c_k={\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;{\left\{Z_k\right\}}_{k=1}^m)}{{\mathrm{var}}_p(X_k;{\left\{Z_k\right\}}_{k=1}^m)}}.$$

In this case,

$$Y\cong {\displaystyle \sum _{k=0}^n}{\displaystyle \frac{{\mathrm{cov}}_p(X_k,Y;{\left\{Z_k\right\}}_{k=1}^m)}{{\mathrm{var}}_p(X_k;{\left\{Z_k\right\}}_{k=1}^m)}}{X}_k,$$

is the best approximation in the sense of least p-variance of the error with respect to the fixed orthogonal variables ${\left\{Z_k\right\}}_{k=1}^m$.

Finally, we point out that p-uncorrelated vectors with respect to fixed orthogonal vectors can be constructed as follows. Let ${\overrightarrow{A}}_m=(a_1,a_2,\dots ,a_m)$ and ${\overrightarrow{B}}_m=(b_1,b_2,\dots ,b_m)$ be two arbitrary vectors, and let ${\left\{{\overrightarrow{Z}}_{k,m}=(z_{k,1},z_{k,2},\dots ,z_{k,m})\right\}}_{k=1}^l$ be a set of fixed orthogonal vectors. Then,

$$\begin{array}{cc}\hfill & \left({\overrightarrow{A}}_m-(1-\sqrt{1-p}){\displaystyle \sum _{k=1}^l}{\displaystyle \frac{{\overrightarrow{A}}_m.{\overrightarrow{Z}}_{k,m}}{{\overrightarrow{Z}}_{k,m}.{\overrightarrow{Z}}_{k,m}}}{\overrightarrow{Z}}_{k,m}\right).\left({\overrightarrow{B}}_m-(1-\sqrt{1-p}){\displaystyle \sum _{k=1}^l}{\displaystyle \frac{{\overrightarrow{B}}_m.{\overrightarrow{Z}}_{k,m}}{{\overrightarrow{Z}}_{k,m}.{\overrightarrow{Z}}_{k,m}}}{\overrightarrow{Z}}_{k,m}\right)\hfill \\ \hfill & ={\overrightarrow{A}}_m.{\overrightarrow{B}}_m-p{\displaystyle \sum _{k=1}^l}{\displaystyle \frac{({\overrightarrow{A}}_m.{\overrightarrow{Z}}_{k,m})({\overrightarrow{B}}_m.{\overrightarrow{Z}}_{k,m})}{{\overrightarrow{Z}}_{k,m}.{\overrightarrow{Z}}_{k,m}}},\hfill \end{array}$$

if only if ${\overrightarrow{Z}}_{k,m}.{\overrightarrow{Z}}_{j,m}=\left({\overrightarrow{Z}}_{j,m}.{\overrightarrow{Z}}_{j,m}\right){\delta }_{k,j}$.