Parallel Simulation Multi-Sample Task Scheduling Approach Based on Deep Reinforcement Learning in Cloud Computing Environment
Abstract
1. Introduction
- (1)
- A parallel scheduling framework for simulation multi-sample tasks was designed. The framework not only supports the parallel execution of all simulation samples but also supports dividing each simulation sample into different groups and scheduling them to different nodes for parallel execution.
- (2)
- A DRL-based scheduling method for multi-sample simulation tasks in cloud computing environments is proposed, where a DRL agent is trained with a designed reward–penalty mechanism to improve resource utilization and reduce overall execution time while satisfying resource constraints.
- (3)
- Extensive experiments have been conducted using a real cloud environment to evaluate the performance of the DRL-based scheduling approach. The experimental results showed that the proposed method can reduce the runtime and costs of executing multi-sample simulation tasks by up to 11% and 33% compared with the round-robin (RR), best fit (BF), and genetic algorithm (GA).
2. Related Work
2.1. Resource Scheduling Based on Heuristic Algorithms
2.2. Resource Scheduling Based on RL
3. Approach for Multi-Sample Task Simulation Scheduling Based on DRL
3.1. Problem Description
3.2. Design of Reinforcement Learning Model
3.3. DQN-Based Simulation Multi-Sample Task Scheduling Algorithm
| Algorithm 1 DQN-based simulation multi-sample task scheduling algorithm |
|
4. Experimental Results and Analysis
4.1. Experimental Setup
4.2. Benchmark Application and Model Setup
| Algorithm 2 The RR Algorithm in Simulation Task Scheduling |
|
| Algorithm 3 The BF Algorithm in Simulation Task Scheduling |
|
| Algorithm 4 The GA Algorithm in Simulation Task Scheduling |
|
4.3. The Network Structure of the DQN Model
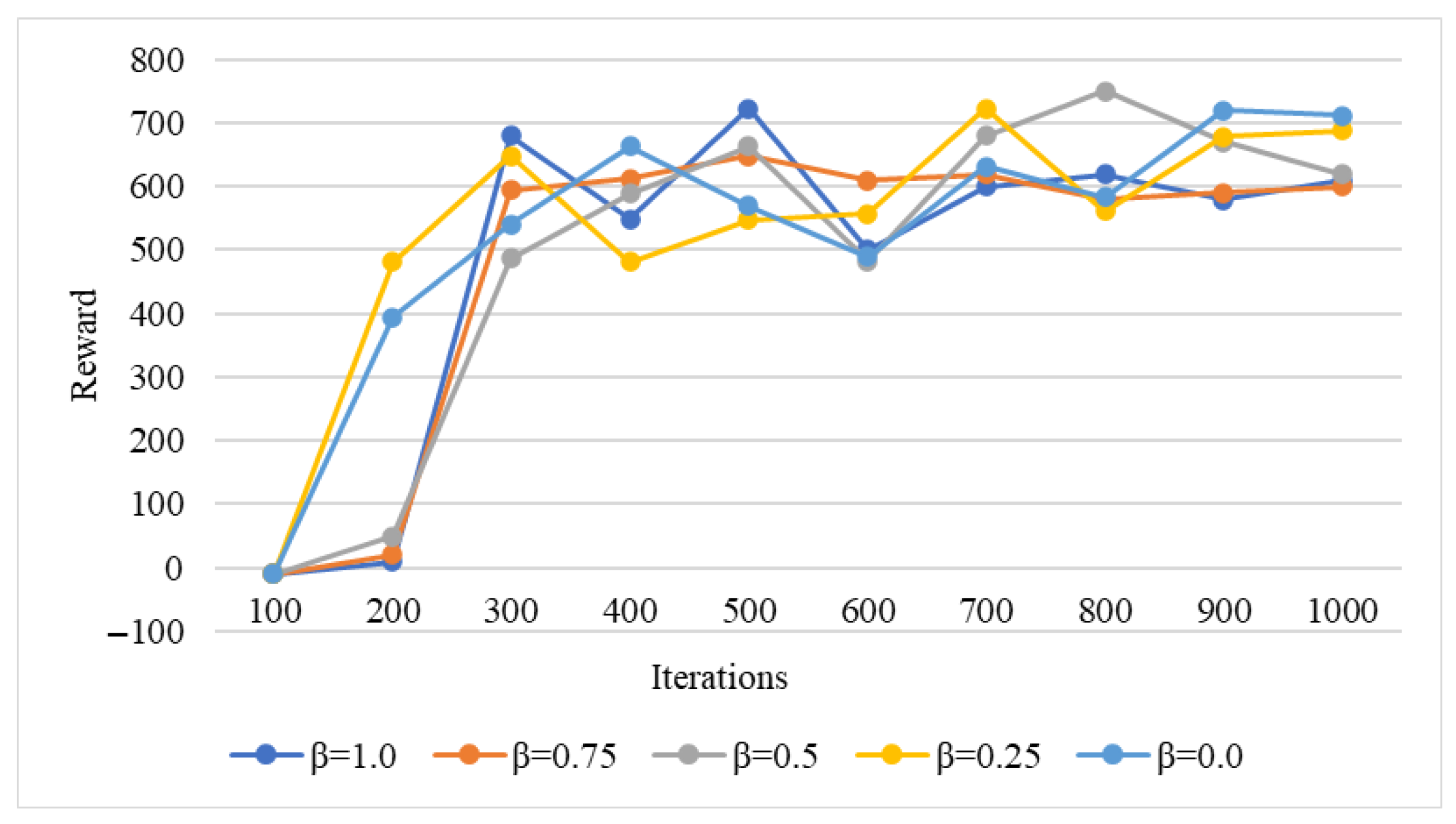
4.4. Model Performance Evaluation
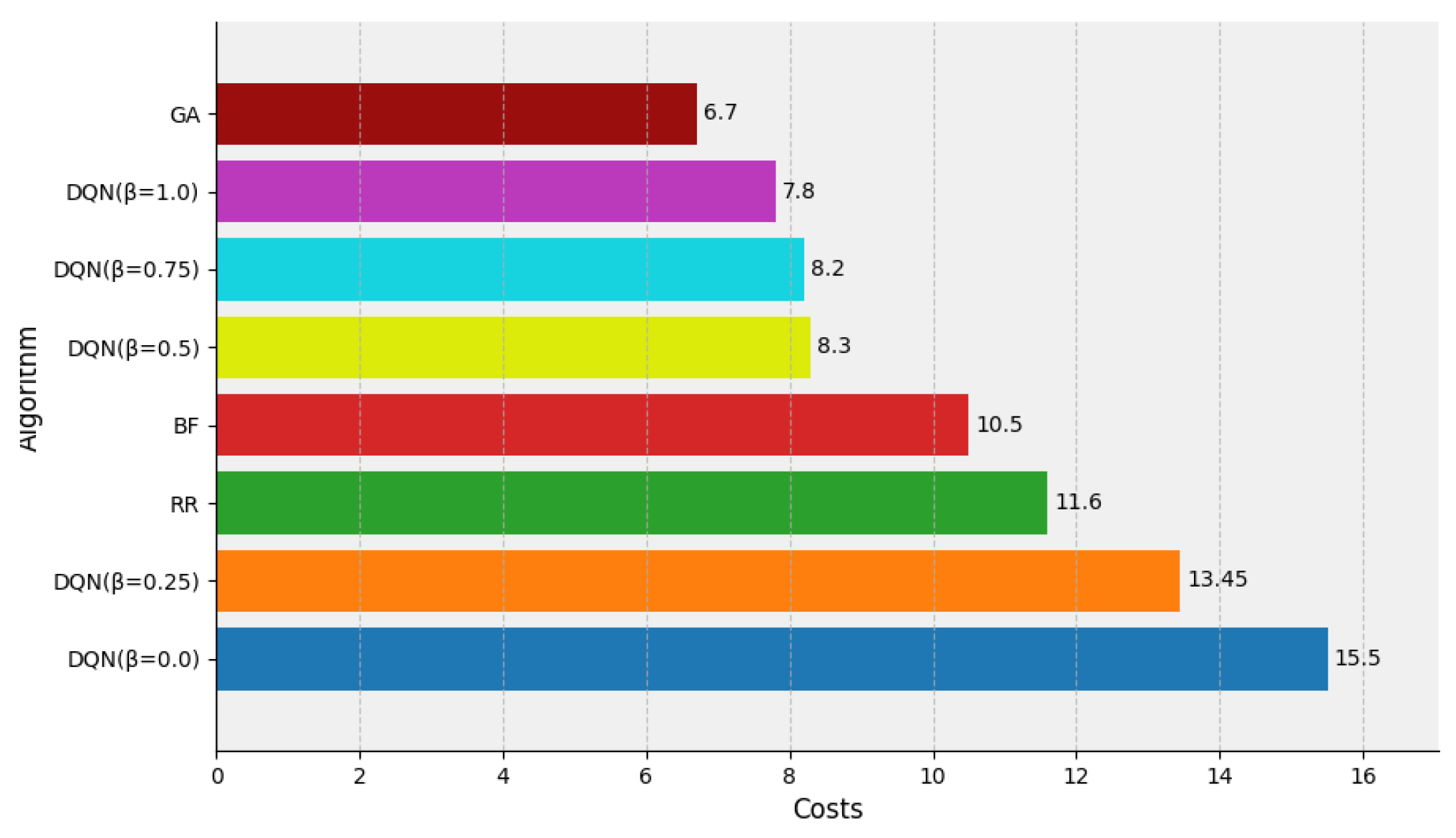
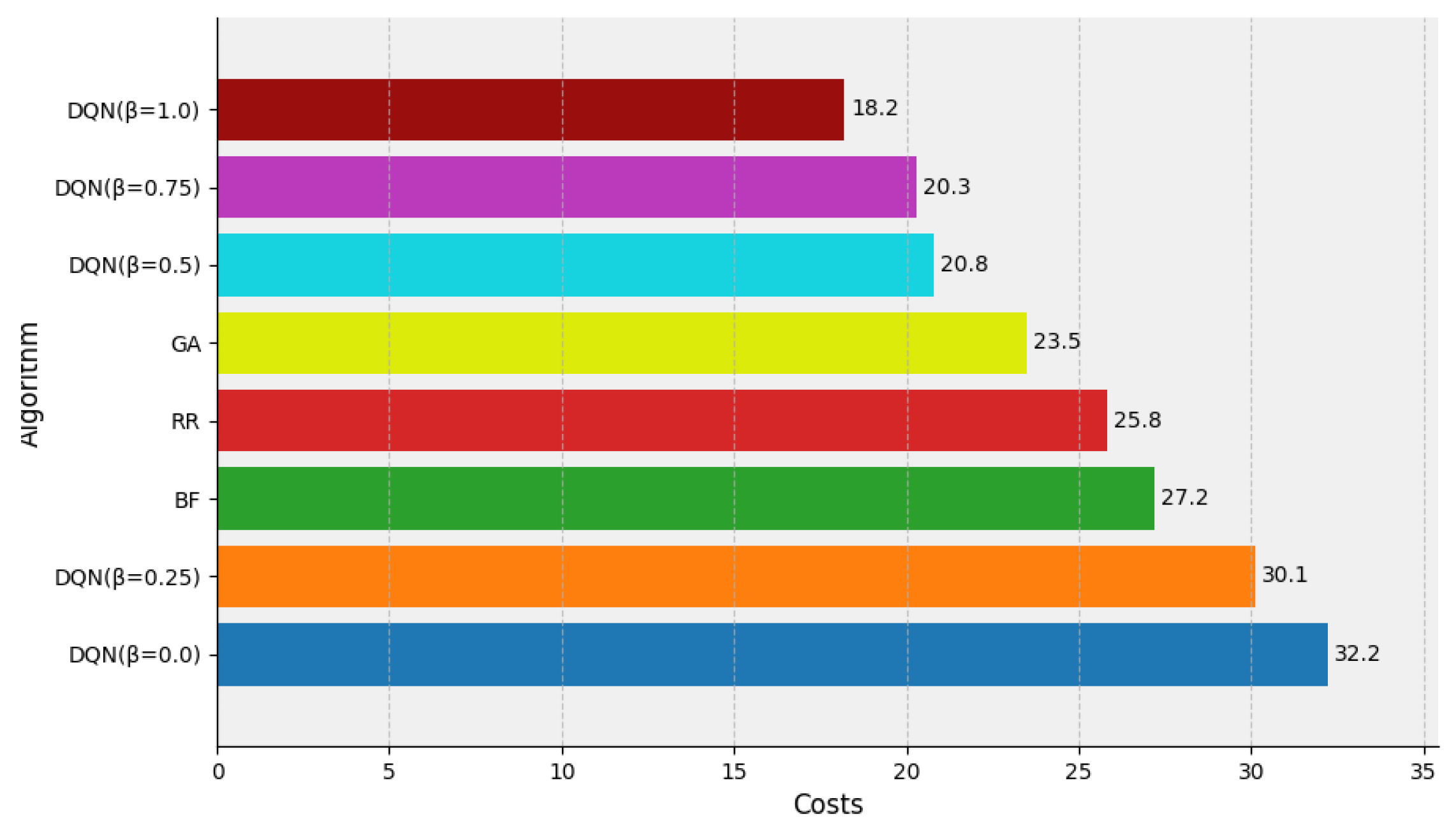
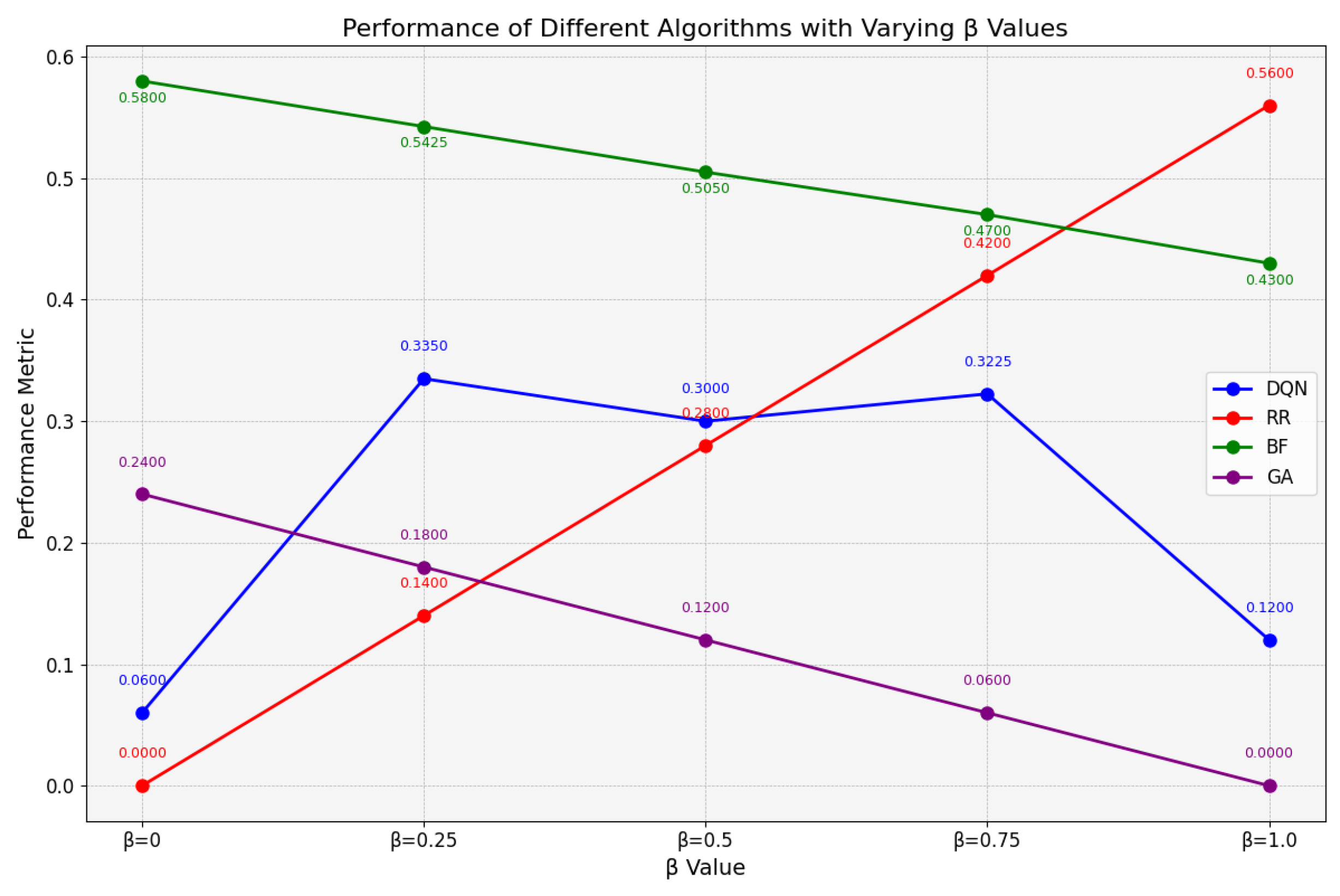
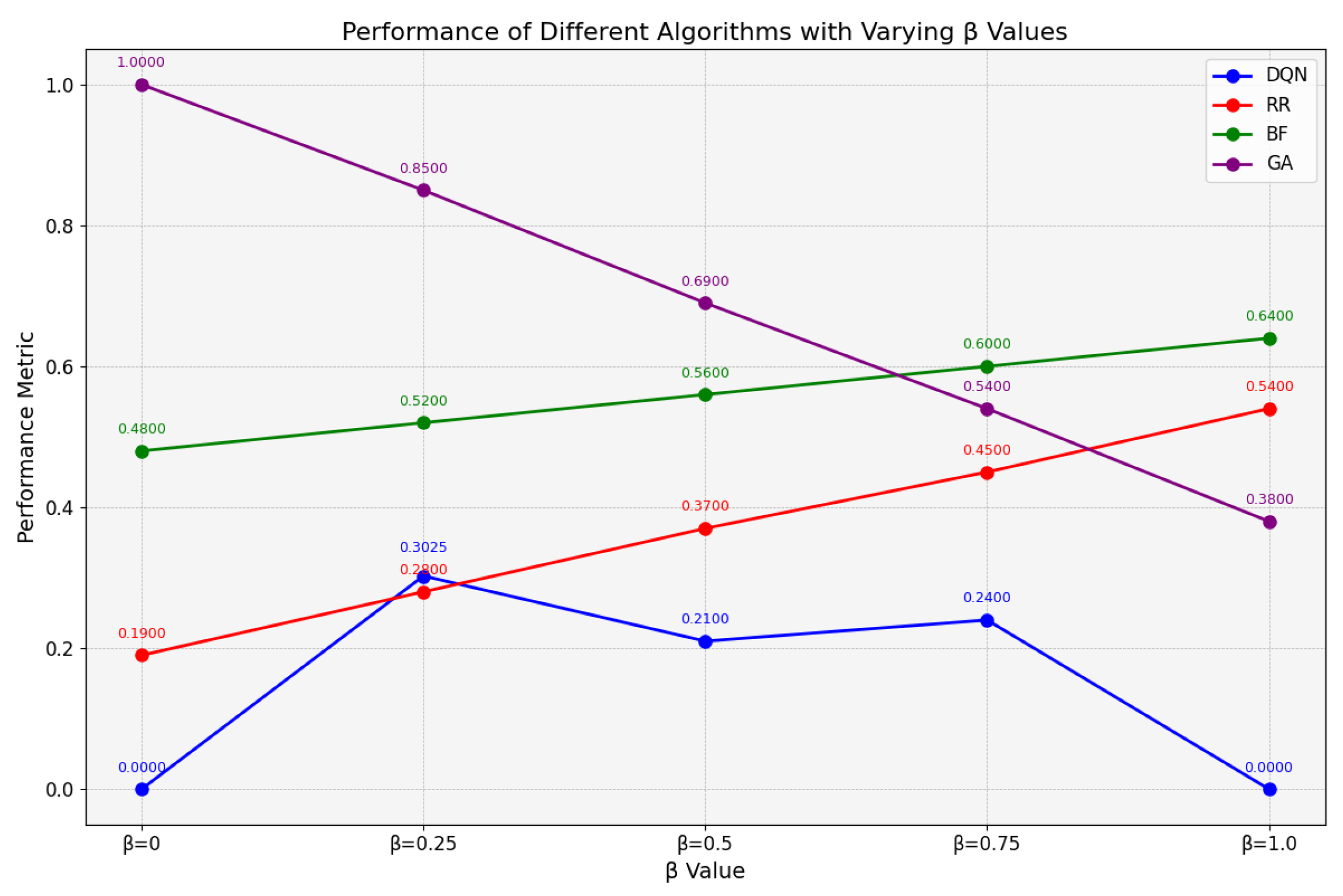
4.4.1. Evaluation of Cost
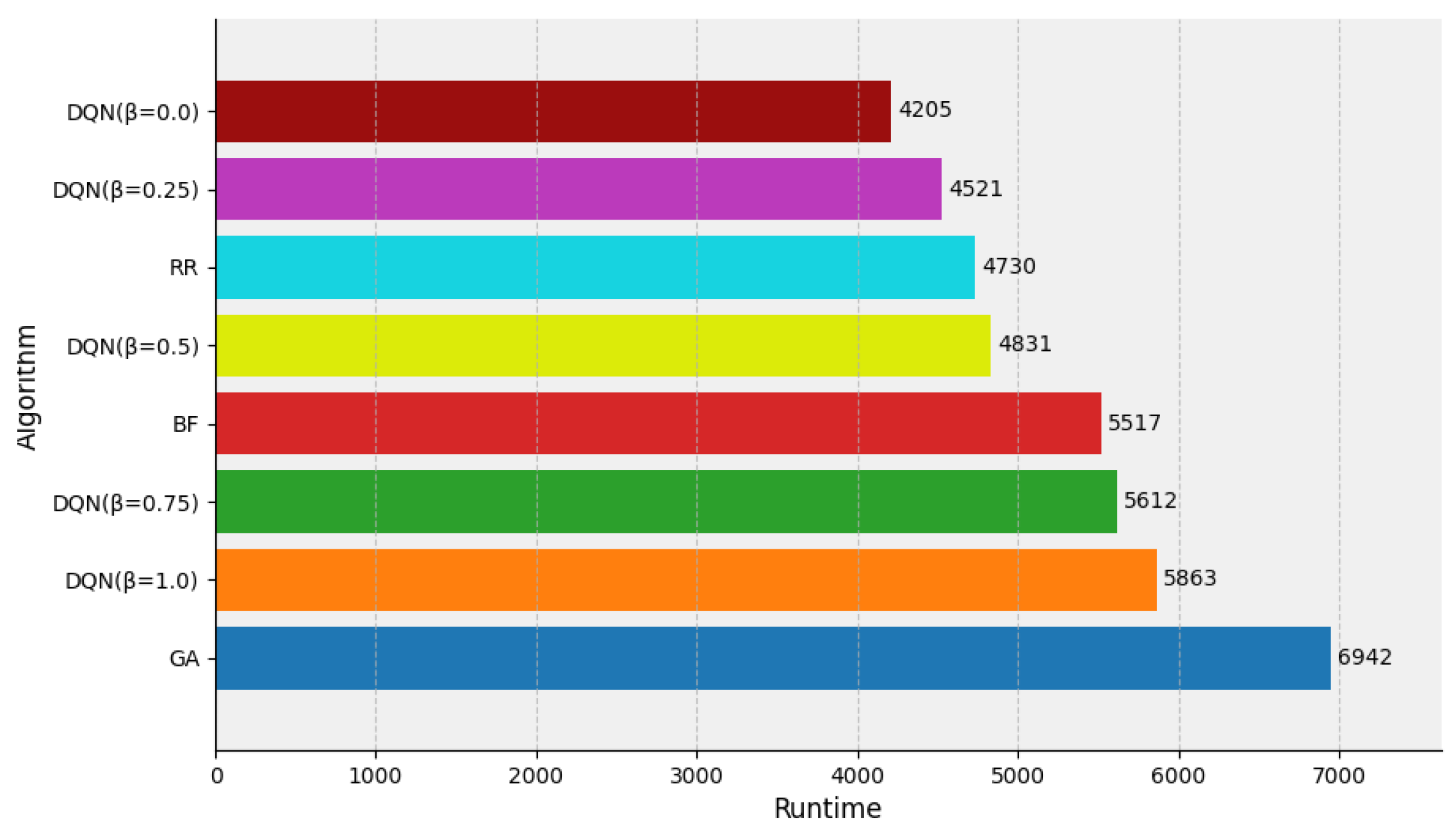
4.4.2. Evaluation of Runtime
4.4.3. Comprehensive Evaluation
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, F.; Liu, F.; Jin, H.; Vasilakos, A.V. Managing performance overhead of virtual machines in cloud computing: A survey, state of the art, and future directions. Proc. IEEE 2013, 102, 11–31. [Google Scholar] [CrossRef]
- Saxena, D.; Kumar, J.; Singh, A.K.; Schmid, S. Performance analysis of machine learning centered workload prediction models for cloud. IEEE Trans. Parallel Distrib. Syst. 2023, 34, 1313–1330. [Google Scholar] [CrossRef]
- Yao, Y.p.; Meng, D.; Zhu, F.; Yan, L.b.; Qu, Q.j.; Lin, Z.w.; Ma, H.b. Three-level-parallelization support framework for large-scale analytic simulation. J. Simul. 2017, 11, 194–207. [Google Scholar] [CrossRef]
- Risco-Martín, J.L.; Henares, K.; Mittal, S.; Almendras, L.F.; Olcoz, K. A unified cloud-enabled discrete event parallel and distributed simulation architecture. Simul. Model. Pract. Theory 2022, 118, 102539. [Google Scholar] [CrossRef]
- Chaudhry, N.R.; Anagnostou, A.; Taylor, S.J. A workflow architecture for cloud-based distributed simulation. Acm Trans. Model. Comput. Simul. 2022, 32, 15. [Google Scholar] [CrossRef]
- Fujimoto, R.M. Research challenges in parallel and distributed simulation. Acm Trans. Model. Comput. Simul. 2016, 26, 22. [Google Scholar] [CrossRef]
- Yoginath, S.B.; Perumalla, K.S. Optimized hypervisor scheduler for parallel discrete event simulations on virtual machine platforms. In Proceedings of the International ICST Conference on Simulation Tools and Techniques, Cannes, France, 5–8 March 2013; pp. 1–9. [Google Scholar]
- Yao, F.; Yao, Y.; Xing, L.; Chen, H.; Lin, Z.; Li, T. An intelligent scheduling algorithm for complex manufacturing system simulation with frequent synchronizations in a cloud environment. Memetic Comput. 2019, 11, 357–370. [Google Scholar] [CrossRef]
- Tang, W.; Yao, Y.; Li, T.; Song, X.; Zhu, F. An adaptive persistence and work-stealing combined algorithm for load balancing on parallel discrete event simulation. Acm Trans. Model. Comput. Simul. 2020, 30, 12. [Google Scholar]
- Song, Y.; Wei, L.; Yang, Q.; Wu, J.; Xing, L.; Chen, Y. RL-GA: A reinforcement learning-based genetic algorithm for electromagnetic detection satellite scheduling problem. Swarm Evol. Comput. 2023, 77, 101236. [Google Scholar] [CrossRef]
- Graham, R.L.; Lawler, E.L.; Lenstra, J.K.; Kan, A.R. Optimization and approximation in deterministic sequencing and scheduling: A survey. Ann. Discret. Math. 1979, 5, 287–326. [Google Scholar]
- Delimitrou, C.; Kozyrakis, C. Quasar: Resource-efficient and qos-aware cluster management. ACM Sigplan Not. 2014, 49, 127–144. [Google Scholar] [CrossRef]
- Maroulis, S.; Zacheilas, N.; Kalogeraki, V. A framework for efficient energy scheduling of spark workloads. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; pp. 2614–2615. [Google Scholar]
- Kaur, K.; Garg, S.; Aujla, G.S.; Kumar, N.; Zomaya, A.Y. A multi-objective optimization scheme for job scheduling in sustainable cloud data centers. IEEE Trans. Cloud Comput. 2019, 10, 172–186. [Google Scholar] [CrossRef]
- Lu, Y.; Sun, N. An effective task scheduling algorithm based on dynamic energy management and efficient resource utilization in green cloud computing environment. Clust. Comput. 2019, 22, 513–520. [Google Scholar] [CrossRef]
- Labba, C.; Saoud, N.B.B.; Dugdale, J. A predictive approach for the efficient distribution of agent-based systems on a hybrid-cloud. Future Gener. Comput. Syst. 2018, 86, 750–764. [Google Scholar] [CrossRef]
- De Grande, R.E.; Boukerche, A. Dynamic balancing of communication and computation load for HLA-based simulations on large-scale distributed systems. J. Parallel Distrib. Comput. 2011, 71, 40–52. [Google Scholar] [CrossRef]
- D’Angelo, G. Parallel and distributed simulation from many cores to the public cloud. In Proceedings of the 2011 International Conference on High Performance Computing & Simulation, Istanbul, Turkey, 4–8 July 2011; pp. 14–23. [Google Scholar]
- Yang, C.; Chai, X.; Zhang, F. Research on co-simulation task scheduling based on virtualization technology under cloud simulation. In Proceedings of the AsiaSim 2012: Asia Simulation Conference 2012, Shanghai, China, 27–30 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 421–430. [Google Scholar]
- Ding, S.; Chen, C.; Xin, B.; Pardalos, P.M. A bi-objective load balancing model in a distributed simulation system using NSGA-II and MOPSO approaches. Appl. Soft Comput. 2018, 63, 249–267. [Google Scholar] [CrossRef]
- Zhang, M.; Peng, Y.; Yang, M.; Yin, Q.; Xie, X. A discrete PSO-based static load balancing algorithm for distributed simulations in a cloud environment. Future Gener. Comput. Syst. 2021, 115, 497–516. [Google Scholar]
- Pandit, M.K.; Mir, R.N.; Chishti, M.A. Adaptive task scheduling in IoT using reinforcement learning. Int. J. Intell. Comput. Cybern. 2020, 13, 261–282. [Google Scholar] [CrossRef]
- Lin, Z.; Tropper, C.; Yao, Y.; Mcdougal, R.A.; Patoary, M.N.I.; Lytton, W.W.; Hines, M.L. Load balancing for multi-threaded PDES of stochastic reaction-diffusion in neurons. J. Simul. 2017, 11, 267–284. [Google Scholar] [CrossRef]
- Zhou, C.; Li, G.; Li, J.; Zhou, Q.; Guo, B. FAS-DQN: Freshness-Aware Scheduling via Reinforcement Learning for Latency-Sensitive Applications. IEEE Trans. Comput. 2022, 71, 2381–2394. [Google Scholar] [CrossRef]
- Li, T.; Ying, S.; Zhao, Y.; Shang, J. Batch Jobs Load Balancing Scheduling in Cloud Computing Using Distributional Reinforcement Learning. IEEE Trans. Parallel Distrib. Syst. 2024, 35, 169–185. [Google Scholar] [CrossRef]
- Wu, C.; Xu, G.; Ding, Y.; Zhao, J. Explore deep neural network and reinforcement learning to large-scale tasks processing in big data. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1951010. [Google Scholar] [CrossRef]
- Razaq, M.M.; Rahim, S.; Tak, B.; Peng, L. Fragmented Task Scheduling for Load-Balanced Fog Computing Based on Q-Learning. Wirel. Commun. Mob. Comput. 2022, 2022, 4218696. [Google Scholar] [CrossRef]
- Xu, J.; Guo, H.; Shen, H.W.; Raj, M.; Wurster, S.W.; Peterka, T. Reinforcement learning for load-balanced parallel particle tracing. IEEE Trans. Vis. Comput. Graph. 2022, 29, 3052–3066. [Google Scholar] [CrossRef] [PubMed]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Yoginath, S.B.; Perumalla, K.S. Efficient parallel discrete event simulation on cloud/virtual machine platforms. ACM Trans. Model. Comput. Simul. 2015, 26, 5. [Google Scholar] [CrossRef]
- Hou, B.; Yao, Y.; Wang, B.; Liao, D. Modeling and simulation of large-scale social networks using parallel discrete event simulation. Simulation 2013, 89, 1173–1183. [Google Scholar] [CrossRef]
- Xiao, Y.; Yao, Y.; Chen, K.; Tang, W.; Zhu, F. A simulation task partition method based on cloud computing resource prediction using ensemble learning. Simul. Model. Pract. Theory 2022, 119, 102595. [Google Scholar] [CrossRef]
- Rasmussen, R.V.; Trick, M.A. Round robin scheduling—A survey. Eur. J. Oper. Res. 2008, 188, 617–636. [Google Scholar] [CrossRef]
- Castillo, C.; Rouskas, G.N.; Harfoush, K. Efficient implementation of best-fit scheduling for advance reservations and qos in grids. In Proceedings of the 1st IEEE/IFIP International Workshop on End-to-End Virtualization and Grid Management (EVGM), San José, CA, USA, 29 October–2 November 2007. [Google Scholar]
- Hartmann, S. A competitive genetic algorithm for resource-constrained project scheduling. Nav. Res. Logist. 1998, 45, 733–750. [Google Scholar] [CrossRef]



| Action | Overview | Reward |
|---|---|---|
| 0 | Agent does not perform scheduling actions | 0 |
| Execute appropriate allocation decisions (meet resource constraints) | 1 | |
| Execution of inappropriate allocation decisions (not meeting resource constraints) | −100 | |
| All simulation samples are assigned and a scheduling training is successfully completed |
| Container Type | CPU Core | Quantity | Price |
|---|---|---|---|
| 0 | 4 | 2 | CNY 1.2/h |
| 1 | 8 | 4 | CNY 2.4/h |
| 2 | 12 | 2 | CNY 3.6/h |
| Parameters | Value |
|---|---|
| Batch size | 32 |
| No. of evaluation episodes | 8 |
| Epsilon | 0.001 |
| Learning rate | 0.01 |
| Collect steps per iteration | 10 |
| Optimization priority | [0.0,0.25,0.50,0.75,1.00] |
| No. of fully connected layers for Q-network | 200 |
| Policy evaluation interval | 100 |
| Discount factor | 0.7 |
| Replay buffer size | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Yao, Y.; Zhu, F. Parallel Simulation Multi-Sample Task Scheduling Approach Based on Deep Reinforcement Learning in Cloud Computing Environment. Mathematics 2025, 13, 2249. https://doi.org/10.3390/math13142249
Xiao Y, Yao Y, Zhu F. Parallel Simulation Multi-Sample Task Scheduling Approach Based on Deep Reinforcement Learning in Cloud Computing Environment. Mathematics. 2025; 13(14):2249. https://doi.org/10.3390/math13142249
Chicago/Turabian StyleXiao, Yuhao, Yping Yao, and Feng Zhu. 2025. "Parallel Simulation Multi-Sample Task Scheduling Approach Based on Deep Reinforcement Learning in Cloud Computing Environment" Mathematics 13, no. 14: 2249. https://doi.org/10.3390/math13142249
APA StyleXiao, Y., Yao, Y., & Zhu, F. (2025). Parallel Simulation Multi-Sample Task Scheduling Approach Based on Deep Reinforcement Learning in Cloud Computing Environment. Mathematics, 13(14), 2249. https://doi.org/10.3390/math13142249





