Abstract
In pursuit of zero-emission targets, increasing sustainability concerns have prompted urban centers to adopt more environmentally friendly modes of transportation, notably through the deployment of electric vehicles (EVs). A prominent manifestation of this shift is the transition from conventional fuel-powered buses to electric buses (e-buses), which, despite their environmental benefits, introduce significant operational challenges—chief among them, the management of battery systems, the most critical and complex component of e-buses. The development of efficient and reliable Battery Management Systems (BMSs) is thus central to ensuring battery longevity, operational safety, and overall vehicle performance. This study examines the potential of intelligent BMSs to improve battery health diagnostics, extend service life, and optimize system performance through the integration of simulation, real-time analytics, and advanced deep learning techniques. Particular emphasis is placed on the estimation of battery state of health (SoH), a key metric for predictive maintenance and operational planning. Two widely recognized deep learning models—Multilayer Perceptron (MLP) and Long Short-Term Memory (LSTM)—are evaluated for their efficacy in predicting SoH. These models are embedded within a unified framework that combines synthetic data generated by a physics-informed battery simulation model with empirical measurements obtained from real-world battery aging datasets. The proposed approach demonstrates a viable pathway for enhancing SoH prediction by leveraging both simulation-based data augmentation and deep learning. Experimental evaluations confirm the effectiveness of the framework in handling diverse data inputs, thereby supporting more robust and scalable battery management solutions for next-generation electric urban transportation systems.
Keywords:
machine learning; deep learning; simulation; agent-based modeling; battery management system; state of health estimation; electric urban buses MSC:
90-10; 90B06; 68T07
1. Introduction
As cities prioritize sustainability, awareness of environmental issues has accelerated the adoption of electric vehicles (EVs). However, private EVs alone are not able to provide a definitive solution to sustainable urban mobility. In this context, electric urban buses play a key role in the transition to greener transportation systems [1]. Public collective transportation systems, such as electric buses, represent an environmentally friendly alternative, offering significant benefits beyond the reduction of greenhouse gas emissions. These include decreasing noise pollution, lower operational costs, and mitigating issues such as traffic congestion and parking spot problems. As highlighted by [2], urban transportation systems are increasingly shifting from conventional fuel-powered buses to electric buses (e-buses) as part of broader efforts to mitigate climate change and meet environmental standards [1]. However, the shift to electric means introduces new challenges to urban transportation management and operations. These issues are particularly related to battery performance and reliability.
Lithium batteries, such as Lithium Cobal Oxide (LiCoO2), Lithium Manganese Oxide (LiMn2O4), and Lithium Iron Phosphate (LiFePO4) are the most used in electric vehicles due to their high energy efficiency, small size, long lifespan, and low self-discharge rate. Batteries power EVs and control their range, efficiency, and operational availability. Issues such as battery degradation, thermal instability, and unexpected failures can disrupt services and compromise public confidence in electric transportation. In fact, lithium batteries are sensitive to overcharging and overheating. For that reason, batteries require comprehensive monitoring to become smart energy storage systems. To address these concerns, advanced Battery Management Systems (BMSs) are required. The BMS monitors key aspects such as state of charge (SoC), state of health (SoH), state of power (SoP), state of function (SoF), cell balancing, remaining useful life (RUL), and thermal regulation to operate the batteries under a safe condition. Therefore, the BMS is an essential component for effective battery operation and its main function is to protect batteries from potential faults by monitoring battery status from terminal voltage, current, and temperature [3].
BMSs employ a variety of methodologies to estimate key states such as SoH or SoC, which can be roughly categorized into physics-based, empirical-based, and data-driven methods. Traditional physics-based methods rely on partial differential equations (PDEs) to model battery dynamics and thus, require a deeper understanding of electrochemical processes, which remains a challenge [4]. Empirical-based approaches, such as equivalent circuit models, offer a simpler implementation but suffer from limited modeling precision under varying operating conditions, compromising the accuracy of SoH estimation [5]. In contrast, machine learning (ML) and deep learning (DL) approaches have emerged as powerful alternatives, requiring no prior knowledge of electrochemical reactions while leveraging large datasets to model the non-linear relationships between battery states and influencing factors [6]. This includes support vector machines, Gaussian process regression, and artificial neural networks, which outperform in accuracy and robustness, particularly when combined with onboard sensor data under natural driving conditions. As the authors of [6] suggest in their study, the future of BMS development is likely to focus on achieving greater accuracy, real-time performance, and robustness through the integration of ML techniques. By integrating advanced machine learning algorithms, deep learning methods, and real-time data analytics, intelligent BMSs can effectively manage key aspects of battery operation and enable real-time diagnostics for decision-making. This study underscores the importance of incorporating artificial intelligence and deep learning, specifically utilizing Multilayer Perceptron (MLP) and Long Short-Term Memory (LSTM) to predict and mitigate potential battery issues and fault diagnosis and optimize battery performance.
In contrast to prior studies that have independently addressed data-driven modeling or physics-based simulation, this work advances a hybrid theoretical framework that bridges these traditionally distinct paradigms. By integrating simulation-generated battery usage profiles—developed using a physics-informed Thevenin circuit and agent-based modeling—with deep learning-based SoH prediction, the study introduces a scalable, application-specific approach for battery diagnostics. This framework addresses a critical gap in the literature: the lack of real-world-operationally aligned synthetic data and its combined use with learning algorithms to enhance predictive accuracy under constrained data availability. Moreover, the incorporation of behavioral realism through ABM adds a system-level abstraction that has not been extensively explored in the context of BMS optimization for electric urban buses.
This study offers four key contributions that collectively advance the current state of knowledge and practical implementation of intelligent Battery Management Systems (BMSs) for electric urban bus fleets.
- (i)
- Simulation-Driven Reframing of BMS Functionality: While BMS technologies are generally considered mature, this work reinterprets their application through the development of an agent-based simulation environment that integrates a physics-informed Thevenin equivalent circuit model with empirically calibrated degradation laws. This novel framework facilitates the generation of synthetic battery usage profiles that closely replicate the duty cycles of electric buses, thereby addressing a significant gap in the literature—namely, the absence of application-specific modeling tailored to public transit operations. Unlike traditional models, this approach provides a scalable and reproducible platform for evaluating intelligent BMS functionality under operationally realistic conditions.
- (ii)
- Dual-Domain Evaluation and Real-Time Edge Deployment of Deep Learning Models: Although the Multilayer Perceptron (MLP) and Long Short-Term Memory (LSTM) architectures are well established, this study distinguishes itself by assessing their predictive performance across two distinct data domains: (a) empirical data from controlled battery aging experiments and (b) synthetic data derived from the simulation environment. Furthermore, both models are converted to TensorFlow Lite and deployed on edge hardware (e.g., Raspberry Pi 4B, Cambridge, UK), thereby demonstrating the feasibility of real-time state-of-health (SoH) prediction in embedded systems. This step extends existing research beyond offline benchmarking by validating both inference speed and predictive accuracy in real-world, resource-constrained settings.
- (iii)
- Integration of Simulation and Machine Learning for SoH Prediction: This research proposes an end-to-end pipeline that couples simulation-based data generation with deep learning–based SoH prediction. This integration not only enables scalable model development in the absence of extensive experimental datasets but also introduces a cost-effective framework for data augmentation, model training, and validation in data-scarce environments—an area often overlooked in prior research.
- (iv)
- Dual-Validation Strategy Leveraging Empirical and Synthetic Data: The presented evaluation framework employs a dual-validation strategy, cross-verifying model performance using both real-world measurements and simulation-derived datasets. This method addresses longstanding concerns regarding reproducibility, generalizability, and scalability in SoH estimation, particularly for fleet-level deployments in electric urban transit systems.
In addition, this study presents a dual-source learning architecture in which deep learning models trained on empirical battery data (specifically, the The Xi’an Jiaotong University XJTU dataset) are validated using high-fidelity synthetic data produced by an agent-based simulation model developed in AnyLogic. This hybrid methodology significantly reduces dependence on costly experimental testing and accelerates the prototyping of BMS solutions—representing a novel integration not extensively explored in the existing literature.
Together, these contributions provide a replicable and extensible foundation for enhancing the theoretical rigor and practical deployment of intelligent BMSs, with broad implications for digital twin development and the advancement of sustainable, smart transportation infrastructure.
To enhance realism, synthetic datasets were developed by combining an equivalent circuit model (Thevenin) with empirical aging laws and stochastic operational scenarios, effectively simulating dynamic e-bus charging/discharging cycles with embedded degradation. This offers a novel pathway for SoH modeling, particularly in resource-constrained settings.
Beyond theoretical contributions, the study demonstrates real-time inference feasibility by deploying the trained models on a Raspberry Pi 4B using TensorFlow Lite. This practical implementation addresses a critical gap in existing BMS research by highlighting hardware-software integration for low-latency, power-efficient edge deployment.
Finally, by comparing MLP and LSTM models across empirical and synthetic data regimes, this research assess model robustness and generalization. This dual-regime evaluation provides actionable insights for model selection—an aspect often overlooked in prior single-model studies.
The rest of the work is structured as follows. Section 2 reviews the relevant literature and methodologies addressing the BMS and battery state estimation for electric vehicles. Section 4 will explain the suggested approach, and Section 6 outlines the computational experiments proposed. In Section 7, the research findings will be discussed, and finally, the conclusions will be described in Section 8.
2. Literature Review
As batteries have evolved, battery models have also been developed. As the authors of [7] pinpoint in their review, these models serve for demonstration and better understanding of the basic features of batteries. Nevertheless, they can represent physical limits and are able to predict behavior under different conditions. Each modeling technique offers various trade-offs in terms of accuracy, computational complexity, and practical applicability. According to comparative reviews [8,9], battery modeling approaches can be classified into three main types: electrochemical models, equivalent circuit models, and data-driven models. While electrochemical models are very accurate and complex, for simulation of electric systems, more simple but less accurate equivalent circuit models are used. Simulation-based studies analyze the real-world performance of BMSs, such as the virtual battery simulation framework proposed by [10] that integrates various external factors, such as temperature, manufacturing quality, and driving behavior, to predict battery performance accurately. Similarly, ref. [11] validate an equivalent circuit model for EV batteries through experimental data and real-world driving scenarios through battery simulations. When it comes to electric buses in particular, ref. [12] focuses on the impact of battery degradation on e-bus operations through the simulation of numerical cases studies of bus operation driving cycles. The authors incorporate a battery degradation model to account for the quantitative relationship between the installation of the charging infrastructure and battery life extension and they demonstrate the importance of considering aging effects in long-term fleet management. Aging effects are a key aspect of batteries and can be addressed experimentally and using modeling approaches to allow comprehensive analysis of aging behavior for real-world applications under different operational conditions as proposed in recent studies [13].
Unlike fuel-powered vehicles, EVs rely on advanced BMSs to ensure the efficiency and safety of their energy storage systems [14]. BMSs are critical for monitoring and controlling key battery states ensuring safe and reliable operation in electric vehicles. Recent reviews of BMS technologies highlight the shift toward data-driven methods and intelligent algorithms, including control architectures [15] and the integration of state-of-the-art estimation methods [16] and providing a comprehensive analysis of ML applications in BMSs [17] and a detailed analysis of the challenges associated with estimating battery states [18]. However, as the authors of [14] conclude in their review, traditional approaches such as Kalman filters and equivalent circuit models are still the most popular despite their limitations in handling complex real-time scenarios.
Machine learning has emerged as a revolutionary approach in BMSs, enabling accurate estimations of battery states without requiring detailed knowledge of electrochemical processes. Studies such as [19] highlight the integration of AI-driven algorithms and neural networks in BMSs, showing that data-driven models and intelligent algorithms not only reduce computational complexity but also improve prediction robustness [20]. Ref. [21] extended this analysis by exploring the integration of AI for predictive fault detection, proving that AI-based methodologies can significantly enhance the safety and operational efficiency of lithium-ion batteries. Moreover, ref. [22] emphasizes the role of ML techniques in SoH and SoC estimation, as they enhance real-time performance addressing critical gaps in traditional methods. In their study, the authors of ref. [23] develop a comparative analysis of four SoC estimation methods in a cloud platform and demonstrate how advanced neural networks like LSTM, feedforward neural networks, and gated recurrent units outperform traditional methods in both computational efficiency and accuracy. Additionally, ref. [24] proposes a real-time SoH estimation model using a hybrid one-dimensional convolutional neural network and a bidirectional gated recurrent unit architecture, and to account for all SoH indicators, the proposed approach uses current, voltage, and temperature measurements, which are readily obtainable from the BMS. Fault diagnosis and prognostics are essential for ensuring the safety and reliability of battery systems for electric buses, where continuous service is crucial. ML techniques such as LSTM, recurrent neural networks, and support vector machine have demonstrated their effectiveness in predictive fault diagnosis and RUL estimation, validating their results with datasets like NASA Ames and CALCE [25]. As stated in [26], combining real-time data with simulation and predictive analytics, digital twin technologies [27] become an accurate tool in the fault diagnosis of the BMS by comparing the predicted states against the threshold values and reporting any abnormalities.
Electric buses are positioned as a solution to the transition toward sustainable urban transportation. However, research specifically focused on the BMS for electric buses remains limited compared to studies on electric vehicle BMSs. Early advancements in electric bus BMSs focused on physics-based methods for lead–acid batteries, which provided SoC, SoH, and cell balancing functionalities in electric buses [28].Traditional methods such as regression analysis and Kalman filtering, as reviewed by [1], have set the basis of battery management for electric buses. However, machine learning-based approaches are gaining interest in the field due to their ability to adapt to dynamic operational scenarios [3]. In their paper, the authors of ref. [29] demonstrate practical applications for SoC and RUL estimation in a small-scale system of campus e-buses. Neural network-based methods, such as radial basis function (RBF) neural networks, have also been applied to battery aging prediction and SoH estimation, providing data-driven solutions to optimize performance [5]. The comparative study in [2] further highlights the potential of integrating traditional techniques with ML to optimize performance, efficiency, and safety, with electric buses offering environmental and operational benefits compared to hybrid and diesel alternatives, including reduced emissions and noise pollution.
Table 1 presents a comparative overview of the contributions with respect to prior studies, emphasizing the algorithms employed and the types of data utilized. Unlike earlier research, which predominantly concentrated either on isolated machine learning techniques or on simulation frameworks relying solely on experimental or synthetic datasets, this study integrates two deep learning models (MLP and LSTM) within a simulation-based modeling paradigm. Specifically, this research leverages both empirical data from the XJTU battery aging dataset and synthetic data generated through a physics-informed simulation model. In addition, the contribution is extended beyond model development by deploying the trained models using TensorFlow Lite, thereby enabling real-time inference on edge devices such as Raspberry Pi and microcontrollers. This aspect of practical deployment and real-world validation, which remains underrepresented in the existing literature, underscores the applied significance of this work.

Table 1.
Comparative framework of related works on machine learning and simulation-based BMS approaches.
3. Dataset
The Xi’an Jiaotong University (XJTU) battery dataset represents a newly developed, large-scale benchmark designed to facilitate performance evaluation [30]. Specifically, it comprises run-to-failure data for 55 lithium-ion batteries that were subjected to six distinct charging and discharging protocols. These batteries, manufactured by LISHEN, employ a cathode material with the chemical composition LiNi0.5Mn0.5O2. Each battery is characterized by a nominal capacity of 2000 mAh and a nominal voltage of 3.6 V, with charge and discharge cut-off voltages of 4.2 V and 2.5 V, respectively. All batteries were cycled to failure using a 40-channel ACTS-5V10A-GGS-D system at ambient room temperature.
The XJTU battery dataset comprises six batches, each characterized by a distinct charging and discharging strategy. In this study, batch five is employed to illustrate the charging and discharging protocols. Batch number five consists of eight batteries and utilizes a random walking strategy, thereby more closely mirroring real-life usage. Specifically, all cells are charged to 4.2 V at a rate of 1C (2 A) using a constant current–constant voltage (CC–CV) mode, followed by a 5 min rest period, and then discharged to 3.0 V. The term “1C” denotes a charging current equivalent to the battery’s nominal capacity (2000 mA or 2 A) [31,32]. The discharge current is a randomly selected integer within the range of two to eight amperes, and the discharge duration is randomly chosen from two to six minutes.
4. Methods
4.1. Study Design
This study adopted a comprehensive methodological approach to examine the efficacy of BMSs in improving battery health, extending lifespan, diagnosing faults, and enhancing overall performance. Specifically, the research concentrated on integrating DL architectures. This is a category of neural network models characterized by multiple layers performing nonlinear transformations to derive meaningful representations from data. These models were utilized to optimize battery operation, with particular attention given to applications within electric vehicles and renewable energy systems.
A primary focus of the investigation was evaluating intelligent BMSs in accurately managing a critical battery parameter known as the SoH. The SoH parameter assesses the battery’s general condition, including the extent of capacity degradation over its operational life. Accurate SoH assessment is essential for determining optimal battery replacement timing, which significantly impacts operational reliability and cost efficiency. This research employed two distinct methodological approaches. The first involved training DL models on empirical data obtained from the XJTU dataset, subsequently validating the performance and robustness of these models. The second approach centered on generating simulated data to serve as input for the previously trained DL models aimed at predicting battery SoH.
The rationale behind employing simulated data is twofold: firstly, to evaluate the accuracy and reliability of predictions derived from simulation in comparison to those based on actual battery data from the XJTU dataset, and secondly, to investigate the feasibility of substituting simulation-generated data for real-world measurements. This substitution holds potential economic benefits, reducing costs associated with data collection from real batteries, and could significantly accelerate the development of cost-effective and efficient intelligent BMSs.
Thus, with the adoption this comprehensive approach, the study aimed to bridge the gap between theoretical models and practical applications in battery management technology. The integration of DL techniques with both real and simulated data represents a novel approach in the field, potentially leading to more robust and adaptive BMS solutions.
4.2. Evaluation Algorithms
To estimate the battery SoH, the study evaluated two prominent deep learning-based models: MLP and LSTM. Notably, only the standard architectures of these models were examined, without incorporating specialized variants. This section presents a concise description of these two algorithms.
The domain of deep learning for battery state estimation encompasses a wide range of promising architectures, including convolutional neural networks (CNNs), gated recurrent units (GRUs), and hybrid frameworks such as CNN-BiGRU, among others. However, in this study, the Multilayer Perceptron (MLP) and Long Short-Term Memory (LSTM) models were deliberately selected based on several considerations [33].
First, both MLP and LSTM are foundational deep learning architectures widely recognized in the literature. The MLP serves as a baseline feedforward neural network, offering interpretability and computational efficiency. In contrast, the LSTM is a recurrent model specifically designed for sequence learning, making it well suited for capturing temporal dependencies inherent in time-series data such as battery voltage and current profiles. Evaluating these two models allowed us to establish a comparative framework grounded in theoretical rigor and enhanced reproducibility.
Furthermore, the practical objective of this study was to enable deployment on edge devices (e.g., Raspberry Pi using TensorFlow Lite). Both MLP and LSTM present favorable trade-offs between model complexity, predictive accuracy, and inference speed, making them particularly suitable for resource-constrained environments.
4.2.1. The Multilayer Perception (MLP)
MLP experienced a significant surge in popularity within the machine learning community during the 1980s, as documented in various studies [34]. Structurally, the MLP features forward architecture, characterized by fully connected layers, as illustrated in Figure 1. This neural network model typically comprises multiple hidden layers, an input layer, and an output layer.
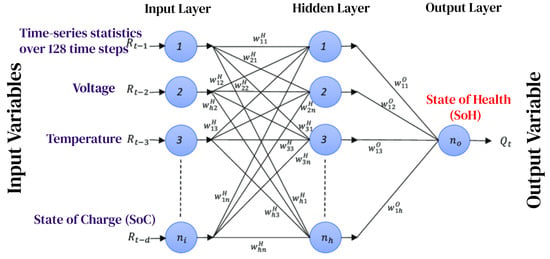
Figure 1.
The diagram of MLP.
The MLP with exactly one hidden layer is formally defined as follows:
- Input Layer: Receives the input feature vector , where d is the dimension of the input. These features include time-series statistics over 128 time steps, comprising voltage, current, temperature, and SoC measurements—each preprocessed through min–max normalization and standardized to a [−1,1] range (as defined in Equation (29)).
- Hidden Layer: Performs a linear transformation followed by a nonlinear activation function :Here, and are the weight matrix and bias vector of the hidden layer, respectively, and m is the number of hidden units.
- Output Layer: Computes the final output through another linear transformation, possibly followed by an activation function (identity, softmax, sigmoid, etc.). The model predicts a scalar value corresponding to the state of health (SoH), computed as a proxy for battery capacity fade. This output is expressed on a normalized scale and subsequently rescaled to the actual SoH domain for interpretability and validation:Here, and are the weight matrix and bias vector for the output layer.
The entire forward pass of this single-hidden-layer MLP can be compactly represented as
Note that common choices for activation functions () include sigmoid and tanh, while common output functions () include identity for regression, sigmoid for binary classification, and Softmax for multi-class classification.
Finally, the training process involves minimizing a loss function such as the Mean Squared Error for regressions in Equation (6) or the Cross-Entropy Loss for classification in Equation (7).
where represents the L1 regularization term that helps prevent overfitting by promoting sparsity in the model weights.
The study employed the following explicit architectural details for the MLP model:
- Input dimension: The input layer consists of 512 neurons, corresponding to the flattened feature space from the four-channel time series (4 × 128 time steps).
- Hidden Layers: The model contains two hidden layers. The first hidden layer comprises 256 neurons, and the second hidden layer contains 64 neurons. Both layers utilize the ReLU activation function to capture non-linear relationships.
- Output Layer: A final dense layer with a single neuron outputs the predicted SoH value using a linear activation function, as the regression task requires continuous output.
- Regularization: L1 regularization and dropout (rate = 0.2) were applied to mitigate overfitting. The dropout was inserted after each hidden layer.
- Optimizer and Loss: The model was optimized using the Adam optimizer (learning rate = ), and training was governed by the MSE loss function.
4.2.2. The Long Short-Term Memory (LSTM)
The LSTM model, first proposed by Hochreiter and Schmidhuber in 1997 [35], is an advanced form of recurrent neural network (RNN) that significantly improves computational effectiveness, especially in addressing the vanishing gradient problem encountered during the training of extensive sequential data. By employing specialized gating mechanisms within its structure, LSTM facilitates better retention and propagation of information across long sequences, thus overcoming limitations inherent to standard RNN architectures. A detailed illustration of the LSTM architecture is provided in Figure 2, offering further clarity on its structural components and functioning.
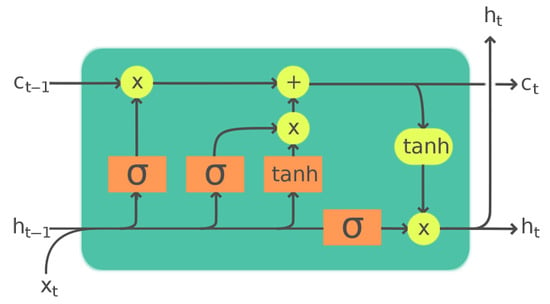
Figure 2.
The diagram of LSTM.
The mathematical formulation of a basic Long Short-Term Memory (LSTM) unit for a time step t involves a series of gating mechanisms that control the flow of information across sequential time steps. An LSTM cell consists primarily of three gates, the input gate , described in Equation (8); forget gate , in Equation (9); and output gate , in Equation (12) each employing sigmoid activations to manage information selectively. Additionally, a candidate memory cell and a memory state , described in Equations (10) and (11), respectively, store and modulate the sequence information. Finally, the hidden state update is described in (13).
where
- : Input vector at time step t;
- : Weight matrices for inputs;
- : Weight matrices for hidden states;
- : Bias vectors;
- : Logistic sigmoid activation function, defined as
- tanh: Hyperbolic tangent activation function;
- ⊙: Element-wise multiplication (Hadamard product).
4.3. Evaluation Metrics
To assess the performance of the models quantitatively, this research employs three evaluation metrics: the Mean Squared Error (MSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE). These metrics were utilized to measure the discrepancy between the estimated SoH and the actual SoH values.
4.3.1. Mean Squared Error (MSE)
MSE, which is the average sum of the squares of each error, is used to measure the difference between the true value and the predicted value. The calculation formula is as follows:
4.3.2. Mean Absolute Error (MAE)
Mean Absolute Error (MAE) is a widely employed metric in predictive modeling and regression analysis, utilized to quantify prediction accuracy by measuring the average magnitude of the errors between predicted and observed values, irrespective of their direction [36]. The formulation is as follows:
where n represents the number of observations, denotes the observed value, and indicates the corresponding predicted value.
4.3.3. Mean Absolute Percentage Error (MAPE)
Mean Absolute Percentage Error (MAPE) is frequently used as a performance metric in predictive modeling and forecasting, quantifying prediction accuracy by expressing errors as percentages of actual observed values [37]. Mathematically, MAPE is defined as:
where n represents the number of observations, is the actual value, and denotes the predicted value.
4.4. Simulation Model
Once the ML models are validated with empirical data, simulated data is generated for predicting the SoH of the battery under controlled and varied operational scenarios. Specifically, simulation-based datasets are created to be used as input for the ML models, allowing us to evaluate their prediction under known conditions. For this aim, an agent-based modeling (ABM) simulation model was developed and the battery operation modes were represented within a statechart. This approach captures the transitions between charging, resting, and discharging states, reflecting a realistic cycle typical of electric vehicles and also the experiments performed to obtain the XJTU battery dataset. Finally, the simulation model was implemented in the commercial software AnyLogic [38]
4.4.1. Battery Simulation Model
To simulate battery behavior, an Equivalent Resistive (R) and Capacitive (C) Circuit Model was implemented (see Figure 3). This equivalent circuit is also known as Thevenin Battery Model and characterizes the internal dynamics of the battery for simulation purposes, as explained in [39]. Both and model the electrochemical polarization capacitance and resistance, is the input ohmic resistance, and represents the open circuit voltage (OCV). The state variable of the circuit is the , that represents the battery voltage and its state space equation is derived from Equations (17)–(23) as
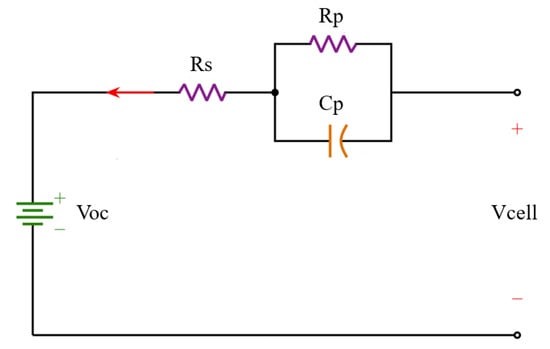
Figure 3.
Equivalent Thevenin circuit model for the battery cell.
The electrical behaviour of the Thevenin model shown in Figure 3 is expressed as
Considering the RC branch, the following differential equation is obtained:
The solution to this differential equation is given by
where the time constant is defined as
Therefore, the complete equation for the battery cell voltage becomes
Considering boundary conditions and initial values,
Thus, it can be formulated as
To implement this formulation in the simulation, it must be discretized to
Following the same procedure, the battery current function is obtained:
This RC equivalent circuit is effective to implement the battery simulation model through a state chart and to capture how the battery voltage (V) and current (I) evolve in each operational mode. Agent-based modeling was chosen due to its flexibility in modeling individual battery cycles and the potential for integrating more complex behaviors in future experiments. The battery is treated as an agent in the simulation framework and its behavior follows the state chart shown in Figure 4 that includes (i) charging, divided into constant current (CC) and constant voltage (CV) modes; (ii) resting (divided into short or long rest states); and (iii) discharging states. The state transition is triggered by time-based events or by thresholds, such as cut-off current, minimum SoC, or cut-off voltage.
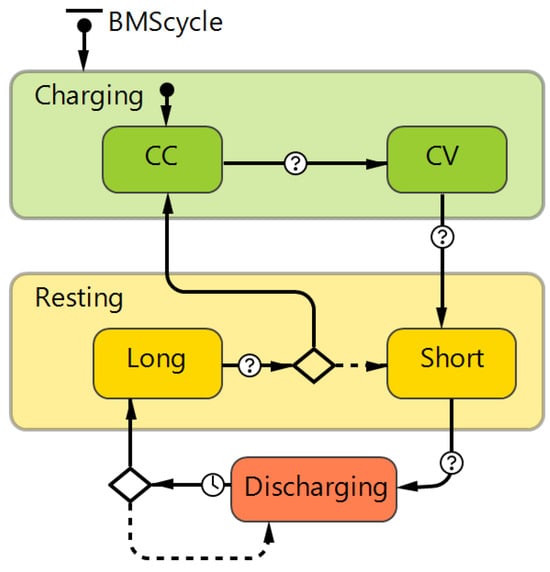
Figure 4.
Battery simulation model statechart in Anylogic software.
The cycle starts at the charging state and the agent transitions from CC to CV once the voltage approaches . After entering CV mode, the battery continues charging at a constant voltage , while the current gradually decreases. The battery transitions from CV mode to the resting state when the charging current drops down to the cut-off current threshold , which indicates the battery is fully charged. The resting state is time-triggered and the resting time is defined as a distribution. When the agent is in a rest state, the simulation sets the battery current to zero. After resting, the agent enters the discharging state initiating the discharge cycle. The duration of this discharging phase is triggered by either a minimum voltage threshold or a minimum SoC threshold.
4.4.2. Battery Aging Model
The battery simulation model described in the previous section represents an ideal scenario in which the battery performance remains stable over repeated cycles without deterioration. However, batteries suffer from degradation with use, repeated charge–discharge cycles, and temperature. To mimic this, an aging component is introduced to the simulation model such that the values of current and voltage are affected through time. The aging model employed is based on the empirical findings of [40], who investigated calendar aging in lithium-ion batteries and established that internal resistance follows a power-law dependency on time (in months), expressed by
where represents the percentage increase in resistance, and a and b are empirical constants derived from accelerated aging experiments. According to the results in [40], a value of provides the best fit for calendar aging data.
In the simulation, the battery degradation is modeled by adjusting the charging parameters that are the time constants associated with the constant current () and constant voltage () charging phases. The effect of resistance increase on the time constant () of the RC equivalent circuit is implemented. Since directly depends on the resistance, the following relationship is established between and :
Given this dependency, changes in over time due to aging can be modeled as
where a is a calibrated coefficient derived from the experimental data. These parameters directly affect the battery charging variables and simulate the gradual degradation of battery health and the resulting performance limitations observed in real world applications.
5. Implementation Details
5.1. Model Training
To ensure consistency and comparability among the evaluated models, each was optimized by minimizing the Mean Squared Error (MSE) loss function. It is important to note that the models implemented in this research are standard versions, devoid of specialized modifications or enhancements.
During the training stage, optimization was performed using the Adam optimization algorithm, initialized with a learning rate of and a weight decay parameter set at . Training was carried out in batches of 128 samples, spanning a total of 100 epochs. To mitigate the risk of overfitting, an early stopping strategy was employed, ceasing training if no performance improvement was observed after 30 consecutive epochs.
Furthermore, a multi-step learning rate scheduler was integrated into the training regimen, dynamically adjusting the learning rate to enhance model convergence. Specifically, the learning rate was reduced by a factor (gamma) of 0.5 at predetermined milestones, which occurred at epochs 30 and 70. These methodological choices were deliberately adopted to maintain a standardized evaluation framework across all compared models.
5.2. Convert Tensorflow Model to TensorFlow Lite
The deployment of machine learning models on edge devices has become increasingly important for applications requiring real-time inference capabilities without cloud connectivity. This section outlines the process of converting TensorFlow models to TensorFlow Lite format and their subsequent deployment on Raspberry Pi hardware.
TensorFlow Lite represents Google’s lightweight solution designed specifically for mobile, embedded, and IoT devices. It offers substantial benefits compared to standard TensorFlow implementations, including reduced model size, decreased inference time, and lower power consumption [41].
The edge deployment paradigm also enhances privacy and security by keeping sensitive data local, reduces bandwidth consumption, and enables applications to function even in disconnected environments [42]. These advantages make Raspberry Pi with TensorFlow Lite an attractive platform for a wide range of AI applications, from smart home devices to industrial monitoring systems.
The TensorFlow Lite converter accepts a TensorFlow model as input and produces an optimized TensorFlow Lite model stored in the FlatBuffer format, distinguished by the (.tflite) file extension. Subsequently, this converted model can be deployed across multiple operating systems or integrated within various microcontroller environments [41]. The selection of TensorFlow Lite was motivated by its optimization for low-power, resource-constrained edge devices such as Raspberry Pi. These platforms are highly relevant for on-board diagnostic systems in electric buses where real-time battery health monitoring is needed without reliance on cloud infrastructure. TensorFlow Lite significantly reduces model size and computational complexity, enabling fast inference and efficient battery SoH prediction in embedded environments.
As detailed in the revised section, the deep learning models (MLP and LSTM) were implemented using TensorFlow and then converted them to the “.tflite” format using the TensorFlow Lite Converter. This involved applying post-training quantization to reduce model precision (e.g., from float32 to int8), thereby lowering memory usage and inference time. The converted models were then tested on a Raspberry Pi 4B (4GB RAM) running Raspberry Pi OS with Python 3.9. Inference tests were directly conducted on the Raspberry Pi using simulated battery data. The models demonstrated robust real-time capability, with MLP inference taking 28 ms and LSTM 49 ms per SoH prediction under a batch size of one. This confirms the feasibility of deploying such models in real-world mobile environments where energy efficiency, inference latency, and model footprint are critical.
The Raspberry Pi was interfaced with battery data acquisition software using GPIO and UART protocols to simulate real-time signal flow. This mimics integration with actual Battery Management Systems (BMSs) in electric buses. By validating this setup, this research demonstrates that the proposed models can be seamlessly embedded into IoT-enabled BMS frameworks, supporting edge AI-based battery diagnostics.
5.3. SoH Estimation Using Simulation-Generated Data
The implementation combines data manipulation and DL inference to transform raw sensor data into actionable predictions.
The pipeline begins by importing the simulation-generated dataset. The data is converted and transposed to align time-series channels along the first dimension. Then, reshaping to dimensions (N, 4, 128) to create a batch-compatible format for DL framework, where the number four likely represents sensor channels and 128 corresponds to time steps.
The numerical array undergoes min-max normalization followed by linear scaling to [−1,1] range using the transformation
This dual normalization approach improves model convergence by ensuring consistent input scales while preserving relative differences between data points.
Following preprocessing, the preprocessed data is fed into a pre-trained DL model, which has been previously optimized and validated on the XJTU battery database for battery SoH prediction. The prediction generated from this pipeline provides insights into battery behavior under specified conditions.
6. Computational Experiments
To prove the effectiveness of the machine learning models in predicting battery SoH, the simulation model is used to generate synthetic operational data. Realistic driving scenarios of an electric vehicle were simulated, assuming a schedule of five charge–discharge cycles per operational day. Under these conditions, a computational experiment of a month of operation is executed to observe the impact of degradation. The aim of this experiment is to capture the battery degradation through the simulation of voltage–current (V-I) curves during a month, which is comparable to the two weeks experiments carried out for the real world XJTU dataset. The dataset obtained from this simulation is utilized as inputs for validating the considered ML models.
In the experiment, the charging and discharging cycles follow the strategy described in the XJTU battery experiments (batch 5): the battery is discharged from V down to a cut-off voltage of V with random discharge currents uniformly selected from the integer range of 2 to 8 A, each maintained for a randomly chosen time between 2 and 6 min. This stochastic approach replicates the operational conditions of an electric vehicle. The degradation parameters and are updated according to the aging model described in Equation (28), affecting the values of V and I. The integration of this aging model allows to generate synthetic battery data, which is utilized to test and validate the performance of the MLP and LSTM models designed for SoH estimation. Table 2 gathers all the parameters considered in the computational experiments. The parameter values were selected to reflect operational conditions of lithium-ion battery cells maintaining consistency with the experimental data provided by the XJTU battery dataset.

Table 2.
Simulation model parameters and their values.
Figure 5 shows an example of the simulation results for the voltage and current profile of the battery across a charge–discharge cycle generated by the ABM model. These curves follow the strategy analyzed in the methodology section and thus the battery follows the sequence of operational states defined in the agent-based state chart model: constant current charging transitions into constant voltage mode up to the maximum voltage 4.2 V, (). During the CV state, the battery voltage is maintained constant, while current gradually decreases until reaching the cut-off current threshold . After some minutes resting, the battery enters the discharging phase, modeled with random discharge currents that show the stepwise pattern depicted in the figure.
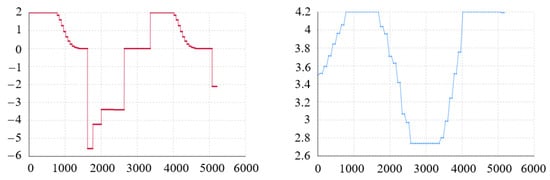
Figure 5.
Battery simulation model current (left) and voltage (right) profiles during a complete charging and discharging cycle.
7. Computational Result
The results of this study provide a comprehensive evaluation of the proposed model’s performance across multiple metrics, offering insights into its accuracy and reliability. The findings are presented systematically, highlighting key trends and comparing them with baseline methods to ensure a thorough analysis. Figure 6 and Figure 7 illustrate the training and validation loss curves of the MLP model and LSTM model, respectively, using the XJTU battery dataset, measured using the MSE loss function. The blue curve represents the training loss, while the orange curve corresponds to the validation loss.
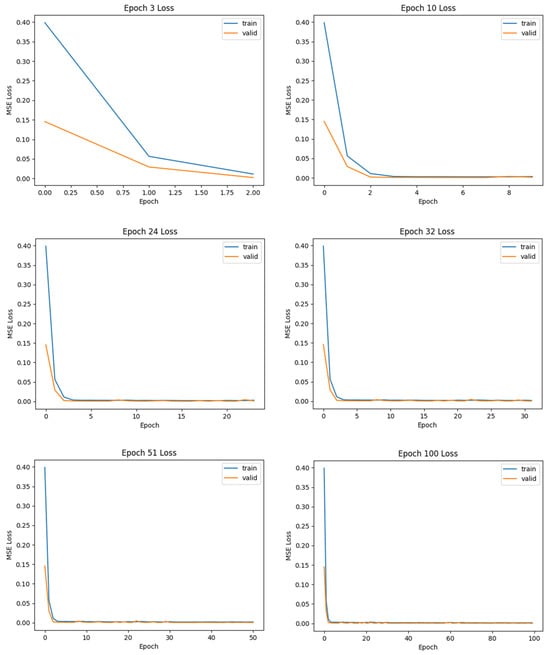
Figure 6.
MLP loss curves for XJTU battery dataset.
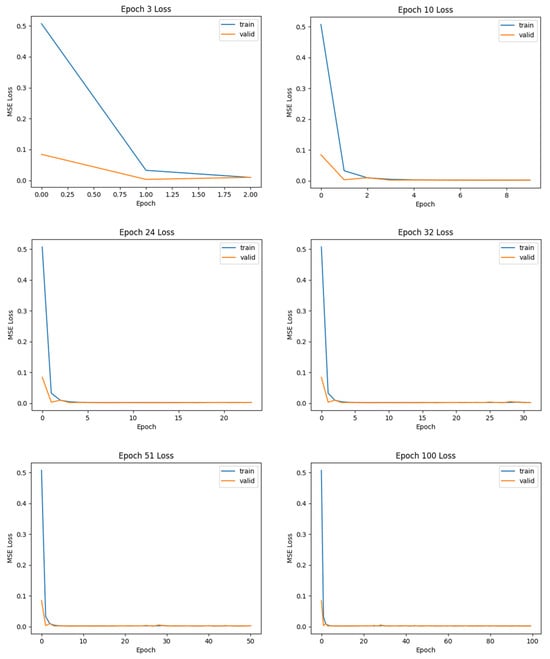
Figure 7.
LSTM loss curves using XJTU battery dataset.
7.1. MLP Model Performance
The progression of model performance during training was evaluated using MSE loss metrics for both the training and validation datasets across varying numbers of epochs. The results are presented in Figure 6, corresponding to epochs 3, 10, 24, 51, and 100, respectively.
At the early training phase (Epoch 3), the MSE loss for both the training and validation datasets exhibited a rapid decline within the initial epochs. The training loss decreased from approximately 0.40 to near-zero values by Epoch 2, while the validation loss followed a similar trend, albeit starting at a lower initial value (0.15). This indicates that the model quickly adapted to the data during the early phase of training, minimizing both overfitting and underfitting.
By Epoch 24, both training and validation losses had stabilized at values close to zero, with negligible differences between the two curves. This stability persisted through Epoch 51, suggesting that the model had achieved convergence. Furthermore, the consistent alignment of training and validation losses implies that the model generalized well without significant overfitting.
Finally, at the final training phase (Epoch 100), The results demonstrate that both training and validation losses remained stable at near-zero values throughout this extended training period. This confirms that additional epochs did not lead to further improvements in performance, indicating that optimal convergence was achieved earlier in training.
Across all epochs analyzed, the model exhibited efficient learning dynamics characterized by rapid initial convergence followed by stable performance. The alignment between training and validation losses throughout suggests robust generalization capabilities. These findings highlight the effectiveness of the model architecture and optimization strategy employed in minimizing prediction errors across datasets.
7.2. LSTM Model Performance
At the early training phase (Epoch 3), both training and validation losses exhibited a steep decline, with the training loss starting at approximately 0.40 and dropping to 0.05 by the end of Epoch 3. Similarly, the validation loss decreased from approximately 0.15 to 0.02 within the same period. This rapid reduction indicates effective learning of the underlying data patterns during early iterations, suggesting that the model is capable of capturing fundamental relationships in the dataset.
By Epoch 24, both training and validation losses largely stabilized, hovering near zero. The convergence of these curves suggests that the model has successfully minimized error on both training and validation datasets without significant overfitting. The close alignment between training and validation losses further supports the robustness of the model’s generalization capabilities.
By Epoch 24 up to 100, training and validation losses remained consistently low, with negligible fluctuations around zero. This sustained performance across prolonged training indicates that the model has reached an optimal state where additional epochs contribute minimal improvement in terms of error reduction.
Across all epochs evaluated, there is no evidence of divergence between training and validation losses which would indicate overfitting. Instead, the consistent alignment of these curves suggests that the model effectively balances learning from the training data while maintaining its ability to generalize to unseen validation samples. Furthermore, the rapid convergence observed in early epochs highlights computational efficiency in achieving optimal performance.
That is, the loss curves show that the model achieves rapid convergence within a few epochs while maintaining stable performance across extended training durations. These findings underscore the efficacy of the model architecture and optimization strategy in minimizing prediction error while ensuring generalization across datasets.
Table 3 presents the outcomes of MAE, MAPE, and MSE for both MLP and LSTM models following normalization within the range [−1,1]. The results demonstrate superior performance by the MLP model, with the LSTM model yielding considerably higher errors in comparison.

Table 3.
Performance of MLP and LSTM models with [−1,1] normalization.
7.3. MLP and LSTM Performance Using Simulation-Generated Data
The synthetic data generated using the battery simulation model was used as input for the MLP and LSTM models to analyze the evolution of battery SoH in the simulated scenarios. The SoH prediction obtained from inputting this synthetic data are notably different when comparing the obtained predictions using MLP and LSTM models, obtaining better results with the last one. Specifically, for MLP, the predicted SoH suggests limited predictive accuracy in this scenario as shown in Figure 8. This significant capacity drop indicates a discrepancy in the structure of the synthetic data compared to the experimental data, which is from that obtained when testing the MLP model on the experimental XJTU dataset. When inputting the simulated data into the LSTM model, the SoH obtained is comparable to the ones obtained with XJTU data, probably due to the fact of how sensitive the model is to time series intervals.
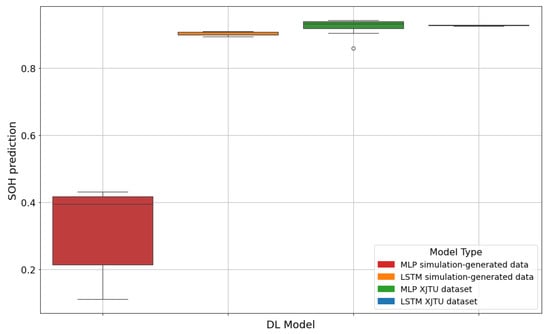
Figure 8.
SoH prediction using MLP and LSTM models based on simulation-generated data (deployment) and XJTU dataset (testing).
One of the main limitations of the simulation-generated synthetic dataset is the lack of real ground truth capacity values. The capacity degradation was not directly simulated; that is, the value of the capacity could not be obtained directly from the simulation, and therefore the SoH values obtained from the ML estimators are approximations rather than experimentally measured targets.
8. Conclusions
This study investigates the feasibility of leveraging deep learning algorithms in conjunction with simulation-based modeling for the estimation of lithium-ion battery state of health (SoH) in urban mobility applications. Specifically, the performance of Multilayer Perceptron (MLP) and Long Short-Term Memory (LSTM) networks was assessed using both empirical data from the XJTU battery aging dataset and synthetic data generated via a calibrated battery simulation model. These models were implemented using the Keras and TensorFlow libraries, then subsequently converted to TensorFlow Lite to enable efficient deployment on edge devices such as Raspberry Pi, thereby facilitating real-time SoH prediction in embedded systems.
The developed battery simulation model is grounded in an equivalent circuit formulation, augmented with generalized empirical degradation laws to emulate the aging behavior of lithium-ion cells. Although this approach reflects broadly validated electrochemical dynamics, it may not fully replicate the specific characteristics of the XJTU experimental cells. This discrepancy likely accounts for the performance variations observed between models trained on synthetic versus real-world data.
To address this, future work should prioritize calibrating the simulation model parameters using empirical degradation measurements, thereby improving the alignment between synthetic and experimental datasets. Such calibration would enhance the realism of the simulated degradation behavior and yield more representative synthetic data for the training and validation of predictive models. Furthermore, expanding the dataset to include operational profiles specific to electric buses could bolster model robustness and applicability.
The integration of synthetic data generation, deep learning-based estimation, and edge-device deployment constitutes a meaningful theoretical contribution by illustrating how hybrid frameworks can address longstanding challenges of scalability, generalizability, and real-time diagnostics in intelligent BMS research. Furthermore, the incorporation of agent-based simulation represents an important methodological step toward modeling operational context with higher behavioral fidelity, advancing the field toward more realistic and practically deployable battery health prediction solutions
In parallel, we plan to validate this approach on widely recognized benchmark datasets, such as those provided by NASA and CALCE. Leveraging these well-established datasets will facilitate a more rigorous and comparative assessment of the models presented in this study relative to the existing body of literature.
Finally, future research will explore the integration of the proposed simulation and machine learning pipeline within a digital twin framework connected to cloud-based battery management systems. This integration aims to enhance real-time monitoring and predictive analytics. Moreover, the development of hybrid models that combine physics-informed techniques with data-driven learning offers a promising avenue for improving predictive accuracy and interpretability. Advancing these directions will contribute significantly to the reliability and sustainability of electric mobility systems, thereby strengthening the current state of the art in battery management technologies.
Author Contributions
Conceptualization, A.A.-R., I.I. and A.S.-H.; methodology, A.A.-R. and I.I.; writing—original draft preparation, A.A.-R. and I.I.; writing—review and editing, A.S.-H. and J.F.; supervision, J.F.; funding acquisition, J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the PID2022-140278NB-I00 project and RED2022-134703-T network from the Spanish Ministry of Science, Innovation, and Universities. Additionally, we acknowledge the support from the UNED Pamplona project (UNEDPAM/PI/PR24/04P).
Data Availability Statement
Simulation data is available upon request. The XJTU battery dataset is publicly accessible at [30] and was used under the terms of academic open-access distribution.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ABM | Agent-Based Modeling |
| BMS | Battery Management System |
| BiGRU | Bidirectional Gated Recurrent Unit |
| CALCE | Center for Advanced Life Cycle Engineering |
| CNN | Convolutional Neural Network |
| CV | Constant Voltage |
| DL | Deep Learning |
| EV | Electric Vehicle |
| GPIO | General Purpose Input/Output |
| GRU | Gated Recurrent Unit |
| LiCoO2 | Lithium Cobalt Oxide |
| LiFePO4 | Lithium Iron Phosphate |
| LiMn2O4 | Lithium Manganese Oxide |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MSE | Mean Squared Error |
| NASA | National Aeronautics and Space Administration |
| RC | Resistive–Capacitive |
| RBF | Radial Basis Function |
| RUL | Remaining Useful Life |
| SoC | State of Charge |
| SoF | State of Function |
| SoH | State of Health |
| SoP | State of Power |
| tflite | TensorFlow Lite |
| UART | Universal Asynchronous Receiver-Transmitter |
| XJTU | Xi’an Jiaotong University |
References
- Manzolli, J.; Silva, R. Comprehensive Review of Electric Bus Technologies and Trends. Renew. Sustain. Energy Rev. 2022, 153, 112211. [Google Scholar] [CrossRef]
- Kapatsila, S.; Johnson, M. Operational Performance of Electric, Hybrid, and Diesel Buses in Transit. Transp. Res. Part D Transp. Environ. 2024, 113, 104120. [Google Scholar] [CrossRef]
- Jarasureechai, J.; Jamvilaiphan, K.; Phramorathat, N.; Ayudhya, P.N.N.; Mujjalinvimut, E.; Kunthong, J.; Sapaklom, T. A Study of Battery Monitoring System Based LoRaWAN for Public Electric Vehicles. In Proceedings of the 2024 13th International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 6–8 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–6. [Google Scholar]
- She, C.; Zhang, Y.; Li, X. Battery Aging Prediction for Electric Buses Using Radial Basis Function Neural Networks. IEEE Trans. Ind. Inform. 2020, 16, 2954–2963. [Google Scholar] [CrossRef]
- Reshma, K.; Kumar, S. SoC, SoH, and RUL Estimation for Electric Bus Batteries Using Dual Adaptive Kalman Filters. Energy Storage 2023, 55, 107573. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Y.; Li, J. Review of Data-driven Methods for Battery State Estimation in Electric Buses. World Electr. Veh. J. 2023, 14, 145. [Google Scholar] [CrossRef]
- Tomasov, M.; Kajanova, M.; Bracinik, P.; Motyka, D. Overview of Battery Models for Sustainable Power and Transport Applications. Transp. Res. Procedia 2019, 40, 548–555. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z.; Lu, Q. Review on the Battery Model and SoC Estimation Method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Adaikkappan, M.; Sathiyamoorthy, N. Modeling, State of Charge Estimation, and Charging of Lithium-ion Battery in Electric Vehicle: A Review. Int. J. Energy Res. 2022, 46, 2141–2165. [Google Scholar] [CrossRef]
- Ju, F.; Wang, J.; Li, J.; Xiao, G.; Biller, S. Virtual Battery: A Battery Simulation Framework for Electric Vehicles. IEEE Trans. Autom. Sci. Eng. 2012, 10, 5–15. [Google Scholar] [CrossRef]
- Jafari, M.; Gauchia, A.; Zhang, K.; Gauchia, L. Simulation and Analysis of the Effect of Real-World Driving Styles in an EV Battery Performance and Aging. IEEE Trans. Transp. Electrif. 2015, 1, 391–401. [Google Scholar] [CrossRef]
- Jeong, S.; Jang, Y.J.; Kum, D.; Lee, M.S. Charging Automation for Electric vehicles: Is a Smaller Battery Good for the Wireless Charging Electric Vehicles? IEEE Trans. Autom. Sci. Eng. 2018, 16, 486–497. [Google Scholar] [CrossRef]
- Irujo, E.; Berrueta, A.; Sanchis, P.; Ursúa, A. Methodology for Comparative Assessment of Battery Technologies: Experimental Design, Modeling, Performance Indicators and Validation with Four Technologies. Appl. Energy 2025, 378, 124757. [Google Scholar] [CrossRef]
- Demirci, E.; Aydin, K. Evaluation of Battery Mnagement System Advancements for Electric Buses. Renew. Energy 2024, 198, 1234–1245. [Google Scholar]
- Ashok, S.; Kumar, R. Comprehensive Review of Control Architectures for Battery Management Systems in Electric Vehicles. J. Energy Storage 2022, 50, 104–115. [Google Scholar]
- Kurucan, E.; Yilmaz, M. Advances and Future Trends in Battery Management Systems. Eng. Proc. 2024, 79, 66. [Google Scholar]
- Lipu, M.; Singh, S. Machine Learning Approaches for Energy-efficient Battery Management Systems. J. Energy Storage 2022, 55, 10221. [Google Scholar]
- Nyamathulla, A.; Dhanamjayulu, C. Challenges and Recommendations for Advanced Battery Management Systems in Electric Vehicles and Energy Storage Systems. Energy Storage Mater. 2024, 45, 789–802. [Google Scholar]
- Farman, M.K.; Nikhila, J.; Sreeja, A.B.; Roopa, B.S.; Sahithi, K.; Kumar, D.G. AI-Enhanced Battery Management Systems for Electric Vehicles: Advancing Safety, Performance, and Longevity. E3S Web Conf. EDP Sci. 2024, 591, 4001. [Google Scholar] [CrossRef]
- Singh, A.K.; Kumar, K.; Choudhury, U.; Yadav, A.K.; Ahmad, A.; Surender, K. Applications of Artificial Intelligence and Cell Balancing Techniques for Battery Management System (BMS) in Electric Vehicles: A Comprehensive Review. Process Saf. Environ. Prot. 2024, 191, 2247–2265. [Google Scholar] [CrossRef]
- Senthilkumar, K.; Anbalagan, E. Comparative Analysis of Traditional And AI Based Fault Detection for Battery Thermal Management System. In Proceedings of the 2024 2nd World Conference on Communication & Computing (WCONF), Raipur, India, 12–14 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–8. [Google Scholar]
- Dineva, A. Evaluation of Advances in Battery Health Prediction for Electric Vehicles from Traditional Linear Filters to Latest Machine Learning Approaches. Batteries 2024, 10, 356. [Google Scholar] [CrossRef]
- Karnehm, D.; Samanta, A.; Anekal, L.; Pohlmann, S.; Neve, A.; Williamson, S. Comprehensive Comparative Analysis of Deep Learning-based State-of-charge Estimation Algorithms for Cloud-based Lithium-ion Battery Management Systems. IEEE J. Emerg. Sel. Top. Ind. Electron. 2024, 5, 597–604. [Google Scholar] [CrossRef]
- Mazzi, F.; Rossi, M. SoH Estimation in Electric Buses Using Hybrid CNN-BiGRU Models. J. Energy Storage 2024, 60, 106573. [Google Scholar]
- Guo, X.; Zhang, W. Fault Diagnosis and RUL Prediction Using LSTM-based Methods for Lithium-ion Batteries. Eng. Appl. Artif. Intell. 2024, 123, 107317. [Google Scholar] [CrossRef]
- Hadraoui, N.; Chen, X. Digital Twin-based Prognostics for Battery Health Management. IEEE Access 2024, 12, 3441517–3441532. [Google Scholar]
- Li, H.; Kaleem, M.B.; Chiu, I.J.; Gao, D.; Peng, J.; Huang, Z. An Intelligent Digital Twin Model for the Battery Management Systems of Electric Vehicles. Int. J. Green Energy 2024, 21, 461–475. [Google Scholar] [CrossRef]
- O’Brien, J. Development of MACT System for Managing Lead-acid Batteries in Buses. IEEE Trans. Ind. Appl. 1994, 30, 1234–1241. [Google Scholar]
- Srirattanawichaikul, S.; Phuritatkul, C. Lightweight Battery Management System for Campus Electric Bus Transit Systems. Int. J. Electr. Comput. Eng. 2020, 10, 6202–6213. [Google Scholar]
- XJTU Battery Dataset—Xi’an Jiaotong University. 2025. Available online: https://wang-fujin.github.io/ (accessed on 2 April 2025).
- Zhou, H.; Yang, Y.; Zhang, Z.; Wang, W.; Yang, L.; Du, X. Charge and Discharge Strategies of Lithium-ion Battery Based on Electrochemical-mechanical-thermal Coupling Aging Model. J. Energy Storage 2024, 99, 113484. [Google Scholar] [CrossRef]
- Battery University: What Is C-Rate? 2024. Available online: https://batteryuniversity.com/article/bu-402-what-is-c-rate (accessed on 2 April 2025).
- Li, K.; Chen, X. Machine Learning-Based Lithium Battery State of Health Prediction Research. Appl. Sci. 2025, 15, 516. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation; MIT Press: Cambridge, MA, USA, 1985; pp. 318–362. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another Look at Measures of Forecast Accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Armstrong, J.S.; Collopy, F. Error Measures for Generalizing about Forecasting Methods: Empirical Comparisons. Int. J. Forecast. 1992, 8, 69–80. [Google Scholar] [CrossRef]
- AnyLogic. Multimethod Simulation Software. 2025. Available online: https://www.anylogic.com (accessed on 2 April 2025).
- Mohamed, M.A.; Yu, T.F.; Ramsden, G.; Marco, J.; Grandjean, T. Advancements in Parameter Estimation Techniques for 1RC and 2RC Equivalent Circuit Models of Lithium-ion Batteries: A Comprehensive Review. J. Energy Storage 2025, 113, 115581. [Google Scholar] [CrossRef]
- Stroe, D.I.; Swierczynski, M.; Kær, S.K.; Teodorescu, R. Degradation Behavior of Lithium-ion Batteries During Calendar Ageing—The Case of the Internal Resistance Increase. IEEE Trans. Ind. Appl. 2017, 54, 517–525. [Google Scholar] [CrossRef]
- Warden, P.; Situnayake, D. TinyML: Machine Learning with TensorFlow Lite on Arduino and Ultra-Low-Power Microcontrollers, 1st ed.; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Garcia-Perez, A.; Miñón, R.; Torre-Bastida, A.I.; Zulueta-Guerrero, E. Analysing edge computing devices for the deployment of embedded AI. Sensors 2023, 23, 9495. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).