Evaluation Algorithms for Parametric Curves and Surfaces
Abstract
1. Introduction
2. Curve Evaluation Algorithms
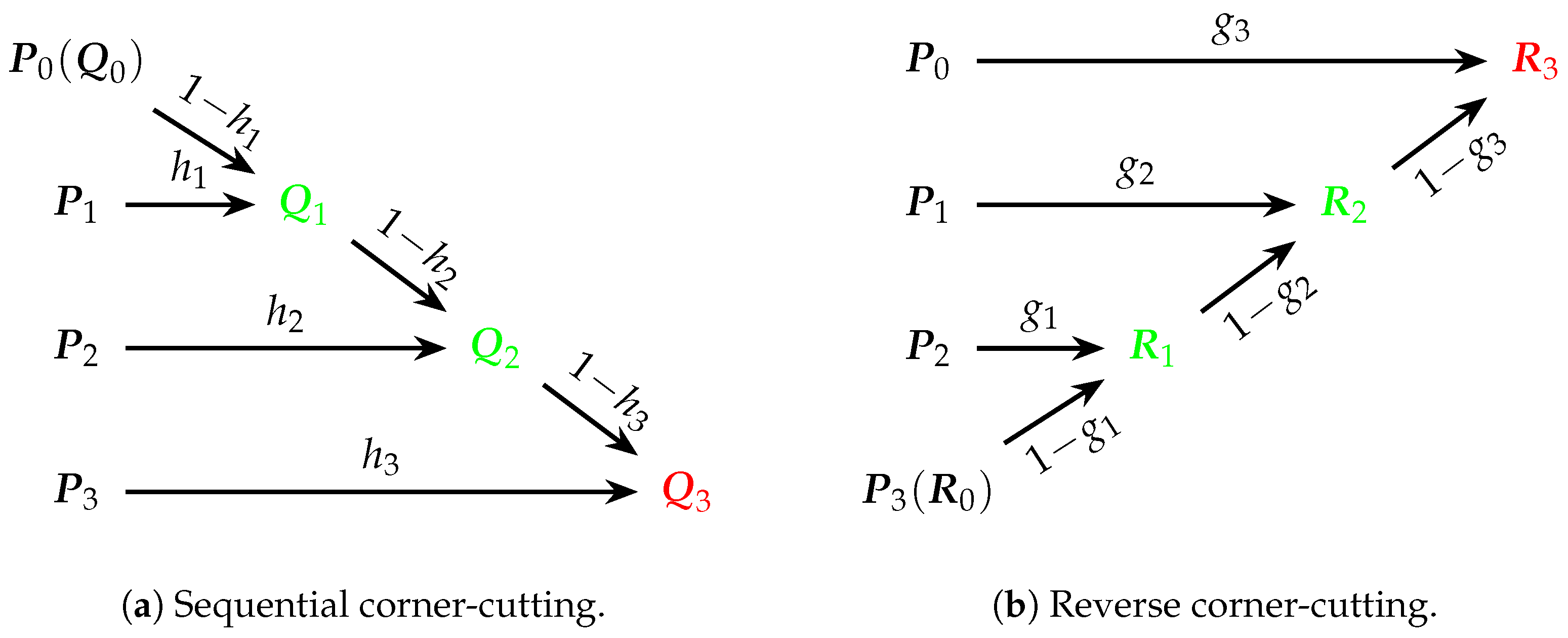
2.1. Sequential Corner-Cutting Algorithm
2.2. Reverse Corner-Cutting Algorithm
2.3. Description of the Curve Evaluation Algorithms
- Form requirement: The algorithms exclusively apply to curves represented in the form of Equation (3), where the curve is a linear combination of control points and basis functions. Classical interpolation schemes (e.g., Lagrange and Hermite) that do not conform to this representation fall outside the scope of this framework.
- Normalization condition: For all parameter values t, the partition of unity must be satisfied (i.e., in Equation (4)). Standard parametric bases (such as Bézier and B-spline) strictly satisfy this condition and are non-negative. However, some interpolation bases proposed in the literature (such as the basis by Yan and Liang [14]) also strictly satisfy the normalization condition but differ from standard bases in lacking non-negativity. The algorithms remain valid as long as normalization is satisfied.
- Symmetry consideration: When , the relationship allows Theorem 2 to be directly derived from Theorem 1. This symmetry is not a necessary condition for the correctness of Theorem 2, as the proof only relies on normalization. For example, the non-symmetric polynomial basis proposed by Hu et al. [15] can still be evaluated using the forward corner-cutting algorithm and backward corner-cutting algorithm.
- Non-negativity and stability: For bases satisfying (such as Bézier and B-spline bases), the weights and belong to , ensuring stable linear interpolation. For the interpolation bases with negative values proposed by Yan and Liang [14], both the forward and backward corner-cutting algorithms can still be used for evaluation, but numerical instability may occur when .
- Discontinuity limitation: For basis functions with discontinuities (e.g., non-uniform B-splines at repeated knots), the algorithm remains mathematically correct if normalization holds piecewise. However, numerical instability may occur near discontinuities due to division by near-zero values of in Equation (5). To mitigate this, two approaches can be adopted. Firstly, we can use adaptive parameter spacing to avoid sampling within for discontinuity at , with recommended (, based on IEEE double-precision floating-point accuracy). Secondly, we can employ hybrid evaluation by switching to the de Boor Algorithm locally at detected discontinuities.
- In Theorem 1, ;
- In Theorem 2, .
2.4. Pseudo-Code and Complexity for Curve Evaluation Algorithms
- For :
- -
- , where ;
- -
- with the initial value .
- For :
- -
- , where ;
- -
- with the initial value .
| Algorithm 1: Sequential corner-cutting algorithm |
 |
| Algorithm 2: Reverse corner-cutting algorithm |
 |
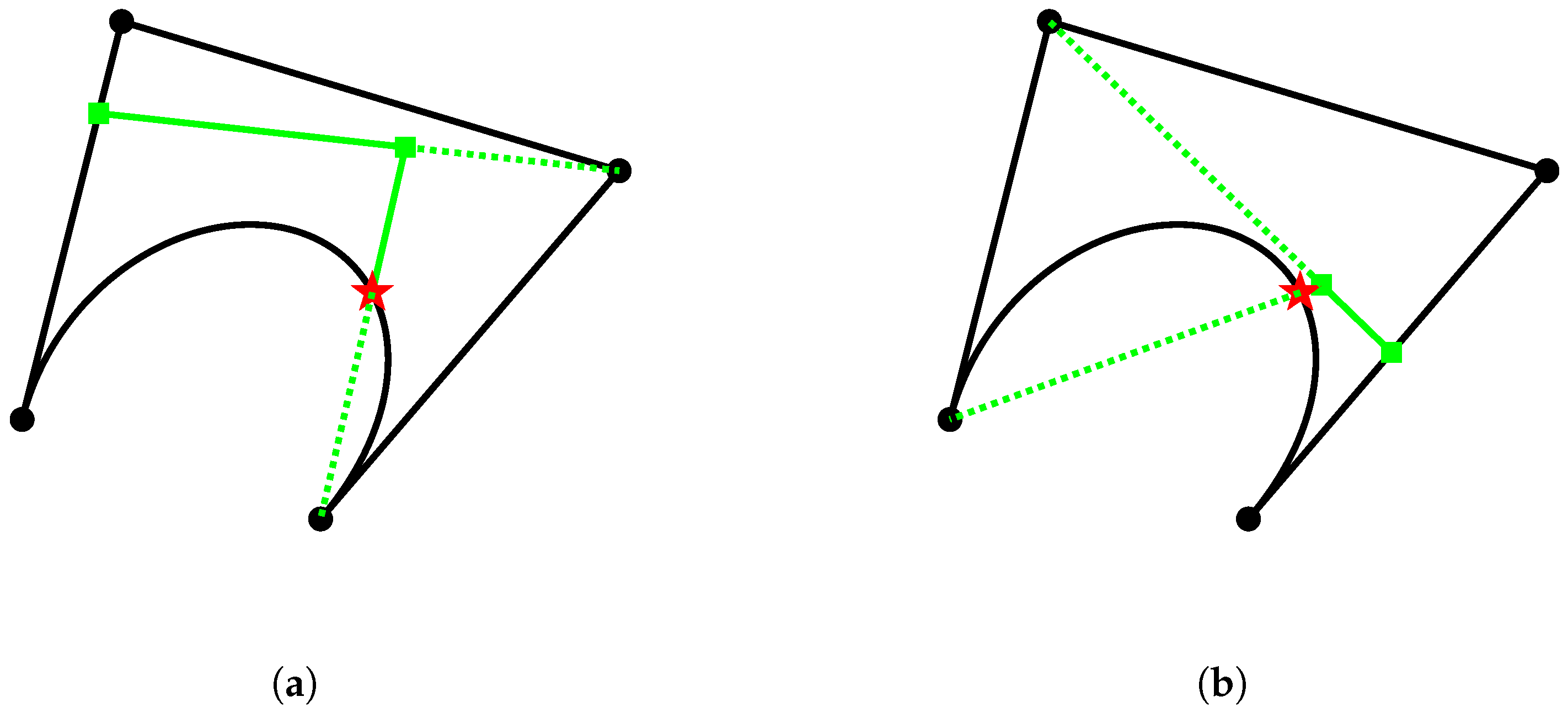
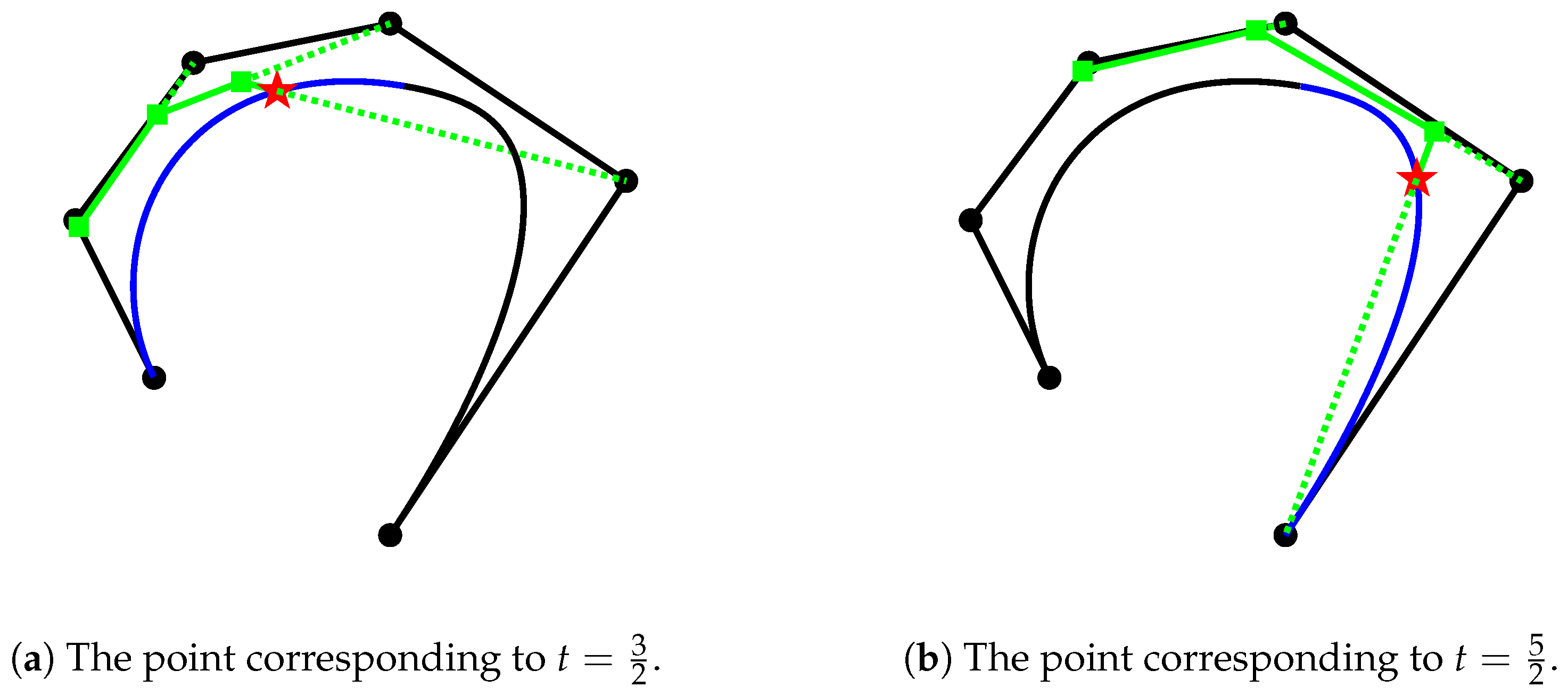
2.5. Application Examples for Curve Evaluation Algorithms
- Identify the segment containing t;
- Determine the active control points and the explicit expressions of the non-zero basis functions for that segment.
- It converts NURBS curves into piecewise rational Bézier curves;
- It determines the rational basis functions that define each segment of the curves.
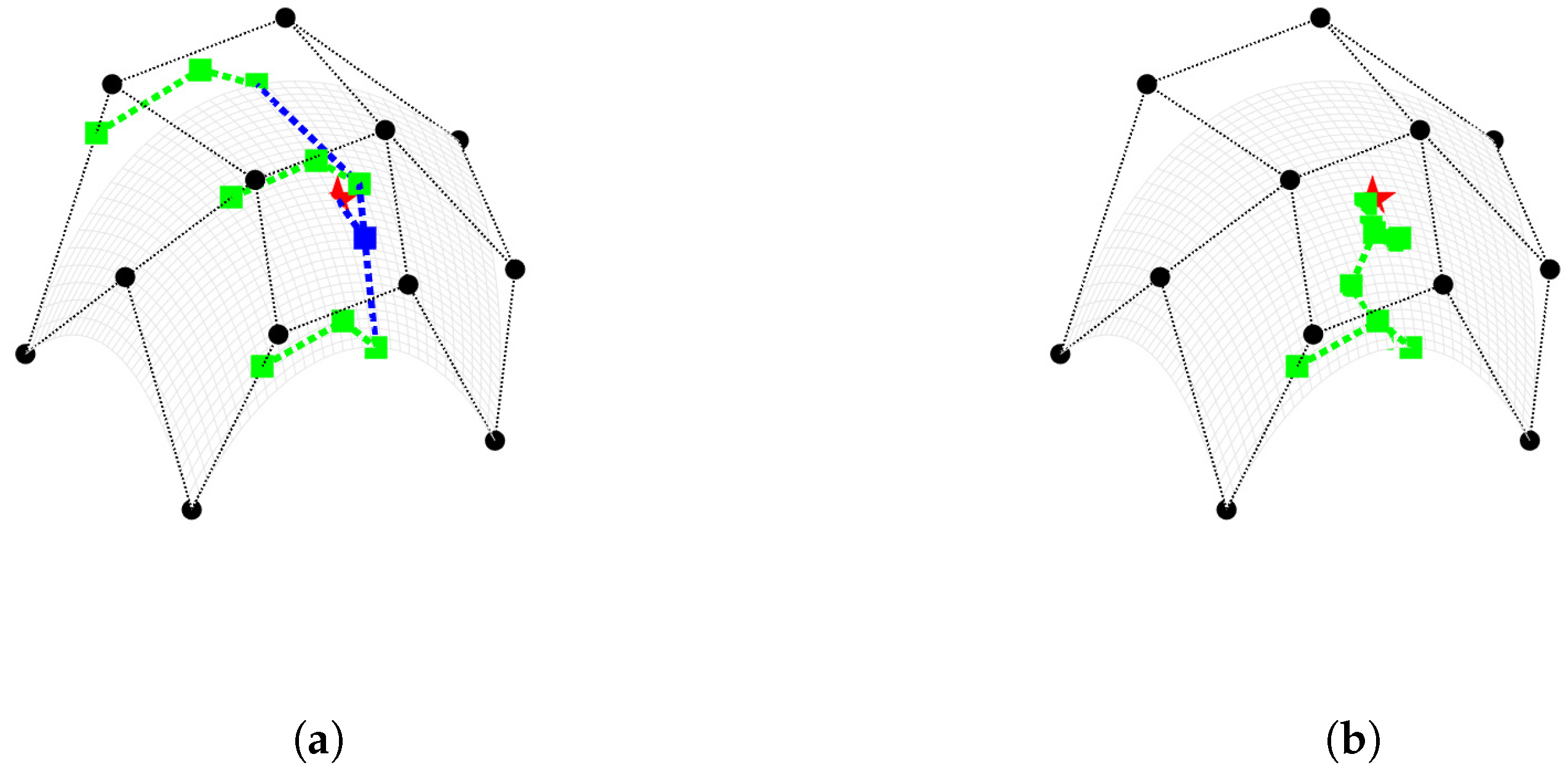
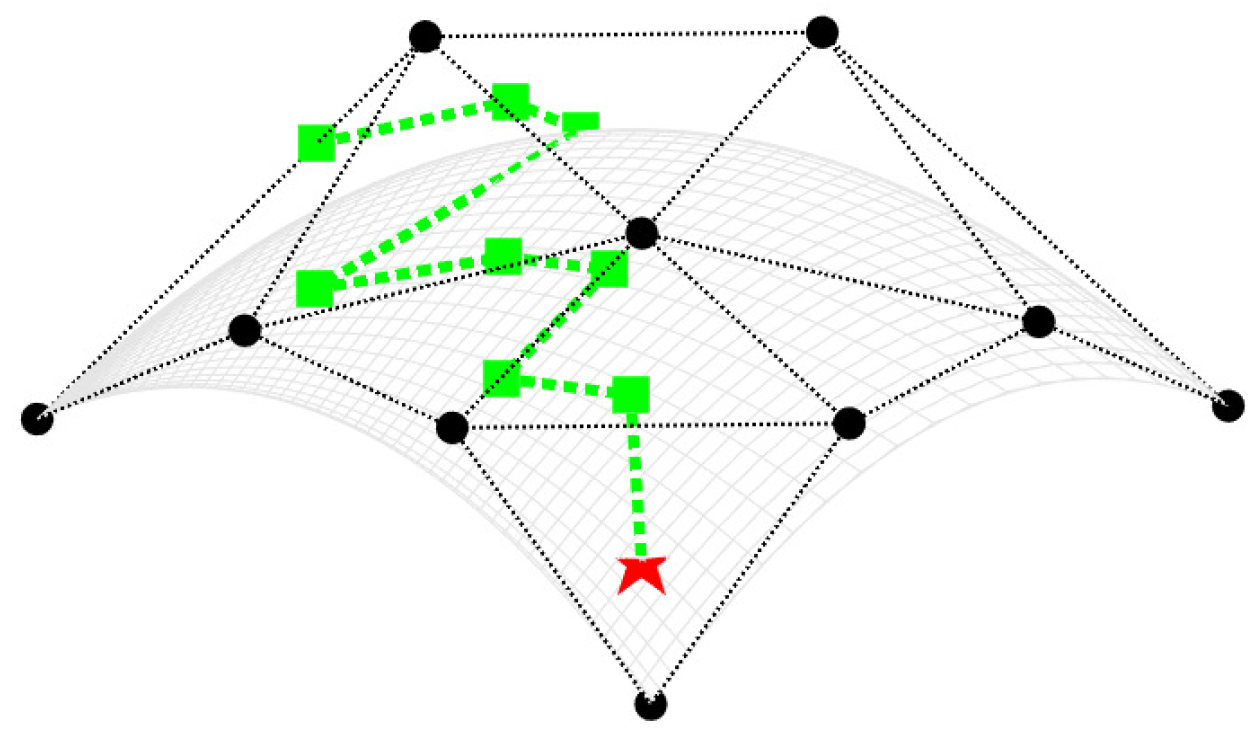
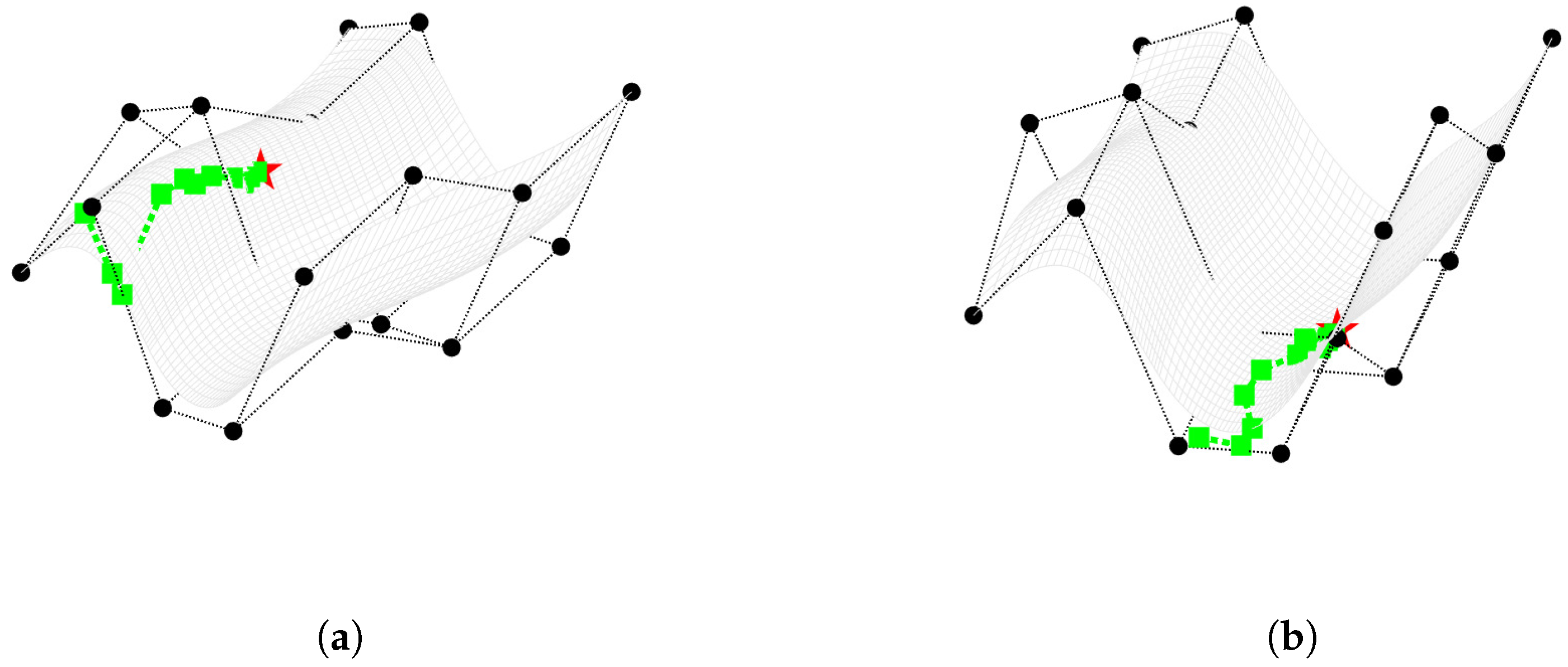
- The black circles represent the initial control points;
- The red pentagrams denote the points on the curves corresponding to the specified parameter values;
- The green squares indicate the new control points generated during the recursive process.
- Preprocessing stage: Using the local Bézier extraction operator in Ref. [16], the NURBS curve is converted into a piecewise rational Bézier form. The complexity of this process is (approximately 64 operations when ).
- Main computation stage: Algorithm 1 is applied to evaluate each curve segment, with the per-point computational complexity being (approximately 4 operations when , compared to operations for the traditional de Boor algorithm).
- Traditional method (e.g., de Boor): ;
- Proposed method: .
- Single-point sampling (): The proposed method is 0.24× slower than de Boor due to preprocessing overhead (64 + 4 = 68 operations vs. 16 operations);
- Dense sampling with 50 points (): The proposed method requires operations, achieving a 3.03× speedup over de Boor ( operations).
- Linear complexity: Algorithm 1 achieved up to 17.37× speedup at , consistent with its complexity compared to the complexity of the de Casteljau algorithm;
- Performance at low degrees: The speedup was only 0.26× at due to the constant overhead of basis function calculations, highlighting that the linear complexity advantage becomes more prominent for higher-degree curves.
3. Surface Evaluation Algorithms
- Tensor-product parametric surfaces: Typical examples include Bézier surfaces and B-spline surfaces. The domain of these surfaces is a rectangular region, and their basis functions can be expressed as the product of two univariate basis functions.
- Non-tensor-product parametric surfaces: Representative examples include rational Bézier surfaces, NURBS surfaces, and triangular domain Bézier surfaces. The domain of these surfaces can be either rectangular or triangular, and their basis functions cannot be expressed as the product of two single-variable basis functions.
3.1. Tensor-Product Surfaces
- First step: Apply the curve evaluation algorithm to the polygons along the s-direction of the control grid using the parameter value s. After m levels of recursion, this results in a polygon with points along the t-direction.
- Second step: Apply the curve evaluation algorithm to this resulting polygon using the parameter value t. After n levels of recursion, a single point is obtained, which is the desired point on the surface.
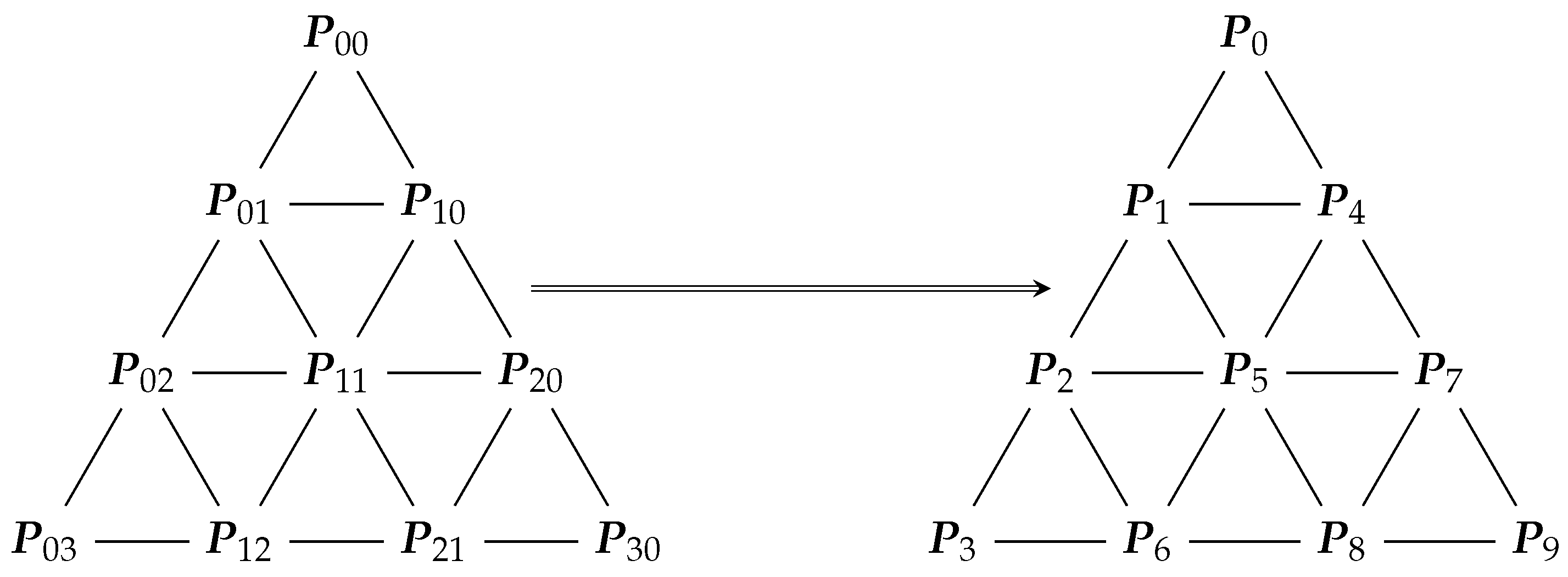
3.2. Non-Tensor-Product Surfaces
3.3. Pseudo-Code and Complexity for Surface Evaluation Algorithms
| Algorithm 3: Tensor-product surface evaluation algorithm |
 |
| Algorithm 4: Non-tensor-product surface evaluation algorithm |
 |
3.4. Examples for Surface Evaluation Algorithms
- Determine which specific surface patch the point lies within;
- Identify the control points that define this surface patch;
- Express the corresponding basis functions explicitly.
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Q.Y.; Wang, G.Z. A class of Bézier-like curves. Comput. Aided Geom. Des. 2003, 20, 29–39. [Google Scholar] [CrossRef]
- Han, X.L. A class of general quartic spline curves with shape parameters. Comput. Aided Geom. Des. 2011, 28, 151–163. [Google Scholar] [CrossRef]
- Zhu, Y.P.; Tang, Y.Y. A class of rational quartic splines and their local tensor product extensions. Comput.-Aided Des. 2023, 164, 103603. [Google Scholar] [CrossRef]
- Zhang, J. C-curves: An extension of cubic curves. Comput. Aided Geom. Des. 1996, 13, 199–217. [Google Scholar] [CrossRef]
- Han, X.A.; Ma, Y.C.; Huang, X.L. The cubic trigonometric Bézier curve with two shape parameters. Appl. Math. Lett. 2009, 22, 226–231. [Google Scholar] [CrossRef]
- Lü, Y.G.; Wang, G.Z.; Yang, X.N. Uniform hyperbolic polynomial B-spline curves. Comput. Aided Geom. Des. 2002, 19, 379–393. [Google Scholar] [CrossRef]
- Xumin, L.; Weixiang, X.; Yong, G.; Yuanyuan, S. Hyperbolic polynomial uniform B-spline curves and surfaces with shape parameter. Graph. Model. 2010, 72, 1–6. [Google Scholar] [CrossRef]
- Jüttler, B.; Schicho, J.; Šír, Z. Apollonian de Casteljau-type algorithms for complex rational Bézier curves. Comput. Aided Geom. Des. 2023, 107, 102254. [Google Scholar] [CrossRef]
- Delgado, J.; Orera, H.; Peña, J.M. An evaluation algorithm for q-Bézier triangular patches formed by convex combinations. J. Comput. Appl. Math. 2023, 428, 115184. [Google Scholar] [CrossRef]
- Schumaker, L.L.; Volk, W. Efficient evaluation of multivariate polynomials. Comput. Aided Geom. Des. 1986, 3, 149–154. [Google Scholar] [CrossRef]
- Hu, S.M.; Wang, G.Z.; Jin, T.G. Properties of two types of generalized ball curves. Comput.-Aided Des. 1996, 28, 125–133. [Google Scholar] [CrossRef]
- Delgado, J.; Peña, J.M. A shape preserving representation with an evaluation algorithm of linear complexity. Comput. Aided Geom. Des. 2003, 20, 1–10. [Google Scholar] [CrossRef]
- Woźny, P.; Chudy, F. Linear-time geometric algorithm for evaluating Bézier curves. Comput.-Aided Des. 2020, 118, 102760. [Google Scholar] [CrossRef]
- Yan, L.L.; Liang, J.F. A class of algebraic–trigonometric blended splines. J. Comput. Appl. Math. 2011, 235, 1713–1729. [Google Scholar] [CrossRef]
- Hu, G.; Wu, J.L.; Qin, X.Q. A novel extension of the Bézier model and its applications to surface modeling. Adv. Eng. Softw. 2018, 125, 27–54. [Google Scholar] [CrossRef]
- Yan, L.L. Conversion from NURBS to Bézier representation. Comput. Aided Geom. Des. 2024, 113, 102380. [Google Scholar] [CrossRef]
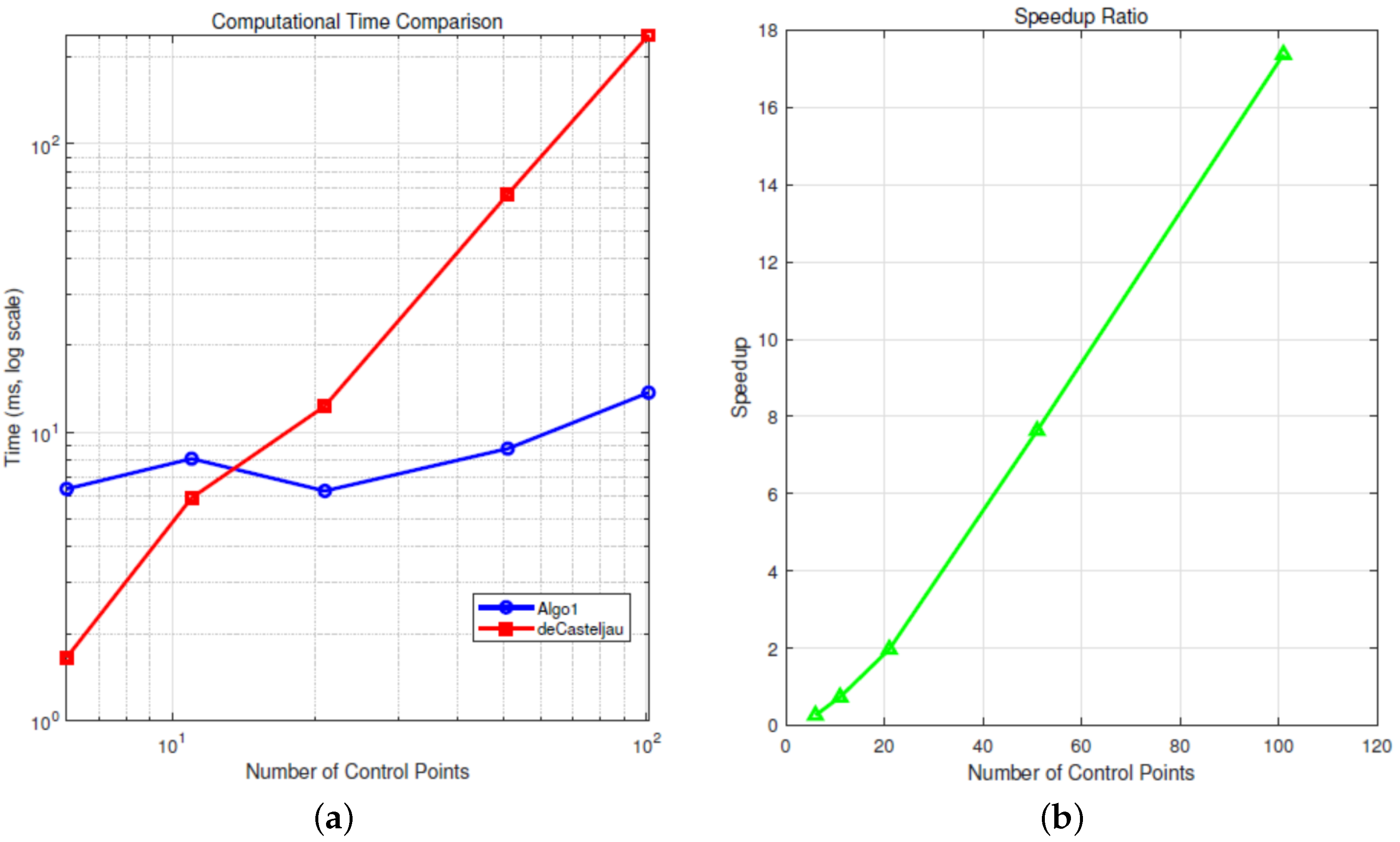
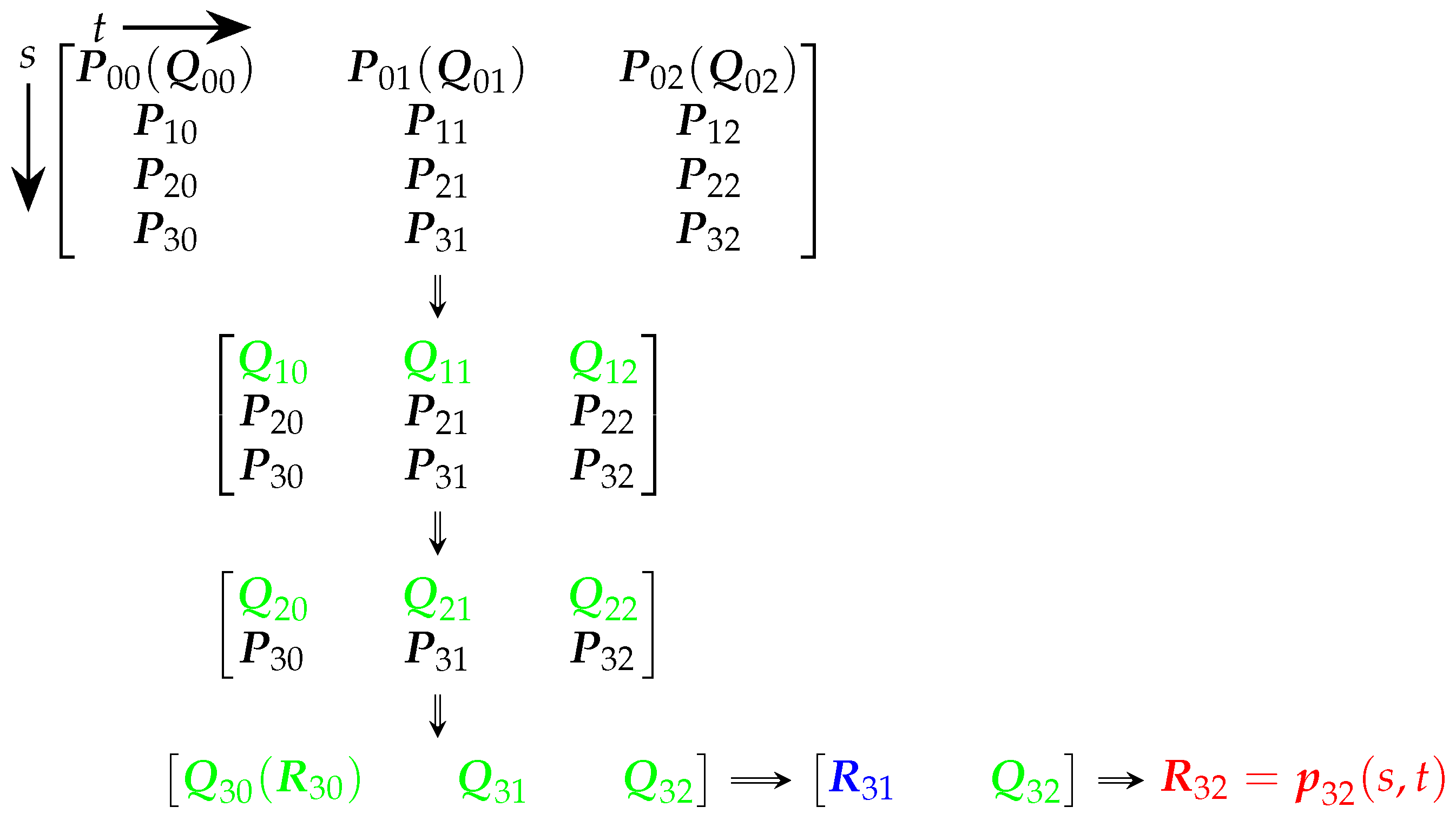
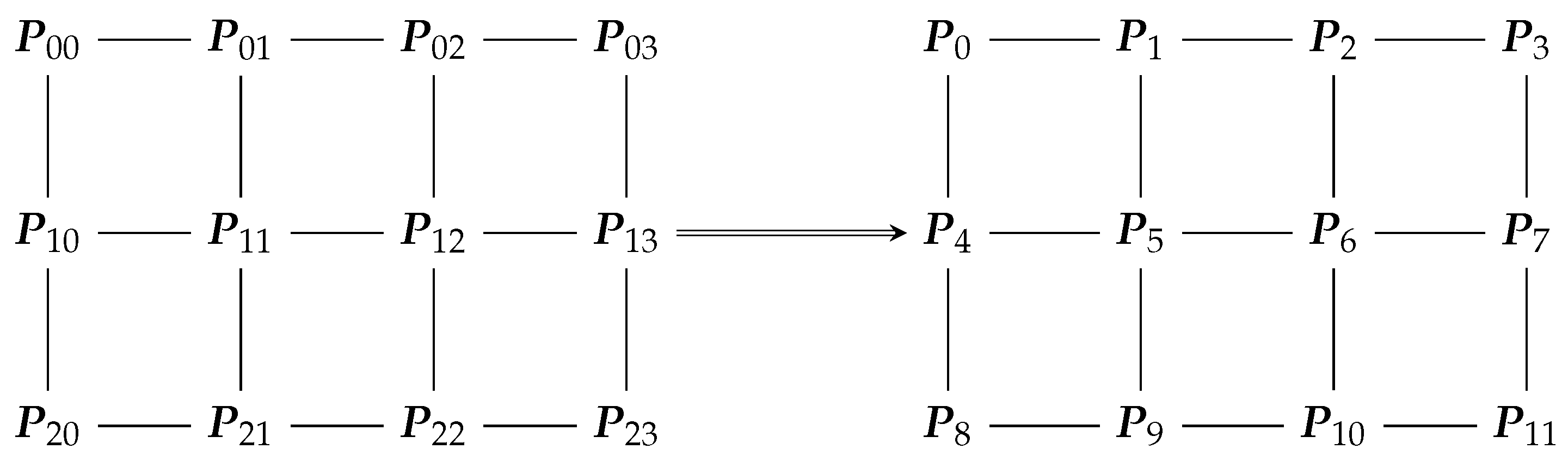
| Control Points | Algorithm 1 | de Casteljau | Speedup Ratio |
|---|---|---|---|
| 6 | 6.36 | 1.65 | 0.26× |
| 11 | 8.09 | 5.92 | 0.73× |
| 21 | 6.25 | 12.32 | 1.97× |
| 51 | 8.77 | 66.89 | 7.63× |
| 101 | 13.71 | 238.14 | 17.37× |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L. Evaluation Algorithms for Parametric Curves and Surfaces. Mathematics 2025, 13, 2248. https://doi.org/10.3390/math13142248
Yan L. Evaluation Algorithms for Parametric Curves and Surfaces. Mathematics. 2025; 13(14):2248. https://doi.org/10.3390/math13142248
Chicago/Turabian StyleYan, Lanlan. 2025. "Evaluation Algorithms for Parametric Curves and Surfaces" Mathematics 13, no. 14: 2248. https://doi.org/10.3390/math13142248
APA StyleYan, L. (2025). Evaluation Algorithms for Parametric Curves and Surfaces. Mathematics, 13(14), 2248. https://doi.org/10.3390/math13142248





