Abstract
Complex scenario analysis and evaluation simulations often involve multiple sets of simulation applications with different combinations of parameters, thus resulting in high computing power consumption, which is one of the factors that limits the efficiency of multi-sample parallel simulations. Cloud computing provides considerable amounts of cheap and convenient computing resources, thus providing efficient support for multi-sample simulation tasks. However, traditional simulation scheduling methods do not consider the collaborative parallel scheduling of multiple samples and multiple entities under multi-objective constraints. Deep reinforcement learning methods can continuously learn and adjust their strategies through interactions with the environment, demonstrating strong adaptability in response to dynamically changing task requirements. Therefore, herein, a parallel simulation multi-sample task scheduling method based on deep reinforcement learning in a cloud computing environment is proposed. The method collects cluster load information and simulation application information as state inputs in the cloud environment, designs a multi-objective reward function to balance the cost and execution efficiency, and uses deep Q-networks (DQNs) to train agents for intelligent scheduling of multi-sample parallel simulation tasks. In a real cloud environment, the proposed method demonstrates runtime reductions of 4–11% and execution cost savings of 11–22% compared to the Round-Robin algorithm, Best Fit algorithm, and genetic algorithm.
MSC:
68T20; 68M20
1. Introduction
Cloud computing is an efficient computing infrastructure architecture that provides flexible, scalable, and affordable computing resources to cloud subscribers in a dynamic, scalable, and virtualized manner [1]. The application of virtual machine/container live migration technology and the design of resource allocation algorithms to optimize resource placement policies at software level can improve resource utilization and meet the performance requirements of cloud subscribers for their application [2]. Large-scale complex system simulations have two computational characteristics: multiple samples and multiple entities [3]. Owing to the probabilistic models in the simulation system, numerous simulation samples must be run repeatedly to achieve stable probability distributions. Each simulation sample typically contains numerous simulation entities, which interact with each other frequently. As the size of simulation samples grows and the number of simulation entities increases, the demand on the computing platform that simulates multiple samples also increases. In recent years, several works have begun deploying large-scale complex system simulation applications on the cloud [4,5]. In the cloud environment, users can adopt either a centralized or distributed strategy to perform multi-sample simulation tasks. However, although distributed strategies can improve the workload of clusters and increase execution efficiency, they can also cause problems, such as wasting computing resources. An unreasonable distributed strategy can reduce the execution efficiency of the simulation application owing to characteristics such as frequent communication and synchronization of entities in the simulation application [6]. A centralized strategy executes simulation tasks in fewer nodes; however, it can considerably reduce the execution efficiency of simulation tasks. Therefore, improving resource utilization of the cloud platform while ensuring the execution efficiency of the simulation application is crucial for parallel simulation in the cloud.
Most of the current cloud-oriented simulation multi-sample task scheduling is implemented using heuristic algorithms such as particle swarm and genetic algorithms [7,8]. These methods typically assume a stable pattern of computational task load (e.g., uniformly distributed over time or increasing gradually) and require the collection of historical load data for computation. However, complex system simulation applications have irregular load variations during execution, and the collected historical data can hardly reflect the load-variation characteristics of the simulation application [9]. Therefore, a new scheduling method is needed to improve the execution efficiency of multi-sample simulation tasks and to optimize the utilization of cloud computing resources. Recently, methods based on reinforcement learning (RL) have been used often to solve complex scheduling problems [10]. RL-based agents can identify the intrinsic features of computing clusters and tasks after extensive training, and thereby achieve more optimal solutions for multiple objectives. RL models do not require access to a priori knowledge of the environment during training and are able to continuously learn knowledge as they interact with the environment, ultimately obtaining policies that maximize long-term returns. By incorporating deep neural networks, the deep reinforcement learning algorithm is able to more efficiently process complex tasks and problems. Therefore, this study proposes a multi-sample simulation resource scheduling method based on Deep Reinforcement Learning (DRL). The proposed method collects cluster load information and simulation application runtime data from the cloud environment as state inputs. A multi-objective reward function focusing on cost-efficiency trade-offs is designed. By considering the priority relationship between computational cost and execution efficiency, a Deep Q-Network (DQN) is employed to train an intelligent agent for parallel scheduling of multi-sample simulation tasks. Experimental results demonstrate that the proposed method can effectively improve the execution efficiency of multi-sample simulations in PDES while also reducing the computational cost.
- (1)
- A parallel scheduling framework for simulation multi-sample tasks was designed. The framework not only supports the parallel execution of all simulation samples but also supports dividing each simulation sample into different groups and scheduling them to different nodes for parallel execution.
- (2)
- A DRL-based scheduling method for multi-sample simulation tasks in cloud computing environments is proposed, where a DRL agent is trained with a designed reward–penalty mechanism to improve resource utilization and reduce overall execution time while satisfying resource constraints.
- (3)
- Extensive experiments have been conducted using a real cloud environment to evaluate the performance of the DRL-based scheduling approach. The experimental results showed that the proposed method can reduce the runtime and costs of executing multi-sample simulation tasks by up to 11% and 33% compared with the round-robin (RR), best fit (BF), and genetic algorithm (GA).
2. Related Work
2.1. Resource Scheduling Based on Heuristic Algorithms
Most cloud platforms, such as Apache Spark 3.0 and Hadoop 3.0, use scheduling methods such as FIFO and polling to reduce the load on individual worker nodes. However, these methods often result in wasted computational resources. Some studies attempted to improve such scheduling strategies using heuristic algorithms. Graham [11] was the first to comprehensively analyze scheduling problems from the perspectives of optimization algorithms, approximation performance, and computational complexity, summarizing the research progress in related fields. Quasar [12] uses a collaborative filtering approach to calculate the impact of different resources on application performance, thus minimizing the resource utilization of the cluster while meeting the computational performance requirements of the user. Maroulis [13] uses dynamic voltage frequency scaling (DVFS) techniques to dynamically adjust incoming CPU computation frequency to reduce energy consumption. Kaur [14] proposes a multi-objective optimization scheme for job scheduling in cloud data centers using service level agreement (SLA), energy cost, and carbon footprint rate (CFR) metrics, and solves the problem using an enhanced heuristic based on greedy policies. Lu [15] proposes a task scheduling algorithm considering time and energy cost, and calculating communication load and computation load to decide the scheduling order of computation tasks. Chahrazed [16] designed a resource prediction framework to evaluate and optimize the deployment cost of multi-intelligent systems in hybrid clouds. This framework focuses on optimizing the overall deployment cost by evaluating the resources consumed by the agents to be deployed at each node. Grande [17] proposed a scheme for balancing the communication and computational load during the execution of distributed simulations, repartitioning policies to determine a distribution of load and minimize imbalances. This method observes distributed load changes and identifies imbalances, reallocating policies to determine load distribution and minimize imbalances. Angelo [18] discussed the potential advantages of executing parallel discrete event simulation (PDES) in a cloud environment and proposed a migration technique for simulation entities to improve simulation performance. Yang [19] proposed a method for scheduling federated simulation tasks in a cloud environment. This method first divides simulation tasks into federated models, then assigns the federated models to virtual machines and considers the effect of network latency during operation. The method aims to maximize the consolidation of simulation tasks onto a single node through dynamic migration, thereby improving simulation efficiency. A simulation load-balancing method, combining the multi-objective genetic algorithm (NSGA-II) and multi-objective particle swarm optimization algorithm, was proposed previously to minimize the computational and communication loads of the simulation application [20]. To solve the load imbalance problem in High-Level Architecture (HLA) simulation applications, a static load-balancing algorithm based on discrete particle swarm was proposed in the literature to adaptively divide HLA simulation federation into individual nodes for execution [21].
The aforementioned approaches rely heavily on global historical load data and build performance prediction models based on different workloads and resource characteristics, or design complex heuristics to achieve one or more objectives. However, such task scheduling algorithms suffer from low adaptability to different task types, long search times, and the tendency to fall into local optimum solutions. In addition, as the amount of computation and communication at each stage of a complex system simulation operation of the application rapidly changes, obtaining timely information on the global load status of all simulation entities through monitoring is challenging. Therefore, a novel approach that can adapt to the dynamic changes in the cluster environment and achieve efficient scheduling performance must be designed.
2.2. Resource Scheduling Based on RL
Machine learning is now being used to efficiently solve combinatorial optimization problems, such as task scheduling. Pandit [22] proposed a new Q-learning-based static task scheduling algorithm that uses a self-learning process in the Q-learning algorithm to rank tasks and a multi-objective scheduling algorithm to allocate resources to tasks, considering the make span and computational cost in the task scheduling problem. Lin [23] proposed an adaptive load-balancing and window-control algorithm for the characteristics of stochastic reaction–diffusion simulation systems. This algorithm first uses a simulated annealing-based load-balancing and dynamic-window-control algorithm to initially divide the simulation entities into threads, and then uses a modified RL Q-learning-based load-balancing algorithm during subsequent runs to achieve dynamic migration of simulation entities. Zhou [24] presents a deep reinforcement learning-based scheduling approach (FAS-DQN) to maximize data freshness in Cyber–Physical Systems, outperforming traditional methods in maintaining up-to-date information for timely responses to dynamic changes. Tian [25] proposes a dynamic load balancing scheduling algorithm based on Distributional Reinforcement Learning for the allocation of computing resources for batch jobs in cloud computing, to ensure the load balance of dynamic clusters and meet user demands. Wu [26] proposed a task allocation algorithm based on deep convolutional neural networks and Q-learning; this method assigns tasks to appropriate physical nodes to maximize long-term payoff while meeting task resource requirements. Rahim [27] proposed a collaborative cloud–edge dynamic load-balancing approach based on RL that meets the performance and security requirements needed for the task while reducing the load on the edge nodes to minimize the average latency. Additionally, Xu [28] proposed an RL-based real-time scheduling method that efficiently runs widely distributed large-scale heterogeneous computing tasks in complex simulation systems by constructing a communication cost model for task migration and training RL agents to migrate tasks from high-load processes to low-load processes.
Nonetheless, research on dynamic scheduling of computing resources for cloud simulation is limited, and most current approaches focus primarily on performance improvements and assume that each task is allocated to only one node. Thus, these approaches have failed to adequately integrate the characteristics of cloud computing and simulation technologies in their design. A simulation multi-sample task in a cloud environment means that multiple samples can be run simultaneously in multiple nodes and a single sample can be executed in parallel in multiple nodes. Therefore, this study combines the advantages of DRL methods to design a simulation multi-sample scheduling method based on DRL. The method not only supports the parallel execution of all simulation samples but also supports dividing each simulation sample into different groups and scheduling them to different nodes for parallel execution. The method does not require any a priori knowledge of clusters or applications, and trains DRL-based intelligence by designing reward and punishment functions to improve resource utilization and reduce the overall execution time of simulation tasks under the premise of satisfying resource constraints.
3. Approach for Multi-Sample Task Simulation Scheduling Based on DRL
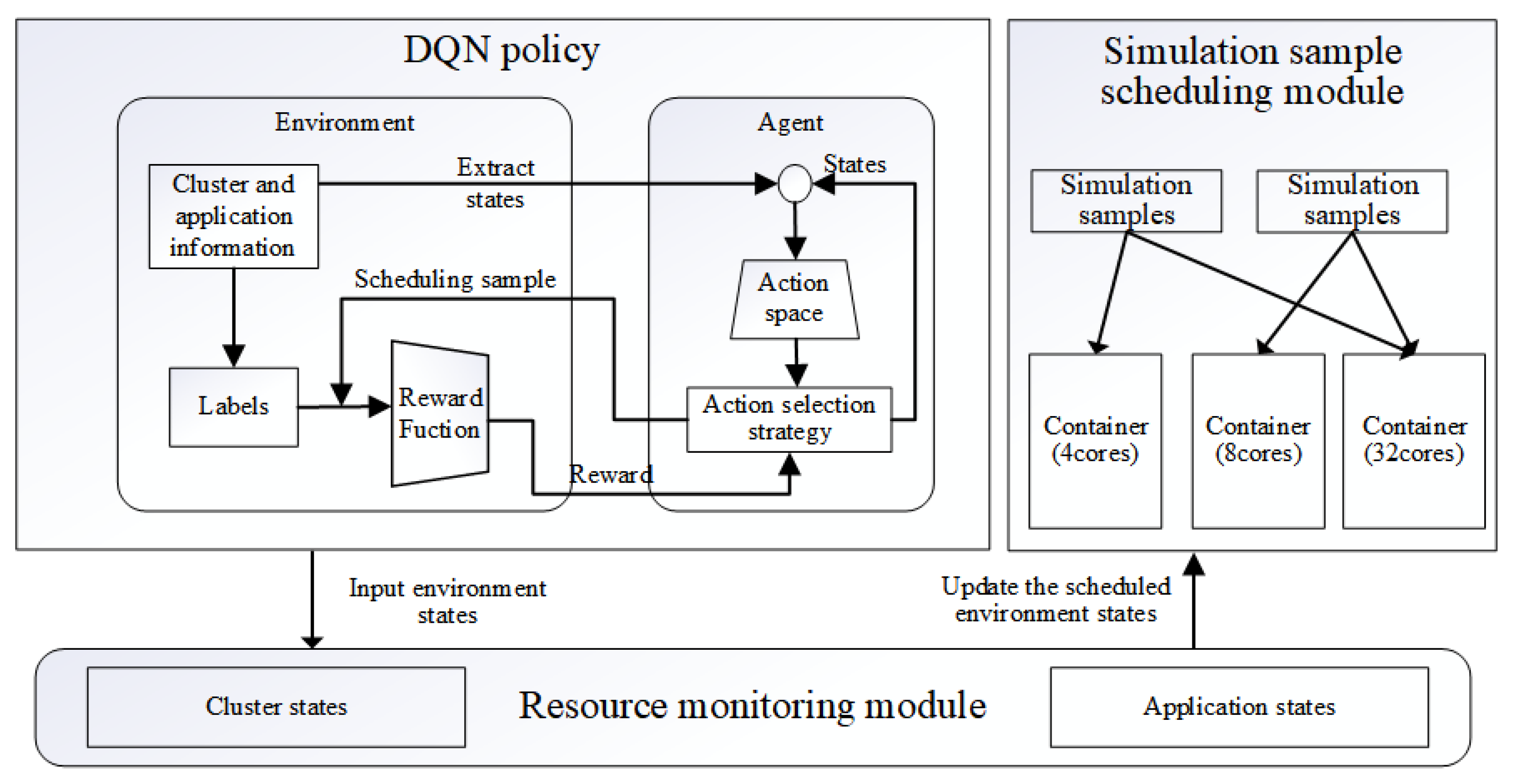
In this study, container virtualization technology was used as a working node to run simulation applications and the containers with different computing resources (number of CPU cores) were assumed to exist in the cloud environment. In the deployed cluster, users can submit one or more simulation tasks and specify resource requirements for their submitted simulation tasks. In each scheduling cycle, the scheduler assigns a single simulation task to either one or multiple containers for parallel execution. When no free computational resources are available in the cluster, the scheduler adopts a wait policy, delaying the allocation until some of the currently executing simulation samples complete and release sufficient resources to accommodate the new task. Figure 1 shows the proposed scheduling framework, which consists of three modules: the resource monitoring module, DRL policy, and simulation sample-scheduling module. The resource monitoring module is responsible for monitoring and collecting the cluster and application states in the entire system. During the simulation execution, the DRL strategy sets parameters based on the collected state data as the training state input, and trains the agent based on the optimization objective to output the optimal mapping scheme from simulation samples to containers. Subsequently, the simulation sample-scheduling module schedules the simulation samples into one or more containers for parallel and distributed computation according to the intelligent scheduling policy output. Finally, the resource monitoring module updates the state of the environment after scheduling and uses it as the state input for the next simulation sample scheduling. Specifically, when users submit multiple simulation tasks, the algorithm first determines the amount of available computing resources in the cluster through the resource monitoring module. Then, it computes the optimal scheduling strategy for assigning simulation samples to available computing resources. For example, a simulation sample requiring four CPU cores (simulation sample 1) and another requiring two CPU cores (simulation sample 2) can be scheduled together to Container 2, which has exactly six idle CPU cores and offers the lowest cost. This approach not only reduces computational costs but also improves overall execution efficiency.
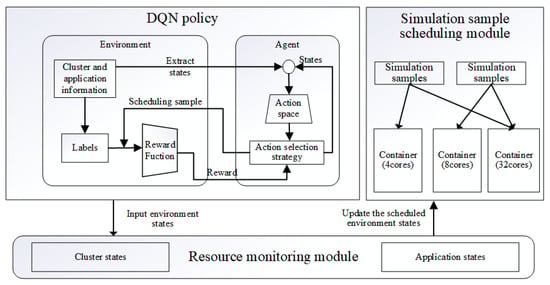
Figure 1.
Deep reinforcement learning-based scheduling framework for parallel simulation multiple sample tasks.
3.1. Problem Description
Here, assume that N is the total number of containers used to deploy the multi-sample simulation application and M is the total number of simulation samples that need to be scheduled. When a task is submitted to the cluster, the scheduler must execute the simulation task in one or more nodes and must satisfy the resource capacity constraint of the node and the resource demand constraint of the current job. The objective function of our method is shown in Equation (1).
where , by setting the value of , specifies the priority of the scheduler. When is 0, the scheduler reduces the total execution time of the simulation task regardless of the cost, whereas when is 1, the lowest cost scheduling scheme is used to execute the simulation task. Then, the constraints are shown in Equation (2)
The Cost mainly represents the total expense of running multiple simulation tasks, calculated as the sum of the runtime of each container multiplied by the unit price. The Time denotes the total execution time of all simulation tasks, determined as the duration from the start of the first task to the completion of the last one, where denotes the number of CPU cores required for the i-th sample in the j-th container. This constraint must be strictly enforced; otherwise, resource contention may occur, leading to potential performance degradation or even task failures in the scheduling process. denotes the unit price of container j; and denotes the runtime of the j-th container. is the physical time from the first simulation application execution; and is the physical time when the last simulation application is executed.
The above optimization problem can be viewed as a mixed integer linear programming and NP (Non-deterministic Polynomial) hard problem. The traditional heuristic-based scheduling methods must predict the execution time of each simulation application to compute the optimal scheduling result. However, increasing complexity of simulation applications and the growing size of simulation samples renders difficulty in determining an efficient method to calculate the execution time of each simulation application and allocate computational resources for it. Therefore, herein, a DRL method was used to train an agent to achieve intelligent scheduling of simulation tasks in a cloud environment.
3.2. Design of Reinforcement Learning Model
RL is the reward-guided behavior of intelligence learned by interacting with the environment in a trial-and-error manner, with the goal of maximizing the reward for the intelligence. In this study, the intelligence performed simulation task scheduling and satisfied the resource demand constraint of the job and the resource capacity constraint of the virtual machine, thereby obtaining the ultimate goal rewards from the environment, such as cost effectiveness and reduction in average job time. Therefore, the solution of the near-optimal policy for simulation task scheduling in RL depends predominantly on the accurate definition of the state action, reward, and punishment functions.
The state space, S, represents the set of states that an agent can perceive from the environment. The state space consists of cluster states and application states . The cluster state includes the number of all containers in the cluster, ; the remaining computational resources currently available for the container, ; the number of simulation application processes running in the container, ; and the price per unit of time used by the container, . The application status indicates the current computing resource requirements of the simulated application to be scheduled . In this work, the complex cluster loading information and simulation data are transformed into numerical features that can be directly fed into the neural network. Specifically, , , , and are encoded as integers to represent discrete attributes of the computing nodes, while is normalized and input as a floating-point number to accurately reflect pricing information. Therefore, in this study, the training of the agents was related only to the cluster state and supported intelligent scheduling of simulation samples of different sizes.
The action space A represents the set of operations that can be performed by the agent. The intelligence selects one or more containers and executes simulation tasks on the containers in parallel. If the cluster does not have sufficient resources to place the current simulation task, the agents wait until the current task is executed. Thus, for a cluster with N containers, a total of actions exist, where denotes the computational resource requirement of the current simulation task toCT be allocated.
The probability transfer function represents the probability of the intelligence transfer from state to state after the action has been performed.
Reward function indicates that the agent is in state and executes the action , and the immediate reward and punishment value are obtained afterward. Among them, positive rewards motivate the agents to take better actions. Conversely, negative rewards train the agents to avoid undesirable behaviors. Therefore, in the proposed model, the intelligence receives a positive reward for each successful placement of the simulation task, and no reward (R = 0) when it does not act (Action = 0). When intelligence is assigned a simulation task that does not satisfy the resource constraint, the training round is stopped and a large negative reward (R = −100) is given. When the intelligence completes all simulation tasks assigned, it receives an overall final reward value R. Thus, when R, which indicates that the training goal of the intelligence is to minimize the cost overhead. When , = R, which indicates that the training goal of the intelligence is to minimize the execution time of all simulation tasks. Finally, we balanced the trade-off between operational cost and performance by setting different values of . The rewards corresponding to specific actions are listed in Table 1.

Table 1.
Action–reward parameter settings.
The transition represents the current state and action observed by the intelligence, state at the next moment, and reward after performing a simulation task assignment process .
The episodes represent the entire process of an agent from the beginning to the end of scheduling, that is, all the transitions contained between the initial assignment and the completion of the assignment of all simulation tasks and the execution of all simulation tasks.
3.3. DQN-Based Simulation Multi-Sample Task Scheduling Algorithm
The Q-learning algorithm is one of the most widely used RL methods in several research areas [29]. In each iteration of the Q-learning algorithm, the agent first observes the current system state and selects an action . After performing that action, the system moves to the next state and receives a feedback value and updates the Q value based on the formula:
where denotes the learning rate; and denotes the penalty term, which is used to help the function converge. During action decision selection for each scheduling, the intelligence uses some strategy to select the action, which accelerates the convergence rate by continuously updating the state space to converge faster toward the optimal direction, thus making its value function (i.e., Q value) continuously approach the optimal direction.
However, the Q-learning approach is limited to contexts where both the action and sample spaces are small and generally discrete. Nonetheless, scheduling tasks for multi-sample simulations in cloud environments often require the construction of complex, huge state and action spaces. To address these limitations, the DQN approach uses a deep neural network to fit the value function, which provides the target value for the deep network based on Q-learning in RL, and continuously updates the network until convergence. Compared with Q-learning, DQN primarily uses convolutional neural networks to approximate the value function, . The network is trained to minimize errors at each step of the training, as follows.
where denotes the distribution of transition samples in the environment {s,a,r, of the distribution.
In addition, to solve the correlation and nonstationary distribution problems, DQN stores all transition samples in playback memory units by designing an experience pool and training on randomly selected samples (mini-batch) at the time of training. Therefore, herein, intelligent scheduling of simulation tasks was implemented in the cloud environment based on the DQN method. The algorithm is designed based on the work of Mnih et al. [30], as detailed in Algorithm 1.
| Algorithm 1 DQN-based simulation multi-sample task scheduling algorithm |
|
Lines 1 to 2 indicate the initialization of the playback memory pool D, the number of data entries N that can be accommodated, and the use of random weights to initialize the action-behavior value function Q.
Lines 5 to 7 indicate that an action is randomly selected using the greedy strategy and executing the action After observing the return value , the state is updated at the next moment as .
Lines 8 to 9 indicate that after performing one simulation assignment, the conversion sample data is recorded and stored in the playback memory pool D.
Line 10 indicates that a uniform random sample of conversion data is sampled from the playback memory D and the target value is calculated .
Line ll indicates the execution of a gradient descent algorithm that updates values and re-runs the loop.
Finally, the algorithm terminates and outputs the results when the maximum number of iterations is reached.
4. Experimental Results and Analysis
This section first discusses the experimental setup, including details of the cluster resources, workload generation, and the baseline scheduler. Next, it presents the evaluation and comparison of the DRL agent with the baseline scheduling algorithm.
4.1. Experimental Setup
The simulation application was deployed in a real cloud environment built by Docker, an open container engine. Container nodes with different resource capacities and prices were built on computing nodes using container virtualization technology (see Ali-Cloud service prices for details); consequently, agents could be trained and evaluated to optimize costs when the cluster was deployed on the public cloud. The specific prices are shown in Table 2.

Table 2.
Container resources: price setting.
4.2. Benchmark Application and Model Setup
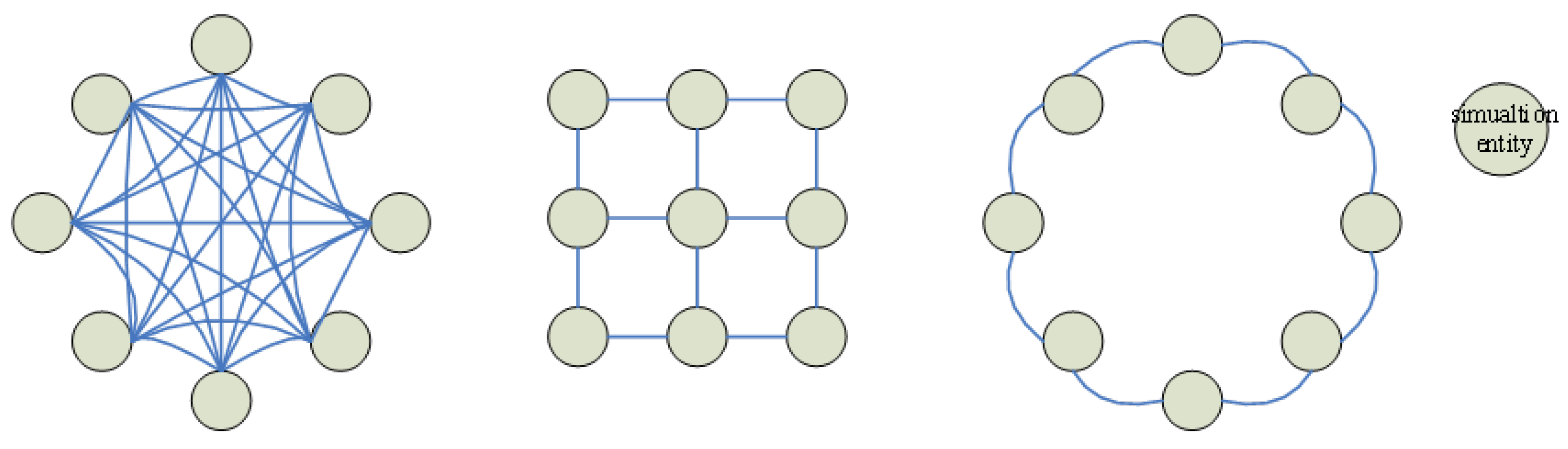
PHOLD is commonly used as a representative benchmark test procedure for evaluating the performance of Parallel Discrete Event Simulation (PDES) [31]. The model assumes that the simulation consists of L logical processes, which are distributed across N computing nodes for execution. Each logical process initializes with an event queue containing M events, resulting in a total of initial events in the system. During the simulation, each entity processes these initial events; upon execution, an event may generate and send a new event with a certain probability, which is then scheduled for processing at a future simulation time. Furthermore, the PHOLD model allows users to adjust its parameters and interaction structures, enabling customization of the simulation’s behavioral characteristics. This flexibility facilitates more realistic modeling of real-world physical systems. Several variants of the PHOLD-based test models are illustrated in Figure 2.
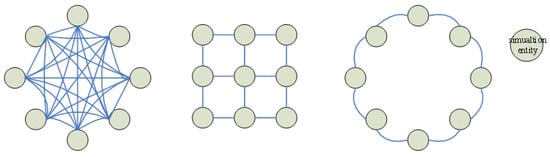
Figure 2.
The structure diagram of the PHOLD model.
Therefore, the PHOLD simulation application is employed to evaluate the performance of the proposed algorithm. A total of 30 simulation samples with resource demands ranging from 1 to 4 CPU cores are generated using a uniform distribution. Finally, the proposed approach was tested in a real-world environment, where the YH-SUPE [32] simulation engine was used to execute the simulation applications. Computing resources were reallocated to the simulation tasks based on the predicted results. The proposed prediction model was evaluated on a desktop computer with a 32-core Intel Xeon Gold 6338 CPU and 64 GB memory based on TensorFlow 2.0 and python 3.7 programming environment.
A larger number of runs can enhance statistical robustness and the reliability of the mean estimate; this study follows the approach of Zhu et al. [33], running 10 experiments to calculate the average of the experimental result. First, three different scheduling methods were tested: the round-robin (RR) algorithm [34], best fit (BF) algorithm [35], and genetic algorithm (GA) [36]. The specific algorithms are shown in Algorithms 2–4. The RR algorithm assigns simulation tasks to available containers in an RR request manner. The BF algorithm assigns as many simulation tasks as possible to the smallest free container. The GA algorithm search for optimal solutions by simulating natural evolutionary processes. Finally, for each scheduling method, the parameter combination that achieved the best performance was selected to compare against our proposed approach.
| Algorithm 2 The RR Algorithm in Simulation Task Scheduling |
|
| Algorithm 3 The BF Algorithm in Simulation Task Scheduling |
|
| Algorithm 4 The GA Algorithm in Simulation Task Scheduling |
|
In each decision step, the entire optimization problem is dynamically generated using the current cluster state and job specifications. To enhance predictive performance, the grid search toolkit was utilized to adjust the model parameters. Finally, the specific parameters of the deep RL model proposed in this study are summarized in Table 3.

Table 3.
DQN model parameter settings.
4.3. The Network Structure of the DQN Model
In the construction of the DQN model, we evaluated the influence of the number of hidden layers and the number of hidden units. The discount factor was set to = 0.7. For the given experimental setup, a network with two hidden layers demonstrated optimal performance. Utilizing three or more hidden layers resulted in overfitting. Furthermore, increasing the number of hidden units improved the model’s performance, with the best results achieved when each layer contained 16 units. Based on these findings, the final network architecture employed in subsequent simulations consisted of two hidden layers, each containing 16 hidden units.
4.4. Model Performance Evaluation
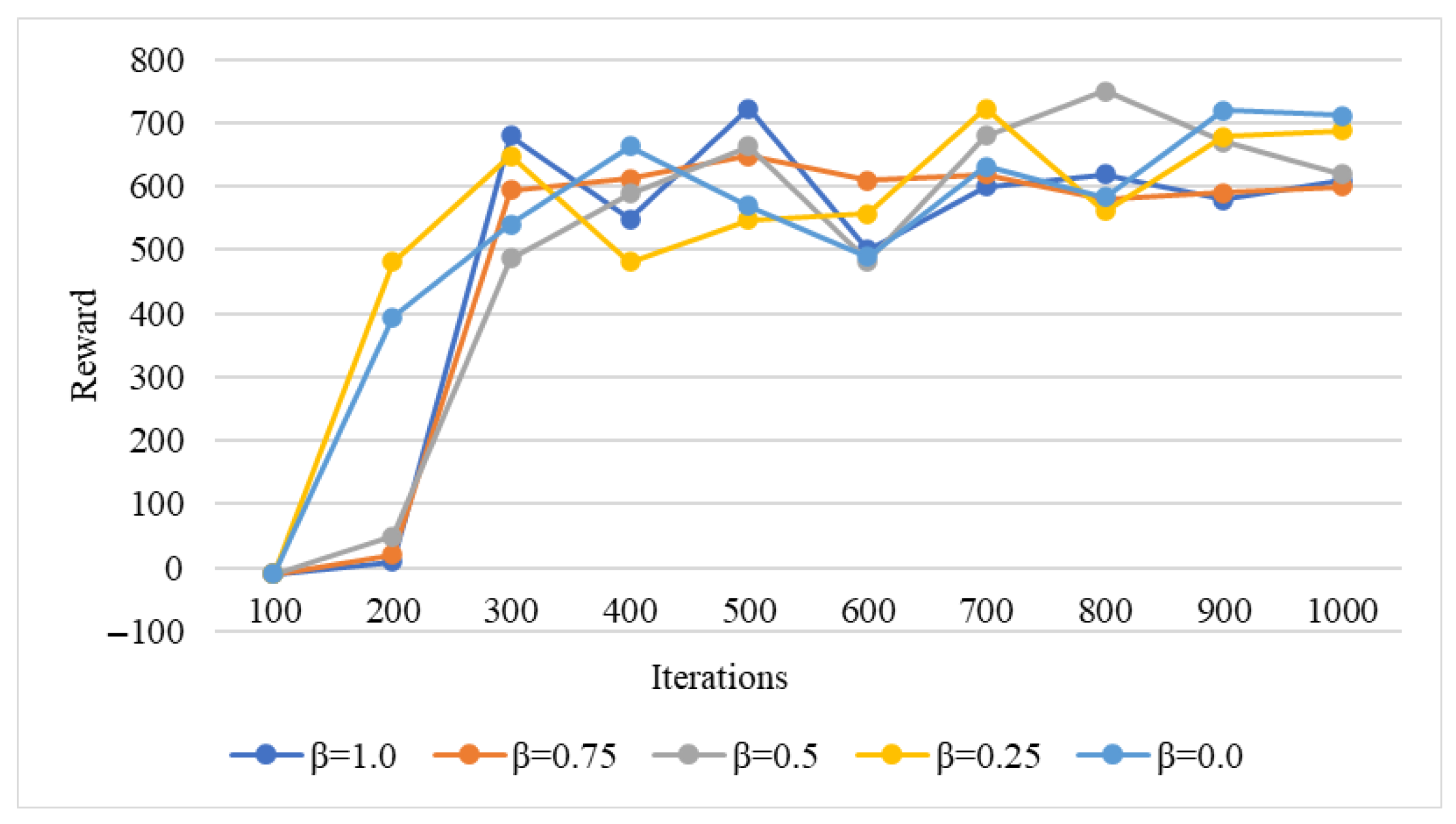
Herein, different parameter values were used to train the DRL model to demonstrate the effectiveness of the method for different optimization objectives. Figure 3 shows the convergence of the DQN algorithm, which represents the average reward accumulated by the DQN agents during training. Higher values indicate that the agents obtain more rewards for reduced node usage cost. Conversely, lower values indicate that the agents are more optimized to reduce the simulation task execution time.
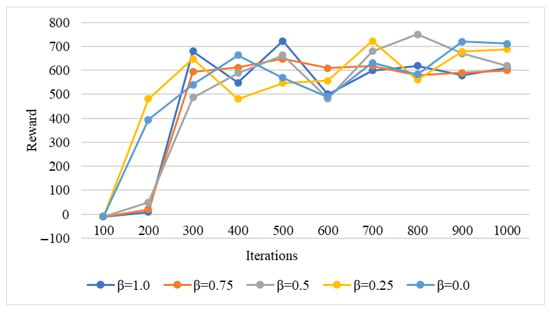
Figure 3.
Convergence of DQN algorithm.
Values between 0 and 1 (e.g., 0.25 and 0.75) indicate a hybrid optimization scheme, where the intelligence attempts optimizing both objectives with different priorities. During the initial training, the average reward of the agents is negative because at the beginning of training, agents often execute scheduling schemes that violate the resource demand constraints and generate large negative rewards. However, after a reasonable allocation decision is taken (assigning simulation samples under satisfying constraints), the environment gives small rewards and motivates the agents to successfully complete the scheduling of all simulation tasks. In addition, without violating the resource constraints, the intelligence continuously learns the scheduling strategy according to the optimization goals and obtains higher rewards. Evidently from Figure 3, within 300 iterations, the agent rapidly improved the overall payoff and converged around 1000 training iterations for different values of .
4.4.1. Evaluation of Cost
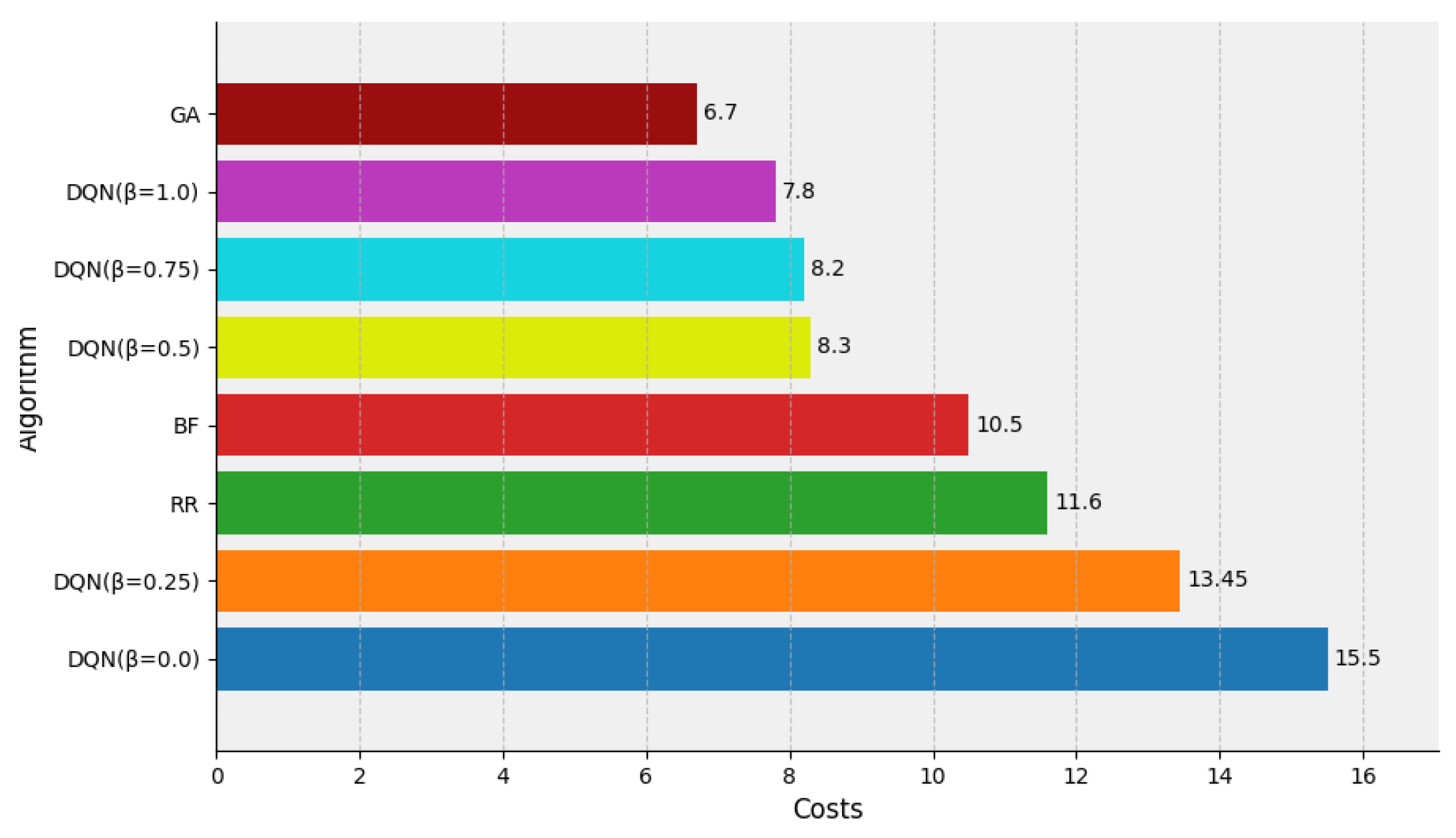
Next, the cost of using cluster computing resources was calculated using the running time of all containers and comparing the proposed DQN-based simulation multi-sample task scheduling method with other scheduling methods. Figure 4 shows the comparison of each method in the cost assessment under sufficient resources. The GA algorithm outperformed all the other algorithms in the case of sufficient resources, i.e., where all simulation tasks can be run simultaneously in the cluster, and achieved the lowest VM usage cost of CNY 6.7. This is because the method collects load information of the global environment, estimates the running time of each simulation task, and assigns the appropriate node for the simulation task to execute. The DQN method demonstrated performance comparable to that of the genetic algorithm (GA) when the parameter was set to 1.0 and 0.75, achieving total costs of CNY 7.8 and CNY 8.2, respectively. Moreover, it significantly outperformed the BF algorithm (CNY 10.5) and RR algorithm (CNY 11.6). Although DQN did not achieve the global optimum in cost minimization, it provided a near-optimal solution for reducing resource usage costs and improving resource utilization, without requiring any prior knowledge of the cluster’s load characteristics.
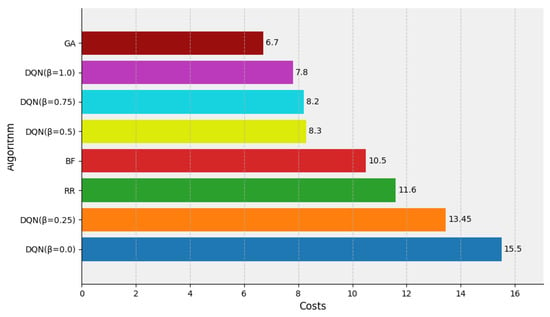
Figure 4.
The comparison of the DQN, RR, BF and GA algorithms in the cost assessment under sufficient resources.
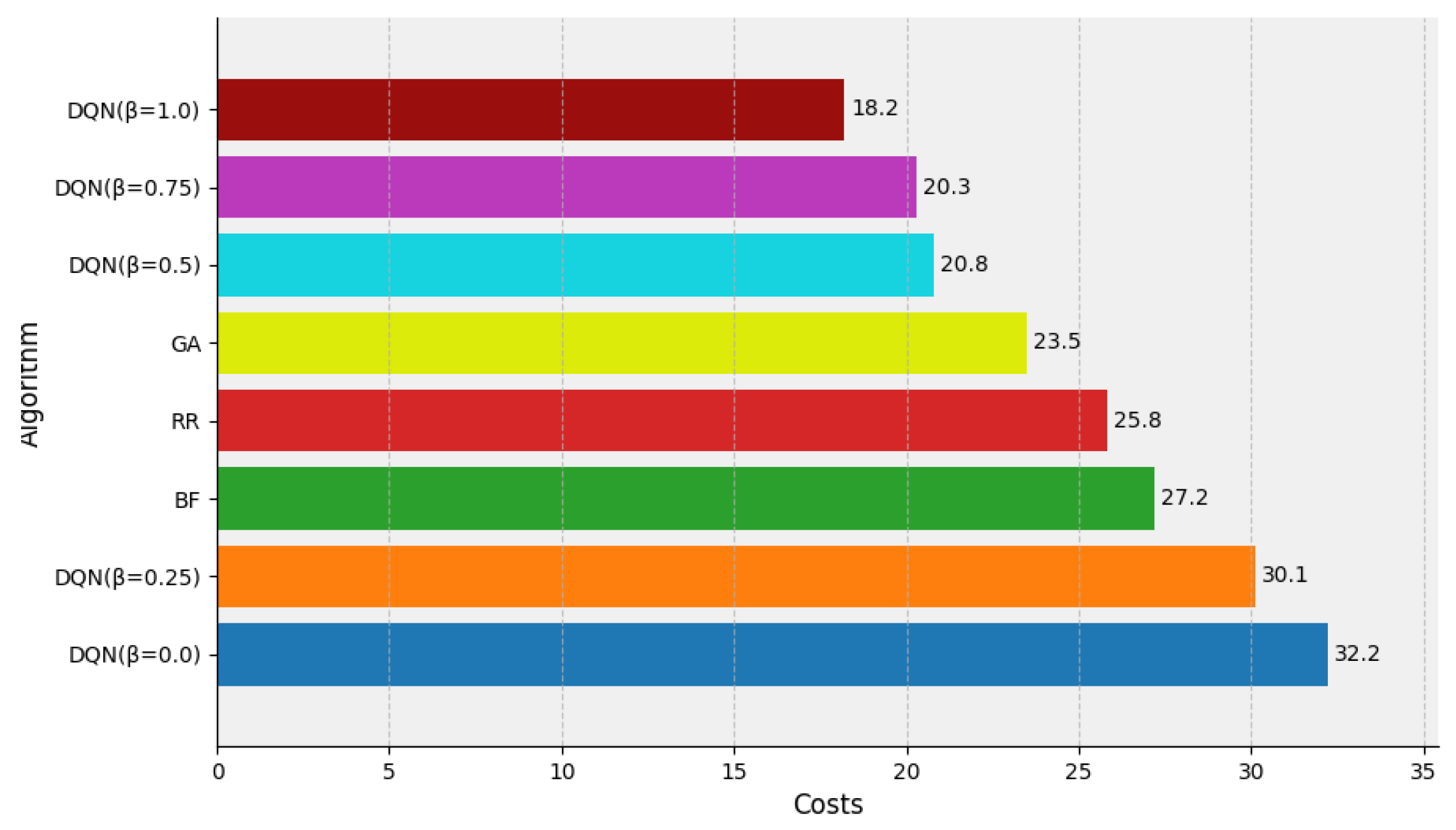
In scenarios with limited resource availability, scheduling algorithms often need to wait for resources to be released by completed simulation tasks due to insufficient cluster capacity to accommodate all jobs simultaneously. As shown in Figure 5, the genetic algorithm (GA) exhibited poor performance. Due to cluster overload, GA struggled to accurately estimate the execution time of each simulation task and implement optimal allocation strategies, resulting in a total cost of CNY 23.5.

Figure 5.
The comparison of the DQN, RR, BF and GA algorithms in the cost assessment under insufficient resources.
The DQN algorithm significantly reduced computational resource costs. When was set to 1.00, 0.75, and 0.50, the corresponding costs were only CNY 18.2, CNY 20.3, and CNY 20.8, respectively. These results represent cost reductions of 11.4% to 22.5% compared to the suboptimal GA method. In comparison with the worst-performing BF algorithm (CNY 27.2), the cost was reduced by up to 33%. Moreover, the RR algorithm incurred a cost of CNY 25.8. This higher cost can be attributed to the RR method’s tendency to limit computation to only a few nodes, which paradoxically increased resource usage costs due to prolonged task execution times.
4.4.2. Evaluation of Runtime
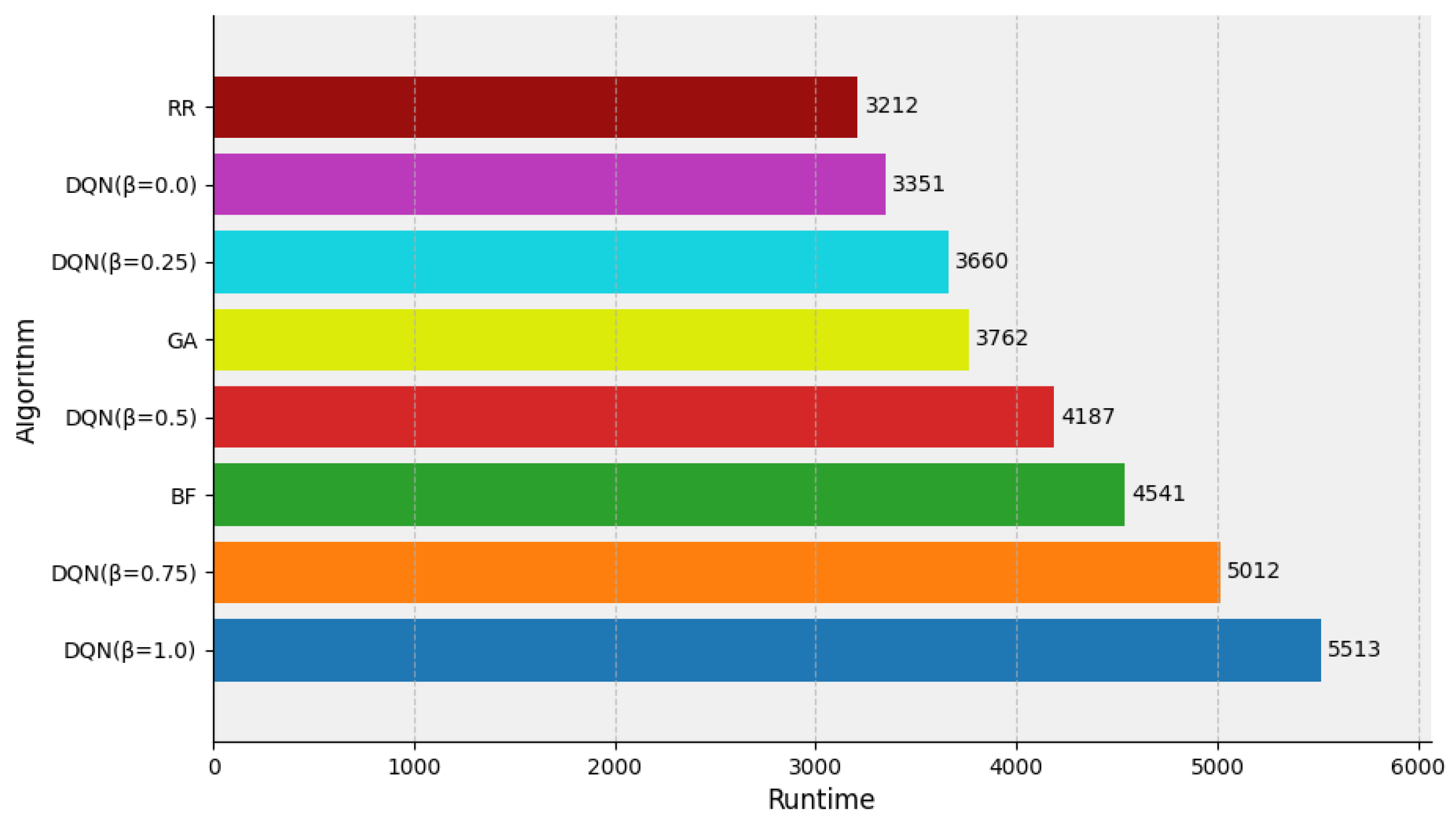
In Figure 6, the overall runtime was collected after the execution of various simulation tasks, and the performance of each scheduling method was evaluated in terms of runtime reduction. For a well-resourced cluster environment, the RR algorithm performed the best with a runtime of 3212 s. This was because the method distributes simulation tasks equally among multiple containers and obtains the shortest execution time. The DQN method ( = 0.0) also achieved near-optimal performance, with a runtime of 3351 s, which is only 3% more than that of the RR method. The BF algorithm performed poorly, with a runtime of 3762 s, owing to its preference to schedule simulation tasks to the same node.
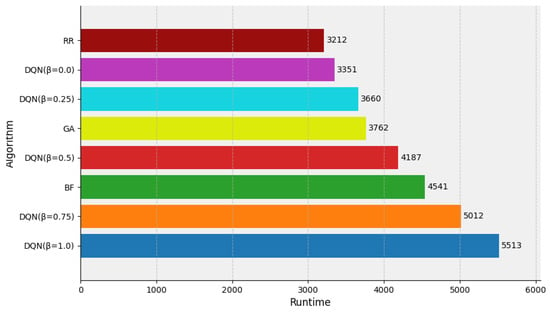
Figure 6.
Runtime evaluation of the DQN, RR, BF, GA algorithm under sufficient resources.
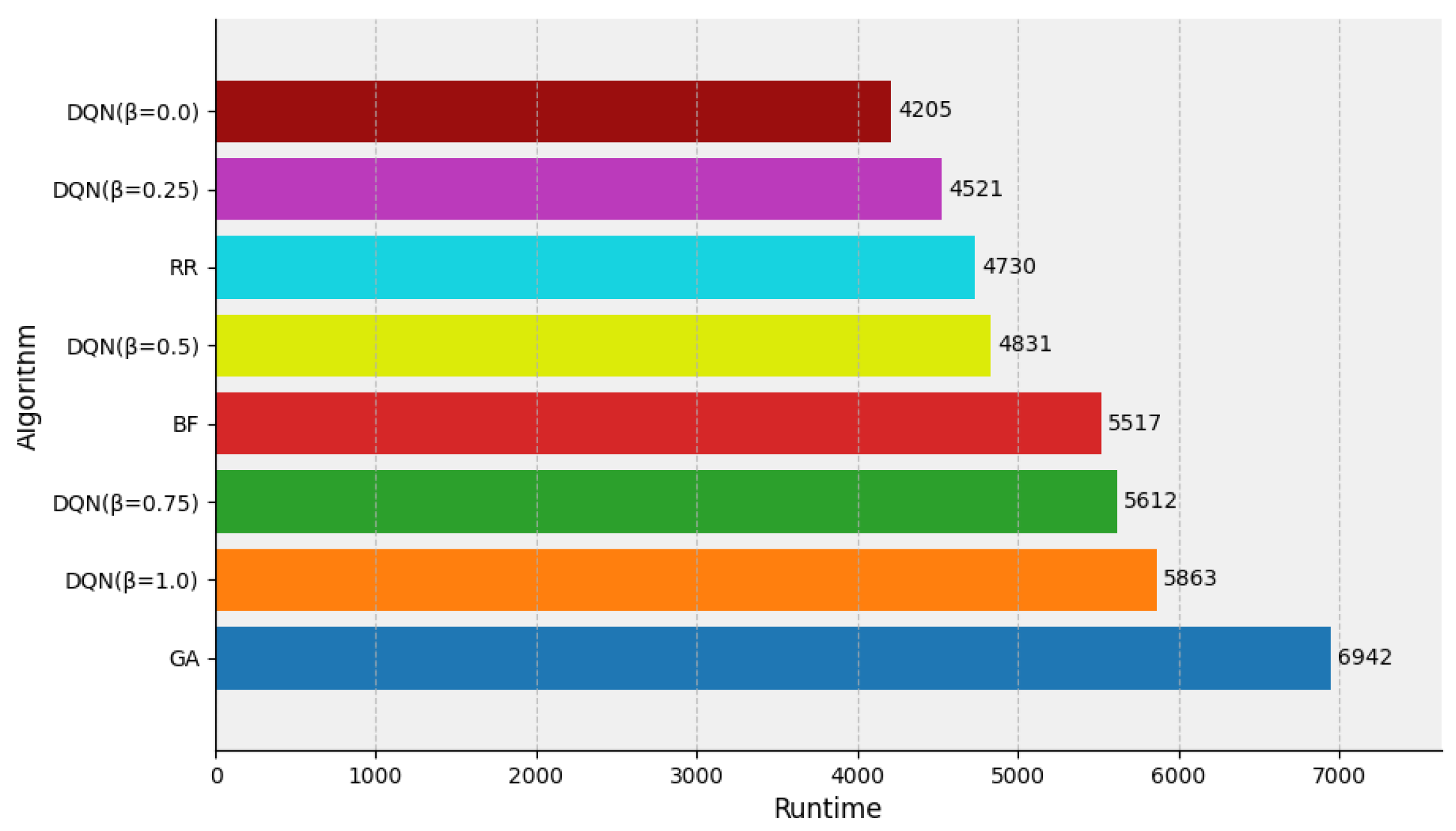
For cluster environments with insufficient resources, simulation samples often have to wait before resources are available. If the simulation samples are assigned to multiple nodes for parallel execution, the execution time of the simulation application may instead increase. As shown in Figure 7, the DQN agent method proposed in this study effectively obtained the deep-level features of the simulation task execution time as well as the simulation task allocation scheme, and used the features as a policy pattern to iteratively train and learn to reduce the overall execution time of the simulation task. The DQN algorithm achieved the best performance with set to 0.0 and 0.25, of 4205 and 4521 s, respectively, corresponding to a reduction in execution time of 4–11% compared with the RR algorithm (4730 s), respectively. The execution time was reduced by up to 40% compared with the worst-performing algorithm (GA).
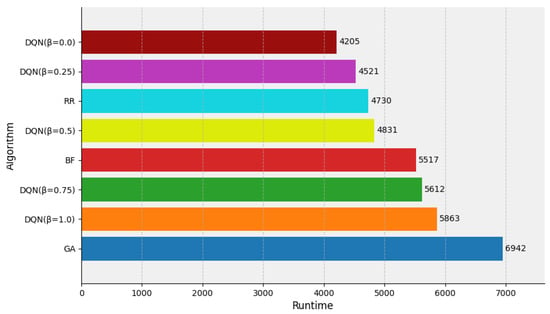
Figure 7.
Runtime evaluation of the DQN, RR, BF, GA algorithm under insufficient resources.
4.4.3. Comprehensive Evaluation
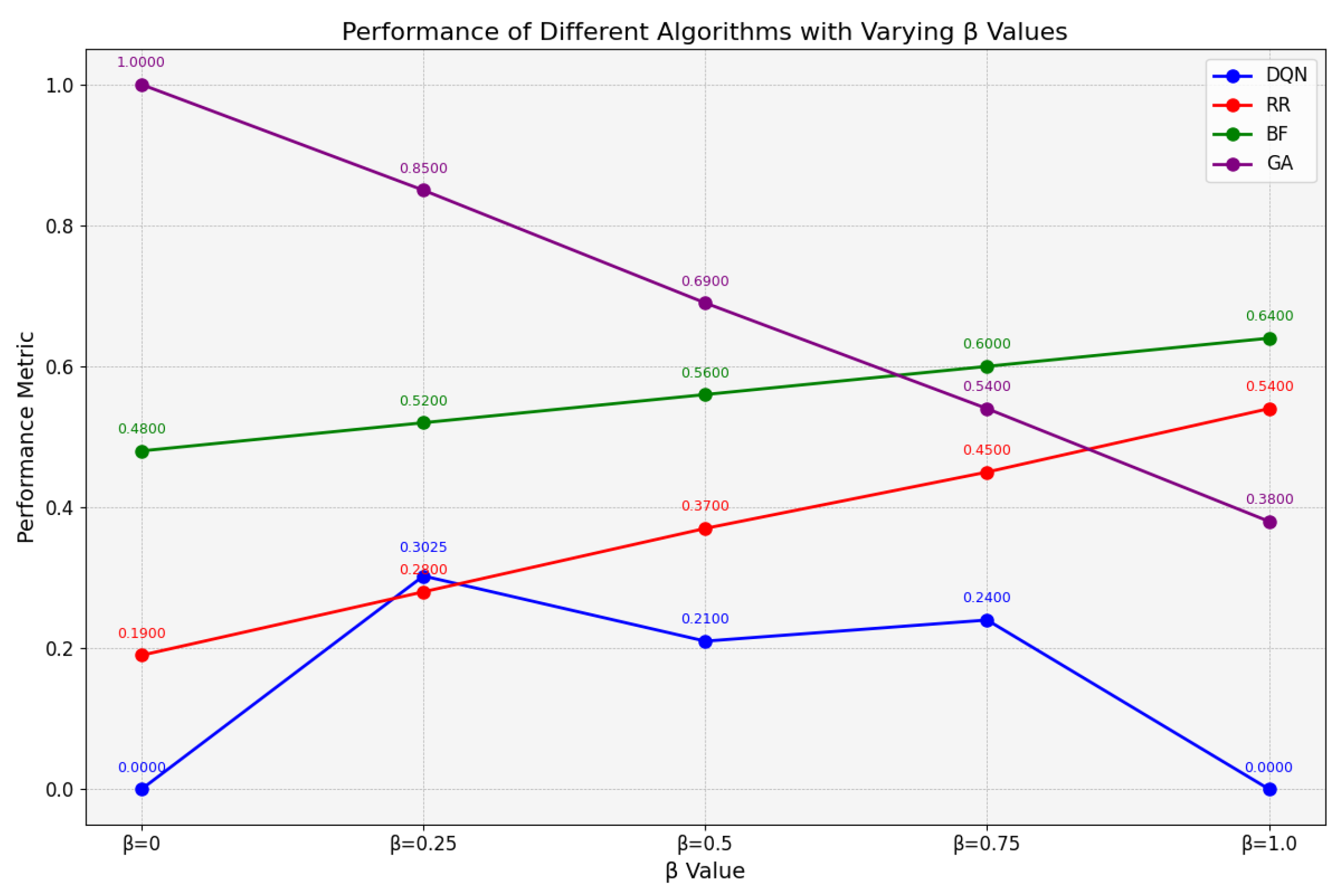
To comprehensively evaluate the effectiveness of the proposed method in optimizing both cost and runtime, this study first applied the min-max normalization technique to standardize the runtime and cost values obtained from the experiments. Subsequently, the overall performance of the DQN method under different values was assessed using Equation (1). It is worth noting that, due to the nature of min-max normalization, the integrated performance score ranges between 0 and 1, where a score of 0 indicates the best overall performance and a score of 1 represents the worst.
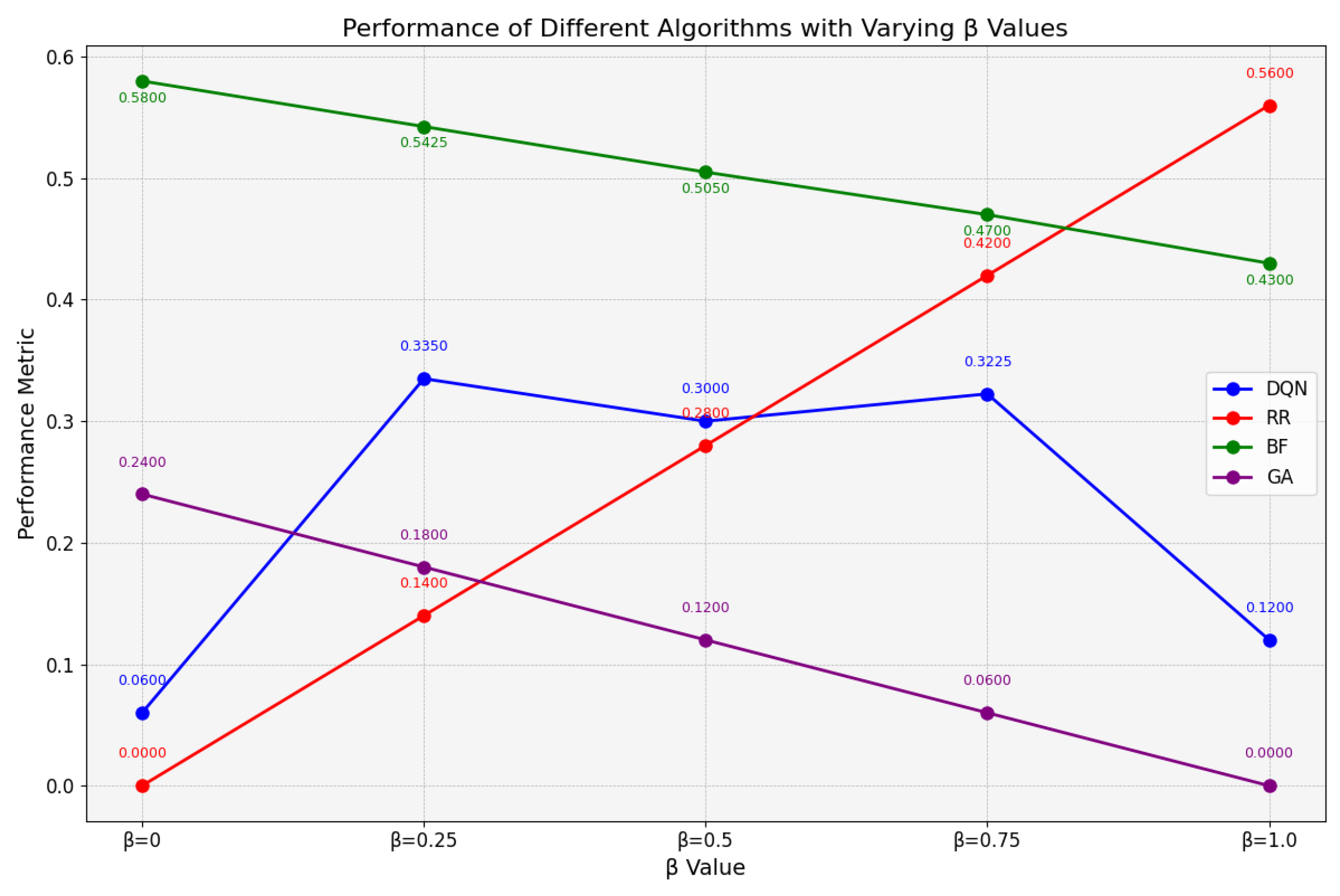
Figure 8 presents the evaluation results of multi-objective optimization under resource-sufficient conditions. The genetic algorithm (GA) demonstrates optimal comprehensive performance, achieving scores of 0.12, 0.06, and 0 when is set to 0.5, 0.75, and 1.0, respectively. However, the DQN algorithm significantly outperforms GA at , achieving a performance score of 0.06 compared to GA’s 0.24. Furthermore, as increases, the DQN method consistently exhibits superior applicability over both the RR and BF algorithms, with performance metrics remaining within the range of 0 to 0.4. These results indicate that, in resource-abundant environments, the DQN algorithm not only achieves optimal performance at but also demonstrates greater stability compared to other scheduling approaches.
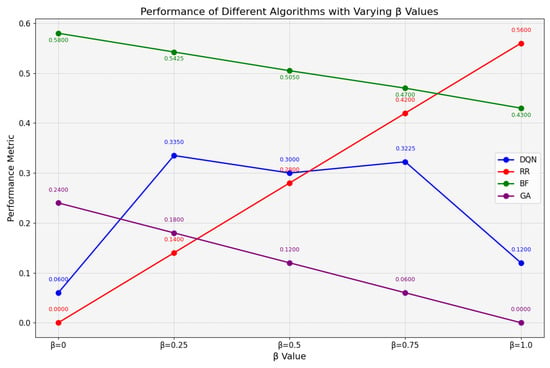
Figure 8.
Comprehensive assessment under sufficient resources.
Figure 9 evaluates the multi-objective optimization performance under resource-constrained conditions. The results demonstrate that the proposed DQN algorithm significantly outperforms other methods across most settings, achieving optimal performance when is set to 0, 0.5, 0.75, and 1.0. At , the DQN algorithm attains near-optimal performance with a score of 0.30, second only to the RR algorithm’s score of 0.28. These findings confirm that the proposed method maintains a considerable advantage over alternative approaches in scenarios with insufficient resource availability.
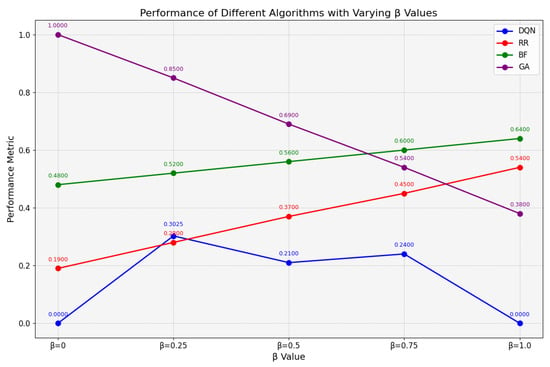
Figure 9.
Comprehensive assessment under insufficient resources.
5. Conclusions and Future Work
Owing to factors such as dynamic changes in the load of complex system simulation applications and frequent synchronization between simulation entities, existing methods cannot effectively schedule computational resources for simulation applications in a cloud environment. In addition, traditional heuristic-based task allocation methods typically need to collect historical load information in advance and cannot be effectively optimized for multiple objectives. To address these problems, this study proposed a DRL-based scheduling method for multi-sample cloud simulation tasks as an efficient and low-cost solution. The method collects cluster load information and simulation application information as the training data, employs deep Q-networks to train an agent to learn the inherent characteristics of clusters and simulation tasks, and designs a reward and punishment function to help the agent learn an intelligent scheduling scheme to reduce cluster resource usage cost and improve simulation task execution efficiency without violating resource constraints.
To demonstrate the advantages of the proposed method, different scheduling schemes were evaluated in a real cloud environment. The experimental results revealed that the method can improve the execution efficiency of multi-sample simulation tasks while reducing the cost of cluster resource usage. In future work, we will further explore the application of deep learning methods to achieve dynamic load balancing among simulation entities in complex system simulation applications, with the aim of improving the execution efficiency of individual simulation tasks. Additionally, we plan to optimize the DQN-based scheduling approach to enable multi-level parallel scheduling both within and across simulation samples, thereby enhancing the overall performance of large-scale parallel simulation workloads.
Author Contributions
Conceptualization, F.Z.; Methodology, Y.Y.; Writing—original draft, Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xu, F.; Liu, F.; Jin, H.; Vasilakos, A.V. Managing performance overhead of virtual machines in cloud computing: A survey, state of the art, and future directions. Proc. IEEE 2013, 102, 11–31. [Google Scholar] [CrossRef]
- Saxena, D.; Kumar, J.; Singh, A.K.; Schmid, S. Performance analysis of machine learning centered workload prediction models for cloud. IEEE Trans. Parallel Distrib. Syst. 2023, 34, 1313–1330. [Google Scholar] [CrossRef]
- Yao, Y.p.; Meng, D.; Zhu, F.; Yan, L.b.; Qu, Q.j.; Lin, Z.w.; Ma, H.b. Three-level-parallelization support framework for large-scale analytic simulation. J. Simul. 2017, 11, 194–207. [Google Scholar] [CrossRef]
- Risco-Martín, J.L.; Henares, K.; Mittal, S.; Almendras, L.F.; Olcoz, K. A unified cloud-enabled discrete event parallel and distributed simulation architecture. Simul. Model. Pract. Theory 2022, 118, 102539. [Google Scholar] [CrossRef]
- Chaudhry, N.R.; Anagnostou, A.; Taylor, S.J. A workflow architecture for cloud-based distributed simulation. Acm Trans. Model. Comput. Simul. 2022, 32, 15. [Google Scholar] [CrossRef]
- Fujimoto, R.M. Research challenges in parallel and distributed simulation. Acm Trans. Model. Comput. Simul. 2016, 26, 22. [Google Scholar] [CrossRef]
- Yoginath, S.B.; Perumalla, K.S. Optimized hypervisor scheduler for parallel discrete event simulations on virtual machine platforms. In Proceedings of the International ICST Conference on Simulation Tools and Techniques, Cannes, France, 5–8 March 2013; pp. 1–9. [Google Scholar]
- Yao, F.; Yao, Y.; Xing, L.; Chen, H.; Lin, Z.; Li, T. An intelligent scheduling algorithm for complex manufacturing system simulation with frequent synchronizations in a cloud environment. Memetic Comput. 2019, 11, 357–370. [Google Scholar] [CrossRef]
- Tang, W.; Yao, Y.; Li, T.; Song, X.; Zhu, F. An adaptive persistence and work-stealing combined algorithm for load balancing on parallel discrete event simulation. Acm Trans. Model. Comput. Simul. 2020, 30, 12. [Google Scholar]
- Song, Y.; Wei, L.; Yang, Q.; Wu, J.; Xing, L.; Chen, Y. RL-GA: A reinforcement learning-based genetic algorithm for electromagnetic detection satellite scheduling problem. Swarm Evol. Comput. 2023, 77, 101236. [Google Scholar] [CrossRef]
- Graham, R.L.; Lawler, E.L.; Lenstra, J.K.; Kan, A.R. Optimization and approximation in deterministic sequencing and scheduling: A survey. Ann. Discret. Math. 1979, 5, 287–326. [Google Scholar]
- Delimitrou, C.; Kozyrakis, C. Quasar: Resource-efficient and qos-aware cluster management. ACM Sigplan Not. 2014, 49, 127–144. [Google Scholar] [CrossRef]
- Maroulis, S.; Zacheilas, N.; Kalogeraki, V. A framework for efficient energy scheduling of spark workloads. In Proceedings of the 2017 IEEE 37th International Conference on Distributed Computing Systems (ICDCS), Atlanta, GA, USA, 5–8 June 2017; pp. 2614–2615. [Google Scholar]
- Kaur, K.; Garg, S.; Aujla, G.S.; Kumar, N.; Zomaya, A.Y. A multi-objective optimization scheme for job scheduling in sustainable cloud data centers. IEEE Trans. Cloud Comput. 2019, 10, 172–186. [Google Scholar] [CrossRef]
- Lu, Y.; Sun, N. An effective task scheduling algorithm based on dynamic energy management and efficient resource utilization in green cloud computing environment. Clust. Comput. 2019, 22, 513–520. [Google Scholar] [CrossRef]
- Labba, C.; Saoud, N.B.B.; Dugdale, J. A predictive approach for the efficient distribution of agent-based systems on a hybrid-cloud. Future Gener. Comput. Syst. 2018, 86, 750–764. [Google Scholar] [CrossRef]
- De Grande, R.E.; Boukerche, A. Dynamic balancing of communication and computation load for HLA-based simulations on large-scale distributed systems. J. Parallel Distrib. Comput. 2011, 71, 40–52. [Google Scholar] [CrossRef]
- D’Angelo, G. Parallel and distributed simulation from many cores to the public cloud. In Proceedings of the 2011 International Conference on High Performance Computing & Simulation, Istanbul, Turkey, 4–8 July 2011; pp. 14–23. [Google Scholar]
- Yang, C.; Chai, X.; Zhang, F. Research on co-simulation task scheduling based on virtualization technology under cloud simulation. In Proceedings of the AsiaSim 2012: Asia Simulation Conference 2012, Shanghai, China, 27–30 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 421–430. [Google Scholar]
- Ding, S.; Chen, C.; Xin, B.; Pardalos, P.M. A bi-objective load balancing model in a distributed simulation system using NSGA-II and MOPSO approaches. Appl. Soft Comput. 2018, 63, 249–267. [Google Scholar] [CrossRef]
- Zhang, M.; Peng, Y.; Yang, M.; Yin, Q.; Xie, X. A discrete PSO-based static load balancing algorithm for distributed simulations in a cloud environment. Future Gener. Comput. Syst. 2021, 115, 497–516. [Google Scholar]
- Pandit, M.K.; Mir, R.N.; Chishti, M.A. Adaptive task scheduling in IoT using reinforcement learning. Int. J. Intell. Comput. Cybern. 2020, 13, 261–282. [Google Scholar] [CrossRef]
- Lin, Z.; Tropper, C.; Yao, Y.; Mcdougal, R.A.; Patoary, M.N.I.; Lytton, W.W.; Hines, M.L. Load balancing for multi-threaded PDES of stochastic reaction-diffusion in neurons. J. Simul. 2017, 11, 267–284. [Google Scholar] [CrossRef]
- Zhou, C.; Li, G.; Li, J.; Zhou, Q.; Guo, B. FAS-DQN: Freshness-Aware Scheduling via Reinforcement Learning for Latency-Sensitive Applications. IEEE Trans. Comput. 2022, 71, 2381–2394. [Google Scholar] [CrossRef]
- Li, T.; Ying, S.; Zhao, Y.; Shang, J. Batch Jobs Load Balancing Scheduling in Cloud Computing Using Distributional Reinforcement Learning. IEEE Trans. Parallel Distrib. Syst. 2024, 35, 169–185. [Google Scholar] [CrossRef]
- Wu, C.; Xu, G.; Ding, Y.; Zhao, J. Explore deep neural network and reinforcement learning to large-scale tasks processing in big data. Int. J. Pattern Recognit. Artif. Intell. 2019, 33, 1951010. [Google Scholar] [CrossRef]
- Razaq, M.M.; Rahim, S.; Tak, B.; Peng, L. Fragmented Task Scheduling for Load-Balanced Fog Computing Based on Q-Learning. Wirel. Commun. Mob. Comput. 2022, 2022, 4218696. [Google Scholar] [CrossRef]
- Xu, J.; Guo, H.; Shen, H.W.; Raj, M.; Wurster, S.W.; Peterka, T. Reinforcement learning for load-balanced parallel particle tracing. IEEE Trans. Vis. Comput. Graph. 2022, 29, 3052–3066. [Google Scholar] [CrossRef] [PubMed]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Yoginath, S.B.; Perumalla, K.S. Efficient parallel discrete event simulation on cloud/virtual machine platforms. ACM Trans. Model. Comput. Simul. 2015, 26, 5. [Google Scholar] [CrossRef]
- Hou, B.; Yao, Y.; Wang, B.; Liao, D. Modeling and simulation of large-scale social networks using parallel discrete event simulation. Simulation 2013, 89, 1173–1183. [Google Scholar] [CrossRef]
- Xiao, Y.; Yao, Y.; Chen, K.; Tang, W.; Zhu, F. A simulation task partition method based on cloud computing resource prediction using ensemble learning. Simul. Model. Pract. Theory 2022, 119, 102595. [Google Scholar] [CrossRef]
- Rasmussen, R.V.; Trick, M.A. Round robin scheduling—A survey. Eur. J. Oper. Res. 2008, 188, 617–636. [Google Scholar] [CrossRef]
- Castillo, C.; Rouskas, G.N.; Harfoush, K. Efficient implementation of best-fit scheduling for advance reservations and qos in grids. In Proceedings of the 1st IEEE/IFIP International Workshop on End-to-End Virtualization and Grid Management (EVGM), San José, CA, USA, 29 October–2 November 2007. [Google Scholar]
- Hartmann, S. A competitive genetic algorithm for resource-constrained project scheduling. Nav. Res. Logist. 1998, 45, 733–750. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).