Dynamics of a Class of Extended Duffing–Van Der Pol Oscillators: Melnikov’s Approach, Simulations, Control over Oscillations

Abstract

The Duffing–van der Pol oscillator is a very prominent and interesting standard model. There is a substantial body of varied literature on this topic. In this article, we propose a new class of oscillators by adding new factors to its dynamics. Investigations in light of Melnikov’s approach are considered. Several simulations are composed. A few specialized modules for testing the dynamics of the hypothetical oscillator under consideration are also given. This will be an essential component of a much broader Web-based scientific computing application that is planned. Possible control over oscillations: approximation with restrictions is also discussed; some probabilistic constructions are also presented.

1. Introduction

The non-autonomous Duffing–van der Pol oscillator is a very prominent and interesting standard model. The literature devoted to this issue is significant in volume and diversity.

The investigations of chemical oscillating reactions in a continuously stirred tank reactor (CSTR) [1,2,3,4,5,6,7,8] have revealed non-equilibrium phenomena such as oscillations, bi-stability, complex oscillations, and quasi-chaotic behavior of the reaction. A detailed study of a nonlinear Duffing-type oscillator driven by two voltage sources can be found in [9]. For some stochastic Duffing equations, see [10,11,12,13,14,15].

Modeling nonlinear dissipative chemical dynamics by a forced modified van der Pol–Duffing oscillator with asymmetric potential is considered in [16]

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -\alpha x-\gamma x^3-\beta +ϵ\left(-\mu (1-x^2)y+Ecos\left(\omega t\right)\right),\hfill \end{array}\right.$$

(1)

where $ϵ$ is a tiny parameter that describes how small the forced and dissipative terms are. Some additional related studies are [17,18,19,20,21].

Chaos in a nonlinear dissipative chemical oscillator, coexisting attractors, and chaos control are considered in [22] (also see [23]).

To be more specific, the authors take the model into the following [22]:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -\alpha x-\gamma x^3-\beta +ϵ\left(-\mu (1-x^2-k_{1}xy-k_2{y}^2)y+fcos\left(\omega t\right)\right).\hfill \end{array}\right.$$

(2)

Simulations and oscillation control of a type of chemical oscillator with asymmetry potential are considered in [24]. More precisely, the next new classes of altered oscillators are presented:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -\alpha x-\gamma x^3-\beta +ϵ\left(-\mu y+{\displaystyle \sum _{j=1}^N}{g}_{j}cos\left(j\omega t\right)\right),\hfill \end{array}\right.$$

(3)

where $0\le ϵ<1$, $\mu >0$, $g_i\ge 0,i=1,2,\dots ,N$, and N is an integer.

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -\alpha x-\gamma x^3-\beta +ϵ\left(-{\mu y\left|y\right|}^{p-1}+{\displaystyle \sum _{j=1}^N}{g}_{j}cos\left(j\omega t\right)\right),\hfill \end{array}\right.$$

(4)

where $0\le ϵ<1$, $\mu >0$, $g_i\ge 0,i=1,2,\dots ,N$, N is an integer, and p is the damping exponent.

In [25], By adding a nonlinear quintic term, the authors take into account an extended Duffing–van der Pol oscillator. The system’s dynamical behavior

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -ax-b{x}^3-c{x}^5+ϵ\left(\mu (1-x^2)y+fcos\left(\omega t\right)\right)\hfill \end{array}\right.$$

(5)

is examined by numerical simulations and Melnikov analysis. Understanding the nature of a particular nonlinear system can be aided by the findings.

Refs. [26,27] contain an analysis of the robustness and mechanism for managing chaos using a random phase. The study of parallelism in random dynamical systems and its impact on system behavior are the main topics of the paper [28]. Numerous academics have thoroughly examined this idea for deterministic dynamical systems. In the cited article, the reader can find additional references. For other results, see [29,30,31,32,33,34,35,36].

Ref. [37] examines the analysis of chaotic behavior in the extended Duffing–van der Pol system under additive non-symmetry biharmonical excitation. More precisely, the following differential model is considered:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -c_{1}x-c_2{x}^3-c_3{x}^5-a(b_1-b_2{x}^2)y+fcos(\mathrm{\Omega }t+\mathrm{\Psi })+\hfill \\ \hfill & & +gsin(\omega t+\sigma \xi (t\left)\right),\hfill \end{array}\right.$$

(6)

where $\sigma$ is the intensity of the typical Winner process and $\xi \left(t\right)$ is the process itself.

The study of fifth-order non-smooth modified Duffing–van der Pol oscillators’ chaotic dynamics is important for upcoming studies in contemporary engineering applications.

The homoclinic and heteroclinic bifurcations in the nonlinear dynamics of models (5) and (6) can be considered in the light of the methodology proposed in the excellent article by Lenci, Menditto, and Tarantino [38].

In the cited article, the reader can find additional references on the topic under discussion.

In [39], the chaotic dynamics of an extended Duffing–van der Pol system of the following sort is examined by the authors:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -ax-b{x}^3-c{x}^5+ϵ\left(\mu (1-x^2)y+fxcos\left(\omega t\right)-dg\left(x\right)\right),\hfill \end{array}\right.$$

(7)

where $a>0,b<0,c>0$ and the excitation amplitude, damping coefficient, excitation frequency, and disturbance amplitude are $f>0,\mu >0,\omega >0,d>0$, respectively.

In (7), $g\left(x\right)$ is considered as a periodic function of x that is not smooth with period $2l$.

Specifically, the differential model that follows has been suggested [39]:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -ax-b{x}^3-c{x}^5+ϵ\left(\mu (1-x^2)y+fxcos\left(\omega t\right)\right.\hfill \\ \hfill & & \left.{\displaystyle -\frac{2d}{\pi }\left({\displaystyle 1-2{\displaystyle \sum _{k=1}^{\infty }}\frac{cos\left(2kx\right)}{4k^2-1}}\right)}\right).\hfill \end{array}\right.$$

(8)

We intend to add new components to the dynamics of this differential system in order to broaden its theoretical foundation. Studies are examined in the context of Melnikov’s methodology [40]. A number of simulations are created. Possible control over oscillations: approximation with restrictions is also discussed. Additionally, we present a few specific modules for examining the dynamics of the hypothetical oscillator under consideration. The obtained results can be included into a much broader scientific computing application; see [41] for additional information.

2. The New Model

We examine a novel class of hypothetical oscillators of the following kind:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -ax-b{x}^3-c{x}^5+ϵ(\mu (1-x^2-m_{1}xy-k_1{y}^2)y+\hfill \\ \hfill & & +x{\displaystyle \sum _{i=1}^N}{g}_{i}cos\left(i\omega t\right)),\hfill \end{array}\right.$$

(9)

where $a>0$, $b<0$, $0\le ϵ<1$, $\mu >0$, $m_1>0$, $k_1>0$, $\omega >0$, $g_i\ge 0,i=1,2,\dots ,N$ (N is an integer), and c is chosen such that $b^2-4ac>0$.

We will note that the physical significance of the above-mentioned restrictive condition in terms of the coefficients of the unperturbed oscillator indicates the periodicity of the unperturbed differential system.

Let

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& f_1(x,y)+ϵg_1(x,y,t)\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& f_2(x,y)+ϵg_2(x,y,t)\hfill \end{array}\right.$$

and ${\mathrm{\Gamma }}_0\left(t\right)=(x_0\left(t\right),y_0\left(t\right))$ be one of the homoclinic orbits. The Melnikov function corresponding to the system is of the form

$$M\left(t_0\right)={\displaystyle {\int }_{-\infty }^{\infty }}{e}^{-\int \nabla .f\left({\mathrm{\Gamma }}_0\left(s\right)\right)\mathrm{d}s}.f({\mathrm{\Gamma }}_0\left(t\right)\wedge g({\mathrm{\Gamma }}_0\left(t\right),t+t_0)\mathrm{d}t.$$

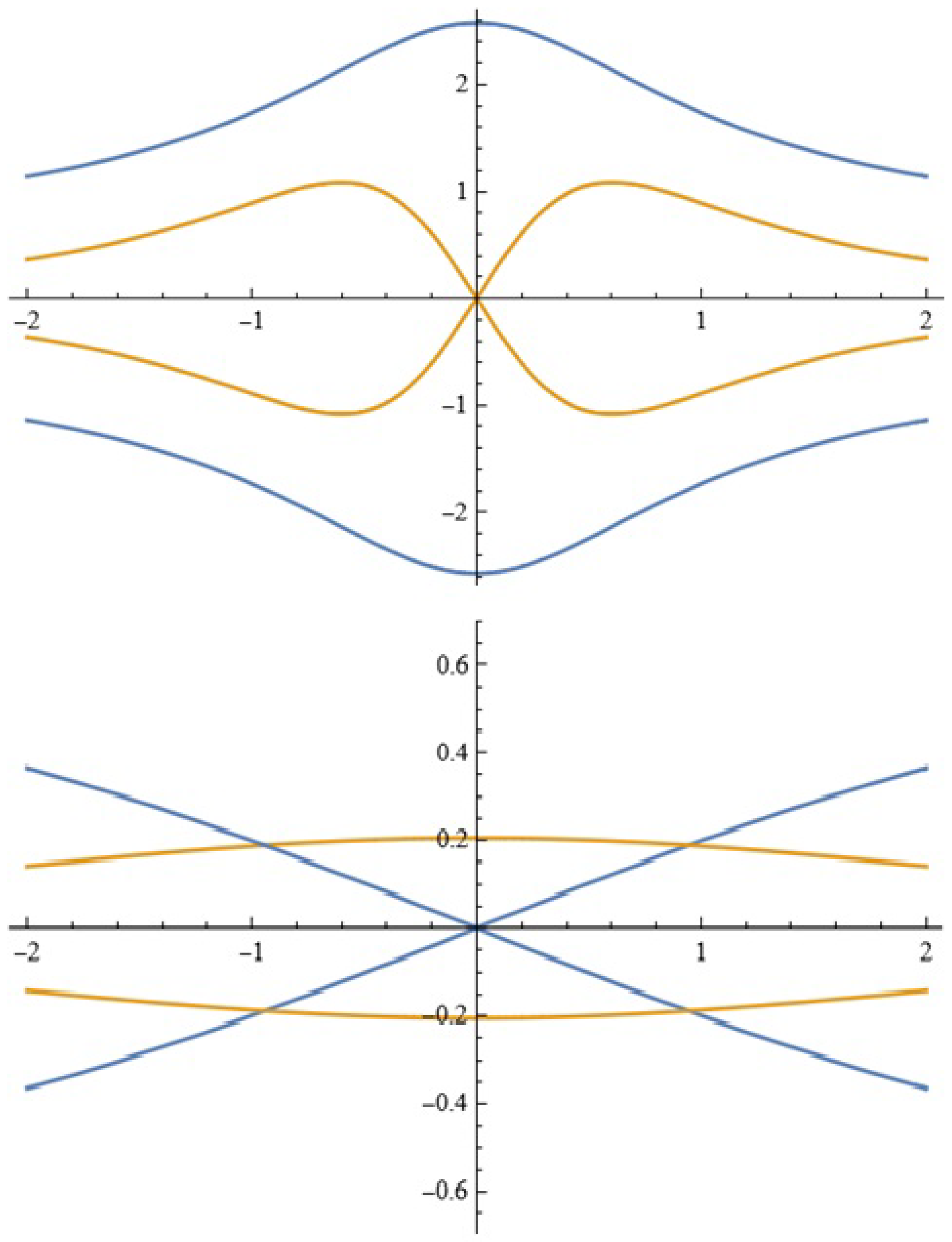
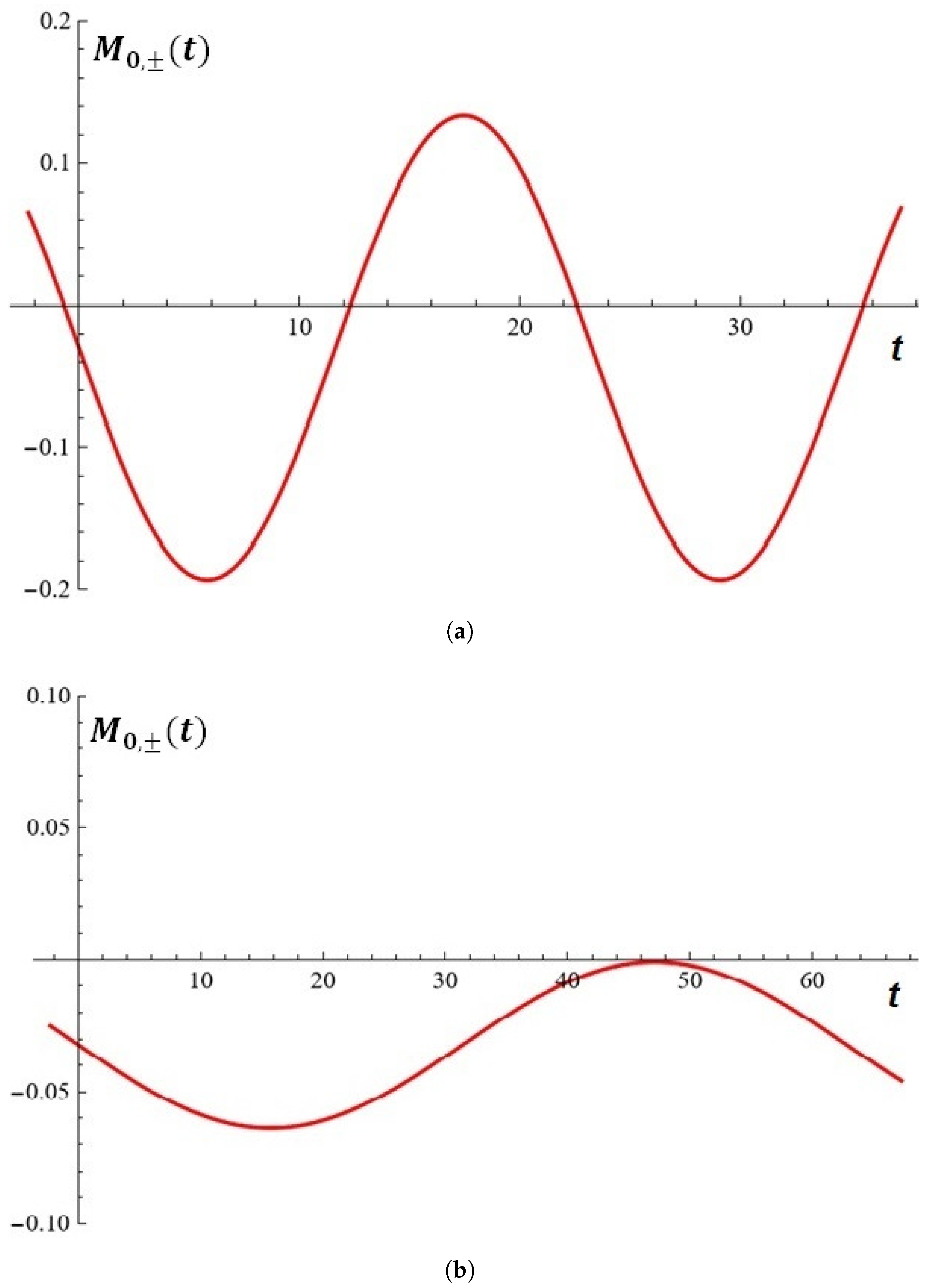
Considerations in the Light of Melnikov’s Approach

There are five equilibrium points for the model (9), defined as $(0,0);(\pm x_1,0);(\pm x_2,0)$, where

$$x_1=\sqrt{{\displaystyle \frac{-b-\sqrt{\mathrm{\Delta }}}{2c}}},x_2=\sqrt{{\displaystyle \frac{-b+\sqrt{\mathrm{\Delta }}}{2c}}},\mathrm{\Delta }=b^2-4ac>0.$$

The homoclinic and heteroclinic orbits connecting saddles $(\pm x_1,0)$ are as follows (see for example [38,39]):

$$\left\{\begin{array}{c}{x}_{0,\pm }\left(t\right)=\pm {\displaystyle \frac{\sqrt{2}{x}_{1}cosh\left(\frac{\gamma }{2}t\right)}{\sqrt{\beta +cosh\left(\gamma t\right)}}}\hfill \\ y_{0,\pm }\left(t\right)=\pm {\displaystyle \frac{\sqrt{2}{x}_1(\beta -1)\gamma sinh\left(\frac{\gamma }{2}t\right)}{2{(\beta +cosh\left(\gamma t\right))}^{\frac{3}{2}}}},\hfill \end{array}\right.$$

$$\left\{\begin{array}{c}{x}_{1,\pm }\left(t\right)=\pm {\displaystyle \frac{\sqrt{2}{x}_{1}sinh\left(\frac{\gamma }{2}t\right)}{{(-\beta +cosh\left(\gamma t\right))}^{\frac{1}{2}}}}\hfill \\ y_{1,\pm }\left(t\right)=\pm {\displaystyle \frac{\sqrt{2}{x}_1(1-\beta )\gamma cosh\left(\frac{\gamma }{2}t\right)}{2{(-\beta +cosh\left(\gamma t\right))}^{\frac{3}{2}}}},\hfill \end{array}\right.$$

where

$$\gamma =x_1^2\sqrt{2c({\theta }^2-1)};\beta ={\displaystyle \frac{5-3{\theta }^2}{3{\theta }^2-1}};\theta ={\displaystyle \frac{x_2}{x_1}}.$$

The homoclinic orbit for $a=0.2;b=-0.5;c=0.1$ is depicted in Figure 1.

When $ϵ\ne 0$, the Melnikov function provides a measure of the leading order distance between the stable and unstable manifolds, which may be used to determine the transverse intersection of the stable and unstable manifolds.

The integral of Melnikov by definition along the homoclinic orbit corresponding to the new model (9) is given by

$$\begin{array}{ccc}{M}_{0,\pm }\left(t_0\right)\hfill & =& {\displaystyle {\int }_{-\infty }^{\infty }}{y}_{0,\pm }\left(t\right)(\mu y_{0,\pm }\left(t\right)-\mu x_{0,\pm }^2\left(t\right)y_{0,\pm }\left(t\right)-\mu m_1{x}_{0,\pm }\left(t\right)y_{0,\pm }^2\left(t\right)-\hfill \\ \hfill & & \mu k_1{y}_{0,\pm }^3\left(t\right)+x_{0,\pm }\left(t\right){\displaystyle \sum _{i=1}^N}{g}_{i}cos\left(i\omega (t+t_0)\right))\mathrm{d}t.\hfill \end{array}$$

(10)

The task of determining the root of $M_{0,\pm }\left(t_0\right)$ is more intriguing from a numerical perspective because the parameters that appear in the suggested differential model are subject to several practical and physical constraints.

It is known that if $M_{0,\pm }\left(t_0\right)=0$ and ${\displaystyle \frac{\mathrm{d}{M}_{0,\pm }\left(t_0\right)}{\mathrm{d}{t}_0}}\ne 0$ for some $t_0$ and some sets of parameters (transversal junction conditions), then a homoclinic bifurcation takes place, indicating the potential for chaotic behavior.

For the Melnikov function $M_{0,\pm }\left(t_0\right)$, in the specific situation $N=1$, we have

$$M_{0,\pm }\left(t_0\right)=\mu \left(I_1-I_2-m_1{I}_3-k_1{I}_4\right)-g_{1}sin\left(\omega t_0\right)I_5,$$

(11)

where

$$I_1={\displaystyle {\int }_{-\infty }^{\infty }}{y}_{0,\pm }^2\left(t\right)\mathrm{d}t,$$

$$I_2={\displaystyle {\int }_{-\infty }^{\infty }}{x}_{0,\pm }^2\left(t\right)y_{0,\pm }^2\left(t\right)\mathrm{d}t,$$

$$I_3={\displaystyle {\int }_{-\infty }^{\infty }}{x}_{0,\pm }\left(t\right)y_{0,\pm }^3\left(t\right)\mathrm{d}t,$$

$$I_4={\displaystyle {\int }_{-\infty }^{\infty }}{y}_{0,\pm }^4\left(t\right)\mathrm{d}t,$$

$$I_5={\displaystyle {\int }_{-\infty }^{\infty }}{x}_{0,\pm }\left(t\right)y_{0,\pm }\left(t\right)sin\left(\omega t\right)\mathrm{d}t.$$

Proposition 1. 

If $N=1$, then the roots of the Melnikov function $M_{0,\pm }\left(t_0\right)$ are given as solutions of the equation $M_{0,\pm }\left(t_0\right)=0$ (see Figure 2).

Remark 1. 

In formulating and proving Proposition 1, we used a significantly specialized module for investigating the dynamics of the considered hypothetical oscillator, implemented in the computer algebraic system for scientific calculations—CAS Mathematica.

Remark 2. 

From Proposition 1, we obtain the condition that the Melnikov function $M_{0,\pm }\left(t_0\right)$ has simple zeros and chaos occurs as follows:

$$\left|{\displaystyle \frac{\mu (I_1-I_2-m_1{I}_3-k_1{I}_4)}{g_1{I}_5}}\right|<1.$$

We leave the detailed study of this criterion (as a function of the parameters of our model (9)) to the reader. Below, we will consider some typical examples.

Remark 3. 

Chaotic features on system parameters for heteroclinic orbit, and also the Melnikov functions and parameter conditions for these orbits, are investigated in a similar way and will be omitted here. It is enough for the reader to strictly follow the research plan proposed for such oscillators in the excellent article in [39].

Example 1. 

For $N=1$, $a=0.37$, $b=-0.5$, $c=0.16$, $\mu =0.5$, $k_1=0.9$, $m_1=0$, $\omega =0.27$, $g_1=0.25$, the Melnikov function is depicted in Figure 3a.

Example 2. 

For $N=1$, $a=0.37$, $b=-0.5$, $c=0.16$, $\mu =0.71$, $k_1=0.06$, $m_1=0$, $\omega =0.1$, $g_1=0.1$, the Melnikov function is depicted in Figure 3b.

Some notes:

• Melnikov’s criterion for the occurrence of the intersection between the disturbed and unperturbed separatrices for a fixed N can be formulated by the reader. In this case, the explicit representation of $M_{0,\pm }\left(t_0\right)$ (moreover, for high values of the parameter N) is laborious. In order to employ specialized modules provided in current computer algebraic systems for scientific study, the user should first conduct a series of preparatory operations on the integrals $I_j$ as previously stated.
• Prior to that, while calculating the integral (8), it is convenient to adopt the following representation: $cos\left(i\omega (t+t_0)\right)=cos\left(i\omega t\right)cos\left(i\omega t_0\right)-sin\left(i\omega t\right)sin\left(i\omega t_0\right)$.

Some extended differential models are examined in the context of Melnikov’s method (see [42,43,44,45,46,47]). Refs. [48,49,50,51] contain numerical techniques for resolving nonlinear equations.

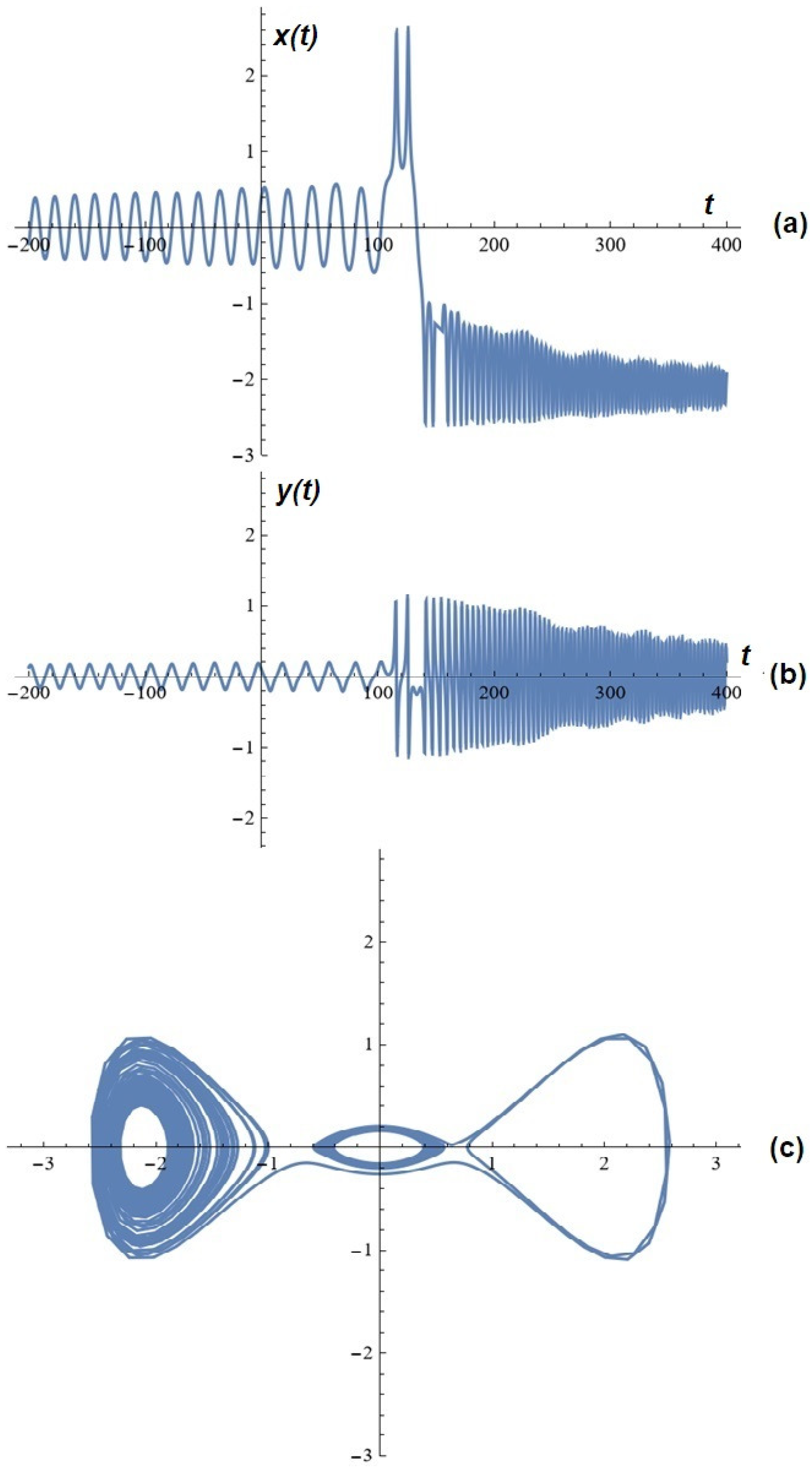
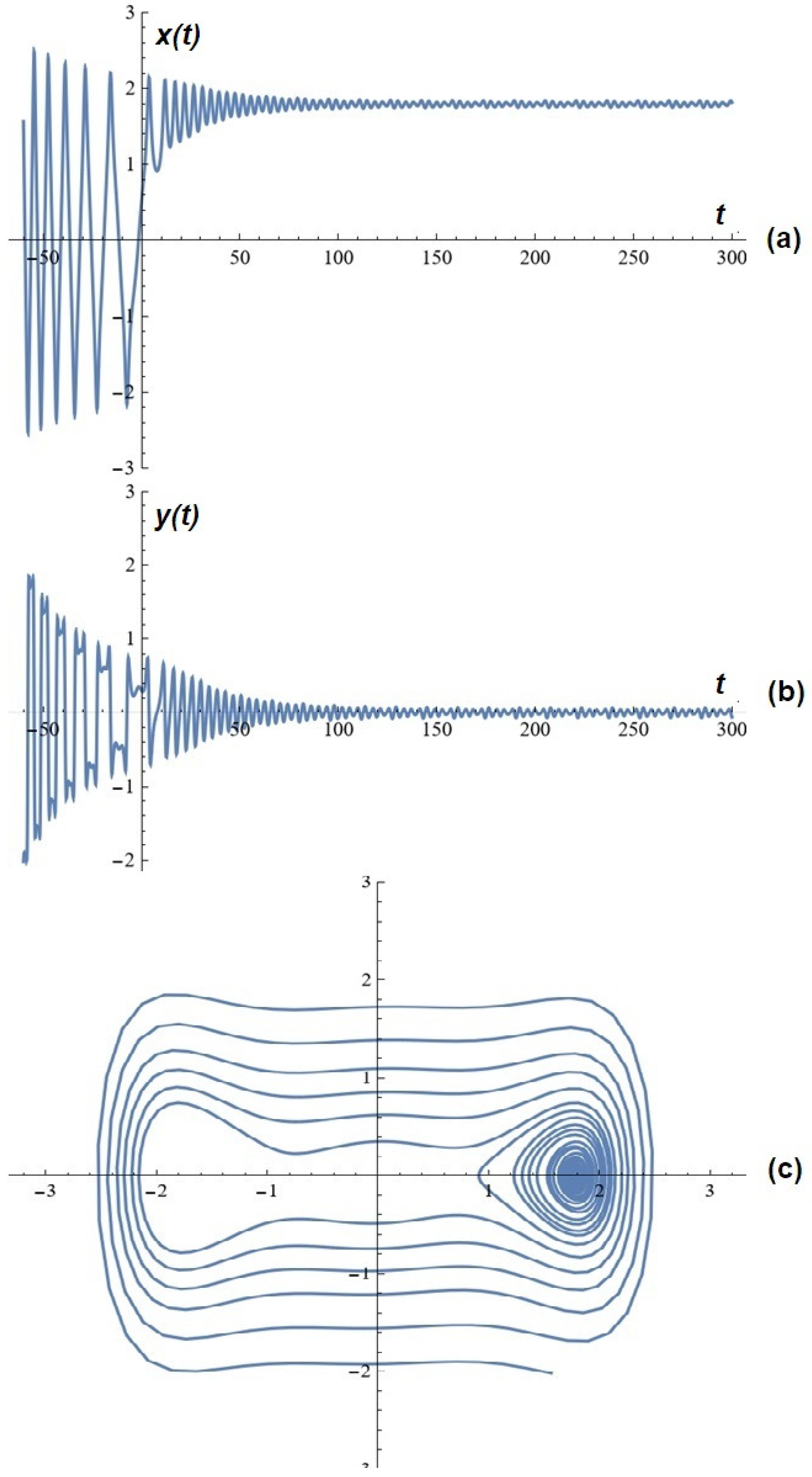
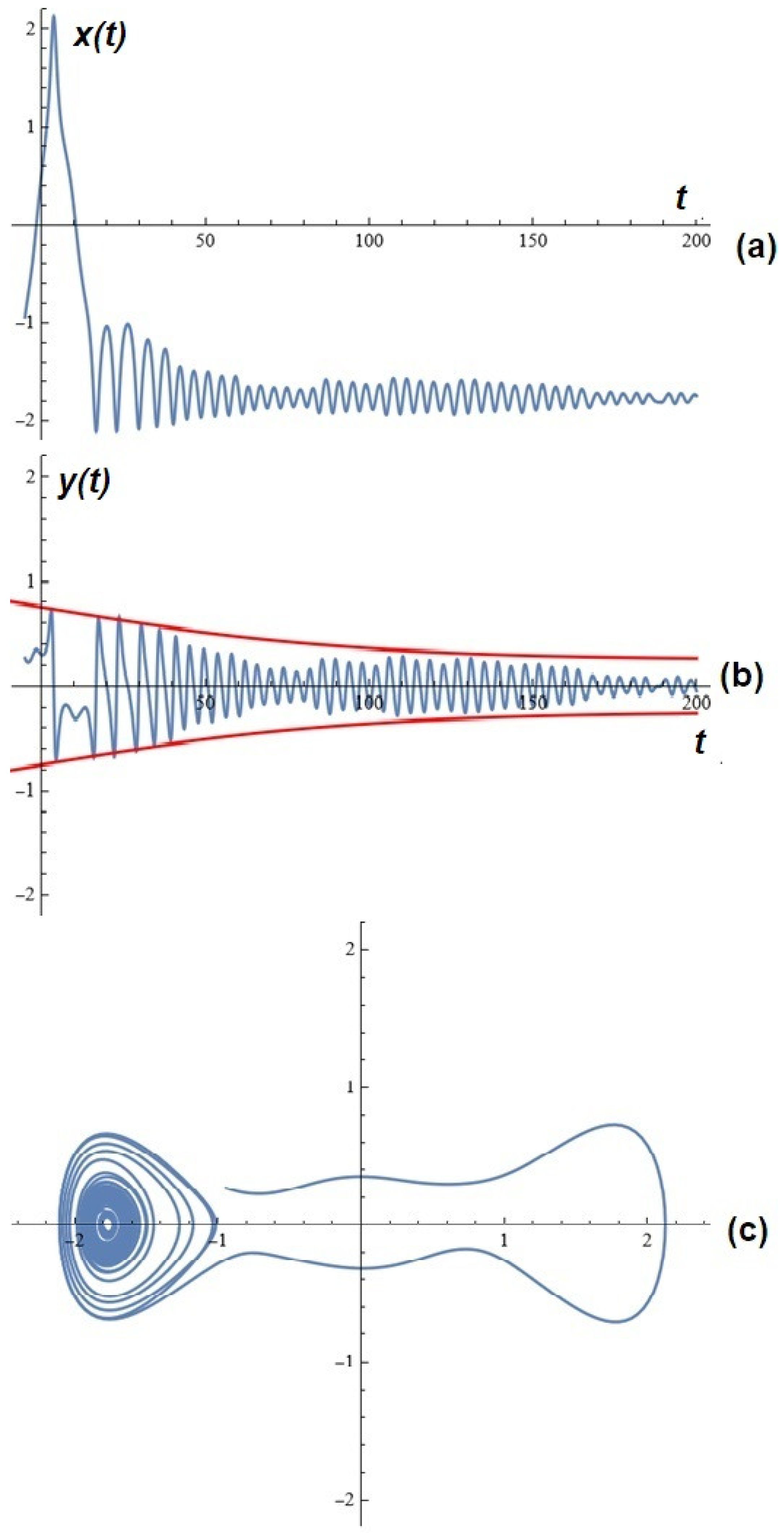
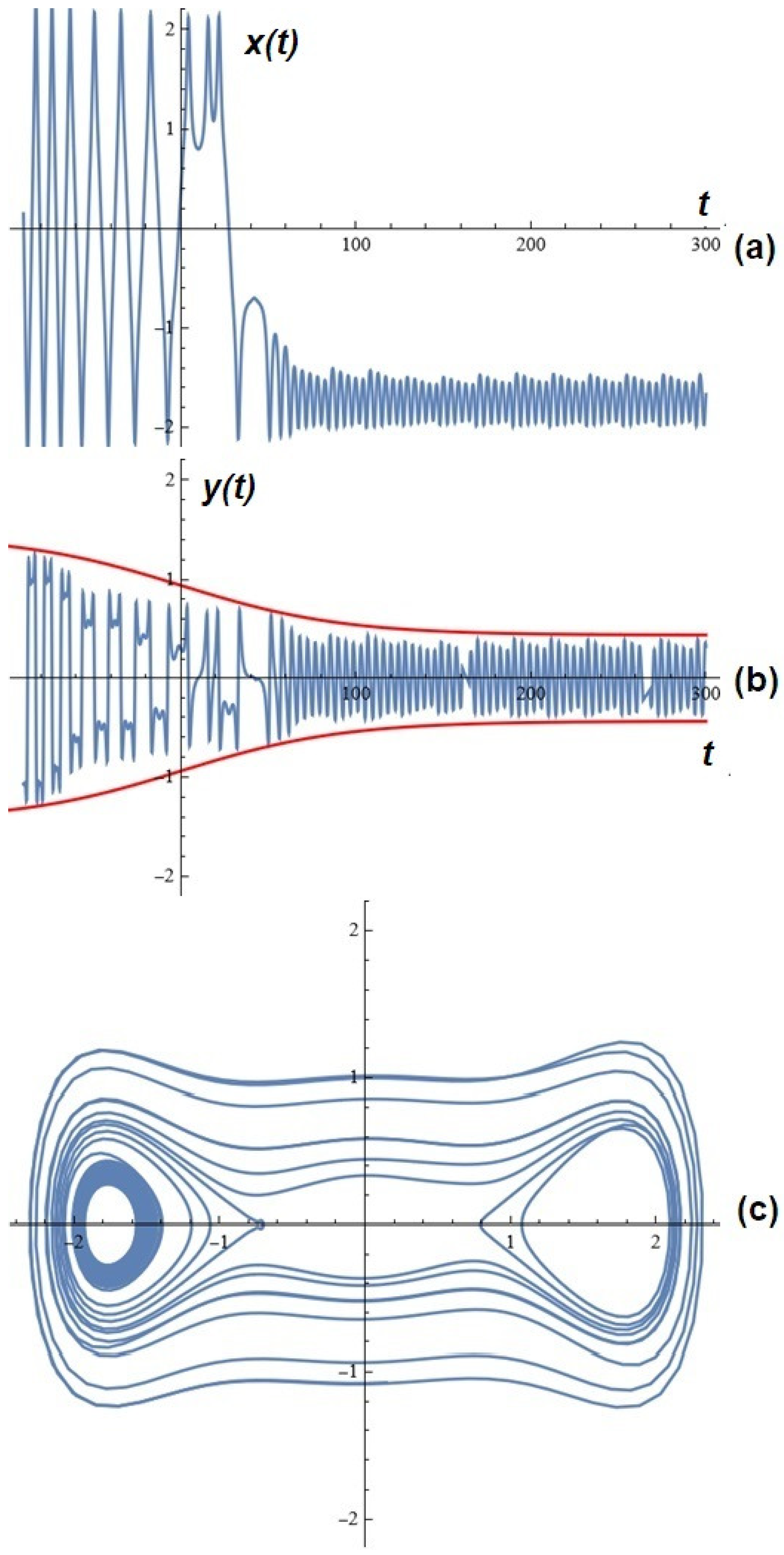
3. A Few Simulations

Here, we will focus on some interesting simulations:

Example 3. 

For given $N=4$, $a=0.2$, $b=-0.5$, $c=0.1$, $\mu =0.2$, $k_1=0.1$, $m_1=0.1$, $\omega =0.4$, $g_1=0.9$, $g_2=0.1$, $g_3=0.3$, $g_4=0.7$, and $ϵ=0.015$, the system’s simulations (9) for $x_0=0.4$ and $y_0=0.1$ are depicted in Figure 4.

Example 4. 

For given $N=6$, $a=0.25$, $b=-0.56$, $c=0.15$, $\mu =3$, $k_1=0.1$, $m_1=0.09$, $\omega =0.4$, $g_1=0.9$, $g_2=0.1$, $g_3=0.3$, $g_4=0.2$, $g_5=0.4$, and $g_6=0.8ϵ=0.015$, the system’s simulations (9) for $x_0=0.5$ and $y_0=0.3$ are depicted in Figure 5.

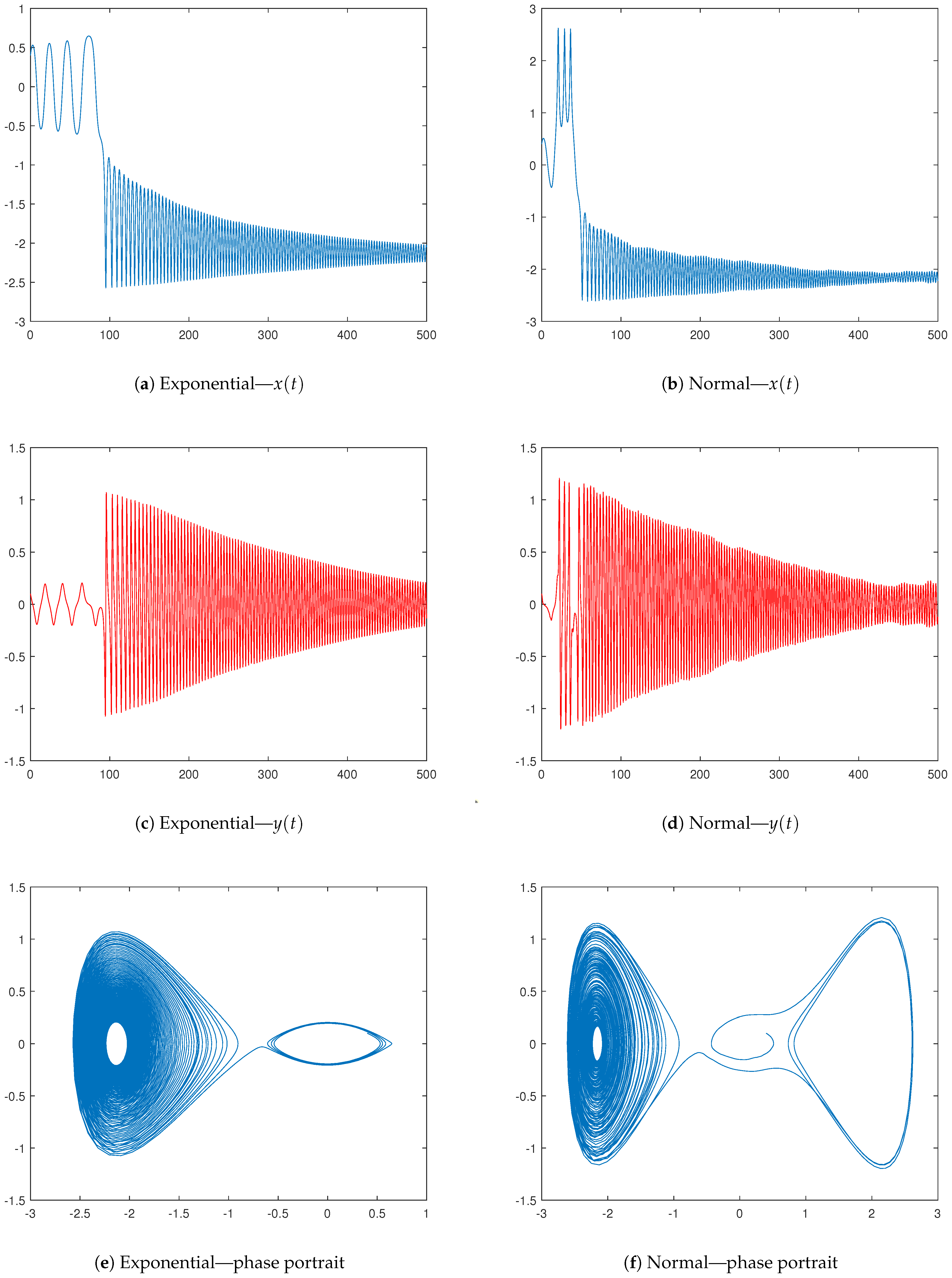
4. Potential Control over Oscillations

A user-preset level (or fork) for the oscillations of the y component of the differential system solution is one of the several free parameters that make the new model (9) appealing for engineering computations.

Assume that the fork or constraint $\left(F\right(t),-F(t\left)\right)$ is of the following type (most typical restriction):

$$F\left(t\right)=a_1+{\displaystyle \frac{a_2}{1+e^{a_{3}t}}}.$$

(12)

To be thorough, we will look at another simulation using the differential model (9) that was previously suggested.

Example 5. 

For given $N=8$, $a=0.256$, $b=-0.567$, $c=0.1545$, $\mu =1.8$, $k_1=0.12$, $m_1=0.078$, $\omega =0.3$, $g_1=0.9$, $g_2=\dots =g_7=0.851$, $g_8=0.9$, and $ϵ=0.01$, the system’s simulations (9) for $x_0=0.5$ and $y_0=0.3$ are depicted in Figure 6.

Using the exponential-type function $F\left(t\right)$ and user-fixed $N=8$

$$F\left(t\right)=-0.25-{\displaystyle \frac{1.01}{1+{\displaystyle e^{0.0211t}}}}$$

for the parameters specified in Example 5 (see Figure 6b), the desired control over oscillations is obtained.

Example 6. 

For given $N=10$, $a=0.256$, $b=-0.567$, $c=0.1545$, $\mu =1.8$, $k_1=0.12$, $m_1=0.078$, $\omega =0.3$, $g_1=0.9$, $g_2=\dots =g_7=0.85$, $g_8=0.9$, $g_9=0.4$, $g_{10}=0.1$, and $ϵ=0.01$, the system’s simulations (9) for $x_0=0.4$ and $y_0=0.3$ are depicted in Figure 7.

With $N=10$ set by the user and the function $F\left(t\right)$ of the kind

$$F\left(t\right)=-0.44-{\displaystyle \frac{0.995}{1+{\displaystyle e^{0.02181t}}}}$$

for the parameters specified in Example 6 (see Figure 7b), the desired control over oscillations is obtained.

Remark 4. 

Depending on the oscillator profile, other approximations may be used, for example, $F\left(t\right)$ may be of the exponential, log-logistic, hyper-log-logistic, piecewise smooth sigmoid, Gompertz, or activation type.

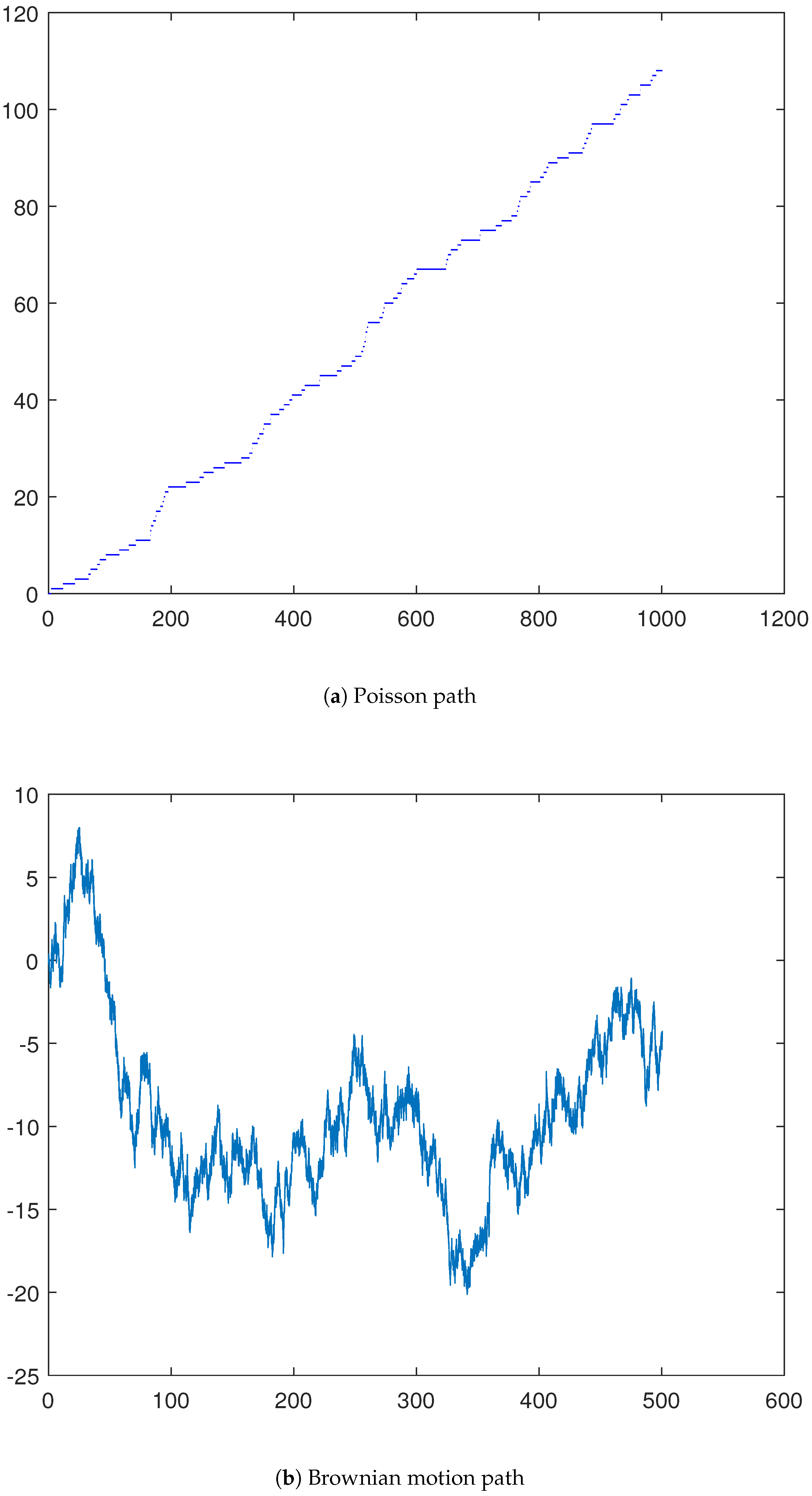
Some Probabilistic Constructions

Suppose that ${\sum }_{j=1}^N{g}_j=1$—this restriction is not essential since we may achieve it after scaling. The probabilities of a random variable $\xi$ specified on the domain $\left\{1,2,\dots ,N\right\}$ can therefore be viewed as the coefficient $g_j$. Let $\mathrm{\Psi }\left(·\right)$ be its characteristic function. Keeping in mind the exponential presentation of the cos function

$$cos\left(x\right)={\displaystyle \frac{e^{ix}+e^{-ix}}{2}},$$

(13)

we transform model (9) into

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}& =-ax-b{x}^3-c{x}^5+ϵ\left(\begin{array}{c}\mu \left(1-x^2-m_{1}xy-k_1{y}^2\right)y\hfill \\ +x{\displaystyle \sum _{j=1}^N}{g}_j{\displaystyle \frac{e^{ij\omega t}+e^{-ij\omega t}}{2}}\hfill \end{array}\right)\hfill \\ \hfill & =-ax-b{x}^3-c{x}^5+ϵ\left(\begin{array}{c}\mu \left(1-x^2-m_{1}xy-k_1{y}^2\right)y\hfill \\ +x{\displaystyle \frac{\mathbb{E}\left[e^{i\omega t\xi }\right]+\mathbb{E}\left[e^{-i\omega t\xi }\right]}{2}}\hfill \end{array}\right)\hfill \\ \hfill & =-ax-b{x}^3-c{x}^5+ϵ\left(\begin{array}{c}\mu \left(1-x^2-m_{1}xy-k_1{y}^2\right)y\hfill \\ +x{\displaystyle \frac{\mathrm{\Psi }\left(\omega t\right)+\mathrm{\Psi }\left(-\omega t\right)}{2}}\hfill \end{array}\right).\hfill \end{array}$$

(14)

We can conclude that the condition $\xi$ to be distributed on the domain $\left\{1,2,\dots ,N\right\}$ is not essential. If we generalize it to the set D, then we can rewrite the dynamics (9) as

$${\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}=-ax-b{x}^3-c{x}^5+ϵ\left(\begin{array}{c}\mu \left(1-x^2-m_{1}xy-k_1{y}^2\right)y\hfill \\ +x\underset{D}{\int }cos\left(u\omega t\right)g\left(du\right)\hfill \end{array}\right).$$

(15)

Note that the probabilities $g_j$ are generalized to the measure $g\left(du\right)$.

We prepare some simulations based on the $\left(q,\sigma \right)$-normal distribution and on the exponential one, whose intensity is denoted by $\lambda$. Their probability densities are

$$\begin{array}{cc}\hfill f_{Gaussian}\left(x\right)& ={\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}{e}^{-{\displaystyle \frac{{\left(x-q\right)}^2}{2{\sigma }^2}}},\hfill \\ \hfill f_{exponential}\left(x\right)& =\lambda e^{-\lambda x}.\hfill \end{array}$$

(16)

The domains are $D=\mathbb{R}$ and $D={\mathbb{R}}^{+}$, respectively. The characteristic functions

$$\begin{array}{cc}\hfill {\mathrm{\Psi }}_{Gaussian}\left(x\right)& =e^{iqx-{\displaystyle \frac{{\sigma }^2{x}^2}{2}}},\hfill \\ \hfill {\mathrm{\Psi }}_{exponential}\left(x\right)& ={\displaystyle \frac{\lambda }{\lambda -ix}}.\hfill \end{array}$$

(17)

Keeping in mind the following relations for the characteristic functions

$$\begin{array}{cc}\hfill & {\mathrm{\Psi }}_{Gaussian}\left(x\right)+{\mathrm{\Psi }}_{Gaussian}\left(-x\right)=2e^{-{\displaystyle \frac{{\sigma }^2{x}^2}{2}}}cos\left(qx\right),\hfill \\ \hfill & {\mathrm{\Psi }}_{exponential}\left(x\right)+{\mathrm{\Psi }}_{exponential}\left(-x\right)=2{\displaystyle \frac{{\lambda }^2}{{\lambda }^2+x^2}},\hfill \end{array}$$

(18)

we transform the dynamics (14) into

$${\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}=-ax-b{x}^3-c{x}^5+ϵ\left(\begin{array}{c}\mu \left(1-x^2-m_{1}xy-k_1{y}^2\right)y\hfill \\ +x{e}^{-{\displaystyle \frac{{\sigma }^2{\omega }^2{t}^2}{2}}}cos\left(q\omega t\right)\hfill \end{array}\right)$$

(19)

for the Gaussian simulation. Let us discuss the effect of the parameters on the model. The expectation q has a scaling role in the periodic function and thus it does not lead to a significant generalization. However, this is not the case for $\sigma$. First, for small time values, $\sigma$ has a more significant impact. When sigma is near zero, the exponent is near one and thus the model is similar to the original formulation with one periodic function. On the other hand, when $\sigma$ tends to infinity, then the exponent vanishes and thus the impact of the periodic function is negligible. The same conclusions can be deduced for the larger values of t but for closer to zero (infinity) values of $\sigma$—at larger t, extreme values of $\sigma$ are necessary to capture the desired behavior.

We have the following for the exponential distribution:

$${\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}=-ax-b{x}^3-c{x}^5+ϵ\left(\begin{array}{c}\mu \left(1-x^2-m_{1}xy-k_1{y}^2\right)y\hfill \\ +x{\displaystyle \frac{{\lambda }^2}{{\lambda }^2+{\omega }^2{t}^2}}\hfill \end{array}\right).$$

(20)

We can see that the exponential distribution introduces a damping x-term in the model reciprocal to the square of the time. The intensity $\lambda$ can be viewed as a scaling parameter—as the larger $\lambda$ is, the larger t has to be. Furthermore, this dependence is linear. We present the x- and y-dynamics as well as the phase portraits in Figure 8. The first column is for the normal distribution ($q=1,\sigma =1$), whereas the exponential simulations with intensity $\lambda =1$ are presented in the second column. For the rest of the parameters, we chose Example 3.

5. Concluding Remarks and Further Work

In this research, we have examined a novel hypothetical differential model that has a large number of free parameters, which makes it appealing to users. To examine the behavior of these oscillators, we present a several specialized modules.

For some of them, a cloud version is available that just requires a browser and an internet connection.

This will be an essential component of a much broader Web-based program for scientific computing that is in the works.

We have tried, as far as possible, to comply with the proposed standard for the publication of new chaotic systems [52].

We envisage future research on the topic—the modeling of chaotic systems with a desired set of properties [53,54].

Last but not least, we provide some simulations based on the idea of [37] to introduce a stochastic element in the dynamical model. We suggest two methods. The first one is inspired by [37]—thus, the dynamics (14) turn into

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}& =-ax-b{x}^3-c{x}^5+ϵ\left(\begin{array}{c}\mu \left(1-x^2-m_{1}xy-k_1{y}^2\right)y\hfill \\ +x{\displaystyle \frac{\mathrm{\Psi }\left(\omega t+N_t\right)+\mathrm{\Psi }\left(-\omega t-N_t\right)}{2}}\hfill \end{array}\right).\hfill \end{array}$$

(21)

We assume that $N_t$ is a homogenous Poisson process. We present in the first column of Figure 9 the related simulations when we consider the exponential modification from Section Some Probabilistic Constructions. The intensity of the Poisson process is assumed to be $\delta =10$. Alternatively, in the second column we present the results for the following dynamics:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}& =-ax-b{x}^3-c{x}^5+ϵ\left(\begin{array}{c}\mu \left(1-x^2-m_{1}xy-k_1{y}^2\right)y\hfill \\ +x{\displaystyle \frac{\mathrm{\Psi }\left(\omega t\right)+\mathrm{\Psi }\left(-\omega t\right)}{2}}+B_t\hfill \end{array}\right),\hfill \end{array}$$

(22)

where $B_t$ is a standard Brownian motion. We apply the Gaussian example from Section Some Probabilistic Constructions. The generated sample paths of the Poisson process and the Brownian motion can be viewed in Figure 10.

The analysis of models (21) and (22) is left for further work.

Analytical estimates of the effect of an amplitude-modulated (AM) signal in nonlinearly damped Duffing–van der Pol oscillators are considered in [55]. More precisely, the authors presented the following model:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& ax-b{x}^3+ϵ(-\gamma (1-x^2)y{\left|y\right|}^{p-1}+\hfill \\ & & +(f+2gcos(\mathrm{\Omega }t\left)\right)sin\left(\omega t\right)),\hfill \end{array}\right.$$

where $2g$ is the degree of modulation, and $\mathrm{\Omega }$ and $\omega$ are the frequencies of the amplitude-modulated (AM) signal.

We plan to expand the theoretical basis of this differential system in a future paper by adding new factors to its dynamics:

$$\left\{\begin{array}{ccc}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}\hfill & =& y\hfill \\ {\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\hfill & =& -ax-b{x}^3-c{x}^5+ϵ(-\gamma (1-x^2)y{\left|y\right|}^{p-1}+\hfill \\ & & +(f+2gcos\left(\mathrm{\Omega }t\right)){\displaystyle \sum _{i=1}^N}{g}_{i}sin\left(i\omega t\right)).\hfill \end{array}\right.$$

Such an interpretation would allow for a detailed study of the dynamics of similar models at a higher energy level. The stochastic analysis of the mentioned model is also left for further work.

The reader may find other results on the topics—chaotic transitions in stochastic dynamical systems and the application of Melnikov processes in engineering, physics, and neuroscience in the book in [56].

Over the past few years, intensive work has been carried out on the important topic of estimating rate-induced tipping via asymptotic series and a Melnikov-like method.

So, for example, in [57], the authors show that a Melnikov-inspired method employing the asymptotic series allows the tipping point to be asymptotically approximated.

Investigations on bifurcation and rate-induced tipping can be found in [58]. For other basic results, see [59,60].

We envisage research in the light of the results obtained in the above-cited articles on new differential models, which are modifications of the models described in the present article.

Examples 5 and 6 considered in Section 4 are study examples. The real task that we set for the students is as follows: For fixed N, $ϵ$, and $x_0$, $y_0$, generate an appropriate simulation of model (9), if the additional user constraint is set, the oscillations on the y- component of the system solutions fall into the fork $(-F(t),F(t\left)\right)$.

After using the specialized module provided by us (with additional approximation and optimization algorithms included) implemented in CAS Mathematica, the students relatively easily arrive at the answer to the task, namely determining all the remaining parameters of the model.

Our problems to be solved are about making the use of modern GPT technologies harder (or even impossible), as they are massively used by students for the realization of their scientific tasks.

We will be glad if this article provokes an interesting discussion about the teaching methodology in this field of scientific knowledge.