Abstract
This paper develops a novel probabilistic theory of belief formation in social networks, departing from classical opinion dynamics models in both interpretation and structure. Rather than treating agent states as abstract scalar opinions, we model them as belief-adoption probabilities with clear decision-theoretic meaning. Our approach replaces iterative update rules with a fixed-point formulation that reflects rapid local convergence within social neighborhoods, followed by slower global diffusion. We derive a matrix logistic equation describing uncorrelated belief propagation and analyze its solutions in terms of mean learning time (MLT), enabling us to distinguish between fast local consensus and structurally delayed global agreement. In contrast to memory-driven models, where convergence is slow and unbounded, uncorrelated influence produces finite, quantifiable belief shifts. Our results yield closed-form theorems on propaganda efficiency, saturation depth in hierarchical trees, and structural limits of ideological manipulation. By combining probabilistic semantics, nonlinear dynamics, and network topology, this framework provides a rigorous and expressive model for understanding belief diffusion, opinion cascades, and the temporal structure of social conformity under modern influence regimes.
Keywords:
two-timescale theory of consensus; structural limits of propaganda efficiency; bounded vs. divergent learning times; logistic-optimal centrality; autopoietic amplification MSC:
15B51; 15A24; 91D30; 91C20
1. Introduction
Information has been used as a tool of power in human society since the dawn of time. Information, as a power tool, goes hand in hand with disinformation. Plato, in the third book of his Republic, writes that disinformation, provided sparingly by the enlightened authoritarian ruler, can be beneficial for society, much like an unpleasant-tasting medicine can be beneficial for the patient [1], 389b:
…So if anyone is entitled to tell lies, the rulers of the city are. They may do so for the benefit of the city, in response to the actions either of enemies or of citizens. No one else should have anything to do with lying, and for an ordinary citizen to lie to these rulers of ours is … a mistake …
So, in plain words, Plato believed that the rulers, and only the rulers, are allowed to provide the citizens with medicinal lies. Almost 2500 years later, most people in democratic societies would certainly disagree with that assessment. It is not hard to agree that the possession of accurate information is the foundation for a well-functioning society. However, Plato’s description of ‘medicinal lies’ was not just for ruling a country—it was also a tool for forming citizens of the right character. Throughout history, various rulers have tried to shape the society they govern and their citizens’ thinking and behavior to their will.
In order to reach that desired outcome, for almost two and a half millenia since Plato, societies provided their citizens with messages that were designed to shape their populace in a certain way. Some of these messages achieved positive results and improved society, whereas some of these social experiments lead to disastrous outcomes for societies and their citizens. Until very recently, the message was centralized, coming from the very top of the government. The more autocratic the government was, the more uniform the centralized messages tended to be. The nature of technology delivering this message changed with progress, from literature, statues, and even coins in the Roman empire, to the radio and then television in the present day [2]. Still, the essence of the method is the same. A centralized message is presented to the citizens and that message, to large extent, has remained unchanged throughout time, compared to the dynamics of opinion formation in society.
While centralized messaging can be effective, it has its limitations, which stem from the theory of opinion dynamics. The centralized message can be viewed as a member of the community that has infinite obstinacy, whereas other members of the community can change their opinions accordingly. In the modern models of opinion dynamics, utilizing the bounded confidence hypothesis [3,4,5,6], the agents interact and exchange opinions only with other agents that have opinions that are close to their own. If the centralized message deviates from the opinion of the people it tries to influence, that centralized message will have very little to no effect.
That paradigm of the centralized message has changed recently with the advent of social media. The presence of bots on social media platforms such as X (formerly Twitter) and Instagram has been known for a long time [7,8,9]. While some bots are relatively harmless, many are used for propaganda purposes in order to spread a desired message among the community. The advantage of bots versus a centralized message is their efficiency; these bots align with the local opinion and can influence it much more precisely compared to the centralized message. In terms of opinion dynamics theory, such bots can act as an agent that is tuned to be close to a certain group of people and can influence the opinions of the groups that are unreachable by the centralized message [10].
The efficiency of bots can also be understood in terms of alternative models of consensus formation, such as the Friedkin–Johnsen [11] and deGroot models [12]. These models do not pose a restriction on the interaction of agents, as the bounded confidence models do, but the interaction between the agents is much slower if the opinion difference is large. Thus, if the agent spreading the centralized message is far from the opinion of a given group, that group is likely to take a long time to align with the centralized message. In contrast, the bot’s message will be closer to the group’s opinion and thus can influence the opinion of the group faster.
A closely related mechanism in the digital manipulation of public perception is the phenomenon of astroturfing, the artificial simulation of grassroots support or opposition. Astroturfing involves coordinated efforts to create a false impression of widespread public backing or resistance to particular ideas, policies, or products. By leveraging bots, fake accounts, and paid influencers, astroturfing campaigns can distort the perceived popularity of a movement, misleading individuals and policymakers alike. This practice is especially effective in the age of social media, where engagement metrics such as likes, shares, and retweets serve as heuristics for credibility and influence [13,14]. The term astroturfing originated in 1985, when Texas Senator Lloyd Bentsen, referring to a flood of letters sent to him under the guise of public advocacy but actually orchestrated by insurance industry lobbyists, remarked “A fellow from Texas can tell the difference between grass roots and ‘AstroTurf’… this is generated mail.” [15]. Bentsen’s analogy highlighted the artificial nature of such orchestrated campaigns, comparing them to AstroTurf™, a synthetic surface designed to mimic real grass.
The mechanisms underpinning models of social opinion formation and the corresponding efficiency of bots can also relate to the theories of social influence, going beyond bounded confidence models. The “spiral of silence” theory proposed by Noelle-Neumann [16] suggests that individuals, fearing social isolation, are less likely to express dissenting opinions if they perceive their views to be in the minority. In an environment where bot-driven interactions artificially amplify certain viewpoints, real users may misinterpret the distribution of social preferences, leading to a cycle of self-censorship and consensus reinforcement. Similarly, Cialdini’s principle of social proof [17] suggests that people rely on cues from their social environment to guide their behavior and opinions—an effect magnified in online spaces where engagement metrics can be artificially manipulated. Bots artificially inflate the perceived number of people having certain opinions for an individual, and thus force the individual to state their allegiance to certain beliefs. Whether such allegiance is sincere or not is a complex question, and is likely dependent on how far the perceived majority opinion for the individual is from their true beliefs.
The structural dynamics of social influence and consensus formation can be understood through network models. For example, in bounded confidence models, the agents establish connections between them if their opinions are close enough. Clearly, the connections between these individuals are dynamic, i.e., the network is changing from one time step to another. Another way to treat social networks is to have graphs that are static and are independent of the opinion dynamics: these are the interactions due to, for example, family, long-term friendships, and employment. Graph theory provides a powerful framework for analyzing the diffusion of opinions in complex systems, where individuals (nodes) influence one another through their connections (edges), forming clusters of agreement or polarization [18,19,20]. This general representation allows to examine how external interventions—such as bot-driven campaigns—can shift collective attitudes by altering perceived majorities. Studies on online polarization have demonstrated that artificial amplification reinforces ideological segregation, fostering echo chambers that inhibit cross-group dialogue [21,22]. Furthermore, empirical research on information cascades suggests that once a critical mass of perceived consensus is established, individuals may conform to the majority opinion, despite personal skepticism [23,24].
The historical use of graphs to represent social and organizational structures dates back to the 19th century. In 1855, Daniel McCallum, the General Superintendent of the New York and Erie Railroad, developed an organizational diagram (Figure 1) that visually depicted hierarchical authority and communication flows [25]. In terms of our discussion, such a network would be static, where the interactions are forced by the organizational structure of their work. This early attempt to structure administrative complexity laid the groundwork for modern network analysis, illustrating how visual representations of influence and control can elucidate hidden patterns within large systems.
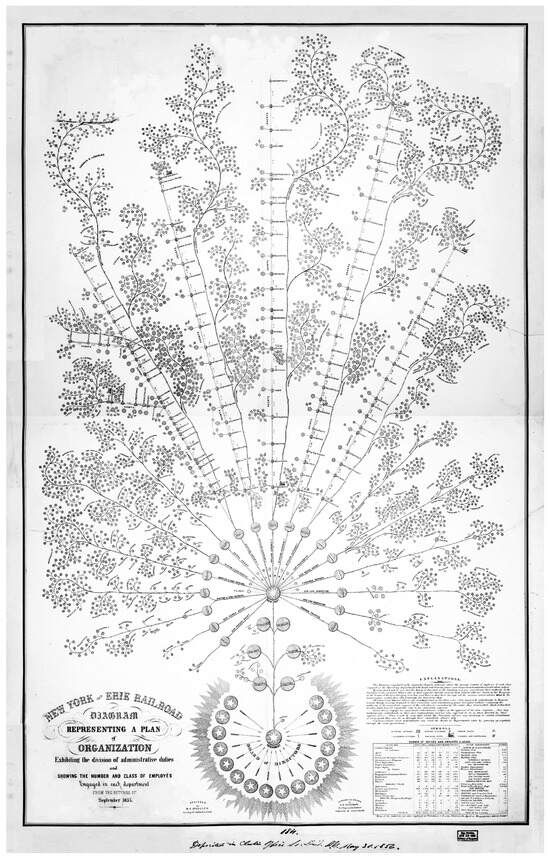
Figure 1.
Organizational diagram of the New York and Erie Railroad, created by D. C. McCallum and G. H. Henshaw in 1855. Retrieved from the Library of Congress (https://www.loc.gov/item/2017586274/, accessed on 1 February 2025).
By analyzing the interplay of algorithmic amplification, artificial engagement, and human psychology, this paper seeks to explore the mechanisms driving opinion shifts in digital environments. Graph-based approaches allow for a systematic examination of social conformity, consensus formation, and influence propagation, providing crucial insights into how disinformation networks can manipulate public perception on a large scale. This phenomenon of disinformation-driven conformity raises important theoretical and practical questions about the relationship between perceived majority opinion and actual individual belief. Why do individuals align so readily with signals of collective support, even when those signals may be artificially engineered? What structural properties of social networks amplify or mitigate these effects? And how does the temporal structure of belief formation—fast local convergence versus slow global consensus—affect the resilience or vulnerability of populations to manipulation?
Our paper develops a comprehensive theoretical framework to explore how structural and temporal factors influence consensus formation and belief propagation in networked societies, emphasizing correlated and uncorrelated social influence. While classical opinion dynamics models typically treat the agent state as an abstract scalar “opinion” lacking clear semantics, our approach adopts a distinctly probabilistic interpretation. Here, explicitly represents the probability of belief adoption or the agent’s readiness for action, embedding a rigorous Bayesian or decision-theoretic meaning into social influence modeling. Although we describe equilibrium beliefs through a static fixed-point equation, the variable t refers to discrete or continuous cycles of external interventions (such as media influence rounds), each sufficiently spaced in time to ensure that local probabilities equilibrate almost instantaneously compared to the scale of these cycles. Thus, our use of t marks successive cycles of global information exposure rather than the short internal equilibration time within local social groups, clearly distinguishing between rapid local consensus formation and slower global belief dynamics.
Furthermore, whereas standard frameworks describe iterative processes converging gradually to equilibrium, we formulate our model (4) as a static fixed-point equation. This explicitly captures instantaneous local consensus formation, modeling equilibrium states reached rapidly within social neighborhoods after each cycle of external influence. Consequently, our approach emphasizes the separation of two distinct timescales: fast local adaptation within immediate social circles and slower global diffusion of beliefs across the broader network, a crucial distinction often absent in standard homogeneous models.
We introduce a novel nonlinear continuous-time formulation, referred to as the matrix logistic differential equation, derived as the limiting case of frequent but independent interventions. The equation is termed matrix logistic because it describes the evolution of a vector of belief probabilities , governed by a fixed row-stochastic matrix that encodes the structure of influence. While can be formally represented as a or array, we use the term vector in the standard linear-algebraic sense, i.e., in the sense of an element of the real vector space , referring simply to an ordered tuple of real-valued belief components, without implying any coordinate transformations or geometric structure as in physical contexts. This allows an analytical exploration of belief trajectories and a precise estimation of mean learning times (MLT) and optimal convergence trajectories, further enriched through the introduction of a logit-transformation linking our probabilistic model with geometric and information-theoretic interpretations.
Moreover, we propose a novel network centrality metric termed logistic-optimal centrality. Unlike traditional centrality measures such as degree or eigenvector centrality, this metric dynamically quantifies a node’s temporal responsiveness, indicating how efficiently it transforms weak initial signals into sustained belief states, and explicitly depends on initial belief distributions.
Our analysis introduces several rigorous results; we derive structural thresholds limiting propaganda effectiveness in conformist groups, demonstrating inherent resilience in large heterogeneous populations and vulnerability in smaller ones. Another key finding, formalized as Theorem 2, demonstrates that correlated belief dynamics lack a finite temporal scale, leading to slow, subexponential convergence and divergent learning times due to cumulative social memory effects. Conversely, we prove that belief propagation under uncorrelated influence exhibits strictly bounded convergence times, enabling rapid consensus even from marginal initial beliefs, a phenomenon termed autopoietic convergence.
The manuscript is structured as follows: Section 2 revisits statistical foundations underpinning collective intelligence; Section 3 presents our probabilistic model of instantaneous local equilibrium formation; Section 4 analytically delineates structural constraints on propaganda efficiency; Section 5 examines temporal divergence under correlated dynamics; and Section 6 analyzes rapid logistic shifts and bounded learning in uncorrelated scenarios. Thus, our approach represents an information-theoretic and probabilistic theory of social conformity, explicitly separating temporal scales, focusing on structural influence topology, and deriving rigorous analytical bounds on the speed and robustness of social consensus formation against systematic manipulation.
2. The Power of Majority: From Local Agreement to Global Consensus
We instinctively align with the majority, as prevailing beliefs often shape perceived truth, an example of argumentum ad populum. This tendency acts as both a cognitive shortcut and a social reinforcement mechanism, fostering acceptance and reducing social risk [26]. Evolution has favored conformity, as adherence to group norms enhanced survival in cooperative societies [27]. Over time, this ingrained bias has driven cultural traditions and institutional structures that sustain social cohesion.
The statistical rationale behind the superiority of collective judgment over individual estimations is rooted in aggregation theory; a group’s prediction is always at least as accurate as the mean individual prediction [28], if the individual predictions have a strong stochastic component. The mathematical foundation of this principle can be derived from the analysis of squared errors. Given a random variable representing the uncertain outcome of some process and a set of n individuals, each making an independent prediction , the collective estimate is defined as the arithmetic mean . The squared error of the collective estimate is given by , while the mean squared individual error is . By applying Jensen’s inequality for convex functions, it follows that
where the equality holds if, and only if, all individuals produce identical predictions. Thus, the existence of a majority implicitly assumes a diversity of perspectives, ensuring that (1) remains a strict inequality in most practical cases. This phenomenon, often referred to as the wisdom of the crowd, has been rigorously analyzed within the framework of error theory, where random individual errors tend to cancel out, resulting in a collective estimate that converges toward the true value [29].
This statistical advantage is further enhanced when individual predictions are uncorrelated, as demonstrated by the variance reduction principle. If individual estimates are characterized by the variance and correlation coefficient between errors, the variance of the collective prediction [30] is given by
As long as , the aggregation mechanism significantly reduces the uncertainty, explaining why heterogeneous groups with independent perspectives tend to outperform even the most knowledgeable individuals. However, if errors are highly correlated , the variance reduction becomes negligible, and the collective judgment offers little to no improvement over individual estimates [31]. In cases of extreme social influence, such as echo chambers and groupthink, the wisdom of the crowd may fail, highlighting the necessity of preserving diversity in decision-making.
The preference for majority alignment is not just statistical optimization but an entropic force driving social cohesion [32]. Evolution has reinforced conformity, as adherence to group norms enhances collective welfare and survival [33], while deviation often leads to exclusion and reduced evolutionary success. However, real-world decision-making rarely operates under ideal conditions of independence and diversity; instead, social influence shapes individual beliefs, leading to varying degrees of conformity.
Consensus formation in the models of opinion formation unfolds in two stages. First, a local consensus emerges rapidly within an individual’s immediate social circle, driven by frequent interactions. Over time, these local clusters interact, leading to a slower process of global consensus formation across the broader network [4,11,12]. Yet, true unanimity remains elusive, as isolated clusters of opinion, while established far apart from each other, have very little chance to merge into a single consensus.
The inherent delay between local and global consensus creates a window of opportunity for manipulating public opinion. Temporary dominance of certain narratives within local clusters can fabricate an illusion of widespread agreement, leading individuals to conform to misleading social signals before a genuine consensus emerges. This phenomenon is theoretically grounded in the gap between fast local saturation and delayed global alignment. Empirically, such effects have been described in communication theory as the “spiral of silence” [16], where perceived majority opinion suppresses dissent. Studies of misinformation propagation and social media clustering [22,34] confirm that users often interpret local signal density as global consensus, especially in filtered online environments. Individuals who rely heavily on social media for opinion cues are particularly vulnerable to this distortion, as automated agents (bots) can exploit this lack of structural awareness to simulate mass agreement.
Thus, understanding the structural and temporal dynamics of consensus formation is crucial. While collective intelligence fosters the stability of information flow, its susceptibility to distortion highlights the need for critical awareness in shaping resilient social and informational networks.
3. Fast Timescale of Local Consensus Formation in Networked Belief Dynamics
Understanding how cognitive biases interact with statistical principles in decision-making calls for a refined probabilistic model that accounts for both individual conviction and social influence. This model advances traditional conformity theories by incorporating network dynamics, resistance to persuasion, and iterative belief updating. A key insight is that consensus forms in two stages: a rapid local alignment shaped by frequent interactions, followed by a slower global convergence. The focus here is on the initial phase, where local consensus emerges within one’s immediate social sphere, laying the groundwork for broader agreement.
To formalize the mechanisms underlying local consensus formation, interactions among individuals can be represented as a graph , where nodes correspond to individuals, and edges E denote influence relationships. The topology of this network—whether centralized, decentralized, or modular—plays a critical role in determining the rate and extent of opinion convergence. To incorporate these structural features into a formal model, we define the influence weight of an edge as , representing the degree to which individual i affects individual j. The social conformity matrix satisfies the row-stochastic constraint, , ensuring that each individual’s posterior probability of adopting a belief or behavior is derived from a weighted sum of social inputs. This constraint guarantees that belief updating follows a Markovian process, enabling iterative convergence to equilibrium.
Building on the probabilistic model of social conformity developed in [35], we assume that each individual j initially holds a prior probability of adopting a particular course of action. Upon interacting with their social neighborhood, this prior is updated to a posterior probability , reflecting the combined influence of personal conviction and external social pressure. To account for resistance to influence, we introduce an obstinacy parameter. Let denote the level of obstinacy, where , with signifying complete independence and total conformity. This resistance reflects empirical findings in social psychology, where cognitive complexity correlates with a lower susceptibility to social pressure [36]. Obstinacy thus acts as a stabilizing force, preventing rapid opinion shifts driven by a single interaction.
While our model shares a formal similarity with opinion dynamics models [11,12], in that represents an evolving state, its interpretation and underlying dynamics are fundamentally different. Unlike those models, where the state is typically treated as an abstract scalar opinion, here, is modeled as the probability of adoption, with a clear Bayesian or decision-theoretic interpretation.
For fully independent individuals, the posterior remains equal to the prior, . For fully conforming individuals, the belief is determined entirely by the collective stance of the group, weighted by the social conformity matrix: . A general formulation incorporating both individual obstinacy and social influence is given by
This equation captures the weighted balance between an individual’s intrinsic beliefs and the influence exerted by their social neighborhood. It naturally extends to a vector formulation, where the full network is described by and . The key relationship governing posterior belief updating is
Equation (4) expresses the fixed-point relation for posterior belief distribution after integrating personal conviction with social influence.
Remark 1.
Since Equation (4) depends explicitly on the diagonal matrix , the posterior belief vector responds continuously to variations in the obstinacy parameters . The mapping is linear and stable as long as the inverse exists. However, as shown in later sections, small changes in μ may lead to nonlinear shifts in convergence time, especially near structural bottlenecks or in highly asymmetric networks.
While structurally similar to iterative update models (e.g., [19]), where each step is defined by
our formulation describes the convergence limit , assuming the process reaches equilibrium. The presence of on both sides in (4) is not a modeling error but reflects this equilibrium assumption.
Unlike previous models (e.g., [19]), which treat obstinacy as a fixed damping parameter relative to the initial opinion, we allow it to dynamically shape the influence aggregation by embedding it directly in the resolvent operator that governs the effective belief integration. This structure allows us to solve the system (4) explicitly:
using the Neumann series expansion for the inverse. This implicit formulation enables the analysis of how structural parameters (e.g., obstinacy and conformity topology) shape final belief states without simulating the full time evolution. While structurally similar to the standard iterative models of opinion dynamics, our model is inherently probabilistic, not diffusive. It computes the posterior probability of belief adoption, rather than an abstract scalar opinion. The underlying logic is rooted in a Bayesian interpretation, where each individual integrates their prior conviction with aggregated social input. The resulting linear system does not describe a time-stepped iteration but rather a fixed-point constraint, a stationary outcome of fast local learning.
In traditional opinion models, agents update their states gradually over time. In contrast, we assume that each individual’s immediate social neighborhood rapidly reaches local equilibrium. From the perspective of our model, this convergence occurs on a fast timescale and is treated as instantaneous relative to the slower dynamics of belief propagation across the global network. Thus, the primary entities in our analysis are not individuals per se, but socially embedded neighborhoods that have already stabilized internally. The long-term evolution of beliefs emerges not from moment-to-moment updates, but from slower “media cycles” or rounds of global exposure, each of which triggers a new local equilibrium. This distinction justifies the presence of posterior beliefs on both sides of the updated Equation (4) and explains why the model retains its probabilistic nature even when written in linear algebraic form.
Since each row sum of in (6) equals one, the sum over each row in is also bounded, ensuring that it is indeed a stochastic matrix. The eigenvalues of remain strictly positive for all and the matrix reflects how the interplay of personal conviction and social conformity shapes the equilibrium belief state. The expansion in (6) reveals that local consensus forms rapidly through repeated interactions within close-knit groups. Early iterations in the series are dominated by direct social inputs, leading to belief synchronization at a fast timescale. In contrast, global convergence unfolds more slowly, shaped by network topology and communication bottlenecks.
This two-timescale structure reflects a fundamental distinction between fast local adaptation and slower global convergence. Rapid local agreement emerges through frequent interpersonal interactions and the reinforcement of shared beliefs. Empirical research on influence networks shows that individuals tend to quickly align their expressed views with those of their immediate social circles, often converging exponentially toward a local consensus [37,38]. Moreover, homophily, the tendency to associate with like-minded peers, further accelerates this process by fostering self-reinforcing opinion clusters that stabilize over short timescales [39]. These findings underscore the critical role of local network structure and interpersonal influence in shaping early belief alignment before any broader consensus takes hold.
4. Structural Limits of Propaganda in Fully Connected Conformist Groups
The probabilistic model of social influence developed in the previous section enables us to assess the structural efficiency of propaganda in tightly connected groups. In such networks, belief formation is shaped by frequent mutual interactions and exposure to persistent external messaging. We focus here on fully connected graphs with uniform influence and obstinacy levels to derive analytical insights into the conditions under which propaganda succeeds or fails.
Consider a fully connected network of individuals, where each agent interacts symmetrically with all others. This setup represents a homogeneous peer group, such as a political community, workplace, or family unit, where individuals share equal exposure to mutual influence. The conformity matrix takes the form
where is the Kronecker delta ensuring no individual prioritizes their own opinion. Under these conditions, the general belief-updating Equation (3) simplifies to
where f represents the expected fraction of individuals who conform to the dominant opinion, given their initial beliefs and obstinacies . This result formalizes a key mechanism of social persuasion; the final stance of an individual is a weighted average of their initial belief and the group’s dominant opinion. Highly conformist individuals () quickly align with the majority, whereas highly obstinate individuals () maintain their initial positions. To incorporate external media influence, following [35], consider a scenario where a family-like group of individuals is exposed to a dominant external source (e.g., television or online media), modeled as a perfectly obstinate -th agent with belief fixed at and obstinacy . The external source exerts influence but does not yet affect the group. Adjusting the normalization to exclude this external source (as it does not update), we have the effective group-level adoption fraction after one exposure cycle:
The terms and explicitly reflect the exclusion of the self-influence of the external agent.
Persuasion rarely occurs in a single step. Instead, the media landscape may evolve iteratively through repeated exposure, where dominant narratives are reinforced over multiple cycles, gradually eroding independent belief formation. In contrast to standard opinion dynamics models [11,12], where iterative averaging governs the process, our formulation treats the belief state as a probability of adoption. We therefore model the evolving adoption fraction as
which expresses that each round persuades a fraction of individuals who remain unconvinced. Solving this recursion yields
indicating exponential convergence to unanimity with a convergence rate set by .
To determine the conditions under which a target adoption level is reached after k rounds of media exposure, we impose , which yields an upper bound on the admissible level of obstinacy:
This condition guarantees that the iterative reinforcement process achieves the desired threshold within k exposures.
An alternative constraint on group size follows from the single-cycle equilibrium (8). Requiring that the adoption level after one round satisfies
and, rearranging terms, we obtain the inequality The structural implications of this bound depend on the relationship between the target threshold and the initial support .
If , the group already satisfies the target level of belief prior to any exposure. The inequality is trivially satisfied for all , and persuasion is guaranteed regardless of group size.
If , the campaign aims to raise adoption beyond its initial level. The inequality yields an upper bound on group size , which exhibits the scaling , highlighting structural resistance to influence in large conformist populations.
These observations can be summarized as follows.
Theorem 1
(Breakdown of Mass Propaganda in Large Conformist Groups). Let a homogeneous group of size with uniform obstinacy and initial belief level be exposed to persistent external influence. Suppose the campaign seeks to elevate belief adoption to a target threshold :
After a single exposure cycle, the goal is achievable only if
After k exposure rounds, a complementary constraint on obstinacy ensures success:
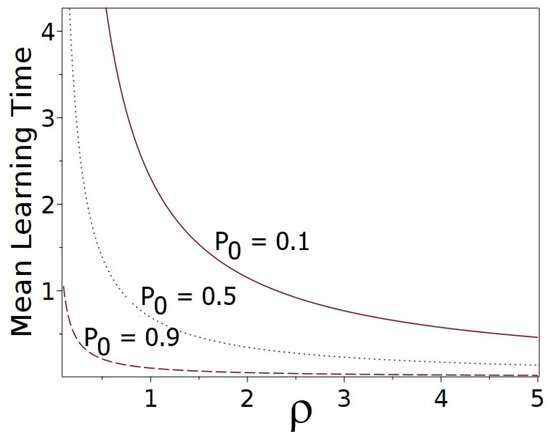
The analysis given above highlights a key fragility of top-down persuasion: in sufficiently large or resistant populations, even persistent messaging fails to shift public belief. The above result assumes a homogeneous group with independent individual responses. In more complex populations with an internal interaction structure, the inequality may underestimate structural reinforcement. However, the scaling remains a robust indicator of the fragility of mass persuasion in large, resistant populations. To visualize the structural limits of persuasion described in the Theorem, in Figure 2 we plot the boundary defined by Equation (11) for several initial belief levels .
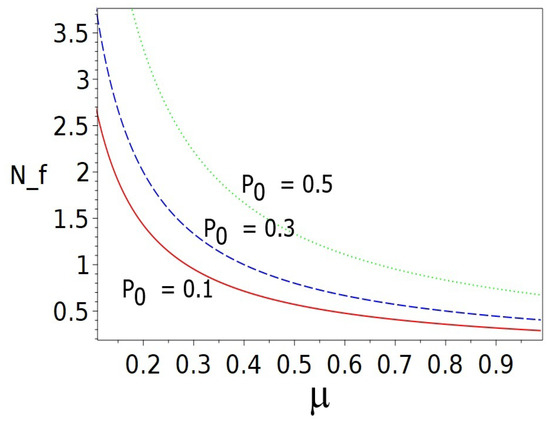
Figure 2.
Critical persuasion boundary in the plane based on Theorem 1 (Equation (13)), for fixed and different values of initial belief . The region below each curve corresponds to the structural feasibility of persuasion; the region above indicates failure.
This figure illustrates how the structural feasibility of propaganda depends jointly on individual obstinacy and the group’s initial belief level . As increases, the persuasive capacity of a campaign diminishes sharply, especially in larger or initially skeptical populations. The inverse relationship manifests here as a steep collapse of the success region for large , highlighting the fragility of belief shifts in conformist environments.
Such dynamics help explain why top-down ideological enforcement often fails in large, homogeneous groups and why authoritarian regimes seek to fragment communities, making centralized narratives easier to impose. Propaganda assumes it can influence broad, diverse populations, yet studies show that its effectiveness diminishes in such settings due to varied opinions and social dynamics. This conclusion aligns with the findings of [40], who observed that while terrorist propaganda follows predictable patterns, its impact varies across groups, highlighting the challenge of uniform messaging in diverse populations. Similarly, studies on media exposure in politically varied contexts suggest that greater media diversity weakens propaganda. Mutz and Martin [41] found that exposure to opposing viewpoints fosters broader political knowledge, counteracting propagandistic effects. Recent research [42] further supports this, showing that even market-driven media diversity can challenge political narratives and limit propaganda’s reach. These examples underscore propaganda’s limitations in large social groups. While small communities may absorb uniform messaging, larger, heterogeneous populations resist centralized narratives due to varied beliefs and complex social dynamics [43].
8. Belief Saturation and Temporal Centrality in Hierarchical Networks with a Teacher
We investigate the structural delays inherent in belief propagation along hierarchical chains, where a marginal node serves as a fully obstinate and initially convinced teacher (, ), while all other nodes share a uniform low initial support () and common obstinacy parameter . Influence is defined by an isotropic bidirectional random walk, yielding a symmetric, localized averaging structure.
Figure 4 presents representative belief trajectories under two regimes; Panel (a) illustrates the weakly autonomous case , dominated by neighbor influence, while Panel (b) corresponds to a balanced regime , where internal conviction begins to contribute appreciably. In both settings, the teacher remains fixed at full belief , while learners evolve gradually under logistic propagation.
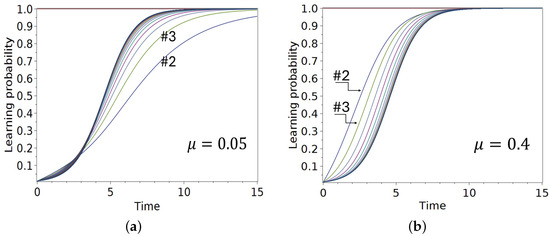
Figure 4.
Time evolution of belief adoption probabilities , , in a linear chain of learners, with a fully obstinate teacher at node (), uniform initial beliefs , and fixed influence structure based on an isotropic random walk. In both panels, despite differing dynamics, most nodes in the chain converge within a narrow time window, reflecting the emergence of bulk synchronization. (a) At low obstinacy , deeper nodes activate faster than early learners (e.g., and ). (b) At moderate obstinacy , belief propagates as a coherent front, with delays increasing with depth.
Notably, the propagation dynamics differ qualitatively. In the weakly autonomous regime, early learners near the teacher (e.g., and ) are, somewhat counterintuitively, delayed in their belief acquisition, whereas deeper bulk nodes activate collectively and earlier than the closest followers, giving rise to a non-monotonic adoption profile. Conversely, in the balanced regime, belief spreads coherently as a sigmoidal front; early learners convert first, followed sequentially by deeper nodes, with the order of adoption aligning with topological depth.
These distinctions manifest clearly in the mean learning time (MLT) profiles. Figure 5 plots as a function of depth k for several values of , revealing how structural synchronization emerges with decreasing obstinacy. At , MLTs decrease with depth, reflecting early suppression and delayed ignition followed by coherent collective activation. At , MLTs increase with depth, as early learners are privileged by their proximity to the source. A critical transition occurs around , where MLTs flatten across the chain, signaling temporal synchronization. Although the figures presented here depict linear chains, we note that similar bottleneck and synchronization patterns were also observed in simulations on tree-structured graphs with the teacher placed at the root. In such trees, all nodes at the same topological depth evolve identically due to structural symmetry, which limits the expressiveness of dynamic variability across the network. Moreover, the number of nodes in regular trees grows exponentially with depth, rapidly inflating both visual complexity and computational cost. By contrast, linear chains allow precise control of topological depth, maximize dynamic resolution per node, and require minimal computational resources. We therefore adopt chains as canonical testbeds for temporal centrality and bottleneck phenomena, without loss of generality.
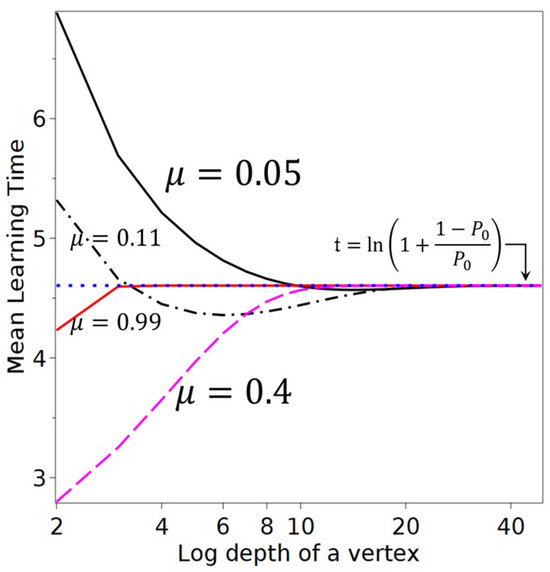
Figure 5.
Mean learning time versus vertex depth k in a chain with a fully obstinate teacher () and uniform initial beliefs . Each curve corresponds to a different obstinacy parameter .
In the autonomous limit , all nodes evolve independently as identical sigmoidal curves, saturating the autonomous MLT bound , marked by the horizontal dotted line. Similar bottleneck and synchronization patterns were observed in tree-structured simulations where the teacher occupied the root node, affirming the generality of the phenomena across hierarchical topologies.
8.1. Coherent Learning in the Limit of Vanishing Individual Autonomy
We now turn to the regime of vanishing individual autonomy, in which the obstinacy parameter and the belief dynamics are entirely governed by mutual influence. In this regime, the system displays emergent coherence for , whereby all deep nodes behave synchronously and evolve as if they were a single logistic unit.
Let the network be a one-dimensional chain of N nodes, with influence governed by a normalized isotropic bidirectional random walk:
with boundary conditions of for a fully obstinate teacher fixed at full belief, while all other nodes (learners) start from the same low initial belief , for , and evolve purely through peer averaging.
Guided by the numerical results from Figure 4a, we assume that for sufficiently large k, all trajectories approximate a common profile . We define the deviation from this profile as , and aim to estimate its decay as a function of depth k. We consider the limiting trajectory as the solution to the standard logistic equation: , . The solution being
Substituting into (31) and linearizing in , we obtain a linear non-autonomous system:
To analyze the behavior of deviations for large k, we note that as , the logistic solution satisfies and with exponential accuracy. Substituting this into (33), we obtain the asymptotic form:
This suggests a depth-dependent solution of the form , where is independent of time. Neglecting the forward term as subdominant for large k, we obtain a recurrence: , or . Thus, the deviation decays as
as for all . This result confirms exponential coherence in depth under purely diffusive dynamics with a fixed boundary.
Theorem 3
(Coherent Learning in the Limit ). Let evolve under matrix logistic dynamics with on a finite chain, with and all for . Then, for all nodes , the deviation , where is the logistic solution (32), satisfies the estimate
exhibiting exponential decay in depth and time.
Corollary 1
(Asymptotic Learning Time in the Collective Limit). In the limit , for all , the mean learning times converge to
That is, the entire chain behaves as a single logistic unit with initial support , converging synchronously to full belief in finite expected time.
Empirical studies of innovation diffusion in structured communities suggest that direct followers of a pioneering agent (such as a teacher or opinion leader) may exhibit slower adoption than more distant actors. In particular, [47] shows that highly connected individuals, due to reputational constraints, often delay adoption until reinforced by multiple peers, while downstream actors adopt rapidly once the innovation gains visibility. Similarly, classic diffusion studies by [48] and summarized by [49] observe that early adopters initiate the awareness phase, but the bulk of the population accelerates adoption after the innovation has been socially legitimized. This phenomenon supports our observation that, in low-autonomy regimes, deep learners within a network may convert earlier than those directly adjacent to the source.
8.2. Belief Saturation and Bottlenecks in the Regime
In the regime where autonomous dynamics are present but not overwhelming (), belief propagation along the chain exhibits a sharply different pattern. Each node approximately follows an independent logistic curve delayed in time, where the delays accumulate recursively based on the integration of upstream trajectories. For small initial belief these delays grow sublinearly with depth and eventually saturate beyond a structural threshold.
Remark 4
(Asymptotic Estimate for the Saturation Depth for ). Let belief propagate over a chain under matrix logistic dynamics with fixed obstinacy and small initial belief . Then the mean learning time at depth k saturates beyond a critical depth approximately given by
The above estimate is asymptotic and captures the heuristic behavior of saturation observed in simulations (see Figure 5) and supported by the following asymptotic analytical arguments.
First, the early growth of belief follows , yielding the MLT .
Second, delays introduced by successive levels decay exponentially, for , as belief is inherited with damping due to . Aggregating these delays gives a convergent geometric sum , which stabilizes once . Inverting yields the estimate (38). While not a rigorous bound, this expression captures the emergence of a structural bottleneck observed in simulations (Figure 5).
The saturation depth defines the minimal number of hierarchical layers required to overcome cognitive inertia and initiate autopoietic propagation. Above this threshold, belief spreads rapidly and near-synchronously. Below it, propagation is significantly slowed by upper-layer resistance. This phenomenon is analogous to nucleation theory, where growth only becomes self-sustaining once a critical cluster size is reached [50].
Empirical evidence supports this structural insight. In hierarchical organizations, early adopters, such as managers or ideological elites, disproportionately influence downstream adoption [51]. Strategic misinformation campaigns exploit these dynamics, prioritizing structural access over volume [52]. Effective belief propagation hinges not on intensity alone, but on timing and topological positioning. Structural depth and temporal centrality jointly govern the diffusion capacity of a network. Understanding their interplay enables more accurate modeling of persuasion dynamics in hierarchical systems.
The MLT offers a natural foundation for defining a dynamic measure of temporal centrality, defined by the MLT ; nodes with shorter exert greater influence in initiating diffusion cascades.
Definition 2
(Temporal Centrality). In matrix logistic belief dynamics, the temporal centrality score of node i is given by
Nodes with higher are temporally more central; they are capable of faster belief adoption and play a disproportionate role in initiating propagation cascades.
Unlike structural centrality measures such as degree or eigenvector centrality, reflects the network’s dynamical geometry and resistance structure, making it a context-sensitive indicator of influence.
9. Autopoietic Amplification of Marginal Beliefs
An important insight emerging from matrix logistic dynamics is that even weak initial signals can be amplified through sustained endogenous feedback, leading to rapid convergence without substantial external pressure. This phenomenon, which we refer to as autopoietic convergence, captures the capacity of a networked system to self-organize and propagate beliefs, transforming marginal prior support into systemic consensus.
Consider the matrix logistic Equation (25) with uniform obstinacy and an influence structure encoded by a row-stochastic matrix . The effective influence matrix is then given by which is well-defined for any irreducible and aperiodic (i.e., ergodic in the Markov sense) matrix . In this context, ergodicity refers to the property that the Markov chain defined by has a unique stationary distribution and converges to it from any initial state. This ensures that the matrix inverse exists and the influence dynamics are globally well-posed. As shown in earlier sections, the belief update rate satisfies and in particular, its lower bound is determined by the spectral radius of . For many structured graphs, the smallest non-zero eigenvalue of is bounded below by , guaranteeing that belief dynamics never become arbitrarily slow.
To estimate the mean learning time for small initial support , we approximate the belief trajectory as a logistic sigmoid, so that the MLT is given by
as . Using the lower bound then yields a universal estimate:
This result formalizes a key structural guarantee; even marginal beliefs will be amplified and adopted within finite time, provided the network is ergodic and agents retain minimal responsiveness. The convergence time grows only logarithmically in the inverse prior , reflecting the information-theoretic surprise of the initial condition.
The mechanism becomes particularly transparent in the case of a complete graph of size N, where the conformity matrix is so that each node is equally influenced by all others. The corresponding matrix has leading eigenvalue and remaining spectrum concentrated near as . In this limit, belief trajectories simplify to and the MLT obeys the refined bound
These analytic results reinforce empirical observations from social psychology. Effects such as group polarization [53,54] and pluralistic ignorance [55] illustrate how even unpopular beliefs can rapidly crystallize into dominant positions under symmetric, decentralized influence structures. The matrix logistic model provides a generative explanation—belief adoption is driven not by initial volume, but by feedback-mediated amplification, a hallmark of autopoietic convergence.
The analytical results presented in this section, including saturation depth, logarithmic bottleneck scaling, and closed-form estimates of mean learning time, rely critically on the hierarchical, tree-like structure of the network. These structures ensure unique propagation paths, acyclic flow, and recursive depth definitions, which make them analytically tractable within the matrix logistic framework.
However, in more general network topologies such as small-world or scale-free graphs, these structural features are lost. The presence of cycles, multiple propagation routes, and highly clustered regions introduces interference effects that preclude closed-form computation. In small-world networks, shortcuts lower geodesic distances but obscure learning depth, while in scale-free networks, hub concentration leads to non-uniform and often non-local belief amplification. As such, the formulas derived here do not extend directly to such settings.
Nonetheless, the qualitative regimes we identify, including geodesic saturation, autopoietic amplification, and bottleneck-induced delays, are expected to persist. Their quantitative behavior in non-hierarchical networks can be investigated via simulations or approximated using effective centrality measures, influence-weighted path statistics, or spectral proxies. Developing such approximations and validating them empirically remains a promising direction for future work.
10. Statistical Isolation of Influence: Techniques for Memory Suppression in Propaganda
Ensuring that each round of propaganda remains statistically independent requires the disruption of memory effects and the prevention of ideological accumulation over time. This can be conceptually interpreted through the lens of memory erasure and belief resetting, as formalized in our uncorrelated learning scenario. Strategically, this corresponds to de-correlation tactics that fragment public memory and prevent cumulative resistance. While this mechanism is modeled abstractly, empirical analogues are discussed in critical media theory [56,57], where control over attention, fragmentation of informational context, and algorithmic obfuscation are shown to suppress long-term narrative coherence. These strategies reinforce continuous susceptibility by impeding reflective or integrative resistance.
One fundamental approach is stochastic resetting, whereby public opinion is periodically reinitialized, either through narrative reversals, purges of ideological figures, or sudden shifts in official policy. This ensures that prior ideological developments do not persist across multiple rounds of influence. Imperial Rome implemented this technique under the name damnatio memoriae, where all images of inconvenient historical figures were purged from records [58]. A more familiar recent example is given by Stalinist Russia, erasing purged officials from records and even photographs, thereby preventing the consolidation of alternative political loyalties [59]. In contemporary contexts, similar methods manifest in sudden shifts in government rhetoric, where public figures previously promoted as authoritative sources are swiftly discredited when their stance no longer aligns with the evolving state narrative.
Closely related is the injection of noise, a technique that floods the information space with contradictory, overwhelming, or misleading narratives to hinder stable belief formation. By generating a high-frequency, high-volume stream of conflicting messages, regimes can create cognitive fatigue, where the audience disengages from critical analysis and instead follows the dominant message of the moment. The “firehose of falsehood” model exemplifies this strategy, leveraging state-controlled media to generate rapid, multi-channel, repetitive, and often contradictory propaganda [60]. This technique, which prioritizes volume over consistency, ensures that each cycle of influence is self-contained, rendering past narratives obsolete and reducing resistance to new messaging.
To further disrupt the formation of ideological continuity, regimes employ randomization of social influence structures. This is achieved through continuous reshuffling of public discourse influencers, such as political leaders, journalists, or digital personalities, preventing long-term trust from forming between the public and any particular information source. Frequent rotations in government figures and controlled opposition movements serve this purpose, ensuring that loyalty does not accumulate within any specific faction. In the modern era, algorithmic censorship on social media platforms contributes to this fragmentation by selectively boosting or suppressing different narratives based on shifting political priorities [61].
To increase the adoption of the message, target segmentation may be used, where smaller groups receive messages that are fine-tuned to that particular groups. As we mentioned before, bots, exploiting the algorithmic power of modern social media, may become devastatingly effective in delivering their messaging to smaller targeted groups.
11. Discussion and Conclusions
The presented research explores the dynamics of belief formation and opinion consensus in social networks under diverse conditions of social conformity, obstinacy, structural topology, and influence propagation mechanisms. Our analytical and numerical findings provide several crucial insights into how individuals integrate social information, form collective judgments, and converge toward consensus, highlighting both the potential and limits of majority-driven decision-making.
We began our analysis by revisiting the classical result known as the wisdom of crowds, demonstrating rigorously how the mean squared error of collective predictions consistently outperforms individual forecasts provided there is diversity and statistical independence among predictions. This advantage arises fundamentally from the cancellation of random individual errors, a phenomenon amplified when individual judgments are minimally correlated. The implications are clear; societal decision-making processes inherently benefit from diversity and decentralization, emphasizing the societal advantage in maintaining heterogeneous sources of information and opinion. Conversely, we found that high correlation among individual errors severely diminishes the accuracy advantage, reflecting situations typical of “echo chambers”, groupthink, or propaganda-saturated environments. Thus, preserving independent thinking and diverse informational sources is not merely beneficial but essential for accurate collective judgment.
Our model further decomposed consensus formation into two distinct phases—rapid local consensus and slow global convergence, clarifying empirical observations that immediate social circles rapidly synchronize beliefs, creating stable local clusters that are resistant to external influence. Such localized equilibrium, confirmed through analytical computations, explains why opinions initially solidify quickly within close-knit groups. However, global consensus emerges much more slowly, constrained by communication bottlenecks and structural divisions within society. This fundamental temporal duality offers critical insights into why social influence strategies often first target local clusters, as rapid internal agreement within smaller communities can then propagate more broadly.
Our detailed study of fully connected conformist networks elucidates the structural limits of propaganda. We derived exact formulas that quantify the effectiveness of external influence in uniform social groups, showing that the impact of persuasive efforts is inversely proportional to the size and obstinacy of the targeted population. Specifically, small, conformist groups rapidly succumb to external messaging, while larger, more resistant populations remain resilient. Our recursive model of repeated exposure further highlights how sustained propaganda efforts can erode initial beliefs, eventually achieving unanimity if the targeted community remains small and sufficiently conformist. Conversely, we established a critical threshold in group size, beyond which propaganda rapidly loses effectiveness due to the prevalence of internal social reinforcement mechanisms.
Examining correlated belief dynamics, we found an unexpected phenomenon: while consensus is guaranteed structurally, the time required to achieve it diverges. When individuals’ belief adoption depends on cumulative social memory, their opinions shift at a progressively diminishing rate, ultimately resulting in a convergence that is unbounded in temporal scale. Our rigorous proof reveals a deep structural constraint of collective cognition—strong dependence on historical interactions creates inertia that slows belief adaptation. Empirically, this underscores the social dangers of collective memory saturation, where excessive reliance on past information effectively paralyzes decision-making processes.
In contrast, our analysis of uncorrelated propaganda scenarios demonstrated that belief adoption under memoryless influence rapidly converges to certainty, governed by logistic dynamics that impose strict upper bounds on mean learning times. We provided explicit, closed-form expressions for the fastest possible convergence trajectories, characterizing conditions under which belief shifts are maximally accelerated. This result implies that societies subject to continuous, memoryless streams of external influence, typical of high-frequency social media environments, can experience rapid ideological shifts. Such conditions amplify marginal initial beliefs into systemic consensus through what we termed autopoietic convergence, highlighting the powerful potential of continuous external signals to shape societal beliefs even when initial support is minimal.
These findings collectively provide profound insights into the mechanisms of opinion formation and manipulation within societies. They demonstrate how structural parameters, such as group size, connectivity, obstinacy, and influence topology, critically shape societal responsiveness to external narratives. The intrinsic vulnerability of small, homogeneous communities to external influence highlights strategic vulnerabilities that are frequently exploited in political propaganda, marketing, and social engineering contexts. Meanwhile, larger, diverse societies inherently resist top-down ideological control, emphasizing the societal benefits of heterogeneity and robust internal communication structures.
Moreover, the demonstrated fragility of collective intelligence under correlated opinion dynamics cautions against overreliance on consensus-driven decision-making in environments prone to memory saturation and information overload. The identified critical role of independent thinking and diversity in maintaining collective accuracy underscores the importance of institutional safeguards that protect informational plurality and encourage critical engagement.
The present study is theoretical in nature and does not rely on empirical datasets or parameter fitting. The phase transitions, learning thresholds, and saturation regimes described throughout, including the emergence of bottlenecks, depth-dependent propagation limits, and critical values of the obstinacy parameter , are derived analytically from the structure of the nonlinear differential system and its coupling to network geometry.
While we include illustrative simulations to visualize these phenomena under controlled structural conditions (e.g., trees, chains, layered graphs), no real-world networks were used to validate the thresholds quantitatively. We therefore view empirical validation as a natural extension of this work. Future research may explore how the theoretical predictions developed here, particularly the mean learning time , saturation depth, and the geodesic-to-autopoietic phase boundary, manifest in observed belief dynamics, whether in social media propagation, controlled opinion experiments, or organizational information flow. Our results provide testable structural hypotheses and functional benchmarks that can be integrated with data-driven inference frameworks.
In conclusion, our study reveals fundamental insights into the structural and dynamic underpinnings of consensus formation and social influence. By rigorously deriving explicit conditions for optimal consensus, exploring the contrasting dynamics of correlated versus uncorrelated influence scenarios, and identifying robust structural limits to external persuasion, we deepen understanding of how societal belief systems evolve and stabilize. Our analysis provides essential tools for diagnosing vulnerabilities in social communication networks and designing resilient informational structures.
While this study is analytical in nature, the predictions obtained, including learning times, belief saturation thresholds, and the structural fragility of mass persuasion, are amenable to empirical validation in controlled experiments or real-world belief diffusion datasets. Experimental studies on social influence in small groups, such as [31], suggest that collective belief updating can exhibit inertia, bias, and suppression of accuracy, phenomena directly linked to the nonlinear effects modeled in this paper. We hope that future work will explore these applications in cognitive, online, and organizational domains.
Future research may extend these theoretical results empirically by testing model predictions in real-world social networks and evaluating how varying levels of correlation, structural diversity, and influence timing affect belief dynamics in specific settings. Such investigations could help determine the extent to which the mechanisms identified in this analytical framework manifest in practice. For example, one could examine belief diffusion on controversial topics using social media datasets, where network structures, echo chamber effects, and temporal dynamics are observable and measurable. Additionally, studying the ethical implications and potential policy responses to structurally mediated influence may offer new strategies for strengthening societal resilience to manipulation and enhancing the robustness of collective decision-making.
Author Contributions
Conceptualization, D.V. and V.P.; methodology, D.V. and V.P.; software, D.V.; formal analysis, D.V. and V.P.; investigation, D.V. and V.P.; resources, D.V. and V.P.; writing—original draft preparation, D.V.; writing—review and editing, D.V. and V.P.; visualization, D.V.; project administration, D.V. and V.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
The authors are grateful to their institution for the administrative and technical support. The authors also gratefully acknowledge Ori Swed (https://www.oriswed.com/) for his valuable insights and stimulating discussions, which significantly contributed to the conceptual development of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviation is used in this manuscript:
| MLT | mean learning time |
References
- Ferrari, G.R. (Ed.) Plato: The Republic, 3rd ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Taylor, P.M. Munitions of the Mind: A History of Propaganda from the Ancient World to the Present Era; Manchester University Press: Manchester, UK, 2013. [Google Scholar]
- Deffuant, G.; Neau, D.; Amblard, F.; Weisbuch, G. Mixing beliefs among interacting agents. Adv. Complex Syst. 2000, 3, 87–98. [Google Scholar] [CrossRef]
- Hegselmann, R.; Krause, U. Opinion dynamics and bounded confidence: Models, analysis and simulation. J. Artifical Soc. Soc. Simul. (JASSS) 2002, 5. [Google Scholar]
- Hegselmann, R.; Krause, U. Opinion dynamics driven by various ways of averaging. Comput. Econ. 2005, 25, 381–405. [Google Scholar] [CrossRef]
- Hegselmann, R. Bounded confidence revisited: What we overlooked, underestimated, and got wrong. J. Artifical Soc. Soc. Simul. 2023, 26, 11. Available online: http://jasss.soc.surrey.ac.uk/26/4/11.html (accessed on 1 February 2025). [CrossRef]
- Mazza, M.; Avvenuti, M.; Cresci, S.; Tesconi, M. Investigating the difference between trolls, social bots, and humans on Twitter. Compu. Commun. 2022, 196, 23–36. [Google Scholar] [CrossRef]
- Liu, X. A big data approach to examining social bots on Twitter. J. Serv. Mark. 2019, 33, 369–379. [Google Scholar] [CrossRef]
- Tunç, U.; Atalar, E.; Gargı, M.S.; Aydın, Z.E. Classification of fake, bot, and real accounts on instagram using machine learning. Politek. Derg. 2022, 27, 479–488. [Google Scholar]
- Swed, O.; Dassanayaka, S.; Volchenkov, D. Keeping it authentic: The social footprint of the trolls’ network. Soc. Netw. Anal. Min. 2024, 14, 38. [Google Scholar] [CrossRef]
- Friedkin, N.E.; Johnsen, E.C. Social influence and opinions. J. Math. Sociol. 1990, 15, 193–206. [Google Scholar] [CrossRef]
- DeGroot, M.H. Reaching a Consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar] [CrossRef]
- Zuckerman, E. Misinformation and manipulation: The rise of astroturfing in digital media. J. Inf. Technol. Politics 2017, 14, 95–108. [Google Scholar]
- Howard, P.N. Lie Machines: How Fake News and Social Media Manipulate the World; Yale University Press: New Haven, CT, USA, 2018. [Google Scholar]
- Bentsen, L. U.S. Senate Proceedings on Lobbying and Grassroots Movements; Congressional Records; U.S. Government Publishing Office: Washington, DC, USA, 1985.
- Noelle-Neumann, E. The Spiral of Silence: A Theory of Public Opinion. J. Commun. 1974, 24, 43–51. [Google Scholar] [CrossRef]
- Cialdini, R.B. Influence: Science and Practice; Allyn & Bacon: Boston, MA, USA, 2001. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Anderson, B.D.; Ye, M. Recent advances in the modelling and analysis of opinion dynamics on influence networks. Int. J. Autom. Comput. 2019, 16, 129–149. [Google Scholar] [CrossRef]
- Centola, D. The Spread of Behavior in an Online Social Network Experiment. Science 2010, 329, 1194–1197. [Google Scholar] [CrossRef]
- Conover, M.D.; Ratkiewicz, J.; Francisco, M.; Gonçalves, B.; Menczer, F.; Flammini, A. Political polarization on Twitter. Proc. Int. AAAI Conf. Web Soc. Media 2011, 5, 89–96. [Google Scholar] [CrossRef]
- Del Vicario, M.; Bessi, A.; Zollo, F.; Petroni, F.; Scala, A.; Caldarelli, G.; Stanley, H.E.; Quattrociocchi, W. The spreading of misinformation online. Proc. Natl. Acad. Sci. USA 2016, 113, 554–559. [Google Scholar] [CrossRef]
- Sunstein, C.R. #Republic: Divided Democracy in the Age of Social Media; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- Barabási, A.-L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- McCallum, D.C.; Henshaw, G.H.; New York and Erie Railroad Company. New York and Erie Railroad Diagram Representing a Plan of Organization: Exhibiting the Division of Academic Duties and Showing the Number and Class of Employés Engaged in Each Department: From the Returns of September; New York and Erie Railroad Company: New York, NY, USA, 1855; [Map]. Retrieved from the Library of Congress. Available online: https://www.loc.gov/item/2017586274/ (accessed on 1 February 2025).
- Bauman, Z. Liquid Modernity; Polity Press: London, UK, 2003. [Google Scholar]
- Boyd, R.; Richerson, P.J. The Origin and Evolution of Cultures; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Page, S.E. The Difference: How the Power of Diversity Creates Better Groups, Firms, Schools, and Societies; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Surowiecki, J. The Wisdom of Crowds; Anchor Books: Palatine, IL, USA, 2004. [Google Scholar]
- Krause, J.; Ruxton, G.D.; Krause, S. Swarm Intelligence in Animals and Humans. Trends Ecol. Evol. 2010, 25, 28–34. [Google Scholar] [CrossRef]
- Lorenz, J.; Rauhut, H.; Schweitzer, F.; Helbing, D. How social influence can undermine the wisdom of crowd effect. Proc. Natl. Acad. Sci. USA 2011, 108, 9020–9025. [Google Scholar] [CrossRef]
- Volchenkov, D. Survival under Uncertainty: An Introduction to Probability Theory and Its Applications; Series Understanding Complex Systems; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Tversky, A.; Kahneman, D. Judgment Under Uncertainty: Heuristics and Biases. Science 1974, 185, 1124–1131. [Google Scholar] [CrossRef] [PubMed]
- Bail, C.A.; Argyle, L.P.; Brown, T.W.; Bumpus, J.P.; Chen, H.; Hunzaker, M.B.; Lee, J.; Mann, M.; Merhout, F.; Volfovsky, A. Exposure to opposing views on social media can increase political polarization. Proc. Natl. Acad. Sci. USA 2018, 115, 9216–9221. [Google Scholar] [CrossRef] [PubMed]
- Krasnoshchekov, P.S. A simplest mathematical model of [collective] behavior. Psychol. Conform. Math. Model. 1998, 10, 76–92. (In Russian) [Google Scholar]
- Sunstein, C.R. Conformity: The Power of Social Influences; New York University Press: New York, NY, USA, 2019. [Google Scholar]
- Moussaïd, M.; Brighton, H.; Gaissmaier, W. The amplification of risk in experimental diffusion chains. Proc. Natl. Acad. Sci. USA 2013, 110, 9354–9359. [Google Scholar] [CrossRef]
- Momennejad, I. Learning Structures: Predictive Representations, Replay, and Generalization. Curr. Opin. Behav. Sci. 2020, 32, 155–166. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- McPherson, M.; Smith-Lovin, L.; Cook, J.M. Birds of a feather: Homophily in social networks. Annu. Rev. Sociol. 2001, 27, 415–444. [Google Scholar] [CrossRef]
- Hahn, L.; Schibler, K.; Lattimer, T.A.; Toh, Z.; Vuich, A.; Velho, R.; Kryston, K.; O’Leary, J.; Chen, S. Why We Fight: Investigating the Moral Appeals in Terrorist Propaganda, Their Predictors, and Their Association with Attack Severity. J. Commun. 2024, 74, 63–76. [Google Scholar] [CrossRef]
- Mutz, D.C.; Martin, P.S. Facilitating communication across lines of political difference: The role of mass media. Am. Polit. Sci. Rev. 2001, 95, 97–114. [Google Scholar] [CrossRef]
- Steinfeld, N.; Lev-On, A. Exposure to diverse political views in contemporary media environments. Front. Commun. 2024, 9, 1384706. [Google Scholar] [CrossRef]
- Gallagher, P. Revealed: Putin’s Army of Pro-Kremlin Bloggers. The Independent, 27 March 2015; [Online]. Available online: https://www.independent.co.uk/news/world/europe/revealed-putin-s-army-of-prokremlin-bloggers-10138893.html (accessed on 26 February 2025).
- DLazer, D.; Baum, M.A.; Benkler, Y.; Berinsky, A.; Greenhill, K.; Menczer, F.; Metzger, M.; Nyhan, B.; Pennycook, G.; Rothschild, D.; et al. The science of fake news. Science 2018, 359, 1094–1096. [Google Scholar]
- Bakshy, E.; Messing, S.; Adamic, L.A. Exposure to ideologically diverse news and opinion on Facebook. Science 2015, 348, 1130–1132. [Google Scholar] [CrossRef] [PubMed]
- He, T.; Minervini, M.S.; Puranam, P. How Groups Differ from Individuals in Learning from Experience. Organ. Sci. 2024, 35, 502–521. [Google Scholar] [CrossRef]
- Centola, D. How Behavior Spreads: The Science of Complex Contagions; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Coleman, J.S.; Katz, E.; Menzel, H. The diffusion of an innovation among physicians. Sociometry 1957, 20, 253–270. [Google Scholar] [CrossRef]
- Rogers, E.M. Diffusion of Innovations, 5th ed.; Free Press: Washington, DC, USA, 2003. [Google Scholar]
- Kelton, K.F.; Greer, A.L. Nucleation in Condensed Matter: Applications in Materials and Biology; Pergamon Materials Series; Elsevier: Amsterdam, The Netherlands, 2010; Volume 15. [Google Scholar]
- Centola, D.; Macy, M. Complex contagions and the weakness of long ties. Am. J. Sociol. 2007, 113, 702–734. [Google Scholar] [CrossRef]
- Vosoughi, S.; Roy, D.; Aral, S. The spread of true and false news online. Science 2018, 359, 1146–1151. [Google Scholar] [CrossRef]
- Sunstein, C.R. The law of group polarization. J. Political Philos. 2002, 10, 175–195. [Google Scholar] [CrossRef]
- Daniel, J.I. Group polarization: A critical review and meta-analysis. J. Personal. Soc. Psychol. 1986, 50, 1141–1151. [Google Scholar]
- Prentice, D.A.; Miller, D.T. Pluralistic ignorance and alcohol use on campus: Some consequences of misperceiving the social norm. J. Personal. Soc. Psychol. 1993, 6, 243–256. [Google Scholar] [CrossRef]
- Tufekci, Z. Algorithmic harms beyond Facebook and Google: Emergent challenges of computational agency. Colo. Technol. Law J. 2014, 13, 203–218. [Google Scholar]
- Zuboff, S. The Age of Surveillance Capitalism: The Fight for a Human Future at the New Frontier of Power; PublicAffairs: New York, NY, USA, 2019. [Google Scholar]
- Varner, E.R. Monumenta Graeca et Romana: Mutilation and transformation: Damnatio Memoriae and Roman Imperial Portraiture; Brill: Leiden, The Netherlands, 2004. [Google Scholar]
- Blakemore, E. How Photos Became a Weapon in Stalin’s Great Purge. History; A&E Television Networks 20 April 2018 (updated 11 April 2022). Available online: https://www.history.com/news/josef-stalin-great-purge-photo-retouching (accessed on 12 March 2025).
- Paul, C.; Matthews, M. The Russian ’Firehose of Falsehood’ Propaganda Model: Why It Might Work and Options to Counter It. RAND Corporation Perspective PE-198. 2016. Available online: https://www.rand.org/pubs/perspectives/PE198.html (accessed on 12 March 2025).
- Tiffert, G. 30 Years After Tiananmen: Memory in the Era of Xi Jinping. J. Democr. 2019, 30, 38–49. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).