Optimal Constructions of Low-Hit Zone Frequency-Hopping Sequence Set Based on m-Sequence
Abstract
1. Introduction
1.1. Background
1.2. Motivation
1.3. Contribution
1.4. Organization
2. Preliminaries
2.1. Hamming Correlation
2.2. LHZ FHS Set and Theoretical Bound
2.3. q-Ary m-Sequences and Its Decimated Sequence
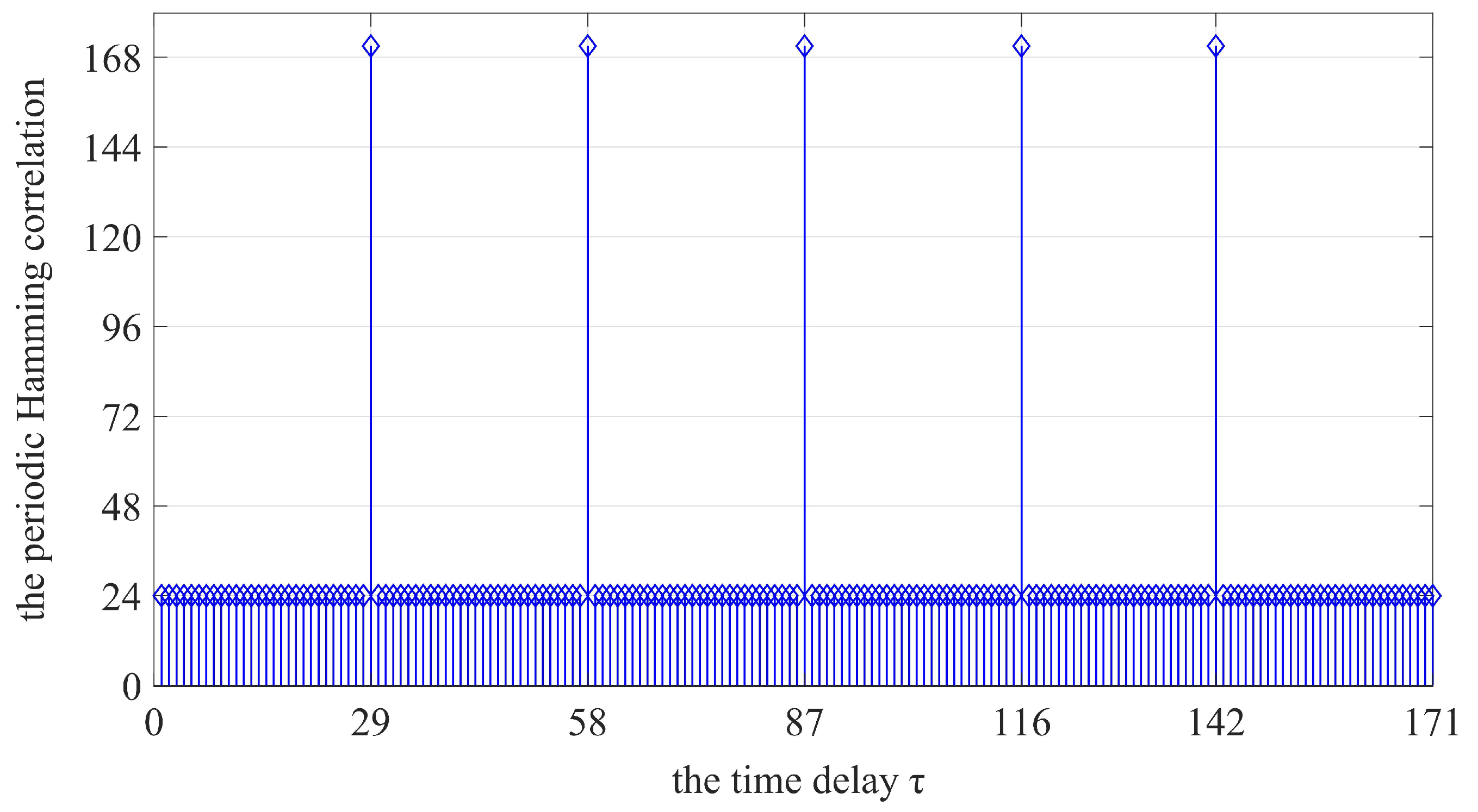
3. LHZ FHS Sets with Optimal Maximum Periodic Hamming Correlation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FHS | frequency-hopping sequence |
| FH | frequency hopping |
| LHZ | low-hit zone |
| MPHC | maximum periodic Hamming correlation |
| MAI | multiple access interference |
| BER | bit error rate |
| LFSR | linear feedback shift register |
| QS-FHMA | quasi-synchronous frequency-hopping multiple access |
References
- Dixon, R. Spead Spectrum with Commercial Application, 3rd ed.; John-Wiley and Sons: New York, NY, USA, 1994. [Google Scholar]
- Simon, M.; Omura, J. Spead Apectrum Communications; Computer Science Press: Rochville, MD, USA, 1985. [Google Scholar]
- Simon, M.; Omura, J. Spead Spectrum Communications Handbook; The Posts and Telecommunications Press: Beijing, China, 2022. [Google Scholar]
- Fan, P.; Darnell, M. Sequence Design for Communications Applications; Research Studies Press, John Wiley & Sons: London, UK, 1996. [Google Scholar]
- Gihousen, K. On the capacity of a cellular CDMA system. IEEE Trans. Veh. Tech. 1991, 40, 303–312. [Google Scholar]
- Ye, W.; Fan, P. Two class of frequency-hopping sequences with no-hit zone. In Proceedings of the Seventh International Symposium on Communications Theory and Applications (ISCTA’2003), Ambleside, UK, 13–18 July 2003; pp. 304–306. [Google Scholar]
- Wang, X.; Fan, P. A class of frequency hopping sequences with no hit zone. In Proceedings of the Fourth International Conference on Parallel and Distributed Computing, Applications and Technologies, (PDCAT’2003), Chengdu, China, 27–29 August 2003. [Google Scholar]
- Sarwate, D.V. Reed-Solomon codes and the design of sequences for spread-spectrum multiple-access communications. In Reed Solomon Codes and Their Applications; Wicker, S.B., Bharagava, V.K., Eds.; IEEE Press: Piscataway, NJ, USA, 1994. [Google Scholar]
- Yang, L.; Giannakis, G.B. Ultra-wideband communications: An idea whose time has come. IEEE Sig. Proc. Mag. 2004, 21, 26–54. [Google Scholar]
- Peng, D.; Fan, P.; Leem, M. Lower bounds on the periodic Hamming correlations of frequency hopping sequences with low hit zone. Sci. China Ser. F Inf. Sci. 2006, 49, 208–218. [Google Scholar]
- Niu, X.; Peng, D.; Liu, F.; Liu, X. Lower Bounds on the Maximum Partial Correlations of Frequency Hopping Sequence Set with Low Hit Zone. IEICE Trans. Fundam. 2010, E93-A, 2227–2231. [Google Scholar]
- Zhou, L.; Peng, D.; Liang, H.; Wang, C.; Han, H. Generalized methods to construct low-hit-zone frequency-hopping sequence sets and optimal constructions. Cryptogr. Commun. 2017, 9, 707–728. [Google Scholar]
- Ma, W.; Sun, S. New designs of frequency hopping sequences with low-hit-zone. Des. Codes Cryptogr. 2011, 60, 145–153. [Google Scholar]
- Han, H.; Peng, D.; Parampalli, U. New sets of optimal low-hitzone frequency-hopping sequences based on m-sequences. Cryptogr. Commun. 2016, 9, 511–522. [Google Scholar]
- Zhou, L.; Peng, D.; Liang, H.; Wang, C.; Ma, Z. Constructions of optimal low-hit-zone frequency hopping sequence sets. Des. Codes Cryptogr. 2017, 89, 219–232. [Google Scholar]
- Niu, X.; Peng, D.; Zhou, Z. New classes of optimal low hit zone frequency hopping sequences with new parameters by interleaving technique. IEICE Trans. Fundam. 2012, E95-A, 1835–1842. [Google Scholar]
- Niu, X.; Peng, D.; Zhou, Z. New classes of optimal frequency hopping sequences with low-hit-zone. Adv. Math. Commun. 2013, 7, 293–310. [Google Scholar]
- Tian, X.; Han, H.; Niu, X.; Liu, X. Construction of Optimal Frequency Hopping Sequence Set with Low-Hit-Zone. Entropy 2023, 25, 1044. [Google Scholar] [CrossRef] [PubMed]
- Niu, X.; Han, L.; Liu, X. New Extension Interleaved Constructions of Optimal Frequency Hopping Sequence Sets With Low Hit Zone. IEEE Access 2019, 7, 73870–73879. [Google Scholar]
- Chung, J.; Yang, K. New classes of optimal low-hit-zone frequency-hopping sequence sets by cartesian product. IEEE Trans. Inform. Theory 2013, 59, 726–732. [Google Scholar]
- Wang, C.; Peng, D.; Zhou, L. New constructions of optimal frequency-hopping sequence sets with low-hit-zone. Int. J. Found. Comput. Sci. 2016, 27, 53–66. [Google Scholar]
- Wang, C.; Zhang, Y. Optimal Constructions of Low-hit-zone Frequency-Hopping Sequence sets via Cyclotomy. IEEE Access 2023, 11, 24128–24136. [Google Scholar]
- Zhou, L.; Wu, H. New Families of Frequency-Hopping Sequence Sets with a Low-Hit-Zone. Entropy 2024, 26, 948. [Google Scholar] [CrossRef] [PubMed]
- Liu, X. Low-hit-zone frequency hopping sequence sets under aperiodic Hamming correlation. Cryptogr. Commun. 2024, 16, 629–645. [Google Scholar]
- Tian, X.; Han, H.; Zhou, L.; Wu, H. Construction of Near-Optimal Frequency Hopping Sequence Set with Low-Hit-Zone. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2023, E106, 1362–1365. [Google Scholar]
- Fan, C.; Cui, X.; Su, W. Constructions of low-hit-zone frequency hopping sequence sets from cyclic codes. Appl. Algebra Eng. Commun. Comput. 2024, 35, 691–701. [Google Scholar]
- Zhou, L.; Kong, Q.; Han, H.; Liu, X.; Wu, H. Low-Hit-Zone Frequency-Hopping Sequence Sets with Wide-Gap and Optimal Hamming Correlation Properties. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2022, E105, 122–125. [Google Scholar]
- Zhou, L.; Liu, X.; Han, H.; Wang, C. Classes of optimal low-hit-zone frequency-hopping sequence sets with new parameters. Cryptogr. Commun. 2021, 14, 1–16. [Google Scholar]
- Golomb, S.; Gong, G. Signal Design for Good Correlation: For Wireless Communication, Cryptography, and Radar; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Zhou, Z.; Tang, X.; Niu, X.; Udaya, P. New classes of frequency-hopping sequences with optimal partial correlation. IEEE Trans. Inform. Theory 2012, 58, 453–458. [Google Scholar]

| Notations & Definitions | Description |
|---|---|
| the maximum quotient when x is divided by y. | |
| the least positive integer of x modulo y. | |
| the operator for cyclic left shift by positions. | |
| the number of g that occurs in any sequence . | |
| , | “the finite field” and “the extension field of a finite field”. |
| the trace function from to . | |
| the set obtained by removing the element 0 from . | |
| the greatest positive integer not exceeding x. | |
| the smallest positive integer that is not less than x. | |
| ⊕ | the addition modulo q over . |
| x does not divide y. | |
| x divides y. |
| Ref. | Parameters | Parameters |
|---|---|---|
| this paper | (511, 32, 16, 170–254, 32) | (511, 48, 16, 127–169, 32) |
| (511, 64, 16, 102–126, 32) | (511, 80, 16, 85–101, 32) | |
| (511, 96, 16, 73–84, 32) | (511, 112, 16, 63–72, 32) | |
| (511, 128, 16, 56–62, 32) | (511, 144, 16, 51–57, 32) | |
| … | … | |
| (511, 2032, 16, 3, 32) | (511, 2720, 16, 2, 32) | |
| [15] | (511, 1168, 16, 6, 32) | (511, 112, 16, 72, 32) |
| Ref. | Parameters | Parameters |
|---|---|---|
| this paper | (171, 4, 7, 57–84, 24) | (171, 6, 7, 42–56, 24) |
| (171, 8, 7, 34–41, 24) | (171, 10, 7, 28–33, 24) | |
| (171, 12, 7, 24–27, 24) | (171, 14, 7, 21–23, 24) | |
| (171, 16, 7, 19 or 20, 24) | (171, 18, 7, 17 or 18, 24) | |
| … | … | |
| (171, 84, 7, 3, 24) | (171, 114, 7, 2, 24) | |
| [15] | (171, 3, 7, 56, 24) | (171, 57, 7, 2, 24) |
| (171, 9, 7, 18, 24) | (171, 19, 7, 8, 24) | |
| [14] | (171, 6, 7, 56, 24) | |
| Ref. | Parameters | Constraints |
|---|---|---|
| [13] | , | |
| - | ||
| ,, | ||
| [14] | ||
| [15] | ||
| [16] | , ,, | |
| ,, | ||
| , | ||
| ,, | ||
| ,, | ||
| , | ||
| ,, | ||
| [17] | ||
| [20] | , | |
| , | ||
| , | ||
| and | ||
| or and | ||
| [12] | , | |
| [21] | ||
| [22] | , | |
| , is even | ||
| Theorem 1 | ||
| Theorem 2 | ||
| Theorem 3 | , is odd prime or odd prime power |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhang, Y.; Yang, W.; Ren, C. Optimal Constructions of Low-Hit Zone Frequency-Hopping Sequence Set Based on m-Sequence. Mathematics 2025, 13, 2228. https://doi.org/10.3390/math13142228
Wang C, Zhang Y, Yang W, Ren C. Optimal Constructions of Low-Hit Zone Frequency-Hopping Sequence Set Based on m-Sequence. Mathematics. 2025; 13(14):2228. https://doi.org/10.3390/math13142228
Chicago/Turabian StyleWang, Changyuan, Yi Zhang, Wanan Yang, and Chunhua Ren. 2025. "Optimal Constructions of Low-Hit Zone Frequency-Hopping Sequence Set Based on m-Sequence" Mathematics 13, no. 14: 2228. https://doi.org/10.3390/math13142228
APA StyleWang, C., Zhang, Y., Yang, W., & Ren, C. (2025). Optimal Constructions of Low-Hit Zone Frequency-Hopping Sequence Set Based on m-Sequence. Mathematics, 13(14), 2228. https://doi.org/10.3390/math13142228





